Representation of spatial sequences using nested rules in human prefrontal cortex

Abstract

Memory for spatial sequences does not depend solely on the number of locations to be stored, but also on the presence of spatial regularities. Here, we show that the human brain quickly stores spatial sequences by detecting geometrical regularities at multiple time scales and encoding them in a format akin to a programming language. We measured gaze-anticipation behavior while spatial sequences of variable regularity were repeated. Participants’ behavior suggested that they quickly discovered the most compact description of each sequence in a language comprising nested rules, and used these rules to compress the sequence in memory and predict the next items. Activity in dorsal inferior prefrontal cortex correlated with the amount of compression, while right dorsolateral prefrontal cortex encoded the presence of embedded structures. Sequence learning was accompanied by a progressive differentiation of multi-voxel activity patterns in these regions. We propose that humans are endowed with a simple “language of geometry” which recruits a dorsal prefrontal circuit for geometrical rules, distinct from but close to areas involved in natural language processing.

Introduction

In a classical paper entitled “the problem of serial order in behavior”(Lashley, 1951), Karl Lashley argued that complex sequential behavior, as occurs when we speak, write or type, cannot be reduced to an associative chain of conditioned responses, but involves a syntax of nested structures or ‘schemas’. Indeed, the ability to grasp the nested structure of sequences is essential for a variety of human cognitive activities such as language, music, mathematics, tool use and problem solving (Dehaene et al., 2015; Greenfield, 1991; Hauser et al., 2002; Rosenbaum et al., 1983). The frontal lobes are broadly known to encode such nested hierarchical structures and to use them for goal-directed behavior (Badre and D'Esposito, 2009). Neuroimaging evidence has shown that the frontal lobes may be functionally organized along a rostral-to-caudal axis to support hierarchical cognitive control, with more rostral regions encoding more abstract forms of control (Badre et al., 2010; Koechlin and Jubault, 2006) (Balaguer et al., 2016; Desrochers et al., 2015).

Language provides a prime illustration of this human propensity for abstract rule-based behavior (Lashley, 1951). Humans can quickly learn new words, rules, or concepts from just one or a few examples, and children can generalize meaningfully via “one-shot learning” (Xu and Tenenbaum, 2007). Even infants can extract abstract patterns and learn hierarchical relations within a few minutes when presented with sequences made of three-syllable words (Kabdebon et al., 2015; Marcus et al., 1999; Saffran and Wilson, 2003). This ability is not, however, confined to auditory language learning. Using spatial sequences, we recently showed that a fast detection of geometrical regularities and embeddings exists in all humans, including Western adults, preschool Western children, and even adults and children with little access to mathematical education (the Munduruku, an indigene group in the Amazon). Within only two presentations of a sequence of 8 locations, participants could detect simple geometrical primitives and combine them in an efficient manner using nested structures, for instance detecting that the sequence comprised four parallel lines, two squares or two rectangles (Amalric et al., 2017).

To date, although simple geometrical regularities have been shown to engage dorsal inferior prefrontal cortex (Bor et al., 2003), how the human brain combines such primitives into complex embedded structures has not been studied. An exciting hypothesis is that the human brain possesses a specific ability, possibly unique amongst primates, to represent recursive structures (Fitch, 2014; Hauser et al., 2002). Comparative fMRI studies of responses to auditory sequences suggest that while both human and non-human primates can recognize algebraic patterns (e.g. AAAB or AAAA) (Wang et al., 2015) or regular languages generated by finite-state automata (Fitch and Hauser, 2004; Wilson et al., 2017), humans may possess the unique additional ability to recursively combine rules in a nested fashion (Dehaene et al., 2015; Fitch and Friederici, 2012).

In the first few months of life, the inferior prefrontal cortex of human infants (“Broca’s area”) already responds to repeated sentences and hierarchical auditory rules and their violation (Basirat et al., 2014; Dehaene-Lambertz et al., 2006; Werchan et al., 2016). In humans compared to other primates, this region is anatomically enlarged, more asymmetrical, specifically interconnected (Neubert et al., 2014; Rilling et al., 2008; Schenker et al., 2010; Smaers et al., 2017) and it shows unique patterns of brain activity during sequence processing (Wang et al., 2015; Wilson et al., 2015). It has therefore been suggested that Broca’s area and its associated fiber pathways could provide a shared and uniquely human substrate for recursion in all domains of human relevance (Jeon, 2014; Koechlin and Jubault, 2006; Makuuchi et al., 2009; Rilling et al., 2008).

The experimental evidence to date is limited and mixed, however. On the one hand, some data indicate that artificial grammars and musical nested structures engage neural circuits that overlap, at least in part, with those involved in language syntax (Patel, 2003). On the other hand, there is also evidence for dissociations. Mathematical thinking, in particular, although clearly involving nested formulas and recursive algebraic structures(Jansen et al., 2003; Schneider et al., 2012), appears to dissociate from language processing (Amalric and Dehaene, 2016; Maruyama et al., 2012; Varley et al., 2005). A functional magnetic resonance imaging (fMRI) study of expert mathematicians has shown that high-level mathematical thinking makes minimal use of language areas, and instead recruit dorsal prefrontal cortex together with posterior circuits initially involved in space and number processing (Amalric and Dehaene, 2016). Furthermore, neurological patients with severe aphasia following left-hemisphere perisylvian lesions may exhibit preserved abilities to engage in algebraic problems involving recursion and structure-dependent operations (Varley et al., 2005).

These findings suggest, but do not prove, that at the brain level, the human ability to learn and to represent non-linguistic nested structures does not engage Broca’s area proper, but is distributed to multiple areas beyond the language network. Clarifying this point is crucial in order to understand the evolutionary origins of human abilities. In the present study, we therefore studied a simple formal language composed of geometrical primitives (symmetries and rotations) and combinatorial rules to produce spatial sequences in a regular octagon (Amalric et al., 2017). We designed a sequential saccade paradigm in which participants were merely required to view a repeating sequence and to move their eyes to successive locations. We then used gaze anticipations to infer whether they understood the underlying geometrical language. Our first goal was to examine whether and how the human brain combines simple primitives in a nested, language-like manner to encode regularities of variable degree of complexity in spatial sequences. If so, the second goal was to determine how nested rules are encoded in the brain with the specific aim of observing whether they share the same brain networks as language processing.

Materials and Methods

Stimulus sequences

Details of the visual sequences and mini-language used to form the sequences have been described in a previous study (Amalric et al., 2017). We designed a formal language capable of describing all 8-locations sequences around a symmetrical octagon. This language comprises a set of primitives shown in Figure 1A, including rotations (0: stay at the same location, +1: next element clockwise, +2, -1: next element counter-clockwise, -2), and symmetries either axial (H: horizontal symmetry, V; vertical symmetry, A & B: symmetries around diagonal axes) or rotational (P: point symmetry). Combining these primitives, any 8-locations sequence can be described. We thus endowed our formal language with recursive combination rules, allowing to repeat any instruction with or without change. For example, a square may be encoded as [+2]^4, i.e. four repetitions of +2). We generated all the 5040 sequences of length 8 on the octagon that always began at the same location and sampled each location once. We then computed their minimum description length, as an approximation of their Kolmogorov complexity (K), in the language defined above. According to our previous study, this measure was a strong predictor of the degree of geometrical regularity and of subjects’ ability to memorize and predict the sequence (Amalric et al., 2017). In the present study, we aimed to search for the neural representation of sequences with different levels of nesting. We selected 12 sequences spanning simple sequences with linear structures, sequences with two or three embedded levels of regularity and sequences of the highest complexity, without any apparent geometrical regularity (Fig. 1B). We briefly describe them below:

• ◦Two simple sequences had a simple linear transition structure: one called “repeat” (complexity: K = 5) contained a single repeated primitive (either +1 or -1), and the other one called “alternate” (K = 7) was generated by applying alternatively +2 and -1 or -2 and +1. Both “repeat” and “alternate” sequences did not involve nesting, but a mere repetition of one or two primitives.
• ◦Four sequences were composed of two embedded levels of regularity: a first level where instructions built a geometrical shape (e.g. a square), and a second level where the shape was repeated with a global transformation (e.g. the square was rotated using the +1/-1 instruction). Sequences of this category were called “2squares” (K = 8), “2arcs” (K = 8), “4segments” (K=7) and “4diagonals” (K = 7). There are four subcategories of “4segments” sequences called “4segments_V”, “4segments_H”, “4segments_A” and “4segments_B”, according to their symmetrical axis
• ◦Two sequences contained three embedded levels of regularity. They were respectively called “2rectangles” (K = 10) and “2crosses” (K = 7), and consisted in an initial segment built using an axial (respectively rotational) symmetry on which a global axial symmetry was applied to draw a rectangle (respectively a cross), on which, in turn, a +2 rotation was applied to transpose the shape to the remaining four points of the octagon.
• ◦The most complex sequence, called “irregular” (K = 16), consisted in a serial presentation of all 8 locations in a fixed order with no apparent regularity.

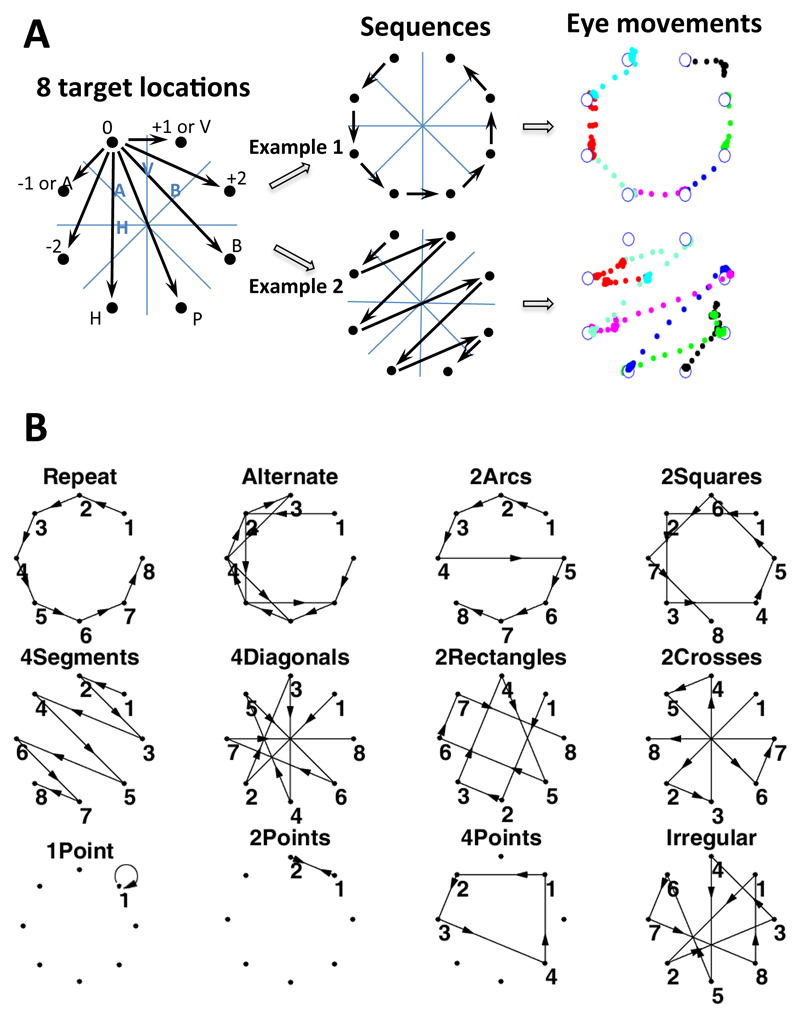
Figure 1. Experimental design.

On each trial, a dot appeared successively at one of eight target locations (A), and subjects were asked to move their eyes to each target as fast as possible. Each 8-location sequence was repeated 4 times in a row, thus allowing subjects to anticipate the next location. Sequences were constructed using basic geometrical rules including rotations (+1, +2, -1, -2), axial symmetries (H: horizontal, V: vertical, A, B: oblique) and point symmetry (P). The right panel shows two example sequences (“repeat” and “4segments”) and their corresponding eye movement trajectories in a representative trial from one subject. Each color indicates one saccade step through the trial, starting from the top left location. (B) Overview of the twelve sequences presented to fMRI participants (in the behavioral experiment, “1point”, “2points” and “4points”, were omitted).

In the fMRI (functional magnetic resonance imaging) experiment, to control for working memory load, three additional irregular sequences were included that spanned only a subset of the 8 locations, called “1point” (K = 5), “2points” (K = 6) and “4points” (K = 9).

Behavioral paradigm

Visual sequences were displayed on a regular octagon (Fig. 1A). The eight locations were indicated by white crosses (35 pixels for horizontal and vertical line) and were constantly visible on the screen (1280 × 1024 pixels) with gray background during experiments. The behavioral and fMRI experiments were organized in short blocks. In each block, subjects were presented with a given sequence of spatial locations and were merely asked to sequentially saccade to each target as accurate and fast as possible. Each sequence was repeated four times in each block. On each trial, a yellow-dot flashing target appeared on one of the eight white crosses for duration of 1000 ms, and then jumped to the next ordinal location with a 150 ms inter-stimulus-interval. The order of sequence was randomized. Each run contained 15 blocks. One run usually took 9.2 minutes. In the fMRI experiment, each run was divided into 2 sub-runs. The behavioral experiment contained 6 runs, and 4 to 6 runs (i.e. 8 to 12 sub-runs) were examined depending on subjects in the fMRI experiment. Visual sequences were presented using the Matlab software (MathWorks, MA) with Psychtoolbox (http://psychtoolbox.org/).

Subjects

In the behavioral study, we tested 44 healthy human subjects (29 females; mean age 26 years). In the fMRI study, we recruited 22 healthy human subjects (10 females, mean age 24 years) with no known neurological or psychiatric pathology. Two subjects did not go through the entire fMRI experiment for being unable to complete the sequential saccade task in the scanner. We collected eye-movement data in twelve of the twenty subjects. Video monitoring allowed us to check the other eight subjects’ eye movements during the saccade task, but the software tracking system sometimes lost the pupil position. After each experimental run and also the end of scanning, we asked the subjects to describe whether there was any regularity in the sequence to ensure that they paid attention on the sequences. All subjects gave written informed consent to participate to this study, which was approved by the local Ethics Committee.

Data Acquisition

Functional images were acquired in a 3T scanner (Siemens, Tim Trio) with a 12-channel head-coil, using a T2*-weighted gradient echo-planar imaging (EPI) sequence (TR = 2.4 s, TE = 30 ms, Matrix = 64 x 64, 3 mm³ voxel size). Eye movements were collected using an EyeLink 1000 eye-tracker (SR Research, ON, Canada). A total of 42 runs from 20 human participants were acquired and analyzed. Human functional volumes were corrected for slice timing differences, realigned for motion correction and spatially normalized to the Montreal Neurological Institute (MNI) template (Lancaster et al., 2000). After image preprocessing, active brain regions were identified by performing voxel-wise GLM analyses implemented in SPM8 (http://www.fil.ion.ucl.ac.uk/spm).

Complete details of the experimental procedures are presented as Supplementary Materials.

Results

Experimental paradigm and behavioral performance

In previous work from our group, we introduced and tested a formal language capable of generating any sequence of movements on a regular octagon (Amalric et al., 2017). The set of primitive instructions is shown in Fig. 1A and includes rotations (0 = stay at the same location, +1 = next element clockwise; and, similarly, -1, +2, -2…) and symmetries (H = horizontal symmetry, V = vertical symmetry, A & B = symmetries around diagonal axes; P = central point symmetry). These all correspond to what we perceive as natural geometric intuitions. The language also allows to recombine these atomic instructions into more sophisticated programs by appending them or by repeating any instruction n times, with or without symmetries and/or variations in starting point.

Although any sequence can be encoded in more than one manner, previous behavioral data showed that humans detect and encode regular sequences in a compressed form (Amalric et al., 2017). For instance, one of the simplest sequences, “Repeat” (Fig. 1A, Example 1) can be captured as a series of successive moves on the octagon, which can be compactly described by the formula [+1]^8 (repeat 8 times the instruction to move to the next item). Humans tend to select the more parsimonious expression that captures each sequence. The framework of minimum description length (MDL) allows to assign a measure of complexity to a given sequence as the length of the shortest expression capable of producing it (Ming, 1997; Romano, 2013). We thus used the MDL as a mathematical definition of the complexity of each sequence, and examined whether this measure could explain saccade anticipation behavior and associated fMRI activity.

Out of all possible 5040 sequences of length 8 without repetition on the octagon, each participant was presented with eight sequences that spanned a broad range of geometrical primitives and regularities, plus one sequence of maximal complexity (called “irregular”). The eight sequences were called “repeat”, “alternate”, “2arcs”, “2squares”, “4segments”, “4diagonals”, “2rectangles”, and “2crosses” (Fig. 1B). Except for “alternate”, these sequences sampled the 8 vertices of the octagon without repetition. To control for the effect of memory demand, we included three additional sequences: “1point”, “2points” and “4points” (Fig. 1B and supplementary information), which were maximally irregular but repeated after spanning only a subset of 1, 2 or 4 locations.

Forty-four participants participated in the initial behavioral task (Fig. 1A). We asked them to track targets with their gaze, and monitored whether their eyes anticipated the next target at a given sequence location. Another twenty participants were recruited in the following fMRI experiment. The behavioral and fMRI experiments were organized in short blocks. In each block, a fixed sequence of 8 items was repeated 4 times (hereafter referred to as 4 “trials”, although note that the 32 locations followed each other seamlessly). From block to block, each category of sequence was presented with variable starting points, so that participants could not immediately recognize it, but could infer its organization after a few items. The length of the sequence (8 locations) challenged participants’ working memory and encouraged them to look for regularities.

Performance (correct response rate) was quantified by examining whether the eye position fell in the target area within a time window of 0-500 ms after the target onset. This window was adopted in order to tolerate a large variation in eye movement time (including anticipations) while still enforcing a relatively rapid response time (less than half of the stimulus onset asynchrony of 1150 ms). Performance was high, between 80% and 96% (see Fig. S1). There was a significant negative correlation between performance and sequence complexity as measured by MDL (r = -0.85, p < 0.003), indicating that participants made more errors for more complex sequences.

Although participants were merely instructed to move their eyes to each successive target, their saccades often anticipated on target appearance. For each successive target location, we next calculated the anticipation index (AI) as the distance, at the onset of the current target, between the actual eye position and the current target position, divided by the distance between the current and the prior target. Thus, AI was equal to 0 when gaze was already focused on the target before it appeared (maximal anticipation), and to 1 when gaze had not left the previous location (no anticipation). The performance for irregular sequences, used as baseline (gray line in Fig. 2A), showed only a modest improvement across the four successive trials (thirty-two targets in total). By contrast, for all regular sequences, participants showed significantly higher anticipation compared to irregular sequences (Fig. 2A, red star on top of each panel denoting p < 0.01 with Wilcoxon signed rank test). Crucially, the amount of anticipation was well predicted by our measure of complexity, as the mean anticipation index was significantly correlated with MDL across sequences (behavioral experiment. R² = 0.86, p < 0.001; fMRI experiment. R² = 0.74, p < 0.001) (Fig. 2B and S2).

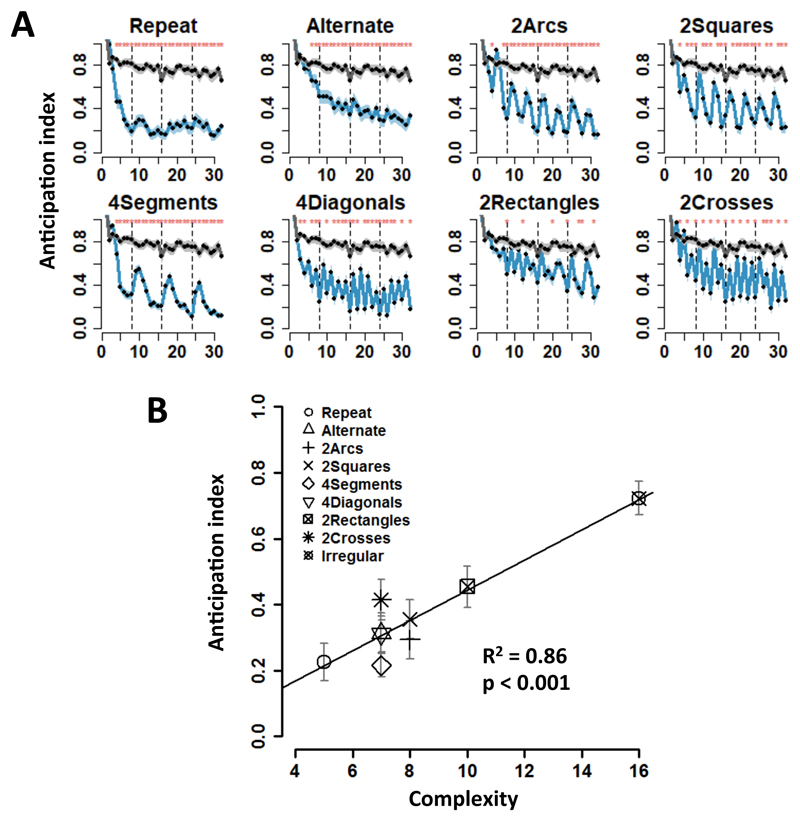
Figure 2. Behavioral performance.

(A) Evolution of saccade anticipation across 4 consecutive presentations (4 “trials”) of each 8-location sequence (shaded area = ±1 SEM). The x-axis represents the 32 consecutive target locations (vertical dashed lines indicate trial boundaries). The y-axis is the anticipation index, calculated as the distance between eye position and the target at the onset of appearance of each target, divided by the absolute distance between the current target and the prior one (Methods). 0 represents maximal anticipation, and 1 no anticipation. As a baseline, the gray curve in each panel shows the saccade anticipation index for irregular sequences. (B) The anticipation index, across sequences, is significantly correlated with sequence complexity (p < 0.001, R² = 0.86). For each sequence, the y-axis denotes the mean anticipation index, averaged across the four trials, and the x-axis indicates sequence complexity (minimum description length).

The participants’ anticipation profile across sequence was also measured by examining saccadic reaction time (Fig. S2A) and fraction of trials with eye position near the corresponding target area at target onset (Fig. S2B). The results showed consistent behavioral performance for all sequences. In subsequent data analysis, we averaged the behavioral indexes from the four variants of the 4segments sequence (“4segments_V”, “4segments_H”, “4segments_A” and “4segments_B”), as they showed highly similar patterns (Fig. S2C; note that only this category had multiple variants). Furthermore, since previous studies indicated that initiation times were influenced by sequence complexity (Hunt and Aslin, 2001; Schneider and Logan, 2006; Verwey et al., 2010), we also examined the anticipation index (AI) in the first points of the 2^nd, 3^rd and 4^th trial (there could be no planning on the 1^st trial of all the sequences) and found a significant correlation between AI and sequence complexity (R² = 0.59, p < 0.02).

We then zoomed in on the structure of each trial by examining anticipation in each of the 8 points of the regular sequence. For the “repeat” sequence, which had the minimum description length and consisted of the repeated application of the +1 or -1 rule, anticipations became evident starting with the fourth data point of the first trial (difference in AI from the corresponding point in the irregular baseline; all ps < 10^-5, signed rank test, normality test violated) (Fig. 2A. The anticipation profile reached an asymptote during the second trial. Those results indicate that participants quickly learned the sequence within the first trial, i.e. during the first presentation of the sequence and before it was even repeated. The alternate sequence showed a similar anticipation effect as repeat (significance from the seventh data point in the first trial, all ps < 0.005, signed rank test) (Fig. 2A).

For other sequences, gaze anticipations showed a temporal structure that reflected the nested, hierarchical organization of the underlying “mental program”, with more anticipation (lower AI) on targets involving a shallower level of nesting (Fig. 2A). Consider for instance the “2arcs” and “2squares” sequences (Fig. 1B). Both involve two nested levels: an elementary operation (respectively +1 or +2) is first repeated four times, then repeated again with a shift in location, thus creating a repetition of repetitions. This structure was reflected in performance. First, the data points corresponding to the application of the first-level rule (2^nd, 3^rd, 4^th and 6^th, 7^th, 8^th within each trial) showed the most anticipation (comparison with irregular: “2arcs”, all ps < 0.01; “2squares”, all ps < 0.05, signed rank test), suggesting that the superficial rule was easily learned. Second, the data points 1 and 5, corresponding to the second-level rule, showed less anticipation than the first-level points (“2arcs”, ps < 10^-6; “2squares”, ps < 10^-7, signed rank test), and became significantly different from the irregular baseline only in the 3^rd and 4^th trials (“2arcs”, all ps < 0.01; “2squares”, all ps < 0.05, signed rank test). Thus, participants learned both first- and second-level nested structures, but the second-level rule was more difficult to learn, perhaps because evidence for this level was scarcer (1/4 of locations for “2arcs” and “2squares”).

The observed behavioral pattern cannot simply be accounted for by sequence transition probabilities: within a sequence, each of the 8 locations is traversed only once in a deterministic manner, hence transition probability is 1. Could subjects adapt to specific transition rules such as +1 (move to the next item) or +2 (skip an item)? While this hypothesis could account for the reduced anticipation on data points 1 and 5 of the “2arcs” and “2squares” sequences, which violate the repetition of +1 or +2 established by the three preceding trials, it fails to explain why these data points still showed significant higher anticipation than all the points of the irregular sequence (ps < 0.001), which had similar transition probabilities. The latter finding establishes that participants ultimately learned two levels of regularities, rather learning merely the most frequent one (e.g. +1 for “2arcs”) and being surprising when it was violated. Performance on the “4segments” and “4diagonals” provided further evidence that both level of structure and amount of repetition are determinants of performance. In those sequences, every other location provides evidence respectively about 1^st-level and 2^nd-level structures (see supplementary information). Accordingly, anticipation relative to the irregular baseline was quickly observed at all data points (“4segments”, all ps < 10^-4; “4diagonals”, all ps < 0.05, signed rank test), yet there were again several indications of a hierarchical program. First, for the “4segments” sequence, there were significantly fewer anticipations at data points 1 and 2 than at data points 3-8 (p < 10^-6, signed rank test, anticipation index was averaged over corresponding points across 4 trials), corresponding to the initial segment. Second, for the “4diagonals” sequence, there were significantly fewer anticipations at odd- than at even-numbered points (p < 10^-5, signed rank test), indicating greater difficulty for the more embedded structure even though it was repeated as often as the less embedded one. Finally, note that while the probabilities of transition rules on even-numbered points of “4segments” and “4diagonals” were identical to those of the “alternate” sequence, the latter did not a similar a jagged anticipation pattern characteristic of a two-level sequence.

We also obtained evidence that the “2rectangles” and “2crosses” sequences, with 3 levels of embedding in our language, were most difficult. Data points 1 and 5, corresponding to the 3^rd-level rule showed no difference compared to the irregular sequence (all ps > 0.1, signed rank test), and even in the fourth trial there was no improvement, suggesting that participants did not acquire the 3^rd-level embedded structure (data points 1 and 5 in the 4^th trial in both AI (Fig. 2A) and reaction time (Fig. S2A, all ps > 0.1, signed rank test). However, data points (3^rd and 7^th) corresponding to the 2^nd-level structure were significantly lower than baseline in the 4^th trial (“2rectangles”: point 3, p < 0.002 and point 7, p < 0.003; “2crosses”: point 3, p < 0.009 and point 7, p = 0.052, signed rank test) (Fig. 2A), suggesting that the participants gradually learned the 2^nd-level structures, but experienced difficulty with the higher 3^rd-level rules in these two sequences.

For the “1point”, “2points” and “4points” sequences in the fMRI experiment, the anticipation patterns were similar to those in the repeat and alternate sequences, i.e. devoid of temporal structures. Those results indicate that, aside from detecting geometrical regularities, participants could also quickly memorize a small number of arbitrary and irregularly spaced locations (Fig. S3A).

A prominent feature of our task is fast rule learning. We quantified the learning rate by calculating the slope of the evolution of the anticipation index across the eight data points in each trial, and found three learning profiles, roughly corresponding to three levels of regularities. The sequence of “repeat” and “alternate” with only one-level regularity, showed a profile of “one-trial learning” (Fig. S4): the learning rate in the first trial was high and significantly higher than those in the subsequent ones (Tukey's HSD (honest significant difference) test, ps < 10^-5), and the learning rates in the 2^nd, 3^rd and 4^th trial were not significant and did not differ from each other (ps > 0.1, Tukey's HSD test). The two-level nested sequences (“2arcs”, “4segments”, “2squares” and “4diagonals”) exhibited a pattern of “incremental learning”, in which the 1^st, 2^nd and 3^rd trials showed a moderate but significant learning rate (all ps < 0.05, Tukey's HSD test) (Fig. S4). For the remaining sequences (“2rectangles”, “2crosses” and “irregular”), the learning rate was small and generally did not reach significance in any trial (Tukey's HSD test, all ps > 0.1), not did it differ between trials (one-way repeated measures ANOVA, “2rectangles”: F (3,129) = 0.6, p > 0.8; “2crosses”: F (3,129) = 2.1, p > 0.6). This learning profile is compatible with a partial understanding of some but not all of the nested levels present in the sequence.

In summary, the behavioral results showed that complexity could predict participants’ saccade anticipation behavior, and that participants learned the single-level sequences (“repeat” and “alternate”) within one trial, and the two-level embedded sequences (“2arcs”, “2squares”, “4segment” and “4diagonals”) with an incremental learning profile, but showed difficulty in learning rules with three levels of embedding (“2rectangles” and “2crosses”). In addition, the 2^nd-level rules were harder to acquire than 1^st-level rules. Finally, the anticipation patterns characteristic of embedded structures could not be attributed to transition probabilities.

Brain activation correlating with complexity (MDL)

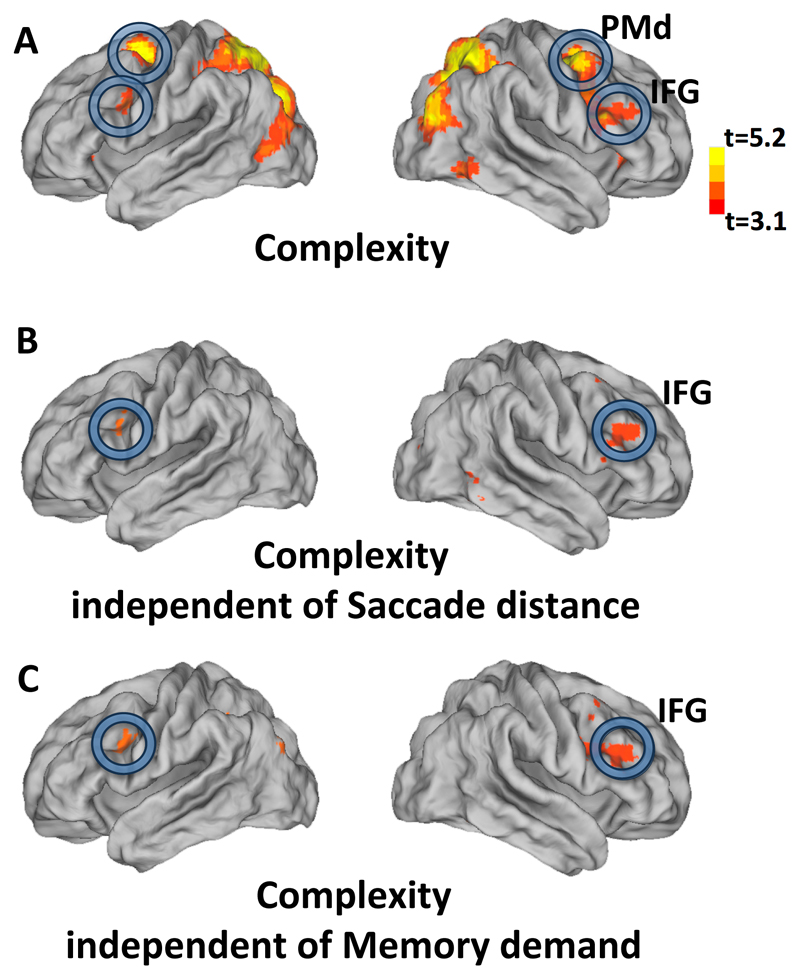
To uncover the brain regions associated with rule-based encoding of spatial sequences, we searched for brain activity positively correlated with sequence complexity (group analysis threshold at t > 3.1, p < 0.05 cluster-level FDR corrected). Several areas showed a positive correlation (Fig. 3A and Table S1), including inferior frontal gyrus (IFG), dorsal premotor cortex (PMd), superior parietal lobule and intra-parietal sulcus (IPS) and surrounding dorsal occipito-parietal cortex, and middle occipital cortex.

Figure 3. Brain activation related to sequence complexity.

(A): Brain regions showing significant correlations of BOLD signal with the complexity (minimal description length) of each sequence (group analysis thresholded at t > 3.1, cluster-level FDR p < 0.05 corrected) projected on lateral view of a slightly inflated brain. (B, C) Same map after exclusion of the voxels that were above threshold (p < 0.05, uncorrected; “exclusive masking”) in the brain map for saccade distance (Fig. S3, B) or memory demand (the contrast of 4points versus 2points sequence, Fig. S3, C) respectively. Abbreviations: PMd, dorsal premotor; IFG, inferior frontal gyrus.

To evaluate alternative interpretations of our results, we also obtained maps of the brain areas where fMRI activation correlated with the average saccade distance in each sequence (Fig. S5A, group analysis threshold at t > 3.1, p < 0.05 cluster-level FDR corrected), and with the memory demand in non-structured sequences (Fig. S5B, contrast of the sequence containing “4 points” versus “2 points”, group analysis threshold at t > 3.1, p < 0.05 cluster-level FDR corrected). These parameters activated an occipito-parieto-premotor network partially similar to the brain regions whose activity increased with sequence complexity. To determine whether parts of this network would activate for complexity, independent of saccade distance and memory demand, we excluded from the brain map of sequence complexity all the voxels above threshold (p < 0.05, uncorrected; “exclusive masking”) in the brain maps of saccade distance and memory demand. We found a significant activation in bilateral IFG (Figs. 3B and 3C). Those results were confirmed by directly examining the voxel-wise contrast for a significantly larger effect of the normalized contrast for complexity than of the normalized contrast for saccade distance (Fig. S5D). Similarly, we also compared the effects of normalized contrasts for complexity and for memory demands (Fig. S5E). In both cases, the entire set of areas correlating with complexity also showed a significantly stronger effect of complexity than of the confounding variables. As an additional control, we also examined the effect of average saccade direction changes, but this map showed no activation in IFG and only weak activation mostly in occipital cortex (Fig. S5C).

Brain activation to participants’ anticipation of nested structures

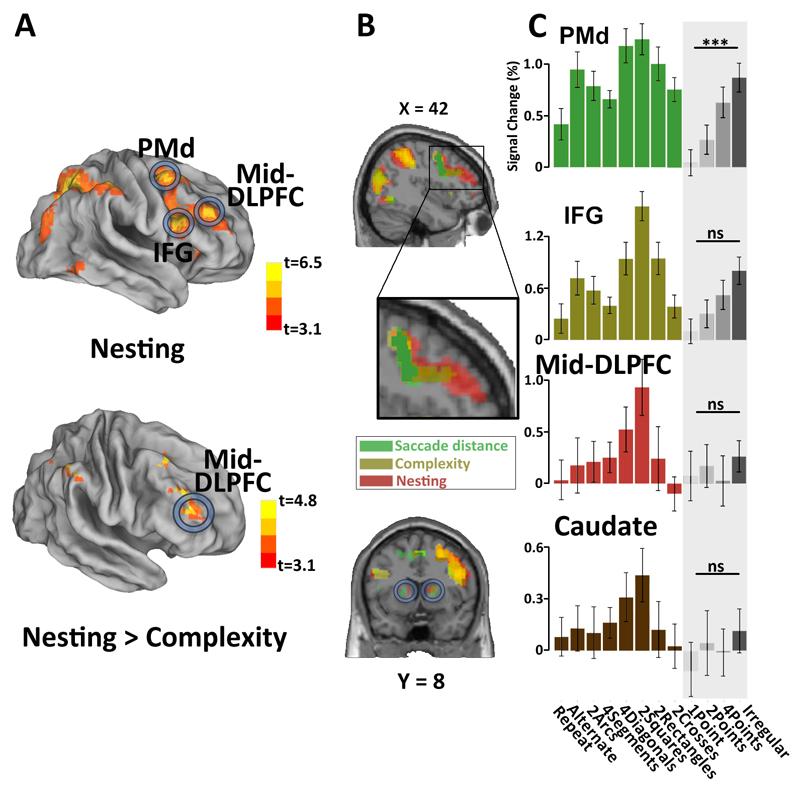
While complexity provided an objective mathematical measure of the amount of structure underlying each sequence, the participants’ anticipation behavior provided a more direct measure of their degree of understanding of those sequences. From this perspective, we thus quantified the extent to which the participant’s anticipation behavior was driven by an understanding of the sequence’s nested structure, and used this behavioral index as a predictor of brain activity. The participants’ anticipation of nested structure (hereafter abbreviated to “sequence nesting”) was quantified as the difference in eye-gaze anticipation between data point 5 in each 8-location sequence (corresponding to second-level rules) and the mean of data points 3 and 7 (corresponding to first-level rules) (see Fig. 2A and supplementary information). We then probed the fMRI activity which was positively correlated with sequence nesting (group analysis threshold at t > 3.1, cluster-level p < 0.05 FDR corrected) and found that the relevant areas included those previously identified with the objective complexity contrast, yet with higher significance in IFG and with additional activation in right mid-dorsal lateral prefrontal cortex (Mid-DLPFC) and bilateral anterior caudate (Fig. 4A upper and Table S2). When excluding the voxels that were above threshold (p < 0.05, uncorrected; “exclusive masking”) in the brain map for sequence complexity (Fig. 3A), only the right Mid-DLPFC showed a significant selective effect of sequence nesting (Fig. 4A lower).

Figure 4. Brain activation related to sequence nesting.

(A) Upper: Brain regions showing significant correlation of the BOLD signal with a behavioral index of the extent to which the participant’s anticipations were driven by nested structures. This index was defined as the difference in anticipation to 2^nd-level and 1^st-level locations in sequences with at least two levels of nested structure (group analysis threshold at t > 3.1, cluster-level FDR p < 0.05 corrected). Lower: same brain map, excluding all voxels that were above threshold (p < 0.05 uncorrected; “exclusive masking”) in the contrast for sequence complexity (Fig. 3A). DLFPC, dorsal lateral prefrontal cortex. (B, C) Brain activations to saccade distance (green), sequence complexity (brown) and nesting (red) effects, projected on a sagittal slice (p < 0.001, cluster-level FDR p < 0.05 corrected). Histograms show the average activation to each of the twelve sequences in the following ROIs by averaging over all the voxels: PMd (15 mm radius sphere at [27 -1 52]), IFG (15 mm radius sphere at [48 11 28]), Mid-DLPFC (15 mm radius sphere at [39 45 15]) and Caudate (15 mm radius sphere at [15 5 4]). Error bars indicate one standard error. ***: p < 0.001; ns: not significant.

Could these activations, especially the Mid-DLPFC activity, be due solely to increasing task difficulty or working memory load (Bor et al., 2003; Braver et al., 1997), as opposed to a rule-based representation? To identify whether those areas were also involved in task difficulty or memory load in the absence of geometrical rules, we searched for increasing brain responses in control sequences (“1point”, “2points”, “4points” and “Irregular”) where the spatial sequence was irregular. Among the regions of interest identified by the previous contrasts (ROIs, Fig. 4A upper) analysis, PMd showed a significant main effect of memory demand (Fig. 4C, one-way repeated measures ANOVA, F(3,57) = 11.88, p < 10^-5) and IFG tended to show a similar effect (Fig. 4C, one-way repeated measures ANOVA, F(3,57) = 2.34, p = 0.08), whereas Mid-DLPFC (Fig. 4C, one-way repeated measures ANOVA, F(3,57) = 0.29, p = 0.8) and anterior caudate (Fig. 4B, one-way repeated measures ANOVA, F(3,57) = 0.59, p = 0.6) did not exhibit such working memory effect (Fig. 4B, histograms with shaded area). In addition, in Mid-DLPFC and anterior caudate, the activity induced by the “irregular” sequence, which has the highest working memory load, was significantly lower than for the two-level embedded sequences “4diagonals” and “2squares” (Student’s paired t-test, Mid-DLPFC t₃₉ = 3.58, p < 0.001; anterior caudate: t₃₉=2.46, p < 0.05) (Fig. 4B). This finding suggests that the Mid-DLPFC and anterior caudate activities were not solely driven by spatial working-memory requirements, but were more specifically associated with the organization of working memory into a structured sequence comprising multiple levels of nesting.

One might argue that the low activation of Mid-DLPFC for the irregular sequence could be simply due to a reduced attention (e.g. if participants gave up learning it). However, behavioral performance (gray lines, Fig. 2A& Fig.S1) indicated that the anticipation index of the “irregular” sequence decreased continuously across the 32 location forming the 4 trials (repeated measures ANOVA, behavioral experiment: F(1,43) = 35.5, p<10^-6; fMRI experiment: F(1,19) = 352.4, p < 10^-12), suggesting a relatively high attention level even for the irregular sequence.

Spatial relationship with the language and mathematical calculation regions

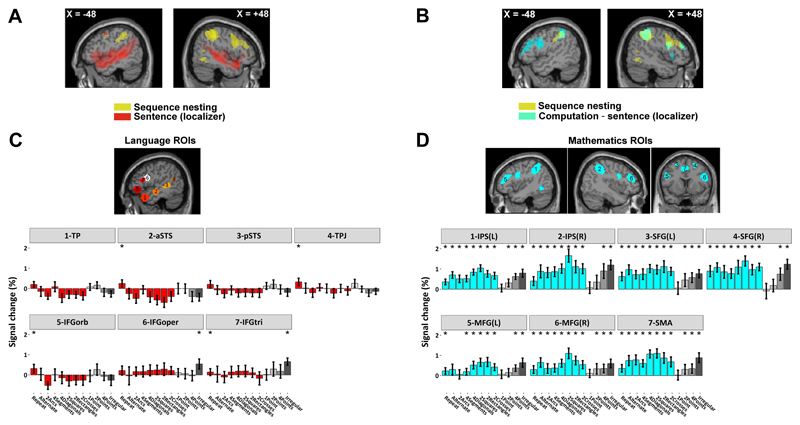
Given that our spatial sequences involve both syntax and geometry, we then examined the relation of the observed activations to previously identified areas involved in language and mathematical calculation, as determined in the same participants using an independent functional localizer (Pinel et al., 2007) (supplementary information). At the whole-brain group level, the areas responsive to geometrical nested structures largely overlapped with the regions active during calculation (Fig. 5B), but not with those involved in sentence processing (Fig. 5A). We next sought to confirm those findings in individual participants by using our functional localizer to identify, within each participant, the subject-specific voxels activated during sentence processing within 7 left-hemispheric language-related regions of interest (ROIs) and during mental calculation within 7 math-related ROIs (supplementary information). The search regions were selected from two previous studies of language constituent structure (Pallier et al., 2011) and mathematical thinking (Amalric and Dehaene, 2016).

Figure 5. Comparison of brain activation in the geometrical task and in localizers for language and mathematics.

(A, B) Sagittal slices show the contrasts for: spoken and written sentence processing relative to rest (in red), calculation relatively to sentence processing (in cyan), and sequence nesting (in yellow). (C, D) Average activation during the geometry task at subject-specific peak voxels responsive to sentence (p < 0.001, uncorrected) and calculation (p < 0.001, uncorrected), within prespecified ROIs. *: p < 0.05 corrected. Abbreviations: TP, temporal pole; aSTS, anterior superior temporal sulcus; pSTS, posterior superior temporal sulcus; TPJ, temporoparietal junction; IPS, intraparietal sulcus; MFG, middle frontal gyrus; SFG, superior frontal gyrus; SMA, supplementary motor area.

Within those subject-specific voxels, identified from independent data, we could then extract and analyzed the activation evoked by each spatial sequence. The results confirmed that math-responsive voxels (Fig. 5D) were significantly activated by spatial sequences, with a profile that matched those reported at the group level (Fig. 4C). By contrast, strikingly, language-responsive voxels were essentially silent or even deactivated during our geometrical saccade anticipation task (Fig. 5C). Even the language-related areas IFG pars opercularis, pars triangularis and pars orbitalis show little or no activity. Examination of the IFG activation associated with geometrical sequence complexity showed that it was located dorsal to any language-related activity, in the most dorsal sector of Brodmann area 44, as previously reported for abstract mathematical reflection (Amalric and Dehaene, 2016).

Examination of the spatial distribution of activations to saccade distance, complexity, and nesting revealed a rostro-caudal organization in prefrontal cortex (Fig. 4B), with saccade distance affected primarily the dorsal precentral sulcus, complexity a more anterior part of dorsal IFG, and nesting an even more anterior sector of dorsolateral PFC. Those findings, similar to previous work (Koechlin et al.), suggest a hierarchical representation of visual-spatial sequences at an increasingly higher degree of abstraction (Fig. S6).

Evolution of representational similarity during learning

The previous analyses are all based on univariate analyses of the correlates of sequence complexity. However, fMRI also affords multivariate analyses of the topographical cortical code activated during a given task(Kriegeskorte et al., 2008). We therefore evaluated whether our fMRI images contained information about the internal code for spatial sequences and its evolution with repeated exposure. Over the course of learning, we hypothesized that the brain regions where the nesting effect was found may progressively converge to a neural code characteristic of the geometrical sequence being learned. Unfortunately, fMRI does not possess the temporal resolution required to identify how this neural code is dynamically organized, and whether it resembles the specific language-like nested structure postulated by our “language of geometry”. However, a simpler prediction is that, during learning, the topographic activation patterns evoked by distinct learned sequences should become increasingly different and unique to each sequence. Furthermore, this differentiation process should occur faster for sequences that are easier to learn.

To test this idea, we examined how the spatial pattern of BOLD signals over voxels evolved over the course of learning, using a multivariate analysis technique known as representational similarity analysis (RSA). Because this technique has reduced statistical power, we did not analyze each sequence individually, but we grouped the sequences based on their distinct behavioral learning profiles: those learned in a single trial, those learned incrementally, and the most complex ones that were only partially learned (Fig. S4). At single-subject level, we computed the representational similarities between all sequences within a group. As noted above, the differentiation hypothesis predicted a decrease in similarity. Such a learning effect was observed in both parietal and frontal ROIs (Fig. 4A) (two-way ANOVA, main effect of Trial, PMd: F(3,57) = 8.9, p < 10^-4; IFG: F(3,57) = 2.7, p < 0.05; Mid-DLPFC: F(3,57) = 8.8, p < 10^-4; IPS: F(3,57) = 8.9, p < 10^-4; SPL: F(3,57) = 6.6, p < 0.001) (Fig. S7). However, only the similarities in frontal IFG and Mid-DLPFC showed significant differences in the slope of this learning effect between groups of sequences (two-way ANOVA, Trial × Group interaction, PMd: F(6,114) = 1.96, p = 0.08; IFG: F(6,114) = 3.6, p < 0.01; Mid-DLPFC: F(6,114) = 3.1, p < 0.01; IPS: F(6,114) = 0.79, p > 0.5; SPL: F(6,114) = 0.64, p > 0.6). Multiple comparisons, performed separately for each trial, found that similarity was significantly different in the third and fourth trial between the partial learning group and the incremental learning group of sequences (IFG, ps < 0.01, t-test; Mid-DLPFC, ps < 0.05, t-test). On the 3^rd trial, there was also a significant difference between the partial learning group and the one-trial learning group (IFG, p < 0.01, t-test; Mid-DLPFC, p < 0.01, t-test) (Fig. S7). Furthermore, the differences observed on the 3^rd trial in the frontal regions were significantly larger than those in the parietal regions (two-way ANOVA, Sequence group × Region interaction, IFG vs. IPS: F(2,38)=4.32, p < 0.03; IFG vs. SPL: F(2,38)=3.24, p < 0.05; Mid-DLPFC vs. IPS: F(2,38)=3.78, p < 0.04; Mid-DLPFC vs. SPL: F(2,38)=3.15, p = 0.054). These results suggest a progressive differentiation of the brain activation patterns in prefrontal cortex in the course of sequence learning, which occurred faster for simpler sequences, thus paralleling the behavior improvements.

Discussion

We designed a novel experimental paradigm in order to probe the human ability to represent spatial sequences using nested combinations of elementary geometrical primitives. Saccadic eye-movement data revealed that the spatial sequences that could be encoded by simple nested geometrical structures were quickly learned, and that the amount of saccadic anticipation could be predicted by the complexity of the sequence, as measured by minimum description length. Using fMRI, we identified a bilateral IFG activation correlating with objective complexity, and an activation in right Mid-DLPFC and bilateral anterior caudate correlating with the subjective anticipation of spatial sequences using embedded rules. Sequence learning was accompanied by a progressive differentiation of multi-voxel activity patterns in parietal-frontal networks. Finally, these parietal-frontal brain regions involved in geometrical sequences overlapped with those activated during mathematical reflection, but bore no relation to classical language-related areas.

Using the same octagon layout, we previously probed memory for spatial sequences using a behavioral task whereby subjects had to explicitly point to the next item, and found that errors increased with complexity in educated adults, uneducated Amazonian adults, and Western preschoolers (Amalric et al., 2017). The present results replicate and extend those findings using an implicit learning task in which subjects were merely asked to follow the items of the sequence with their eyes. In both studies, participants showed difficulties in learning the 2rectangles and 2crosses sequences with three-level embedded structures. This could be due to the fast presentation rate and limited number of sequence repetitions, both of which left participants limited time to think and generate predictions. The performance in these two sequences nevertheless was better than for the irregular sequence, suggesting that participants did learn some of the shallower primitives (e.g. +1/-1, +2/-2 and symmetries), though not the full overarching structure.

Our fMRI results indicate that such structures are represented in prefrontal areas such dorsal IFG and PFC. Several other experimental and psychological accounts can be excluded. First, could the IFG involvement be associated with basic parameters of the eye-movement behavior (e.g. saccade distance)? This seems unlikely as the group analyses showed that the IFG was more activated by complexity than by those eye movement parameters (Figs. 3 and S4). Brain activity associated with saccade parameters was observed, as expected, but it did not encompass the IFG region. Second, could the activation in Mid-DLPFC and basal ganglia reflect working memory load or general task demands rather than the extraction and representation of nested rules? We found no significant working memory load effect in Mid-DLPFC and basal ganglia when we examined the activity differences among the control sequences “1point”, “2points”, “4points” and “irregular” (Fig. 4C), which did not possess any geometrical regularities but varied in difficulty and load. Furthermore, crucially, Mid-DLPFC activations during the “2squares” and “4diagonals” sequences were significantly higher than during the more demanding “irregular” sequence, suggesting that task demands or difficulty was not likely the main reason for the Mid-DLPFC activity. In this respect, our results replicate and extend previous work by Bor et al. (Bor et al., 2003), who found greater inferior prefrontal and parietal activity to structured spatial sequences than to unstructured ones, and concluded that the capacity to parse the sequence into meaningful chunks was the major determinant of PFC activity. Similar work done by Desrochers et al.(Desrochers et al., 2015) also showed ramping activity in the rostrolateral prefrontal cortex and complexity effect in the pre-PMd region. Like them, we conclude that the IFG or Mid-DLPFC/basal ganglia activities in our task do not simply reflect eye movements, general task difficulty or attention level, but can only be explained by a parsing mechanism akin to a “language of geometry”, as initially demonstrated through behavioral analysis of a similar touch-screen task (Amalric et al., 2017).

Our finding that individual saccade movements, sequence complexity, and anticipation of nested rules were respectively represented along a rostro-caudal axis of the frontal lobe, from PMd (the peak of the cluster at [27 -1 52]) to IFG (peak at [48 11 28]) and to Mid-DLPFC (peak at [39 45 15]), is consistent with previous proposals of a hierarchy of increasing abstract rules (Badre and D'Esposito, 2009; Badre et al., 2010) or an information cascade for executive control in prefrontal cortex (Koechlin and Jubault, 2006; Koechlin et al., 2003; Koechlin and Summerfield, 2007). Specifically, the spatial relationship of the three clusters is compatible with the hierarchical map in frontal cortex proposed by Badre et al. (Badre and Nee, 2018), where the first-order (sensory-motor, Y = -7), second-order (contextual control, Y = 15) and the third-order (schematic control, Y = 49) were defined hierarchically. Frontal cortex appears to be functionally organized to represent increasingly abstract frames of perception or action, with information gradually changing from a narrow (current stimulus) to an increasingly broader context (Bahlmann et al., 2015; Nee and D'Esposito, 2016; O'Reilly, 2010; Wendelken et al., 2012). In the present study, it seemed that the more anterior frontal regions (e.g. Mid-DLPFC and IFG) were sensitive to increasingly abstract encodings of saccade movements. A plausible hypothesis, which should be tested in future work, is that anterior regions generate top-down signals that help organize subordinately lower-level actions in more posterior regions (Dehaene and Changeux, 1997; Koechlin and Summerfield, 2007).

Human language abilities imply a unique competence for nested tree structures (Hauser et al., 2002). Previous studies have suggested a neural circuit involving left superior temporal sulcus, temporal poles, temporo-parietal junction and especially the left inferior frontal gyrus (“Broca’s area”) was highly correlated with the syntactic complexity of sentences (Pallier et al., 2011). A major goal of the present study was to examine whether our “language of geometry” with recursive embedding structures also engaged the same set of language-related areas. The answer was unambiguous: the language of geometry recruited a non-linguistic neural network, distinct from language areas, and involving the bilateral prefrontal, parietal and inferior temporal regions that were previously found to encode number, space, time and other mathematical abstractions (Amalric and Dehaene, 2016; Dehaene, 2011). Their bilateral frontal recruitment might reflect the visuospatial nature of the stimuli used in current study. In that respect, the present results replicate, in a much simple geometrical setting, the previous findings that high-level mathematical thinking activates a cortical network distinct from, and dorsal to, classical language areas (Amalric and Dehaene, 2016, 2017). Importantly, Amalric et al. presented mathematical stimuli in sentential form, and thus activating temporal and inferior frontal language areas; as such, the results merely proved that language areas were not more activated by mathematical thinking than by reflection on general semantic knowledge. By contrast, the present results are stronger is that they show that with non-verbal stimuli generated by a formal spatial language, language areas remain strictly silent (Fig. 5C) even though behavior and brain activity in other math-responsive areas (Fig. 5D) provide direct evidence that those stimuli were represented as nested language-like structures. Thus, the human brain houses multiple, possibly parallel circuits for tree-like structures in mathematics versus sentence processing.

We recently proposed that any incoming sequence may be encoded internally at one of five possible levels of abstraction from transition probabilities, chunking, ordinal knowledge to algebraic patterns and nested tree structures (Dehaene et al., 2015). In agreement with Karl Lashley (Lashley, 1951), the present findings suggests that humans do not simply associate each successive item with the next one in a chain-like fashion, but also grasp multi-item sequential structures at different levels of abstraction. The neural representation of such a system with nested and hierarchical structures seems to lie in prefrontal and parietal areas. The fact that dissociated activation patterns during learning were found in the frontal but not parietal regions might reflect the distinct roles within the system. While parietal areas are activated whenever we learn or memorize low-level information about spatial locations, the present data suggest that prefrontal cortex is involved in encoding information in a more abstract, integrated and efficient fashion, thus compressing sequences into a structured representation that leads to enhanced spatial working-memory performance.