Abstract
Background and Purpose
Receptor internalisation is by nature kinetic. Application of a standard equilibrium dose response model to describe the properties of a ligand inducing internalisation, while commonly used, are therefore problematic. Here, we propose two quantitative approaches to address this issue—(a) a model‐free method and (b) a kinetic modelling approach—and systematically evaluate the performance of these methods against traditional equilibrium methods to characterise the internalisation profiles of cannabinoid CB1 receptor agonists.
Experimental Approach
Kinetic internalisation assays were conducted using a concentration series of six CB1 receptor ligands. Internalisation rate analysis and snapshot equilibrium analysis were performed. A model‐free method was developed based on the mean residence time of internalisation. A kinetic internalisation model was developed under the quasi‐steady state assumption.
Key Results
Rates of receptor internalisation depended on both agonist and concentration. Agonist potencies from snapshot equilibrium analysis increased with stimulation time, and there was no single time point at which internalisation profiles could infer agonist properties in a comparative manner. The model‐free method yielded a time‐invariant measure of potency/efficacy for internalisation. The kinetic model adequately described the internalisation of CB1 receptors over time and provided robust estimates of both potency and efficacy.
Conclusion and Implications
Applying equilibrium analysis to a non‐equilibrium pathway cannot provide a reliable estimate of agonist potency. Both the model‐free and kinetic modelling approaches characterised the internalisation profiles of CB1 receptor agonists. The kinetic model provides additional advantages as a method to capture changes in receptor number during other functional assays.
Abbreviations
- 2‐AG
2‐arachidonoylglycerol
- AEA
anandamide/N‐arachidonoylethanolamine
- AUMC
area under the first moment curve
- BAY
BAY59,3074
- CP
CP55,940
- HEK293, HEK
human embryonic kidney cell
- MRT
mean residence time
- THC
Δ9‐tetrahydrocannabinol
- WIN
WIN55,212‐2.
What is already known
• Receptor internalisation is a kinetic process, but standard equilibrium models are traditionally used for analysis.
What this study adds
• Two novel non‐equilibrium analysis approaches are proposed and applied, for characterising ligand‐induced CB1 receptor internalisation.
What is the clinical significance
Applying equilibrium analyses to dynamic data results in misinterpretation of drug responses.
Non‐equilibrium analysis may improve the success rate of translating lead compounds into innovative clinical therapies.
1. INTRODUCTION
Receptor theory has long recognised cell surface receptor density as a critical factor for determining the magnitude (efficacy) of receptor‐mediated signalling responses (Black & Leff, 1983; Furchgott, 1966). For GPCRs, internalisation is a commonly used pharmacological “signalling” end point and receptor internalisation as a mechanism to decrease cell responsiveness to agonists is now seen as a critical component of both the regulation of physiological GPCR function and prevention of toxic system overstimulation (Calebiro & Godbole, 2018; Hanyaloglu & von Zastrow, 2008; von Zastrow, 2003).
Functional selectivity (agonist bias) is also an important current theme in GPCR pharmacology (Smith, Lefkowitz, & Rajagopal, 2018; Urban et al., 2007). Recently, the effect of time on the interpretation of agonist bias at D2 dopamine receptors has been investigated (Klein Herenbrink et al., 2016). This seminal paper made the point that virtually, all pharmacological studies to date make an implicit analytical assumption that all pathways are in states of equilibrium (i.e., all concentrations of all drugs, in all pathways compared, are assumed to be spatiotemporally stable; Klein Herenbrink et al., 2016), which is patently not the case. For example, the transient “peak‐and‐decay” nature of GPCR‐mediated phosphorylation of ERK in human embryonic kidney (HEK) cells is well documented (Eishingdrelo & Kongsamut, 2013; Luttrell & Luttrell, 2003). Similarly, many methods for assaying the effect of GPCR activity of cAMP levels (a prototypical G protein‐mediated signal) are accumulation assays (as opposed to real‐time kinetic assays). This means that cAMP levels may progressively increase with incubation time, due to the inclusion of a PDE inhibitor in the assay medium, decreasing the turnover of cAMP (Hunter & Glass, 2015).
System non‐equilibrium is further illustrated by bias analysis itself. It has been shown that ligand‐dependent pathway kinetic differences result in reversals of agonist bias outcomes for some ligand‐pathway combinations at different time points. Thus, it appears that agonists that dissociate slowly from their receptors become “favoured” (in bias terms) at later time points, whereas other agonists that dissociate quickly are favoured at earlier time points. This was also apparent in simple EC50 comparisons, where potencies left‐shifted or right‐shifted over time respectively (Klein Herenbrink et al., 2016). Interestingly, the method for bias analysis employed in this study, Operational analysis (Kenakin, Watson, Muniz‐Medina, Christopoulos, & Novick, 2012; van der Westhuizen, Breton, Christopoulos, & Bouvier, 2014), explicitly treats receptor amount as a constant, thereby discounting the role of receptor internalisation in determining the activity kinetics of the other pathways characterised in the study. It could be argued that the “snapshot” approach for utilising Operational analysis is therefore undermined by this factor.
The cannabinoid CB1 receptor is a family A GPCR which exhibits complex pharmacology (Howlett et al., 2002; Pertwee et al., 2010). Interestingly, several of the studies to date that have examined CB1 receptor trafficking have focused primarily on post‐endocytic receptor fate (Grimsey, Graham, Dragunow, & Glass, 2010; Leterrier, Bonnard, Carrel, Rossier, & Lenkei, 2004) rather than on internalisation per se. This may be because ligand‐specific parameters (such as rates and extents of internalisation) are not inherently meaningful unless they either involve comparisons between ligands or examine the association with signalling pathway activities. In general, descriptions to date of agonist‐driven receptor internalisation have arisen mainly from “traditional” pharmacological experimental approaches where Emax model curves are fitted to concentration–response data obtained at only one or two time points. In some other examples, agonist time courses were performed at just one concentration of agonist (Ayoub et al., 2015; Levoye et al., 2015; Shayo et al., 2001). To our knowledge, there has been little attention given to investigating the kinetic aspect of agonist‐specific effects on GPCR internalisation, by employing assay designs that consider both agonist concentration and time.
CB1 receptors are particularly appropriate GPCRs in which to investigate internalisation, because it is possible to measure receptor internalisation as a pure process. This is because, in HEK cells, CB1 receptors degrade following internalisation (Grimsey et al., 2010) and therefore, internalisation data are not confounded by the recycling of receptor molecules, thus repopulating the cell surface.
The current study set out to systematically investigate the ligand specificity of CB1 receptor internalisation with a view to determining how best to capture agonist internalisation activity profiles (both activity kinetics and concentration dependence). This information will be valuable in future studies involving additional pathways and end points (i.e., functional selectivity studies). We have previously compared the activity of the same six CB1 receptor agonists used in this study, in another context (CP55,940 [CP]; WIN55,212‐2 [WIN]; anandamide [AEA]; 2‐arachidonoylglycerol [2‐AG]; Δ9‐tetrahydrocannabinol [THC] and; BAY59,3074 [BAY]) and chose to continue to characterise this mini panel of ligands in the current study on the basis of their structural heterogeneity and variable pharmacology (Finlay et al., 2017). We propose two quantitative approaches to characterise agonist activity: (a) a model‐free method and (b) a kinetic modelling approach. Though applied only to GPCR internalisation data in this report, we believe that similar approaches may have general applicability for the quantification of any non‐equilibrium pharmacological pathway response.
2. METHODS
The methods are described in two parts. In the first part, the technical details of the experimental assays are provided. In the second part, three analysis methods for internalisation data are introduced: (a) traditional methods; (b) model‐free method; and (c) kinetic modelling approach.
2.1. Part 1
2.1.1. Agonist preparation and use
CP, WIN, and BAY were purchased from Tocris Bioscience (Bristol, UK); AEA and 2‐AG were purchased from Cayman Chemical Company (Ann Arbor, MI); and (−)‐trans‐Δ9‐THC was purchased from THC Pharm (Frankfurt, Germany). All drugs were prepared as stocks in absolute ethanol at concentrations of either 10 mM or 31.6 mM such that final ethanol concentrations in assays would be 1:1,000 (vehicle was maintained constant in all assay conditions). Drugs were stored as single‐use aliquots at −80°C prior to use. In order to allow for concerns about potential confounding of data due to the presence of endocannabinoids in serum, all drug stimulations were performed in the absence of FBS and following a short period of serum starvation (as described below).
2.1.2. Cell culture
Cell culture medium was purchased from Hyclone Laboratories (GE Healthcare Life Sciences), all other culture reagents were purchased from Thermo Fisher Scientific (Waltham, MA), and culture plasticware was purchased from Corning (Corning, NY). The 3HA‐hCB1 HEK293 cell line (ATCC, Manassas, VA; Cat# CRL‐1573, RRID:CVCL_0045 transfected with 3HA‐hCB1; Cawston et al., 2013) was cultured in DMEM supplemented with 10% FBS and 250‐μg ml‐1 Zeocin™, in a 5% CO2, 37°C humidified incubator.
2.1.3. Competition binding assays
Homogenate radioligand competition binding assays were performed as previously described (Finlay et al., 2017), except that radioligand ([3H]‐CP) was used at its predefined pKD of 1.6 nM (Finlay et al., 2017). Full concentration‐displacement curves were performed for each displacer ligand (WIN, AEA, 2‐AG, THC, and BAY).
2.1.4. Receptor internalisation assays
For agonist‐induced internalisation, all the internalisation assays were performed with eight different concentration levels (serial dilutions) of six CB1 receptor ligands: CP, WIN, AEA, 2‐AG, THC, and BAY. Terminal sampling of agonist‐induced internalisation was taken at 0, 2, 4, 8, 15, 30, and 60 min. For constitutive internalisation assays (which were performed in the absence of agonist), terminal sampling was performed at 0, 30, 60, 90, 120, 180, 240, 300, 360, and 480 min. The longer time course was required due to the much slower rate of constitutive internalisation.
Internalisation assays were performed largely as described in Grimsey, Narayan, Dragunow, and Glass (2008). In brief, 3HA‐hCB1 HEK cells were plated into poly‐D‐lysine coated 96‐well, clear culture plates (Nunc, Roskilde, Denmark), at a density of 4 × 104 cells per well. After approximately 16 hr of culture, medium was aspirated and cells were then serum starved in DMEM supplemented with 1‐mg·ml−1 BSA (SFM) for at least 1 hr. Primary mouse anti‐haemagglutinin clone 16B12 monoclonal antibody (BioLegend San Diego, CA; Cat# 901502, RRID:AB_2565007) was diluted 1:500 in SFM. Antibody dilution was pre‐warmed to 37°C and dispensed in a staggered fashion so that every time point was exposed to primary antibody for 30 min prior to drug stimulation. At the end of the 30‐min antibody incubation, the antibody dilution was aspirated, and wells were washed with pre‐warmed SFM. SFM was immediately aspirated, and a serial dilution of agonist was dispensed (pre‐warmed to 37°C). The plate was immediately returned to the incubator. The primary antibody labelling, washing, and drug stimulation were repeated at subsequent time points as appropriate, such that all time points assayed on each microplate would conclude at the same time. At this point, plates were moved to an ice bed for approximately 5 min to arrest receptor trafficking. Drug dilutions were then aspirated, and secondary Alex Fluor® 488 goat anti‐mouse antibody (1:300; Thermo Fisher Scientific Cat# A‐11029, RRID:AB_2534088) was dispensed in SFM. Plates were incubated at room temperature for 30 min, and antibody dilution was then aspirated and wells were washed twice with SFM. SFM was aspirated, and cells fixed in 4% paraformaldehyde (Sigma Aldrich, St Louis, MO) in 0.1‐M phosphate buffer for 10 min. Paraformaldehyde was aspirated, and wells were washed twice with PBS. Finally, nuclei were stained with Hoechst 33258 (Sigma Aldrich; 4 mg·ml−1 in milliQ, diluted 1:500 in PBS supplemented with 0.2% Triton‐X100, PBS + T) for 15 min, and wells were washed twice with PBS + T prior to imaging.
As antibodies do not permeate live cells, only receptors resident at the cell surface at the beginning of the stimulation and labelled with primary antibody that were still resident at the cells surface at the conclusion of stimulation were labelled with secondary antibody. Thus, declining fluorescence intensity correlates with increased internalisation. This protocol is given the shorthand designation “live‐at‐start,” to reflect the fact that the primary antibody labelling was performed at the start of the assay (prior to the trafficking stimulation).
2.1.5. Image acquisition and analysis
The receptor internalisation assay method described in the previous section is amenable to quantitative immunocytochemistry analysis. Images were acquired utilising the ImageXpress® Micro XLS High‐Content System (automated microscope) and quantified with its associated image analysis platform, MetaXpress® v6.2.3.733 (MetaXpress, RRID:SCR_016654; Molecular Devices, Sunnyvale, CA, USA). Images were acquired with filters for both 488 and Hoechst wavelengths for four sites per well, at 10× objective magnification. Exposure times were set empirically by testing the expected brightest wells and adjusting so the resulting pixel intensities would be approximately 50% of the maximum limit of detection (typically 1,500 ms for 488, 120 ms for Hoechst). This was necessary in order to avoid image saturation, which results in a loss of information because the relative intensities of bright pixels cannot be distinguished. Images in both channels were saved as 16‐bit tiff images, with pixel intensities (“grey levels”) scaled 0–65,535.
Image analysis in MetaXpress® was performed by the application of an analysis method first reported by Grimsey et al. (2008), with modifications reported in Finlay, Joseph, Grimsey, and Glass (2016). This analysis entailed calculating fluorescence intensity per cell above background (based on a user‐defined intensity threshold) and is reported in arbitrary units for total grey value per cell.
2.2. Part 2
2.2.1. General aspects of data analysis
The data and statistical analysis comply with the recommendations of the British Journal of Pharmacology on experimental design and analysis in pharmacology (Curtis et al., 2018). Concentration–response and time course data were replicated in three independent experiments. This may appear to conflict with the BJP minimum experimental replication requirement (n = 5). However, as the data are analysed by simultaneous global fitting of responses at six time points and eight concentration levels, the effective sample size is much larger than five. Furthermore, no statistical comparison was performed on these data; rather, they were used for the development of the mechanistic kinetic model of internalisation. All the plots and curve fittings were obtained using GraphPad Prism v7.0 (GraphPad Prism, RRID:SCR_002798). Plots show representative data (mean ± SEM) of technical replicates, unless otherwise specified.
Internalisation rate analysis
As receptor internalisation is progressive (longer time results in more internalisation), the surface receptors that were initially labelled with the primary antibody would eventually be fully internalised if enough time was given (i.e., plateau equal to zero). Hence, the time course of internalisation for each ligand at every concentration level was separately fitted with a one‐phase decay model (parameter “Plateau” constrained to 0) in GraphPad Prism v7.0. Rates (t 1/2) were obtained from these curve fits and reflect the time for each concentration of a ligand to induce internalisation of 50% of the receptor on the cell surface.
Traditional “snapshot” equilibrium analysis
For each ligand, separate concentration–response curves were plotted at each assay time point (2, 4, 8, 15, 30, and 60 min) using the mean of the technical replicates to provide a concentration–response curve. The three‐parameter Emax model (n H constrained to 1) was fitted to each set of data in GraphPad Prism v7.0. These fits were used to obtain concentration–response parameters (i.e., Emax and pEC50). Where concentration–response curves could not be fitted, connecting lines were drawn between data points to help visualise trends.
2.2.2. Model‐free method
Model‐free metric for quantifying internalisation
In the area of pharmacokinetics, mean residence time (MRT) is widely used as a model‐free metric for estimating the average time a drug stays in the human body (Gabrielsson & Weiner, 2001; Gibaldi & Perrier, 1982). It is defined as the ratio of the area under the first moment curve (AUMC) and the AUC of concentration versus time.
| (1) |
Although this summary variable has its roots in pharmacokinetics, it is ideally suited for describing receptor loss associated with the kinetics of receptor internalisation. Here, instead of drug concentration, we are dealing with the fluorescence intensity that is assumed to be proportional to receptor density. Here, MRT reflects the average time a labelled receptor remains on the membrane surface.
It is noted that MRT is highly influenced by the measurements at the terminal phase of the curve. If there are inadequate samples to cover the terminal phase, MRT estimates may be unreliable. In this case, constitutive internalisation of CB1 receptors occurs more slowly than the agonist‐induced internalisation and only a small change in receptor density occurs by the end of the experiment (1 hr). Therefore, the estimated MRT will be substantially greater than the experiment duration (1 hr) and may be imprecisely estimated. Utilising the inverse of MRT, , takes advantage of the fact that for slow internalisation cases, absolute error is small even though estimates are imprecise. This is because in such instances, values of would approach 0 anyway.
| (2) |
For the calculation of , AUC was approximated by (AUC until last time point) and AUMC was approximated by (AUMC until last time point). Hence, the model‐free metric for quantifying receptor internalisation ( ) can be expressed as the ratio of to (Equation 3). The detailed calculation of and is described in the Appendices A.
| (3) |
Concentration–response analysis
The model‐free metric was utilised to evaluate the concentration–response relationship in receptor internalisation. The concentration–response curve of each ligand was analysed using the three parameter Emax model (n H constrained to 1) in GraphPad Prism v7.0.
2.2.3. Kinetic modelling approach
Agonist‐induced internalisation model
The schematic plot shown in Figure 1 illustrates the kinetic model for receptor internalisation. The natural turnover of receptor is controlled by the receptor synthesis rate (Rsyn) and the constitutive internalisation rate constant (kcon). In addition, two micro‐rate constants (kon and koff) regulate the ligand‐binding process. The agonist‐induced internalisation rate constant (kint) is responsible for the internalisation of formed ligand–receptor complex (AR). CB1 receptor recycling is assumed to be negligible on the basis of prior research (Grimsey et al., 2010), and therefore not implemented in the kinetic model of CB1 receptor internalisation.
Figure 1.
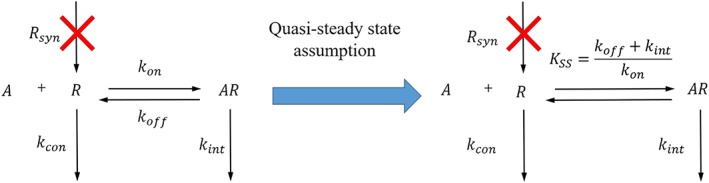
The schematic plots of the full kinetic model (left) and the quasi‐steady state model (right) for agonist‐induced internalisation in a “live‐at‐start” internalisation assay
In the “live‐at‐start” internalisation assay, newly synthesised receptors are not detectable because they are not labelled by the primary antibody at the beginning of internalisation assay. In addition, there is an excess of free ligand (A). Hence, it is reasonable to assume that binding and internalisation would not significantly alter the concentration of free ligand. Taking these into account, two model assumptions are made here:
Assumption 1
The receptor synthesis rate (Rsyn) of labelled receptor is equal to 0.
Assumption 2
The free ligand concentration is constant over time.
According to these two assumptions, the kinetic model for agonist‐induced receptor internalisation was derived.
| (4) |
| (5) |
In order to make inferences about the standard Emax parameters (e.g., efficacy and potency), it is necessary to evaluate the system at the steady state, that is, a point at which there is no change in the species R and AR over time. However, due to the kinetic nature of internalisation, there is no single steady state time point. On the other hand, if one part of the system reacts much faster than any other parts, then the fast parts of the system can be assumed to be at steady state even while the system continues to change over time. This assumption is termed quasi‐steady state (Gibiansky, Gibiansky, Kakkar, & Ma, 2008). The quasi‐steady state assumption has been widely applied to derive a useful simplification of target‐mediated drug disposition model of biologics (e.g., denosumab, tocilizumab, and canakinumab; Chakraborty et al., 2012; Gibiansky et al., 2012; Gibiansky & Frey, 2012). In this case, the receptor binding and agonist‐induced internalisation are much faster than the constitutive internalisation of receptor. We therefore assumed that ligand–receptor complex (AR) was at the quasi‐steady state (Assumption 3; Equation 6, the same as eq. 20 in Gibiansky et al., 2008):
| (6) |
Here, setting to zero means that the free ligand, the free receptor, and the ligand–receptor complex is at a quasi‐steady state (as opposed to static‐steady state), where the binding rate is balanced by the sum of the dissociation and internalisation rates on the scale of the other processes. It is noted that at the same time, (Equation 4) is not equal to zero, meaning that the free receptor is changing over time. Given the relationship among the free ligand, the free receptor, and the ligand–receptor complex (Equation 6), the ligand–receptor complex will change along with the free receptor. Because of the fast ligand–receptor association (large kon) and dissociation (large koff), and also fast internalisation of the ligand–receptor complex (large kint), this change can be considered to be instantaneous compared to the time scale of the other processes.
Reorganising Equation (6) yields the expression of quasi‐steady state K (KSS):
| (7) |
It is noted that KSS contains both receptor binding (KD, equilibrium K D) and internalisation ( ) information. In general, KSS will therefore be larger than KD. It is noted that the rapid binding assumption (i.e., equilibrium binding, see Figure S1) can be considered a special case of the quasi‐steady state assumption when agonist‐induced internalisation (kint) is considerably slower than the dissociation of ligand–receptor complex (koff; Gibiansky et al., 2008). In such cases, KSS is approximately equal to KD, and the quasi‐steady state model (Equation A7) collapses into the simpler rapid binding model (Equation S5). In the current study, the agonist‐induced internalisation of CB1 receptor is very rapid. Hence, the rate constant of agonist‐induced internalisation (kint) is not negligible compared to the dissociation rate constant (koff) and therefore, the quasi‐steady state approach is preferred.
An analytical expression for fluorescence intensity (FI; see Appendix A.2 for details) is shown.
| (8) |
Here, FI0 is defined as the initial fluorescence intensity.
For curve‐fitting purposes, the parameter KSS was recast in logarithm form (i.e., ), yielding the final equation used for direct curve fitting:
| (9) |
Constitutive internalisation
The constitutive internalisation model (Equation 10) was a sub‐model of the agonist‐induced internalisation model (Equation 9) when the ligand (A) was not added (i.e., set A to 0).
| (10) |
Kinetic modelling analysis
The constitutive internalisation model and the quasi‐steady state model of agonist‐induced internalisation were implemented in GraphPad Prism v7.0, as user‐defined equations. The codes for these equations are available in the Supporting Information. For model fitting, the least squares (ordinary) fit method in GraphPad Prism was used. A hands‐on tutorial is also included in the Supporting Information to show how to conduct kinetic modelling of internalisation in Prism.
2.3. Nomenclature of targets and ligands
Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY (Harding et al., 2018), and are permanently archived in the Concise Guide to PHARMACOLOGY 2017/18 (Alexander et al., 2017).
3. RESULTS
3.1. Rate of receptor internalisation is agonist and concentration dependent
The agonist‐induced internalisation assay results revealed that the six CB1 receptor ligands included in the screen had varying profiles (Figure 2). High concentrations of all six agonists resulted in a majority of surface receptors internalising after 60 min of stimulation, and the rate of internalisation was clearly concentration dependent, with higher concentrations of all six agonists driving receptor internalisation more rapidly than lower concentrations (Figure 2).
Figure 2.
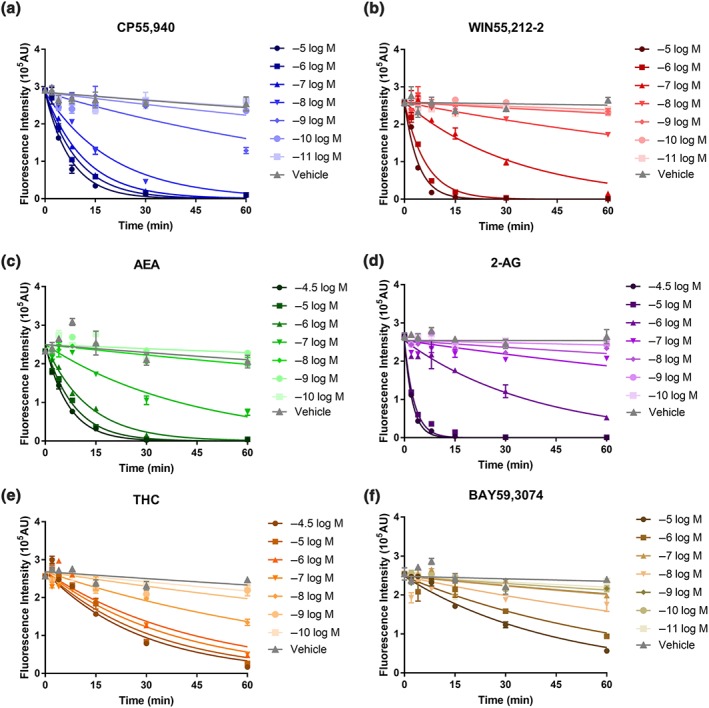
Representative “live‐at‐start” internalisation time courses, showing agonist‐induced internalisation of surface 3HA‐hCB1 in HEK cells upon stimulation with concentration series of CP55,940 (a), WIN55,212‐2 (b), AEA (c), 2‐AG (d), THC (e), and BAY59,3074 (f). Symbols represent raw data (demonstrating mean ± SEM of technical duplicate) and the lines represent the prediction from one phase decay model with parameter “Plateau” constrained to zero
In spite of the concentration‐dependent features within each agonist's concentration–response series, maximal rates of internalisation (where increasing agonist concentration does not further increase the rate of internalisation) were highly variable between agonists. The maximum internalisation t 1/2 for each ligand (±SEM), in decreasing order (fastest to slowest), were as follows: 1.44 ± 0.16 min (2‐AG, Figure 2d), 2.32 ± 0.95 min (WIN, Figure 2b), 4.67 ± 1.07 min (CP, Figure 2a), 5.96 ± 1.64 min (AEA, Figure 2c), 18.24 ± 0.81 min (THC, Figure 2e), and 28.16 ± 1.72 min (BAY, Figure 2f). Agonists can therefore be clustered into two approximate groups on the basis of maximum internalisation rate: fast internalisers with t 1/2 less than 6 min (2‐AG, WIN, CP, and AEA) and slow internalisers with substantially larger t 1/2 (THC and BAY).
3.2. Snapshot equilibrium‐based potencies of agonist‐induced internalisation increases with stimulation time
The data shown in Figure 2 have been represented in conventional concentration–response format (Figure 3) so that pharmacological parameters (i.e., Emax and pEC50) could be obtained. It is apparent that there are large differences in apparent internalisation potency for all agonists depending on the selected time point for the assay. For example, between 4 and 60 min of stimulation, the apparent pEC50 of CP internalisation increased from 7.90 to 9.33 (Table 1). Apparent potency shifts were also seen for all the other agonists. Importantly, it is noted that the fast internalisation agonists (e.g., 2‐AG, Figure 3d) demonstrate smaller apparent potency shifts than the slower internalisation agonists (e.g., THC, Figure 3e). At short stimulation time points, the internalisation data could not be fitted by the Emax model for some agonists as insufficient internalisation had occurred (e.g., all time points shorter than 30 min for BAY, Figure 3f). Fundamentally, these observations mean that there is no single time point at which all agonist activity profiles may be used to infer agonist properties comparatively, as is required in contemporary empirical pharmacological applications.
Figure 3.
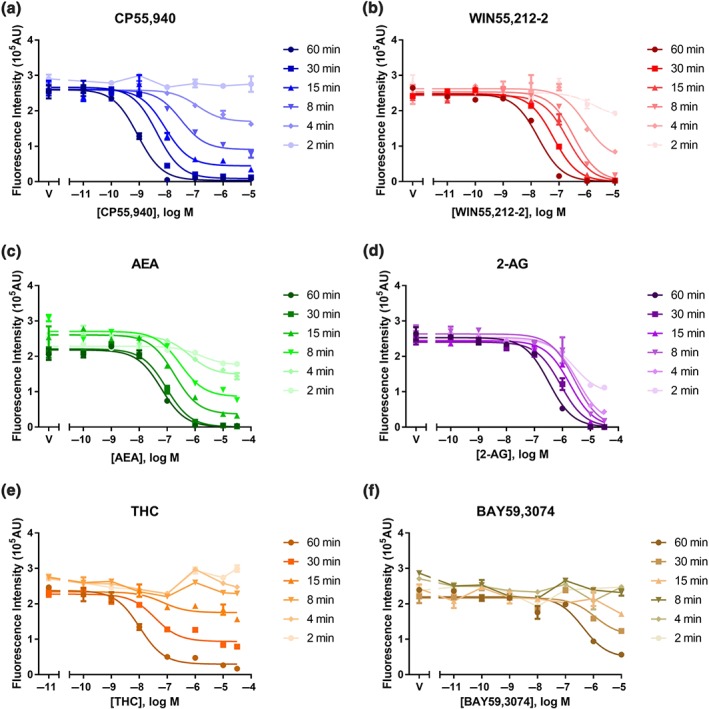
Representative “live‐at‐start” internalisation concentration–response curves, showing agonist‐induced internalisation of surface 3HA‐hCB1 in HEK cells upon stimulation for six different time points with CP55,940 (a), WIN55,212‐2 (b), AEA (c), 2‐AG (d), THC (e), and BAY59,3074 (f). Symbols represent raw data (demonstrating mean ± SEM of technical duplicate) and the curves shown are classic three‐parameter Emax model fits (n H constrained to one)
Table 1.
CB1 receptor agonist‐induced internalisation potencies (pEC50 ± SEM) in 3HA‐hCB1 HEK cells from the traditional “snapshot” equilibrium analysis across six stimulation time points (n = 3, unless indicated otherwise).
| Ligand | Assay time point | |||||
|---|---|---|---|---|---|---|
| 60 min | 30 min | 15 min | 8 min | 4 min | 2 min | |
| CP55,940 | 9.33 ± 0.14 | 8.69 ± 0.19 | 8.29 ± 0.14 | 7.93 ± 0.21 | 7.90 ± 0.52 | 7.64 ± 0.62 (n = 2) |
| WIN55,212‐2 | 7.70 ± 0.10 | 7.37 ± 0.12 | 6.95 ± 0.16 | 6.65 ± 0.12 | 6.32 ± 0.15 | 6.16 ± 0.20 |
| AEA | 7.11 ± 0.11 | 6.73 ± 0.19 | 6.59 ± 0.42 | 6.31 ± 0.74 | 5.30 ± 0.89 (n = 2) | 4.88 ± 0.92 (n = 2) |
| 2‐AG | 6.46 ± 0.07 | 6.18 ± 0.07 | 5.85 ± 0.07 | 5.61 ± 0.10 | 5.50 ± 0.05 | 5.47 ± 0.06 |
| THC | 7.88 ± 0.08 | 7.53 ± 0.08 | 7.31 ± 0.14 | 6.91 (n = 1) | N.D.[Link] | N.D.[Link] |
| BAY59,3074 | 6.52 ± 0.08 | 6.20 ± 0.13 | 6.49 ± 0.58 (n = 2) | N.D.[Link] | N.D.[Link] | N.D.[Link] |
N.D. ‐ The potency could not be determined for THC and BAY because the internalisation data could not be fitted by the Emax model as insufficient internalisation at short stimulation time points.
3.3. A model‐free method renders time invariant potency/efficacy for agonist‐induced internalisation
Through the model‐free approach, the inverse of MRT for the labelled receptors on the membrane surface ( ) was calculated from the “live‐at‐start” internalisation assay data. Based on this metric, receptor internalisation concentration–response curves were constructed for the six CB1 receptor ligands. As shown in Figure 4 and Table 2, the six CB1 receptor ligands induced receptor internalisation differentially. Agonists showed large variations in internalisation potency, with pEC50 values varying from 4.68 to 8.55. In addition, large variations in Emax values were observed (Figure 4), with differences in efficacies proceeding 2‐AG (most efficacious) > WIN > AEA > CP > THC ≈ BAY (Table 2).
Figure 4.
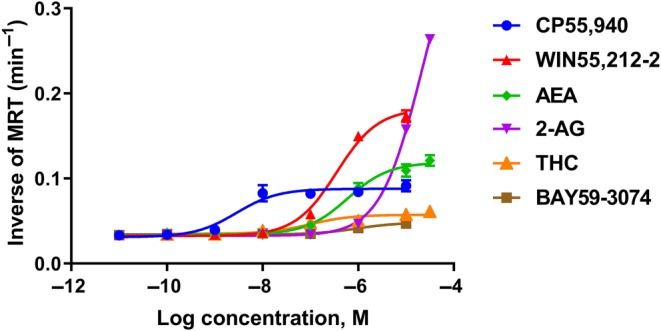
Concentration–response curves generated by model‐free analysis of kinetic internalisation data (the inverse of mean residence time) showing 3HA‐hCB1 HEK cells signalling on stimulation with a panel of six agonists: CP55,940, WIN55,212‐2, AEA, 2‐AG THC and BAY59,3074 Symbols represent model‐free metric calculated from raw data (demonstrating mean ± SEM of technical duplicates) and the curves shown are classic three‐parameter Emax model fits (n H constrained to one)
Table 2.
The potency/efficacy of CB1 receptor agonists for internalisation in 3HA‐hCB1 HEK cells using the model‐free approach with the inverse of mean residence time as the response metric
| Ligand | Parameter estimate [RSE%] | |
|---|---|---|
| pEC50 | Emax (min−1) | |
| CP55,940 | 8.55 [2.2] | 0.088 [3.4] |
| WIN55,212‐2 | 6.45 [0.96] | 0.18 [2.3] |
| AEA | 6.22 [1.6] | 0.12 [2.6] |
| 2‐AG | 4.68 [0.63] | 0.42 [2.9] |
| THC | 7.01 [2.6] | 0.057 [2.3] |
| BAY | 6.03 [1.9] | 0.048 [1.9] |
Abbreviation: RSE, relative standard error.
3.4. Findings from the kinetic modelling approach are consistent with findings from the model‐free method
As shown in Figure S2 and Figure 5, the developed kinetic model could adequately describe the observations from constitutive and agonist‐induced internalisation of the six tested CB1 receptor ligands. In addition, all the kinetic internalisation parameters were precisely estimated with relative standard error values less than 50% (Table 3). It was also noted that agonist‐induced internalisation was much more rapid than constitutive internalisation. Similar to the findings from the model‐free approach, significant between‐ligand variability was observed in the potency and efficacy values derived from kinetic modelling of CB1 receptor internalisation (Table 3); the potency parameter (pKSS) ranged from 4.41 to 7.83. Of all the tested CB1 receptor ligands, CP exhibited the highest potency and 2‐AG the lowest. Furthermore, there was around 40‐fold difference in the efficacies (kint) proceeding 2‐AG (most efficacious) > WIN > AEA ≈ CP > THC ≈ BAY (Table 3). All findings were consistent with the results from the model‐free method.
Figure 5.
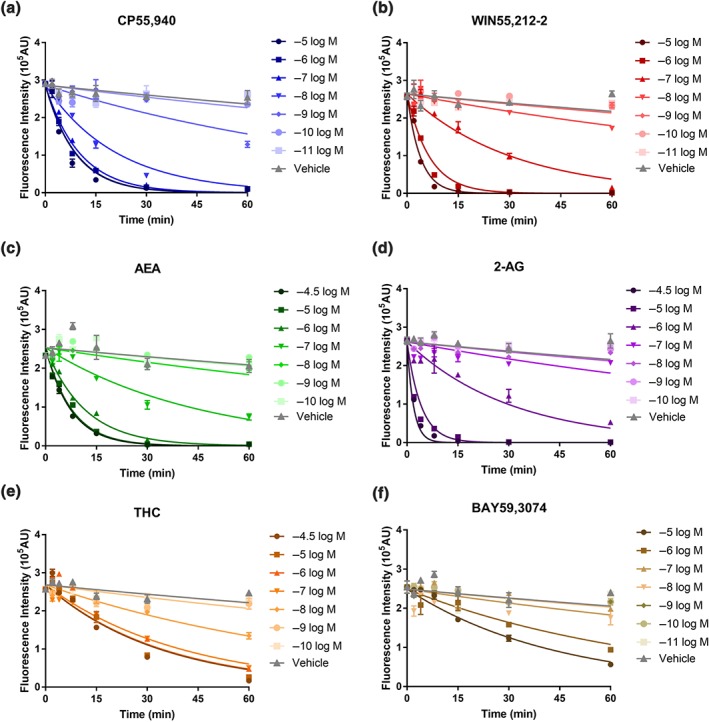
The fitting results of the quasi‐steady state internalisation model for agonist‐induced internalisation in 3HA‐hCB1 HEK cells on stimulation with six CB1 receptor ligands: CP55,940 (a), WIN55,212‐2 (b), AEA (c), 2‐AG (d), THC (e), and BAY59,3074 (f). The line here represents the prediction from quasi‐steady state model of agonist‐induced internalisation for “live‐at‐start” assay and the symbols (mean ± SEM) here are the observed data from the internalisation assay
Table 3.
Summary of parameter estimates from the quasi‐steady state internalisation model for agonist‐induced internalisation in 3HA‐hCB1 HEK cells on stimulation with six CB1 receptor agonists
| Parameter | Definition | Parameter estimate [RSE%] | |
|---|---|---|---|
| kcon (min−1) | Constitutive internalisation rate constant | 0.0032 [6.6%] | |
| kint (min−1) | Agonist‐induced internalisation rate constant | CP55,940 | 0.11 [5.9] |
| WIN55,212‐2 | 0.28 [9.3] | ||
| AEA | 0.14 [6.6] | ||
| 2‐AG | 1.17 [31.0] | ||
| THC | 0.029 [5.6] | ||
| BAY | 0.025 [13.2] | ||
| pKSS | Negative logarithm of quasi‐steady state K | CP55,940 | 7.83 [0.9] |
| WIN55,212‐2 | 6.07 [1.2] | ||
| AEA | 6.21 [1.1] | ||
| 2‐AG | 4.41 [3.7] | ||
| THC | 7.67 [1.5] | ||
| BAY | 5.99 [3.2] | ||
3.5. The relationship between the model‐free and kinetic modelling methods
Through theoretical evaluation, it was demonstrated that the relationship between internalisation metric ( ) and ligand concentration (A) follows an Emax model (Equation 11, the derivation is detailed in Appendix A.3). Hence, the potency parameter EC50 from the model‐free approach can be directly linked to the potency parameter (KSS) in the kinetic model. Similarly, the efficacy parameter (Emax) from model‐free approach can be directly linked to the efficacy parameter (kint) in the kinetic model as well.
| (11) |
Apart from the theoretical evaluation, a numerical comparison was also conducted to explore the correlation between potency/efficacy parameters derived from kinetic modelling (Table 3) and model‐free approaches (Table 2). As shown in Figure 6, the potency/efficacy parameters estimated from kinetic modelling are highly correlated with those obtained from model‐free approach (potency: r2 = 0.87; efficacy: r2 = 0.98). Furthermore, the potency and efficacy rank order of six CB1 receptor agonists was preserved across both methods.
Figure 6.
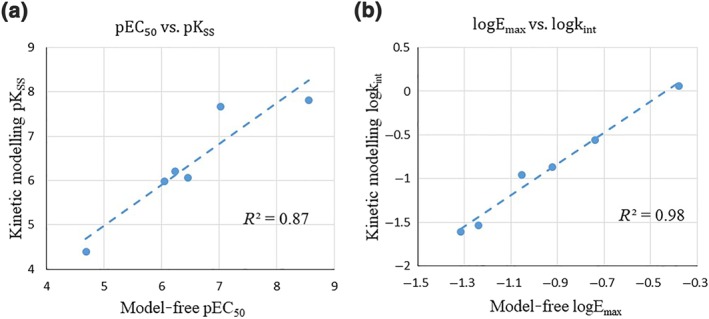
Comparison of the potency/efficacy of CB1 receptor agonists for internalisation in 3HA‐hCB1 HEK cells derived from model‐free method (the inverse of mean residence time) and kinetic modelling approach (the quasi‐steady state internalisation model). (a) Correlation between potencies of CB1 receptor ligands for internalisation derived from kinetic modelling (pKSS) and model‐free approach (pEC50; r2 = 0.87). (b) Correlation between efficacies of CB1 receptor ligands for internalisation derived from kinetic modelling (logkint) and model‐free approach (logEmax; r2 = 0.98). Here, the blue dashed line indicates the trend line from linear regression
3.6. Comparison of Ks derived from kinetic internalisation and equilibrium binding
As shown in Figure 7, the values of pKSS estimated from quasi‐steady state model of internalisation are highly correlated with the values of pKD obtained from equilibrium competitive binding assay (r2 = 0.75) and have the similar rank order. As anticipated, there is a systematic deviation for the observed higher potency in equilibrium competitive binding compared to kinetic internalisation. This is consistent with the quasi‐steady state assumption where KSS is defined as the sum of KD (receptor binding term) and (internalisation term; Equation 7).
Figure 7.
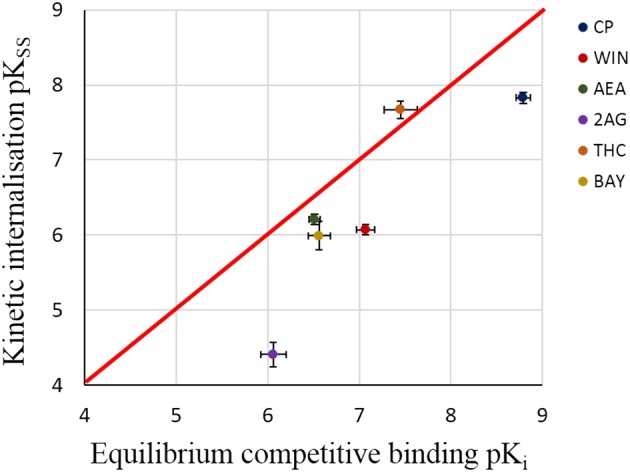
Correlation between pKSS derived from kinetic internalisation assay in the whole cells and pKi derived from equilibrium competitive binding assay in membrane homogenates. Here, the red line indicates the identity line and the error bar indicates the standard error. Data generally fall below the line of unity as would be expected if the quasi‐steady state assumption is valid. The data for pKSS are presented in Table 3 and the data for pKi are included in Table S1
4. DISCUSSION
The purpose of current study is to determine possible approaches for characterising agonist internalisation activity profiles from non‐equilibrium assay data. The proposed approaches were compared to the performance of traditional internalisation analysis methods, where an equilibrium time point is (erroneously) assumed. This analysis highlighted a limitation of the traditional method due to the existence of the confounding factors of time and agonist concentration, demonstrating that apparent potency clearly shifted over time and that this shift was inconsistent between ligands. Two approaches were proposed and used to characterise internalisation activity. These were (a) a model‐free method and (b) a full kinetic modelling approach. These approaches were derived and evaluated based on internalisation profiles of a set of CB1 receptor agonists. Both methods performed well and gave equivalent results.
It was evident using the traditional analysis method that no single time point was useful for inferring agonist properties in an internalisation pathway across agonists (Table 1). Furthermore, and as anticipated, the estimated potency of the agonist was time‐varying, demonstrating an artefactual potency left‐shift over time (Figure 3). This clearly indicates that standard equilibrium assumptions inherent in traditional pharmacological approaches are invalid for non‐equilibrium data such as internalisation. Therefore, this analysis indicates that it is essential to incorporate time into the analysis of internalisation data for meaningful characterisation of agonist properties.
Two quantitative approaches were proposed for characterising the agonist‐specific properties in internalisation in order to accommodate non‐equilibrium conditions. In the model‐free method, the effect of time is integrated out via the construction of a model‐free metric, . The inverse of MRT ( ) reflects the inverse of the average time a labelled receptor remains on the membrane surface. This model‐free metric can be utilised to evaluate the concentration–response relationship in receptor internalisation. For the kinetic modelling approach, agonist concentration and time are naturally incorporated into a time‐based model derived from a mechanistic approximation of receptor internalisation.
Thus, the current study shows that internalisation data can be analysed by either the model‐free or kinetic modelling methods, and both methods provide comparable results (Figure 6). The choice of method should therefore depend on the aim of the analysis. If the primary goal is to determine the agonist specific potency/efficacy parameters for internalisation pathway (e.g., E max and EC 50), then the model‐free method might be preferred as it is contingent upon fewer underlying assumptions than kinetic modelling and can be automated. However, if the study involves analysis and inference of additional pathways, then a full kinetic modelling approach that provides a mechanistic basis for co‐incident pathway activities would be ideal.
The current analysis of internalisation assay data provides an alternative to established methods (e.g., radioligand binding) for characterising ligand–receptor binding. It is shown that the results from internalisation assay are highly correlated with those from binding assays (r 2 = 0.75). However, there is a systematic deviation in these descriptions of ligand binding: the Ks from binding assays are lower than those from internalisation assays (Figure 7). One possible explanation is that the rapid agonist‐induced internalisation of CB1 receptors may decrease cell responsiveness to agonists. This may cause the internalisation assay (which is conducted in intact cells) to report lower apparent ligand affinities than the binding assay (which is conducted in membrane homogenates, so internalisation does not occur). Another alternative explanation is that agonist affinity in functional assays may be system dependent. In this case, the internalisation assay system results in lower agonist affinities than the binding assay system. Regardless of the cause of this deviation, this study suggests that the K from internalisation assays can be used to infer the relative affinities of agonists. On the other hand, the current analysis of internalisation assay also renders a potentially valuable ligand specific parameter (kint) for efficacy in internalisation. The biological interpretation of kint would be the rate constant of internalisation at the maximally effective concentration of agonist (Equation A8 and Equation S6).
However, sometimes, it is difficult or impossible to estimate every kinetic micro‐rate constant from typical functional assays for kinetic modelling (Hoare, Pierre, Moya, & Larson, 2018). Hence, there is a need to develop a reduced kinetic model that contains the essential features of the full kinetic model (Gibiansky et al., 2008; Mager & Krzyzanski, 2005). As demonstrated in our case, with certain assumptions, the agonist‐specific K can be estimated from non‐equilibrium data with the reduced kinetic model. This “middle‐out” approach could reduce the data requirement for kinetic modelling and provide mechanistic insights into the kinetic behaviours of signalling pathways given the data from typical functional assays.
Assumption evaluation is a crucial but often overlooked part of model development (EFPIA MID3 Workgroup et al., 2016; Karlsson, Jonsson, Wiltse, & Wade, 1998; Ooi, Wright, Isbister, & Duffull, 2018). Two findings from this study highlighted the utility of assumption evaluation. First, the violation of the equilibrium assumption underpinning traditional pharmacological models caused an artefactual potency shift over time (Figure 3). Assumption evaluation helped pick up this fault, and later, the relaxation of the equilibrium assumption allowed development of a kinetic internalisation model. Second, two competing assumptions (rapid binding vs. quasi‐steady state, Figure S1 and Figure 1, respectively) rendered the same mathematical form of the kinetic internalisation model but different interpretations of the K. The K determined under rapid binding conditions is KD (see Supporting Information), but when the quasi‐steady state assumption applies, the K is KSS which incorporates both binding and internalisation parameters. The form of the K can be identified by comparing the internalisation model‐derived K with the equilibrium K D determined by traditional competition displacement binding assays (i.e., KD). A systematic deviation between the internalisation model‐estimated K and the “binding assay” KD (as was the case in this instance, Figure 7) indicates that the quasi‐steady state assumption was preferred and therefore, the K determined is the quasi‐steady state K (KSS).
The development of the quasi‐steady state internalisation model is simple for receptors, such as the CB1 receptors, for which all known orthosteric ligands (certainly all six agonists used in this study) bind a shared site. This one‐site binding principle (and its consequence; that cooperative binding is not relevant) is a standard assumption in this type of experimental paradigm, and the resulting kinetic model could adequately describe all the internalisation data produced. However, for other candidate receptors for which cooperative binding of ligands (and multi‐site binding) are possible, we note that the quasi‐steady state internalisation model can be generalised to account for cooperative binding with non‐unity Hill slope (n) and individual initial fluorescence intensity (FI0i; detailed in the Supporting Information).
The in vitro internalisation system can be regarded as a simplified version of the in vivo internalisation system. In vivo, the assumption of constant ligand concentration (Assumption 2) is invalid as the ligand concentration will change over time due to the pharmacokinetics of the ligand. By incorporating a pharmacokinetic model of the ligand into the in vitro internalisation model, this assumption can be generalised and thus an in vivo internalisation model could be proposed. We also note that this generalisation has already been considered within the framework of target‐mediated drug disposition (generally) for monoclonal antibodies (Gibiansky et al., 2008; Mager & Jusko, 2001).
Characterisation of ligand signalling is a critical component of drug discovery. The quality of the decisions made during the drug characterisation process depends on the robustness and accuracy of the models utilised to analyse the data. The use of analysis paradigms that rely on assumptions of equilibrium conditions, when the actual data are dynamic (lacking a single equilibrium time point), is therefore a major limitation of prevailing approaches. One direct consequence of this is that such models misrepresent ligand responses (resulting in misinterpretation of drug effects)—examples of which we have clearly demonstrated in the current study (see Figures 2 and 3). Development of non‐equilibrium analysis paradigms, such as those reported in the current study, can overcome this problem. This approach helps guide efficient drug discovery and improves the success rate of translating lead compounds into innovative clinical therapies.
In conclusion, we have systematically evaluated the performance of two new analysis methods for evaluating internalisation activity profiles of CB1 receptors. Both methods, the model‐free method and kinetic modelling approach, performed equivalently and demonstrated accurate characterisation of these profiles. It was noted that the traditional equilibrium analysis technique did not perform well and was highly sensitive to the time that equilibrium was assumed. The proposed techniques have generality beyond the CB1 receptor and can be used when quantifying any receptor internalisation but would also be generally applicable to other types of non‐equilibrium functional data.
AUTHOR CONTRIBUTIONS
X.Z. and D.B.F. designed and performed experiments. M.G. and S.B.D. designed experiments. X.Z., D.B.F., M.G., and S.B.D. analysed the data. X.Z., D.B.F., M.G., and S.B.D. wrote the paper.
CONFLICT OF INTERESTS
The authors declare no conflicts of interest.
DECLARATION OF TRANSPARENCY AND SCIENTIFIC RIGOUR
This Declaration acknowledges that this paper adheres to the principles for transparent reporting and scientific rigour of preclinical research as stated in the BJP guidelines for Design & Analysis, and as recommended by funding agencies, publishers and other organisations engaged with supporting research.
Supporting information
Table S1. CB1 Ligand affinity from equilibrium competitive binding assay (pKi ± SEM, n=5)
Figure S1. The schematic plot of the rapid binding model of agonist‐induced internalisation for “live‐at‐start” internalisation assay.
Figure S2. The model fitting results of constitutive internalisation. The line here represents the prediction from constitutive internalisation model and the dots (mean ± SEM) are the observed data of constitutive internalisation from “live‐at‐start” internalisation assay.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge grants to M.G. from the University of Auckland, School of Medical Sciences; X.Z. is supported by a University of Otago Doctoral Scholarship; and D.B.F. was supported by a University of Auckland Doctoral Scholarship.
APPENDICES A.
A.1. Calculation of and
The linear trapezoidal method is used to calculate the AUC, which is the standard for bioequivalence trials in the area of pharmacokinetics. For a given time interval (ti+1 − ti), the AUC can be calculated as the product of the average signal (fluorescence intensity in this case) over the time interval ( ) and the duration of time (ti+1 − ti). Summing all the intervals together yields the total exposure of fluorescence intensity from the first time point to the last ( ).
| (A1) |
where ∆ti = ti+1 − ti and tlast denotes the time of the last measured fluorescence intensity.
Similarly, the linear trapezoidal method can also be used to calculate the AUMC. The only difference here is that the signal is the product of time and fluorescence intensity for the calculation of AUMC. In this sense, AUMC captures the time and averaged intensity of the interval ∆ti.
| (A2) |
A.2. The derivation of quasi‐steady state internalisation model
The measured florescence intensity reflected the amount of all the labelled receptors remaining on the surface. Hence, it was the sum of both the labelled free receptor (R) and labelled occupied receptor (AR):
| (A3) |
Solving Equation (7) and Equation (A3) yielded the expressions for R and AR:
| (A4) |
| (A5) |
From Equations (4) and (5), the changing rate of total labelled receptor (RT) was derived:
| (A6) |
Substituting Equations (A4) and (A5) into Equation (A6) yielded the quasi‐steady state model (Equation A7) for receptor internalisation in the “live‐at‐start” assay.
| (A7) |
It is noted that kint is the rate constant of internalisation at the maximally effective concentration of agonist (Equation A8).
| (A8) |
From the Equation (A7), the analytical solution (Equation A9) could be derived:
| (A9) |
Since the fluorescence intensity (FI) was detected to reflect the density of labelled receptor on the surface, a fundamental assumption for this analysis was that the measured fluorescence intensity should be proportional to the amount of labelled surface receptor remaining on the surface of membrane (Assumption 4). Here, α was a coefficient to link the unit of receptor density and fluorescence intensity (Equation A10).
| (A10) |
Substituting Equation (A9) into Equation (A10) yielded the model for quantifying receptor internalisation in “live‐at‐start” assay:
| (A11) |
Due to an identifiability issue, it was not possible to separately estimate α and R0. In order to circumvent this problem, α and R0 were therefore reduced into a single identifiable quantity (FI0), defined as the initial fluorescence intensity. This provided the equation of quasi‐steady state model for agonist‐induced internalisation.
| (A12) |
A.3. Theoretical evaluation of the relationship between model‐free method and kinetic modelling approaches
In the kinetic modelling approach, the AUC of fluorescence intensity verse time (AUC) can be directly integrated from the quasi‐steady state model of internalisation (Equation A13).
| (A13) |
Remembering that , the corresponding AUMC is computed as
| (A14) |
Taking the ratio of AUC and AUMC yields the expression of the internalisation metric ( ) within the kinetic internalisation model framework (Equation A16):
| (A15) |
| (A16) |
Zhu X, Finlay DB, Glass M, Duffull SB. Model‐free and kinetic modelling approaches for characterising non‐equilibrium pharmacological pathway activity: Internalisation of cannabinoid CB1 receptors. Br J Pharmacol. 2019;176:2593–2607. 10.1111/bph.14684
Xiao Zhu and David B. Finlay contributed equally.
Contributor Information
Michelle Glass, Email: michelle.glass@otago.ac.nz.
Stephen B. Duffull, Email: stephen.duffull@otago.ac.nz.
REFERENCES
- Alexander, S. P. , Christopoulos, A. , Davenport, A. P. , Kelly, E. , Marrion, N. V. , Peters, J. A. , … CGTP Collaborators . (2017). The Concise Guide to PHARMACOLOGY 2017/18: G protein‐coupled receptors. British Journal of Pharmacology, 174(Suppl 1), S17–S129. 10.1111/bph.13878 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayoub, M. A. , Landomiel, F. , Gallay, N. , Jegot, G. , Poupon, A. , Crepieux, P. , & Reiter, E. (2015). Assessing gonadotropin receptor function by resonance energy transfer‐based assays. Frontiers in Endocrinology, 6, 130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Black, J. W. , & Leff, P. (1983). Operational models of pharmacological agonism. Proceedings of the Royal Society of London ‐ Series B: Biological Sciences, 220, 141–162. [DOI] [PubMed] [Google Scholar]
- Calebiro, D. , & Godbole, A. (2018). Internalization of G‐protein‐coupled receptors: Implication in receptor function, physiology and diseases. Best Practice & Research. Clinical Endocrinology & Metabolism, 32, 83–91. 10.1016/j.beem.2018.01.004 [DOI] [PubMed] [Google Scholar]
- Cawston, E. E. , Redmond, W. J. , Breen, C. M. , Grimsey, N. L. , Connor, M. , & Glass, M. (2013). Real‐time characterization of cannabinoid receptor 1 (CB1) allosteric modulators reveals novel mechanism of action. British Journal of Pharmacology, 170, 893–907. 10.1111/bph.12329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborty, A. , Tannenbaum, S. , Rordorf, C. , Lowe, P. J. , Floch, D. , Gram, H. , & Roy, S. (2012). Pharmacokinetic and pharmacodynamic properties of canakinumab, a human anti‐interleukin‐1β monoclonal antibody. Clinical Pharmacokinetics, 51, e1–e18. 10.2165/11599820-000000000-00000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtis, M. J. , Alexander, S. , Cirino, G. , Docherty, J. R. , George, C. H. , Giembycz, M. A. , … Ahluwalia, A. (2018). Experimental design and analysis and their reporting II: Updated and simplified guidance for authors and peer reviewers. British Journal of Pharmacology, 175, 987–993. 10.1111/bph.14153 [DOI] [PMC free article] [PubMed] [Google Scholar]
- EFPIA MID3 Workgroup , Marshall, S. F. , Burghaus, R. , Cosson, V. , Cheung, S. Y. , Chenel, M. , … Visser, S. A. (2016). Good practices in model‐informed drug discovery and development: Practice, application, and documentation. CPT: Pharmacometrics & Systems Pharmacology, 5, 93–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eishingdrelo, H. , & Kongsamut, S. (2013). Minireview: Targeting GPCR activated ERK pathways for drug discovery. Current Chemical Genomics and Translational Medicine, 7, 9–15. 10.2174/2213988501307010009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finlay, D. B. , Cawston, E. E. , Grimsey, N. L. , Hunter, M. R. , Korde, A. , Vemuri, V. K. , … Glass, M. (2017). Gαs signalling of the CB1 receptor and the influence of receptor number. British Journal of Pharmacology, 174, 2545–2562. 10.1111/bph.13866 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finlay, D. B. , Joseph, W. R. , Grimsey, N. L. , & Glass, M. (2016). GPR18 undergoes a high degree of constitutive trafficking but is unresponsive to N‐Arachidonoyl Glycine. PeerJ, 4, e1835 10.7717/peerj.1835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furchgott, R. (1966). The use of β‐haloalkylamines in the differentiation of receptors and in the determination of dissociation constants of receptor‐agonist complexes. Advances in Drug Research, 3, 21–55. [Google Scholar]
- Gabrielsson, J. , & Weiner, D. (2001). Pharmacokinetic and pharmacodynamic data analysis: Concepts and applications (3rd ed.). Stockholm: Swedish Pharmaceutical Press. [Google Scholar]
- Gibaldi, M. , & Perrier, D. (1982). Pharmacokinetics (2nd ed.). New York: Marcel Dekker. [Google Scholar]
- Gibiansky, L. , & Frey, N. (2012). Linking interleukin‐6 receptor blockade with tocilizumab and its hematological effects using a modeling approach. Journal of Pharmacokinetics and Pharmacodynamics, 39, 5–16. 10.1007/s10928-011-9227-z [DOI] [PubMed] [Google Scholar]
- Gibiansky, L. , Gibiansky, E. , Kakkar, T. , & Ma, P. (2008). Approximations of the target‐mediated drug disposition model and identifiability of model parameters. Journal of Pharmacokinetics and Pharmacodynamics, 35, 573–591. 10.1007/s10928-008-9102-8 [DOI] [PubMed] [Google Scholar]
- Gibiansky, L. , Sutjandra, L. , Doshi, S. , Zheng, J. , Sohn, W. , Peterson, M. C. , … Pérez‐Ruixo, J. J. (2012). Population pharmacokinetic analysis of denosumab in patients with bone metastases from solid tumours. Clinical Pharmacokinetics, 51, 247–260. 10.2165/11598090-000000000-00000 [DOI] [PubMed] [Google Scholar]
- Grimsey, N. L. , Graham, E. S. , Dragunow, M. , & Glass, M. (2010). Cannabinoid receptor 1 trafficking and the role of the intracellular pool: Implications for therapeutics. Biochemical Pharmacology, 80, 1050–1062. 10.1016/j.bcp.2010.06.007 [DOI] [PubMed] [Google Scholar]
- Grimsey, N. L. , Narayan, P. J. , Dragunow, M. , & Glass, M. (2008). A novel high‐throughput assay for the quantitative assessment of receptor trafficking. Clinical and Experimental Pharmacology & Physiology, 35, 1377–1382. 10.1111/j.1440-1681.2008.04991.x [DOI] [PubMed] [Google Scholar]
- Hanyaloglu, A. C. , & von Zastrow, M. (2008). Regulation of GPCRs by endocytic membrane trafficking and its potential implications. Annual Review of Pharmacology and Toxicology, 48, 537–568. 10.1146/annurev.pharmtox.48.113006.094830 [DOI] [PubMed] [Google Scholar]
- Harding, S. D. , Sharman, J. L. , Faccenda, E. , Southan, C. , Pawson, A. J. , Ireland, S. , … NC‐IUPHAR . (2018). The IUPHAR/BPS guide to PHARMACOLOGY in 2018: Updates and expansion to encompass the new guide to IMMUNOPHARMACOLOGY. Nucl Acids Res, 46, D1091–D1106. 10.1093/nar/gkx1121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoare, S. R. , Pierre, N. , Moya, A. G. , & Larson, B. (2018). Kinetic operational models of agonism for G‐protein‐coupled receptors. Journal of Theoretical Biology, 446, 168–204. 10.1016/j.jtbi.2018.02.014 [DOI] [PubMed] [Google Scholar]
- Howlett, A. C. , Barth, F. , Bonner, T. I. , Cabral, G. , Casellas, P. , Devane, W. A. , … Pertwee, R. G. (2002). International Union of Pharmacology. XXVII. Classification of cannabinoid receptors. Pharmacological Reviews, 54, 161–202. 10.1124/pr.54.2.161 [DOI] [PubMed] [Google Scholar]
- Hunter, M. R. , & Glass, M. (2015). Increasing the flexibility of the LANCE cAMP detection kit. Journal of Pharmacological and Toxicological Methods, 71, 42–45. 10.1016/j.vascn.2014.10.008 [DOI] [PubMed] [Google Scholar]
- Karlsson, M. O. , Jonsson, E. N. , Wiltse, C. G. , & Wade, J. R. (1998). Assumption testing in population pharmacokinetic models: Illustrated with an analysis of moxonidine data from congestive heart failure patients. Journal of Pharmacokinetics and Biopharmaceutics, 26, 207–246. 10.1023/A:1020561807903 [DOI] [PubMed] [Google Scholar]
- Kenakin, T. , Watson, C. , Muniz‐Medina, V. , Christopoulos, A. , & Novick, S. (2012). A simple method for quantifying functional selectivity and agonist bias. ACS Chemical Neuroscience, 3, 193–203. 10.1021/cn200111m [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein Herenbrink, C. , Sykes, D. A. , Donthamsetti, P. , Canals, M. , Coudrat, T. , Shonberg, J. , … Lane, J. R. (2016). The role of kinetic context in apparent biased agonism at GPCRs. Nature Communications, 7, 10842 10.1038/ncomms10842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leterrier, C. , Bonnard, D. , Carrel, D. , Rossier, J. , & Lenkei, Z. (2004). Constitutive endocytic cycle of the CB1 cannabinoid receptor. The Journal of Biological Chemistry, 279, 36013–36021. 10.1074/jbc.M403990200 [DOI] [PubMed] [Google Scholar]
- Levoye, A. , Zwier, J. M. , Jaracz‐Ros, A. , Klipfel, L. , Cottet, M. , Maurel, D. , … Bachelerie, F. (2015). A broad G protein‐coupled receptor internalization assay that combines SNAP‐tag labeling, diffusion‐enhanced resonance energy transfer, and a highly emissive terbium cryptate. Frontiers in Endocrinology, 6, 167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luttrell, D. K. , & Luttrell, L. M. (2003). Signaling in time and space: G protein‐coupled receptors and mitogen‐activated protein kinases. Assay and Drug Development Technologies, 1, 327–338. 10.1089/15406580360545143 [DOI] [PubMed] [Google Scholar]
- Mager, D. E. , & Jusko, W. J. (2001). General pharmacokinetic model for drugs exhibiting target‐mediated drug disposition. Journal of Pharmacokinetics and Pharmacodynamics, 28, 507–532. 10.1023/A:1014414520282 [DOI] [PubMed] [Google Scholar]
- Mager, D. E. , & Krzyzanski, W. (2005). Quasi‐equilibrium pharmacokinetic model for drugs exhibiting target‐mediated drug disposition. Pharmaceutical Research, 22, 1589–1596. 10.1007/s11095-005-6650-0 [DOI] [PubMed] [Google Scholar]
- Ooi, Q. X. , Wright, D. , & Isbister, G. , & Duffull, S. (2018). Evaluation of assumptions underpinning pharmacometric models. PAGE 27 Abstr 8538 [www.page‐meeting.org/?abstract=8538]. [DOI] [PubMed]
- Pertwee, R. G. , Howlett, A. C. , Abood, M. E. , Alexander, S. P. , Di Marzo, V. , Elphick, M. R. , … Ross, R. A. (2010). International Union of Basic and Clinical Pharmacology. LXXIX. Cannabinoid receptors and their ligands: Beyond CB(1) and CB(2). Pharmacological Reviews, 62, 588–631. 10.1124/pr.110.003004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shayo, C. , Fernandez, N. , Legnazzi, B. L. , Monczor, F. , Mladovan, A. , Baldi, A. , & Davio, C. (2001). Histamine H2 receptor desensitization: Involvement of a select array of G protein‐coupled receptor kinases. Molecular Pharmacology, 60, 1049–1056. 10.1124/mol.60.5.1049 [DOI] [PubMed] [Google Scholar]
- Smith, J. S. , Lefkowitz, R. J. , & Rajagopal, S. (2018). Biased signalling: From simple switches to allosteric microprocessors. Nature Reviews. Drug Discovery, 17, 243–260. 10.1038/nrd.2017.229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urban, J. D. , Clarke, W. P. , von Zastrow, M. , Nichols, D. E. , Kobilka, B. , Weinstein, H. , … Mailman, R. B. (2007). Functional selectivity and classical concepts of quantitative pharmacology. The Journal of Pharmacology and Experimental Therapeutics, 320, 1–13. [DOI] [PubMed] [Google Scholar]
- van der Westhuizen, E. T. , Breton, B. , Christopoulos, A. , & Bouvier, M. (2014). Quantification of ligand bias for clinically relevant β2‐adrenergic receptor ligands: Implications for drug taxonomy. Molecular Pharmacology, 85, 492–509. 10.1124/mol.113.088880 [DOI] [PubMed] [Google Scholar]
- von Zastrow, M. (2003). Mechanisms regulating membrane trafficking of G protein‐coupled receptors in the endocytic pathway. Life Sciences, 74, 217–224. 10.1016/j.lfs.2003.09.008 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1. CB1 Ligand affinity from equilibrium competitive binding assay (pKi ± SEM, n=5)
Figure S1. The schematic plot of the rapid binding model of agonist‐induced internalisation for “live‐at‐start” internalisation assay.
Figure S2. The model fitting results of constitutive internalisation. The line here represents the prediction from constitutive internalisation model and the dots (mean ± SEM) are the observed data of constitutive internalisation from “live‐at‐start” internalisation assay.


