Abstract
Purpose
The desire to quantitatively discriminate the extra‐ and intracellular tissue 1H2O MR signals has gone hand‐in‐hand with the continual, historic increase in MRI instrument magnetic field strength [B 0]. However, recent studies have indicated extremely valuable, novel metabolic information can be readily accessible at ultra–low B 0. The two signals can be distinguished, and the homeostatic activity of the cell membrane sodium/potassium pump (Na+,K+,ATPase) detected. The mechanism allowing 1H2O MRI to do this is the newly discovered active transmembrane water cycling (AWC) phenomenon, which we found using paramagnetic extracellular contrast agents at clinical B 0 values. AWC is important because Na+,K+,ATPase can be considered biology’s most vital enzyme, and its in vivo steady‐state activity has not before been measurable, let alone amenable to mapping with high spatial resolution. Recent reports indicate AWC correlates with neuronal firing rate, with malignant tumor metastatic potential, and inversely with cellular reducing equivalent fraction. We wish to systematize the ways AWC can be precisely measured.
Methods
We present a theoretical longitudinal relaxation analysis of considerable scope: it spans the low‐ and high–field situations.
Results
We show the NMR shutter‐speed organizing principle is pivotal in understanding how trans–membrane steady–state water exchange kinetics are manifest throughout the range. Our findings illuminate an aspect, apparent population inversion, which is crucial in understanding ultra‐low field results.
Conclusions
Without an appreciation of apparent population inversion, significant misinterpretations of future data are likely. These could have unfortunate diagnostic consequences.
Keywords: active water cycling, apparent population‐inversion, shutter‐speed
1. INTRODUCTION
1.1. Discerning tissue water compartmentalization
The major water compartmentalization in tissue is intra‐ and extracellular (“inside”/“outside”). In almost all parenchymal tissue, the vascular space comprises a small volume fraction. Thus, in the simplest approximation, this is a two site situation. A reliable way to quantitatively discriminate in vivo 1H2Oi and 1H2Oo NMR signals has been a very long quest.
1.2. Active transmembrane water cycling
Recently, this pursuit has gained much greater importance. It has been discovered that the pseudo‐first‐order rate constant for homeostatic cellular water efflux (kio) has an energetically active component, kio(a), as expressed in Equation 1, and
| (1) |
elaborated in Equation 2. The passive component, kio(p), is 〈A/V〉PW(p), where: 〈A/V〉 represents
| (2) |
the voxel average or region of interest average 〈cell surface area/volume〉 ratio, and PW(p) is the diffusive (“passive”) cell membrane water permeability coefficient. In this study, quantities in brackets, 〈〉, represent voxel or region of interest averages. All symbols and acronyms are defined in the Appendix. It was previously thought kio = kio(p): there was no active component. However, this is not the case: kio(a) is always present, and often dominant.1, 2, 3, 4 It is elaborated as (x/([H2Oi]〈V〉))cMRNKA, where cMRNKA is the cellular metabolic rate of the cell membrane Na+,K+‐ATPase (NKA) (fmol(ATP)hydrolyzed/cell/s), [H2Oi] is the intracellular water concentration, and x is the stoichiometric mole ratio of water actively cycled to ATP hydrolyzed by NKA [fmol(H2O)/fmol(ATP)]. Thus, an enzymatic activity generates a membrane permeability. Active transmembrane water cycling (AWC) is a fundamental aspect of water biology not previously described.
This is important because NKA can be considered biology’s most vital enzyme, but its in vivo homeostatic activity has never been measurable or amenable to mapping.1, 2, 3, 4 Significantly, it has been found that kio correlates with metastatic potential in breast5 and melanoma6 cell lines, and with neuronal firing in brain tissue.4 This is a new imaging biomarker with potentially great power.
Previously, the main candidate techniques for 1H2Oi/1H2Oo signal discrimination required the use of an exogenous, extracellular paramagnetic contrast agent (CAo) to increase the 1H2Oo R1o (≡ 1/T1o) value selectively.3, 7, 8 This will be detailed below. Indeed, studies on model systems,1, 2, 3, 4, 9, 10 in which constant [CAo] ≥ 5 mM can be sustained during complete relaxation recovery measurement, were required to confirm the (x/([H2Oi]〈V〉))cMRNKA term in Equation 2. However, this approach is problematic for in vivo human study.3
Since the beginning of NMR, there has been a seemingly inexorable march to instruments with higher magnetic field (B 0) values.11 This has been driven by the increased signal/noise ratio and spectral dispersion. However, this trend has not been particularly helpful for the discrimination of 1H2Oi and 1H2Oo. Even though CA detectability increases slightly with increasing B 0,12 the diminished relaxivity (r1) of approved CAs at current clinical B 0 values13 requires large CA doses. Consequently, safety and environmental regulatory restrictions preclude achieving the high, sustained [CAo] values sufficient for precise kio determination in vivo.3 Recently, Aime and co‐workers have demonstrated CA‐free 1H2Oi/1H2Oo discrimination, again in an animal model and cell suspensions, at ultra‐low B 0 values.5, 10 Here, we present a comprehensive analysis of the fundamental principles spanning the high and low field experiments.
2. METHODS
2.1. Intrinsic sample or voxel compartmental properties
There are two intrinsic NMR properties of interest: R1i and R1o, R1i is the 1H2Oi R1 value. For CA‐enhanced MRI, the 1H2Oo R1 value is given by Equation 3,
| (3) |
where r1o is the extracellular CA longitudinal relaxivity [CAo], the extracellular CA concentration, and R1o0 the R1o value in the absence of CA. In addition to being temperature–dependent, the R1i, r1o, and R1o0 properties are also B 0–dependent.
There are two intrinsic cell biology properties of interest: pi, and kio. The quantity pi is the mole fraction (“population”) of water that is intracellular. The intracellular volume fraction, vi, is given by Equation 4, where fM is
| (4) |
the tissue volume fraction inaccessible to mobile aqueous solutes.2, 8 When the vascular fraction is neglected, Equations (5a), (5b)a and 5b obtain, where po and vo are the respective extracellular mole and volume fractions.
| (5a) |
| (5b) |
The pseudo‐first‐order rate constant for homeostatic cellular water efflux is kio. (The parameter kio is the reciprocal of the mean intracellular water molecule lifetime, 1/τi. The τi value is often reported in the literature.) Because we assume a steady‐state, kio is also given by Equation 6, where koi is the corresponding influx rate constant. While still
| (6) |
temperature‐dependent, pi, fM, kio, and koi do not depend on B 0 or [CAo].
Figure 1 illustrates the isothermal behavior of realistic, representative intrinsic NMR properties over a very large range. The ordinate measures R1: the R1i curves are blue, while the R1o curves are red. The abscissa is bifurcated: the left side measures an increase in log v L, the Larmor resonance frequency (proportional to log B 0: the 1H magnetogyric ratio is 0.023 T/MHz), with [CAo] = 0; while the right side measures an increase in [CAo], with v L constant at 43 MHz (B 0 = 1.0 T), the largest v L reached on the left. The smooth R1i and R1o curves on the left pass through fitted values for a murine xenograft TS/A breast cancer tumor.5 They exhibit the familiar dispersive shape [an R1i inflection point near 0.1 MHz (0.002 T)]. The R1 B 0‐dependence has long been referred to as NMR dispersion. The R1o values on the right are calculated using r1o = 3.8 s−1(mM)−1, typical for approved Gd(III) chelates.7 All magnitudes are for T = 37°C.
Figure 1.
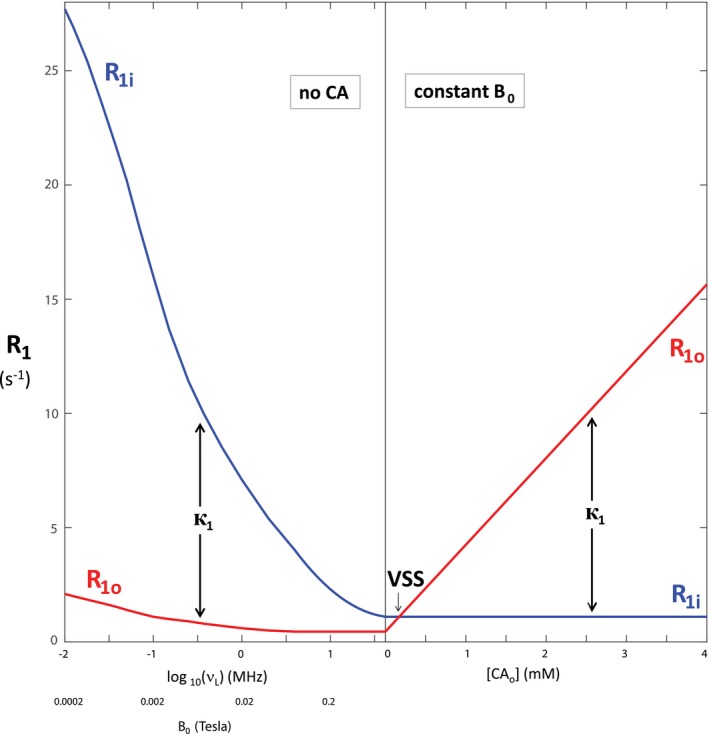
The dependences of the stipulated intrinsic compartmental longitudinal relaxation rate constants, R1, on the: magnetic field, B 0 (left), and extracellular CA concentration, [CAo] (right). The left abscissa has a log B 0 scale, with fixed [CAo] = 0. The right abscissa is linear in [CAo], with fixed B 0 = 1.0 T. The intracellular R1i (blue) and extracellular R1o (red) rate constants on the left include those reported in Ruggiero et al.5 The R1o values on the right were calculated from Equation 3 with extracellular CA relaxivity, r1o = 3.8 mM−1s−1. The longitudinal MR shutter–speed, к1 (Equation 9), and the VSS condition are indicated. It is important to note these would be the experimentally measured R1 rate constants if there was no trans‐cytolemmal water exchange [k = 0]
Figure 2 illustrates the behavior of the intrinsic cell biology properties: we take representative values of pi (0.8) and kio (1 s−1).3, 5 (Thus, po = 0.2, and koi = 4 s−1 [kio + koi = 5 s−1]). The left ordinate measures the p values (pi, blue; po, red), while the right ordinate measures the overall exchange rate constant, k, given by Equation 7. The abscissa is
| (7) |
Figure 2.
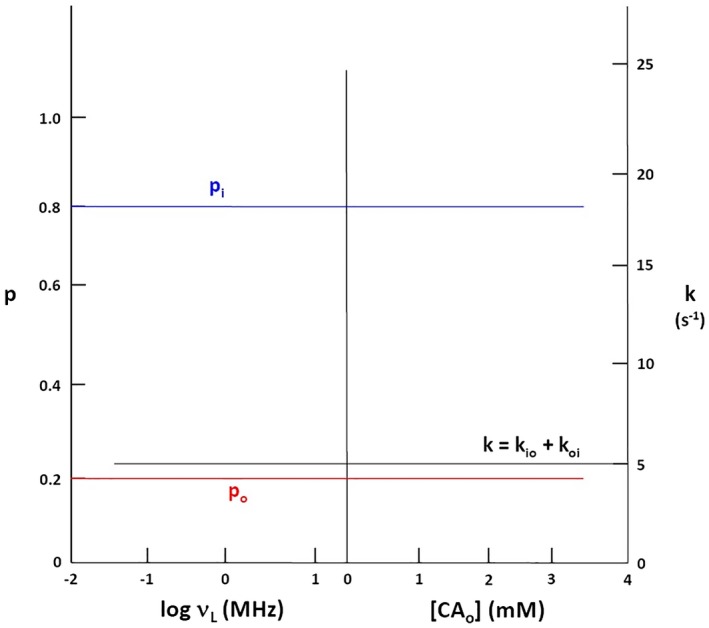
The non‐dependences of the stipulated intrinsic compartmental mole fractions (“populations”), p, and intercompartmental exchange rate constant, k (Equation 7), on: (left) the B 0 and (right) the [CAo]. The abscissa is the same as in Figure 1. The intracellular pi (blue) and extracellular po (red) populations are measured on the left ordinate, while k is measured on the right ordinate
the same as for Figure 1. Because these are isothermal plots, these properties exhibit horizontal lines.
2.2. Magnetic field‐dependence
It has long been known the tissue 1H2O (the observed, approximated monoexponential R1 value) increases with decreasing B 0 (reviewed in Rooney et al11). In the absence of CAo, the 1H2O longitudinal relaxation mechanism is generally dominated by water intramolecular 1H – 1H magnetic dipole fluctuations at the v L frequency. As B 0 decreases, the v L value decreases toward the increased probability of experiencing such fluctuations (“spectral density”) found in tissue.14 In contrast, the 1H2O R1 value of pure water is not very B 0–dependent: the inherent fluctuations have much greater frequency [reciprocal of the molecular rotational (“tumbling”) correlation time constant, τr −1 ≅ 1012 s−1] than v L, and thus are too fast for efficient relaxation.11, 14 Therefore, it has long been suspected the inverse R1, v L relationship is due to the presence of macromolecules in tissue. Macromolecular tumbling is much slower than that of the molecules in pure water.15 The fluctuation is τr −1 ≅ 1.7/MW, where MW is the macromolecular mass in kDa. (Thus, even a smallish 100 kDa macromolecule has τr −1 ≅ 1.7 × 107 s−1.) To our knowledge, there is no simple physical model that predicts the B 0‐dependence of tissue 1H2O . Any attempt to match data with, say, a superposition of Lorentzian functions requires an empirical distribution of τr values.11
The extra‐ and intracellular tissue spaces both contain macromolecules,3 and one could not know for certain if extra‐ or intracellular macromolecules, or both, dominated the effect. One avoids this uncertainty by writing Equation 8 for iron‐free tissue.11 In this expression: r1M is the tissue macromolecular relaxivity, and R1H2O is
| (8) |
the pure water R1 at physiological temperature. (An extra term can be added if a tissue contains a sufficient amount of paramagnetic iron.11) The greater r1M decrease with increasing B 0 compared with that of r1o is the cause of the aforementioned slight CA detectability increase.12
However, Ruggiero and co‐workers used a Matrigel phantom as a model for extracellular space.5 They found the R1o value, so approximated, exhibits only a very slight NMR dispersion, as seen in Figure 1 (left). This supports a long‐held suspicion that the B 0‐dependence is dominated by an increasing R1i value with decreasing B 0.16 This is attributed to sites for water molecules that are characterized as “buried” within macromolecules (H2Obu), and the surmise that such sites are more abundant in intracellular than in extracellular macromolecules.16 Water molecules in such sites can more fully experience the slower macromolecule rotation, and thus particularly effective slow intramolecular 1H – 1H fluctuations. Such macromolecules are endogenous, intracellular contrast agents, CAis. Although their concentrations do not increase with decreasing B 0, their relaxivities do. (Relaxivities and concentrations always appear together as products,2, 17, 18 as in Equation 3.) Nonetheless, the miniscule number of H2Obu molecules are still in rapid exchange (rate constant > 104 s−1)19 with the vastly greater number of all other H2Oi molecules, certainly as compared with the kio magnitude. They could even use the Grotthuss proton hopping mechanism.15 In any case, the cytoplasm is “well–mixed.” This is depicted in the Figure 3 cartoon. Some very large heterogeneous compartments (e.g., Xenopus oocyte [〈V〉 = 840 nL] cytoplasms)20 can exhibit inhomogeneous 1H2O resonances. However, most tissue cell 〈V〉 values range from hundreds of fL to a few pL.21 In such small cells, even a conservatively small diffusion coefficient leads to good water mixing in any NMR experimental time period.9
Figure 3.
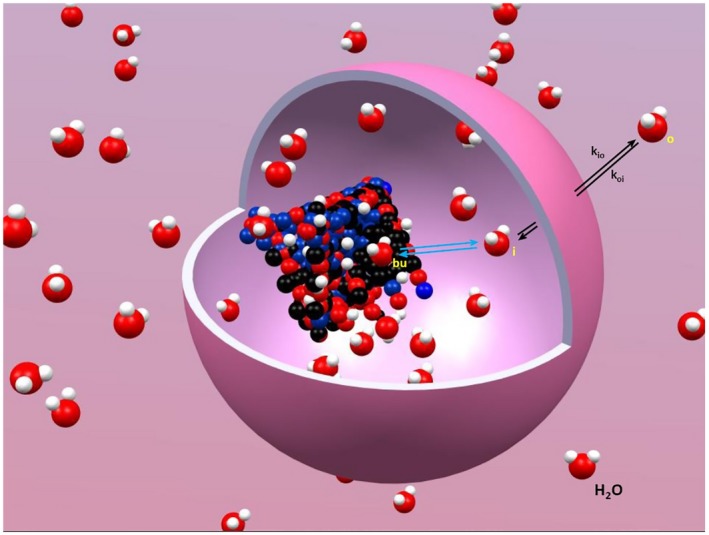
A stylized cartoon depiction of the steady‐state water exchange processes that dominate the tissue 1H2O MR signal longitudinal relaxation at ultra‐low‐field. The trans‐cytolemmal process has a kio (Equation 2) and a koi (Equation 6) rate constants. The exchange of water out of and into macromolecular buried sites, H2Obu, is much faster than k = kio + koi. For the considerations here, cytoplasmic water is “well‐mixed.” This figure was prepared with the help of Gangxu Han
The steady‐state transmembrane water molecule exchange process, k = kio + koi, is rate‐limiting; i.e., slower than essentially all other water molecule interaction kinetics in tissue. And, this has been the source of considerable confusion in the in vivo MRI literature. If the exchange kinetics were exceedingly slow, or exceedingly fast, the interpretation of experimental 1H2O data would be straightforward. But slow and fast are rather misleading adjectives. Figure 2 shows the k does not depend on B 0 or [CAo]. This is why we introduced18 the concept of the longitudinal NMR relaxation shutter‐speed, к1,3, 8 the absolute value function defined in Equation 9. The comparison of k with к1
| (9) |
determines the “exchange condition” of the tissue 1H2O MR signal. If k is insufficiently greater than к1, a “slow” condition obtains: but if it is sufficiently larger, the system is in a “fast” condition. In experimental terms, a slow condition means the longitudinal relaxation is non‐monoexponential, and a fast condition means the relaxation is monoexponential. The kio measurement precision depends on the extent κ1 exceeds k. Obviously, the greater the k value, the larger the к1 required.
As Figures 1 and 4 indicate, in biological tissue it is к1 that can be manipulated by the investigator [by means of B 0 and/or [CAo]], usually not k (almost all in vivo studies are isothermal). Because k does not change, the exchange reaction does not go “faster” or “slower.” Using these terms is meaningful only if one thinks of к1 changes as “warping” time. Thus, a slow condition is more profitably understood as a “large‐shutter‐speed” (LSS) condition; and a fast condition as a “small‐shutter‐speed” (SSS) condition. These distinctions are important because the nature of the exchange condition strongly influences the correct interpretation of the experimental result. This is described by the well‐known Bloch–McConnell‐Woessner (BMW) Rate Law Equations18, 22, 23, which elaborate the phenomenological signal equation.
Figure 4.
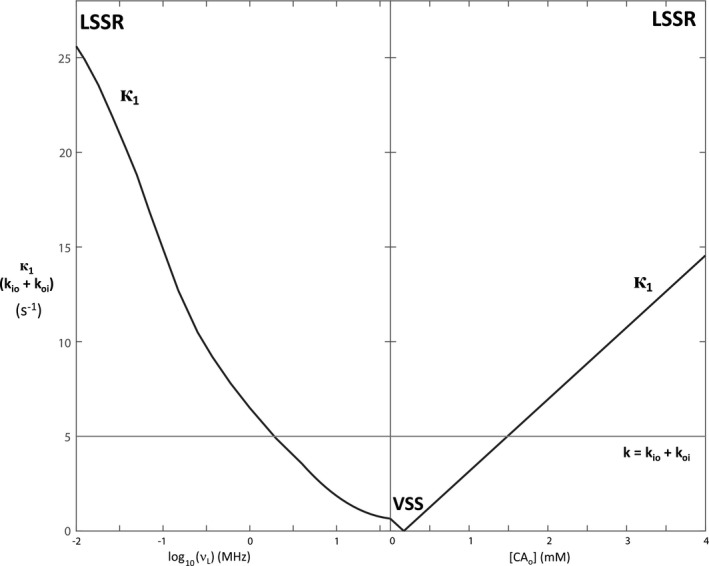
The dependences of the stipulated MR shutter‐speed, к1 (Equation 9), and intercompartmental exchange rate constant, k (Equation 7), on (left) the B 0 and (right) the [CAo]. The abscissa is the same as in Figure 1, and the ordinate the same as on the right in Figure 2. The vanished shutter‐speed VSS condition is indicated. The rate constant kio can be determined with precision only when к1 >> k, the large shutter‐speed regime LSSR period
2.2.1. Apparent sample or voxel compartmental properties
The experimental relaxation decay is often fitted with an empirical bi–exponential expression, with apparent fast and slowly relaxing components that are not coupled by molecular exchange, Equation 10, where: S can be a recovery time‐course signal or a multi‐pulse MR steady‐state
| (10) |
signal, S0 is the Boltzmann signal, and the apparent populations, and and are fractional recovery or longitudinal and transverse relaxation saturation factor functions (running from 1 to 0). When transverse relaxation cannot be ignored, the saturation factor functions can be complicated. These are left implicit in Equations 11 and 12,
| (11) |
| (12) |
where time is the recovery period, and α, TR, and TE are the steady‐state acquisition pulse flip angle, repetition time, and echo time, respectively. (We have presented examples of recovery2, 9 and longitudinal steady‐state7 functions.) Each apparent component is defined to have single (, ) and complicated (, ) values.
However, in the vast majority of in vivo MR experiments, there is molecular exchange (steady–state) between the populations, and this makes the situation completely different from the empirical bi–exponential description. This is true even if, to simplify the subsequent derivation, we set = = 1. (As we will see below, however, this is probably, and importantly, not true for in vivo experiments, where multipulse acquisition, with incomplete recovery, is required for imaging purposes.) For nonimaging studies of model systems, S can be measured with α = 90° and complete recovery (large TR). Thus, the longitudinal saturation components in Equations 11 and 12 can be dealt with.
With these caveats, the apparent longitudinal relaxation rate constants, R1′, and longitudinally “fully relaxed” (“unsaturated”) apparent mole fractions, p′, are expressed, in the isochronous (v Lo = v Li) BMW two‐site‐exchange (2SX) exchange Equations (13), (14), (15), (16) through (13), (14), (15), (16), as functions of the intrinsic system parameters.7, 18, 22, 23
| (13) |
| (14) |
| (15) |
| (16) |
(These equations correct typographical errors in Equations 6 and 7 of Li et al.7 The term that was printed as pi(1 – pi)/τi in Equation 6 should have been pi/[(1 – pi)τi], and the square root should have been of the Equation 7 denominator.) Each apparent parameter has contributions from both analogous intrinsic parameters.
3. RESULTS
It is very important to recognize the experimentally measured relaxation rate constants and mole fractions ( and ) are not the same as the system R1 and p values that are desired. We input the Figures 1 and 2 intrinsic parameter values into Equations (13), (14), (15), (16) to “reverse engineer” typical parameters from experiments. This is illustrated in Figures 5 and 6, where expected and values, respectively, are plotted with abscissae identical to that of Figures 1, 2, and 4. The Figure 5 ordinate is identical to that of Figure 1, while the Figure 6 ordinate is identical to the Figure 2 left ordinate. The empirical labels are given outside the right ordinates: (Equation 13) and (Equation 14) for Figure 5, and (Equation 16) and (Equation 15) for Figure 6. In Figure 1, the R1i and R1o values cross (point): R1,cross = R1i = R1o = 1.1 s−1 at [CAo] = 0.17 mM. This would be the experimental result if there was no exchange: k = 0, the no‐exchange‐limit (NXL). However, when exchange kinetics are finite this crossing is avoided (Figure 5). (See also Figure 3 of Bai et al24 and Figure 4 of Labadie et al.25) This result is a property of the “mixing” inherent in any coupled differential equations, such as those giving rise to Equations (13), (14), (15), (16).
Figure 5.
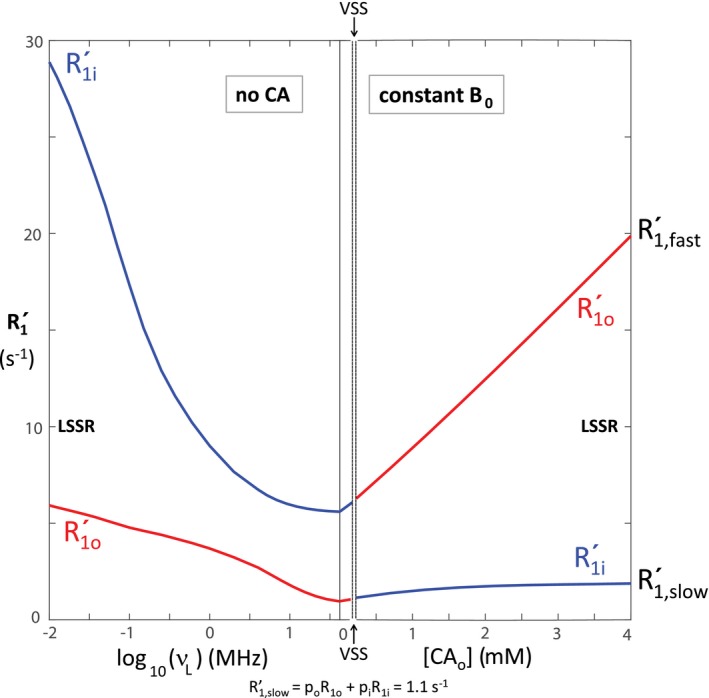
With the intrinsic parameters from Figures 1 and 2, we calculated the dependences of the expected apparent compartmental longitudinal relaxation rate constants, (, Equation 13; , Equation 14) on (left) the B 0 and (right) the [CAo]. The and rate constant segments are colored blue and red, respectively. The colors switch when the curves pass through the VSS condition. The abscissa is the same as in Figure 1, and the ordinate the same as on the left in Figure 1
Figure 6.
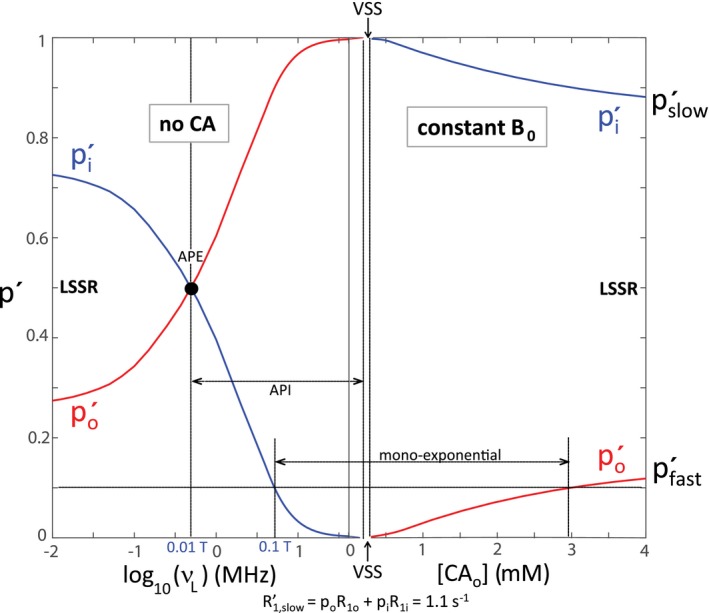
With the intrinsic parameters from Figures 1 and 2, we calculated the dependences of the expected (longitudinally) fully relaxed apparent compartmental populations, (, Equation 16; , Equation 15) on (left) the B 0 and (right) the [CAo]. The and population segments are colored blue and red, respectively. The colors switch when the curves pass through the VSS condition. The abscissa is the same as in Figure 1, and the ordinate the same as on the left in Figure 2. An apparent population equality APE point is indicated, as is the region of apparent population inversion API, along with a conservatively small monoexponential relaxation regime. Unfortunately, current clinical MRI protocols fall within this latter region: the system is constrained to the vast shutter–speed “wasteland” exhibited in Figure 4
At the smallest B 0 (0.0002 T; v L = 0.01 MHz) and largest [CAo] (4 mM) values simulated, when к1 is maximally different from k (Figure 4), the and values are just approaching the LSS limit (LSSL) condition (к1 >> k) values: = R1i + kio (28 + 1 = 29 s−1) on the left, and = R1o + koi (15 + 4 = 19 s−1) on the right; = R1o + koi (2 + 4 = 6 s−1) on the left, and = R1i + kio (1 + 1 = 2 s−1) on the right (Figure 5). However, more importantly, the p′ values (Figure 6) have clearly not yet reached the LSSL p′ values (pi = 0.8, po = 0.2) (Figure 2). For in vivo human studies, it is currently not very practical to work near the earth’s field (~0.0001 T),26 and it is essentially disallowed to achieve [CAo] of even transiently 3 mM.27 Thus, realistic clinical MR examinations are constrained to never even approach the LSSL condition. The shutter‐speed cannot be increased sufficiently.
Therefore, one must account for steady‐state trans‐cytolemmal water exchange kinetics [k] if one wishes to extract accurate system pi and po values. This has been experimentally demonstrated for myocardium,28 where po (extracellular volume fraction, ECF) is an extremely important biomarker.3 Changes in pi and po report tissue edema (a net intercompartmental water transfer) because the mean cell volume 〈V〉 = vi/ρ, where ρ is the cell (number) density (e.g., cells/μL): the relationship between vi and pi is given in Equation 4. Assuming either k = ∞ (as has frequently been done), or k = 0, is incorrect.
3.1. Relaxation exponentiality
Figure 6 is very informative. It is unproductive to consider only the empirical , , , and parameters. What are important are the intrinsic parameters with which they correlate. Because we have simulated over such a wide range, we can assign segments of the apparent curves correctly (blue for and ; red for and ). When к1 approaches zero, the faster relaxing apparent component vanishes ( → 0; Figure 3 of Bai et al,24 Figure 2 of Vétek et al29), and the experimental relaxation time‐course becomes monoexponential ( is single‐valued). When к1 is actually zero, the vanished shutter‐speed (VSS, Figures 1, 4, 5, 6) condition, R1′ is given by Equation 17.30
| (17) |
The signal arises from all the water: the kio parameter does not enter the equation, and thus is intrinsically indeterminate.
Practically speaking, however, it is hard to experimentally detect a small minority component even when it is present. We draw a horizontal line at p′ = 0.1 in Figure 6. It strikes the blue curve on the left at log v L ≅ 0.7 (v L ≅ 4.3 MHz; B 0 ≅ 0.1 T), and the red curve on the right at [CAo] ≅ 2.9 mM. Because all current human MR instruments have B 0 > 0.1 T and (as suggested above) [CAo] values > 3 mM cannot be sustained, clinical 1H2O data are constrained to exhibit apparent monoexponential longitudinal relaxation (single‐valued ). The accessible shutter speeds are too small (Figure 4): clinical MRI is trapped in a vast shutter‐speed “wasteland.” This regime indicated is conservatively small: it can be experimentally difficult to detect a minority component even with p′ somewhat greater than 0.1.
To extract kio and pi when the relaxation is effectively monoexponential, when one is in the wasteland, one must vary [CAo] (as pharmacokinetically, after a bolus injection) or – now ‐ B 0, and take advantage, to the extent possible, of the nonlinear [CAo]– or B 0‐dependence in this regime (Figure 5). Neglecting the () contribution is the most common shutter–speed (dynamic‐contrast‐enhanced) DCE–MRI version [fast‐exchange‐regime‐allowed (FXR‐a)].1, 7, 8, 17, 27, 31 One can see (Figure 6) the term is mostly vanished by the exchange effect. However, precision can be poor, and kio indeterminate in circumstances of insufficient CA extravasation, negligibly small [CAo], as in the normal‐appearing brain.3
We neglect potential non‐monoexponential contributions from vascular H2O or magnetization transfer (MT) from macromolecular 1H resonances.32 The model study systems are avascular, or effectively so. In vivo, the vascular contribution is generally limited to the initial portion of the DCE time‐course.8 Also, the low α, on–resonance RF pulse in a 3D imaging acquisition is generally not very MT sensitive.33, 34, 35
The contention that kio can never be accessed by DCE‐MRI is predicated on the supposed longitudinally fully relaxed and contributions.36 The longitudinal saturation expressions (the α, TR, , and functions of Equations 11 and 12 have been assessed (Figure S1 of Li et al31; Figure 6 of Buckley36). If not unity, these weight disproportionately relative to . (That is, they make and each less than unity, but > .) However, taking this into account and forcing data fittings with the fully longitudinally relaxed biexponential expressions (Equations (10), (11), (12), (13), (14), (15), (16) has been found to introduce unacceptable systematic errors, cause kio to become artificially indeterminate,7, 31 and sometimes to make fittings poorer.36 When the two components cannot be experimentally discriminated and separately fitted, the and B 0‐ and [CAo]‐dependences tend to counteract one another (the “avoided crossing,” Figure 5), and thus reduce kio influence (Equations 13 and 14). It seems the contribution is disproportionately (essentially exclusively) acquired. So, we consider the transverse saturation expressions (the TE, , and functions of Equations 11 and 12). In DCE, TR is often < 5 ms, so TE must be very small. Although the saturation expressions can be very complicated,33, 34, 35 an infinitely small TE is equivalent to = = 0. We have proposed, however, it is quite plausible that and are sufficiently nonzero due to magnetic susceptibility gradients.7, 31
During the bolus CA passage, there are significant paramagnetic CA concentration gradients across capillary walls and cell membranes. Plasma [CA] can exceed 5 mM immediately upon CA arrival in the tissue.27, 36 Susceptibility gradients due to such concentration differences have been shown to significantly increase R′2 values.37 The fully relaxed contribution has already been rendered much smaller than by exchange (it vanishes in the VSS condition), Figure 6. Thus, even if and are equally elevated, it is easy to imagine the fortuitous consequence that is completely saturated (“quenched”), leaving partially saturated as the meaningful component. Whatever the mechanism, considerable experimental evidence has accumulated that kio can be usefully estimated in many DCE–MRI experiments (see the Discussion section)
A truly noninvasive diffusion‐weighted imaging (DWI) analysis that does not require a CA or a shutter–speed shows considerable promise in determining kio.3 This novel DWI approach works at clinical B 0 values, seems to measure large kio values with more precision, and allows separation of the irreducible vi cell biology factors, ρ and 〈V〉. These pathology‐related properties are very important in their own right, and in discriminating the 2 Equation two terms to access xcMRNKA itself: ρ and 〈V〉 are not accessible with DCE‐MRI.3
3.2. Apparent Population Inversion
Somewhere below 0.1 T, one can begin to detect non‐monoexponential T1 relaxation caused by kio.5, 10 Figure 6 exhibits further interesting features. When the field value is small enough to observe apparent biexponential relaxation, but not yet as small as ~0.01 T, the apparent minority component does not extrapolate to the true minority component, po (red), but to the true majority component, pi (blue). Between B 0 ≅ 0.01 T and the VSS, there is an apparent population inversion (API). This has been noted previously (Figure 4 of Lee and Springer38). If one conducts only an empirical biexponential analysis (Equations (10), (11), (12) of such experimental data, one would find the minority component (blue p′ in Figure 6) has the faster relaxation (blue in Figure 5). If the apparent minority p′ value is near 0.2, as is quite likely, one would be tempted to incorrectly assign it to 1H2Oo, or any population other than H2Oi, because pi is commonly understood to be near 0.8. This is a common problem with the inappropriate application of an empirical biexponential analysis to data that do not have an intrinsic biexponential nature.39 The condition of apparent population equality (APE) (pi′ = po′ = 0.5; log v L ≅ −0.35 in Figure 6; v L = 0.43 MHz, B 0 = 0.01 T), and thus API, occurs only when the true majority component (pi here) has the faster relaxation (R1i on the left), and at the point given by Equation 18 (derived from Equations 15 and 16), where the к1 argument (argк1) is (R1i – R1o).
| (18) |
4. DISCUSSION
4.1. Why does API happen?
The curves in Figures 5 and 6 are generated from the BMW 2SX Equations (13), (14), (15), (16). On their RHSs, the shutter‐speed argument (R1i – R1o) appears in many places, and it plays a pivotal role. It is the only factor that changes sign from the left to the right of Figures 5 and 6: being positive on the left, and negative on the right. As a consequence, it is always the population with the apparent faster relaxation that vanishes as the system approaches the VSS condition (two vertical dashed lines in Figures 5 and 6), which is where argк1 changes sign. This behavior can be seen graphically in simulated (Figure 3 of Lee and Springer38) and experimental (Figure S1 of Zhang et al9) decay curves, and can be derived from Equations 15 and 16. Thus, if the VSS is approached from the left in Figure 6, by increasing B 0, it is that goes to zero. On the other hand, if the VSS is approached from the right, by decreasing [CAo], it is po′ that goes to zero. Our simulations here are all for k = 5 s−1. However, the rate of vanishing does depend on k: all other parameters held fixed, the greater the k the more shallow the vanishing.24 As a corollary, when a system passes through the VSS condition, the assignments of the apparent relaxation rate constants (s) and populations (p′s) must be switched; from blue to red and vice versa in Figure 6. This can be observed in experimental data (Figure 3 of Zhang et al40).
The deviation of an observed p′ from its corresponding inherent compartmental p does have a physical basis. There are subcompartmental spin populations with different diffusion (phase diagram)41 and/or exchange31 histories. Thus, these can have different R1 values, but surely they exist in continua.42 Given these complications, the emphasis must remain on the inherent p values, which enjoy the well‐mixed attribute, and these can be extracted only with 2SX analyses of experimental data. Furthermore, this is also the only way to determine kio with a shutter–speed experiment.
4.2. Implications
Many results indicate the new metabolic kio biomarker can be very powerful. As befitting the crucial NKA role in intermediary metabolism, kio has been reported responsive to several different metabolic alterations (Table 1). For instance, entries a, d, l, and t suggest that kio reports from ground zero of the oncogenic transformation: it may increase because of the very ion transporter up–regulation that triggers K‐Ras/rapidly accelerated fibrosarcoma kinase/mitogen‐activated protein kinase signaled uncontrolled cell proliferation.3 This suggests its potential for early cancer detection. These consequences are surely due to the cMRNKA contribution to kio(a). Because of its vital nature, cMRNKA is likely to be altered in most, if not all, pathologies. Another example is systemic multiple sclerosis.52 The Table 1 entries arising from DCE‐MRI estimation are clearly marked with a superscript #. It is important to note that entries d and t show DCE‐MRI results that have been validated with more precise ultra‐low field model experiments not subject to the DCE uncertainties.
Table 1.
kio Responsiveness to Metabolic Changes
| kio increases with: | a | Increased NKA pump expression (5,9*) |
| b | Increasing cytoplasmic ATP (9*) | |
| c | Increasing [Ko +] (at low [Ko +]), with an NKA Michaelis‐Menten signature (4,43) | |
| d | Hypoxia (10,44#) | |
| e | Cisplatin‐induced apoptosis (45) | |
| f | Xenograft tumor apoptotic regions (46#) | |
| g | Human brain metastasis radiosurgery (47#) | |
| kio decreases with: | h | Ouabain NKA pump inhibition (2,5,9*,43) |
| i | Increasing [Ko +] (at sufficient [Ko +] to cause membrane depolarization) (4) | |
| j | WZB117 glucose uptake inhibition (5) | |
| k | O2 → N2 switch (9*) | |
| l | Increasing mitochondrial reducing equivalents (6#) | |
| m | Intracellular lonidamine (48#) mitochondrial complex II inhibition (49) | |
| n | Extracellular tetrodotoxin voltage‐gated sodium channel inhibition (4) | |
| o | Extracellular AP5 plus DNQX† post‐excitatory neuronal activity inhibition (4) | |
| p | Glutamine deprivation (10) | |
| q | Hypertension in myocardium (28#) | |
| r | Chemotherapy of human breast tumors (50#) | |
| s | Phosphatase activation breast tumor therapy (51#) | |
| kio correlates with: | t | Tumor metastatic potential (5,6#) |
| u | Neuronal firing (4) | |
| v | Oxidative phosphorylation rate (52&) | |
| w | O2 consumption rate (4) | |
| x | Head and neck cancer mortality (53#) | |
| y | 18Fluoro‐2‐deoxy‐D‐glucose breast tumor uptake (54#) |
ATP, adenosine triphosphate; kio, water efflux k (1/τi); NKA, Na+,K+‐ATPase (sodium pump).
For yeast, pump is PMA1, inhibitor is ebselen.
Employed shutter‐speed (к1) dynamic‐contrast‐enhanced‐MRI.
(2R)‐Amino‐5‐phosphonovaleric acid plus 6,7‐dinitroquinoxaline‐2,3‐dione.
Indirect.
Damadian’s early ex vivo 0.6 T 1H2O MR study to discriminate malignant and normal tissue55 was cited by Lauterbur56 as part of the motivation for developing MRI.57 The fact that subsequent research showed sensitivity and specificity are insufficient for robust cancer detection has been one of the major drivers for the seemingly inexorable increase in B 0 strength (moving to the right in the figures) in clinical MRI.11, 58 So, particularly the fact that Ruggiero and co‐workers’ results (although nonimaging) were obtained at very small B 0 values, with a fast field cycling study (modest detection B 0) of an in vivo murine xenographic tumor model,5 will stimulate renewed interest in ultra–low field MRI (moving to the left in the figures). It is exciting to find AWC is the molecular process that dominates the ultra‐low field 1H2O signal.
Ruggiero and co‐workers’ finding5 that it is mainly the kio increase with malignancy that leads to decreasing provides an explanation for Damadian’s classic observation of the latter phenomenon.55 It suggests his ex vivo NMR acquisitions within five min of rat euthanasia were soon enough to retain most of the in vivo cellular ATP. Also, the increase of kio with concomitant po increase in malignancy5 is consistent with metabolic competition between cancer cells.3 The greater the cell density, ρ, the slower the NKA activity per cell.
There has been only a small amount of fast field cycling work in human studies: a recent report at 0.06 T has been published.59 However, significant efforts to produce such human‐sized instruments are under way. The same is true for “portable” low‐field scanners, with possibly B 0 < 0.1 T (Garwood MG, personal communication). 60 These could become very valuable metabolic instruments.
Figure 6 illustrates, however, that B 0 values sufficiently small to access the LSSL condition are quite unlikely to be reached. This emphasizes the importance of the BMW 2SX analysis detailed here. Otherwise, the bi–exponential relaxation results that will be obtained can be very easily miss–interpreted. This would cause quite unfortunate confusion, and actually represent a medical set–back.
ACKNOWLEDGMENTS
We thank Eric Baker, Thomas Barbara, Peter Basser, Michael Garwood, Erin Gilbert, Wei Huang, Shalom Michaeli, Martin Pike, William Rooney, Christopher Sotak, Lawrence Wald, Gregory Wilson, and Mark Woods for stimulating discussions, as well as Gangxu Han for Figure 3. X.L. and C.S.S. were supported in part by the Brenden–Colson Center for Pancreatic Care and the OHSU Advanced Imaging Research Center.
APPENDIX 1. ACRONYMS AND SYMBOLS
| APE | apparent population equality |
| API | apparent population inversion |
| ATP | adenosine triphosphate |
| 〈A/V〉 | mean cell area/volume ratio |
| AWC | active water cycling |
| α | read pulse flip angle |
| B 0 | main magnetic field |
| BMW | Bloch‐McConnell‐Woessner |
| CA | contrast agent |
| CAi | intracellular CA |
| CAo | extracellular CA |
| [CAo] | CAo concentration |
| DCE | dynamic‐contrast‐enhanced |
| DWI | diffusion‐weighted imaging |
| ECF | tissue extracellular volume fraction |
| FXL | fast‐exchange limit |
| FXR | fast‐exchange‐regime |
| fM | tissue macromolecular volume fraction |
| H2Obu | buried water |
| H2Oi | intracellular water |
| H2Oo | extracellular water |
| [H2Oi] | H2Oi concentration |
| 1H2O | water proton MR signal |
| 1H2Oi | H2Oi MR signal |
| 1H2Oo | H2Oo MR signal |
| k | steady‐state water exchange rate constant |
| kio | water efflux k (1/τi) |
| kio(a) | active kio contribution |
| kio(p) | passive kio contribution |
| koi | water influx k |
| K‐Ras | Kirsten rat sarcoma virus oncogene |
| к1 | longitudinal MR shutter‐speed (SS) |
| LSS | large SS condition (formerly, SXR) |
| LSSL | large SS limit (formerly, SXL) |
| cMRNKA | cellular NKA metabolic rate |
| MW | molecular mass |
| NKA | Na+,K+‐ATPase (sodium pump) |
| NXL | no‐exchange‐limit |
| v L | Larmor frequency (often v 0) |
| v Li | 1H2Oi v L |
| v Lo | 1H2Oo v L |
| p | tissue water mole fraction (“population”) |
| pi | intrinsic H2Oi p |
| po | intrinsic H2Oo p |
| p′ | apparent p |
| p′fast | fast‐relaxing component p′ (formerly, aS) |
| p′i | H2Oi p′ |
| p′slow | slow‐relaxing component p′ (formerly, aL) |
| p′o | H2Oo p′ |
| PMA1 | plasma membrane H+‐ATPase |
| PW | membrane water permeability coefficient |
| PW(p) | passive PW |
| R1 | longitudinal relaxation rate constant |
| R1,cross | = R1i = R1o |
| R1i | intrinsic 1H2Oi R1 |
| R1H2O | pure water R1 |
| R1o | intrinsic 1H2Oo R1 |
| R1o0 | R1o in the absence of CAo |
| R′1 | apparent, approximate single R1 value |
| R′1,fast | fast‐relaxing component R′1 (formerly, R1S) |
| R′1i | apparent R1i |
| R′1o | apparent R1o |
| R′1,slow | slow‐relaxing component R′1 (formerly, R1L) |
| R2 | transverse relaxation rate constant |
| R′2 | apparent R2 |
| R′2,fast | fast‐relaxing component R′2 |
| R′2,slow | slow‐relaxing component R′2 |
| RHS | right‐hand side |
| r1 | longitudinal relaxivity |
| r1M | macromolecular r1 |
| r1o | CAo r1 |
| ρ | cell (number) density |
| S | tissue 1H2O signal strength |
| S0 | Boltzmann S |
| S′fast | apparent fast‐relaxing saturation factor |
| S′slow | apparent slow‐relaxing saturation factor |
| SS | shutter‐speed (к1) |
| SSS | small SS condition (formerly, FXR) |
| SXL | slow‐exchange‐limit |
| SXR | slow‐exchange‐regime |
| TE | pulse sequence magnetization echo time |
| TR | pulse sequence repetition time |
| T1 | longitudinal relaxation time constant |
| T1o | intrinsic 1H2Oo T1 |
| τi | mean H2Oi molecule lifetime (1/kio) |
| τr | molecular rotational correlation time |
| 〈V〉 | mean cell volume |
| VSS | vanished SS condition (formerly, FXL) |
| v | tissue volume fraction |
| vi | intracellular v |
| vo | extracellular v (formerly, ECF) |
| 2SX | two‐site‐exchange |
Li X, Mangia S, Lee J‐H, Bai R, Springer CS Jr. NMR shutter‐speed elucidates apparent population inversion of 1H2O signals due to active transmembrane water cycling. Magn Reson Med. 2019;82:411–424. 10.1002/mrm.27725
Funding information Brenden‐Colsen Center for Pancreatic Care; Advanced Imaging Research Center
REFERENCES
- 1. Springer CS, Li X, Tudorica LA, et al. Intratumor mapping of intracellular water lifetime: metabolic images of breast cancer? NMR Biomed. 2014;27:760–773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Bai R, Springer CS, Plenz D, Basser PJ. Fast, Na+/K+ pump driven, steady‐state transcytolemmal water exchange found in neuronal tissue: a study of rat brain cortical cultures. Magn Reson Med. 2018;79:3207–3217. [DOI] [PubMed] [Google Scholar]
- 3. Springer CS. Using 1H2O to measure and map sodium pump activity in vivo. J Magn Reson. 2018;291:110–126. [DOI] [PubMed] [Google Scholar]
- 4. Bai R, Springer CS, Plenz D, Basser PJ. Brain active trans‐membrane water cycling measured by MR is associated with neuronal activity. Magn Reson Med. 2019;81:1280–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Ruggiero MR, Baroni S, Pezzana S, Ferrante G, Crich SG, Aime S. Evidence for the role of intracellular water lifetime as a tumor biomarker obtained by in vivo field‐cycling relaxometry. Angew Chem Int Ed Engl. 2018;57:7468–7472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Li LZ, Zhou R, Xu HN, et al. Quantitative magnetic resonance and optical imaging biomarkers of melanoma metastatic potential. Proc Natl Acad Sci U S A. 2009;106:6608–6613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Li X, Priest RA, Woodward WJ, et al. Cell membrane water exchange effects in prostate DCE‐MRI. J Magn Reson. 2012;218:77–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Li X, Rooney WD, Springer CS. A unified MRI pharmacokinetic theory for intravascular and extracellular contrast reagents. Magn Reson Med. 2005;54:1351–1359. [Erratum; 55, 1217 (2006)]. [DOI] [PubMed] [Google Scholar]
- 9. Zhang Y, Poirier‐Quinot M, Springer CS, Balschi JA. Active trans‐plasma membrane water cycling in yeast is revealed by NMR. Biophys J. 2011;101:2833–2842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Ruggiero MR, Baroni S, Aime S, Crich SG. Relaxometric investigations addressing the determination of intracellular water lifetime: a novel tumor biomarker of general applicability. Mol Phys. 2018. 10.1080/00268976.2018.1527045 [DOI] [Google Scholar]
- 11. Rooney WD, Johnson G, Li X, et al. The magnetic field and tissue dependences of human brain longitudinal 1H2O relaxation in vivo. Magn Reson Med. 2007;57:308–318. [DOI] [PubMed] [Google Scholar]
- 12. Rooney W, Sammi M, Grinstead J, et al. Contrast reagent detection sensitivity increases with B0: 3 T and 7 T comparisons of the human head In: Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City, Utah, 2013. Abstract 1224. [Google Scholar]
- 13. Avedano S, Botta M, Haigh JS, Longo DL, Woods M. Coupling fast water exchange to slow molecular tumbling in Gd3+ chelates: why faster is not always better. Inorg Chem. 2013;52:8436–8450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Andrew ER, Bydder G, Griffiths J, Iles R, Styles P. Principles of magnetic resonance imaging In: Clinical Magnetic Resonance: Imaging and Spectroscopy. Chichester: John Wiley & Sons; 1990:36. [Google Scholar]
- 15. Ball P. Water is an active matrix of life for cell and molecular biology. Proc Natl Acad Sci U S A. 2017;114:13327–13335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Persson E, Halle B. Cell water dynamics on multiple time scales. Proc Natl Acad Sci U S A. 2008;105:6266–6271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Li X, Cai Y, Moloney B, et al. Relative sensitivities of DCE‐MRI pharmacokinetic parameters to arterial input function (AIF) scaling. J Magn Reson. 2016;269:104–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Landis CS, Li X, Telang FW, et al. Equilibrium transcytolemmal water exchange kinetics in skeletal muscle in vivo. Magn Reson Med. 1999;42:467–478. [DOI] [PubMed] [Google Scholar]
- 19. Persson F, Halle B. Transient access to the protein interior: simulation versus NMR. J Am Chem Soc. 2013;135:8735–8748. [DOI] [PubMed] [Google Scholar]
- 20. Sehy JV, Banks AA, Ackerman JJH, Neil JJ. Importance of intracellular water apparent diffusion to the measurement of membrane permeability. Biophys J. 2002;83:2856–2863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Tzur A, Kafri R, LeBleu VS, Lahav G, Kirschner MW. Cell growth and size homeostasis in proliferating animal cells. Science. 2009;325:167–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. McConnell HM. Reaction rates by nuclear magnetic resonance. J Chem Phys. 1958;28:430–431. [Google Scholar]
- 23. Woessner DE. Nuclear transfer effects in nuclear magnetic resonance pulse experiments. J Chem Phys. 1961;35:41–48. [Google Scholar]
- 24. Bai R, Springer CS, Basser PJ. The vanishing shutter‐speed limit In: Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, Hawaii, 2017. Abstract 1918. [Google Scholar]
- 25. Labadie C, Lee J‐H, Vétek G, Springer CS. Relaxographic imaging. J Magn Reson B. 1994;105:99–112. [DOI] [PubMed] [Google Scholar]
- 26. Lee SK, Möβle M, Myers W, et al. SQUID‐detected MRI at 132 μT with T1–weighted contrast established at 10 μT to 300 mT. Magn Reson Med. 2005;53:9–14. [DOI] [PubMed] [Google Scholar]
- 27. Landis CS, Li X, Telang FW, et al. Determination of the MRI contrast agent concentration time course in vivo following bolus injection: effect of equilibrium transcytolemmal water exchange. Magn Reson Med. 2000;44:563–574. [DOI] [PubMed] [Google Scholar]
- 28. Coelho‐Filho OR, Mongeon F‐P, Mitchell R, et al. Role of transcytolemmal water‐exchange in magnetic resonance measurements of diffuse myocardial fibrosis in hypertensive heart disease. Circ Cardiovasc Imaging. 2013;6:134–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Vétek G, Sammi MK, Lee J‐H, Springer CS. Equilibrium exchange effects in relaxographic imaging: quantitative analysis In: Proceedings of the 4th Annual Meeting of ISMRM, New York, New York, 1996. Abstract 1560. [Google Scholar]
- 30. Wilson GJ, Woods M, Springer CS, Bastawrous S, Bhargava P, Maki JH. Human whole‐blood 1H2O longitudinal relaxation with normal and high‐relaxivity contrast reagents: influence of trans‐cell‐membrane water exchange. Magn Reson Med. 2014;72:1746–1754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Li X, Huang W, Morris EA, et al. Dynamic NMR effects in breast cancer dynamic‐contrast‐enhanced MRI. Proc Natl Acad Sci U S A. 2008;105:17937–17942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Prantner AM, Bretthorst GL, Neil JJ, Garbow JR, Ackerman JJH. Magnetization transfer induced biexponential relaxation. Magn Reson Med. 2008;60:555–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Murase K. Generalized equation for describing the magnetization in spoiled gradient‐echo imaging. Magn Reson Imaging. 2011;29:723–730. [DOI] [PubMed] [Google Scholar]
- 34. Springer F, Steidle G, Martirosian P, Claussen CD, Schick F. Effects of in‐pulse transverse relaxation in 3D ultrashort echo time sequences: analytical derivation, comparison to numerical simulation and experimental application at 3 T. J Magn Reson. 2010;206:88–96. [DOI] [PubMed] [Google Scholar]
- 35. Ou X, Gochberg DF. MT effects and T1 quantification in single‐slice spoiled gradient echo imaging. Magn Reson Med. 2008;59:835–845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Buckley DL. Shutter‐speed dynamic contrast‐enhanced MRI: is it fit for purpose? Magn Reson Med. 2019;81:976–988. [DOI] [PubMed] [Google Scholar]
- 37. Wilson GJ, Springer CS, Bastawrous S, Maki JH. Human whole blood 1H2O transverse relaxation with gadolinium‐based contrast reagents: magnetic susceptibility and transmembrane water exchange. Magn Reson Med. 2017;77:2015–2027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Lee J‐H, Springer CS. The effects of equilibrium exchange on diffusion‐weighted NMR signals: the diffusigraphic ‘shutter‐speed’. Magn Reson Med. 2003;49:450–458. [Erratum; 51, 222 (2004)]. [DOI] [PubMed] [Google Scholar]
- 39. Mulkern RV, Balasubramanian M, Maier SE. On the perils of multiexponential fitting of diffusion MR data. J Magn Reson Imaging. 2017;45:1545–1547. [DOI] [PubMed] [Google Scholar]
- 40. Zhang Y, Poirer‐Quinot M, Springer CS, Balschi JA. Discrimination of intra‐ and extracellular 23Na+ signals in yeast cell suspensions using longitudinal magnetic resonance relaxography. J Magn Reson. 2010;205:28–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Hürlimann MD, Helmer KG, de Swiet TM, Sen PN, Sotak CH. Spin echoes in a constant gradient and in the presence of simple restriction. J Magn Reson A. 1995;113:260–264. [Google Scholar]
- 42. Sukstanskii AL, Ackerman JJH, Yablonskiy DA. Effects of barrier‐induced nuclear spin magnetization inhomogeneities on diffusion‐attenuated MR signal. Magn Reson Med. 2003;50:735–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Zhang Y, Balschi JA. Water exchange kinetics in the isolated heart with Na+/K+ ATPase activity: potentially high spatiotemporal resolution in vivo MR access to cellular metabolic activity In: Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City, Utah, 2013. Abstract 4045. [Google Scholar]
- 44. Koch CJ, Jenkins WT, Jenkins KW, et al. Mechanisms of blood flow and hypoxia production in rat 9L‐epigastric tumors. Tumor Microenviron Ther. 2013;1:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Bailey C, Giles A, Czarnota GJ, Stanisz GJ. Detection of apoptotic cell death in vitro in the presence of Gd‐DTPA‐BMA. Magn Reson Med. 2009;62:46–55. [DOI] [PubMed] [Google Scholar]
- 46. Bailey C, Moosvi F, Stanisz GJ. Mapping water exchange rates in rat tumor xenografts using the late‐stage uptake following the bolus injections of contrast agent. Magn Reson Med. 2014;71:1874–1887. [DOI] [PubMed] [Google Scholar]
- 47. Mehrabian H, Desmond KL, Chavez S, et al. Water exchange rate constant as a biomarker of treatment efficacy in patients with brain metastases undergoing stereotactic radiosurgery. Int J Radiat Oncol Biol Phys. 2017;98:47–55. [DOI] [PubMed] [Google Scholar]
- 48. Nath K, Paudyal R, Nelson DS, et al. Acute changes in cellular‐interstitial water exchange rate in DB‐1 melanoma xeongrafts after lonidamine admistration as a marker of tumor energetics and ion transport In: Proceedings of the 22nd Annual Meeting of ISMRM, Milan, Italy, 2014. Abstract 2757. [Google Scholar]
- 49. Guo L, Shestov AA, Worth AJ, et al. Inhibition of mitochondrial complex II by the anticancer agent lonidamine. J Biol Chem. 2016;291:42–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Tudorica A, Oh KY, Chui SY‐C, et al. prediction and evaluation of breast cancer response to neoadjuvant chemotherapy using quantitative DCE‐MRI. Transl Oncol. 2015;9:8–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Springer CS, Li X, Jayatilake ML, et al. Metabolic imaging of early tumor therapy In: Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Canada, 2015. Abstract 3860. [Google Scholar]
- 52. Rooney WD, Li X, Sammi MK, Bourdette DN, Neuwelt EA, Springer CS. Mapping human brain capillary water lifetime: high‐resolution metabolic neuroimaging. NMR Biomed. 2015;28:607–623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Chawla S, Loevner LA, Kim SG, et al. Dynamic contrast‐enhanced MRI‐derived intracellular water lifetime (τi): a prognostic marker for patients with head and neck squamous cell carcinomas. Am J Neuroradiol. 2018;39:138–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Inglese M, Cavaliere C, Monti S, et al. A multi‐parametric PET/MRI study of breast cancer: evaluation of DCE‐MRI pharmacokinetic models and correlation with diffusion and functional parameters. NMR Biomed. 2018;e4026. [DOI] [PubMed] [Google Scholar]
- 55. Damadian R. Tumor detection by nuclear magnetic resonance. Science. 1971;171:1151–1153. [DOI] [PubMed] [Google Scholar]
- 56. Lauterbur PC. One path out of many – how MRI actually began. Encly NMR. 1996;1:445–449. [Google Scholar]
- 57. Lauterbur PC. Image formation by induced local interactions: examples employing nuclear magnetic resonance. Nature. 1973;242:190–191. [PubMed] [Google Scholar]
- 58. Budinger TF, Bird MD, Frydman L, et al. Toward 20 magnetic resonance for human brain studies: opportunities for discovery and neuroscience rationale. MAGMA. 2016;29:617–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Ross PJ, Broche LM, Lurie DJ. Rapid field‐cycling MRI using fast spin‐echo. Magn Reson Med. 2015;73:1120–1124. [DOI] [PubMed] [Google Scholar]
- 60. McDaniel PC, Cooley CZ, Stockmann JP, Wald LL. A 6.3 kg single‐sided magnet for 3D, point‐of‐care brain imaging In: Proceedings of the 26th Annual Meeting of ISMRM, Paris, France, 2018. Abstract 943. [Google Scholar]


