Weak Pnictogen Bond with Bismuth: Experimental Evidence Based on Bi−P Through‐Space Coupling

Abstract

To study pnictogen bonding involving bismuth, flexible accordion‐like molecular complexes of the composition [P(C₆H₄‐o‐CH₂SCH₃)₃BiX₃], (X=Cl, Br, I) have been synthesised and characterised. The strength of the weak and mainly electrostatic interaction between the Bi and P centres strongly depends on the character of the halogen substituent on bismuth, which is confirmed by single‐crystal X‐ray diffraction analyses, DFT and ab initio computations. Significantly, ²⁰⁹Bi–³¹P through‐space coupling (J=2560 Hz) is observed in solid‐state ³¹P NMR spectra, which is so far unprecedented in the literature, delivering direct information on the magnitude of this pnictogen interaction.

Weak interactions are elementary bonding forces, which have an impact on the structure of molecular assemblies. The properties of materials strongly depend on the strength and orientation of noncovalent interactions; thus, a fundamental understanding of their nature is essential for the design of new molecular assemblies with bespoke physical and chemical properties.1 Besides the well‐known hydrogen bonding, more recently the concepts of other “element‐specific” interactions such as triel,2 tetrel,3 pnictogen,4 chalcogen,5 halogen6 and aerogen7 bonding for group 13–18 elements, respectively, have been established. Although interactions between pnictogen centres had been observed much earlier, some pioneering works at the beginning of this decade,4, 8 initiated a vivid scientific discussion on the theoretical aspects of pnictogen bonding. Analogously to the definition of a halogen bond,9 a pnictogen bond is defined as a weak, attractive interaction between the electrophilic region of a pnictogen atom (termed as pnictogen bond donor) and a Lewis base (termed as pnictogen bond acceptor, which is not necessarily another pnictogen centre).10 Because the strength of pnictogen interactions can be comparable to that of hydrogen bonds,11 pnictogen bonding can be envisioned to be a potential linking motif in molecular assemblies.8 Very recently the idea of employing pnictogen bonds in organocatalysis arose12 and was successfully realised experimentally.13

A plethora of computational studies have revealed two main interactions, that contribute to pnictogen bonds (besides minor effects such as dispersion forces): 1) The electrostatic interaction, whereby the lone pair of a Lewis base (the pnictogen bond acceptor) interacts with the positively charged belt around the lone pair of a pnictogen, is considered to make the leading contribution. Due to this anisotropic electron density distribution around the pnictogen centre the pnictogen bond belongs to the so‐called σ‐hole interactions.14 2) To a lesser extent, charge transfer also contributes to the pnictogen bonding: the lone pair of a Lewis base donates electron density into the σ*(Pn−X) antibonding orbitals at the pnictogen Pn.4, 8a, 15

In contrast to the large number of theoretical studies that have been disclosed, experimental investigations on pnictogen bonding are mainly limited to single‐crystal X‐ray studies.16, 17 Notably, only a few spectroscopic investigations have been reported8b, 13a, 18 even though methods such as NMR spectroscopy are ideally suited for gaining fundamental understanding of pnictogen bonding. However, minor changes in chemical shifts may only be expected due to the weak nature of these interactions. In contrast, coupling patterns and spin–spin coupling constants derived therefrom can be very meaningful; however, their observation is usually limited to systems with spin I=$1/2$ nuclei whereas coupling to quadrupolar nuclei (I>$1/2$ ) is seen comparatively rarely due to fast relaxation.

Here, we present our experimental and theoretical studies on pnictogen interaction in a series of accordion‐like, bridged compounds 2 a–c shown in Scheme 1, which were designed based on the following considerations: Phosphorus and bismuth were chosen as bridge‐head atoms and in our hypothesis the linkers are flexible enough to allow electronic communication between the pnictogens. On one hand, phosphorus has outstanding NMR properties among the pnictogens and may act as a pnictogen bond acceptor (electron pair donor). On the other hand, the strongest pnictogen interaction is expected for bismuth (due to its largest polarisability), and its electronic properties may be tuned by the halogen substituents.

Scheme 1.

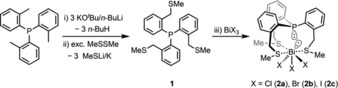
Synthesis of ligand 1 and compounds 2 a–c. i) hexane, rt; ii) toluene, −78 °C; iii) toluene (2 a,b)/THF (2 c), rt.

To obtain the target molecules, we first developed a facile and reproducible two‐step synthetic protocol for the preparation of the tris‐γ‐substituted thioether phosphine 1 (P(C₆H₄‐o‐CH₂SCH₃)₃, Scheme 1) as the central building block.19 This involves metallation of the commercially available tris(o‐tolyl)phosphine with Schlosser's base20 and subsequent reaction with dimethyl disulfide. Compound 1 (³¹P δ=−36.8 ppm) can be isolated as a colourless solid in moderate yield (36 %).

We attempted to synthesise the 1:1 complexes of 1 with all the four bismuth trihalides (BiX₃, X=F, Cl, Br, I). The reaction of compound 1 with bismuth trichloride or tribromide in toluene delivers adducts 2 a or 2 b, respectively, as bright yellow precipitates (soluble in acetonitrile, slightly soluble in chloroform and benzene and insoluble in hexane) (Scheme 1). Due to the low solubility of bismuth triiodide, the analogous dark‐red iodo complex 2 c was synthesised using THF as solvent. All the three complexes 2 a–c were isolated in good yields and characterised by multinuclear NMR‐spectroscopy, elemental analysis and single‐crystal X‐ray diffraction studies (vide infra). In contrast, we could not synthesise the analogous adduct with bismuth trifluoride despite varying reaction conditions (THF or acetonitrile as solvent, prolonged reaction times, elevated temperatures), presumably due to the low solubility of bismuth trifluoride.21

The connectivity of molecules 2 was proven by X‐ray crystallography on single crystals obtained from saturated solutions of the compounds in acetonitrile (Figure 1).

Figure 1.

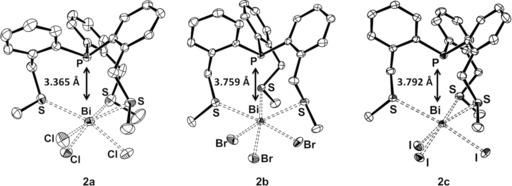
ORTEP plots of 2 a, 2 b and 2 c (thermal ellipsoids are drawn at 50 % probability). Hydrogen atoms have been omitted for clarity. Selected atomic distances (Å): 2 a: P−Bi 3.365(1), Bi−S1 3.106(1), Bi−S2 3.075(2), Bi−S3 3.076(1), Bi−Cl1 2.572(2), Bi−Cl2 2.547(1), Bi−Cl3 2.574(1); 2 b: P−Bi 3.759(7), Bi−S1 3.047(9), Bi−S2 3.088(8), Bi−S3 3.079(8), Bi−Br1 2.700(4), Bi−Br2 2.712(4), Bi−Br3 2.680(4); 2 c: P−Bi 3.792(9), Bi−S1 3.074(8), Bi−S2 3.136(8), Bi−S3 3.130(8), Bi−I1 2.911(3), Bi−I2 2.923(3), Bi−I3 2.893(3).

The three molecular complexes 2 a–c are isostructural and exhibit bridged [4.4.4] structures, which locate the P and Bi atoms in the bridgehead positions. Based on the symmetry of the free ligand 1 (C ₃) and the bismuth trihalides (C _3v) one might also expect a C₃ axis for complexes 2 a–c. However, some asymmetry is visible in the Bi−X and the Bi−S bond lengths in 2 a–c. For example in the case of 2 a the lengths of two Bi−Cl bonds are rather similar (2.574(1) Å and 2.572(2) Å) but different from that of the third one (2.547(1) Å). A similar phenomenon is observable in the case of the Bi−S bonds (e.g., 3.076(1) Å and 3.075(2) Å vs. 3.106(1) Å for 2 a). The effect of asymmetry is even more pronounced in the S‐Bi‐S bond angles, especially in 2 a: one of the S‐Bi‐S bond angles (133.1°) is significantly larger than the other two (82.4°, 104.0°), which lie relatively close to the ideal 90° of an octahedral arrangement (see Figure S18, Supporting Information). Thus, the bismuth centres are in an asymmetric, distorted octahedral coordination sphere (particularly in 2 a) and the distortion from an ideal C₃ symmetry can be rationalised by the presence of a stereochemically active lone pair at the bismuth centre (vide infra). In contrast, the phosphorus centres reside in a nearly symmetric pyramidal geometry (e.g., C‐P‐C angles in 2 a: 105.0°, 101.8°, 105.6°).

The Bi−X bonds in 2 a–c are significantly longer than those in the corresponding uncomplexed bismuth trihalides BiX₃ (e.g., for 2 a d(Bi−Cl_average)=2.56(1) Å vs. 2.42(1) Å measured for the BiCl₃ monomer in the gas phase),22 while the Bi−S distances in 2 a–2 c are comparable to those in the coordination complex [Bi₂I₈(SMe₂)₂]²⁻ (3.054(8) Å).23

Significantly, comparing the complexes of the different bismuth halides, the distance between the bridgehead atoms P and Bi increases from 3.365(1) Å in 2 a to 3.759(7) Å in 2 b and 3.792(9) Å in 2 c. Note that the P−Bi distance of 2 b resembles 2 c more than that of 2 a, something likely to result from 2 b and 2 c crystallising in the same space group C2/c, which is different from that of 2 a (P2₁/c). The increasing order of the P−Bi distances is also observed on structures optimised in the gas phase (vide infra); thus, we conclude that these structural changes are not simply due to crystal packing effects. This clearly indicates the proposed flexibility of the linkers (accordion‐like behaviour), which allows a rather large change in the position of the bridgehead atoms. The P−Bi atomic distances in 2 a–c (especially in 2 a) are smaller than the sum of van der Waals radii of these elements (3.87 Å)24 denoting a secondary interaction. Importantly, as the P−Bi distance gradually decreases across the series 2 c>2 b>2 a, the attractive pnictogen interaction influenced by the nature of the halogen increases in the same direction.

Further insights into pnictogen interactions can be gained from solution and solid‐state ³¹P NMR spectroscopy. The solution ³¹P NMR spectra of complexes 2 a–c in C₆D₆ exhibit broad singlet resonances at −37.0, −38.7 and −39.2 ppm for 2 a, 2 b and 2 c, respectively, which show no temperature dependency. The significant line broadening observed for complexes 2 (W _1/2 >30 Hz in contrast to the sharp singlet resonance of 1, W _1/2 ≈3 Hz) again hints at a weak interaction between the ³¹P and the quadrupolar ²⁰⁹Bi nuclei. The chemical shifts of 2 a–c lie at lower frequency compared to that of the free ligand 1 (indicating that the P is a pnictogen bond acceptor), which is consistent with a recent NMR study on P⋅⋅⋅I interactions, involving triphenyl phosphane acting as a halogen bond acceptor.25 The deshielding effect of the increasing pnictogen interaction going from 2 c towards 2 a is indicated by a slight shift of the resonances to higher frequencies.

While the ³¹P solution NMR spectra deliver only limited information on the bonding situation, more insight can be gained by ³¹P NMR spectroscopic experiments on solid‐state samples (note that conclusive ²⁰⁹Bi MAS solid‐state NMR spectra could not be obtained due to extreme line broadening, probably due to the low symmetry of the compounds).26 Complexes 2 a–c were analysed at three different temperatures (256, 298 and 323 K) by CP‐MAS solid‐state ³¹P NMR spectroscopy. At room temperature, the three spectra (Figure 2) exhibit broad resonances centred at similar chemical shifts (−35.5 ppm (2 a), −37.5 ppm (2 b) and −37.0 ppm (2 c)) to those determined for the solution spectra. Whereas in solution all three spectra show singlet resonances, in the solid‐state spectra only the spectrum of 2 c displays a singlet peak with a remarkably large signal width (W=42 ppm). In contrast, the line shapes of the signals of 2 a and 2 b do not resemble simple Gaussian type functions corresponding to a singlet resonance, but rather a broadband shape likely consisting of several overlapping components.

Figure 2.

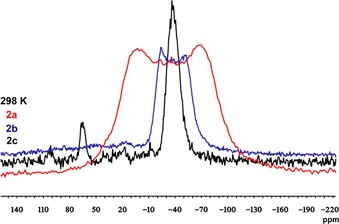
³¹P CP‐MAS NMR spectra of solid samples of 2 a (red), 2 b (blue) and 2 c (black) measured at 298 K with a spin rate of 10 kHz (2 a) and 6 kHz (2 b, 2 c). Compound 2 c contains an impurity at 65 ppm.

To shed light on the origin of the unusual appearance and large line width of the band corresponding to 2 a, we performed variable temperature solid‐state NMR spectroscopic studies (Figure 3). Whereas the increase in temperature (323 K) only causes a collapse of the original signal to a very broad singlet (W≈200 ppm), at lower temperature (256 K) a well‐resolved signal with ten approximately equidistant lines is visible in the spectrum. This dectet is consistent with the coupling of the ³¹P nucleus with the ²⁰⁹Bi nucleus (I=9/2, 100 % natural abundance) and a coupling constant of J=2560 Hz can be measured.27 Note that the same value is obtained at different magnetic field strengths as well as differing spinning rates. Remarkably, this is the first experimental evidence for a ²⁰⁹Bi–³¹P spin–spin coupling. According to the literature, coupling to ²⁰⁹Bi nuclei is observed extremely rarely. To the best of our knowledge the only reported spin–spin coupling constants between ²⁰⁹Bi and any nuclei are restricted to the highly symmetric [BiF₆]⁻ and [Bi(OTeF₅)₆]⁻ anions (one‐bond ²⁰⁹Bi–¹⁹F and two‐bond ²⁰⁹Bi–¹²⁵Te J coupling, respectively).28

Figure 3.

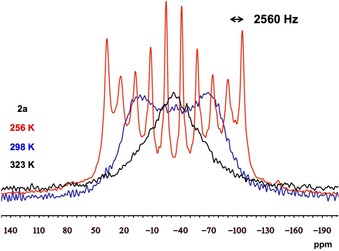
³¹P CP‐MAS NMR spectra of a solid sample of 2 a measured at 256 K (red), 298 K (blue) and 323 K (black) with spin rates of 6 kHz (256 K and 323 K) and 10 kHz (298 K), respectively. Acquired with a recycle delay of 60 s and 4 ms contact time.

In contrast to these clearly through‐bond couplings, the coupling pattern shown in Figure 3 is the result of a non‐covalent through‐space pnictogen interaction. Even though through‐space coupling is not rare,29 this is the first example with a ²⁰⁹Bi nucleus. For complexes 2 b and 2 c it was not possible to find appropriate experimental conditions (by systematically changing parameters such as temperature, magnetic field strength and spinning rate of the samples) to detect resolved multiplet signals and thus coupling constants could not be obtained. However, the width of the band shape significantly increases in the direction of 2 c→2 b→2 a (2.9, 3.8 and 9.6 kHz, respectively). We anticipate that similar through‐space coupling also exists in the case of 2 b and 2 c and the bandwidth can be used as an indicator for this interaction. Hence, the increase in the band width in the order 2 c<2 b<2 a reflects that the interaction between the two pnictogens strengthens in the same order.30

To gain insight into the nature of the interaction between the bridgehead atoms verified by X‐ray crystallography and solid‐state NMR spectroscopy, DFT and ab initio calculations have been performed. As the weak interactions play an important role, we have chosen methods that take dispersion effects into account, such as ωB97XD, B3LYPD3 and second‐order Møller–Plessett perturbational method (MP2) in combination with the cc‐pVDZ basis set, including pseudo potential (‐PP) for the heavier atoms (for details see the Supporting Information).

In agreement with the crystallographic results (vide supra), the gas‐phase optimised structures of 2 a–c show a distortion away from an ideal C₃ symmetry due to the presence of a stereochemically active lone pair at the Bi centres (see HOMO of 2 a in Figure 4).

Figure 4.

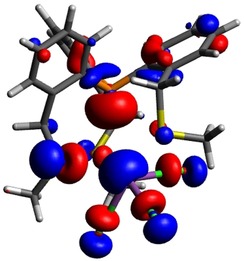
HOMO of 2 a at a contour value of 0.040 a.u. at the ωB97XD/cc‐pVDZ(‐PP) level of theory.

The calculated geometrical parameters are very similar in the case of the DFT methods; however, compared to these the MP2 calculations predict somewhat shorter distances for the weak interactions, but still show the same tendencies. In the following, we discuss the results at the ωB97XD/cc‐pVDZ(‐PP) level, which are broadly similar to the ones obtained experimentally in the solid state. The largest discrepancies are seen for the Bi−P distances: As discussed above, in the solid state d(Bi−P) of 2 b (3.759(7) Å) is closer to that of 2 c (3.792(9) Å) than that of 2 a (3.365(1) Å), whereas the gas‐phase calculations show a more balanced distribution of these atomic distances (3.576 Å (2 a), 3.631 Å (2 b), 3.732 Å (2 c)). We attribute these deviations to the different phases in the calculations and the experiments: whereas in the gas phase a single molecule is calculated, in the solid state the crystal packing also influences these weak interactions.

We estimated the total interaction energies of the Bi−P and Bi−S pairs from complex formation energies of 2 a–c and model complexes (Table 1, for more details see the Supporting Information). The energy of the Bi−P interaction increases in the order of 2 c (7.1 kcal mol⁻¹) <2 b (8.0 kcal mol⁻¹) <2 a (8.8 kcal mol⁻¹), and these values are somewhat larger than that of an average Bi−S interaction (6.3–6.5 kcal mol⁻¹). As usually two interactions (electrostatic and charge transfer (donor–acceptor)) contribute to the pnictogen bonding, we performed further investigations to clarify which of the two plays a more important role here. Because it is more difficult to obtain quantitative information on the electrostatic contributions, in the following we first search for evidences of charge transfer interactions based on natural bonding orbital (NBO) analysis.

Table 1.

Experimental and calculated Bi−P atomic distances (d, Å), interaction energy of the Bi−P interaction (ΔE _int, kcal mol⁻¹), Wiberg bond indices (WBI, −), NPA charges (q, electron) and net charge donation from the ligand to the BiX₃ moiety (Δq calculated as the sum of partial NPA charges in the ligand fragment) at the ωB97XD/cc‐pVDZ(‐PP) level of theory. The partial NPA charge at the P centre in the free ligand 1 is 0.833 e. Properties at the bond critical point: electron density (ρ _bcp, a.u.), Laplacian of the electron density (▿² ρ _bcp, a.u.), η=|λ ₁|/λ ₃ where λ ₁ and λ ₃ are the smallest and largest eigenvalues of the electron density Hessian matrix, respectively, total energy density (H, a.u.), ratio of potential and kinetic energy density (|V|/G, −).

	2 a	2 b	2 c
d(Bi−P)exp	3.365(1)	3.759(7)	3.792(9)
d(Bi−P)calc	3.576	3.631	3.732
ΔE int	8.8	8.0	7.1
WBI (Bi−P)	0.085	0.077	0.062
q(P)	0.838	0.840	0.839
q(Bi)	1.360	1.146	0.847
Δq	0.326	0.332	0.306
ρ bcp	0.0131	0.0121	0.0103
▿2 ρ bcp	0.0267	0.0244	0.0207
η	0.191	0.188	0.182
H	6.2×10−4	6.5×10−4	6.4×10−4
|V|/G	0.897	0.881	0.859

To measure the covalent character of a bond, Wiberg bond indices (WBIs) have been obtained, which correlate with the optimised atomic distances (Table 1 and SI). The WBIs (and bond lengths) of the Bi−S bonds in 2 a–c show no significant differences or trends; however, the Bi−P WBIs clearly indicate the increasing interaction in the direction of 2 c→2 b→2 a. Note that even the largest WBI of a Bi−P interaction (0.09 for 2 a) is substantially smaller than that of a Bi−S bond (0.14–0.16), indicating that the Bi−P interactions in 2 a–c have a much smaller covalent character than the Bi−S bonds. Because the Bi−X bonds significantly elongate (and weaken according to the WBIs) upon complexation in all the three complexes 2 a–c, donor–acceptor interactions from the lone pairs of the S and/or P atoms into the antibonding σ*(Bi−X) orbitals have to be taken into account.31 To find the origin of the bond elongation, natural population analyses (NPA) have been carried out. The net charge donation from the ligand to the BiX₃ moiety (Δq) is very similar in the three complexes 2 a–c and amounts to approximately 0.32 e. In 2 a–c the sulfur centres are by 0.04–0.05 e more positively charged compared to those in the free ligand (see Table S9 in the Supporting Information), indicating significant charge transfer from the sulfur lone pairs.32 In contrast, the partial charge on the P atoms is very similar in the free ligand and in the complexes 2 a–c, which means that the charge transfer from the P lone pair is negligible.33

As the WBIs and NPA analyses demonstrate that the donor–acceptor contribution in the Bi−P interaction is not too significant in complexes 2 a–c (especially much less compared to the Bi−S interactions), it is proposed that this interaction is mainly electrostatic in nature. This is supported by the partial charges at the Bi in complexes 2 a–c, which substantially increase in the direction 2 c (0.847 e) <2 b (1.146 e) <2 a (1.360 e), whereas the charge at the P remains unchanged (see Table 1). Thus, the Coulombic attraction between the Bi centres and the P lone pairs grows in the order 2 c<2 b<2 a, which is consistent with the increasing ionic character of the Bi−X bonds due to the increasing electronegativity of the halogen.

The presence of an attractive interaction between the Bi and P centres was proven by atoms in molecules (AIM) analysis34 of the calculated electron density: a bond critical point between the Bi and P nuclei with a moderate electron density was detected in each of the three compounds 2 a–c and no cage critical point was found (Figure 5). The electron density values at these bond critical points show a reversed trend to the atomic distances d(Bi−P) (Table 1).

Figure 5.

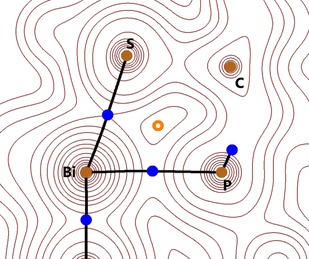
Atoms in molecules (AIM) contour plot of 2 a in one of the Bi/S/P planes at the ωB97XD/cc‐pVDZ(‐PP) level of theory. Brown and blue dots denote nuclei (3, +3) and bond critical points (3, −1), respectively. The ring critical point (3, +1) is marked with an orange circle.

Further analysis of the electron density can deliver information about the shared shell (covalent) or closed shell (van der Waals or ionic) nature of the interaction. The Laplacian of the electron density is negative for covalent bonds and positive for noncovalent interactions, therefore the positive values for the Bi−P interactions in 2 a–c suggest dominant closed‐shell interactions. Similarly, the η parameter (η=|λ ₁|/λ ₃, where λ ₁ and λ ₃ are the smallest and largest eigenvalues of the electron density Hessian matrix) is clearly smaller than unity (around 0.2), showing another indication of noncovalent interactions. The sign of the total electronic energy density H, the sum of the kinetic and the potential energy density (G and V, respectively), can distinguish between shared shell and closed shell interactions. In noncovalent bonds, the kinetic energy overcompensates the potential energy resulting in an H value larger than zero and consequently the |V|/G ratio is smaller than unity. These characteristics at the bond critical points between the Bi and P atoms in 2 a–c (H>0, |V|/G=0.86 to 0.90) again indicate the chiefly noncovalent nature of these interactions. These findings were further corroborated by NCI (noncovalent interaction) analyses,35 which shows an attractive weakly bonding domain between the P and Bi atoms (see Figure S22 in the Supporting Information).

To gain insight into the nature of the coupling between P and Bi, we simulated the coupling constants J(²⁰⁹Bi–³¹P) for 2 a–c in the gas phase at the PBE1/TZ2P level with scalar ZORA approximation. The Fermi contact (FC), the diamagnetic spin‐orbit (DSO) and the paramagnetic spin‐orbit (PSO) terms were separately calculated; furthermore, the sums of spin‐dipolar contributions (SD) and cross terms were also obtained (see Table 2).

Table 2.

Calculated P−Bi coupling constant J(²⁰⁹Bi–³¹P) contributions for 2 a–c (Hz).

	2 a	2 b	2 c
FC	1301.7	1147.7	906.6
DSO	0.1	0.1	0.2
PSO	−0.6	−0.3	0.0
SD+cross terms	2.6	1.9	0.8
Total	1303.8	1149.4	907.6

Although the calculated J(²⁰⁹Bi–³¹P) coupling constant (1303.8 Hz) deviates substantially from the experimentally obtained one (J=2560 Hz), the tendency observed for the decreasing bandwidths going in the direction 2 a to 2 c are reproduced by the computations. Note that the precise estimation of indirect spin–spin coupling constants is especially challenging for weak interactions and heavy elements; furthermore, the calculations were performed in the gas phase, whereas the experimental coupling constant value of 2 a was measured by solid‐state NMR spectroscopy. Based on the different terms, the Fermi contact is by far the largest contribution to the total coupling and the DSO, PSO and SD terms are practically negligible.

Thorough theoretical studies on through‐space ¹⁹F–¹⁹F coupling mechanisms have outlined that the through‐space couplings are transferred by a large Fermi contact term with a positive sign, whereas for the through‐bond couplings significant PSO and SD contributions are characteristic.36 As the J(²⁰⁹Bi–³¹P) coupling constants in 2 a–c are ruled by the Fermi contact term and the PSO and SD contributions are insignificant, this coupling mechanism is through‐space in nature, in accord with the Mallory‐type lone pair overlap theory reported for ¹⁹F–¹⁹F, ¹⁹F–¹⁵N and ³¹P–³¹P through‐space couplings.37 The s‐character of the P and Bi lone pairs in compounds 2 a–c is very similar (approximately P: 55 %, Bi: 97 %), however, the overlap of the two lone pairs depends on the distance between the two atoms, which is clearly determined by the strength of the pnictogen interaction.38

In conclusion, we have developed accordion‐like compounds with flexible skeletons to study bismuth as a pnictogen bond donor. Employing X‐ray crystallography and theoretical calculations, we have verified the existence of a secondary interaction between the two pnictogens P and Bi. Quantum chemical calculations (NBO, AIM and NCI analyses) show that this interaction is mainly electrostatic in nature and that its strength can be tuned through variation of the halogen substituents on the bismuth. Remarkably, using solid‐state ³¹P NMR spectroscopy, we have discovered indirect spin–spin coupling between the P and Bi centres, which is a direct manifestation of pnictogen interaction. The coupling mechanism was studied by DFT calculations, which indicate that this coupling is through‐space in nature. This is, to the best of our knowledge, the first observation of a coupling between the two nuclei ²⁰⁹Bi and ³¹P, and also the first through‐space coupling involving bismuth. Furthermore, the solid‐state NMR spectra deliver valuable information on the strength of the pnictogen interaction.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

R. Mokrai, J. Barrett, D. C. Apperley, A. S. Batsanov, Z. Benkő, D. Heift, Chem. Eur. J. 2019, 25, 4017.