Abstract
Purpose
To investigate the sequence‐specific impact of amplitude mapping on the accuracy and precision of permittivity reconstruction at 3T in the pelvic region.
Methods
maps obtained with actual flip angle imaging (AFI), Bloch–Siegert (BS), and dual refocusing echo acquisition mode (DREAM) sequences, set to a clinically feasible scan time of 5 minutes, were compared in terms of accuracy and precision with electromagnetic and Bloch simulations and MR measurements. Permittivity maps were reconstructed based on these maps with Helmholtz‐based electrical properties tomography. Accuracy and precision in permittivity were assessed. A 2‐compartment phantom with properties and size similar to the human pelvis was used for both simulations and measurements. Measurements were also performed on a female volunteer’s pelvis.
Results
Accuracy was evaluated with noiseless simulations on the phantom. The maximum bias relative to the true distribution was 1% for AFI and BS and 6% to 15% for DREAM. This caused an average permittivity bias relative to the true permittivity of 7% to 20% for AFI and BS and 12% to 35% for DREAM. Precision was assessed in MR experiments. The lowest standard deviation in permittivity, found in the phantom for BS, measured 22.4 relative units and corresponded to a standard deviation in of 0.2% of the average value. As regards precision, in vivo and phantom measurements were comparable.
Conclusions
Our simulation framework quantitatively predicts the different impact of mapping techniques on permittivity reconstruction and shows high sensitivity of permittivity reconstructions to sequence‐specific bias and noise perturbation in the map. These findings are supported by the experimental results.
Keywords: accuracy and precision, B1 mapping, Helmholtz‐based EPT, permittivity mapping
1. INTRODUCTION
Knowledge of electrical tissue properties is necessary to build patient‐specific electromagnetic (EM) models, which are fundamental for radiofrequency (RF) safety1, 2 and treatment planning for therapeutic heating of malignant tissues using RF or microwave antennas.3, 4, 5, 6, 7 For example, patient‐specific electrical properties may be used as input for planning in locoregional hyperthermia treatment of patients with pelvic tumors (e.g., cervix) with phased arrays of 70‐130 MHz antennas.6, 7 In this frequency range, however, electrical properties might vary (e.g., the permittivity variation is 11% in muscle and 15% in the cervix) because of their dispersive nature8; thus, electrical properties should be characterized at a frequency near the frequency used for treatment in order to improve the reliability of treatment planning. Moreover, a great body of literature has shown differences between the electrical properties of healthy and malignant human tissues9, 10, 11, 12, 13, 14, 15, 16, 17; such differences could potentially be exploited for diagnostic purposes. Therefore, measuring electrical tissue properties, being permittivity (εr) and conductivity (σ), has since long been an important research question.8, 18, 19, 20
A relatively recent MR‐based technique, called electrical properties tomography (EPT),1, 21, 22 extracts noninvasively the in vivo electrical properties of tissues from the spatial modulation of the circularly polarized component () of the transverse RF transmit field, which is responsible for spin excitation. This spatial modulation in the complex field is determined by induced conduction and displacement currents (which are governed by tissue conductivity and permittivity distributions), the applied RF frequency (e.g., 128 MHz at 3T proton imaging), and the incident RF field.23, 24, 25 To the leading order, the permittivity is encoded in the amplitude of the field (), whereas the conductivity is reflected in the phase of such field.25, 26, 27, 28 Therefore, measuring accurate and precise amplitude and phase maps is essential in EPT, given that the quality of these maps intrinsically influences the quality of both property estimates. Indeed, Lee et al theoretically demonstrated that the precision of permittivity and conductivity reconstructed with a Helmholtz‐based algorithm depends linearly on the precision of amplitude (or ) and phase maps, respectively.29 Seemingly, the accuracy of both properties is expected to be proportional to the accuracy of the measured amplitude and phase maps,21, 30 although it has never been verified.
To date, several techniques for field mapping have been used in EPT studies (e.g., standard spin echo, gradient echo, and balanced steady‐state free precession for phase mapping and actual flip angle imaging (AFI)31 and double‐angle methods32 for mapping) and numerous algorithms have been proposed to disentangle both properties from the field.1, 27, 28, 29, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45 Based on measured field maps, in vivo conductivity maps have been derived (e.g., see previous works1, 27, 28, 33, 37, 44, 45) and also preliminarily tested for clinical oncologic applications, for example, in brain,17, 46, 47, 48 breast,16, 49 and uterine cervix.50 At the same time, a few studies have reported in vivo permittivity maps,27, 37, 51, 52 but no study has exploited permittivity maps in clinical scenarios. Regardless of the chosen EPT reconstruction algorithm, the precision of these permittivity maps was poorer than that of conductivity images. These inferior results were attributed to higher noise levels in experimental maps.27, 51, 52
The underlying precision of amplitude and phase maps is dissimilar because both maps are measured independently and differently. The phase distribution is typically approximated with the phase image acquired with standard MR sequences. Thus, its precision is linearly proportional to the signal‐to‐noise ratio (SNR) of the MR image.53 On the other hand, the is mapped with dedicated mapping sequences (e.g., see previous works31, 32, 54, 55, 56). These sequences utilize a model describing the sequence‐specific encoding mechanism to derive the information from acquired MR images. This model regulates the noise propagation that leads to finite precision in the map. Moreover, the encoding model, which normally relies on approximations or assumptions, might degrade the accuracy of the calculation and therefore bias the estimated distribution.
mapping sequences that share similar encoding mechanisms (e.g., the double‐angle and AFI‐based techniques) are expected to have comparable accuracy and precision in the and consequently similar influence on the permittivity. However, although the accuracy and precision of maps obtained with some mapping sequences have already been assessed in studies unrelated to EPT,57, 58, 59, 60 the impact of acquisition on accuracy and precision of the permittivity map remains still unknown.
Hence, in this study, we investigate the specific impact of the sequence on permittivity mapping. To this aim, we examined three commonly commercially available sequences (namely, AFI,31 Bloch–Siegert [BS] shift,54 and dual refocusing echo acquisition mode [DREAM]55), which have distinct encoding mechanisms. Clinically acceptable scanning times are essential, and therefore the three techniques were set to image the in the pelvic region within 5 minutes. maps of the pelvic region at 3T were of interest to estimate permittivity at ~128 MHz, which falls within the frequency range (70–130 MHz) applied for locoregional hyperthermia treatments of cervical cancers.61 By designing a methodological framework consisting of (1) mathematical models, (2) numerical simulations, and (3) MR measurements that take the sequence‐specific generation of the distribution into account, we quantified to what extent the quality of different amplitude maps affects accuracy and precision of the resulting permittivity maps. Comparing these permittivity maps highlighted the impact of sequence‐specific accuracy and precision on the permittivity.
2. METHODS
Phantom MR simulations and measurements and in vivo measurements were performed with AFI, BS, and DREAM techniques, which were set to map amplitude distribution in the pelvic region within 5 minutes at 3T. From these data, permittivity maps were obtained. Figure 1 illustrates the complete workflow of our study. Subsequently, accuracy and precision of both and permittivity maps have been evaluated and compared. Hereafter, we define accuracy as the bias caused by model imperfections between the estimate of the quantity and the true quantity (in our case, this quantity could be amplitude or the permittivity), in the absence of noise. The precision, instead, is inversely related to the standard deviation (std) of the estimate (i.e., precision = (std)–2) and generally reflects the propagation of noise. Moreover, we will use the term “ map” to refer to the amplitude map, unless explicitly stated otherwise.
Figure 1.
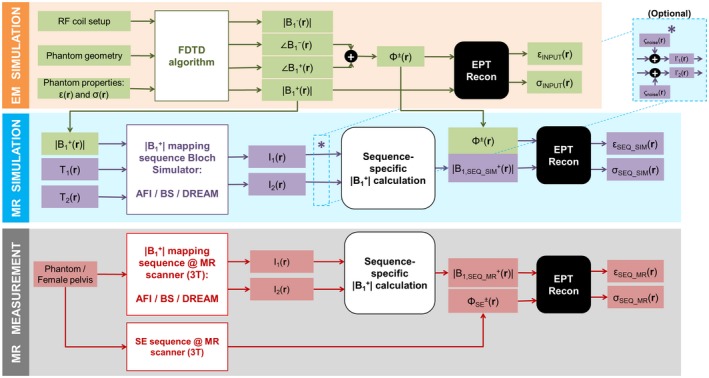
From generation to permittivity (εr) reconstruction: workflow of our study, consisting of an EM simulation, MR simulations, and MR measurements on a phantom and in vivo MR measurements on a female pelvis. For the MR simulations, Gaussian noise ςnoise could be optionally added separately to both real and imaginary parts of the signals I1 and I2 (denoted by the asterisk and the block “Optional”). In the MR measurements, a separate SE sequence was performed to retrieve a transceive phase map (ΦSE ±) needed for EPT reconstruction. The sequence‐specific calculations were performed according to the formulas reported in the Appendix. The subscript “SEQ” refers to any sequence among AFI, BS, and DREAM
2.1. Phantom and in vivo
For simulations and measurements, a pelvic‐sized phantom was used consisting of 2 compartments62: an elliptically shaped cylinder and an inner sphere (Figure 2). The outer cylinder was made of poly(methyl methacrylate). The inner sphere was ~7.5 mm thick and was made of polystyrene. Phantom composition, dielectric properties, and relaxation times are listed in Table 1. Dielectric properties of the solutions contained in the inner and outer compartments were measured with a dielectric probe (85070E; Agilent Technologies, Santa Clara, CA) and matched those of the uterus and the average female pelvis, respectively, based on literature values.8 Measurements were also conducted on the pelvis of a female volunteer (whose written informed consent was obtained).
Figure 2.
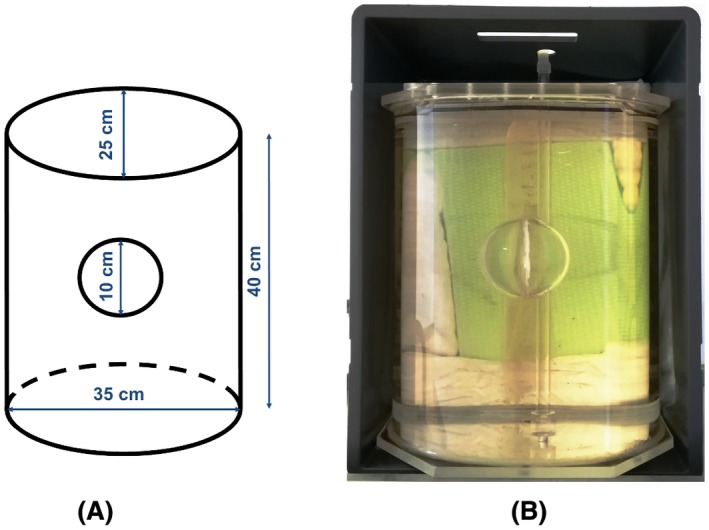
Phantom used for simulations and measurements. A, Schematic view of the phantom, with its dimensions. B, Picture of the phantom
Table 1.
Phantom characteristics
| Inner compartment | Outer compartment | |
|---|---|---|
| Composition | 6 g/L NaCl | Ethylene glycol + 64 g/L NaCl |
| εr (rel. units)a | 80 | 36 |
| σ (Sm–1) | 0.99 | 0.47 |
| T1 (ms)b | 3929 | 500 |
| T2 (ms) | 433 | 74 |
Values for permittivity εr and conductivity σ were measured with a dielectric probe (85070E; Agilent Technologies, Santa Clara, CA) from samples of both solutions.
T1 and T2 values are average values taken from T1 and T2 maps measured with a vendor‐specific “mix‐TSE” sequence (single slice, isotropic voxel size = 5 mm).
2.2. MR experiments
All experiments were performed on a 3T scanner (Ingenia; Philips Healthcare, Best, Netherlands), using a 28‐channel torso array for reception. For all three techniques, a 3D acquisition was chosen because of its inherently higher SNR compared to 2D acquisition, essential for EPT. For each sequence, settings were chosen to achieve a scan length of 5 minutes for a field of view (FOV) = 480 × 260 × 80 mm3 with voxel size 2.5 × 2.5 × 5 mm3 (transverse orientation; Table 2). A multislice spin echo sequence was used to map the transceive phase. To obtain an eddy‐current–free transceive phase map, 2 identical spin echo scans with opposed gradient polarity were acquired.1 For all MR scans, the vendor‐specific CLEAR option was enabled.63 With CLEAR, the combined transceive phase of the body coil and the torso array is converted to the transceive phase of the body coil only.
Table 2.
Protocol parameter settings for both simulations and measurements
| AFI | BS | DREAM | SEa | ||
|---|---|---|---|---|---|
| FOV (mm3) | 480 × 260 × 80 | 480 × 260 × 80 | 480 × 260 × 80 | 480 × 260 × 80 | |
| Voxel size (mm3) | 2.5 × 2.5 × 5 | 2.5 × 2.5 × 5 | 2.5 × 2.5 × 5 | 2.5 × 2.5 × 5 | |
| Spatial encoding | 3D | 3D | 3D | 2D multislice | |
| Imaging flip angle (°) | 60 | 60 | 15 | 90 | |
| TE (ms) | 2.5 | 12 | TE1/TE2 = 2.1/4.6 | 6 | |
| TR (ms) | TR1/TR2 = 30/155 | 93 | 7.7 | 1000 | |
| Fast imaging mode | None | None | Ultrafast GRE, 2 shots | None | |
| Sequence‐specific options | N.A. |
Fermi pulse angle: 725° Fermi pulse duration: 8 ms Fermi pulse offset frequency: 4 kHz KBS: 90.2 rad/G2 |
STE‐first scheme STEAM flip angle: 40° STEAM slice thickness: 20 mm Shot interval length: 3900 ms |
N.A. | |
| Pixel BW (Hz) | 409.8 | 479.4 | 790.5 | 586.5 | |
| NSA | 1 | 1 | 2 | 1 | |
| Scan duration (min:sec) | 5:00 | 5:02 | 5:05 | 7:06 | |
Settings apply for both phantom and in vivo cases.
NSA = number of signal averages; N.A. = not applicable; GRE = gradient echo.
The SE technique was used only for MR measurements to map the transceive phase. Its scan time duration refers to the time needed to acquire 2 identical SE scans with opposed gradient polarity (for compensation of eddy currents).
2.3. MR simulations
The complex field pattern in the phantom, as generated by a 16‐rod birdcage RF coil, was simulated using an in‐house developed FDTD (finite‐difference‐time‐domain) algorithm.64 The coil was tuned at 128 MHz (3T) and driven in quadrature mode. A resolution of 2.5 × 2.5 × 5 mm3 was used for the simulation. The resulting components of the magnetic field were combined to obtain the complex magnetic transmit field () and complex magnetic receive field (; Figure 1).
Subsequently, the MR experiment for each mapping sequence was emulated in Matlab (R2015a; The MathWorks, Inc., Natick, MA) by using a Bloch simulator.65 Input for these simulations were the geometry of the phantom model, the amplitude map from the FDTD simulation (also called “input ” in this study), and T1 and T2 values (see Figure 1 and Table 1). The input map was normalized to the average value in the central slice. Therefore, all values relating to are reported as relative units.
Rectangular‐shaped RF excitation pulses were used, except for the off‐resonant Fermi pulse in BS. All pulses were set to achieve an average flip angle equal to the chosen nominal flip angle in the experiments (Table 2) and were scaled by the input transmit field. Imaging gradients were also approximated as rectangular blocks. Furthermore, we assumed ideal spoiling of the transverse magnetization at the end of each TR. Two different simulation approaches were used according to the acquisition regime of each sequence. For the steady‐state sequences (AFI and BS), the voxel signal corresponded to the signal value at TE (i.e., the value at the center of k‐space). Differently, to mimic the multishot imaging modality of DREAM, the full readout and phase‐encoding gradient schemes were implemented. Thus, the full k‐space was collected and then Fourier transformed into the image domain to obtain the MR image.
For each sequence, the output of each simulation was two MR images (I1 and I2; Figure 1). These images were combined to form the map according to the sequence‐specific encoding mechanism, as outlined in the Appendix. To simulate the full phantom volume, the sequence simulation was looped over all slices.
2.4. Permittivity reconstruction
Permittivity maps were reconstructed with a Helmholtz‐based EPT method. This method is based on a finite‐difference Laplacian implementation: specifically, the noise‐robust kernel was used for the Laplacian operator.28 The kernel size was 7 × 7 × 5 voxels.
The EPT reconstruction requires the complex field as input data (i.e., both the amplitude and phase distribution maps). Because the phase of the transmit field (ϕ+) is not directly measurable in MR, the transceive phase assumption26 was used. The transceive phase assumption approximates the phase as half of the transceive phase (ϕ±), namely the sum of and phases. Van Lier et al28 and Balidemaj et al62 showed that this approximation introduced a minor phase error in both the brain at 7T and the pelvis at 3T.
We reconstructed permittivity maps based on complex data from both simulations and experiments. The amplitude map was derived from AFI, BS, and DREAM measurements or simulations. The transceive phase was derived from the spin‐echo–based transceive phase map (measurements) and from the sum of and phases obtained in the EM simulation (Figure 1). We also reconstructed the permittivity from the true “ ” amplitude and transceive phase (i.e., the maps without influence of the mapping technique). We called this permittivity map “input permittivity.” Note that this input permittivity represents the best permittivity that could be obtained with the abovementioned reconstruction method.
2.5. Effect of transceive phase assumption
To assess the impact of the transceive phase assumption on permittivity, we simulated two types of permittivity: the first permittivity was reconstructed from the amplitude map and the transceive phase map, and the second was based on the amplitude and phase maps.
2.6. Region‐of‐interest delineation
For both measurements and simulations, two regions of interest (ROIs) corresponding to the two compartments were manually delineated. All ROI delineations did not include the boundary errors caused by Helmholtz‐based EPT reconstruction. In vivo, three ROIs were defined corresponding to the whole pelvis, bladder, and fat tissues. These ROIs were based on thresholding on magnitude images followed by further erosion to exclude the aforementioned EPT boundary errors.
2.7. Accuracy assessment
As there is no reference technique (“golden standard”) for mapping in experiments, accuracy (bias) of was assessed on noiseless simulated maps of the phantom. The bias in the pattern was illustrated by an error map representing the difference between the sequence map and the true distribution. To evaluate the isolated impact of the sequence‐specific bias on accuracy in permittivity, we first reconstructed the permittivity maps on the abovementioned simulated maps. Then, we calculated the permittivity error (i.e. bias) maps, namely difference maps between the sequence‐based permittivity and input permittivity. Moreover, an average accuracy for permittivity was estimated in both phantom simulations and measurements by calculating permittivity mean values in the ROIs.
2.8. Precision assessment
Because precision and std are inversely related, we will use the std of the quantity under consideration as a measure for its precision. To avoid confusion with the conductivity symbol, we will denote the std with “ς.” Hence, we will indicate hereafter noise level, std in the amplitude, and std in permittivity with ςnoise, , and respectively.
An analytical expression for the std in the map, , was determined with the law of error propagation66 for each mapping sequence (see the Appendix for more details) and used to generate maps in measurements and simulations. As shown in the Appendix, depends on sequence settings, the magnitudes or phases of the original images I1 and I2, and their SNRs (SNR1 and SNR2). To obtain the map from measured data, SNR maps corresponding to the images I1 and I2 were calculated with Kellman’s method.67 Implementation of Kellman’s method was validated with the temporal SNR method (SNRmult in an earlier work68) in previous experiments (not shown). For both phantom and in vivo experiments, mean and std values for were calculated in the respective aforementioned ROIs.
In MR simulations (phantom only), instead, the real and imaginary parts of the images I1 and I2 were corrupted independently with a Gaussian noise level ςnoise. Subsequently, fictitious SNR1 and SNR2 maps were generated from the ratio of the noiseless image amplitude maps and ςnoise. Finally, a single map for was obtained. This procedure was repeated by using a range of realistic noise levels common to each technique. For each sequence and ςnoise, the resulting simulated maps for SNR1 (and SNR2) and were then spatially averaged inside the phantom. With these average values we predicted the relationship between and the image SNRs for the three sequences.
To determine the effect of realistic precision on the reconstructed permittivity, we performed a Monte‐Carlo–based simulation (1000 iterations). In this case, the noise level used to corrupt the images in each technique was chosen such that the simulated image SNRs approximated the sequence‐specific experimental image SNRs. In each iteration, a map was retrieved from these noisy images and used to reconstruct the permittivity. Subsequently, the permittivity mean and std maps over all iterations were calculated and eventually averaged inside the ROIs.
The std in permittivity, , was calculated on measured permittivity data in the ROIs corresponding to both compartments. Permittivity precision was then correlated with the precision found experimentally in the phantom.
3. RESULTS
3.1. Simulation results
3.1.1. Accuracy
Noiseless simulations showed that all the techniques were able to reveal the field in the phantom (Figure 3A). Although these maps appeared to have perfect resemblance with the input field, difference maps exposed the subtle sequence‐specific errors (Figure 3B). The maximum relative accuracy (i.e., ) was 0.2% for AFI, 0.3% for BS, and 6.1% for DREAM in the inner compartment. In the outer compartment, the maximum relative accuracy was 1.5% for AFI, 0.3% for BS, and 15.4% for DREAM. Figure 3C depicts the permittivity maps reconstructed on these sequence‐specific maps and the permittivity reconstructed on the input , dubbed “input permittivity.” For all these cases, the transceive phase obtained from the EM simulation was used together with the amplitude. The difference between the sequence‐specific and input permittivity is reported in Figure 3D. This difference revealed the inaccuracies introduced by the mapping technique. The seemingly small bias in obtained with AFI and BS led to substantial errors in the permittivity maps. In the inner compartment, the relative bias for the permittivity (defined as ) was, on average, 7.4% for AFI and BS; in the outer compartment, it was 19.5% for AFI and 17.9% for BS. In the case of DREAM, the higher inaccuracies caused a further distorted permittivity map (e.g., the rim around the phantom perimeter and mild spurious fluctuations in Figure 3D). In this case, average relative errors of 12% in the inner compartment and 35.4% in the outer compartment were observed, with peak errors up to 264% around the phantom perimeter. In general, the mean permittivity was offset from the input permittivity of ~6 units for both AFI and BS and of ~13 to 15 units for DREAM in both compartments (Table 3).
Figure 3.
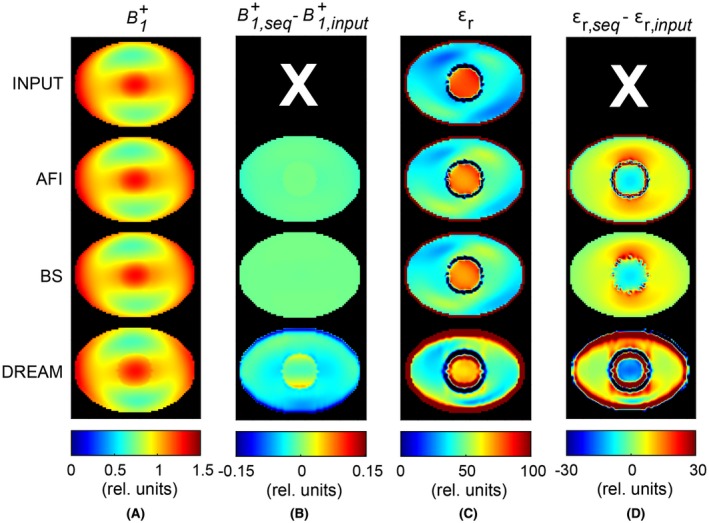
Phantom simulation study to assess the accuracy of both and εr, which were obtained with the EM simulation (“input,” first row), AFI (second row), BS (third row), and DREAM (fourth row). No noise was added. A, maps. Values for the maps were normalized to the average value in the central slice. B, Map of the error in (B + 1,sequence – B + 1,input ). C, Permittivity maps, which were reconstructed from the maps shown in (A) and the simulated transceive phase. D, Map of the error in εr (εr,sequence – εr,input ). Note that the input permittivity (εr,input) accounts for the transceive phase assumption and is therefore the best permittivity that can be obtained with this EPT reconstruction method
Table 3.
Phantom permittivity (in relative units) obtained from simulations and measurements
| Simulations | Measurements | |||||||
|---|---|---|---|---|---|---|---|---|
| and phase (noiseless) | and transceive phase (noiseless) | a and transceive phase | and transceive phase | |||||
| Inner compartment | Outer compartment | Inner compartment | Outer compartment | Inner compartment | Outer compartment | Inner compartment | Outer compartment | |
| TRUEb | 80 | 36 | 80 | 36 | 80 | 36 | 80 | 36 |
| INPUTc | 80.64 ± 0.59 | 36.42 ± 0.76 | 80.45 ± 2.76 | 36.21 ± 5.94 | — | — | — | — |
| AFI | 74.69 ± 2.28 | 43.28 ± 3.46 | 74.49 ± 3.13 | 43.07 ± 6.66 | 73.79 ± 95.75 | 43.04 ± 26.14 | 83.77 ± 103.00 | 38.65 ± 31.85 |
| BS | 74.71 ± 2.26 | 42.74 ± 3.63 | 74.52 ± 3.11 | 42.52 ± 6.78 | 74.52 ± 44.02 | 42.57 ± 12.48 | 72.34 ± 47.65 | 38.40 ± 22.38 |
| DREAM | 65.02 ± 10.68 | 49.03 ± 13.86 | 64.81 ± 10.76 | 48.80 ± 14.86 | 63.52 ± 17.00 | 47.98 ± 28.93 | 56.87 ± 48.71 | 55.31 ± 46.69 |
Mean ± std values were calculated in 2 ROIs corresponding to both compartments. The boundary errors attributed to EPT reconstruction were excluded from the ROIs.
Monte Carlo simulation to emulate the MR measurements. maps were affected by noise, which corrupted the original images I1 and I2.
TRUE refers to the permittivity values measured with the dielectric probe and already reported in Table 1.
INPUT refers to the permittivity values calculated from the input permittivity (i.e. the permittivity based on the input obtained directly from the EM simulation).
3.1.2. Effect of transceive phase assumption
The effect of the transceive phase assumption on permittivity is illustrated in Supporting Information Figure S1 for our phantom. The transceive phase error (ϕ±/2‐ϕ+; Supporting Information Figure S1A) appeared as left‐right antisymmetry and was larger in the outer compartment, where the validity of the assumption degrades. The maximum error was 0.15 rad. A peripheral antisymmetric pattern was also reflected in the permittivity reconstructed with the transceive phase combined with the amplitude (Supporting Information Figure S1C). This led to a maximum bias of 15% with respect to the permittivity calculated based on the phase and amplitude. In general, using the transceive phase contributed mostly to the spread of permittivity values (Table 3). Similar effects have been observed for conductivity in previous studies.28, 62
3.2. Measurement results
Figure 4 presents the measurement results in the phantom for all methods. First, the SNR1, namely the SNR of the first image (the highest in magnitude between the two signals), is shown. Second, the measured map is reported. Overall, each technique showed similar spatial distributions. Comparing maps from AFI and DREAM with respect to BS‐based map resulted into differences of <±0.15 rel. units, similar to the accuracy found in simulations (not shown). Third, maps for the std in () are shown, which were calculated from measured data as described in the Appendix. Despite its lowest SNR1, DREAM introduced the smallest in the inner compartment (average = 4.3 · 10–3 rel. units). BS had a slightly higher (5.9 · 10–3 rel. units), and AFI had almost two‐fold (1.1 · 10–2 rel. units). In the outer compartment, the average for DREAM was slightly lower than for AFI (3.5 · 10–3 versus 4.9 · 10–3 rel. units), but higher than BS (= 2.2 · 10–3 rel. units). Finally, the corresponding permittivity maps are reported. Although affected by noise, BS‐ and DREAM‐based permittivity maps displayed a bias pattern which resembles the permittivity reconstructions on simulated maps (Figure 3C): note, for instance, the rim of higher values and spurious fluctuations in the outer compartment periphery in DREAM‐based permittivity. The measured permittivity mean values were, nonetheless, biased with respect to the values predicted with noisy simulations (~5 units in the outer compartment for all sequences and ~10, 2, and 8 units for AFI, BS, and DREAM, respectively, in the inner sphere). Also permittivity std values were offset. These offsets were likely caused by experimental factors that were not simulated, such as ringing and ghosting due to fluid motion as a result of gradient switching.
Figure 4.
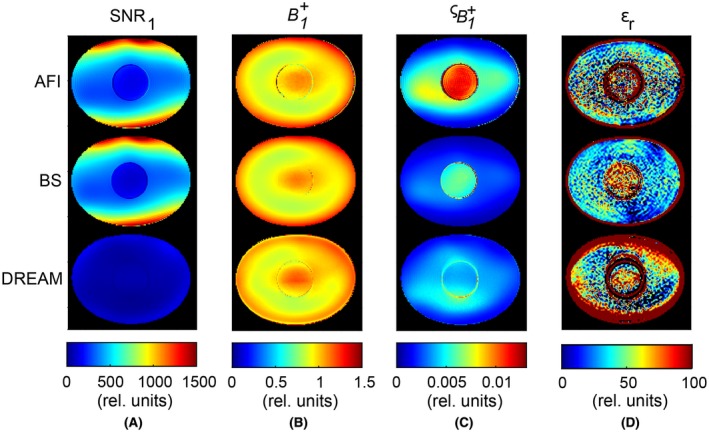
Phantom MR measurements. For each mapping technique (AFI, top row; BS, center row; DREAM, bottom row) the following maps are reported: A, SNR1, namely the SNR relative to the image I1; B, the field distribution. Values for the maps were normalized to the average value in the central slice; C, the standard deviation , as calculated in the Appendix; and D, the permittivity εr
Figure 5 presents in vivo results, which can be compared to the phantom results. In terms of precision (Figure 5C), the phantom inner sphere and the bladder were alike: the std in (average = 2.1 · 10–2 rel. units) was considerably poorer in AFI than for the other two methods (4.4 · 10–3 and 5.1 · 10–3 rel. units for BS and DREAM, respectively). With respect to the outer compartment, on average slightly lower values were measured in fat (2.2 · 10–3, 1.1 · 10–3, and 4.0 · 10–3 rel. units for AFI, BS, and DREAM, respectively). Overall, the averaged over the whole pelvis was 5.3 · 10–3, 4.7 · 10–3, and 5.1 · 10–3 rel. units for AFI, BS, and DREAM. On the other hand, the measured maps (Figure 5B) exhibited different types of disturbances than the phantom measurements. AFI map was hampered by bowel motion. DREAM map showed sharp transitions at tissue interfaces (e.g., hip bone/muscle). In BS map, ghosting because of the flowing blood in iliac vessels appeared between hip bone and bladder. As expected, these disturbances were enhanced by the derivative kernel used for EPT reconstruction and generally corrupted the permittivity distribution. Nevertheless, the posterior part in BS‐based permittivity map was unaffected by the abovementioned artifact. For the fat in that particular region, a permittivity of 5.3 ± 26.3 rel. units (mean ± std) was calculated, by excluding EPT boundary errors. The average value found was close to the literature value (5.9 rel.units8).
Figure 5.
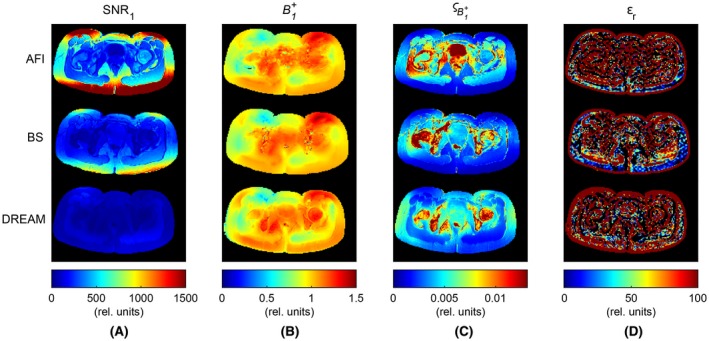
In vivo MR measurements on a female pelvis. For each mapping technique (AFI, top row; BS, center row; DREAM, bottom row) the following maps are reported: A, SNR1, namely the SNR relative to the image I1; B, the field distribution. Values for the maps were normalized to the average value in the central slice; C, the standard deviation , as calculated in the Appendix; and D, the permittivity εr
3.2.1. Precision
In Figure 6, the relationship between the SNR1 and is shown for the three sequences. In all cases, the simulated curves predicted the measured trends. The most favorable ‐ SNR1 curve was found for DREAM, i.e. high precision was achieved for a relatively low image SNR. Note, however, that the measured SNR1 range for DREAM was rather limited (measured max SNR1 <350) in comparison to the SNR1 obtained with AFI and BS (measured max SNR1 >1000). Figure 6 also displays the asymptotic behavior of , which implies that large jumps of image SNR would be necessary for rather small gains in precision.
Figure 6.
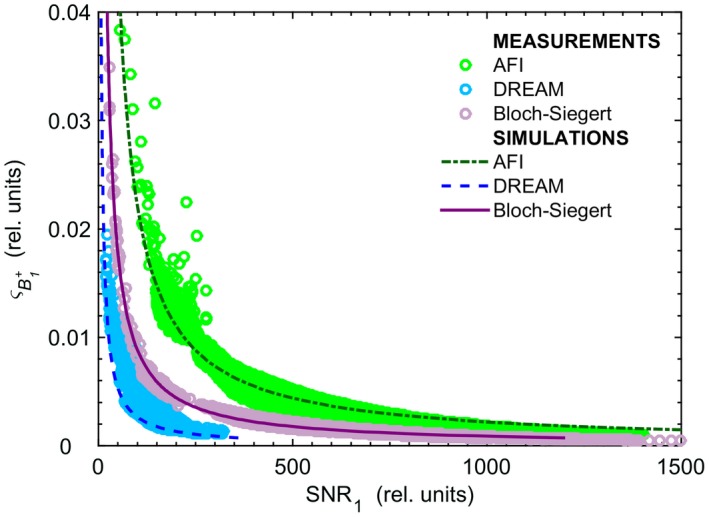
std (indicated by ) as a function of SNR1, the SNR of the first image (I1) for each technique, plotted for the central slice. The circles and lines represent the measured and simulated data, respectively. In simulations, different maps for SNR1 and , corresponding to different levels of ςnoise, were generated. For each ςnoise, SNR1 and maps were averaged inside the phantom. The simulated trends shown in this figure are the result of the averaging operation. In the measured data, the voxels related to the plastic borders of both compartments were excluded. The simulated curves predicted well the behavior found in measurements
Figure 7 illustrates our phantom experimental findings on the relationship between precision and permittivity precision. Also shown is the relationship for the EPT kernel used in this study, as theorized by Lee et al.29 We found that BS achieved the smallest in both compartments (22.4 and 47.6 rel. units in the inner and outer compartment, respectively) and that AFI‐derived permittivity had the greatest values (103.0 and 31.8 rel. units in the inner and outer compartments, respectively). Regarding DREAM, was biased by the distorted permittivity distribution caused by sequence‐related inaccuracies affecting the map. Overall, our results agreed well with Lee et al’s theoretical model. Note that experimental factors, as mentioned earlier, might have slightly biased values. Nonetheless, it is worth noticing that deviations of the same order of magnitude from the theoretical model were reported in the work by Lee et al29 for an analytical complex map (i.e., no sequence dependence, transceive phase assumption, and experimental factors).
Figure 7.
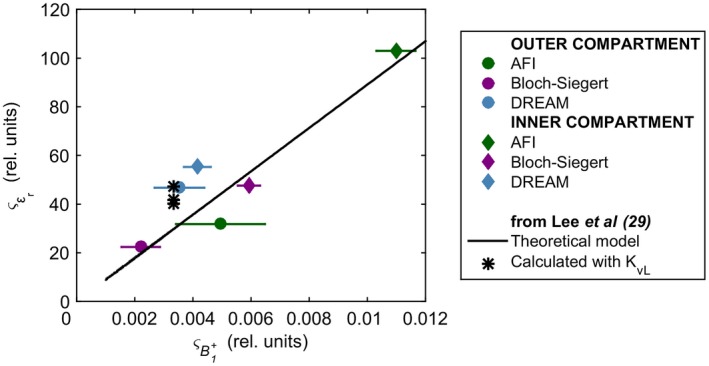
Experimental relationship between and . Both and were evaluated in 2 manually delineated ROIs matching the phantom inner and outer compartments. For , the average value is displayed. The horizontal bars indicate the spread (std) of the in both ROIs. The black line represents the theoretical model29 relating and for the noise‐robust kernel KvL (Equation 18 in Lee et al,29 where Ntot= 117, L =√67, G = 290.2, and ≈ 1/). The black asterisks refer to the std values of the permittivity calculated by Lee et al29 inside 3 ROIs, for a simulated phantom map with fictitious = 300
4. DISCUSSION
We investigated, for the first time, the impact of acquisition on permittivity mapping. To this end, we designed a framework to predict and validate the sensitivity of the permittivity reconstruction to the sequence‐specific accuracy and precision effectively achieved by the amplitude map at 3T. Moreover, we compared the accuracy and precision of Helmholtz‐based permittivity maps reconstructed on maps measured with AFI, BS, and DREAM sequences. According to our definition, accuracy was associated with imperfections specific to the adopted sequence whereas precision (inverse of variance) was related to noise propagation. Our analysis demonstrated how the permittivity reconstruction is influenced by the sequence‐specific error and noise propagation in the depending on which mapping sequence is used. More generally, we found that Helmholtz‐based permittivity is extremely sensitive to both bias and noise in the map.
Regarding accuracy, BS‐ and AFI‐based permittivity maps were comparably accurate in our phantom (Figures 3 and 4; Table 3). The maps from which these permittivity maps were reconstructed were also comparably accurate, which is in line with other studies.58, 59, 60 DREAM‐based permittivity, instead, deviated from the expected permittivity distribution because of inaccuracies in the map, which were larger at compartment interfaces. In vivo, permittivity maps were corrupted by under‐ and overshooting errors (also called “boundary errors”) arising in correspondence of discontinuities in the distribution (Figure 5). These discontinuities manifested evidently at tissue interfaces in DREAM map and were likely caused by imperfect T1 or T2 decay of the stimulated echo.55, 69 Analogously, in vivo BS distributions were disturbed by ghosting artifacts due to sensitivity to flow, as a result of its “phase‐based” encoding mechanism.54
Considering precision, we found that the permittivity std () differed when the permittivity was derived from different sequences. For the most commonly used AFI technique, for example, the permittivity std was 1.5 to 2 times greater than for BS (Figure 7; Table 3). Note that, on average, the underlying std in () for AFI was double the std in for BS. Similar findings on precision of AFI and BS were reported in previous works.59, 70 Although permittivity precision in the pelvis was not estimated because of the aforementioned boundary errors disturbing the permittivity map, the precision trends found in the phantom were also observed in the female pelvis, particularly in bladder, uterus, and fat (Figure 5). Thus, we expect the in vivo permittivity precision to be in the same order of magnitude as the phantom permittivity precision, because the noise propagation from the to Helmholtz‐based permittivity is linear, as theoretically demonstrated by Lee et al.29 Furthermore, by comparing the precision of the three sequences, our results experimentally validated Lee et al’s theoretical model for the noise propagation from to permittivity (Figure 7).
Overall, extremely small errors in the map created considerable deviations in the permittivity distribution reconstructed with Helmholtz‐based EPT. For example, BS results in the outer compartment showed that a less than 1% deviation in accuracy (or bias) in the simulated map (Figure 3B) resulted in 20% relative bias in permittivity (Figure 3D) and that a = 2.0 · 10–3 rel. units, namely 0.2% of the average measured , led to = 22.4 rel. units (Figure 7). In the pelvis, the std in measured, on average, 0.5% at 3T for all the sequences, with values as low as 0.1% in fat for BS and peaks higher than 2% in the bladder for AFI (Figure 5D). All these values, nevertheless, were far from the precision required to achieve = 5 units (≈ 0.05%; Figure 7), which we deem a considerable improvement for permittivity precision, in relation to the range of tissue permittivity (i.e., 20 ≤ εr ≤ 85 rel. units for the majority of tissues at 128 MHz, except fat (see, e.g., due studies8, 18, 19, 20)). Such a low std in would be reached only for image SNR1 ≥2500, 1500, and 500 rel. units for AFI, BS, and DREAM, respectively (Figure 6), but these SNRs were not achieved in our experimental setup (pelvis FOV in 5 minutes at 3T). Hence, we deduce that a Helmholtz‐based approach cannot reconstruct precise permittivity maps for the precision clinically achieved by three commonly available sequences (at 3T for scan times ≤5 minutes).
Investigating more noise‐robust solutions for permittivity mapping was beyond the scope of this study, but brain permittivity maps with superior quality were shown at 7T for Helmholtz‐based EPT51 and gEPT combined with multichannel systems.37 Higher field strengths, in fact, benefit permittivity mapping not only for the intrinsic SNR gain, but also because the imprint of the displacement currents on the is stronger.29, 51 Moreover, improved permittivity results have very recently been reported by using newly formulated EPT reconstruction methods on maps from EM simulations. For example, using a quasi‐Newton approach, Rahimov et al have shown a permittivity precision of ~20% in the brain.39 In Guo et al, the std in permittivity, converted from the reported interquartile ranges according to the procedure in Wan et al,71 was ~8 rel. units in white and gray matter and ~17 rel. units in cerebrospinal fluid.41 In both studies, the simulated was directly corrupted with a noise level = 3.1 · 10–3 (i.e., = 316). Provided that these results are experimentally corroborated, using such less noise‐sensitive EPT reconstruction methods or denoising techniques52 could be preferred when precise permittivity maps obtained with clinical MR scanners (1.5 or 3T) are desired.
Our findings on accuracy also revealed that the slight perturbations of the field resulting from realistic permittivity variations (already studied in, e.g., Vaidya et al25 and Brink et al72) can be in the same order of magnitude as the sequence‐specific errors in the maps. Thus, although the severity of these errors on permittivity accuracy may vary depending on the chosen reconstruction technique and on the imaged body geometry, we conclude that using only electromagnetic simulations of the field is insufficient to fully investigate the accuracy of a permittivity reconstruction.
Despite the fact that our in vivo permittivity maps did not provide reliable quantitative estimates, we remark that we pragmatically tackled the unprecedented problem of assessing to what extent the acquisition influences the permittivity reconstruction. In light of all our results, we cannot give definitive solutions, but we can propose several directions for improvement, ranging from recommendations on sequence selection for permittivity mapping to suggestions on how to fully assess the quality of the reconstructed permittivity map. BS and AFI techniques should be preferred over DREAM for clinical applications where accurate permittivity estimates are of utmost importance, as is the case of hyperthermia treatment planning.3 Strategies to mitigate some sequence‐specific imperfections contaminating in vivo and permittivity distributions were beyond the scope of this study, but are worthy of further investigation (e.g., using flow compensation for BS or acceleration techniques to reduce motion artifacts for AFI). Alternatively, when precise reconstruction of the permittivity of certain tissues is desired, for example for tissue contrast visualization purposes, bear in mind that DREAM or BS had more favorable “ precision‐to‐image SNR” performance than AFI. This recommendation is also valid when EPT algorithms prone to noise amplification (e.g., derivative‐based methods) are used for permittivity reconstruction. Besides, if shorter scan durations are intended, then DREAM could allow the greatest time reduction (of ~3 minutes for our FOV), because of a higher flexibility in parameter settings; however, this might come at a cost of accuracy (e.g., by decreasing the shot interval length69) and loss of precision (e.g., by reducing the number of averages). More generally, to validate or predict the permittivity accuracy obtained with any new reconstruction method, or even to train a neural network,73 we recommend taking the used mapping technique into account, for example by running Bloch simulations emulating the sequence, in addition to electromagnetic simulations of the field. Likewise, in order to predict or validate the method performance under clinically realistic noise levels valid for the majority of body tissues, we advise testing newly developed reconstruction methods against noise levels between 0.5% and 2.5% of the average (i.e., ).
5. CONCLUSION
In conclusion, the merit of our work is to provide a methodology to assess the sensitivity of permittivity reconstruction to bias and noise in maps. Despite addressing only one reconstruction method and three mapping sequences, we emphasize that our framework, outlined in Figure 1, is reproducible for any type of mapping sequence (but also phase mapping sequence, if conductivity were of interest) and EPT reconstruction algorithm. By using this framework, two major findings were obtained. First, the mapping sequence affects the accuracy and precision of the permittivity reconstruction according to the sequence‐specific error propagation determined by its encoding mechanism. This implies that attention should be paid to select the most appropriate mapping sequence in relation to the accuracy and precision desired in the final permittivity map. Second, the precision achieved by commonly available mapping techniques was below the precision needed to decrease the permittivity standard deviation to only 5 to 10 units, which means that the extreme sensitivity of Helmholtz‐based EPT to noise perturbations, together with boundary errors, renders permittivity reconstruction not feasible at 3T in clinically acceptable times.
Supporting information
FIGURE S1 Effect of the transceive phase assumption on permittivity, for the phantom case. (a) Transceive phase error map, calculated as the difference between half of the transceive phase, ϕ±/2, and the transmit phase ϕ+; (b) permittivity map reconstructed with the transmit phase; and (c) permittivity map reconstructed with the transceive phase. An antisymmetric pattern appears in the permittivity when the transceive phase assumption is used. In (b) and (c), the input B1+ amplitude map was used
APPENDIX 1. Derivation of error propagation (precision) in the ,
In each examined technique, two images, I1 and I2, are acquired. Their magnitude/phase representation is I1 = S1 exp(iθ1) and I2 = S2 exp(iθ2). Either the amplitudes or the phases of such images are then combined to form a map according to a sequence‐specific function f(x1,x2) where x1 and x2 are the input data (either magnitude or phase, depending on the mapping technique). In this section, a short summary and the sequence‐specific function f(x1,x2) are presented for each technique. Next, as a measure for precision, the std in the amplitude, , for all the 3 methods is derived by applying the law of error propagation66 (Equation A1):
| (A1) |
where and are the standard deviations of the noise corresponding to, respectively, the signals x1 and x2.
Note that in the following expressions the represents the (dimensionless) spatial modulation of the transmit field, ( r). Also known in literature as transmit sensitivity, ( r) corresponds to the absolute field (in Tesla) normalized by the nominal value in T.
AFI
The AFI technique is a steady‐state spoiled gradient‐echo sequence with 2 interleaved repetition times TR1 and TR2 after an imaging pulse with constant nominal tip angle αnom. Two images are acquired in each TR interval. Under the assumptions of perfect spoiling and repetition times shorter than T1, the ratio of the magnitude images is related to the transmit field as follows31 (Equation A2):
| (A2) |
where n = TR 1 /TR 2. Note that x1 = S1 and x2 = S2.
The expression for the std, , is (Equation A3):
| (A3) |
where is the std of the noise in the magnitude data. Note that this quantity is related to the SNR as , for i = 1, 2.
BS
The BS technique is a steady‐state spoiled gradient echo sequence with an off‐resonance pulse (in this case a Fermi pulse) inserted between the excitation and acquisition. The off‐resonance pulse induces a B1‐dependent frequency shift, which is translated into a phase shift in the image. Acquiring 2 signals with opposite offset frequencies and subtracting their phase images leads to a phase shift difference that is related to the amplitude,54 as expressed below (Equation A4):
| (A4) |
with x1 = θ1 and x2 = θ2. Apeak,Fermi is the Fermi pulse peak value. KBS is a pulse‐related constant that depends on the pulse waveform B 1 ,normalized(t), its duration TFermi and its offset frequency ωFermi, as in Equation A5:
| (A5) |
The std for BS is expressed by (Equation 6):
| (A6) |
where is the std of the phase data θi, and is related to the image SNR by formula (15.84) in Haacke et al,53 that is, (radians), for i = 1, 2.
Note that Equation A6 coincides with Equation 20 of Pohmann and Scheffler59 if Apeak,Fermi is replaced by the expression of a (fictitious) block pulse with nominal flip angle αnom, peak value Apeak,Fermi, and duration τ.
DREAM
In DREAM, a STEAM sequence,74 is utilized to encode the information. The STEAM segment serves as a magnetization preparation before an imaging step composed by a train of RF pulses (also called shot) with gradient echo readout. A stimulated echo and a free‐induction decay signals are acquired quasi‐simultaneously in a single acquisition. The ratio of their magnitudes (x1 = S1 and x2 = S2) is related to as indicated below55 (Equation A7):
| (A7) |
Applying Equation A1 for DREAM yields the following expression (Equation A8):
| (A8) |
where is the std of the noise in the magnitude data and is related to the image SNR as , for i = 1, 2.
Gavazzi S, van den Berg CAT, Sbrizzi A, et al. Accuracy and precision of electrical permittivity mapping at 3T: the impact of three mapping techniques. Magn Reson Med. 2019;81:3628–3642. 10.1002/mrm.27675
Funding information
Dutch Cancer Society (KWF; project UVA 2014‐7197)
[Correction added after online publication 13 March 2019. The authors have corrected minor typographical and grammar issues throughout the article.]
REFERENCES
- 1. Katscher U, Voigt T, Findeklee C, Vernickel P, Nehrke K, Dössel O. Determination of electric conductivity and local SAR via B1 mapping. IEEE Trans Med Imaging. 2009;28:1365–1374. [DOI] [PubMed] [Google Scholar]
- 2. Zhang X, Schmitter S, Van De Moortele PF, Liu J, He B, Bin He. From complex B1 mapping to local SAR estimation for human brain MR imaging using multi‐channel transceiver coil at 7T. IEEE Trans Med Imaging. 2013;32:1058–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. van de Kamer JB, van Wieringen N, De Leeuw AA, Lagendijk JJW. The significance of accurate dielectric tissue data for hyperthermia. Int J Hyperth. 2001;17:123–142. [DOI] [PubMed] [Google Scholar]
- 4. Kok HP, Kotte ANTJ, Crezee J. Planning, optimisation and evaluation of hyperthermia treatments. Int J Hyperth. 2017;33:593–607. [DOI] [PubMed] [Google Scholar]
- 5. Hahn GM, Kernahan P, Martinez A, et al. Some heat transfer problems associated with heating by ultrasound, microwave or radio frequency. Ann N Y Acad Sci. 1980;335(1 Thermal Chara):327–346. [DOI] [PubMed] [Google Scholar]
- 6. Crezee J, Bennis M, Gavazzi S, et al. Development of electrical properties tomography for hyperthermia treatment planning In: 2017 First IEEE MTT‐S International Microwave Bio Conference (IMBIOC). New York, NY: IEEE; 2017:1–4. [Google Scholar]
- 7. Balidemaj E, Kok HP, Schooneveldt G, et al. Hyperthermia treatment planning for cervical cancer patients based on electrical conductivity tissue properties acquired in vivo with EPT at 3 T MRI. Int J Hyperthermia. 2016;32:558–568. [DOI] [PubMed] [Google Scholar]
- 8. Gabriel C. Compilation of the Dielectric Properties of Body Tissues at RF and Microwave Frequencies. San Antonio, TX: Air Force Materiel Command, Brooks Air Force Base; 1996. [Google Scholar]
- 9. Schepps JL, Foster KR. The UHF and microwave dielectric properties of normal and tumor tissues variation in dielectric properties with tissue water content. Phys Med Biol. 1980;25:1149–1159. [DOI] [PubMed] [Google Scholar]
- 10. Rogers JA, Sheppard RJ, Grant EH, Bleehen NM, Honess DJ. The dielectric properties of normal and tumour mouse tissue between 50 MHz and 10 GHz. Br J Radiol. 1983;56:335–338. [DOI] [PubMed] [Google Scholar]
- 11. Joines WT, Zhang Y, Li C, Jirtle RL. The measured electrical properties of normal and malignant human tissues from 50 to 900 MHz. Med Phys. 1994;21:547–550. [DOI] [PubMed] [Google Scholar]
- 12. Lazebnik M, Popovic D, McCartney L, et al. A large‐scale study of the ultrawideband microwave dielectric properties of normal, benign and malignant breast tissues obtained from cancer surgeries. Phys Med Biol. 2007;52:6093–6115. [DOI] [PubMed] [Google Scholar]
- 13. O’Rourke AP, Lazebnik M, Bertram JM, Converse MC, Hagness SC, Webster JG, et al. Dielectric properties of human normal, malignant and cirrhotic liver tissue: In vivo and ex vivo measurements from 0.5 to 20 GHz using a precision open‐ended coaxial probe. Phys Med Biol. 2007;52:4707–4719. [DOI] [PubMed] [Google Scholar]
- 14. Gavazzi S, Limone P, De Rosa G, Molinari F, Vecchi G. Comparison of microwave dielectric properties of human normal, benign and malignant thyroid tissues obtained from surgeries: a preliminary study. Biomed Phys Eng Express. 2017;4:47003. [Google Scholar]
- 15. Halter RJ, Zhou T, Meaney PM, et al. The correlation of in vivo and ex vivo tissue dielectric properties to validate electromagnetic breast imaging: Initial clinical experience. Physiol Meas. 2009;30:S121–S136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Shin J, Kim MJ, Lee J, et al. Initial study on in vivo conductivity mapping of breast cancer using MRI. J Magn Reson Imaging. 2015;42:371–378. [DOI] [PubMed] [Google Scholar]
- 17. Tha KK, Katscher U, Yamaguchi S, et al. Noninvasive electrical conductivity measurement by MRI: a test of its validity and the electrical conductivity characteristics of glioma. Eur Radiol. 2018;28:348–355. [DOI] [PubMed] [Google Scholar]
- 18. Wang H, He Y, Yan Q, et al. Correlation between the dielectric properties and biological activities of human ex vivo hepatic tissue. Phys Med Biol. 2015;60:2603–2617. [DOI] [PubMed] [Google Scholar]
- 19. Schwan HP. Electrical properties of tissues and cell suspensions: mechanisms and models In Proceedings of the 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Baltimore, MD, 1994. pp. 70–71. [Google Scholar]
- 20. Pethig R. Dielectric properties of biological materials: biophysical and medical applications. IEEE Trans Electr Insul. 1984;EI‐19:;453–474. [Google Scholar]
- 21. Katscher U, van den Berg CAT. Electric properties tomography: biochemical, physical and technical background, evaluation and clinical applications. NMR Biomed. 2017;30:e3729. [DOI] [PubMed] [Google Scholar]
- 22. Liu J, Wang Y, Katscher U, He B. Electrical properties tomography based on B1 maps in MRI: principles, applications, and challenges. IEEE Trans Biomed Eng. 2017;64:2515–2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Yang QX, Wang J, Zhang X, et al. Analysis of wave behavior in lossy dielectric samples at high field. Magn Reson Med. 2002;47:982–989. [DOI] [PubMed] [Google Scholar]
- 24. Collins CM, Liu W, Schreiber W, Yang QX, Smith MB. Central brightening due to constructive interference with, without, and despite dielectric resonance. J Magn Reson Imaging. 2005;21:192–196. [DOI] [PubMed] [Google Scholar]
- 25. Vaidya MV, Collins CM, Sodickson DK, Brown R, Wiggins GC, Lattanzi R. Dependence of B1− and B1+ field patterns of surface coils on the electrical properties of the sample and the MR operating frequency. Concepts Magn Reson Part B Magn Reson Eng. 2016;46:25–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Wen H. Noninvasive quantitative mapping of conductivity and dielectric distributions using RF wave propagation effects in high field MRI In: Yaffe MJ, Antonuk LE, eds. Proc SPIE 5030, Medical Imaging: Physics of Medical Imaging. Bellingham, WA: International Society for Optics and Photonics; 2003:471–477. [Google Scholar]
- 27. Voigt T, Katscher U, Doessel O. Quantitative conductivity and permittivity imaging of the human brain using electric properties tomography. Magn Reson Med. 2011;66:456–466. [DOI] [PubMed] [Google Scholar]
- 28. van Lier ALHMW, Brunner DO, Pruessmann KP, et al. B1+ phase mapping at 7 T and its application for in vivo electrical conductivity mapping. Magn Reson Med. 2012;67:552–561. [DOI] [PubMed] [Google Scholar]
- 29. Lee SK, Bulumulla S, Hancu I. Theoretical investigation of random noise‐limited signal‐to‐noise ratio in MR‐based electrical properties tomography. IEEE Trans Med Imaging. 2015;34:2220–2232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Zhang X, Zhu S, He B. Imaging electric properties of biological tissues by RF field mapping in MRI. IEEE Trans Med Imaging. 2010;29:474–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Yarnykh VL. Actual flip‐angle imaging in the pulsed steady state: a method for rapid three‐dimensional mapping of the transmitted radiofrequency field. Magn Reson Med. 2007;57:192–200. [DOI] [PubMed] [Google Scholar]
- 32. Cunningham CH, Pauly JM, Nayak KS. Saturated double‐angle method for rapid B1+ mapping. Magn Reson Med. 2006;55:1326–1333. [DOI] [PubMed] [Google Scholar]
- 33. Bulumulla SB, Lee SK, Yeo DTB. Conductivity and permittivity imaging at 3.0T. Concepts Magn Reson Part B Magn Reson Eng. 2012;41B:13–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Sodickson DK, Deniz CM, Ben‐Eliezer N, et al. Generalized local maxwell tomography for mapping of electrical property gradients and tensors Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City, UT, 2013. p. 4175. [Google Scholar]
- 35. Hafalir FS, Oran OF, Gurler N, Ider YZ. Convection‐reaction equation based magnetic resonance electrical properties tomography (cr‐MREPT). IEEE Trans Med Imaging. 2014;33:777–793. [DOI] [PubMed] [Google Scholar]
- 36. Balidemaj E, Van Den Berg CAT, Trinks J, et al. CSI‐EPT: a contrast source inversion approach for improved MRI‐based electric properties tomography. IEEE Trans Med Imaging. 2015;34:1788–1796. [DOI] [PubMed] [Google Scholar]
- 37. Liu J, Zhang X, Schmitter S, Van de Moortele PF, He B. Gradient‐based electrical properties tomography (gEPT): a robust method for mapping electrical properties of biological tissues in vivo using magnetic resonance imaging. Magn Reson Med. 2015;74:634–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Serralles JEC, Daniel L, White JK, Sodickson DK, Lattanzi R, Polimeridis AG. Global maxwell tomography: a novel technique for electrical properties mapping based on MR measurements and volume integral equation formulations In Proceedings of the 2016 IEEE International Symposium on Antennas and Propagation/USNC‐URSI National Radio Science meeting, Fajardo, Puerto Rico, 2016. pp. 1395–1396. [Google Scholar]
- 39. Rahimov A, Litman A, Ferrand G. MRI‐based electric properties tomography with a quasi‐Newton approach. Inverse Probl. 2017;33: 105004 10.1088/1361-6420/aa7ef2. [DOI] [Google Scholar]
- 40. Liu C, Jin J, Guo L, et al. MR‐based electrical property tomography using a modified finite difference scheme. Phys Med Biol. 2018;63:145013. [DOI] [PubMed] [Google Scholar]
- 41. Guo L, Jin J, Liu C, Liu F, Crozier S. An efficient integral‐based method for three‐dimensional MR‐EPT and the calculation of the RF‐Coil‐Induced Bzfield. IEEE Trans Biomed Eng. 2018;65:282–293. [DOI] [PubMed] [Google Scholar]
- 42. Leijsen RL, Brink WM, van den Berg CAT, Webb AG, Remis RF. Three‐dimensional contrast source inversion‐electrical properties tomography. IEEE Trans Med Imaging. 2018;37:2080–2089. [DOI] [PubMed] [Google Scholar]
- 43. Arduino A, Bottauscio O, Chiampi M, Zilberti L. Magnetic resonance‐based imaging of human electric properties with phaseless contrast source inversion. Inverse Probl. 2018;34: 084002. [Google Scholar]
- 44. Katscher U, Herrmann M, Amthor T, Findeklee C, Doneva M. Dictionary‐based Electric Properties Tomography for brain conductivity imaging In Proceedings for the 26th Annual Meeting of ISMRM, Paris, France, 2018. p. 5102. [Google Scholar]
- 45. Chung HJ, Kim JM, Jeong YJ, Kim JH, Lee C, Oh CH. Electro‐magnetic property mapping using Kalman filtering with a single acquistion at 3.0 T and 7.0 T MRI In Proceedings for the 26th Annual Meeting of ISMRM, Paris, France, 2018. p. 5081. [Google Scholar]
- 46. van Lier ALHMW, Hoogduin JM, Polders DL, et al. Electrical conductivity imaging of brain tumours In Proceedings of the 19th Annual Meeting of ISMRM, Montréal, Canada, 2011. p. 4464. [Google Scholar]
- 47. Voigt T, Väterlein O, Stehning C, Katscher U, Fiehler J. In vivo glioma characterization using MR conductivity imaging In Proceedings of the 19th Annual Meeting of ISMRM, Montréal, Canada, 2011. p. 2865. [Google Scholar]
- 48. Huhndorf M, Stehning C, Rohr A, Helle M, Katscher U, Jansen O. Systematic brain tumor conductivity study with optimized EPT sequence and reconstruction algorithm In Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City, UT, 2013. pp. 3626. [Google Scholar]
- 49. Katscher U, Abe H, Ivancevic MK, Keupp J. Investigating breast tumor malignancy with electric conductivity measurements In Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Canada, 2015, p. 3306. [Google Scholar]
- 50. Balidemaj E, de Boer P, van Lier ALHMW, et al. vivo electric conductivity of cervical cancer patients based on B1+ maps at 3T MRI. Phys Med Biol. 2016;61:1596–1607. [DOI] [PubMed] [Google Scholar]
- 51. van Lier ALHMW, Raaijmakers A, Voigt T, et al. Electrical properties tomography in the human brain at 1.5, 3, and 7T: a comparison study. Magn Reson Med. 2014;71:354–363. [DOI] [PubMed] [Google Scholar]
- 52. Michel E, Hernandez D, Cho MH, Lee SY. Denoising of B1 + field maps for noise‐robust image reconstruction in electrical properties tomography. Med Phys. 2014;41:102304. [DOI] [PubMed] [Google Scholar]
- 53. Haacke EM, Brown RW, Thompson MR, Venkatesan R, eds. Magnetic Resonance Imaging: Physical Principles and Sequence Design, 1st edn New York, NY: John Wiley & Sons; 1999. [Google Scholar]
- 54. Sacolick LI, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch‐Siegert shift. Magn Reson Med. 2010;63:1315–1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Nehrke K, Börnert P. DREAM—a novel approach for robust, ultrafast, multislice B1 mapping. Magn Reson Med. 2012;68:1517–1526. [DOI] [PubMed] [Google Scholar]
- 56. Morrell GR. A phase‐sensitive method of flip angle mapping. Magn Reson Med. 2008;60:889–894. [DOI] [PubMed] [Google Scholar]
- 57. Wade T, Rutt B. Comparison of current B1‐mapping techniques In Proceedings of the 15th Annual Meeting of ISMRM, Berlin, Germany, 2007. p. 354. [Google Scholar]
- 58. Morrell GR, Schabel MC. An analysis of the accuracy of magnetic resonance flip angle measurement methods. Phys Med Biol. 2010;55:6157–6174. [DOI] [PubMed] [Google Scholar]
- 59. Pohmann R, Scheffler K. A theoretical and experimental comparison of different techniques for B1 mapping at very high fields. NMR Biomed. 2013;26:265–275. [DOI] [PubMed] [Google Scholar]
- 60. Park DJ, Bangerter NK, Javed A, Kaggie J, Khalighi MM, Morrell GR. A statistical analysis of the Bloch‐Siegert B1 mapping technique. Phys Med Biol. 2013;58:5673–5691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. De Greef M, Kok HP, Correia D, Borsboom PP, Bel A, Crezee J. Uncertainty in hyperthermia treatment planning: the need for robust system design. Phys Med Biol. 2011;56:3233–3250. [DOI] [PubMed] [Google Scholar]
- 62. Balidemaj E, van Lier ALHMW, Crezee H, Nederveen AJ, Stalpers LJA, van den Berg CAT. Feasibility of electric property tomography of pelvic tumors at 3T. Magn Reson Med. 2015;73:1505–1513. [DOI] [PubMed] [Google Scholar]
- 63. Voigt T, Homann H, Katscher U, Doessel O. Patient‐individual local SAR determination: in vivo measurements and numerical validation. Magn Reson Med. 2012;68:1117–1126. [DOI] [PubMed] [Google Scholar]
- 64. Van de Kamer JB, De Leeuw AA, Hornsleth SN, Kroeze H, Kotte AN, Lagendijk JJ. Development of a regional hyperthermia treatment planning system. Int J Hyperthermia. 2001;17:207–220. [DOI] [PubMed] [Google Scholar]
- 65. Hargreaves B. Bloch Equation Simulator. http://mrsrl.stanford.edu/~brian/blochsim/.
- 66. Ku HH. Notes on the use of propagation of error formulas. J Res Natl Bur Stand Sect C Eng Instrum. 1966;70C:263. [Google Scholar]
- 67. Kellman P, McVeigh ER. Image reconstruction in SNR units: a general method for SNR measurement. Magn Reson Med. 2005;54:1439–1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Dietrich O, Raya JG, Reeder SB, Reiser MF, Schoenberg SO. Measurement of signal‐to‐noise ratios in MR images: influence of multichannel coils, parallel imaging, and reconstruction filters. J Magn Reson Imaging. 2007;26:375–385. [DOI] [PubMed] [Google Scholar]
- 69. Nehrke K, Versluis MJ, Webb A, Börnert P. Volumetric B1+ mapping of the brain at 7T using DREAM. Magn Reson Med. 2014;71:246–256. [DOI] [PubMed] [Google Scholar]
- 70. Khalighi MM, Sacolick LI, Rutt BK. Signal to noise ratio analysis of Bloch‐Siegert B1+ mapping In 18th Annual Meeting of ISMRM, Stockholm, Sweden, 2010. p. 2842. [Google Scholar]
- 71. Wan X, Wang W, Liu J, Tong T. Estimating the sample mean and standard deviation from the sample size, median, range and/or interquartile range. BMC Med Res Methodol. 2014;14:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Brink WM, Boernert P, Nehrke K, Webb AG. Ventricular B1+ perturbation at 7T—real effect or measurement artifact? NMR Biomed. 2014;27:617–620. [DOI] [PubMed] [Google Scholar]
- 73. Mandija S, Meliadò EF, Huttinga NRF, Luijten PR, van den Berg CAT. Opening a new window on MR‐based electrical properties tomography with deep learning. arXiv. arXiv:1804.00016 [physics.med‐ph]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Haase A, Frahm J, Matthaei D, et al. MR imaging using stimulated echoes (STEAM). Radiology. 1986;160:787–790. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
FIGURE S1 Effect of the transceive phase assumption on permittivity, for the phantom case. (a) Transceive phase error map, calculated as the difference between half of the transceive phase, ϕ±/2, and the transmit phase ϕ+; (b) permittivity map reconstructed with the transmit phase; and (c) permittivity map reconstructed with the transceive phase. An antisymmetric pattern appears in the permittivity when the transceive phase assumption is used. In (b) and (c), the input B1+ amplitude map was used


