The mixed model for the analysis of a repeated‐measurement multivariate count data

Abstract

Clustered overdispersed multivariate count data are challenging to model due to the presence of correlation within and between samples. Typically, the first source of correlation needs to be addressed but its quantification is of less interest. Here, we focus on the correlation between time points. In addition, the effects of covariates on the multivariate counts distribution need to be assessed. To fulfill these requirements, a regression model based on the Dirichlet‐multinomial distribution for association between covariates and the categorical counts is extended by using random effects to deal with the additional clustering. This model is the Dirichlet‐multinomial mixed regression model. Alternatively, a negative binomial regression mixed model can be deployed where the corresponding likelihood is conditioned on the total count. It appears that these two approaches are equivalent when the total count is fixed and independent of the random effects. We consider both subject‐specific and categorical‐specific random effects. However, the latter has a larger computational burden when the number of categories increases. Our work is motivated by microbiome data sets obtained by sequencing of the amplicon of the bacterial 16S rRNA gene. These data have a compositional structure and are typically overdispersed. The microbiome data set is from an epidemiological study carried out in a helminth‐endemic area in Indonesia. The conclusions are as follows: time has no statistically significant effect on microbiome composition, the correlation between subjects is statistically significant, and treatment has a significant effect on the microbiome composition only in infected subjects who remained infected.

1. INTRODUCTION

Microbiome data are overdispersed multivariate counts; for each sample, counts across multiple taxa are observed. If one is interested in the change of the microbiome composition over time, subjects are measured longitudinally.1 Such data are subject to two sources of correlation, namely, the correlation between the counts of a sample and between multiple samples across time of a subject. For this type of data, the available statistical models are still limited.

The microbiome data set considered in this paper is obtained by sequencing the amplicon of the bacterial 16S rRNA gene, where the sequencing procedure follows the HMP standardized protocol.2 Chimeric sequences were filtered out and the resulting sequences are either categorized based on similarity into operational taxonomical units followed by annotation or directly annotated using relevant databases (eg, Ribosomal Database Project, Greengenes, or Silva). The counts for a specific category represent the abundances of the bacteria at a biological taxonomy level. Data sets generated through this sequencing process comprise features that have not been adequately accounted for by currently available statistical methods.3 Firstly, the data set might be represented by a matrix of taxonomical counts with a compositional structure, which imposes a correlation between taxa.4 Secondly, overdispersion might exist due to unobserved heterogeneity in the sampling procedure, the presence of taxa with rare abundance (zero‐inflation), and pooling of categories. Another source might be differences in total sequence reads per sample, which might be caused by technical difficulties or by sampling or individual variability. This is commonly addressed by dividing the bacteria for each categories with the total count of the smallest reads (normalization), which results in a constant total bacterial count for all samples. Alternatively, an offset can be used in the model.

Our work is motivated by the microbiome measurements from an epidemiological study carried out in a helminth endemic rural area in Indonesia.5 The primary research question of this study is to analyze the joint effect of helminth infections and albendazole treatment on the microbial composition comprising multiple bacterial taxa. It has been hypothesized that the presence of helminths is linked with the microbial dysbiosis. However, recent findings report inconsistencies, probably due to limitation in the study design.1, 6, 7 For our study, the stool samples were collected and measured on a subset of subjects participating in a randomized placebo‐controlled trial. Thus, we included the microbiome data from infected subjects who received placebo, which makes our study unique. The bacterial count and the helminth infection status were assessed in samples before and 21 months after the first treatment. Details of the study can be found elsewhere.8 In a previous paper,5 we identified an effect of treatment on the microbiome composition in subjects who were infected at baseline and at follow up. This relationship was studied in the post‐treatment samples, whereas the microbiome composition at baseline was not used. Here, we model all the available data simultaneously and hence need to address the correlation structure.

The objective of this paper is to develop a parametric model for the analysis of the overdispersed multivariate count data in the repeated‐measurement setting. To date, several statistical parametric methods for analysis of microbiome data are available, which take into account the features of the data such as overdispersion and the presence of rare taxa. One approach is to consider a univariate taxa of interest and model the association of this taxa with biological covariates. Several regression models for this simplified problem exist. Zero‐inflated models or hurdle models have been proposed to deal with rare taxa.9 These models are also available for longitudinal studies. This approach however ignores the multivariate structure of the data. A second approach, which considers the compositional feature of the microbiome data, models the multivariate count outcome across taxa by a multinomial distribution. To deal with overdispersion, the underlying parameters are assumed to follow the conjugate distribution.10 This formulation has an advantage that the marginal distribution has a closed‐form formula.

The correlation due to repeated‐measurements within the same person is often modeled by including a normally distributed random effect in the linear predictor, ie, generalized linear mixed model. The overdispersion is typically accounted for by the conjugate distribution.10, 11, 12 Molenberghs et al13, 14 and Booth et al15 introduced a combined model, where the conjugate distribution for the overdispersion is used and the correlation over time is modeled by normally distributed random effects, ie, generalized linear mixed model. The authors only consider single categorical count data; hence, these models cannot be directly applied to our data, where we have to acknowledge the compositional feature. Therefore, in spirit of the combined model, we propose an extension of the Dirichlet‐multiomial regression model with random effects to incorporate the correlation due to repeated measurements. We will use the reparameterization of the work of Guimarães and Lindrooth,12 in which the overdispersion is a function of the covariates and the random effects.

This manuscript is organized as follows. In Section 2, we briefly describe the formulation of the loglinear model in the setting of multivariate count data and derive the likelihood of the multinomial distribution obtained by conditioning on the total count. We show the derivation of this method in the case where the count is overdispersed. The model is then extended to include the correlation due to repeated measurements over time. In Section 3, simulation studies are described to investigate the performance of the proposed methods and the results of the analyses of the motivating data set are presented in Section 4. In Section 5, we conclude and discuss the proposed method.

2. METHODS

A novel mixed model is considered for the relationship between counts of six phyla categories and the binary variables of infection status and treatment allocation before and after the first treatment round. Due to the normalization, the total count per sample is fixed at 2000 at each time point. Before introducing our new model, we will review various models for categorical count data in the cross‐sectional setting, namely, for independent count data (the loglinear and the multinomial logistic regression model) and for count data subject to overdispersion (the negative binomial and the Dirichlet‐multinomial model).16, 17

We first introduce the following notations. Let $C_i^{(t)}=\{C_{i1}^{(t)},\text{…},C_{iJ}^{(t)}\}$ be the J‐dimensional vector of the multivariate microbial count with $C_{ij}^{(t)}$ the abundance of bacteria taxa j ( j = 1,…,J) for subject i (i = 1,…,N) at time‐point t. The total count for each subject i at time‐point t is fixed and denoted as $C_{i+}^{(t)}={\sum }_{j=1}^J{C}_{ij}^{(t)}$. Let P be the number of categorical covariates and $X_i^{(t)}$ be the P‐dimensional vector of covariate values for subject i at time‐point t. When modeling microbiome data as described earlier, either the sequence count itself can be considered or the normalized count related to the total sequence read, ie, compositional data. Multiple counts distributed over categories are usually represented by a contingency table. We briefly review models for the cross‐sectional setting and therefore suppress the superscript t in the model formulation in Section 2.1.

2.1. Cross‐sectional setting

2.1.1. The loglinear model for two categorical variables

The loglinear model is commonly used to model the association between multivariate categorical count data and predictors of categorical or continuous value. In the case where all variables are categorical, the data can be represented by a contingency table. Consider two categorical variables E and F, with J and K levels, respectively. The count outcome c _jk is associated with the jth level of predictor E and kth level of predictor F, which could be described in a J × K contingency table (Table 1) as follows.

Table 1.

The J × K contingency table

		F
		k
	j	1	…	K
	1	c 11	…	c 1K
E	2	c 21	…	c 2K
	⋮	⋮	⋮	⋮
	J	c J1	…	c JK
Marginal		c +1	…	c +K

Each cell's count outcome c _jk is assumed to follow a Poisson distribution with a mean μ _jk. Here, the saturated loglinear model for such contingency table is given by

$$\log ({\mu }_{jk})={\lambda }_0+{\lambda }_j^E+{\lambda }_k^F+{\lambda }_{jk}^{EF},$$ (1)

where λ ₀, ${\lambda }_0+{\lambda }_j^E$, ${\lambda }_0+{\lambda }_k^F$, and ${\lambda }_0+{\lambda }_k^F+{\lambda }_j^E+{\lambda }_{jk}^{EF}$ represent the overall mean, the marginal mean of categorical variable E at the jth level, the marginal mean of variable F at the kth level, and the mean when variables E and F taking the value j and k, respectively. Because there are J × K cells, the J + K + JK + 1 parameters of the saturated loglinear model (1) are not uniquely identifiable and, thus, constraints are needed to ensure the model identifiability. Two sets of constraints are commonly used, namely, the baseline and the symmetrical constraint, given by

$$\begin{array}{ll}{\lambda }_1^E={\lambda }_1^F& ={\lambda }_{j1}^{EF}={\lambda }_{1k}^{EF}=0\\ & \text{and}\\ {\displaystyle \sum _{j=1}^J}{\lambda }_j^E={\displaystyle \sum _{k=1}^K}{\lambda }_k^F& ={\displaystyle \sum _{j=1}^J}{\lambda }_{j1}^{EF}={\displaystyle \sum _{k=1}^K}{\lambda }_{1K}^{EF}=0,\text{for all}j,k,\end{array}$$

respectively. In this manuscript, we use the baseline constraint.

Note that, in model (1), the response (bacterial categories) E and predictor F are exchangeable. The loglinear model (1) could be written in the regression format for the bacterial outcome as follows:

$$\log ({\mu }_{jk})={\xi }_{0j}+{\xi }_{1jk}[F=k],j=1,\text{…},J,k=1,\text{…},K,$$

with [.] as the indicator function. To show the equivalence between two models, note that the following j runs over the category and k runs over the predictor levels. For a subject with their predictor in category k = 1, the regression model {ξ ₀₁,ξ ₀₂,…ξ _0J} with ξ _0j for j = 2,…,J corresponds to ${\lambda }_0+{\lambda }_j^E$. For subjects with their predictor in other categories k, the regression model {ξ ₀₁ + ξ _11k,ξ ₀₂ + ξ _12k,…,ξ _0J + ξ _1Jk}, where ξ _1jk for j = 2,…J, corresponds to ${\lambda }_k^F+{\lambda }_{jk}^{EF}$. Thus, in the context of regression, the ${\lambda }_{jk}^{EF}$ represents the effect of the categorical variable F on outcome category j relative to the reference category.

To estimate the parameters, we assume that each cell's entry represents a realization from the Poisson distribution. The maximum likelihood estimate of λ or of ξ can be obtained by maximizing the following likelihood function. Specifically, for subject i, it is given by

$$\begin{array}{ll}{L}_i(\mathit{\lambda })& ={\prod }_j{f}_{\text{Pois}}(\mathit{\lambda };c_{ijk})\\ & ={\prod }_j\frac{\exp (-{\mu }_{jk}){\mu }_{jk}^{c_{ijk}}}{c_{ijk}!},\end{array}$$ (2)

where person i belongs to category k and has counts in each bacteria category  j. The model could be straightforwardly generalized to incorporate more categorical covariates, which results into more than two‐way contingency table. For instance, when incorporating the infection and treatment status, we will have a three‐way contingency table. As previously, the categorical variable E corresponds to the bacteria category, variable F to the treatment randomization arm, and G to the infection status. The corresponding loglinear model can be written as follows:

$$\begin{array}{ll}\log ({\mu }_{jkl})& ={\lambda }_0+{\lambda }_j^E+{\lambda }_k^F+{\lambda }_{jk}^{EF}+{\lambda }_l^G+{\lambda }_{jl}^{EG}+{\lambda }_{kl}^{FG}+{\lambda }_{jkl}^{EFG},j=2,\text{…},J;k=l=2\\ & \text{or in the regression format as}\\ & ={\xi }_{0j}+{\xi }_{1j}\text{Treatment}+{\xi }_{2j}\text{Infection}+{\xi }_{3j}\text{Treatment}\times \text{Infection},j=1,\text{…},J,k=l=1,2.\end{array}$$ (3)

Here, the baseline constraint is applied on the first equation, whereas, for the second equation, this is not needed because there are only J × P parameters. This last equation represents the loglinear model written in terms of regression coefficients ξ and covariate values, where Treatment and Infection are binary variables. To assess the statistical significance of the pth covariate (p = 1,…,P) on the multivariate count distribution, the null hypothesis ξ _p = 0 should be tested. We will use the standard likelihood ratio test, which follows a χ ² distribution with J degrees of freedom.

2.1.2. Multinomial logistic regression

In our data example, the total bacterial count is fixed to a constant for all samples. Under this constraint of a fixed total count, it is sufficient to model the counts for J − 1 categories and (J − 1) × P parameters are uniquely identified. Guimarães and Lindrooth12 showed that the distribution of the multivariate counts under the constraint that the total is a constant could be derived from the distribution of the unconstrained multivariate counts earlier by using the conditional log likelihood given the total count. When the counts in each category are independently Poisson distributed with mean μ _jkl, the total count c _+kl follows a Poisson distribution with mean ${\sum }_{j=1}^J{\mu }_{jkl}={\mu }_{+kl}$. The distribution of the multivariate counts conditional on the total for each subject i is therefore given by

$$\begin{array}{ll}\mathrm{Pr}({\mathit{c}}_i=\{c_{1kl},\text{…},c_{Jkl}\}|c_{+kl})& =\frac{\mathrm{Pr}(c_{1kl},\text{…},c_{Jkl},c_{+kl})}{\mathrm{Pr}(c_{+kl})}\\ & =\frac{{\displaystyle \prod _{j=1}^J}{f}_{\text{Pois}}(c_{jkl};{\mu }_{jkl})}{f_{\text{Pois}}(c_{+kl};{\mu }_{+kl})}=c_{+kl}!{\displaystyle \prod _{j=1}^J}\left(\frac{1}{c_{jkl}!}\right){\left(\frac{{\mu }_{jkl}}{{\mu }_{+kl}}\right)}^{c_{jkl}}\\ & \sim \text{Multinomial}(c_{+kl};{\pi }_{1kl},\text{…},{\pi }_{Jkl}),\text{where}{\pi }_{jkl}=\frac{{\mu }_{jkl}}{{\mu }_{+kl}}.\end{array}$$ (4)

Thus, under the baseline constraint and the constraint that the total count is fixed, the distribution of the multivariate count is equivalent to the multinomial distribution with parameter ${\pi }_j=\frac{{\mu }_j}{{\mu }_{+}}$. This model is the multinomial logistic regression model. Note that the parameters λ of the loglinear model (1) cancel out. In the multinomial logistic regression model, the parameters of the reference category are typically assumed to be equal to zero, although other constraints can be used as well.

2.1.3. Overdispersed count data

When the count data are overdispersed, the variance of the cell count is no longer equal to its expected value and the Poisson distribution cannot be used. A common approach to deal with overdispersion is to assume that the conditional mean of the count outcome is a random variable following the conjugate distribution. Consider a count at category j and let $\exp ({\eta }_{ij})$ be the random effect for overdispersion following the Gamma distribution (conjugate for Poisson) with parameter θ. Guimarães and Lindrooth formulated the model for an overdispersed count outcome as follows:

$$\begin{array}{ll}{C}_{ij}|\exp ({\eta }_{ij})& \sim \text{Pois}({\tilde{\mu }}_{ij}),j=1,\text{…},J\\ {\tilde{\mu }}_{ij}& =\exp ({\eta }_{ij}){\mu }_{ij},\text{where}\exp ({\eta }_{ij})\sim \mathrm{\Gamma }(\text{shape}={\theta }^{-1}{\mu }_{ij},\text{rate}={\theta }^{-1}{\mu }_{ij})\\ {\tilde{\mu }}_{ij}& =\exp ({\eta }_{ij}){\mu }_{ij}\sim \mathrm{\Gamma }(\text{shape}={\theta }^{-1}{\mu }_{ij},\text{rate}={\theta }^{-1}).\end{array}$$

Here, μ _ij corresponds to the mean of the count in the nonoverdispersed model. Now, the marginal distribution for the count at category j in person i, C _ij, can be obtained by integrating out the random effect $\exp \left({\eta }_{ij}\right)$ as

$$\begin{array}{ll}\mathrm{Pr}(C_{ij})& ={\displaystyle \underset{0}{\overset{\infty }{\int }}}\mathrm{Pr}(C_{ij}|\exp ({\eta }_{ij}))g(\exp ({\eta }_{ij}))d\exp ({\eta }_{ij})\\ & =\frac{\mathrm{\Gamma }({\theta }^{-1}{\mu }_{ij}+C_{ij})}{C_{ij}!\mathrm{\Gamma }({\theta }^{-1}{\mu }_{ij})}{\left(\frac{1}{{\theta }^{-1}+1}\right)}^{C_{ij}}{\left(\frac{{\theta }^{-1}}{{\theta }^{-1}+1}\right)}^{{\theta }^{-1}{\mu }_{ij}}.\end{array}$$

This corresponds to a negative binomial distribution with parameters $\left({\theta }^{-1}{\mu }_{ij},\frac{{\theta }^{-1}}{1+{\theta }^{-1}}\right)$. By the properties of the negative binomial random variable, the total count for subject i also follows the negative binomial distribution

$$C_{i+}\sim \mathrm{NB}\left({\theta }^{-1}{\mu }_{i+},\frac{{\theta }^{-1}}{1+{\theta }^{-1}}\right).$$

The likelihood for subject i in this setting is given by

$$\begin{array}{ll}{L}_i\left(\theta ,\mathit{\lambda }\right)& =\prod _j{f}_{\text{NB}}\left(\mathit{\lambda },\theta ;C_{ij}\right)\\ & =\prod _j\frac{\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{ij}+C_{ij}\right)}{C_{ij}!\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{ij}\right)}{\left(\frac{1}{{\theta }^{-1}+1}\right)}^{C_{ij}}{\left(\frac{{\theta }^{-1}}{{\theta }^{-1}+1}\right)}^{{\theta }^{-1}{\mu }_{ij}}.\end{array}$$ (5)

Note that, in this setting, parameter θ, which models the overdispersion and the intercept λ ₀, is not identifiable. An often used solution is to absorb the overdispersion parameter into the grand mean λ ₀, ie, ${\theta }^{-1}\exp ({\lambda }_0)={\delta }_0^{-1}$.12

2.1.4. Overdispersed multinomial

We briefly review the overdispersed count data introduced by Guimarães and Lindrooth as follows. To guarantee that the parameters of the count for each category follows a Gamma distribution with the same rate parameter, the overdispersion parameter $\exp ({\eta }_{ij})$ needs to be a function of the linear predictor μ _ij. For such a distribution, theorem 1 in the work of Mossiman18 can be applied. This theorem states that, if C _i = {C _i1,C _i2,…,C _iJ} are independently Gamma distributed random variables with parameters $({\tilde{\mu }}_{i1},{\tilde{\mu }}_{i2},\text{…},{\tilde{\mu }}_{iJ})$ with the same scale parameter θ ⁻¹, then the random variables Π _i = {Π_i1,Π_i2,…,Π_i J} with ${\mathrm{\Pi }}_{ij}=\frac{C_{ij}}{{\sum }_{j=1}^J{C}_{ij}}$ have a multivariate beta distribution (Dirichlet distribution) with parameters $\{{\tilde{\mu }}_{i1},{\tilde{\mu }}_{i2},\text{…},{\tilde{\mu }}_{iJ}\}$. Note that the Dirichlet distribution is the conjugate for the multinomial distribution. Hence, the marginal distribution for the random variable Π _i is obtained by integrating out the Dirichlet random effects. Now, the corresponding Dirichlet‐multinomial distribution is given by

$$\begin{array}{ll}\mathrm{Pr}({\mathbf{\Pi }}_i)=\frac{\mathrm{\Gamma }({\tilde{\mu }}_{i+})C_{i+}!}{\mathrm{\Gamma }({\tilde{\mu }}_{i+}+C_{i+})}{\displaystyle \prod _{j=1}^J}\frac{\mathrm{\Gamma }({\tilde{\mu }}_{ij}+C_{ij})}{\mathrm{\Gamma }({\tilde{\mu }}_{ij})C_{ij}!}.& \end{array}$$ (6)

Alternatively, we consider the conditional likelihood of the multivariate negative binomial given the total count. The contribution for the ith subject is given by

$$\begin{array}{ll}{L}_i(\mathit{\lambda },\theta )=\mathrm{Pr}({\mathit{C}}_i|C_{i+})& =\frac{{\prod }_{j=1}^J{f}_{\text{NB}}(C_{ij};{\tilde{\mu }}_{ij})}{f_{\text{NB}}(C_{i+};{\tilde{\mu }}_{i+})}\\ & =\frac{\mathrm{\Gamma }({\theta }^{-1}{\mu }_{i+})C_{i+}!}{\mathrm{\Gamma }({\theta }^{-1}{\mu }_{i+}+C_{i+})}{\displaystyle \prod _{j=1}^J}\frac{\mathrm{\Gamma }({\theta }^{-1}{\mu }_{ij}+C_{ij})}{\mathrm{\Gamma }({\theta }^{-1}{\mu }_{ij})C_{ij}!}.\end{array}$$ (7)

By ${\tilde{\mu }}_{ij}={\theta }^{-1}{\mu }_{ij}$, it follows that the likelihood (7) is equivalent to the Dirichlet‐multinomial distribution (6). Here, parameter θ is unidentifiable. Similar to (5), we apply the parameterization in the work of Guimarães and Lindrooth,12 where the overdispersion is absorbed in the grand mean λ ₀ such that ${\theta }^{-1}\exp ({\lambda }_0)={\delta }_0^{-1}$ in the reference category. In contrast to the nonoverdispersed multinomial model, the intercepts of the overdispersed multinomial model do not cancel out.

2.2. Repeated‐measurement of overdispersed count

In addition to the overdispersion due to the presence of multiple bacteria within one sample, there is also correlation between measurements of the same person at the two time‐points, ie, at the pre‐ and post‐treatment. To deal with this correlation, we propose to include a random effect u _i in the linear predictor of the model and assume that, conditional on this random effect, the observations of the two time points are independent. We further assume that the random effect u _i follows a normal distribution with zero mean and variance ${\sigma }_u^2$. The idea of using different distributions for the random effects representing overdispersion and correlation was introduced by Molenberghs et al13, 14 and Booth et al.15 Molenberghs and Booth modeled the mean of an outcome as a multiplication of overdispersion and the linear predictor. However, to guarantee that the theorem 1 in the work of Mossimann holds, ie, that the proportion of each bacterial category has Dirichlet‐multinomial distribution, we need to model the overdispersion as a function of the linear predictor.

In the rest of this section, we describe three different mixed models for multivariate count data with overdispersion in the repeated‐measurement setting using random effects, conditional on the random effect u _i: the counts follow the multivariate negative binomial distribution; the counts follow the conditional multivariate negative binomial distribution given the total count; and the proportions (cell's count divided by total count) follow the Dirichlet‐multinomial distribution. In all models, we will add the random effect u _i to the linear predictor. These models are therefore extensions of the models for overdispersed multivariate count given in Section 2.1. Specifically, for the first model, we assume that, conditional on the random effects $\exp \left({\eta }_{ij}^{(t)}\right)$ and u _i, the count $C_{ij}^{(t)}$ follows a Poisson distribution with mean equal to

$$\begin{array}{ll}\mathrm{E}\left[C_{ij}^{(t)}\left|\exp \left({\eta }_{ij}^{(t)}\right)\right.,u_i\right]& =\exp \left({\eta }_{ij}^{(t)}\right)\exp \left({\tilde{\mu }}_{ij}^{(t)}\right),\text{where}{\tilde{\mu }}_{ij}^{(t)}={\mathit{X}}_i{\mathit{\xi }}_j+u_i,j=1,\text{…},J.\\ \exp \left({\eta }_{ij}^{(t)}\right)& \sim \mathrm{\Gamma }\left(\text{shape =}{\theta }^{-1}\exp \left({\tilde{\mu }}_{ij}^{(t)}\right),\text{rate =}{\theta }^{-1}\exp ({\mathit{X}}_i{\mathit{\xi }}_j+u_i)\right).\end{array}$$ (8)

Thus, given the random effect u _i, the two vectors of counts $C_i^{(t)}$ for t = 1 and t = 2 are independently distributed and follow the negative binomial distribution. The corresponding likelihood can be written as follows:

$$\begin{array}{ll}{L}_{\text{UNBM}}\left(\mathit{\xi },\theta ,{\sigma }_u^2\right)=\prod _i\mathrm{Pr}\left({\mathit{C}}_i^{(t)}\right)& =\prod _i\underset{u_i}{\int }\mathrm{Pr}\left(C_{i1}^{(t)},\text{…},C_{iJ}^{(t)},u_i\right)d{u}_i\\ & =\prod _i\underset{u_i}{\int }{\displaystyle \prod _{t=1}^2}{\displaystyle \prod _{j=1}^J}\mathrm{Pr}\left(C_{ij}^{(t)}|u_i\right)\mathrm{Pr}\left(u_i\right)d{u}_i,\end{array}$$ (9)

and we denote the regression model under this likelihood to be the unconstrained negative‐binomial mixed model (UNBM).

For the second approach, we consider the counts following the conditional multivariate distribution given the total count. When each categorical count conditional on the total count follows the negative binomial with the same rate parameter, the total count $C_{i+}^{(t)}|u_i$ follows the negative binomial distribution with parameters $\left({\sum }_{j=1}^J\exp \left({\eta }_{ij}^{(t)}\right)\exp \left({\tilde{\mu }}_{ij}^{(t)}\right),\frac{{\theta }^{-1}}{1+{\theta }^{-1}}\right)$. Thus, the corresponding conditional likelihood is given by

$$\begin{array}{ll}{L}_{\text{CNBM}}\left(\mathit{\xi },\theta ,{\sigma }_u^2\right)=\prod _i\mathrm{Pr}\left({\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)}\left|C_{i+}^{(1)},C_{i+}^{(2)}\right.\right)& ={\text{∏}}_i\frac{{\int }_{u_i}\mathrm{Pr}\left(\left.{\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)},C_{i+}^{(1)},C_{i+}^{(2)}\right|u_i\right)\mathrm{Pr}\left(u_i\right)d{u}_i}{{\int }_{u_i}\mathrm{Pr}\left(C_{i+}^{(1)},C_{i+}^{(2)},u_i\right)d{u}_i}\\ & ={\text{∏}}_i\frac{{\int }_{u_i}{\prod }_{t=1}^2{\prod }_{j=1}^2\mathrm{Pr}\left(\left.C_{ij}^{(t)}\right|u_i\right)\mathrm{Pr}(u_i)d{u}_i}{{\int }_{u_i}{\prod }_{t=1}^2\mathrm{Pr}\left(\left.C_{i+}^{(t)}\right|u_i\right)\mathrm{Pr}(u_i)d{u}_i}.\end{array}$$ (10)

The model corresponding to this likelihood is denoted as the conditional negative‐binomial mixed model (CNBM). However, when the total counts depends on u _i, the total count should be a random variable. This is not the case in our data set. Therefore, we propose the third method with the assumption that the total count is independent of u _i.

In the third approach, we model the multivariate counts in terms of the relative abundance. We assume that the vector of proportions ${\mathrm{\Pi }}_i^{(t)}$ conditional on the random effect u _i follows the Dirichlet multinomial distribution, ie,

$$\begin{array}{ll}\left.\left\{\frac{C_{i1}^{(t)}}{C_{i+}^{(t)}},\text{…},\frac{C_{i1}^{(t)}}{C_{i+}^{(t)}}\right\}\right|\left\{{\alpha }_{i1}^{(t)},\text{…},{\alpha }_{ij}^{(t)}\right\},u_i& \sim \text{Mult}\left({\tilde{\pi }}_{i1}^{(t)},\text{…},{\tilde{\pi }}_{iJ}^{(t)}\right)\\ \left\{{\tilde{\pi }}_{i1}^{(t)},\text{…},{\tilde{\pi }}_{iJ}^{(t)}\right\}& \sim \text{Dir}\left({\alpha }_{i1}^{(t)},\text{…},{\alpha }_{iJ}^{(t)}\right)\\ {\alpha }_{ij}^{(t)}& ={\theta }^{-1}{\mu }_{ij}^{(t)},\end{array}$$ (11)

where ${\mu }_{ij}^{(t)}$ is the linear predictor as in the loglinear model for the Poisson count. With this parameterization, the expected multinomial parameter becomes

$${\tilde{\pi }}_{ij}^{(t)}=\frac{\exp \left({\eta }_{ij}^{(t)}\right)\exp \left({\tilde{\mu }}_{ij}^{(t)}\right)}{{\sum }_{j=1}^J\exp \left({\eta }_{ij}^{(t)}\right)\exp \left({\tilde{\mu }}_{ij}^{(t)}\right)}.$$

The likelihood for each subject i is then formulated as follows:

$$\begin{array}{ll}{L}_{\text{DMM}}\left(\mathit{\xi },\theta ,{\sigma }_u^2\right)=\mathrm{Pr}\left(\frac{{\mathit{C}}_i^{(1)}}{C_{i+}^{(1)}},\frac{{\mathit{C}}_i^{(2)}}{C_{i+}^{(2)}}\right)& =\underset{u_i}{\int }\mathrm{Pr}\left(\left.\frac{{\mathit{C}}_i^{(1)}}{C_{i+}^{(1)}},\frac{{\mathit{C}}_i^{(2)}}{C_{i+}^{(2)}}\right|u_i\right)\mathrm{Pr}\left(u_i\right)d{u}_i\\ & =\underset{u_i}{\int }{\displaystyle \prod _{t=1}^2}\frac{\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{i+}^{(t)}\right)C_{i+}^{(t)}!}{\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{i+}^{(t)}+C_{i+}^{(t)}\right)}{\displaystyle \prod _{j=1}^J}\frac{\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{ij}^{(t)}{C}_{ij}^{(t)}\right)}{\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{ij}^{(t)}\right)C_{ij}^{(t)}!}\mathrm{Pr}\left(u_i\right)d{u}_i.\end{array}$$ (12)

The corresponding regression model under this likelihood is denoted as the Dirichlet‐multinomial mixed model (DMM). It is shown in Appendix A that, in the case where the total count does not depend on the random effect u _i, the likelihoods (10) and (12) are equivalent.

The variance of the random effect u ( ${\sigma }_u^2$) represents the correlation between the samples of the same subject across time. However, this value is hard to interpret and the marginal correlation between categorical count outcomes might be more interesting. This correlation is given by

$$\begin{array}{ll}\text{Corr}\left({C_{ij}}^{(t)},C_{i{j}^{\ast }}^{(t^{\ast })}\right)=\frac{{\sigma }_{{C_{ij}}^{(t)},C_{i{j}^{\ast }}^{(t^{\ast })}}}{\sqrt{{\sigma }_{C_{ij}^{(t)}}^2·{\sigma }_{C_{i{j}^{\ast }}^{(t^{(\ast )})}}^2}}.& \end{array}$$

The marginal correlation can be computed from Monte‐Carlo estimates of the first and second moments.

The program language R is used for all the computations except for data application with categorical‐specific random effects. When maximizing the likelihoods, the integrals are approximated by the adaptive Gauss‐Hermite quadrature method,19 and we used the functions available in the ecoreg package20 to compute the integral. R implementations are available in github (https://github.com/IvonneMartin/CombinedMultinomial).

2.3. The categorical‐specific random effect

In the aforementioned parameterization, we assume that the subject‐specific effect u _i is univariate and is the same for all bacteria categories and time points. Alternatively, a J‐dimensional vector of random effects can be used. Equation (8) now becomes

$$\begin{array}{ll}{\tilde{\mu }}_{ij}^{(t)}& ={\mathit{X}}_i{\mathit{\xi }}_j+u_{ij},j=1,\text{…},J.\\ u_{ij}& \sim \text{MVN}\left(\mathbf{0},{\mathrm{\Delta }}_{J\times J}\right).\end{array}$$ (13)

Here, each bacterial category has its own realization of the random effect and the random effects solely model correlation between the categories over time. The vector u _i of length J follows a multivariate normal distribution with a J by J diagonal variance matrix Δ with ${\sigma }_j^2$ as diagonal elements. In addition to the general model (13), we consider a model with common variance ${\sigma }_j^2={\sigma }_u^2$, for all j, to reduce the parameter space. Since the overdispersion already takes care of the correlation among the categories, this model might be better interpretable. However, a drawback of this model is that computation of the likelihood function involves an intractable J‐dimensional integral.

3. SIMULATION STUDY

3.1. Simulation setting

Three sets of simulation studies were conducted to evaluate the performance of the proposed methods. With regard to estimation of the fixed effect parameters and variance components, we first investigated the performance of the DMM models for a subject‐ and categorical‐specific random effects. We reported the bias and MSE as well as the sensitivity and specificity for these parameters. The sensitivity and the specificity of the likelihood ratio test statistics were computed for the following pairs of hypotheses (for fixed and variance of random effect, respectively):

$$\begin{array}{ll}{\mathrm{H}}_0& :{\mathit{\xi }}_p=\mathbf{0}\text{vs}{\mathrm{H}}_1:\text{at least one of}{\mathit{\xi }}_p\ne 0,\\ {\mathrm{H}}_0& :{\sigma }_u^2=0\text{vs}{\mathrm{H}}_1:{\sigma }_u^2>0.\end{array}$$

In the second set, we want to estimate the marginal correlation given the distribution of the random effect. The purpose of this study is to verify whether the marginal intraclass correlation observed in our motivating data set can be represented by our models (UNBM and DMM). For this purpose, we vary the standard deviation of the random effect and we used 10 000 Monte‐Carlo simulation for estimating the marginal intraclass correlation.

In the third set, we aimed to study the robustness of the parameter estimates by fitting the DMM models when the true model is UNBM. For this purpose, we generated data sets with three categories from the UNBM model.

3.1.1. Data set generation

To reduce the computational burden, data sets with only three categories at two different time‐points t were considered. The total count per sample S was 25, 50, or 2000, and the number of samples N was 150 or 500. Two sets of parameters were used, namely, λ was fixed at $\{{\lambda }_2^F,{\lambda }_2^E,{\lambda }_3^E,{\lambda }_{22}^{EF},{\lambda }_{32}^{EF}\}=\{0.5,-1,0.1,0.8,-2\}$ as well as the parameters from the data set (results are given in Supporting Information Table S1). To increase the power, the parameter values of the first set are relatively larger. Note that the parameter λ ₀ is fixed at zero to guarantee identifiability of the overdispersion parameter. The overdispersion parameter was fixed at θ = 0.1. For the standard deviation of the random effects, we considered values σ _u of 0.5, 0.8, and 1.

Specifically, for the Dirichlet‐multinomial mixed (DMM) model with a univariate random effect, multivariate counts were generated as follows.

1. For each subject i,i = 1,…,N, we randomly generate binary covariates $X_i^t$ for each time‐point t and a random effect $u_i\sim N(0,{\sigma }_u^2)$.

2. The mean for each category j is computed as ${\tilde{\mu }}_{ij}^{(t)}={\theta }^{-1}\exp (\mathit{\lambda }+u_i)$, where λ correspond to ξ.

3. A multivariate count with mean ${\tilde{\mu }}_{ij}^{(t)}$ is generated.

For the DMM model with multivariate random effect, a similar procedure was used except that the random effects in step (1) are now generated from the multivariate normal distribution with a diagonal covariance matrix Σ. We considered three sets of values for the standard deviations of random effects, namely, ${\mathit{\sigma }}_u=({\sigma }_{u_1},{\sigma }_{u_2},{\sigma }_{u_3})$ is (0.5,0.6,0.5), (0.8,0.9,0.8), or (1,0.9,1).

For the second set of simulation, six bacterial categories are used and parameters for the simulation are obtained from the data set. Finally, for the unconstrained negative binomial mixed (UNBM) model, the second step was replaced by computation of the expected count outcome for each category j of ${\tilde{\mu }}_{ij}={\theta }^{-1}\exp (\log (S)+\mathit{\lambda }+u_i)$. Here, the offset $\log (S)$ is incorporated to take into account the total bacteria count S. For each scenario mentioned earlier, 1000 replicates were generated. The models were fitted to each of the replicates.

3.2. Simulation results

3.2.1. Evaluation of DMM model

The performance of the method in estimating the parameters is described in Figure 1. Overall, the bias and MSE appear to be improved when either the total bacterial count (from S = 25 to S = 50 and the sample size was N = 500) or the sample size was increased (from N = 150 to N = 500 and the total count was S = 2000). For a small value of ${\sigma }_u$, both the bias and the MSE of this estimate are relatively large. Similar results are obtained for the model with categorical‐specific random effects (Figure S1). The sensitivity of the likelihood ratio test for the fixed effects parameters that are obtained from the data set are very low for all scenarios except when the total sample size is large (Table S2A). For testing the zero variance component, the likelihood ratio test has a high sensitivity and specifity when the sample size and variance component are large (Table S2B).

Figure 1.

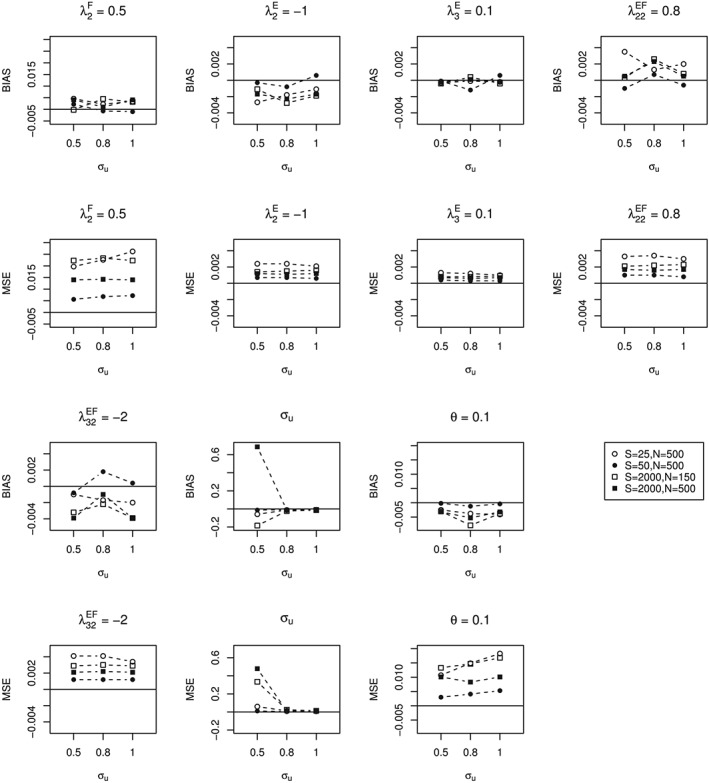
Bias and mean squared error (MSE) of data sets generated from the Dirichlet‐multinomial mixed model with subject‐specific random effect. λ: a vector of parameters in loglinear model. σ _u: the standard deviation of the between individual variation. θ the overdispersion

Since the model with the categorical‐specific random effect is time consuming to fit, we also investigate the robustness of assuming a subject‐specific random effect, whereas the data sets were generated by using a vector of random effects following the multivariate normal distribution. The results are given in Table 2. It appears that, for a random effect with smaller standard deviation ( $\log ({\sigma }_u)$ of −1.309), the biases of the estimates of fixed effect parameters and of $\log ({\sigma }_u)$ are relatively small, whereas, for a random effect with larger standard deviation $\log ({\sigma }_u)=0$ (σ _u of 1), the biases are relatively large.

Table 2.

The mean estimates (standard deviation) over 1000 replicates when data sets were generated from the Dirichlet‐multinomial mixed model with categorical‐specific random effect with common variance

	${\mathit{\lambda }}_{\mathbf{2}}^{\mathit{F}}=$ 0.5	${\mathit{\lambda }}_{\mathbf{2}}^{\mathit{E}}=$ −1	${\mathit{\lambda }}_{\mathbf{3}}^{\mathit{E}}=$ 0.1	${\mathit{\lambda }}_{\mathbf{22}}^{\mathit{E}\mathit{F}}=$ 0.8	${\mathit{\lambda }}_{\mathbf{32}}^{\mathit{E}\mathit{F}}=$ −2	$\mathbf{\text{log}}\left({\mathit{\sigma }}_{\mathit{u}}\right)=$ −1.309	$\mathbf{\text{log}}(\mathit{\theta })=$ −2.302	Loglik
Subj‐sp	0.418(0.130)	−0.959(0.059)	0.096(0.050)	0.765(0.071)	−1.900(0.075)	−1.680(0.754)	−1.886(0.094)	−3918.581(18.333)
Cat‐sp	0.438(0.172)	−1.007(0.116)	0.108(0.109)	0.809(0.084)	−2.017(0.086)	−0.704(0.005)	−2.366(0.125)	−3961.971(14.865)
	${\mathit{\lambda }}_{\mathbf{2}}^{\mathit{F}}=$ 0.5	${\mathit{\lambda }}_{\mathbf{2}}^{\mathit{E}}=$ −1	${\mathit{\lambda }}_{\mathbf{3}}^{\mathit{E}}=$ 0.1	${\mathit{\lambda }}_{\mathbf{22}}^{\mathit{E}\mathit{F}}=$ 0.8	${\mathit{\lambda }}_{\mathbf{32}}^{\mathit{E}\mathit{F}}=$−2	$\mathbf{\text{log}}\left({\mathit{\sigma }}_{\mathit{u}}\right)=$ −0.693	$\mathbf{\text{log}}(\mathit{\theta })=$ −2.302	Loglik
Sub‐sp	0.359(0.130)	−0.882(0.080)	0.096(0.077)	0.695(0.088)	−1.739(0.095)	−0.973(0.334)	−1.320(0.099)	−4064.461(18.503)
Cat‐sp	0.462(0.170)	−1.000(0.122)	0.110(0.117)	0.794(0.085)	−1.997(0.083)	−0.607(0.028)	−2.253(0.129)	−3988.959(16.392)
	${\mathit{\lambda }}_{\mathbf{2}}^{\mathit{F}}=$ 0.5	${\mathit{\lambda }}_{\mathbf{2}}^{\mathit{E}}=$ −1	${\mathit{\lambda }}_{\mathbf{3}}^{\mathit{E}}=$ 0.1	${\mathit{\lambda }}_{\mathbf{22}}^{\mathit{E}\mathit{F}}=$ 0.8	${\mathit{\lambda }}_{\mathbf{32}}^{\mathit{E}\mathit{F}}=$ −2	$\mathbf{\text{log}}\left({\mathit{\sigma }}_{\mathit{u}}\right)=$ −0.223	$\mathbf{\text{log}}(\mathit{\theta })=$ −2.302	Loglik
Sub‐sp	0.300(0.132)	−0.766(0.099)	0.092(0.105)	0.602(0.11)	−1.509(0.121)	−0.766(0.196)	−0.698(0.112)	−4171.966(17.482)
Cat‐sp	0.455(0.194)	−1.004(0.173)	0.099(0.17)	0.795(0.089)	−1.985(0.096)	−0.237(0.049)	−2.235(0.165)	−4011.262(19.136)
	${\mathit{\lambda }}_{\mathbf{2}}^{\mathit{F}}=$ 0.5	${\mathit{\lambda }}_{\mathbf{2}}^{\mathit{E}}=$ −1	${\mathit{\lambda }}_{\mathbf{3}}^{\mathit{E}}=$ 0.1	${\mathit{\lambda }}_{\mathbf{22}}^{\mathit{E}\mathit{F}}=$ 0.8	${\mathit{\lambda }}_{\mathbf{32}}^{\mathit{E}\mathit{F}}=$ −2	$\mathbf{\text{log}}\left({\mathit{\sigma }}_{\mathit{u}}\right)=$ 0	$\mathbf{\text{log}}(\mathit{\theta })=$ −2.302	Loglik
Sub‐sp	0.270(0.129)	−0.691(0.112)	0.092(0.117)	0.541(0.122)	−1.376(0.133)	−0.699(0.187)	−0.367(0.117)	−4193.591(19.342)
Cat‐sp	0.449(0.200)	−1.003(0.213)	0.100(0.197)	0.795(0.088)	−1.985(0.101)	−0.020(0.046)	−2.225(0.177)	−3993.517(23.146)

Each rows started with Sub‐sp represents the estimates (standard deviation) when data sets were fitted with the DMM model with subject‐specific random effect and rows started with Cat‐sp represents the estimates (standard deviation) when data sets were fitted with DMM model with categorical‐specific random effect having common variance.

λ,σ _u,θ are as explained in Figure 1.

Loglik represents the loglikelihood value obtained using the corresponding model.

Rows in gray represent the estimation when the standard deviation of the normally distributed random effect is small.

In Table S3, the marginal correlations are given for the subject‐specific random effects. It appears that the correlation between categories are all negative and the correlation between samples across time are very small. These results are not affected by the standard deviation of the random effect for our considered values. Table S4 lists the marginal correlations using categorical‐specific random effects, where each category‐specific random effect has the same standard deviations σ _u. We notice that a part of the correlations between categories is now positive and the correlation between the same categories across time is larger. Moreover, these correlations tend to increase with a larger variance of the random effects.

3.2.2. Simulations under the UNBM model

The marginal correlations for the UNBM with a subject‐specific random effect are listed in Table S5. It appears that the correlations between categories are positive as well as negative. The correlations of the same category between time points are all positive and increase with σ _u. A similar result is observed for the UNBM model with categorical‐specific random effects (Table S6) although, here, the correlation varies more across categories.

Next, we investigated the robustness of the models. Data sets were generated using the multivariate negative binomial mixed model without conditioning on the total count (UNBM model). The results of fitting the unconditional multivariate negative binomial mixed model (UNBM), the multivariate negative binomial mixed model conditional on the total (CNBM), and the Dirichlet‐multinomial mixed model (DMM) are given in Figure 2 for the fixed effect parameters and Figure 3 for the variance component.

Figure 2.

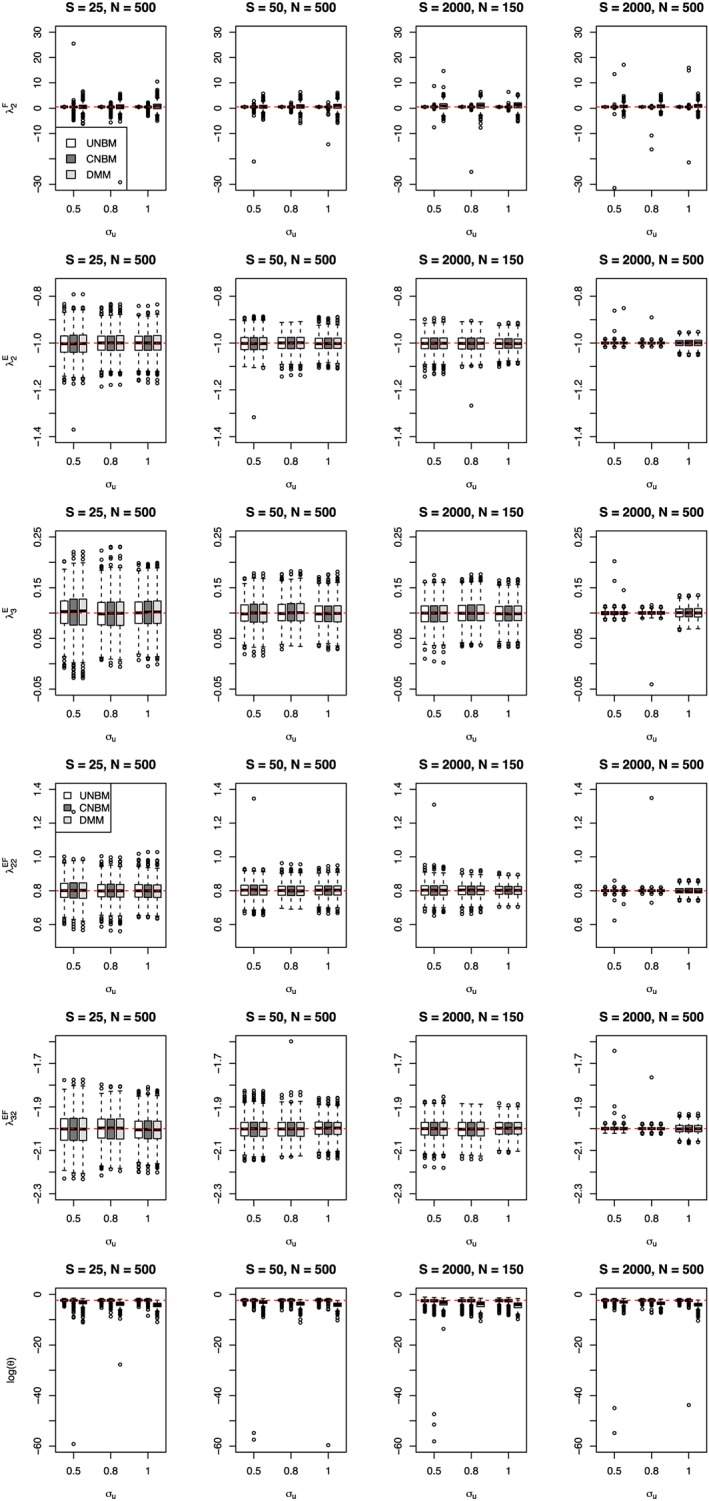
Estimates of the fixed effect and overdispersion parameters obtained from three different models (UNBM, CNBM, and DMM) when data sets were generated using UNBM model. CNBM, conditional negative‐binomial mixed model; DMM, Dirichlet‐multinomial mixed; UNBM, unconstrained negative binomial mixed [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 3.

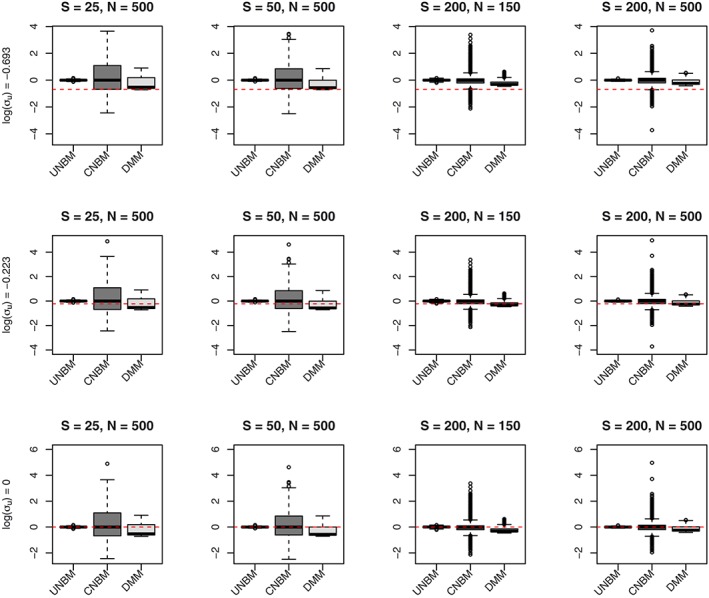
Estimates for the variance components obtained from three different models (UNBM, CNBM, and DMM) when data sets were generated using the UNBM model. CNBM, conditional negative‐binomial mixed model; DMM, Dirichlet‐multinomial mixed; UNBM, unconstrained negative binomial mixed [Colour figure can be viewed at wileyonlinelibrary.com]

In general, the fixed effect parameters obtained from these three different models are unbiased except the estimates of the intercepts ( ${\lambda }_2^F$) for the CNBM model and the DMM model. Since the model used for analysis and generating the data are the same, the estimates of the fixed effect parameters in Figure 2 are unbiased and the variance of the estimator decreases when the total count was increased (from S = 25 to S = 50) or the sample size is increased (from N = 150 to N = 500). When using the conditional distribution, given the total, the estimates of the fixed effect parameters in Figure 2 are biased when the total bacterial count is small (S = 25 and S = 50). When the total count is relatively large (S = 2000), the estimates of the fixed effects (including the intercept ${\lambda }_2^F$) are less biased. When estimating the fixed effect parameters using the DMM model, the estimate of the fixed effects are unbiased except for the intercept term ${\lambda }_2^F$ and increasing the sample size does not improve the estimation.

The estimates of the random effect parameters in the UNBM model are unbiased and, by increasing the total bacterial count or the sample size, improve the precision. In the CNBM model, when the total bacterial count is small (S = 25 and S = 50), we observe that the standard deviation of u _i is overestimated and that the bias in the estimate of the overdispersion parameter is small. When the total count is large S = 2000, the estimate of the standard deviation of u _i appears to be less biased, whereas the overdispersion parameters are underestimated. When fitting the DMM model to the data, the estimates of the random effect parameters are biased in all scenarios.

4. DATA APPLICATION

We used the DMM models to analyze the effect of helminth infections and treatment on microbiome composition. For this purpose, we first consider the fixed effect structure and fitted several DMM models to our data set assuming (common) random effect for each category. Next, we will investigate the best random effect structure and we will verify whether the parameter estimates of the fixed effects are affected by the random effect structure.

The microbiome data set considered here was measured in a subset of a randomized clinical trial performed in a helminth‐endemic area in Nangapanda subdistrict, Indonesia, described elsewhere8 and is publicly available at Nematode.net (http://nematode.net/Data/Indonesia_16S/S1_Table.xlsx). In brief, households were randomized to receive either a single dose of 400 mg albendazole or placebo, once every three months for a period of one and a half years. To assess the effect of treatment on the prevalence of soil transmitted helminth infections, yearly stool samples were collected on a voluntary basis. T. trichiura infection was detected by microscopy and a multiplex real‐time PCR was used to detect the DNA of hookworm (Ancylostoma duodenale or Necator americanus) and Ascaris lumbricoides. A subject was regarded as infected if it was infected with at least one helminth species.

For the current study, paired DNA samples before and at 21 months after the first treatment round from 150 inhabitants in Nangapanda were selected based on the treatment allocation and infection status, as well as the availability of complete stool data at pre‐ and post‐treatment. The procedure for sample collection and processing was already described in the work of Wiria et al.8 The 16s rRNA gene from the stool samples was processed through the 454 pyrosequencing technique, and the classification of the sequence resulted in counts of 18 bacterial phyla. For the current analyses, we retained the five most prevalent phyla and pooled the remaining into one category, resulting in six phyla categories: Actinobacteria, Bacteroidetes, Firmicutes, Proteobacteria, unclassified, and pooled category.

The description of relative abundance of each bacterial phyla at each time points is given in Table S7. Firmicutes has the highest relative abundance at each time points (around 68%), followed by Actinobacteria (around 12%), Proteobacteria (around 10%), Bacteroidetes (around 6%), and unclassified and pooled category (each around 1%). The dispersions are estimated by the ratio between the variance and mean. All bacteria counts show dispersion larger than 1, indicating the presence of overdispersion. Since zero‐inflation might lead to overdispersion, we investigated the number of the samples with zero counts for the six categories at the two time points. Only for the following three categories, a small number of samples with zero counts was observed: Bacteroidetes (5 samples at post‐treatment), unclassified bacteria (1 at pre‐treatment and post‐treatment), and the pooled category (15 at pretreatment and 6 at posttreatment). The corresponding histograms can be found in Figure S2. From this, we conclude that zero‐inflation is not present, hence the overdispersion is probably caused by other sources. We will therefore account overdispersion by additional random effects.

Table 3 gives the observed correlations between categories and of categories between time points. The order j for $C_j^{(t)}$ are Firmicutes, Actinobacteria, Bacteroidetes, Proteobacteria, and unclassified and pooled category. The observed correlations between Firmicutes and the three most abundant bacteria (Actinobacteria, Proteobacteria, and Bacteroidetes) are relatively high and negative (around −0.50), indicating an increase of Firmicutes corresponding to the decrease of these bacterial categories. These correlations are relatively similar for both time points, except for the correlation between Firmicutes and Actinobacteria, which becomes smaller at the second time point (−0.27). The correlations between Firmicutes and unclassified, and the pooled category, are relatively small. The intraclass correlations of bacterial categories between the two time points are always positive. Firmicutes and Actinobacteria show the highest correlation between two time points (0.14 and 0.17).

Table 3.

The observed marginal correlation of the motivating data set

	${\mathit{C}}_{\mathbf{1}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{2}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{3}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{4}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{5}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{6}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{1}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{2}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{3}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{4}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{5}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{6}}^{(\mathbf{2})}$
$C_1^{(1)}$	1	−0.46	−0.43	−0.48	−0.12	−0.23
$C_2^{(1)}$	·	1	−0.29	0.13	0.02	0
$C_3^{(1)}$	·	·	1	−0.27	−0.19	0
$C_4^{(1)}$	·	·	·	1	0.1	0.06
$C_5^{(1)}$	·	·	·	·	1	0.01
$C_6^{(1)}$	·	·	·	·	·	1
$C_1^{(2)}$	0.14	−0.11	−0.05	−0.01	0	−0.13	1	−0.27	−0.53	−0.57	0.04	−0.14
$C_2^{(2)}$	−0.14	0.17	0.04	0.03	−0.01	−0.05	·	1	−0.27	−0.15	−0.05	0.01
$C_3^{(2)}$	0.04	0.05	0.01	−0.07	−0.08	−0.1	·	·	1	−0.07	−0.22	−0.11
$C_4^{(2)}$	−0.11	−0.02	0.01	0.07	0.05	0.3	·	·	·	1	0.02	0.09
$C_5^{(2)}$	0.06	−0.25	0.09	0.01	0.05	0.01	·	·	·	·	1	−0.05
$C_6^{(2)}$	−0.07	0.08	−0.06	−0.01	0.23	0.17	·	·	·	·	·	1

$C_j^{(t)}$ represents the bacterial phyla j,j = 1,…,6 at time‐point t. The order of j are Firmicutes, Actinobacteria, Bacteroidetes, Proteobacteria, Unclassified and pooled category.

The baseline characteristics of the study participants were given in Table 4. In each of the randomization arms, there are four possible combinations of infection status at pre‐ and post‐treatment, namely, uninfected subjects who either remained uninfected (condition 1) at post‐treatment or became infected at post‐treatment (condition 2) and infected subjects who either became uninfected at post‐treatment (condition 3) or remained infected at post‐treatment (condition 4). The number of samples in each conditions at pre‐ and post‐treatment are given in Figure 4. It has been shown previously that treatment had an effect on the composition at post‐treatment in infected subjects who remained infected (condition 4).5 Here, we want to reanalyze this data set by using a joint model for the microbiome data at pre‐ and post‐treatment to assess the treatment effect in the infected subjects who remained infected. Additionally, we want to estimate the time effect while adjusting for other variables such as infection status and treatment allocation. The following loglinear model is considered. Let D,E,F,G,H represent the categorical variables: bacterial taxa, infection (INF), treatment (TRT), baseline infection status (BHelm), and time (t) with J,K,L,M,N levels for each variable. For bacterial phyla, the Firmicutes was considered as a reference category. Now, the following model was fitted to the data

$$\begin{array}{ll}\log \left({\mu }_{ijklm}^{DEFGH}\right)& =\left(\log \left({\delta }_0^{-1}\right)+{\lambda }_j^D\right)+\left({\lambda }_k^E+{\lambda }_{jk}^{DE}\right)+\left({\lambda }_n^H+{\lambda }_{jn}^{DH}\right)+\left({\lambda }_{ln}^{FH}+{\lambda }_{jln}^{DFH}\right)\\ & +\left({\lambda }_{mn}^{GH}+{\lambda }_{jmn}^{DGH}\right)+\left({\lambda }_{lmn}^{FGH}+{\lambda }_{jlmn}^{DFGH}\right)+\left({\lambda }_{klmn}^{EFGH}+{\lambda }_{jklmn}^{DEFGH}\right)+u_i\\ & \text{with the baseline constraint at}J=K=L=M=N=1,u_i\sim N\left(0,{\sigma }_u^2\right).\end{array}$$ (14)

Table 4.

Characteristics at baseline for study participants

Characteristics	albendazole	placebo
	(N = 69)	(N = 81)
Age (in years), mean (sd)	28.38 (16.52)	27.85 (16.91)
Sex, female, n(%)	39 (56.52)	45 (55.56)
Helminth Infections, n(%)
A. lumbricoides	17 (24.64)	18 (22.22)
Hookworm	26 (37.681)	23 (28.40)
N. americanus	25 (36.23)	23 (28.40)
A. duodenale	2 (2.90)	2 (2.47)
T. trichiura	20 (28.99)	22 (27.16)
Any helminths	47 (68.12)	47 (58.03)
Proportion (in %) of the 6 most abundant bacteria phyla, mean(sd)
Actinobacteria	12.49 (8.95)	10.96 (7.98)
Bacteroidetes	7.41 (11.35)	6.42 (11.04)
Firmicutes	66.83 (13.46)	70.05 (13.66)
Proteobacteria	9.78 (7.86)	9.16 (8.37)
Unclassified#	1.95 (2.22)	2.68 (3.22)
Pooled*	1.54 (3.67)	0.73 (1.22)

^# Unclassified represents sequences that cannot be assigned to a phyla.

^* Pooled category consists of the remaining 13 phyla having average relative abundance among samples less than 1%.

Figure 4.

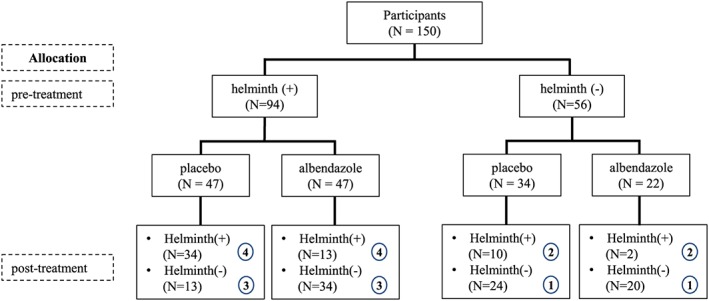
The profile of the microbiome study. The chart shows the number of subjecs infected with at least one of the prevalent soil transmitted helminths (Helminth (+)) or free of helminth infections (Helminth (‐)) that belonged to either the placebo or albendazole treatment group, at pre‐treatment and 21 months after the first treatment round. The circled number represents the condition explained in Section 4 [Colour figure can be viewed at wileyonlinelibrary.com]

Alternatively, the model could be written in terms of regression coefficients as follows:

$$\begin{array}{ll}\log \left({\mu }_{ij}^{(t)}\right)& ={\xi }_{0j}+{\xi }_{1j}\mathrm{INF}+{\xi }_{2j}t+{\xi }_{3j}\text{TRT}\times t+{\xi }_{4j}\text{BHelm}\times t+{\xi }_{5j}\text{BHelm}\times \text{TRT}\times t\\ & +{\xi }_{6j}\mathrm{INF}\times \text{BHelm}\times \text{TRT}\times t+u_i,\end{array}$$

where ${\xi }_{0j}=\log ({\delta }_0^{-1})+{\lambda }_j^D$, ${\xi }_{1j}={\lambda }_l^F+{\lambda }_{jl}^{DF}$, and so forth. In this model, there are 6 × 7 estimable covariate effects on each bacterial phyla. In condition 4, the difference in the microbiome composition between the albendazole and placebo arm is represented by ξ _3j + ξ _5j + ξ _6j, whereas, in condition 3, the difference in the microbiome composition between two arms by ξ _3j + ξ _5j. In the subjects who are uninfected at baseline, the treatment effect is represented by ξ _3j, irrespective of their infection status at post‐treatment. The change of microbiome composition, when subjects were uninfected at baseline, remained uninfected at post‐treatment, and received placebo, is modeled by ξ _2j. Two interaction terms with BHelm were included in this model (14) (ie, the coefficient ξ _4j and ξ _5j) to model the effect of having infection at pre‐treatment and still being infected at follow up, irrespective of treatment by albendazole. The coefficient ξ _4j represents the effect of having infection at pre‐treatment in the placebo group. We first included a subject‐specific random effect u _i in the model. Statistical significance for each covariate was assessed by the likelihood ratio test with 6 degrees of freedom and the significance of the random effect was assessed using the likelihood ratio test with mixture of ${\chi }_{[0,1]}^2$ distribution.

The parameter estimates from the loglinear model with subject‐specific random effects (14) are given in Table S8. The between subject variation over time is estimated by the standard deviation σ _u of 0.269 (s.e. of 0.053). The variance of this random effect is significantly different from zero (p‐value <0.001, LRT with mixture of ${\chi }_{[0,1]}^2$ distribution), indicating that the microbiome counts of a person over time are correlated. The regression coefficients for the covariates BHelm×t (ξ _4j) and BHelm×TRT×t (ξ _5j) appear not to be significantly associated with the microbiome (p−values >0.05), indicating that having infection at pre‐treatment does not influence the microbiome composition. These two covariates were present at the second time point for subjects in conditions 3 and 4. Being the terms ξ _4j + ξ _5j almost zero for all categories, the change of microbiome in these conditions appears to be not affected by these two covariates.

To obtain a model with less parameters, we first eliminated the covariate BHelm×TRT×t. The covariate BHelm×t was also not significant in this reduced model (p−value of 0.795). Hence, we reduced model (14) further by eliminating this covariate. In this updated model, BHelm×TRT×t was still not significant (p−value of 0.843). Finally, we fitted the following model:

$$\begin{array}{ll}\log \left({\mu }_{ij}^{(t)}\right)& ={\xi }_{0j}+{\xi }_{1j}\mathrm{INF}+{\xi }_{2j}t+{\xi }_{3j}\text{TRT}\times t+{\xi }_{4j}\mathrm{INF}\times \text{BHelm}\times \text{TRT}\times t+u_i.\end{array}$$ (15)

In this final model for fixed effects, assuming a subject‐specific random effect (15), 6 × 4 parameters represent the covariate effects on the microbiome composition. The treatment effect is modeled by ξ _3j for all conditions except for condition 4. The difference in the microbiome composition in condition 4 between the albendazole and placebo arm is represented by ξ _3j + ξ _4j. The estimated log odds ratio for each bacterial category compared to Firmicutes is given in Table S9. Moreover, for this model, the standard deviation of random subject‐specific effect u _i is significantly greater than zero (p−value <0.001). Albendazole has no direct effect in subjects who remained uninfected as the odds ratios for each bacterial category are approximately 1. On the other hand, when subjects remained infected, the odds of Actinobacteria to Firmicutes at the second time point compared to the first time point increases about 55%, whereas the odds ratio for Bacteroidetes to Firmicutes decreases about 62%.

Next, we considered a six‐dimensional random effects structure for this data. We fitted DMM model (15). The results are listed in Tables 5 and S10. Overall, the estimates of the fixed effects and overdispersion are very similar for these random effect structures. This is in line with the result of the simulation study. However, when we fitted the DMM model with categorical‐specific random effects, we observed the following. As the estimated variance component over time for the first three categories are relatively large ( ${\sigma }_{u_1}^2$ = 0.369 to ${\sigma }_{u_3}^2$ = 0.536), for the last three categories (Proteobacteria, Unclassified and Pooled) are small, and hence, the random effects for these categories can be omitted.

Table 5.

The log odds ratio (95% CI) when data set were fitted with Dirichlet‐multinomial mixed with categorical‐specific random effect having common variance^*

Categories	INF	t	TRT×t	Bhelm × INF × TRT×t
Actinobacteria	−0.006 (−0.218, 0.207)	0.050 (−0.155, 0.256)	0.046 (−0.235, 0.326)	0.326 (−0.042, 0.694)
Bacteroidetes	0.220 (−0.056, 0.496)	−0.119 (−0.395, 0.157)	−0.012 (−0.381, 0.356)	−0.916 (−1.573, −0.259)
Protobacteria	0.171 (−0.054, 0.396)	0.056 (−0.161, 0.273)	0.035 (−0.256, 0.326)	0.026 (−0.376, 0.427)
Unclassified	−0.024 (−0.304, 0.257)	0.129 (−0.149, 0.407)	−0.099 (−0.476, 0.277)	−0.159 (−0.727, 0.410)
Pooled	0.166 (−0.158, 0.490)	0.195 (−0.124, 0.515)	−0.030 (−0.449, 0.388)	−0.180 (−0814, 0.454)
Loglik	−8285.5	$\widehat{\theta }$ (s.e)	0.08 (0.01)
${\widehat{\sigma }}_u$ (s.e)	0.22 (0.03)

^* Fitted with SAS procedure NLMIXED with 3 quadrature points of adaptive Gauss‐Hermite approximation.

Finally, we investigated whether the correlations induced by the model correspond to the observed correlations; the marginal correlation induced by the DMM model with a subject‐specific random effect (Table S11A), a categorical specific random effect with common variance (Table 6) and with categorical‐dependent variance for the random effects (Table S11B). For all DMM models, the pairwise correlations at each time points between Firmicutes and the other three prevalent bacterial phyla are relatively high and similar to the observed marginal correlations (Table 6, Table S11A‐B). With regard to the correlation of categories between the two time points, the DMM model with categorical‐specific random effects with common variance showed a similar correlation structure to the observed one (Table 6). For the DMM model with categorical‐specific random effect, the correlation between the same category over time seems to be too high compared to the data set (Table S11B). Therefore, we concluded that the DMM model with a categorical specific random effect having common variance across categories is the model, which describes our data best.

Table 6.

The estimated marginal correlation of the data set obtained by Dirichlet‐multinomial mixed model with categorical‐specific random effect having common variance across categories

	${\mathit{C}}_{\mathbf{1}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{2}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{3}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{4}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{5}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{6}}^{(\mathbf{1})}$	${\mathit{C}}_{\mathbf{1}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{2}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{3}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{4}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{5}}^{(\mathbf{2})}$	${\mathit{C}}_{\mathbf{6}}^{(\mathbf{2})}$
$C_1^{(1)}$	1	−0.55	−0.35	−0.51	−0.3	−0.22
$C_2^{(1)}$	·	1	−0.06	−0.09	−0.05	−0.03
$C_3^{(1)}$	·	·	1	−0.04	−0.03	−0.02
$C_4^{(1)}$	·	·	·	1	−0.05	−0.03
$C_5^{(1)}$	·	·	·	·	1	−0.02
$C_6^{(1)}$	·	·	·	·	·	1
$C_1^{(2)}$	0.19	−0.12	−0.06	−0.1	−0.05	−0.04	1	−0.57	−0.3	−0.51	−0.3	−0.23
$C_2^{(2)}$	−0.12	0.13	0.03	0.03	0.02	0.02	·	1	−0.07	−0.08	−0.06	−0.04
$C_3^{(2)}$	−0.05	0.02	0.05	0.02	0.01	0.01	·	·	1	−0.05	−0.02	−0.01
$C_4^{(2)}$	−0.1	0.02	0.02	0.12	0.02	0.01	·	·	·	1	−0.05	−0.03
$C_5^{(2)}$	−0.05	0.02	0.01	0.02	0.05	0.01	·	·	·	·	1	−0.02
$C_6^{(2)}$	−0.04	0.02	0.01	0.01	0.01	0.03	·	·	·	·	·	1

5. DISCUSSION

We proposed a novel parametric multivariate method to model microbiome data from an epidemiological study using a repeated‐measurements design. Current parametric models that account simultaneously for overdispersion and repeated‐measurements use a combination of a conjugate and a normal distribution. This method was introduced by Booth et al for count data. Molenberghs et al reviewed the combined model for the binary21 and time‐to‐event data.22 The multinomially distributed data were however not considered in these papers. The rationale of this combined model is the simplification to the parent distribution when overdispersion is absent and, furthermore, the conditional distribution given the normally distributed random effect has a closed‐form formula, which reduces computational time. Thus, this model has an advantage over the generalized linear mixed models, where multivariate normal distributions were used to model correlation due to overdispersion and repeated measurements. Our proposed model is also an extension of the econometrics model for the analysis of choice probabilities in the cross‐sectional setting.12 We considered two models for the analysis of repeatedly measured microbiome data, namely, models corresponding to the unconditional distribution and to conditional distribution given the total count of a sample. For the latter distribution, we considered the situations where the total counts either vary or are fixed. We showed that, for the last situation, ie, total count is fixed, the likelihood is equivalent to the likelihood of the multinomial logistic model. Since, in our data set, the total number of counts per sample is constant, we prefer to use the DMM model.

In a simulation study, we showed that the DMM model provides unbiased estimates for the fixed and random effects independent of the used random effect structure to model the correlation between subjects across time. The sensitivity of the likelihood ratio test for the fixed and random effect components are relatively high when the sample size is large as in the case of our data application. We also showed that the models provided similar estimates for the fixed and random effects when data sets were generated from DMM model with different random effect structure. Two structures of the random effects were considered in the DMM model; one is the simplest subject‐specific random effect, where the variation of each categorical count outcomes is the same, and the second is to assume a diagonal covariance structure with the same variance for each category. With regard to the marginal correlation for each category between time points, we observed that different correlations can be obtained by changing the random effect structure. The simple random effect structure provides small correlations, whereas, for the model with categorical‐specific random effect, the correlations are larger and increased with the size of variance component. Hence, if the interest is solely on the fixed effects and random effect estimates, the simple model with subject‐specific random effect can be used. On the other hand, when the correlation structure between the same category across time is of interest, a more complex DMM model with categorical‐specific random effects should be used.

For our data application, we were interested in the parameters modeling the variability between subjects and the effect of covariates on microbiome composition; therefore, we used a subject‐specific random effect. Following the generalized linear mixed model framework, the random effect u _i is linked to the expected outcome and measures the variation of the count outcome for certain category between subjects. The variability of the categorical count between subjects is then captured by a single estimate of the standard deviation of the random effect and its significance reveals that the variability between subjects should be taken into account in the model. The estimate of the standard deviation in our data analysis is 0.269 (s.e. of 0.053, p‐value <0.001), which is relatively small; hence, our assumption of a subject‐specific random effect is justified. The standard deviation although small is significant; hence, our extensive model is necessary for this data. With regard to the fixed effects, their estimates describe the contribution of the covariate to the odds ratio of two bacterial categories. One advantage from our model is to model the change of microbiome in different strata over time. For instance, we showed in the motivating data set that the change of microbiome over time in subject who remained uninfected in the placebo arm could be inferred from the estimate of the time coefficients. Using the same model, we could also infer the change of microbiome when subjects remained uninfected in the albendazole arm as well as the change of microbiome when subjects remained infected. In the previous analyses, we selected subjects who were infected at pre‐treatment and fit the Dirichlet‐multinomial regression at post‐treatment to observe the effect of having long term infection and treatment on microbiome composition. The statistical test using that model showed subjects who remained infected, and received albendazole harbored significantly different microbiome composition compared to subjects who remained infected and received placebo. This result is confirmed by the analysis in this manuscript.

On the other hand, for the data application, when the interest is on the marginal correlation, the random effect structure has to be correctly modeled. For our data set, we considered three structures, namely, subject‐specific random effects, categorical‐specific random effects with common variance, and with categorical‐dependent variances. The second correlation structure represents our data best, suggesting that the first structure is too restricted, and in the third structure, there were too many parameters for which there is no sufficient information in our data to estimate all of them.

Several challenges in modeling the microbiome data using this method exist. Firstly, in our data application, we were able to fit a categorical‐specific random effects structure; however, the computational burden was large. More research is needed to obtain computational efficient methods. The second challenge is related to the number of categorical count outcome involved in the study. Typically, categories with rare count (bacteria only presence in the small number of samples) are pooled. One might argue that this rare count might be due to systematic error rather than sequencing error and thus pooling could be viewed as losing the information. Future research should address the issue of the number of categories included in the analyses and, consequently, a development of computationally efficient method is needed to take into account the category‐dependent random effect.

Several alternatives for our approach can be considered. Although modeling overdispersion with the conjugate distribution has computational advantages, it might be too simple because all correlation is modeled by one additional parameter. Extensions to more complex correlation structures would be of interest. Secondly, the choice of six categories is arbitrary. More categories can be analyzed if the dimension of the parameter space is reduced, for example, using penalization.10, 23 Thirdly, the interpretation of the fixed effect parameters are all conditional on the random effects. In practice, one might be interested in marginal parameters.24, 25 To this end, marginalized models for multivariate counts need to be developed. Finally, it is of interest to analyze the microbiome data jointly with other outcomes such as diseases or immunological markers. For example, we would like to model the effect of helminths and treatment on microbiome composition and cytokines. This is a topic of an ongoing research.

Supporting information

SIM_8101‐Supp‐0002‐20190129_SupportingInformationSIM.pdf

APPENDIX A.

DERIVATION OF THE JOINT MULTIVARIATE DISTRIBUTION

1. Joint multivariate distribution for proportions

Conditioned on the random effect u _i, the relative abundances are independent. Thus, the joint distribution for the multivariate relative abundance for subject i could be formulated as follows:

$$\begin{array}{ll}\mathrm{Pr}\left(\frac{{\mathit{C}}_i^{(1)}}{C_{i+}^{(1)}},\frac{{\mathit{C}}_i^{(2)}}{C_{i+}^{(2)}}\right)& =\underset{u_i}{\int }\mathrm{Pr}\left(\frac{{\mathit{C}}_i^{(1)}}{C_{i+}^{(1)}},\frac{{\mathit{C}}_i^{(2)}}{C_{i+}^{(2)}},u_i\right)d{u}_i\\ & =\underset{u_i}{\int }\mathrm{Pr}\left(\left.\frac{{\mathit{C}}_i^{(1)}}{C_{i+}^{(1)}}\right|u_i\right)\mathrm{Pr}\left(\left.\frac{{\mathit{C}}_i^{(2)}}{C_{i+}^{(2)}}\right|u_i\right)\mathrm{Pr}\left(u_i\right)d{u}_i\\ & =\underset{u_i}{\int }{\displaystyle \prod _{t=1}^2}\mathrm{Pr}\left(\frac{{\mathit{C}}_i^{(t)}}{C_{i+}^{(t)}}\right)\mathrm{Pr}\left(u_i\right)d{u}_i\\ & =\underset{u_i}{\int }{\displaystyle \prod _{t=1}^2}\frac{\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{i+}^{(t)}\right)C_{i+}^{(t)}!}{\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{i+}^{(t)}+C_{i+}^{(t)}\right)}{\displaystyle \prod _{j=1}^J}\frac{\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{ij}^{(t)}+C_{ij}^{(t)}\right)}{\mathrm{\Gamma }\left({\theta }^{-1}{\mu }_{ij}^{(t)}\right)C_{ij}^{(t)}!}\mathrm{Pr}\left(u_i\right)d{u}_i,\end{array}$$ (A1)

with ${\mu }_{i·}^{(t)}$ is the loglinear mean.

2. Joint multivariate distribution under condition on total count

We will show that the distribution given in Equations (9) and (10) is in general not equivalent. The distribution in Equations (10) and (12) is not equivalent except for the situation where the total count is fixed.

We denote ${\mathit{C}}_i^{(t)}$ as the multivariate count outcome at time t for subject i and the total count to be $C_{i+}^{(t)}$. Thus, the multivariate count outcome for subject i conditional on their total is as follows:

$$\begin{array}{ll}\mathrm{Pr}\left(\left.{\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)}\right|C_{i+}^{(1)},C_{i+}^{(2)}\right)& =\frac{\mathrm{Pr}\left({\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)},C_{i+}^{(1)},C_{i+}^{(2)}\right)}{\mathrm{Pr}\left(C_{i+}^{(1)},C_{i+}^{(2)}\right)}\\ & =\frac{{\int }_{u_i}\mathrm{Pr}\left({\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)},C_{i+}^{(1)},C_{i+}^{(2)},u_i\right)d{u}_i}{{\int }_{u_i}\mathrm{Pr}\left(C_{i+}^{(1)},C_{i+}^{(2)},u_i\right)d{u}_i}\\ & =\frac{{\int }_{u_i}\mathrm{Pr}\left(\left.{\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)}\right|C_{i+}^{(1)},C_{i+}^{(2)},u_i\right)\mathrm{Pr}\left(C_{i+}^{(1)},C_{i+}^{(2)},u_i\right)d{u}_i}{{\int }_{u_i}\mathrm{Pr}\left(C_{i+}^{(1)},C_{i+}^{(2)},u_i\right)d{u}_i}.\end{array}$$ (A2)

The probability $\mathrm{Pr}(C_{i+}^{(1)},C_{i+}^{(2)},u_i)$ could be rewritten as follows:

$$\begin{array}{ll}\mathrm{Pr}\left(C_{i+}^{(1)},C_{i+}^{(2)},u_i\right)& =\mathrm{Pr}\left(\left.C_{i+}^{(1)},C_{i+}^{(2)}\right|u_i\right)\mathrm{Pr}\left(u_i\right)\\ \text{(by conditional independence)}& =\mathrm{Pr}\left(\left.C_{i+}^{(1)}\right|u_i\right)\mathrm{Pr}\left(\left.C_{i+}^{(2)}\right|u_i\right)\mathrm{Pr}\left(u_i\right)\\ \text{(conditional distribution)}& =\frac{\mathrm{Pr}\left(C_{i+}^{(1)},u_i\right)}{\mathrm{Pr}\left(u_i\right)}\frac{\mathrm{Pr}\left(C_{i+}^{(2)},u_i\right)}{\mathrm{Pr}\left(u_i\right)}\mathrm{Pr}\left(u_i\right)\\ & =\frac{\mathrm{Pr}\left(u_i\left|C_{i+}^{(1)}\right.\right)\mathrm{Pr}\left(C_{i+}^{(1)}\right)}{\mathrm{Pr}\left(u_i\right)}\frac{\mathrm{Pr}\left(u_i\left|C_{i+}^{(2)}\right.\right)\mathrm{Pr}\left(C_{i+}^{(2)}\right)}{\mathrm{Pr}\left(u_i\right)}\mathrm{Pr}\left(u_i\right)\\ & =\frac{\mathrm{Pr}\left(u_i\left|C_{i+}^{(1)}\right.\right)\mathrm{Pr}\left(C_{i+}^{(1)}\right)·\mathrm{Pr}\left(u_i\left|C_{i+}^{(2)}\right.\right)\mathrm{Pr}\left(C_{i+}^{(2)}\right)}{\mathrm{Pr}\left(u_i\right)}.\end{array}$$

Thus, the joint probability of multivariate count outcome given in Equation (A2) can be written as follows:

$$\begin{array}{ll}\mathrm{Pr}\left(\left.{\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)}\right|C_{i+}^{(1)},C_{i+}^{(2)}\right)& =\frac{\underset{u_i}{\int }\mathrm{Pr}\left(\left.{\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)}\right|C_{i+}^{(1)},C_{i+}^{(2)},u_i\right)\frac{\mathrm{Pr}\left(u_i\left|C_{i+}^{(1)}\right.\right)\mathrm{Pr}\left(C_{i+}^{(1)}\right)·\mathrm{Pr}\left(u_i\left|C_{i+}^{(2)}\right.\right)\mathrm{Pr}\left(C_{i+}^{(2)}\right)}{\mathrm{Pr}\left(u_i\right)}d{u}_i}{\underset{u_i}{\int }\frac{\mathrm{Pr}\left(u_i\left|C_{i+}^{(1)}\right.\right)\mathrm{Pr}\left(C_{i+}^{(1)}\right)·\mathrm{Pr}\left(u_i\left|C_{i+}^{(2)}\right.\right)\mathrm{Pr}\left(C_{i+}^{(2)}\right)}{\mathrm{Pr}\left(u_i\right)}}\\ & =\underset{u_i}{\int }\mathrm{Pr}\left({\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)}\left|C_{i+}^{(1)},C_{i+}^{(2)},u_i\right.\right)\left[\frac{\mathrm{Pr}\left(u_i\left|C_{i+}^{(1)}\right.\right)\mathrm{Pr}\left(u_i\left|C_{i+}^{(2)}\right.\right)}{\mathrm{Pr}\left(u_i\right){\displaystyle \underset{u_i}{\int }}\frac{\mathrm{Pr}\left(u_i\left|C_{i+}^{(1)}\right.\right)\mathrm{Pr}\left(u_i\left|C_{i+}^{(2)}\right.\right)}{\mathrm{Pr}\left(u_i\right)}d{u}_i}\right]d{u}_i.\end{array}$$ (A3)

Since Pr(u _i) is not equal to the term in bracket in Equation (A3), then Equations (9) and (10) are not equivalent. However, when the total count is fixed, the following equation holds: $\mathrm{Pr}(u_i|C_{i+}^{(t)})=\mathrm{Pr}\left(u_i\right)$. Now, using the last equation in (A3), the joint distribution becomes

$$\begin{array}{ll}\mathrm{Pr}\left(\left.{\mathit{C}}_i^{(1)},{\mathit{C}}_i^{(2)}\right|C_{i+}^{(1)},C_{i+}^{(2)}\right)& =\underset{u_i}{\int }\mathrm{Pr}\left({\mathit{C}}_i^{(1)}\left|C_{i+}^{(1)},u_i\right.\right)\mathrm{Pr}\left({\mathit{C}}_i^{(2)}\left|C_{i+}^{(2)},u_i\right.\right)\mathrm{Pr}\left(u_i\right)d{u}_i\\ & =\underset{u_i}{\int }\frac{\mathrm{Pr}\left(\left.{\mathit{C}}_i^{(1)},C_{i+}^{(1)}\right|u_i\right)\mathrm{Pr}\left(\left.{\mathit{C}}_i^{(2)},C_{i+}^{(2)}\right|u_i\right)}{\mathrm{Pr}\left(C_{i+}^{(1)}\right)\mathrm{Pr}\left(C_{i+}^{(2)}\right)}\mathrm{Pr}\left(u_i\right)d{u}_i.\end{array}$$ (A4)

Since the count at each category $C_{ij}^{(t)}|u_i\sim \text{NB}\left({\theta }^{-1}{\mu }_{ij}^{(t)},\frac{{\theta }^{-1}}{1+{\theta }^{-1}}\right)$, where $\log \left({\mu }_{ij}^{(t)}\right)={\mathit{X}}_i{\mathit{\xi }}_j+u_i$, we obtain similar formulation as the conditional likelihood at the cross‐sectional setting. Thus, in the case where the total count is fixed, the formulation is equivalent to the distribution of the multivariate relative abundance (A1).

Martin I, Uh H‐W, Supali T, Mitreva M, Houwing‐Duistermaat JJ. The mixed model for the analysis of a repeated‐measurement multivariate count data. Statistics in Medicine. 2019;38:2248–2268. 10.1002/sim.8101