Dynamics of the Bulk Hydrated Electron from Many‐Body Wave‐Function Theory

Abstract

The structure of the hydrated electron is a matter of debate as it evades direct experimental observation owing to the short life time and low concentrations of the species. Herein, the first molecular dynamics simulation of the bulk hydrated electron based on correlated wave‐function theory provides conclusive evidence in favor of a persistent tetrahedral cavity made up by four water molecules, and against the existence of stable non‐cavity structures. Such a cavity is formed within less than a picosecond after the addition of an excess electron to neat liquid water, with less regular cavities appearing as intermediates. The cavities are bound together by weak H−H bonds, the number of which correlates well with the number of coordinated water molecules, each type of cavity leaving a distinct spectroscopic signature. Simulations predict regions of negative spin density and a gyration radius that are both in agreement with experimental data.

The bulk hydrated electron,1 $e_{aq}^{-}$ , discovered in 19621b is a key species in aqueous radiation1c and plasma chemistry.1e Its structure, however, had long been elusive. First, no classical chemical formula corresponds to $e_{aq}^{-}$ and the very term “structure” had to be refined to include spin density distribution and the solvation shells. Second, it is a short‐lived species which cannot be separated or even concentrated. Therefore, the structure of $e_{aq}^{-}$ is barely accessible for direct structural approaches, diffraction or NMR spectroscopy.1 The only explicitly geometry‐related property derived from the spectroscopic data is the spin density gyration radius.2 Directly observed structure‐related properties are optical spectra in UV‐1b, 3 and IR‐regions,4 EPR g‐factors5 and the binding energy.6 The lack of direct experimental measurements of the structure of the hydrated electron calls for theory, although reliable modelling of $e_{aq}^{-}$ is at least equally challenging as the corresponding experiments.

An example of the debate originated in different theoretical approaches is whether the hydrated electron occupies a cavity or not.7 Although the conventional view of the cavity structure is supported by most theoretical studies, the non‐cavity model has also been able to predict the observables close to the measured ones.7a,7f,7g The time evolution as obtained from molecular dynamics (MD) simulation8 enriches the picture: after generation of $e_{aq}^{-}$ , a regular cavity is being formed from a bulk structure of water within several picoseconds via less regular intermediates. Consequently, the delocalized structures must exist, although their exact shapes, life times and relevance for chemistry are yet to be revealed. Another ongoing discussion has to do with the distinguishable surface and bulk structures of the hydrated electron.9

Much of the theoretical uncertainty results from the limitations of the computational approaches applied:10 to name a few, static calculations of clusters with density functional theory DFT and correlated wave function methods,11 MD of clusters with DFT12 and correlated wave function methods,13 condensed‐phase and cluster molecular dynamics (MD) with one‐electron pseudopotentials/Hamiltonians7e,7g, 9b, 14 and with DFT, including the generalized gradient approximation (GGA),15 GGA‐based QM/MM,8 and an ad hoc constructed dispersion‐corrected hybrid functional.16 DFT, the work horse of ab initio MD, exhibits a number of well‐known shortcomings. One of them is the inaccurate description of bulk liquid water, for which even modern functionals are not able to provide a balanced description of structure, dynamics and thermodynamics simultaneously.17 In contrast, the issue is satisfactorily addressed by the second‐order Møller‐Plesset perturbation theory (MP2).18 Another shortcoming of GGA DFT is the infamous delocalization (self‐repulsion) error,19 which is expected to spuriously delocalize $e_{aq}^{-}$ charge distribution. This leads to significant errors in the redox properties of aqueous species due to errors in solvation shell description and band structure.20

To guarantee reliable results for simulations of the bulk hydrated electron, one may formulate requirements for the computational model. First, it should be MD‐based to capture the formation and dynamic transformations of the cavity. Second, a many‐body correlated electronic structure level is highly recommended since this avoids the delocalization error and delicate correlation effects have been found crucial to predict the solvation of the electron accurately without empirical parameters. Third, the simulation should be performed in the bulk under periodic boundary conditions to avoid the formation of the surface structure. Finally, the method should provide an accurate description of liquid water. Such calculations, however, have been technically impossible until recent method developments (including those by our groups) enabled massively parallel many‐body theory calculations in the condensed phase on state‐of‐the‐art supercomputers.21

Herein, we report MD simulations of bulk $e_{aq}^{-}$ at the second‐order Møller‐Plesset perturbation theory (MP2) level of electronic structure under periodic boundary conditions21 in a cell containing 47 water molecules, which fulfills all of the above requirements (See Supporting Information, 1). Dynamics are supplemented by G ₀ W ₀ band gap calculations22 (See Supporting Information, 2). Two trajectories over 2 ps long are presented: one starts from a prepared cavity, trajectory 1, the second starts from the neat liquid water structure, trajectory 2. Another trajectory of 1 ps long starting from the neat liquid water, trajectory 3, is reported in Supporting Information, 6. The time scale of the production runs is restricted to ca. five picoseconds due to computational cost of the state‐of‐the‐art electronic structure method applied. We will show that this time span suffices to obtain important insights and reproduce essential experimental observations, although a full dynamic picture $e_{aq}^{-}$ can only be obtained with a more extensive sampling. For similar reasons, the unit cell is restricted to 47 water molecules.

Atoms‐in‐molecules (AIM) analysis23 of the MP2 electron densities along the trajectories identifies contacts between H atoms of the water molecules forming the cavity: the electron density value at the bond critical point is approximately 0.01 a.u. and both atoms bear negative charge. The distances between the atoms in contact are systematically shorter than those between the non‐contact atoms and are distributed between 1.8 and 2.8 Å. This range is compatible with that of hydrogen bonds.24 Therefore, we will call the contacts weak H−H bonds and use them to classify the cavity structures.

For trajectory 1, we have chosen the preformed cavity to be confined by four hydrogen atoms of four different water molecules (see Figure 1, top right panel), with O−H bonds pointing towards the center as proposed in Ref. 11a. In this structure, the four water molecules in the coordination sphere are bound by three H−H bonds as shown in Figure 1, top. We observe that the preformed cavity remains stable over the whole MP2‐trajectory of more than 2 ps, while no structures with five coordinating water molecules as in Figure 1. bottom, appeared. The two isomeric structures differing by the distributions of the bonds among the cavity‐forming molecules are identified (1 and 1′ in Figure 1) and remain in dynamic equilibrium. Importantly, regions of negative spin density are present at the cavity‐forming molecules (see Figure 1, top). Spin density spreads significantly beyond the cavity‐forming molecules to include the second‐solvation shells and even farther regions. The averaged gyration radius of spin density derived from the preformed cavity simulation is found to be 2.02 Å. The band gap remains stable at approximately 1.8 eV with a moderate spread correlating with the gyration radius (see Figure 2). Time evolution of the bonding pattern and the band gap, revealing the stability of both, is shown in Figure S2 in the Supporting Information.

Figure 1.

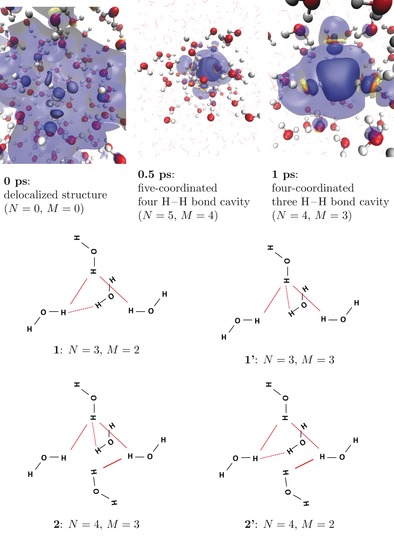
Dynamic structure of the hydrated electron: N is the number of H−H bonds; M is the maximum number of H−H bonds formed by one atom. The number of water molecules forming the cavity is almost everywhere equal to N+1. Top: evolution of the hydrated electron's spin density exhibits rapid cavity formation. Blue: positive spin density; yellow: negative spin density. Spin density isovalues: opaque: ±0.0015 a.u.; transparent: ±0.0001. Bottom: Typical structures of the hydrated electron's cavity with bonding schemes: structures 1 and 1′, 2 and 2′ are isomeric.

Figure 2.

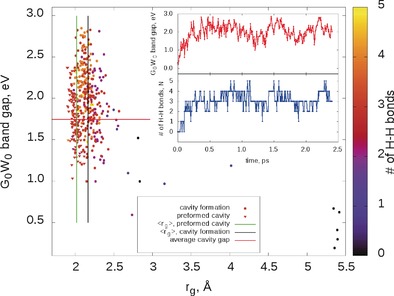
Band gaps, gyration radii, r_g of the spin density distribution and bonding: Vertical lines are average gyration radii, ⟨r_g⟩. Data from the second half (1 ps) of the preformed cavity trajectory are given and used for averaging r_g. Data for all the cavity formation trajectory (2.4 ps) are given, the first 0.5 ps is neglected for averaging r_g. Band gaps and gyration radii have been calculated along the trajectories every 7.5 fs. Inset: time evolution of band gaps and bonding patterns along the cavity formation trajectory. Structures with different bonding patterns have specific spectroscopic signatures.

After addition of the excess electron to the unperturbed liquid water (trajectory 2), we found that a cavity is formed rapidly within 250 fs (see insets in Figure 2). The localization process begins near an elongated hydrogen bond, which acts as a “trap” and subsequently breaks (see Supporting Information, 7). No stable delocalized solvated electron structures7 have been observed. However, a number of non‐tetrahedral cavities existing for considerable time (up to 100 fs) have been identified. Those are five‐coordinated isomeric structures linked by four H−H bonds (2 and 2′ in Figure 1, bottom) and less common six‐coordinated structures linked by five H−H bonds (not plotted). Those also exhibit similar regions of negative spin density. With time the regular tetrahedral four‐coordinated cavity prevails (see Figure 2). The band gap strongly depends on the cavity structure type correlating well with the number of H−H bonds: the more bonds, the higher the band gap (see Figure 2 (inset) and Figure S3 in the Supporting Information).

The gyration radius has a larger spread than in case of preformed cavity dynamics as shown in Figure 2 and the average value after six‐, five‐ and four‐coordinated cavities have been formed is 2.16 Å. We expect that equilibration will further improve agreement. Similar results are observed in a second shorter (1 ps) cavity formation trajectory (see Supporting Information, 6: Figures S4 and S5).

Our main finding is that bulk MP2 simulations $e_{aq}^{-}$ fail to find any evidence of non‐cavity structures7e of the bulk hydrated electron neither as stable nor as metastable states. A four‐coordinated tetrahedral cavity with three H−H bonds is the most stable configuration since once formed it does not transform to cavities of different types. This motif is similar to a recently suggested minimal representative model of the hydrated electron11a and corresponds to a coordination number of four described in Ref. 14d Other cavity structures—five‐ and six‐coordinated with four and five H−H bonds—come into existence during cavity formation and as fluctuations from the four‐coordinated structure. In most cases, the number of water molecules forming the cavity is equal to N+1, where N is the number of H‐H bonds, as shown in Figures S2, S3 and S4.

Importantly, we observe the regions of negative spin density, giving rise to a negative isotropic hyperfine coupling and essential for explaining EPR spectra.5 Negative spin density regions have not been reported in the bulk DFT‐based QM/MM studies,8 although they are predicted by most simulations.1a, 11a As it can be seen in Figure 1, our study based on MP2 correlated wave function MD confirms negative spin density regions in the condensed phase. Significant spin density spread beyond the cavity‐forming molecules is in agreement with previous results8a, 14c and rule out an oversimplified view of the cavity.

The gyration radius of the preformed cavity simulation (averaged over the second picosecond of simulation), 2.02 Å, is less than the one derived from the experiment, 2.35 Å.2 The gyration radius in the cavity formation trajectory (averaged after 0.2 ps) is 2.16 Å, closer to those derived indirectly from experimental measurements. We expect the gyration radius to increase towards the experimental value with a larger simulation cell as this reduces spurious interaction between periodic images, and lets liquid density to adjust. On the other hand, the QM/MM simulations8 employing a larger periodic cell reducing the spurious Coulomb repulsion predict a much larger value of 2.65 Å, which can be traced back to the delocalization error19 of which MP2 is free.

Although the G ₀ W ₀ band gaps are not equivalent to optical absorption line positions, the considerable differences in the former (up to 1 eV) for different cavity types are expected to lead to a distinct spectroscopic signature of each one. The band gap dependence on the number of the H−H bonds (or on the coordination number) is much more pronounced than that on the gyration radius, a criterion used previously.8b

Herein, we provide much stronger theoretical evidence for the cavity model of the bulk hydrated electron, and predict that the various H−H bonding motives could be visible in optical spectroscopies. This is the first dynamic simulation of a complex chemical species in the condensed phase at the correlated wave function level of theory, providing evidence of the potential of the employed methods.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

J. Wilhelm, J. VandeVondele, V. V. Rybkin, Angew. Chem. Int. Ed. 2019, 58, 3890.