Abstract
This study used Monte Carlo simulations to examine the ability of the two-stage least-squares (2SLS) estimator and two-stage residual inclusion (2SRI) estimators with varying forms of residuals to estimate the local average and population average treatment effect parameters in models with binary outcome, endogenous binary treatment, and single binary instrument. The rarity of the outcome and the treatment were varied across simulation scenarios. Results showed that 2SLS generated consistent estimates of the LATE and biased estimates of the ATE across all scenarios. 2SRI approaches, in general, produced biased estimates of both LATE and ATE under all scenarios. 2SRI using generalized residuals minimized the bias in ATE estimates. Use of 2SLS and 2SRI is illustrated in an empirical application estimating the effects of long-term care insurance on a variety of binary healthcare utilization outcomes among the near-elderly using the Health and Retirement Study.
1. INTRODUCTION
Instrumental variables (IV) methods are used to obtain causal estimates of the effects of endogenous variables on outcomes using observational data. These methods mediate potential bias from unmeasured confounders affecting observed treatment through identifying and specifying an instrumental variable, which may represent a “natural experiment” affecting treatment through satisfying two principle assumptions: the instrument is sufficiently correlated with the endogenous variable (strength), and the instrument is uncorrelated with the error term in the outcome equation (validity). IV methods are usually implemented using a two-stage approach where the first-stage estimates an expectation of the endogenous variable conditional on measured confounders and one or more instrumental variables. The second stage model then predicts outcomes as a function of the estimated treatment values from the first-stage, measured confounders, and potentially other control variables.
In what has been popularly dubbed as the two-stage least-squares (2SLS) approach, the first and second stage models are parametrized using ordinary least squares regression, where the model fit is chosen through minimizing the sum of squared residuals from linear models. The 2SLS approach is a special case of the more general two-stage predictor substitution (2SPS) method, which follows the procedure described above but may apply alternative methods for estimating first- and second-stage models. Alternatively, one can obtain the residuals from the first stage regression and then run the second stage regression with the original endogenous variable, observed confounders and the residuals from the first stage as an added covariate. This approach, known as the two-stage residual inclusion (2SRI) approach, is analogous to the 2SLS approach when both first- and second-stage models are linear.
These estimation methods were originally derived in a linear setting with continuous endogenous treatments and continuous outcome measures. The target parameter for these estimations is the average causal effect, which is the average of the partial derivative of a continuous outcome with respect to a continuous endogenous variable. However, these estimators but are often applied to what may be considered an inherently non-linear setting, such as with binary treatment or outcome measures. When treatment (exposure) or outcome is binary and therefore has a conditional expectation that follows a probability scale, a non-linear model featuring a convenient cumulative density function (CDF) is often used to model the conditional mean of the treatment indicator in the first-stage or outcome in the second-stage. Popular approaches include using probit or logit regression models.
In these settings, it is well established that the 2SPS approach produces biased estimates of the population average treatment effect (ATE) (Blundell and Powell 2001; Terza et al. 2008). Under full parametric assumptions of joint-normality, bi-variate probit models can be used to model the two stages simultaneously (Bhattacharya et al. 2006) and estimate the ATE
Alternatively, it has been suggested that nonlinear 2SRI is the appropriate approach for estimation when first- or second-stage models have a dependent variable that is binary or otherwise suited for non-linear regression; especially when full parametric assumptions, where statistical joint distribution of error terms of the exposure and outcomes are specified, are not wanted (Blundell and Powell 2003, 2004; Terza et al. 2008). Nonlinear 2SRI methods identify the ATE through relying on the concepts that support control function methods (Blundell and Powell 2003, 2004), which were developed in the context of continuous endogenous variables. However, applicability of nonlinear 2SRI to models with binary endogenous treatments remains contentious.
Finally, with a non-linear data-generating process for outcomes, treatment effects are heterogeneous by construction. This raises complexity and confusion in that the specific treatment effect parameter identified by the 2SLS or 2SRI approaches may differ and generally depends on whether treatment effects are heterogeneous across the population and vary across levels of observed or unobserved confounders (aka essential heterogeneity). In such a situation, it is well–established that traditional IV approaches such as 2SLS identify an average treatment effect across only the subgroup of “marginal” individuals whose treatment choices were affected by changes in the specified instrumental variable(s) (Heckman 1997; Heckman et al. 2006, Basu et al. 2007). When the instrumental variable is binary (which is the focus of this paper), this effect is known as the local average treatment effect (LATE) (Imbens and Angrist 1994). It is an average of the treatment effects for each individual at the margin, or the marginal treatment effects, whose treatment choice would be affected by the change in the level of the instrument (Heckman 1997; Heckman et al. 2006, Basu et al. 2007; Kowalski 2016). Both 2SLS and the analogous strictly linear application of 2SRI will generate consistent estimates of LATE as long as the linear mean model specifications in both stages are correct.1
Terza et al. (2007, 2008) claimed that nonlinear 2SRI, but not 2SLS or 2SPS, produced consistent estimates of ATE in models with inherently nonlinear dependent variables. However, it is not clear which treatment effect parameter is being estimated under a 2SRI approach for a binary treatment. Particularly in applications with binary IVs, the 2SRI approach relies on functional form assumptions for identification (as explained below) that are difficult to test in most applied setting and many analysts, especially economists, have favored the 2SLS approach regardless of whether treatment and outcome are continuous or binary. As such, many questions remain about the best approaches to IV estimation with such data. On one hand, linear probability models may not provide a good fit to the data, especially when treatment or outcome variables are “rare” or otherwise imbalanced in nature, which in turn may lead to imprecise estimates. On the other hand, probit and logit models may provide a better fit to observed data overall but generate biased estimates depending on the support of the residual distribution (across all X’s).
For example, Chapman and Brooks showed that small changes to the simulation settings of Terza et al. (2007) resulted in different results and conclusions about the properties of 2SLS and 2SRI. They showed that 2SLS produced consistent estimates of LATE across alternative scenarios while 2SRI estimates were not generally consistent for either ATE or LATE. However, the evidence produced by Chapman and Brooks is limited in that their scenarios all included two continuous instrumental variables and had treatment and outcome rates near 50%, a setting that may have inadvertently favored the 2SLS method.
Moreover, there is a debate in the health econometrics literature about the right form of the residual to be used in 2SRI approaches. Garrido et al. (2012) compared results from 2SRI models with different versions of residuals when applied to health expenditure data. They found that results varied widely depending on the type of residuals they use in the second stage. They raised the concern that raw residuals may not be the right control function variable. However, there is no theoretical rationale as to why different forms of the residual matter and the authors did not perform simulations to show which one is better. Chapman & Brooks’ only considered 2SRI with raw residuals when showing general inconsistency of 2SRI for ATE and LATE. Further, Chapman & Brooks did not report coverage probabilities for their estimates, a necessary component for making comparisons on properties of 2SLS and nonlinear 2SRI methods and for considering potential strengths and limitations of these approaches in practice.
In this paper, we try to provide theoretical and empirical evidence to inform these debates.2 We first extend the recent assessment conducted by Chapman & Brooks using a simple scenario with binary outcome, a binary treatment that is made endogenous by a continuous unobserved confounder, binary instrument, and a binary measured confounder. There is an abundance of examples in the applied health literature where such a full binary setting is of relevance. Our empirical example illustrates this case. 2SRI and 2SLS methods can also be applied to other settings such as for count data and expenditure models. This paper does not say anything about the performance of these estimators in those settings.
After a theoretical discussion on the properties and expected behaviors of alternative estimators, we test the capability of 2SLS and alternative specifications of 2SRI methods for estimating alternative average treatment effect concepts across a range of simulation scenarios varying by the rarity of the treatment and the outcomes using extensive Monte-Carlo simulation exercises.
Results show that the 2SLS method with binary IV produced consistent estimates of LATE across the entire range of rarity for either treatment or the outcome. The rarity of either did not affect the coverage probabilities of these estimators. In contrast, the 2SRI approach with any residuals studied was a biased estimator for LATE. In principle, nonlinear 2SRI estimators are designed to estimate the ATE parameter. However, 2SRI estimates of ATE were also generally biased, with the level of bias varying by residual form and outcome rarity. General conclusions from results of these simulation models are consistent with those of the more limited scenarios considered by Chapman & Brooks. Among 2SRI models, those using generalized residuals were most often least biased in estimating ATE, though 2SRI with Anscombe residuals generated less biased estimates in scenarios with very rare outcomes (<5%). Implications of these results are discussed.
Finally, we examined the implications of model choice using an empirical setting that resembles the simulated scenario with endogenous binary treatment, binary outcomes, and binary observable confounders. The alternative instrumental variable methods were applied to evaluate the effect of long-term care insurance on a variety of health care utilization outcomes using tax treatment as an instrument for long-term care insurance holding, as has been validated in the literature (Goda 2011; Konetzka, et al. 2014, Coe, Goda and Van Houtven 2015). The results from applying the alternative estimators are discussed in the context of our simulation results.
2. ECONOMETRIC THEORY & METHODS
In what follows, we provide an intuitive explanation of the underlying theory of these methods rather than the full formal theory
Consider the binary structural response model
| (1) |
where the latent variable yi* follows a linear model of the form
| (2) |
where xi is a row vector of covariates and ui is a stochastic disturbance term for individual i. Throughout this section, bold-face is used to represent a vector. If ui is independent of xi, a single index regression model such as:
| (3) |
can be used to obtain consistent estimates of β. However, it may often be the case that ui is not independent of xi because some component of xi, say di, is determined jointly with yi* such that
| (4) |
where indicates statistical independence. Let the reduced form of di, which we denote to be the endogenous binary treatment variable, be given as
| (5) |
where zi = vector of instrumental variables, λ is the true function through which di is determined by wi and zi, vi is a stochastic disturbance term, and E(vi | wi, zi) = 0 by construction. It is assumed throughout that expectation of d is a non-trivial function of z given w.
For evaluation research, interest generally lies in estimating β parameters or, more specifically, the components of β that represent the causal effect of an exogenous shift in treatment, di, on the response probabilities. The interpretation of those parameters of interest then must be considered. The broadest and perhaps most intuitive treatment effect parameter is the average treatment effect (ATE), which represents the mean change in outcome that would be realized if everyone in a target population changed from not receiving treatment to receiving treatment. The ATE can be written as
| (6) |
where ATE (w) represents the conditional average treatment effect for a sample, which may be distinct in the mix of characteristics w.
If it is the case that treatment effects are heterogenous across the population and this heterogeneity is related to treatment choice (i.e., essential heterogeneity) then treatment effectiveness will vary over levels of ui when components of w are unmeasured by the researcher (i.e., there are unmeasured confounders). As a result, identification of ATE will require strong assumptions. First, the ATE can be estimated through identification of the function represented by G(.), which is to akin to identifying the full parametric distribution of ui. In the absence of full parametric assumptions, the ATE can be identified in special cases using instrumental variables methods, where the specified IV(s) fully identify the conditional distribution of ui | vi, which can then be integrated over the distribution of vi identified in the IV-based first-stage model. More simply put, the specified IV(s) must be considered as potentially influencing treatment choice for all types of individuals in the sample, defined by their levels of observed and unobserved characteristics. These IV assumptions may be particularly difficult to satisfy when a single binary instrument is used, as only two points of support in the distribution of vi are identified non-parametrically.
More generally, as Imbens and Angrist (1994) have shown, the IV effect estimated using a single binary IV, zi, is referred to as the local average treatment effect (LATE) and is given as:
| (7) |
The LATE reflects the average causal effect of di on the probability of yi among those (marginal) individuals whose treatment statuses would likely change with a change in the level of the instrumental variable (Angrist & Imbens 1994, 1996; Heckman 1997). The LATE parameter is only “locally” interpretable in the context of the instrument specified. Even with very strong instruments that lead all patients in the sample to be marginal, LATE will not often converge to the ATE because, unlike randomization, the instrument may put more weight on some marginal patient than others. Therefore, since it is often difficult to identify the marginal patients directly (i.e., to know for whom the instrument affected choice), it may also be difficult to understand to whom the estimate applies (Heckman 1997; Newhouse and McClellan, 1998). In some cases where a binary IV is related to a specific policy, LATE may be interpretable as the effect of changing di among those individuals who would be induced to change their treatment status by the policy (Heckman et al. 2006). Naturally, if the true treatment effect is constant then the true LATE and ATE are the same.
The following discussion focuses on three popular approaches for estimation of mean effects on response probabilities from an instrument-driven exogenous shift in the treatment di: the fully parametric bivariate probit (BVP) model, the semi-parametric residual inclusion (2SRI) approach, and the linear two-stage least squares (2SLS) approach. Each of these methods employ different assumptions and attempt to identify different parameters. In fact, Chiburis et al. (2012) have argued that many of the documented differences in the treatment effect estimates from 2SLS and bi-variate probit models in the literature may be driven by the fact that they are estimating different parameters to begin with. We now look at these estimators in detail.
2.1. Approach 1 (Fully parametric): e.g. Bivariate-Probit
If the joint distribution of the structural error term ui and the reduced form error term vi were parametrically specified (e.g. Gaussian), and λ(wi, zi) is parametrically specified, then under some normalization of the Var(ui) (Blundell and Smith 1986),
| (8) |
where ρ is the vector of population regression coefficients of ui on vi. The parameters β, λ(.) and ρ can be estimated using maximum likelihood estimation. When both yi and di are binary, this approach can be implemented using a bivariate probit regression (Heckman 1978). However, bivariate probit models can be sensitive to heteroscedasticity and are usually more robust when treatment probabilities approach 0 or 1 (Chiburis et al. 2012). If the underlying distributions are correctly specified, this method structurally recovers the average treatment effect (ATE) parameter since ui | vi, identified through the IV, is structurally linked to ui through the parametric assumption.
The sample analog for the population treatment effect parameter identified by this approach is given by:
| (9) |
where indicates that these quantities have been estimated from the data at hand.
2.2. Approach 2 (Semi-parametric): e.g 2SRI
The semi-parametric approach uses estimates of the reduced form error term, vi, to control for endogeneity of di in the outcomes structural model (Blundell and Powell 2004). The identification of β1 and the distribution functions of the error term, ui, is through distributional exclusion restrictions, the first of which requires that the dependence of ui on each of di, wi and zi are completely characterized by the reduced form error vector vi:
| (10) |
Under this assumption,
| (11) |
where F(.) is the conditional c.d.f. of -ui given vi.
The marginal distribution function G(.) with respect to -ui could be identified using a control function approach such as (Blundell and Powell 2004):
| (12) |
where Hv is the distribution function of v. Consequently, ATE can be identified using (6). Note that, unlike the fully parametric approach, one can be agnostic about the parametric distribution of ui and vi as long as the distributional exclusion criterion is met. However, Blundell and Powell’s (2003) identification relies on a continuous vi. Moreover, the identification of ATE relies on the fact that the error term in the outcomes model is additively separable. These conditions allow for a counterfactual to be determined without the need for any additional functional form assumptions given that the β are consistently estimated. However, in non-linear models, such as those in (2), these counterfactuals inherently depend on the functional form assumption of the control function.
For example, in practice, this approach is implemented through “residual inclusion”, which follows estimating the error term in the first–stage regression and then including these estimated residuals as a covariate in the second-stage outcomes regression. A recycled predictions approach can then be used to recover the marginal effect of di on E(yi).
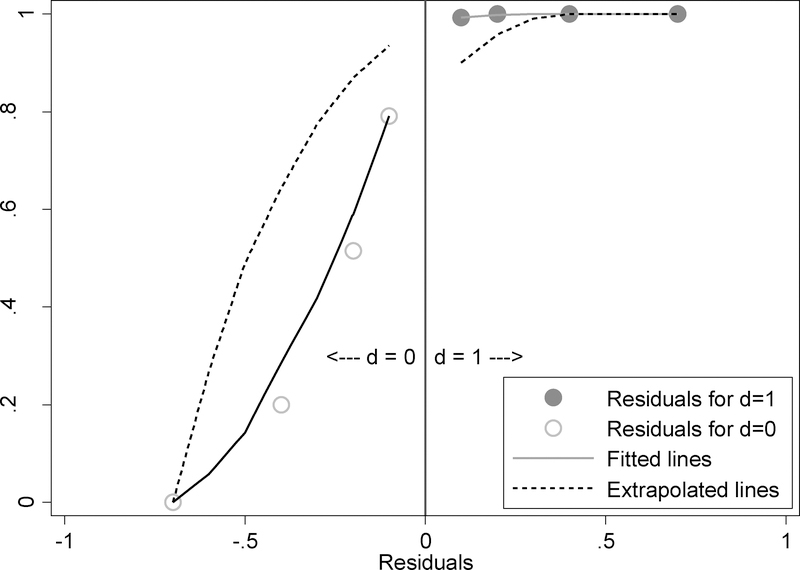
However, when implementing this approach for a binary treatment variable, the residuals from the first stage would always be positive for treatment recipients and negative for non-recipients. Hence, in a non-linear outcomes model, the conditional treatment effect, conditional on any level of the estimated vi (say, ), must be obtained via extrapolation. Figure 1 illustrates this idea for a group of individuals with the same wi, which is kept implicit, but different values of zi, which leads to difference values of . Suppose the residuals among treatment recipients are 0.1, 0.2, 0.3, 0.4, 0.7 and those among non-recipients are −0.1, −0.2, −0.3, −0.4, −0.7. Conditional on a positive level of the residual vi+, is obtained from the data where y1 is the potential outcome under treatment. However, the counterfactual outcome, i.e. the corresponding potential outcome y0 for treatment recipients, which are supposed to be estimated from the outcomes of similar patients under no treatment, cannot be directly estimated as there are no non-recipients that have a positive level of the residual by construction.
Figure 1:
Illustration of residual inclusion approach for binary treatment variable.
Once the parameters of the F(), the CDF-based regression function used to model the binary outcome as a function of d and the residuals, are estimated, the counterfactual outcomes for treatment recipients over the distribution of positive residuals has to be obtained via extrapolation of the functional specification of F() over the positive residuals and turning off the indicator d to 0.. Similar extrapolation is required for estimating the counterfactual outcomes y1 for treatment non-recipients over the distribution of negative residuals. Figure 1(a) illustrates this extrapolation. The overall treatment effect is then obtained by averaging the conditional treatment effects obtained over the distribution of .
Symmetry in the distribution of , to the extent that it can be attained, can facilitate this extrapolation. Most forms of residuals used in non-linear settings attempt to mimic a normal distribution. Alternate forms of residuals, such as standardized, deviance, Anscombe, and generalized (Gourieroux et.al., 1987), may also be used in the residual inclusion approach and have been explored Garrido et al. 2012). When estimated by a nonlinear approach, such as probit or logit, raw-scale residuals for a binary treatment variable will always lie between 0 and 1 in absolute values. Therefore, each type of residual transformation is likely to spread the support of the residual distribution on the real line. For example, if predicted Pr(d|z) = 0.4 and 0.7 for two observations with d = 1, then the raw-scale residuals will be 0.6 and 0.3 respectively, but the standardized residuals will be 1.22 and 0.65 respectively. Consequently, standardized residuals may provide a better fit to the outcomes data and increase the robustness of extrapolations. For example, when the treatment is rare, the raw-scale residuals on either the negative or the positive side are likely to be far away from zero. Transformation can help these residuals to spread out, so as to increase accuracy when estimating the functional form of the outcome conditional on these residuals. A priori, it is difficult to predict what form of residuals from a binary treatment model would best approximate the non-separable error term in the outcomes equation.
It is worth reiterating that a central problem, beyond the issue of non-overlap in support of as discussed above, when the instrumental variable is also binary is that only two points on the support of are identified for any level of w. Model fit and extrapolation is based only on those two points in the support for
2.3. Approach 3 (Non-parametric): e.g. 2SLS
Distinct from BVP and 2SRI approaches discussed above, which are designed to identify the ATE, a 2SLS approach is designed to estimate the LATE parameter. A 2SLS approach attempts to estimate the LATE from the data non-parametrically by estimating the slope of outcomes and exposure, conditional on the instrument. In the case of a single binary instrument, this slope is based upon the two points of support identified by the two levels of the instrument. That is, it plugs in the sample analogs of the numerator and the denominator in the LATE parameter defined above. However, this process assumes that the mean outcomes and the exposure models are linear in terms of wi.3 When one or both of these linear specifications are violated, 2SLS may be a biased estimator for the outcome probabilities (Horace and Oaxaca 2006). While this could, in turn, induce bias in the estimation of LATE, some have suggested that risk of such bias is minimal in many applied settings and concerns are exaggerated. (Angrist and Fernandez-Val 2001)
The 2SLS approach of linear IV models can be viewed as a special case of control function methods (Telser 1964), where both first and second stage regressions are linear. However, since 2SLS approaches rely only on mean–independence requirements, and not on the full conditional independence of the distribution as in (8), demands the “correct” specification of the first-stage to provide consistent estimates of the second-stage parameters (Blundell and Powell, 2004). However, this requirement seems to apply mostly for the estimation of ATE; as the LATE value is not necessarily equivalent or determined by the true structural parameters under essential heterogeneity. It is unclear how violation of this requirement affects estimation of LATE. We expect that for a binary treatment in the first stage, a linear approximation of the conditional mean is likely to be most appropriate when the mean treatment is close to 50%. Chapman and Brooks (2016) simulation results showed that 2SLS methods produced unbiased estimates of the IV effect (i.e weighted average of LATEs defined by the continuous IVs that they use) in models with treatment rates near 50%, but did not consider binary instruments.
These discussions establish the rationale for the simulations in this paper. It is conjectured that 2SRI approach applied to binary endogenous variables can produce biased results when extrapolations are not appropriate. Alternative versions of the residuals could improve the performance of 2SRI approaches through mutating the scale of the residual distribution used, which could influence the estimation of the underlying structural functions through the 2SRI approach as was observed in Garrido et al. (2012). Second, when the endogenous binary variable becomes rare, the linear model specification in the first-stage could break down, resulting in biased estimation of second-stage parameters in the 2SLS approach. These biases could then compound biases from misfit of the linear model to rare outcomes in the second-stage.
3. SIMULATIONS
We consider the simplest case where we have a binary outcome (yi), a binary treatment (di), three binary controls (wi) and a binary instrument (zi). We chose three binary controls so that the residuals from the first stage regression have at least thirty unique values in their support. The central questions we try to answer with these simulations are: Can linear approximation (2SLS) provide consistent estimates of the LATE for a binary outcome/binary endogenous variable model? What form of residuals are most suited to a correctly specified nonlinear 2SRI (Probit-Probit) approach? How do the results change if outcomes (yi) and/or treatment (di) become rare?
The data generating processes (DGPs) are described below (subscripts i are suppressed for clarity).
3.1. Exposure (treatment) DGP
| (13) |
where (α1, α2, α3) = (0.5, 1, 2), αU = 1, αZ = 1. Observed variables w1, w2, w3 and z are all binary variables with mean equal to 0.5, generated by dichotomizing standard normal variables around the value of 0. Together, (αU· wU – ω) represents the empirical error term for the treatment model and consists of the binary unobserved confounder, wU, which is also based on dichotomizing a Normal (0,1), and the continuous model disturbance term, ω ~ Normal(0,1). Observed treatment, d, is derived from the index function (d* > 0) and Pr(d) = Φ( (α0 + 2.25)/√3.5625)). We vary the model intercept, α0, to take on values of −2, −1.25, −0.3, 0.5, and 1.5 which correspond to Pr(d) = 0.55, 0.70, 0.85, 0.93, and 0.995 respectively.
3.2. Outcomes DGP
| (14) |
Together (βU· wU – ε) represents the empirical error term, u, from the theoretical outcomes model under Section 2. Across all simulation models, true values of coefficients (β 1, β 2, β3) were set to (1,1,1), the coefficient for the unmeasured confounder, βU, was set to 2, and coefficient on treatment, βD, was set to 1. The model disturbance term ε ~ Normal(0,1) and Pr(y|d) = Φ( (β 0 + β D· d + 1.5)/√5.75)). We vary β 0 across simulations to take on values of −2, 0.5, 1.5, and 2.5 which correspond to Pr(y) = 0.51, 0.82, 0.93 and 0.96 respectively.
3.3. Target parameters
The primary target parameters were the ATE and the LATE. True values for the ATE and LATE concepts were calculated in each simulation as:
| (15) |
| (16) |
where w = (w1, w2, w3, wu). The true value of the LATE parameter was simulated based on 100 samples of 1 million observations each.
3.4. Simulations
Estimates were generated using Monte-Carlo simulation methods, using 1,000 samples of 50,000 observations each to mitigate finite sample issues and also to align our simulation with our empirical example. For each of the 1,000 simulated samples, 500 bootstrap re-samples were drawn and used to calculate standard error and coverage values. Percent bias was calculated as ( - LATE)*100/LATE or ( - ATE)*100/ATE averaged over all simulated samples, where is the estimated treatment effect for sample k. The coefficient of variation is based on the standard deviation of the mean estimates across the 1,000 Monte-Carlo samples divided by the average of the mean estimates from those samples. Finally, coverage probabilities for LATE and ATE were determined by averaging I (( – 1.96* ) ≤ LATE ≤ ( + 1.96* )) and I (( – 1.96* ) ≤ ATE ≤ ( + 1.96* )), respectively, across all 1,000 samples, where I() is an indicator function and is the sample-specific standard error obtained via bootstrap.
Simulations were repeated using a sample size of 5,000 to magnify any finite sample issues, and those results are presented in the appendix.
3.5. Estimators
We compared the following estimators:
IV regression with LPM (2SLS)
-
Probit-Probit 2SRI with
raw residuals as ,
standardized (Pearson) residuals given by ,
deviance residuals, given by and
Anscombe residuals, , where and B() is a Beta Function.
Generalized residuals (Gourieroux et al. 1987):
Bi-variate probit regression model, which is the MLE for the DGPs.
3.6. Results
Descriptive statistics for our DGPs are provided in Table 1. As expected, the true mean average treatment effect (ATE) parameter values varied across scenarios varying the intercept in the outcome models, β 0, but not across scenarios varying the intercept in the treatment models. LATE, however, varies with the intercepts in both the outcome and treatment choice models. As outcomes become rare, following an underlying probit model, both ATE and LATE decrease.
Table 1:
Descriptive statistics for alternative data generating processes.
| Outcomes DGP (β0) | Exposure DGP (α0) |
||||
|---|---|---|---|---|---|
| −2 | −1.25 | −0.3 | 0.5 | 1.5 | |
| −2 | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
| E(Y) = 0.51 | E(Y) = 0.54 | E(Y) = 0.57 | E(Y) = 0.57 | E(Y) = 0.58 | |
| ATE = 0.165 | ATE = 0.165 | ATE = 0.165 | ATE = 0.165 | ATE = 0.165 | |
| TT= 0.168 | TT= 0.176 | TT= 0.176 | TT= 0.172 | TT= 0.170 | |
| TUT =0.160 | TUT =0.140 | TUT =0.101 | TUT =0.071 | TUT =0.031 | |
| LATE = 0.212 | LATE = 0.198 | LATE = 0.150 | LATE = 0.098 | LATE = 0.046 | |
| 0.5 | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
| E(Y) = 0.82 | E(Y) = 0.84 | E(Y) = 0.86 | E(Y) = 0.87 | E(Y) = 0.89 | |
| ATE = 0.097 | ATE = 0.097 | ATE = 0.097 | ATE = 0.097 | ATE = 0.097 | |
| TT= 0.044 | TT= 0.060 | TT= 0.078 | TT= 0.088 | TT=0.93 | |
| TUT =0.162 | TUT =0.181 | TUT =0.202 | TUT =0.201 | TUT =0.172 | |
| LATE = 0.100 | LATE = 0.141 | LATE = 0.192 | LATE = 0.218 | LATE = 0.203 | |
| 1.5 | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
| E(Y) = 0.93 | E(Y) = 0.93 | E(Y) = 0.93 | E(Y) = 0.95 | E(Y) = 0.95 | |
| ATE = 0.058 | ATE = 0.058 | ATE = 0.058 | ATE = 0.058 | ATE = 0.058 | |
| TT=0.017 | TT=0.025 | TT=0.038 | TT=0.047 | TT=0.054 | |
| TUT =0.109 | TUT =0.133 | TUT =0.168 | TUT =0.197 | TUT =0.217 | |
| LATE = 0.045 | LATE = 0.075 | LATE = 0.127 | LATE = 0.178 | LATE =0.220 | |
| 2.5 | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
| E(Y) = 0.96 | E(Y) = 0.96 | E(Y) = 0.96 | E(Y) = 0.98 | E(Y) = 0.98 | |
| ATE = 0.029 | ATE = 0.029 | ATE = 0.029 | ATE = 0.029 | ATE = 0.029 | |
| TT=0.005 | TT=0.008 | TT=0.014 | TT=0.020 | TT=0.023 | |
| TUT =0.059 | TUT =0.077 | TUT =0.110 | TUT =0.144 | TUT =0.185 | |
| LATE = 0.015 | LATE = 0.029 | LATE = 0.062 | LATE = 0.107 | LATE = 0.175 | |
TT: Effect on the Treated; TUT: Effect on the Untreated; True values of TT and TUT are provided for information only
Simulation results are presented in Tables 2 and 3. Table 2 reports percent bias, the coefficient of variation, and coverage probabilities on the LATE. We find that 2SLS always provides consistent estimates of LATE, irrespective of the treatment rarity or outcomes rarity. This indicates that 2SLS can consistently estimate the LATE effect even if the linear probability model misfits the data and produces out of range predictions. Results do not show any major drop in coverage probabilities for LATE across simulation design points. Estimates from nonlinear 2SRI and bi-variate probit were generally biased for the LATE.
Table 2:
Simulations results (N=50,000) for Local Average Treatment Effects (LATEs) - %Bias (Coeff. Var.) {Coverage Pr}
| E(Y) | Estimators | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
|---|---|---|---|---|---|---|
| 0.50~0.60 | Naïve Probit | 170 [.01] {0} | 182 [.01] {0} | 242 [.01] {0} | 382 [.01] {0} | 846 [.01] {0} |
| 2SLS | −1 [.08] {.96} | −1 [.1] {.96} | −2 [.21] {.95} | −5 [.59] {.94} | −30 [4.64] {.94} | |
| 2SRI | −49 [.19] {0} | −33 [.16] {.17} | 42 [.12] {.34} | 205 [.12] {0} | 774 [.15] {.01} | |
| 2SRI - sres | 12 [.08] {.75} | 36 [.09] {.17} | 109 [.11] {0} | 267 [.14] {0} | 799 [.2] {.04} | |
| 2SRI - dres | −106 [−1.45] {0} | −102 [−5.19] {0} | −50 [.42] {.36} | 126 [.19] {.15} | 834 [.12] {0} | |
| 2SRI - ares | −91 [1.07] {0} | −84 [.68] {0} | −34 [.3] {.62} | 120 [.19] {.18} | 775 [.15] {0} | |
| 2SRI - gres | −48 [.18] {0} | −33 [.15] {.13} | 22 [.14] {.73} | 150 [.15] {.03} | 656 [.22] {.05} | |
| Bi.Probit | −23 [.1] {.17} | −17 [.1] {.5} | 9 [.15] {.92} | 63 [.3] {.75} | 171 [1.57] {.84} | |
| 0.80 ~0.90 | Naïve Probit | 233 [.01] {0} | 185 [.01] {0} | 156 [.01] {0} | 161 [.01] {0} | 228 [.02] {0} |
| 2SLS | 0 [.17] {.91} | 0 [.13] {.92} | 0 [.12] {.92} | 0 [.17] {.93} | −1 [.51] {.93} | |
| 2SRI | −1 [.16] {.92} | −38 [.19] {.09} | −75 [.38] {0} | −86 [.8] {0} | −79 [1.38] {.25} | |
| 2SRI - sres | 75 [.06] {0} | 71 [.05] {0} | 63 [.06] {0} | 72 [.08] {0} | 134 [.11] {0} | |
| 2SRI - dres | −71 [.69] {.04} | −97 [3.72] {0} | −107 [−1.15] {0} | −101 [−6.45] {0} | −59 [.65] {.38} | |
| 2SRI - ares | −48 [.34] {.15} | −68 [.39] {0} | −79 [.42] {0} | −74 [.42] {0} | −35 [.45] {.67} | |
| 2SRI - gres | −1 [.15] {.92} | −31 [.17] {.17} | −55 [.2] {0} | −65 [.3] {0} | −62 [.69] {.35} | |
| Bi.Probit | −3 [.13] {.93} | −31 [.14] {.08} | −50 [.15] {0} | −56 [.19] {0} | −51 [.44] {.33} | |
| 0.9 ~ 0.95 | Naïve Probit | 322 [.02] {0} | 232 [.02] {0} | 166 [.02] {0} | 144 [.02] {0} | 162 [.02] {0} |
| 2SLS | −1 [.29] {.94} | −1 [.18] {.95} | −1 [.13] {.95} | −1 [.15] {.94} | −2 [.31] {.96} | |
| 2SRI | 61 [.12] {.1} | −12 [.16] {.82} | −76 [.41] {0} | −102 [−3.35] {0} | −108 [−1.19] {0} | |
| 2SRI - sres | 134 [.06] {0} | 97 [.05] {0} | 68 [.06] {0} | 51 [.08] {0} | 63 [.11] {.02} | |
| 2SRI - dres | −18 [.34] {.9} | −78 [.77] {.01} | −103 [−2.91] {0} | −105 [−1.29] {0} | −96 [2.73] {0} | |
| 2SRI - ares | 7 [.23] {.91} | −47 [.28] {.11} | −71 [.32] {0} | −78 [.39] {0} | −68 [.49] {.04} | |
| 2SRI - gres | 56 [.12] {.14} | −11 [.15] {.83} | −52 [.19] {0} | −73 [.31] {0} | −84 [.8] {0} | |
| Bi.Probit | 29 [.16] {.66} | −22 [.15] {.48} | −54 [.17] {0} | −67 [.2] {0} | −73 [.38] {0} | |
| 0.95~0.98 | Naïve Probit | 493 [.02] {0} | 324 [.02] {0} | 203 [.02] {0} | 151 [.03] {0} | 133 [.04] {0} |
| 2SLS | −2 [.6] {.95} | −1 [.32] {.96} | −1 [.19] {.97} | −2 [.17] {.97} | −3 [.25] {.96} | |
| 2SRI | 174 [.1] {0} | 32 [.14] {.62} | −67 [.36] {0} | −108 [−.99] {0} | −111 [−.33] {0} | |
| 2SRI - sres | 244 [.06] {0} | 142 [.06] {0} | 87 [.07] {0} | 48 [.09] {.01} | 30 [.12] {.4} | |
| 2SRI - dres | 88 [.22] {.45} | −43 [.44] {.63} | −95 [2.42] {0} | −104 [−1.66] {0} | −102 [−2.92] {0} | |
| 2SRI - ares | 111 [.17] {.16} | −11 [.23] {.94} | −60 [.29] {0} | −76 [.32] {0} | −78 [.49] {0} | |
| 2SRI - gres | 164 [.1] {0} | 25 [.14] {.72} | −44 [.21] {.05} | −74 [.3] {0} | −89 [.82] {0} | |
| Bi.Probit | 90 [.24] {.48} | −2 [.19] {.96} | −53 [.2] {0} | −73 [.22] {0} | −83 [.4] {0} | |
2SRI – sres: 2SRI with standardized residuals; 2SRI – dres: 2SRI with deviance residuals; 2SRI – ares: 2SRI with Anscombe residuals; 2SRI-gres: 2SRI with generalized residuals; Shaded cells highlight estimator with lowest percentage bias.
Table 3:
Simulations results (N=50,000) comparing to Average Treatment Effects (ATEs) - %Bias (Coeff. Var.) {Coverage Pr}
| E(Y) | Estimators | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
|---|---|---|---|---|---|---|
| 0.50~0.60 | Naïve Probit | 248 [.01] {0} | 237 [.01] {0} | 211 [.01] {0} | 187 [.01] {0} | 164 [.01] {0} |
| 2SLS | 28 [.08] {.28} | 18 [.1] {.69} | −11 [.21] {.92} | −43 [.59] {.78} | −80 [4.64] {.86} | |
| 2SRI | −34 [.19] {.28} | −20 [.16] {.66} | 28 [.12] {.55} | 82 [.12] {.03} | 144 [.15] {.09} | |
| 2SRI - sres | 44 [.08] {.05} | 63 [.09] {.01} | 90 [.11] {0} | 119 [.14] {.02} | 151 [.2] {.18} | |
| 2SRI - dres | −108 [−1.45] {0} | −103 [−5.19] {0} | −55 [.42] {.19} | 35 [.19] {.71} | 161 [.12] {.01} | |
| 2SRI - ares | −88 [1.07] {0} | −80 [.68] {0} | −40 [.3] {.42} | 31 [.19] {.74} | 144 [.15] {.05} | |
| 2SRI - gres | −33 [.18] {.3} | −20 [.15] {.63} | 11 [.14] {.88} | 49 [.15] {.42} | 111 [.22] {.36} | |
| Bi.Probit | −1 [.1] {.95} | −1 [.1] {.97} | −1 [.15] {.95} | −3 [.3] {.94} | −25 [1.57] {.85} | |
| 0.80 ~0.90 | Naïve Probit | 244 [.01] {0} | 314 [.01] {0} | 407 [.01] {0} | 489 [.01] {0} | 587 [.02] {0} |
| 2SLS | 3 [.17] {.9} | 45 [.13] {.25} | 98 [.12] {.01} | 125 [.17] {.1} | 107 [.51] {.78} | |
| 2SRI | 2 [.16] {.9} | −10 [.19] {.85} | −49 [.38] {.25} | −68 [.8] {.26} | −55 [1.38] {.72} | |
| 2SRI - sres | 80 [.06] {0} | 149 [.05] {0} | 224 [.06] {0} | 289 [.08] {0} | 390 [.11] {0} | |
| 2SRI - dres | −71 [.69] {.04} | −95 [3.72] {0} | −114 [−1.15] {0} | −103 [−6.45] {.01} | −13 [.65] {.89} | |
| 2SRI - ares | −47 [.34] {.22} | −54 [.39] {.1} | −58 [.42] {.1} | −42 [.42] {.56} | 36 [.45] {.88} | |
| 2SRI - gres | 2 [.15] {.92} | 0 [.17] {.91} | −10 [.2] {.89} | −20 [.3] {.8} | −20 [.69] {.87} | |
| Bi.Probit | 0 [.13] {.94} | 0 [.14] {.91} | 0 [.15] {.93} | 0 [.19] {.94} | 2 [.44] {.93} | |
| 0.9 ~ 0.95 | Naïve Probit | 226 [.02] {0} | 327 [.02] {0} | 484 [.02] {0} | 649 [.02] {0} | 891 [.02] {0} |
| 2SLS | −24 [.29] {.79} | 27 [.18] {.76} | 117 [.13] {.02} | 204 [.15] {0} | 272 [.31] {.38} | |
| 2SRI | 24 [.12] {.6} | 13 [.16] {.89} | −48 [.41] {.36} | −107 [−3.35] {.04} | −131 [−1.19] {.19} | |
| 2SRI - sres | 81 [.06] {0} | 154 [.05] {0} | 268 [.06] {0} | 365 [.08] {0} | 519 [.11] {0} | |
| 2SRI - dres | −37 [.34] {.6} | −72 [.77] {.09} | −107 [−2.91] {0} | −115 [−1.29] {0} | −85 [2.73] {.42} | |
| 2SRI - ares | −18 [.23] {.85} | −31 [.28] {.59} | −37 [.32] {.5} | −32 [.39] {.7} | 19 [.49] {.95} | |
| 2SRI - gres | 21 [.12] {.67} | 14 [.15] {.85} | 4 [.19] {.95} | −17 [.31] {.83} | −39 [.8] {.76} | |
| Bi.Probit | 0 [.16] {.92} | 0 [.15] {.95} | 0 [.17] {.94} | 1 [.2] {.95} | 1 [.38] {.93} | |
| 0.95~0.98 | Naïve Probit | 203 [.02] {0} | 328 [.02] {0} | 549 [.02] {0} | 819 [.03] {0} | 1292 [.04] {0} |
| 2SLS | −50 [.6] {.62} | 0 [.32] {.96} | 111 [.19] {.26} | 259 [.17] {.02} | 482 [.25] {.13} | |
| 2SRI | 40 [.1] {.23} | 33 [.14] {.60} | −29 [.36] {.78} | −128 [−.99] {.03} | −164 [−.33] {.06} | |
| 2SRI - sres | 76 [.06] {0} | 144 [.06] {0} | 301 [.07] {0} | 444 [.09] {0} | 679 [.12] {0} | |
| 2SRI - dres | −4 [.22] {.96} | −42 [.44] {.66} | −89 [2.42] {.1} | −114 [−1.66] {.02} | −112 [−2.92] {.21} | |
| 2SRI - ares | 8 [.17] {.91} | −10 [.23] {.94} | −15 [.29] {.89} | −12 [.32] {.91} | 30 [.49] {.97} | |
| 2SRI - gres | 35 [.1] {.32} | 26 [.14] {.7} | 19 [.21] {.91} | −3 [.3] {.95} | −36 [.82] {.8} | |
| Bi.Probit | −3 [.24] {.94} | −1 [.19] {.96} | 0 [.2] {.96} | 0 [.22] {.97} | 2 [.4] {.94} | |
2SRI – sres: 2SRI with standardized residuals; 2SRI – dres: 2SRI with deviance residuals; 2SRI – ares: 2SRI with Anscombe residuals; 2SRI-gres: 2SRI with generalized residuals; Shaded cells highlight estimator with lowest percentage bias.
Table 3 reports percent bias, the coefficient of variation and coverage probabilities on the ATE. As expected, given the DGPs, bi-variate probit always produced the least biased estimates of the ATE. Also as expected, 2SLS produced biased estimates of ATE, especially as the ATE and LATE became increasingly distinct in value with rarer treatment and outcome. Results showed that all of the 2SRI estimators produced substantially larger biases (and poor coverage probabilities) than bi-variate probit in estimating ATE. This highlights the difficulty of estimating the ATE through extrapolation using the first-stage residuals. Among the residual inclusion approaches, 2SRI with generalized residual appeared to have the least bias in estimating ATE in most cases. However, the corresponding coverage probabilities were low.
One interesting observation was that, for rare outcomes (such as those below 5%), 2SRI with Anscombe residuals produced the least bias in estimating ATE, with coverage probabilities close to 95% in each case. The coverage probabilities did not detoriorate when treatment also became rare. This may indicate that the Anscombe transformation of the first-stage residuals are helping to better approximate the distribution of ui|vi where the outcomes are rare and, therefore, abetting the extrapolation for the counterfactuals.
Results for patterns of bias with 2SLS and 2SRI held similar for the simulations with a sample size of 5000 (Appendix Tables A2 and A3).
4. EMPIRICAL EXAMPLE
To illustrate the potential impact of the estimation method on empirical results, we use the case of long-term care insurance (LTCI) and its impact on long-term care (LTC) utilization. This issue has been studied by Konetzka, He, Guo and Nyman (2014) and Coe, Goda and Van Houtven (2015). This application is fitting to illustrate the concepts examined in the simulation models, as it is characterized by: 1) a relatively low E(Y) -- few elderly hold long-term care insurance; 2) an empirically strong and widely accepted instrumental variable – state tax policies that reduce the cost of insurance influence LTCI holding; and 3) multiple outcomes, at varying means Pr(Y).
4.1. Data
Three main data sources were used, following Coe, Goda and Van Houtven (2015): (1) the Health and Retirement Study (HRS) (including RAND versions) (http://hrsonline.isr.umich.edu/); (2) the HRS restricted geographic identifiers (HRS/G), in order to match the individual to the state of residence, and (3) state-level tax subsidy data for the purchase and holding of state-approved LTCI policies (GS Goda, 2011).
Data from ten waves of the HRS (1996–2010), a publicly available, bi-annual survey of the near elderly in the U.S. were used.4 Respondents were ages 50 and older when they initially entered the sample and many respondents are observed long enough to have used some type of long-term care. To increase the relevance of the instrumental variable used for analysis – the state tax subsidy – the sample was limited to individuals who report filing taxes and individuals in the top half of the income distribution in our sample. The sample size consisted of 46,639 individual-wave observations. The Cross-Wave Geographic Information (State) file matches respondents to their state of residence, which is then matched to hand-collected data from individual state income tax return forms from 1996–2010 that describe tax subsidy programs for private long-term care insurance.
4.2. Measures and Descriptive Statistics
Five binary outcome measures were created; the measures had varying means to illustrate the bias due to the estimation methods. Each outcome measure is created from HRS data one wave (approximately two years) ahead of the data used to create explanatory measures described below. Descriptive statistics for the data are shown in Table 3.
Informal Helper
Defining informal care in the HRS requires an algorithm based on several variables. The process first identifies whether the person received care for specific IADLS and ADLS and then uses information from relationship codes measured in the helper file to determine whether the care was from a child, a friend or another relative to ensure that the care recipient was not paid. We create 3 variables based on who provided the informal care: 60 percent of the sample receives informal care from any person; 43 percent receive informal care from a child; 16.5 percent receive care from other relatives.
Home Health care
The formal home health care variables are: “Since the previous interview, has any medically-trained person come to your home to help you, yourself?” In 2000, the HRS clarified that medically-trained persons include professional nurses, visiting nurse’s aides, physical or occupational therapists, chemotherapists, and respiratory oxygen therapists, which may represent an expansion of the definition of home health care. 6.8 percent received home health care.
Nursing home care
The HRS asks: “Since (Previous Wave Interview Month-Year/In the last two years), have you been a patient overnight in a nursing home, convalescent home, or other long-term health care facility?” For individuals who died between waves, nursing home use was measured from data in the HRS exit interviews. 2.3 percent received nursing home care.
LTCI (mean=0.157)
Starting in the 1996 wave, respondents were asked to respond yes or no to the following question: “Not including government programs, do you now have any long term care insurance which specifically covers nursing home care for a year or more or any part of personal or medical care in your home?”. LTCI status is defined as having LTCI in year t, based on the recorded response to this question; 15.7 percent of individual-waves had long-term care insurance.
State Tax Subsidy (an instrument for LTCI)
Following the literature, a binary variable indicating whether a state has a tax subsidy available in a particular year was created to be used as an instrument for LCTI. The state tax subsidy indicated any subsidy, regardless of the form of the subsidy (i.e., credit or a deduction), the fraction of premiums eligible, monetary caps on the value of the subsidy, income limits, or whether the state subsidy was available in addition to the federal subsidy (GS Goda, 2011; Konetzka et al. 2014; Coe, Goda and Van Houtven 2015). The availability of a state tax subsidy varied considerably over time and across states; while only three states had tax incentives for LTCI in 1996, a total of 24 states plus the District of Columbia had adopted a subsidy by 2008. Prior literature has provided evidence that the state tax subsidy is empirically important in whether someone holds an LTCI policy and meets essential criteria for use as an instrumental variable in this context. In the first stage regression, the estimated coefficient on the binary state tax subsidy variable suggested that individuals in states with subsidies are about three percentage points more likely to own LTCI (F-stat: 65.93, p<0.001).
Individual-level control variables
Control variables in the models included binary variables indicating respondent’s marital status, sex, number of children, retirement status, education, income, race, ethnicity, health status (fair or poor self-reported health and the presence of any limitations in the activities of daily living (ADLs)), and age fixed effects.
Fixed-effects
All models include year and state fixed-effects. The year fixed-effects account for time trends in the data while the state fixed-effects account for non-time-varying differences across states. The inclusion of state fixed-effects suggests that the empirical models identify the effect of LTCI coverage on outcome for individuals whose LTCI coverage was sensitive to within-state differences in the state tax policy.
Analyses included use of all estimators represented in the simulations models described in the previous section. Each estimator was used to estimate the effect of long-term care insurance on each of the five outcomes described above, using the binary state tax subsidy variable as an instrumental variable. For each estimator, estimates from 500 clustered bootstrap samples were used to compute standard errors for the marginal effect in each case.
4.3. Results
The simulation results indicated that 2SLS should produce consistent estimates of LATEs, regardless of treatment or outcome rarity. Conversely, results suggested 2SRI models were likely to produce bias in estimating average treatment effects on outcomes (ATE or LATE), with generalized residuals estimator (2SRI-Gres) producing the least bias. For very rare outcome, such as nursing home care and home health care in our empirical application, 2SRI with Anscombe residual (2SRI-ares) may produce estimates close to the unbiased estimates of ATE.
Table 4 provides summary statistics for outcomes and other variables used in the empirical models. The marginal effects and their bootstrapped standard errors are shown in Table 5.
Table 4:
Descriptive Statistics for HRS dataset
| Binary Variables | Mean (sd) |
|---|---|
| Outcomes | |
| Informal Care from Any Source | 0.60 (0.49) |
| Informal Care from Child | 0.43 (0.50) |
| Informal Care from other Relative | 0.165 (0.37) |
| Home Health Care | 0.068 ( 0.25) |
| Any Nursing Home Care | 0.023 (0.15) |
| Treatment | |
| LTCI coverage | 0.157 (0.364) |
| IV | |
| Subsidies | 0.335 (0.472) |
| Other covariates | |
| Marital status==2 | 0.11 (0.32) |
| Marital status ==3 | 0.17 (0.37) |
| Marital status==4 | 0.06 (0.24) |
| Female | 0.56 (0.5) |
| No. of children==1 | 0.1 (0.3) |
| No. of children==2 | 0.31 (0.46) |
| No. of children==3 | 0.22 (0.42) |
| No. of children==4 | 0.13 (0.34) |
| No. of children==5 | 0.15 (0.36) |
| No. of children==6 | 0.01 (0.11) |
| Retired | 0.47 (0.5) |
| Education category ==2 | 0.35 (0.48) |
| Education category ==3 | 0.26 (0.44) |
| Education category ==4 | 0.3 (0.46) |
| Income category==2 | 0.36 (0.48) |
| Income category==3 | 0.64 (0.48) |
| Race category ==2 | 0.06 (0.25) |
| Race category ==3 | 0.03 (0.18) |
| Fair/Poor health | 0.17 (0.37) |
| Any ADL | 0.1 (0.29) |
Table 5:
Effects of long-term care insurance on different outcomes.
| Outcomes→ | Informal Care from Any Source | Informal Care from Child | Informal Care from other Relative | Home Health Care | Any Nursing Home Care |
|---|---|---|---|---|---|
| Estimators | Pr(Y) = 0.60 | Pr(Y) = 0.43 | Pr(Y) = 0.165 | Pr(Y) = 0.07 | Pr(Y) = 0.023 |
| Naïve Probit | −0.037 (0.006)++ | −0.032 (0.006)++ | −0.015 (0.004)++ | −0.005 (0.003) | 0.001 (0.002) |
| 2SLS | −0.302 (0.165)+ | −0.329 (0.165)++ | 0.161 (0.114) | −0.252 (0.089)++ | 0.087 (0.055) |
| 2SRI | −0.319 (0.103)++ | −0.238 (0.099)++ | −0.091 (0.062) | −0.142 (0.031)++ | 0.063 (0.097) |
| 2SRI - sres | −0.118 (0.029)++ | −0.074 (0.029)++ | −0.06 (0.017)++ | −0.028 (0.013)++ | 0.008 (0.012) |
| 2SRI - dres | −0.392 (0.085)++ | −0.28 (0.082)++ | −0.126 (0.052)++ | −0.127 (0.032)++ | 0.072 (0.102) |
| 2SRI - ares | −0.297 (0.07)++ | −0.198 (0.068)++ | −0.114 (0.038)++ | −0.085 (0.026)++ | 0.038 (0.055) |
| 2SRI – gres | −0.268 (0.062)++ | −0.179 (0.061)++ | −0.111 (0.032)++ | −0.077 (0.023)++ | 0.029 (0.041) |
| Bi.Probit | −0.283 (0.055)++ | −0.179 (0.059)++ | −0.147 (0.044)++ | −0.117 (0.033)++ | 0.023 (0.028) |
Pr(long-term care insurance) in these data = 0.157. 2SRI – sres: 2SRI with standardized residuals; 2SRI – dres: 2SRI with deviance residuals; 2SRI – ares: 2SRI with Anscombe residuals
p-val≤ 0.10
p-val≤0.05
The 2SLS-based consistent LATE estimates for LTCI were −0.302 (Informal care from any source), −0.329 (Informal care from child), 0.161 (Informal care from relatives), −0.252 (home health care), and 0.087 (Any nursing home care). The interpretation of LATE always refers to the marginal individuals. For example, in the model predicting informal care from any source, the LATE estimate suggests that LTCI decreases the use of informal care from any source by 30 percentage points among people who are moved to acquire LTCI due to the subsidy. Sometimes, LATE can provide treatment effects estimates that are difficult to interpret, and may even be considered nonsensical, even when the IV is policy-driven. For example, assuming that access to LTCI would increase receipt of formal care, which will act as a substitute for all forms of informal care, the effect of LTCI on Informal care from any source would perhaps not be expected to be smaller than the effect on Informal care from child, yet that is what LATE suggests. Similarly, it is difficult to envision how the effect from having LTCI, for those who have insurance due to state subsidies, increases informal care from a relative; though this LATE estimate does not reach statistical significance. One may invoke complicated stories about complementarity between formal care and informal care from relatives and particularities about the generosity of LTCI for those who have it due to state subsidies, to explain these result. Then again, the real world is full such complexities and taking the time to disentangle such nuanced relationships may be considered worthwhile. Note that the LATEs for different outcomes belong to the same marginal group of patients who are influenced by this specific IV.
Treatment effect estimates produced from the 2SRI models are often quite different from the 2SLS-based LATE estimates. This was expected. The 2SRI-Gres estimates of ATE for LTCI are −0.268 (Informal care from any source), −0.179 (Informal care from child), −0.111 (Informal care from relatives), −0.077 (home health care) and 0.023 (Any nursing home care). Taken at face value, these estimates did not have the contextual inconsistencies, as it relates to our a priori theory about the relationships under study, that were seen in LATE estimates. The 2SRI estimates were also quite similar to those produced by the Bi-Probit model, especially when outcomes mean was close to 0.50. It is quite plausible that the underlying distribution of outcomes is well approximated by a normal distribution when the binary outcome mean is close to 0.50, and hence, for these outcomes, the bi-probit model is likely to produce consistent estimates of ATE.5 For rarer outcomes, the bi-probit estimates and the 2SRI-gres estimates differ and it is not clear if any of those estimates are unbiased estimates of ATE.
For any nursing home care, which is the rarest outcome, 2SRI-ares (with Anscombe residuals) estimates of ATE are close to being unbiased, according to our simulations. Although this point estimate of 0.038 differs from that of Bi-probit (= 0.023), neither reach statistical significance. Hence, it is reasonable to conclude that the overall average effect of LTCI in the entire population does not significantly affect any nursing home care.
5. CONCLUSIONS
The economics literature is teeming with applications where linear probability models are used for binary outcomes. In case of instrumental variables methods, both the binary treatment (in 1st stage) and the binary outcome (in 2nd stage) are often modeled with linear probability models with two-stage least squares (2SLS) estimators. In contrast, a control function approach may be used with non-linear models (e.g. probit or logit applied to first and/or second stage models) where the estimated residuals from the first stage are used as an additional covariate in the second stage. However, the residual inclusion approach does not identify a treatment effect non-parametrically. Instead, it relies on extrapolation for the counterfactual outcomes conditional of the level of a residual using the functional form used. The proper characterization of these residuals is thought to be important to carry out such extrapolations. This research considered the case where a local average treatment effect (LATE) parameter is non-parametrically identified using a binary instrument in the presence of all binary covariates. Extensive simulations that varied the rarity of both the outcome and treatment were performed to answer questions of whether 2SLS or 2SRI methods with different forms of residuals has the least bias in estimating the LATE or the ATE parameters.
Results show that the 2SLS method with binary IV, applied to a binary endogenous treatment and a binary outcome, produces consistent estimates of LATE across the entire range of rarity for either treatment or the outcome. The rarity of either does not affect the coverage probabilities of these estimators. In contrast, the 2SRI approach with any residuals studied was a biased estimator for LATE. However, in principle, the 2SRI estimators are designed to estimate the ATE parameter. Yet, still, results showed that 2SRI does not appear dependable for producing unbiased estimates of ATE. Rather, there were varying levels of bias associated with 2SRI estimates of ATE. Among the residual forms, 2SRI with generalized residuals appeared to produce the least biased estimates of the ATE. For very rare outcomes (<5%) 2SRI with Anscombe residual generated the least bias in estimating ATE. We conjecture that the symmetric transformation of these residuals may be leading to better extrapolation properties of the 2SRI estimators. However, whether these findings represent a general operating characteristic of 2SRI or are unique to our simulation settings is not known.
Results from this study conform with the simulation results of Chapman and Brooks (2016), who compared 2SLS and nonlinear 2SRI with raw residuals in simulation models with binary treatment, binary outcome, and continuous instruments to find that 2SLS produced consistent estimates for the IV effect while 2SRI did not reliably estimate either the ATE or the IV effect. However, their study did not examine models with binary instruments, vary rarity of treatment or outcome from approximately 0.5, examine alternative forms of 2SRI residuals, or report coverage probabilities of estimates. The results of this study provide additional and more comprehensive evidence showing how 2SLS are consistent estimators of LATE over a wide range of scenarios varying by rarity of binary outcomes and binary treatments.
We hope that this work will help the applied researcher to cautiously approach and interpret the results generated from IV estimation in models with binary treatment, binary outcome and binary instrumental variable. Careful interpretation of treatment effects that are identified and being estimated, as well as the potential for bias arising from methodologic decisions, are key factors to consider in conducting these analyses and responsibly reporting the results from them. While estimating the LATE may be straightforward given a valid instrument, the interpretation of LATEs is often nuanced and may heighten the potential for unintentionally misleading or erroneous inferences and conclusions. On the other hand, interpreting population mean treatment effect parameters such as the ATE is straight-forward but estimating them is often problematic and potentially infeasible, as doing so demands either richer data or a slew of statistical assumptions that may not be met. Moreover, under settings of essential heterogeneity in treatment effectiveness, the potential usefulness of a population wide average effect may be limited and more nuanced parameters are required for practical impact. It’s important that researchers understand precisely the assumptions underlying identification of alternative treatment effect concepts and the related theory to support an approach for estimating them. We are hopeful that our results and discussions can help untangle these challenges.
Acknowledgments
Basu acknowledges support from NIH research grants RC4CA155809 and R01CA155329. Coe acknowledges support from National Institute of Nursing Research grant NIH 1R01NR13583 (PI: Van Houtven). We thank two anonymous reviewers for their very useful comments. Opinions expressed are ours and do not reflect those of the University of Washington or the NBER. All errors are our own.
Appendix
Table A1:
Simulations results (N=5,000) for Local Average Treatment Effects (LATEs) - %Bias (Coeff. Var.) {Coverage Pr}
| E(Y) | Estimators | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
|---|---|---|---|---|---|---|
| 0.50~0.60 | Naïve Probit | 170 [.02] {0} | 182 [.03] {0} | 242 [.03] {0} | 381 [.03] {0} | 845 [.04] {0} |
| 2SLS | −1 [.27] {.94} | −2 [.35] {.95} | −4 [.71] {.96} | −11 [2.08] {.96} | −61 [27.76] {.97} | |
| 2SRI | −47 [.59] {.67} | −31 [.5] {.83} | 44 [.37] {.86} | 208 [.35] {.45} | 476 [.85] {.58} | |
| 2SRI - sres | 11 [.27] {.92} | 32 [.29] {.82} | 96 [.33] {.59} | 215 [.42] {.52} | 428 [.99] {.53} | |
| 2SRI - dres | −103 [−9.25] {.14} | −99 [38.24] {.28} | −47 [1.25] {.82} | 131 [.58] {.76} | 534 [.75] {.5} | |
| 2SRI - ares | −88 [2.74] {.24} | −81 [1.98] {.41} | −32 [.94] {.86} | 123 [.59] {.79} | 488 [.81] {.54} | |
| 2SRI - gres | −46 [.56] {.65} | −32 [.49] {.82} | 24 [.44] {.91} | 155 [.46] {.67} | 399 [.98] {.61} | |
| Bi.Probit | −22 [.31] {.83} | −16 [.34] {.89} | 9 [.49] {.93} | 54 [1.06] {.87} | 297 [1.83] {.47} | |
| 0.80 ~0.90 | Naïve Probit | 233 [.04] {0} | 185 [.04] {0} | 155 [.04] {0} | 160 [.04] {0} | 226 [.06] {0} |
| 2SLS | −3 [.52] {.95} | −1 [.37] {.95} | −1 [.36] {.94} | −2 [.53] {.95} | −7 [1.74] {.96} | |
| 2SRI | −3 [.47] {.95} | −36 [.54] {.75} | −70 [1.01] {.33} | −78 [1.71] {.42} | −44 [1.71] {.79} | |
| 2SRI - sres | 74 [.19] {.39} | 69 [.17] {.32} | 57 [.18] {.41} | 61 [.22] {.52} | 106 [.34] {.55} | |
| 2SRI - dres | −75 [2.27] {.73} | −95 [7.59] {.26} | −103 [−9.52] {.09} | −94 [5.58] {.22} | −33 [1.26] {.82} | |
| 2SRI - ares | −52 [1.07] {.83} | −68 [1.09] {.49} | −76 [1.15] {.23} | −70 [1.18] {.44} | −18 [1.02] {.84} | |
| 2SRI - gres | −4 [.45] {.96} | −31 [.47] {.8} | −51 [.58] {.5} | −59 [.87] {.51} | −38 [1.35] {.79} | |
| Bi.Probit | −5 [.4] {.94} | −31 [.4] {.74} | −47 [.45] {.43} | −52 [.62] {.47} | −33 [1.11] {.8} | |
| 0.9 ~ 0.95 | Naïve Probit | 322 [.05] {0} | 232 [.05] {0} | 165 [.05] {0} | 143 [.06] {0} | 160 [.08] {0} |
| 2SLS | −2 [.96] {.93} | 0 [.61] {.93} | 1 [.46] {.93} | 0 [.52] {.93} | −5 [1.15] {.95} | |
| 2SRI | 58 [.44] {.82} | −9 [.54] {.92} | −69 [1.18] {.41} | −94 [4.73] {.22} | −83 [3.52] {.53} | |
| 2SRI - sres | 134 [.19] {.15} | 97 [.19] {.19} | 64 [.2] {.43} | 43 [.21] {.66} | 51 [.29] {.77} | |
| 2SRI - dres | −27 [1.35] {.94} | −77 [2.57] {.69} | −97 [10.3] {.19} | −98 [12.3] {.14} | −77 [2.09] {.51} | |
| 2SRI - ares | 0 [.86] {.94} | −45 [.96] {.83} | −66 [.98] {.4} | −72 [1.08] {.34} | −55 [1.13] {.64} | |
| 2SRI - gres | 52 [.43] {.81} | −8 [.51] {.91} | −47 [.63] {.57} | −66 [.9] {.34} | −67 [1.47] {.57} | |
| Bi.Probit | 24 [.54] {.92} | −21 [.51] {.88} | −50 [.57] {.45} | −62 [.71] {.29} | −60 [1.09] {.55} | |
| 0.95~0.98 | Naïve Probit | 492 [.07] {0} | 322 [.07] {0} | 202 [.08] {0} | 150 [.09] {0} | 130 [.12] {0} |
| 2SLS | −3 [2] {.94} | −4 [1.1] {.94} | −2 [.66] {.94} | 0 [.58] {.95} | −1 [.9] {.95} | |
| 2SRI | 158 [.47] {.83} | 34 [.53] {.99} | −61 [1.22] {.64} | −101 [−37.55] {.25} | −92 [6.21] {.51} | |
| 2SRI - sres | 236 [.29] {.32} | 144 [.21] {.17} | 84 [.24] {.56} | 41 [.26] {.81} | 19 [.34] {.92} | |
| 2SRI - dres | 56 [1.15] {.95} | −52 [2.02] {.98} | −92 [5.92] {.45} | −98 [15.37] {.19} | −87 [2.92] {.41} | |
| 2SRI - ares | 86 [.82] {.95} | −14 [.91] {1} | −55 [.96] {.64} | −70 [.98] {.39} | −65 [1.27] {.53} | |
| 2SRI - gres | 148 [.47] {.81} | 25 [.52] {.99} | −38 [.7] {.73} | −67 [.89] {.43} | −74 [1.64] {.48} | |
| Bi.Probit | 26 [2.05] {.85} | −7 [.78] {.97} | −50 [.73] {.64} | −68 [.74] {.34} | −70 [1.25] {.46} | |
2SRI – sres: 2SRI with standardized residuals; 2SRI – dres: 2SRI with deviance residuals; 2SRI – ares: 2SRI with Anscombe residuals; 2SRI-gres: 2SRI with generalized residuals
Table A2:
Simulations results (N=5,000) comparing to Average Treatment Effects (ATEs) - %Bias (Coeff. Var.) {Coverage Pr}
| E(Y) | Estimators | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
|---|---|---|---|---|---|---|
| 0.50~0.60 | Naïve Probit | 248 [.02] {0} | 237 [.03] {0} | 210 [.03] {0} | 187 [.03] {0} | 163 [.04] {0} |
| 2SLS | 28 [.27] {.88} | 18 [.35] {.91} | −13 [.71] {.94} | −47 [2.08] {.94} | −89 [27.76] {.96} | |
| 2SRI | −32 [.59] {.86} | −17 [.5] {.9} | 31 [.37] {.89} | 84 [.35] {.66} | 61 [.85] {.71} | |
| 2SRI - sres | 44 [.27] {.81} | 58 [.29] {.68} | 78 [.33] {.64} | 88 [.42] {.68} | 47 [.99] {.67} | |
| 2SRI - dres | −104 [−9.25] {.3} | −99 [38.24] {.39} | −52 [1.25] {.8} | 38 [.58] {.85} | 77 [.75] {.69} | |
| 2SRI - ares | −85 [2.74] {.42} | −78 [1.98] {.53} | −38 [.94] {.84} | 33 [.59] {.86} | 64 [.81] {.69} | |
| 2SRI - gres | −31 [.56] {.86} | −18 [.49] {.90} | 12 [.44] {.91} | 52 [.46] {.81} | 39 [.98] {.7} | |
| Bi.Probit | 1 [.31] {.93} | 0 [.34] {.93} | −1 [.49] {.93} | −8 [1.06] {.86} | 11 [1.83] {.5} | |
| 0.80 ~0.90 | Naïve Probit | 244 [.04] {0} | 314 [.04] {0} | 407 [.04] {0} | 488 [.04] {0} | 582 [.06] {0} |
| 2SLS | 0 [.52] {.95} | 43 [.37] {.84} | 97 [.36] {.71} | 121 [.53] {.82} | 95 [1.74] {.93} | |
| 2SRI | 0 [.47] {.95} | −7 [.54] {.95} | −40 [1.01] {.81} | −49 [1.71] {.77} | 17 [1.71] {.9} | |
| 2SRI - sres | 79 [.19] {.36} | 145 [.17] {.07} | 213 [.18] {.02} | 262 [.22] {.07} | 331 [.34] {.31} | |
| 2SRI - dres | −74 [2.27] {.74} | −93 [7.59] {.53} | −105 [−9.52] {.39} | −87 [5.58] {.59} | 40 [1.26] {.89} | |
| 2SRI - ares | −50 [1.07] {.83} | −53 [1.09] {.78} | −51 [1.15] {.75} | −32 [1.18] {.81} | 71 [1.02] {.89} | |
| 2SRI - gres | −1 [.45] {.97} | 1 [.47] {.94} | −3 [.58] {.92} | −8 [.87] {.88} | 29 [1.35] {.88} | |
| Bi.Probit | −2 [.4] {.94} | 0 [.4] {.95} | 4 [.45] {.95} | 9 [.62] {.91} | 41 [1.11] {.9} | |
| 0.9 ~ 0.95 | Naïve Probit | 226 [.05] {0} | 327 [.05] {0} | 482 [.05] {0} | 648 [.06] {0} | 883 [.08] {0} |
| 2SLS | −25 [.96] {.91} | 28 [.61] {.91} | 121 [.46] {.68} | 208 [.52] {.65} | 260 [1.15] {.85} | |
| 2SRI | 22 [.44] {.9} | 18 [.54] {.94} | −32 [1.18] {.84} | −80 [4.73] {.64} | −37 [3.52] {.86} | |
| 2SRI - sres | 81 [.19] {.3} | 154 [.19] {.05} | 260 [.2] {0} | 340 [.21] {.02} | 472 [.29] {.19} | |
| 2SRI - dres | −44 [1.35] {.93} | −70 [2.57] {.81} | −93 [10.3] {.59} | −93 [12.3] {.57} | −13 [2.09] {.85} | |
| 2SRI - ares | −23 [.86] {.93} | −29 [.96] {.91} | −25 [.98] {.87} | −14 [1.08] {.86} | 71 [1.13] {.93} | |
| 2SRI - gres | 18 [.43] {.92} | 18 [.51] {.94} | 17 [.63] {.91} | 3 [.9] {.9} | 27 [1.47] {.9} | |
| Bi.Probit | −4 [.54] {.95} | 2 [.51] {.94} | 10 [.57] {.93} | 16 [.71] {.91} | 52 [1.09] {.93} | |
| 0.95~0.98 | Naïve Probit | 202 [.07] {0} | 326 [.07] {0} | 546 [.08] {0} | 815 [.09] {0} | 1277 [.12] {0} |
| 2SLS | −50 [2] {.89} | −3 [1.1] {.94} | 110 [.66] {.86} | 265 [.58] {.7} | 491 [.9] {.79} | |
| 2SRI | 32 [.47] {.96} | 35 [.53] {.99} | −16 [1.22] {.95} | −103 [−37.55] {.71} | −50 [6.21] {.79} | |
| 2SRI - sres | 72 [.29] {.79} | 146 [.21] {.17} | 295 [.24] {.03} | 417 [.26] {.03} | 612 [.34] {.24} | |
| 2SRI - dres | −20 [1.15] {.96} | −52 [2.02] {.98} | −83 [5.92] {.8} | −94 [15.37] {.71} | −25 [2.92] {.83} | |
| 2SRI - ares | −5 [.82] {.96} | −14 [.91] {1} | −4 [.96] {.96} | 10 [.98] {.93} | 109 [1.27] {.93} | |
| 2SRI - gres | 27 [.47] {.95} | 26 [.52] {.99} | 32 [.7] {.98} | 21 [.89] {.94} | 55 [1.64] {.91} | |
| Bi.Probit | −36 [2.05] {.94} | −6 [.78] {.97} | 7 [.73] {.94} | 18 [.74] {.93} | 78 [1.25] {.93} | |
2SRI – sres: 2SRI with standardized residuals; 2SRI – dres: 2SRI with deviance residuals; 2SRI – ares: 2SRI with Anscombe residuals; 2SRI-gres: 2SRI with generalized residuals
Table A3:
Simulations results (N=50,000) for Average Treatment Effects (LATEs) with logit Data generating Process - %Bias (Coeff. Var.) {Coverage Pr}
| E(Y) | Estimators | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
|---|---|---|---|---|---|---|
| 0.50~0.60 | 2SRI | −13 [.23] {.84} | −5 [.21] {.91} | 11 [.2] {.89} | 24 [.21] {.82} | 35 [.3] {.84} |
| 2SRI - ares | −46 [.42] {.38} | −30 [.33] {.72} | 4 [.23] {.91} | 40 [.19] {.69} | 82 [.19] {.37} | |
| 2SRI - gres | −13 [.23] {.81} | −5 [.21] {.91} | 11 [.2] {.91} | 24 [.21] {.83} | 35 [.3] {.84} | |
| 0.80 ~0.90 | 2SRI | 2 [.2] {.9} | −11 [.25] {.88} | −28 [.35] {.76} | −42 [.54] {.7} | −60 [1.26] {.68} |
| 2SRI - ares | −32 [.37] {.62} | −39 [.4] {.54} | −26 [.34] {.75} | −2 [.29] {.93} | 40 [.3] {.86} | |
| 2SRI - gres | 2 [.2] {.85} | −11 [.25] {.83} | −28 [.35] {.74} | −42 [.54] {.7} | −60 [1.26] {.68} | |
| 0.9 ~ 0.95 | 2SRI | 13 [.2] {.85} | 0 [.23] {.92} | −25 [.36] {.8} | −52 [.68] {.65} | −82 [2.68] {.57} |
| 2SRI - ares | −19 [.34] {.82} | −29 [.37] {.71} | −25 [.36] {.79} | −8 [.32] {.9} | 30 [.35] {.93} | |
| 2SRI - gres | 13 [.2] {.74} | 0 [.23] {.88} | −25 [.36] {.78} | −52 [.68] {.64} | −82 [2.68] {.57} | |
| 0.95~0.98 | 2SRI | 22 [.19] {.78} | 11 [.23] {.9} | −16 [.37] {.87} | −52 [.84] {.65} | −94 [9.6] {.53} |
| 2SRI - ares | −9 [.32] {.88} | −18 [.36] {.84} | −18 [.38] {.84} | −6 [.37] {.9} | 26 [.41] {.96} | |
| 2SRI - gres | 22 [.19] {.66} | 11 [.23] {.85} | −16 [.37] {.86} | −52 [.84] {.67} | −94 [9.6] {.53} | |
2SRI – ares: 2SRI with Anscombe residuals; 2SRI-gres: 2SRI with generalized residuals
Table A4:
Simulations results (N=50,000) for Average Treatment Effects (LATEs) with cloglog Data generating Process - %Bias (Coeff. Var.) {Coverage Pr}
| E(Y) | Estimators | Pr(D) = 0.55 | Pr(D) = 0.70 | Pr(D) = 0.85 | Pr(D) = 0.93 | Pr(D) = 0.995 |
|---|---|---|---|---|---|---|
| 0.50~0.60 | 2SRI | −25 [.23] {.64} | −18 [.21] {.78} | −4 [.2] {.92} | 7 [.21] {.93} | 16 [.31] {.9} |
| 2SRI - ares | −54 [.43] {.19} | −40 [.33] {.44} | −10 [.23] {.91} | 21 [.19] {.85} | 59 [.19] {.51} | |
| 2SRI - gres | 27 [.09] {.68} | 35 [.1] {.45} | 83 [.1] {0} | 162 [.09] {0} | 250 [.07] {.01} | |
| 0.80 ~0.90 | 2SRI | 1 [.2] {.93} | −11 [.24] {.9} | −28 [.34] {.76} | −42 [.53] {.7} | −59 [1.19] {.68} |
| 2SRI - ares | −32 [.35] {.69} | −38 [.38] {.58} | −26 [.33] {.77} | −1 [.29] {.93} | 41 [.3] {.85} | |
| 2SRI - gres | 33 [.08] {.67} | 37 [.1] {.61} | 39 [.15] {.6} | 57 [.25] {.63} | 174 [.47] {.65} | |
| 0.9 ~ 0.95 | 2SRI | 27 [.19] {.74} | 12 [.23] {.91} | −15 [.36] {.88} | −45 [.68] {.72} | −77 [2.47] {.63} |
| 2SRI - ares | −9 [.33] {.9} | −20 [.37] {.85} | −14 [.36] {.88} | 6 [.33] {.93} | 48 [.34] {.88} | |
| 2SRI - gres | 26 [.08] {.95} | 36 [.11] {.79} | 43 [.16] {.69} | 48 [.26] {.77} | 109 [.66] {.88} | |
| 0.95~0.98 | 2SRI | 64 [.19] {.43} | 49 [.23] {.68} | 14 [.37] {.94} | −33 [.81] {.85} | −89 [7.68] {.67} |
| 2SRI - ares | −13 [.31] {.97} | 10 [.36] {.92} | 11 [.38] {.93} | 27 [.37] {.94} | 70 [.4] {.93} | |
| 2SRI - gres | 14 [.1] {1} | 26 [.12] {.98} | 41 [.18] {.84} | 45 [.27] {.86} | 101 [.73] {.94} | |
2SRI – ares: 2SRI with Anscombe residuals; 2SRI-gres: 2SRI with generalized residuals
Footnotes
The LATE effect is non-parametrically identified in a 2SLS setting within any cell defined by levels of all observed covariates X (Imbens and Angrist 1994). However, in a regression setting with many X’s, where a full saturated model is typically not used, the consistency of estimating LATE would rely on the appropriateness of the linear model specification.
There are other forms of estimators that deal with a binary outcome and a binary endogenous treatment model, such as a GMM approaches (McCarthy and Tchernis 2011) and semi-parametric estimators (Abadie 2003; Abrevaya et al. 2009, Chiburis 2010; Shaikh and Vytlacil 2011). However, these estimators are not as popular as the 2SLS and the 2SRI approaches and so we do not cover them in this paper.
There can certainly be a more elaborate model building exercise that can overcome this problem, but such exercises are seldom found in the economics and health economics literature. In any case, such exercises typically lead one away from a simple linear model into the realm of non-linear models.
Earlier waves of the survey are omitted because of the lower quality information on the LTCI question (Finkelstein and McGarry, 2006) and state information is not yet available for later waves.
Note that in contrast to our simulations, where we generate all outcomes under the normal distribution and found the BVP perform better for rare outcomes, here we are suggesting that when the outcomes mean is around 50% its underlying data-generating process is more likely to be normal.
Contributor Information
Anirban Basu, The Comparative Health Outcomes, Policy, and Economics (CHOICE) Institute, Departments of Pharmacy, Health Services and Economics, University of Washington, Seattle, 1959 NE Pacific St, Box-357630, Seattle WA 98195.
Norma Coe, Department Medical Ethics and Health Policy, Perelman School of Medicine, University of Pennsylvania, 3641 Locust Walk Philadelphia, PA 19104-6218.
Cole G. Chapman, University of South Carolina, Health Services Policy and Management, Arnold School of Public Health, 915 Greene Street, 303C, Columbia SC 29208
REFERENCES
- ABADIE A Semiparametric Instrumental Variable Estimation of Treatment Response Models.” Journal of Econometrics 2009; 113:231–63. [Google Scholar]
- ABREVAYA J, HAUSMAN JA, and KHAN S Testing for casual effects in a generalized regression model with endogenous regressors. Economterica 2010; 78(6): 2043–2061. [Google Scholar]
- ANGRIST J, and FERNANDEZ-VAL I ExtrapoLATE-ing: External Validity and Overidentification in the LATE Framework In Advances in Economics and Econometrics: Theory and Applications, Tenth World Congress, Volume III: Econometrics. Econometric Society Monographs, 2013. [Google Scholar]
- BASU A, HECKMAN JJ, NAVARRO-LOZANO S, and URZUA S Use of instrumental variables in the presence of heterogeneity and self-selection: An application to treatments of breast cancer patients. Health Economics 2007; 16(11): 1133–1157. [DOI] [PubMed] [Google Scholar]
- BHATTACHARYA J, GOLDMAN D, McCAFFREY D. Estimating probit models with self-selected treatments. Statistics in Medicine 2006; 25(3): 389–413. [DOI] [PubMed] [Google Scholar]
- BLUNDELL RW and POWELL JL Endogeneity in Nonparametric and Semiparametric Regression Models, in Dewatripont M, Hansen LP and Turnovsky SJ (eds.) Advances in Economics and Econometrics: Theory and Applications, Eighth World Congress, Vol. II (Cambridge: Cambridge University Press; ), 2003. [Google Scholar]
- BLUNDELL RW and POWELL JL Endogeneity in semiparametric binary response models. Review of Economic Studies 2004; 71, 655–679. [Google Scholar]
- BLUNDELL RW and SMITH RJ An Exogeneity Test for a Simultaneous Tobit Model, Econometrica 1986; 54, 679–685. [Google Scholar]
- BLUNDELL RW and SMITH RJ Estimation in a Class of Simultaneous Equation Limited Dependent Variable Models. Review of Economic Studies 1989; 56, 37–58. [Google Scholar]
- CHAPMAN CG, BROOKS JM. Treatment effect estimation using nonlinear two-stage instrumental variable estimators: Another cautionary note. Health Services Research 2016; 51(6): 2375–2394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CHIBURIS R Semiparametric Bounds on Treatment Effects. Journal of Econometrics 2010; 159(2):267–275. [Google Scholar]
- CHIBURIS R, DAS J and LOKSHIN M A practical comparison of the bivariate probit and linear IV estimators. Economic Letters 2012; 117(3): 762–766. [Google Scholar]
- COE NB, GODA GS, AND VAN HOUTVEN CH Long-term Care Insurance and Family Behavior. NBER Working paper w21483, 2015. [DOI] [PMC free article] [PubMed]
- FINKELSTEIN AN and MCGARRY K . Multiple Dimensions of Private Information: Evidence from the Long-Term Care Insurance Market. American Economic Review 2006; 96(4), 938–58. [PubMed] [Google Scholar]
- GARRIDO MM, DEB P, BURGESS JF, PENROD JD Choosing models for cost analyses: Issues of nonlinearity and endogeneity. Health Services Research 2012; 47(6): 2377–2397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- GODA GS. “The Impact of State Tax Subsidies for Private Long-Term Care Insurance on Coverage and Medicaid Expenditures.” Journal of Public Economics 2011; 95(7–8), 744–57. [Google Scholar]
- GOURIEROUX CA, MONFORT, TROGNON A Generalised residuals. Journal of Econometrics 1987; 34: 5–32 [Google Scholar]
- HECKMAN JJ “Dummy Endogenous Variable in a Simultaneous Equations System”, Econometrica 1978; 46, 931–959. [Google Scholar]
- HECKMAN JJ. Instrumental Variables: A study of implicit behavioral assumptions used in making program evaluations. Journal of Human Resources 1997; 32 (3): 441–462. [Google Scholar]
- HECKMAN JJ, URZUA S, VYTLACIL E. Understanding instrumental variables in models with essential heterogeneity. Review of Economics and Statistics 2006; 88(3): 389–432. [Google Scholar]
- HORRACE WC, OAXACA RL. Results on the bias and inconsistency of ordinary least squares for the linear probability model. Economic Letters 2006; 321–327. [Google Scholar]
- IMBENS G, ANGRIST J Identification and estimation of local average treatment effects. Econometrica 1994; 62(2): 467–475. [Google Scholar]
- KONETZKA RT, HE D, GUO J and NYMAN J. 2014. “Moral Hazard and Long-Term Care Insurance.” Working paper available: http://business.illinois.edu/nmiller/mhec/Konetzka.pdf
- KOWALSKI AE. Doing More When You’re Running LATE: Applying Marginal Treatment Effect Methods to Examine Treatment Effect Heterogeneity in Experiments. NBER Working Paper No. 22363, 2016.
- MCCARTHY IM AND TCHERNIS R On the Estimation of Selection Models when Participation is Endogenous and Misclassied In Drukker D (Ed.) Advances in Econometrics, Missing-Data Methods: Cross-sectional methods and Applications 2011; 27:179–207. London: Emerald Group Publishing. [Google Scholar]
- NEWHOUSE J, MCCLELLAN MB. Econometrics in Outcomes Research: The Use of Instrumental Variables. Annual Review of Public Health 1998; 19:17–34. [DOI] [PubMed] [Google Scholar]
- SHAIKH AM and Vytlacil EJ Partial identification in triangular systems of equation with binary dependent variables. Econometrica 2011; 79(3): 949–955. [Google Scholar]
- TELSER LG Iterative Estimation of a Set of Linear Regression Equations. Journal of the American Statistical Association 1964; 59, 845–862. [Google Scholar]
- TERZA JV, BRADFORD WD, DISMUKE CE. The use of linear instrumental variables methods in Health Services Research and Health Economics: A cautionary note. Health Services Research 2007; 43(3): 1102–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- TERZA JV, BASU A, RATHOUZ PJ. Two-stage residual inclusion estimation: Addressing endogeneity in health econometric modeling. Journal of Health Economics 2008; 27(3):531–543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WOOLDRIDGE J Control function methods in applied econometrics. The Journal of Human Resource 2015; 50(2): 420–445. [Google Scholar]