The effectiveness–efficiency trade-off in health care: The case of hospitals in Lombardy, Italy

Abstract

We study the presence and the magnitudes of trade-offs between health outcomes and hospitals’ efficiency using a data set from Lombardy, Italy, for the period 2008–2011. Our goal is to analyze whether the pressures for cost containment may affect hospital performance in terms of population health status. Unlike previous work in this area, we analyze hospitals at the ward level so comparisons can be made across more homogeneous treatments. We focus on two different health outcomes: mortality and readmission rates. We find that there is a trade-off between mortality rates and efficiency, as more efficient hospitals have higher mortality rates. We also find, however, that more efficient hospitals have lower readmission rates. Moreover, we show that focusing the analysis at the ward level is essential, since there is evidence of higher mortality rates in general medicine and surgery, while in oncology mortality is lower in more efficient hospitals. Furthermore, we find that consideration of spatial processes is important since mortality rates are higher for hospitals subject to high degree of horizontal competition, but lower for those hospitals having strong competition but high efficiency. This implies that the interplay of efficient resource allocation and hospital competition is important for the sustainability and effectiveness of regional health care systems.

1. Introduction

The recent worldwide growth of health care expenditures has raised strong concerns about cost containment. In the secondary care sector, the main attempts to achieve this goal have focused on health policies to increase the efficiency of hospitals’ management and at eliminating possible waste of resources. One central feature of many such policies is the adoption of a prospective payment system (PPS), regulating hospitals’ reimbursements for the treatments they provide. Under PPS, these reimbursements are classified according to DRG codes and have introduced strong incentives to reduce patients’ Length of Stay (LOS). As a response to these incentives, hospitals’ managers have adopted procedures and guidelines to increase labor and capital productivity, mainly through the increase of total discharges per bed and per unit of labor. These trends have raised concerns regarding the quality of care.¹ From this perspective, it becomes important to investigate whether there is in the hospital sector a trade-off between hospital efficiency and effectiveness in achieving health outcomes. The goal of this paper is to provide some new empirical evidence on this topic.

In dealing with this issue we introduce two factors that may lead to a better understanding of the impacts of pursuing efficiency in the realm of health outcomes: (1) the analysis is conducted at the hospital ward level and (2) the impacts of several spatial features of the hospitals’ environment are considered. This analysis will be performed by applying a three-stage econometric model to a large administrative data set on all patients admitted in the hospitals of Lombardy, an Italian region with a population of approximately ten million, over four years from 2008 to 2011.

Focusing on the ward level should enhance the investigation of efficiency and effectiveness because, as noted by Carey and Burgess (1999), “the hospital level of analysis is too general to be capable of revealing variation in quality as measured by rate-based adverse events”.² This suggests that hospital-level estimates may be too broad and incapable of describing the effectiveness achieved by the different structures operating within the same organization.³ Hence, computing outcomes at the hospital level may lead to biased – or at least uninformative – estimates of the trade-offs’ magnitudes and signs.

The analytical structure used in this paper is related to the earlier work of Carey and Burgess (1999), Deily and McKay (2006) and, most specifically, McKay and Deily (2008). Carey and Burgess (1999) study the relationship between cost and quality on a sample of US Department of Veterans Affairs hospitals during the period 1988–93. They show a positive trade-off between costs and quality. McKay and Deily (2008) examine in the context of U.S. acute care hospitals a variety of relationships involving cost inefficiency and health outcomes. The authors hypothesize that, holding constant other factors, cost inefficiency itself may be a determinant of health outcomes at the hospital level. Whereas costs per se may be positive contributors to good outcomes (working through higher levels of productive inputs, most obviously), cost inefficiency is unlikely to be productive of good health. The policy relevance of such a distinction is clear, since intervention efforts to control cost inefficiency may be very different in nature than interventions directed toward controlling the level of total costs associated with efficient use of inputs.⁴ The authors find no consistently strong impacts of cost inefficiency on health outcomes, where the particular health outcomes of interest are inpatient mortality and inpatient complications.

While related in some ways to the Deily–McKay (DM) work, the analytical approach used in this paper is somewhat different. First, we estimate risk-adjusted measures of health outcomes starting from administrative data covering all the relevant population and not a sample of it. In contrast, DM employ estimates of health outcomes provided by a private health care information company, Solucient.⁵ Second, DM do not utilize a multilevel model for estimating health outcomes and, hence, do not take into account the hierarchical structure of the data. Third, DM estimate both health outcomes and efficiency at the aggregate hospital level. Hence, they analyze each health organization without taking into account that this aggregate level is not able to provide a picture of the complexity of both health outcomes and efficiency scores within hospitals. Our data permit a more detailed analysis in which estimation is at the hospital ward level. Fourth, we estimate hospital efficiency through a production function and not a cost function. The latter may produce biased estimates to the extent that measured input prices do not reflect true prices (for DM, they are taken from balance accounts). Production function estimates are instead based on observed input data. Finally, our estimated trade-offs are able to control for the impacts of exogenous variables and ward effects.

In the first stage we estimate hospitals’ effectiveness in achieving health outcomes. This means measuring changes in the patients’ health status. In general, evaluating hospital performance in terms of effectiveness involves investigating improvements across a very broad range of indicators, varying from Quality Adjusted Life Years (QALY) to lower mortality rates. These improvements are achieved through the provision of health services (Donabedian, 1988) during hospitalization. Since patients’ characteristics and hospitals’ procedures may affect changes in the health status, risk-adjusted methods are widely adopted in the literature (Goldstein and Spiegelhalter, 1996). As shown by Goldstein (2003), in evaluating hospitals’ effectiveness, multilevel models are more appropriate since patients are nested within health structures and the corresponding data have strong hierarchical relationships. We apply a multilevel model to individual data, and estimate hospitals’ effectiveness at the ward level. We consider two indicators: mortality rate (MR) and readmission rate (RA).⁶

In the second stage we measure hospitals’ efficiency. This means evaluating the performance of a productive unit, i.e., the ratio among outputs and inputs (or among costs and production). In this paper we focus on technical efficiency, i.e. a production function frontier. The latter is estimated using a stochastic frontier (SF) model (Aigner et al., 1977), whose estimates allow one to distinguish between failures in achieving the maximum feasible output level due to managerial inefficiency from those due to random shocks. SF models have been widely applied to measure hospitals’ efficiency.⁷ We apply a SF model to data on hospitals’ inputs and outputs, and estimate hospitals’ efficiency scores at the ward level. Furthermore, we analyze two output measures: (1) yearly number of discharges and (2) yearly revenues. In Lombardy, hospitals’ revenues are given by the DRG tariff that the regional government sets at the beginning of each year for each discharge in a specific DRG. More complicated DRGs receive higher tariffs. Hence revenues take into account the differing complexity of treatments when assessing hospital technical efficiency.

Finally, in the third stage we provide some empirical evidence on the presence, the sign, and the magnitude of a trade-off between efficiency and effectiveness controlling for hospitals’ characteristics (ownership, specialization, teaching), spatial variables, ward effects, and the interaction effects among these variables.

An important innovation of this paper is the inclusion of hospital competition in the analysis. Tay (2003) points out that the irrelevance of money prices in the choice of a specific hospital by a consumer (in Lombardy the consumer does not directly pay for a hospital treatment, since it is covered by the national health system) makes competition among hospitals mainly focused on location, i.e., horizontal product differentiation based on travel or time costs. Taking this perspective, Propper et al. (2004, 2008) have examined the impact of hospital competition on hospitals’ mortality rates for patients with Acute Myocardial Infarction (AMI) in the UK in the 1990s. They find that competition has a negative impact on health outcomes measured by mortality rates. Kessler and McClellan (2000) also investigate patients affected by AMI in the US over the period 1985–1994 and find that hospital competition has instead a beneficial effect on mortality rates. These contributions measure competition through distance but they do not compute travel times. Unlike the present paper, these authors use fixed boundaries for the hospital’s catchment areas and straight-line distances. Distances in our work are computed without imposing exogenous boundaries and are measured through the available road network; we believe that these more accurate travel times provide a more appropriate measure of hospitals’ competition in the Lombardy context. Another dimension of hospitals’ competition is through vertical product differentiation (quality), as suggested by Tay (2003): as a proxy for this variable we consider the percentage of patients admitted in regional hospitals but living outside the region, i.e., those patients who incur in higher mobility costs in their care seeking. The intuition is that the attraction of patients living at greater distances is a signal of hospital’s reputation. Such measures have not been considered in previous studies.

The paper is organized as follows. In Section 2 we briefly describe the regional hospital sector in Lombardy and the main features of the regional DRG regime. In Section 3 we specify the empirical strategy, while the main features of the data set are described in Section 4. The empirical results are presented in Section 5, while the main conclusions are highlighted in Section 6.

2. The hospital sector in Lombardy

Major reforms affecting the hospitals operating in Lombardy were introduced in 1997. Since then, all hospitals satisfying some requirements compose the so-called mixed market hospital sector, including public, private not-for-profit and private for-profit hospitals. The organizations belonging to this mixed market receive a predetermined reimbursement from the regional government for each discharge they make. These reimbursements are determined according to the DRG regime and are established by law at the beginning of each year. The DRG tariffs are revised to take into account hospitals’ costs and possible management distortions (e.g., upcoding). These public regional reimbursements represent the vast majority of revenues for acute discharges in all hospitals of Lombardy: out-of-pocket reimbursements comprise only a tiny share of hospital revenues (only 2.2% of regional acute discharges, while the percentage of people with a private insurance in Italy is only 7%). As in every Italian region, universal coverage for health care services in Lombardy is provided by the Italian NHS, which was introduced in 1978. The NHS is funded through general taxation. Financial resources are then transferred to the various regions that are in charge of managing their local systems. This implies that price is not a strategic variable when dealing with hospital competition.

The regional government is attempting to keep health expenditures –that currently give rise to about 75% of the regional budget – under control. Given the population’s growing age and corresponding pressures on health care use and spending, tighter regulation and DRG tariffs are designed in order to increase the hospitals’ managers incentive to control costs. In Lombardy the budget assigned to each hospital is based on two-stage bargaining between the hospital and the regional officers. In the first stage, before the beginning of a year, there is an agreement on the overall budget assigned to each hospital. This agreement is achieved bilaterally between the managers of each hospital and the region. The ex-ante budget is a monetary ceiling fixing the maximum reimbursement that a specific hospital may receive the coming year from the region. Hospital managers are free to choose how to obtain this maximum reimbursement; in particular, they may decide to increase some treatments and to reduce others. The treatments are indeed reimbursed according to the pre-determined DRG-tariff scheme that is uniform for all the hospitals operating within the region. Hence, managers may decide to allocate a hospital’s resources in the different wards according to the different remuneration levels provided by the DRG-tariffs scheme, up to the budget ceiling. When they get close to this ceiling, usually to-ward autumn, hospital managers and regional officers start the second stage bargaining. They agree on an extra budget, which is the possibility for hospitals to provide further treatments (otherwise they have either to provide services for free or to stop treatments). The first stage budget is agreed taking into account two components: (1) the historical budget; and (2) an incentive scheme. The latter is currently based only upon health outcomes, and it consists of a − 1%-+ 1% change on the historical budget. Each hospital is evaluated according to different health outcomes (including risk-adjusted mortality rates and readmission rates) and receives a score. The median hospital in the score ranking gets 0, hospitals below the median one receive a penalty while those above the median hospital obtain a premium.⁸

In Lombardy the hospital’s general manager is indeed lawfully responsible for all the activity performed in her/his hospital. Hence, we can investigate whether the regulators’ pressure on cost containment has induced managers to give more weight to efficiency, introducing a negative or positive trade-off between it and effectiveness.

3. The empirical strategy

Our aim is to investigate the presence and the magnitude of a trade-off between health outcomes and efficiency in the hospital sector. In order to achieve this goal we need to obtain estimates of health outcomes and estimates of hospitals’ efficiency and then investigate the relation between them, always at the ward level. Hence our empirical analysis is split in three stages: in the first stage we estimate models of health outcomes; in the second stage we study hospitals’ efficiency; and in the third stage we investigate the trade-off between effectiveness and efficiency.

3.1. Measuring health outcomes

In the hospital sector improvements in health outcomes are evaluated using a broad range of ex-post indicators.⁹ Ex-post indicators are risk adjusted, i.e., they consider the influence that patients’ individual characteristics (e.g., their health status) and hospitals’ procedures (e.g., some treatments are more complex than others and therefore more risky) have on health outcomes. Risk adjustment methods are widely employed in the literature in order to evaluate, ceteris paribus, those hospitals providing better outcomes than others. Among the risk adjustment models, multilevel methods are typically more suitable than linear models, since they take into account that patients are nested within wards and hospitals, so that the data have a hierarchical structure (Goldstein and Spiegelhalter, 1996; Leyland and Goldstein, 2001). Unlike linear models, which assume that observations are uncorrelated, multilevel models control for the existence of an intra-hospital (or intra-ward) correlation, which may make patients within a hospital – in general, and in particular patients in the same ward – more alike than patients coming from different hospitals (the inter-hospital variation).¹⁰

In our setting, a multilevel model considers that patient i is nested within ward w of hospital j. Hence, if π_iwjt denotes the probability of an event y_iwjt (i.e., an indicator of hospitals’ health outcomes, being a binomial variable) occurring for patient i, admitted in ward w and hospital j in period t, then the latter may depend upon a set of variables representing (1) the patient’s characteristics, (2)the disease severity, the type of treatment received during the hospitalization period, a ward-effect and (5) a hospital-effect. A multilevel model explains the logit transformation (η_iwjt) of the probability π_iwjt as the following equation:

$${\eta }_{iwjt}={\gamma }_0+\beta {\mathcal{X}}_{iwjt}+u_{wjt}+u_{jt}+{ϵ}_{iwjt}$$ (1)

where η_iwjt = ln(π_iwjt/(1 − π_iwjt)), β is a vector of coefficients and x_iwjt an observed vector of covariates. u_wjt is a random effect identifying the impact of ward w nested within hospital j in period t on the observed health outcomes, capturing the latent heterogeneity of ward w. u_jt is also a random effect representing the impact of hospital j on the observed health outcome. Both u_wjt and u_jt are IID with zero mean and constant variances equal to, respectively, ${\sigma }_{u1}^2$ and ${\sigma }_{u2}^2$. Hence, they are random effects representing the intra-group impact (at the ward level and at the higher hierarchical level given by the hospital) on individual health outcomes. As in standard random effect panel data models, u_wjt and u_jt are assumed to be uncorrelated with the regressors.

Having estimated Eq. (1), we can compute the predicted health outcomes at the ward level in each hospital, defined as follow:

$$\widehat{H}{O}_{wjt}=\sum _{i=1}^I\frac{\widehat{H}{O}_{iwjt}}{I}$$ (2)

where I is the total number of patients admitted in ward w of hospital j, and HO_iwjt is the individual i’s predicted health outcome, given by:

$$\widehat{H}{O}_{iwjt}=\frac{{\exp }^{{\widehat{\gamma }}_0+\widehat{\beta }{\mathcal{X}}_{iwjt}}}{1+{\exp }^{{\widehat{\gamma }}_0+\widehat{\beta }{\mathcal{X}}_{iwjt}}}$$ (3)

with ${\widehat{\gamma }}_0$ and ${\widehat{\beta }}_0$ estimated with (1). These are risk-adjusted predicted health outcomes computed for each ward operating in a specific hospital, so that it is possible to compare performance in terms of effectiveness of units providing similar treatments. We have two predicted outcomes for each ward operating in a hospital of the regional system: mortality rate and readmission rate. Regarding the first outcome, we consider total mortality rates, i.e., the sum of in-hospital and 30-day post-discharge mortality rates. The second outcome, readmission, is an attempt to measure post-surgical adverse events.¹¹

A mis-specification test for the multilevel model is performed by studying the significance of the intraclass correlation coefficient (ICC), defined as the ratio between the estimated variances ${\sigma }_{u1}^2$, ${\sigma }_{u2}^2$ and the total variance observed in model (1), i.e., $\text{ICC}=({\sigma }_{u1}^2+{\sigma }_{u2}^2)/({\sigma }_{u1}^2+{\sigma }_{u2}^2+{\sigma }_{ϵ}^2)$. It shows whether there is a variability significantly different from 0 among the higher level units, i.e., the wards and the hospitals. The null hypothesis is that ICC = 0 i.e., ${\sigma }_{u1}^2={\sigma }_{u2}^2=0$ Our data cover four years (2008–2011). We estimate model (1) for each period to get yearly estimates of hospital health outcomes. We estimate model (1) at the ward level, i.e., one regression for each available ward, for four years.

The exogenous variables in Eq. (1) are GENDER (a dummy equal to 1 if patient is male), AGE (patient’s age), DRGWEI (the DRG weight capturing the treatment complexity), HEARTDIS (a dummy equal to 1 if the patient is affected by heart disease), CANCERDIS (a dummy equal to 1 if the patient affected by cancer disease), EUNIT (a dummy equal to 1 if the patient is admitted through emergency unit), COMORB (patient degree of comorbidity), ICU (days spent in intensive care unit) and TRANSF (a dummy equal to 1 if the patient is transferred to another hospital).

3.2. Estimation of hospital efficiency

The second-stage analysis provides estimates of hospital efficiency. We apply a stochastic frontier time-varying efficiency model (Battese and Coelli, 1995) for panel data, which allows to estimate hospital efficiency in each of the considered periods. Hence, we estimate the following equation:

$$y_{wjt}=\alpha +\beta {\mathcal{X}}_{wjt}+v_{wjt}-k_{wjt}.$$ (4)

The dependent variable y_wjt is the observed output of ward w in hospital j in period t; α is a constant, β is a vector of parameters and x is an observed vector of covariates, representing inputs. The error term is split into two components: v_wjt represents the white noise residuals, while k_wjt is the hospitals’ inefficiency score, which has to be estimated by the model. The error component v_wjt is a two-sided disturbance capturing the effect of random shocks, while the error component k_wjt is a one-sided non-negative disturbance, distributed as a truncated normal, reflecting the effect of inefficiency. The model is estimable by maximizing the log-likelihood function of the normal-truncated normal stochastic frontier (Kumbhakar and Lovell, 2000).¹²

The estimated efficiency scores for each ward-hospital pair are then obtained by computing their exponential transformation, i.e., exp^−kwjt, so that they vary between 0 and 1. An efficiency score equal to 1 means that ward w of hospital j in period t is on the estimated frontier, i.e., it is efficient. The closer is to 0 the lower is its efficiency. Hence, we obtain a set of estimated efficiency scores, denoted by ES_wjt.

We consider as the functional form for the production frontier a translog model (Christensen et al., 1973). Hence, we estimate the following equation:

$$\log \left(y_{wjt}\right)=\alpha +\sum _{h=1}^H{\beta }_h\log \left({\mathcal{X}}_{wjth}\right)+\frac{1}{2}\sum _{h=1}^H\sum _{l=1}^L{\beta }_{jtl}\log \left({\mathcal{X}}_{wjth}\right)\log \left({\mathcal{X}}_{wjtl}\right)$$ (5)

where x_jth is input h in hospital j at period t. We consider five inputs, computed at the ward level: the number of beds (BEDS), the yearly job time hours of physicians (PHYS), nurses (NURS), and other employees (OTHER).¹³ For labor we consider the yearly hours of activity. Furthermore, to take into account of the impact of technical progress on hospitals’ activity, we introduce a variable capturing the technology level adopted in each hospital (TECH). The latter is defined as follows: we identified as technological a hospital that can provide recovery in an intensive care unit (ICU). Since we cannot use information about specific technological equipment, we use this proxy to classify the hospitals. This feature fits very well for all wards except heart surgery and neurosurgery (since all these wards have an ICU). Hence, for these two wards we identify a set of treatments that require high-tech equipment.¹⁴

Concerning hospital outputs at the ward level, we analyze two different variables: yearly discharges (DIS) and yearly revenues from discharges (REV). The first variable captures the relationship between two quantitative levels: patients and inputs. The second output variable also includes the monetary incentives coming from admitting patients, and links them to inputs through the production function. It is given by the product of the DRG tariff times the yearly number of discharges in that DRG. Since the DRG tariff is a function of the treatment’s complexity, revenues take also into account the severity of the health care procedure provided to the patient.

Model (5) is estimated at the ward level. We estimate it using as the dependent variable first the logarithm of discharges and then the logarithm of hospital revenues.

3.3. Estimating the trade-off between health outcomes and efficiency

The main issue investigated in this paper is the trade-off between health outcomes and technical efficiency in the hospital sector. This is explored in the third-stage analysis, where we take the estimated health outcomes HO_wjt obtained in the first-stage by estimating model (1), the estimated efficiency scores ES_wjt obtained by estimating model (5), and then estimate the following equation:

$$\begin{gathered} \widehat{H}{O}_{wjt}=a_0+b_{ES}\widehat{E}{S}_{wjt}+b_{OP}OWNPU{B}_{jt}+b_{ONFP}OWNNF{P}_{jt}+ \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}+b_{M}MON{O}_{jt}+b_{T}TEAC{H}_{jt}+b_{F}FLO{W}_{wjt}+b_{C}COM{P}_{wjt}+{ϵ}_{wjt}. \end{gathered}$$ (6)

Eq. (6) shows that, in addition to estimated efficiency scores, we consider also the impact of some hospital characteristics on the estimated health outcomes. We control for hospital ownership, i.e., the dummy variable OWNPUB equals1 if the hospital is public, while the dummy variable OWNNFP is equal to 1 if the hospital is a private not-for-profit organization. This implies that the baseline ownership type is a for-profit hospital. Furthermore, we control for a hospital’s specialization in specific health treatments (e.g., a hospital focuses only on cardiology, or on orthopedics); hence, the dummy variable MONO equals 1 if the hospital is specialized. Last, we control for teaching hospitals, with the dummy variable TEACH equal to 1 if the hospital has a faculty of medicine.

We also control for some spatial variables capturing hospital product differentiation. The first is given by the extra-regional flows of patients admitted in hospitals of Lombardy. This may be considered as a proxy of hospitals’ vertical differentiation, since hospitals with good reputations may induce patients to incur higher travel costs and, in turn, this may have an impact on health outcomes. Hence, the variable FLOW is the percentage of discharges for patients living outside Lombardy, computed at the ward level. The second spatial variable is a measure of spatial competition, built taking into account distance among all the hospitals in Lombardy, given the current road network. This is the variable COMP, computed as follow:

$$COM{P}_{wjt}=\sum _{f=1}^N{r}_{fj}{s}_{wft}(f\ne j)$$ (7)

where N is the number of hospitals in the region where a ward w is operating, $s_{wjt}=\frac{y_{wft}}{y_{wt}}$ is the share of regional patients in year t admitted in the ward w of hospital f (computed on the total number of patients admitted in ward w), and rfj are elements of a spatial weight matrix, where rfj is the distance in traveling time between hospital j and hospital f. The traveling time is computed by a program in Visual Basic, which gets the minutes required for driving from hospital j to hospital f with the current road map, using Google Maps. The intuition is that, since traveling times are a crucial variable when the patient selects a hospital, the degree of competition exposure of hospital j is not simply given by the share of regional patients that are admitted in all other regional hospitals, but it is weighted by the distance. The patients admitted in hospitals located at a long distance from hospital j have lower weight than patients admitted in hospitals close to it. The index COMP varies between 0% (meaning no competition since all patients are admitted in hospital j) and 100% (implying the highest competition since all patients are admitted to hospitals at one-minute distance from hospital j).

Model (6) is estimated on a panel data set: the unit of observation is the ward w in hospital j during year t. Hence, in the third-stage we estimate a panel data model with ward effects. We test whether a fixed effect or a random effect model is more appropriate by estimating Eq. (6) under both specifications and then applying a Hausman test. Under the fixed effect approach we implement a least square dummy variable model (LSDV); this implies adding to Eq. (6) the following ward-level dummy variables: CARDIO_jt (equal 1 if the ward in hospital j at period t is cardiology), GENMED_jt (equal 1 if the ward is general medicine), HEARTSUR_jt (equal 1 if the ward is heart surgery), NEURO_jt (equal 1 if the ward is neurology), NEUROSUR_jt (equal 1 if the ward is neurosurgery), ONCO_jt (equal 1 if the ward is oncology), and SURGE_jt (equal 1 if the ward is surgery). Hence the baseline ward effect is orthopedics.

Moreover, we investigate if there is a specific trade-off effect for each hospital characteristic, spatial variable and for each ward through the inclusion of interaction effects. Hence, we introduce in Eq. (6) four interaction effects for studying the impact of hospital characteristics on the possible trade-off: ES_wjt × OWNPUB_jt (providing evidence on whether there is a trade-off in public hospitals), ES_wjt × OWNNFP (in private not-for-profit hospitals), ES_wjt × MONO_jt (in specialized hospitals) and ES_wjt × TEACH_jt (in teaching hospitals). In addition, we specify two interaction effects investigating the impact of the spatial variables on the trade-off: ES_wjt × FLOW_wjt (a possible trade-off between efficiency and extra-regional patient flows) and ES_wjt × COMP_wjt (a trade-off between efficient and hospital spatial competition).

Furthermore, we introduce seven interaction effects to identify the presence of a trade-off in different wards: ES_wjt × CARDIO_jt, ES_wjt × GENMED_jt, ES_wjt × HEARTSUR_jt, ES_wjt × NEURO_jt, ES_wjt × NEUROSUR_jt ES_wjt × ONCO_jt and ES_wjt × SURGE_jt.

Fig. 1 provides a summary of our empirical strategy, split in the three-stage econometric model and highlighting, for each stage, the dependent variable, the explanatory variables and the estimated results. Table 1 provides the variables’ definitions.

Fig. 1.

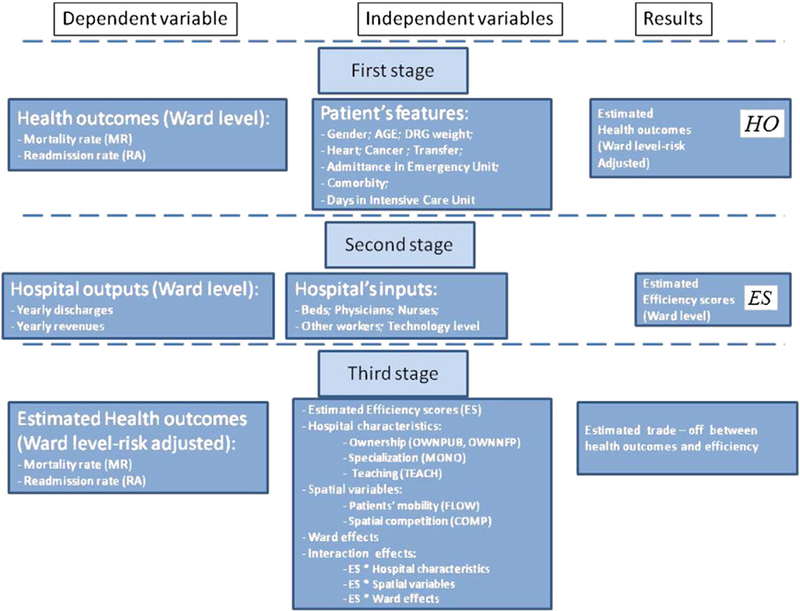
The three-stage empirical strategy.

Table 1.

Definition of variables.

Variable	Description
GENDER	Patient sex, dummy variable equal to 1 if patient is male
AGE	Patient age, in years
DRGWEI	Weight of the DRG, number
HEARTDIS	Patient already affected by heart disease, dummy variable equal to 1
CANCERDIS	Patient already affected by cancer, dummy variable equal to 1
EUNIT	Patient admitted through emergency unit, dummy variable equal to 1
COMORB	Patient comorbidity at admittance, number ranging from 0 to 5
ICU	Days spent in intensive care unit during the discharge, in days
TRANSF	Transfer in a different hospital, dummy variable equal to 1
TEACH	Teaching (non-teaching) hospital, dummy equal to 1 (0)
MONO	Monospecialistic (General) hospital, dummy equal to 1 (0)
OWNNFP	Private not-for-profit hospital, dummy equal to 1
OWNPUB	Public hospital, dummy equal to 1
FLOW	Outside region patients, percentage of total outside region patients
COMP	Spatial competition, percentage ranging between 0 and 100
DIS	Annual discharges, number
REV	Annual revenues from discharges, euros
BEDS	Beds, number
PHYS	Physicians, yearly hours of job time
NURS	Nurses, yearly hours of job time
OTHER	Other employees, yearly hours of job time
TECH	High-tech ward, dummy = 1
WARDS	Cardiology (dummy = 1), general medicine, heart surgery, neurology Neurosurgery, oncology, surgery (baseline = orthopedics)

Two possible alternatives to our econometric approach deserve discussion.¹⁵ First, in third stage, the trade-off between the risk-adjusted health outcomes and hospitals’ efficiency might be investigated via a simple correlation between these two variables, and among outcomes and other hospitals’ characteristics. However, a correlation analysis, as well as a simple linear regression, while indicating the presence of a trade-off, does not allow estimation of a coefficient for efficiency after having taken into account the impact of other variables that may have an effect on health outcomes, such as hospitals’ competition, characteristics, ward effects and interaction effects. Moreover, it will not be possible to make any inference about the statistical significance of the estimated coefficients (and of their signs). Second, since modeling the analysis at three separate stages implies that we lose some information on data variability, we could investigate the trade-off in a single model. Two considerations arise. First, efficiency scores need to be estimated using a specific econometric method—the stochastic frontier approach— which cannot be embedded into hierarchical models. Second, our goal is also to analyze the impact of hospitals’ competition on the health outcomes. As shown by Kessler and McClellan (2000), this may lead to an endogeneity problem, since hospitals’ quality (measured in terms of their health outcomes) can influence competition. Hence, it is not possible to use observed health outcomes and to consider predicted ones, after having taken into account the influence of hospital effects (including patients’ perceived quality). For these reasons we choose to adopt a three-stage approach.

4. The data

Our data are extracted from a large administrative data set covering the full population of patients and hospitals operating in Lombardy between 2008 and 2011. The data are provided by the Health Care Department of the Lombardy Region. We have information coming from all individual Hospital Discharge Charts (HDC), which include information regarding the patient (gender, age, residence), the hospital (regional code) and the treatments received during the hospitalization period (DRG, comorbidity, principal and secondary procedures, etc.). This information has been linked with another data set from the Lombardy Health Care Department that describes hospitals’ features (inputs and some exogenous factors such as ownership).

Table 2 shows some descriptive statistics concerning the variables used in the three-stage econometric approach. The data cover 147 hospitals located in Lombardy and 2,434,595 discharges. We analyze eight wards: cardiology, general medicine, heart surgery, neurology, neurosurgery, oncology, orthopedics and surgery. The total discharges in these eight wards cover 65% of total yearly discharges in Lombardy. General medicine wards in Lombardy are the most common (N = 125), while heart surgery wards are the least common (N = 19). Table 2 also shows the mean and standard deviation of the explanatory variables adopted in model (1).¹⁶

Table 2.

Descriptive statistics on first-stage variables.

	GENDER	AGE	DRGWEI	HEARTDIS	CANCERDIS	EUNIT	COMORB	ICU	TRANSF	MR	RA	Hospitals
Cardiology
Mean	63.57	69.51	1.66	0.93	0.01	0.19	0.53	0.24	0.03	0.02	0.23	73
St. dev.		13.44	1.10	0.26	0.09	0.39	0.77	0.43	0.17	0.15	0.41
General medicine
Mean	48.73	73.38	1.07	0.52	0.16	0.15	0.82	0.02	0.02	0.15	0.15	125
St. dev.		15.48	0.74	0.50	0.36	0.36	0.91	0.12	0.13	0.36	0.36
Heart surgery
Mean	66.09	65.34	4.94	0.91	0.01	0.11	0.48	0.76	0.01	0.02	0.13	19
St. dev.		15.67	2.73	0.28	0.08	0.31	0.75	0.43	0.11	0.12	0.34
Neurology
Mean	49.22	64.32	1.05	0.55	0.05	0.30	0.48	0.02	0.02	0.06	0.10	47
St. dev.		18.14	1.09	0.50	0.22	0.46	0.72	0.14	0.14	0.24	0.30
Neurosurgery
Mean	53.97	56.61	1.99	0.16	0.10	0.19	0.10	0.17	0.04	0.02	0.12	22
St. dev.		17.76	2.59	0.37	0.29	0.39	0.37	0.37	0.19	0.15	0.32
Oncology
Mean	52.45	64.94	1.21	0.13	0.76	0.05	0.71	0.01	0.01	0.18	0.35	35
St. dev.		13.34	0.77	0.34	0.43	0.22	0.68	0.08	0.09	0.39	0.47
Orthopedics
Mean	47.58	56.21	1.28	0.04	0.01	0.02	0.07	0.01	0.01	0.01	0.06	109
St. dev.		21.26	0.57	0.19	0.09	0.13	0.30	0.12	0.08	0.09	0.24
Surgery
Mean	51.62	59.12	1.21	0.17	0.20	0.07	0.17	0.04	0.01	0.02	0.09	120
St. dev.		18.41	1.00	0.37	0.40	0.26	0.46	0.19	0.07	0.15	0.29

Table 3 presents the means of the dependent and explanatory variables used in the second-stage estimation of hospitals’ efficiency.¹⁷ In Lombardy 62.6% of hospitals are public, while private for-profit hospitals represent 26.2% of the total, and private not-for-profit 11.2%. Specialized hospitals are only 2.4%, while teaching hospitals are 16.8%. Regarding our spatial measures, the average flow of patients living outside Lombardy and admitted in a regional hospital is 8.6%, while the average degree of spatial competition is (2.4%).

Table 3.

Descriptive statistics (averages) on second-stage variables.

	Cardiology	General medicine	Heart surgery	Neurology	Neurosurgery	Oncology	Orthopedics	Surgery
Discharges (number)	1108.8	1313.0	508.4	753.0	744.3	567.7	1141.7	1307.3
Revenues (Euros)	5,975,178.6	4,032,765.0	8,146,189.7	2,358,690.4	5,303,045.8	1,874,102.4	4,286,855.5	4,470,049.0
Beds (number)	22.3	44.0	22.6	24.4	24.0	18.1	27.3	32.6
Physicians (hours)	321,811.0	220,105.7	544,060.6	390,778.6	542,200.7	388,846.1	233,317.1	234,110.9
Nurses (hours)	595,330.6	412,557.2	947,413.6	717,045.9	971,580.3	693,765.8	436,128.8	432,041.8
Others (hours)	474,262.3	335,981.0	801,540.3	568,818	809,805.8	552,258.4	355,154.5	354,945.4
Tech (dummy)	89.7%	59.9%	35.0%	94.4%	73.9%	81.5%	65.8%	64.7%

Fig. 2 displays the location of the 75 hospitals with a cardiology ward and the 19 hospitals with a heart surgery ward in the region and the magnitude (the size of the circle) of their specific index of spatial competition (COMP). It is evident that hospitals located in the Milan area (the most populated city in Lombardy) are subject to higher competition than the other hospitals, for both wards considered. On the contrary, many hospitals seem to operate in a regime of local monopoly, especially outside the Milan area and in heart surgery wards. Similar arguments apply to all other wards.

Fig. 2.

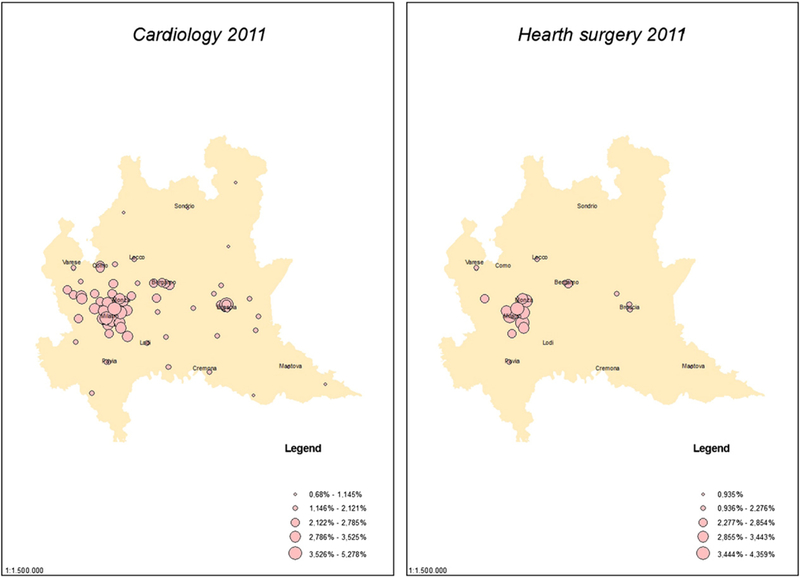
The index of hospital spatial competition.

5. Results

In this section we present our empirical results. The discussion is in three parts: first, we describe the estimates of hospitals’ health outcomes obtained in the first-stage analysis by applying a multilevel model to patients’ individual data. Second, we present the estimates of hospitals’ efficiency scores. Last, we discuss the empirical evidence regarding the trade-off between effectiveness and hospital’s efficiency, obtained in the third-stage analysis.

5.1. Estimation of effectiveness in achieving health outcomes

The estimated coefficients of the variables affecting observed health outcome in each year in multilevel model (1) are shown in Table 4.¹⁸ It presents the coefficients’ estimates for cardiology. Similar results have been found for the other wards, since the regressors included in the analysis are the main determinants of individual risk adjusted health outcomes. Table 4 presents the results for eight model specifications, i.e., two health outcomes for four years.

Table 4.

Determinants of health outcomes: Cardiology.

Indep. variables	2008		2009		2010		2011
	Health outcome		Health outcome		Health outcome		Health outcome
	MR	RA	MR	RA	MR	RA	MR	RA
Intercept	−11.4091***	−3.0969***	−10.9423***	−3.2999***	−11.6516***	−2.9754***	−12.0305***	−3.1343***
GENDER	0.1720***	0.2530***	0.0162	0.3012***	0.1256**	0.2104***	0.1416***	0.3154***
AGE	0.0950***	0.0037***	0.0881***	0.0060***	0.0931***	0.0057***	0.0982***	0.0073***
DRGWEI	−0.2136***	−0.0230***	−0.2243***	−0.0584***	−0.1582***	−0.0420***	−0.2433***	−0.0423***
HEARTDIS	0.1169	0.9831***	−0.0656	1.0220***	−0.3540***	0.6999***	0.0386	0.5871***
CANCERDIS	1.9181***	−0.4044***	1.7535***	−0.2710***	1.6349***	−0.2176**	1.8139***	−0.1861*
EUNIT	1.2523***	0.0660***	1.3103***	0.0943***	1.2705***	0.0493*	1.2426***	−0.0184
COMORB	0.0916***	0.1349***	0.0573*	0.1687***	0.2481***	0.1726***	0.1769***	0.1083***
ICU	0.1117	0.1936***	0.087	0.2253***	0.1082	0.1862***	0.0527	0.2364***
TRANSF	0.4550***	3.7426***	0.6138***	3.8990***	0.4631***	3.7082***	0.5335***	3.7516***

Legend: MR = Mortality; RA = Readmissions.

^***1% significance.

^**5% significance.

^*10% significance.

For all the models estimated, we find that most of the coefficients regarding patients’ characteristics are statistically significant. For mortality rates gender and age are estimated to have positive effects; hence estimated mortality rates are higher when the patient is male and old. An increase in the mortality rate is observed also when the patient suffers from heart disease, cancer, if she/he is admitted through an emergency unit and if her/his comorbidity level is high. Interestingly, the mortality rate is higher if the patient is transferred to another hospital. This may be interpreted as a signal that patients in very bad health status are not treated in the first hospital where they are admitted and are instead transferred to other structures. In addition, mortality is higher the lower is the DRG weight.

Readmission rates are greater if the patient is male, old, suffers from heart disease, is admitted through an emergency unit, has a high comorbidity level, spends some days in the intensive care unit, and, again, is transferred to another hospital. Readmission rates are lower for patients with high DRG weight and suffering from cancer.

In order to test for a possible model mis-specification we compute the intra-class correlation coefficient (ICC), defined in Section 3. Table 5 shows the values of ICC when we estimate model (1). The intraclass correlation coefficient ICC is generally highly significant, implying that the inclusion of the ward level on top of the individual level is important to get efficient and unbiased estimates of the model coefficients and, in turn, of the predicted health outcomes.

Table 5.

Estimated ICC at the hospital and ward levels.

Wards	2008		2009		2010		2011
	Health outcomes		Health outcomes		Health outcomes		Health outcomes
	MR	RA	MR	RA	MR	RA	MR	RA
Cardiology	0.088***	0.022***	0.083***	0.024***	0.118***	0.022***	0.116***	0.024***
General medicine	0.056***	0.020***	0.043***	0.022***	0.051***	0.019***	0.053***	0.021***
Hearth surgery	0.065**	0.005*	0.091**	0.012**	0.084**	0.011**	0.119**	0.007**
Neurology	0.091***	0.014***	0.075***	0.015***	0.075***	0.019***	0.080***	0.013***
Neurosurgery	0.113***	0.049**	0.119**	0.045***	0.110***	0.034***	0.076**	0.023***
Oncology	0.147***	0.149***	0.171***	0.131***	0.130***	0.139***	0.105***	0.090***
Orthopedics	0.215***	0.029***	0.242***	0.031***	0.190***	0.025***	0.190***	0.033***
Surgery	0.138***	0.031***	0.162***	0.027***	0.128***	0.033***	0.140***	0.033***

Legend: M = Mortality; RA = Readmissions.

^***1% significance.

^**5% significance.

^*10% significance.

The box-plots regarding the distribution among hospitals of the predicted risk-adjusted mortality rates are shown in Fig. 3, for each ward considered. Oncology has the higher dispersion, while the smallest is in heart surgery and orthopedics. Fig. 4 presents the box-plots for the predicted risk-adjusted readmission rates: again, oncology has the highest dispersion, while orthopedics has the lowest.

Fig. 3.

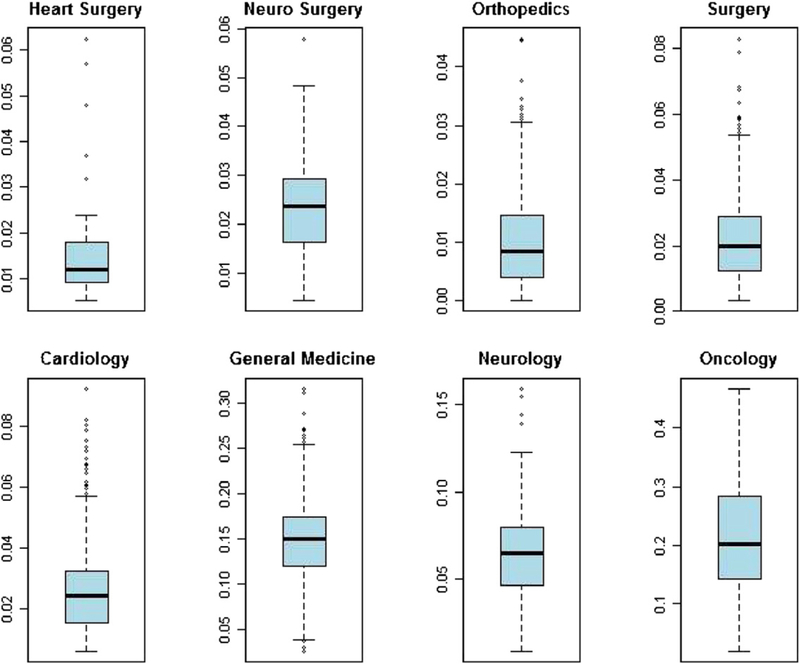
Distribution of predicted mortality rate by ward.

Fig. 4.

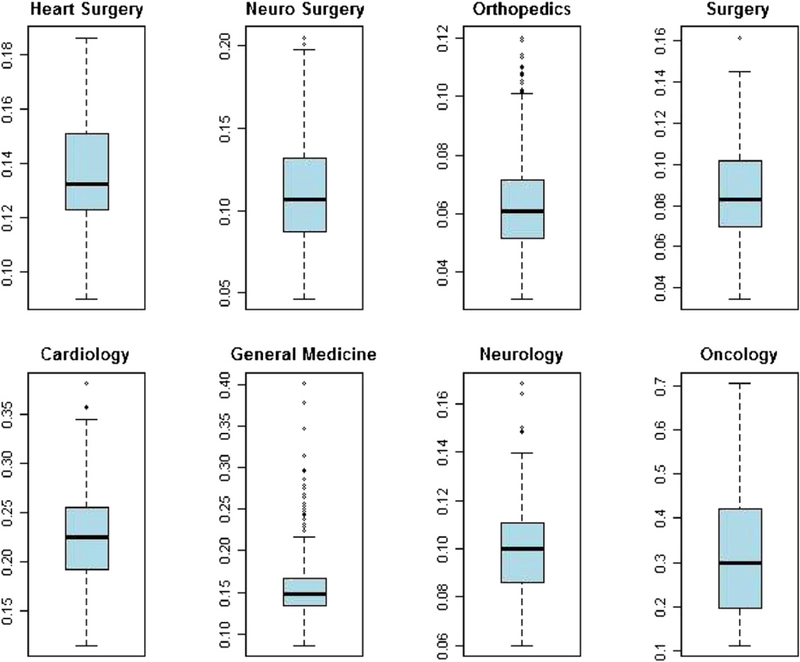
Distribution of predicted readmission rate by ward.

5.2. Estimation of hospitals’ efficiency scores

In this section we present the estimated hospital efficiency scores, obtained by applying the SF translog production function presented in Eq. (5) to our data. Table 6 displays the average (among all the hospitals and over the four years) estimated efficiency scores both for the discharges and the revenues’ output variables. In general, there is considerable heterogeneity in efficiency among wards. The high specialty wards (e.g., neurosurgery) tend to have higher efficiency scores. Table 6 also shows that the correlation between the estimated efficiency scores when using discharges and revenues as output is rather high in all wards. This implies that hospitals that are more efficient when the output is given by discharges are also more efficient when revenues are the dependent variable of the production function.

Table 6.

Estimates of hospitals efficiency scores: ward averages.

	Cardiology	General medicine	Heart surgery	Neurology	Neurosurgery	Oncology	Orthopedics	Surgery
Discharges
Mean	0.62	0.69	0.74	0.70	0.79	0.62	0.51	0.69
Min	0.21	0.18	0.16	0.19	0.38	0.23	0.12	0.15
Max	0.98	0.97	0.97	0.98	0.98	0.98	0.97	0.99
St. Dev.	0.17	0.18	0.22	0.17	0.16	0.19	0.19	0.17
Revenues
Mean	0.56	0.64	0.75	0.69	0.77	0.69	0.53	0.65
Min	0.12	0.14	0.19	0.20	0.36	0.18	0.07	0.11
Max	0.98	0.98	0.98	0.96	0.97	0.96	0.97	0.99
St. Dev.	0.20	0.18	0.23	0.19	0.17	0.19	0.20	0.19
Correlation discharges/revenues	0.91	0.88	0.95	0.89	0.77	0.89	0.83	0.83

Fig. 5 displays the box-plots of the estimated efficiency scores among the different wards. Fig. 5(a) is related to the efficiency scores when discharges are the hospitals’ output, while Fig. 5(b) regards hospitals’ revenues. It is evident that the distribution of the two considered outputs among the different wards is similar.

Fig. 5.

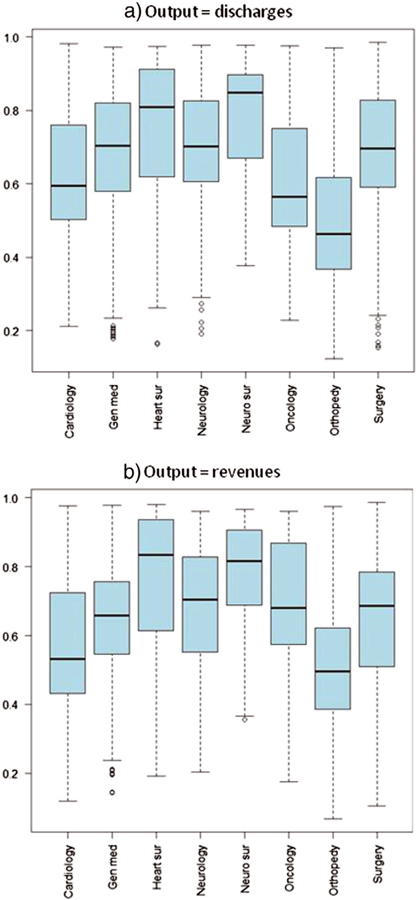
Estimated efficiency scores.

Table 7 displays the coefficients’ estimates regarding the inputs of the translog production frontier presented in Eq. (5). The top rows display the estimated coefficients when discharges are the output variable, while the bottom rows of Table 7 show the estimated coefficients when revenues are the dependent variable. For all the wards the estimated coefficient γ, given by ${\sigma }_k^2/({\sigma }_k^2+{\sigma }_v^2)$ (with ${\sigma }_k^2$ being the variance of the different wards the one-side error component representing efficiency, and ${\sigma }_v^2$ the variance of the white noise disturbances) and indicating the importance of inefficiency in explaining the distance from the estimated frontier and the observed output, is highly statistically significant and very large. It means that a large part of the difference between the estimated frontier and hospitals’ observed outputs is due to inefficiency, and not to random shocks. When we specify discharges as the hospital output, the inputs’ estimated coefficients are particularly significant for general medicine, neurology and orthopedics. Similar results are obtained when using revenues as the output variable, with significantly estimated coefficients for cardiology, general medicine, heart surgery, orthopedics and surgery. The variable TECH is positive and statistically significant in cardiology and neurology when discharges are the hospital output. When the latter is given by revenues, it is positive and statistically significant in cardiology, general medicine, neurology, orthopedics and surgery. It is negative and significant in neurosurgery if output is given by discharges.

Table 7.

Estimates of hospitals production functions.

	Cardiology	General medicine	Heart surgery	Neurology	Neurosurgery	Oncology	Orthopedics	Surgery
Output: Discharges
Intercept	5.88	−0.97	7.56	11.23***	−2.50	−10.68	−5.67***	4.56**
BEDS	0.78	−0.71	−0.53	0.54	−0.61	4.16**	0.88	−0.08
PHYS	0.71	−0.50	3.17	2.97**	1.60	−2.44	0.30	−0.11
NURS	−0.13	2.30***	−2.77	−3.62**	−1.37	4.42*	1.47**	−0.02
OTHER	−0.71**	−0.63***	−0.34	−0.19	1.23*	−0.65	−0.06	0.40*
BEDS2	−0.11*	0.10	0.25*	0.27***	−0.05	0.05	0.20***	0.14
BEDS × PHYS	−0.28***	−0.09	−0.21	−0.07	0.01	−0.01	−0.04	0.11
BEDS × NURS	0.32***	0.32***	0.19	−0.03	0.02	−0.29	0.02	−0.12
BEDS × OTHER	−0.04	−0.16***	0.02	0.06	0.08	0.02	−0.07	0.04
PHYS2	0.02	0.13**	0.04	−0.54*	−0.26	−0.12	−0.18**	0.08
PHYS × NURS	−0.04	−0.18**	−0.47	0.47	0.19	0.48	0.15	−0.08
PHYS × OTHER	0.03	0.13***	0.26	−0.18	−0.06	−0.19	0.02	−0.02
NURS2	−0.09	−0.05	0.45	−0.48	−0.07	−0.61	−0.12	0.18
NURS × OTHER	0.07	−0.04	0.17	0.31**	−0.01	−0.11	−0.16**	−0.08
OTHER2	−0.04	0.01	−0.42**	−0.14**	−0.04	0.35**	0.19***	0.05
TECH	0.84***	0.04	−0.01	0.94	−0.40***	0.38*	0.16*	−0.11*
γ	0.98***	0.95***	0.98***	0.96***	0.94***	0.96***	0.97***	0.96***
Output: Revenues
Intercept	8.24	5.39***	2.92***	26.82***	−4.22	13.49*	2.92*	11.56***
BEDS	2.00***	−0.52	−0.50	−0.49	−1.48	1.11	1.55***	0.46
PHYS	0.10	−0.87**	−0.91	−1.02	3.71**	−2.38*	−0.30	−0.17
NURS	0.97	2.95***	−1.21	−0.72	−1.55	1.02	1.74***	0.15
OTHER	−0.58	−0.71***	0.23	−0.28	1.14*	0.80	−0.05	0.23
BEDS2	−0.42***	−0.06	0.13	0.34***	−0.25**	0.50**	0.22***	0.09
BEDS × PHYS	−0.29***	−0.09	−0.09	0.08	0.48**	0.15	−0.09	0.18**
BEDS × NURS	0.30**	0.38***	−0.03	−0.09	−0.23	−0.26	0.02	−0.29***
BEDS × OTHER	−0.02	−0.19***	0.15***	0.03	−0.01	−0.01	−0.07*	0.12**
PHYS2	0.00	0.20***	0.60	0.29	−0.55	0.03	−0.01	0.27***
PHYS × NURS	0.00	−0.26***	−0.80**	−0.26	0.34	0.00	−0.02	−0.32***
PHYS × OTHER	0.07	0.17***	0.32**	0.04	−0.20	0.12	0.09	0.03
NURS2	−0.17	−0.01	1.04***	0.18	−0.39	0.21	0.03	0.45***
NURS × OTHER	0.02	−0.08	−0.19	0.15	0.26	−0.23	−0.17**	−0.08
OTHER2	−0.05	0.03	−0.17	−0.19**	−0.16	0.06	0.12**	−0.01
TECH	1.12***	0.28***	0.01	1.02***	−0.17	0.37*	0.43***	0.17**
γ	0.97***	0.96***	0.99***	0.96***	0.94***	0.95***	0.97***	0.97***
Observations	296	497	78	187	91	145	437	476

^***1% significance.

^**5% significance.

^*10% significance.

The output elasticity of inputs for the different wards is shown in Table 8, for both output variables. In a translog production function, the output elasticity of input h is defined as follows:

$${ϵ}_{y,h}=\frac{\partial \log \left(y_{wjt}\right)}{\partial \log \left({\mathcal{X}}_{wjth}\right)}={\beta }_h\log \left({\mathcal{X}}_{wjth}\right)+\frac{1}{2}\sum _{l=1}^L{\beta }_{jl}\log \left({\mathcal{X}}_{wjtl}\right).$$ (8)

Table 8.

Hospital production functions: inputs’ elasticities.

Ward	Output	Inputs
		Beds	Physicians	Nurses	Others	SR hours
Cardiology	Discharges	0.63	0.02	−0.05	−0.03
	Revenues	0.81	0.06	−0.08	−0.05
General medicine	Discharges	0.67	−0.02	0.16	0.01
	Revenues	0.66	0.02	0.10	−0.01
Heart surgery	Discharges	0.39	0.11	−0.07	−0.12
	Revenues	0.34	0.11	−0.13	−0.04
Neurology	Discharges	0.79	−0.13	−0.01	−0.001
	Revenues	0.78	0.00	0.05	−0.11
Neurosurgery	Discharges	0.62	−0.04	0.09	−0.01
	Revenues	0.73	−0.12	0.24	−0.11
Oncology	Discharges	0.70	−0.10	0.12	0.10
	Revenues	0.90	−0.02	0.17	−0.003
Orthopedics	Discharges	0.56	0.04	−0.18	0.18
	Revenues	0.54	0.09	−0.13	0.13
Surgery	Discharges	0.67	0.07	−0.05	0.02
	Revenues	0.67	0.08	0.12	−0.11

We find that bed elasticities are always positive and rather large in cardiology, neurology, neurosurgery, oncology and surgery. Positive elasticities for physicians are estimated in cardiology, heart surgery, orthopedics and surgery. Negative elasticities for physicians are instead estimated in neurosurgery and oncology (mixed results are obtained in general medicine and neurology). Nurses are estimated to have positive elasticities in general medicine, neurosurgery and oncology; negative nurse elasticities are estimated in cardiology, heart surgery and orthopedics. The other hospital workers have positive elasticity only in orthopedics, while negative elasticities are estimated in cardiology, heart surgery, neurology and neurosurgery. Negative elasticities may be interpreted as excessive endowments of that input; hence, in some wards there are excessive physicians and nurses, while in most wards there are other kinds of workers in excess.

5.3. The trade-off between effectiveness and efficiency

In this section we analyze the possible presence of a trade-off between hospital effectiveness and efficiency. The estimates of efficiency scores obtained from the two estimated translog production frontiers are used as explanatory variables in applying the model shown in Eq. (6), adding the ward effects and the interaction effects. First, Table 9 reports the results of the Hausman test, applied to check whether a fixed effect or a random effect panel data model provides a more appropriate econometric specification of Eq. (6). If the LSDV fixed effect model does not survive the Hausman test, Eq. (6) is estimated with a random effect panel data model. Given the results of the Hausman test, Eq. (6) is estimated with a fixed effect panel data model when the health outcome is mortality rate and hospitals’ efficiency is computed using discharges as output, and with a random effect panel data model in all the other cases.¹⁹ The econometric results, applied to the two different health outcomes investigated in this paper, are shown in Tables 10 and 11.

Table 9.

Model mis-specification test: Fixed vs random effect models.

Output	X2	P-value	H0: Random effect
Health outcome: Mortality rate
Discharges	53.16	0.000	Reject
Revenues	−40.48	NA	Not reject
Health outcome: Readmission rate
Discharges	−69.55	NA	Not reject
Revenues	−12.14	NA	Not reject

Table 10.

The trade-off between mortality rate and hospital efficiency.

Discharges			Revenues
Indep. variables	Coeff	S.E.	Indep. variables	Coeff	S.D.
Intercept	−0.019*	0.010	Intercept	0.085***	0.024
ESDIS	0.044***	0.016	ESREV	−0.024	0.038
Hospital characteristics
OWNPUB	0.040***	0.006	OWNPUB	−0.031**	0.015
OWNNFP	0.001	0.008	OWNNFP	−0.037**	0.019
MONO	−0.113***	0.016	MONO	0.097***	0.035
TEACH	−0.023***	0.008	TEACH	0.004	0.019
Spatial variables
FLOW	0.001	0.028	FLOW	0.052	0.044
COMP	0.635**	0.284	COMP	−0.220	0.664
Ward effects
CARDIO	0.024***	0.009	CARDIO	0.158***	0.021
GENMED	0.113***	0.008	GENMED	0.100***	0.019
HEARTSUR	0.009	0.015	HEARTSUR	0.018	0.026
NEURO	0.077***	0.011	NEURO	0.008	0.027
NEUROSUR	−0.002	0.019	NEUROSUR	0.070	0.045
ONCO	0.313***	0.011	ONCO	0.084***	0.026
SURGE	0.020**	0.008	SURGE	−0.005	0.019
Interaction effects
ESDIS × OWNPUB	−0.046***	0.009	ESREV × OWNPUB	0.049**	0.022
ESDIS × OWNNFP	−0.020*	0.012	ESREV × OWNNFP	0.050*	0.028
ESDIS × MONO	0.107***	0.023	ESREV × MONO	−0.117**	0.051
ESDIS × TEACH	0.021*	0.011	ESREV × TEACH	0.005	0.026
ESDIS × FLOW	−0.037	0.044	ESREV × FLOW	−0.048	0.069
ESDIS × COMP	−1.125**	0.442	ESREV × COMP	−0.267	1.023
ESDIS × CARDIO	−0.011	0.014	ESREV × CARDIO	0.011	0.035
ESDIS × GENMED	0.039***	0.012	ESREV × GENMED	−0.015	0.031
ESDIS × HEARTSUR	0.010	0.020	ESREV × HEARTSUR	0.066	0.035
ESDIS × NEURO	−0.026	0.016	ESREV × NEURO	0.040	0.040
ESDIS × NEUROSUR	0.030	0.024	ESREV × NEUROSUR	−0.029	0.058
ESDIS × ONCO	−0.162***	0.017	ESREV × ONCO	0.275***	0.042
ESDIS × SURGE	−0.007	0.012	ESREV × SURGE	0.038	0.031
R2	0.82		R2	0.73
Observations	2205		Observations	2205

^***1% significance.

^**5% significance.

^*10% significance.

Table 11.

The trade-off between readmission rate and hospital efficiency.

Discharges			Revenues
Indep. variables	Coefficient	S.E.	Indep. variables	Coefficient	S.E.
Intercept	0.085***	0.024	Intercept	0.112***	0.024
ESDIS	−0.024*	0.038	ESREV	−0.080**	0.039
Hospital characteristics
OWNPUB	−0.031**	0.015	OWNPUB	−0.021	0.015
OWNNFP	−0.037**	0.019	OWNNFP	−0.049**	0.019
MONO	0.097***	0.035	MONO	0.093***	0.035
TEACH	0.004	0.019	TEACH	0.009	0.020
Spatial variables
FLOW	0.052	0.044	FLOW	−0.002	0.046
COMP	−0.220	0.664	COMP	−0.814	0.609
Ward fixed effects
CARDIO	0.158***	0.021	CARDIO	0.194***	0.019
GENMED	0.100***	0.019	GENMED	0.089***	0.019
HEARTSUR	0.018	0.026	HEARTSUR	0.032	0.033
NEURO	0.008	0.027	NEURO	0.000	0.026
NEUROSUR	0.070	0.045	NEUROSUR	0.002	0.045
ONCO	0.084***	0.026	ONCO	0.263***	0.028
SURGE	−0.005	0.019	SURGE	−0.017	0.019
Interaction effects
ESDIS × OWNPUB	0.049**	0.022	ESREV × OWNPUB	0.036	0.023
ESDIS × OWNNFP	0.050	0.028	ESREV × OWNNFP	0.074**	0.030
ESDIS × MONO	−0.117**	0.051	ESREV × MONO	−0.115**	0.051
ESDIS × TEACH	0.005	0.026	ESREV × TEACH	0.000	0.027
ESDIS × FLOW	−0.048	0.069	ESREV × FLOW	0.063	0.074
ESDIS × COMP	−0.267	1.023	ESREV × COMP	0.754	0.980
ESDIS × CARDIO	0.011	0.035	ESREV × CARDIO	−0.048	0.033
ESDIS × GENMED	−0.015	0.031	ESREV × GENMED	0.011	0.031
ESDIS × HEARTSUR	0.066	0.035	ESREV × HEARTSUR	0.055	0.043
ESDIS × NEURO	0.040	0.040	ESREV × NEURO	0.059	0.039
ESDIS × NEUROSUR	−0.029	0.058	ESREV × NEUROSUR	0.064	0.059
ESDIS × ONCO	0.275***	0.042	ESREV × ONCO	−0.015	0.042
ESDIS × SURGE	0.038	0.031	ESREV × SURGE	0.068**	0.030
R2	0.73		R2	0.72
Observations	2205		Observations	2205

^***1% significance.

^**5% significance.

Table 10 presents the results when the health outcome is hospitals’ mortality rate, under the two hospital output specifications, i.e., discharges and revenues. First we analyze the results for discharges. The estimated coefficient for the efficiency scores ESDIS is positive and statistically significant. This implies that at the sample level hospital efficiency has a negative relationship with mortality rates, since those hospitals having higher efficiency scores have also higher risk adjusted mortality rates. Hence, if we consider discharges, there is a trade-off between mortality rate and efficiency, given that hospitals tend to treat more patients per inputs and this induces a higher mortality rate. If we look at hospital characteristics, public hospitals (OWNPUB) have higher mortality rates (in comparison with private for-profit hospitals), since the estimated coefficient is positive and statistically significant. On the contrary private not-for-profit hospitals (OWNNFP) have no significant impact on mortality rates in comparison with private for-profit ones, with the estimated coefficient positive but not statistically significant. Specialized hospitals (MONO) have lower mortality rates than general hospitals, given that the estimated coefficient is negative and statistically significant. Teaching hospitals (TEACH) have lower mortality rates than non-teaching hospitals.

The impact of spatial variables on mortality rates is positive and not statistically significant for FLOW, i.e., a high percentage of patients living outside the region has no impact on mortality rates. This implies that high-quality hospitals (those with the higher degree of vertical differentiation), attracting patients willing to incur high travel costs to access treatment (and, hence, possibly have more complicated health problems than patients not living far from the hospital), are also able to treat them without a significant difference in health outcomes (considering total mortality rates) in comparison with hospitals having a lower degree of vertical differentiation. Spatial competition among hospitals has a positive effect on mortality rates, since COMP has a positive and statistically significant estimated coefficient. Hence, considering mortality rates and discharges, it seems that hospital competition based on horizontal product differentiation leads to worse health outcomes: hospitals with higher degree of competition end up having higher risk-adjusted mortality rates.

If we focus on ward effects, we find that higher mortality rates (in comparison with orthopedics, the base ward) are estimated for cardiology (CARDIO), general medicine (GENMED), neurology (NEURO), oncology (ONCO) and surgery (SURGE). All these wards have positive and statistically significant estimated coefficients.

Concerning the interaction effects between efficiency and hospital characteristics, we find that mortality rates are lower in public hospitals that are more efficient: the estimated coefficient for ESDIS × OWNPUB is negative and statistically significant. Combined with the evidence that public hospitals have higher mortality rates, this is an interesting insight: it implies that in general public hospitals achieve worse health outcomes (i.e., higher mortality rates) but those of them having higher efficiency in treating patients are able to get better health outcomes. Hence, in public hospitals the pressure to be efficient acts as a stimulus also for achieving lower mortality rates, i.e., it is not producing a perverse incentive of getting more patients at the cost of worse health outcomes. Not-for-profit hospitals that are more efficient do not have any effect on mortality rates. Specialized hospitals that are more efficient have higher mortality rates, implying that the incentive to be efficient induces a distortion on health outcomes in specialized structures. Teaching hospitals that are more efficient have no effect, as well as hospitals with high flows of patients coming from other regions.

Interestingly, while hospitals exposed to a higher degree of competition have higher mortality rates, those of them that are more efficient have lower mortality rates. The estimated coefficient of the interaction term ESDIS × COMP is negative, statistically significant, and large (in absolute value). Hence, competition seems not to harm health outcomes when it is combined with managers’ efforts to be efficient; on the contrary, it appears to induce hospitals to be both efficient and effective. Similarly, oncology wards that are more efficient (ESDIS × ONCO) have lower mortality rates than oncology wards that are less efficient. The latter interaction effect is very interesting since even finding that oncology wards have higher mortality rates at the sample level, we find, when studying the interaction with efficiency scores, a positive trade-off between mortality rates and efficiency levels. Last, general medicine wards that are more efficient have higher mortality rates (ESIDS × GENMED): hence, general medicine wards have, in general, higher mortality rates (GENMED), and those of them that are more efficient have even higher mortality rates. We find evidence of a relevant tradeoff between efficiency and effectiveness in these wards that accounts for a high percentage of discharges.

Table 10 also presents the results when hospitals’ efficiency is computed using revenues as output. There is no evidence of a statistically significant trade-off between mortality rate and efficiency at the sample level, even if the estimated coefficient for ESREV is positive. Hence, when we consider also the monetary incentives linked with discharges, hospitals that are more efficient, i.e., with higher revenues given the amount of inputs, achieve this result with no effect on mortality rates.

Regarding hospital characteristics, we find that public hospitals (OWNPUB) have higher mortality rates, while private not-for-profit hospitals (OWNNFP) have no effects on this health outcome. Specialized hospitals (MONO) have lower mortality rates while teaching hospitals (TEACH) have no effects. The two spatial variables have no effects, even if the estimated coefficient for the degree of competition is positive. Regarding ward effects, cardiology, general medicine, neurology and oncology have higher risk-adjusted mortality rates (in comparison with orthopedics), while the other wards have no significant impacts.

If we look at interaction effects between efficiency and hospital characteristics, we find a statistically significant estimated coefficient only for specialized hospitals (ESREV × MONO): the coefficient is positive and this implies that while specialized hospitals have lower mortality rates at the sample level, those of them with higher efficiency have instead a higher mortality rates. All estimated models have rather high R² goodness of fit, since the values of R² are 0.82 for discharges and 0.80 for revenues.

The empirical evidence provided on the factors affecting mortality rates confirms the presence of a trade-off between mortality rates and efficiency levels at the sample level, and of specific ward trade-offs, with negative and positive relations between efficiency and risk-adjusted mortality rates across the different wards.

Table 11 presents the results regarding the trade-off between readmission rates and hospital efficiency. First we examine the evidence when efficiency is computed using discharges as hospital output. We find no evidence of a trade-off between hospital efficiency and health outcome at the sample level: the coefficient of ESDIS is negative but not statistically significant. Concerning hospital characteristics, lower readmission rates are observed in public hospitals (OWNPUB) and in private not-for-profit hospitals (OWNNFP), in comparison with private for-profit ones. Higher readmission rates are found for specialized hospitals (MONO) at the sample level. No significant effects of teaching hospitals on risk-adjusted readmission rates are observed.

Spatial variables have no estimated significant effects, even if FLOW has a positive coefficient and COMP a negative one. Regarding ward effects, higher readmission rates are found for cardiology (CARDIO), general medicine (GENMED) and oncology (ONCO), having all positive and significant estimated coefficients. If we look at the interaction effects among efficiency, hospital characteristics and spatial variables, readmission rates are higher in public hospitals that are more efficient (ESDIS × OWNPUB has a positive and significant coefficient); hence, while public hospitals have lower readmission rates at the sample level, they show a trade-off between efficiency and risk-adjusted readmission rates: public hospitals that are more efficient have higher readmission rates, signaling lower health outcomes according to this variable. On the contrary, specialized hospitals have a positive effect on readmission rates if they are efficient, since the estimated coefficient of ESDIS × MONO is negative and statistically significant, implying lower risk-adjusted readmission rates. Regarding the interaction effects among efficiency and wards, only oncology has a statistically significant trade-off: the estimated coefficient for ESDIS × ONCO is positive. This implies that oncology wards that are more efficient have higher risk-adjusted readmission rates.

Table 11 also displays the results regarding the factors affecting readmission rates when hospitals’ efficiency is computed using revenues as hospital output. In this case there is evidence of a statistically significant trade-off between hospital efficiency and readmission rates at the sample level: the estimated coefficient for ESREV is negative and statistically significant. Hence, if we look at readmission rates, we find that efficiency does not work against health outcomes, different from the mortality rate results. Regarding the impact of hospitals’ characteristics, readmission rates are higher in specialized hospitals (MONO) but lower in private not-for-profit hospitals. Again, no effect of our spatial variables is found, even though both FLOW and COMP have negative estimated coefficients. Regarding ward effects, higher readmission rates are found in cardiology, general medicine and oncology. In addition to the general positive relation between efficiency and readmission rates found at the sample level, there is a further evidence of no trade-off in specialized hospitals. There is instead evidence of a tradeoff between risk-adjusted readmission rates and efficiency in private not-for-profit hospitals (ESREV × OWNNFP), and in surgery wards (ESREV × SURGE). Again, all regressions have rather high R² goodness of fit: R² = 0.73 for discharges and 0.72 for revenues.

To sum up, these are our main results. First, considering ward-level effects is essential, since the relation between health outcomes and efficiency may have different signs across wards. This is particularly relevant, in the case of Lombardy, for general medicine (for mortality rates), and oncology and surgery (for readmission rates). Second, we show that considering spatial variables is important since hospital competition based on horizontal differentiation leads to lower mortality rates if competition is high and hospitals are efficient; in absence of efficiency it may instead increase mortality rates. Third, there is some evidence of a trade-off between mortality rates and efficiency; moreover, we find no effect of efficiency on readmission rates. If such relationships are causal, this implies that efforts to enhance efficiency may penalize patients since mortality rates deteriorate, yet reducing the possibility of being readmitted in the short-run for the same treatment. The different impact of efficiency on readmission may be due to the presence of regional incentives to reduce the readmission rates included in the regional payment scheme. Last, on hospitals’ characteristics, we find that specialization has a mixed effect on the trade-off: more efficient specialized hospitals have lower mortality rates but higher readmission rates. Regarding ownership, we find that public hospitals that are more efficient have lower mortality rates, while private not-for-profit hospitals with high efficiency have higher readmission rates.

The above results yield some interesting policy implications. They show that efficiency and ward effects should be taken into consideration in the health care payment scheme. Hence, our policy implications, based on the provided empirical evidence, are as follows. First, it is important to evaluate hospitals at the ward level and not just at the aggregate hospital level since there are relevant ward effects. Second, hospitals’ efficiency should be included in the evaluation scheme, since we show that efficiency has an impact on health outcomes. This implies designing an incentive scheme based upon two dimensions: health outcomes and efficiency (while the current scheme is based only on health outcomes). Hospitals with good health outcomes but low efficiency have either to receive a lower premium or to be penalized, since low efficiency leads to medium/long-run sustainability problems in funding health care treatments. Finally, spatial hospital competition is not an obstacle toward health outcomes if it combined with positive incentives for achieving efficiency, since we show that hospitals facing a high degree of competition that are more efficient achieve better health outcomes.

6. Summary and conclusions

We study whether the pressure to increase efficiency in the secondary care segment leads hospitals to lower effectiveness. We apply a three-stage econometric model to individual data on patients admitted in hospitals in Lombardy during the period 2008–2011. Unlike previous contributions (Carey and Burgess, 1999; Deily and McKay, 2006; McKay and Deily, 2008) focused on hospital level effects, we estimate health outcomes at the ward level and furthermore estimate production functions at the ward level. We also consider the impact on health outcomes of some hospital characteristics (ownership, specialization etc.), of spatial variables (hospital competition based on horizontal product differentiation and patients’ mobility due to reputation effect), of ward effects, and of the interaction of all these measures with the estimated efficiency scores. These interaction effects allow us to investigate the presence and the sign of a trade-off between health outcomes and efficiency in the regional system, for some hospital characteristics, spatial variables and in some wards.

We find that considering wards and not hospitals is essential since the impact of efficiency on mortality and readmission rates is different across wards. Furthermore, we show that hospitals’ competition must be combined with efficiency in order to achieve good health outcomes. This implies providing hospitals’ managers incentives to allocate efficiently their resources. Last, at the sample level there is a tradeoff between efficiency and mortality rates, while, on the contrary, efficiency leads to lower readmission rates.

Our results may be extended by estimating a distance stochastic frontier function, where hospitals are considered multi-product firms (producing both acute and day hospital discharges). Furthermore, it is possible to consider more sophisticated measures of hospital competition. These extensions are left for future research.