Abstract
We present a scalable weakly supervised clustering approach to learn facial action units (AUs) from large, freely available web images. Unlike most existing methods (e.g., CNNs) that rely on fully annotated data, our method exploits web images with inaccurate annotations. Specifically, we derive a weakly-supervised spectral algorithm that learns an embedding space to couple image appearance and semantics. The algorithm has efficient gradient update, and scales up to large quantities of images with a stochastic extension. With the learned embedding space, we adopt rank-order clustering to identify groups of visually and semantically similar images, and re-annotate these groups for training AU classifiers. Evaluation on the 1 millon EmotioNet dataset demonstrates the effectiveness of our approach: (1) our learned annotations reach on average 91.3% agreement with human annotations on 7 common AUs, (2) classifiers trained with re-annotated images perform comparably to, sometimes even better than, its supervised CNN-based counterpart, and (3) our method offers intuitive outlier/noise pruning instead of forcing one annotation to every image. Code is available.1
1. Introduction
Facial action unit (AU) analysis has been a long-standing problem in computer vision and psychology [9, 30]. Automated AU annotation enables numerous applications such as human-robot interaction, digital marketing, psychological and behavioral research. Most existing approaches to AU detection rely on either supervised methods (i.e., training on fully annotated data) or semi-supervised methods (i.e., training on partly annotated data). Although the amount of online facial images has been growing at an exponential rate, it remains unclear how AU detectors can benefit from large, freely available web images with inaccurate annotations (i.e., annotations with errors). The need for alleviating the constraints of annotations, therefore, has increased considerably.
Reviewing the literature, an AU detector can be trained with full supervision using methods based on either static models (e.g., boosting [25], SVM [50], DBN [44], CNN [14, 51]), dynamic models (e.g., HMM [23], CRF [5], LSTM [45]), or their combinations (e.g., [11, 24]). Given different degrees in the number of samples, these methods impose regularization in space and/or time during learning to improve model generalizability. Another trend of model regularization belongs to semi-supervised learning (SSL), which makes use of partial supervision by considering additional unannotated data. To our best knowledge, most SSL approaches resort to unannotated test samples due to their availability at prediction time. The test samples are often predicted by personalized classifiers (e.g., [7, 47]) or removing a person’s identity [37, 46]. We refer interested readers to [29, 35, 38] for more comprehensive reviews.
Training AU detectors with either fully or partly annotated data encounters several limitations. First, collecting AU annotations requires labor-intensive coding processes by FACS experts. With an experienced coder, manually coding 1 AU for a one-minute video can take 30 minutes or more. Due to this demanding coding process, datasets in the literature (e.g., CK+ [27], SEMAINE [41], AM-FED [32], DISFA [31], BP4D [49]) are still constrained by the number of coded AUs, samples, and subjects. Second, most existing datasets lack assessment of inter-rater reliability, resulting in potentially error-prone or inaccurate annotations [54]. Classifiers trained on such annotations are likely to make inconsistent predictions and thus hinder performance. Lastly, existing pre-trained models can only be applied to the detection phenomena described by FACS experts, i.e., unable to correct images mis-annotated by human coders.
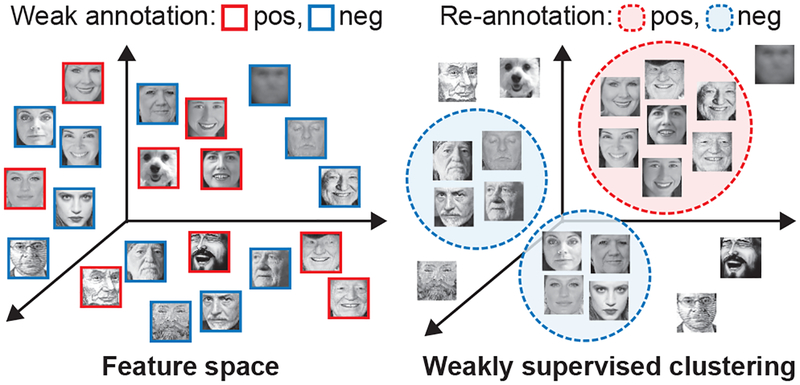
To address these challenges, we propose a weakly-supervised clustering (WSC) approach for learning AUs. Our approach exploits a largely, free web image set with weak annotations that are often obtained from either pre-trained models or query strings. Fig. 1 illustrates our main idea. In the input feature space, neighboring images could suffer from discrepancy in semantics due to non-optimized representation. WSC optimizes for a new embedding space, preserving both similar appearance and annotations. Our approach is efficient, and extends naturally with stochastic approximation that accommodates web-scale images. Clusters in the learned embedding space are re-annotated to be the same class by majority voting, and will be later used to train AU detectors. We show the effectiveness of our approach on the EmotioNet dataset [13] that consists of 1 million facial images collected from the Internet. Our results suggest that our learned annotations yield high agreement with human annotations, and AU detectors trained with the re-annotated images can perform closely to, sometimes better than, their supervised counterpart. We also show our approach is able to prune outliers/noise by design, instead of forcing an annotation on each image.
Figure 1.
An illustration of weakly-supervised clustering: Unlike the original feature space (left) that encloses different semantics and noisy annotations in neighboring images, weakly supervised clustering (right) finds a new embedding space where image clusters possess visual-semantic coherence. The proposed approach scales up to a large number of images, and offers outlier/noise pruning by design. Each cluster is re-annotated as the same class by majority voting, and will be included for training AU detectors.
2. Related Work
Learning-based AU detection:
Algorithms for automated AU detection have evolved along with the scale of datasets and available annotations. For small datasets, challenges were addressed progressively. For instance, given the observation that an AU occurs only in sparse facial regions, sparsity-induced algorithms (e.g., [40, 50, 53]) were exploited to select informative regions so that the influence of uncorrelated facial regions can be reduced or neglected. To alleviate errors caused by individual differences, transductive learning (e.g., [7, 46, 47]) was applied to train AU detectors with consideration of unannotated test samples. Another challenge involves AU correlations, i.e., occurrence of an AU could increase or decrease the likelihood of other AUs. Considering AU correlations, algorithms based on multi-label learning (e.g., [12,50]) or DBN (e.g., [44]) yield a multi-label AU classifier to jointly predict multiple AUs. Temporal modeling, on the other hand, captures transition between consecutive frames. For instance, a temporal manifold (e.g., [24]) models onset, apex, and offset phases within an AU segment, or overlapping sliding windows [21] produces fixed-length representations for variable-length motions. We refer interested readers to [29, 35, 38] for comprehensive reviews.
For larger datasets, Convolutional Neural Networks (CNN) have become a dominating approach due to their capacity and capability of representation learning. Strategies for small datasets start to migrate to CNN-based methods. Given AU relations, [14, 51] learn a unified model to predict multiple AUs. Temporal modeled as the Long Short-Term Memory (LSTM) is aggregated to CNN architecture to construct fusion models (e.g., [8, 19]). In the view of peak and non-peak frames corresponding to the same semantic (e.g., expressions), [52] applies a siamese-like CNN model to learn the feature responses of non-peak frames towards those of peak ones. These methods are mostly fully supervised. In contrast, the proposed Weakly Supervised Clustering (WSC) utilizes unannotated images.
Learning with unannotated images:
Methods tackling with unannotated images can be broadly categorized into two-fold: semi-supervised and weakly supervised learning. Semi-supervised learning aims to leverage unannotated data by assuming that unannotated data follow continuity or form cluster with annotated data. For instance, to alleviate individual differences between the training and the test set, STM [7] trains a personalized classifier for each test subject. Similary, CPM [48] remedies subjects discrepancy by iteratively training SVM classifiers with test samples annotated by pre-trained classifiers. GFK [15] learns an intermediate space that can describe distribution similarities on a Grassmann manifold. In addition, instead of only unannotated test data, LapSVM [33] and TSVM [20] exploits all available unannotated data into learning.
On the other hand, weakly supervised learning exploits inexact, incomplete or inaccurate annotations [54] (i.e., weak annotations), and has proven effectiveness in vision tasks. For semantic segmentation, treating an object-level annotation on an entire image as weak supervision, Liu et al. [26] combined spectral clustering and a discriminative classifier to learn the mapping between superpixels and object-level annotations. Similarly, Vezhnevets et al. [42] presented a family of CRF models to predict classes for superpixels by encouraging neighboring superpixels to share the same class label. For object detection, the presence or absence of an object is also given at image-level. Bilen et al. [3] utilized a latent SVM with convex clustering to locate high probable windows. For human-object interaction, without human and object location, action label could be a clue for weak supervision. For instance, Prest et al. [36] used an action classifier and a human detector to determine the relevant object for an action and its relative location to a human. In contrast, WSC can not only learn from weakly annotated images (i.e., inaccurate annotation), but can prune noisy annotations by design.
3. Scalable Weakly Supervised Clustering
The proposed weakly-supervised clustering comprises two components. First, we propose Weakly-supervised Spectral Embedding to find an embedding space. Then, we re-annotate images in the embedding space using rank-order clustering. Below we describe each in turn.
3.1. Weakly-supervised Spectral Embedding
The first component, Weakly-supervised Spectral Embedding (WSE), finds an embedding space that preserves coherence in both visual similarity and weak annotation (i.e., inaccurate supervision [54]). Conventional methods that consider only one factor could suffer from the gap between visual features and semantic. For instance, images that are close in the feature space may not carry the same semantics, while weak annotations often contain noise/outlier and are thus not fully trustworthy. Through WSE, we aim to achieve a proper balance between the two factors.
Formulation:
A promising method to find good clusters has recently emerged into spectral clustering [43], due to its simplicity in avoiding parametric density estimators and local minima encountered in iterative algorithms (e.g., K-means). Inspired by empirical successes (e.g., [16, 26]), we adopt the objective of spectral clustering to find a new embedding space. Denote N data samples in the data matrix , we form a symmetric mutual k-nearest neighbor graph [43] by computing each component of an affinity matrix :
| (1) |
where is the set of k-nearest neighbors of xj measured by a distance function d(·, ·) (we used L2), and γ is a parameter for normalization. A graph Laplacian is obtained as L = D − A (or for a normalized Laplacian), where D is the degree matrix for a finite graph represented by A. Spectral clustering solves for an embedding by:
| (2) |
where is an identity matrix and K is the dimension of the learned embedding space. Solving (2) yields an embedding space where convex regions directly correspond to clusters with visually similar images, whereas clusters in the original space usually do not [43]. Taking weak annotations into account, we denote a “group” as the set of images annotated as the same class yi, and then associate images with weak annotations to a set of groups . This association allows a general representation for binary and multi-label weak annotations due to the independence between groups. As will be shown later, this method allows each to be optimized independently.

Given the representation of “groups”, we define as a scatter measure of the g-th group, where wi is the i-th row of W and is the mean of rows of W that belong to the g-th group. The scatter measure can be rewritten as a compact matrix form: , where is an ng × ng centering matrix, ng is the number of images in group and 1 is a vector of ones. That is, smaller value of indicates higher agreement of weak annotations within the same group. Let be the scatter over all groups, we formulate WSE as:
| (3) |
where f(W, L) denotes the spectral clustering objective in Problem (2), serves as a regularizer that encourages images with similar weak annotations to be close in the learned embedding space, and λ ≥ 0 is a trade-off between visual similarity and weak annotations. The goal of WSE is to pull together images that share both similar appearance and annotations.
Optimization:
For smooth convex functions, first-order gradient method can be applied with convergence rate . However, WSE in Problem (3) is non-smooth due to the group regularizer , especially when contains overlapping groups. To perform effective and efficient optimization, we propose a fast algorithm with convergence rate based on accelerated gradient descent [6]. First, we expand (3) with the first-order Taylor expansion of f(W):
| (4) |
where 〈A, B〉 = Tr(A⊤B) denotes the inner product of matrices, and M is the coefficient of Taylor expansion. Let and qL(V) = minW QL(W, V) be the smoothed problem, we can rewrite Eq. (4) as:
| (5) |
Define , (5) can be decomposed into each group:
| (6) |
Seeing each group g separately, we obtain a group-wise optimization for each Wg:
| (7) |
The optimal solution for (7) can be obtained as , yet the numerical solution to inverse operation is usually slow and numerically unstable. Instead, we derive a closed-form solution as , where , , and Wi and Vi are the i-th row of Wg and the i-th row of Vg, respectively. Algorithm 1 summarizes the optimization procedure with accelerated gradient updates. Please see supplementary materials for detailed derivation and theoretical rationale. We used a stopping condition as the changes in objective value (Eq. (4)) is less than 1e-5.
Fig. 2 illustrates the convergence process of WSE on synthetic data. To synthesize weak annotations, we randomly introduce 30% noisy samples to ground truth annotation. While the number of iteration increases, WSE gradually converges to two clusters that group neighboring samples and preserve information of the noisy supervision. Upon convergence at iteration #100, WSE is able to prune noisy annotations, resulting in a distribution that closely resembles ground truth. This shows WSE’s capability of coupling visually similar images with their weak annotations.
Figure 2.
A synthetic example for solving Eq. (3) with λ = 256. Left to right: Objective value in Eq. (4) v.s. #iterations, clustering effect at selected iterations, and weak annotations (30% noise added to ground truth). Red circles ( ) and blue rectangles (
) and blue rectangles ( ) indicate samples assiociated with different annotations. Upon convergence at #100, noisy annotations are removed, resulting in distributions closer to ground truth. As can be seen, our method is able to group neighboring samples while preserving their relationship to the weak annotations.
) indicate samples assiociated with different annotations. Upon convergence at #100, noisy annotations are removed, resulting in distributions closer to ground truth. As can be seen, our method is able to group neighboring samples while preserving their relationship to the weak annotations.
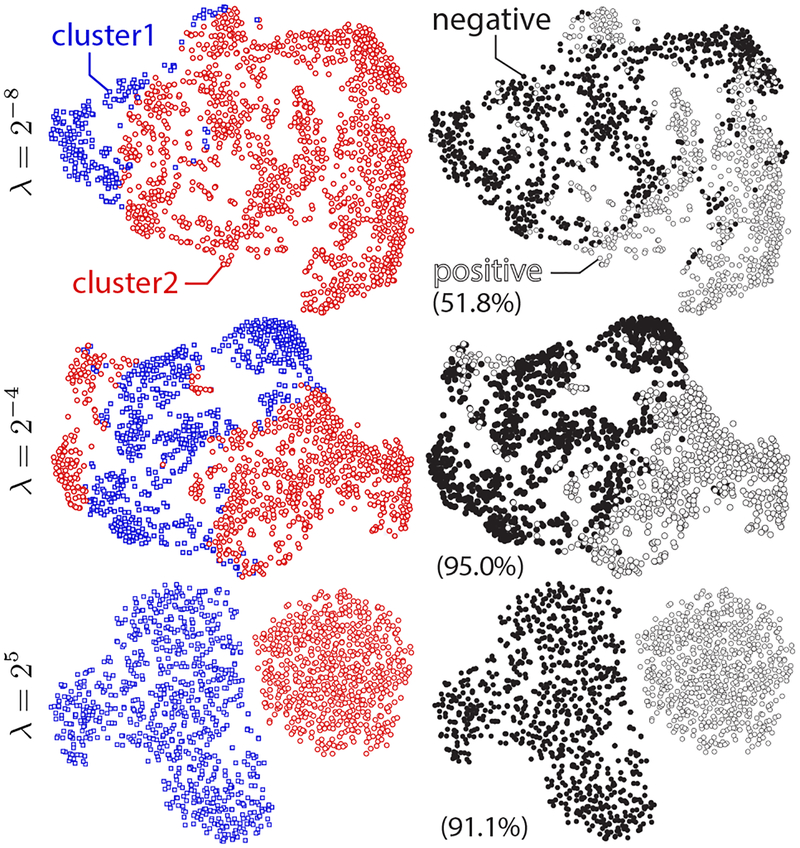
Influence of λ:
Fig. 3 shows the learned embedding W projected onto 2-D PCA space according to different choices of λ. In this particular example, we used 10k web images in the EmotioNet dataset [2], with weak annotation of AU12 from an AlexNet model pre-trained on the BP4D dataset [49]. As can be seen, WSE with small λ (top row) tends to group visually similar images due to their closeness in the feature space (left column), yet fails to maintain semantics in neighboring images (right column). As a result, the agreement (i.e., accuracy) of WSC re-annotation with ground truth annotation is only 51.8%. On the contrary, WSE with large λ (bottom row) enforces the algorithm to trust completely on the weak annotations, leading to a clean-cut clustering result and a 91.1% agreement with ground truth. An appropriate λ lies in-between (middle row), where WSE is able to preservie images that are both close in the feature space and possess the same annotations. With an appropriate λ, the agreement with ground truth annotation reaches 95.0%.
Figure 3.
Illustration of the learned W with different λ on real data of AU12. Each sample is colored by cluster ID (left column) or weak-annotations, i.e., positive v.s. negative (right column). Parentheses indicate the % of agreement between WSC re-annotation and ground truth (higher better). A good balance is found at λ = 2−4 where WSC achieved highest agreement.

Stochastic extension of WSE:
Applying WSE to largescale web images can be expensive for both building the Laplacian and parameter update in Algorithm 1. We introduce a scalable version of WSE to deal with large amount of images using stochastic approximation. Denote as an “edge-sampled” version of L [10] that ensures the expectation condition . Here, are set to be Lij if the edge between the i-th and j-th nodes in the graph are sampled, and 0 otherwise. Under this condition, the local convergence rate becomes . Algorithm 2 summarizes the optimization procedure.
3.2. Rank-order clustering for re-annotation
With the learned embeddings from WSE, the second component aims at improving the weak annotations. Fig. 4 summarizes the re-annotation process. First, we build an undirected graph of the learned embeddings using rank-order distance [34], which measures the distance between two samples by their orders in each other’s neighbors. Observing that samples of the same class often have similar distributions of closest neighbors, we found the rank-order distance is more robust to biased distribution of AU data (i.e., large negative-positive ratio) compared to standard absolute L1/L2 distance. Given the undirected graph, we used breadth-first hierarchical clustering to find clusters with high intra-cluster density and low inter-cluster density. We term this process Rank-Order Clustering (ROC).
Figure 4.
Pipeline for WSC re-annotation
To describe the quality of clustering results, we modified the notion of Modularization Quality Index (MQI) [28]. MQI was designed originally to evaluate directed graphs in programming language. We revise the formation to evaluate modularization on undirected graphs, and term it “uMQI”. Denote as the i-th cluster, mi and ni as the number of edges and the number of nodes of , and mij as the number of edges between and , we define uMQI on clustering results as:
| (8) |
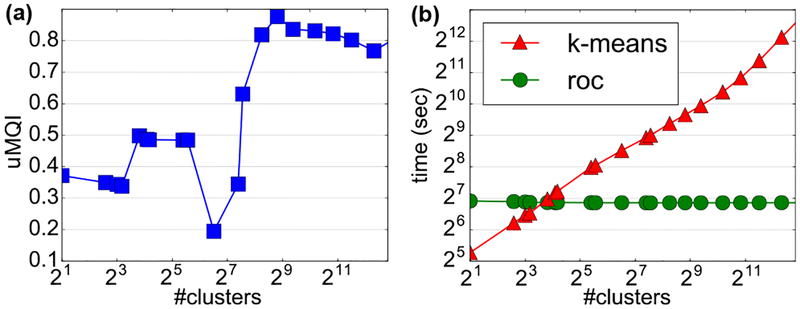
where measures the intra-cluster density, and measures the inter-cluster density. uMQI computes the difference between expectations of intra-cluster and inter-cluster densities, resulting in a value in [−1, 1]. The higher uMQI is, the better clustering results preserve modularization. To avoid trivial solution, we consider only the clusters with non-single element by setting δ = 1. As illustrated in Fig. 5(a), uMQI serves as an objective criteria to choose #clusters.
Figure 5.
Two properties of rank-order clustering: (a) uMQI v.s. #clusters, showing an objective criteria for choosing #clusters, (b) Running time v.s. #clusters between k-means and ROC.
Compared to conventional clustering (e.g., k-means), ROC offers numerous benefits for our task: (1) ROC stands on hierarchical clustering, and is exempt from requiring #clusters as an input. (2) ROC enables intuitive noise/outlier pruning by identifying clusters with rare samples, while standard clustering methods tend to assign a cluster label to each sample. (3) ROC scales up easily to large number of samples. The complexity of ROC is , given k the number of nearest neighbors for each node. A naive k-means takes for running t iterations with K clusters. As in Fig. 5(b), the running time of ROC is unrelated to #clusters, unlike k-means. Finally, images of the same cluster were simply treated to be the same class based on majority voting. As will be showing in experiments, this simple approach is effective in improving annotation quality and excluding undesired outlier/noise, which sum to better performance.
3.3. Comparison with semi-supervised methods
WSC shared similarities with existing semi-supervised methods, i.e., STM [7], CPM [48], GFK [15], LapSVM [33] and TSVM [20]. Compared to fully supervised methods (e.g., DRML [51]), semi-supervised methods aim to utilize unannotated data for learning. However, they differ in several aspects, as summarized in Table 1. GFK, STM, and CPM recruit unannotated data from the test set. These methods hold assumptions on the distribution: GFK assumes a geodesic flow kernel from training set to test set to minimize the mismatch, while STM and CPM assume the unannotated test data belong to the same identity. In contrast, LapSVM and TSVM require no such assumptions, and can be generalized to any form of unannotated data. However, LapSVM and TSVM cannot scale to large dataset for their kernel-based design. In addition, common to all these approaches involves their limitations in pruning noisy annotations. Overall, WSC is exempt from strong assumptions, scales up to large amount of samples, and can prune noisy annotations by design.
Table 1.
Comparisons with related methods
| Methods | UD | PN | SL | IE |
|---|---|---|---|---|
| DRML [50] | × | × | ✓ | ✓ |
| STM [7], CPM [48] | ✓ | × | × | × |
| GFK [15] | ✓ | × | × | ✓ |
| LapSVM [33], TSVM [20] | ✓ | × | × | ✓ |
| WSC (ours) | ✓ | ✓ | ✓ | ✓ |
UD: Unannotated data, PN : Pruning noisy annotation, SL: Scalability, IE: Identity exemption.
4. Experiments
4.1. Settings
Dataset:
We evaluated the effectiveness of WSC on the EmotioNet dataset [2], which contains 1 million images collected from the Internet. 50,000 images were manually labeled with multiple AUs by expert annotators. We followed the train/test partition in [2], ending up with with 25,000 images in each. 7 AUs with base rate larger than 5% (as shown in Table 2) were chosen for the experiments. The remaining 950,000 samples were used to exhibit the benefits of the use of unannotated web images. Throughout the experiments, we reported on the test set.
Table 2.
Base-rate (%) of each AU in EmotioNet [2]
| AU | 1 | 2 | 4 | 5 | 6 | 9 | 12 | 17 | 20 | 25 | 26 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | 6.2 | 3.1 | 11.5 | 5.7 | 20.5 | 2.2 | 38.7 | 2.1 | 0.6 | 50.0 | 8.6 |
| Test | 5.6 | 4.1 | 6.3 | 6.0 | 24.7 | 0.7 | 41.2 | 0.9 | 0.6 | 50.0 | 8.4 |
Metric:
We reported two standard metrics for AU detection: F1 score and S score (i.e., free marginal kappa coefficient) [4]. F1 score captures specific agreement on the positive class, and, despite its popularity, known to be sensitive to unbalanced distribution such as AUs (e.g., Table 2). As an alternative, we reported S score, which is more robust to prevalence and bias [4]. For each metric, we also reported their average over all AUs (denoted as Avg.).
Comparative methods:
For a thorough comparison, we applied the annotations learned by WSC to two popular models for AU detection, i.e. AlexNet [22] and DRML [51]. There are semi-supervised approaches that utilize unannotated images for AU detection, i.e., STM [7], CPM [48], GFK [15], LapSVM [33] and TSVM [20]. However, STM and CPM depend on strong assumptions that unannotated images are correlated and belong to the same identity, and thus are not applicable to our task. To understand the impact of annotation quality on model performance, we set up four types of annotations: (1) “gt” denotes ground truth annotations, (2) “wlb” denotes weak annotations, (3) “wsc” denotes annotations provided by our approach, (4) “ulb” denotes no annotations. We noted each annotation type with the number of images to indicate different scale of experiments, e.g., “wlb10k” and “wsc25k” indicate 10k weakly annotated images and 25k images annotated by WSC. Throughout the experiments, we will use the braces “{}” to indicate one or combination of annotation types.
Implementation details:
For AlexNet [22], we appended batch norm [18] to each relu layer, and revised the output of fc7 to 256-D. For DRML, considering a fair comparison with AlexNet, we applied binary softmax loss instead of multi-label cross-entropy loss used in the original paper. Instead of the hand-crafted shape and Gabor features as provided originally in the EmotioNet dataset [2], we extracted 256-D features by an AlexNet model trained on the BP4D dataset [49] and then fine-tuned on EmotioNet training set. According to our analysis, the learned features performed more reliably than the hand-crafted features (details in supplementary materials). We used the learned features as inputs for GFK, LapSVM and TSVM.
For GFK, we set the subspace dimension as 100-D and randomly select 5,000 samples per random trials. For LapSVM, we apply RBF kernel and train the classifier in primal. For TSVM, we search the tuning parameter λ within {10−5, …,102}. To understand the impact of leveraging unannotated images over annotated ones, we used AU predictions of the fine-tuned AlexNet as weak annotations for the 950,000 unannotated images. During training, we used 1:1 positive-negative ratio for each mini-batch by oversampling positive images if the distribution of an AU is overly skewed. All hyper-parameters were set following the original work. For WSE, we search the tuning parameter λ within {2−10, …,210}. The dimension of the learned embedding space was set to 100-D, which was chosen empirically but found robust to all AUs. For rank-order clustering, we set the number nearest neighbors for each node as 100, and implemented randomized k-d tree using the FLANN library [1] to get the list of neighboring nodes. We applied Alg. 2 to all experiments for scalability concerns. For getting WSE embedding for 200k samples, it took 2 min on a single machine with Intel i7 CPU.
4.2. Results
Tables 3, 5, and 6 show the main results on EmotioNet under different conditions. All instantiations of our approach demonstrate that the models trained with our re-annotated images outperform variants of existing models.
Table 3.
Performance comparison on EmotioNet [2] test set. Braces indicate training images with different amount and annotations (see Sec. 4.1 for details). Bracketed and bold numbers indicate the best and second best performance.
| AU | F1 | S score | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AlexNet |
AlexNet |
AlexNet |
DRML |
AlexNet |
DRML |
AlexNet |
AlexNet |
AlexNet |
DRML |
AlexNet |
DRML |
|
| 1 | 11.8 | 19.8 | 24.2 | 25.3 | 25.3 | [26.3] | [83.6] | 82.6 | 76.1 | 76.5 | 78.2 | 78.9 |
| 4 | 23.9 | 32.5 | 34.7 | [35.7] | 34.5 | 35.5 | 53.9 | [63.9] | 63.0 | 61.8 | 62.9 | 61.9 |
| 5 | 26.6 | 37.6 | 39.5 | 40.0 | 39.3 | [40.3] | [87.5] | 86.4 | 80.1 | 79.6 | 79.2 | 80.1 |
| 6 | 58.8 | 73.5 | 73.1 | 75.3 | 75.6 | [78.7] | 69.4 | 74.8 | 77.3 | 78.5 | 78.6 | [79.6] |
| 12 | 82.1 | 87.1 | 86.8 | 86.6 | 87.4 | [88.1] | 73.9 | 79.1 | 79.5 | 78.1 | 80.5 | [80.8] |
| 25 | 82.1 | 84.3 | 88.5 | [88.9] | 88.8 | [88.9] | 61.4 | 67.2 | 77.1 | 78.8 | 78.6 | [78.9] |
| 26 | 24.3 | 40.2 | 45.6 | 46.2 | 47.7 | [49.1] | [79.1] | 68.5 | 75.7 | 76.7 | 77.6 | 78.2 |
| Avg. | 44.2 | 53.6 | 56.1 | 56.9 | 57.0 | [58.1] | 72.6 | 74.6 | 75.5 | 75.7 | [76.5] | 75.9 |
Table 5.
Results of alternative methods that use unlabeled images
| AU | F1 | S score | ||||
|---|---|---|---|---|---|---|
| GFK |
LapSVM |
TSVM |
GFK |
LapSVM |
TSVM |
|
| 1 | 19.3 | 1.2 | 24.1 | 66.1 | 82.3 | 70.2 |
| 4 | 31.0 | 25.7 | 32.3 | 61.1 | 85.3 | 62.5 |
| 5 | 31.8 | 23.1 | 40.3 | 61.1 | 60.7 | 80.6 |
| 6 | 73.8 | 58.3 | 75.7 | 71.7 | 70.0 | 79.1 |
| 12 | 85.1 | 57.7 | 87.4 | 75.5 | 50.9 | 80.2 |
| 25 | 85.8 | 88.9 | 88.2 | 72.4 | 79.4 | 78.5 |
| 26 | 39.0 | 5.0 | 47.0 | 69.5 | 83.2 | 78.4 |
| Avg. | 52.2 | 37.0 | 56.4 | 68.2 | 73.1 | 75.6 |
Table 6.
Large-scale evaluation of WSC (F1-score)
| 20k | 200k | 400k | 1M | |||||
|---|---|---|---|---|---|---|---|---|
| AU | wlb | wsc | wlb | wsc | wlb | wsc | wlb | wsc |
| 1 | 17.6 | 18.3 | 17.8 | 19.3 | 16.9 | [21.3] | 17.6 | 21.2 |
| 4 | 20.3 | 20.5 | 19.0 | 20.4 | 18.9 | 21.3 | 18.4 | [22.1] |
| 5 | 28.5 | 28.9 | 30.1 | 30.8 | 31.5 | 33.4 | 30.8 | [41.6] |
| 6 | 72.4 | 74.1 | 75.9 | 76.9 | 76.3 | 78.6 | 77.4 | [79.3] |
| 12 | 76.7 | 85.8 | 79.1 | 86.4 | 79.3 | 87.8 | 81.4 | [88.2] |
| 25 | 84.7 | 85.7 | 85.4 | 85.9 | 79.4 | 86.1 | 86.1 | [89.1] |
| 26 | 32.4 | 34.9 | 32.7 | 36.0 | 33.3 | 36.1 | 33.3 | [47.2] |
| Avg. | 47.5 | 49.7 | 48.5 | 50.8 | 47.9 | 52.1 | 49.3 | [55.5] |
WSC vs. weak annotation:
We evaluated WSC against weak annotations (“wlb” hereafter) by comparing their annotation quality and improvement in model performance. To compare annotation quality, we evaluated the agreement of (wlb, wsc) with human annotations (gt). Table 4 shows the % of agreement on wlb of AlexNet (wlb10k) and wsc of AlexNet (wsc10k). The agreement is consistently higher (on average 2.1%) between wsc and gt than between wlb and gt, and particularly yields 98.6% for AU12. Sampled AU12 images that wlb and wsc disagreed are shown in Table 4, where we observed WSC was able to rectify incorrect weak annotations in wlb. For model performance, we compared AlexNet (wlb10k) and AlexNet (wsc10k) in Table 3, and observed 17.9% improvement of F1 averaged over 7 AUs, and even >50% improvement of F1 on AUs (1, 4, 26). AUs (1, 4, 26) are highly unbalanced (see Table 2), and thus are more sensitive to annotation quality. All highlights that WSC produces better quality of annotations than wlb.
Table 4.
Agreement with ground truth annotation (%) comparing weak annotations (wlb) and our approach (wsc)

|
WSC vs. human annotation:
We also compared WSC with the gold standard—human annotations. Interestingly, models trained with our automatically annotated images performed close to, sometimes even better than, models trained with human annotations. Take AlexNet (wsc10k) and AlexNet (gt25k) in Table 3 for example, the average F1 and S-score of AlexNet (wsc10k) are only 4.6 and 1.2 points lower than AlexNet (gt25k). For AUs (6, 12), F1 of AlexNet (wsc10k) are (0.4, 0.3) points even higher than AlexNet (gt25k). If we further increased the amount of re-annotated images (i.e., AlexNet (wsc25k)), the performance on AlexNet increased from (56.1, 75.5) to (57.0, 76.5) in terms of (F1, S) scores. Additionally, to prove the same strategy can be generalized to different models, we evaluated performance on the state-of-the-art DRML [51]. Similar to AlexNet, with 25k more re-annotated images, the performance on DRML improved 2.1% over the baseline DRML trained with all available human annotated images. WSC bridges the long-standing gap between using weakly annotated images and improvement of model performance.
WSC vs. alternative methods:
Close to WSC is SSL and transfer learning, for their use of unannotated images (denoted as “ulb”). Table 5 shows the results of GFK [15], LapSVM [33] and TSVM [20]. Compared to Table 3, the averaged F1 of AlexNet (wsc25k) and DRML (wsc25k) are (11.5%, 57.0%, 3.5%) higher than GFK, LapSVM, and TSVM, respectively. Note that the number of unannotated images for LapSVM was set to be 10k due to the expense in building the Laplacian matrix, i.e., {gt25k + ulb10k} consumed more than 32G memory and took >6hrs. Recall that these methods applied an additional SVM on top of deep features. Our WSC showed better scalability, more efficient to run, and performed best with existing CNNs.
#images:
Finally, we investigated the impact of the number of images on model performance. Table 6 shows the results of models trained with only images that are weakly annotated or re-annotated by WSC. Comparing the results between wlb (200k) and wlb (400k), the averaged F1 decreased from 48.5 to 47.9. One explanation is due to polluted supervision introduced by weak annotations. On the contrary, WSC consistently outperforms wlb, achieving 4.6%, 4.7%, 8.8%, and 12.6% higher on the scale of 20k, 200k, 400k, and 1M images, respectively. Not surprisingly, the more images added to training, the larger improvement we observed in WSC. Both cues indicate WSC’s capability of gathering meaningful images with high visual-semantic coherence and cleaning undesired ones (detailed in next section). We also observed that most AUs saturated when the number of images went beyond 400k. We suspect models with higher capacity (e.g., ResNet [17] or VGG-16 [39]) might yield further improvement, and leave this investigation for future work.
4.3. Pruning noisy annotations
Beyond the capability of preserving visual-semantic coherence, WSC offers an intuitive noise and outlier pruning. This is done in the re-annotation step: Only clusters that contain more than δ images are qualified for uMQI evaluation. In other words, clusters of ≤ δ images receive limited support from its neighborhood, and thus are likely to be noise (i.e., not real faces) or outlier (i.e., uncommon/challenging cases). Fig. 6 shows the clusters with δ = 1, i.e., each image represents a single cluster. WSC produced quite compelling results. As EmotioNet was collected with generic face detectors, WSC is able to identify noise (e.g., cartoon face, sketch, artistic), and expose false detection from the face detector (e.g., dog face and face-like images). Additionally, WSC identifies outliers that involved blurry face, large pose, and shadow/occlusion on the face. Including noise and outlier images can degrade the performance of AU detection. Unlike conventional clustering approaches that tend to assign a label to each image, WSC allows for excluding noise and outlier images, suggesting a more principled approach for data preparation.
Figure 6.
Undesired images identified by WSC: noise (left) and outlier (right). We note noise images as the ones that are not true faces (e.g., cartoon, sketch, etc), and outlier images as uncommon/challenging cases including blur, large pose, shadow, and occlusion.
5. Conclusion
We have presented a weakly spectral clustering (WSC) approach to leverage web images for learning AUs. We proposed weakly-supervised spectral embedding, a scalable algorithm that learns an embedding space considering visual-semantic coherence. Given the learned space, we introduced rank-order clustering that finds high-density clusters based on uMQI and meanwhile prunes noise/outlier. We showed the effectiveness and scalability of WSC on the 1 million EmotionNet dataset. Results indicate that models trained with WSC consistently outperform models with naive weak annotations, and perform comparably to models trained with human annotations. Adding more images annotated by WSC, we showed further improvement over all variants of baseline and state-of-the-art. Future work includes incorporating WSC with multiple labels, replacing models with larger capacity, and extending WSC to more applications such as video and scene classification.
Supplementary Material
Acknowledgements
Research reported in this paper was supported in part by the Natural Science Foundation of China under grant 61701032 and Fundamental Research Funds for the Central Universities (2017RC08) to KZ, and the National Institutes of Health under grant R01-DC-014498 to AMM.
Footnotes
References
- [1]. https://www.cs.ubc.ca/research/flann/.
- [2].Benitez-Quiroz CF, Srinivasan R, Feng Q, Wang Y, and Martinez AM. Emotionet challenge: Recognition of facial expressions of emotion in the wild CVPRW, 2017. [Google Scholar]
- [3].Bilen H, Pedersoli M, and Tuytelaars T. Weakly supervised object detection with convex clustering In CVPR, 2015. [Google Scholar]
- [4].Brennan RL and Prediger DJ. Coefficient kappa: Some uses, misuses, and alternatives. Educational and psychological measurement, 41(3):687–699, 1981. [Google Scholar]
- [5].Chang K-Y, Liu T-L, and Lai S-H. Learning partially-observed hidden conditional random fields for facial expression recognition In CVPR, 2009. [Google Scholar]
- [6].Chen X, Pan W, Kwok JT, and Carbonell JG. Accelerated gradient method for multi-task sparse learning problem In ICDM, 2009. [Google Scholar]
- [7].Chu W-S, De la Torre F, and Cohn JF. Selective transfer machine for personalized facial action unit detection In CVPR, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Chu W-S, De la Torre F, and Cohn JF. Learning spatial and temporal cues for multi-label facial action unit detection In Automatic Face and Gesture Conference, 2017. [Google Scholar]
- [9].Cohn JF and Kanade T. Use of automated facial image analysis for measurement of emotion expression Handbook of emotion elicitation and assessment, pages 222–238, 2007. [Google Scholar]
- [10].Collins MD, Liu J, Xu J, Mukherjee L, and Singh V. Spectral clustering with a convex regularizer on millions of images In ECCV, 2014. [Google Scholar]
- [11].Ding X, Chu W-S, De la Torre F, Cohn JF, and Wang Q. Facial action unit event detection by cascade of tasks In ICCV, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Eleftheriadis S, Rudovic O, and Pantic M. Multi-conditional latent variable model for joint facial action unit detection In ICCV, 2015. [DOI] [PubMed] [Google Scholar]
- [13].Fabian Benitez-Quiroz C, Srinivasan R, and Martinez AM. Emotionet: An accurate, real-time algorithm for the automatic annotation of a million facial expressions in the wild In CVPR, 2016. [Google Scholar]
- [14].Ghosh S, Laksana E, Scherer S, and Morency L-P. A multi-label convolutional neural network approach to cross-domain action unit detection In ACII, 2015. [Google Scholar]
- [15].Gong B, Shi Y, Sha F, and Grauman K. Geodesic flow kernel for unsupervised domain adaptation In CVPR, 2012. [Google Scholar]
- [16].Han Y and Filippone M. Mini-batch spectral clustering IJCNN, 2017. [Google Scholar]
- [17].He K, Zhang X, Ren S, and Sun J. Deep residual learning for image recognition In CVPR, 2016. [Google Scholar]
- [18].Ioffe S and Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift In ICML, 2015. [Google Scholar]
- [19].Jaiswal S and Valstar M. Deep learning the dynamic appearance and shape of facial action units In WACV, 2016. [Google Scholar]
- [20].Joachims T. Transductive inference for text classification using support vector machines In ICML, 1999. [Google Scholar]
- [21].Koelstra S, Pantic M, and Patras I. A dynamic texture-based approach to recognition of facial actions and their temporal models. TPAMI, 32(11):1940–1954, 2010. [DOI] [PubMed] [Google Scholar]
- [22].Krizhevsky A, Sutskever I, and Hinton GE. Imagenet classification with deep CNNs In NIPS, 2012. [Google Scholar]
- [23].Lien JJ-J, Kanade T, Cohn JF, and Li C-C. Detection, tracking, and classification of action units in facial expression. Robotics and Autonomous Systems, 31(3):131–146, 2000. [Google Scholar]
- [24].Liu M, Shan S, Wang R, and Chen X. Learning expressionlets on spatio-temporal manifold for dynamic facial expression recognition In CVPR, pages 1749–1756, 2014. [Google Scholar]
- [25].Liu P, Han S, Meng Z, and Tong Y. Facial expression recognition via a boosted DBN In CVPR, 2014. [Google Scholar]
- [26].Liu Y, Liu J, Li Z, Tang J, and Lu H. Weakly-supervised dual clustering for image semantic segmentation In CVPR, 2013. [Google Scholar]
- [27].Lucey P, Cohn JF, Kanade T, Saragih J, Ambadar Z, and Matthews I. The extended cohn-kanade dataset (ck+): A complete dataset for action unit and emotion-specified expression In CVPRW, 2010. [Google Scholar]
- [28].Mancoridis S, Mitchell BS, Rorres C, Chen Y, and Gansner ER. Using automatic clustering to produce high-level system organizations of source code In International Workshop on Program Comprehension, pages 45–52, 1998. [Google Scholar]
- [29].Martinez A and Du S. A model of the perception of facial expressions of emotion by humans: Research overview and perspectives. JMLR, 13(May):1589–1608, 2012. [PMC free article] [PubMed] [Google Scholar]
- [30].Martinez AM. Computational models of face perception. Current directions in psychological science, 26(3):263–269, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Mavadati SM, Mahoor MH, Bartlett K, Trinh P, and Cohn JF. DISFA: A spontaneous facial action intensity database. TAC, 4(2):151–160, 2013. [Google Scholar]
- [32].McDuff D, El Kaliouby R, Senechal T, Amr M, Cohn JF, and Picard R. Affectiva-MIT facial expression dataset (AM-FED): Naturalistic and spontaneous facial expressions collected in-the-wild CVPRW, 2013. [Google Scholar]
- [33].Melacci S and Belkin M. Laplacian support vector machines trained in the primal JMLR, 2011. [Google Scholar]
- [34].Otto C, Jain A, et al. Clustering millions of faces by identity TPAMI, 2017. [DOI] [PubMed] [Google Scholar]
- [35].Pantic M and Bartlett MS. Machine analysis of facial expressions. 2007.
- [36].Prest A, Schmid C, and Ferrari V. Weakly supervised learning of interactions between humans and objects. TPAMI, 34(3):601–614, 2012. [DOI] [PubMed] [Google Scholar]
- [37].Rudovic O, Pavlovic V, and Pantic M. Context-sensitive dynamic ordinal regression for intensity estimation of facial action units. TPAMI, 37(5):944–958, 2015. [DOI] [PubMed] [Google Scholar]
- [38].Sariyanidi E, Gunes H, and Cavallaro A. Automatic analysis of facial affect: A survey of registration, representation, and recognition. TPAMI, 37(6):1113–1133, 2015. [DOI] [PubMed] [Google Scholar]
- [39].Simonyan K and Zisserman A. Very deep convolutional networks for large-scale image recognition arXiv preprint arXiv:1409.1556, 2014. [Google Scholar]
- [40].Taheri S, Qiu Q, and Chellappa R. Structure-preserving sparse decomposition for facial expression analysis. TIP, 23(8):3590–3603, August 2014. [DOI] [PubMed] [Google Scholar]
- [41].Valstar MF, Almaev T, Girard JM, Mckeown G, Mehu M, Yin L, Pantic M, and Cohn JF. FERA 2015 - Second Facial Expression Recognition and Analysis Challenge In AFGR, 2015. [Google Scholar]
- [42].Vezhnevets A, Ferrari V, and Buhmann JM. Weakly supervised structured output learning for semantic segmentation In CVPR, 2012. [Google Scholar]
- [43].Von Luxburg U. A tutorial on spectral clustering. Statistics and computing, 17(4):395–416, 2007. [Google Scholar]
- [44].Wang Z, Li Y, Wang S, and Ji Q. Capturing global semantic relationships for facial action unit recognition In ICCV, 2013. [Google Scholar]
- [45].Wöllmer M, Kaiser M, Eyben F, Schuller B, and Rigoll G. LSTM-Modeling of continuous emotions in an audiovisual affect recognition framework. IVC, 31(2):153–163, 2013. [Google Scholar]
- [46].Yang S, Rudovic O, Pavlovic V, and Pantic M. Personalized modeling of facial action unit intensity In ISVC, pages 269–281, 2014. [Google Scholar]
- [47].Zen G, Sangineto E, Ricci E, and Sebe N. Unsupervised domain adaptation for personalized facial emotion recognition In ICMI, 2014. [Google Scholar]
- [48].Zeng J, Chu W-S, De la Torre F, Cohn JF, and Xiong Z. Confidence preserving machine for facial action unit detection In ICCV, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Zhang X, Yin L, Cohn JF, Canavan S, Reale M, Horowitz A, and Liu P. A high-resolution spontaneous 3d dynamic facial expression database In AFGR, 2013. [Google Scholar]
- [50].Zhao K, Chu W-S, De la Torre F, Cohn JF, and Zhang H. Joint patch and multi-label learning for facial action unit detection In CVPR, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Zhao K, Chu W-S, and Zhang H. Deep region and multi-label learning for facial action unit detection In CVPR, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Zhao X, Liang X, Liu L, Li T, Han Y, Vasconcelos N, and Yan S. Peak-piloted deep network for facial expression recognition In ECCV, 2016. [Google Scholar]
- [53].Zhong L, Liu Q, Yang P, Huang J, and Metaxas DN. Learning multiscale active facial patches for expression analysis. Transactions on Cybernetics, (99), 2014. [DOI] [PubMed] [Google Scholar]
- [54].Zhou Z-H. A brief introduction to weakly supervised learning National Science Review, 2017. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.