Prognostic models for spinal metastatic disease: evolution of methodologies, limitations, and future opportunities

Abstract

Advances in cancer biology and therapy have increased survival of metastatic disease patients and, in turn, the rates of metastatic epidural spinal cord compression (MESCC). Surgery can improve patient quality of life, but accurate estimation of postoperative survival is critical for appropriate patient selection, multidisciplinary management, and shared decision making. Survival estimation on the basis of clinician judgement alone has been shown to be inaccurate and unreliable. Numerous prognostic scoring systems have been developed to address this need but the inputs to these models, the modeling methodologies, and the model outputs have evolved significantly over time. Here we discuss the available scoring systems, existing limitations, and future opportunities.

Spinal metastatic disease is present in 70% of cancer patients at autopsy with historical estimations of metastatic epidural spinal cord compression (MESCC) occurring in 2.5–10% of cancer patients in the last years of life (1-3). As a reference, 14.1 million new cases of cancer were diagnosed in 2012 and 22 million new cases are predicted to be diagnosed in 2030 (4).

Improvements in cancer therapy have increased survival of patients with metastatic disease and, in turn, the rate of MESCC (5,6). Simultaneously, randomized controlled trials showing improved quality of life with surgery and radiotherapy versus radiotherapy alone for MESCC have increased enthusiasm for and rates of surgical intervention (7,8). Surgical intervention to address spinal instability or cord compression is often undertaken to reduce pain, address neurologic deficit, or stabilize the spine (5,9-11). However, determination of the appropriateness of surgery requires preoperative estimation of postoperative survival, as well as postoperative complications, ambulatory status, neurologic deficit, and patient-reported quality of life. This assessment can inform multidisciplinary management and shared decision making with patients and families to consider timing of surgery, degree of invasiveness, expected postoperative recovery and alternative options of radiotherapy, medical management, and palliative therapy.

Regrettably, survival prediction on the basis of clinician judgement alone has been shown to be inaccurate and unreliable (12-14). Given the critical decisions that hinge on accurate survival prediction in MESCC, numerous predictive models have been developed to complement clinician judgement (15-36). Some of these scoring systems include Tokuhashi [1990], Bauer [1995], modified Bauer, Tomita [2001], Katagiri [2005], Sioutos [2005], van der Linden [2005], Oswestry Spinal Risk Index [2013], Bollen [2014], revised Katagiri [2014], New England Spine Metastasis (NESMS) Score [2015], SORG Nomogram [2016], SORG Classic [2016], and SORG Machine Learning algorithms [2019]. This article will focus specifically on survival prediction models in MESCC, as these are the most mature. However, the recommendations provided here can be translated to additional outcomes of interest as highlighted above.

Fundamentally, the motivation for predictive models is grounded in approximating the true relationship (transformation) between data available in the present (input) and survival expected in the future (output) (Figure 1).

Figure 1.

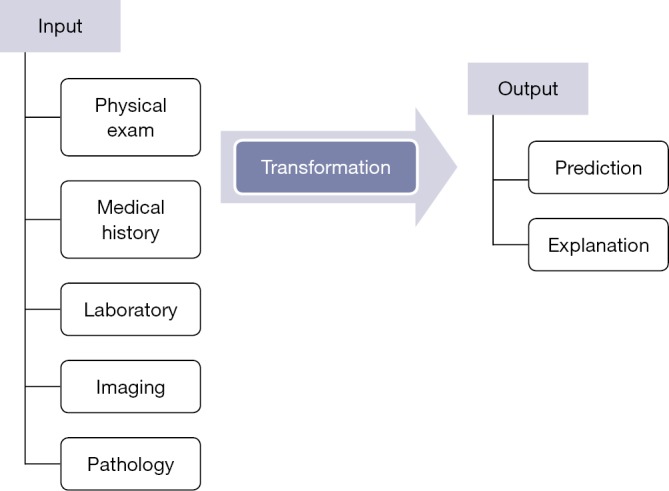
Pipeline of predictive modeling in MESCC. MESCC, metastatic epidural spinal cord compression.

Input

The inputs of models for MESCC consist of the factors gathered from the physical exam, medical history, laboratory tests, imaging, and pathology. Comparison of the predictive factors included by selected models is shown in Table 1. Other scoring systems and predictive factors include:

Table 1. Predictors included in each scoring system for spinal metastatic disease.

Score	Harrington	Tokuhashi	Bauer	Modified Bauer	Tomita	Katagiri	Sioutos	Revised Tokuhashi	van der Linden	ORI	Bollen	Revised Katagiri	NESMS	SORG Nomogram and Classic	SORG ML
Year	1986	1990	1995	–	2001	2005	2005	2005	2005	2013	2014	2014	2015	2016	2019
Demographics
Age														X
Body mass index															X
History and exam
Pain	X
Performance/functional status		X				X		X	X	X	X	X		X	X
Neurologic deficit	X						X								X
Previous systemic therapy						X						X		X	X
Ambulatory status													X
Severity of comorbid disease															X
Pathology
Primary tumor histology		X	X	X	X	X	X	X	X	X	X	X	X	X	X
Imaging
Visceral metastasis		X	X	X	X	X		X	X		X	X	X	X	X
Number of vertebral metastases		X					X	X						X	X
Brain metastasis						X					X	X		X	X
Bone metastasis		X	X	X	X	X		X				X	X
Spinal tumor location
Pathologic fracture/vertebral instability	X		X
Laboratory data
White blood cell												X		X
Hemoglobin/hematocrit												X		X	X
Platelet												X			X
Absolute lymphocyte															X
Absolute neutrophil															X
NLR															X
PLR															X
Albumin												X	X		X
Alkaline phosphatase															X
Creatinine															X
Bilirubin												X
C-reactive protein												X
Lactate dehydrogenase												X
INR															X

INR, international normalized ratio; NESMS, New England Spine Metastasis Score; NLR, absolute neutrophil to lymphocyte ratio; ORI, Oswestry Risk Index; PLR, platelet to lymphocyte ratio; SORG, Surgical Outcomes Research Group.

• ❖ North [2005]: surgical intervention greater than two spinal segments, recurrent disease after radiotherapy of operative site, primary tumor histology, cervical tumor location;

• ❖ Rades [2013]: primary tumor histology, bone metastasis, visceral metastasis, time from diagnosis to MESCC, ambulatory status before radiotherapy, timing of motor deficits relative to radiotherapy

The most common factors included in the prognostic models are primary tumor histology, metastatic tumor burden (e.g., visceral or brain metastasis, number of vertebral metastases), and performance/functional status (15-19,23,26,36). Considering the models developed in the last decade, additional factors included are previous systemic therapy and laboratory data (albumin, white blood cell, hemoglobin, neutrophil to lymphocyte ratio). Furthermore, the use of primary tumor histology in the models has changed dramatically. For example, early scoring systems stratified patients on the basis of the primary tumor location alone (e.g., lung versus breast). However, more recent systems such as the revised Katagiri not only include primary tumor location but also reflect advances in cancer biology with molecular characterization of the primary tumor (hormone dependent versus hormone independent breast cancer and molecularly targeted non-small cell lung cancer versus other lung cancers).

Advancements in cancer biology and novel biologic therapies (immunotherapy, targeted therapy) for specific expression profiles in primary tumor histologies would suggest inclusion of these important factors for accurate survival prediction. Other scoring systems developed for MESCC patients undergoing radiotherapy are more sophisticated in this manner. For example, previous studies have developed separate histology and age-specific MESCC radiotherapy scoring systems for prostate cancer (n=436), elderly prostate cancer (n=243), breast cancer (n=510), elderly breast cancer (n=218), non-small cell lung cancer (n=356), elderly lung cancer (n=201), colorectal cancer (n=121), elderly colorectal cancer (n=57), renal cell carcinoma (n=69), elderly renal cell carcinoma patients (n=71), myeloma (n=216), elderly myeloma (n=116), head-and-neck cancer (n=58), elderly patients with unknown primary (n=104), melanoma (n=27), gastric cancer (n=29), elderly gastric cancer (n=20), pancreatic cancer (n=15), esophageal cancer (n=27), hepatocellular carcinoma (n=8), salivary gland patients (n=9), and gynecologic malignancy (n=22) (37-52).

Most of the points above highlight the variety of the input data available for modeling. Spine surgeons should also be aware of the other 4 V’s (variety, volume, velocity, veracity), used most commonly with reference to “big data”, but also important for predictive modeling in general. Variety refers to the diversity of data included as highlighted above. Volume refers to sufficient quantities of patients to allow for reliable modeling as described below. Velocity is the expected rate of new data collection and availability for model derivation, update, and refinement. Veracity, perhaps the most important, defines the reliability of the input data and is a necessary pre-requisite for the trustworthiness of all subsequent steps in the modeling process. As the adage goes “garbage in, garbage out”, meaning that inaccurate or unreliable data will result in similarly unreliable models and outputs. Retrospective versus prospective study design, single-center versus multi-center, single-surgeon versus multiple, and one geography versus multiple all inform veracity of the data.

For the next step in evolution of inputs to MESCC prognostication models, there is a need for large multi-center prospective studies with granular, histology-specific data. The granular data should consist of the laboratory and biochemical prognostic factors identified previously but should also include information such as genomics, unstructured DICOM imaging, and passive and actively collected patient-reported outcomes (digital phenotyping). By integrating diverse data streams for focused populations, advancements in both basic cancer biology and computational methods can be applied for the benefit of MESCC patients.

Transformation and assessment methodology

Over time, the methodologies used for modeling the relationship between the preoperative MESCC patient data and the expected survival have evolved as well. Nearly all MESCC risk scores have used techniques such as proportional hazards regression or multivariable logistic regression. However, recent MESCC scoring systems (SORG) have explored more flexible modeling strategies such as stochastic gradient boosting, decision trees, random forests, kernel-based algorithms (Bayes point machine, support vector machines), neural networks, and elastic-net penalized logistic regression (23,32,36). The choice of fixed versus flexible modeling strategies depends on the tradeoff between bias and variance (53). In the context of MESCC, bias can be defined as the residual error in estimating the predicted survival on the basis of the available inputs. Variance can be defined as the generalizability of the model performance from the development population to future patients or external, independent populations. In general, a model can achieve nearly zero bias by employing the most flexible modeling strategy to perfectly memorize the relationship between the available inputs and outputs (observed survival). However, even if the model is 100% accurate on the population of patients used to develop the model, this does not guarantee that the model will be similarly accurate on future patients or external independent populations. In general, the bias (error on development population) decreases as the flexibility increases but the variance (error on future patients and independent populations) increases as the flexibility increases (53).

The purpose of modeling the transformation function between the available inputs in MESCC patients and the observed survival outcome is to achieve a balance between these competing forces. On the one hand, strategies such as multivariable logistic regression require and assume pre-specified relationships between the inputs and outputs. On the other hand, more flexible techniques such as convolutional neural networks act as universal functional approximators without requiring these pre-specified relationships. Determination of the appropriateness of one strategy over the other continues to be debated. Spine surgeons should be aware of both options and understand the strengths and limitations of each approach.

Steyerberg et al. previously described the (“ABCD”) principles that must be followed for validation of clinical prediction models (54). A and B refers to model calibration, C refers to model discrimination, and D refers to decision curve analysis (55). Calibration plots are constructed by plotting the models output (predicted) versus the observed events in the population of interest (Figure 2). “A” refers to calibration in the large and represents the intercept of the calibration plot. A perfect model would have calibration intercept =0. If the calibration intercept is greater than 0 and the predicted outcome is survival, the model tends to overestimate survival in the population relative to the observed outcome. The reverse occurs if the calibration intercept is less than zero. B refers to the calibration slope and represents the alignment of the predictor effects in the model relative to the observed outcome in the population. Perfect models have calibration slope =1.

Figure 2.

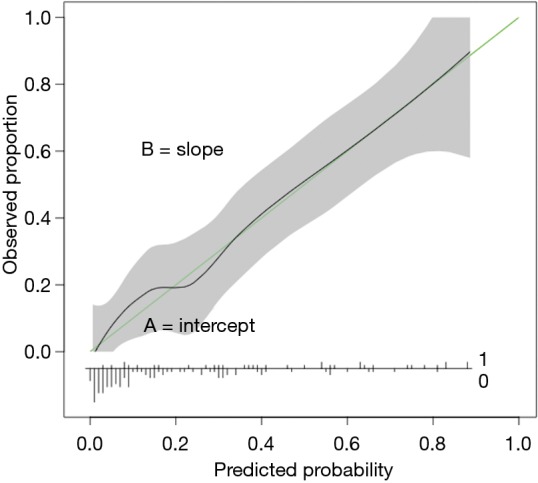
Example of a calibration plot.

C refers to the model discrimination and represents the area under the receiver operating curve (AUC) (Figure 3). Perfect models have c-statistic or AUC =1. This metric conveys the probability that the model will be able to distinguish two patients from one another with respect to the outcome. This metric does not capture how the predictions align with the observed outcome. For example, consider that a model assigns a survival probability of 0.02 to every patient who dies at 90 days and assigns a probability of 0.03 to every patient who survives at 90 days. The c-statistic of the model will be perfect, but the calibration will be poor because we would expect that for 100 patients that the model predicts a survival probability of 0.03, only 3 of those 100 patients should be alive at 90 days. In fact, the reality will be very different, as reflected by the poor calibration.

Figure 3.

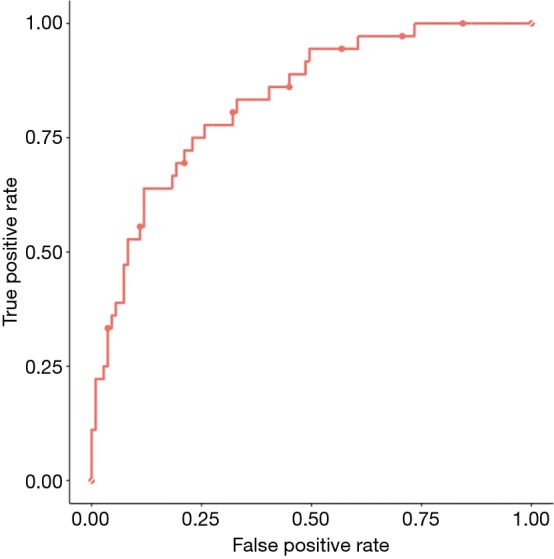
Example of a receiver operating curve.

Finally, D refers to decision curve analysis, which is critical because neither discrimination nor calibration take into account the impact of true positives and false positives generated by these models (55). Decision curves are based on the idea of net benefit, which takes into account the impact of potential benefit and potential harm from the use of predictive models. Net benefit can be calculated for the model in the derivation or validation population by assessing the number of true positives, the number of false positives, the relative weight of true positives to false positives and finally the total number of patients in the population. The relative weight is calculated from the threshold probability, which is the probability above or below which the clinician will change management. For example, if the considered management change is a less invasive operation for MESCC, a potential threshold probability might be a predicted probability of survival less than 40% at 90 days. Curves are constructed for all threshold probabilities and the algorithm’s performance is compared to the default strategies for changing management for no patients or for all patients (Figure 4). In addition, decision curves are useful for comparing various scoring systems in order to identify the model that maximizes net benefit.

Figure 4.

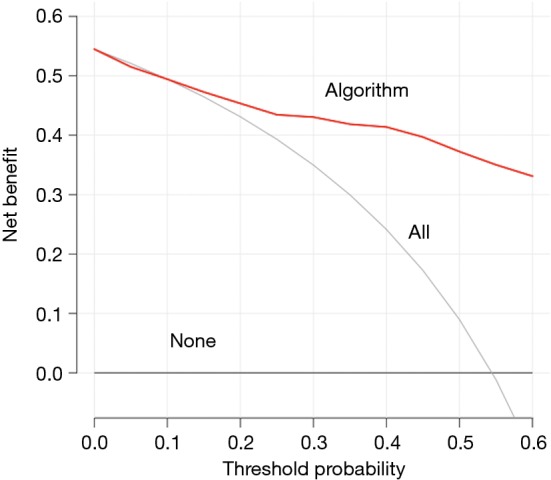
Example of decision curve analysis.

Ahmed et al. compared the SORG Classic, SORG nomogram, Tokuhashi, revised Tokuhashi, Tomita, Bauer, modified Bauer, Katagiri, and van der Linden scoring systems in 176 MESCC patients who underwent surgical resection at a single institution and found that the SORG nomogram had the highest AUC for 30-day (0.81) and 90-day (0.70) mortality (26). The original Tokuhashi score was best for 365-day survival (AUC =0.78) (26). A recent study comparing the Tokuhashi, revised Tokuhashi, Tomita, Bauer, van der Linden, Bartels, Oswestry Spinal Risk index, and Bollen scores in a prospective North American multi-center registry of 142 surgically treated MESCC patients found that the best c-statistic was Bartels (0.68) (56).

The same study was the first full validation of those models on both discrimination and calibration in accordance with the Transparent Reporting of Multivariable Prediction Model for Individual Prognosis or Diagnosis (TRIPOD) guidelines (57). The best performing model on discrimination, Bartels, had a calibration slope of 0.45 and calibration plots of all scoring systems showed fair to poor calibration overall. Recent systems such as the SORG Machine Learning algorithms have included full assessment of the validation metrics advocated by Steyerberg et al. by assessing discrimination, calibration, and decision curve analysis. Future studies in MESCC that seek to develop or compare scoring systems should consider assessment of these important metrics, especially calibration and decision curve analysis as these represent the expected utility of these scoring systems in practice.

Output and model presentation

MESCC models can be presented as risk score tables, nomograms, and digital applications. Most of the available risk scores offer predictions in terms of an aggregate score that can be used against pre-specified categories defined in the derivation cohort. For example, application of the revised Tokuhashi score results in an aggregate score between 0 and 15. If patients have scores 0–8, they are predicted to survive less than 6 months, if they have scores 9–11, 6 months or more, if scores 12–15, 1 year or more. Drawbacks of risk scores are lack of predicted probabilities at specific time points critical for preoperative decision making. The SORG nomogram can be printed and used to compute a summary score based on the patient characteristics. This summary score is then scaled to probabilities of survival at specific time points (30 days, 90 days, 1 year). Alternatively, the SORG Machine Learning algorithms are available through an open-access web application for smartphones, tablets, or desktop computers and currently output probabilities and explanations for predicted survival at 90 days and 1 year after surgery (36).

Ideally, these scoring systems would be integrated into electronic health records. Such integration could allow the algorithms to automatically collect the relevant input data from the patient medical record. Subsequently, surgeons could access the outputs of these models when formulating the assessment and plan. The output would consist of both survival predictions and explanations for these predictions. With the model explanations, surgeons would have increased transparency into the factors used by the algorithms to make the predictions. Progress in machine learning methodologies allow for the use of flexible modeling strategies while maintaining the transparency required for clinicians to double-check the predictions of such algorithms against their own clinical expertise.

Final thoughts

Advances in basic biology and computational methodologies have created a host of opportunities for improving the care of MESCC patients; scoring systems represent an important subset of these opportunities. As highlighted in this article, spine surgeons should gain more familiarity with the evolution of existing scoring systems and the unique strengths and limitations in the pipeline of predictive analytics ranging from input to transformation to output. Future directions for the improvement of existing algorithms include several opportunities at each step in the model development pipeline; for example, inputs may be improved through the inclusion of more granular factors, such as tumor expression profiles, and assessment of emerging areas, such as unstructured data. Integration of algorithms into modern electronic health records may further facilitate the decision-making process in the future. Though clinician judgement alone may not be sufficient for prognostication in MESCC, clinician judgement is critical for maximizing the potential of more sophisticated and flexible modeling techniques. Previous studies have shown that patients benefit more from a combination of human (natural) intelligence and artificial intelligence rather than either alone (58). Finally, learnings from continued improvements in survival prediction models can subsequently be translated to developing models for complications, ambulatory status, neurologic deficit, and patient-reported outcomes.