ESTIMATING UNCERTAINTY OF TARGET VALUES FOR DEQAS SERUM MATERIALS.

Abstract

The External Quality Assessment (EQA) scheme for vitamin D metabolites (DEQAS) distributes human serum samples to laboratories across the world to assess their performance in measuring serum total 25-hydroxyvitamin D [25(OH)D], i.e. the sum of the concentrations of serum 25(OH)D₂ and 25(OH)D₃. In 2013 DEQAS, in collaboration with the Vitamin D Standardization Program (VDSP), became an accuracy-based EQAS when the National Institute for Standards and Technology (NIST) began assigning 25(OH)D target values to DEQAS serum samples using their Joint Committee for Traceability in Laboratory Medicine (JCTLM) approved reference measurement procedure (RMP). Historically, NIST has performed 4 determinations of 25-OHD2 and 25-OHD3 on each sample and used the mean values to calculate a single ‘target value’ for Total 25-OHD against which performance was judged. By definition the target values cannot be exact and each is associated with a level of uncertainty. The total uncertainty (U_NIST) has two components, one from the 25(OH)D₂, and 25(OH)D₃ measurements and the other associated with the calibration procedure. The total combined uncertainty is calculated by adding up these uncertainties. In future, uncertainties will be attached to the target value in each DEQAS serum sample, starting with the next distribution cycle in 2019. Confidence intervals obtained using these uncertainties will allow DEQAS participants to determine if their result agrees with the NIST assigned target value. Furthermore, if the value falls within the confidence interval the laboratory’s assay would be regarded as traceable, i.e. standardized, to the NIST RMP.

Introduction

The Vitamin D External Quality Assessment Scheme (DEQAS) has been distributing human serum samples to laboratories across the world to assess their performance in measuring 25-Hydroxyvitamin D [25(OH)D]. Recently in 2013, DEQAS initiated an accuracy-based scheme with target values for serum samples assigned by the NIST Reference Measurement Procedure for 25(OH)D₂ and 25(OH)D₃. Historically, NIST performs 4 determinations per sample following calibration using SRM 972[1]. The assigned or “target” value to each sample is calculated as the sample mean of the 4 determinations. Due to random sampling, the calculated target values cannot be exact and each is associated with a level of uncertainty. The total uncertainty in measurement has two components, one derived from the within-lab measurement error and the other from the procedure used to calibrate assay standards. In future, uncertainties will be attached to the target value in each DEQAS serum sample, starting with the next distribution cycle in 2019. Confidence intervals obtained using these uncertainties will allow DEQAS participants to determine if their result agrees with the NIST assigned target value. Furthermore, if the value falls within the confidence interval the laboratory’s assay would be regarded as traceable, i.e. standardized, to the NIST RMP.

This paper describes the theoretical background behind the estimation of this uncertainty and it additionally provides an example to illustrate the calculation. An appendix presents a layman’s introduction to confidence interval estimation, which is the basis for reporting target value uncertainty.

Methods

When sample sizes are moderately large, say over 25–40 values, we usually compute 95% confidence intervals for the true mean (i.e. target value for 25(OH)D₂ or 25(OH)D₃) following four basic steps:

1. Compute the Mean value

2. Compute the standard deviation, SD

3. Compute the standard error, SE (I am calling this standard uncertainty to follow NIST document naming convention[2], as $SE=\frac{SD}{\sqrt{N}}$, with N the sample size

4. 95% confidence interval is: Mean ± 2*SE. The number 2 should really be 1.96 (It is known as the 97.5^th percentile of the standard normal distribution).

When sample sizes are not large enough, then the 97.5^th percentile is calculated using the so-called t-distribution, which requires calculating degrees of freedom (Here we note that when the degrees of freedom are large, say 25–40 or larger, then this percentile will be about 1.96).

DEQAS is mainly concerned with the estimation of total 25(OH)D, defined as the sum of 25(OH)D₂ and 25(OH)D₃. The four steps listed above for the estimation of the 95% confidence interval for the total 25(OH)D are:

1. Compute the Total 25(OH)D as 25(OH)D₂ + 25(OH)D₃;

2. Compute the standard deviation for each 25(OH)D₂ and 25(OH)D₃. Call these values sd₂ and sd₃.

3. Compute the standard error to the estimation of total 25(OH)D, as $SE=\sqrt{\frac{s{d}_2^2+s{d}_3^2}{n}}$.

4. The 95% confidence interval is computed as before if n, the number of determinations, is large.

The problem at hand, estimation of total 25(OH)D, involves the additional technical difficulties,

1. Small sample size, since n = 4

2. The standard deviation for the estimation of 25(OH)D₂ and 25(OH)D₃ are not equal

3. The error in calibration has to be accounted for.

The following sections of this paper address these technical issues, including the estimation of standard, combined, and expanded uncertainty as described in the NIST guidelines for evaluating and expressing uncertainty[2].

Standard Uncertainty Estimation

Let x₁, x₂, …,x_n represent measured values of the “true” level of 25(OH)D₂ for a DEQAS sample in a specific distribution. Similarly, let y₁, y₂, …,y_n be the corresponding values for the “true” level of 25(OH)D₃ for the same sample. The assigned values for the true levels of 25(OH)D₂ and 25(OH)D₃ are then given by

$$D_2=\frac{x_1+x_2+\cdots +x_n}{n}\Leftarrow Assignedvaluetotrue25(OH)D_2$$

$$D_3=\frac{y_1+y_2+\cdots +y_n}{n}\Leftarrow Assignedvaluetotrue25(OH)D_3$$

The within laboratory uncertainty for the estimation of the true values of 25(OH)D₂ and 25(OH)D₃, is the Standard Error of the Mean,

$$u_2=\frac{s{d}_2}{\sqrt{n}}\Leftarrow StandardUncertaintyofthe\text{ 25 }(OH)D_{2}Estimator$$

$$u_3=\frac{s{d}_3}{\sqrt{n}}\Leftarrow StandardUncertaintyofthe\text{ 25 }(OH)D_{3}Estimator$$

Where

$$s{d}_2=\sqrt{\frac{{\left(x_1-D_2\right)}^2+{\left(x_2-D_2\right)}^2+\cdots +{\left(x_n-D_2\right)}^2}{n-1}}\Leftarrow StandardDeviation$$

$$s{d}_3=\sqrt{\frac{{\left(y_1-D_3\right)}^2+{\left(y_2-D_3\right)}^2+\cdots +{\left(y_n-D_3\right)}^2}{n-1}}\Leftarrow StandardDeviation$$

Reference Materials

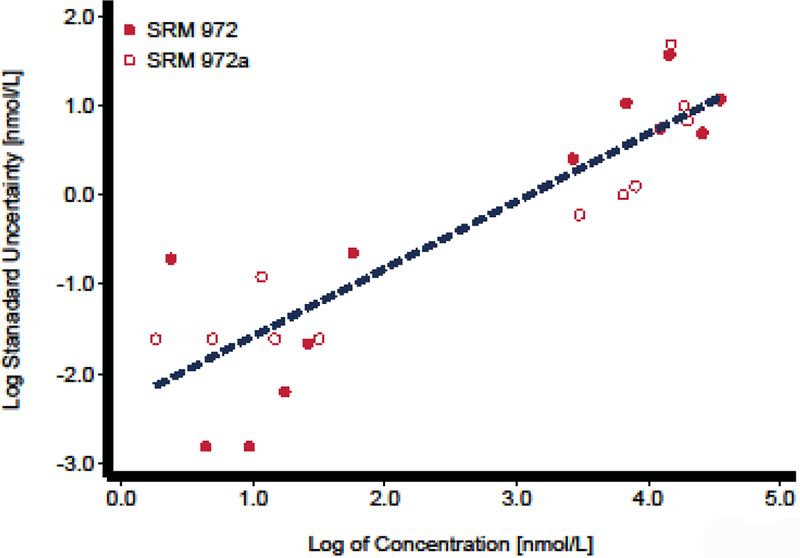
In order to account for all the uncertainty associated with the value assignment, we need to incorporate the uncertainty derived from the calibration process. NIST has carried out measurements of the reference materials SRM 972 and SRM 972a at the various levels available.

The levels of these materials and the estimated errors are reported by NIST[3, 4] and listed in Tables 1. These values, depicted in Figure 1, were used to fit a linear regression equation relating the logarithm of the error, ln (u(D)), and the logarithm of the SRM assigned value, D, ln (D). Some of the key ideas included in this manuscript, along with the regression equation generated have been reported as a unpublished white paper[5] to investigators participating in the Vitamin D Standardization Program (VDSP). Precisely, the mathematical model relating vitamin D concentration with error is given by:

$$\text{ln}[u(D)]=-3.08+0.77\times \text{ln}(D)$$

or equivalently

$$u(D)=\text{exp}[-3.08+0.77\times \text{ln}(D)]$$

Table 1:

Certified and Reference Concentration Values for Vitamin D Metabolites in Serum: SRM 972 and SRM 972a

Certified Concentration Values
	SRM 972		SRM 972a
	ng/mL	nmol/L	ng/mL	nmol/L
Level 1
25-Hydroxyvitamin D2	—	—	—	—
25-Hydroxyvitamin D3	23.9 ±0.8	59.6 ±2.1	28.8 ± 1.10	71.8 ±2.7
3-epi-25-Hydroxyvitamin D3	—	—	1.81 ± 0.10	4.5 ± 0.2
Level 2
25-Hydroxyvitamin D2	1.71 ±0.08	4.14 ± 0.19	0.81 ±0.06	2.0 ±0.2
25-Hydroxyvitamin D3	12.3 ± 0.6	30.8 ± 1.5	18.1 ±0.4	45.1 ±1.0
3-epi-25-Hydroxyvitamin D3	—	—	1.28 ± 0.09	3.2 ± 0.2
Level 3
25-Hydroxyvitamin D2	26.4 ±2.0	64.1 ±4.8	13.3 ±0.3	32.3 ±0.8
25-Hydroxyvitamin D3	18.5 ±1.1	46.2 ±2.8	19.8 ±0.4	49.5 ± 1.1
3-epi-25-Hydroxyvitamin D3	—	—	—	—
Level 4
25-Hydroxyvitamin D2	2.40 ± 0.21	5.81 ± 0.52	—	—
25-Hydroxyvitamin D3	33.0 ±0.8	82.3 ±2.0	29.4 ±0.9	73.4 ± 2.3
3-epi-25-Hydroxyvitamin D3	37.7 ± 1.2	94.1 ± 2.9	26.0 ±2.2	64.8 ± 5.4
Reference Concentration Values
	SRM 972		SRM 972a
	ng/mL	nmol/L	ng/mL	nmol/L
Level 1
25-Hydroxyvitamin D2	0.60 ±0.20	1.46 ±0.49	0.54 ±0.06	1.3 ± 0.2
25-Hydroxyvitamin D3	—	—	—	—
3-epi-25-Hydroxyvitamin D3	1.39 ± 0.04	3.46 ± 0.11	—	—
Level 3
25-Hydroxyvitamin D2	—	—	—	—
25-Hydroxyvitamin D3	—	—	—	—
3-epi-25-Hydroxyvitamin D3	0.76 ±0.02	1.19 ± 0.06	1.17 ± 0.14	2.9 ± 0.4
Level 4
25-Hydroxyvitamin D2	—	—	0.55 ± 0.10	1.3 ± 0.2
25-Hydroxyvitamin D3	—	—	—	—
3-epi-25-Hydroxyvitamin D3	1.06 ± 0.03	2.65 ± 0.06	—	—

Fig. 1.

Uncertainty Contribution from Calibration. The amount of 25(OH)D3, 25(OH)D2, and 3-Epid-25(OH)D3 concentration in NIST Standard Reference materials (SRM) 972 and 972a and estimated standard uncertainty.

Combined Uncertainty

The combined uncertainty for each sample, incorporating both the measurement and calibration errors is then estimated by:

$$u_{2c}=\sqrt{u_2^2+u^2\left(D_2\right)}$$

$$u_{3c}=\sqrt{u_3^2+u^2\left(D_3\right)}$$

A 95% confidence interval for the true levels of 25(OH)D₂ and 25(OH)D₃ in this sample can be calculated as

$$D_2\pm t_{v_{2,0.975}}\times u_{2c}\Leftarrow 25(OH)D_2$$

$$D_3\pm t_{v_{3,0.975}}\times u_{3c}\Leftarrow 25(OH)D_3$$

where the degrees of freedom are calculated according the Welch-Satterthwaite formula[6].

$$v_2=\frac{{\left[u_2^2+u^2\left(D_2\right)\right]}^2}{\frac{{\left[u_2^2\right]}^2}{n-1}}$$

$$v_3=\frac{{\left[u_3^2+u^2\left(D_3\right)\right]}^2}{\frac{{\left[u_3^2\right]}^2}{n-1}}$$

The expressions for degrees of freedom, above, can be obtained directly from the Welch-Satterthwaite formulae assuming infinity degrees of freedom for the variance component attributable to calibration. An alternative derivation was reported by Maity and Sherman[7], where they calculate the degrees of freedom for the two sample t-test when one of the two variances is known.

Total 25(OH)D is calculated as the sum of 25(OH)D₂ and 25(OH)D₃. That is

$$Total 25(OH)D=D_2+D_3$$

The variance and corresponding standard uncertainty of the estimator attributable to the within-laboratory dispersion are calculated under the assumption that the concentration of 25(OH)D₂ and 25(OH)D₃ are uncorrelated in the context of DEQAS samples. The rationale behind this supposition rests on the following:

1. Patients with vitamin D deficiency are likely to present an association of low concentration of 25(OH)D₃ and high concentration of 25(OH)D₂ owing to deliberate supplementation with the latter;

2. Patients without vitamin D supplementation are likely to present a wide range of concentration of 25(OH)D₂, regardless of their concentration of 25(OH)D₃;

3. The DEQAS samples are not sera from single patients, but result from mixing sera to achieve particular concentration targets.

$$VarianceTotalD=u_2^2+u_3^2$$

$$StandardUnceartainty=\sqrt{u_2^2+u_3^2}$$

whereas the combined (within-laboratory dispersion and uncertainty attributable to calibration) variance and standard deviation are given by

$$VarianceTotal{D}_c=u_2^2+u_3^2+u^2[TotalD]$$

$$u_c=CombinedStandardUncertaint{y}_c=\sqrt{u_2^2+u_3^2+u^{\text{2}}[TotalD]}$$

The corresponding degrees of freedom, assuming the component of uncertainty due to calibration has infinity degrees of freedom, is obtained using the Welch-Satterthwaite formula[6, 8], as follows:

$$v=\frac{{\left[u_2^2+u_3^2+u^2[TotalD]\right]}^2}{\frac{{\left[u_2^2\right]}^2}{n-1}+\frac{{\left[u_3^2\right]}^2}{n-1}}$$

Where

$$u[TotalD]=\text{exp}[-3.08+0.77\times ln(TotalD)]$$ Eq. 1

A 95% confidence interval the estimated total 25(OH)D is computed as

$$TotalD\pm t_{v,0.975}\times CombinedStandardUncertaint{y}_c$$

Expanded Uncertainty

Following the recommendations described in the NIST guidelines for evaluating and expressing uncertainty, we define expanded uncertainty, U, as

$$U=k\times u_c$$

where u_c represents the combined uncertainty and k is a coverage factor determined by the level of confidence desired by the confidence interval defined by

$$y-k\times u_c\le Y\le y+k\times u_c$$

Here Y stands for the measurand of interest, i.e., Total 25(OH)D, and y is an estimate of the measurand, based on the n=4 determinations. Using the notation from the previous section

$$k\text{ = }{t}_{v,0.975}$$

For instance, when ν, the degrees of freedom, is a large number then k = 1.96 ≈ 2.0.

Results

Table 2, below, depicts the 4 repeated measures of 25(OH)D₂ and 25(OH)D₃ for each of the 5 DEQAS samples corresponding to the 646.02-13-0.15 distribution, along with the assigned NIST values and standard uncertainty estimates. Table 3 shows the estimated combined uncertainty, degrees of freedom from the Welch-Satterthwaite formula, as well as the lower/upper 95% confidence limits for the true value of 25(OH)D₂, 25(OH)D₃, and their sum (Total 25(OH)D).

Table 2:

NIST assigned values for 646.02-13-0.15

Serum 25-Hydroxyvitamin D2 [nmol/L]
	Repeat				Assigned Value (D2)	Standard Deviation (sd2)	Standard Uncertainty (u2)
DEQAS ID	1	2	3	4
421	0.96	0.94	0.87	1.04	0.952	0.071	0.036
422	1.68	1.71	1.63	1.71	1.681	0.035	0.017
423	1.04	0.94	1.01	0.96	0.989	0.045	0.023
424	1.01	1.01	1.01	0.94	0.995	0.037	0.019
425	1.01	0.91	0.96	0.91	0.952	0.047	0.024
Serum 25-Hydroxyvitamin D3 [nmol/L]
	Repeat				Assigned Value (D3)	Standard Deviation (sd3)	Standard Uncertainty (u3)
DEQAS ID	1	2	3	4
421	57.56	56.88	57.05	57.61	57.277	0.368	0.184
422	36.86	36.58	36.61	36.05	36.528	0.342	0.171
423	84.35	84.52	83.38	85.70	84.486	0.950	0.475
424	46.34	45.52	46.36	46.28	46.126	0.404	0.202
425	46.03	46.21	46.13	46.06	46.107	0.081	0.040

Table 3:

NIST assigned values for 646.02-13-0.15 and estimated uncertainty

Serum 25-Hydroxyvitamin D2 [nmol/L]
DEQAS ID	Assigned Value	Combined Uncertainty	Degrees Of Freedom	Lower Limit 95% CI	Upper Limit 95% CI
421	0.95	0.06	19.32	0.83	1.07
422	1.68	0.07	805.23	1.54	1.82
423	0.99	0.05	77.32	0.89	1.09
424	0.99	0.05	151.14	0.90	1.09
425	0.95	0.05	60.59	0.85	1.05
Serum 25-Hydroxyvitamin D3 [nmol/L]
DEQAS ID	Assigned Value	Combined Uncertainty	Degrees Of Freedom	Lower Limit 95% CI	Upper Limit 95% CI
421	57.28	1.05	3227.62	55.21	59.34
422	36.53	0.75	1125.43	35.05	38.01
423	84.49	1.48	280.75	81.58	87.40
424	46.13	0.90	1184.35	44.36	47.89
425	46.11	0.88	681706.75	44.38	47.83
Serum Total 25-Hydroxyvitamin D [nmol/L]
DEQAS ID	Assigned Value	Combined Uncertainty	Degrees Of Freedom	Lower Limit 95% CI	Upper Limit 95% CI
421	58.23	1.14	3393.27	56.00	60.45
422	38.21	0.87	1284.93	36.51	39.91
423	85.48	1.57	290.06	82.38	88.57
424	47.12	1.00	1261.64	45.16	49.08
425	47.06	0.91	649327.13	45.27	48.85

Example

Let us consider sample 421 from Table 2. The serum sample was processed by the NIST lab yielding the following results:

$$25(OH)D_2=0.96,0.94,0.87,1.04nmol/L$$

$$25(OH)D_3=57.56,56.88,57.05,57.61nmol/L$$

The corresponding standard uncertainties are then

$$D_2=\frac{0.96+0.94+0.87+1.04}{4}=0.952nmol/L$$

$$D_3=\frac{57.56+56.88+57.05+57.61}{4}=57.277nmol/L$$

The uncertainty due to within laboratory dispersions are then

$$s{d}_2=0.07\Rightarrow u_2=\frac{0.07}{\sqrt{4}}=0.036$$

$$s{d}_3=0.37\Rightarrow u_3=\frac{0.37}{\sqrt{4}}=0.184$$

The assigned value to Total 25(OH)D is

$$D_2+D_3=0.952+57.277=58.299nmol/L$$

The uncertainty attributable to within laboratory dispersion is

$$u_2^2+u_3^2={(0.036)}^2+{(0.184)}^2=0.035152$$

From Eq. 1 above, the contribution of calibration to the total uncertainty estimate of the assigned value is

$$u[TotalD]=\text{exp}[-3.08+0.77\times ln(\mathrm{0.58.229})]=1.0508247$$

$$u^2[TotalD]={(1.0508386)}^2=1.1042618$$

$$\begin{gathered} VarianceTotal{D}_c=u_2^2+u_3^2+u^2[TotalD] \\ ={(0.036)}^2+{(0.184)}^2+{(1.0508247)}^2 \\ =1.1393846 \end{gathered}$$

$$\begin{gathered} CombinedstandardUncertaint{y}_c=\sqrt{u_2^2+u_3^2+u^2[TotalD]}=\sqrt{1.1393846} \\ =1.0674196 \end{gathered}$$

The degrees of freedom, ν, are calculated using the Welch-Satterthwaite formula[6, 8].

$$\begin{gathered} degressoffreedom=v=\frac{{\left[u_2^2+u_3^2+u^2[TotalD]\right]}^2}{\frac{{\left[u_2^2\right]}^2}{3}+\frac{{\left[u_3^2\right]}^2}{3}} \\ =\frac{{\left[{(0.036)}^2+{(0.184)}^2+{(1.0508247)}^2\right]}^2}{\frac{{\left[{(0.036)}^2\right]}^2}{3}+\frac{{\left[{(0.184)}^2\right]}^2}{3}} \\ =3392.7721 \end{gathered}$$

The 97.5^th percentile of the t distribution with ν = 3393.77 degrees of freedom is 1.96. Thus, the 95% confidence interval for the true value of the total 25(OH)D level is

$$58.23\pm 1.96\times 1.0674196\Rightarrow [56.00,60.45]$$

The expanded uncertainty for 95% confidence is then

$$U=k\times u_c=1.96\times 1.0674196$$

Results for the 5 human serum samples corresponding to distribution 646.02-13-0.15 are presented in Table 3.

Summary

The purpose of this paper is to demonstrate how the NIST assigned values for total 25-Hydroxyvitamin D are obtained, as well as how the various contributors to the uncertainty of the assigned value are calculated and combined. The assigned value is computed as the average of the 4 determinations performed by NIST. The components of uncertainty include, the standard uncertainty, as well as the uncertainty due to calibration, which sum results in the total or combined uncertainty. The expanded uncertainty is also calculated following the recommendation of the NIST guidelines for evaluating and expressing uncertainties, that is the combined uncertainty is multiplied by a factor, k, determined by the level of a confidence interval for the true concentration of total 25-Hydroxyvitamin D. An example is provided to illustrate the calculations. A confidence interval with a desired level of confidence could be used to determine whether a lab measurement is standardized to the NIST reference measurement procedure.

Highlights:

• Estimation of Total 25-Hydroxyvitamin D target values require estimation of uncertainty around them

• Total combined uncertainty of target values can be decomposed into assay and calibration components

• Total uncertainty and confidence intervals of target values can be used to determine whether a laboratory assay is traceable to the NIST RPM

• Total uncertainty and confidence intervals of target values used by DEQAS will be provided to laboratories participating in DEQAS, which could inform their performance and enhance 25(OH)D measurement.