h-Type Membrane Current Shapes the Local Field Potential from Populations of Pyramidal Neurons

Abstract

In cortex, the local field potential (LFP) is thought to mainly stem from correlated synaptic input to populations of geometrically aligned neurons. Computer models of single cortical pyramidal neurons showed that subthreshold voltage-dependent membrane conductances can also shape the LFP signal, in particular the hyperpolarization-activated cation current (I_h; h-type). This ion channel is prominent in various types of pyramidal neurons, typically showing an increasing density gradient along the apical dendrites. Here, we investigate how I_h affects the LFP generated by a model of a population of cortical pyramidal neurons. We find that the LFP from populations of neurons that receive uncorrelated synaptic input can be well predicted by the LFP from single neurons. In this case, when input impinges on the distal dendrites, where most h-type channels are located, a strong resonance in the LFP was measured near the soma, whereas the opposite configuration does not reveal an I_h contribution to the LFP. Introducing correlations in the synaptic inputs to the pyramidal cells strongly amplifies the LFP, while maintaining the differential effects of I_h for distal dendritic versus perisomatic input. Previous theoretical work showed that input correlations do not amplify LFP power when neurons receive synaptic input uniformly across the cell. We find that this crucially depends on the membrane conductance distribution: the asymmetric distribution of I_h results in a strong amplification of the LFP when synaptic inputs to the cell population are correlated. In conclusion, we find that the h-type current is particularly suited to shape the LFP signal in cortical populations.

SIGNIFICANCE STATEMENT The local field potential (LFP), the low-frequency part of extracellular potentials recorded in neural tissue, is often used for probing neural circuit activity. While the cortical LFP is thought to mainly reflect synaptic inputs onto pyramidal neurons, little is known about the role of subthreshold active conductances in shaping the LFP. By means of biophysical modeling we obtain a comprehensive, qualitative understanding of how LFPs generated by populations of cortical pyramidal neurons depend on active subthreshold currents, and identify the key importance of the h-type channel. Our results show that LFPs can give information about the active properties of neurons and that preferred frequencies in the LFP can result from those cellular properties instead of, for example, network dynamics.

Introduction

The local field potential (LFP) is the low-frequency part (below ∼500 Hz) of the extracellular potentials recorded in the brain. The LFP signal in the mammalian cortex reflects the activity of thousands of neurons (Buzsáki et al., 2012; Einevoll et al., 2013) and is commonly used to study the network dynamics underlying e.g., sensory processing, motor planning, attention, memory, and perception; (Roux et al., 2006; Szymanski et al., 2011; Liebe et al., 2012). The LFP signal has further increased in importance in recent decades because of the development of high-density silicon-based microelectrodes, allowing simultaneous recording of the LFP at thousands of positions spanning entire brain regions (Normann et al., 1999; Buzsáki, 2004; Frey et al., 2009; Lambacher et al., 2011). Furthermore, the LFP shows promise for steering neuroprosthetic devices as it is easier and more stably recorded in chronic settings than single-unit spiking activity (Andersen et al., 2004; Markowitz et al., 2011; Jackson and Hall, 2017).

The biophysical origins of the LFP are the transmembrane currents of neurons in the vicinity of the recording electrode (Nunez and Srinivasan, 2006). The extracellular potentials induced by the transmembrane currents can be calculated using the well established volume conductor theory (Rall and Shepherd, 1968; Holt and Koch, 1999; Nunez and Srinivasan, 2006; Lindén et al., 2013). The main contribution to the cortical LFP is thought to stem from synaptic inputs and the ensuing return currents (Mitzdorf, 1985; Pettersen et al., 2008; Einevoll et al., 2013; Haider et al., 2016). However, cortical neurons are known to express many voltage-dependent (or active) currents (Migliore and Shepherd, 2002; Lai and Jan, 2006; Major et al., 2013) that may contribute to the LFP, either by subthreshold processing of synaptic inputs or through somatic and dendritic spikes. Reimann et al. (2013) recently studied the combined effects of all active currents on the LFP in a large cortical population model and found substantial effects of these currents. However, their approach did not allow for an easy separation between the effects of spiking currents and the effect of subthreshold active currents; hence, it is still debated to what extent such subthreshold active currents contribute to the LFP. We recently investigated this using computational models of single neurons (Ness et al., 2016) and found that subthreshold active currents can strongly amplify or dampen the lowest frequencies of the LFP power spectrum, in the latter case leading to a resonance in the LFP. We identified the key importance of the hyperpolarization-activated cation current (I_h), and, in particular, we observed that for synaptic input that selectively targeted the apical dendrites of cortical layer 5 pyramidal cells, I_h caused a strong resonance peak in the LFP power spectrum. However, how the observed effect of I_h on the LFP would transfer from a single cell to a neural population remained an open question.

Using a modeling approach, we here investigate the effect of subthreshold active conductances on the LFP from cortical neural populations. The populations consisted of layer 5 pyramidal cells, as these numerous, large, and geometrically aligned cells are thought to be a main contributor to the cortical LFP (Einevoll et al., 2013; Hagen et al., 2016). We demonstrated the key importance of I_h in shaping the LFP from pyramidal cell populations and found that it does this in two fundamentally different ways, depending on the synaptic input. First, for synaptic input to the distal apical dendrites of the neurons, we observed a strong dampening of the lowest LFP frequencies, leading to a resonance in the LFP power spectrum. It has been argued that the cortical LFP is dominated by populations of neurons receiving correlated synaptic input (Lindén et al., 2011; Łęski et al., 2013), and we found that such correlations increased the expression of the I_h-induced resonance. Second, for correlated synaptic input that was uniformly distributed on the cells, we instead observed a novel and strong low-frequency amplification that could increase the power of the LFP by up to two orders of magnitude. Hence, the h-type current with its asymmetric distribution and its nature to generate resonances is particularly suited to shape the LFP in cortical populations.

Materials and Methods

Neuron models.

Simulations for Figures 1, 2, 3, and 8 were performed using a model of a cortical layer 5 pyramidal cell from Hay et al. (2011). The cell model is available from ModelDB (Hines et al., 2004; Hay et al., 2011, parameters from their Table 3, accession #139653, “cell #1,”). This model was fitted to experimental data by multiobjective optimization with an evolutionary algorithm and has 10 active ionic conductances. This model can exhibit both somatic and dendritic spikes; however, note that in this study we focus only on the subthreshold regime. For the model labeled “passive,” all active conductances were removed from the model. For the model labeled “passive + I_h,” all active conductances, save for I_h, were removed. For the model labeled “passive + frozen I_h,” the dynamics of the remaining I_h conductance was also removed by keeping the gating variable of the h-current constant, yielding an additional passive conductance. The leak reversal potential of each cell compartment was set such that the resting potential of the cell was uniform at −70 mV (Carnevale and Hines, 2006; Ness et al., 2016) as this simplifies the interpretation of the results. Note that this was not done for the model labeled “BBP with complex synapses” used in Figure 9, without the overall conclusions being affected.

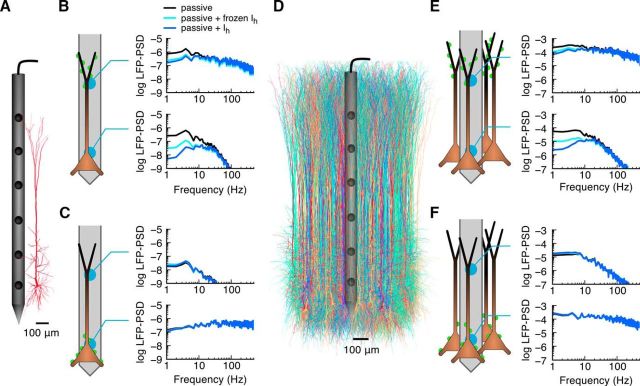
Figure 1.

Distal synaptic input to pyramidal cells with h-type conductances results in resonances in single-cell and population LFPs. A, Illustration of reconstructed cortical pyramidal cell and recording electrode. B, C, For a single cell, the LFP power spectral density (LFP-PSD) is shown in the somatic and apical regions of the cell for synaptic input that arrives at the distal tuft or the basal dendrite respectively. Different lines correspond to different versions of the model: a model with one active h-type conductance (blue curves), a passive model where the increased membrane conductance from the h-type channel is included, but with the dynamics removed (cyan curves), and a passive model that only has the passive parameters of the original cell model (black curves). D, Illustration of a population of 10,000 cells, centered around a recording electrode. E, F, Same as B and C, but for the population of cells. The LFP-PSDs are shown in log₁₀ scale with units of μV²/Hz.

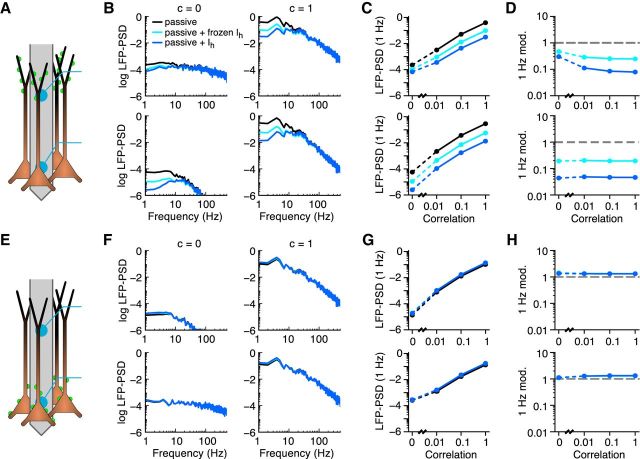
Figure 2.

Correlations in synaptic input to distal or proximal dendrites amplify the LFP signal while retaining the effect of I_h. A, B, LFP-PSD in apical and somatic regions resulting from distal tuft synaptic input (A), with different levels of correlation, c, between the synaptic inputs (B, columns), to a population of 10,000 cortical layer 5 pyramidal cells. Different curves correspond to the different cell models used in Figure 1. C, LFP-PSD at 1 Hz as a function of the synaptic input c value. D, The PSD modulation at 1 Hz as a function of the synaptic input correlation. The PSD modulation is defined as the LFP-PSD from the passive + I_h model (blue curves) or the passive + frozen I_h model (cyan curves), divided by the LFP-PSD from the passive model. E–H, Same as A–D, but with basal synaptic input. The LFP-PSDs are shown in log₁₀ scale with units of μV²/Hz.

Figure 3.

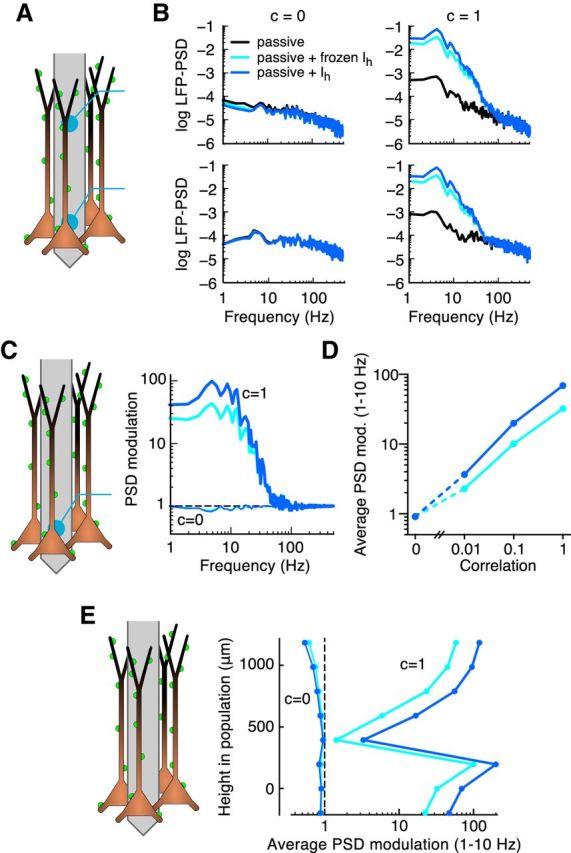
Membrane conductance gradient amplifies the LFP signal for a population receiving correlated uniformly distributed synaptic input. A, B, LFP-PSD resulting from uniform synaptic input (A) with different levels of c between the synaptic inputs (B, columns) to a population of 10,000 cortical layer 5 pyramidal cells. Different curves correspond to the different cell models used in Figures 1 and 2. The LFP-PSDs are shown in log₁₀ scale with units of μV²/Hz. C, PSD modulation, defined as the LFP-PSD from the passive + I_h model (blue curves) or passive + frozen I_h model (cyan curves), divided by the LFP-PSD from the passive model, for c = 0 (thin lines) or c = 1 (thick lines). D, Average of the PSD modulation between 1 and 10 Hz as a function of the synaptic input c value. E, Average of the PSD modulation between 1 and 10 Hz for different positions along the axis of the apical dendrites, in the middle of the population, for c = 0 (thin lines) or c = 1 (thick lines).

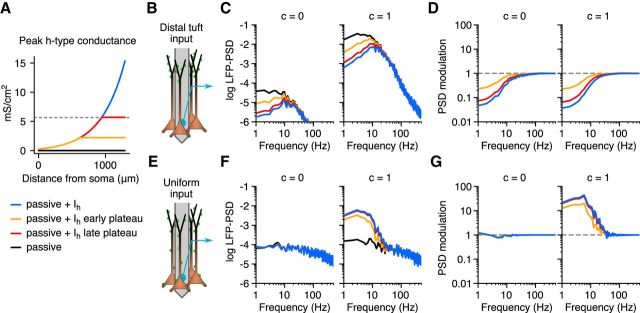
Figure 8.

The effect of I_h is independent of exact subcellular conductance distribution. A, Different distributions of the peak I_h conductance along the apical dendrite. B–D, The LFP-PSD for distal tuft synaptic input (B) with different levels of correlation (C, columns), as well as the corresponding PSD modulations (D). E–G, Same as B–D, but for uniformly distributed synaptic input. The LFP-PSDs are shown in log₁₀ scale with units of μV²/Hz, and the PSD modulation is defined in Figures 2, 3, 4, and 7.

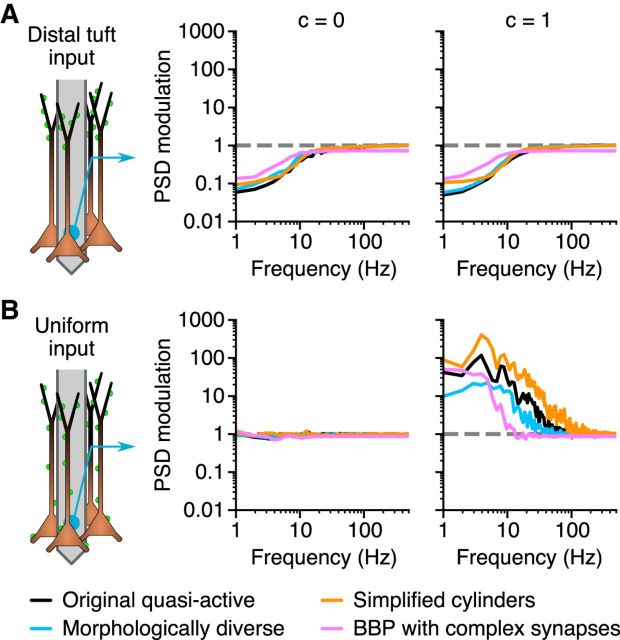
Figure 9.

Findings generalize to both more complex and simplified populations. The PSD modulation, defined as the LFP-PSD from a population with an I_h-like conductance, normalized by the LFP-PSD from the same population with the I_h-like conductance removed. A, B, The synaptic input is distributed at the distal apical dendrite (A), or uniformly on the entire cell (B), and is either uncorrelated (c = 0) or fully correlated (c = 1). Results from four different population types are shown in different colors: (1) black, The quasi-active model used in Figures 4 (column 1), 6, and 7, with 1000 cells; (2) cyan, a population of 1000 cells with a similar quasi-active conductance, but composed of 67 distinct cell morphologies; (3) pink, a population of 1000 reconstructed cortical layer 5 pyramidal cells from the Blue Brain Project (Markram et al., 2015), receiving conductance-based synaptic input with a realistic time course (synaptic time constant, 2 ms; the PSD modulation is calculated from the LFP-PSD of a population with a single I_h conductance, normalized by the LFP-PSD from a passive population; however, using the fully active cell models with all 11 active conductances gave similar results); and (4) orange, a simplified population of 1000 cylindrical cell models (1000 μm long, 2 μm thick) receiving current-based, white-noise synaptic input (i.e., very short synaptic time constant), in this case distributed either to the top half (A) or uniformly along the entire cell (B). The PSD modulation was calculated by the LFP-PSD from a population with a single quasi-active restorative conductance that was fivefold stronger in the top half of the cells, normalized by the LFP-PSD from a population with a uniform passive conductance. For all cases, the LFP-PSD is calculated at a single position in the lower region of the population (corresponding to the somatic region for the pyramidal cells).

Simulations for Figures 4, 6, and 7 used the same complex morphology as described above, but instead of the original active conductances, used a single so-called quasi-active conductance (Mauro et al., 1970; Koch, 1984; Hutcheon and Yarom, 2000; Remme, 2014). Voltage-dependent membrane currents often behave in a near-linear fashion for small perturbations around a holding potential; hence, one can make use of linear approximations of the nonlinear ionic currents, thereby greatly reducing the parameter space, while retaining the generic features of the system. This quasi-active description highlights that active conductances basically come in two classes, regenerative or restorative, functioning as positive or negative feedbacks by amplifying or counteracting changes in the membrane voltage, respectively. The implementation was the same as in Ness et al. (2016), except that the strength of the quasi-active peak conductance was halved to increase the stable voltage regime of the quasi-active conductance. This was needed since we did not use the balanced excitation and inhibition that was used in Ness et al. (2016). The quasi-active description allowed for a systematic study of the effect on the LFP of quasi-active conductances of different classes (i.e., regenerative or restorative) and different cellular distributions (i.e., linear decrease or increase in membrane conductance strength with distance from the soma, as well as a uniform distribution). The quasi-active peak conductance was ḡ_w(x) = 71.3 − 0.0543x μS/cm² for the model with the linear decrease in conductance with distance (x in μm) from the soma, ḡ_w(x) = 2.64 + 0.121x μS/cm² for the model with the linear increase with distance from soma, and ḡ_w(x) = 50 μS/cm² for the uniform distribution. For all three of these different membrane conductance distributions, the total resting membrane conductance (i.e., summed for the entire membrane surface) was the same. The same quasi-active conductance was used for the model labeled “simplified cylinders” in Figure 9, where cells were represented by single cables with a length of 1000 μm and a diameter of 2 μm. The top half of the cable had a fivefold increased strength of the quasi-active conductance, compared with the bottom half, which had ḡ_w(x) = 33.3 μS/cm². In Figure 9 (“BBP with complex synapses”), we used a cell model from the Blue Brain Project cortical microcircuit (available from https://bbp.epfl.ch/nmc-portal; Markram et al., 2015) named “L5_TTPC2_cADpyr232_2.”

Figure 4.

Asymmetry in the distribution of membrane conductance or synaptic input enhance the effect of membrane conductances on the LFP. Systematic study with three different synaptic input distributions (rows A1–A3, B1–B3, C1–C3) and three different membrane conductance distributions (columns) for a population of 10,000 cortical pyramidal cells. The LFP-PSD from the passive+frozen population is shown for c = 0 (black curves) and c = 1 (gray curves). The LFP-PSDs are shown in log₁₀ scale with units of μV²/Hz. The PSD modulation (i.e., the LFP-PSD of the population with a regenerative (red curves) or restorative (blue curves) conductance, divided by the LFP-PSD from the population with a passive + frozen conductance) is shown for c = 0 and c = 1. Note that each of the different cell models has the same total membrane conductance. Freq., Frequency.

Figure 6.

Synaptic input correlation can boost restorative resonance above noise level. A, B, LFP-PSD for the apical (top row) and somatic (bottom row) regions for distal tuft (A, pink) or uniformly distributed (B, green) synaptic inputs to the cortical cell population with an increasing restorative (I_h like) quasi-active conductance. Columns show different correlation levels from c = 0 to c = 1. The sum of the LFPs from the two populations is shown in black. The LFP-PSDs are shown in log₁₀ scale with units of μV²/Hz.

Figure 7.

LFP amplification for uniform synaptic input to I_h-like conductance requires correlation and a minimum population size. A, B, For cell populations with increasing radius (A), the average of the PSD modulation between 1 and 10 Hz, is shown for different levels of synaptic correlation (B). The PSD modulation is defined as the LFP-PSD from a population with a quasi-active I_h-like conductance, divided by the LFP-PSD from a passive model, similar to Figures 2 and 3. A population with the full radius but half the original cell density is also shown (dark red, dashed line). C, The same data as in B, but with the average PSD modulation between 1 and 10 Hz for different correlation levels (c) as a function of the population radius.

Population models.

Models of cortical populations were constructed by placing layer 5 pyramidal cell models with the somata uniformly distributed within a disc, and with the apical dendrites oriented along the same axis. The cells were randomly rotated along the axis of the apical dendrite. Unless otherwise specified, the populations contained 10,000 cells, the thickness of the disc was 200 μm, and the radius of the disc was 1000 μm, resulting in a planar cell density of ∼3000 cells/mm² (Lindén et al., 2011; Łęski et al., 2013). In most cases, all cell models were duplicates of one and the same cell morphology, but we also constructed a population consisting of 67 distinct morphologies from adult rat somatosensory cortex L5 pyramidal cells (see Fig. 9). These cell morphologies were downloaded from NeuroMorpho.org (Ascoli et al., 2007; Chen et al., 2014; Hamada et al., 2016) and equipped with the single quasi-active conductance described in the previous paragraph.

Synaptic input.

For the model used in Figure 9, labeled “BBP with complex synapses,” we used conductance-based synapses, with instantaneous jumps in conductance of 0.01 nS followed by an exponential decay with a time constant of 2 ms. For all other figures, the synaptic inputs were current-based synapses modeled with very short time constants (3 time steps), effectively making them delta pulses with a white-noise (i.e., flat) power spectrum (Łęski et al., 2013). This ensured that all observed deviations from a flat LFP power spectrum were caused by cell properties (Lindén et al., 2010; Łęski et al., 2013; Ness et al., 2016). In all cases, each cell received 1000 different spike trains, and the individual spike trains were independent Poisson processes with a mean rate of 5 spikes/s. Correlations were in all cases introduced by drawing the presynaptic spike trains of all the cells from a large common pool of spike trains. The spike trains were drawn without replacement for each cell, i.e., for any given cell all 1000 spike trains were different and independent. Different levels of correlation were obtained by varying the size of the common pool of spike trains, which decides the average fraction (c) of common spike trains that two random cells would share. For c = 0, the synaptic inputs are uncorrelated, and for c = 1 all cells share the exact same 1000 presynaptic spike trains. Note, however, that the spike trains did not target the exact same postsynaptic locations on different cells. Synaptic input to the distal tuft only targeted the apical dendrites above z = 900 μm, where the somas are distributed in a disc centered at z = 0 μm (see Population models). Basal synaptic input targeted the basal dendrites and the soma, and the uniformly distributed synaptic input targeted all cell compartments. Within the targeted region, postsynaptic cell compartments were randomly selected with uniform area-weighted probability.

Calculation of extracellular potentials.

Extracellular potentials were calculated using volume conductor theory. From a simulated multicompartmental neuron model (Rall, 1962; Butz and Cowan, 1974; Koch, 1999), the transmembrane currents, I_n(t), are obtained from each compartment n at position r→_n. The extracellular potential φ(r→, t) at position r→ resulting from these transmembrane currents can then be calculated as follows (Holt and Koch, 1999; Lindén et al., 2013):

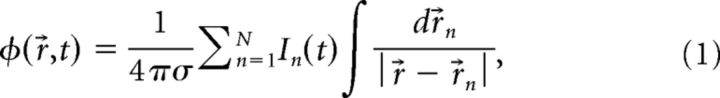where the conductivity of the extracellular medium was given by σ = 0.3 S/m (Goto et al., 2010), and was assumed to be homogeneous, isotropic, and frequency independent (Miceli et al., 2017). This line-source formula assumes that the transmembrane currents are evenly distributed along the axes of cylindrical neural compartments (for a detailed description, see Lindén et al., 2013). All simulations and computations of the extracellular potentials were performed using LFPy (Lindén et al., 2013), an open-source Python package that provides an interface to NEURON (Carnevale and Hines, 2006). For most cases, the LFP-PSD is shown for both the somatic region (z = 0 μm) and the apical region (z = 1000 μm).

To obtain the power spectral density (PSD) of the LFP, we used Welch's method. Note that the term LFP commonly refers to the extracellular potential after it has been low-pass filtered (below ∼300–500 Hz) to remove spikes. Here, we focused only on the subthreshold regime; hence, since no spikes are present, we simply refer to the unfiltered extracellular potential as the LFP. The time step of the neural simulation was one-sixteenth of a microsecond. For all simulations, the first 2000 ms was discarded to avoid initialization effects, and the total simulation time was 2¹³ = 8192 ms, where the power of 2 was chosen to speed up the calculation of the PSDs.

All simulation code used to produce the figures in this study are available from the on-line repository: https://github.com/torbjone/aPop.

Results

The aim of the current study is to investigate the effect of subthreshold voltage-dependent conductances on the LFP produced by a biophysical model of a population of pyramidal neurons. As a reference point, we start by showing the LFP produced by a single pyramidal neuron model in response to ongoing synaptic input, as in the study by Ness et al. (2016).

Active conductances shape single-cell and population LFPs for asymmetrically distributed synaptic input

We used a morphologically reconstructed cortical pyramidal cell from layer 5 (Hay et al., 2011; Fig. 1A) and provided the cell with 1000 excitatory current-based synaptic inputs that were activated by independent Poisson statistics. The synaptic inputs were distributed within different target regions with uniform area-weighted probability. The time course of the synaptic inputs was made very short, giving the input a flat power spectral density (PSD) so that the input itself does not shape the LFP-PSD profile (Łęski et al., 2013; see Materials and Methods). The original, experimentally constrained cell model included 10 active conductances, and we demonstrated previously that the h-type conductance was sufficient to capture the active contributions to the subthreshold LFP response (Ness et al., 2016). For simplicity, we will for most results consider a simplified model with only I_h (passive + I_h).

The I_h conductance is distributed asymmetrically across the dendrites of many types of pyramidal cells, with a strong increase in conductance density along the apical dendrite away from the soma (Magee, 1998, 1999; Hu et al., 2002, 2009; Kole et al., 2006; Angelo et al., 2007; Hay et al., 2011; Almog and Korngreen, 2014). When restricting the subthreshold synaptic input to the distal dendritic tuft, the LFP-PSD from the model with the h-type conductance showed a resonance (but see also Hutcheon et al., 1996; Narayanan and Johnston, 2008) when measured close to the soma (i.e., a peak in the PSD at ∼10 Hz; Fig. 1B, bottom, blue curve). This resonance was not present for the following two different passive models: one where the I_h conductance was completely removed (Fig. 1B, bottom, passive, black); and one where the increased resting membrane conductance that results from the h-type conductance was included, but the dynamics of the conductance were removed (i.e., a so-called frozen conductance; Fig. 1B, bottom, passive + frozen I_h, cyan curve). The h-type conductance had a much weaker effect on the single-cell LFP when the input targeted the basal dendrites, where I_h was only weakly expressed (Fig. 1C). Note also that the LFP-PSD exhibited a much steeper falloff with frequency when measured on the side opposite to the synaptic input (Fig. 1B, C). This is due to intrinsic dendritic filtering, as described in detail by Lindén et al. (2010) and Łęski et al. (2013).

The above single-cell effects of active conductances were previously described in the study by Ness et al. (2016). To investigate whether these effects carry over to the LFP produced by a population of pyramidal neurons, we next constructed a population of 10,000 pyramidal cells, with the somata distributed within a disc of radius 1000 μm and a thickness of 200 μm (Fig. 1D), giving a planar cell density of ∼3000 cells/mm² (Lindén et al., 2011; Łęski et al., 2013). The cells were randomly rotated along the axis of the apical dendrite. The extracellular potential was calculated at different positions along the axis of the disc (in the center of the population). Each cell received input that was similar to that for the single cell described above (i.e., 1000 excitatory synaptic inputs that were activated by independent Poisson processes). As in the single-cell simulations, we found that the resonance due to the h-type conductances was indeed present in the LFP-PSD from the population model when the cells received uncorrelated synaptic input to the distal tuft dendrites (Fig. 1E, bottom). In fact, for uncorrelated synaptic input, all tested combinations of synaptic input regions and distributions of the conductance resulted in population LFP-PSDs that were very similar in shape to the single-cell LFP-PSDs; the difference was mainly a magnitude scaling factor (Fig. 1, compare B, E, and C, F). This was not surprising. Because of the linearity of extracellular potentials, the LFP from a population of cells is just the sum of the single-cell LFPs, and summing uncorrelated signals with similar frequency content should not change the overall shape of the LFP-PSD (Lindén et al., 2011; Łęski et al., 2013).

Synaptic input correlations amplify the LFP for asymmetrically distributed input and preserve I_h-induced resonance

Although the above results could be expected on the basis of the linear summation of LFP signals, the results are not straightforward when correlations are introduced among the synaptic inputs to a population of neurons. Previous studies showed that such correlations have a strong effect on the LFP (Lindén et al., 2011; Łęski et al., 2013). We introduced correlations by varying the c value of input fibers that each pair of neurons shared (see Materials and Methods), i.e., c = 0 means that each neuron receives different input spike trains, and c = 1 means that every cell receives the exact same 1000 spike trains (note that they arrive at random postsynaptic positions). We found that the correlations caused a strong amplification of the LFP-PSD when the population received synaptic input to the distal tuft (Fig. 2A, B). For the passive population at 1 Hz, the amplification from c = 0 to c = 1 in the input region was a factor of ∼1700 (Fig. 2C). The origin of this frequency-dependent amplification with correlation has been thoroughly investigated previously by Łęski et al. (2013). Linearity assures us that we can consider the high and low frequencies of membrane currents separately. The high frequencies of the synaptic return currents tend to be close to the synaptic input, and the locally random orientation of the dendrites therefore ensures that the orientation of the resulting currents dipoles will also be predominately random. For the more spatially distributed low-frequency currents, however, the geometrically aligned nature of pyramidal cells becomes important in aligning the current dipoles. The implication of this is that the conversion of synaptic input correlations into correlations between single-neuron LFP contributions is more efficient at low frequencies, giving stronger LFP-PSD amplification for synaptic correlations at low frequencies (Łęski et al., 2013).

A similar phenomenon of a correlation-dependent slope of the membrane potential PSD was reported by El Boustani et al. (2009), and in the single-cell model used therein, this phenomenon was found to be dependent on the distribution of the individual delays for each presynaptic spike train. In the present study, we did not have any individual time delays for the presynaptic spike trains. However, based on the findings of El Boustani et al. (2009), we expect that introducing such individual time delays would result in an additional adjustment of the LFP-PSD slope by decreasing the LFP-PSD power at high frequencies for correlated synaptic input.

The I_h-induced attenuation of low frequencies for distal tuft synaptic input was also present for correlated input (Fig. 2D, dark blue). To quantify the effect of the I_h conductance, we calculated the PSD modulation i.e., the LFP-PSD from the population with either the original or the frozen I_h conductance, normalized by the LFP-PSD from the passive population. At the lowest considered frequency of 1 Hz, the attenuating effect of I_h increased with correlation in the apical region (Fig. 2D, top), while remaining constant with correlation in the basal region (Fig. 2D, bottom). As a consequence, the LFP-PSD in the somatic and apical regions look very similar for fully correlated input (Fig. 2B, second column). This can be understood in the following way: as the input correlations are increased, the dynamics of the different cells in the population will become increasingly similar. For the highest correlation, c = 1, the entire population behaves as a single current dipole such that the LFP-PSD is very similar in the apical and somatic regions (except with opposite phase; data not shown, but see Łęski et al., 2013; Fig. 2B, F, rightmost panels). For basal synaptic input (i.e., input to the region where the I_h density was low; Fig. 2E), we found a strong signal power amplification with increasing correlation (Fig. 2F, G), but no effect of the h-type conductance for any correlation level (Fig. 2H).

Synaptic input correlations amplify the LFP for uniformly distributed input when membrane conductances are distributed asymmetrically

For a population of passive neurons (i.e., without the h-type conductance) where the synaptic inputs were not targeted to either apical or basal dendrites but instead were uniformly distributed across all dendrites (Fig. 3A), we found relatively weak effects of input correlations (Fig. 3B, black curve, passive), which is in line with findings from Łęski et al. (2013). Note that the passive properties of the cell model from Hay et al. (2011) are not completely uniform; we will confirm below that a cell model with completely uniform passive properties shows no effect from input correlations (see below; Fig. 4B2). This was in stark contrast to what we found for the models that included the asymmetrically distributed h-type conductance, in which case we observed a strong amplification for frequencies below ∼30 Hz (Fig. 3B, C, cyan and blue curves). This effect was present for the passive model with the frozen h-type conductance and even somewhat stronger for the model with the original, active h-type conductance. Note that this result is opposite to the usual observation that the h-type conductance always leads to a dampening of low frequencies compared with the passive conductance (Ness et al., 2016). We will return to this result below. To isolate the effect of the intrinsic conductances, we normalized the LFP-PSDs recorded in the somatic region by the signal from the passive population, which highlighted that the h-type conductance had no effect for c = 0 (Fig. 3C, thin curves), but caused an up to 100-fold amplification for c = 1 at frequencies below ∼10 Hz (Fig. 3C, thick curves). This low-frequency amplification was found to steadily increase with correlation (Fig. 3D), and it was present for most extracellular positions along the apical dendrite, except in the zero-crossing region of the dipole (Fig. 3E).

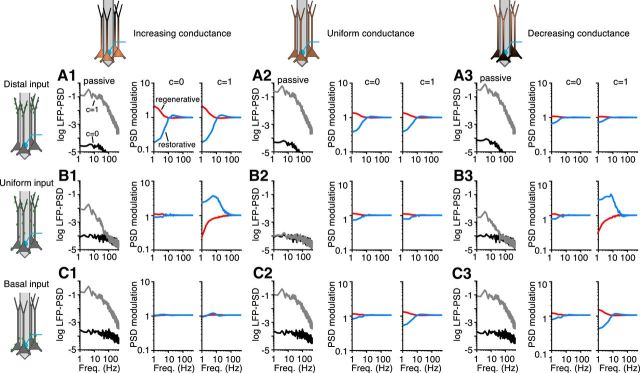
Asymmetry in the distribution of membrane conductance or synaptic input enhance the effect of membrane conductances on the LFP

The active properties of pyramidal neurons vary across cell layers, brain region, and animal species, and can, for example, change during development or be under the control of neuromodulators. It is therefore not possible to know a priori the combinations of ion channel type, distribution, synaptic input regions, and synaptic input correlation that are shaping the LFP in a given setting. The effect of nonuniform membrane conductances on the membrane potential has been studied previously for passive membranes (Kawato, 1984; Schierwagen, 1989; London et al., 1999) and for I_h (Angelo et al., 2007; Zhuchkova et al., 2013). To allow for a systematic study of the effects of active conductances on the LFP, we made use of the so-called quasi-active description of voltage-dependent conductances (see Materials and Methods). For small deviations of the membrane potential around a holding potential, these linear approximations can capture the dynamics of a broad variety of subthreshold active currents very well (Remme and Rinzel, 2011 and Ness et al., 2016). The quasi-active approximation highlights that voltage-dependent conductances come in two different forms, regenerative and restorative. The h-type conductance is a restorative conductance i.e., it functions as a negative feedback by counteracting changes in the membrane voltage. In contrast, regenerative conductances (e.g., persistent sodium) function as positive feedbacks, amplifying changes in the membrane potential. The effect of the dynamics of either of these two conductance classes can be evaluated by looking at the LFP-PSD modulation i.e., the LFP-PSD from the population with either the regenerative or restorative conductance, normalized by the LFP-PSD from the passive population. Note that the different cell models all had the same total resting membrane conductance; hence, we are comparing the quasi-active conductance to a passive-frozen conductance (comparable to the passive + frozen I_h case in Figs. 1, 2, 3). To investigate the effect of the distribution of the conductances, we used a uniformly distributed conductance as well as a conductance that was linearly increasing or linearly decreasing in density with distance from the soma. There was a 60-fold increase or decrease in the conductance density along the length of the cell, similar to what has been reported for the h-type conductance in pyramidal cells in layer 5 of the neocortex and in the hippocampus (Lörincz et al., 2002; Kole et al., 2006; Nusser, 2009; Mishra and Narayanan, 2015). These three distributions of the membrane conductance were combined with three different distributions of the synaptic input: uniform, only to the distal tuft, or only to the basal dendrites.

First focusing on the cell populations with passive-frozen conductances (Fig. 4, gray and black curves), we found that the LFP-PSD was strongly amplified by input correlations for all combinations of synaptic input distributions and membrane conductance distributions, except when both distributions were uniform (Fig. 4B2, gray vs black curves). We quantified the effects of the quasi-active conductances by normalizing the LFP-PSD to that of the corresponding passive-frozen case (Fig. 4, red and blue curves). For distal tuft synaptic input to a population with an increasing membrane conductance distribution (i.e., I_h like), we found that the restorative conductance resulted in a strong decrease for the lowest frequencies, over fivefold at 1 Hz, of the LFP-PSD compared with the passive-frozen case, thereby producing a resonance (Fig. 4A1, blue curves). For the regenerative conductance, there was instead a low-frequency amplification of more than a factor 2 at 1 Hz (Fig. 4A1, red curve; Ness et al., 2016). We found that for most cases the LFP-PSD modulation by the regenerative or restorative conductance was similar for uncorrelated and correlated inputs (Fig. 4, red and blue curves; c = 0 vs c = 1). A notable exception was seen for populations with asymmetric conductance distributions, receiving uniform synaptic input. In this case, the LFP-PSD modulation by the quasi-active conductances was up to a factor of ∼4 for correlated inputs (c = 1) for both the restorative and regenerative conductances (Fig. 4B1, B3). However, as noted above, the modulation by either current was in a direction opposite to what we observed in all other conditions (see below). Comparing the LFP-PSD modulation from all combinations of membrane conductance distributions and synaptic input regions, we found that especially the I_h-like conductance (i.e., restorative) and distribution (i.e., linearly increasing) had a strong ability to shape the LFP-PSD (Fig. 4, left column, gray and blue traces): This configuration produced a (passive) amplification of the LFP-PSD for correlated input (Fig. 4, gray traces in leftmost panels), while the contribution of the I_h-type dynamics (blue curves) carried the following: (1) a resonance for apical synaptic input; (2) no modulation for basal input; and (3) a signal amplification for uniform input. This demonstrates the unique potential of the h-type current for shaping the LFP as a function of input region and input correlation.

Asymmetric membrane conductance distributions cause a strong LFP amplification

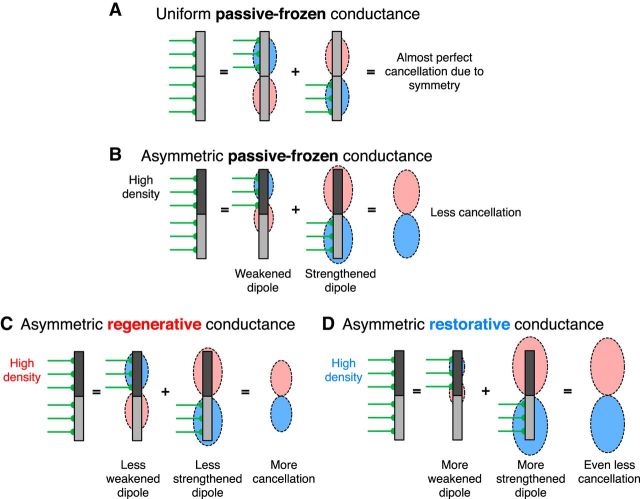
The counterintuitive result that the LFP from a population receiving uniformly distributed synaptic input was strongly amplified by an asymmetric membrane conductance distribution—and even further amplified by the dynamics of the h-type conductance (Figs. 3, 4)—can be understood in the following way. Because of linearity, the LFP from a population receiving uniformly distributed synaptic input can be factorized into two subpopulations: one receiving synaptic input to the top half of the cells, and the other to the bottom half. The LFP signals from these two subpopulations will, for a uniform membrane conductance distribution, be almost perfect mirror images. Hence, the superposition of these two signals will cancel almost entirely and cause a very weak LFP signal (Fig. 5A). This is different for an asymmetric passive conductance, because currents from synaptic input to a region with a high membrane conductance can more easily exit locally, giving a decreased current dipole moment, while currents from synaptic input to a region with low membrane conductance can exit less easily locally, giving an increased current dipole moment. An asymmetric passive conductance will therefore lead to less dipole cancellation and a stronger LFP signal (Fig. 5B). A regenerative conductance is partly working against the above-described effect of the asymmetric passive conductance by increasing the current dipole moment for synaptic input to strong conductance regions. Synaptic input to the weak conductance region will also depolarize the strong conductance region and initiate a regenerative current that opposes the synaptic currents, thereby decreasing the current dipole moment for synaptic input to weak conductance regions (Ness et al., 2016). Therefore, the resulting cancellation is larger than that for the asymmetric passive case (Fig. 5C). A restorative conductance is enhancing the effect of the asymmetric passive conductance by further decreasing the current dipole moments of synaptic inputs to a high-conductance region. Synaptic input to the weak conductance region will also depolarize and initiate a restorative current in the strong conductance region, thereby increasing the current dipole moments of synaptic inputs to a low-conductance region (Fig. 5D). Note that even though linearity means that one can sum LFP time traces, one cannot directly sum LFP-PSDs without taking into account the phase information (which we do not show here). For example, apical synaptic and basal synaptic inputs result in opposite LFP dipoles (Fig. 5A), which in the frequency domain correspond to opposite phases. Therefore, the sum of these two LFPs will be smaller than either of the separate cases.

Figure 5.

For asymmetric membrane conductance distributions, uniformly distributed correlated synaptic input causes an amplification in the LFP due to less dipole cancellation. Schematic illustration of mechanism underlying the amplified LFP-PSD for uniformly distributed input to a cell population with a spatially asymmetric membrane conductance. Schematic cylindrical neuron with two cell regions is shown in gray, and synapses in green. Due to linearity, the LFP from uniformly distributed synaptic input to a population can be decomposed into the sum of the LFPs from synaptic input to two different cell regions. A, For a uniform passive membrane conductance, top and bottom synaptic inputs cause opposite dipoles, leading to an almost perfect cancellation of the summed LFP. B, An asymmetric passive conductance weakens the symmetry and leads to less dipole cancellation. C, An asymmetric regenerative conductance will partly counteract the effect of the asymmetric passive conductance. D, An asymmetric restorative conductance will strengthen the effect of the asymmetric passive conductance.

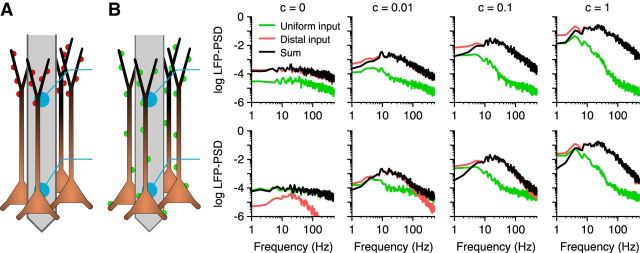
Restorative resonance can be amplified above noise level by synaptic input correlations

An important question is whether the resonance caused by the h-type conductance (Figs. 1, 2, 4) can be expected to appear in an experimental setting. The resonance was present only for asymmetric synaptic input, and, in an in vivo experimental setting, synaptic input might not exclusively target only one region of a population of cells for sufficient time for the resonance to be visible in recordings. We compared the LFP-PSD resulting from a population receiving distal tuft synaptic input (Fig. 6A) to a population receiving uniformly distributed synaptic input (Fig. 6B). For both cases, we used the quasi-active formalism with the single, I_h-like, restorative conductance. The sum of the LFPs from these two cases would, because of linearity, correspond to a mixed population of cells receiving either distal tuft or uniform synaptic input. For this example, we assumed that the correlation between the two populations was the same as the correlation between the cells within a population (i.e., we used the same common pool of spike trains for both populations). We found that for uncorrelated input, no resonance was visible in the PSD of the soma region LFP sum, since the signal was dominated by close-by (“Uniform”) white-noise synaptic input (Fig. 6, c = 0, bottom). However, input correlations amplify the LFP signal for asymmetric input more than they amplify the LFP signals for uniform input. For nonzero correlation levels, we found the LFP-PSD from the population receiving distal tuft input to be strongest in the frequency region around the resonance peak (at ∼10–20 Hz; Fig. 6, c = 0.01–1). This makes it plausible that an I_h-induced resonance could be detectable in vivo. It should be noted, however, that both the strength of the resonance (Fig. 6A) and the strength of the amplification for the uniform synaptic input (Fig. 6B) are parameter dependent.

Effect of h-type conductance on LFP is a robust phenomenon

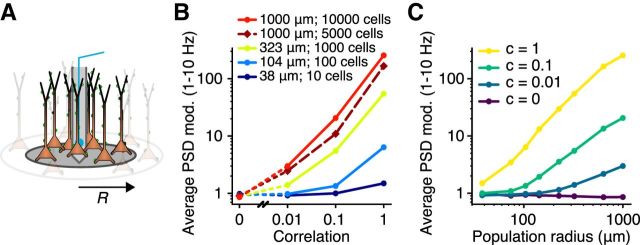
The I_h-induced resonance that we observed for apical synaptic input was found to be very robust with regard to the population parameters. For the LFP-PSD from the original cell model from Hay et al. (2011), I_h-induced resonance was expressed for a single cell (Fig. 1B) as well as for all correlation levels of the synaptic input to a population (Fig. 2A). As expected, it was therefore also present for different population sizes (10–10,000 cells) and for a population with half the original cell density (results not shown).

The low-frequency amplification for an asymmetric conductance distribution and uniformly distributed synaptic input was, however, not present for a single cell and required correlated synaptic input to a population of neurons, and we therefore performed further investigations of the robustness of this phenomenon. We quantified the amplification by calculating the average PSD modulation i.e., the LFP-PSD from the population with the I_h-like conductance, normalized by the LFP-PSD from the passive population, in the low-frequency range (1–10 Hz). We found the low-frequency amplification to be present for uniformly distributed synaptic input with correlation levels of c = 0.01 and above for many different population sizes as well as for a population with half the original cell density, and the amplification was increasing in strength with both the correlation and the population size (Fig. 7). For the highest correlation level (c = 1), a small amplification could be seen for as little as 10 cells.

The strength of the h-type conductance is, as previously discussed, known to strongly increase along the apical dendrite of L5 cortical pyramidal neurons. In the cell model from Hay et al. (2011), based on results from Kole et al. (2006), the peak conductance of the h-type current increased exponentially with distance from the soma (Fig. 8A, blue line). However, a recent study by Harnett et al. (2015) suggests that the conductance density of the h-type current reaches a plateau after the main bifurcation of the pyramidal cell apical dendrite, with a maximum peak conductance value of ∼5.6 mS/cm² (Fig. 8A, horizontal dotted line). This means that the cell model from Hay et al. (2011) used in Figures 1, 2, and 3 might reach unrealistically high h-type conductance densities in the distal part of the apical dendrite. We therefore constructed population models consisting of 1000 pyramidal cells that had modified spatial distributions of the h-type conductance. First, we tested a model where the h-type conductance plateaus after the main bifurcation of the pyramidal cell (Fig. 8A, orange line); however, this particular morphology has a relatively proximal bifurcation, and therefore this model had a plateau value for the peak h-type conductance density of less than half the value found by Harnett et al. (2015). We therefore also tested a model with a plateau density corresponding to the numerical value given by Harnett et al. (2015) of 5.6 mS/cm² (Fig. 8A, red line).

For both these cases, the h-type conductance had an effect on the LFP-PSD similar to that observed previously, but the effect was, as expected, less than that for the original model from Hay et al. (2011) since the total amount of h-type current in the distal apical dendrites was reduced (Fig. 8B–G). For the cell model that used the late plateau at the h-type conductance value reported by Harnett et al. (2015), the results were, however, very similar to those from the original model (Fig. 8D, G), demonstrating that our results are not caused by an unrealistically high h-type conductance.

All of the populations used so far have consisted of (rotated and shifted) duplicates of one particular cell morphology; however, to exclude the possibility that using a single morphology biased our results, we also constructed populations of 1000 cells based on 67 distinct morphologies from rat somatosensory cortex layer 5 pyramidal cells (downloaded from neuromorpho.org; see Materials and Methods). The cells were equipped with a single quasi-active I_h-like conductance, and we found that the effect of the I_h-like conductance, characterized by the PSD modulation, was very similar to the results for the single-morphology population (Fig. 9, compare cyan, black).

The resonance and amplification were also expressed by a population consisting of the original cell models from Hay et al. (2011) (i.e., with all 10 active conductances present; results not shown). The same holds for a much more complex population of 1000 cortical layer 5 pyramidal cells from the Blue Brain Project cortical microcircuit model (https://bbp.epfl.ch/nmc-portal; Markram et al., 2015), where we used conductance-based synapses with a realistic time course (synaptic time constant, 2 ms; Fig. 9, pink). Note that in contrast to the previously shown results, we did not enforce a uniform resting membrane potential for the cell models in this case, resulting in a membrane potential gradient along the apical dendrites of the cells due to I_h (Kole et al., 2006; Hay et al., 2011; Harnett et al., 2015).

Finally, the LFP-PSD resonance and amplification effects were also produced by a strongly simplified population consisting of 1000 cylindrical cell models with a restorative quasi-active conductance with a fivefold increased density on the top half of the cylinder (Fig. 9, orange).

Discussion

In the present article, we have investigated the role of subthreshold active currents in shaping the LFP from cortical neural populations. Using models of populations of 10,000 cortical layer 5 pyramidal cells, we found that the dominant subthreshold active conductance, I_h, is particularly suited to modulate the LFP in a manner that reflects the spatial distribution of the synaptic input, the degree to which the synaptic inputs are correlated, and the spatial distribution of the I_h channels.

For synaptic input that targeted the apical dendrite of the cell population, I_h gave rise to a prominent resonance peak in the LFP-PSD (Fig. 1). Furthermore, we demonstrated that the introduction of correlations to asymmetrically distributed synaptic input caused a strong signal amplification, while the effect of I_h was also more strongly expressed (Fig. 2). For uniformly distributed correlated synaptic input, we found, surprisingly, that the asymmetric distribution of the h-type conductance caused a strong low-frequency amplification of the LFP-PSD (Figs. 3, 5). Hence, the same active conductance has two opposite effects on the LFP-PSD, depending on the following input specifics: a low-frequency dampening (yielding a resonance) for apical input or a low-frequency amplification for correlated uniformly distributed input.

We next systematically studied the effect on the LFP of different combinations of conductance types, conductance distributions, and synaptic input regions, using quasi-active conductances, which are linear approximations of the voltage-dependent currents (Mauro et al., 1970; Koch, 1984; Remme and Rinzel, 2011; Ness et al., 2016). The quasi-active description strongly reduces the number of parameters needed to describe an active current, which enabled us to systematically study the effects of active currents on the LFP signal from cortical populations. These linear descriptions highlight that active currents basically come in the following two forms: regenerative (e.g., the persistent sodium current) and restorative (e.g., I_h). We demonstrated that these two types of active currents affect the lowest frequencies of the LFP-PSD in opposite manners, by amplification or dampening, depending on the spatial distribution and correlation level of the synaptic input (Fig. 4). For an I_h-like conductance (i.e., a restorative conductance that was increasing in strength with distance from the soma), the above-described effects of I_h on the LFP were observed also in this more general model. Importantly, this systematic study demonstrated that the restorative dynamics and the strongly asymmetric conductance distribution of I_h are in fact the ideal combination for an active current to shape the LFP (Fig. 4). The observed I_h-induced resonance could be of substantial experimental value (see below) if present in in vivo LFP recordings, and we showed how the large signal amplification of spatially asymmetric correlated synaptic input can potentially make this resonance experimentally detectable (Fig. 6).

We demonstrated that the effect of the h-type conductance on the LFP-PSD (i.e., the resonance for apical input and the amplification for uniformly distributed correlated input) was a very robust phenomenon. First, the described effects were present for different population sizes and cell densities (Figs. 1, 7). Second, they were present for different types of synaptic input, both current based with a short synaptic time constant (Figs. 1, 2, 3, 4, 5, 6, 7) and conductance based with a realistic synaptic time constant (Fig. 9). Third, they were present for different types of I_h-like conductances i.e., an experimentally constrained h-type conductance with an exponential increase with distance from the soma (Hay et al., 2011; Figs. 1, 2, 3) and a quasi-active restorative conductance with a linear increase in density with distance from the soma (Figs. 4, 5, 6, 7, 9). Finally, the effects were present for different cell morphologies i.e., detailed reconstructed cell models (Figs. 1, 2, 3, 4, 5, 6, 7, 9) and simplified cylindrical models (Fig. 9).

Implications for interpretations of extracellular brains signals

We have demonstrated that subthreshold active conductances, and in particular the h-type conductance, can have an important role in molding the return currents following synaptic input to populations of pyramidal neurons, leading to large, qualitative changes in the shape of the LFP. Other important brain signals, such as the electrocorticography, electroencephalography (EEG), and magnetoencephalography signals, which reflect the neural activity of larger brain volumes than the LFP, are all still expected to predominantly reflect the same underlying process, namely synaptic input to populations of geometrically aligned pyramidal neurons (Mitzdorf, 1985; Nunez and Srinivasan, 2006; Buzsáki et al., 2012; Cohen, 2017). Therefore, our findings are relevant not only for the interpretation of LFPs, but also for these other widely studied brain signals.

Our findings have several implications for the interpretation of the experimental data. First, the two opposite effects on the LFP-PSD that we observed from the same h-type conductance, depending on the synaptic input, have interesting consequences for the information content of the LFP signal. It implies that the LFP contains information about both the distribution of synaptic inputs and the level of synaptic correlation. Different input pathways to pyramidal neurons are known to target specific cell regions (Petreanu et al., 2009; Hooks et al., 2013); hence, the emergence of a resonance in the LFP-PSD could indicate the activation of an apical input pathway to a neural population in the vicinity of the recording electrode. Likewise, the emergence of an amplification of the low frequencies of the LFP-PSD could indicate an increase in correlations between synaptic inputs that target the entire neuron.

A second implication concerns peaks observed in the LFP-PSD, which are commonly interpreted as oscillations in the firing rate of the neural populations that drive the LFP-generating neurons (Buzsáki and Draguhn, 2004; Nolan et al., 2004; Roberts et al., 2013; Hadjipapas et al., 2015). We demonstrated that peaks in the LFP-PSD can also be caused by apical input to populations of I_h-expressing pyramidal cells. Hence, further signal analysis and/or experiments would be needed to establish the source of such peaks in the LFP-PSD.

Third, our findings have implications for the interpretation of putative power laws in recorded brain signals like the LFP and EEG. Various origins of such putative power laws have been proposed (Beggs and Plenz, 2003; Bédard et al., 2006; Bédard and Destexhe, 2009, El Boustani et al., 2009; Miller et al., 2009; Pettersen et al., 2014). Here, we observed that the slope of the PSD was strongly affected by the synaptic input site and the synaptic correlation level (but see also Łęski et al., 2013), as well as by the type and distribution of membrane conductances (Fig. 4), which implies that the asymmetric cellular distribution of the h-type conductance might affect putative power laws in LFP and EEG signals.

Effect of spiking

The cortical LFP is thought to predominantly reflect synaptic input and the associated return currents (Pettersen et al., 2008; Haider et al., 2016); however, it might contain components from both subthreshold and suprathreshold activity (Suzuki and Larkum, 2017). The combined effects of all active conductances on the cortical LFP have previously been explored in comprehensive network simulations with spiking neurons (Reimann et al., 2013). Our study instead attempts to disentangle the important factors in shaping the LFP, focusing on the subthreshold activity. The characterization of the importance of spiking and the nature of the effect on the LFP should be addressed in a separate study, but note that any contribution from spiking activity would, because of linearity, come in addition to the effects of the subthreshold active currents. Last, note that even though we expect the cortical LFP to be dominated by synaptic input, the hippocampal LFP is expected to contain a much larger spiking component because of the strongly correlated firing associated with, for example, sharp-wave ripples (Schomburg et al., 2012; Scheffer-Teixeira et al., 2013; Sinha and Narayanan, 2015; Taxidis et al., 2015).

Outlook

Experimental verification of our model predictions could be pursued, for example, through in vitro cortical slice experiments. Using an experimental paradigm that allows for region-specific activation of cortical pyramidal cells (Petreanu et al., 2009; Hooks et al., 2013), one can provide correlated basal, apical, or homogeneous input to a population of layer 5 pyramidal cells, with or without the presence of an I_h blocker, like ZD7288. We predict that (1) for basal input, the effect of the blocker on the LFP-PSD will be small; (2) for apical input, the blocker will remove a resonance in the LFP-PSD; and (3) for homogeneous input, the blocker will substantially decrease power at low frequencies of the LFP-PSD.

The overall effect of I_h on the LFP will be twofold: (1) I_h will affect the timing of the synaptic inputs by modifying the spiking dynamics of the network (Hutcheon et al., 1996, 2000; Magee, 1999; Migliore et al., 2004; Nolan et al., 2004; Angelo et al., 2007; Narayanan and Johnston, 2008; Neymotin et al., 2013); and (2) I_h will affect the LFP by molding the return currents following each synaptic input (Ness et al., 2016). In this study, we were able to isolate the effect of the second point by using identical synaptic inputs to populations of cells with different intrinsic conductances. Under these conditions, we gained a thorough understanding of the direct effects on the LFP from subthreshold active conductances, and in particular I_h. However, now that we have developed a good understanding of the direct effect of I_h on the LFP, a natural extension of this project would be to use this knowledge to address the next question: what is the overall effect of I_h on the LFP?

Closing statement

Identifying I_h as the cause of a low-frequency amplification or a resonance in the LFP-PSD would be difficult in complex simulations with network interactions and spiking, and even more so in experiments. However, having identified I_h as a key player, its signatures can be searched for in LFPs both from large-scale brain simulations (Markram et al., 2015; Hagen et al., 2016) and from experimental data. This highlights the importance of working with simplified models, as it allows the dissection of complicated brain signals. We believe that this work is an important step in the direction of a better understanding of the cortical LFP signal, which is needed to take full advantage of this brain signal in the future.