Neural Dynamics of Variable Grasp-Movement Preparation in the Macaque Frontoparietal Network

Abstract

Our voluntary grasping actions lie on a continuum between immediate action and waiting for the right moment, depending on the context. Therefore, studying grasping requires an investigation into how preparation time affects this process. Two macaque monkeys (Macaca mulatta; one male, one female) performed a grasping task with a short instruction followed by an immediate or delayed go cue (0–1300 ms) while we recorded in parallel from neurons in the grasp preparation relevant area F5 that is part of the ventral premotor cortex, and the anterior intraparietal area (AIP). Initial population dynamics followed a fixed trajectory in the neural state space unique to each grip type, reflecting unavoidable movement selection, then diverged depending on the delay, reaching unique states not achieved for immediately cued movements. Population activity in the AIP was less dynamic, whereas F5 activity continued to evolve throughout the delay. Interestingly, neuronal populations from both areas allowed for a readout tracking subjective anticipation of the go cue that predicted single-trial reaction time. However, the prediction of reaction time was better from F5 activity. Intriguingly, activity during movement initiation clustered into two trajectory groups, corresponding to movements that were either “as fast as possible” or withheld movements, demonstrating a widespread state shift in the frontoparietal grasping network when movements must be withheld. Our results reveal how dissociation between immediate and delay-specific preparatory activity, as well as differentiation between cortical areas, is possible through population-level analysis.

SIGNIFICANCE STATEMENT Sometimes when we move, we consciously plan our movements. At other times, we move instantly, seemingly with no planning at all. Yet, it's unclear how preparation for movements along this spectrum of planned and seemingly unplanned movement differs in the brain. Two macaque monkeys made reach-to-grasp movements after varying amounts of preparation time while we recorded from the premotor and parietal cortex. We found that the initial response to a grasp instruction was specific to the required movement, but not to the preparation time, reflecting required movement selection. However, when more preparation time was given, neural activity achieved unique states that likely related to withholding movements and anticipation of movement, shedding light on the roles of the premotor and parietal cortex in grasp planning.

Introduction

Some actions, such as reacting to a spilling cup of coffee, demand an instant response. Others, such as waiting before a traffic light, require withholding our actions for the right moment. Most of our actions lie on the continuum between the two, and although many actions are carefully planned before they are executed (Kutas and Donchin, 1974; Ghez et al., 1997), we are often required to act with little or no warning. Various studies have examined how movements are prepared and held in memory in the primate brain (Wise, 1985; Riehle and Requin, 1989), but only a few have contrasted well-planned movements with situations where little or no planning is possible (Wise and Kurata, 1989; Crammond and Kalaska, 2000; Churchland et al., 2006; Yu et al., 2009; Ames et al., 2014). None, to our knowledge, has systematically probed the transition between immediate and planned grasping movements in the behaving primate.

Delayed-movement paradigms, in which actions must be withheld before they are executed, have shown that activity in the premotor and parietal cortex can be used to decode and disentangle object properties and hand shapes during preparation (Baumann et al., 2009; Fluet et al., 2010; Townsend et al., 2011; Schaffelhofer et al., 2015; Schaffelhofer and Scherberger, 2016) and during movement (Menz et al., 2015). Furthermore, preparatory activity in the premotor (Churchland et al., 2006; Afshar et al., 2011) and parietal cortex (Snyder et al., 2006; Michaels et al., 2015) is correlated with reach-and-grasp reaction time, and perturbing this preparation state in the premotor cortex delays subsequent movement (Day et al., 1989; Churchland and Shenoy, 2007; Gerits et al., 2012), a clear indication of a functional contribution to action planning and execution.

Recent studies have employed a state space framework of population activity (for review, see Cunningham and Yu, 2014). Under this framework, the firing of each neuron represents a dimension in a high-dimensional space of all neurons where the firing of all neurons at a particular time represents a single point in the space of all potential network states. For example, preparatory activity in the motor cortex acts as an initial state for subsequent movement dynamics (Churchland et al., 2012), and when reaches are cued, the neural population in the dorsal premotor cortex (PMd) immediately bypasses the state space achieved during delayed movements (Ames et al., 2014), suggesting that successful preparation of the same reach may be achieved through different neural trajectories. While some studies show that after adequate preparation time, activity stabilized in the state space, other studies suggest that the premotor cortex may track time or expectation (Carnevale et al., 2015). Only an analysis of the full continuum of preparation from immediate to fully planned movements can provide an understanding of the complex interaction between movement planning and execution. Furthermore, it has been proposed that delayed and immediate movements are controlled quite differently, termed proactive and reactive control, respectively (Braver, 2012), a feature that has not been investigated in the premotor cortex.

To address these questions, we recorded neural populations from the grasping circuit consisting of the hand area (F5) of the ventral premotor cortex and the anterior intraparietal area (AIP) while two macaque monkeys performed a delayed grasping task, with a memory component, in which preparation time was systematically varied using 12 discrete delays (0–1300 ms). We found that the neural states achieved during longer delays were bypassed during immediately cued grasps. However, the initial trajectory was specific to each grip type, but the same regardless of delay, providing evidence that this activity may be required for movement selection. Activity in the AIP was less dynamic than in F5 during the memory period. Both populations included a representation of anticipation throughout the memory period that predicted reaction time. However, prediction was better from F5 neurons. Interestingly, activity in both areas formed distinct long-delay and short-delay clusters following the go cue, demonstrating that a network-wide shift occurs when movements are withheld and executed from memory.

Materials and Methods

Basic procedures.

Neural activity was recorded simultaneously from area F5 and the AIP in one male and one female rhesus macaque monkey (Macaca mulatta; Monkeys B and S; body weight, 11.2 and 9.7 kg, respectively). Animal care and experimental procedures were conducted in accordance with German and European law and were in agreement with the Guidelines for the Care and Use of Mammals in Neuroscience and Behavioral Research (National Research Council, 2003). Authorization for conducting this experiment was delivered by the Animal Welfare Division of the Office for Consumer Protection and Food Safety of the State of Lower Saxony, Germany (permit no. 032/09 and 14/1442).

Basic experimental methods have been described previously (Michaels et al., 2015; Dann et al., 2016). We trained monkeys to perform a delayed grasping task. They were seated in a primate chair and trained to grasp a handle with the left hand (Monkey B) or the right hand (Monkey S; Fig. 1a). A handle, placed in front of the monkey at chest level at a distance of ∼26 cm, could be grasped either with a power grip (opposition of fingers and palm) or precision grip (opposition of index finger and thumb; Fig. 1b, insets). Two clearly visible recessions on either side of the handle contained touch sensors that detected thumb and forefinger contact during precision grips, whereas power grips were detected using an infrared light barrier inside the handle aperture. The monkey was instructed which grip type to make by means of two colored LED-like light dots projected from a thin-film transistor (TFT) screen (CTF846-A; screen size: 8 inch digital; resolution: 800 × 600; refresh rate: 75 Hz) onto the center of the handle via a half mirror positioned between the monkey's eyes and the target. A mask preventing a direct view of the image was placed in front of the TFT screen and two spotlights placed on either side could illuminate the handle. Apart from these light sources, the experimental room was completely dark. In addition, one or two capacitive touch sensors (Model EC3016NPAPL, Carlo Gavazzi) were placed at the level of the monkey's mid-torso and functioned as hand-rest buttons, preventing any premature movement of the hands. The nonacting arm of Monkey B was placed in a long tube, preventing it from interacting with the handle. Monkey S was trained to keep her nonacting hand on an additional hand-rest button.

Figure 1.

Task design, implantation, and behavior. a, Illustration of a monkey in the experimental setup. The cues were presented on a masked monitor and reflected by a mirror such that cues appeared superimposed on the grasping handle. b, Delayed grasping task with two grip types (top, power grip; bottom, precision grip). Trials were presented in pseudorandom order in darkness and with the handle in the upright position. c, d, Plots of RT and MT against delay length for all successful trials of both monkeys. Boxes represent the median and 25th/75th percentiles for each delay bin, while whiskers mark ∼±2.7 SDs. Outliers are shown as individual points. e, f, Array locations for Monkeys S (e) and B (f). Two arrays were placed in F5 on the bank of the arcuate sulcus (AS) and two were placed in the AIP toward the lateral end of the intraparietal sulcus (IPS). In Monkey B two more arrays were placed on the bank of the central sulcus (CS). These were not used in this study. The cross shows medial (M), lateral (L), anterior (A), and posterior (P) directions. Note that Monkey S was implanted in the left hemisphere and Monkey B was implanted in the right hemisphere.

Eye movements were measured using an infrared optical eye tracker (Model AA-ETL-200, ISCAN) via a heat mirror directly in front of the monkey's head. To adjust the gain and offset, red calibration dots were shown at different locations at the beginning of each session for 25 trials that the monkey fixated for ≥2 s. Eye tracking and the behavioral task were controlled by custom-written software implemented in LabView Realtime (National Instruments) with a time resolution of 1 ms. An infrared camera was used to monitor behavior continuously throughout the experiment, additionally ensuring that monkeys did not prematurely move their hands or arms.

Task design.

The trial course of the delayed grasping task is shown in Figure 1b. Trials started after the monkey placed the acting hand on the resting position and fixated a red dot (fixation period). The monkey was required to keep the acting hand or, in the case of Monkey S, both hands completely still on the resting position until 150 ms after the go cue. After a variable period of 400–700 ms, two flashlights illuminated the handle for 300 ms, followed by 600 ms of additional fixation. In the cue period, a second light dot was then shown next to the red one to instruct the monkey about the grip type for this trial (grip cue). Either a green or white dot appeared for 300 ms, indicating a power or a precision grip, respectively. After that, the monkey had to either react immediately or memorize the instruction for a variable memory period (also referred to as delay length). This memory period lasted for 0–1300 ms, in discrete memory period bins of 0, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, or 1300 ms (i.e., the go cue could appear simultaneously with the grip cue, which was always presented for 300 ms regardless of the length of the delay). Switching off the fixation light then cued the monkey to reach and grasp the target (movement period) to receive a liquid reward. Monkeys were required to hold the appropriate grip for 300 ms. A failed trial occurred if the monkeys stopped fixating the central point before movement onset, moved their hand from the hand-rest sensor, performed the incorrect grip, or took >1100 ms to complete the movement following the go cue. Additionally, no-movement trials were randomly interleaved (8% of trials), in which a go cue was never shown and the monkey only received a reward if it maintained fixation and kept hands on the hand rests for 2000 ms following the grip cue. All trials were randomly interleaved and, apart from the 300 ms handle-illumination period, conducted in total darkness.

Surgical procedures and imaging.

Upon completion of behavioral training, each monkey received an MRI scan to locate anatomical landmarks for subsequent chronic implantation of microelectrode arrays. Each monkey was sedated (e.g., 10 mg/kg ketamine and 0.5 mg/kg xylazine, i.m.) and placed in the scanner (GE Healthcare 1.5T or Siemens Trio 3T) in a prone position. T1-weighted volumetric images of the brain and skull were obtained as described previously (Baumann et al., 2009). We measured the stereotaxic location and depth orientation of the arcuate and intraparietal sulci to guide placement of the electrode arrays.

An initial surgery was performed to implant a head post (titanium cylinder; diameter, 18 mm). After recovery from this procedure and subsequent training of the task in the head-fixed condition, each monkey was implanted with floating microelectrode arrays (FMAs; MicroProbes for Life Science) in a separate procedure. Monkey B was implanted with six electrode arrays in the right hemisphere, each with 32 electrodes (Fig. 1f). Two such arrays were implanted in area F5, two in the AIP, and two in area M1. Monkey S was implanted with four FMAs in the left hemisphere and received two arrays in each area (Fig. 1e). The arcuate sulcus of Monkey S did not present a spur, but in the MRI a small indentation was visible in the posterior bank of the arcuate sulcus, ∼2 mm medial to the knee, which we treated as the spur. We placed both anterior FMAs lateral to that mark. FMAs consisted of nonmoveable monopolar platinum-iridium electrodes with initial impedances ranging between 300 and 600 kΩ at 1 kHz measured before implantation and verified in vivo. Lengths of electrodes were between 1.5 and 7.1 mm.

All surgical procedures were performed under sterile conditions and general anesthesia (e.g., induction with 10 mg/kg ketamine, i.m., and 0.05 mg/kg atropine, s.c., followed by intubation, 1–2% isofluorane, and analgesia with 0.01 mg/kg buprenorphene). Heart and respiration rate, electrocardiogram, oxygen saturation, and body temperature were monitored continuously. Systemic antibiotics and analgesics were administered for several days after each surgery. To prevent brain swelling while the dura was open, the monkey was mildly hyperventilated (end-tidal CO₂, ∼30 mmHg) and mannitol was kept at hand. Monkeys were allowed to recover fully (∼2 weeks) before behavioral training or recording experiments commenced.

Neural recordings and spike sorting.

Signals from the implanted arrays were amplified and digitally stored using a 128-channel recording system (Cerebus, Blackrock Microsystems; sampling rate, 30 kS/s; 0.3–7500 Hz hardware filter). Data were first filtered using a median filter (window length, 3 ms) and the result subtracted from the raw signal, corresponding to a nonlinear high-pass filter. Afterward, the signal was low-pass filtered with a non-causal Butterworth filter (5000 Hz; fourth order). To eliminate common noise sources (i.e., movement noise, common component induced by reference and ground), principal components analysis (PCA) artifact cancellation was applied for all electrodes of each array (Musial et al., 2002; Dann et al., 2016). To ensure that no individual channels were eliminated, PCA dimensions with any coefficient >0.36 (with respect to normalized data) were retained. Spike waveforms were extracted and semiautomatically sorted using a modified version of the off-line spike sorter Wave_clus (Quiroga et al., 2004; Kraskov et al., 2009; Dann et al., 2016).

Units were classified as single or nonsingle units, based on the following five criteria: (1) the absence of short (1–2 ms) intervals in the interspike interval histogram for single units, (2) the homogeneity and SD of the detected spike waveforms, (3) the separation of waveform clusters in the projection of the first 15 features (a combination for optimal discriminability of principal components, single values of the wavelet decomposition, and samples of spike waveforms) detected by Wave_clus, (4) the presence of well-known waveform shapes characteristics for single units, and (5) the shape of the interspike interval distribution.

After the semiautomatic sorting process, redetection of the average waveforms (templates) was done to detect overlaid waveforms (Gozani and Miller, 1994). Filtered signals were convolved with the templates starting with the biggest waveform. Independently for each template, redetection and resorting were run automatically using linear discriminant analyses for classification of waveforms. After the identification of the target template, the shift-corrected template (achieved by up and down sampling) was subtracted from the filtered signal of the corresponding channel to reduce artifacts for detection of the next template. This procedure enabled detection of templates up to an overlap of 0.2 ms. Unit isolation was evaluated again as described before to determine the final classification of all units into single or multiple units. Units were only classified as single if they unambiguously met the five criteria.

Experimental design and statistics.

Three macaque monkeys participated in this study (see Basic procedures and Additional experiment). However, statistical analysis was performed across recorded units or populations of units across recording sessions, as commonly accepted in primate system neurophysiology. Statistical procedures are described in the following sections.

Data preprocessing.

Although units were classified as single or multiple units, all recorded units with an average firing rate of ≥2 Hz were used. A detailed list of recording sessions can be found in Table 1. After spike sorting, spike events were binned in nonoverlapping 1 ms windows. For all analyses, single-trial spike trains were smoothed with a Gaussian window (σ = 50 ms) and down-sampled to 100 Hz. Data were aligned to two events: the presentation of the grip cue and movement onset, i.e., the time when the monkey's hand left the hand-rest button. The cue alignment proceeded from 100 ms before cue onset until the go cue. The movement onset alignment proceeded from movement onset minus the median RT for each delay condition until 400 ms after movement onset. These two alignments were concatenated in time to produce a continuous signal. Average firing rates were then calculated by averaging over all trials of the same condition.

Table 1.

Trial counts, performance, and number of units recorded for all datasets

Session	Trial count	Correct performance	Units recorded in F5	Units in F5 meeting retention criteria	Units Recorded in the AIP	Units in the AIP meeting retention criteria
B1–B6
B1	485	91%	78	48	36	26
B2	685	96%	86	53	38	28
B3	586	96%	57	35	32	18
B4	814	96%	60	38	26	19
B5	775	96%	66	34	27	18
B6	745	97%	65	44	33	21
Mean	682	95.3%	68.7	42.0	32.0	21.7
S1–S6
S1	502	98%	108	74	139	102
S2	514	97%	116	75	134	100
S3	571	97%	132	99	127	102
S4	658	99%	133	92	131	109
S5	590	99%	139	103	136	100
S6	546	98%	129	98	130	98
Mean	564	98.0%	126.2	90.2	132.8	101.8

Dimensionality reduction.

To extract an informative set of projections in our neural populations (see Fig. 3), we applied separately for each area and recording session a form of targeted dimensionality reduction (Mante et al., 2013) to all units from 100 ms before cue onset to movement onset. In the case of the no-movement condition, we used activity from 100 ms before cue onset to reward onset. In this method, the z-scored activity of each unit over all trials was first regressed against a set of predetermined task signals, which is expressed as follows (Eq. 1): r_k,i = β_i,1grip_k + β_i,2cueGrip_k + β_i,3moveGrip_k + β_i,4CI_k + β_i,5cueCI_k + β_i,6moveCI_k + β_i,7goCI_k + β_i,8, where r_k,i is the normalized firing rate of unit i of N across all time points of each trial k, and β ∈ R^N×8 is the set of regression weights. The task signals were constructed as follows: grip was 0 before grip cue onset, and either 1 or −1 for the rest of each trial, for precision and power grip, respectively. cueGrip was 1 or −1 during the grip cue depending on the grip type, and 0 all other time points. moveGrip was 0 until 200 ms before movement onset, after which it was 1 or −1, depending on the grip type. CI was a condition-independent signal that was 0 during fixation and 1 all other time points. cueCI was a signal that was 1 during the 300 ms grip cue and 0 all other time points. moveCI was 0 until 200 ms before movement onset and 1 after. goCI was 0 until the go cue and 1 after.

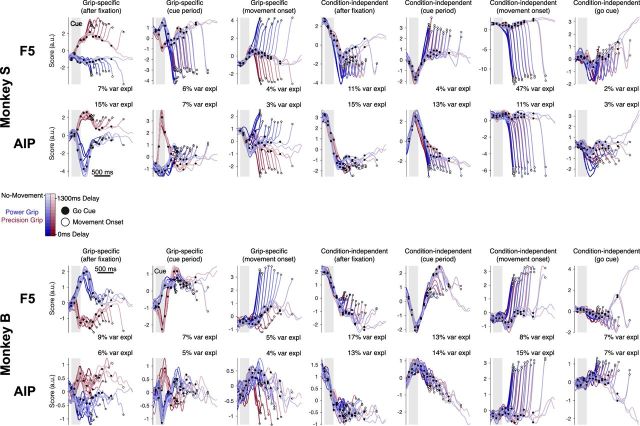
Figure 3.

Targeted dimensionality reduction of neural trajectories in F5 and the AIP. Population data of all conditions, for each area and dataset separately, were projected into a seven-dimensional task space as determined by targeted dimensionality reduction (see Materials and Methods). A single-session trial-averaged example is shown for Monkey S (Session S4, top) and Monkey B (Session B2, bottom). Trajectories begin 100 ms before the grip cue and end at movement onset. For the no-movement condition, data is plotted from 100 ms before the grip cue until reward onset.

To capture independent variance in each of our task-specific axes, we orthogonalized the task dimensions using QR-decomposition, expressed as follows (Eq. 2): β = QR, where Q is an orthogonal matrix and R is an upper triangular matrix. The orthogonal axes, β_⊥, are then constructed from the first seven columns of Q.

Finally, to estimate the contribution of the neural population to the task-specific dimensions, we projected the z-scored, trial-averaged data onto the orthogonal task axes, as follows (Eq. 3):

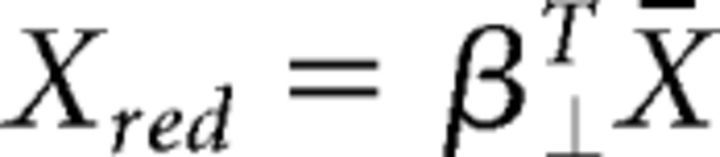where X̄ ∈ ℝ^N×CT is the z-scored and trial-averaged neural data, C is the number of conditions, and T is the average number of time points per condition. Note that a different number of time points was used for each condition due to the varying delays.

Variance explained per dimension was calculated by zeroing all columns of β_⊥ except the dimension of interest and calculating the R-square between X̄ and β_⊥(β_⊥^TX̄).

Distance analysis.

To find the neural distance between two conditions over time, we calculated the minimum Euclidean distance (point-to-curve distance) between the two trajectories in the full neural space. Three versions of this analysis were performed. For the distance in Figure 4a, we iterated through all time points on a delayed trajectory (in steps of 10 ms) and calculated the Euclidean point-to-curve distance from the delayed (1000 ms) trajectory to the nondelayed (0 ms) trajectory, where the point-to-curve distance is the minimum distance from a specific time point on the delayed trajectory to all points on the nondelayed trajectory. Minimum distance, as a conservative measure, was used to overcome the different time courses of the conditions being compared. Small distances indicate that the two trajectories achieve a similar point in neural space at some point in time, while large distances indicate that the two trajectories do not pass through a similar point in the high-dimensional space. Euclidean distances were normalized by the square root of number of units to make spaces with different number of units comparable.

Figure 4.

Point-to-curve distance between delayed (1000 ms) and nondelayed (0 ms) trajectories. a, Minimum Euclidian distance in the full neural space between each time point on the delayed trajectory (in steps of 10 ms) and the entire nondelayed trajectory over time for two example datasets (B2-Power, S6-Precision) from both areas and monkeys. The black line represents the minimum point-to-curve distance between the delayed and nondelayed trajectory, while the gray line represents the chance level (see Materials and Methods). Black bars along the top of plots denote times when the distance is significantly greater than chance level (bootstrapping procedure with 1000 resamples, p = 0.01; see Materials and Methods). Error bars represent the fifth and 95th percentiles of the distances generated by the bootstrapping procedure. b, Fraction of significant distances over all datasets and grip types (6 datasets × 2 grip types). Error bars represent the SEM over datasets and grip types. c, Difference in onset of grip and delay separation over all datasets and grip types (6 datasets × 2 grip types).

For the distance analysis in Figure 4c, distance between the delayed trajectories (1000 ms) of each grip type was calculated in the same manner to determine when grip information becomes present in the population.

For the distance analysis in Figure 5, the Euclidean distance was calculated between all pairs of time points on the same trajectory and used in conjunction with the bootstrapping procedure (next section) to determine whether two points significantly differed.

Figure 5.

Neural trajectory stability over the course of no-movement trials. a, Mean Euclidean distance in the full neural space for the no-movement trials between all pairs of time points over both grip types for example datasets in each monkey (Sessions B5, S3). Cue, cue epoch; Mem, mem epoch; Rew, reward epoch. All plots are clipped at 8 spikes/s for visualization. b, For each pair of time points, distance results were tested for a significant difference using a bootstrapping procedure (1000 resamples in steps of 50 ms, p = 0.01). Panels show time pairs where a significant difference was found in the dataset of a for both grip types (white), one grip type (gray), or in no condition (black). c, Percentage of time points showing a significant difference over all datasets and grip types (6 datasets × 2 grip types) separately for each monkey and area. d, Mean distance between all time points during the stable portion of the memory period (650–1800 ms after cue onset; a, dashed box) for all individual datasets and grip types (6 datasets × 2 grip types) across areas and paired according to recording session. Stars indicate a significant difference (Wilcoxon sign-rank test, p < 0.001).

Bootstrap procedure.

To gain an estimate of underlying trial-to-trial variability, we performed a bootstrap analysis. This procedure was in general the same, but with slight variations for the different distance analyses presented above. We resampled trials from each condition randomly, with replacement, of the same size as the number of recorded trials in that condition. We then constructed average firing rates for each condition and carried out the appropriate distance analysis as described above (e.g., minimum distance between delayed and nondelayed trajectory). This resampling was done 1000 times, producing a distribution of distances.

To obtain an estimate of how much distance is expected between trajectories by chance, we carried out another resampling in which a trajectory was resampled from itself to determine its underlying variability. Trajectories were resampled once with the number of trials observed in that condition and once using the number of trials recorded in the other trajectory in the comparison. Then the Euclidean distance was calculated as described in the previous section. The overlap of these distributions was then used to generate a p value for each time point. This analysis enabled us to determine when an observed distance was significantly greater than the distance expected if two trajectories were generated from the same underlying distribution.

For chance analyses in Figure 5, resampling of trials was carried out 1000 times, with replacement, for each condition and dataset. For each of the 1000 resampling steps the same trajectory was resampled twice, termed p and p′. Then, for every pair of time points (t₁ and t₂), the resampled distance along the first trajectory d = d[p(t₁), p(t₂)] was compared with the two intertrajectory distances at time t₁ and t₂: d₁ = d[p(t₁), p′(t₁)] and d₂ = d[p(t₂), p′(t2)]. We determined the percentile of resamples (across all 1000) for which the along-trajectory distance d exceeded both intertrajectory distances: d > max(d₁, d₂). This percentile determined a specific p value for each time pair (t₁, t₂). The resampled distance, d, was then considered significant if p < 0.01. In this way, the significance level was dependent on which time points were compared along the trajectory, establishing a conservative estimate of the underlying trial-to-trial variability.

Additional experiment.

For Figure 6, we analyzed data from an additional experiment originally described by Michaels et al. (2015). Monkey Z performed a similar task to the current study requiring the monkey to grasp a handle with the same two grip types (6 datasets × 2 grip types × 3 task types: Instructed, Free choice, and Delayed instructed). Only Instructed trials with the same cues and cue length as the task of this study were used for this analysis, leading to an average (±SD) of 267 ± 55 trials per session. Furthermore, the memory period was also variable (1100–1500 ms). However, all trials resulted in movement, regardless of condition. The average (±SD) number of units recorded in F5 and AIP were 85 ± 18 and 81 ± 24, respectively.

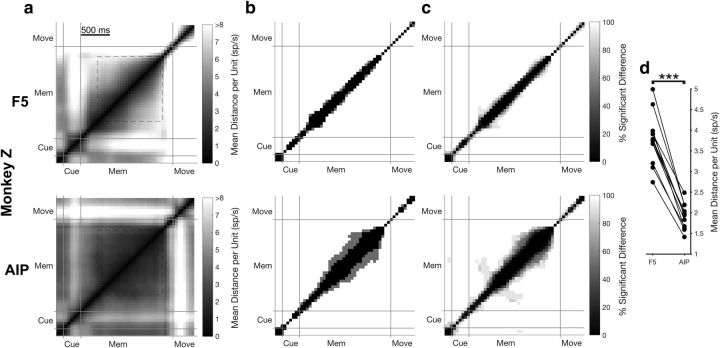
Figure 6.

Neural trajectory stability over the course of instructed trials for an additional experiment. Same layout as Figure 5. a, Mean Euclidean distance in the full neural space for the Instructed trials between all pairs of time points over both grip types for an example dataset in Monkey Z (see Materials and Methods). Cue, cue epoch; Mem, memory epoch; Move, movement epoch. All plots are clipped at 8 spikes/s for visualization. b, For each pair of time points, distance results were tested for a significant difference using a bootstrapping procedure (1000 resamples in steps of 50 ms, p = 0.01). Panels show time pairs where a significant difference was found in the dataset of a for both grip types (white), one grip type (gray), or in no condition (black). c, Percentage of time points showing a significant difference over all datasets and grip types (6 datasets × 2 grip types). d, Mean distance over the stable portion of the memory period (650 ms after cue onset; go cue; a, dashed box) for all individual datasets and grip types (6 datasets × 2 grip types) across areas and paired according to recording session. Stars indicate a significant difference (Wilcoxon sign-rank test, p < 0.001).

Hazard rate.

To classify the temporal evolution of activity during the memory period, the z-scored, single-trial firing rate of each unit for the no-movement condition from cue onset until reward onset was fit with an anticipation function using the same targeted dimensionality technique described earlier (see Materials and Methods). The anticipation function can be described as the conditional probability that a movement will be required at a given moment, given that it has not occurred until this point. This type of anticipation has been termed the hazard rate, and we present it here precisely as presented by Janssen and Shadlen (2005). The hazard rate can be expressed as follows (Eq. 4):

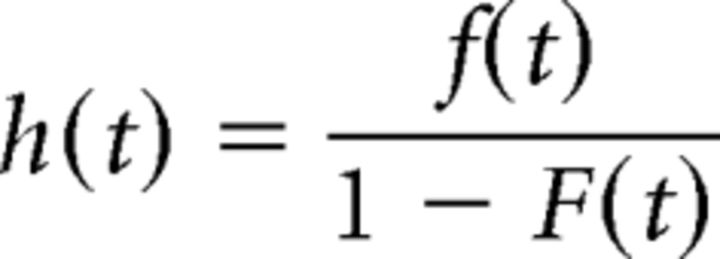where f(t) is the probability that a go cue will come at a given time after cue onset in 1 ms bins, and F(t) is the cumulative distribution, ∫_s=0^tf(s)ds.

As in Janssen and Shadlen (2005), to obtain an estimate of the monkey's internal representation of anticipation we calculate “subjective anticipation” based on the assumption that the animal is uncertain about time and that this uncertainty scales with time since an event. Therefore, before calculating hazard rate, we smoothed our probability density function, f(t), with a normal distribution where SD is proportional to elapsed time (Eq. 5):

The coefficient of variation, φ, is a Weber fraction, under the assumption that the experience of elapsed time carries uncertainty proportional to the true duration (Weber's Law). For all analyses, we used a value of 0.26, as has been calculated from behavioral experiments and used previously (Leon and Shadlen, 2003; Janssen and Shadlen, 2005). To obtain the final subjective anticipation function h̃(t), f̃(t) was substituted into Equation 4, along with its cumulative distribution, F̃(t).

Clustering analysis.

To evaluate whether delay trajectories leading up to movement onset clustered in a distinct way, we calculated the Euclidean distance between all pairs of linearly spaced delays (0–1000 ms, in steps of 10 ms) in the full neural space and looked for community structure (i.e., distinct clusters of similar value) in the resulting distance matrix. We employed a well-known modularity analysis that iteratively finds nonoverlapping groups of conditions that minimizes the within-group distance between conditions and maximizes the between-group distance (Newman, 2004; Reichardt and Bornholdt, 2006). We used γ sensitivities of 0.66 and 0.77 for Monkeys S and B, respectively. These γ levels were automatically selected so that ≤2 clusters were found. Note that this sensitivity does not force the existence of multiple clusters at any time. Each distance matrix was normalized to the maximum value over all time and subtracted from a matrix of ones to prepare them for analysis. To ensure that the found structure was not due to chance, we randomly permuted the distance matrix (1000 permutations, while conserving matrix symmetry) and compared the modularity index Q between the empirical and permuted data. The percentile of instances where the permuted distribution values exceeded the empirical value corresponds to the p value.

Results

Task and behavior

To investigate the continuum of grasp-movement preparation, we trained two macaque monkeys (B and S) to perform a delayed grasping task, with a memory component, in which the amount of preparation time was systematically varied between nondelayed (0 ms) and a long delay (1300 ms) in 12 distinct increments (see Materials and Methods). Monkeys fixated a central point (red dot), received a grip cue (300 ms) corresponding to either precision (white dot) or power grip (green dot), and were cued to perform this grip following a variable delay when the central fixation point turned off (Fig. 1a,b). The performance of both monkeys was high, correctly completing trials after receiving grip information 95 and 98% of the time for Monkeys B and S, respectively (Table 1). In addition to the normal task, we also randomly inserted no-movement trials to ensure that monkeys waited for the go cue before acting. Both monkeys completed these trials successfully (Monkey B: 100%; Monkey S: 97.7%).

In addition to number of correctly executed trials, reaction times (RTs) and movement times (MTs) of the monkeys provided useful insight into the performance of the task. RTs decreased steadily with increasing amounts of preparation (Rosenbaum, 1980), approaching a minimum after ∼400 ms of preparation (Fig. 1c), in line with previous findings (Churchland et al., 2006). RTs increased slightly for the longest delay. For Monkey S, MTs did not correlate with length of the delay period (Fig. 1d; r = 0.002, p = 0.91), indicating that although RT was slower for short delays, movements were only initiated once they were fully prepared. In Monkey B, there was a small positive correlation between delay and MT (Fig. 1d; r = 0.11, p < 0.001). Movement kinematics were likely similar regardless of delay, since the variability in mean MTs between different delay lengths was extremely small. The SDs in mean MTs (Monkey S: precision grip, 3.5 ms SD; power grip, 1.8 ms SD; Monkey B: precision grip, 14.2 ms SD; power grip, 10.8 ms SD) provide evidence that the kinematics of the movements did not vary between delays, especially for Monkey S. The number of errors showed no clear relationship to the length of the delay period, and the number of errors was extremely low, providing evidence that the monkeys could complete all conditions equally well.

Neural responses

We recorded six sessions of each monkey using floating microelectrode arrays for a total of 128 channels (64 in each area) simultaneously in F5 and the AIP (Fig. 1e,f) and single-unit and multi-unit activity was isolated (see Materials and Methods). For Monkey B, there were significantly more units recorded in area F5 than in the AIP (paired t test, p < 0.001), while for Monkey S, there was no significant difference (paired t test, p = 0.31). For individual session information see Table 1. For all analyses, we pooled single and multiple units together (mean ± SD recorded per session: Monkey S, 78 ± 8 single and 115 ± 5 multiple; Monkey B, 21 ± 6 single and 43 ± 7 multiple) and excluded units with a mean firing rate <2 Hz (on average 69% of units were retained; Table 1). All further analyses were based on these neural population sets. We evaluated grip-type tuning in both areas to ensure that the task successfully elicited task-related tuning. The average percentage of units tuned for grip type during the 200 ms following movement onset was 75 and 66% for F5 and the AIP, respectively (t test, p < 0.05). Additionally, on average 99 and 89% of units in F5 and the AIP, respectively, were significantly modulated from baseline (100 ms before cue onset) for ≥1 time point in one condition of the task (paired t test, p < 0.05, steps of 10 ms, Bonferroni-corrected for number of time-point comparisons). Amounts of grip tuning were very similar between monkeys and to previous studies of both F5 and the AIP (Lehmann and Scherberger, 2013; Michaels et al., 2015; Schaffelhofer et al., 2015; Michaels and Scherberger, 2018).

Interestingly, a wide variety of mixed activity patterns were present in both areas (Fig. 2). In many cases, the initial grip cue response was suppressed when the go cue appeared concurrently with the grip information (Fig. 2a,d), while in other cases the initial cue response was present regardless of delay (Fig. 2b,e). Other interesting responses were observed, such as a lone peak in activity strictly during the memory period (Fig. 2c) and typical movement-related activity specific to the grip type (Fig. 2f). All of these diverse types of responses were present in both F5 and the AIP. The broad variety of unit responses reveals a complex interaction between differing amounts of preparation, making strict categorization of individual neurons difficult.

Figure 2.

Example average firing rate curves of single units for delayed (1300 ms) versus nondelayed (0 ms) grasps. a–c, Example single units from area F5 of both monkeys showing (a) a suppressed cue response during nondelayed grasps, (b) an identical cue response for either delay, and (c) a large condition-independent response restricted to the delay period. d, e, Similar single-unit examples from the AIP of both monkeys. f, A typical movement period response selective for grip type. Delayed data were aligned to two events, grip cue onset and movement onset, and are separated by a gap, which marks the go cue. Nondelayed data were only aligned to movement onset. The later cue period was only present for nondelayed grasps. The cue was always presented for 300 ms regardless of delay. Curves and shaded bands represent mean and SEM, respectively.

Visualizing the population response

An alternative approach to categorizing single units is the state space framework, in which all units are considered as a high-dimensional space in which the firing of each unit represents one dimension. Due to the high dimensionality of neural data, we employed a targeted dimensionality reduction (TDR) method to find task-specific projection axes for visualization (see Materials and Methods). In this technique, projections of the neural population are found that are partially explained by task-specific signals, such as the presence of a grip cue, when the movement occurs, or grip-specific activity throughout the trial. In total, we regressed neural activity against a set of seven task-specific signals. Figure 3 shows the neural trajectories of exemplar data of each monkey (Sessions S4, B2). In both example sessions, a significant portion of the variance is explained by these projections (S4: 81% in F5, 67% in the AIP; B2: 65% in F5, 64% in the AIP). These example projections capture only 10% less variance than the first seven principal components that specify the optimal linear model. It's important to note that although we regressed neural activity on these specific signals, the information in each dimension is not restricted to explaining these signals, and therefore also varies with other internal processes.

In general, the condition-independent movement signal captured a large amount of variance, a feature observed previously in the motor cortex (Kaufman et al., 2016). The condition-independent signals tended to capture the most variance overall. The grip-specific signals independently separated the two grip conditions during their respective epochs: after fixation, during the cue period, and during movement. Additionally, activity separated by grip type quickly after grip cue onset (∼150 ms earlier; Fig. 3; grip-specific cue period signal), but did not appear to separate based on when the go cue appeared until later (∼≥300 ms; Fig. 3; condition-independent go cue signal). Together, the amount of variance explained and the high visual similarity between the projections across areas and monkeys indicate that our TDR reliably extracted task-specific signals. While this analysis is useful for visualization, it does not capture all neural variability. Therefore, almost all further analyses consider the entire neural population.

Unique memory state for delayed grasping movements

Given the large variability in population activity during the memory period seen in Figure 3, it is unclear whether memory states traversed during long delays are also traversed during immediately cued (nondelayed) movements. To test this possibility statistically, we used a continuous distance analysis (see Materials and Methods). We measured the minimum Euclidean distance (known as point-to-curve) between each time point on the trajectory of a delayed condition (1000 ms delay condition in steps of 10 ms) and the entire nondelayed trajectory (0 ms delay condition). For each recording session and each grip type, this was done separately in the full neural population space (all units with an average firing rate of ≥2 Hz) in each area to determine which points in the state space were traversed by both conditions and which were unique to longer-delayed movements. After the grip cue, distance between delayed and nondelayed trajectories rose and remained significantly above chance level until around movement onset or later in example datasets of both areas and monkeys (Fig. 4a; Sessions B2-Power, S6-Precision; bootstrapping procedure with 1000 resamples, p < 0.01; see Materials and Methods). Over all grip types and datasets, the same effect is present (Fig. 4b), showing that distance between the trajectories was most prevalent until around movement onset. The amount of divergence between the delayed and nondelayed trajectories was very similar in F5 and the AIP, indicating that when grasps are cued without a delay, the neural population of both areas bypass the states achieved by longer delays.

As mentioned earlier, it appeared in Figure 3 that the difference between grip types was present before the difference between delays. In other words, the effect of the grip cue appeared before the effect of the go cue. To test this, we repeated the distance analysis and additionally tested the Euclidean distance between grip conditions (Fig. 4c; see Materials and Methods). Comparing the first onset of significance between delay and grip effects for each dataset separately revealed that grip separation consistently appeared before delay separation in both areas and monkeys (Wilcoxon sign-rank test: F5 Monkey S, p = 0.002; AIP Monkey S, p < 0.001; F5 Monkey B, p = 0.003; AIP Monkey B, p = 0.016). On average across monkeys and areas, grip separation occurred 151 ms after cue onset and delay separation occurred 309 ms after cue onset.

Together, these results provide evidence that large portions of the state space traversed after the first ∼300 ms do not seem to be necessary for successfully executing grasping movements, and the activity in the first ∼300 ms likely represents unavoidable movement selection.

Dynamic memory states

Given that the trajectories of delayed and nondelayed grasps only overlap for the first ∼300 ms of preparation, what are the dynamics of the memory-period activity? To analyze the dynamics of the memory period, we systematically compared the Euclidean distance between all pairs of time points along the trajectories for the no-movement trajectories (Fig. 5a, example sessions S3 and B5). Dynamic activity should appear as large distances between trajectories everywhere except the diagonal (points close in time), while less dynamic activity should appear as a “block” of activity with a small distance between trajectories.

The strongest differences occurred shortly after grip cue onset and near reward. The neuronal trajectory during the memory period in F5 seemed to continuously progress in the absence of behavioral events. Meanwhile, the neuronal trajectory in the AIP was less dynamic. The effect becomes clearer when visualizing the time points that significantly differed (Fig. 5b; see Materials and Methods), showing a stereotypical “block” pattern in the AIP partially visible over all datasets (Fig. 5c). Taking the average distance during the portion of the memory period unaffected by cue or reward (650–1800 ms after cue onset) showed a significantly more dynamic representation in F5 than in the AIP (Fig. 5d; Wilcoxon signed-rank test, p < 0.001). Repeating the same analysis on delayed-movement trials (1300 ms delay) led to the same difference between F5 and the AIP in Monkey S (Wilcoxon signed-rank test, p = 0.01) and Monkey B (Wilcoxon signed-rank test, p = 0.002). Given the dynamic nature of population activity, especially in F5, is it possible that there were unique subsets of neurons that were drifting rather than remaining stable? To test this possibility, we repeated the Euclidean distance analysis in Figure 5 on all individual units separately, additionally z-scoring all units before analysis. However, the distribution of distances in both F5 and the AIP showed no signs of bimodality, supported by Hartigan's dip test (F5: p = 0.99; AIP: p = 0.80).

It is also important to consider that the probability of having to perform a movement did not remain constant throughout the trial, since the probability of being in the no-movement condition increased with time spent in the memory period. Therefore, it could be that the dynamic nature of the memory period in F5 reflects the change in necessity of the motor plan. To rule out this possibility, we repeated the current analysis on data of a similar experiment, in which movements were required in all conditions (see Materials and Methods). We found that the same interarea differences were present in this additional experiment (Fig. 6), lending further support to the observed dissociation between areas.

Tracking temporal signals in memory-period activity

Given the dynamic nature of activity during the memory period, does this activity follow any predictable pattern? As mentioned earlier, some units appeared to change their activity strictly during the memory period (Fig. 2c), even in the absence of behavioral cues. The observed pattern appears similar to the hazard rate, which in the current experiment is the probability of a go cue occurring at any moment, given that the go cue has not appeared yet (Janssen and Shadlen, 2005). The form of the hazard rate during no-movement trials and corresponding subjective anticipation function, which takes the monkey's uncertainty about time into account (see Materials and Methods), is shown in Figure 7a. RT was well predicted by subjective anticipation for short delays (0–400 ms), with a mean R-square of 0.55 and 0.60 for Monkey S and B, respectively, while RT was not well predicted by subjective anticipation for longer delays (500–1300 ms), with a mean R-square of 0.01 and 0.06.

Figure 7.

Representation of subjective anticipation across F5 and the AIP. a, Illustration of the probability of a go cue at all times during the delay (binned into 25 ms bins for visualization purposes), the hazard rate (Eq. 4), and the subjective anticipation function (Eq. 5 substituted into Eq. 4). b, Subjective anticipation axis as determined by targeted dimensionality reduction for all single trials of the no-movement condition across both brain regions (Session S5). c, Projection of F5 and the AIP onto the subjective anticipation axis 100 ms before the go cue correlated with single-trial RT for two delay bins in the same example dataset. d, Summary of RT prediction over all datasets. Stars denote a significant difference between areas (Wilcoxon sign-rank test, p < 0.05). e–g, Same as b–d for Monkey B (Session B4).

To extract neural correlates of this signal, we implemented TDR using only a single task dimension, in this case subjective anticipation, to predict the activity of individual units across both areas during the no-movement condition. To avoid overfitting, regression was cross-validated (leave-one-out) and regularized with an L2 penalty with weight 0.001. The L2 weight was determined by performing Bayesian optimization for each dataset (Matlab function: “fitrlinear”), then taking the median value across all datasets. Projection of single-trial neural data from the no-movement condition onto this axis fits the subjective anticipation function well, with an average R-square of 0.61 for Monkey S and 0.67 for Monkey B (p < 0.001), indicating that anticipation is significantly represented. Example datasets are shown in Figure 7b,e (data from Session S5 and B4). Interestingly, activity on the subjective anticipation axis appeared to be farthest away from the mean activity at movement onset when anticipation was highest at ∼1100 ms postcue (Fig. 7b,e, dashed lines), a finding that was replicated across all datasets of both monkeys. On average across datasets, the subjective anticipation axis explained 7 and 6% of the single-trial variance in F5 and the AIP, respectively.

Next, we projected neural data on movement trials of each area (all weights from nontarget area set to 0) onto the subjective anticipation axis. For this analysis, regression weights were averaged across cross-validation folds from the previous section to yield a single set of weights for each dataset. Interestingly, plotting the subjective anticipation axis activity conservatively measured 100 ms before the go cue against RT on all single trials revealed a consistent positive correlation that appeared to have two clear distributions (Fig. 7c,f) consisting of delays < or >500 ms. This relationship is especially evident in the example F5 dataset of Monkey B (Fig. 7f). The correlation with RT was positive for both delay distributions, both areas, and all datasets, indicating that higher anticipation along this axis led to slower RTs. Furthermore, for the longer delay bin there was a clear difference in prediction of RT between the areas in both monkeys (Fig. 7d,g; Wilcoxon sign-rank test, stars indicate p < 0.05), although this relationship was not present in the shorter delay bin in Monkey S.

Clustering of immediate and withheld movements from memory

While activity during the memory period was distinctly different for long and short delays (Fig. 4), activity had largely converged shortly after movement onset. Therefore, we wondered whether all delay length converged during movement initiation in a uniform manner or in distinct clusters. To visualize the clustering of individual unit activity for example datasets in F5, we plotted the activity of all linearly spaced delays (0–1000 ms) of a single grip type around movement onset (Fig. 8a). Looking specifically at ∼100 ms before movement onset, trajectories from the conditions with a delay of 0–500 ms and from the conditions with a delay of 500–1000 ms seem to form two clusters. This effect is also present in the AIP, where trajectories deflect into two distinct groups in a similar fashion (Fig. 9).

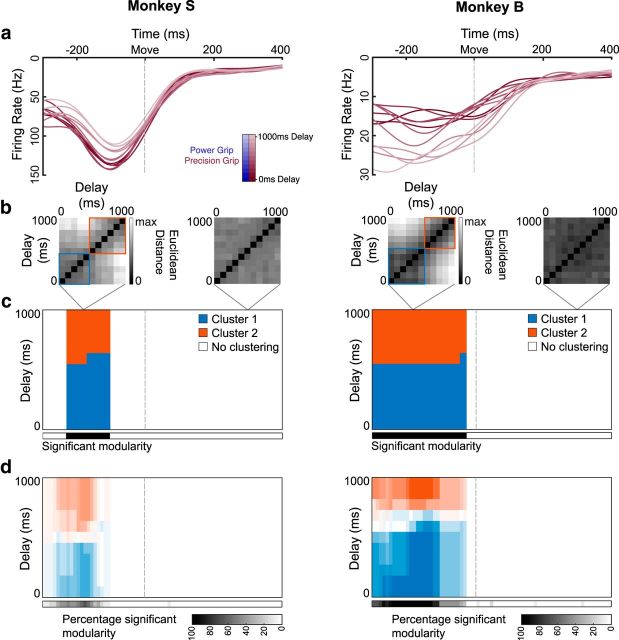
Figure 8.

Clustering of movement-initiation activity in F5. a, Example individual unit activity in F5 over all linearly spaced delays (0–1000 ms) for an example dataset from each monkey (Sessions S5-Precision, B2-Precision), aligned to movement onset. b, Euclidean distance between all pairs of delays in the full neural space for two example time points of the example dataset, including identified clusters, using a clustering analysis that finds community structure (see Materials and Methods). c, Clusters identified in the distance matrices over time (in steps of 10 ms) for the example dataset. Black significance bar shows time points where the modularity statistic exceeded chance level (permutation test, p < 0.01). d, Same analysis as c averaged over all datasets and grip types (6 datasets × 2 grip types).

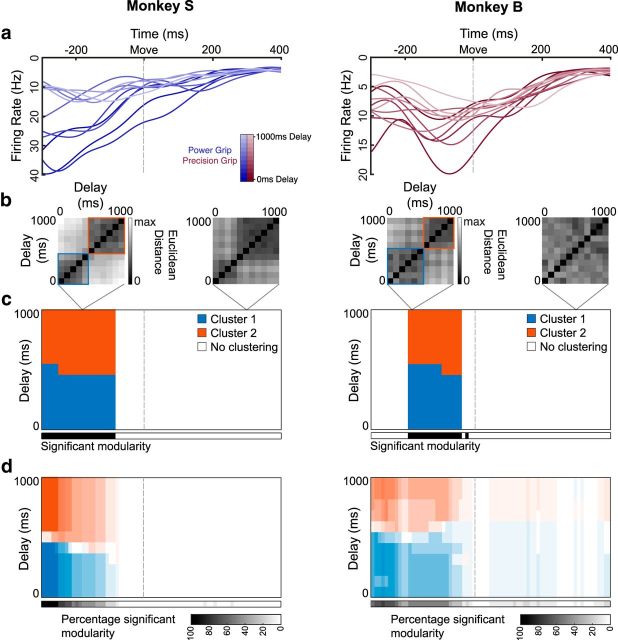
Figure 9.

Clustering of movement initiation activity in the AIP. Same layout as Figure 8. a, Example individual unit activity in the AIP over all linearly spaced delays (0–1000 ms) for an example dataset from each monkey (S3-Power, B2-Precision), aligned to movement onset. b, Euclidean distance between all pairs of delays in the full neural space for two example time points of the example dataset, including identified clusters, using a clustering analysis that finds community structure (see Materials and Methods). c, Clusters identified in the distance matrices over time (in steps of 10 ms) for the example dataset. Black significance bar shows time points where the modularity statistic exceeded chance level (permutation test, p < 0.01). d, Same analysis as c averaged over all datasets and grip types (6 datasets × 2 grip types).

To quantify clustering at the population level, we calculated the Euclidean distance between all pairs of delay lengths for each grip type separately in the full neural space (Fig. 8b) and looked for clusters in the distance matrices without assuming clustering a priori (see Materials and Methods). Two clusters were identified for the example dataset (Fig. 8c), showing a split around the 400–500 ms delay point that lasts until shortly before movement onset (permutation test, p < 0.01; see Materials and Methods). This pattern was very similar over all datasets (Figs. 8d, 9d), did not differ between grip types, and was present in both areas and monkeys, indicating that the state change that occurs between short and long delays spans both the frontal and parietal lobes.

Clustering is not likely due to different movement kinematics, since the MTs were nearly identical for all delay lengths (Fig. 1d), especially for Monkey S. However, since the time of movement onset is determined by the monkey's behavior, the time that has elapsed since the visual grip cue was presented could introduce a potential confound. Yet, differences in how long ago the grip cue was presented is unlikely to explain the two clusters, since repeating the same clustering analysis on the behavioral data (i.e., the mean time between cue presentation and movement onset for all delays) does not produce significant clustering for either grip type (permutation test: Precision grip, p = 0.97; Power grip: p = 0.97). These controls suggest that the separation of the neural trajectories into two distinct clusters reflects a robust effect of delay length in F5 and the AIP.

Discussion

To systematically probe the interplay between planning and movement in the grasping network, we recorded neural populations in premotor area F5 and the parietal AIP while two macaque monkeys performed a delayed grasping task with 12 distinct preparation times (0–1300 ms). First, the initial part (∼300 ms) of the neural space traversed was the same for all delays, but was grip-specific, providing evidence that this activity was an unavoidable part of selecting the correct movement. Next, population activity shifted into a separate state that was not achieved during short delays. The memory state was more dynamic in F5 than in the AIP, tracking subjective movement anticipation over time in both areas, but predicting RT more strongly in F5. Last, activity during movement initiation formed two distinct clusters, demonstrating a network-wide shift when movements need to be withheld. Our findings reinforce the notion that more global aspects of movements, such as the movement plan, as well as dynamic aspects, such as cue anticipation, can be well extracted at the population level.

As shown in Figure 4, separation between the neural trajectories occurred ∼150 ms earlier between the two grips than between long and short delays. This novel result indicates that while grip information is swiftly encoded in F5 and the AIP following the cue, responses to the go cue are delayed ≥150 ms relative to the grip information to facilitate the completion of the motor plan. Afterward, areas of the state space traversed by longer delays are not strictly necessary to produce successful movements, similar to the results of Ames et al. (2014) in the PMd.

In F5, the memory-period activity did not congregate in a specific region of the state space, a feature of F5 never before observed to our knowledge. This finding differs from the results of Ames et al. (2014) for the nearby PMd. They postulated that delay-period activity may act as an attractor state into which all trials would congregate given enough preparation time. It is possible that PMd activity would be more dynamic if an experimental design with a memory period were used, a point supported by studies showing that activity from some subregions of the premotor cortex can encode prior knowledge of when events are likely to occur (Mauritz and Wise, 1986; Carnevale et al., 2015). However, given current evidence, our results support the notion that strongly dynamic memory-period activity is a genuine feature of F5.

One possibility is that the temporal dynamics during the memory period are a result of an internalized representation of the likelihood of task events occurring at specific times throughout the memory period, known as hazard rate and previously observed in the lateral intraparietal cortex (Leon and Shadlen, 2003; Janssen and Shadlen, 2005). We observed a significant representation of subjective anticipation rate across both areas, although RT was more readily predicted from F5's projection onto this axis. Time dependence has been identified in prefrontal areas (Genovesio et al., 2006) and a growing body of literature suggests that time keeping is an intrinsic property of all neural networks (for review, see Goel and Buonomano, 2014). A mechanistic explanation for the dynamics observed during the memory period could be that recurrent networks of neurons in these areas generate temporal dynamics similar to a time code. The strongest evidence for this view comes from a recent study in which the presence or absence of a sensory stimulus on a given trial had to be reported (Carnevale et al., 2015). The authors found that the neural state space of the premotor cortex evolved over the course of the trial and was more sensitive to incoming sensory information during the fixed window that the monkeys knew would or would not contain the stimulus. Importantly, Carnevale et al. (2015) showed that a recurrent neural network model trained for optimal response sensitivity provided a sound explanation for the behavior of the monkey.

The results of Carnevale et al. (2015) raise important questions about the current results. They observed that delay activity should be closer to the decision boundary during the period most likely to contain stimulus information. However, in the current experiment, we explicitly observe that activity on the subjective anticipation axis moves away from the movement-initiation state (Fig. 7). How can these results be reconciled? The largest difference between our experiments is that in the work of Carnevale et al. (2015), detection of the stimulus is necessary to select a motor goal (left or right reach), while in our case the goal is specified by a separate cue and detection of the go cue is mainly necessary to decide when to act. Furthermore, the go cue is a very salient stimulus that persists throughout the remainder of the trial, requiring no heightened sensitivity. Therefore, we propose that the primary function of activity along the subjective anticipation axis in F5 and the AIP is to suppress movement, a conclusion supported by current theories of preparatory activity (Wong et al., 2015), our finding that RT is significantly predicted from this axis (Fig. 7), and our finding that activity on this axis moves away from the movement-initiation state.

One of the most striking features in both areas was that the population activity was highly variable at the time of go cue, yet converged rapidly leading up to movement onset (Figs. 3, 8). We propose that the broadly tuned nature of activity at the go cue provides the motor system with ample flexibility in movement initiation. Similar to the dynamics observed during the memory period, it could be that once movement is triggered, recurrent networks of neurons within these areas rapidly reduce variability within particular regions of the neural space to ensure correct muscle activation during initiation (Sussillo et al., 2015; Michaels et al., 2016). Under this framework, selecting between multiple movement plans would only require the neural population to be within a general region of activity. Such a framework is also in line with the finding that preparatory activity in PMd/M1 projects into the null space of upper-limb muscles and transitions into the potent space during movement (Kaufman et al., 2014), as this transition likely takes place during movement initiation when variability between movement plans is heavily reduced (Churchland et al., 2006). Once movement is initiated, activity would fall onto a common trajectory unique to each action plan. Future work must tackle the question of to what degree local circuit features or extrinsic inputs can account for the rapid decrease in trial-to-trial variability taking place before movement execution.

While variability decreased leading up to movement onset, trajectories clustered into two distinct groups splitting between delay conditions < or >400–500 ms (Figs. 8, 9). Given that fully taking advantage of preparatory time takes ∼400 ms, evidenced by the leveling of the RT curve (Fig. 1d), the two clusters could correspond to movements executed “as fast as possible” and movements executed from memory where the monkey must first wait for the go signal. Our results indicate that shifting between immediate movements and withheld movements from memory may cause a state shift in the frontoparietal network that produces the two clusters during movement initiation. Once the state has been changed, the trajectories continue to cluster for the entire period of movement initiation (up to shortly before movement onset). Specifically, the underlying cause of the shift is likely the transition from reactive to proactive control, i.e., the increased ability to properly anticipate a go cue after sufficient preparation times (Braver, 2012). This sensitivity to task timing is inherent in highly trained tasks and has been shown in the supplementary motor area (SMA; Chen et al., 2010) and in the medial frontal cortex (Stuphorn and Emeric, 2012). Humans with SMA lesions are not able to execute timed behavior as well as humans without SMA lesions (Halsband et al., 1993). This supports our findings, since F5 is closely connected to the pre-SMA (Luppino et al., 1993).

It remains a possibility that systematic differences in hand-shaping latencies or final posture between different delay lengths could contribute to the observed clustering. However, clustering of delay conditions was almost nonexistent after movement onset, especially in F5, making differences in final posture improbable. Although differences in hand-shaping during movement cannot be ruled out, the extreme similarity in MTs between delays (see Results), especially for Monkey S, makes this possibility unlikely.

In summary, our results provide novel insights and build on delayed reaching and grasping literature in the premotor (Cisek et al., 2003; Lucchetti et al., 2005; Fluet et al., 2010) and parietal cortex (Murata et al., 1996; Snyder et al., 2006; Baumann et al., 2009). We show that dissociation of global and dynamic aspects of movement, such as the movement plan and the anticipation over time, respectively, can be coherently extracted at the level of neural populations and allow for comparison and dissociation between interacting cortical areas.