Active Braking of Whole-Arm Reaching Movements Provides Single-Trial Neuromuscular Measures of Movement Cancellation

Abstract

Movement inhibition is an aspect of executive control that can be studied using the countermanding paradigm, wherein subjects try to cancel an impending movement following presentation of a stop signal. This paradigm permits estimation of the stop-signal reaction time or the time needed to respond to the stop signal. Numerous countermanding studies have examined fast, ballistic movements, such as saccades, even though many movements in daily life are not ballistic and can be stopped at any point during their trajectory. A benefit of studying the control of nonballistic movements is that antagonist muscle recruitment, which serves to actively brake a movement, presumably arises in response to the stop signal. Here, nine human participants (2 female) performed a center-out whole-arm reaching task with a countermanding component, while we recorded the activity of upper-limb muscles contributing to movement generation and braking. The data show a clear response on antagonist muscles to a stop signal, even for movements that have barely begun. As predicted, the timing of such antagonist recruitment relative to the stop signal covaried with conventional estimates of the stop-signal reaction time, both within and across subjects. The timing of antagonist muscle recruitment also attested to a rapid reprioritization of movement inhibition, with antagonist latencies decreasing across sequences consisting of repeated stop trials; such reprioritization also scaled with error magnitude. We conclude that antagonist muscle recruitment arises as a manifestation of a stopping process, providing a novel, accessible, and within-trial measure of the stop-signal reaction time.

SIGNIFICANCE STATEMENT The countermanding or stop-signal paradigm permits estimation of how quickly subjects cancel an impending movement. Traditionally, this paradigm has been studied using simple movements, such as saccadic eye movements or button presses. Here, by measuring upper limb muscle activity while human subjects countermand whole-arm reaching movements, we show that movement cancellation often involves prominent recruitment of antagonist muscles that serves to actively brake the movement, even on movements that have barely begun. The timing of antagonist muscle recruitment correlates with traditional estimates of movement cancellation. Because they can be detected on a single-trial basis, muscle-based measures may provide a new way of characterizing movement cancellation at an unprecedented within-trial resolution.

Introduction

Sudden events often require the abrupt cancellation of an impending movement. Movement cancellation is an aspect of executive control that can be studied using the countermanding (or stop-signal) paradigm (Logan et al., 1994), which requires subjects try to cancel an impending movement following presentation of a stop signal. The countermanding paradigm permits estimation of the time needed to react to the stop signal (the stop signal reaction time [SSRT]) (Logan et al., 1984). Although the SSRT cannot be empirically measured, its estimation provides a temporal marker to which neural activity can be related, differentiating neural activity plausibly involved in movement cancellation (Hanes et al., 1998; Paré and Hanes, 2003; Mirabella et al., 2011) from that related to involved in performance monitoring or other aspects of executive control (Scangos and Stuphorn, 2010; Stuphorn et al., 2010). SSRT estimation also has clinical relevance in psychiatric disorders characterized by poor inhibitory control, such as obsessive-compulsive disorder, schizophrenia, or Parkinson's disease (Gauggel et al., 2004; Lipszyc and Schachar, 2010).

Movement cancellation has been best studied using rapid, seemingly ballistic, movements, such as saccades (Hanes and Schall, 1995; Hanes and Carpenter, 1999), button press responses (Logan and Cowan, 1984; Logan and Irwin, 2000), or utterances (Xue et al., 2008). Stop signal performance on such tasks is easily categorized into canceled or noncanceled subtypes. However, many movements are not ballistic. For example, whole-arm reaching moves a multisegmental body part that is endowed with considerable inertia; the motion itself also lasts long enough to permit the opportunity for modification. Reaching movements are under control throughout their entire trajectory (Georgopoulos et al., 1981), meaning that an ongoing movement can either be arrested or superseded by a new movement in midflight (for review, see Battaglia-Mayer et al., 2014; Gaveau et al., 2014). Accordingly, the definition of cancellation with these and other manual movements is arbitrary (de Jong et al., 1990; McGarry and Franks, 2003): is a successfully canceled movement one that is stopped just before reaching the movement goal or one that features absolutely no sign of an overt movement? Complicating matters further, even overtly canceled movements where no obvious movement occurs may exhibit initial patterns of muscle recruitment, meaning that the movement commands were not fully inhibited (de Jong et al., 1990; Burle et al., 2002; McGarry and Franks, 2003).

There are potential benefits for studying cancellation of nonballistic movements. Chief among these is that cancellation often requires active braking via recruitment of antagonist muscles (Kudo and Ohtsuki, 1998; Goonetilleke et al., 2010). If one presumes that antagonist muscle recruitment arises in response to the stop signal, then time between the stop signal and the onset of antagonist recruitment, which we term the antagonist latency, provides a within-trial measure of the SSRT. In support of this, during head-free gaze shifts, SSRT estimates for gaze shift cancellation correlate with the timing and variance of the antagonist latency measured from neck muscles (Goonetilleke et al., 2010, 2012). Such neck muscle antagonist latencies also vary with immediate trial history (Corneil et al., 2013), showing proactive adjustments of movement cancellation at a single-trial resolution that surpasses what could be gained via SSRT estimates.

Here, we investigate the relationships between SSRT estimates of movement cancellation and antagonist latencies during whole-arm reaching movements, targeting muscles of the upper limb that contribute to movement generation and active braking. Reaching movements offer a novel platform for studying the correlates of movement cancellation in the periphery, given the well-known proximal-to-distal muscle recruitment sequence during whole arm reaching (Karst and Hasan, 1991). We present a rich dataset consisting of quantifiable responses to the stop signal in the motor periphery, even on trials where movements have barely begun. Moreover, an analysis of immediate trial history shows an unexpected weighting of error magnitude, with larger post-error adjustments occurring after larger-magnitude errors.

Materials and Methods

Participants.

Nine subjects (2 female, mean ± SD aged 30.2 ± 8.7 years, all right-handed) participated with informed consent and received payment. This sample size is somewhat lower than that typically found in stop-signal studies in humans because of the use of intramuscular fine-wire electrodes. Participants did not report any neurological deficits, and all had normal or corrected-to-normal vision. All procedures were approved by the University Research Ethics Board for Health Science Research at the University of Western Ontario and were in accordance with the Declaration of Helsinki. Participants were aware that they could terminate testing at any time. Two participants (pp3 and pp7, B.D.C. and J.A., respectively) were authors and hence were knowledgeable about the specific goals of the experiment. Their results did not differ from the remaining participants who were naive to the experimental goals. Five subjects had also never participated previously in either a stop-signal or a whole-arm reaching study, and their results also did not differ from those of other subjects.

Apparatus.

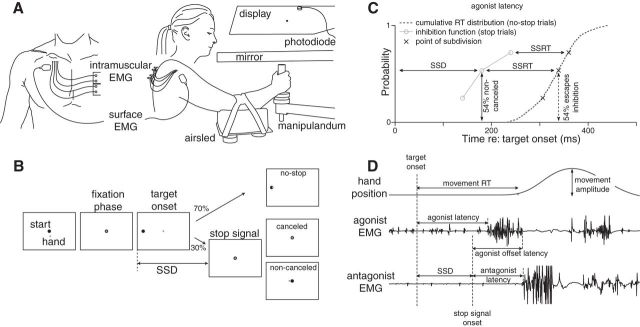
The reaching apparatus and EMG recording setup have been described previously (Wood et al., 2015; Gu et al., 2016). Briefly, participants performed leftward or rightward reaching movements in the horizontal plane while holding the handle of a robotic manipulandum (InMotion Technologies) with the right arm (Fig. 1A). The x and y positions of the manipulandum were recorded at 600 Hz at a submillimeter resolution. Stimuli were generated using Tool Command Language. A custom-built air sled was positioned under the right elbow to reduce friction. Real-time feedback of hand position was displayed as a red dot (2.9 mm radius) on a white background by a downward facing LCD (Sony Bravia KDL-46V3000, output 150 Hz, input 60 Hz), viewed via an up-facing mirror that obscured view of the hand and manipulandum. A photodiode, placed at target height at the right edge of the display, recorded target and stop-signal onset times. No background loading force was applied to the arm.

Figure 1.

Experimental setup, countermanding task, and analysis. A, Participants held a robotic manipulandum with the right hand. Surface and intramuscular EMG recordings were made from the clavicular head of the pectoralis muscle, and from the posterior deltoid muscle. Stimuli and virtual hand position were viewed via a mirror. B, Each trial started by fixating a central starting position. After 1–2 s, a target appeared either to the left or right. Subjects moved their hands so that the cursor representing hand position intersected the target stimulus as quickly as possible. In 30% of the trials, the target jumped back to the starting position after an SSD, instructing the participant to try to withhold the planned movement. If the hand remained within 0.01 m of the start location, the stop trial was classified as successfully canceled; otherwise, it was classified as noncanceled. C, Depiction of the integration method for estimating SSRT. D, Overview of the kinematic and EMG measures. Movement RT is defined as the time at which the hand crosses the 0.01 m radius around the starting location, relative to the time of target presentation. The antagonist latency is the time from presentation of the stop signal to the onset of antagonist muscle activation.

EMG.

EMG activity from the clavicular head of the right pectoralis major (PEC) and posterior deltoid (DELT) were recorded using two pairs of intramuscular fine-wire electrodes and one surface electrode per muscle. Both muscles are proximal muscles that span the shoulder joint and are recruited very early during whole-arm reaching movements (Karst and Hasan, 1991). In our setup, PEC and DELT are active before leftward or rightward movements of the right arm, respectively (Wood et al., 2015). In this manuscript, we focus primarily on intramuscular EMG recordings as its higher signal-to-noise ratio promotes improved detection of rapid changes in muscle recruitment, although surface EMG recordings led to similar conclusions. We had to rely on surface recordings of DELT in participants pp1 and pp4, as the intramuscular recordings were lost during their session. For each intramuscular recording, we inserted two monopolar electrodes (A-M Systems) staggered by ∼1 cm to enable recording of multiple motor units. For PEC, insertions were aimed ∼1 cm inferior to the inflection point of the clavicle. For DELT, insertions were aimed at the middle belly of the posterior deltoid. Intramuscular EMG activity was recorded with a Myopac Junior system (Run Technologies, low-pass filter modified to 2 kHz). Surface EMG was recorded with doubled-differential electrodes (DE-2.1, Delsys), placed on the same muscle fiber belly, but displaced from the intramuscular electrodes. Both the surface and intramuscular EMG signals were digitized at 4 kHz.

Behavioral task.

Subjects performed a center-out reaching task with a countermanding component, which required them to move to a peripheral target on 70% of all trials (no-stop trials), but to try to cancel this movement when a stop signal appeared (stop trials; 30% of all trials). Subjects began each trial by reaching to black central stimulus (8.2 mm radius) that served as the central starting position. After a randomized delay (1–2 s), a peripheral black target (8.2 mm radius) appeared randomly 0.2 m to the left or right of the central position, at a visual angle of ∼20° relative to the central starting position (derived from the geometry of the apparatus). On no-stop trials, subjects were instructed to reach as soon as possible to the target and had 1.5 s in which to do so. On stop trials, the black central stimulus reappeared after a predetermined delay (stop signal delay [SSD]). Subjects were instructed to try to keep the hand at the central position on stop trials; hence, they returned their hand to the central position after small errors. The next trial began after another randomized delay (1–2 s).

A stop trial was considered successfully canceled when the hand remained within the 0.01 m radius of the starting position, and noncanceled when the hand crossed the 0.01 m radius (Fig. 1B). No feedback was given regarding the outcome of a stop trial. The SSD was varied adaptively via a 1-up/1-down staircase with a step size of ∼28 ms, so that participants were able to cancel movements within these constraints on approximately half of all stop trials. This staircasing method will preferentially sample SSDs where p(move) ∼ 0.5 and will rarely sample p(move) < 0.2 or p(move) > 0.8. SSDs were constrained between 50 and 500 ms, and the first SSD was set to 150 ms. Because the input and output refresh rate of the display did not match, there was some scatter in SSD timings (SD ∼15 ms). The actual SSD presented to the subject was used whenever possible (e.g., for calculation of measures related to antagonist muscle recruitment). However, because this scatter would have occasionally reduced the number of observations from a given SSD below that needed for the integration method of calculating SSRT, SSDs were binned (16.7 ms width) for the construction of the inhibition function (see below).

Each participant completed one session with a total of 1600 trials, preceded by at least 100 practice trials. After each block of 200 trials, the experiment was paused for at least 2 min. The experiment, including electrode placement, took ∼2 h.

Analysis of movement kinematics.

Data analyses were performed offline. Hand position recordings were analyzed in the left-right dimension only. Movement RT was defined as the interval between target onset and the moment the hand departed from a circle of 0.01 m radius, centered around the starting position. For both the RT measure and the classification of stop trials, the same, albeit arbitrary, criterion was used. To quantify movement amplitude for all trials (including canceled stop trials), we computed the maximum deviation of hand position, relative to the position at target onset, in the direction of the target within 1 s after target onset.

Independent race model.

Performance in the countermanding paradigm can be analyzed within the framework of an independent race model (Logan and Cowan, 1984). In this model, the outcome of a stop trial depends on which process finishes first: a “go process” initiated upon target presentation which results in movement generation toward the target, or a “stop process” initiated by stop signal presentation which results in movement inhibition. The two processes are assumed to proceed independently.

One way the SSRT can be inferred is via the “integration method” (Logan et al., 1994), which requires the RT distribution from no-stop trials, and the inhibition function that plots the proportion of noncanceled trials as a function of SSD (Fig. 1C). At each SSD, the SSRT is determined by subtracting the SSD from the point that subdivides the RT distribution into the proportion of noncanceled trials from the inhibition function. The rationale here, given the assumed independence of the stop and go processes, is that this point differentiates those trials that would have escaped inhibition on stop trials (which lie below the point of subdivision) from those that would have been canceled (above the point of subdivision) had a stop-signal been provided. As suggested previously (Logan et al., 1994), we avoided SSDs where the probability of movement fell below 0.1 or exceeded 0.9. SSRT mean and variance are then derived from SSRTs estimated at qualifying SSDs. Another way of estimating the SSRT is to fit a cumulative Weibull function to the inhibition function (similar to that used in Scangos and Stuphorn, 2010), and the SSD at which p(move) = 0.5 is extracted (we term this the “Weibull method”). This SSD is then subtracted from the mean of the RT distribution to extract the SSRT. In theory, SSRTs estimated via both methods are equivalent. Consistent with this, SSRT estimates calculated via either method were very similar within a subject (Table 1). With the exception of some tests of the independent race model that require SSRT estimates at each SSD, reported SSRTs are the average of that obtained via the two methods.

Table 1.

SSRT values computed for each subject via the integration method or extracted via the Weibull fit

Subject	SSRT (ms)
	Integration method	Weibull fit	Average
1	234 ± 13	235	235.5
2	265 ± 31	283	274.0
3	251 ± 15	249	250.0
4	217 ± 34	213	215.0
5	216 ± 51	215	215.5
6	260 ± 29	266	263.0
7	225 ± 24	223	224.0
8	291 ± 14	299	295.0
9	225 ± 53	225	225.0

Determining the onset and offset of muscle recruitment.

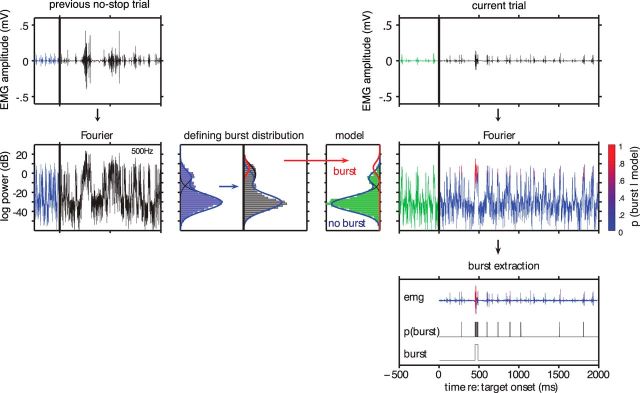
Central to our experimental aim is the timing of changes in muscle recruitment. Defining both the onset and offset of bursts of EMG activity within a single trial at a high temporal resolution is not straightforward, given the variability of background EMG activity before target onset, and the fact that recruitment on canceled stop trials can be both brief and small. Rather than adopting a simple thresholding approach (e.g., based on transitions across 2–3 SDs above mean baseline activity), we adopted an algorithm for detecting recruitment timing based on the work by Liu et al. (2015). This work characterizes the logarithmic distribution of the EMG signal as a mixture of Gaussian normal distributions, including low-power baseline distributions and a high-power “burst” distribution (Fig. 2). Using this Gaussian mixture model, at each time point (0.25 ms steps), a burst presence probability was estimated for several frequency bands in parallel, and together with a clustering algorithm the burst of interest was extracted (for full details, see Gaussian mixture model (GMM)). The algorithm was run from 110 ms after target onset to avoid the stimulus-locked response (SLR), which is a burst of EMG recruitment time-locked to peripheral stimulus onset (Pruszynski et al., 2010; Wood et al., 2015; Gu et al., 2016). All detected onset and offset times were visually inspected by a trained observer, using a custom-written MATLAB program, and corrected where needed (6.7% of instances). Figure 1D provides an overview of the within-trial measures. The agonist latency is defined as the interval between target onset and the start of the detected agonist burst. The antagonist latency is defined as the interval between stop signal onset and the start of the detected antagonist burst. We also defined the agonist offset latency as the interval between stop signal onset and the end of the agonist burst, as an alternative measure to the antagonist latency. Agonist offset was less pronounced and therefore less reliable than the antagonist onset.

Figure 2.

Burst detection algorithm. A discrete Fourier transform was applied to get EMG power in several frequency bands (one band is shown here). The power distribution was parameterized using three normal distributions: two baseline distributions (blue), which are fitted on the baseline period (500 ms before target onset); and one burst distribution with higher power (red), which complements the baseline fit to describe the trial period (which runs for 2 s after target onset). At each trial, these distributions were fitted anew using the previous three no-stop trials (one trial shown). From this fit, only the burst distribution was used, together with the baseline fit of the current trial, to compute the burst probability over time. The burst probability vectors of the three frequency bands that dissociated best between burst and baseline were averaged to get to a single p(burst) vector. Finally, using a low pass filter, the burst of interest was extracted. For further details, see Materials and Methods.

Gaussian mixture model (GMM).

The log power signal obtained from differential EMG electrodes can be modeled by a mixture of Gaussian normal distributions (Liu et al., 2015). We estimated EMG power by applying a discrete Fourier transform (4 ms, 16 sample Hamming window, with 0.25 ms overlap) to produce 9 distinct frequency bands (0, 250–2000 Hz). Power values were expressed in decibels referenced to the band's mean power as follows:

We analyzed EMG activity in the frequency domain because EMG activity can oscillate in a broad range of frequencies, some of which contain more information than others regarding the presence of a burst. Each band was initially analyzed separately, with information being combined only at a later step for frequency bands that best informed about burst presence or absence (see below).

One difference from the method proposed by Liu et al. (2015) is that we defined three, not two, states of muscle activity: rest (s = 1, low power), baseline activity (s = 2, intermediate power), and burst (s = 3, high power). Having three states provided a better characterization of EMG activity, particularly during the baseline period where EMG activity consisted of brief occasional bursts of activity. Thus, our GMM consists of three components as follows:

where p(s = k) is the a priori probability of state k, which is modeled by parameter Φ_k (with ∑_k=1³Φ_k = 1), and p(x|s = k) is the conditional probability distribution of observing log power value x given state k, modeled by a normal probability density function as follows:

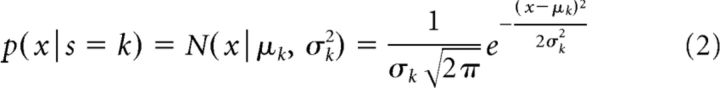where μ_k and σ_k² are the mean and variance of the Gaussian distribution for the given hypothesis s = k. Using Bayes rule, we can infer the probability of state k given x as follows:

This forms the basis for estimating the burst probability p(s = 3 | x). The parameter set Φ ≜ {Φ₁, Φ₂, Φ₃}, μ ≜ {μ₁, μ₂, μ₃}, and σ ≜ {σ₁, σ₂, σ₃} is estimated for every trial in a series of steps, which follow from the following assumptions:

1. In the 500 ms “baseline” period preceding target onset, the state of the muscle is either rest (s = 1) or baseline (s = 2), but never burst (s ≠ 3). Thus, the probability density of x in the baseline period can be estimated with a two-component GMM.

2. If an arm movement is made toward the target, then the probability density of x in the 2000 ms period after target onset resembles the GMM of the baseline period, but with a third component added (s = 3) with μ₃ > μ₂ > μ₁. The 2000 ms duration ensures that muscle activity related to both the outgoing and return movement is included.

3. We expect the burst state parameters Φ₃, μ₃, and σ₃ to change slowly over time (e.g., fatigue), whereas the baseline parameters are expected to change more rapidly from trial to trial (e.g., because of posture changes).

Fits were performed using MATLAB's fminsearch function by maximizing the log likelihood of the signal under the model (The MathWorks). The baseline fit provided the trial's μ₁, μ₂, σ₁, σ₂ and preliminary weights Φ̃₁ and Φ̃₂ (with Φ̃₂ = 1 − Φ̃₁). These weights are termed preliminary because they were lowered once Φ₃ was known. Not all trials contain movements: a muscle may never reach State 3 on a stop trial. Thus, to estimate the third component (Φ₃, μ₃, and σ₃), we used the previous three no-stop trials, as the muscle must have reached the burst state at some point on these trials. Using the previous three no-stop trials instead of a single no-stop trial resulted in more robust fits. For these three reference trials, the baseline periods were taken together and fitted using a two-component GMM. Then, for these trials, the 2000 ms periods after target onset were taken together and fitted with the three-component GMM in which the first two components were adopted from the two-component fit with their weights (Φ) fixed proportionally to each other. Now the full GMM for the reference trials is known, only Φ₃, μ₃, and σ₃ are transferred to the current trial's GMM fit with the first two weights now being: Φ₁ = Φ̃₁(1 − Φ₃) and Φ₂ = Φ̃₂(1 − Φ₃).

Once the three-component GMM for a given trial is established, the probability of the muscle being in burst state at the i'th time point, p(s_i = 3|x_i) can be computed using Equation 3. However, this ignores the variability between samples that are close in time. For example, we assume that muscles will transition into or out of a burst state intermittently. Accordingly, our analysis of burst state probability not only includes sample x_i, but also a few nearby samples to make the state estimate more reliable. However, EMG activity was Fourier-transformed with a 16 sample window; hence, samples that are too close in time will already be highly correlated. Instead, we found that including x_i−8, x_i, and x_i+8 into the computations at time point i provided reliable results. The burst probability at x_i is now given by the following:

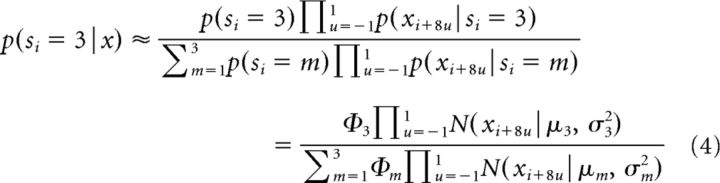The parameter and state estimations were performed for all 9 frequency bands independently. The inferred weighting parameter Φ₃ provided information regarding which frequency bands best differentiated the presence or absence of a burst. If Φ₃ < 0.005 or Φ₃ ≥ 0.3, we excluded the band for that trial because it is unlikely that the muscle was in a burst state <0.5% or >30% of the time in the previous go trials.

Next, the overlap of the distribution p(s = 3|x) with the combined distribution p(s = 1|x) + p(s = 2|x) was estimated for each frequency band. The frequency bands showing the least overlap were included for the actual burst detection, as these could dissociate best between the burst and no-burst states (up to three bands were included). The burst probability vectors of the included frequency bands were then averaged and transformed into a binary vector: p(s = 3|x) > p(s = 1|x) + p(s = 2|x).

Because hand kinematics were also recorded, we used the time at which hand velocity crossed 0.01 m/s in the direction of the target to constrain the timing of acceptable bursts. The window for acceptable agonist or antagonist onsets began 150 or 80 ms before this velocity crossing, respectively. If hand velocity did not cross 0.01 m/s within a trial (as on canceled stop trials), agonist and antagonist onsets that occurred up to 1 s after target onset were considered. In addition, the antagonist onset was only accepted if it occurred after the agonist onset. To remove noise from the binary vector, sequential bursts (a cluster of adjacent ones) that totaled <4 ms were removed. Subsequently, bursts were concatenated if they were <50 ms apart. The first detected burst was considered the burst of interest, taking into account the constraints noted above.

Data exclusion.

A trial was excluded from the analyses when the antagonist latency was >350 ms (1.0% of all stop trials) or when the agonist offset latency was negative (i.e., agonist withdrawal occurred before stop signal onset) (1.0% of all stop trials) because these occurrences are not linked to prompt processing of the visual stop signal. Furthermore, when on visual inspection the burst onset appeared ambiguous because of a gradual increase in muscle recruitment, or when an initial small movement was followed by a larger movement a few hundred milliseconds later, the trial was excluded (3.8%). For one participant (pp8), agonist onsets could not be determined reliably because of tonic cocontraction before movement onset. Therefore, agonist onset markers of this participant were discarded.

Model simulations.

We tested aspects of our observed data against that predicted by an independent race between manifestations of the go and stop process. To do this, bootstrapping simulations were conducted by taking random samples from the observed agonist latency (relative to the go signal), antagonist latency (relative to the stop signal), and the sampled SSD. Each sample of these three values then produced an interval between agonist and antagonist burst onset, which as an example we could use to predict the movement amplitude that would be associated with such an interval (using a fitted cumulative Gaussian).

Experimental design and statistical analysis.

All statistical analyses were performed in MATLAB (version R2104b, The MathWorks). When applicable, results are expressed as mean ± SD, unless otherwise noted. Comparisons of within-subject or across-subject results were conducted via paired or two-sample t tests, respectively. Pearson's correlation was used to correlate various measures, as reported in Results. The level of significance was set to p < 0.05. Effect sizes are reported as Cohen's d for t tests and partial η² for ANOVAs.

Results

We studied muscle recruitment during whole-limb reaching movements in a countermanding task. We hypothesized that the timing of antagonist muscle recruitment arises from the completion of the stop process and, hence, should relate to both stop signal onset and the estimated SSRT. First, we describe behavior on the basis of hand position recordings in the conventional manner used in countermanding studies. Then we present the patterns of muscle recruitment on agonist and antagonist muscles. We conclude with an investigation of the agonist and antagonist recruitment latencies with trial history, to examine whether they provide evidence for proactive and opposing adjustments in processes related to movement generation and inhibition, as has been reported previously in neck muscles during control of orienting eye-head gaze shifts (Corneil et al., 2013).

Continuous control of reaching

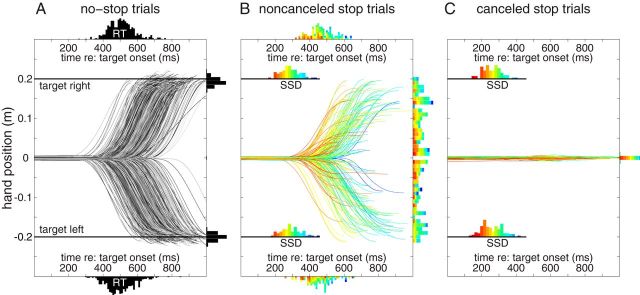
Figure 3 shows the horizontal component of hand movement traces of a representative participant. In this plot, each trace represents a single trial, aligned to the onset of either the right or left target. In the no-stop trials (Fig. 3A), movement amplitudes scatter around the target (rotated histograms to the right of the movement traces). As expected, there is substantial variance in movement RT, as summarized by the respective RT distributions above or below the movement traces.

Figure 3.

Movement traces on no-stop (A) and stop trials (subdivided into noncancelled, B; and canceled, C; subtypes). Traces are drawn until the point of maximum deviation toward the target. Stop trials are color-coded by SSD. SSD histograms represent the proportion of times a given SSD was sampled. A, On no-stop trails, movement amplitudes are ∼0.2 m (tilted histograms on the right). B, Movement amplitudes on noncanceled trials varied considerably. Earlier stop signals are accompanied with earlier but smaller movements, as represented by the histograms. C, When the movement was successfully canceled, amplitudes are typically <0.01 m.

In stop trials, the target suddenly jumps back to the central position after a variable SSD, instructing the participant to try to withhold the movement. The data in Figure 3B, C are further segregated based on whether the participant generated a movement beyond the 0.01 m criterion (Fig. 3B, noncanceled trials) or not (Fig. 3C, canceled trials). For this participant, the SSD ranged between 125 and 425 ms (color-coded SSD histograms just above position traces; note preferential sampling of intermediate SSDs). A substantial proportion of noncanceled movements failed to attain the target but were arrested in midflight (e.g., compare movement amplitude histograms in Fig. 3A,B). Furthermore, noncanceled trials have shorter RTs than no-stop trials (compare RT histograms in Fig. 3A,B; no-STOP RTs = 501 ± 77 ms, noncanceled RTs = 463 ± 75 ms; two-tailed t test t₍₁₂₅₀₎ = 6.56, p < 10⁻¹⁰, Cohen's d = 0.51), suggesting that presumably long RT movements can be canceled on trials with long SSDs. The color coding of the movement RT distributions supports this supposition: for short SSDs (red/orange), only movements with short RTs escape inhibition. In contrast, the movement traces on canceled trials barely deviate at all (Fig. 3C), and there are more canceled trials with early SSDs compared with noncanceled trials, and more noncanceled trials with late SSDs than canceled trials. Thus, as expected, the probability of successfully canceling a movement increases the earlier the stop signal is presented.

As mentioned, the reach behavior of this participant was representative of our sample. To show this, Figure 4 illustrates the movement amplitudes of all participants on no-stop trials (Fig. 4A) versus noncanceled stop trials (Fig. 4B). Note how movement amplitude for noncanceled trials ranged from the target location down to the 0.01 m boundary between canceled and noncanceled movements. This observation reinforces the nonballistic nature of these whole-arm reaching movements, so that ongoing movements can be canceled at any point before reaching the target.

Figure 4.

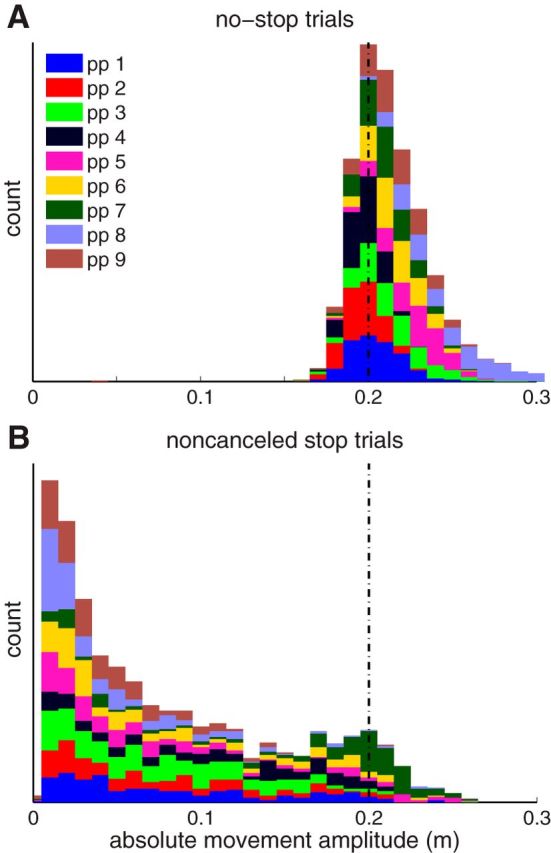
Histogram of movement amplitudes with all participants stacked for no-stop trials (A) and noncanceled stop trials (B). Vertical dashed line indicates target position.

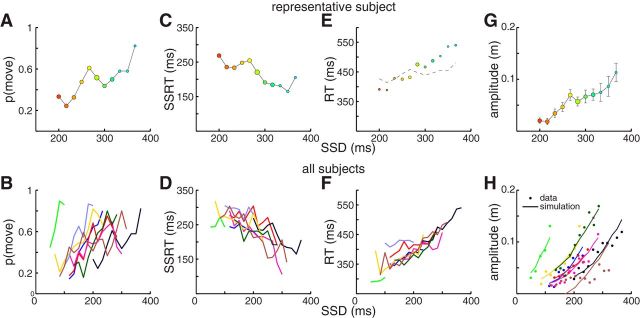
In Figure 5, we quantify a number of other observations both for the representative participant (top row) and across our sample (bottom row). The inhibition functions (Fig. 5A,B) show the proportion of noncanceled stop trials as a function of SSD; and as expected, the proportion of noncanceled trials increases with longer SSDs (Lappin and Eriksen, 1966). All participants exhibited this pattern, although there was substantial intersubject variability in where this function was centered along the x-axis (Fig. 5B), in part due to how quickly subjects reacted on no-stop trials. These inhibition functions are primarily centered near p(move) = 0.5 and did not extend to p(move) < 0.1 or p(move) > 0.9; this is due to our use of the one-up/one-down stepping procedure used to determine the SSD on the next trial. The inhibition function can be used along with the RT distributions to estimate the SSRT, or the time needed to react to the stop signal. Across our sample, SSRTs derived from the integration method and Weibull method were very similar (Table 1; linear regression, r = 0.970, t₍₇₎ = 16.235, p < 10⁻⁶⁾, justifying averaging. SSRTs averaged 244 ± 28 ms (mean ± SD), ranging from 215 to 295 ms, which conforms well with previously reported SSRTs for a variety of manual responses (Mirabella et al., 2006; Boucher et al., 2007; Brunamonti et al., 2012).

Figure 5.

Variation in countermanding performance as a function of SSD. Top row indicates data from the representative subject (color codes as in Fig. 3; disc radius proportional to number of samples). Bottom row indicates data across all subjects (color codes as in Fig. 4). A, B, Inhibition function, expressing movement probability versus SSD. C, D, SSRTs estimated via the integration method are negatively correlated with SSD. E, F, RTs on noncanceled trials increase as a function of SSD, although as shown in E, such increases are greater than that predicted by the independent race model (thin line). G, H, The amplitude of noncanceled trials increases with SSD; this increase was well predicted by a bootstrapping simulation of movement amplitude based on independent sampling of agonist and antagonist onsets (see Materials and Methods). H, Lines indicate predictions of simulations.

Movements conform to the independent race model

The independent race model makes a number of predictions about reaching behavior that we can test against our observations. For example, the independent race model predicts that SSRTs should decrease for longer SSDs because only those stop processes that proceed faster can produce movement inhibition in such cases (Logan and Cowan, 1984). To test this, we used the integration method to estimate the SSRT at each SSD and plotted this as a function of SSD. As shown for our representative participant (Fig. 5C) and across our sample (Fig. 5D), SSRTs did decrease as a function of SSD (a significantly negative correlation was observed in 7 of 9 subjects, at p < 0.05).

According to the independent race model, the RT on noncanceled trials at a particular SSD should be predicted by subdividing the no-stop RTs into the proportion of trials that would or would not have escaped inhibition, had a stop signal been provided at that particular SSD (Fig. 1C) (Logan and Cowan, 1984); a corollary of this test is that RTs on noncanceled trials should increase for longer SSDs because longer SSDs permit more slowly proceeding go processes to still escape inhibition. Across our sample, the observed RTs of noncanceled trials did increase with SSD (Fig. 5E,F, linear regression, r = 0.855, slope = 0.614, t₍₈₆₎ = 15.29, p < 10⁻²⁵; a significantly positive correlation was observed in 7 of 9 subjects, at p < 0.05), although we found that the trend in observed RTs was generally steeper than predicted, with RTs at higher SSDs being particularly underestimated (Fig. 5E).

Finally, our observation of highly variable amplitudes for noncanceled movements is consistent with both the nonballistic nature to these movements and the continued processing of the stop signal after the movement is launched. We found a straightforward relationship between movement amplitude and SSD: movement amplitudes tended to be greater for longer SSDs, both in our representative participant (Fig. 5G) and across our sample (Fig. 5H) (all positive correlations, p < 0.05). The relationship between movement amplitude and SSD was accurately captured with our simulation of the independent race model for 8 of our 9 subjects (Fig. 5H, lines indicate simulation results). All correlations between observed and simulated data were significant at p < 0.005; r values exceeded 0.9 for 8 subjects but was 0.75 for the subject shown by the brown line.

Muscle recruitment on no-stop trials

Having established that participants performed in a manner consistent with an independent race model, we now turn to the profile of muscle recruitment accompanying this task. In particular, we address whether changes in muscle recruitment provide a proxy of movement cancellation.

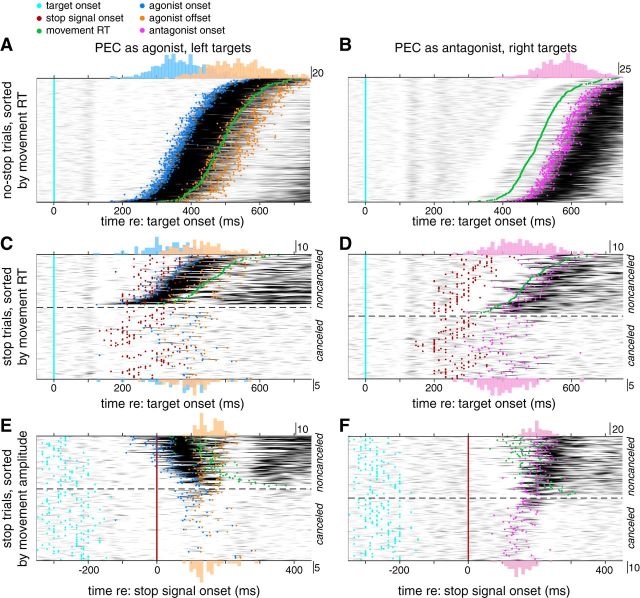
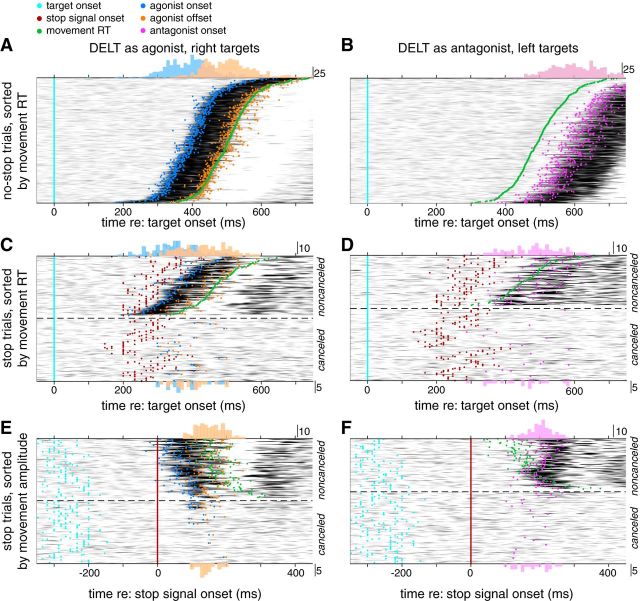
We measured surface and intramuscular EMG activity of the right PEC and DELT muscles, which in our setup contribute to either leftward or rightward planar movements of the right upper limb as an agonist muscle, respectively, and would be expected to actively brake movements proceeding in the opposite direction as an antagonist muscle. Figures 6 and 7, respectively, show intramuscular PEC and surface DELT activity recorded from the same subject during the classified trials types (no-stop, noncancelled, and canceled), vertically stacked by either movement RT (Figs. 6A–D, 7A–D) or movement amplitude (Figs. 6E,F, 7E,F). These figures are organized in a muscle, rather than direction-specific fashion; hence, the appreciation of how the muscles work together can be gained by comparing Figure 6 (left column) with Figure 7 (right column), or vice versa. Surface EMG recordings are shown for DELT in this example because intramuscular recordings were lost with this participant; we also wish to emphasize that similar observations can be made using either intramuscular or surface recordings.

Figure 6.

Rectified intramuscular EMG data from PEC from the representative participant, smoothed with a 40 ms Gaussian for display purposes. EMG voltage above baseline is proportional to the darkness of the gray shade. Colored dots indicate the timing of variety of events (see legend). Trials are vertically stacked based on movement RT (A–D) or movement amplitude (E, F).

Figure 7.

Surface activity recorded from the DELT muscle of the representative subject. Same format as Figure 6. Left column represents rightward movements, for which DELT acts as an agonist.

We focus first on the recruitment of these muscles during no-stop trials, aligned to target onset and vertically sorted by movement RT. As expected of agonist muscles, large bursts of activity preceded movement onset, leading leftward movements by 123 ms for PEC (Fig. 6A) and leading rightward movements by 112 ms for DELT (Fig. 7A). Across our sample, the lead between agonist onset and RT tended was greater for PEC than DELT (157 ± 32 and 137 ± 26 ms, respectively, paired t test, t₍₈₎ = 4.37, p = 0.002). For each subject, the burst onset in both muscles was highly correlated with the direction-appropriate RT on a trial-by-trial basis (linear regressions, r² = 0.86 ± 0.17, PEC; and r² = 0.92 ± 0.076, DELT; all p < 10⁻⁵⁸). Similarly, when these muscles served as antagonists on no-stop trials, they both exhibited a prominent burst of activity that led movement offset across our sample by 254 ± 38 ms (PEC; Fig. 6B) or 262 ± 33 ms (DELT; Fig. 7B). These profiles of recruitment resemble the first two phases of the triphasic profile of activation that accompany rapid goal-directed movements of an inertial object (Hallett et al., 1975); the third phase of agonist muscle recruitment is visible for the shortest latency movements in Figures 6A and 7A.

One other aspect of PEC muscle recruitment that is apparent on no-stop trials is the banding that begins ∼100 ms after target presentation, with activity increasing (Fig. 6A) or decreasing (Fig. 6B) after leftward or rightward target presentation, respectively, before progressing through a series of ∼15 Hz oscillations in advance of the main burst of muscle recruitment. This feature is the SLR (Pruszynski et al., 2010; Wood et al., 2015; Gu et al., 2016). An SLR was observed in 8 of 9 participants on PEC and in 2 of 9 participants on DELT. Our analyses of agonist and antagonist burst onsets began after the SLR (>110 ms after target onset).

Muscle recruitment on stop trials

We now examine the profiles of muscle recruitment observed on stop trials (Figs. 6C–F, 7C–F), subdividing such data based on target direction and into noncanceled or canceled stop trials (above and below the dashed line, respectively). Stop trial data in Figures 6 and 7 are aligned either to target (Figs. 6C,D, 7C,D, cyan lines or dots) or stop signal onset (Figs. 6E,F, 7E,F, red lines or dots). On noncanceled trials, we observed a straightforward relationship between stop signal onset and agonist muscle recruitment: late noncanceled movements escaped inhibition only when the stop signal was late (Figs. 6C, 7C). On such trials, agonist muscle activity commenced as expected but exhibited a shorter burst duration compared with no-stop trials (123 ± 30 ms compared with 207 ± 83 ms, mean ± SD across participants, paired t test, t₍₈₎ = 3.61, p = 0.007); on such trials, antagonist muscle activity relative to the agonist onset also started earlier compared with no-stop trials (149 ± 26 ms compared with 242 ± 75 ms). These features (foreshortening of the agonist burst, earlier antagonist recruitment) are consistent with the arm movements being arrested in mid-flight.

Two further observations of muscle recruitment on stop trials are important to note. First, as is particularly apparent in Figure 6C, D, the SLR preceded stop signal appearance and, hence, persisted regardless of whether a stop signal was present or not. Second, there were a number of instances of detectable muscle recruitment even on canceled trials, in which the hand did not leave the starting position (traces below dashed lines: Figs. 6C–E, 7C–E). This was a consistent observation across all subjects in our sample, as shown in Table 2. A cessation of the agonist recruitment was detected on 39 ± 15% (PEC, mean ± SD across participants) and 35 ± 19% (DELT) of canceled trials, whereas antagonist activation was detected on 67 ± 10% (PEC) and 41 ± 24% (DELT) of canceled trials; the magnitudes of such recruitment can be quite subtle on canceled trials, when aligned to target onset (Figs. 6C,D, 7C,D). Clearly, despite the absence of overt movement of the limb, both PEC and DELT are being recruited on just over half of all canceled stop trials. Thus, movement cancellation does not imply the absences of changes in muscle recruitment; however, changes in muscle recruitment did not always accompany movement cancellation.

Table 2.

Number of movement sequences on stop-trials, and the number and proportion of trials from with either agonist offset or antagonist muscle onset could be extracted on canceled stop trials^a

Subj.	PEC as agonist (leftward movement)					PEC as antagonist (rightward movements)
	No. of stop trials	No. of noncanceled	No. of canceled	No. of agonist offset	% agonist offset	No. of stop trials	No. of noncanceled	No. of canceled	No. of antagonist offset	% antagonist offset
1	234	110	124	45	36.2	235	115	120	72	60.0
2	217	94	123	49	39.8	223	110	113	74	65.4
3	229	185	44	17	38.6	236	130	106	84	79.2
4	219	91	128	41	32.0	225	110	115	68	59.1
5	224	86	138	50	36.2	236	127	109	74	67.8
6	231	100	131	43	32.8	235	126	109	66	60.5
7	229	79	150	48	32.0	232	142	90	47	52.2
8	231	122	109	85	77.9	236	107	129	107	82.9
9	232	97	135	37	27.4	240	127	113	82	72.5
					39 ± 15					67 ± 10

	DELT as agonist (rightward movements)					DELT as antagonist (leftward movements)
1	235b	115b	120b	23b	19.1b	234b	110b	124b	42b	33.8b
2	223	110	113	35	30.9	217	94	123	46	37.3
3	236	130	106	61	57.5	229	185	44	29	65.9
4	225b	110b	115b	21b	18.2b	219b	91b	128b	21b	16.4b
5	236	127	109	38	34.8	224	86	138	66	47.8
6	235	126	109	21	19.2	231	100	131	17	12.9
7	232	142	90	34	37.7	229	79	150	67	44.6
8	236	107	129	95	73.6	231	122	109	95	87.1
9	240	127	113	29	25.6	232	97	135	28	20.7
					35 ± 19					41 ± 24

^aData are presented in a muscle-specific fashion, following the convention in Figures 6 and 7. PEC acts as an agonist on leftward movements and an antagonist on rightward movements (vice versa for DELT). Summary data presented as mean ± SD.

^bData extracted from surface recordings.

Next, we asked whether the timing of muscle events, and in particular the timing of antagonist onset, relate to the timing of the stop signal. To examine this, we realigned stop-trial data on stop signal onset (Figs. 6E,F, 7E,F). This tightened the trial-by-trial variability in the timing of antagonist muscle onset (e.g., Figs. 6F, 7F, magenta histograms) and agonist muscle offset (e.g., Figs. 6E, 7E, orange histograms), compared with the variability observed when these features are aligned to target onset (Figs. 6C,D, 7C,D). Realigning the data in this way also makes the level of antagonist muscle recruitment on canceled trials more apparent (Fig. 6F). Across our sample, realigning data to stop signal onset reduced the SDs of the antagonist onset distributions by a factor of 1.78 ± 0.91 for PEC (paired t test, t₍₈₎ = 4.47, p = 0.002) and 1.85 ± 1.05 for DELT (t₍₈₎ = 4.74, p = 0.002). The agonist offset distributions were reduced in a similar way (PEC: 1.79 ± 1.01, t₍₈₎ = 4.87, p = 0.002; DELT: 1.60 ± 0.61, t₍₈₎ = 4.01, p = 0.004). Across participants, the average antagonist latencies relative to stop signal onset were 182 ± 16 ms for PEC and 195 ± 18 ms for DELT. Average agonist offset latencies were 165 ± 22 ms for PEC and 164 ± 18 ms for DELT. Although the agonist offset relative to the stop signal may theoretically provide another measure of movement cancellation, in practice this measure was less reliable than that provided by antagonist onsets in our experimental configuration. Evidence for this point can be found by comparing the proportion of trials from which a given muscle can yield a quantifiable change in muscle recruitment when acting as an agonist or antagonist (Table 2); across our sample, measures of antagonist muscle recruitment were available on a larger proportion of trials (paired t test, t₍₁₇₎ = 4.69, p = 0.0002). When both agonist offset and antagonist onset were present on the same trial for canceled and small noncanceled trials (<0.05 m), the duration between these measures was 25 ± 18 ms, with 93% of these observations being >0. Thus, the agonist and antagonist muscles were rarely coactivated, perhaps due to spinal circuits that prevent cocontraction in this task.

The trials in Figures 6E, F, and 7E, F have been stacked in order of increasing movement amplitude; this is possible even for canceled trials, which featured movements that did not exceed the position threshold. Ordering trials this way reemphasizes how larger movements are associated with earlier agonist onsets (blue dots) relative to the stop signal (i.e., note how agonist muscle bursts start earlier for larger noncanceled trials). In contrast, both agonist offsets and antagonist onsets related to movement amplitude in a reciprocal way: the earlier the antagonist onset, the less motion occurred (Figs. 6F, 7F). Further, note as well that the antagonist onsets relative to the stop signal do overlap for noncanceled and canceled trials (Fig. 6F); we attribute this overlap to the variability in reacting to both the target and to the stop signal, the SSD, to the ambiguity in differentiating noncanceled from canceled trials, and to the continued processing of the STOP signal after movement onset.

Although not visible in Figures 6 and 7 because of the chosen grayscale, we also observed that antagonist muscle recruitment on stop trials was brisker than on no-stop trials, ramping up more quickly to the peak level of within-trial recruitment. This is illustrated in Figure 8, which shows the average burst profile of the agonist (Fig. 8A) and antagonist (Fig. 8B) muscles, pooled across participants, for no-stop trials and for stop trials associated with a variety of different movement amplitudes. The initial ∼100 ms of agonist muscle recruitment (Fig. 8A) was largely similar on no-stop trials and larger noncanceled movements (Fig. 8A, red and green traces) but muted for smaller noncanceled movements (Fig. 8A, blue traces). In contrast, the initial ∼100 ms of antagonist muscle recruitment was gradual on no-stop trials, peaking ∼80 ms after burst onset, but sharp on noncanceled movements regardless of movement amplitude, peaking within ∼30 ms (Fig. 8B). The peak of antagonist muscle recruitment was also largest on the noncanceled movements of intermediate amplitudes (Fig. 8B, green lines). Our interpretation of this result is that antagonist muscle recruitment actively brakes the ongoing limb movement on trials altered in mid-flight in an acceleration- and/or velocity-dependent manner, requiring more recruitment on intermediate (Fig. 8B, green traces) versus small (Fig. 8B, blue traces) noncanceled. However, because some of the larger (Fig. 8B, red traces) are nearing completion, they may already be decelerating at the time a braking pulse is required, which is why there is a smaller recruitment peak on larger-amplitude noncanceled trials. To further support our contention that antagonist muscle recruitment actively brakes the ongoing limb movement on many stop trials and is not simply linked to the triphasic pattern of recruitment seen on no-stop trials, we calculated the slope from burst onset to peak EMG activity. When examining the agonist muscle activity, we found no difference in the slope for no-stop trials compared with the average slope of the stop trials across different movement amplitudes (paired t test, t₍₈₎ = 0.51, p = 0.62). However, we did find a steeper slope for antagonist muscle recruitment on stop trials compared with no-stop trials (t₍₈₎ = 3.83, p = 0.005).

Figure 8.

Averaged rectified EMG activity aligned to burst onset for no-stop (black traces) and stop trials with large (red), intermediate (green), and small (blue) movement amplitudes, for either the agonist muscle (A) or antagonist muscle (B). The contours subtend the mean ± SE of EMG activity and are normalized to the peak movement-related activity on no-stop trials, pooled across movement direction, averaged across all trials within a participant, and then averaged across participants.

Together, these finding support our hypothesis that characteristics of muscle recruitment, such as the antagonist onset, provide a proxy measurement of the stop signal RT.

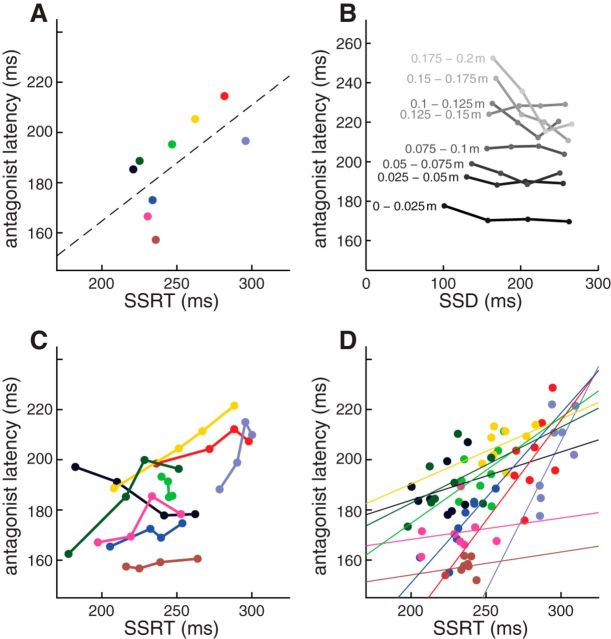
Antagonist latencies relate to SSRTs

We now turn to relationships between the antagonist latency and the SSRT, testing the hypothesis that the antagonist onset provides a proxy measurement for stopping. If so, one would predict similar variations in SSRT and antagonist latency across and within subjects. As predicted, mean antagonist latencies correlated with SSRT estimates on a subject-by-subject basis (Fig. 9A; linear regression, r = 0.852, slope = 0.828, t₍₇₎ = 4.31, p < 0.005): subjects with longer SSRTs tended to have longer antagonist latencies. On average, antagonist latency preceded the estimated SSRT by 45 ± 5 ms (mean ± SEM). Although it may seem curious that SSRT exceeds the antagonist latency, changes in muscle recruitment can precede SSRTs in manual response tasks (Scangos and Stuphorn, 2010); and as mentioned in Discussion, SSRTs vary depending on the criterion separating canceled from noncanceled movements on stop trials.

Figure 9.

Relationships between SSRT and antagonist latency. Color codes as in Figure 4. A, Mean antagonist latency correlates with SSRT across subjects. B, Across subjects, the antagonist latency is negatively correlated with SSD over the whole range of movement amplitudes. C, Positive relationship between SSRT and antagonist latency within and across subjects (stop trial data divided into quartiles based on SSD). D, Same as in A, but now for each participant the mean observation from each block of 200 trials is depicted (dots). Lines indicate linear fits, all with positive slopes, meaning that blocks with longer SSRTs tended to have longer antagonist latencies.

We also wished to examine how the antagonist latency related to the SSD because, as predicted by the independent race model (and as seen for the relationship between SSRT and SSD shown in Fig. 5D), longer SSDs permit less time for stopping. However, conducting this analysis is potentially confounded by movement amplitude because, as noted above, smaller amplitude movements tend to be associated both with shorter SSDs (Fig. 5G,H) and with shorter antagonist latencies (e.g., Fig. 6F, position of pink dots relative to red line, stacked as a function of movement amplitude). To circumvent this potential confound, we examined the relationship between antagonist latency and SSD for movements binned into 0.025 m amplitude bins and then averaged the antagonist latencies across all participants. As shown in Figure 9B (with SSDs grouped into quartiles for convenience), antagonist latency tended to decrease with increasing SSDs over most movement amplitudes, although we did not test the significance of this correlation because there were only four data points. Thus, providing one accounts for how much the hand moves before being stopped, the antagonist latency appeared to decrease for later SSDs.

To directly compare antagonist latency and SSRT, we split the SSDs into quartiles and then plotted the observed antagonist latency against the estimated SSRT at each quartile. As shown in Figure 9C, doing so revealed a positive relationship between antagonist latency and SSRT in 7 of 9 participants, although we did not test the significance of this correlation because there were only 4 data points.

Finally, we wished to examine whether there were relationships between the SSRT and antagonist latency. We found that the antagonist latency and SSRT tended to cofluctuate through time, as participants shifted priority between going and stopping over the course of the experiment (Bissett and Logan, 2011; Corneil et al., 2013). To analyze this aspect of our data, we compared the estimated SSRT and the mean antagonist latency in each of the eight blocks of 200 trials. In all participants, we observed a positive relationship between antagonist latency and SSRT (Fig. 9D; this correlation reached significance in 1 of 9 subjects, at p < 0.05), meaning that blocks with longer SSRTs tended to have longer antagonist latencies.

Opposing and scaled post-error adjustments across different movement sequences

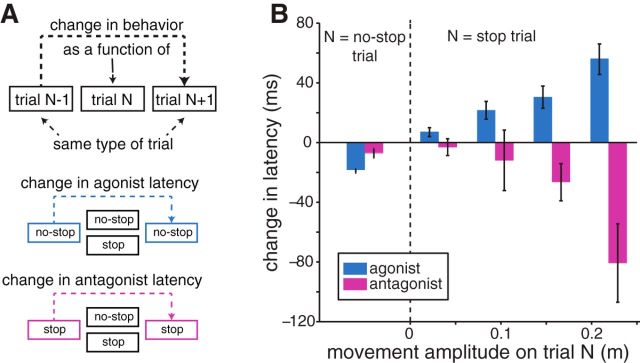
We now turn to analyses that would not be possible using conventional estimates of SSRT, given that such estimates require many trials. A well-documented effect in countermanding tasks is post-error slowing of the RT on no-stop trials (Emeric et al., 2007; Enticott et al., 2009; Bissett and Logan, 2012b). Previous work on countermanding eye-head gaze shifts has shown that the antagonist latency on neck muscles is also adjusted based on recent trial history, but in a direction opposite to that observed for RTs (Corneil et al., 2013). Such results were attributed to strategic and opposing shifts in the balance between movement generation and inhibition. Here we looked for a similar trial history effect on both movement generation and inhibition using a “triplet analysis” (Nelson et al., 2010) that allows assessment of the change in agonist latency relative to target onset, or antagonist latency relative to stop signal onset, across different trial sequences (Fig. 10A). The triplet analysis permits pooling of results across participants because all measures are referenced to the n − 1 trial.

Figure 10.

Triplet analysis. A, Graphical depiction of the logic of the analysis, wherein the change in the agonist or antagonist latency across the n − 1 and n + 1 trial is assessed as a function of the intervening trial (e.g., whether trial n was a stop or no-stop trial). B, When the intervening trial was a no-stop trial (left of dashed line), both agonist latency (blue) and antagonist latency (magenta) decreased. When the intervening trial was a stop trial (right of dashed line), agonist latency increased but antagonist latency decreased as a function of movement amplitude on the intervening trial.

The effect of trial history on movement generation was assessed via the change in the agonist latency (Fig. 10B, blue bars). In agreement with previous studies (Nelson et al., 2010; Corneil et al., 2013), agonist latency decreases across a no-stop–no-stop–no-stop sequence (Fig. 10B, left; one-sample t test, t₍₄₀₇₄₎ = −14.7, p < 10⁻⁴⁶), reflecting a hastening in movement generation across no-stop trials with an intervening no-stop trial. In contrast, if the intervening trial was a stop trial, agonist latency increased (one-sample t test, t₍₁₈₁₃₎ = 6.04, p < 10⁻⁸). Moreover, this post-error slowing across such sequences scaled with movement amplitude (Fig. 10B, right), being moderate for small movements (which would include canceled and small-amplitude noncanceled trials) and progressively larger for larger-amplitude noncanceled movements (linear regression; r = 0.14, t₍₁₈₁₂₎ = 6.05, p < 10⁻⁸). Thus, not only was the movement generation process delayed after an intervening stop trial, but the magnitude of the delay scaled with the magnitude of any error that the subject made on the intervening trial.

We conducted a similar analysis on antagonist latency. We found that the antagonist latency tended to decrease across an intervening stop trial, with a larger decrease occurring when the subject produced a larger error on the intervening stop trial (Fig. 10B, right; linear regression; r = −0.26, t₍₁₂₇₎ = −3.21, p = 0.002). Thus, in contrast to what was seen with the movement generation process, the movement inhibition process was expedited after an intervening stop trial, with the magnitude of such an adjustment scaling with error magnitude on the intervening trial. Finally, in contrast to previous findings (Corneil et al., 2013), the antagonist latency decreased if an intervening trial was a no-stop trial (Fig. 10B, left; one-sample t test, t₍₄₁₄₎ = −2.30, p = 0.022). Our failure to replicate previous findings may relate to the effect of movement amplitude on the n − 1 and n + 1 stop trials on the antagonist latency, which could obscure any effects on trial history.

In sum, we found evidence for opposing trial-to-trial adjustments in both the agonist and antagonist latency across trial sequences with an intervening stop trial, in line with opposing reprioritization of movement generation or inhibition with immediate trial history. The opposing directions of these scaled adjustments on measures of movement generation and inhibition across an intervening stop trial can be best appreciated in Figure 10B (right), as the adjustments of agonist or antagonist latency increase or decrease, respectively.

Fewer trials are required to assess the latency of stopping using antagonist latency versus the SSRT

In the final analysis, we examine how many trials are required to obtain accurate measures of either the antagonist latency or SSRT. To address this, we performed post hoc simulations in which “x” number of trials was randomly taken from the dataset. Under the assumption that after 1600 trials (with 30% stop trials), we obtained the true value of the SSRT or antagonist latency, we asked how many trials would be required to obtain measures than lay within an arbitrary 10 ms of this true value. Across our sample, 440 ± 98 total trials (mean ± SEM, with 30% stop trials, or ∼132 stop trials across all SSDs) were required to derive SSRTs within 10 ms of the true value. This finding compares favorably to the simulation results reported by Band et al. (2003), where it was shown that ∼50 stop trials per SSD are required to yield SSRT estimates with 95% CIs of ∼10 ms. In contrast, only 64 ± 14 total trials (or ∼19 stop trials) were required to obtain average antagonist latencies within 10 ms of the true value. This analysis illustrates that the antagonist latency could be used to provide a more rapid assessment of inhibitory control than that currently used via estimation of the SSRT.

Comparing results from surface versus intramuscular recordings

Our analysis largely, although not exclusively, relied on EMG recordings made via intramuscular electrodes. The output of the burst detection algorithm was also screened on a trial-by-trial basis. Given that intramuscular recordings are invasive (which limited our sample size) and trial-by-trial screening time-consuming, we investigated whether similar conclusions could have been reached from surface recordings, and without manual screening. To do this, we took advantage of the fact that PEC was recorded via two sets of intramuscular recordings (the “selected” and the “unselected” channel; for the selected channel, we reverted to measures obtained directly from the burst detection algorithm, before manual screening) and one surface recording. We then compared the mean antagonist latency obtained from each of these three channels to each other and to the SSRT. As expected, all muscle measures correlated well with each other on a subject-by-subject basis (Table 3); hence, subjects with longer antagonist latencies with the selected intramuscular recording tended to have longer antagonist latencies with unselected surface recording (linear regressions, r > 0.76, p < 0.01 for the three possible comparisons). Antagonist latencies measured via surface recordings tended to be longer than those obtained from the selected (paired t test, t₍₈₎ = 4.71, p = 0.0015) but not unselected (paired t test, t₍₈₎ = 2.11, p = 0.07) intramuscular recordings, and the values from the selected and unselected intramuscular recordings did not differ significantly (paired t test, t₍₈₎ = 1.30, p = 0.22). Finally, the positive correlation between SSRT and the antagonist latency remained regardless of whether the antagonist latency was derived from the selected intramuscular recording (Fig. 11A; linear regression, r = 0.75, slope = 0.31, t₍₇₎ = 3.01, p = 0.02), unselected intramuscular recording (Fig. 11B; linear regression, r = 0.78, slope = 0.43, t₍₇₎ = 3.30, p = 0.01), or the surface recording (Fig. 11C; linear regression, r = 0.67, slope = 0.36, t₍₇₎ = 2.38, p = 0.05; compare both with Fig. 9A).

Table 3.

Mean antagonist latencies from canceled trials (in ms) for the selected and unselected intramuscular recording, and the unselected surface recording^a

Subject	Selected intramuscular	Unselected intramuscular	Unselected Surface
1	174	172	193
2	188	191	210
3	181	181	191
4	172	167	184
5	167	162	171
6	181	192	194
7	178	191	182
8	188	198	193
9	152	154	157

^aAll recordings obtained from PEC.

Figure 11.

Comparison of the relationship between SSRT and the antagonist latency for PEC, with the latter extracted from the selected intramuscular recording (A), the unselected intramuscular recording (B), or the surface recording (C). A differs from Figure 9A because the latter combined antagonist latencies across both PEC and DELT, after manual screening. Same format as Figure 9A.

Using agonist muscle offset to assess movement cancellation

As mentioned above, movement cancellation was often associated with a cessation of agonist muscle recruitment that preceded antagonist muscle onset, on average by ∼25 ms. The analyses shown in Figures 9 and 10 relied on the timing of antagonist muscle recruitment relative to the stop signal, given that this measure was obtained on a higher proportion of stop trials. We repeated the same analyses using the timing of agonist muscle offset, and observed many of the same tendencies, although these tendencies approached but did not reach significance. Briefly, the mean of the agonist offset latency correlated on a subject-by-subject basis with the SSRT (subject-by-subject correlation of means: r = 0.76, slope = 0.78, t₍₇₎ = 2.15, p = 0.018; compare with Fig. 9A). However, presumably due to the fewer observations from which an agonist offset latency could be derived, block-by-block correlations between agonist offset and SSRT trended upward in only 6 of 9 subjects (as opposed to 9 of 9 subjects when using the antagonist onset; Fig. 9D), and the agonist offset latency did not trend downward across a stop trial in a manner that depended on the movement amplitude in the intervening trial, as was the case for the antagonist onset in Figure 10B. Thus, although aspects of movement cancellation appear accessible with agonist muscle offset, antagonist muscle onset provided a more reliable measure in our experimental configuration that permitted a finer-grained assessment of movement cancellation.

Discussion

We studied the cancellation of whole-arm reaching movements in humans while recording upper limb activity from agonist and antagonist muscles. The timing of changes in muscle recruitment relative to a stop signal provides a within-trial measure of the stopping latency. Such measures can be obtained via surface recording techniques, converge on stable values within <100 total trials, and enable examination of the prioritization of stopping at an unprecedented resolution.

Mid-flight cancellation of an inertial body segment

The limb has considerable inertia, which imposes a lag between the changes in muscle recruitment and changes in movement kinematics. Moreover, the whole-arm reaching movements studied here lasted ∼300 ms. Accordingly, such whole-arm reaching movements can be stopped at any point in mid-flight, ranging from instances where the movement has barely begun to those where the stop signal was presented after agonist muscle onset (Fig. 4B). Clearly, the stop signal continues to be processed after movement commitment. Movement duration may be a crucial factor determining whether a movement is ballistic or not; whereas small-amplitude saccades offer limited time for control, larger eye-head gaze shifts can be arrested or adjusted in mid-flight (Corneil et al., 1999; Corneil and Elsley, 2005).

The wide range of amplitudes on stop trials emphasizes the arbitrariness of the criterion dividing stop trials into canceled or noncanceled subtypes. Our 1 cm criterion (∼5% of movement amplitude on no-stop trials) produced SSRT estimates similar to those reported previously (Mirabella et al., 2006; Boucher et al., 2007; Brunamonti et al., 2012). Post hoc analysis showed that SSRTs would have increased by 42 ± 17 ms (mean ± SD) or 72 ± 34 ms had we used a stopping criterion of either 50% of 95% of the entire movement amplitude, respectively. Shorter SSRTs that match or precede the antagonist latency could be obtained by constraining the stopping criterion even further. The arbitrariness of what constitutes success in a nonballistic system, and the associated changes in SSRT estimates, are relevant for neurophysiological studies of stopping, where the SSRT differentiates whether candidate neural activity could be involved in movement control or not. The confidence one has in applying this logic depends on how closely the SSRT matches central processes related to movement inhibition. Measuring changes in muscle recruitment offers an alternative, empirical measure of movement inhibition that is less prone to arbitrariness: any central stopping process must necessarily precede changes in peripheral muscle recruitment for it to contribute to movement control.

Although our SSRT estimates compare favorably with previous reports, the types of manual responses are quite different. Manual responses studied in the countermanding framework include squeezes of a dynamometer (de Jong et al., 1990), keyboard presses (Logan and Irwin, 2000), deflections or movements of a joystick or manipulandum (Boucher et al., 2007; Scangos and Stuphorn, 2010), pointing movements on a touchscreen or toward a pushbutton (Mirabella et al., 2006, 2011), single-joint deflections of the elbow (McGarry and Franks, 1997; Kudo and Ohtsuki, 1998), or some combination thereof (Brunamonti et al., 2012). Distinct profiles of EMG activity are needed to control distinct manual responses, reflecting differences in the specific biomechanics and force requirements of the task. For some manual responses, cancellation may entail the absence of departure from a starting position, accomplished perhaps by withdrawing or cancelling agonist muscle recruitment without requiring antagonist muscle recruitment; Scangos and Stuphorn (2010) did not observe any antagonist muscle recruitment in a task requiring translation of a horizontal manipulandum. In our setup, antagonist muscle recruitment on proximal limb muscles was detected on ∼50% of successfully canceled trials even when the hand stayed within a 1 cm radius window (Table 2).

Thus, successful cancellation in our task may or may not produce quantifiable changes in muscle recruitment. de Jong et al. (1990) forwarded the notion of central or peripheral cancellation, and our work and that of others (Burle et al., 2002; Servant et al., 2015) extend this to a single-trial resolution. The presence of trials where quantifiable changes in muscle recruitment were absent does not detract from the value of such measures, when available, in characterizing the stop process. Further, more advanced analytical methods may be able to extract peripheral signatures of cancellation on an even higher proportion of canceled trials, perhaps by assessing recruitment across multiple agonist and antagonist muscles (Corneil et al., 2010) or within a higher-dimensional space (Shenoy et al., 2013).

Using a trial-by-trial measure of movement cancellation to study effects of trial history

Our results supported the hypothesis that the antagonist latency is a manifestation of the stop process. We also found a relationship between trial history and the recruitment timing of both agonist (relative to target onset) and antagonist (relative to stop signal onset) muscles. These measures trended in opposing directions after a stop trial, with antagonist latencies decreasing and agonist latencies increasing across sequences with an intervening stop trial. Such results are suggestive of proactive and opposing adjustments that shift priority to expedite stop processes at the expense of slowing go processes (Bissett and Logan, 2012a; Corneil et al., 2013; Marcos et al., 2013). A novel finding of our study is that the magnitude of such adjustment scales with the magnitude of the intervening error, with larger adjustments occurring following larger errors. Thus, not only is the balance of stopping versus going affected by the presence of a stop trial, but adjustments depend on the performance on that stop trial in a continuous as opposed to binary fashion.

In contrast, both agonist and antagonist latencies decreased across no-stop trial sequences, in contrast to that observed in the oculomotor domain, where agonist latencies decreased while antagonist latencies increased across a no-stop trial sequence (Corneil et al., 2013). Our failure to replicate these previous results may be because antagonist latencies on the neck were derived from a small set of “head-only” errors when the head moved even though gaze remained stable (Goonetilleke et al., 2010, 2012). Alternatively, the effects of trial history may be obscured by the effect of movement amplitude on the n − 1 and n + 1 stop trials on the antagonist latency, or to the need to pool antagonist latencies across PEC and DELT to obtain a sufficient number of stop–no-stop–stop sequences, even though antagonist latencies were ∼13 ms shorter on PEC. More precise analysis of how antagonist latencies during manual responses change across a no-stop trial sequence may require a unidirectional task to generate enough such sequences with similar error amplitudes on the n − 1 and n + 1 trials.

Challenges associated with assessing movement control with EMG

Measuring antagonist latencies can advance the understanding of movement inhibition, revealing, for example, evidence for proactive adjustments of inhibition based on trial history. Further, providing a movement task is chosen that features prominent antagonist muscle recruitment (in our case, occurring on ∼75% of all stop trials, or ∼50% of canceled stop trials), accurate assessments of inhibition via the antagonist latency can be obtained in <100 total trials, rather than the several hundreds or more required for accurate SSRT estimations (Band et al., 2003; Teichert and Ferrera, 2015). Requiring fewer trials may help assessment of clinical or pediatric populations not amenable to performing a large number of trials. Study of such populations is also potentiated by our findings that antagonist recruitment can be recorded via surface EMG.

Assessing inhibition via EMG measurements does present challenges. Single-trial EMG measures are noisy, requiring complex algorithms to detect burst onset or offset and separate signal from noise. The limb is also a complex and asymmetric motor plant, requiring informed choices of agonist and antagonist muscles. In our study, PEC and DELT were not recruited symmetrically as agonist-antagonist pairs, as was the case for bilaterally recorded neck muscles (Goonetilleke et al., 2010); instead, PEC served more of a prime mover than DELT, being recruited sooner relative to target onset when serving as an agonist, and sooner relative to stop signal onset when serving as an antagonist. The magnitude and timing of control exerted through these muscles are not identical, complicating analysis of trail history. Finally, antagonist EMG signals associated with active braking may only occur in conjunction with the motion of body parts endowed with significant inertia, such as whole-arm reaching movements or orienting head movements, and hence may be absent during simpler joystick-, button-, or touchscreen-based movements. For such movements, within-trial measures of cancellation may be accessible via recordings of the withdrawal of agonist muscle recruitment.

These challenges aside, the application of EMG within a countermanding framework provides a rich dataset suited to trial-by-trial examination that can advance the neurophysiological and theoretical understanding of movement inhibition. We note as well that our use of EMG within the countermanding framework parallels the rise of using EMG recordings, down to the level of single trials, to advance the understanding of how the brain arrives at decisions (Burle et al., 2002; Servant et al., 2015; Jana et al., 2017).