Neural Representations of Sensorimotor Memory- and Digit Position-Based Load Force Adjustments Before the Onset of Dexterous Object Manipulation

Abstract

Anticipatory load forces for dexterous object manipulation in humans are modulated based on visual object property cues, sensorimotor memories of previous experiences with the object, and, when digit positioning varies from trial to trial, the integrating of this sensed variability with force modulation. Studies of the neural representations encoding these anticipatory mechanisms have not considered these mechanisms separately from each other or from feedback mechanisms emerging after lift onset. Here, representational similarity analyses of fMRI data were used to identify neural representations of sensorimotor memories and the sensing and integration of digit position. Cortical activity and movement kinematics were measured as 20 human subjects (11 women) minimized tilt of a symmetrically shaped object with a concealed asymmetric center of mass (CoM, left and right sided). This task required generating compensatory torques in opposite directions, which, without helpful visual CoM cues, relied primarily on sensorimotor memories of the same object and CoM. Digit position was constrained or unconstrained, the latter of which required modulating forces beyond what can be recalled from sensorimotor memories to compensate for digit position variability. Ventral premotor (PMv), somatosensory, and cerebellar lobule regions (CrusII, VIIIa) were sensitive to anticipatory behaviors that reflect sensorimotor memory content, as shown by larger voxel pattern differences for unmatched than matched CoM conditions. Cerebellar lobule I–IV, Broca area 44, and PMv showed greater voxel pattern differences for unconstrained than constrained grasping, which suggests their sensitivity to monitor the online coincidence of planned and actual digit positions and correct for a mismatch by force modulation.

SIGNIFICANCE STATEMENT To pick up a water glass without slipping, tipping, or spilling requires anticipatory planning of fingertip load forces before the lift commences. This anticipation relies on object visual properties (e.g., mass/mass distribution), sensorimotor memories built from previous experiences (especially when object properties cannot be inferred visually), and online sensing of where the digits are positioned. There is limited understanding of how the brain represents each of these anticipatory mechanisms. We used fMRI measures of regional brain patterns and digit position kinematics before lift onset of an object with nonsalient visual cues specifically to isolate sensorimotor memories and integration of sensed digit position with force modulation. In doing so, we localized neural representations encoding these anticipatory mechanisms for dexterous object manipulation.

Introduction

Dexterous object manipulation relies on adapting fingertip forces to the object's physical properties via sensory feedback and anticipatory mechanisms (Westling and Johansson, 1987; Johansson and Westling, 1988; Schneider and Hermsdörfer, 2016). Because feedback processing of performance error (slip, tilt/roll) is delayed, anticipatory fingertip force modulation (before lift onset) is essential to minimize error. Anticipatory force modulation is based primarily on visual cues and internal representations of previous experiences with similar objects (referred to as sensorimotor memories). Sensorimotor memories are especially useful when key object properties are hidden or misleading. Behavioral studies on the nature of sensorimotor memories use a paradigm whereby visual cues are unhelpful for the task goal of minimizing roll at lift onset of a symmetrically shaped object with an asymmetric center of mass (CoM) (Salimi et al., 2000, 2003; Lukos et al., 2007; Bursztyn and Flanagan, 2008; Fu et al., 2010; Zhang et al., 2010). Subjects learn to generate a compensatory torque in the opposite direction of the CoM by asymmetrically partitioning digit load forces during load phase (e.g., more thumb than index finger load force with a left CoM object), thereby minimizing roll shortly after lift onset. Later studies adapted the task with unconstrained digit positions and found that subjects can maintain task performance despite trial-to-trial digit position variability by accurately modulating load forces (Fu et al., 2010; Fu and Santello, 2014; Mojtahedi et al., 2015; Marneweck et al., 2016). This suggests an online component to anticipatory force modulation, namely, to sense and integrate digit position variability before lift onset. Therefore, load forces can be modulated anticipatorily as a function of visual feedback (when available and conveying veridical object property information), sensorimotor memories, and integrating online sensing of digit position with force modulation.

It is unclear how the brain represents these mechanisms contributing to anticipatory force modulation because studies have rarely isolated them from each other or from feedback of object properties emerging after lift onset. The cerebellum has been proposed as a locus for sensorimotor memory representations (Miall et al., 1993; Wolpert et al., 1998); however, anticipatory grip force is impaired in some cerebellar degeneration cases, but not others (Fellows et al., 2001; Diedrichsen et al., 2005; Rabe et al., 2009), suggesting that sensorimotor memory representations might extend beyond cerebellum. Transcranial magnetic stimulation (TMS) to motor, premotor, and parietal regions alters prelift motor output, suggesting a regional network of sensorimotor memory representations (Chouinard et al., 2005; Davare et al., 2006, 2007, 2009, 2010; Dafotakis et al., 2008; Koch et al., 2010; Loh et al., 2010; White et al., 2013; Parikh et al., 2014). The most convincing studies incorporate designs with unhelpful visual object cues (Chouinard et al., 2005; Dafotakis et al., 2008; Loh et al., 2010). However, these protocols disrupt anticipatory force measures, but rarely task success (usually specified as a simple object lift). Such tasks might not demand the precision or dexterity, and thus precise anticipatory force control, required for explicit performance-based tasks like roll minimization.

Representational similarity analysis (RSA) of fMRI data was used to investigate representations of anticipatory mechanisms contributing to load force modulation for dexterous object manipulation. fMRI activity and movement kinematics were measured as subjects minimized roll of a symmetrically shaped object with a concealed asymmetric CoM in blocked trials to the left and right. The two blocks of CoM require opposite compensatory torques, which, without salient visual CoM cues, rely primarily on the sensorimotor memories of the same object and CoM. Regions representing sensorimotor memories should show larger voxel pattern differences when contrasting trials with different, unmatched CoMs than when contrasting trials with the same, matched CoMs. In some blocks, digit position was unconstrained, requiring modulation of load force beyond what can be recalled from sensorimotor memories to compensate for the additional digit position variability. Regions representing online digit position-based force adjustments should show larger voxel pattern differences in unconstrained than constrained grasping. We hypothesized a broad motor–premotor–cerebellar network of sensorimotor memory and digit-position-based anticipatory force adjustments.

Materials and Methods

Participants

Twenty healthy, right-handed subjects (median age: 22 years; range: 18–32; 11 women) with normal or corrected to normal vision participated in the experiment. Data from four subjects (2 women) were excluded due to equipment failure (n = 3) and due to not finishing the experiment (n = 1). All study procedures were approved by the Human Subjects Committee, Office of Research, University of California–Santa Barbara, and all subjects gave written informed consent.

Materials, design, and procedure

Subjects lay supine in the MRI scanner with their head, neck, and shoulders firmly padded and kept in place with sandbag cushions to minimize excessive head and body motion. Sandbag cushions were also placed under the right upper arm to minimize upper limb movement during the reach and execution stages of a given trial. Subjects wore headphones to hear audio cue instructions and to minimize scanner noise. After structural T1- and T2*-weighted anatomical scans, BOLD activity was measured while subjects grasped and lifted an inverted T-shaped object at constrained and unconstrained grasp contacts with a concealed off-centered CoM using the tip of their right thumb and index finger with the aim of preventing object roll.

Materials.

The custom-made inverted T-shaped Plexiglas object (Fig. 1A) consisted of a horizontal base (height: 0.5 cm; width: 18.0 cm; depth: 5 cm) and a vertical Plexiglas column (height: 13.0 cm; width: 3.4 cm; depth: 5.0 cm). On either side of the vertical column were removable balsa-wood-covered grip surfaces (distance between grip surfaces: 9.0 cm). The grasp surfaces used when subjects grasped the object with the tip of the thumb and index finger at constrained and unconstrained locations were of circular (diameter: 1.5 cm) and rectangular shapes (height: 7.0 cm; width: 2.2 cm), respectively. A rectangular brass mass (height: 2.5 cm; width: 6.5 cm; depth: 2.5 cm; 372 g) was placed on the horizontal base either on the left or the right side of the vertical column, which created an off-centered CoM. The added mass to the left or right of the object's vertical column causes a counterclockwise or clockwise torque of 180 Newton millimeter (Nmm) that subjects experience after object lift onset. To prevent object roll (task goal), subjects had to generate a compensatory torque in the opposite direction of the CoM.

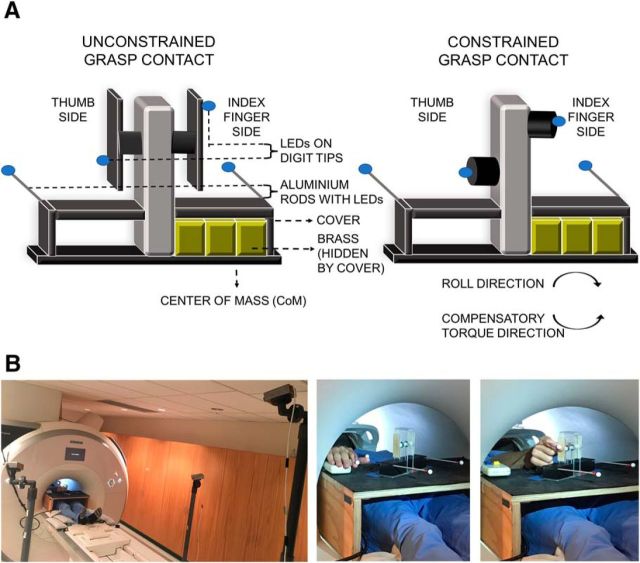
Figure 1.

A, Illustration of the custom-built inverted T-shaped object with an off-centered concealed CoM (right-sided in the example) with removable balsa-wood-covered unconstrained (left) and constrained (right) grasp surfaces. LED markers on aluminum rods and on digit tips are depicted by blue circular shapes. To prevent object roll (task goal), subjects were to generate a compensatory torque in the opposite direction of the CoM (counterclockwise in this example). For each grasp contact condition, the CoM was on the left and the right, thus giving four experimental conditions performed in four blocks of trials within each of six functional runs. B, Photographs showing in-scanner setup with the three radiofrequency-shielded cameras situated in a standard position relative to the scanner bore (left) and a subject during the button-down phase (middle) and contact-to-lift phases (right), respectively.

Black covers (height: 3.4 cm; width: 7.2 cm; depth: 5 cm) on both sides of the vertical column concealed the location of the CoM. Two aluminum rods (length: 12.4 cm) were firmly affixed to the outer edge of the top of the black covers (furthest away from the vertical column). Wiring from a battery pack was fed through each rod, ending in LED markers at the rod tips (for measuring object position and roll, see below). The total mass of the object was 610 g.

The inverted T-shaped object was positioned at arm's length on a wooden table sitting over the hips of the subject. The object start position did not face forward (i.e., parallel to the edge of the table), but rather was rotated in a counterclockwise direction at a 30° offset. Piloting showed that this position maximized the biomechanical ability to use digit position asymmetry (thumb higher than index finger and index finger higher than thumb) in achieving the task goal with the CoM on the left and right side, respectively. This object position also minimized biomechanical constraints that influence object roll (e.g., the wrist would be stiffened more when picking up the facing forward than angled object, the former of which would minimize the object rolling in a clockwise direction). A button box was affixed to the right side of the table, which subjects were instructed to hold down with the palm of their hand between trials. A mirror attached to the head coil allowed subjects to see the object (statically and during task-related movement) and their digit positioning on the object as if they were looking directly at it.

Anatomical and fMRI data were collected using a Siemens 3T Magnetom Prisma Fit (64-channel phased-array head coil). High-resolution 0.94 mm isotropic T1-weighted (TR = 2500 ms, TE = 2.22 ms, FA = 7°, FOV = 241 mm) and T2*-weighted (TR = 3200 ms, TE = 566 ms, FOV = 241 mm) sagittal sequence images were acquired of the whole brain. Next, as subjects performed the object manipulation task, BOLD contrast was measured with a multiband T2*-weighted echoplanar gradient-echo imaging sequence (TR = 400 ms, TE = 35 ms, FA = 52°, FOV = 192 mm, multiband factor 8). Each functional image consisted of 48 slices acquired parallel to the AC–PC plane (3 mm thick; 3 × 3 mm in-plane resolution).

Digit position and object position and roll were tracked by a radiofrequency-shielded three-camera motion tracking system (Precision Point Tracking System; Worldviz; see Fig. 1B for in scanner setup) that recorded six degrees of freedom positions of near-infrared LEDs (frame rate: 150 Hz; camera resolution: 640 × 480 VGA; at the focal distance, the spatial accuracy is submillimeter). The cameras were always positioned in the same spot (380 cm, 771 cm, 452 cm, respectively, horizontally from the scanner bore). These camera positions were selected based on piloting for adequate tracking of the object position and digit positions on the object. An individual LED marker was positioned on the tip of the index fingernail and on the thumbnail (to measure digit position) and on either side of the T-shaped object on the outer tip of the aluminum rods (to measure object roll and position).

Experimental design and procedure.

The experimental task consisted of four conditions: manipulating an object with a left and right CoM at unconstrained grasp contacts and with a left and right CoM at constrained grasp contacts. Subjects first completed 40 practice trials (10 trials for each condition). The digit position for the 10 constrained practice trials was set to a generic position across subjects, with a 2 cm vertical spacing between the digits. The mean digit position of the thumb and index finger during each of the 10 unconstrained practice trials (with the CoM on the left and the right, respectively) was used to set the position of the constrained grasp surfaces for test trials. The rationale for this was to equalize as much as possible the mean digit force distribution between the unconstrained and constrained conditions (such that any differences arising in voxel patterns between unconstrained and constrained conditions were not due to differences in mean force distribution patterns). After practice, subjects performed six functional runs each consisting of 40 trials (10 blocked trials for each condition). Stimulus timings for each block of trials were controlled by a custom script (Vizard Virtual Reality Software Toolkit, version 4.0; Worldviz). The intertrial interval was randomly chosen to be between 2, 3, 4, 5, or 6 s and there was a rest period between each of the 4 blocks of trials. The rest period was ∼30 s, but varied slightly depending on the time it took the experimenter to change the CoM and/or grasp surfaces. The experimenter changing the CoM/grasp surfaces signaled the completion of the change to another experimenter, who then initiated the script to run the next block of trials. The order of the blocks of unconstrained and constrained trials (and the order of the blocked CoM within each of those trials) was counterbalanced across runs and subjects.

On each trial, subjects started with their right hand in a relaxed position holding down a button with the palm of their hand. An audio start cue instructed them to release the button, reach for the object, lift it, hold it to the height of a marker (5 cm), and minimize object roll. Subjects were required to hold the object at the marker height until a third audio cue (4 s after button release time) instructed them to place the object back in its start position and return their hand to the button. The start audio cue for each trial always coincided with the beginning of a new functional image. An “error” audio cue was played after the hand was back on the button if the object rolled >5° in either direction at any time during the trial. With the mirror attached to the head coil, subjects could at all times see the object and their hand (when in a static position and when in motion during a trial).

For trials requiring object manipulation at constrained grasp contact points, the audio start cue consisted of two identical sounds played in quick succession. For trials requiring object manipulation with the unconstrained grasp surfaces, the audio start cue consisted of two sounds that were either the same or different. If the two cues sounded the same (three of every 10 trials in a block), subjects were to grasp the object with their index finger and thumb collinearly (i.e., grasping the object's grasp surface at the same vertical height relative to the object's base). If the two auditory cues differed (i.e., one tone was higher than the other; seven of every 10 trials in a block), subjects were to grasp the object with their digits noncollinearly (i.e., thumb higher than the index finger). Therefore, the number of auditory cues was matched between constrained and unconstrained conditions. Subjects were encouraged to vary the vertical distance between the index fingertip and thumb during the unconstrained trials. The rationale for this extra instruction was to increase variability in digit position on a trial-to-trial basis (requiring trial-to-trial modulation of digit forces) when manipulating the object with unconstrained grasp surfaces. It was expected that subjects would be able to modulate digit forces to these variable digit positions on each trial, as demonstrated by previous work in which subjects were asked to change digit position by increasing or decreasing the number of digits involved in the grasp (Fu et al., 2011).

Validation study materials, design, and procedure.

Data were collected on 10 different subjects (six women) performing the same object manipulation task outside of the scanner (20 trials each for 80 trials total). Force transducers (Nano 17 Force/Torque transducer; ATI Industrial Automation) attached to the grasp contact surfaces measuring grip force, load force, and torques applied (resolution = 0.05 N, 0.025 N, and 0.125 Nmm respectively). An electromagnetic sensor (Polhemus Fasttrack, 0.005 mm of range, 0.025° resolution) attached to the top of the vertical column of the object measured the vertical position and the roll of the grip device. This allowed calculating the mean time from load force initiation (0.1 N) to lift onset (i.e., load phase) during unconstrained and constrained trials, respectively. The mean load phase on successful trials was 380 and 320 ms for constrained and for unconstrained trials, respectively. Mean load phases were used to estimate the onset of contact-to-lift phases of trials inside the scanner. This phase was the focus of all fMRI analyses because load phase is known to be the time during which load forces are recruited in an anticipatory fashion before feedback about object properties becomes available after object lift onset. This anticipatory force modulation is based on sensorimotor memories and also when digit position is variable from trial to trial, as in an unconstrained grasp case, based on online feedback about digit position.

Statistical analyses

Kinematic data processing and analyses.

Data collected were filtered using a fourth-order Butterworth filter with a cutoff frequency of 5 Hz. Movement phases (Fig. 2) were defined for each trial in the following way. The reach phase was defined as the time from the button box release onset to the contact-to-lift phase onset. The contact-to-lift phase was defined as the time from load force initiation of 0.1 N to lift onset (i.e., load phase). Lift onset was defined as the time at which the vertical position of the object went above 1 mm and subsequently remained above this value for at least 20 samples. Load force initiation was set to a fixed time (320 ms for unconstrained trials, 380 ms for constrained trials) before lift onset. The fixed timings were set to the mean time between load force initiation and lift onset during unconstrained and constrained trials that were collected with force transducers outside of the scanner during the validation study (see “Validation study materials, design, and procedure” section). The mean load phase durations from the validation study were not statistically different from the contact-to-lift phases from the fMRI study for each grasp type condition (unconstrained: p = 0.92; constrained: p = 0.05). The execution phase was defined as the time from lift onset to the onset of the button-down phase. Finally, the button-down phase onset was defined as the time at which the hand was back on the button after execution. The duration of the button-down phase of each grasp contact condition matched its corresponding contact-to-lift phase (i.e., 320 ms for unconstrained trials, 380 ms for constrained trials).

Figure 2.

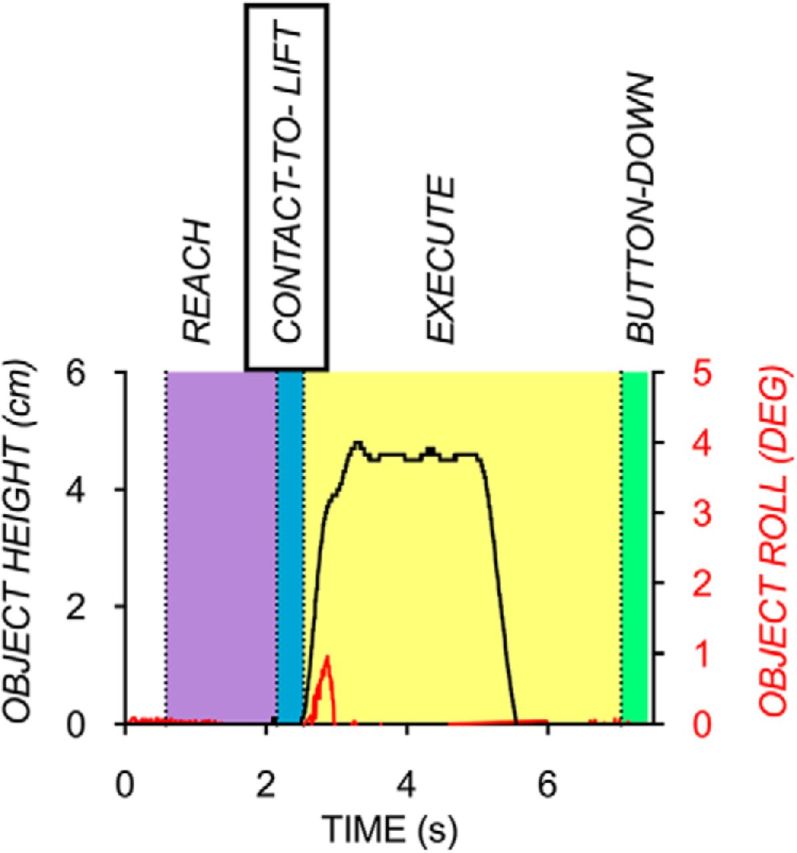
Representative traces (one subject) showing object height (black) and roll (red) of a successfully performed trial during the reach, contact-to-lift, execute, and button-down phases.

Object roll was defined as the angle of the object in the frontal plane. Peak object roll was recorded shortly after lift onset (∼250 ms) before somatosensory feedback resulted in corrective responses to counter object roll. Trials with object roll >5° were classified as errors. Subjects generally complied to the task instructions of minimizing roll, with on average only a small subset of trials (20 of 240 trials, i.e., 8%) being characterized by a larger error (mean roll on error trials = 7.03°, SD = 0.82°). These error trials were not included in the RSAs, but, as described below, were modeled as a predictor variable in the general linear model (GLM) of each run for each subject. Finally, the difference in thumb and index finger position at lift onset was calculated (thumb position − index finger position). Positive values indicate thumb higher than index finger position, whereas negative values indicate index finger higher than thumb position. A median split of digit position was performed within each of the four conditions such that each condition had two subconditions: one in which subjects' digit position was above the median digit position difference and another in which subjects' digit position difference was below or equal to the median digit position difference. The rationale for this median split was to evaluate whether unconstrained grasping trials gave larger differences between these subconditions (due to trial-to-trial variability in digit position) than constrained grasping trials.

Four sets of statistical analyses were performed on the kinematic data. First, a two-way ANOVA examined the effect of CoM (left and right) on digit position partitioning, the aim of which was to ensure that mean digit positioning partitioning was different between CoM conditions in both grasp contact conditions. Second, a two-way ANOVA examined whether variability of digit position (SD) was higher in the unconstrained than constrained grasp contact conditions, regardless of CoM. Third, it was determined whether differences in digit position partitioning were larger between CoM conditions (i.e., unmatched) than within a given CoM condition (i.e., matched CoM) within each grasp contact condition, respectively. A two-way ANOVA [with CoM correspondence (matched and unmatched) and grasp contact (unconstrained and constrained) as factors] compared the difference between digit positioning partitioning above and below the median (mean from both CoM conditions for each grasp contact condition separately) with the difference in digit positioning partitioning between CoM conditions (mean of four differences in digit position partitioning between the left and right CoM conditions, for each grasp contact condition separately) as follows: (1) above median left CoM − above median right CoM; (2) above median left CoM − below median right CoM; (3) below median left CoM − below median right CoM; and (4) below median left CoM − above median right CoM. Fourth, two sets (one for each CoM) of two-way ANOVAs determined whether, as expected, the difference in digit position created by a median split (i.e., below vs above median comparison) was significantly larger in the unconstrained than constrained grasp contact conditions.

MRI data preprocessing and analyses.

MRI data were preprocessed and analyzed using SPM12 (Wellcome Trust Center for Neuroimaging). Functional images across all runs were spatially realigned to a mean EPI image using second degree B-spline interpolation, all of which were coregistered to the subject's T1 image. Two between-subject spatial normalization methods were used, one for cerebellum and one for the rest of the brain. Between-subject normalization of cerebellum was conducted using the SUIT SPM toolbox (Diedrichsen, 2006; Diedrichsen et al., 2009, 2011; Diedrichsen and Zotow, 2015). Using SUIT, the cerebellum was isolated and segmented into tissue types. The full volume was cropped to include the infra-tentorial structures and then tissue types were used to calculate the posterior probability of each voxel to belong to cerebellum or brainstem (Ashburner and Friston, 2005). Next, these tissue segmentation maps created an affine transformation matrix and a 4D nonlinear flow field to normalize each subject's individual cerebellum into the SUIT atlas space (interpolation: trilinear; voxel size: 2 × 2 × 2 mm). Between-subject registration of the rest of the brain was conducted with SPM's normalize function, which aligned each subject's T1 and its coregistered functional images into standard ICBM/MNI-152 atlas space (interpolation: fourth degree B-spline; voxel size: 3 × 3 × 3 mm).

Two first-level GLMs were conducted. The first of these was a convolution-based model with events convolved with the standard canonical HRF basis function. This was estimated for each run separately for each subject. Onsets and durations were entered for separate predictors for each of 15 experimental conditions: reach (1 condition), contact-to-lift (8 conditions, see below), execute (1 condition), and button-down phases (4 conditions for the four experimental conditions) of a given trial and a full movement phase of error trials, if any (1 condition). Three subjects did not make any errors on 1 (n = 2) or 2 (n = 1) functional runs, so the GLMs for those runs did not include an error condition. The four experimental conditions manipulating CoM and grasp contact (i.e., unconstrained left CoM, unconstrained right CoM, constrained left CoM, and constrained right CoM) were subdivided into eight contact-to-lift conditions. For each condition (unconstrained/constrained; left/right COM), trials in which digit position difference were above the median split were assigned to one condition and trials in which digit position difference were below the median split were assigned to the other condition. The reach, execute, and button-down conditions were not analyzed further in this analysis.

The second GLM used a finite impulse response (FIR) deconvolution approach. The purpose was to test whether the voxel pattern differences from the RSA between unmatched and matched CoM conditions (see below) reflect differences in anticipatory sensorimotor memories for the different CoMs before or at the point of contact, before execution or object liftoff had commenced. To this end, an FIR function was selected as a basis function (window length: 6.8 s; order: 400 ms), yielding 17 400 ms time bins. We chose this time window length to track activations sufficiently through the peak of the HRF, which we assumed was <6 s. The onsets of each of the eight contact-to-lift conditions were set 400 ms before contact-to-lift onset. To avoid a rank-deficient design matrix and to minimize overfitting of the GLM, the reach, execution, and button-down phases were included as part of the baseline. The FIR analysis identified at which time point unmatched CoM distances (as measured by RSA, see below) were significantly greater than matched CoM distances in each of our ROIs over the course of 17 × 400 ms time bins (400 ms before contact-to-lift to 6 s after contact-to-lift).

The RobustWLS Toolbox in SPM (Diedrichsen and Shadmehr, 2005) was used to obtain unbiased estimates of noise variance of each image and to down-weight those images with high variance to account for movement artifacts. Any arm movement occurring during contact-to-lift phase is minimal because this is the time during which the subject makes contact with the object to the time that the subject lifts the object—in other words, the arm is likely stationary (and supported by sand bags) during this phase. Nevertheless, any arm movement occurring during this phase is arguably part of the anticipatory plan alongside the digit position and forces necessary to lift the object and minimize roll. The hand-to-target trajectories during reach phase are also similar across all conditions; therefore, it is unlikely that differences seen in RSA patterns are driven by differences in arm movement. Furthermore, head motion mean rotations and translations (with minimum and maximum values in parentheses) were minimal: x: −0.02 mm (−0.38, 0.34); y: −0.29 mm (−0.86, 0.29); z: 0.76 mm (−0.42, 1.72); pitch: −0.008° (−0.02, 0.008); roll: −0.001° (−0.009, 0.006); and yaw: 0.002° (−0.005, 0.01). Altogether, motion unrelated to anticipatory control of object manipulation was unlikely to have affected the results.

An RSA approach (Kriegeskorte et al., 2008; Walther et al., 2016) identified neural representations of anticipatory mechanisms, sensorimotor memory content, and digit-position-based force adjustments involved in dexterous object manipulation. This approach was chosen over a traditional univariate fMRI approach because the latter is limited to the detection of magnitude-based differences in activity within a given region. It is unlikely that a region would more strongly activate when manipulating an object with a left compared with a right CoM in our task. Instead, subtle differences were predicted between the pattern of activity across voxels in a given regions between such conditions, as has been demonstrated extensively in previous studies of visual and motor encoding (Eisenberg et al., 2010, 2011; Haxby et al., 2014; Ejaz et al., 2015; Fabbri et al., 2016).

RSAs were performed in predefined regions of interest (ROIs). Left hemisphere (ROIs, Fig. 3) were preselected from motor (4a, 4p, PMv, PMd, SMA), parietal (SPL5, SPL7, AIP, PF), and somatosensory regions (S1/PSC, OP), Broca area (BA) 44, and right hemisphere cerebellar lobule regions were preselected (I–IV, V, VI, Crus I, Crus II, VIIb, VIIIa, VIIIb), all of which have been suggested to be involved in anticipatory force control (Schneider and Hermsdörfer, 2016). This conservative, hypothesis-driven approach was chosen over a data-driven, exploratory approach (e.g., whole-brain searchlight analysis) to establish that this novel analysis in this domain could indeed identify unique representations of anticipatory control and to avoid potential biases and false-positives associated with the large number of comparisons. Right hemisphere cortical ROIs and left hemisphere cerebellar lobule ROIs were not included in the current set of analyses because we focused on regions that control right-handed hand movements directly. All patterns except those from premotor areas were extracted using the ROIs in the SPM Anatomy Toolbox (Eickhoff et al., 2005, 2006, 2007). Premotor ROIs were based on predefined anatomical parcellations (Geyer et al., 1996; Picard and Strick, 2001; Tomassini et al., 2007; Destrieux et al., 2010): PMv, PMd, and SMA regions were free-drawn on a standardized surface mesh in SUMA (Saad et al., 2004), projected to a standard MNI space, and then mapped back to the subject's native space using their own T1-weighted image (Barany et al., 2014).

Figure 3.

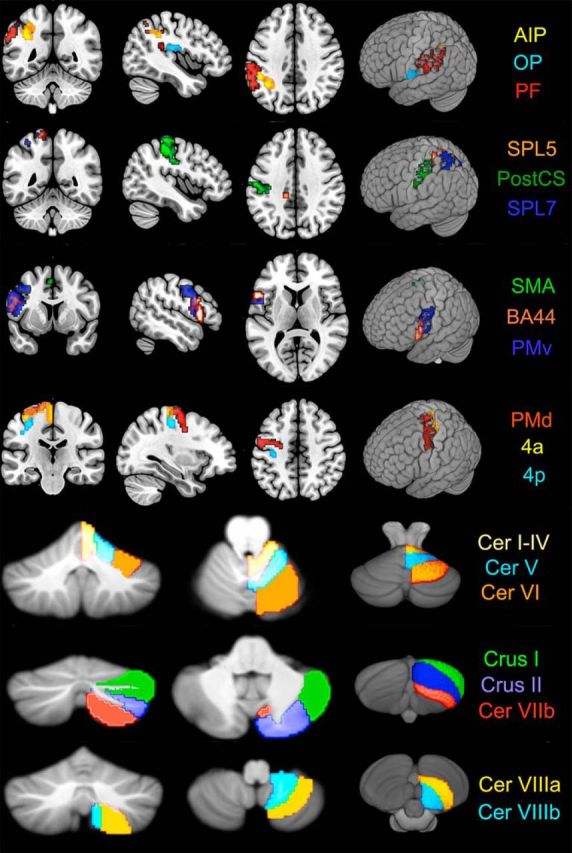
Anatomical ROIs displayed on the MNI-152 atlas using the visualization software MRIcro (http://www.mccauslandcenter.sc.edu/crnl/mricro).

The cross-validated Mahalanobis distance (also known as crossnobis distance) was used to estimate the distance between two voxel patterns rather than the simpler Euclidean distance. The Mahalanobis distance incorporates a multivariate noise normalization, leading to more reliable distance estimates than univariate noise normalization, and it gives less weight to the information contained in two voxels that are highly correlated in their random variability than to information contained in two uncorrelated voxels. For each region, run, and subject, vectors of GLM residuals and β-coefficients from the first-level GLM analysis were tabulated. The estimate of the noise covariance within a region was obtained from each run's residuals (Walther et al., 2016) and averaged across the six runs. The resulting mean noise covariance per region was used to prewhiten the corresponding regression coefficients separately for each run and subject. One way to calculate the Mahalanobis distance is to calculate the Euclidean distances of the prewhitened regression coefficients for each of the six runs and then average these together. However, there is residual noise in each coefficient that differs for each run and that will enter into the quadratic distance metric, causing a positive bias; activity patterns will always be larger than zero and the expected value of the distance estimate will increase with increasing noise. This complicates the comparison of distances between different brain regions or individuals, which can differ considerably in the level of measurement noise. To circumvent this bias, an unbiased estimate was obtained for the pattern distances by using cross-validation. For each subject, the distance between the prewhitened regression coefficient for one condition from one run was compared with the coefficient of another condition from another run (which has different noise). This was repeated for all possible pairs between runs and the distances were averaged. This is referred to as cross-validated Mahalanobis distances and was calculated for each of the eight contact-to-lift conditions for each subject in each ROI. This procedure was repeated for the second set of GLM results derived from the FIR deconvolution.

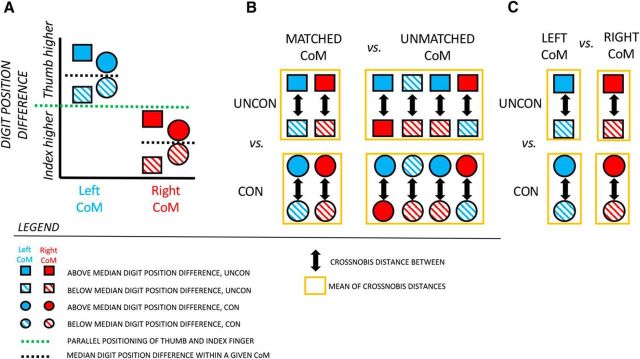
To identify regions that are sensitive to anticipatory differences between left and right CoM conditions that would minimize roll of an object, voxel pattern differences were compared between conditions with matched and unmatched CoM distributions (Fig. 4B); this analysis was done on the convolution-based and the deconvolution-based data. As shown schematically in Figure 4A and quantitatively in Figure 6, there was a smaller difference when comparing digit position partitioning above and below the median within a given CoM condition (i.e., matched CoM) than when comparing digit position partitioning between CoM conditions (i.e., unmatched CoM). Given this, regions were identified in which the voxel pattern differences were sensitive to these behavioral differences in matched and unmatched CoM contrasts. For each ROI, a two-way ANOVA was performed with CoM correspondence (matched or unmatched) and grasp contact (unconstrained and constrained) as factors. The matched CoM variable (for each grasp contact condition) was calculated from the mean crossnobis distances of the two CoM conditions differentiating patterns during which the digit position difference was below compared with above the median. The unmatched CoM variable (for each grasp contact condition) was calculated from the mean of the four possible distance estimates differentiating left from right CoM within each grasp contact condition (Fig. 4B).

Figure 4.

Schematic illustrations of the contact-to-lift conditions and the comparisons of mean voxel pattern distances between these conditions in our main representational similarity analyses. A, Schematic illustration of the eight contact-to-lift conditions based on lifting an object with a given CoM (blue, left; red, right) at constrained (CON; circular shapes) and unconstrained (UNCON; rectangular shapes) grasp contacts with the subject's expected digit position difference above (solid pattern) and below (dashed pattern) the median (black horizontal dotted line). Digit position above and below the green dotted line (indicative of parallel positioning of thumb and index finger) indicates thumb higher than index finger position, and index finger higher than thumb position, respectively. Note the depiction of larger differences in digit position partitioning in unconstrained than constrained grasping, as that shown in Figure 7; B, to identify regions that are sensitive to behavioral differences between different CoM conditions, the mean voxel pattern distance in matched CoM conditions (mean distance between above vs below median digit position partitioning for left and right CoM conditions) is compared with the mean voxel pattern distance between unmatched CoM conditions (mean of four distances of digit position partitioning that differentiate left from right CoM) for each grasp contact respectively; C, to identify regions that are sensitive to behavioral differences of trial-to-trial variation in digit position between grasp contact conditions, the voxel pattern distance of above and below median digit position difference is compared between unconstrained and constrained grasp contact conditions for the left and right CoM conditions.

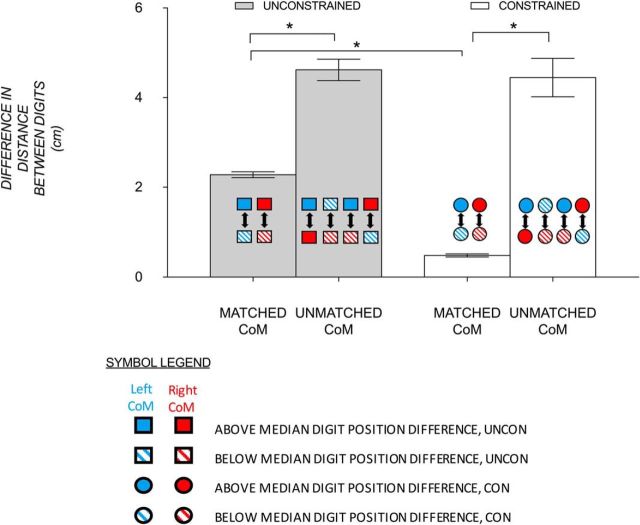
Figure 6.

Mean (±1 SE) difference in distance between digits within (i.e., matched) and between (i.e., unmatched) CoM conditions for unconstrained (gray) and constrained (clear) conditions. As the colored symbols show, the matched CoM variables are the mean distances between above versus below median digit position partitioning for left and right CoM conditions and the unmatched CoM variables are the mean of four distances of digit position partitioning that differentiate left from right CoM for each grasp contact, respectively. Statistical significance (p < 0.001) is shown with an asterisk.

To identify regions that are sensitive to anticipatory behavioral differences between unconstrained and constrained grasping (within a given CoM), voxel pattern distances between digit positions above and below the median split were compared between unconstrained and constrained grasping in both CoM conditions (Fig. 4C). A two-way ANOVA was performed with grasp contact (unconstrained and constrained) and CoM (left and right) as factors and the crossnobis distance contrasting digit position difference above and below its median as the dependent variable.

Critically, with these planned RSAs, a distance relative to a null model is not of interest; with noise in the data, there will always be a residual distance within a given RSA comparison. Instead, the focus is on the relative difference in voxel patterns distances between RSA comparisons. All analyses report the adjusted false discovery rate using the Holm's Sequential Bonferroni Procedure (Holms, 1979).

Results

Kinematic movement analyses

Significant differences in mean digit position between CoM conditions and larger digit position variability in unconstrained than constrained grasp contact conditions

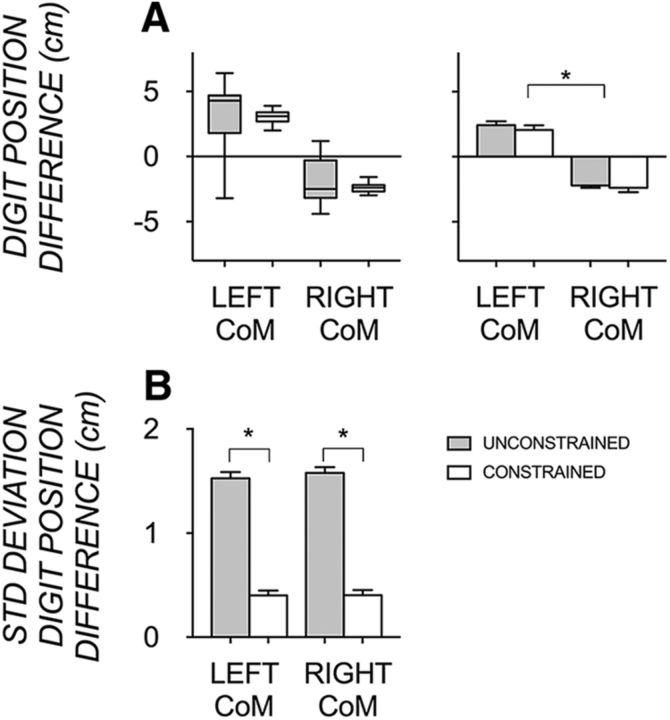
To compare the representational voxel patterns associated with left and right CoM conditions and to make inferences about their differences being reflective of anticipatory behavioral differences, it is essential to first establish that behavior (i.e., digit position partitioning) actually differs between left and right CoM conditions. Furthermore, to compare the representational voxel patterns associated with constrained and unconstrained conditions and to make inferences about their differences being reflective of digit position variability, it is essential that digit position variability differs between these conditions. Figure 5 shows a representative subject plot and group mean and SD plots of digit positioning differences at lift onset of an object with a left and a right CoM with unconstrained and constrained grasp contacts, respectively. As Figure 5A shows, digit positions were significantly different depending on CoM, with a main effect (F_(1,15) = 213.94, p < 0.001, η_p² = 0.93) and no interaction (p = 0.53). Whereas digit position partitioning was similar on average between grasp contact conditions (p = 0.11), it was shown to be more variable (Fig. 5B) in the unconstrained than constrained grasp contact conditions (F_(1,15) = 500.09, p < 0.001, η_p² = 0.97). Object roll was also not statistically different between grasp contact conditions across CoM conditions (p = 0.60), suggesting that any difference in voxel patterns between these grasp contact conditions were not due to overall performance-related differences.

Figure 5.

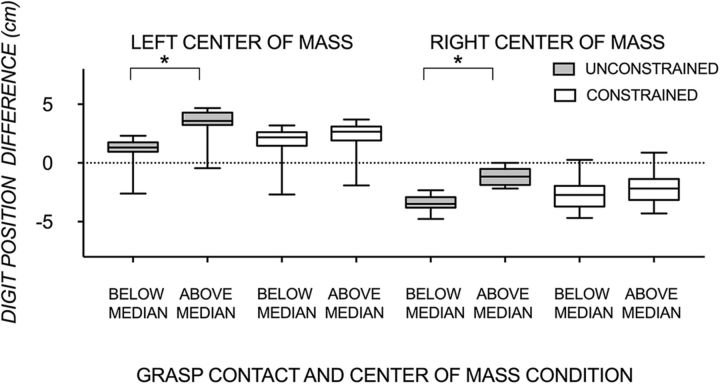
A, Representative subject box-and-whisker plot (left) and group mean bar plot (±1 SE; right) showing the difference in digit position of the thumb and index finger at lift onset when manipulating the object at unconstrained (gray) and constrained (clear) grasp contact points with the object's CoM on the left and right, respectively. A digit position difference above zero indicates thumb higher than index finger digit positioning, a digit position difference below zero indicates index finger higher than thumb positioning, and a digit position difference of zero indicates symmetrical, parallel digit positioning. B, Group SD of digit position difference for each of the four conditions. Statistical significance is shown with an asterisk.

Larger differences between digit positions between unmatched than matched CoM conditions

To identify the region where voxel patterns are sensitive to sensorimotor memories associated with different anticipatory digit positions for different CoMs, it is essential to demonstrate that, at a behavioral level, the partitioning of trials by a median split led to significant differences in digit position for different CoMs. As Figure 6 shows, differences in digit positioning partitioning were much larger in unmatched than matched CoM conditions in both grasp contact conditions. As expected, there were larger differences within a given CoM in the unconstrained than constrained conditions. There was a significant main effect of CoM match (F_(1,15) = 103.75, p < 0.001, η_p² = 0.87), grasp contact (F_(1,15) = 37.21, p < 0.001, η_p² = 0.71), and a significant interaction (F_(1,15) = 22.53, p < 0.001, η_p² = 0.60), which was driven by the differences between grasp contact conditions seen in the matched CoM variable (i.e., larger differences between above and below median digit position difference in unconstrained than constrained; also confirmed below).

Larger differences between digit positions above and below the median in unconstrained than constrained grasp conditions

To identify regions with voxel patterns that are sensitive to anticipatory differences of digit position for different trials, it is essential to demonstrate greater effects of a median split on unconstrained than constrained trials. Figure 7 shows the difference in digit position above and below the median in the unconstrained and constrained grasp contact condition within each CoM. For both CoM conditions, there was a significant effect of the median split comparison (left CoM: F_(1,15) = 672.50, p < 0.001, η_p² = 0.98; right CoM: F_(1,15) = 686.23, p < 0.001, η_p² = 0.98), with a position by grasp contact interaction (left CoM: F_(1,15) = 376.39, p < 0.001, η_p² = 0.96; right CoM: F_(1,15) = 407.62, p < 0.001, η_p² = 0.97) and no effect of grasp contact (left CoM: F_(1,15) = 2.66 p = 0.12, η_p² = 0.15; right CoM: F_(1,15) = 0.21, p = 0.65, η_p² = 0.01). These results suggest that the difference between digit positions above and below a median split varied depending on the grasp condition, being larger in the unconstrained (due to more digit position variability) than in the constrained grasp contact condition.

Figure 7.

Box-and-whisker group plots showing a below and above median split of the difference in digit position of the thumb and index finger when manipulating the object with a left and right center of mass at unconstrained (gray) and constrained (clear) grasp contacts. Above the horizontal dotted line depicts thumb higher than index finger digit positioning; below the dotted line depicts index finger higher than thumb positioning; on the dotted line depicts symmetrical, parallel digit positioning. Statistical significance (p < 0.001) is shown with an asterisk.

Univariate analyses of fMRI data

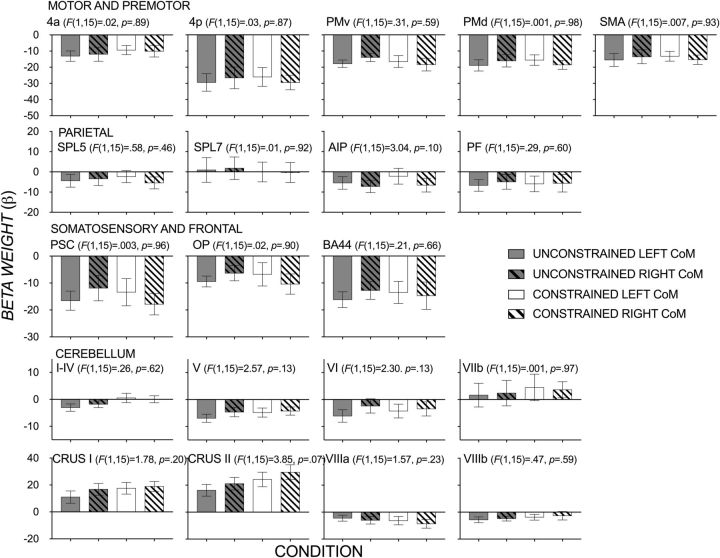
A traditional univariate analysis on the data showed, unsurprisingly, no difference in mean activity within each region when comparing conditions with a left compared with a right CoM, and when comparing unconstrained and constrained grasp conditions. In addition, there was no CoM × grasp interaction in any of the ROIs. This suggests that no ROI is more active during dexterously manipulating an object as a function of the two different mass distributions or unconstrained versus constrained grasp types (Fig. 8).

Figure 8.

Mean β weights (±1 SE) in preselected ROIs during contact-to-lift phase of lifting an object with a left (solid bars) and right (patterned bars) CoM at unconstrained (gray bars) and constrained (clear bars) contact points across the six functional runs. ANOVA results show no significant effect of CoM for any of the ROIs. There was also no significant effect of grasp or grasp × CoM interaction.

Representational similarity analyses of fMRI data: convolution model

Regions with voxel patterns sensitive to digit position difference as a function of CoM

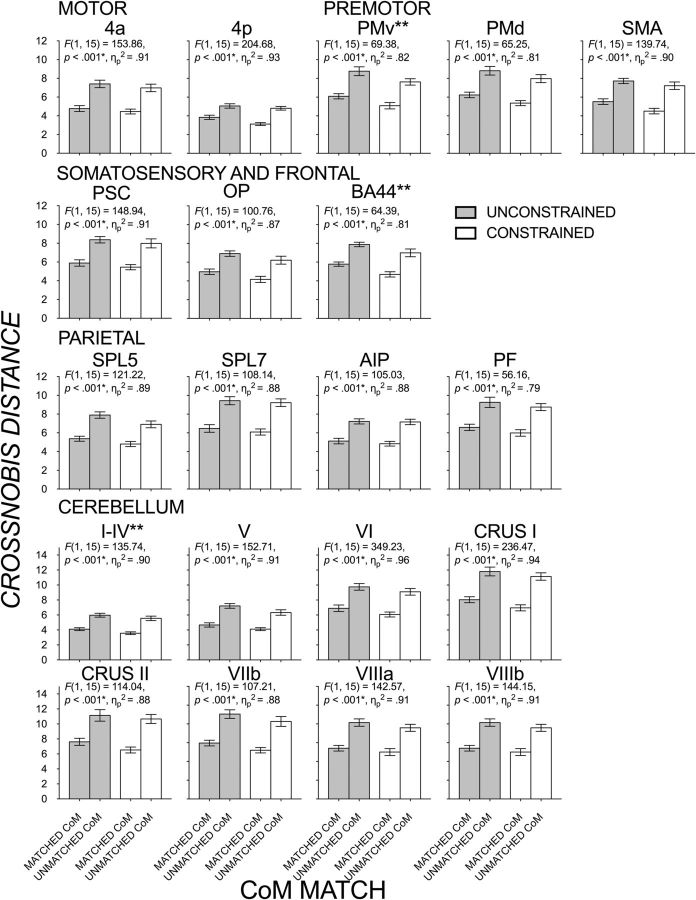
As reported in Figure 6, there was a larger difference when comparing digit position partitioning above and below the median in unmatched than matched CoM conditions. RSAs were used to identify regions that would be sensitive to such behavioral differences, as reflected by larger voxel pattern differences in unmatched than matched CoM conditions. Figure 9 shows that all regions showed significantly larger distances between conditions with unmatched than matched CoM distributions. Effect sizes were typically large to very large, with the largest magnitudes (η_p² > 0.90) seen in motor region, 4a, 4p, SMA, somatosensory region, PSC/S1, and cerebellar lobule regions, I–IV, V, VI, Crus I, VIIIa, and VIIIb. We found no interactions of CoM match × grasp contact in any of the regions (suggesting that the differences in distances between matched and unmatched CoM distributions were not dependent on a given grasp contact). Interestingly, three regions, PMv (F_(1,15) = 16.70, p = 0.001, η_p² = 0.53), BA44 (F_(1,15) = 16.38, p = 0.001, η_p² = 0.52), and cerebellar lobules I–IV (F_(1,15) = 15.48, p = 0.001, η_p² = 0.51), also gave significant, moderately sized effects of grasp contact, with larger distances in the unconstrained than constrained conditions regardless of CoM match. This grasp contact effect is explored further below.

Figure 9.

Mean crossnobis distances (±1 SE) between conditions with matched and unmatched CoM distributions for a given grasp contact (gray bars, unconstrained; clear bars, constrained). ANOVA results of CoM match effect, FDR-corrected significance (*), and partial η square are displayed for each ROI. Double asterisks denote ROIs that gave significant effects of grasp contact condition in addition to significant effects of CoM match.

Regions with voxel patterns sensitive to digit position differences as a function of grasp contact

The previous analyses showed greater voxel pattern differences in both matched and unmatched CoM contrasts in unconstrained than constrained grasping in PMv, BA44, and cerebellar lobules I–IV. The next analyses investigated whether the greater distances in these contrasts might be a function of greater trial-to-trial variability of digit position in unconstrained than constrained grasping. Crossnobis distances were compared within a given CoM when digit position difference was above compared with below the median, as shown schematically in Figure 4C. The aim of this analysis was to identify whether regions PMv, BA44, and cerebellar lobules I–IV were sensitive to larger differences in digit position across trials.

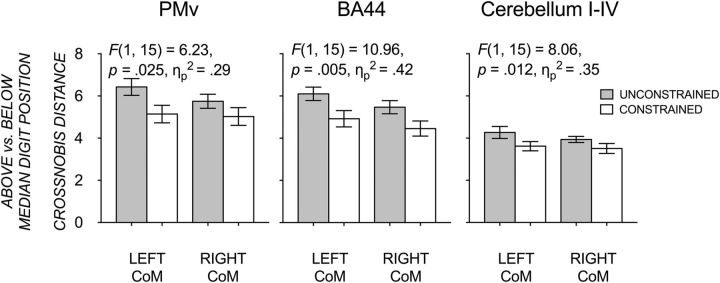
As Figure 10 shows, the crossnobis distance between trials in which digit position was above compared with below the median digit position was always larger (i.e., more dissimilar) during unconstrained than constrained grasp contact conditions. The effect of grasp contact was significant in PMv, BA44, and cerebellar lobules I–IV, with no significant effect or interaction with CoM. This suggests that these three regions were sensitive to larger differences in digit position across trials in the unconstrained than constrained grasp case.

Figure 10.

Mean crossnobis distances (±1 SE) between trials with above median digit positioning and trials below median digit positioning within a given CoM condition and grasp contact condition, respectively (gray bars, unconstrained; clear bars, constrained). ANOVA results for the effect of grasp contact, FDR-corrected significance levels, and partial η square are displayed.

Representational similarity analyses of fMRI data: deconvolution model

Although the previous fMRI results were modeled for a time window corresponding to the contact-to-lift phase, the HRF convolution method could blur the temporal distinction with adjacent reach and execution periods. Therefore, it is possible that the differences between conditions from the two RSA analyses (unmatched vs matched; unconstrained vs constrained) were due to differences between these conditions after object liftoff (i.e., resultant of differences in somatosensory feedback of object properties between conditions). To account for this possibility, we used an FIR deconvolution approach to characterize temporal changes of RSA distances between matched and unmatched CoM distributions beginning just before the onset of contact to lift. This approach could specifically localize regions representing the sensorimotor memory anticipatory process without contamination from the execution process by examining between-condition distances estimated from the HR response at contact to lift and 400 ms before. The RSA distances for the above versus below median distances between unconstrained and constrained grasp conditions were not re-estimated because the deconvolution design matrix included in its baseline the reach and execution phases of movement. This limits its sensitivity in detecting relative changes of BOLD during an online feedback-based correction process that involves executed movement (i.e., load force adjustment based on digit position).

Table 1 highlights the time bins in which unmatched CoM conditions gave an FDR-corrected significantly greater distance than matched CoM conditions for each of the preselected ROIs. As the table shows, the same pattern was observed as that showed in the convolution-based analyses. All ROIs showed significantly larger distances in unmatched than matched CoM conditions across many consecutive time points. Strikingly, differences between matched and unmatched CoM conditions were present at very early time points. Differences between these CoM conditions were already present at the very first time point for cerebellar (Crus II, VIIIa), premotor (PMv), and somatosensory regions (PSC/S1, OP).

Table 1.

FDR-corrected significant p values from comparing mean crossnobis distances between matched and unmatched center of mass conditions for each of 17 time bins from 400 ms before the onset of contact to lift (corresponding to time 0) for each of preselected ROIs

Time (ms)	−400	0	400	800	1200	1600	2000	2400	2800	3200	3600	4000	4400	4800	5200	5600	6000
C-CrusII	0.0040	0.0040	0.0004	0.0004	0.0010	0.0004	0.0010	0.0010	0.0004	0.001	0.0003	0.0002	0.0007	0.0004	0.0240	0.0070
C-VIIIa	0.0060	0.0020	0.0030	0.0010	0.0001	0.0004	0.0010	0.0010	0.0002	0.0003	0.0004	0.0003	0.0010	0.0090
Pmv	0.0003	0.0010	0.0040	0.0020		0.0010	0.0020	0.0004	0.0001	0.0003				0.0010	0.0010
PSC/S1	0.0004	0.0030	0.0020	0.0050	0.0030	0.0001	0.0002	0.0002	0.0003	0.0030	0.0040	0.0010	0.0040	0.0020	0.0030	0.0210
OP	0.0050		0.0010	0.0110	0.0010	0.0003	0.0020	0.0020	0.0004	0.0010	0.0020	0.0003	0.0010	0.0040	0.0030
C-CrusI		0.0050	0.0010	0.0010	0.0010	0.0010	0.0010	0.0010	0.0010	0.0010	0.0004	0.0001	0.0001	0.0020	0.0110		0.0150
4a		0.0010	0.0010	0.0030	0.0001	0.0030	0.0010	0.0040	0.0010	0.0040	0.0010	0.0002		0.0060
BA44		0.0020	0.0030	0.010	0.0020	0.0020	0.0010	0.0001	0.0020	0.0050	0.0010	0.0003	0.0001	0.0040	0.0040
PMd		0.0020	0.0040	0.0010	0.0020	0.0080	0.0004	0.0010	0.0010	0.0000	0.0003	0.0050	0.0010	0.0060	0.0040
C-V			0.0000			0.0010			0.0004			0.0004		0.0020
C-VIIb			0.0004	0.0001	0.0000	0.0010	0.0003	0.0010	0.0003	0.0000	0.0000	0.0003	0.0001	0.0004
C-VIIIb			0.0010	0.0002	0.0010	0.0001	0.0020	0.0020	0.0030	0.0010	0.0020	0.0070	0.0060
SMA			0.0040		0.0020	0.0020	0.0010	0.0060	0.0010	0.0003	0.0010	0.0010	0.0050	0.0002
SPL5				0.0030		0.0004	0.0030		0.0040	0.0010	0.0020			0.0000
SPL7				0.0050	0.0050	0.0060	0.0020	0.0030	0.0010	0.0060	0.0030	0.0010	0.0010	0.0010	0.0010
C-I-IV					0.0010			0.0001			0.0030			0.0030
C-VI					0.0050	0.0010	0.0004	0.0010	0.0010	0.0010	0.0004	0.0002	0.0001	0.0030	0.0040
4p						0.0020				0.0030			0.0030
AIP						0.0040		0.0010		0.0010	0.0004	0.0010	0.0030
PF						0.0020	0.0030		0.0000	0.0004		0.0010	0.0004

Time 0 is contact-to-lift onset. Blank cells correspond to p-values that were not significant after FDR correction.

C, Cerebellar lobule.

Discussion

We identified neural representations of anticipatory mechanisms enabling dexterous manipulation of objects with asymmetric CoMs at unconstrained and constrained grasp contacts in the absence of salient visual cues about the object's CoM. RSA showed large voxel pattern differences between unmatched and matched CoM conditions in many ROIs (from convolution-based data), suggesting that the sensorimotor system is involved broadly in the control of load force modulation during dexterous manipulation of objects with asymmetric mass distributions. A deconvolution analysis showed that in PMv, cerebellar (CrusII, VIIIa), and somatosensory (S1, OP) regions, between-CoM voxel pattern differences were unequivocally anticipatory and likely representative of sensorimotor memories. Furthermore, moderately sized voxel pattern differences between unconstrained and constrained grasp conditions in cerebellar lobules I–IV, BA44, and PMv are suggestive of representations related to online force adjustment as a function of digit position variability.

To infer that voxel pattern differences between unmatched and matched CoM conditions reflect differences in anticipatory sensorimotor memories, it is necessary to establish that the observed behavioral differences between CoM conditions are a product of differences in sensorimotor memories and that the estimated activation for this strictly reflects the anticipatory process. We used an explicit performance-based task (roll minimization of a symmetrically shaped object with a concealed asymmetric CoM) that has been used previously to study the nature of sensorimotor memories. Because the visual cues of the object's CoM are nonsalient and object property feedback can only be used after lift onset, subjects must primarily rely on sensorimotor memories from previous trials with the same asymmetric CoM for compensatory torque generation and roll minimization at lift onset (Salimi et al., 2000, 2003; Lukos et al., 2007; Bursztyn and Flanagan, 2008; Fu et al., 2010; Zhang et al., 2010). The relied-upon sensorimotor memory content would have to be unique to the object CoM because resulting anticipatory behavior is unique to the given CoM. Specifically, the appropriate torque is in opposite directions for minimizing roll with the CoM on the left and right. This torque is achieved by load force partitioning either solely (Salimi et al., 2000; Bursztyn and Flanagan, 2008) or combined with digit position partitioning strategies (Fu et al., 2010, 2011; Zhang et al., 2010; Marneweck et al., 2015) and varies depending on the CoM (i.e., higher force and position by the digit closest to the CoM). Kinematic measures in the current study confirmed that these different torques were generated (evidenced by roll minimization) by differing digit positioning partitioning strategies. Digit positioning differences were also larger in unmatched than matched CoM conditions.

Although the RSA results on the convolved data of between-CoM voxel pattern differences might be a function of somatosensory feedback of object properties after object liftoff (which varies between CoM conditions), the RSA results on the deconvolved data characterizes purely anticipatory differences between CoM conditions before object liftoff. Furthermore, the CoM conditions required the same hand-to-target trajectories during the reach phase of the trial, with hand shape being practically identical in these conditions. Therefore, the predominant variation between CoM conditions during this anticipatory stage of movement is the sensorimotor memory content used to modulate load force for successfully generating a torque at lift onset. This gives strong evidence that differences in the subset of cerebellar, premotor, and somatosensory ROIs are reflective of anticipatory sensorimotor memory processes before somatosensory feedback become available after lift onset. These findings are novel in four ways. First, anticipatory processes were reliably separated from execution processes of dexterous manipulation. This has not been done in most previous fMRI studies (Schmitz et al., 2005; Jenmalm et al., 2006; Ehrsson et al., 2007), which makes it difficult to gauge whether a given region encodes a sensorimotor memory, the discrepancy in predicted and actual sensory feedback, or updates to the sensorimotor memory. Second, the behavioral paradigm allowed the study of sensorimotor memories in the absence of salient visual cues. This has rarely been done in those TMS studies and a couple of fMRI studies that have separated anticipatory from execution processes (Davare et al., 2006, 2007, 2009, 2010; Koch et al., 2010; van Nuenen et al., 2012; White et al., 2013; Gallivan et al., 2014; Parikh et al., 2014). Third, we used an explicit performance-based task that requires precision and dexterity and thus more precise anticipatory force control than typically used simple object lifting tasks (the latter of which are rarely unsuccessfully executed). Finally, a novel RSA approach identified spatial variation in pattern differences between conditions that were undetectable by traditional univariate approaches.

The involvement of cerebellar Crus II and VIIIa fit the general consensus that the cerebellum is a locus for sensorimotor memory representations (Miall et al., 1993; Wolpert et al., 1998). However, current results suggest that sensorimotor memory representations are more broadly distributed. The exact contents of encoded sensorimotor memories and whether different regions encode different aspects of anticipatory behaviors (e.g., digit position/force partitioning, digit position sensing, higher-order task goal of generating a direction-specific torque) cannot be ascertained fully here. However, based on previous work, somatosensory regions (Schabrun et al., 2008) and PMv (Davare et al., 2006) might encode digit position sensing, which varies between CoM conditions. Conversely, somatosensory and cerebellar regions were insensitive in detecting voxel pattern differences between unconstrained and constrained grasping (which gave slight differences in digit position and, thus, load forces), which suggests that these regions might encode the higher-order task goal regardless of the variety of ways in which it can be achieved.

PMv, BA44, and cerebellar lobules I–IV showed larger voxel pattern differences for unconstrained than constrained grasping. The voxel pattern differences between grasp conditions could not be explained by differences in mean digit position or task performance (shown by kinematic measures inside the scanner) or digit force distributions (shown by kinetic measures outside the scanner). The only difference between these grasp cases is that, in unconstrained grasping, forces undergo modulation based on sensing where the digits are, whereas in constrained grasping, they are expected to be mostly driven by implementing a memory-based control. Therefore, these voxel pattern differences most likely reflect online sensing and integration of digit position variability and subsequent load force fine tuning. We are the first to have studied this online control process by fMRI.

Cerebellar lobule IV (Bostan et al., 2013) and PMv (Dum and Strick, 2002) project directly to M1 and PMv has direct connections with spinal motoneurons, making them ideal sites for swiftly orchestrating the process of sensing digit position and fine tuning load force adjustments. The cerebellum is known to serve as a comparator of motor output and sensory predictions (Therrien and Bastian, 2015). Our work adds to this concept by showing that it generates representations for sensorimotor memories and online digit position sensing. In doing so, it can determine whether predicted and actual sensory consequences match and correct for a mismatch by swiftly adjusting load force. Mismatches occur more so in unconstrained than constrained grasping, thus explaining the larger voxel pattern differences in unconstrained grasping. BA44 has similarly been found to be involved in comparing predicted and actual sensory consequences (Johnson-Frey et al., 2003; Schmitz et al., 2005), which the current results support. Finally, Davare et al. (2006) also implicated PMv's involvement in digit position sensing before object liftoff. Particularly, rTMS to PMv increased digit position variability and noncollinearity on a symmetrically mass-distributed object requiring a simple lift. The consequent position changes failed to disrupt task success because subjects always managed to lift the object. It might be that the task did not demand precision and dexterity and thus anticipatory control process needs. Alternatively, our results suggest that PMv is capable of dealing with digit position variability, even with more explicit performance-based task goals (minimizing roll), by fine tuning force adjustments and sending the adjusted motor command to the M1 or spinal level.

Digit-position-based force adjustments should conceivably be communicated in part to M1. Therefore, it was curious that M1 was insensitive to differences between grasp conditions. These fine motor adjustments might only become apparent in M1 at a later time point, very close to, at lift onset, or after lift onset, which our paradigm was not optimized to detect. AIP was also insensitive to pattern differences between grasp conditions, which is in contrast to previous reports of its sensitivity to digit position (Davare et al., 2007) and force adjustment based on hand posture orientation (Tunik et al., 2005). However, AIP likely represents dynamics related to the visual object properties before and after liftoff, which was not manipulated here.

In summary, the ability to modulate load forces to manipulate objects dexterously with different mass distributions seems to be a function of a widespread sensorimotor network. Within this network, cerebellar (CrusII, VIIIa), somatosensory (S1, OP), and PMv regions are sensitive to anticipatory behavior that reflect sensorimotor memory content for scaling load forces to an object's CoM, and cerebellar lobules I–IV, PMv, and BA44 seem sensitive to the fundamental online control feature of digit forces compensating for the natural variation of digit position.