Dual Coding of Frequency Modulation in the Ventral Cochlear Nucleus

Abstract

Frequency modulation (FM) is a common acoustic feature of natural sounds and is known to play a role in robust sound source recognition. Auditory neurons show precise stimulus-synchronized discharge patterns that may be used for the representation of low-rate FM. However, it remains unclear whether this representation is based on synchronization to slow temporal envelope (ENV) cues resulting from cochlear filtering or phase locking to faster temporal fine structure (TFS) cues. To investigate the plausibility of those encoding schemes, single units of the ventral cochlear nucleus of guinea pigs of either sex were recorded in response to sine FM tones centered at the unit's best frequency (BF). The results show that, in contrast to high-BF units, for modulation depths within the receptive field, low-BF units (<4 kHz) demonstrate good phase locking to TFS. For modulation depths extending beyond the receptive field, the discharge patterns follow the ENV and fluctuate at the modulation rate. The receptive field proved to be a good predictor of the ENV responses for most primary-like and chopper units. The current in vivo data also reveal a high level of diversity in responses across unit types. TFS cues are mainly conveyed by low-frequency and primary-like units and ENV cues by chopper and onset units. The diversity of responses exhibited by cochlear nucleus neurons provides a neural basis for a dual-coding scheme of FM in the brainstem based on both ENV and TFS cues.

SIGNIFICANCE STATEMENT Natural sounds, including speech, convey informative temporal modulations in frequency. Understanding how the auditory system represents those frequency modulations (FM) has important implications as robust sound source recognition depends crucially on the reception of low-rate FM cues. Here, we recorded 115 single-unit responses from the ventral cochlear nucleus in response to FM and provide the first physiological evidence of a dual-coding mechanism of FM via synchronization to temporal envelope cues and phase locking to temporal fine structure cues. We also demonstrate a diversity of neural responses with different coding specializations. These results support the dual-coding scheme proposed by psychophysicists to account for FM sensitivity in humans and provide new insights on how this might be implemented in the early stages of the auditory pathway.

Introduction

It is generally agreed that the auditory system is adapted and optimized for the encoding of naturalistic stimuli (Nelken et al., 1999; Lewicki, 2002; Woolley et al., 2005; McDermott and Simoncelli, 2011). Among the features characterizing natural sounds, low-rate, frequency modulation (FM) may play a specific role. Consistent with this view, salient FM, together with other forms of temporal modulations such as amplitude modulation (AM), are systematically found at low rates (<20 Hz) in speech and animal vocalizations, as well as in environmental and musical sounds (Attias and Schreiner, 1997; Wang, 2000; Singh and Theunissen, 2003; Rees and Malmierca, 2005; Varnet et al., 2017). Moreover, there is clear evidence that speech recognition performance in quiet and in the presence of background sounds are constrained by human auditory sensitivity to low-rate FM (Zeng et al., 2005; Binns and Culling, 2007; Ruggles et al., 2011; Johannesen et al., 2016).

Numerous psychophysical studies have investigated the detection of low-rate sinusoidal frequency modulation (SFM). Zwicker (1952, 1956) and Maiwald (1967a,b) put forth an “excitation pattern model” in which SFM is perceived via temporal envelope cues (ENV). This mechanism is often referred to as “FM-to-AM conversion” because frequency-dependent attenuation of the FM caused by the cochlear filters results in AM (Saberi and Hafter, 1995). However, the excitation pattern model has often been challenged and several studies have demonstrated that changes over time in the pattern of neural phase locking to temporal fine structure (TFS) cues may be used to perceive SFM at low carrier frequencies (Demany and Semal, 1986, 1989; Moore and Sek, 1996; Whiteford and Oxenham, 2015; Paraouty et al., 2016; Paraouty and Lorenzi, 2017). This additional mechanism is assumed to be “sluggish” and restricted to the processing of low rate (<5–10 Hz) FM (Moore and Sek, 1996).

Neurophysiological studies have addressed this issue by using frequency sweeps, but knowledge regarding the underlying mechanisms of SFM coding in the early auditory pathway is relatively sparse. In addition, most studies examining FM responses in the cochlear nucleus (CN) predate the detailed physiological and morphological classifications of CN neurons. Responses of single auditory nerve fibers (ANFs) to FM sweeps have been studied in the cat (Britt and Starr, 1976; Sinex and Geisler, 1981) and were described as similar to responses to pure tones; that is, ANFs discharged for each frequency transition that crossed the response area. At the CN level, Britt and Starr (1976) described the responses of primary-like units to FM sweeps as simple relays, whereas onset and pauser units responded more to one direction of sweep. Only a few studies by Moller (1972a,b) examined the responses of CN units to SFM and showed that the response patterns were synchronized to the ENV. Fernald and Gerstein (1972) also showed that the mean discharge patterns of CN units followed the modulations of the ENV cues in response to triangular periodic FM. To our knowledge, no former study has examined and characterized neural phase locking to TFS in the responses of CN neurons to low-carrier and low-rate SFM stimuli.

This work aims at narrowing the gap between the psychophysical findings regarding SFM coding (Whiteford and Oxenham, 2015; Paraouty et al., 2016) and the physiological responses of auditory neurons to SFM. This was achieved by the characterization of the relative contributions of ENV and TFS coding of ventral cochlear nucleus (VCN) neurons, with a wide range of best frequencies (BFs: 0.14–22 kHz) in response to low-rate SFM (<10 Hz). The results demonstrate the capacity of VCN neurons to encode FM information using both ENV and TFS cues. The data further show contrasting ENV and TFS specializations in different unit types, providing a possible neural basis for a dual-encoding scheme of FM in the early auditory pathway.

Materials and Methods

Preparation.

Experiments were performed on 10 male and 17 female pigmented guinea pigs (Cavia porcellus) weighing between 300 and 800 g. The animals were anesthetized with urethane (1.0 g/kg, i.p.) and hypnorm (or fentanyl) was administered as supplementary analgesia (1 ml/kg, i.m.). Anesthesia and analgesia were maintained at sufficient depth to abolish the pedal withdrawal reflex of the front paw. Additional doses of hypnorm or urethane were administered on indication. Core temperature was monitored with a rectal probe and maintained at 38°C using a thermostatically controlled heating blanket (Harvard Apparatus). The trachea was cannulated and on signs of suppressed respiration, the animal was ventilated artificially with a pump (Bioscience). Surgical preparation and recordings took place in a sound-attenuated chamber (Industrial Acoustics). The animal was placed in a stereotaxic frame, which had ear bars coupled to hollow speculae designed for the guinea pig ear. A midsagittal scalp incision was made and the periosteum and the muscles attached to the temporal and occipital bones were removed. The bone overlaying the left bulla was fenestrated and a silver-coated wire was inserted into the bulla to contact the round window of the cochlea for monitoring compound action potentials (CAPs). The hole was resealed with petroleum jelly. The CAP threshold was determined at selected frequencies at the start of the experiment and thereafter upon indication. If the thresholds had deteriorated by >10 dB and were nonrecoverable (e.g., by removing fluid from the bulla), the experiment was terminated. A craniotomy was performed exposing the left cerebellum. The overlying dura was removed and the exposed cerebellum was partially aspirated to reveal the underlying cochlear nucleus. The hole left from the aspiration was then filled with 1.5% agar in saline to prevent desiccation. The experiments performed in this study have been carried out under the terms and conditions of the project license issued by the United Kingdom Home Office to I.M.W.

Neural recordings.

Responses of single units were recorded extracellularly with glass-coated tungsten microelectrodes (Merrill and Ainsworth, 1972; Microelectrodes.net). Electrodes were advanced in the sagittal plane by a hydraulic microdrive (650 W; David Kopf Instruments) at an angle of 45°. Neural spikes were discriminated and stored as spike times and were analyzed off-line using custom-written MATLAB programs (The MathWorks). Single units were isolated using broadband noise as search stimulus. All stimuli were digitally synthesized in real time with a PC equipped with a DIGI 9636 PCI card that was optically connected to an AD/DA converter (ADI-8 DS; RME Audio Products). The AD/DA converter was used for digital-to-analog conversion of the stimuli as well as for analog-to-digital conversion of the amplified (1000×) neural activity. The sample rate was 96 kHz. The AD/DA converter was driven using the ASIO (Audio Streaming Input Output) and SDK (Software Developer Kit) from Steinberg. After digital-to-analog conversion, the stimuli were equalized (phonic graphic equalizer, model EQ 3600; Apple Sound) to compensate for the speaker and coupler frequency response and fed into a power amplifier (Rotel RB971) and a programmable end attenuator (0–75 dB in 5 dB steps, custom built) before being presented over a speaker (Radio Shack 30-1777 tweeter assembled by Mike Ravicz, MIT, Cambridge, MA) mounted in the coupler designed for the ear of a guinea pig. The stimuli were monitored acoustically using a condenser microphone (Bruël and Kjær model 4134) attached to a calibrated 1-mm-diameter probe tube that was inserted into the speculum close to the eardrum.

Unit classification.

Upon isolation of a unit, its BF and excitatory threshold were first determined manually using audiovisual criteria and then verified offline using an automated fitting procedure. The receptive field (or response map) for each unit was computed from 50 ms responses to pure tones played for a set of different stimulation levels: from 14–94 dB SPL in 5-dB steps and for a set of frequencies below and above the unit's BF: 2 and 3 octaves, respectively, for BFs <5 kHz and 1 and 2 octaves, respectively, when BFs were >5 kHz (in 0.1 steps per octave). Both level and frequency were presented randomly. Peristimulus time histograms (PSTHs) with a bin width of 0.2 ms were generated from spike times collected in response to 250 sweeps of a 50 ms tone (with randomized starting phase and 1 ms raised-cosine ramps) at the unit's BF at 20 and 50 dB above threshold. The tone bursts were repeated with a period of 250 ms. Spontaneous activity was measured over a 10 s period. Single units were classified based on their pure-tone PSTHs, the first-order interspike interval (ISI) distribution and the coefficient of variation (CV) of the discharge regularity.

The CV was calculated by averaging the ratios of the SD divided by the mean ISI between 12 and 20 ms after onset (Young et al., 1988; Wright et al., 2011). On the basis of differences in the CV, the population of chopper units was divided into sustained choppers (CS, CV <0.3) and transient choppers (CT, CV ≥0.3) (Blackburn and Sachs, 1989). All units were classified as primary-like (PL), primary-like with notch (PN), chopper-sustained (CS), chopper-transient (CT), onset-chopper (OC), and other onset types (onset: O, onset-L: OL, and onset-I: OI). The onset units were subdivided according to the scheme introduced by Winter and Palmer (1995). For some units with very low BFs (∼<0.5 kHz), it was not possible to assign them to one of the above categories. In the absence of a definitive classification, these are grouped together as “low-frequency” (LF) units. For the population data, all recorded units were categorized into three major groups: (1) primary-likes and low-frequency (including PL, PN, and LF units), (2) choppers (including CS and CT units), and (3) onsets (including OC, O, OL, and OI units). In this study, no other types of units were included (for instance, pauser, buildup, or other dorsal cochlear nucleus response patterns).

SFM stimuli.

An SFM was imposed on a pure tone stimulus (the carrier) with frequency (fc) set at the unit's BF. The modulation rate (fm) was 2, 5, or 10 Hz. Modulation depth (Δf) was 2, 4, 8, 16, or 32% relative to the BF. SFM tones were 1 s long, including 5 ms raised-cosine ramps at the start and end of the stimuli. The time interval between two stimuli was 1 s and the presentation level was set to 55 dB SPL. The SFM was presented at positive and negative starting polarities (Φ_C: starting carrier phases), whereas the starting phase of the modulator (Φ_M) was fixed (see equation below and Fig. 1). For each carrier phase, responses to 25 presentations of SFM stimuli were recorded. All of the different experimental conditions were randomized. SFM responses at different stimulation levels were also recorded when possible and the number of units (n) = 29 for lower sound levels (20–45 dB SPL) and n = 40 for higher sound levels (60–90 dB SPL) compared to 55 dB SPL. In addition, for a subset of 15 units, SFM tones were played off-BF, with fc above and/or below the BF of the unit (from 0.5 to 2 octaves).

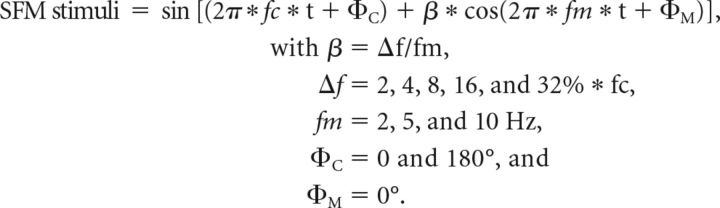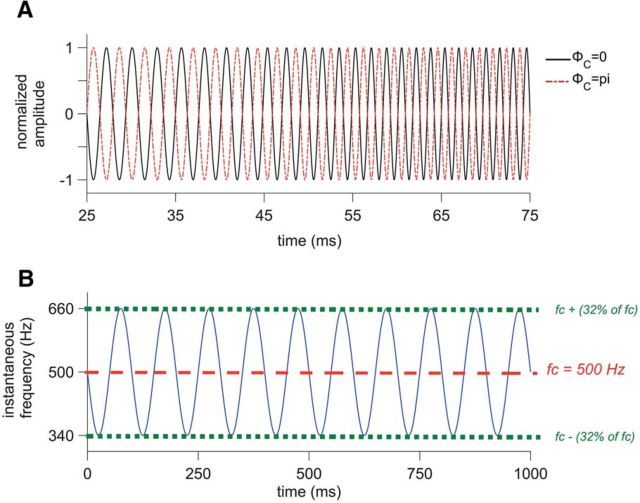
Figure 1.

Description of SFM stimuli. A, SFM, normalized in amplitude and plotted as a function of time from 25 to 75 ms. Black line shows the standard stimulus with Φ_C = 0 and the red dotted line shows the polarity-inverted stimulus (i.e., Φ_C = 180°). B, Instantaneous frequency of the SFM plotted in blue as a function of time from 0 to 1000 ms. The carrier frequency is 500 Hz (indicated with the red dotted line) and the fm is 10 Hz. The instantaneous frequency varies from 340 to 660 Hz since the modulation depth (Δf) is 32% of 500 Hz.

Analyses.

Spike times collected in response to 25 sweeps of the 1 s SFM stimuli were analyzed and SFM-PSTHs were generated for the two different starting polarities (0° and 180°, with bin width = 0.2 ms). Period histograms to the modulation rate were computed for the 0° starting phase condition, as well as the vector strengths. To avoid onset effects, spikes in response to the first modulation cycle were discarded.

To examine the respective contributions of ENV and TFS coding for each unit, shuffled correlograms were computed (Joris, 2003; Joris et al., 2006). Shuffled correlograms provide a smoother representation of the temporal characteristics present in the neural responses compared to standard all-order interval histograms (Louage et al., 2004). To compute the shuffled auto-correlograms (SACs), spike trains to repeated presentations of the SFM stimulus were compared pairwise by counting the number of instances that spikes were fired at the same instant in time (i.e., coincidences). Starting with the first spike of the first spike train, all forward intervals between this reference spike and all other spikes in nonidentical spike trains were measured and tallied in a histogram. Only intervals across spike trains were considered; intervals within spike trains were excluded to avoid the effect of the refractory period. In counting the number of coincidences, a 50 ms window was defined over which two spikes were regarded as being coincident (Joris et al., 2006). The whole procedure was repeated for all spikes in all spike trains and, again, all forward intervals between the reference spike and all other spikes in nonidentical spike trains were measured and tallied in the same histogram. SACs were then normalized (Louage et al., 2004; Joris et al., 2006) such that the bin values were independent of average firing rate r, number of presentations N, choice of bin width Δt, and stimulus duration D. This normalized number of coincidences was achieved by dividing by N(N − 1)r² Δt D. Here, N corresponded to 25 and Δt to 0.00005 s and D was 1 s. The SAC is displayed symmetrical around 0 ms; each positive interval of spike train pair (sweep 1, sweep 2) has a negative interval in pair (i.e., sweep 2, sweep 1). A peak height of 1 of the normalized SAC at 0 ms delay indicates a lack of stimulus-induced temporal structure. Larger values indicate that the spike times tend to be correlated between the different spike trains and lower values indicate anticorrelation (Joris et al., 2006).

Like SACs, shuffled cross-correlograms (XACs) are also similar to all-order interval histograms but, here, the spike times are compared across responses to two different stimuli: the standard stimulus with Φ_C = 0° and the polarity-inverted stimulus, with Φ_C = 180°, rather than across responses to the same stimulus (as for the SAC, in which responses to only the standard stimulus are examined). XACs were normalized by N² r₁r₂ Δt D, where r₁ is the mean firing rate to the presentation of the standard stimulus and r₂ is the mean firing rate to the presentation of the polarity-inverted stimulus. A peak height of 1 at 0 ms delay of the normalized XAC indicates a lack of stimulus-induced temporal structure, similarly to the SAC.

The peak heights of the SAC and the XAC indicate the strength of temporal coding, of either ENV or TFS or any mixture of both ENV and TFS. To disambiguate and quantify the strength of TFS and ENV coding, the Sumcor and Difcor were computed (Joris et al., 2006; Heinz and Swaminathan, 2009). The Sumcor is the average of the SAC and the XAC and the Difcor is the difference between SAC and XAC. The response component that changes upon inverting the polarity (i.e., Φ_C) is due to synchronization to TFS, whereas the response component common to the standard stimulus (Φ_C = 0°) and the polarity-inverted stimulus (Φ_C = 180°) reflects synchronization to ENV. By taking the average of the SAC and XAC (i.e., the Sumcor), the common contribution of ENV coding is emphasized and the contribution of TFS coding is minimized. For the Difcor, a value of 0 indicates the number of coincidences expected from chance (rather than a value of 1 as in the other correlograms: SAC, XAC, and Sumcor). The TFS contributions do not always cancel out completely in the Sumcor (Heinz and Swaminathan, 2009). This leakage of TFS into the Sumcor reflects distortion that arises from rectification associated with neural responses. The undesirable contribution of TFS coding to the Sumcor was eliminated according to Heinz and Swaminathan (2009) by considering only the envelope spectra below CF. In addition, the ENV contributions do not always cancel out completely in the Difcor (Heinz and Swaminathan, 2009). However, the influence of ENV coding on the Difcor can be argued to be small based on the small effect of sound level on Difcor peak heights (Louage et al., 2004; Heinz and Swaminathan, 2009).

The shuffled correlogram analyses are applicable to any repeatable stimulus, such as AM tones (Kale and Heinz, 2010), as well as to broadband noise (Joris, 2003; Louage et al., 2004, 2005; Swaminathan and Heinz, 2011) or chimaeric speech (Heinz and Swaminathan, 2009). They are also widely used to analyze responses to monaural stimuli (Joris, 2003; Heinz and Swaminathan, 2009; Kale and Heinz, 2010; Swaminathan and Heinz, 2012). A limitation of these stationary shuffled correlogram analyses is that they only estimate the overall strength of ENV and TFS averaged across the whole duration of the SFM stimuli (1000 ms). In other words, they do not account for the temporal dynamics of the SFM stimuli. Therefore, a sliding short-time analysis was also carried out to explore the “nonstationarity” of the temporal structure of the SFM stimulus. Shuffled all order ISI histograms were computed using a windowing procedure similar to (Sayles et al., 2015). The analysis window was centered over 50 ms and positive ISIs were analyzed in this 50 ms time bin, creating an ISI histogram. The latter was computed based on the calculation of ISIs between ordered pairs of nonidentical spike trains. A sliding window of 5 ms was used and the 1000 ms response recorded was analyzed. The normalized number of coincidences (normalization factor: N(N − 1)r² Δt D) for each time window analyzed were computed. A running correlogram was then built from those normalized ISI histograms, showing the modulated ISI distribution as a function of time (i.e., SFM duration = 1000 ms).

Statistical methods.

All statistical analyses were computed using STATISTICA software (StatSoft). t tests for independent samples were used for comparison between datasets in Figure 5E. A p-value of <0.05 was used for the significance limit.

Figure 5.

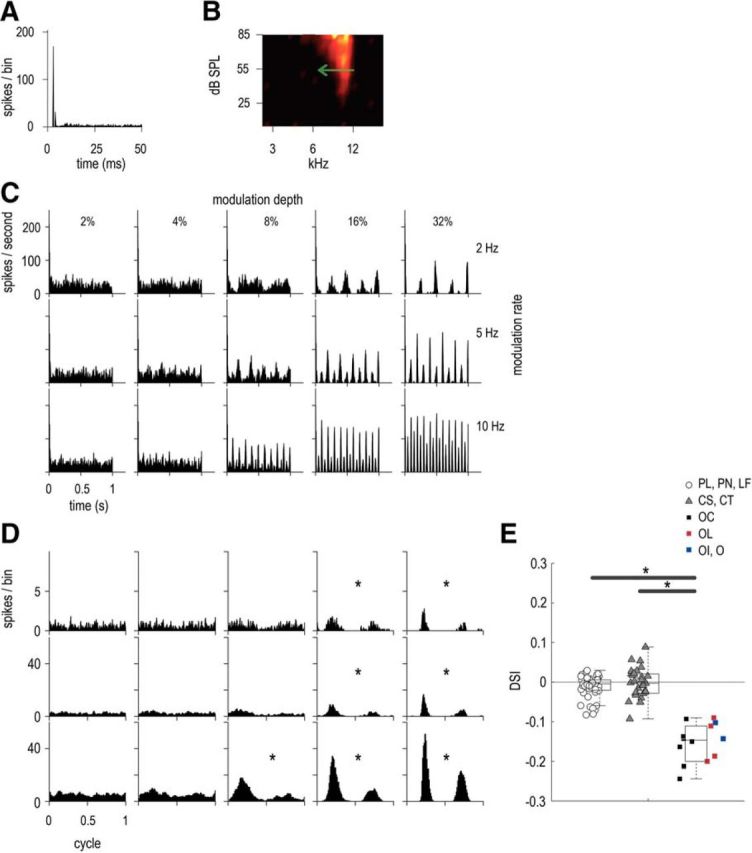
Asymmetric ENV responses of an OC unit, with BF = 10.1 kHz, SR = 0.9 spikes/s, T = 47 dB SPL. A, Pure tone PSTH (50 dB above threshold). B, Receptive field, with a green arrow indicating direction of preference (for the downward-going part of the SFM). C, PSTHs in response to 55 dB SPL SFM presented at BF at 3 modulation depths: 8, 16, and 32% (indicated in different columns) and 3 modulation rates: 2, 5, and 10 Hz (indicated in different rows). D, Period histograms to the modulation rate (similar experimental conditions as in C). Significant vector strength values are indicated by asterisks according to Rayleigh's criterion. E, DSI for all units (SFM at modulation rate = 10 Hz across all modulation depths). Three categories of units are described in the legend: (1) primary-likes and low-frequency (including PL, PN, and LF units), in white circles; (2) choppers (including CS and CT units), in gray triangles; and (3) onsets (including OC, O, OL, and OI units), in squares (OC are represented in black, OL in red, and O and OI in blue). The BFs of OC units varied between 4.1 and 22.3 kHz, whereas those of OL units varied between 1.9 and 14.7 kHz and those of O and OI varied between 2.2 and 9.1 kHz. Individual DSI values are plotted for all units, as well as box plots for the three unit categories. A DSI value of 0 corresponds to a symmetric response to both upward- and downward-going frequencies. A positive DSI value corresponds to a preference for upward-going sweep and a negative DSI value corresponds to a downward-going preference. Significant differences are indicated by asterisks (here, p < 0.0001 in both cases).

A one-factor ANOVA was conducted with the dependent variable corresponding to the Sumcor peak heights of all units analyzed to assess the differences between unit types regarding the strength of ENV coding (see Fig. 8A). The factor “unit type” had seven levels for the different unit types: LF, PL, PN, CS, CT, OC, and O (see “Unit classification” section). Post hoc tests with Bonferroni corrections were also computed. Similarly, another one-factor ANOVA was conducted with the dependent variable corresponding to the Difcor peak heights of all analyzed units to assess the differences between unit types regarding the strength of TFS coding (see Fig. 8B).

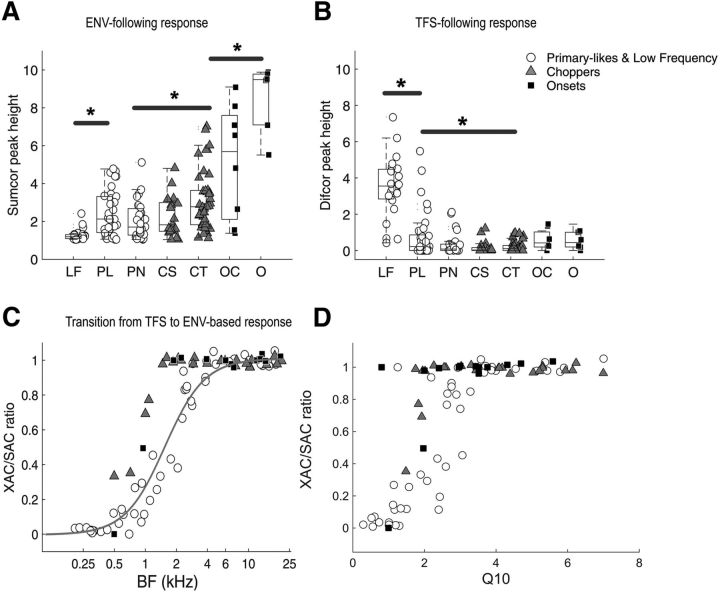
Figure 8.

Population data: ENV- and TFS-following responses. A, ENV-following response (peak height of Sumcor at zero delay) for all units. Seven unit types are shown: LF, PL, PN, CS, CT, and OC, and other onset types (including O, OI and OL). Three main categories of units are described in the legend: (1) primary-likes and low-frequency (including PL, PN and LF units), in white circles; (2) choppers (including CS and CT units), in gray triangles; and (3) onsets (including OC, O, OL, and OI units), in black squares. Asterisks indicate significant differences between Sumcor values of different unit types. B, TFS-following response (peak height of Difcor at zero delay) for all units. Same legend as for A. C, Ratio of XAC to SAC as a function of BF for all units recorded. A ratio of 0 indicates a purely TFS-following response and a ratio of 1 indicates s purely ENV-following response. D, Ratio of XAC to SAC as a function of Q10 (or Q_{10 dB}) calculated from the receptive fields for all units recorded. Small Q10 values indicate sharp filter bandwidths and larger Q10 values indicate broader filter bandwidth.

A repeated-measures ANOVA was conducted on the Sumcor peak heights (and the Difcor peak heights) to assess the effect of the modulation rate of the SFM (see Fig. 9A,B). The ANOVA was computed separately for the three major groups of units: (1) primary-likes and low-frequency, (2) choppers, and (3) onsets. The factor “modulation rate” had 3 levels corresponding to 2, 5, and 10 Hz. Similarly, repeated-measures ANOVAs were also conducted on the Sumcor peak heights (and the Difcor peak heights) for the three major unit types separately to assess the effect of the modulation depth of the SFM (Fig. 9C,D). The factor “modulation depth” had 5 levels corresponding to 2, 4, 8, 16, and 32%.

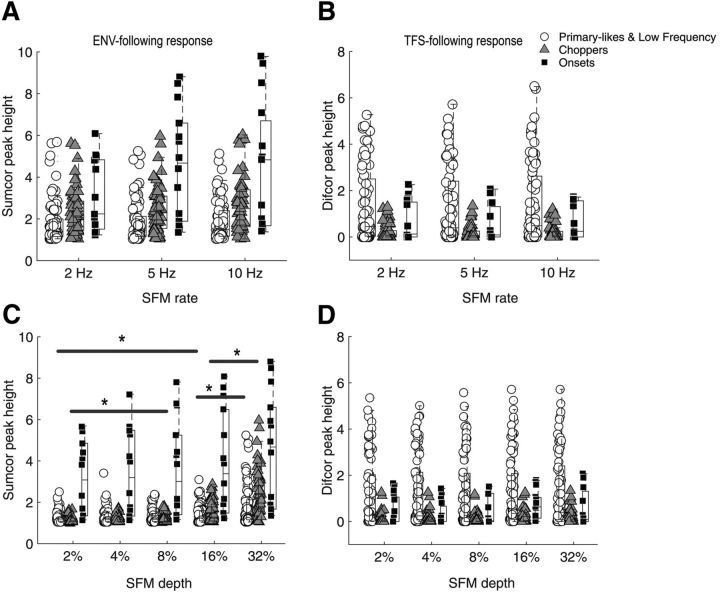
Figure 9.

Strengths of ENV and TFS coding in response to SFM at different modulation rates and depths. A, ENV-following response (peak height of the Sumcor at 0; see Materials and Methods) for each unit as a function of modulation rate, 2, 5, and 10 Hz, for a fixed modulation depth of 32%. B, TFS-following response (peak height of the Difcor at 0) for each unit as a function of modulation rate, 2, 5, and 10 Hz, for a fixed modulation depth of 32%. C, Envelope-following response for each unit as a function of modulation depth: 2, 4, 8, 16, and 32%, for a fixed modulation rate of 5 Hz. Significant differences (p < 0.05) are indicated by asterisks. D, TFS-following response for each unit as a function of modulation depth, 2, 4, 8, 16, and 32%, for a fixed modulation rate of 5 Hz.

Modeling.

The purpose of the modeling was to assess to what extent the receptive field of a unit could predict the ENV responses observed (i.e., resulting from FM-to-AM conversion). The raw receptive field measured for each unit was thus used to predict the amount of ENV fluctuations in the PSTHs in response to SFM. For each SFM condition (i.e., the three modulation rates and five modulation depths), the firing rates were modeled from the receptive field and plotted on the recorded PSTH (see Fig. 10). In addition, for each SFM condition, the correlation between the recorded PSTH and the predicted PSTH was computed, as well as an overall root-mean-square error (RMSE). The model was also used to predict the level dependence of ENV responses, as well as off-BF responses (see Fig. 10).

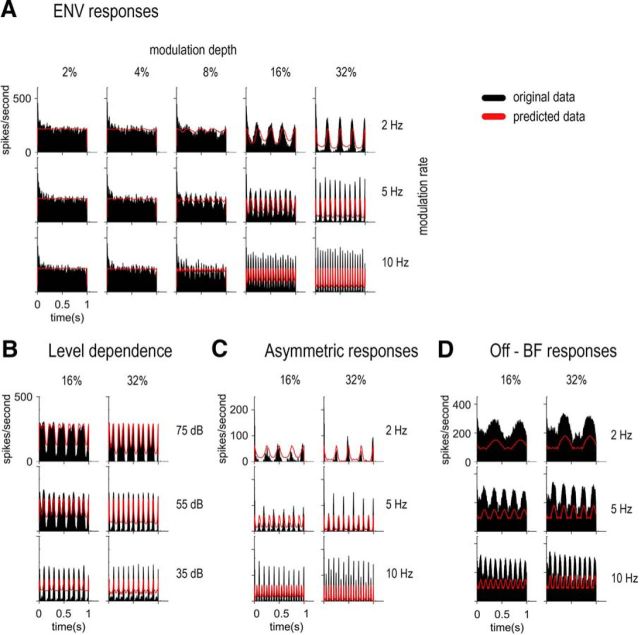
Figure 10.

Prediction of ENV responses from the raw receptive fields. A, PSTHs of the PL unit from Figure 2 for different SFM conditions (black) with the predicted shape of the PSTHs from the receptive field of the PL unit (red). B, PSTHs of the CS unit from Figure 4 for different SFM conditions (black) at three different levels (shown in the three rows) with the predicted shape of the PSTHs from the receptive field of the CS unit (red). C, PSTHs of the OC unit from Figure 5 (black) showing asymmetric responses with the predicted shape of the PSTHs from the receptive field of the OC unit (red). D, PSTHs of the CS unit from Figure 7 for different SFM conditions (black) presented off-BF (Fig. 7C) with the predicted shape of the PSTHs from the receptive field of the CS unit (red).

This model did not include other peripheral factors (e.g., short-term neural adaptation, amplitude compression, or lateral suppression) or CN factors (e.g., intrinsic neural properties, neural circuitry), which also contribute to the responses of CN units. The effects of those factors can be observed indirectly from what this simple model cannot predict.

Results

A total of 115 neurons were recorded in the VCN in response to SFM stimulus, played at different modulation rates (fm= 2, 5, and 10 Hz) and different modulation depths (Δf = 2, 4, 8, 16, and 32% of BF). The carrier frequency was adjusted for each unit and set to the unit's BF (i.e., fc= BF). PSTHs and period histograms to the modulation rate were computed. In addition, the responses of each unit were analyzed using shuffled autocorrelograms and cross-correlograms (SAC and XAC) and the strengths of ENV and TFS coding were quantified using the peak heights of the Sumcor and Difcor, respectively. The relative strength of ENV to TFS was calculated using the ratio of the XAC to SAC. Data from single units are shown first (see Figs. 2, 4, 5, 6, 7), followed by the population analyses (see Figs. 8, 9) and the modeled responses (see Fig. 10). Units were classified as follows: LF (number of units, n = 16), PL (n = 23), PN (n = 19), CS (n = 9), CT (n = 23), OC (n = 9), and other onset-type (including O, OL, and OI, n = 6). Units which did not “respond” to the SFM were excluded from the analysis.

Figure 2.

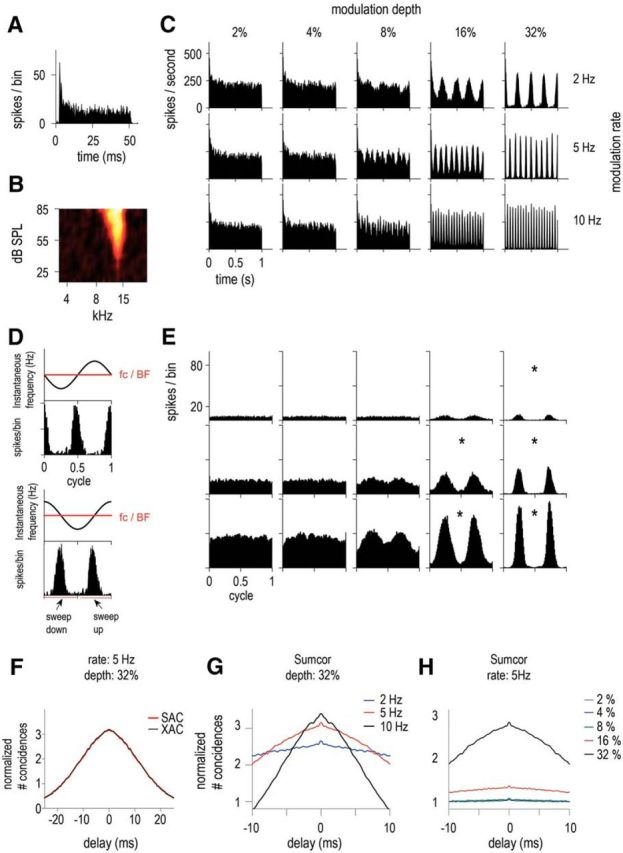
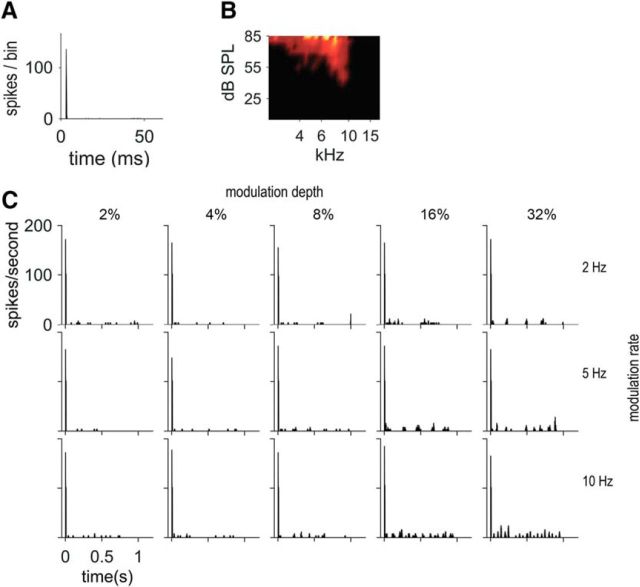
ENV responses of a high-BF unit characterized as PL, with BF = 13.3 kHz, spontaneous rate (SR) = 20.5 spikes/s, and threshold (T) = 36 dB SPL. A, Pure tone PSTH (20 dB above threshold). B, Receptive field. C, PSTHs in response to SFM presented at 55 dB SPL at 5 modulation depths: 2, 4, 8, 16, and 32% (in columns) and 3 modulation rates: 2, 5, and 10 Hz (in rows). D, Schematic illustration of how the period histogram is computed, with the top plot showing raw data and the bottom plot data after reorganization of the spike times to compare sweep-up and sweep-down. Sweep-up values correspond to an instantaneous frequency going upward and sweep-down values correspond to the instantaneous frequency going downward. E, Period histograms to the modulation rate for each of the different condition of modulation rates and depths (same as in C). Significant vector strength values are indicated by asterisks according to Rayleigh's criterion. F, Normalized SAC (red) and XAC (black) for 5 Hz SFM at modulation depth = 32%. G, Sumcor (average SAC and XAC) for the 3 modulation rate conditions for a fixed modulation depth of 32% (2, 5, and 10 Hz in blue, red, and black, respectively). H, Sumcor for the 5 modulation depth conditions for a fixed modulation rate of 5 Hz (2, 4, 8, 16, and 32% in gray, blue, green, red, and black, respectively).

Figure 4.

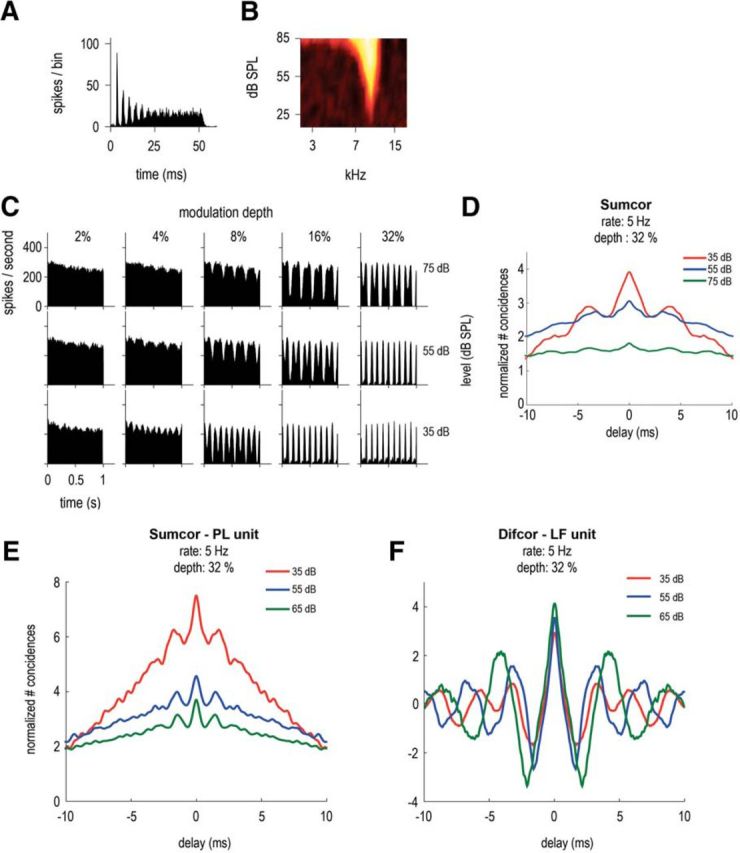
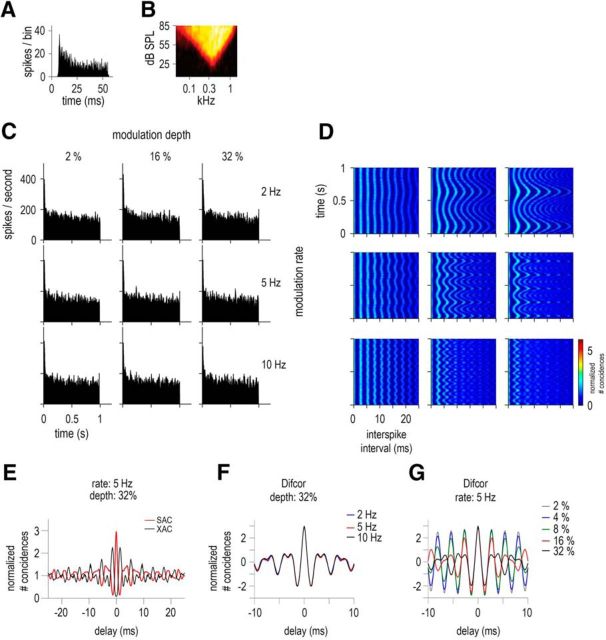
Level dependence of the ENV responses of a CS unit, with BF = 9.5 kHz, SR = 35.4 spikes/s, T = 23 dB SPL. A, Pure tone PSTH (20 dB above threshold). B, Receptive field. C, PSTHs in response to 5 Hz SFM presented at BF and at 3 stimulation levels: 35, 55, and 75 dB SPL (in rows) and 5 modulation depths: 2, 4, 8, 16, and 32% (in columns). D, Sumcor (average SAC and XAC) for 5 Hz SFM stimuli at modulation depth = 32% at the 3 presentation levels (35, 55, and 75 dB SPL in red, blue and green). E, Sumcor of another high-BF unit: PL, BF = 9.2 kHz, at different presentation levels in dB SPL (in response to SFM stimuli: 5 Hz rate and 32% depth). F, Difcor of a low-BF unit: LF, BF = 417 Hz, at different presentation levels in dB SPL (in response to SFM stimuli: 5 Hz rate and 32% depth).

Figure 6.

Some onset units respond primarily to the onset of the SFM. An OI unit is shown here, with BF = 9.1 kHz, SR = 0.0 spikes/s, T = 45 dB SPL. A, Pure tone PSTH (50 dB above threshold). B, Receptive field. C, PSTHs in response to 55 dB SPL SFM presented at BF, at 5 modulation depths: 2, 4, 8, 16, and 32% (in columns) and 3 modulation rates: 2, 5, and 10 Hz (in rows). An ongoing response can be seen only at the highest modulation depths (16 and 32%).

Figure 7.

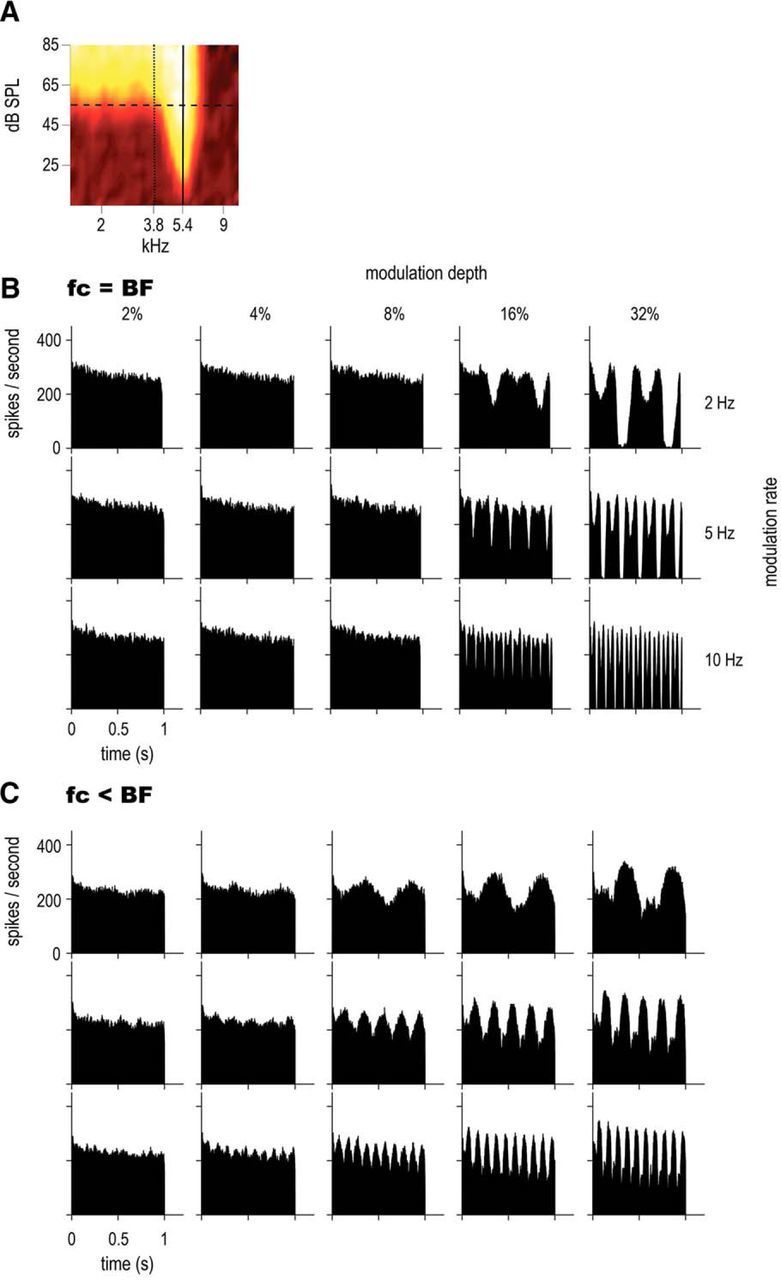
Comparison of on-BF and off-BF responses of a CS unit, with BF = 5.4 kHz, SR = 71.0 spikes/s, T = 20 dB SPL. A, Receptive field. The solid line indicates the on-BF position (carrier frequency at BF) and the dotted line the off-BF position. B, PSTHs in response to on-BF SFM presented at 55 dB SPL (horizontal dashed line) at 3 rates: 2, 5, and 10 Hz (in rows) and 5 modulation depths: 2, 4, 8, 16, and 32% (in columns). The fc was set to the same value as BF (5.4 kHz). C, PSTHs in response to off-BF SFM (same conditions as B); fc was set to 3.8 kHz.

ENV synchronized responses

An example of a high-BF PL unit (13.3 kHz) is shown in Figure 2, with the pure tone PSTH presented at 20 dB above the unit's threshold (Fig. 2A), together with its receptive field (Fig. 2B). Figure 2C shows the PSTHs in response to the 1-s-long SFM tone played at 55 dB SPL at 5 modulation depths, 2, 4, 8, 16, and 32% of BF, and 3 modulation rates, 2, 5, and 10 Hz. At 2% and 4% modulation depths, the PSTHs showed no obvious ENV-following response; however, at 8% depth (frequency sweeping from 12.2 to 14.3 kHz), the discharge rate starts to follow the ENV cues resulting from FM-to-AM conversion; that is, the overall firing rate is modulated. At that presentation level (55 dB SPL), the low-frequency edge of the response area corresponds to 11.5 kHz and the high-frequency edge to 15.2 kHz. The frequencies swept by the SFM approach both the low and high edges of the receptive field when the modulation depth is between 8% and 16%. At 32% depth (frequency sweeping from 9.0 to 17.5 kHz), the PSTH represents the SFM fully sweeping in and out of the receptive field and the firing rate drops to zero when the frequencies of the SFM are outside of the receptive field. Figure 2D illustrates schematically how the period histograms to the modulation rate in Figure 2E are constructed. The top plot shows the period histogram computed from the raw data obtained and the bottom plot shows the period histogram with the first half cycle representing “sweep-down”; that is, when the instantaneous frequency goes from high to low frequencies (also referred to as “downward-going”) and the second half cycle representing “sweep-up”; that is, when the instantaneous frequency goes from low to high frequencies (also referred to as “upward-going”). In Figure 2E, all period histograms are computed as the latter plot. The period histograms to the modulation rate are shown for the various modulation rates and depths as in Figure 2C after excluding the response to the first cycle of the stimuli. To assess the strength of synchronization to the ENV, the vector strength was calculated (Huffman et al., 1998). Significant vector strengths (i.e., p < 0.05 according to Rayleigh's criterion) are indicated by an asterisk. The period was taken (2*1/f) as the ENV had twice the modulation frequency of the stimulus. The ENV responses were more salient for the higher modulation rates and depths. There was no direction preference and the firing rate was similar when the SFM sweeps from high-to-low or from low-to-high frequencies. Figure 2F shows the normalized shuffled correlogram (SAC and XAC) in response to a 5 Hz SFM at 32% depth. The SAC and XAC overlap completely. Figure 2G shows the normalized Sumcors for the 32% depth SFM at 3 different modulation rates: 2, 5, and 10 Hz. The peak height of the Sumcor increases as the modulation rate increases (from fm = 2 to 10 Hz), showing better ENV coding at the highest modulation rate. The normalized Sumcors for the 5 Hz modulation rate SFM at the 5 different modulation depths, 2, 4, 8, 16, and 32%, are shown in Figure 2H. The ENV representation, as assessed by the Sumcor peak height, is higher at 32% depth compared to the lower modulation depths. Overall, SFM (at the highest modulation rates and depths) can be represented via synchronization to the ENV cues in CN units, as described previously in the cat (Fernald and Gerstein, 1972) and in the rat (Moller, 1972a,b). The Difcor (data not shown) is flat for this 13.3 kHz PL unit, showing no TFS coding at all since the difference between the SAC and XAC (Fig. 2F) leads to 0 in this case.

Phase locking to TFS cues

An example of responses of an LF unit (BF = 372 Hz) is given in Figure 3. The PSTHs in response to the SFM (Fig. 3C) showed no obvious ENV-following response. This was expected as the frequencies swept by the SFM stimuli remain within the receptive field even at 32% modulation depth. At this modulation depth, the SFM stimuli sweeps from 253 to 491 Hz, well within the low (141 Hz) and high (797 Hz) frequency edges of the receptive field. Figure 3E shows the normalized shuffled correlogram (SAC and XAC) in response to a 5 Hz SFM at 32% depth and Figure 3, F and G, represent the normalized Difcors (SAC-XAC) for the different modulation depths and rates. The damped oscillatory shaped Difcor has the same frequency as the BF of the unit, reflecting the carrier frequency of the SFM. The unit is phase locking to the carrier of the stimulus (i.e., to the TFS). The Difcor peak heights are similar for all modulation rates and depths, indicating similar strengths of TFS coding. The Sumcor in this case (data not shown) is flat and has a value of 1, indicating no ENV coding. Figure 3D shows the running correlograms (or interval histograms) computed to account for the temporal dynamics of the SFM stimuli (see Materials and Methods). The running correlograms are shown for the same experimental conditions as in Figure 3C (i.e., 3 modulation rates, 2, 5, 10 Hz, and 3 modulation depths, 2%, 16%, 32%). The TFS information is represented in the temporal dynamics of the firing pattern of the LF unit. The first peak (corresponding to the smallest ISI) in all the running correlograms occurs at 2.7 ms, which is equivalent to the fc of the SFM (also equivalent to the unit's BF = 372 Hz). The changes in instantaneous frequency of the stimuli with time are well represented in the spike timings, with 2, 5, and 10 cycles for the 2, 5, and 10 Hz SFM, respectively, in 1 s. The modulation depths, that is, the frequencies swept by the stimuli, are also well represented in the running correlograms. Overall, the TFS information is present in the ISI of low-BF units and is conveyed to higher structures of the auditory brainstem.

Figure 3.

TFS responses of a low-BF unit characterized as LF, with BF = 372 Hz, SR = 0.4 spikes/s, and T = 24 dB SPL. A, Pure tone PSTH (20 dB above threshold). B, Receptive field. C, PSTHs in response to 55-dB SPL SFM presented at 3 modulation depths: 2, 16, and 32% (in columns) and 3 modulation rates: 2, 5, and 10 Hz (in rows). D, Running correlograms for positive ISIs (see Materials and Methods). Responses to different rates and depths as illustrated in C. The color scale bar applies to all running correlograms. E, Normalized SAC (red) and XAC (black) for 5 Hz SFM at modulation depth = 32%. F, Difcor (SAC − XAC) corresponding to the 3 modulation rates conditions (2, 5, and 10 Hz) for a fixed modulation depth of 32%. G, Difcor corresponding to the 5 modulation depths conditions (2, 4, 8, 16, and 32%) for a fixed modulation rate of 5 Hz.

Level dependence of ENV and TFS coding

The responses as a function of sound level are shown in Figure 4C for a CS unit (BF = 9.5 kHz), at 3 levels over a 40 dB range. Like the PL unit shown in Figure 2, at low modulation depths (2%), the PSTHs are flat and an ENV-following response emerges from the 4% depth condition. This unit also illustrates a common finding among the units recorded, the phenomenon of “peak separation” in the PSTH (i.e., the doublets of the peaks in the PSTH). This is consistent with data recorded from cat CN (Fernald and Gerstein, 1972) and reflects the asymmetry of the receptive field, particularly at high levels. As the SFM tone sweeps in and out of the receptive field, at high levels, most of the energy is outside at the high-frequency end (firing rate decreases to zero) while still remaining within the receptive field at the low-frequency end (hence, only a small decrease in firing rate). This phenomenon is well predicted by the model developed in the current study based on the receptive field as shown in Figure 10B. In Figure 4D, the Sumcor peak height at zero increases with decreasing stimulus level reflecting better ENV-following responses at lower levels. The bandwidth of the receptive field is sharper at low levels compared to higher levels, so the ENV representation is enhanced at low levels. Another example of a high-BF unit (PL unit with BF = 9.2 kHz, Fig. 4E) is given in response to SFM played at 5 Hz rate and 32% deviation. For this PL unit as well, the peak height of the Sumcor increases with decreasing stimulation level, showing better ENV representation at low levels. When considering the population data for all recorded units, there is a significant difference in Sumcor peak height (paired t test: p = 0.009) between responses evoked at lower sound levels (<55 dB SPL) and responses evoked at higher sound levels (>55 dB SPL).

The Difcors of an LF unit (BF = 417 Hz) in response to SFM played at different levels are shown in Figure 4F. The Difcor peak heights are similar at all three levels. When considering the population data, there is no significant difference in Difcor peak heights for all recorded units (t test: p = 0.429) between responses evoked at lower sound levels (<55 dB SPL) and responses evoked at higher sound levels (>55 dB SPL). The TFS-based representation is thus very similar at different stimulation levels above threshold (Johnson, 1980). This is consistent with Palmer and Russell (1986) and their data from ANFs of the guinea pig, in which phase locking, as measured by vector strength, increased with stimulation level and reached a saturation point ∼20 dB above threshold.

Asymmetric responses of onset units

PL and PN units, as well as CT and CS units, discharge similarly for both the upward-going and downward-going parts of the SFM. However, this was often not the case for units classified as onsets (Winter and Palmer, 1995). An example of an OC unit with an asymmetric ENV-following response is given in Figure 5. The first half cycle of the period histograms to the modulation rate (D) corresponds to the responses for the downward-going part of the SFM (i.e., from high to low frequencies), whereas the second half cycle corresponds to the responses for the upward-going part of the SFM (i.e., from low to high frequencies). The unit discharges preferentially to the downward-going part of the SFM stimulus (i.e., in the same direction as the green arrow on the receptive field). A direction selectivity index (DSI) was calculated as (number of spikes for sweep-up) − (number of spikes for sweep-down) divided by the (total number of spikes for sweeps-up and down), as described by Mendelson and Cynader (1985). For the current OC, the DSI was −0.17 for a 10 Hz SFM rate and 32% depth.

Figure 5E shows the DSI for all units in response to the SFM played at 10 Hz merged across all modulation depths. The units are separated in three main groups: (1) open circles representing primary-like and low-frequency units (i.e., PL, PN, and LF), (2) gray triangles representing chopper units (i.e., CS and CT), and (3) squares representing onset units (with black squares for OC, red squares for OL, and blue squares for OI and O). The asymmetric responses of the present onset units altogether are quite small (DSI values <0.3) compared to the asymmetric responses obtained in the inferior colliculus of the bat (DSI values >0.6) in response to SFM (Casseday et al., 1997) and the auditory cortex of the cat (>0.3) using upward- and downward-going FM sweeps at different speeds (Mendelson and Cynader, 1985). Nevertheless, the values of DSI obtained for the current onset units are significantly different from those of primary-like and low-frequency units (t test for independent samples: p < 0.0001) and chopper units (p < 0.0001).

It is important to point out that some OI units did not “respond” to the SFM except with one precise first spike at the beginning of the stimulus and very few spikes afterward. Figure 6A shows the pure tone PSTH presented at 50 dB above the unit's threshold, followed by the receptive field (Fig. 6B). Figure 6C shows the PSTHs in response to the SFM played at 55 dB SPL at various modulation rates and depths. Very few spikes are obtained in most conditions and an ongoing response can only be seen at the highest modulation depths (16% and 32%).

Off-BF responses

For a subset of 15 units, responses to off-BF SFM were also recorded. An example is given in Figure 7 for a CS unit. The PSTHs are plotted for different modulation rates and depths on-BF (Fig. 7B, fc = 5.4 kHz) and off-BF, with a carrier frequency at approximately half an octave below BF (Fig. 7C, fc = 3.8 kHz), in order for the energy of the SFM stimulus to fall within the tail of the receptive field. The PSTH shape changes with off-BF stimulation and only one peak is present in the PSTH instead of two peaks (as in the on-BF condition). In other words, off-BF responses show modulations in their PSTH at the SFM rate, whereas on-BF responses are modulated at twice the SFM rate. The shape of the off-BF responses can be accurately predicted from the receptive field of the unit (see Fig. 10D). In addition, the ENV-following response in the PSTH is present at a lower modulation depth condition (8%), whereas for the on-BF stimuli, the PSTHs are modulated only at 16% modulation depth condition. There is a trend for enhanced ENV-following responses (i.e., fluctuations in the PSTH) in off-BF conditions at low modulation depths, which are also predicted from the receptive field. However, at the 32% modulation depth, the peak heights of the Sumcors were very similar (data not shown) across the two conditions (on-BF and off-BF presentations). The Difcors also remained flat in both cases, showing no more TFS processing in the tail of the receptive field compared to the tip (data not shown). This was consistent across several units examined and may be due to the low sound levels used (55 dB SPL). Altogether, these data are partly consistent with the notion, initially formulated by psychophysicists, that FM detection can be achieved by monitoring off-frequency channels tuned to lower (or higher) frequencies than the carrier frequency (Zwicker, 1956; Ernst and Moore, 2010).

Different coding specializations for different unit types

The peak heights of the Sumcors (Fig. 8A) and the Difcors (Fig. 8B) at zero delay are shown in Figure 8 for all units. The Sumcor peak heights correspond to the strength of the ENV-based representation in the neural response and the Difcor peak heights correspond to the strength of the TFS-based representation in the neural response. Different symbols indicate the three main unit types: (1) primary-like and low-frequency units (PL, PN, and LF), (2) chopper units (CS and CT), and (3) onset units (OC, O, OL, and OI) in response to SFM at a modulation rate of 10 Hz and a modulation depth of 32% (stimulation level = 55 dB SPL).

Different unit types have different ENV and TFS-following responses. Onset and chopper units are the best ENV encoders, whereas PL and PN units, particularly LF units, are the best TFS encoders. Two one-factor ANOVAs revealed a significant effect of unit type for both the ENV- and the TFS-following responses (ENV response: F_(6,150) = 23.6, p < 0.0001; TFS-response: F_(6,150) = 30.8, p < 0.0001). Onset units are significantly better than all other unit types for ENV coding (confirmed by post hoc tests with Bonferroni correction and by t test, e.g., when comparing O and CT, p < 0.0001), whereas chopper units are significantly better than primary-like units (e.g., comparing CT and PN, p = 0.008), which are in turn significantly better than LF units (comparing PL and LF, p < 0.0001). LF units are significantly better than all other unit types for TFS coding (e.g., comparing LF and PL, p < 0.0001), whereas primary-like units are significantly better than chopper units (e.g., comparing PL and CT, p = 0.023), which are relatively similar to onset units (e.g., comparing CT and O, p = 0.638).

Ratio of ENV and TFS coding

The shuffled correlograms (SAC and XAC) allow quantification of the individual strengths of ENV and TFS coding by the Sumcor and Difcor metrics and the relative strength of ENV and TFS coding can be quantified by the ratio of the peak heights of XAC to SAC at zero delay (Louage et al., 2004, 2005; Kale and Heinz, 2010). A ratio of 0 represents primarily TFS coding and a ratio of 1 represents primarily ENV coding. For a low-BF unit, the SAC and the XAC are inverted in polarity (Fig. 3E), leading to an XAC/SAC ratio close to 0, whereas for a high-BF unit, the SAC and XAC are overlapping (Fig. 2E), leading to an XAC/SAC ratio close to 1.

The XAC/SAC ratio for all units is shown in Figure 8C as a function of BF in response to SFM played at 55 dB SPL, with modulation rate = 5 Hz and modulation depth = 2%. At this modulation depth, all of the energy of the stimulus remained within the receptive field of the unit even for high-BF units. The transition region whereby units change from a more TFS-based response to a more ENV-based response ranges from 1 to 4 kHz. TFS coding is no longer present beyond 4 kHz. Similarly to Louage et al. (2005), responses are defined as ENV dominated for XAC/SAC ratio ≥0.9 and the frequency cutoff value at this ratio corresponds to ∼4 kHz for primary-like and low-frequency units. Chopper and onset units show higher ENV-following responses compared to primary-like units, at least for BFs <2 kHz. Those units are poor TFS encoders, but good ENV encoders. Therefore, they have a lower transition region from TFS to ENV coding compared to primary-like and low-frequency units.

As the SFM used in the current study was at fixed modulation depths and not adjusted to the bandwidth of the unit under study, the transition from TFS to ENV can be thought of as mainly due to the bandwidth of the unit. In other words, the sharper the bandwidth, the more salient the ENV cues (resulting from FM-to-AM conversion) are, independently of unit types. Figure 8D shows the distribution of the XAC/SAC ratio as a function of Q10 (or Q_{10 dB}) calculated from the receptive fields of all units. Indeed, for primary-like and low-frequency units, the transition in ratio observed is quite similar to the transition observed in Figure 8C. In contrast, for onset and chopper units, even when the SFM stimuli are well within the filter bandwidth, those units do not encode the TFS information as well as the primary-like and low-frequency units. In other words, at similar Q10 values to primary-like and low-frequency units, the XAC/SAC ratio for chopper and onset units are higher compared to those of primary-like and low-frequency units. There is, however, quite a large variability in the Q10 values. Nevertheless, some onset and chopper units, despite having relatively small Q10 values (<3), have an XAC/SAC ratio of 1. Altogether, this suggests that the filter bandwidth (expressed here as Q10) does indeed constrain FM-to-AM conversion and the strength of ENV coding. However, chopper and onset units show enhanced ENV coding and reduced TFS coding at similar Q10 or BF values as primary-like and low-frequency units, demonstrating coding specializations as well.

FM coding as a function of modulation rate and depth

The Sumcor (Fig. 9A) and the Difcor (Fig. 9B) peak heights at zero delay for the different unit types are shown in Figure 9 as a function of the modulation rate (2, 5, and 10 Hz) in response to SFM at a fixed modulation depth of 32%. The ENV-based representation and the TFS-based representation are similar across modulation rates for all unit categories. A repeated-measures ANOVA revealed no significant effect of modulation rate for onset units (f_(2,22) = 2.7, p = 0.09).

Figure 9 also shows the Sumcor (Fig. 9C) and Difcor (Fig. 9D) peak heights for the different unit types as a function of the modulation depth (2–32%), in response to SFM at a fixed modulation rate of 5 Hz. Although the TFS-based representation is constant across modulation depths, the ENV-based representation is significantly enhanced with modulation depth for all three unit categories (repeated-measures ANOVA: for primary-like and low-frequency units: F_(4,296) = 30.7, p < 0.0001; for chopper units: F_(4,220) = 66.8, p < 0.0001; and for onset units: F_(4,52) = 4.7, p = 0.003). Significant differences are obtained between the responses of particular unit types at different modulation depths (e.g., primary-like and low-frequency units from 2 to 16%, paired t test: p = 0.010, chopper units from 2 to 8%, p = 0.001). At higher modulation depths, the SFM stimuli sweep across a wider range of frequencies, so the possibility of crossing the edges of the receptive field of a particular unit is increased, leading to more ENV cues.

Modeling results

To quantify the ENV representation at different modulation rates and depths, the raw receptive field (i.e., without any smoothing) of each unit was used to predict the FM-to-AM conversion; that is, the ENV fluctuations in the PSTH. Figure 10A shows the PSTH of the PL unit from Figure 2 and the predicted ENV responses modeled from the receptive field of the PL unit. Differences in overall spiking rate are expected as the receptive field is computed from 50 ms responses to pure tones, whereas the PSTH is computed from 1000 ms responses to SFM. In addition, the model did not take into account any physiological characteristic of CN neurons nor physiological peripheral processes. However, the shape of the PSTHs and the ENV responses (the fluctuations in the PSTHs) are well predicted as quantified by the correlation value (e.g., p < 0.001 for 2, 5, and 10 Hz SFM conditions at 32% depth). The overall RMSE for this unit = 51.1. The differences in spiking rate between the data and the predictions cause the RMSE to be rather large despite the fact that the ENV shape is quite accurately modeled. At 2% and 4% modulation depths, the predicted PSTHs are flat, showing no obvious ENV-following response, consistent with the original data (except for the onset response and the adaptation observed). At higher modulation depths (starting at 8%), the PSTH shows fluctuations well captured by the model.

Level differences in ENV coding can also be well predicted from the receptive field, as shown in Figure 10B. The PSTHs of the CS unit from Figure 4 are shown together with the predicted ENV responses at 75, 55, and 35 dB SPL. The filter shape and bandwidth can predict the sharper ENV responses at decreasing stimulation level (p < 0.001 for 32% depth condition at all 3 levels). Figure 10C shows the PSTHs of the OC unit from Figure 5, with an asymmetric response to the upward-going and downward-going parts of the SFM. The measurements derived from the receptive field do not predict this asymmetry. Conversely, off-BF responses can be accurately predicted, as shown in Figure 10D. The overall firing rate is not accurate, but the shape of the predicted PSTHs match closely those from the original data of the CS unit from Figure 7C. Overall, a simple model based on the receptive field can accurately predict the shape of the ENV fluctuations in the PSTH for all conditions presented here except for the asymmetric ENV responses.

Discussion

The present study assessed the relative contributions of ENV and TFS coding for a population of VCN single units in response to low-rate SFM. The results provide clear evidence that FM can be encoded via 1) synchronization to ENV cues generated at the output of cochlear filters and represented in the fluctuations of the firing pattern and, 2) phase locking to TFS cues which are represented in the precise spike timing. The diversity in the responses of different unit types provides new insights regarding how this dual-coding scheme might be implemented in the early auditory system.

Unit specialization for ENV and TFS coding

The data show that onset units (multipolar and octopus cells) are specialized in ENV coding. At similar BFs, onset units show higher ENV synchronization than chopper units, which in turn show higher ENV responses than primary-like units (onset > chopper > primary-like). This is consistent with previous studies demonstrating the hierarchy of ENV representation in the CN using AM stimuli (Frisina et al., 1990; Rhode and Greenberg, 1994; Wang and Sachs, 1994; Joris et al., 2004). Precise inhibitory circuits have been proposed to underlie ENV enhancement at various levels of the auditory pathway (Koch and Grothe, 1998; Backoff et al., 1999; Krishna and Semple, 2000; Caspary et al., 2002; Ter-Mikaelian et al., 2007). Onset I units (octopus cells) have been shown to be exceptional AM encoders (Rhode, 1994; Golding et al., 1995). Here, most onset-I units only fired at the onset of the stimuli. This lack of response may be due to the low modulation rates and depths used here as octopus cells are particularly sensitive to the rate of depolarization (Ferragamo and Oertel, 2002) and have been shown to fire when a wide array of ANFs are synchronously active (Oertel, 2005).

Low-frequency and primary-like units (bushy cells) with BFs <3 kHz show strong phase locking to TFS cues, consistent with the notion that bushy cells provide fast-fluctuating TFS information to the superior olivary complex and form part of the binaural sound localization stream (Yin, 2002). The current data also show that the strength of phase locking to TFS was relatively independent of the modulation rate, depth, and level of stimulation of the SFM. Therefore, compared to ENV cues, which are highly dependent on modulation depth (Fig. 7C) and stimulation level (Fig. 3), TFS cues provide an invariant and robust code. However, F0-related periodicity information has been shown to be degraded in the presence of both reverberation and F0-modulation (Sayles and Winter, 2008; Sayles et al., 2015).

The significant degradation of ENV coding with increasing stimulation level is consistent with ANF data (Joris and Yin, 1992; Wang and Sachs, 1994; Louage et al., 2004; Dreyer and Delgutte, 2006) and with the saturating character of rate level functions. In the current study, the observed level responses are due to the combined effect of saturation and receptive field bandwidth at different stimulation levels. In other words, the strength of ENV elicited from FM-to-AM conversion decreases as the stimulus level increases as the tuning of CN neurons are broader at higher sound levels compared to lower ones.

Limit of phase locking to TFS

A coding scheme for FM based on TFS cues would be restricted to relatively low carriers due to the limit of neural phase locking. In the current data, the transition region where units' responses change from being TFS driven to being ENV driven is ∼4 kHz (Fig. 6, XAC/SAC ratio = 0.9) for primary-like and low-frequency units. The upper limit of phase locking in ANFs, as assessed with vector strength measurements, is known to vary across species; 5–6 kHz in squirrel monkeys and cats (Rose et al., 1967; Johnson, 1980) and 4–5 kHz in guinea pigs and chinchillas (Harrison and Evans, 1979; Palmer and Russell, 1986). The owl is exceptional in this respect as phase locking is constant up to 9–10 kHz (Sullivan and Konishi, 1984; Köppl, 1997).

In agreement with previous reports examining temporal coding for a population of ANFs (Louage et al., 2004; Kale and Heinz, 2010), the current CN data show a sigmoidal relationship between the ratio of TFS to ENV coding (i.e., the XAC/SAC ratio) and frequency (i.e., BF). The transition frequency from a TFS-based to an ENV-based representation found here is consistent with ANF responses to sinusoidal AM in the chinchilla (∼3 kHz, Kale and Heinz, 2010). In response to broadband noise, ANF responses showed the same trend (Louage et al., 2004), with a cutoff of ∼5 kHz in the cat. Louage et al. (2005) examined the responses of trapezoid body fibers and reported a lower cutoff (∼4 kHz) for primary-like responses compared to ANFs. Indeed, several studies have shown a decrease in the phase-locking cutoff along the ascending auditory pathway (Nelson et al., 1966; Schuller, 1979; Rees and Møller, 1983; Gaese and Ostwald, 1995; Lu and Wang, 2000). This decrease has been proposed to reflect the conversion of temporally synchronized cues into a rate-based representation, allowing the integration of auditory information with other sensory input at the cortical level (Wang et al., 2008).

The human phase-locking cutoff is still unknown (at least ∼3 kHz; Joris and Verschooten, 2013). In addition, SFM coding via synchronization to ENV cues is highly dependent on the frequency selectivity of the cochlear filters as it constrains the amount of ENV. It is very likely that the current results underestimate ENV cues from FM-to-AM conversion in humans since the latter have been estimated to have sharper tuning (2–3 times) than cats, chinchillas, and guinea pigs (Shera et al., 2002; but see Ruggero and Temchin, 2005, Joris et al., 2011). Therefore, the dual-coding scheme of FM demonstrated here in the guinea pig should be similar or even more efficient for humans, at least regarding ENV coding when considering the output of several overlapping sharp auditory filters. From the current model predictions (Fig. 10), the global fluctuations in spiking rate (ENV responses) are well accounted for when considering only FM-to-AM conversion. However, the small differences between the data and the predictions and the absence of asymmetric responses from the current model suggest that additional mechanisms (e.g., intrinsic neural properties of CN units, neural circuitry of the VCN) and more complex models of CN units (Manis and Campagnola, 2018) need to be considered.

Direction selectivity

Physiological data regarding direction selectivity in the auditory system appear to be dependent on species, as well as on the recording site. In contrast to the visual system, where direction selectivity is observed at the very beginning of sensory processing (Fried et al., 2002), ANFs show symmetrical discharge patterns to ascending and descending parts of FM signals, suggesting a lack of direction preference (Britt and Starr, 1976; Sinex and Geisler, 1981). However, as early as the CN, neurons show asymmetrical responses (Erulkar et al., 1968; Moller, 1974a,b; Godfrey et al., 1975; Britt and Starr, 1976). These early reports did not unequivocally identify the class of unit type or the region of the cochlear nucleus from which they were recorded, making comparisons with the present study difficult. Consistent with some of these early reports, however, the current results show a small but significant preference for onset units to respond preferentially to the descending part of the SFM (from high to low frequencies). Although direction selectivity was not prominent in the rat CN (Moller, 1969), a preference for descending sweeps was found at high sweep rates (Moller, 1971) and, in the cat CN, a small preference for ascending sweeps was found in onset units (Rhode and Smith, 1986). At the cortical level, neurons selective to ascending and descending directions are equally abundant (Poon et al., 1991; Nelken and Versnel, 2000; Zhang et al., 2003; Kuo and Wu, 2012). Auditory neurons of bats present a strong downward preference and it has been noted that downward frequency sweeps are common in their echolocation calls (Suga, 1965; Andoni et al., 2007; Razak and Fuzessery, 2008). Interestingly, some differences have also been reported in the perception of rising and falling frequency sweeps for human listeners, with a preference for rising glides (Collins and Cullen, 1978; Carlyon and Stubbs, 1989).

Previous studies (Suga, 1988) have suggested that the distribution of excitatory and inhibitory regions may underlie direction selectivity and higher DSI values may be obtained for larger FM depths than examined here as the effect of any inhibitory sideband would be exacerbated. To our knowledge, there is no evidence for inhibition playing a role in the responses of onset units.

In a previous study by Rhode and Smith (1986), the OI unit category showed the strongest direction selectivity. The arrangement of ANF inputs on the dendrites of octopus cells (Oertel et al., 2000; McGinley et al., 2012) suggests that these cells may perform across-frequency processing and this may contribute to the asymmetry. It is unclear why we failed to observe this, but it might be due to different stimulation parameters or species differences. In a computational model of octopus cells (presumed OI units), Levy and Kipke (1997) also failed to observe any directional selectivity. It is worth noting that, in the present study, the onset classification scheme adopted was that of Winter and Palmer (1995). From the Winter and Palmer dataset, OC and OL units were modeled as a continuum (Kalluri and Delgutte, 2003). Others, however, have suggested that OL units are associated with globular bushy cells and form a continuum with the PN response type (Spirou et al., 2005). Across-frequency coincidence detection has previously been shown in PN units (Carney, 1990; Wang and Delgutte, 2012). They are thus sensitive to local changes in the spatiotemporal pattern of AN activity. Monaural cross-frequency coincidence detection results in a temporal sharpening across frequency channels, which may be useful in pitch perception, although the importance of across-fiber spike timing remains unclear in monaural processing (but see Carney, 1990; Joris et al., 1994; Heinz et al., 2001). It is possible that these properties would lead to a preference for sweep direction in PN units or the OL units hypothesized to form a continuum with them. The DSI values of the OL units in the present study are closer to the OC units than the PN units. Finally, other neural mechanisms such as adaptation (Bleeck et al., 2006; Ingham et al., 2016) or rate of depolarization (McGinley and Oertel, 2006) could contribute to the observed directional selectivity.

Dual-code subserving FM detection

A better understanding of the underlying mechanisms of FM coding should improve our knowledge of how the auditory system processes speech and other natural sounds. The current results are consistent with data obtained for SFM detection in human listeners. For low carrier frequencies (<5 kHz) and modulation rates (<5–10 Hz), several studies suggest that human listeners mostly use TFS cues for SFM detection (Moore and Sek, 1996; Paraouty et al., 2016; Wallaert et al., 2016, 2017; Paraouty and Lorenzi, 2017). In comparison, for high carriers and rates, listeners seem to mostly use ENV cues (Ernst and Moore, 2010, 2012).

The current findings support the view that low-rate FM is encoded by two sensory mechanisms based on synchronization to slow ENV cues resulting from cochlear filtering and phase locking to faster TFS cues. The absence of differences in the TFS-following responses across modulation rates tested here (2–10 Hz) indicates that the locus of sluggishness for TFS processing postulated by psychophysicists (Moore and Sek, 1996) is more central than the CN. A dual-coding scheme has several advantages compared to a single ENV coding scheme. For high sound (conversational) levels, most low-threshold, high-spontaneous-rate fibers are saturated when the SFM stimuli is played at BF, leading to reduced ENV synchronization (Sachs and Young, 1979; Joris and Yin, 1992). Conversely, off-BF responses are less affected at high sound levels (Wang and Sachs, 1993) and the ENV cues would still be salient. Phase locking to TFS cues also remains relatively robust at high sound levels. In addition, in the presence of noise or competing backgrounds, phase locking to TFS cues provides a more robust representation compared to synchronized ENV responses (Shamma and Lorenzi, 2013). In reverberant environments, TFS coding of linear-frequency-swept harmonic complexes was found to be degraded, which in turn, impairs stream segregation (Sayles and Winter, 2008; Sayles et al., 2015). Overall, phase locking to TFS cues is likely to play a crucial role in the robust representation of speech and other ecologically important sounds in a broad range of acoustic situations. The dual-coding scheme is thus adapted to the constraints of natural listening conditions, which are constantly changing.