The Nucleus Reuniens Controls Long-Range Hippocampo–Prefrontal Gamma Synchronization during Slow Oscillations

Abstract

Gamma oscillations are involved in long-range coupling of distant regions that support various cognitive operations. Here we show in adult male rats that synchronized bursts of gamma oscillations bind the hippocampus (HPC) and prefrontal cortex (mPFC) during slow oscillations and slow-wave sleep, a brain state that is central for consolidation of memory traces. These gamma bursts entrained the firing of the local HPC and mPFC neuronal populations. Neurons of the nucleus reuniens (NR), which is a structural and functional hub between HPC and mPFC, demonstrated a specific increase in their firing before gamma burst onset, suggesting their involvement in HPC–mPFC binding. Chemical inactivation of NR disrupted the temporal pattern of gamma bursts and their synchronization, as well as mPFC neuronal firing. We propose that the NR drives long-range hippocampo–prefrontal coupling via gamma bursts providing temporal windows for information exchange between the HPC and mPFC during slow-wave sleep.

SIGNIFICANCE STATEMENT Long-range coupling between hippocampus (HPC) and prefrontal cortex (mPFC) is believed to support numerous cognitive functions, including memory consolidation occurring during sleep. Gamma-band synchronization is a fundamental process in many neuronal operations and is instrumental in long-range coupling. Recent evidence highlights the role of nucleus reuniens (NR) in consolidation; however, how it influences hippocampo–prefrontal coupling is unknown. In this study, we show that HPC and mPFC are synchronized by gamma bursts during slow oscillations in anesthesia and natural sleep. By manipulating and recording the NR–HPC–mPFC network, we provide evidence that the NR actively promotes this long-range gamma coupling. This coupling provides the hippocampo–prefrontal circuit with a novel mechanism to exchange information during slow-wave sleep.

Introduction

Slow-wave sleep is important for memory consolidation (Rasch and Born, 2013). Recently acquired memories in the hippocampus (HPC) can be replayed during the periods of large, synchronous oscillations (0.1–4 Hz) that characterize slow-wave sleep (Steriade et al., 1993). Hippocampal sharp wave-ripples (SPW-Rs; 80–250 Hz bursts that can be observed during slow-wave sleep and quiescent states) provide a way to exchange information between the HPC and the cortex (Buzsáki, 2015), in particular with the medial prefrontal cortex (mPFC), which is directly involved in memory consolidation (Siapas and Wilson, 1998; Maingret et al., 2016; Latchoumane et al., 2017). Other rhythms may act as vectors of information during slow-wave sleep, such as gamma band oscillations (30–90 Hz), which are ubiquitous in the brain (Buzsáki and Wang, 2012). Neuronal gamma-band synchronization has been proposed as a fundamental process in cognitive operations, including those during sleep (Fries, 2009; Valderrama et al., 2012; Cardin, 2016; Sohal, 2016). The time window provided by a gamma cycle (10–30 ms) is optimal for information exchange between partner neurons (Csicsvari et al., 2003; Buzsáki and Wang, 2012; Cardin, 2016), as it can entrain neurons from downstream regions (Peyrache et al., 2011). Whether gamma oscillations play a role in information exchange between the HPC and mPFC is not known. Gamma rhythms are mostly local phenomena (Csicsvari et al., 2003; Fries et al., 2007), therefore long-range synchronization between locally generated gamma oscillations may be an efficient way to ensure communication between the HPC and mPFC (Buzsáki and Schomburg, 2015; Fries, 2015). Before investigating whether such an information exchange can occur between the HPC and mPFC, it is necessary to first prove that synchronized gamma activities exist between the two structures and that cell behavior during these gamma events fulfills criteria for information exchange. This constitutes the first goal of our study. We focus on slow oscillations, such as those found during slow-wave sleep, because gamma oscillations finely organize neuronal activity in conjunction with slower timescales (Isomura et al., 2006; Buzsáki and Wang, 2012; Buzsáki and Schomburg, 2015). Our second goal is to determine a possible mechanism of long-range gamma synchronization between the HPC and mPFC. Although the HPC projects directly to the mPFC, the time delays imposed by the distance between the two regions may disrupt coupling (Buzsáki and Wang, 2012). The nucleus reuniens (NR), a thalamic midline nucleus, is ideally posed to synchronize HPC and mPFC activities (Herkenham, 1978; Hoover and Vertes, 2012; Varela et al., 2014). The NR is bidirectionally connected to the HPC and mPFC (Vertes et al., 2007; Hoover and Vertes, 2012), and numerous studies have demonstrated that the three regions form a network involved in mnemonic processes and consolidation (Dolleman-van der Weel et al., 2009; Loureiro et al., 2012; Wheeler et al., 2013; Xu and Südhof, 2013; Pereira de Vasconcelos and Cassel, 2015; Hallock et al., 2016; Ali et al., 2017). Recent studies show that NR neurons' firing participates in fear memory generalization (Wheeler et al., 2013; Xu and Südhof, 2013), working memory (Davoodi et al., 2009; Hembrook et al., 2012; Hallock et al., 2013, 2016; Duan et al., 2015; Griffin, 2015), and spatial navigation (Jankowski et al., 2014, 2015; Ito et al., 2015). The bidirectional projection of the NR to HPC and mPFC led to the hypothesis that the activity of NR neurons could influence the finer time scale of the interactions between these regions (Varela et al., 2014; Pereira de Vasconcelos and Cassel, 2015). However, how NR neuronal firing shapes HPC–mPFC interactions is not known.

To address the possibility that NR neurons are involved in gamma synchronization between HPC and mPFC, we recorded and manipulated the NR–mPFC–HPC circuit during slow oscillations under anesthesia, which resembles sleep patterns and provide long periods for analysis. We confirmed the gamma synchronization during natural slow-wave sleep and show that NR neurons control long-range gamma synchronization between the HPC and mPFC during slow oscillations.

Materials and Methods

Ethics

All experiments were conducted in accordance with Aix-Marseille Université and Inserm Institutional Animal Care and Use Committee guidelines. The protocol was approved by the French Ministry of National Education, Superior Teaching, and Research, approval number 01451-02. All surgical procedures were performed under anesthesia and every effort was made to minimize suffering.

Experimental model and subject details

A total of 16 rats were used in this study. In seven male Wistar Han IGS rats (250–400 g; RRID:RGD_2308816; Rats A–G) data were simultaneously collected from the mPFC, NR, and HPC (CA1 SP) under anesthesia. In four other anesthetized rats (Rats H–K), both NR and HPC (CA1) were recorded simultaneously. In an additional group of three rats (Rats L–N), a local injection of a fluorophore-conjugated muscimol was delivered in the NR and data from the mPFC and the HPC (CA1) was simultaneously acquired. Finally, only the mPFC and the HPC (CA1) were recorded during natural sleep in one adult male Long–Evans rat (Rat O; RRID:RGD_2308816), and one adult male rat (Wistar Han IGS; Rat P). All the animals were maintained on a 12 h light/dark schedule with lights off at 8:00 pm.

Animal surgery

Rats (A–N) were anesthetized with urethane (1.5 g/kg, i.p.; Sigma-Aldrich) and ketamine/xylazine (20 and 2 mg/kg, i.m.) with additional doses of ketamine/xylazine (2 and 0.2 mg/kg) given during the electrophysiological recordings. Heart rate, breathing rate, pulse distension, and arterial oxygen saturation were also monitored with an oximeter (MouseOX; StarrLife Sciences) during the duration of the experiment to ensure the stability of the anesthesia and monitor the vital constants. The head was secured in a stereotaxic frame and the skull was exposed and cleaned. Two miniature stainless-steel screws, driven into the skull above the cerebellum, served as ground and reference electrodes. Up to three craniotomies were performed to target, from bregma: the prelimbic area of the mPFC at +3 mm AP and +0.8 mm ML; the CA1 field of the intermediate HPC at −5.6 mm AP and +4.3 mm ML; and the NR at −1.8 mm AP and −2 mm ML. These coordinates were chosen with respect to the known anatomical connectivity between mPFC, HPC, and NR (Dolleman-Van der Weel et al., 1997). The recap list below informs on the structures targeted, the devices used, and their depth (DV coordinates from brain surface):

In Rats A to G, we recorded the mPFC (Edge 5 mm 32-site silicon probe at [−2.5 −3.1] mm to reach layer 5; NeuroNexus Technologies), NR (Edge 10 mm 32-site silicon probe at −7.2 mm with a 15.5° ML angle; NeuroNexus Technologies), and HPC (50 μm tungsten electrode at −2.2 mm to reach CA1 stratum pyramidale).

In Rats H to K, we recorded the NR (same as previously in Rats A–G) and HPC (linear 6 mm 32-site or Edge 5 mm 32-site silicon probe; NeuroNexus Technologies) at [−2.8 −3.0] mm placed perpendicularly to the CA1 field from stratum oriens to stratum lacunosum moleculare.

In Rats L to N, we recorded the mPFC (same as in Rats A–G) and HPC (same as for Rats H–K), while the NR was infused with the fluorophore TMR-X-conjugated GABA_A agonist, BODIPY-Muscimol (Invitrogen), which has similar electrophysiological and behavioral effects as the classic form of muscimol. Injection of muscimol (GABAa agonist) induces an inactivation of neurons without targeting neuronal processes en-passant (Allen et al., 2008; Cholvin et al., 2013). The injection needle was inserted in the NR (using the same DV coordinates as the probes) and 0.70 nm of muscimol in 0.3 μl of PBS (Cholvin et al., 2013) was delivered over 60 s through a micropump (UltraMicroPump, WPI). The needle was left in place for 3 additional minutes to allow for adequate diffusion of the drug, and then carefully removed.

All implanted devices were mounted on individual stereotaxic manipulator and lowered independently using a motorized descender (IVM, Scientifica). The online positioning of the electrodes was refined by using the presence of unit activity in cell body layers and the presence of ripples [100 200] Hz in stratum pyramidale.

Rats O and P were anesthetized using only isoflurane 2% in 1 L/min of O₂. The surgical procedure (Csicsvari et al., 2003) was the same as described above except that recording electrodes were mounted on a custom-built (Rat O) or commercial (Rat P; Cambridge NeuroTech) microdrives fixed on the skull and secured in a copper-mesh hat. In Rat O, the mPFC and HPC (CA1) were simultaneously recorded with a 50 μm tungsten electrode (same coordinates as previously described) and a Poly2 5 mm 32-site silicon probe (NeuroNexus Technologies; as described in Rats H–K), respectively. In Rat P, mPFC and HPC were recorded with two-shank 6 mm 32-site silicon probes (Cambridge NeuroTech; as described in Rats L–N). They were progressively moved until they reached their targets and then adjusted every day to optimize yield and stability. A camera was placed next to the cage to monitor sleep and the video signal was synchronized with electrophysiological recordings.

Data collection and initial analysis

The extracellular signals were amplified (1000×), bandpass filtered (1 Hz to 5 kHz) and acquired continuously at 32 kHz with a Digital Lynx (NeuraLynx; 20 kHz with Amplipex for Rat O) at 16-bit resolution. Raw data were preprocessed using NEUROSUITE (Hazan et al., 2006; http://neurosuite.sourceforge.net/; RRID:SCR_008020). The signals were downsampled to 1250 Hz for the local field potential (LFP) analysis. Spike sorting was performed automatically, using KLUSTAKWIK (Harris et al., 2000; http://klustakwik.sourceforge.net/; RRID:SCR_008020; RRID:SCR_014480), followed by manual adjustment of the clusters, with the help of autocorrelogram, cross-correlogram, and spike waveform similarity matrix with KLUSTERS software (Hazan et al., 2006; RRID:SCR_008020). After spike sorting, the spike features of units were plotted as a function of time, and the units with signs of significant drift over the period of recording were discarded. Moreover, only units with clear refractory periods and well defined cluster were included in the analyses. Recording sessions were divided into brain states of theta and slow oscillation periods. The epochs of stable theta or slow oscillation periods were visually selected from ratios of the whitened power in the theta band [3 6] Hz and the power of neighboring bands [1 3] and [7 14] Hz of CA1 stratum pyramidale LFP and from the ratio of the whitened power in the slow oscillation band [0.5 2] Hz and the power of neighboring band [20 30] Hz of mPFC layer 5 LFP, respectively and were assisted by visual inspection of the raw traces (Quilichini et al., 2010).

Single unit identification

Neurons were assigned as “NR neurons” by determining the approximate location of their somata relative to the recordings sites (with the largest-amplitude unit corresponding to the putative location of the soma), the known distances between the recording sites, the histological reconstruction of the recording electrode tracks and subsequent estimation of the recording sites. The neurons recorded from sites located near the close contour of the NR were discarded. Neurons located at a minimal distance of 200 μm of the NR border and located within contours of the ventromedian, submedian or anteromedian thalamic nuclei were classified as “other thalamic neurons” and used in the analysis presented in Figures 5 and 6. Using this method, 126 of the 237 recorded units were classified as NR neurons, and 46 of the 237 units as “other thalamic neurons”.

Figure 5.

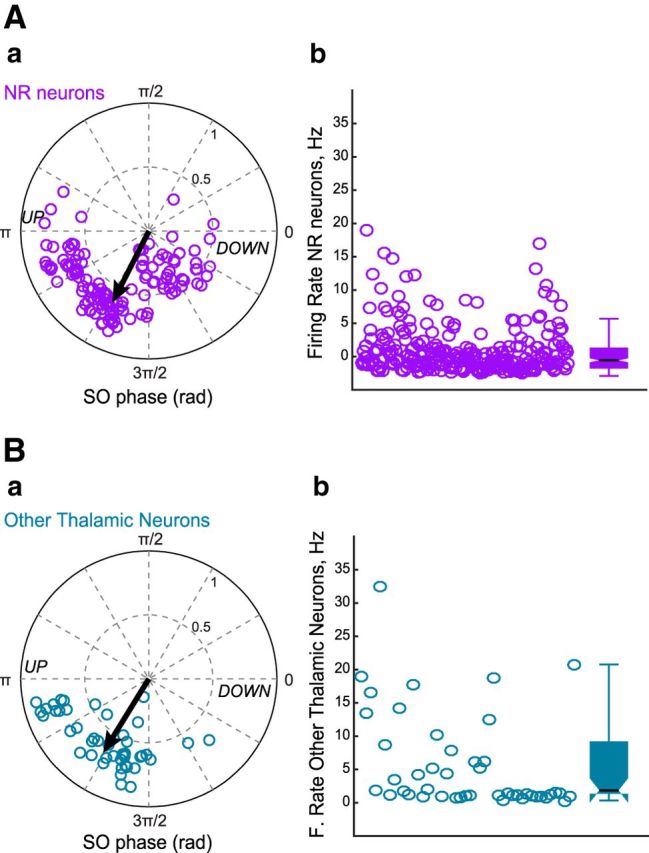
Firing properties of thalamic neurons. Aa, Polar diagram of preferred phase and modulation strength of NR neurons referenced to slow oscillation cycle. The black arrow indicates the mean phase and strength of modulation (Rayleigh statistics). Ab, Mean firing rates calculated during slow oscillation episodes for NR neurons. The box plots represent the grouped data statistics for the 126 NR neurons recorded (n = 7 experiments). Ba, Polar representation of preferred phase and modulation depth for neurons belonging to thalamic nuclei neighboring NR (n = 46, 4 experiments) referenced to slow oscillation cycle. Bb, Mean firing rates calculated during slow oscillation episodes for other thalamic neurons (grouped data statistics).

Figure 6.

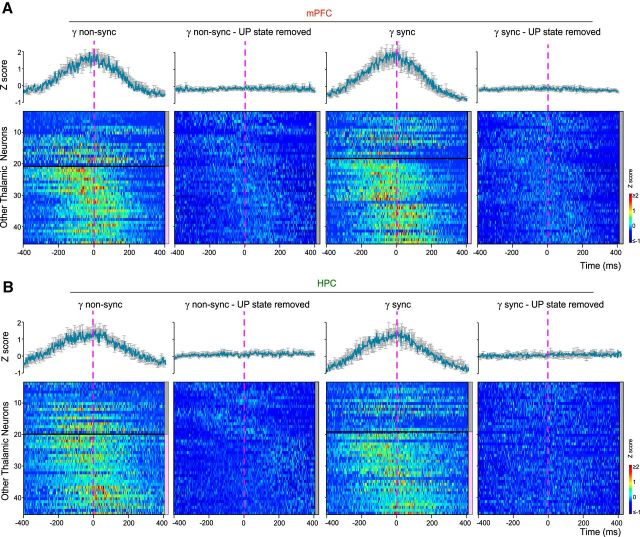
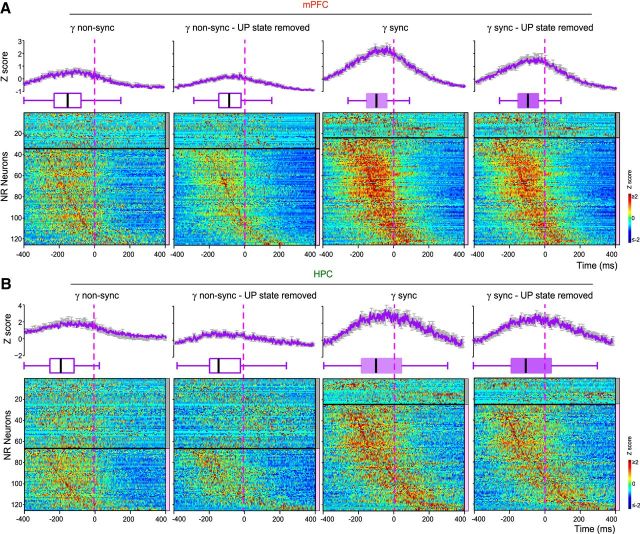
Dynamics of other thalamic neurons firing before gamma onset. A, Peri-gamma burst z-scored firing probability raster plots and average (shaded error bars) firing probability curves for other thalamic neurons with respect to non-sync and sync mPFC gamma burst onset (dashed vertical line), with and without the UP state contribution (UP state removed). The neurons are separated into two subgroups (horizontal black line) based on the significant increase of their firing with respect to gamma bursts, as indicated by the color scale (right): gray: p ≥ 0.05; pink: p < 0.05 (see Materials and Methods). The increase in firing disappears when the influence of the UP state is removed. B, Peri-gamma burst z-scored firing probability raster plots and firing probability curves for the same neurons as in A with respect to HPC gamma burst onset. The increase in firing disappears when the influence of the UP state is removed.

Burst index denotes the propensity of neurons to discharge in bursts. We estimated the amplitude of the burst spike autocorrelogram (1 ms bin size) by subtracting the mean value between 40 and 50 ms (baseline) from the peak measured between 0 and 10 ms. Positive burst amplitudes were normalized to the peak and negative amplitudes were normalized to the baseline to obtain indexes ranging from −1 to 1. Neurons displaying a value of 0.6 were considered bursting.

Putative principal cells and interneurons identification.

Putative principal cells and interneurons were separated based on their auto-correlograms, waveforms and mean firing rates (Quilichini et al., 2010). The combination of trough-to-peak latency (“half-width”), the asymmetry index of the filtered [0.8–5] kHz spike waveform, and firing rate provided the best separation between putative principal cells and interneurons. We used the hyperplane that divided the population in two to separate units into putative interneurons and putative pyramidal cells (see Fig. 3B). No attempt was made to distinguish between the many interneuron classes.

Figure 3.

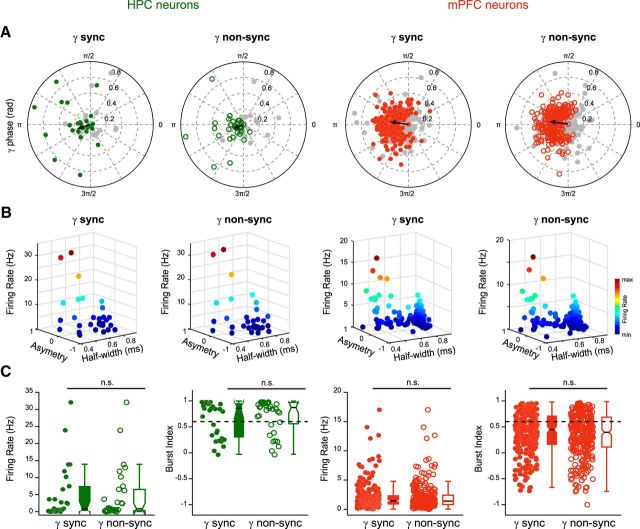
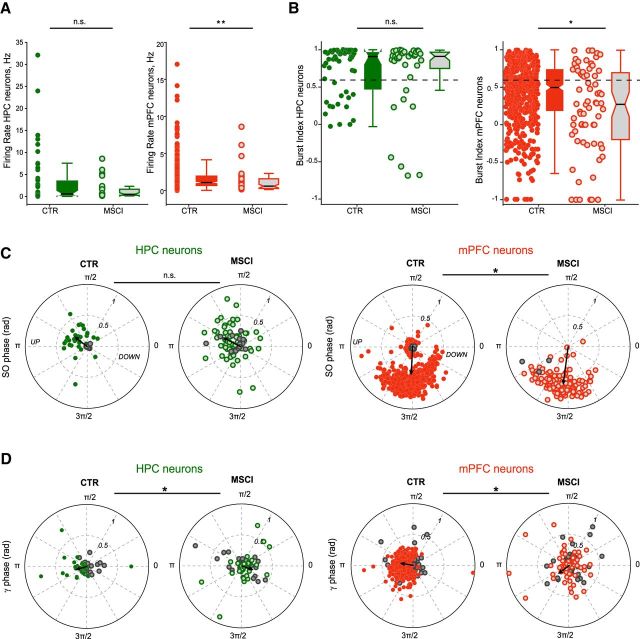
Gamma bursts entrain local neuronal populations. A, Polar plots of preferred phase and modulation depth of HPC (green) and mPFC (red) neurons referenced to sync and non-sync gamma bursts (grouped data, n = 8). The gray circles correspond to nonsignificantly entrained neurons (Rayleigh test, p ≥ 0.05). The black arrow indicates the mean phase and strength of modulation for the significantly entrained neurons only (gamma cycle peak = 0°). There was no significant difference in the mean phase and strength of the modulation between sync and non-sync groups (circular ANOVA, p ≥ 0.05, respectively). B, Relationship between spike half-width, asymmetry, and firing rate for the HPC and mPFC units significantly entrained by sync and non-sync gamma bursts as defined in A. Note the division into two groups, separating putative excitatory (right) from inhibitory (left) neurons (see Materials and Methods). C, Firing rates and burst indices of HPC and mPFC units significantly entrained by sync gamma bursts were no different from those entrained by non-sync gamma bursts (Wilcoxon test, p ≥ 0.05) indicating that both types of bursts did not segregate different neuronal populations.

Histological analysis

At the end of the recording, the animals were injected with a lethal dose of pentobarbital Na (150 mg/kg, i.p.) and perfused intracardially with 4% paraformaldehyde solution in 0.12 m phosphate buffer (PB), pH 7.4. The brains were removed and postfixed at 4°C overnight. They were then rinsed in PB, and sliced into 60-μm-thick coronal sections by a Vibratome. The position of the electrodes was revealed by the presence of DiIC18(3) (Interchim), which was applied on the back of the electrodes before insertion and confirmed histologically on fluorescent Nissl-stained sections (Neuro-Trace 500/5225 Green Fluorescent Nissl Stain, Invitrogen). Only experiments with the appropriate position of the electrodes were used for analysis. For the inactivation experiments, the fluorescent muscimol allows us to visualize the spread of the drug in the NR on fluorescent Nissl-stained sections and only experiments with the correct target sites were included in data analysis.

Spectral analyses

Spectral analyses were performed on pre-whitened LFPs using direct multitaper estimates (Quilichini et al., 2010). Slow oscillation periods analyzed had a median duration of 70 min for Rats A–K (minimum duration = 43 min, maximum duration = 99 min), and median duration of 12 min of natural slow-wave sleep for Rats O and P (minimum duration = 3 min, maximum duration = 31 min). In inactivation experiments, slow oscillation epochs of 30 min (15 min after the injection (Edeline et al., 2002) were used for comparing spectra of control and muscimol LFPs. For spectral analysis of oscillatory patterns, we used a modified version of the multitaper FFT MATLAB package by Mitra and Pesaran (1999): FFT window size of 4 s, three to five tapers, frequency bins = 0.15 Hz, no overlap between successive windows, time bandwidth = 3 (Mitra and Pesaran, 1999; Quilichini et al., 2010). The coherence between the LFPs in mPFC and HPC was assessed by spectral methods using custom-written MATLAB (RRID:SCR_001622; RRID:SCR_008020) scripts. We used the previously defined “comodugram” analysis (Buzsáki et al., 2003; Isomura et al., 2006; Quilichini et al., 2010; Sullivan et al., 2011) to assess the power-power correlation of HPC and mPFC LFPs for each pair of frequencies between 30 and 150 Hz using the FFT parameters detailed previously. The correlation coefficients between normalized spectral power values of the respective signals at all pairs of frequencies were calculated with the “corrcoef.m” MATLAB function.

To quantify slow oscillation phase-gamma amplitude coupling, the power of the gamma frequency band [30–90] Hz was calculated in short [50–100] ms overlapping windows, correlated with the instantaneous phase of slow oscillations (20° bins), obtained from the Hilbert transformation of the [0.5–2] Hz filtered LFP and initially checked for circular uniformity (von Mises distribution).

Gamma bursts were detected from HPC CA1 stratum pyramidale and mPFC layer 5 LFPs with the MATLAB plugin RippleLab (Navarrete et al., 2016; https://github.com/BSP-Uniandes/RIPPLELAB; RRID:SCR_015876) using the short line-length detector (frequency range = [30 90] Hz, filter window = 30 ms for each 3 min epoch, threshold percentile = [65 80], minimum event duration = 90 ms). Automatically detected events were individually reviewed and refined manually. The normalized peak power and mean frequency of each detected burst was extracted from the wavelet decomposition.

Synchronized gamma bursts were defined as all HPC and mPFC events showing latencies greater than the ones obtained by chance (nonparametric significance test based on jittering of event timings, see section Statistics), e.g., above the 95% confidence intervals obtained after 1000 surrogate tests (n = 1000 surrogates), in the HPC–mPFC gamma burst cross-correlations. The total number of synchronized bursts in mPFC and HPC are not always identical. In some instances, two gamma bursts occurred successively in the HPC and were classified as “synchronized” with a single burst in mPFC, which resulted in a difference in total burst count. The other events were tagged as not synchronous (no sync) events.

To remove the influence of slow oscillation entrainment on gamma bursts (Figs. 2Eb,Ed, 7Eb), we first detected DOWN states from the whitened mPFC LFP. They were defined as periods where the processed normalized signal was at least 0.75 SD below the mean for at least 100 ms. The remaining epochs (100 ms of minimal duration) were considered as “UP states”. We then created a set of surrogate data by selecting UP states associated with both mPFC and HPC gamma bursts. First, we computed the distribution of the actual mPFC gamma burst onset latencies from the UP state beginning. Second, we randomly chose an identical number of UP states and attributed in each a virtual mPFC gamma onset based on their true distribution. We then recomputed the cross-correlation of the surrogate mPFC gamma onsets with HPC gamma burst onsets for anesthesia, natural slow-wave sleep (SWS), and inactivation experiments. This procedure keeps the time lag of each event relative to the onset of the UP state fixed but changes the identity of the UP state randomly for each event. An average of such shuffled gamma-triggered firing probability (1000 shuffled events) gives an estimate of the gamma cross-correlation or firing probability for each unit that is independent of the slow oscillation modulation (Isomura et al., 2006). The same procedure was used to remove the influence of slow oscillation entrainment on thalamic neurons firing (see Figs. 4, 6), with the difference that we created a set of surrogate data by selecting UP states not associated with gamma bursts, computed the distribution of the actual gamma burst onset latencies from the UP state beginning then randomly chose an identical number of UP states and attributed in each a virtual gamma onset based on the true distribution. We then recomputed the cross-correlation of the surrogate gamma onsets with NR and “other thalamic” neurons action potentials.

Figure 2.

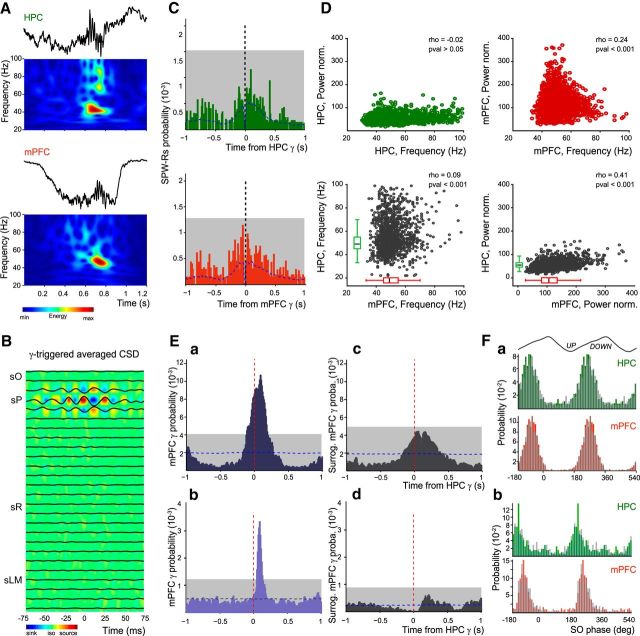
Synchronous gamma bursts in HPC and mPFC during the slow oscillation state. A, Example of gamma bursts simultaneously recorded in HPC and mPFC and their corresponding normalized wavelet transforms. B, The gamma-triggered average CSD (computed from a template experiment) depicts an alternation of sinks and sources only around SP, suggesting a local generation of gamma bursts. sO, stratum oriens; sR, stratum radiatum; sLM, stratum lacunosum moleculare. C, Cross-correlation between HPC SPW-Rs and gamma bursts (grouped data, n = 8) detected in HPC (green bars) and in mPFC (red bars). Dashed vertical lines indicate zero-time lag; blue dashed lines indicate the mean of time-jittered gamma bursts. Note that no bin in both cross-correlograms is above the chance level (gray box; 0.01% significance level). D, Correlations between frequency and normalized power of HPC and mPFC gamma bursts (grouped data, n = 8). Note the low values of the correlation coefficients (rho; Pearson correlation). Ea, Cross-correlation between mPFC and HPC gamma bursts, using HPC gamma bursts as reference (dashed red line; grouped data, n = 8 animals), showing a significant correlation peak during slow oscillations in anesthesia. Dashed blue line: mean of time-jittered HPC gamma; gray box: 0.01% significance level (see Materials and Methods). Eb, Predicted cross-correlation between the surrogate mPFC gamma onsets (see Materials and Methods) with the regular HPC gamma onsets (grouped data, n = 8). Note the disappearance of the peak correlation. Ec, Cross-correlation between mPFC and HPC gamma bursts during natural slow-wave sleep (grouped data, n = 2 animals). Ed, Predicted cross-correlation between the surrogate mPFC gamma onsets and HPC ones during natural sleep. Note again the absence of correlation. F, Distribution histograms of gamma burst entrainment by slow oscillation phase for HPC and mPFC bursts during (Fa) anesthesia slow oscillations and (Fb) natural SWS (grouped data, n = 8). The plain bars (green, HPC; red, mPFC) represent the distribution of sync gamma events, and the overlaid gray bars correspond to the non-sync gamma bursts.

Figure 7.

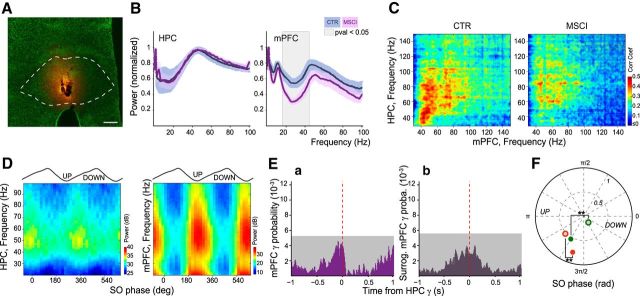
Chemical inactivation of NR abolishes the gamma synchrony. A, Visualization of the extent of BODIPY-Muscimol (MSCI: 0.7 nm in 0.3 μl; orange staining) injection in the NR (dashed line shows the NR contours) over green fluorescent Nissl-stained section of a template experiment. Scale bar, 250 μm. B, Normalized power spectra of mPFC and HPC LFPs in control (CTR; blue curves; n = 7) compared with MSCI (pink curves; n = 3) conditions. The ± SEM is presented as the lighter blue (control) and lighter pink (MSCI) bands. Gray zone: p < 0.05, t test. C, Mean comodugrams showing the power–power correlation between HPC and mPFC LFPs in control (left; n = 7) and MSCI (right; n = 3) conditions. Note the decrease in correlation in the [30 90] Hz band. D, Gamma amplitude-slow oscillation phase modulation plots of LFPs in HPC and mPFC during NR inactivation calculated from a template experiment. Note the drastic decrease in the modulation of HPC gamma and the phase shift compared with control (Fig. 1C). E, Cross-correlation between (Ea) mPFC gamma bursts and (Eb) the surrogate mPFC gamma onsets (see Materials and Methods) with respect to HPC gamma bursts (dashed red line) during NR inactivation. There was no significant peak in the correlation compared with the control condition (Fig. 2Ea) and the predicted cross-correlation did not show any correlation either. Gray box: 0.01% significance level; grouped data, n = 3. F, Polar plot of the mean preferred slow oscillation phase and modulation strength of HPC (green) and mPFC (red) gamma bursts in control (filled circles; n = 7) and MSCI experiments (open circles; n = 3). NR inactivation induced a significant phase shift (circular ANOVA, p < 0.001 for both comparisons) and a decrease of modulation strength (t test, p < 0.001 for both) of gamma bursts in both structures.

Figure 4.

Dynamics of NR neurons firing before gamma onset. A, Peri-gamma burst z-scored firing probability raster plots for all NR neurons, average (shaded error bars) firing probability curves and statistical boxes for all the NR neurons firing with respect to non-sync, sync, with or without the UP state contribution (UP state removed) mPFC gamma burst onset (dashed vertical line). The neurons are separated into two subgroups (horizontal black line) based on the significant increase of their firing with respect to mPFC gamma bursts, as indicated by the color scale (right): gray: p ≥ 0.05, pink: p < 0.05 (see Materials and Methods). The early increase of the firing in the significant group [−200 0] ms before sync gamma onset subsists after removing the UP state influence. Such behavior is less prominent for the non-sync events. B, Peri-gamma burst z-scored firing probability raster plots for all NR neurons, average firing probability curves and statistical boxes for all the NR neurons firing with respect to gamma bursts detected in HPC (dashed vertical line) constructed as in A.

The procedure of SPW-Rs detection in the HPC stratum pyramidale LFP was based on those described previously (Isomura et al., 2006). Briefly, the LFP was digitally bandpass filtered [80 250] Hz, and the power (root-mean-square) of the filtered signal was calculated. The mean and SD of the power signal were calculated to determine the detection threshold. Oscillatory epochs with a power of 5 or more SD above the mean were detected. The beginning and the end of oscillatory epochs were marked at points where the power fell <0.5 SD.

Current source density analysis

Current source density (CSD) analysis of the simultaneously recorded potentials from strata oriens to lacunosum moleculare (LM) in CA1 HPC was used to eliminate volume conduction and reveal the spatial segregation of gamma bursts. CSD was computed as the second spatial derivative of the recorded LFPs and smoothed spatially with a triangular kernel (Quilichini et al., 2010). Activity from the malfunctioning sites was eventually interpolated from the neighboring sites.

Statistics

All results reported are based on a significance threshold α = 0.05 unless otherwise stated and all groups included enough samples to enable rejection of the null hypothesis at that level. We used nonparametric testing in most cases: two-sided paired testing Wilcoxon's signed-rank test for paired groups and two-sided Mann–Whitney U test for unpaired groups, and provided the median value for each group. For data with normal distribution (tested with Lilliefors test), we used two-tailed t test and expressed the mean values ± the SD around the mean (SEM).

Circular statistics.

The phase of the mPFC slow oscillations was determined from the filtered LFP in the [0.5 2] Hz. The instantaneous phase was computed as the angle of the Hilbert transform, and the distribution of the phases in each session was tested for uniformity before analysis. To establish the gamma-phase modulation of units, the gamma bursts in HPC and mPFC during slow oscillation epochs were concatenated, and the instantaneous phase of gamma oscillation was estimated by Hilbert transform of the [30 90] Hz filtered signal. Using linear interpolation, a value of phase was assigned to each event (units or gamma onsets). The slow oscillation and gamma phase modulation of events were determined by Rayleigh circular statistics; p < 0.05 was considered significant. Circular uniformity of the data was first assessed with a test for symmetry around the median (Berens, 2009) and group comparison tests of circular variables were performed using circular ANOVA for uniformly distributed data and using a nonparametric multisample test for equal medians “CM-test”, similar to a Kruskal–Wallis test, for non-uniformly distributed data (Berens, 2009; https://philippberens.wordpress.com/code/circstats), and p < 0.05 was considered significant.

Cross-correlations and jittering.

A nonparametric significance test based on jittering was used to assess significance of cross-correlations of point processes (e.g., gamma burst onset and units), as described previously in detail for spike trains (Fujisawa et al., 2008; Quilichini et al., 2010; Amarasingham et al., 2012). In brief, for each pair, the referred point-process in the original dataset was randomly and independently jittered on a uniform interval of [−100 +100] ms, to form a surrogate dataset. The process was repeated independently 1000 times to form 1000 such surrogate datasets. Then, the cross-correlograms were constructed for surrogate datasets as a function of latency across the interval [−400 +400] ms. Global bands at 99% acceptance level were constructed for the cross-correlogram from the maximum and minimum of each jitter surrogate cross-correlogram across the interval [−400 +400] ms. The latency peak in the original cross-correlogram was determined to be statistically significant (at p < 0.01) when the counts in the cross-correlogram were atypical over at least three bins with respect to the upper global band.

Results

Synchronized gamma bursts between HPC and mPFC during slow oscillations

We first asked whether synchronized gamma oscillations were occurring during slow oscillations in both HPC and mPFC. We used anesthesia conditions to obtain long duration recordings and reach strong statistical significance. The protocol used here provided an alternation between slow and theta oscillations, which resemble the oscillatory patterns of SWS and paradoxical sleep, respectively (Isomura et al., 2006; Clement et al., 2008; Quilichini et al., 2010). During slow oscillations, the frequency content of the mPFC and HPC LFPs measured in layer V and CA1 stratum pyramidale (sP) displayed peaks in the dominant frequency (∼1 Hz) and in the gamma range (30 90 Hz; Fig. 1Aa), respectively. Power-power comodugrams revealed a large correlation between HPC and mPFC LFPs in the (30 90 Hz) gamma band (Fig. 1Ab). In contrast, there was no correlation in the gamma band between the two structures during theta oscillations (Fig. 1B). Gamma power was strongly modulated by the slow oscillation phase as it was locked to the trough and ascending phase of the cycle, i.e., during the UP state, in both structures (Fig. 1C).

Figure 1.

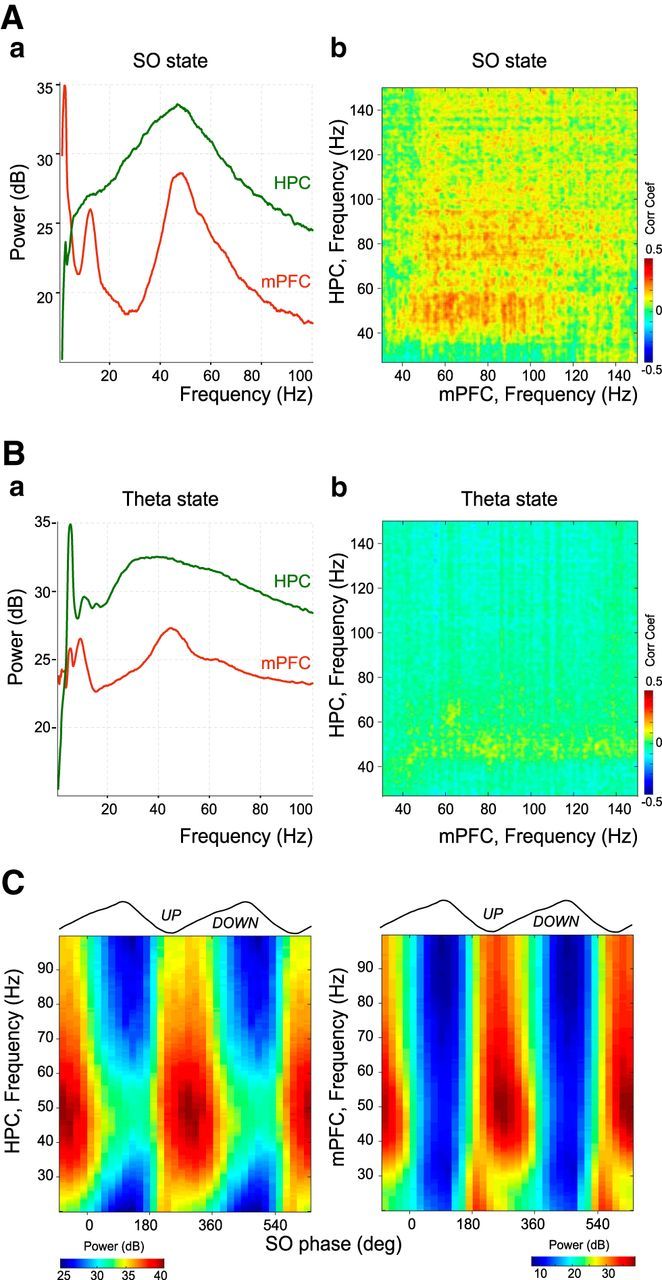
HPC and mPFC interactions during theta and slow oscillation states. Aa, Whitened power spectra of mPFC and HPC LFPs during slow oscillation state (sO) from a template experiment. Ab, Comodugram describing the power relationship between HPC and mPFC LFPs shown in Aa in the gamma band. The correlation coefficient is color-coded. Ba, Whitened power spectra of mPFC and HPC LFPs during theta state from the same template experiment as in A. Bb, Comodugram between HPC and mPFC LFPs shown in Ba in the gamma band. Note the absence of correlation compared with the slow oscillation state (sO). C, Gamma amplitude-slow oscillation phase modulation plots of LFPs in HPC and mPFC from the same template experiment as in A. The gamma power dominated the trough and beginning of the ascending phase of mPFC slow oscillations.

These periods of large gamma power corresponded, at least in part, to gamma bursts in the LFP (median frequency mPFC = 49 Hz, median duration: 156 ms, present in 13 ± 2% of UP states, 3740 bursts; HPC = 52 Hz, 167 ms, present in 11 ± 2% of UP states, 3605 bursts; n = 8; Fig. 2A). CSD confirmed the presence and the segregation of these gamma bursts in sP of the CA1 area, with an alternation of sinks and sources (Fig. 2B; n = 4). Bouts of gamma power also occur in strata radiatum and LM at different phases of the slow oscillations (Isomura et al., 2006). Recordings spanning the CA1 hippocampus from strata oriens to LM showed that gamma bursts were not cooccurring with any other gamma events in other strata (Fig. 2B; n = 4). SPW-Rs are another prominent type of hippocampal activity during slow oscillations (Buzsáki, 2015). Although both gamma bursts and SPW-Rs are modulated by the phase of the slow oscillations (Sirota and Buzsáki, 2005; Isomura et al., 2006; Fig. 1C), their co-occurrence was very rare during slow oscillations (HPC: 2.6 ± 0.9%; mPFC: 3.0 ± 1.0%, over a [−500 500] ms window around gamma onset; Fig. 2C). Together these results establish that SP gamma bursts during slow oscillations constitute a specific pattern of activity complementing the previously described other hippocampal gamma oscillations and sharp wave-ripples.

There was only a weak relationship between the power and frequency of gamma bursts within HPC and mPFC, as well as between them (Fig. 2D), but there was no correlation between the duration of HPC and mPFC bursts (p = 0.3452; data not shown). Most gamma bursts occurred during UP states (97 ± 1% for mPFC; 82 ± 4% for HPC) and many hippocampal bursts co-occurred with mPFC ones (59 ± 4%). Many of these bursts (39% in HPC, 37% in mPFC) were significantly synchronized (i.e., delays greater than the ones obtained by chance from a nonparametric significance test based on jittering of event timings; p < 0.001, see Materials and Methods) with a mPFC gamma burst onset probability peaking at ∼100 ms ([−110 190] ms range) after the onset of the HPC gamma burst (Fig. 2Ea). Whether synchronized (sync; as defined previously) or not (non-sync), all gamma bursts were phase-locked to the trough and ascending phase of the slow oscillations (HPC: sync = 238 ± 2°, non-sync = 243 ± 1°, p = 0.1255; mPFC: sync = 254 ± 1°, non-sync = 253 ± 1°, p = 0.4882; circular ANOVA; Fig. 2Fa). To remove the influence of the UP state, we computed a predicted cross-correlation revealing how often mPFC and HPC gamma bursts co-occur because of the UP state entrainment (see Materials and Methods). The cross-correlation between the surrogate mPFC gamma onsets with the regular HPC gamma onsets indicated no significant synchronization (Fig. 2Eb). This shows that the fine time correlation between mPFC and HPC gamma bursts is independent of the UP state influence.

We found similar results during natural SWS with 52% (302/582) of sync events in HPC, 54% (315/585) in mPFC, and a similar latency (∼90 ms, [50 130] ms range) between HPC and mPFC gamma bursts (2 animals; Fig. 2Ec,Ed). Phase locking was also similar (Fig. 2Fb), although gamma bursts occurred earlier in the cycle (HPC: sync = 222 ± 3°, p < 0.001, non-sync = 223 ± 4°, p = 0.012; mPFC: sync = 223 ± 2°, p < 0.001, non-sync = 225 ± 1°, p < 0.001, circular ANOVA). CSD revealed a similar alternation of sinks and sources in sP (data not shown).

Gamma burst synchronization may provide a functional substrate for information transfer between HPC and mPFC during slow oscillations. This raises the question of the mechanisms underlying this coupling. Gamma oscillations are locally produced, and therefore we first reasoned that HPC and mPFC neurons would display different firing signatures during sync and non-sync gamma bursts. More than half of the neurons were entrained (p < 0.05, Rayleigh test) by the gamma oscillations in each structure (HPC: 29/43, 68%, for sync bursts and 33/52, 64%, for non-sync bursts; mPFC: 266/495, 54%, for sync bursts and 279/495, 56% for non-sync bursts; Fig. 3A). The phase modulation was similar for both neuronal populations with a preference for the trough of the gamma cycle (mean phases: HPC: 195 ± 10° for sync bursts, 201 ± 9° for non-sync bursts; mPFC: 169 ± 2° for sync bursts, 170 ± 2° for non-sync bursts; Fig. 3A). Furthermore, we distinguished putative principal neurons (pPYR) and interneurons (pIN) and found that an equivalent number of cells in HPC (12 pIN, 17 pPYR for sync bursts; 11 pIN, 22 pPYR for non-sync bursts) and in mPFC (44 pIN, 222 pPYR for sync bursts; 43 pIN, 236 pPYR for non-sync bursts) was significantly entrained (as defined by the Rayleigh statistics shown in Fig. 3A,B), by sync or non-sync bursts. However, their firing pattern did not correlate with either sync or non-sync bursts (HPC: firing rates p = 0.6948, burst indices p = 0.6948; mPFC: firing rates p = 0.5641, burst indices p = 0.4374; Wilcoxon test; Fig. 3C). Although HPC and mPFC cells display classical features of entrainment by gamma oscillations, we did not find differences in their activity during sync and non-sync bursts suggesting that they may not participate in the synchronization process between HPC and mPFC.

Nucleus reuniens neurons fire specifically before gamma onset

What could be at the origin of such synchronization? Numerous studies show that the thalamus plays a key role in coordinating activity between HPC and mPFC (Xu and Südhof, 2013; Pereira de Vasconcelos and Cassel, 2015; Latchoumane et al., 2017). In particular, because of its specific bidirectional connectivity pattern with these structures, the NR is ideally posed to act as a nodal hub to influence hippocampo–prefrontal interactions (Hoover and Vertes, 2012; Cassel et al., 2013; Varela et al., 2014). We tested whether NR neurons display specific firing patterns when gamma bursts occur. To this aim, we performed simultaneous LFP and unit recordings in the HPC, mPFC, and NR (n = 7). Most NR neurons increased their firing −98.4 ms before the sync gamma burst onset (median lag for 100/126 neurons with significant firing increase before mPFC gamma bursts; Fig. 4A; see B, −70.9 ms prior HPC gamma burst onset). The firing increase was less prominent during non-sync gamma bursts, their peak firing before gamma onset was delayed and their increase of firing less robust (median lag: −152.4 ms for 93/126 neurons; p = 0.0014; two-sample Kolmogorov–Smirnov test; mean z-scored firing probability: non-sync = 0.52 ± 0.03, sync = 1.09 ± 0.05; p < 0.001, two-sample t test; Fig. 4A; see B, −192.0 ms prior the HPC gamma burst onset).

NR neurons were also entrained by the slow oscillation phase, preferentially during the UP state (mean phase = 246 ± 4°, mean r = 0.58 ± 0.01, 126/126 significantly modulated neurons, p < 0.05, Rayleigh test; median firing = 2.5 Hz; Fig. 5A), and because of this the early firing described above may only correspond to slow oscillation-driven firing. To assess the relationship between NR neuronal firing and gamma bursts in HPC and mPFC, we removed the influence of the UP state. To do so, we created a set of surrogate data by selecting UP states not associated with gamma bursts in either mPFC or HPC, attributed each a virtual gamma onset and computed the correlation between NR neuron firing and virtual gamma onsets, then subtracted this gamma-independent firing to the previously computed firing. The results still showed a significant increase of the firing probability of NR neurons before sync gamma onset (mean z-scored firing probability: 0.85 ± 0.02 for 100/126 neurons; Fig. 4A; see B, 0.80 ± 0.04 prior HPC gamma burst onset). Thus, early firing of NR neurons may play a role in coordinating gamma bursts and cell firing in HPC and mPFC, independently from their entrainment by the UP state. NR neurons behavior appeared to be specific to gamma bursts because no increase of firing probability was detected prior sharp wave-ripples (data not shown).

As a negative control, we took advantage of four experiments in which the silicon probe did not reach the NR, but recorded the neighboring thalamic nuclei, which are not known to project to both mPFC and HPC as NR does. Some neurons displayed an increase of their firing around mPFC or HPC gamma burst onsets, whether sync (26/46 neurons) or not (30/46) (Fig. 6A,B). They also exhibited a strong modulation of their firing by the slow oscillations, reaching its peak at the beginning of the UP state (mean phase: 228 ± 4°, mean R: 0.67 ± 0.02; 46/46 neurons significantly entrained, p < 0.001, Rayleigh test; median firing = 1.6 Hz; Fig. 5B). Once this modulation was removed the increase in firing around the gamma bursts disappeared (mean z-scored firing probability < 0.001; Fig. 6A,B). Together these results show that the early firing prior sync gamma bursts, and to a lesser extent to non-sync ones, is specific to NR neurons.

Nucleus reuniens activity is necessary for mPFC–HPC gamma coupling

To test causality between NR neuronal firing and gamma coupling, we performed chemical inactivation of the NR with muscimol (MSCI) in 3 animals (Fig. 7A). The LFP spectra only showed a decrease in the low gamma power in mPFC but not in HPC ([18 44] Hz, p = 0.025, t test on normalized spectra; Fig. 7B). There was no statistical difference between the mean slow oscillation power ([0.5 2] Hz band in the mPFC LFP; Fig. 7B; CTR: 31.0 ± 2.2 dB; MSCI: 33.7 ± 1.1 dB; p = 0.4756, t test) frequency (CTR: 1.05 ± 0.05 Hz; MSCI: 1.07 ± 0.00 Hz; p = 0.7972, t test), and in the UP states duration (median CTR: 0.55 s; median MSCI: 0.58 s; p = 0.2671, two-sided Mann–Whitney U test). The comodugrams revealed a strong reduction in the HPC–mPFC LFP correlation in the [30 90] Hz range (p < 0.05, t test; Fig. 7C). Moreover, the gamma power in both HPC and mPFC was less strongly modulated by the slow oscillation phase and was phase shifted, particularly in the HPC (Fig. 7D). Gamma bursts were still present in HPC and mPFC and occurred at an unchanged frequency (in 12 ± 2%, p = 0.67 and 10 ± 3%, p = 0.52 of UP states, respectively; Mann–Whitney U test). However, NR inactivation disrupted the temporal organization of gamma bursts in both regions. There was a drastic decrease of co-occurrence of gamma bursts between HPC and mPFC (16 ± 1%, p = 0.0167) and importantly, NR inactivation fully abolished HPC–mPFC gamma synchronization (Fig. 7Ea). Removing the influence of the UP state did not change this mPFC–HPC burst cross-correlation (Fig. 7Eb). Only 60 ± 2% of HPC bursts were associated to UP states (p = 0.0029; Mann–Whitney U test), with no significant change for mPFC bursts (96 ± 2%, p = 0.95). During the slow oscillation cycle, HPC gamma bursts were delayed, whereas mPFC bursts occurred earlier (HPC: CTR = 241 ± 1°, MSCI = 304 ± 2°, p < 0.001; mPFC: CTR = 253 ± 1°, MSCI = 234 ± 2°, p < 0.001; circular ANOVA; Fig. 7F). The strength of their entrainment was also reduced (HPC: CTR = 0.54 ± 0.02, MSCI = 0.19 ± 0.03, p < 0.001; mPFC: CTR = 0.78 ± 0.02, MSCI = 0.53 ± 0.03, p < 0.001; two-sample t test; Fig. 7F).

NR inactivation modified the firing properties of mPFC, but not that of HPC neurons, median firing rates: HPC: CTR = 0.59 Hz, MSCI = 0.49 Hz, p = 0.62; mPFC: CTR = 1.07 Hz, MSCI = 0.58 Hz, p < 0.001, Mann–Whitney U test (Fig. 8A), and median burst indices: HPC: CTR = 0.91, MSCI = 0.92, p = 0.92; mPFC: CTR = 0.50, MSCI = 0.28, p = 0.006, Mann–Whitney U test (Fig. 8B). However, their entrainment by slow oscillations was not changed (HPC: CTR = 132 ± 8°, MSCI = 155 ± 7°, p = 0.095; mPFC: CTR = 266 ± 2°, MSCI = 258 ± 3, p = 0.0524; circular ANOVA; Fig. 8C). Although both sync and non-sync gamma bursts entrained similarly HPC and mPFC neurons in control conditions, NR inactivation changed their entrainment properties (Fig. 8D). Fewer HPC and mPFC neurons (HPC = 33/67, 49%; mPFC = 65/139, 46%) were significantly entrained (p < 0.05, Rayleigh test) by gamma bursts when NR was inactivated compared with control conditions (HPC = 32/52, 62%; mPFC = 342/495, 69%). The gamma phase-modulation was also changed (mean phase, HPC: CTR = 199° ± 8°, MSCI = 342 ± 9°, p < 0.001; mPFC: CTR = 168 ± 2°, MSCI = 217 ± 7°, p < 0.001; circular ANOVA test), whereas the strength of this entrainment remained unaffected (mean R, HPC: CTR = 0.17 ± 0.02, MSCI = 0.20 ± 0.02, p = 0.4947; mPFC: CTR = 0.19 ± 0.01, MSCI = 0.18 ± 0.02, p = 0.4038, two-sample t test). These results demonstrate that NR is not only instrumental in gamma burst synchronization between HPC and mPFC, but that it also controls the firing of mPFC neurons and the coordination of HPC and mPFC neuronal activity during gamma bursts.

Figure 8.

Firing properties of HPC and mPFC neurons during NR inactivation. A, Mean firing rates calculated during slow oscillation episodes in control (CTR) and during NR inactivation (MSCI) for HPC (CTR n = 55, MSCI n = 37) and mPFC neurons (CTR n = 496, MSCI n = 71). The box plots represent the grouped data statistics (CTR n = 7 experiments, MSCI n = 3). Only mPFC neurons showed a significant decrease of their firing rate (Mann–Whitney U test, **p < 0.001 for mPFC, p = 0.62 for HPC). B, Mean burst indices for the HPC and mPFC neurons shown in A. Note that, again, only mPFC neurons fired less in bursts (Mann–Whitney U test, *p = 0.006 for mPFC, p = 0.92 for HPC). C, Comparison of preferred phase and modulation depth of HPC and mPFC neurons referenced to the slow oscillation cycle in the control condition and during NR inactivation. The black arrow indicates the mean phase and strength of modulation. n.s., Not significant, *p < 0.05. D, Polar plots of preferred phase and modulation depth of HPC and mPFC neurons referenced to all the gamma bursts detected in HPC and mPFC, respectively, in the control condition and during NR inactivation. The nonsignificantly entrained neurons are depicted by the gray circles (Rayleigh test, p ≥ 0.05). The black arrow indicates the mean phase and strength of modulation for the significantly entrained neurons only. Both groups display a shift of the mean phase (circular ANOVA, *p < 0.001 for both) but not of the mean strength (two-sample t test, HPC p = 0.4947, mPFC p = 0.4038) of the modulation during NR inactivation compared with control.

Discussion

Using a combination of multisite high-density LFPs and unit recordings, as well as pharmacological inactivation in anesthetized rats, we examined the mechanisms of the interactions between the HPC, mPFC, and NR. We have found that: (1) HPC and mPFC are coupled during slow oscillations through synchronized gamma bursts. (2) These gamma bursts entrain in turn the local populations of neurons in HPC and mPFC. (3) A large increase of NR firing specifically occurs prior sync gamma bursts. (4) NR is central for gamma burst synchronization and controls the firing properties of mPFC neurons. Such NR-dependent gamma-driven cortico–hippocampal coupling may open temporal windows for information transfer during slow oscillations.

Gamma oscillations promote functional binding of distant regions, which is central for numerous cognitive functions including sensory binding (Singer, 1999), working memory (Montgomery and Buzsáki, 2007; Benchenane et al., 2011; Yamamoto et al., 2014; Lundqvist et al., 2016), and learning (Sirota et al., 2008; Buzsáki and Wang, 2012). An efficient way to bind distant regions for information exchange (e.g., forming cell assemblies) is via the modulation of gamma power by slower oscillations (Buzsáki and Wang, 2012). Cross-frequency coupling has been extensively studied between theta and gamma oscillations, with the magnitude of theta-gamma correlating with cognitive load and performance (Lundqvist et al., 2011; Buzsáki and Wang, 2012; Buzsáki and Schomburg, 2015). Compared with theta, slow oscillations offer longer time windows for information transfer and increase neuronal firing because slow oscillations are associated with larger membrane potential changes. Slow oscillation-gamma coupling could reveal itself as an efficient way to exchange information during sleep. Our study provides the first evidence of long-range synchronization of gamma oscillations during slow oscillations and SWS. This mechanism may complement other known processes used to transfer/consolidate information during sleep, such as spindles and sharp wave-ripples (Siapas and Wilson, 1998; Maingret et al., 2016; Latchoumane et al., 2017). In keeping with this proposal, gamma bursts and sharp wave-ripples overlapped very rarely.

Multiple types of gamma rhythms can be distinguished based on their frequency band and their spatial location. In the hippocampus, specific increases in gamma power are found in sP, radiatum, and LM (Isomura et al., 2006). During slow oscillations, gamma oscillations appeared as short-duration (∼150 ms) bursts (i.e., not just a background gamma power), satisfying the condition for opening transient temporal windows to transfer information between HPC and mPFC. Approximately 60% of the gamma bursts were not synchronized between the two structures and two-thirds of them were detected in only one region, suggesting that they may be involved in other processes. Another major finding of the present study is the role of the NR in the timing of gamma bursts in HPC and mPFC. Approximately 40% of gamma bursts were synchronized between HPC and mPFC, as defined by a co-occurrence in a [−110 190] ms time window, and such synchronization was independent of the influence of the UP state. Such coupling disappeared following NR inactivation, whereas the gamma bursts overall number was not affected. This suggests that the NR is involved in the synchronization between HPC and mPFC during slow oscillations on fine timescales. The drop in mPFC–HPC gamma power correlation could be at least partly credited to gamma burst desynchronization. In the absence of NR influence, gamma bursts occur at the same rate, but their temporal organization is disrupted. Thus, the NR acts as a key node in this thalamo–hippocampo–prefrontal circuit for the temporal control of gamma oscillations and phase locking of cell firing during gamma bursts.

The fact that NR neurons increase their firing rate specifically before the gamma burst coupling (i.e., it persisted once the confounding slow oscillation modulation was removed) strongly suggests that NR acts as a driver. In addition, HPC and mPFC coupling appears to require a larger increase in NR firing compared with non-sync bursts. The gradual recruitment of NR neurons before gamma bursts supports the involvement of different neuronal types (with different firing properties, chemical content, and/or input and output connectivity, etc.) in the NR (Bokor et al., 2002). Such behavior was not found in neighboring thalamic nuclei that, as far as we know, do not possess the same connection pattern as the NR does. The upstream mechanism underlying the increase in NR activity remains to be determined considering that many regions project to NR in addition to HPC and mPFC (Van der Werf et al., 2002; McKenna and Vertes, 2004; Cassel et al., 2013). Downstream, at least in the HPC, NR neurons cannot only act on principal cells (Dolleman-Van der Weel et al., 1997) but potentially also on parvalbumin-containing basket cells (Dolleman-Van der Weel and Witter, 2000; Di Prisco and Vertes, 2006), whose dendrites extend to LM, the projection zone of NR in CA1 (Wouterlood et al., 1990). Gamma oscillations recorded in sP during theta are supported by parvalbumin-expressing basket cell activation (Lasztóczi and Klausberger, 2014). However, a detailed description of connectivity patterns between NR and the different hippocampal cells is still lacking. Unfortunately, much less is so far known about the NR–mPFC anatomical circuit (Di Prisco and Vertes, 2006). Several types of cells may exist in the NR (Bokor et al., 2002; Cassel et al., 2013). In particular, a subset (∼8%) of NR neurons project both to mPFC and HPC, and these neurons may be central to consolidation of memory traces (Varela et al., 2014). It is tempting to speculate that some of the neurons increasing their firing before gamma onset could correspond to the double-projecting NR neurons as they are in an ideal position to control synchronization. The lack of specific molecular markers for these neurons (and for NR neurons in general) and the gradual recruitment of NR neurons prior to gamma bursts prevent, at present, optogenetic and pharmacogenetic approaches to test this hypothesis.

In conclusion, these results revealed a novel role of the NR in synchronizing gamma bursts between HPC and mPFC during slow oscillations. These sync gamma bursts may constitute another actor in memory transfer/consolidation during SWS.