Hippocampal Ripple Oscillations and Inhibition-First Network Models: Frequency Dynamics and Response to GABA Modulators

Abstract

Hippocampal ripples are involved in memory consolidation, but the mechanisms underlying their generation remain unclear. Models relying on interneuron networks in the CA1 region disagree on the predominant source of excitation to interneurons: either “direct,” via the Schaffer collaterals that provide feedforward input from CA3 to CA1, or “indirect,” via the local pyramidal cells in CA1, which are embedded in a recurrent excitatory-inhibitory network. Here, we used physiologically constrained computational models of basket-cell networks to investigate how they respond to different conditions of transient, noisy excitation. We found that direct excitation of interneurons could evoke ripples (140–220 Hz) that exhibited intraripple frequency accommodation and were frequency-insensitive to GABA modulators, as previously shown in in vitro experiments. In addition, the indirect excitation of the basket-cell network enabled the expression of intraripple frequency accommodation in the fast-gamma range (90–140 Hz), as in vivo. In our model, intraripple frequency accommodation results from a hysteresis phenomenon in which the frequency responds differentially to the rising and descending phases of the transient excitation. Such a phenomenon predicts a maximum oscillation frequency occurring several milliseconds before the peak of excitation. We confirmed this prediction for ripples in brain slices from male mice. These results suggest that ripple and fast-gamma episodes are produced by the same interneuron network that is recruited via different excitatory input pathways, which could be supported by the previously reported intralaminar connectivity bias between basket cells and functionally distinct subpopulations of pyramidal cells in CA1. Together, our findings unify competing inhibition-first models of rhythm generation in the hippocampus.

SIGNIFICANCE STATEMENT The hippocampus is a part of the brain of humans and other mammals that is critical for the acquisition and consolidation of memories. During deep sleep and resting periods, the hippocampus generates high-frequency (∼200 Hz) oscillations called ripples, which are important for memory consolidation. The mechanisms underlying ripple generation are not well understood. A prominent hypothesis holds that the ripples are generated by local recurrent networks of inhibitory neurons. Using computational models and experiments in brain slices from rodents, we show that the dynamics of interneuron networks clarify several previously unexplained characteristics of ripple oscillations, which advances our understanding of hippocampus-dependent memory consolidation.

Introduction

The hippocampal local field potential (LFP) displays various oscillations that are associated with different behavioral states (Buzsáki and Draguhn, 2004). Theta and gamma oscillations occur during locomotor activities (Vanderwolf, 1969; Buzsáki et al., 1983; Bragin et al., 1995) at which sensory information is temporarily stored in the hippocampus. Sharp wave-ripple complexes (SWRs) are prominent in periods of immobility, consummatory behaviors, and slow-wave sleep in rodents (Buzsáki et al., 1983, 1992; Buzsáki, 1986; Wilson and McNaughton, 1994; Karlsson and Frank, 2009) and humans (Bragin et al., 1999; Axmacher et al., 2008). During SWRs, previously acquired information is replayed (Wilson and McNaughton, 1994; Nádasdy et al., 1999; Lee and Wilson, 2002; Foster and Wilson, 2006; Diba and Buzsáki, 2007; Gupta et al., 2010). SWRs were proposed to assist memory consolidation (Buzsáki, 1989, 1998; Siapas and Wilson, 1998; Girardeau and Zugaro, 2011). In support, the suppression of SWRs impairs spatial memory (Girardeau et al., 2009; Ego-Stengel and Wilson, 2010; Jadhav et al., 2012). However, mechanisms underlying the generation of SWRs are not well understood (Buzsáki and Lopez da Silva, 2012).

SWRs consist of a fast (∼90–200 Hz) oscillation, the ripple, superimposed on a transient deflection of the LFP, the sharp wave (Buzsáki et al., 1992). The activity of various cell types is locked to ripple oscillations, but the pace-making mechanisms are unclear, although many in vivo and in vitro studies addressed this question (Ylinen et al., 1995; Draguhn et al., 1998; Nádasdy et al., 1999; Csicsvari et al., 2000; Klausberger et al., 2003, 2005; Maier et al., 2003, 2011; Lapray et al., 2012; Hájos et al., 2013; Pangalos et al., 2013; Gan et al., 2017). Current hypotheses agree that the fast component emerges from interactions between neurons, but models differ on where and how such oscillatory activity is generated. Excitation-first models propose that oscillations originate in pyramidal cells that, in turn, entrain interneurons via local principal cell-to-interneuron connections. Generative mechanisms in such models rely on propagation of activity between pyramidal cells via axonal gap junctions (Draguhn et al., 1998; Traub et al., 1999) or, alternatively, via chemical synapses and supralinear dendritic integration (Memmesheimer, 2010). In inhibition-first models, in contrast, the generation of the oscillation is critically dependent on a recurrent interneuron network (Buzsáki et al., 1992; Ylinen et al., 1995; Taxidis et al., 2012; Malerba et al., 2016). Upon stimulation, such an interneuron network generates fast oscillations, providing rhythmic inhibition that paces principal cells. Models of this class may differ on whether interneurons are predominantly driven by direct Schaffer collateral input (Schlingloff et al., 2014) or indirectly via local pyramidal cells (Stark et al., 2014).

Ripples display several features that constrain the type of pace-making mechanism. First, single oscillatory episodes in vivo can exhibit frequencies either in the ripple band (140–220 Hz) or the fast-gamma band (90–140 Hz) (Csicsvari et al., 1999; Sullivan et al., 2011). Second, both ripple and fast-gamma events exhibit intraripple frequency accommodation (IFA): an initially high oscillation frequency during the first half of the event is followed by a monotonic deceleration (Ponomarenko et al., 2004; Nguyen et al., 2009; Sullivan et al., 2011). And third, the ripple frequency in vitro is insensitive to GABA modulators (Papatheodoropoulos et al., 2007; Koniaris et al., 2011; Viereckel et al., 2013), in stark contrast to other forms of inhibition-based oscillations (Whittington et al., 1995; Traub et al., 1996).

So far, models of SWRs have focused on the ripple band, and have not accounted for IFA (Traub et al., 1996; Memmesheimer, 2010; Taxidis et al., 2012; Malerba et al., 2016). Moreover, previous inhibition-first models are frequency-sensitive to changes in GABAergic transmission (Taxidis et al., 2012; Malerba et al., 2016; but see Brunel and Wang, 2003), which supports excitation-first models (Viereckel et al., 2013).

The present computational and experimental study demonstrates how the inhibition-first hypothesis can account for all the aforementioned features of ripples, advancing our understanding of hippocampus-dependent memory formation.

Materials and Methods

Here we aimed at assessing the explanatory power of ripple models that rely on an interneuron network as the primary pacemaker. We therefore focused on the oscillatory response of a physiologically constrained model of a parvalbumin-immunoreactive (PV⁺) basket cell (BC) network in CA1. The parameters of the model were constrained by data obtained from studies using rodents, mostly rats. In few cases, if data from rats were not available, we also used data obtained from mice (for a review on ripple features in these species, see Maier and Kempter, 2017).

Model neurons.

Both pyramidal cells and interneurons were described by single-compartment, leaky integrate-and-fire models, in which the dynamics of the subthreshold membrane potential V_m obeyed as follows:

where E_rest is the leak (resting) potential, C_m is the capacitance, and g_leak is the leak conductance. The symbols I_syn and I_app indicate the synaptic and injected (applied) currents, respectively. When V_m reaches a threshold voltage V_thres, the unit emits a spike. After spiking, V_m is reset to a potential V_reset and the cell remains refractory for a period t_ref.

For interneurons, the parameters of the leaky integrate-and-fire model were tuned to resemble the behavior of a fast-spiking BC in CA1. The leak potential E_rest was set to −65 mV (Wang and Buzsáki, 1996; Bartos et al., 2002). The values C_m = 100 pF and g_leak = 10 nS yield a membrane time constant of 10 ms (Buhl et al., 1996). The spiking parameters V_thres, V_reset, and t_ref were set to −52 mV, −67 mV, and 1 ms, respectively. Although higher values of V_thres have been reported in the literature (Ferguson et al., 2013), we opted to remain consistent with previous models (Wang and Buzsáki, 1996; Taxidis et al., 2012) because this parameter is not critical for the phenomena described here. To check for the consistency of the chosen parameter values, we empirically measured the current-frequency curve of the interneuron model by varying the value of I_app between 0 and 1.0 nA in the absence of synaptic currents. The obtained current-frequency curve exhibited a slope of 380 Hz/nA (measured at I_app = 0.6 nA) and a rheobase of 0.13 nA, in agreement with hippocampal PV⁺ BCs recorded in vitro (Pawelzik et al., 2002; Ferguson et al., 2013) and more sophisticated models of fast-spiking BCs (Wang and Buzsáki, 1996; Ferguson et al., 2013).

For pyramidal cells, the parameters of the leaky integrate-and-fire model were adjusted according to Bähner et al. (2011): E_rest = −67 mV, C_m = 275 pF, and g_leak = 25 nS, which yield a membrane time constant of 11 ms, and the spiking parameters V_thres, V_reset, and t_ref were set to −50 mV, −60 mV, and 2 ms, respectively.

Model synapses.

The total synaptic current I_syn is described according to a conductance-based model as follows:

where g_e and g_i are the phasic excitatory and inhibitory conductances, respectively, resulting from the presynaptic activity, and g_t corresponds to a tonic excitatory conductance that could be externally driven. E_i and E_e are the reversal potentials of inhibition and excitation, respectively. For interneurons, E_i was set to −75 mV, in accordance with reported values (Buhl et al., 1995) and previous models (Wang and Buzsáki, 1996; Bartos et al., 2002). For pyramidal cells, E_i was set to −68 mV (Maier et al., 2003; Bähner et al., 2011). E_e was set to 0 mV for both interneurons and pyramidal cells.

The time course of a postsynaptic conductance due to a presynaptic spike is described by a normalized dual exponential as follows:

for t ≥ τ₁ and g(t) = 0 otherwise. The scaling factor s was set such that g(t) reaches the maximum value g^peak, and τ_r and τ_d are the rise and decay time constants, respectively. There is a latency of τ_l = 1 ms between a presynaptic spike and the start of the postsynaptic conductance.

Two types of phasic synapses were used: fast GABAergic and AMPA-type. The values for GABAergic synapses were tuned according to Bartos et al. (2002): GABA on interneurons had τ_r = 0.45 ms, τ_d = 1.2 ms, and g^peak = 5 nS. GABA on CA1 pyramidal cells had τ_r = 0.4 ms, τ_d = 2 ms, and g^peak = 9 nS. AMPA-type synapses on CA1 interneurons had τ_r = 0.5 ms, τ_d = 2 ms, and g^peak = 0.8 nS when driven by Schaffer collateral activity (Taxidis et al., 2012), and τ_r = 0.5 ms, τ_d = 1.2 ms, and g^peak = 3.0 nS when driven by CA1 pyramidal cell activity (Pawelzik et al., 2002). AMPA-type synapses on pyramidal cells had τ_r = 0.5 ms, τ_d = 1.8 ms, and g^peak = 0.9 nS (Maier et al., 2011).

Network model of inhibitory neurons.

SWRs can be observed in the isolated CA1 area of ventral-to-middle hippocampal slices (Maier et al., 2003, 2011; Nimmrich et al., 2005). We therefore constrained the model according to the PV⁺ BC network in such a small volume of tissue. To set the number of interneurons in the network, we obtained two consistent estimates for the number of PV⁺ BCs. The first estimate is based on the volume of the stratum pyramidale in a hippocampal slice and the density of PV⁺ BCs in this region. The typical thickness of a hippocampal slice (0.4 mm) and the dimensions of the CA1 stratum pyramidale in ventral hippocampus (0.13 mm × 1.1 mm) (Dougherty et al., 2012) yield a volume of 0.057 mm³. The density of PV⁺ cells in the stratum pyramidale was estimated to be 5.4 × 10⁺³ cells/mm³ (Aika et al., 1994). Considering that 60% of PV⁺ cells in CA1 are BCs (Bezaire and Soltesz, 2013), we calculated 185 PV⁺ BCs contained in a slice.

A second estimate for the number of interneurons was obtained by scaling the total number of 5530 PV⁺ BCs in the hippocampus (Bezaire and Soltesz, 2013) by the fraction of the volume of a 400 μm slice. If we approximate the geometry of the hippocampus to a cylinder and consider its septotemporal extension to be ∼10 mm (Patel et al., 2012), a 400 μm slice represents 4% of the total volume. This fraction yields 221 PV⁺ BCs in a slice. Approximately consistent with both estimates, our simulated network consisted of 200 interneurons.

To estimate the connectivity in our network, we note that a single PV⁺ BC can contact on average 64 other PV⁺ cells (Sik et al., 1995). If we consider that 60% of those PV⁺ cells are BCs (Bezaire and Soltesz, 2013), then a PV⁺ BC contacts on average 38 other cells of the same type. This number corresponds to a connectivity of 20.5% for 185 cells and 17% for 221 cells. In our simulations, we used 20% connectivity.

To keep the model as simple as possible, we assumed that pairs of PV⁺ BCs are connected with equal probability. In consequence, there is no spatial structure in the connectivity, in contrast to previous models (Wang and Buzsáki, 1996; Bartos et al., 2002; Taxidis et al., 2012).

In summary, the interneuron network model consisted of 200 fast-spiking BCs that are randomly connected with a connection probability of 20%. Thus, on average, each interneuron in the network received 40 synaptic contacts from other interneurons.

Phasic excitatory input to interneurons.

In the hippocampus, AMPA-type synapses on interneurons in CA1 can be driven by Schaffer collaterals from CA3, or by local fibers from CA1 pyramidal cells (Takács et al., 2012). In our model, two populations of pyramidal cells (CA3 and CA1) were randomly connected to CA1 interneurons via AMPA-type synapses. Here we explain how we constrained the number of pyramidal cells in both populations and their connectivity with the interneuron network described above. In the intact hippocampus, the total number of pyramidal cells in CA3 and CA1 was estimated as 204,700 and 311,500, respectively (Bezaire and Soltesz, 2013). We scaled these numbers down to the ratio 0.04 of the volumes of a slice and the intact hippocampus to obtain ∼8200 CA3 and ∼12,000 CA1 pyramidal cells providing input fibers to CA1 interneurons. The connectivity between CA3 pyramidal cells and interneurons in the model (see Fig. 3A) was obtained from the estimated number of synapses per interneuron and the total number of CA3 pyramidal cells. In the intact hippocampus, each interneuron receives 7,952–17,476 synapses from Schaffer collaterals (Bezaire and Soltesz, 2013). Such collaterals stem from pyramidal cells located within the proximal two-thirds of the ∼10 mm septotemporal extension of CA3 (Li et al., 1994). If we consider that each of those synapses corresponds to a pyramidal cell located within such an extension (∼6.7 mm) and that the thickness of a typical hippocampal slice preserves 6% of that extension (0.4 mm/6.7 mm), we expect that ∼6% of the total number of excitatory synapses can be driven by the ∼8200 CA3 pyramidal cells. From this estimate, we obtained 480–1050 input synapses per interneuron. From the ratio between the number of synapses per interneuron and the number of pyramidal cells in CA3, we estimated a connection probability between CA3 pyramidal cells and interneurons, p_share, that ranged from 0.06 to 0.13. This number also describes the average shared input across interneurons and therefore quantifies the correlations introduced by the connectivity. For the simulations, we chose an intermediate value p_share = 0.095, which corresponds to ∼780 excitatory synapses per interneuron. Interneurons did not project back to CA3 pyramidal cells.

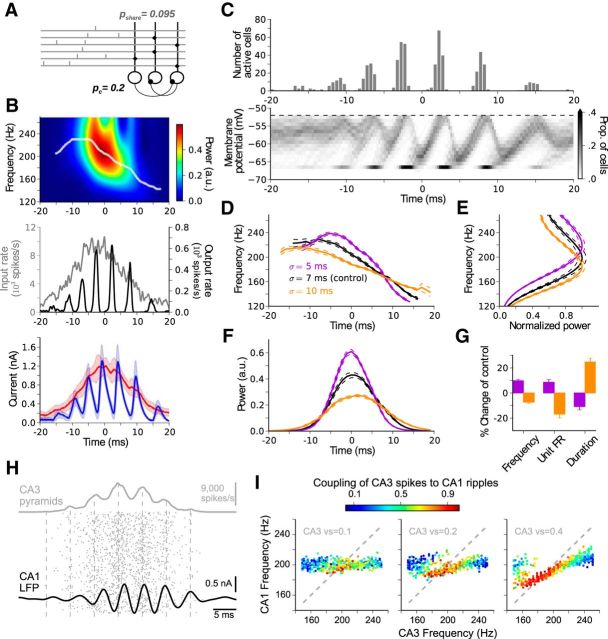
Figure 3.

Interneuron-network response to excitatory bursts from CA3. A, Interneurons (black circles) are randomly interconnected with probability p_c = 0.2. The driving population is randomly connected to the interneuron network with probability p_share = 0.095. Excitatory fibers (gray lines, only 6 shown) from the bursting subpopulation (1400 units) fire once with a normally distributed timing. The remaining 6800 fibers fire randomly and provide a total background rate of 1200 spikes/s to each interneuron. B, Top, Wavelet spectrogram and instantaneous peak frequency (white) of the transient response (middle, black). The transient response exhibits IFA. Middle, Overlay of the total input activity (gray, input rate) and response of the interneuronal network (black, output rate). The network responds with a modulated oscillation whose envelope lags the input burst. Bottom, Mean synaptic currents across the population generated by the excitatory input (red) and the inhibitory recurrent response (blue). On the ascending phase of the input, inhibitory peaks remain slightly below the ongoing excitatory current. The opposite occurs during the descending phase. C, Spike-time histogram (top) and time course of membrane-potential distribution (bottom). During an initial stage (t ≲ −5 ms), a wider distribution of membrane potentials shows subthreshold oscillations that increase in amplitude, denoting an unsaturated (high noise) state. This initial stage is followed by a saturated (low noise) state (t ≳ 0 ms). D, Average IFA signatures obtained at different burst widths σ. Black represents control value σ = 7 ms, used also in B and C. Broader input bursts (σ = 10 ms, orange) evoke shallower IFA signatures, whereas narrower input bursts (σ = 5 ms, violet) evoke sharper IFA signatures (see also Fig. 2B₃). E, Average power spectra obtained for the same burst widths as in D. Broader input bursts evoke slower ripples. F, Average time course of power obtained for the same burst widths as in D. Broader input bursts evoke longer lasting but weaker transient responses. G, Changes in frequency, firing rate (FR), and duration with respect to the control value σ = 7 ms. B–G, Average traces were obtained from 20 simulations. H, In a ripple-modulated CA3 burst (gray), spikes (dots) are phase-locked (vector strength v_s = 0.2) to a local rhythm (180 Hz, vertical dashed lines at input-rate peaks). The CA1 LFP response (black; see Materials and Methods) oscillates at 200 Hz, and CA3 spikes are weakly coupled to the CA1 LFP (v_s = 0.08). I, CA1 frequency as a function of CA3 frequency for different CA3 modulation depths. Colored dots represent simulated events; CA3 vector strength v_s = 0.1 (left), 0.2 (middle), and 0.4 (right). At v_s = 0.1 and 0.2, CA1 oscillates at its intrinsic frequency (∼200 Hz), almost independently of the CA3 frequency (dashed line indicates identity). The coupling of the CA3 spikes to the CA1 LFP becomes prominent when CA3 frequencies are close to the CA1 intrinsic frequency (∼200 Hz). At v_s = 0.4 (right), the CA3 ripple affects the CA1 frequency at a wider range. The coupling of CA3 spikes to the CA1 ripples (vector strength, color coded) is normalized to the vector strength of the input, individually for each CA3 modulation depth.

The connection probabilities between CA1 pyramidal cells (pyr) and interneurons (int) (see Fig. 4A) were adjusted according to the reported connectivity between pyramidal cells and PV⁺ BCs in vitro (Pawelzik et al., 2002): pyr → int = 0.1; int → pyr = 0.3. Local pyramidal cells were also reciprocally connected with probability 0.01 (Deuchars and Thomson, 1996).

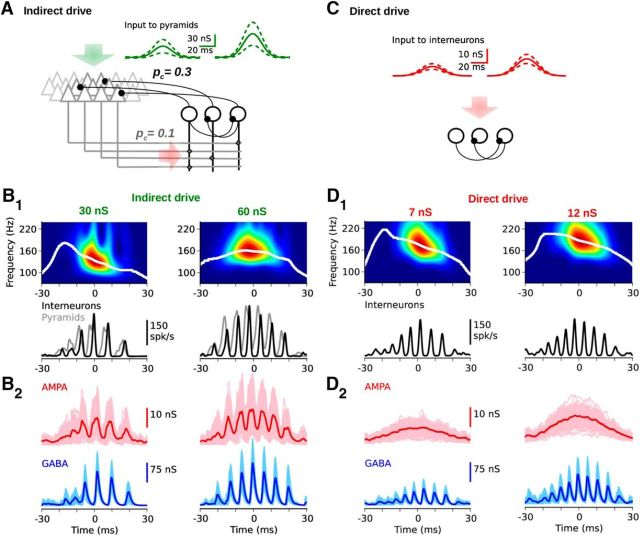
Figure 4.

Induced oscillations under two driving conditions. A, A population of pyramids (pyr; gray triangles, 12,000 units) is reciprocally interconnected with an interneuron network (int; black circles, 200 units; connection probabilities p_c: pyr → int = 0.1, int → pyr = 0.3, pyr → pyr = 0.01). During indirect drive, a subpopulation of 100 pyramids is excited with Gaussian bursts (green, σ = 13 ms). Burst amplitudes were normally distributed across neurons (green: mean; dashed line, ±SD). Two input levels (30 nS and 60 nS) are shown. B, Network response to indirect-drive for the two input levels depicted in A (green, left and right, respectively). B₁, Top, Wavelet spectrogram and instantaneous peak frequency (white) of the interneuron population activity (bottom, black). At low input (30 nS, left), the transient response exhibits IFA at ∼130 Hz. At high input (60 nS, right), the frequency peaks at ∼155 Hz and there is no IFA. Bottom, Overlay of the activities of the pyramidal (gray) and interneuronal (black) populations. Pyramids lead interneurons. B₂, Synaptic conductances across the interneuron population. C, The isolated interneuron network (black circles) is directly driven with normally distributed Gaussian bursts (red). Burst profiles and variability were adjusted to resemble the filtered (<30 Hz) excitatory conductances shown in B₂ (left and right, light red), yielding profiles with σ = 14 ms and average peaks: 7 nS and 12 nS, respectively. D, Same as B when the interneuron network is directly excited with the profiles depicted in C. The network response displays the stereotypical IFA shape at ∼172 Hz (left) and ∼186 Hz (right). The directly driven interneuronal network requires comparably lower excitation to generate oscillations in the ripple band.

Stimulation paradigms.

To study the oscillatory behavior of the interneuron network under both its steady-state and transient regimes, we applied different forms of persistent and transient excitation to interneurons, respectively. Stimulation was applied either directly to interneurons (i.e., in the absence of feedback inhibition; sketched in Figs. 3A, 4C) or indirectly via depolarization of local CA1 pyramidal cells (sketched in Fig. 4A). Direct stimulation was delivered either via spiking activity of the CA3 population of pyramidal cells (see, e.g., Fig. 3A), or by activation of tonic excitatory conductances (g_t in Eq. 2) on interneurons (as in Schlingloff et al., 2014) (see Fig. 4C). Indirect stimulation, on the other hand, was delivered by activation of tonic excitatory conductances on CA1 pyramidal cells (as in Stark et al., 2014) (see Fig. 4A). In what follows, we describe in detail the various combinations of stimulus paradigms.

Persistent stimulation was always applied directly to the interneurons. During persistent spiking stimulation (see Figs. 1, 2, and 9A), every pyramidal cell in CA3 fired according to a homogeneous Poisson process with a constant rate. In this condition, the total Poisson rate delivered to each interneuron corresponds to the number of synapses per interneuron (here: 780) multiplied by the rate of a single pyramidal cell, which was varied in a wide range between 1.28 and 19.23 spikes/s. The input strength of the network is then given as the total rate per cell (range, 1,000–15,000 spikes/s), which corresponds to the number of excitatory synaptic events experienced by a single interneuron per unit time. For persistent stimulation via tonic conductance activation (see Fig. 9B), constant values of g_t were normally distributed across the population with a mean of 17.4 nS and an SD of 0.5 nS, yielding a coefficient of variation (CV) of 3%, as in interneuron-network gamma models (Traub et al., 1996; Wang and Buzsáki, 1996).

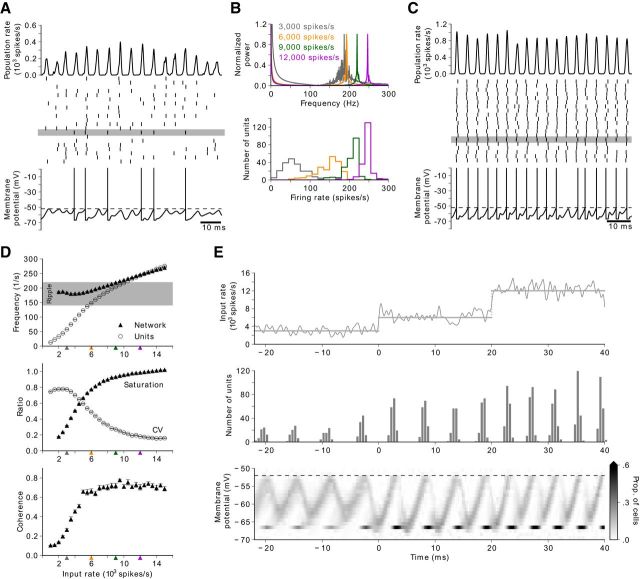
Figure 1.

Steady-state oscillations in a model of the CA1 BC network. A, Network activity at an input rate of 3000 spikes/s. Oscillations in the population rate (top) emerge from units that fire irregularly (middle: spike raster plot for 20 of 200 units). Bottom, Membrane potential of a unit (spike times: middle, horizontal gray bar). Subthreshold oscillations are superimposed on random fluctuations. B, Power spectral density of population activity (top) and firing-rate histogram of units (bottom) at four levels of input rates (gray corresponds to activity depicted in A). C, Network activity at an input rate of 9000 spikes/s (B, green). Oscillations in the population rate (top) emerge from units that fire regularly and rarely skip cycles of the population activity (middle). Bottom, Membrane potential of a unit (spike times: middle, gray bar). D, Steady-state network response as a function of input strength (input levels depicted in B are indicated by colored triangles below the horizontal axis). Top, Network frequency (triangles) and mean firing rate of units (circles). Gray area represents the ripple band (140–220 Hz). Middle, The saturation (triangles) is the average fraction of units recruited in one cycle. Irregularity of firing is described by the average CV (circles) of the interspike interval of units. Bottom, Coherence of network oscillations. Error bars are smaller than marker size. E, Sequence of three input levels (top), spike-time histogram of network activity (middle; bin width 0.5 ms), and membrane-potential distribution across the interneuron population (bottom). At an input rate of 3000 spikes/s (t < 0 ms), the distribution of membrane potentials exhibits a subthreshold sinusoidal mean. The tail of the distribution reaches the threshold (dashed line; see also A, bottom). At 6000 spikes/s (0 < t < 20 ms), ∼75% of the population is recruited (middle) in every cycle. Because the network is close to saturation, a further increase to 12,000 spikes/s (t ≥ 20 ms) reduces the time between bursts of activity (middle). The threshold is then reached in the rising (excitatory) phase of the membrane potentials.

Figure 2.

Network response to changing input rate is asymmetric. A, A double ramp input rate (top, gray) consists of a linear increase (t < 0 ms), a plateau (0 ≤ t < 40 ms), and a linear decrease (t ≥ 40 ms). The network response (top, black) is asymmetric with respect to the input. The membrane-potential distribution (bottom) shows that the network is in a high-noise state (bottom, t ≤ −20 ms) and synchronizes in the middle of the ascending input ramp at t ≈ −20 ms. The network then remains in a low-noise state during the plateau and the entire descending phase (bottom, 40 < t ≤ 75 ms). B, Time courses of input (top), average frequency responses (middle), and average saturations (bottom) for different parameters of the double ramp. During the ascending phase (solid line), the onset frequency (∼220 Hz) is independent of the amplitude (B₁), slope (B₂), and combinations of these two parameters (B₃), regardless of its steady-state value (dotted line). Frequency decays with input during the descending phase (dashed line). C, Frequency (top) and saturation (bottom) as a function of input rate (obtained from B). Frequency is more sensitive to input on the descending phase (top, dashed line), which is consistent with the respective higher saturation (bottom, dashed line). Each average trace was obtained from 50 simulations. Error bars (data not shown) were comparable with the line width. B₂, B₃, Black traces are respectively identical.

Figure 9.

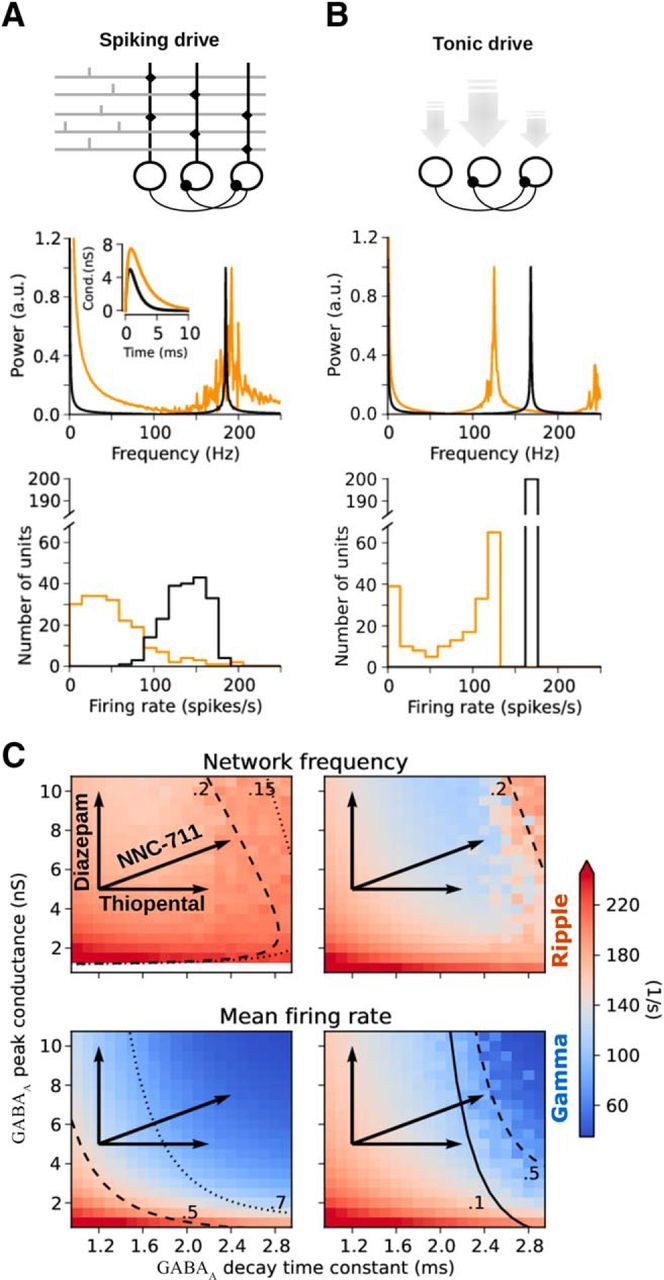
Differential effects of GABA_A parameters on network response for spiking and tonic drives. A, Network driven by uncorrelated spiking activity (top). Normalized power spectral densities (middle) and firing-rate histograms (bottom) for the control condition (black) and for the simulated application of the GABA-uptake blocker NNC-711 (orange). Under the effect of the drug on the postsynaptic conductance (inset), the network peak frequency is almost unaffected, but the distribution of firing rates is shifted to lower values. B, Network driven by tonic conductances (top). Tonic conductances (gray arrows) were distributed across the population with low variability (CV = 0.03). Under the action of the drug (A, inset), both the peak frequency and the firing rates are shifted to lower values. C, Dependence of network peak frequency (top) and mean firing rate (bottom) on GABA_A decay-time constant and peak conductance for spiking drive (left column) and tonic drive (right column). Black arrows indicate the changes in GABA_A parameters induced by different drugs. For spiking drive (left), the peak frequency remains relatively insensitive to changes in GABA_A kinetics, whereas the mean firing rate is strongly affected. For tonic drive (right), both peak frequency and mean firing rate are rather sensitive to GABA_A parameters. Solid, dashed, and dotted lines outline different levels of coherence (top) and CV of firing rate (bottom).

To provide transient stimulation, interneurons were driven either by a modulated Poissonian activity (e.g., see Fig. 2A, top, gray), or a burst of excitatory activity (e.g., see Figs. 3B,H, 4C). In all cases, also a weak Poissonian synaptic activity was delivered at a total rate of 1200 spikes/s, which summarizes the synaptic noise due to random activity and spontaneous synaptic release stemming from both CA1 and CA3 pyramidal cells. The burst consisted of a Gaussian temporal profile that was delivered either directly or indirectly. To directly deliver a burst in the form of CA3 spiking activity (see Figs. 3, 8), we considered that a small fraction of the pyramidal cells in CA3 (∼17%) fires once during a single SWR event (Hájos et al., 2013). Accordingly, in our simulations, 1400 of 8200 units of the CA3 driving population participated in the SWR. Each driving unit in this bursting subpopulation fires once at a point in time which is drawn from a normal distribution with a SD of 5, 7, or 10 ms.

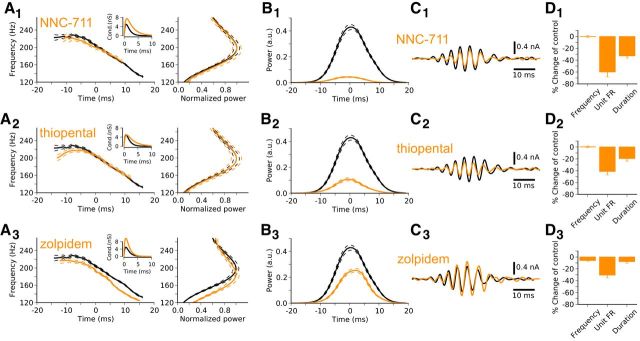
Figure 8.

Simulation of the effect of three different GABA modulators: 1, Uptake-blocker NNC711; 2, thiopental; and 3, zolpidem. A, Left, Average IFA signatures obtained for control (black, identical to Fig. 3D) and under the effect of the drug (orange). Insets, The action of the drug on the inhibitory postsynaptic conductance. Right, Normalized average power spectra of network activity for control (black) and during exposure to the drug (orange). B, Average time courses of ripple power of network activity for control (black) and during exposure to the drug (orange). C, Examples of simulated ripple extracellular potentials obtained from the average inhibitory current across the population (see Materials and Methods). D, Changes in frequency, firing rate (FR), and duration with respect to control values. Each average trace was obtained from 20 simulations.

To modulate the transient activity of CA3 pyramidal cells at ripple frequencies (Fig. 3H,I), we modified the probability distribution from which the spike times of the bursting population were drawn. The modified distribution consisted of a train of Gaussian peaks with jitter σ_jitter that were separated by a constant interpeak interval T (i.e., no IFA from CA3). This train (at ripple frequency 1/T) was in turn modulated by a Gaussian envelope (σ = 7 ms), as in the control condition in Figure 3A, and the train of Gaussian peaks was randomly aligned (across simulated SWR events) to the Gaussian envelope. In this way, the excitatory firing rate delivered to the interneuron network remained the same, regardless of the values of T and σ_jitter. To quantify phase locking, the vector strength v_s resulting from the wrapped peak distributions was set by adjusting σ_jitter/T in

In our simulations, we used reference values v_s = 0.1 and 0.2 of CA3 modulation depths, which correspond to the upper bound observed for ripples in vivo (Sullivan et al., 2011), and the average reported for fast-gamma in vivo (Tukker et al., 2013), respectively. We also used v_s = 0.4 to illustrate an extreme case.

To compare our results regarding the coupling between CA3 units and CA1 LFP with those obtained by Both et al. (2008), we translated their measure “coupling strength” of unit locking (called S_Both here) into vector strength v_s in the following manner: Both et al. (2008) estimated the time-span around the central peak of the cross correlogram that entails 50% of its area, and then expressed this time as a percentage of the ripple period (their Figs. 2, right, and 4C for single-unit recordings with S_Both = 0.37, bottom right). In a normal distribution, such a width corresponds to ∼4/3 of its SD (± 2/3 SDs around the peak). The fraction S_Both of the ripple cycle covered by such a width is therefore S_Both = 4/3 · σ_jitter/T. Using S_Both = 0.37 yields v_s = 0.22.

For the indirect-drive condition in Figure 4A, a random subpopulation of 100 local pyramids was depolarized by driving their tonic excitatory conductances (g_t in Eq. 2) with Gaussian intensity profiles (σ = 13 ms). The amplitudes of such profiles were normally distributed across the population with a variability described by the ratio between the SD and the mean of the normal distribution (i.e., by its CV). The variability was kept constant at CV = 0.5 across simulations, only the mean amplitude of this distribution was varied to provide different levels of input to the pyramids. For the direct-drive condition (see Fig. 4C), interneurons were depolarized by driving their tonic excitatory conductances with Gaussian intensity profiles, as was done with pyramids. Such intensity profiles were adjusted according to the excitatory activity measured on interneurons during the indirect-drive condition. For every average level of input applied to the pyramids during indirect-drive, the resulting excitatory conductances measured at the interneurons were low-pass filtered (<30 Hz) to generate a sample of 200 reference conductance traces (one for each interneuron). From that sample, an average trace and its SD were measured. The average trace and variability obtained were then used to adjust the Gaussian intensity profiles that were delivered directly to the interneurons via their tonic excitatory conductances.

Numerical simulations.

Simulations consisted of 1 s or 100 ms simulated time (time step = 10 μs) for the persistent and transient paradigms, respectively. For each numerical simulation, a new instance of the model was created (i.e., the network and the external input connectivity were randomly rewired). All simulations, data analysis, and visualization of results were performed in Python (www.python.org). The network model was implemented using the spiking network simulator Brian (Goodman and Brette, 2009).

Analysis of the network activity.

For simulations performed under persistent stimulation, power spectra of the network activity were computed from the Fourier transform of the autocorrelogram of the population activity (see Figs. 1B, 9B). The network frequency was obtained from the peak of the power spectrum. The network saturation was defined as the average number of inhibitory units recruited in a network oscillation cycle (see Fig. 1D, middle). Because in our simulations units rarely fired more than once in each cycle, we obtained an approximation of the saturation from the average number of spikes generated by the population in one cycle. Unit firing rates were estimated from the number of spikes generated during the time of a simulation (1 s). Regularity of unit firing was measured by the CV of the interspike interval. The coherence of the oscillation (see Fig. 1D, bottom) was derived from the power spectrum as the square root of the ratio between the power of the peak and the power at zero frequency (Kempter et al., 1998).

For simulations performed under transient stimulation, we calculated the wavelet spectrogram of the corresponding transient response (see, e.g., Fig. 3B, top). To obtain this spectrogram, the population spiking activity was first smoothed with a Gaussian kernel (σ = 0.2 ms); that is, each spike was replaced by a Gaussian and then convolved with Gabor wavelets covering the band 120–270 Hz in steps of 1 Hz.

To reveal the time course of the instantaneous frequency of single ripple events, we located the maximum activation at every time step in the spectrogram (see Fig. 3B, top, white). Likewise, the time course of the power was calculated by averaging the wavelet spectrogram across frequencies for every time step (see Fig. 3F). The duration of a transient response was calculated as the length of the time interval during which the power exceeded 4 SDs above the baseline, where the baseline corresponds to the mean power generated by the network in response to the background input activity. The power spectrum was calculated by averaging the wavelet spectrogram across time for each frequency (see Fig. 3E). The leading frequency was obtained from the peak of the power spectrum. The unit firing rate was calculated by dividing the number of spikes the interneurons generated during an event by the duration of the transient response.

Model of extracellular field ripples.

We assumed that ripples in the extracellular field, as measured in the CA1 stratum pyramidale, are mainly generated by perisomatic inhibitory currents in pyramids, and that such currents reflect the collective activity of PV⁺ BCs (Schlingloff et al., 2014; Gan et al., 2017). To obtain an approximation of the LFP of ripples from our model, we assumed that the perisomatic inhibitory activity experienced by interneurons in the network is similar to that experienced by CA1 pyramidal cells. We therefore considered the bandpass filtered (120–300 Hz) average inhibitory current experienced by the population of interneurons as an approximation for the LFP ripple in CA1 (see Figs. 3H and 8C). It could be argued that GABA_A channels expressed in the perisomatic area of pyramids have peak conductances and decay time constants different from those in interneurons. However, because here the purpose of modeling the LFP is simply to evaluate phase locking (see Fig. 3) and to illustrate qualitative changes in LFP ripple amplitude as caused by drugs that alter GABA_A parameters (see Fig. 8), the initial (control) condition of such parameters and their absolute amplitudes are irrelevant.

Slice preparation and electrophysiology in vitro.

Experimental procedures were similar to those described previously (Maier et al., 2009). Briefly, horizontal slices (400 μm) were prepared from ventral to mid-hippocampus of C57Bl/6 male mice 3–4 weeks old, and slices were maintained in an interface chamber superfused with oxygenated ACSF at ∼35°C. ACSF contained the following (in mm): 119 NaC, 2.5 KCl, 1.3 MgSO₄, 2.5 CaCl₂, 10 glucose, 1.0 NaH₂PO₄, and 26 NaHCO₃. Osmolarity of ACSF was routinely checked to range between 290 and 310 mosmol/L. Slices were incubated for 1–4 h before being transferred to a submerged chamber for recordings at 31°C-32°C. Extracellular LFPs from the CA1 field were recorded with ACSF-filled borosilicate glass electrodes of 0.2–0.3 MΩ resistances. Within a distance of ∼160 μm from the LFP electrode (range, 37–157 μm), simultaneous whole-cell recordings were performed from two pyramidal cells. Borosilicate glass electrodes (2–5 MΩ) were filled with Cs-based intracellular solution that contained the following (in mm): 120 gluconic acid, 10 KCl, 2.0 MgSO₄, 3.0 MgATP, 1.0 NaGTP, 5.0 EGTA, 10 HEPES, and 2–3 mg/ml biocytin, pH adjusted to 7.4 with CsOH. Signals were amplified 1000×, low-pass filtered at 0.7 or 2 kHz and 4 or 8 kHz (LFP and intracellular signals), sampled at 16 bit resolution (National Instruments), and digitized at 10 or 20 kHz. Data were recorded in Igor Pro (WaveMetrics) using a Multiclamp 700A amplifier (Molecular Devices). Series resistance (R_S) was monitored continuously throughout experiments; cells were rejected if R_S exceeded 20 MΩ or varied >30% during recordings or between cells recorded in parallel. No R_S compensation was used. Voltages were not corrected for liquid junction potentials.

Experimental design and statistical analysis.

Experimental data were obtained from seven hippocampal slices from 5 male mice (Mouse 1: three slices; Mice 2–5: one slice each). SWR-associated postsynaptic currents were simultaneously recorded from pairs of CA1 pyramidal cells. Obtained data were used to test theoretically formed predictions. No statistical comparisons were performed. Data in the text are presented as mean ± SD.

Results

The basic building block of inhibition-first models of hippocampal ripples is a network of recurrently connected PV⁺ BCs (Klausberger et al., 2003; Katona et al., 2014; Schlingloff et al., 2014; Gan et al., 2017). We therefore began by analyzing the oscillatory response of an in silico model of such a network of interneurons to different configurations of excitatory drive. The model, which aimed at describing the scenario in CA1 in an acute hippocampal slice and in a local network in vivo, consisted of a population of 200 interneurons that were randomly interconnected via fast GABAergic synapses with a connection probability of 20%. Excitatory input was delivered either directly by a population of 8200 CA3 pyramidal cells or indirectly by depolarizing a subpopulation of local CA1 pyramidal cells (as in Stark et al., 2014). Both pyramidal cell populations were randomly connected to the interneurons via fast AMPA-type synapses with a connection probability of ∼10%. Interneurons projected back only to the local pyramidal cells with probability 30% (Pawelzik et al., 2002) (for a motivation of this particular choice of numbers, see Materials and Methods). The magnitude of excitation delivered to the interneuron network was described by the total input rate, which corresponds to the average number of excitatory synaptic events per unit time experienced by a typical interneuron. Alternatively, input was also described in terms of the mean excitatory conductance per interneuron.

Steady-state oscillations in a model of the CA1 BC network

We set off by analyzing the oscillatory response of an isolated CA1 interneuron network driven by constant levels of spiking excitatory activity. In such a direct-drive condition, there were no feedback projections from the interneurons to the driving excitatory population.

Previous modeling studies have shown that interneuron networks subject to constant levels of excitatory input can sustain two distinct modes of oscillation that respond differentially to the magnitude of the excitatory drive. In the sparsely synchronized mode, the frequency is insensitive to the input drive (Brunel and Wang, 2003; Brunel and Hakim, 2008), whereas in the fully synchronized mode, the network frequency increases monotonically with the input drive (Traub et al., 1996; Wang and Buzsáki, 1996). Here, we reproduce and extend these generic results in our specific hippocampal model, and we show how low and high input rates favor the emergence of sparsely and fully synchronized oscillations, respectively (Fig. 1). We focus on the dependence of network oscillation frequency on input rate because it provides the basis to explain the phenomenon of IFA that emerges in the transient response, which we study later in this manuscript (see Figs. 2–5).

Figure 5.

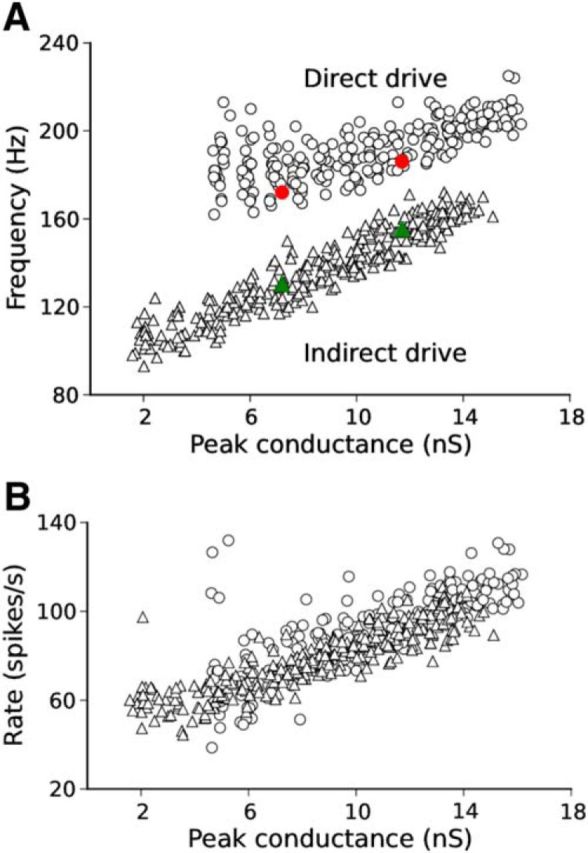
Network-frequency response for indirect versus direct drive of interneurons. A, Network frequency as a function of the peak input conductance to interneurons. For indirect drive (triangles, 280 simulations), the network frequency increased linearly with peak conductance, covering the fast-gamma range (90–140 Hz) and part of the lower ripple band (range, 93–172 Hz). For direct drive (circles, 240 simulations), frequency was limited to the ripple band (range, 162–225 Hz). B, Firing rate of interneurons as a function of the peak input conductance to interneurons. Units expressed similar firing rates in both direct (open circles) and indirect (open triangles) conditions. Green triangles and red circles correspond to the examples shown in Figure 4B and Figure 4D, respectively.

We first delivered a persistent stimulation to the CA1 interneuron network by allowing each pyramid in the CA3 population to fire randomly at a constant rate that was varied between 1.3 and 19.3 spikes/s. Given that each interneuron has ∼780 AMPA-type synapses (see Materials and Methods), the total input rates varied between 1000 and 15,000 spikes/s.

Driving strength modulates the oscillatory regime

Figure 1A shows the response of the network when a total input rate of 3000 spikes/s was applied to each interneuron. At such an input level, a prominent and stable ripple-like oscillation was apparent in the population activity throughout the stimulation (Fig. 1A, top). Interestingly, oscillations in the population activity emerged from units that fired irregularly, as indicated by the rastergram (Fig. 1A, middle). The membrane potential of a typical interneuron in the network showed subthreshold oscillations that reflected the oscillatory population activity (Fig. 1A, bottom). Such oscillations of the membrane potential constrain the timing of the spiking response of interneurons by providing windows of opportunity at which they are more likely to fire. Random fluctuations, here due to the Poissonian excitatory drive, occasionally depolarize the membrane potential above threshold. As a result, units skip cycles randomly, giving rise to a firing pattern that is irregular but in phase with the population activity. The prominence and coherence of network oscillations were further revealed in the spectrum of the population activity by a peak at ∼187 Hz (Fig. 1B, top, gray). In contrast, the distribution of firing rates in the population showed that units fired at a broad range of rates, and firing rates were much lower than the frequency of the oscillatory population activity (Fig. 1B, bottom, gray) (Bähner et al., 2011).

The behavior of the interneuron network at such a weak input rate (3000 spikes/s) was consistent with “sparsely synchronized oscillations” (Brunel and Hakim, 2008). Such a regime emerges in conditions of high noise, and it is characterized by units that fire irregularly at rates lower than the frequency of the oscillations in the population activity (Brunel, 2000; Brunel and Wang, 2003). In this regime, the network frequency is determined by the delay of the recurrent interactions (transmission latency and rise time of IPSCs), and it is therefore largely independent of the level of excitation provided (Brunel and Wang, 2003).

Consistent with the sparsely synchronized regime, a doubling in the excitatory input from 3000 spikes/s to 6000 spikes/s shifted the distribution of interneuron firing rates toward much higher values, but the network frequency increased only by 3% (Fig. 1B, gray, orange). However, when the input strength was increased beyond 6000 spikes/s, also the network frequency markedly increased with input strength (Fig. 1B, top). This change of behavior was accompanied by an increasingly larger fraction of units firing at rates close to the network frequency (Fig. 1B, bottom). Such a change in the network response with increasing input rate suggested a change in the oscillatory regime. Figure 1C shows the response of the network when a total input rate of 9000 spikes/s was applied. In stark contrast to the situation depicted in Figure 1A, oscillations in the population activity (Fig. 1C, top) emerged from units that fired regularly and rarely skipped cycles (Fig. 1C, middle, bottom). Accordingly, units fired at mean rates close to the peak frequency of the oscillatory population activity (Fig. 1B, green).

The behavior of the interneuron network at such a high input rate (9000 spikes/s) was consistent with “fully synchronized oscillations” (Brunel and Hakim, 2008). In this mode, units fire regularly at rates close to the population frequency, as also demonstrated previously in interneuron network models expressing gamma oscillations (Traub et al., 1996; Wang and Buzsáki, 1996; Bartos et al., 2002).

Although such a transition from sparse to full synchrony in response to increased input rate was predicted by previous theoretical studies (Brunel and Wang, 2003), an in depth understanding of underlying mechanisms is still lacking. Figure 1D summarizes such a transition by showing key properties of the network as a function of input rate. Figure 1D (top) shows that a minimum input rate of ∼2000 spikes/s was sufficient to generate a ripple-like network oscillation (∼186 Hz). The network exhibited sparsely synchronized oscillations at input rates between ∼2000 and ∼6000 spikes/s where the unit firing rate remained well below the network frequency. At input rates ≳6000 spikes/s, the network entered a state that resembled a fully synchronized regime where the network frequency and the firing rate were similar, and both increased monotonically with input rate. Thus, an indicator for the regime is the ratio of firing rate and network frequency (i.e., the fraction of the population recruited in any given cycle), which we called the network saturation (Fig. 1D, middle). Saturation increased with increasing input rate. The unit activity became also more regular, which is quantified by the decreasing CV of the interspike intervals. We refer to a CV ≳ 0.5 as a high-noise state of the network, where units fire irregularly, whereas ≳0.5 will be termed low-noise state, where units fire regularly. Another marker for the regime is the coherence of the network oscillations (Fig. 1D, bottom). Coherence increased rapidly with increased input rate during the high-noise state and saturated in the low-noise state.

Mechanisms underlying the regime transition

To better understand the network behavior at different input rates, we studied the time course of membrane potentials across units in relation to the oscillatory population activity at different levels of excitatory drive. Figure 1E shows an input rate that increases abruptly every 20 ms (top), the resulting population activity (middle), and the underlying distribution of membrane potentials (bottom).

The basic process sustaining the oscillations in the population activity can be explained as follows (Brunel and Hakim, 1999; Brunel and Wang, 2003): We consider a trough of the oscillatory distribution of membrane potentials shown in Figure 1E (bottom) as the starting point of a cycle. At that point, all the units are below threshold; therefore, the population is silent. The excitatory input charges the membranes of the interneurons, pushing the distribution of membrane potentials toward more depolarized values. Eventually, part of the distribution reaches the threshold (Fig. 1E, bottom, dashed line) and the corresponding subset of units fires (Fig. 1E, middle). Conduction and synaptic delays introduced by the recurrent connections allow the spiking activity to further build up before being fed back to the network as inhibitory currents. The inhibitory currents induced by the population activity shift the distribution of membrane potentials to more hyperpolarized values, and thereby the spiking activity is reduced and eventually silenced. As inhibitory currents decay, the excitatory input recharges the membranes. The distribution of membrane potentials is again pushed toward depolarized values, and a new cycle is initiated.

How is this process affected by the level of excitatory input? At an input rate of 3000 spikes/s, where the sparsely synchronized regime is expressed (Fig. 1E, t < 0 ms; see also Fig. 1A), the membrane potentials were highly variable across cells due to the uncorrelated noisy input. In this case, the noise in the system is not only resulting from the random excitatory activity but also from the mostly irregular inhibitory activity that was delivered by the network itself via sparse recurrent connections (Brunel and Hakim, 1999).

At an input rate of 3000 spikes/s, a large fraction of the units remains subthreshold at any given time point, and the mean membrane potential is oscillatory. In such a condition, population activity is generated via noise fluctuations, preferentially near the maxima of the mean membrane potential (see also Fig. 1A, bottom). Under this fluctuation-driven regime (Renart et al., 2006), stable network oscillations are possible only if the sinusoidal mean and the population activity are mutually consistent in phase and amplitude (Brunel and Wang, 2003; Brunel and Hansel, 2006). The phase consistency limits the frequencies at which oscillations can be expressed to a narrow range that is mostly determined by the latency and rise time of inhibitory synaptic transmission. The amplitude consistency, on the other hand, allows some variability in the firing rate of single units (e.g., due to changes in excitatory drive) without affecting the network frequency (for a detailed analysis, see Brunel and Wang, 2003).

Figure 1E (middle) (0 < t < 20 ms) shows the behavior of the population when the input rate was doubled to 6000 spikes/s. Because of the stronger excitatory currents, the distribution of membrane potentials exhibited a steeper ascending phase (increase in the voltage-time derivative), the “escape rate” at the firing threshold increased, and more units fired before this activity affected the network in the form of inhibitory currents. Because more cells were recruited in any given cycle, the amount of negative charge delivered back to the network was larger, and the membrane potentials were shifted toward more hyperpolarized values. Thus, the steeper ascending phase of the membrane potential distribution (due to a stronger excitation) was compensated for by a more hyperpolarized trough (due to the increased inhibitory activity). As a result, the network frequency was similar for input rates of 3000 and 6000 spikes/s, although the mean firing rates were approximately doubled. However, this doubling of the input rate led to a narrower distribution of membrane potentials (Fig. 1E, t > 0 ms), and nearly all the units reached the threshold (dashed line) and fired within a small fraction of a cycle. In this case, the strong network synchronization has introduced correlations in the inhibitory synaptic activity, reducing the variability of membrane potentials across the population, and thereby the noise in the system (Brunel, 2000); the network has entered a mean-driven or low-noise regime, as predicted by Brunel and Wang (2003).

Once a large fraction of the population is recruited at a cycle, further increases in excitatory input can no longer be compensated for by a larger recruitment of interneurons. To illustrate this effect, let us consider the transition from the input rate 6000 to 12,000 spikes/s depicted in Figure 1E at time t = 20 ms. In this case, the fraction of units recruited in a cycle increased only from ∼0.8 to ∼0.9, which means that the inhibition fed back to the network in a given cycle only slightly increased, and could therefore not compensate the doubled excitatory input. Thus, the oscillation period is dominated by the duration of the ascending phase of the membrane-potential distribution, which depends on the level of mean excitatory drive.

In summary, the amount of excitatory drive can modulate the oscillatory state of a recurrent interneuron network. At low input rates, the network expresses sparsely synchronized oscillations, where the network frequency is relatively insensitive to changes in input rate. With increasing input rates, the network frequency becomes gradually more sensitive to excitation as it transits toward a fully synchronized regime. In line with previous models that investigated the latter type of oscillations (Traub et al., 1996; Wang and Buzsáki, 1996), the network frequency increases monotonically with increasing excitatory drive.

Network response to direct transient stimulation

So far, to explain basic oscillatory regimes, we have analyzed the response of a CA1 interneuron network only to persistent stimulation, which is an unrealistic scenario given the transient nature of SWRs. During SWRs, interneurons in the CA1 network experience an excitatory current that increases and decreases within a few tens of milliseconds (Buzsáki and Chrobak, 1995; Csicsvari et al., 2000; Schlingloff et al., 2014; Stark et al., 2014). To understand the network dynamics during such a transient activation, we first focused on the response of the network to excitatory activity that increased and decreased linearly (Fig. 2). Here, we show that the frequency is relatively stable during the ascending phase of excitation, but it decays monotonically during the descending phase. As a consequence, when the network is driven by a burst of activity resembling that of pyramidal cells in CA3 during a SWR, the transient response exhibits IFA (Fig. 3), as in experiments.

Network response to changing input rate exhibits synchrony hysteresis

We analyzed the response of the interneuron network to random spiking activity that was modulated by a double ramp input as the one depicted in Figure 2A (top, gray). In this example, the input rate increased from a baseline of 1200 spikes/s to a maximum of 9000 spikes/s within 40 ms. After remaining in a plateau for 40 ms, it decreased back to baseline with the same slope as the ascending phase. Remarkably, the network response (top, black) exhibited a prominent asymmetry with respect to the input (top, gray): The population started synchronizing at ∼220 Hz in the middle of the ascending phase of excitation (t ≈ −20 ms). In contrast, the population persisted oscillating during the entire descending phase (40 ms ≤ t ≤ 80 ms), at decelerating frequency.

To study this asymmetry in more detail, we tracked the evolution of the network state by observing the membrane potential distribution underlying the network activity (Fig. 2A, bottom). At an initial stage, the population exhibited a wide distribution of membrane potentials that hovered below the threshold (Fig. 2A, bottom, t ≲−20 ms). In the middle of the ascending phase of the excitatory activity (−20 ≤ t <−10 ms), the network exhibited a short phase of a high-noise oscillatory state (Fig. 2A, top; see also Fig. 1E; t < 20 ms). At this time interval, the increase in excitatory drive was counterbalanced by the increase in network (i.e., inhibitory) activity. This compensation was also reflected in the increasing amplitude of the membrane potential oscillations; that is, membrane potentials gradually reached more hyperpolarized values until the network entered a low-noise state (t ≈−10 ms). Interestingly, after the end of the plateau (t > 40 ms), the saturated network remained synchronized in a low-noise state for almost the entire descending phase of excitation.

The state transition from the asynchronous irregular balanced state to the high noise oscillatory activity observed during the ascending phase of excitation predicts an onset frequency that is independent of the ramp slope and amplitude. According to Brunel and Wang (2003), oscillatory instabilities of the initial balanced state depicted in Figure 2A (bottom, t ≲ −20 ms) emerge when a critical level of interneuronal activity is reached. Such oscillations appear with an onset frequency that is exclusively determined by the time constants describing the dynamics of the GABAergic synaptic transmission. With the parameters used in our model, their theory predicts an onset frequency of ∼237 Hz (Brunel and Wang, 2003, their Eq. 16), which is consistent with our simulations (see below). The subsequent low-noise oscillatory state observed during the plateau and descending phase of the input predicts that the frequency should be modulated by both the ramp amplitude and its descending slope. Such a behavior has been observed in a previous low-noise model subject to decaying excitatory drive (Traub et al., 1996).

To test these predictions in a systematic way, we analyzed the network response to double ramps with different amplitudes and slopes (Fig. 2B, top). In this manner, we could gradually drive the network activity from baseline toward different levels of saturation and then back to baseline at different speeds. For each input-rate profile (Fig. 2B, top), we calculated the instantaneous frequency (Fig. 2B, middle) from the time interval between the peaks of the population activity, and the saturation (Fig. 2B, bottom) by determining the fraction of units that were active within a cycle (see Materials and Methods). Each average curve for the instantaneous frequency and the saturation was obtained from 50 responses.

We first focused on the response to double ramps that reached different plateau levels at a fixed slope (Fig. 2B₁, top). Consistent with an initial condition of high noise (Fig. 2A, t <−20 ms), the onset frequency at which oscillations emerged during the ascending phase (Fig. 2B₁, middle, solid lines) was ∼220 Hz, which was close to the ∼237 Hz predicted by the theory (Brunel and Wang, 2003, their Eq. 16). Once the input reached its plateau (Fig. 2B₁, t = 0), the frequency settled at the steady-state value of the respective input level (Fig. 2B₁, middle, dotted lines; see corresponding colors in Fig. 1B,D). During the descending phase of the input (Fig. 2B₁, t > 40), the frequency decreased monotonically and followed the time course of the descending excitation down to frequencies much lower than those expressed during the rising phase (Fig. 2B₁, middle, dashed lines).

To characterize this hysteresis phenomenon in more detail, we plotted frequency and saturation as a function of the input rate (Fig. 2C₁). The frequency characteristic showed a markedly lower sensitivity to input rate in the ascending phase compared with the descending phase (Fig. 2C₁, top, solid and dashed lines, respectively). Such a differential sensitivity to the input rate was consistent with a much lower saturation expressed during the ascending phase compared with the descending phase (Fig. 2C₁, bottom, solid and dashed lines, respectively).

We hypothesized that the hysteresis characteristic of the saturation, which captures the noise asymmetry in the system, is mediated by the temporal lag of the instantaneous population activity with respect to the excitatory input that drives it: Once oscillations are established, every peak of activity in the transient response (e.g., Fig. 2A, top, black) results from the interaction between excitation and inhibition during the preceding oscillation cycle. Thus, during the ascending phase, every peak of interneuronal activity provides an inhibitory input that is confronted with an excitation that is higher than the one that generated the peak. The opposite occurs during the descending phase, where the synchronized inhibition is confronted with a subsequent lower excitation. Thereby, the ascending phase is dominated by random excitation, which increases noise, and the descending phase is dominated by synchronized inhibition, which reduces noise.

This mechanism predicts that the prominence of the hysteresis effect should be modulated by the slopes of the input ramps: An input that grows and decays with shallower slopes can be tracked more closely by the network response, and thereby the balance mismatch is reduced. To test this prediction, we focused on the response to double ramps that reached a plateau of 9000 spikes/s in 10, 20, or 40 ms (Fig. 2B₂, top). Again, the onset frequency at the ascending phase (Fig. 2B₂, middle, solid lines) was ∼220 Hz, regardless of the ramp's slope. In contrast, during the descending phase, the frequency was strongly modulated by the input rate (Fig. 2B₂, middle, dashed lines). The prominence of the saturation hysteresis (Fig. 2C₂, bottom), which is typically described by the area between the ascending and descending characteristics (Fig. 2C, bottom, solid and dashed lines, respectively), increased with steeper slopes. This behavior was confirmed in simulations where different ramp slopes were combined with different plateau levels of the input (Fig. 2B₃,C₃).

To conclude, Figure 2 supports the idea that the network begins to synchronize in a high-noise state during the ascending phase, where the frequency is relatively insensitive to the excitatory input. After reaching saturation during the plateau, the network remains in a low-noise state during the descending phase, where the frequency decays with the decreasing excitation.

Intraripple frequency dynamics

To connect our findings with experimental results, we studied the response of the interneuron network to excitatory input that resembled the activity of pyramidal cells in CA3 during an SWR (Fig. 3A). In particular, we aimed at testing the predictions of the noise-state transition (Fig. 2) in a more realistic model of SWRs. Here, an excitatory burst was generated by allowing 1400 units (∼17% of the population of CA3 pyramidal cells in a slice) to fire once at a random time drawn from a normal distribution with SD = 7 ms (Hájos et al., 2013). The remaining ∼6800 CA3 pyramidal cells fired randomly at a rate ∼1.85 spikes/s, providing a total input rate of 1200 spikes/s. Such a background activity summarizes the synaptic noise due to random spiking and spontaneous synaptic release stemming from both local and CA3 pyramidal cells (for details, see Materials and Methods).

In response to such a stimulation (Fig. 3B, middle, gray), the interneuron network generated a few cycles of oscillatory activity in the ripple-frequency range (Fig. 3B, middle, black). This time, we obtained the instantaneous frequency of the population activity (Fig. 3B, top, white line) from its wavelet spectrogram (Fig. 3B, top), for better comparison with experimental results. During the first half of the event, the ripple frequency exhibited a peak that was followed by a monotonic decrease during the second half. Such a signature in the instantaneous frequency has been reported in the literature and termed IFA (Ponomarenko et al., 2004; Nguyen et al., 2009; Sullivan et al., 2011).

The IFA in the simulations in Figure 3D resembled the asymmetry of the frequency response with respect to the input that we observed during the double-ramp stimulation (Fig. 2B, middle). If both situations share the same mechanism, we should be able to observe a noise transition in the burst response, mediated by a lag of the network activity with respect to the input (as in Fig. 2A). Indeed, the burst response (Fig. 3B, middle, black) conformed a modulated oscillation with an envelope that lagged the transient input (Fig. 3B, middle, gray) by a few milliseconds. Such a delayed response with respect to the input generated a time course of synaptic activity that was initially dominated by excitation (Fig. 3B, bottom, red), which increases noise in the system, and a subsequent phase that was dominated by synchronized inhibition (Fig. 3B, bottom, blue), which reduces noise. The time axis was centered (t = 0) to the peak of the mean excitatory current because this enables a comparison with the in vitro experiments described below. Consistently, the distribution of membrane potentials in relation to the network activity (Fig. 3C) showed a gradual transition from a high-noise state toward a low-noise state that persisted for most of the descending phase of excitation (Fig. 3C, bottom; as in Fig. 2A).

Input burst width affects frequency dynamics

The proposed mechanism governing IFA predicts that the prominence of the effect can be reduced by providing a transient excitatory stimulus that develops more slowly (as in Fig. 2B₂,C₂). To test this prediction, we analyzed the response of the model to input bursts with different widths. The burst width was specified by the SD of the distribution from which the spike times of the driving population were drawn. Narrower distributions give rise to input rates that develop faster and exhibit higher peak values. Because every unit in the driving population fires once during the burst, the burst width affects only the rate at which spikes are delivered to the network; the total number of input spikes (∼1400) generated during a single burst remains unchanged.

Figure 3D shows the average IFA signatures obtained at three different values of input burst widths (σ = 5, 7, and 10 ms). Such burst parameters provided input slopes and amplitudes similar to those of the double ramp depicted in Figure 2B₃ (top, see corresponding colors). Consistent with an initial high-noise state, the onset frequency remained nearly the same for the three conditions. Broader input bursts (larger σ) stretched the IFA signature in time, resulting in frequency traces that started to decay earlier and slower. To quantify this effect, we show in Figure 3E, F the normalized power spectra and the time courses of power in the ripple band for the three analyzed conditions, respectively. Broader and lower-amplitude input bursts generated responses with lower frequencies (Fig. 3E), lower maximum power, and longer durations (Fig. 3F). The mean firing rate decreased with broader input bursts (Fig. 3G).

To conclude, IFA can be explained by interactions within the interneuron network. Its delayed response to the excitatory input burst generates a time course of synaptic currents that is initially dominated by coarse excitation and later by the synchronized inhibition. This timing of excitation and inhibition initially favors the emergence of a high-noise, sparsely synchronized state characterized by a high oscillation frequency, and later favors a low-noise, fully synchronized state in which the network frequency is sensitive to the decreasing input drive.

Entrainment of oscillations in CA1 by CA3 input

So far, we have considered CA1 interneuron networks that receive transient excitatory input devoid of ripple-like oscillations. However, CA3 cells are entrained by ripples in their local network (Maier et al., 2003; Both et al., 2008; Tukker et al., 2013), which adds an oscillatory component to the CA1 input (Sullivan et al., 2011; Schönberger et al., 2014). Despite such a ripple-modulated drive, CA1 can oscillate independently from CA3, typically at higher frequencies (Maier et al., 2003, 2011; Sullivan et al., 2011). Notwithstanding, spikes of CA3 pyramidal cells can be coupled to the ripple oscillations in CA1 (Both et al., 2008; Sullivan et al., 2011).

To test whether interneuron networks in CA1 can generate ripple oscillations independently of those stemming from CA3, and to assess the prominence of phase locking between the CA3 spikes and the CA1 ripple, we performed numerical simulations with ripple-modulated excitatory input (Fig. 3H,I). The example in Figure 3H shows a CA3 Gaussian excitatory burst with σ = 7 ms (same as in Fig. 3B) whose spikes are entrained by a 180 Hz rhythm with a vector strength v_s = 0.2 (for details, see Materials and Methods). The CA1 network oscillated at ∼200 Hz, which was similar to the case without ripple-locked input (Fig. 3E). In Figure 3H, the spikes in CA3 (dots) were coupled to the CA1 LFP ripple (black trace) with a vector strength of ∼0.08.

Figure 3I summarizes the dependency of the CA1 frequency on the CA3 input frequency for three different CA3 input vector strengths (v_s = 0.1, 0.2, and 0.4; for details, see Materials and Methods), and the resulting coupling (color coded) of CA3 spikes to CA1 ripples. At physiologically feasible CA3 modulations (v_s = 0.1 and v_s = 0.2, left and middle, respectively), ripple events in CA1 oscillated at ∼200 Hz, almost independently of the CA3 input frequency. Nevertheless, CA3 spikes were phase-locked to CA1 ripples, and the locking was strong when the CA3 frequency was close (± 10%) to CA1's intrinsic frequency ∼200 Hz. For high CA3 modulation (v_s = 0.4; Fig. 3I, right), the CA1 frequency was affected by the CA3 frequency, and phase locking of CA3 and CA1 was prominent for a wider range of frequencies.

The numerical simulation at CA3 input vector strength v_s = 0.2 (Fig. 3I, middle) could account for the experimental results by Both et al. (2008), who reported a coupling strength between CA3 units and the LFP in CA1 of ∼0.22 during ripples in vitro (for a derivation of this number, see Materials and Methods). If we assume that the CA3 input vector strength is v_s ∼0.2 and consider a CA3 oscillation frequency ∼10% below the CA1 natural frequency, as observed in vitro (Maier et al., 2003; Both et al., 2008), one could expect a coupling of CA3 spikes to the CA1 LFP of 0.2. The much lower CA3 spike to CA1-LFP coupling observed in vivo, on the other hand, could be explained by the larger and more variable frequency difference between the two areas and/or by a weaker local entrainment of CA3 pyramidal cells (Sullivan et al., 2011; Buzsáki, 2015).

In conclusion, the interneuron network model is compatible with the idea that ripples are generated de novo in CA1 (i.e., not inherited from CA3) (Csicsvari et al., 1999; Sullivan et al., 2011), and it accounts for the apparent coupling between CA3 spikes and CA1 fields (Both et al., 2008; Sullivan et al., 2011). Because the topic of coupled oscillators is complex enough in itself, in what follows we return to CA3 input that is not ripple-locked. This simplification will allow us to uncover further interesting features of the generation of ripple oscillations within a local network, such as CA1.

Network response to indirect transient stimulation

In the previous section, we showed that the slow time course of excitation plays a pivotal role in the development of IFA (e.g., Fig. 3D). However, we only considered the case of an isolated interneuron network that is driven by a feedforward excitatory projection (Schaffer collaterals from CA3). In such a scenario, interneurons cannot provide inhibitory feedback to the pyramidal cell population that is driving them. How would the frequency dynamics be affected when interneurons are driven by the local pyramidal cells in CA1 to which they also project? Would IFA be disrupted in such a closed-loop scenario? To address these questions, we extended the interneuron network model by including local pyramidal cells. The parameters describing the pyramidal cells were adjusted according to Bähner et al. (2011). In this new model, the 200 units in the interneuron network were reciprocally interconnected with a population of 12,000 CA1 pyramids. Pyramids were randomly connected to the interneurons with a probability p_c = 0.1 via fast AMPA-type synapses (Pawelzik et al., 2002). The interneurons, in turn, were connected back to the pyramids with probability p_c = 0.3 (Pawelzik et al., 2002) via fast and strong GABA-type synapses (Bartos et al., 2002). Pyramids were also reciprocally and sparsely interconnected with probability p_c = 0.01 via AMPA-type synapses (for details, see Materials and Methods).

Induced high-frequency oscillations in silico

To analyze the response of the closed-loop network upon depolarization of local pyramidal cells, we implemented an in silico version of the experiment described by Stark et al. (2014). In this experiment, fast oscillations (>80 Hz) were evoked by optogenetic depolarization of a small group (80–100) of pyramidal cells in CA1. Such induced high-frequency oscillations provide a model of hippocampal SWRs that is amenable to an in silico implementation.

To emulate this experiment, pyramids in the model were equipped with excitatory conductances aimed at mimicking channelrhodopsins. To evoke induced high-frequency oscillations in the model, a random subpopulation of 100 pyramids was depolarized by driving their excitatory conductances with Gaussian intensity profiles (σ = 13 ms). The peak conductances applied to the cells were normally distributed across the population with CV = 0.5 (see Materials and Methods) to provide variable levels of input to the pyramids (Fig. 4A, solid and dashed green traces: mean ± SD, respectively).

Figure 4B shows the response of the network at two levels of mean input conductances to the pyramids, as depicted in Figure 4A (left and right, respectively). Both pyramids and interneurons displayed a transient oscillation in their population activities, with pyramids leading interneurons (Fig. 4B₁, gray and black, respectively). Consistently, interneurons experienced strongly modulated excitatory and inhibitory inputs (Fig. 4B₂, red and blue, respectively). At low excitatory input to pyramids (30 nS, left), the transient response exhibited IFA at ∼130 Hz (Fig. 4B₁, top left). When the input to pyramids was increased to 60 nS (right), the frequency of the oscillation increased to 155 Hz, but the instantaneous frequency lost the stereotypical IFA shape (Fig. 4B₁, top right).

With increasing input level, the interneuron network responded not only with a higher network frequency but also with stronger activity (Fig. 4B₁, black), resembling a state of higher saturation. As a consequence, for high enough input, the network achieved a level of high saturation already at the beginning of the event, as evidenced by the instantaneous frequency that followed the time course of the excitatory input.

Network response under indirect versus direct drive

We have shown that, during the indirect-drive condition, interneurons experienced strongly modulated excitatory activity stemming from the entrained population of pyramids (Fig. 4B₂, red). We wondered how the isolated interneuron network would respond if it was directly driven by the same levels of excitatory input but devoid of oscillatory modulation. To do that, we equipped the interneurons with the same channelrhodopsin-mimicking conductances used to depolarize pyramids and directly drove them with Gaussian bursts, as in Schlingloff et al. (2014) (Fig. 4C). During this direct-drive condition, the Gaussian bursts in Figure 4C were tuned to resemble a low-pass (<30 Hz) version of the excitatory conductances depicted in Figure 4B₂ (light red). The slow (<30 Hz) component of such conductances exhibited average peaks of 7 and 12 nS, both with a variability of CV = 0.28 across cells. Both mean traces were approximately Gaussian with σ = 14 ms. When those conductances were directly delivered to the interneurons, the network activity displayed oscillations at frequencies of ∼172 Hz and ∼186 Hz (Fig. 4D₁, top left and right, respectively). Compared with the indirect-drive condition, it was apparent that the interneuronal network activity was lower (Fig. 4D₁, black). This lower unit activity during the direct-drive condition is indicative of a lower state of saturation of the network, which explains why the IFA signature was rescued at higher channelrhodopsin input in this condition (Fig. 4D₁, top right).

The phenomenology described in Figure 4 suggests that the network frequency exhibits different responses to excitatory input under the indirect-drive versus the direct-drive conditions. To characterize this differential response in a systematic way, we focused on the network frequency in response to a wide range of input levels that were delivered under both conditions (Fig. 5A). In both cases, we explored a range of excitation levels that evoked firing rates of interneurons within the physiological range observed in vivo (Lapray et al., 2012; Varga et al., 2012; Katona et al., 2014) (Fig. 5B).

For the direct-drive condition, we tested a range of peak conductances spanning from 4.5 nS (the minimum required to evoke oscillations) to 16 nS. Oscillations evoked in this condition exhibited frequencies constrained to the ripple band (range, 162–225 Hz; Fig. 5A, circles). Remarkably, this range of frequencies resembled those observed in vitro (e.g., 160–240 Hz) (Maier et al., 2011). Frequencies were also only weakly sensitive to the peak excitatory input delivered (see also Fig. 1D). In this direct-drive condition, network frequencies were considerably higher than the unit firing rates (Fig. 5A,B, respectively, circles), yielding saturation levels that ranged from 30% to 50%. Consistently, network frequency became gradually more sensitive to input at higher input levels (see also Fig. 1D).

For the indirect-drive condition, on the other hand, we applied peak conductances to the pyramids within a range from 10 to 75 nS. This range of input resulted in peak excitatory conductances to the interneurons spanning from 1.5 to 15 nS. For easier comparison with the direct-drive condition (Fig. 5A, circles), we plotted the network frequency of each event in the indirect-drive condition as a function of the average peak of the filtered (<30 Hz) excitatory input experienced by interneurons (Fig. 5A, triangles). Within the range of inputs tested, the network frequency increased linearly with excitatory input to interneurons, covering almost the entire fast-gamma range and part of the ripple band (range, 93–172 Hz). These results indicate that the network operated at a high saturation level. Indeed, if we consider the ratios of unit firing rate to their corresponding network frequencies for that condition (Fig. 5B,A, respectively, triangles), we can estimate a saturation of ∼60% for the entire range tested. Consistent with such a level of saturation, the interneuron network frequency increases with excitatory input (see also Fig. 1D).

In summary, oscillations evoked in transiently excited interneuron networks can exhibit IFA when the interneurons are driven both directly or indirectly by depolarization of the local pyramids to which they project. Under direct drive, IFA is robust, but its expression is limited to the ripple band. On the other hand, in oscillations evoked by depolarization of local pyramidal cells, as in Stark et al. (2014), IFA is limited to the fast gamma band. In both cases, when IFA is expressed, the model predicts a peculiar relationship between the time courses of the instantaneous frequency and the transient excitatory input to interneurons: the network frequency exhibits a peak during the ascending phase of excitation (Figs. 3D, 4B₁, left, D₁).

Frequency dynamics during ripples in vitro

To test the prediction of the in silico model, that the maximum frequency precedes the peak of excitatory input, we resorted to a previously established in vitro model of hippocampal SWRs in CA1 (Maier et al., 2009). In this preparation, we aimed at tracking the instantaneous frequency of the putative interneuron network activity while simultaneously observing the time course of the excitatory input to CA1 during SWR events. In other words, we were specifically interested in the fine temporal “ripple” structure of inhibition and the slower temporal “sharp wave” structure of excitation. This information can be extracted from whole-cell recordings of pyramidal cells in voltage-clamp mode. However, inhibitory and excitatory currents cannot be measured simultaneously in a single cell. Hence, we performed simultaneous patch-clamp recordings from two neighboring pyramidal cells within area CA1. By isolating excitatory synaptic activity in one cell and inhibitory synaptic activity in another, we could extract the relevant information to test the model prediction.

The described approach rests on the assumption that the currents in two different pyramidal cells are correlated. This assumption is supported by the structure of the projections: pyramidal cells receive input from a large sample of converging inhibitory (mostly local collaterals) and excitatory (mostly Schaffer collaterals) fibers. Therefore, the synaptic current measured in a single cell can provide information about the overall activity of the respective converging population. To test this assumption, we first voltage-clamped pairs of pyramidal cells at the same holding potential and assessed the temporal relationship between the measured currents. Clamping both cells at the reversal potential of inhibition reveals excitatory currents. On the other hand, clamping both cells at the reversal potential of excitation reveals inhibitory currents. We first investigated these two cases in detail and checked whether inputs were indeed correlated.

Phase alignment of inhibitory ripples in pairs of pyramidal cells

Can the inhibitory current measured in one CA1 pyramidal cell provide information about the inhibitory current in another pyramidal cell? We reasoned that, if a pair of pyramids receives input from two inhibitory subpopulations that are entrained by a common rhythm (i.e., a ripple), the ripple-locked compound IPSCs recorded in the two cells should be temporally aligned or, equivalently, their ripple components should be phase-locked with a phase difference close to 0. Therefore, we analyzed the phase relationship between inhibitory ripples.

To isolate inhibitory currents, two simultaneously recorded cells were clamped at the reversal potential of excitation. In both cells, we observed compound IPSCs that co-occurred with the extracellularly recorded SWRs (Fig. 6A) and exhibited a temporal structure consistent with a rhythmic inhibitory input (Fig. 6A, bottom). For every SWR event, two inhibitory ripples were obtained from bandpass filtered currents (120–300 Hz). We then calculated the Hilbert transform of the two ripples and obtained their envelopes (Fig. 6B, top) and instantaneous phase angles. The instantaneous phase shift between the two ripple oscillations was obtained by subtracting the angles yielded by their respective Hilbert transforms (Fig. 6B, bottom). Then the phase shift of a single SWR event was calculated as the circular mean of the instantaneous phase shift in the time interval where both ripple envelopes exceeded 3 SDs of the baseline (Fig. 6B, gray box); and the quality of phase locking was described by the vector strength of the instantaneous phase shift during this overlap. The phase shift, which is an angle, and the vector strength, which is a number between 0 and 1, were determined for all SWR events recorded in a cell pair (Fig. 6C, gray circles). From all these phase vectors obtained in a simultaneous recording, we calculated an average phase vector (Fig. 6C, black circle). Inhibitory ripples were strongly phase-locked at low phase shift angles in all simultaneous recordings analyzed (Fig. 6D). For the seven recordings analyzed, the average vector strength was 0.76 ± 0.03 (range, 0.63–0.82) and the average phase shift was 2 ± 8 degrees (range, −32 to 31 degrees). The range of phase shifts observed corresponds to time lags <0.5 ms for a ripple frequency of 200 Hz. From these results, we conclude that the inhibitory input to one pyramid predicts the phase of inhibitory input to other pyramids well. Moreover, the inhibitory current can be used to assess the phase of the putative interneuron network activity and therefore its instantaneous frequency.

Figure 6.

Inhibitory and excitatory currents in pairs of CA1 pyramidal cells during SWRs in vitro. A, To isolate inhibitory currents, two cells were clamped at 6 mV. Top (black), Extracellular SWR. Bottom, Simultaneously recorded inhibitory currents (gray) and bandpass filtered versions (as indicated, blue). B, Magnification and overlay of the two filtered currents and their envelopes as derived from the Hilbert transform (top). The instantaneous phase shift (bottom, gray) between the two ripple oscillations was obtained by subtracting the angles yielded by their respective Hilbert transforms. The average phase shift (−4 degrees) and the quality of phase locking (vector strength 0.99) were estimated from the time span where both envelopes exceed 3 SD of baseline (gray box). C, Average phase shifts and vector strengths of inhibitory currents for 124 SWR events (gray circles) recorded in one cell pair. Black circle represents the average phase vector (phase shift: −32 degrees; vector strength: 0.81) across events. D, Average phase vectors for 7 cell pairs (symbols). E, To isolate excitatory currents, two cells were clamped at −55 mV. Top (black), Extracellular SWR. Bottom, Simultaneously recorded excitatory currents (gray) and low-pass filtered versions (as indicated, red). F, Overlay of the two filtered and rectified currents (top), their temporal derivatives (middle), and the cross-correlation of the derivatives (bottom). The maximum of the cross-correlation (0.97) indicates the strength of the correlation, and the time of this peak (0.7 ms) denotes the time lag of the two excitatory inputs for a particular SWR. G, Time lags as a function of the maximum correlation (top, gray dots) and histogram of maximum correlations (bottom) for 191 events (gray dots) recorded in one cell pair. Black circle represents the average correlation (0.79 ± 0.01) and the average time lag (0.9 ± 0.5 ms) across events. H, Average time lag versus average correlation for 7 cell pairs. The grand average time lag (across cell pairs) was −0.04 ± 0.54 ms (range, −2.9 to 1.4 ms).

Alignment of excitatory sharp waves in pairs of pyramidal cell

In a second set of experiments, we aimed at testing whether the time course of the excitatory current recorded in one pyramidal cell is a reliable predictor of the overall time course of excitatory input to the network. We reasoned that, if a pyramidal cell receives input from a large sample of Schaffer collateral fibers, we should be able to use the excitatory current recorded in any pyramid to track the time course of the excitatory burst. We specifically tested whether the slow component of excitation is aligned in pairs of pyramidal cells.

To isolate excitatory currents, two simultaneously recorded cells were clamped at the reversal potential of inhibition. In both cells, we observed ripple-locked compound EPSCs that co-occurred with the extracellularly recorded SWRs (Fig. 6E) (Maier et al., 2011). To keep track of the coarse excitatory input, we focused on the low-frequency components of the measured currents. For every SWR, we obtained a low-pass filtered version (0–50 Hz) of the co-occurring SWR-locked compound EPSCs. The rectified version of such a slow current describes the time course of the excitatory input that we refer to as excitatory sharp wave (eSW, Fig. 6F, top). To be able to precisely characterize the time course of an eSW, we calculated its first derivative. This allowed us to reduce the eSW to a single cycle in which a positive part marks the ascending phase of the eSW, the zero crossing demarcates the peak, and the subsequent negative part marks the descending phase (Fig. 6F, middle). The relative timing of the two simultaneously recorded eSWs can be described by their cross-correlation. The lag of the peak of the cross-correlation quantifies the time lag between the signals, and the peak value determines the amount of correlation (Fig. 6F, bottom). Figure 6G shows the peak correlations and the time lags of eSWs obtained for all the events recorded in one pair of cells (gray dots). From all the events in one recording, we calculated the average time lag and the average correlation coefficient (black circle). Figure 6H shows the average time lag and the average correlation values in seven cell pairs. In all of these recordings, high values of correlation coefficients (range, 0.66–0.92) and low time lags (range, −2.9 to 1.4 ms) were observed. High correlation values between pairs of cells imply that the time course of excitation recorded in one cell is a reliable predictor of the excitatory input experienced by other cells in the network. From these results, we concluded that it is possible to use the excitatory synaptic input onto a single pyramid to assess the phase of the excitatory burst driving the CA1 network.

IFA and its relation to the time course of excitation

Having confirmed our main assumptions on the correlation of SWR-associated currents in pairs of pyramids, we could use one pyramidal cell (of a pair) to probe the output of the inhibitory CA1 network while we simultaneously used another pyramidal cell to probe the excitatory input to CA1. For every SWR recorded in the LFP, the inhibitory current was recorded in one cell by holding its membrane potential at the reversal potential of excitation. Simultaneously, the excitatory current was recorded in another cell by holding it at the reversal potential of inhibition (Fig. 7A). An inhibitory ripple and a coarse excitation were obtained from the bandpass (120–300 Hz) and low-pass (0–50 Hz) filtered versions of the respective currents. From the inhibitory ripple current obtained in one cell, the instantaneous frequency was calculated using the wavelet spectrogram (Fig. 7B, top, middle). From the rectified coarse excitation, we obtained an eSW. By combining the instantaneous frequency with the eSW (Fig. 7B, bottom), we were able to describe the temporal relationship between the instantaneous frequency of inhibition and the time course of excitatory input onto CA1 during a single SWR.

Figure 7.

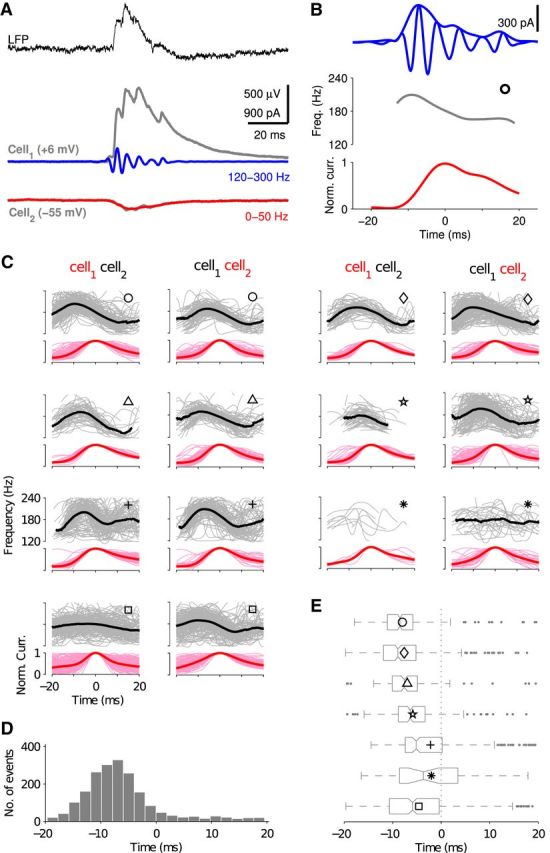
IFA and its relation to the time course of excitation in CA1 pyramidal cells in vitro. A, During an SWR in the LFP (top), the inhibitory current was recorded in cell 1 (middle), whereas the excitatory current was simultaneously recorded in cell 2 (bottom). B, Illustration of the analysis of a single event. From the inhibitory ripple current obtained from cell 1 (blue, top), the instantaneous frequency (middle) was calculated from its wavelet spectrogram. The instantaneous-frequency trace (middle, gray) is plotted only for the time interval where the envelope of the ripple oscillation exceeds 3 SD of the baseline (here from −6 to 20 ms). The simultaneously recorded, low-pass filtered signal that represents excitation (red, bottom) has a peak at a time at which the instantaneous frequency is decreasing. Here, the time is set relative to the peak of the excitatory input current (t = 0). C, Instantaneous ripple frequencies and time courses of excitatory currents for 7 cell pairs (symbols at top right corners matched to Fig. 6). For all but one cell pair, we recorded in two conditions by switching the holding potentials (6 and −55 mV) of the two cells. Each subplot shows an overlay of instantaneous frequencies (gray) and normalized excitatory currents (pink) for all SWR events recorded in one recording condition for a cell pair. The average instantaneous frequency (black) is calculated only at times where at least 10 traces overlap. Red represents average excitatory currents. In 6 (of 7) cell pairs, the average instantaneous ripple frequency has a peak before the mean excitation reaches its maximum. D, Time of frequency peak for 1972 events recorded from 7 pairs. On average, the instantaneous ripple frequency has a peak 6.2 ± 0.2 ms before the mean excitation reaches its maximum. E, Time of frequency peak for all events recorded in each cell pair. Symbols represent the mean and identify the cell pair. Average time across cells pairs: −5.3 ± 0.9 ms (range, −8.0 to −2.0 ms).

We collected data in one configuration of holding potentials (i.e., cell 1 at 6 mV and cell 2 at −55 mV), and then switched the holding potentials (i.e., cell 1 at −55 mV and cell 2 at 6 mV). This approach allowed us to control for any bias that might be introduced by the particular cells used. Figure 7C shows the instantaneous ripple frequencies obtained from inhibitory currents and its relation with the time course of excitatory currents. We confirmed the prediction of the model in 6 of 7 pairs: the instantaneous frequency peaked during the ascending phase of excitation, and the instantaneous frequency started to decay before the peak of excitation was reached. To characterize the typical time at which the frequency peaked with respect to the maximum excitation, we measured this interval in all 1972 recorded events across cells and conditions (Fig. 7D), obtaining an average delay of −6.2 ± 0.2 ms. We also obtained average times of the frequency peaks for all events recorded in each cell pair (Fig. 7E). Pairs displayed times of frequency peaks ranging from −8.0 to −2.0 ms. The average across cell pairs was −5.3 ± 0.9 ms.

To conclude, inhibitory oscillations during SWRs in vitro exhibit prominent IFA in the ripple band. Experiments confirmed the model prediction that during SWRs the oscillation frequency exhibits its peak during the ascending phase of the coarse excitatory input.

Effect of GABA modulators on inhibitory networks

The modeling and experimental results presented so far support the idea that the frequency dynamics of ripples in vitro is well described by a directly driven interneuron network. Could such a model also account for the impact of GABA modulators on ripple frequency as reported in the literature? The oscillation frequency of ripples in vitro is remarkably resistant to drugs that alter the time constant and peak conductance of GABAergic synaptic transmission (Papatheodoropoulos et al., 2007; Koniaris et al., 2011; Viereckel et al., 2013) and such resistance has been used as an argument against a ripple pacemaker relying on interneuronal networks (e.g., Viereckel et al., 2013). To investigate the validity of this argument, we tested the effect of GABA modulators on ripple oscillations generated by a directly driven CA1 interneuron network model (Figs. 8, 9).

The effect of GABA modulators on ripples in silico

We focused on the effect of three drugs that induce changes in the GABAergic synaptic transmission, namely, NNC-711 (Viereckel et al., 2013), thiopental (Whittington et al., 1996; Dickinson et al., 2002), and zolpidem (Whittington et al., 1996; Thomson et al., 2000). Remarkably, during SWRs in vitro, these drugs have little effect on the ripple frequency, despite the marked changes they induce in other features such as the neuronal activity and the ripple duration (Papatheodoropoulos et al., 2007; Koniaris et al., 2011; Viereckel et al., 2013).

Here, we used the interneuron-network response to an excitatory burst from CA3 as a model of ripples in vitro (Fig. 3). The action of a drug was simulated by modifying the peak conductance g_peak and/or the decay time constant τ_D of inhibitory conductances in the model (Fig. 8A, insets). The altered characteristics due to the simulated application of the drugs are shown as orange traces juxtaposed against the control (black) traces in Figure 8, which are identical to the black traces in Figure 3D–G.

The action of the GABA uptake-blocker NNC-711 was simulated by increasing τ_D by 100% and g_peak by 50% (Viereckel et al., 2013) (Fig. 8A₁, inset). To simulate thiopental, we increased τ_D by 80% and kept g_peak unaltered, as reported for a concentration of 50 μm (Whittington et al., 1996) (Fig. 8A₂, inset). Finally, we simulated the effect of a benzodiazepine, such as diazepam or zolpidem, by selectively increasing g_peak by 100% without affecting τ_D (Fig. 8A₃, inset) (Whittington et al., 1996; Pawelzik et al., 1999; Thomson et al., 2000; but see Zarnowska et al., 2009).

NNC-711 and thiopental showed qualitatively similar effects that were consistent with those reported in the literature (Papatheodoropoulos et al., 2007; Viereckel et al., 2013). The overall network frequency was not affected by these drugs (Fig. 8A₁,A₂), but the network activity was largely reduced, as revealed by the average time course of the power (Fig. 8B₁,B₂). Such a reduction in activity was paralleled by a reduction in the ripple duration (Fig. 8D₁,D₂). For ripples in vitro, bath application of thiopental at the concentration simulated here (50 μm) did not affect the frequency but reduced multiunit activity by ∼44%, and ripple duration by ∼20% (Papatheodoropoulos et al., 2007), remarkably close to the ∼40% and ∼20% reductions obtained from our simulations, respectively (Fig. 8D₂).

In slight contrast, the simulated application of zolpidem induced an overall frequency decrease of 6%, which was reflected in both the IFA signature and in the average power spectrum (Fig. 8A₃, left and right, respectively). The power and duration of the transient response also decreased (Fig. 8B₃,D₃) but to a much lesser extent than the previous drugs.

At this point, it is important to bear in mind that, in general, the effect of a drug is not limited to the synapses between PV⁺ BCs but also affects the currents generating the LFP. This is of particular importance when comparing experimental results with those obtained in silico. In experiments, ripple oscillations are often measured in the stratum pyramidale where the LFP is mostly contributed by perisomatic GABAergic synapses onto pyramidal cells. This implies that, in addition to the effect exerted on the interneuron network activity, the drug may also affect the amplitude of the ripple measured in the extracellular field. To capture qualitative changes in the ripple amplitude that might stem from this “double effect,” we used the bandpass filtered (120–300 Hz) inhibitory currents generated by the interneurons in the model as an approximation of the LFP in the ripple band (Fig. 8C; see Materials and Methods). In the case of the NNC-711 and thiopental, for example, the model predicts only a mild reduction in LFP amplitude (Fig. 8C₁ and Fig. 8C₂, respectively), despite the large reduction in network activity (Fig. 8B₁ and Fig. 8B₂, respectively). In this respect, zolpidem is a particularly interesting case in which the reduction in unit activity (Fig. 8B₃) is overcompensated by the increase in the GABAergic conductance. This overcompensation resulted in an increase in the LFP-ripple amplitude (Fig. 8C₃), consistent with the reported effect of zolpidem on ripples in vitro (Koniaris et al., 2011).

In summary, the effect of simulated GABAergic modulators on the transient response of the interneuron network model was consistent with effects reported in several experimental studies. Notably, increases in the GABAergic transmission are counterbalanced by a reduction in the network (i.e., unit) activity. The model can explain why drugs that induce an increase in decay time constant of GABAergic synaptic transmission can reduce ripple duration and interneuron firing rates without affecting ripple frequency.

To further generalize our results, we now return to the case of persistent stimulation of an interneuron network.

The role of input noise in frequency sensitivity

In stark contrast to ripples, pharmacologically evoked oscillations in the gamma band that rely exclusively on inhibition are frequency-sensitive to GABA modulators (Whittington et al., 1995, 1996; Traub et al., 1996; Fisahn et al., 2004). In agreement, in silico models of such interneuron-network gamma (ING) exhibit oscillations whose frequency is sensitive to manipulation of GABA parameters (Traub et al., 1996; Wang and Buzsáki, 1996; Bartos et al., 2002). How can interneuron networks generate oscillations that are frequency insensitive (as in our ripple model) and also frequency sensitive (as in ING models)?

One commonality to ING models is that interneurons are driven by tonic currents that are distributed across cells with low variability (CV = 3%) (Traub et al., 1996; Wang and Buzsáki, 1996). Such a tonic driving input is intended to mimic the steady currents induced by activation of metabotropic channels during pharmacologically evoked ING. Would such a homogeneous tonic drive generate frequency-sensitive oscillations in our model? To examine this question and connect it to previous results, we compared the response of the network to GABA modulators under two different driving conditions: spiking drive (as during persistent stimulation; see Fig. 1) and tonic drive (as in ING models). The results are summarized in Figure 9.

We first tested the effect of the GABA-uptake blocker NNC-711 (Fig. 9A, middle, inset) during persistent stimulation at a rate of 5500 spikes/s (Fig. 9A, see also Fig. 1). In the control condition, the network oscillated at a frequency of 185 Hz (Fig. 9A, middle, black) and units fired at an average rate of 138 spikes/s (range, 70–179 spikes/s) (Fig. 9A, bottom, black). Under the drug, the frequency of the oscillation in the population exhibited only a 4% increase (Fig. 9A, top, orange). In contrast, the distribution of firing rates across units was shifted to much lower values (Fig. 9A, bottom, orange). This effect of the drug closely resembled the effect of a decrease in the excitatory drive (Fig. 1B,D).

We then stimulated the same network by driving the interneurons with tonic excitatory conductances that were distributed across the population with low (CV = 0.03) variability (Fig. 9B, top). The mean value of the excitatory conductance used (17.4 nS) was equivalent to the value induced by the spiking stimulation at 5500 spikes/s. The SD of the conductances was set to 3% of the mean, in accordance with previous ING models (Traub et al., 1996; Wang and Buzsáki, 1996). Under such conditions of low noise in the input, the network oscillated at 168 Hz (Fig. 9B, middle, black) and all units fired at 168 spikes/s (Fig. 9B, bottom, black), consistent with a fully synchronized (“low noise”) regime.

When NNC-711 was applied under the tonic-drive condition, the network-oscillation frequency markedly decreased from 168 Hz to 125 Hz (Fig. 9B, middle, orange). Also, the peak of the firing-rate distribution decreased, matching the network-oscillation frequency (Fig. 9B, bottom, orange). It is noteworthy that the distribution of firing rates was not only shifted but also smeared out to lower values (bimodal distribution in Fig. 9B, bottom). Although a large fraction of units fired at a rate close to the network frequency, the remainder of the distribution revealed units that skipped cycles. The subpopulation expressing low firing rates (≲50 spikes/s) spiked irregularly but consistently with the population oscillations (data not shown). Thus, the simulated application of NNC-711 under tonic drive not only decreased the network frequency but also allowed the emergence of a sparsely synchronized subpopulation in the network.

How do other drugs that alter GABAergic synaptic transmission affect the network oscillations under the two input conditions? To outline the predictions of the in silico model regarding the effects of GABAergic modulators in general, we measured the network frequency and the mean unit firing rate at different combinations of g_peak and τ_D under the two driving conditions depicted in Figure 9A, B. Figure 9C shows the network peak frequency (top row) and the mean firing rate across units (bottom row) as a function of g_peak (range, 1–10 nS) and τ_D (range, 1–3 ms). Such a representation of the parameter space allows us to visualize the effect of a drug as a displacement vector that starts at the control value τ_D = 1.2 ms and g_peak = 5.0 nS and points at the new values induced by the drug (Fig. 9C, black arrows).

During the spiking-drive condition (Fig. 9C, left column), the network frequency remained in the ripple band for a wide range of values of g_peak and τ_D. This behavior indicates that drugs affecting the two parameters would induce only minor changes in the network frequency, which is also consistent with the transient regime investigated in Figure 8. Remarkably, however, a drug could induce small but variable changes depending on the initial condition (i.e., control) in the parameter space. For example, an increase in τ_D from 1.2 to 2.2 ms (e.g., thiopental) would result in a small or no change in the network frequency if g_peak = 5 nS in the control condition. In contrast, the same change in τ_D would induce a slight increase in the network frequency if g_peak = 8 nS in the control condition. The mean firing rate, on the other hand, was much more sensitive to g_peak and τ_D and ranged from <60 to >220 spikes/s in the simulated parameter space (Fig. 9C, bottom left). Firing rates strongly decreased when g_peak or τ_D increased.

During the tonic-drive condition, in contrast, both the network frequency and the mean firing rate were highly sensitive to changes in g_peak and τ_D (Fig. 9C, right column). The gradient of network frequencies in the observed parameter space showed that frequency and firing rate were inversely related to both g_peak and τ_D. This trend is consistent with experimental results in the context of induced gamma oscillations in vitro (Whittington et al., 1995, 1996; Traub et al., 1996; Fisahn et al., 2004).

Interestingly, close to the highest values of τ_D and g_peak tested (upper right corners in color plots) in the tonic-drive condition (Fig. 9C, right column), high network frequencies emerged from units firing at low rates. This suggests that changes in τ_D and g_peak of GABAergig synaptic transmission can also affect the oscillatory regime. To figure out the expression of different regimes in the observed parameter space, we measured the average CV of unit activity (Fig. 9C, bottom, black contour lines). In both conditions of driving input, increasing τ_D and/or g_peak increased the CV, which means that units fired more irregularly. The transition from full to sparse synchrony may be indicated by CV = 0.5 (dashed line). For spiking drive, a sparsely synchronized regime was observed in most of the shown parameter space (Fig. 9C, bottom left). For tonic drive, on the other hand, full synchrony appeared in a large area around the control values. It is noteworthy that the CV within this region is considerably lower than the lowest level that could be achieved during the persistent-drive condition at very high rates (Fig. 1D, middle).

In summary, the noise provided by spiking excitatory stimulation favors the emergence of oscillations whose frequency is insensitive to GABA modulators. On the other hand, the conditions of low noise provided by the tonic excitation with low neuron-to-neuron variability, typically used in ING models, favor the emergence of oscillations whose frequency is sensitive to GABA modulators. In conclusion, the fact that ripple oscillations are frequency-insensitive to GABA modulators cannot rule out an interneuronal pacemaker.

Discussion

Using a physiologically constrained computational model of the PV⁺ BCs network in CA1 and an in vitro model of SWRs, we described mechanisms underlying the generation of fast oscillations in the ripple (140–220 Hz) and fast gamma (90–140 Hz) ranges. In the computational model, we analyzed the transient oscillatory responses of the PV⁺ BCs network under two configurations of excitatory drive to interneurons. Under direct drive, interneurons did not provide inhibitory feedback to the pyramidal cells exciting them (Schlingloff et al., 2014). Under indirect drive, on the other hand, the firing of the local pyramidal cells in CA1 excited the interneurons, which projected back to the pyramids (Stark et al., 2014). In both cases, we explored excitation levels that evoked firing rates of interneurons within the physiological range observed in vivo. The computational model showed that (1) under direct drive, oscillation frequencies only weakly depended on the excitation level, and remained constrained to the ripple range; (2) single responses under such a condition exhibited IFA and were frequency-resistant to GABA modulators; (3) under indirect drive, the oscillation frequency increased monotonically with the excitation level, covering the entire fast gamma range and the lower ripple band; (4) IFA under indirect drive was expressed in the fast gamma range only; (5) when IFA was present, the maximum frequency occurred several milliseconds before the peak of excitation. In the in vitro model, we showed that (6) SWRs in vitro exhibit IFA, and (7) double recordings from CA1 pyramidal neurons during SWRs confirmed the relationship between the instantaneous ripple frequency and the time course of excitation predicted by the computational model.

IFA and excitation-first models

Hippocampal ripples exhibit IFA both in vivo (Ponomarenko et al., 2004; Nguyen et al., 2009; Sullivan et al., 2011; Stark et al., 2014; Hulse et al., 2016) and in vitro, as shown here for the first time. The finding that IFA is expressed in transiently excited interneuron-networks poses a challenge to excitation-first models, which so far have not accounted for the phenomenon. To produce IFA, an excitatory pacemaker should be able to slow down its frequency within the time course of a single SWR. In the axon-plexus model (Traub and Bibbig, 2000), for example, one factor that could dynamically control the frequency is the spike-to-spike propagation latency. Such a latency depends on the action-potential amplitude, which has been shown to decrease with somatic depolarization of pyramidal cells (Shu et al., 2006, 2007).

The role of noise in frequency-sensitivity to GABA modulators

As shown here and elsewhere (Brunel and Wang, 2003; Maex and De Schutter, 2003), the sensitivity of frequency to GABA modulation is not an intrinsic property of interneuronal network oscillations but rather depends on the noise and heterogeneities in the system. The higher sensitivity of previous inhibition-first models of ripple oscillations can be explained by factors that favor a low-noise oscillatory state, such as homogeneously distributed driving currents in the absence of noise (Taxidis et al., 2012) or all-to-all connectivity (Malerba et al., 2016). In contrast to these models, we drove units with excitatory conductances that were heterogeneously distributed across the population in the presence of random synaptic activity, which led to the generation of frequency-resistant ripple oscillations.

Fast hippocampal oscillations may reflect two distinct processes

The sharp wave associated fast oscillations emerging in CA1 during slow-wave sleep and awake immobility express a wide range of frequencies spanning from ∼80 to ∼220 Hz (Csicsvari et al., 1999; Sullivan et al., 2011). These events co-occur with sharp wave sinks in the stratum radiatum, which reflect the depolarization of the apical dendrites of CA1 pyramidal cells due to the input from CA3. Given the correlation between sharp wave-sink amplitude and ripple frequency, it has been suggested that an indirect-drive model (Fig. 4A) can account for most of the features of SWRs in vivo and in vitro (Stark et al., 2014). Indeed, this model alone can generate a wide range of frequencies depending on the excitatory input provided, allowing a continuum that encompasses both fast-gamma and ripple bands into a single process (Fig. 5A). However, the indirect-drive condition alone is still at odds with several features of SWRs: First, during slow-wave sleep, a bimodal distribution of ripple frequencies emerges from a unimodal distribution of sharp wave-sink amplitudes (Sullivan et al., 2011). Second, during transient periods of immobility, ripple-frequency does not correlate with sharp wave amplitude (Buzsáki, 2015, his Fig. 4). Third, during SWRs in vitro, oscillations that are limited to the ripple band (Maier et al., 2003, 2011; Papatheodoropoulos et al., 2007; Koniaris et al., 2011) emerge under extremely weak (0.0038 spikes/s) CA1 pyramidal-cell activity (Bähner et al., 2011). In line with these data, Sullivan et al. (2011) suggested that transient oscillations in CA1 reflect the presence of two “voltage-controlled” oscillators that exhibit different frequency gains but share anatomical substrates and mechanisms. Here, we propose that these two “voltage-controlled” oscillators correspond to the same interneuronal network that is recruited either by direct excitatory drive or by indirect excitatory drive via depolarization of local pyramids, conforming a “ripple oscillator” and a “fast-gamma oscillator,” respectively. These putative oscillators cover different frequency ranges and exhibit different excitation-frequency curves that overlap at higher frequencies (Fig. 5A).

Anatomical substrates for the fast-gamma and ripple oscillators

The difference in connectivity of deep versus superficial pyramidal cells and PV⁺ BCs in CA1 could provide the substrate for the selective recruitment of the putative oscillators proposed here (Lee et al., 2014). Pyramidal cells in the deep layers of stratum pyramidale (i.e., closer to stratum oriens) are interconnected with PV⁺ BCs in a scheme that is dominated by feedback inhibition (as in our indirect-drive condition). Conversely, pyramidal cells in the superficial layer of stratum pyramidale (i.e., closer to stratum radiatum) project heavily onto PV⁺ BC and receive comparably little inhibition from them (a scheme more reminiscent of our direct-drive condition). We therefore hypothesize that the selective depolarization of the deep calbindin-immunonegative (CB⁻) pyramidal cells generates oscillations preferentially in the fast gamma range whereas depolarization of the superficial calbindin-immunoreactive (CB⁺) pyramidal cells favors the expression of oscillations in the ripple band. The selective activation of these cell types in vivo could be mediated by anatomically segregated excitatory pathways (Mizuseki et al., 2011; Slomianka et al., 2011). In the general case where both subclasses of pyramidal cells and PV⁺ BC receive concurrent excitatory input, the intralaminar connectivity between pyramidal cells and PV⁺ BC could function as a winner-take-all network where ripples and fast gamma oscillations compete for expression (Viriyopase et al., 2016).

Ripple oscillations in vitro

In stark contrast to their in vivo counterparts, SWRs in vitro are characterized by frequencies that are limited to the ripple range (Maier et al., 2003, 2011; Papatheodoropoulos et al., 2007; Koniaris et al., 2011) and by much lower firing rates of local pyramidal cells (e.g., in vitro: 0.038 spikes/s vs in vivo: 12.8 spikes/s on average) (Bähner et al., 2011; English et al., 2014). This low activity of pyramidal cells in CA1 is consistent with weak excitation; in a hippocampal slice, the input to CA1 pyramidal cells through excitatory afferents is indeed compromised (Ishizuka et al., 1990; Li et al., 1994). Our dual-pathway model suggests that the excitation to pyramidal cells in CA1 in vitro is not strong enough to engage the pyramidal-interneuron-network feedback loop into an oscillatory regime (Brunel and Hakim, 2008), which explains the absence of fast-gamma oscillations. The remaining excitatory afferents might still be sufficient to drive the more excitable direct pathways to interneurons, granting the expression of oscillations in the ripple band. In such a scenario of weakened excitatory input, pyramidal cells are dominated by a strong rhythmic perisomatic inhibition that allows only a very sparse but precisely timed firing of pyramidal cells. Such rhythmic excitatory activity is revealed as a ripple component in the excitatory currents measured in pyramidal cells (Maier et al., 2011) (Fig. 6E). We further hypothesize that, in the isolated CA1 region, the more excitable superficial pyramids can also excite the local interneurons in a direct-drive fashion to evoke ripples (Maier et al., 2003, 2011), provided they can initiate a sharp wave, presumably in a manner similar to CA3 (de la Prida et al., 2006; Bazelot et al., 2016).

In conclusion, in the context of memory replay and consolidation (Buzsáki, 1989, 1998; Siapas and Wilson, 1998; Lee and Wilson, 2002), ripple oscillations synchronize the activity among large ensembles of cells, which amplifies the output messages of CA1 and may boost plasticity in downstream brain structures. The observed bimodality in ripple frequency (Csicsvari et al., 1999; Sullivan et al., 2011) may be underlied by two distinct processes involving functionally different subpopulations of pyramidal cells in CA1 (Valero et al., 2015), which receive input from and project to different source and target areas, respectively (Slomianka et al., 2011).