Correlations Between Primary Motor Cortex Activity with Recent Past and Future Limb Motion During Unperturbed Reaching

Abstract

Many studies highlight that human movements are highly successful yet display a surprising amount of variability from trial to trial. There is a consistent pattern of variability throughout movement: initial motor errors are corrected by the end of movement, suggesting the presence of a powerful online control process. Here, we analyze the trial-by-trial variability of goal-directed reaching in nonhuman primates (five male Rhesus monkeys) and demonstrate that they display a similar pattern of variability during reaching, including a strong negative correlation between initial and late hand motion. We then demonstrate that trial-to-trial neural variability of primary motor cortex (M1) is positively correlated with variability of future hand motion (τ = ∼160 ms) during reaching. Furthermore, the variability of M1 activity is also correlated with variability of past hand motion (τ = ∼90 ms), but in the opposite polarity (i.e., negative correlation). Partial correlation analysis demonstrated that M1 activity independently reflects the variability of both past and future hand motions. These findings provide support for the hypothesis that M1 activity is involved in online feedback control of motor actions.

SIGNIFICANCE STATEMENT Previous studies highlight that primary motor cortex (M1) rapidly responds to either visual or mechanical disturbances, suggesting its involvement in online feedback control. However, these studies required external disturbances to the motor system and it is not clear whether a similar feedback process addresses internal noise/errors generated by the motor system itself. Here, we introduce a novel analysis that evaluates how variations in the activity of M1 neurons covary with variations in hand motion on a trial-to-trial basis. The analyses demonstrate that M1 activity is correlated with hand motion in both the near future and the recent past, but with opposite polarity. These results suggest that M1 is involved in online feedback motor control to address errors/noise within the motor system.

Introduction

Many studies highlight that movements are highly variable from trial to trial (Messier and Kalaska, 1999; Todorov and Jordan, 2002; van Beers et al., 2004) and that this trial-to-trial variability can originate from both internal (e.g., neuromuscular noise) (Faisal et al., 2008) and external noise (e.g., perturbations). Previous studies have demonstrated that movement errors are rapidly corrected before the end of reaching, suggesting a powerful online control process (Messier and Kalaska, 1999; Todorov and Jordan, 2002; van Beers et al., 2004; Nashed et al., 2012).

How does the motor system generate online corrections? Previous studies have shown that neurons in primary motor cortex (M1) exhibit rapid, goal-dependent responses following mechanical or visual perturbations, suggesting that M1 plays a key role in online motor corrections, at least when there is a discrete disturbance on the order of several millimeters of hand displacement (Herter et al., 2009; Pruszynski et al., 2011, 2014; Omrani et al., 2014; Scott et al., 2015; Stavisky et al., 2017). We have also shown that corrective responses are observed for small discrete disturbances that approach the range of natural variability observed during unperturbed reaching (Crevecoeur et al., 2012). Therefore, we hypothesize that a similar feedback process in M1 manages errors/noise generated internally by the motor system during unperturbed reaching.

Here, we examine this hypothesis by quantifying how variations in the activity of M1 neurons covary with natural variations in hand motion on a trial-to-trial basis. Our basic assumption is that, if M1 neurons are involved in online corrections to counter natural variability during reaching, then trial-to-trial variations of M1 activity should covary with hand motion in the recent past. Furthermore, if this modulation causally generates a corrective response, it should covary with future hand motion. Therefore, M1 activity should covary with hand motion in both the recent past and immediate future.

In this study, we introduce an analytical approach to comprehensively measure the correlations of trial-to-trial variation of signals during reaching. We first demonstrate that variability at the initiation of reaching is rapidly compensated by hand motion in the opposite direction during reaching, as demonstrated in human studies (Messier and Kalaska, 1999; Todorov and Jordan, 2002; van Beers et al., 2004). Then, we show that the trial-to-trial variability of M1 neuron activity is correlated with past and future hand motion. Furthermore, partial correlation analysis also highlights that these correlations of M1 neuron with the past and future hand motions are independent, suggesting that M1 activity reflects an online feedback process during unperturbed reaching.

Materials and Methods

Animals and apparatus.

Five male rhesus monkeys (Macaca mulatta, 6–17 kg, Monkeys A–E) were used in this study following procedures approved by the Queen's University Animal Care Committee. They were trained to perform reaching tasks with their right arm while wearing a robotic upper-limb exoskeleton (KINARM; BKIN Technologies) that permitted horizontal shoulder and elbow motion and monitored those joint motions (Scott, 1999). A virtual reality system presented visual targets and a white cursor representing hand position in the workspace while also permitting the monkeys to view their entire limb.

Behavioral task.

We trained monkeys to perform a center-out reaching task, which has been described previously (Kurtzer et al., 2006). In brief, Monkeys A–D began each trial by maintaining their fingertip within a circular start target (0.8 cm radius). This start target was positioned near the center of the hand's workspace (∼30° and 90° at the shoulder and elbow joints, respectively). After a random waiting period (1.5–2.0 s), a peripheral target (1.2 cm radius) appeared at 1 of 8 possible target locations (all 6 cm away from central target). The monkey then moved from the start target to the peripheral target within 220–350 ms, which resulted in total reach times of ∼500 to 600 ms including motion within the targets. Trial completion was rewarded by a drop of water. Monkey E performed the same center-out reaching task, but the peripheral target was a 2.0 cm square, the target location was 5 cm away, and the time limit to get the peripheral target was set to <750 ms. Monkeys A and B reached to eight targets distributed approximately uniformly in joint-torque space: 45°, 67.5°, 90°, 180°, 247.5°, 270°, 315°, and 337.5°, where 0° is to the right and positive rotation is counterclockwise. In contrast, Monkeys C and D reached to eight targets distributed uniformly in hand space: 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315° or 22.5°, 67.5°, 112.5°, 157.5°, 202.5°, 247.5°, 292.5°, and 337.5°. Targets were presented in random order within a block of eight trials and blocks were repeated five to seven times. Monkey E reached to eight targets distributed uniformly in hand space: 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°. In this monkey, blocks of eight trials were repeated 30 times.

Data collection.

For Monkeys A–D, we used standard techniques for extracellular single-unit recordings in the shoulder/elbow region of left M1 (Scott and Kalaska, 1997; Scott et al., 2001). In brief, under aseptic conditions, we performed surgery to attach a recording chamber over the arm area of left M1 and a head fixation post with dental acrylic. On each recording day, a tungsten microelectrode was advanced through M1 while the monkey was performing a reaching task. Neurons active during the task were isolated and examined for their response to passive limb movement. Neurons responding predominantly to shoulder or elbow movements were studied further. For Monkey E, a 96-channel Utah Array (Blackrock Microsystems) with 1.5 mm length electrodes was chronically implanted on the cortical surface in the arm area of M1. Spike activity was sorted offline by isolating clusters within a space defined by the top two principle components and peak-trough amplitude of the spike waveforms (Offline Sorter; Plexon). Only well isolated single units were included in the present dataset. Neuron firing was binned into 5 ms bins (i.e., 200 Hz) and the spike counts per bin were stored for analyses. Joint kinematic data (shoulder/elbow) were simultaneously recorded at 1000 Hz (Monkeys A and E) or 4000 Hz (Monkeys B–D) and downsampled to 200 Hz.

Data analyses.

All analyses were performed using MATLAB (The MathWorks, RRID:SCR_001622).

Hypothesis and predictions.

The main goal of this study was to examine the hypothesis that M1 is involved in the online correction of the limb. To this end, we quantified how variations in the activity of M1 neurons covary with natural variations in hand motion on a trial-to-trial basis. Figure 1 highlights our predictions for correlations between trial-to-trial fluctuations of hand motion and correlations between M1 activity and hand motion. To begin, consider two reaching trials to the same target (Fig. 1A), but one with a larger initial lateral deviation (red) and one with a smaller deviation (blue). Therefore, online corrections must be larger for the red trial and smaller for the blue trial to reach the target (Fig. 1A). This online correction can be depicted as a mirror reversal of lateral hand velocity during movement (LatVel, t1 and t2; Fig. 1B). Across all trials, this will generate a negative correlation between initial and later LatVel (Vel-Vel correlation; Fig. 1D).

Figure 1.

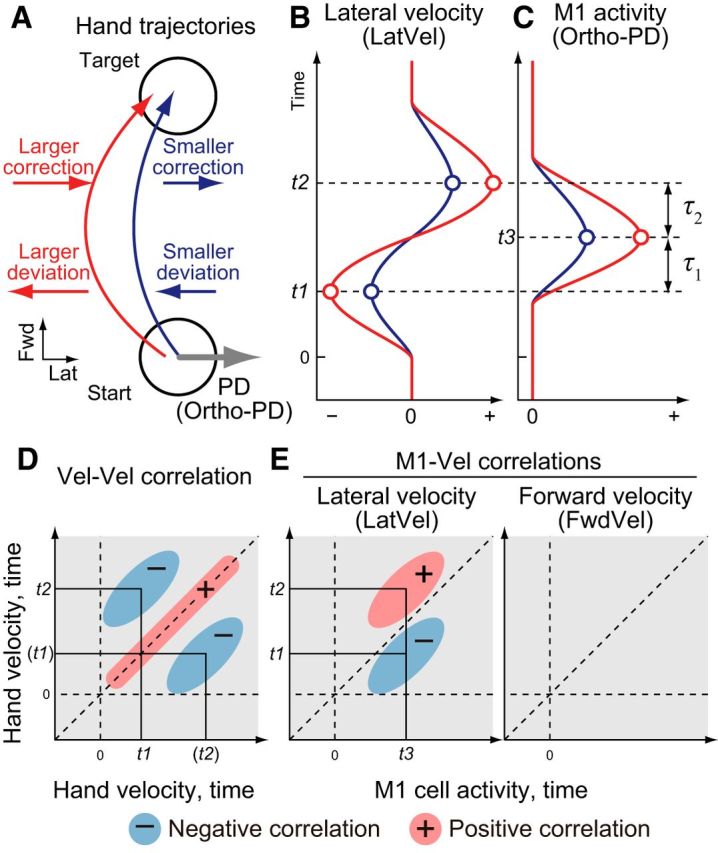
Predictions for intertrial correlation between M1 neuron activity and hand velocities during reaching. A, Schematic illustration of two reaching trajectories from a start target to a goal target: one with a smaller deviation (blue) and one with a larger deviation (red). B, Predicted lateral hand velocity (LatVel) for each trial. t1 and t2 represents the timing of the initial deviation (t1) and later correction (t2). C, Predicted M1 activity with ortho-PD based on our hypothesis that M1 activity leads feedback corrections in its PD. D, Prediction for intertrial correlation between LatVels at different time points (Vel-Vel correlation). Vertical and horizontal axes indicate timing of LatVel data for intertrial correlation. Vertical and horizontal dashed lines denote the time of movement onset and diagonal dashed line is a unity line. We predicted that LatVel of initial deviation (t1) is negatively correlated to those at later timing (t2, blue circles). E, Prediction for intertrial correlation between M1 neuron activity and LatVel across time (M1-Vel correlation). Same format as D but horizontal axis indicates timing for M1 neuron activity. We predict that activity of neurons with ortho-PD should positively correlate with LatVel in the near future (t3 vs t2, red circle) and negatively correlate with LatVel in the recent past (t3 vs t1, blue circle). M1 neurons with ortho-PD should also show minimal correlations with FwdVel.

Next, if M1 neurons are involved in online control of the limb, then trial-to-trial variations in their firing should correlate with variations in lateral hand motion. This link reflects that M1 is involved in selecting the timing and magnitude of muscle activity, which in turn generates corrective motion of the hand (Scott, 1997; Pohlmeyer et al., 2007; Cherian et al., 2011; Yakovenko et al., 2011; Heming et al., 2016). For simplicity, M1 activity can be related to the direction of hand motion where a neuron becomes most active (i.e., preferred direction, PD). If M1 is involved in feedback processing, then an M1 neuron with a PD orthogonal to target direction (ortho-PD; Fig. 1A) should increase its firing more for the red trial with the larger motor correction compared with the blue trial (Fig. 1C). This relation results in a negative correlation with past hand motion (M1-Vel correlation; Fig. 1E, left, t3 vs t1) and a positive correlation with future hand motion (Fig. 1E, left, t3 vs t2). Finally, these correlations should be directionally selective: a neuron with an ortho-PD should show minimal correlations with forward hand velocity (FwdVel; Fig. 1E, right).

Note that, although we used hand motion to explain M1 activity, we do not suggest that activity of M1 represents hand motion explicitly (Scott et al., 2001). Measures such as electromyographic activity likely have a more direct link to the activity in M1 (Cherian et al., 2011; Heming et al., 2016), but are very noisy signals. In contrast, hand velocity is a relatively simple measure of limb motion that can be used as a surrogate of motor output.

Intertrial correlation of kinematic signal.

We first examined correlations between trial-to-trial fluctuations of hand kinematics during reaching, referred to as “intertrial correlations.” We examined from 500 ms before to 1000 ms after reach onset, defined as the moment when hand velocity rose >10% of peak hand velocity. Then, we decomposed hand velocity into a forward (FwdVel) and a lateral (LatVel) velocity relative to target direction. We computed intertrial correlations by calculating a Pearson correlation coefficient (r) between trial-to-trial fluctuations of hand velocities obtained from different time points. We repeated the calculation of intertrial correlation for all time-point pairs and created a 2D Vel-Vel correlation map. We made this correlation map for each reaching dataset and for each individual target.

These individual correlation maps were pooled and averaged across datasets from all monkeys. It is known that simple averaging of correlation coefficients leads to underestimation because the sampling distribution of the correlation coefficients is skewed (Silver and Dunlap, 1987). Therefore, we applied Fisher z-transformation before the averaging, as follows:

Where archtanh is the inverse hyperbolic tangent function and z is the transformed value. This transformation corrects the skew in the distribution of r (Silver and Dunlap, 1987). Then, we averaged the z values and applied the inverse transformation (hyperbolic tangent function, tanh) to get the averaged r.

Data shuffling.

To evaluate chance level in the correlations, we created similar correlation maps for shuffled data. For each pair of signals, we shuffled the trial numbers with replacement and then calculated r with this shuffled data. Only the trial numbers were shuffled so that the temporal structure of signal was not modified by this procedure. We repeated this shuffling 100 times and averaged them to get a shuffled r value for each correlation map.

When we calculated the shuffled r, we added a small Gaussian noise (0.0001 SD of original data) to the shuffled data because shuffling with replacement sometimes selects the same value for all the trials. The addition of the small random noise has almost no effect on the correlation value (∼0.01). After we obtained the shuffled correlation map for individual datasets, we averaged across all datasets as performed with the original data; that is, Fisher z-transformation, averaging, and then the inverse transformation.

Significance test.

The significant difference between the original and shuffled correlation maps was tested by pooling all datasets and applying the paired t test for each pixel of the correlation map (p < 0.05). However, this repeated test causes a multiple-comparisons problem resulting in too many false positives. A popular way to solve this problem is by applying the Bonferroni correction. However, this correction is too conservative in our situation because this correction assumes independent samplings for the individual tests. In our data, the kinematic and neural signals are usually highly correlated between the neighboring time points, so the Bonferroni correction is not suitable for our dataset. The random field theory (RFT) gives another solution to correct for this multiple-comparisons problem, which is often used for analyses of functional imaging data (Worsley et al., 1992; Friston et al., 1994). The RFT assumes a null hypothesis that the signals are derived from a Gaussian random field with a certain spatial smoothness. Based on this assumption, RFT infers how many clusters exceed a threshold by chance and the size of each cluster. This function is defined with Euler characteristics (Worsley et al., 1992). Therefore, by identifying the spatial smoothness of the signal, we are able to obtain the significant limit for the cluster size at a certain significance level. To begin, we created 2D t-statistic maps by applying the paired t test between the original and shuffled maps for each pixel of the correlation map. Then, we transformed this t-statistic map to a Z-score map by matching the probability density functions of both distributions. The resultant Z-score map assumes a normal distribution with unit variance. Then, we estimated the spatial smoothness (FWHM in each dimension) of the Z-score map by applying the derivative method (Worsley et al., 1992). From this FWHM and total data size (301² = 90,601 pixels), we estimated the significant limit of the cluster size according to Euler characteristics (p < 0.05). Finally, we accepted the clusters as significant only if the cluster size exceeded this threshold for the cluster size.

Intertrial correlation between M1 activity and kinematic signals.

The PD of M1 neurons was obtained using a plane fit based on the spike counts within a time interval from 150 ms before to 100 ms after reach onset. We tested a significance of the plane fitting with the standard F test for regression analysis at the 5% level. We categorized movements based on the neuron's PD into three groups. ortho-PD movements were for target locations from +135° to +45° (clockwise PD: CW-PD) and from −45° to −135° (counterclockwise PD: CCW-PD) relative to the neuron's PD. Similarly, pro-PD movements were for target locations <45° relative to the neuron's PD. Finally, anti-PD movements were for target locations >135° relative the neuron's PD. As a pilot study, we also computed the PDs at velocity peak (from 125 ms before to 125 ms after the velocity peak) and at reach offset (from 250 to 0 ms before reach offset) and confirmed that most neurons display similar PDs between these epochs and an average shift of PD from the one around reach onset was −3.6 ± 52.6° and 1.8 ± 64.0° at the velocity peak and the end of reach, respectively (mean ± SD).

The time series of neural firing was obtained by convolving the spike trains with a double exponential kernel (rise time = 1 ms, fall time = 20 ms) that mimics a postspike potential (Thompson et al., 1996). To match the temporal smoothness between neural firing and kinematic signals, we further smoothed the neural signal with a Gaussian kernel (SD = 40 ms). Then, we calculated the intertrial correlation between M1 activity and hand velocity signals (FwdVel and LatVel) for each neuron–target pair (M1-Vel correlation map). For the ortho-PD groups, direction of LatVel was set to −90° (CW-PD) or +90° (CCW-PD) to make positive LatVel indicate hand velocity in the neuron's PD. For the intertrial correlation map with neural activity, we applied an additional 2D Gaussian smoothing (SD = 10 ms). Finally, we averaged the correlation map among each movement category (ortho-, pro-, or anti-PD). For averaging and the statistical tests of the maps, we used the same methods for the kinematic signals; that is, Fisher z-transformation, averaging, inverse transformation, shuffling, t test, and the cluster size correction. In addition to the map-based analysis, we also applied a time-window-based analysis. For a certain test time window, we averaged the z-transformed correlation coefficients for the original and shuffled data and then applied paired t tests between the averaged values.

Partial correlation analysis between M1 activity and kinematic signals.

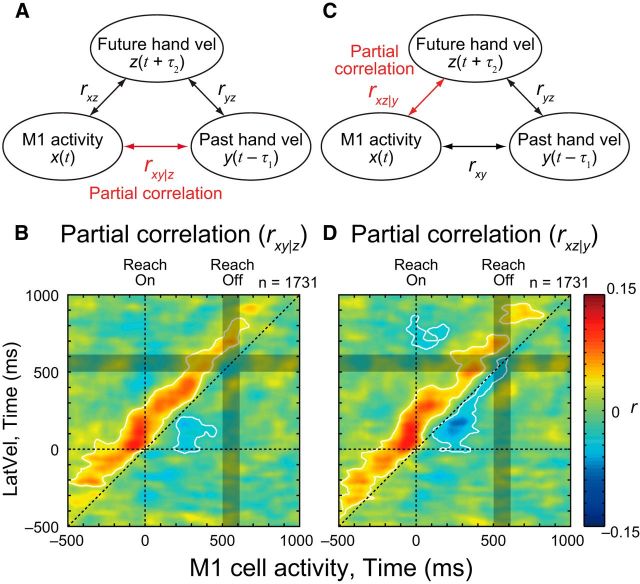
Correlations between M1 activity and hand motion in the past could be a spurious byproduct given that M1 activity is related to future hand motion and future is correlated to past hand motion. We examined this possibility by computing a partial correlation between M1 neuron activity and hand velocity after removing the effect of the future hand velocity. For time point t, we computed partial correlation between M1 activity at t [i.e., x(t)] and hand velocity at t − τ1 [i.e., y(t − τ1)] while controlling the effect of future hand velocity at t + τ2 [i.e., z(t + τ2)]. Time differences between past (y) and future (z) hand velocities was fixed to τ1 + τ2 = 250 ms based on our results from the intertrial correlation analysis. Formally, the partial correlation was computed as follows. First, linear regression of z was individually applied to x and y to remove a linear effect of z. Then, the partial correlation (r_xy|z) was computed as a correlation between those residuals. Practically, this calculation was achieved as follows:

where r_xy, r_xz, and r_yz indicate a correlation coefficient between parameters. We also computed a partial correlation between M1 neuron activity and future hand velocity while controlling past hand velocity (r_xz|y) by replacing the parameters of y and z.

Mutual information between M1 activity and kinematic signals.

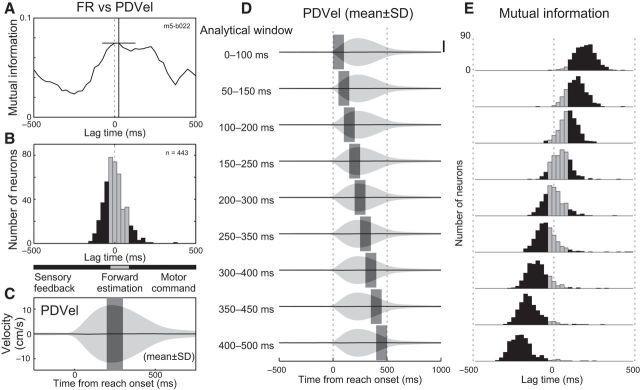
We calculated mutual information between M1 neuron activity and hand velocity following the approach used by Mulliken et al. (2008). We pooled the M1 activity and hand velocity data across reaching for eight targets for each M1 neuron. We projected the hand velocity to the PD of each M1 neuron to obtain hand velocity in the neuron's PD (PDVel). As with Mulliken et al. (2008), we selected the analytical time window from the middle of a trial (200–300 ms after reach onset). We discretized firing rate and PDVel signals into 16 groups based on the rank order (i.e., first group includes values from 0 to 1/16 percentile, second group from 1/16 to 2/16 percentile, and so on). Then, we calculated the normalized Shannon mutual information between the discretized M1 activity and PDVel (formulae 4, 5, and 6 in Mulliken et al., 2008).

We determined peak lag time for the mutual information by shifting the analytical time window from −500 to +500 ms for PDVel relative to M1 activity. The lag time that contained the maximal mutual information was defined as the peak lag time, denoting the relative time at which a neuron's firing rate contained the most information about the PDVel. Positive and negative time lag indicates M1 activity encodes future and past PDVel, respectively. We divided the peak lag times for each M1 neuron into 25 ms bins and made a histogram. Based on Mulliken et al. (2008), we categorized encoded information as sensory feedback (lag < 30 ms), forward estimation (30 ≤ lag ≤ 90 ms), or motor commands (lag > 90 ms).

Results

Temporal change of intertrial correlation of hand velocity

Our first objective was to quantify the intertrial variability in hand motions to each spatial target. Five rhesus monkeys were trained to perform a center-out reaching task (Fig. 2A). Figure 2B illustrates for a single dataset that the initial trajectory of the hand to a target was highly variable. For example, the red trial in Figure 2B was initially directed counterclockwise and the blue trial was directed clockwise relative to target direction. Importantly, these initial deviations in hand trajectories were corrected later, leading to motion in the opposite direction to attain the goal (Fig. 2B). This illustrates the common observation that reaching movements tend to be slightly curved and variable during reaching (van Beers et al., 2004; Nashed et al., 2012).

Figure 2.

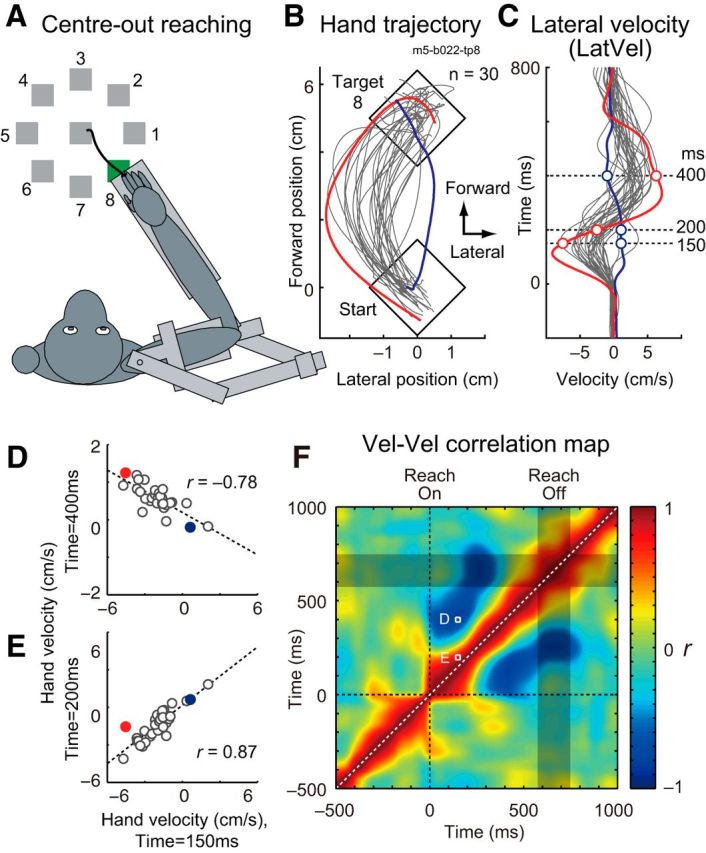
Example of intertrial correlation of lateral hand velocity during a reaching. A, Basic center-out reaching task in which a monkey moves its hand from a central target to peripheral targets equally spaced around a circle (movement distance = 5 cm). B, Hand trajectories of an exemplar set of trials (target 8 of Monkey E, 30 trials). Axes are rotated to match the vertical and horizontal axis to the target direction and the lateral to target direction, respectively. Two exemplar trials are highlighted and color-coded throughout this figure (red and blue). C, LatVel of the same trials. Traces are aligned to reach onset. Horizontal dashed lines indicate the time points displayed in D and E. D, Intertrial correlation of LatVel between 150 versus 400 ms after reach onset. Dashed line denotes linear regression (Pearson correlation coefficient, r). E, Same format as D except between 150 versus 200 ms. F, Intertrial correlation map for LatVel (Vel-Vel correlation map) in this sample set. Color indicates correlation coefficient (r) at each time point pair. Gray rectangle indicates a time interval where 50% of movement offsets occurred. Data points shown in D and E are denoted as white squares.

To quantify how lateral deviation of hand motion is corrected within a reaching movement, we decomposed the velocity into lateral (LatVel) and forward (FwdVel) components relative to target direction. Figure 2C illustrates LatVel for the dataset shown in Figure 2B, highlighting a reciprocal pattern, early versus late during reaching. For example, LatVel for the red trial was initially negative and then became positive halfway through movement. The blue trial displayed the opposite pattern. We calculated intertrial correlations by calculating how LatVel at a given time point for all trials in a dataset correlated with their respective values at other time points during the trial. Figure 2D illustrates the intertrial correlation for a data point early (150 ms after reach onset) versus late (400 ms) in movement. The plot clearly shows a strong negative correlation (r = −0.78), indicating that initial deviations were corrected later during reaching. In contrast, correlations were very positive for two time points early in the movement (150 ms vs 200 ms, r = 0.87; Fig. 2E). A full comparison of all intertrial correlations for the entire movement creates a 2D correlation map (Vel-Vel correlation map; Fig. 2F). Note that the diagonal is always 1 because it corresponds to the correlation between identical values and top-left and bottom-right halves are identical mirror images (i.e., the correlation map is a symmetric matrix). This correlation map clearly shows that there are two phases during movement: the initial LatVel during reaching remains positively correlated for ∼200 ms and then becomes negatively correlated to LatVel for the rest of the reaching movement (∼300–500 ms).

We created a grand average of the Vel-Vel correlation maps of LatVel by pooling datasets from all monkeys (960, 435, 1470, 392 and 264 neuron–target pairs from Monkeys A–E; Fig. 3A). The grand average highlights the temporal dynamics of intertrial correlations: the initial LatVel during early reaching (0–250 ms) is positively correlated and then becomes negatively correlated to LatVel during the later phase of reaching (250–500 ms). A bootstrap analysis showed that both the positive and negative correlations significantly exceeded chance levels expected from trial-shuffled data (p < 0.05 with cluster size correction, paired t test; Fig. 3B). Note that the largest negative correlation is observed at the time-point pair between 195 and 445 ms (Fig. 3A, white arrow, only shown in top left half). Because this point is well before the end of reaching (<10% of peak velocity; Fig. 3A, gray shades), we suggest that the motor correction is made online during reaching rather than after the end of reaching.

Figure 3.

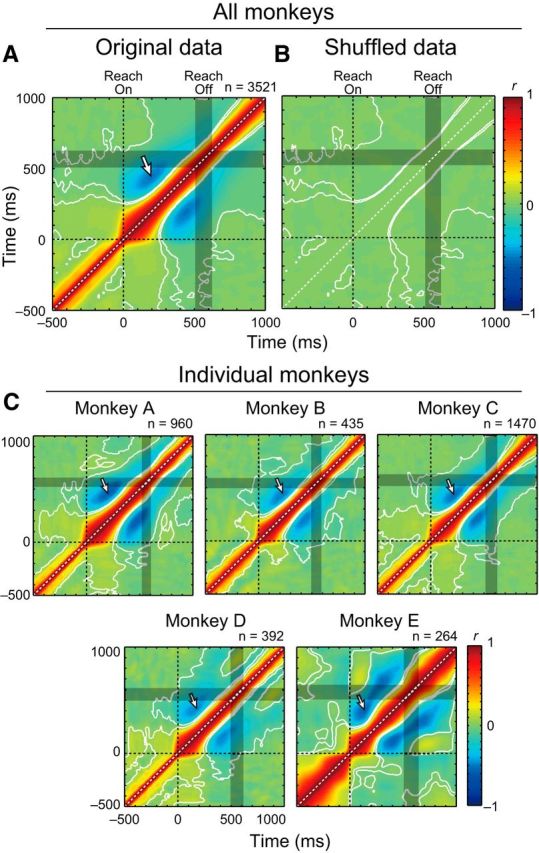
Vel-Vel correlations during reaching. A, Vel-Vel correlation maps of LatVel were averaged across datasets obtained from all monkeys (n = 3521 neuron–target pairs). Contours indicate the area where r was significantly different from the shuffled data (p < 0.05 with cluster size correction, paired t test; see Materials and Methods). Data were aligned to reach onset (horizontal and vertical dashed lines). Gray rectangle indicates a time interval where 50% of movement offsets occurred. White arrow indicates the largest negative correlation (horizontal: 195 ms, vertical: 445 ms). B, Same format as A but for shuffled data. C, Vel-Vel correlation maps for individual animals. Same format as A.

A similar pattern of intertrial correlations was observed in each monkey (Fig. 3C). These correlation maps demonstrate similar basic features: initial positive and later negative correlations and the most negative point was well before reaching offset (200 vs 460 ms, 225 vs 450 ms, 215 vs 440 ms, 175 vs 425 ms, and 135 vs 410 ms for Monkeys A–E, respectively). These results are consistent with our prediction (Fig. 1D).

Intertrial correlation between M1 neuron activity and hand velocity

Our next question was whether variations in M1 activity across trials was coupled to these variations in hand motion. Specifically, if M1 is involved in online control of reaching, then we predict that M1 activity should show positive and negative correlations with future and past motion of the hand, respectively. These correlations with hand motion are dependent on the directional tuning (PD) of each neuron relative to target direction (Fig. 1E). Figure 4A illustrates activity of an M1 neuron from monkey E that is directionally tuned to movements to the left (PD = 151°). We classified each target direction relative to the neuron's PD to predict how the neuron's activity should relate to lateral and forward velocity of the hand (Fig. 1E). For this neuron, we categorized targets 2, 3, 6, and 7 as an ortho-PD (Fig. 4A, left). Similarly, we also categorized other targets as a pro-PD (targets 4 and 5) and an anti-PD (targets 1 and 8).

Figure 4.

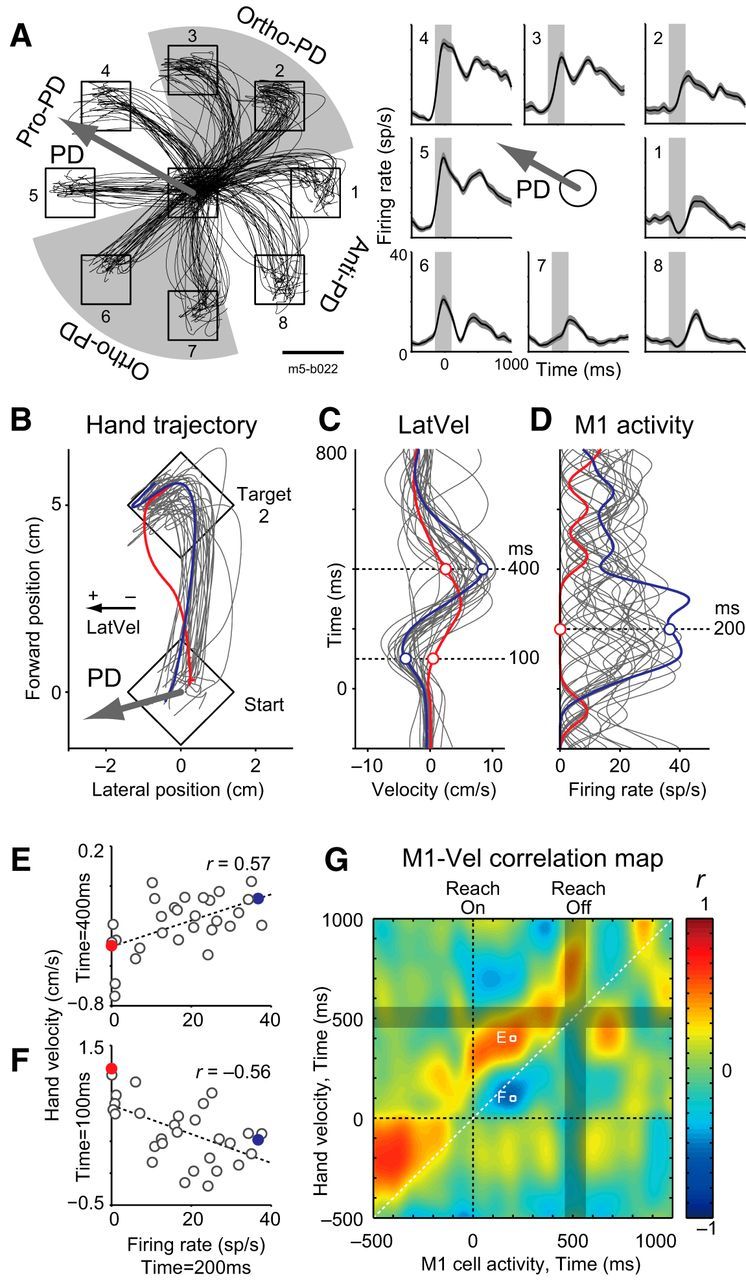
Example of intertrial correlation between M1 neuron activity and hand velocity. A, Classification of reach directions according to an example neuron's PD (m5–b022). Left, Hand trajectories for eight different target locations by Monkey E (30 trials). Right, Activity of M1 neuron for each target location averaged across trials. Traces were aligned to reach onset. Solid line and shaded area indicates mean and SEM, respectively. Vertical gray rectangle indicates the time window for calculation of the neuron's PD. The arrow defines the PD of this neuron (PD = 151°). According to the neuron's PD, targets were separated into four equally spaced areas and then categorized into three groups: targets in the PD (pro-PD), opposite to the PD (anti-PD), and orthogonal to the PD (ortho-PD). Traces denote the hand trajectories for each target. Scale bar, 3 cm. B, Hand trajectory for an ortho-PD target (target 2, movement direction is rotated to vertical for presentation purposes). The arrow indicates the neuron's PD relative to the target direction. Two exemplar trials are highlighted and color-coded throughout this figure (red and blue). C, LatVel corresponding to B. Traces are aligned to reach onset. Horizontal dashed lines indicate the time points displayed in E and F. D, The neuron's activity for each trial. Same format as C but the horizontal axis represents neuron's firing rate (spikes per second, sp/s). E, Intertrial correlation between M1 activity at 200 ms and LatVel at 400 ms after reach onset. Dashed line denotes linear regression (Pearson correlation coefficient, r). F, Same format as E except between M1 activity at 200 ms versus LatVel at 100 ms after reach onset. G, Intertrial correlation map between activity of this neuron and LatVel (M1-Vel correlation map). The basic format is same as Figure 2F, but the horizontal axis represents the timing of M1 activity.

Then, we examined the intertrial correlation between this neuron's activity and hand velocities. Figure 4B shows hand trajectories during reaching to an ortho-PD target (target 2; Fig. 4A). We hypothesized that, in this case, the neuron's activity would display a positive correlation with LatVel in the very near future and a negative correlation with LatVel in the recent past. Figure 4, C and D, shows LatVel and M1 activity in the same dataset. The blue line denotes a trial when LatVel was negative at the beginning of movement and positive at the end of movement. In this case, the activity of the M1 neuron was high during movement. In contrast, the red line denotes a trial when the magnitude of LatVel remained smaller and, in turn, the activity of the M1 neuron was minimal or absent during movement.

Figure 4, E and F, illustrates the intertrial correlation between the activity of this M1 neuron 200 ms after reach onset compared with LatVel at two time points: 100 and 400 ms after reach onset. M1 activity is negatively correlated with the former and positively correlated with the latter. Figure 4G illustrates a full comparison of all intertrial correlations for the entire movement between the activity of this M1 neuron and LatVel as an M1-Vel correlation map. This map clearly shows this neuron's activity has a negative correlation with past hand motion (below the diagonal) and positive correlation with future hand motion (above the diagonal). These correlations indicate that this neuron tends to have a higher firing rate when the hand had just deviated away from the neuron's PD (i.e., negative correlation) and is about to deviate toward the neuron's PD (i.e., positive correlation), respectively. These correlations are consistent with our prediction based on the hypothesis that M1 neuron is involved in online feedback control of the limb (Fig. 1E).

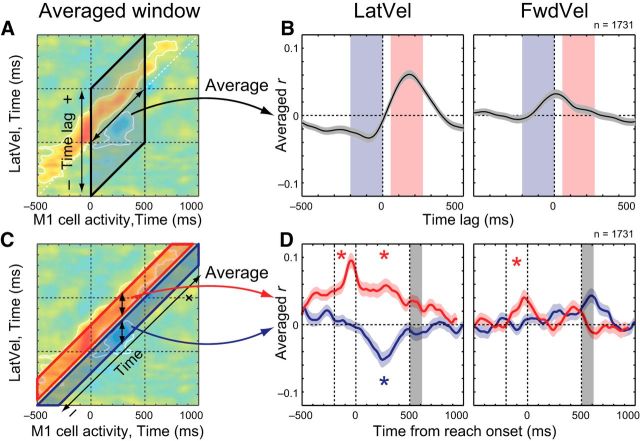
We then created a grand average of these correlation maps across all neuron–target pairs for ortho-PD targets to investigate the details of the M1-Vel correlations. In total, we identified 324 neurons with activity that was significantly tuned to the direction of reaching (73, 30, 155, 33 and 33 in Monkeys A–E). Each dataset included five to seven reaches (Monkey A–D) or 30 reaches (Monkey E) for a given target. Some neurons were recorded multiple times (2, 3, and 4 datasets for 48, 31, 3 neurons, respectively). In total, there were 3521 neuron–target pairs (ortho-PD: 1731, pro-PD: 895, and anti-PD: 895 pairs).

In the ortho-PD group, M1 activity had a significant positive correlation with LatVel in the future (above the diagonal) and a negative correlation with LatVel in the past (below the diagonal; Fig. 5B, left). The white bands around the red and blue regions denote significant differences from shuffled data (p < 0.05 with cluster size correction, paired t test). In contrast, the ortho-PD group was less correlated with FwdVel (Fig. 5B, right). Again, these results are consistent with our prediction (Fig. 1E). We also made a separate M1-Vel correlation map for individual monkeys with LatVel (Fig. 5C). As the figure highlights, the basic correlation patterns, positive and negative correlations with future and past hand motions, are consistent across monkeys, although they are noisier due to a small size of samples. We also confirmed that these correlation patterns were generally observable when examining each M1-Vel map for each target direction (data not shown).

Figure 5.

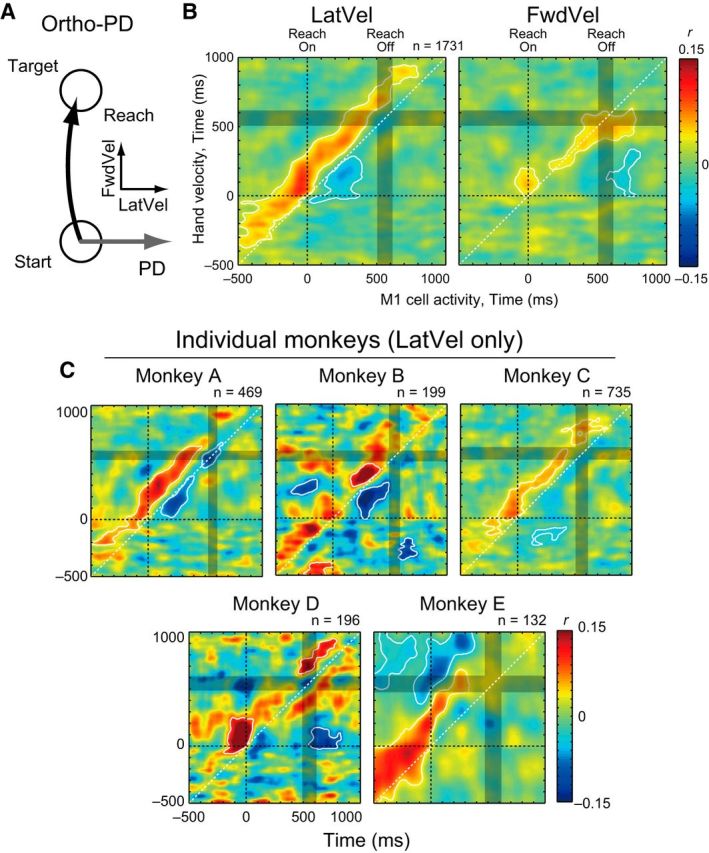
M1-Vel correlation during ortho-PD reaching. A, Schema about the PD and hand velocities. B, M1-Vel correlation map between M1 activity for ortho-PD target direction with LatVel (left) and FwdVel (right). Maps were averaged across datasets (1731 neuron–target pairs). The basic format is same as Figure 3A, but the horizontal axis represents the timing of M1 activity. White contours indicate the area where r was significantly different from the shuffled data (p < 0.05 with cluster size correction, paired t test). C, M1-Vel correlation maps for individual animals. Same format as B.

We estimated the peak time lags for the positive and negative correlations between M1 activity and LatVel (Fig. 6A). Effectively, this was done by averaging the correlations relative to the matrix diagonal (double-headed arrow) from 0 to 500 ms after reach onset. Figure 6B shows the average correlation coefficient for each time lag from M1 activity and highlights that M1 activity is most positively correlated with LatVel at 165 ms in the future and most negatively correlated with LatVel at 90 ms in the past. These positive and negative peaks with future and past hand motions were not observed for FwdVel (Fig. 6B, right).

Figure 6.

Temporal profiles of M1-Vel correlation map. A, Schema for the averaging method. Correlation coefficients were averaged in a direction parallel to the matrix diagonal (double-headed arrow) from 0 to 500 ms after reach onset. B, Intertrial correlation between M1 activity and hand velocity (left: LatVel, right: FwdVel) was averaged within reaching time (from 0 to 500 ms after reach onset). The horizontal axis indicates the time lag between M1 activity and hand velocity, where positive and negative values indicate that an increase in M1 activity precedes and lags an increase in hand velocity, respectively. Red and blue shades indicate selected time windows used in C and D. C, Schema showing the averaging method. Correlation coefficients were averaged along vertical strips (double-headed arrows) from 50 to 250 ms (future, red area) and −200 to 0 ms (past, blue area). D, Intertrial correlation between M1 activity and hand velocity (left: LatVel, right: FwdVel) averaged within 200 ms time window before (from −200 to 0 ms, blue) or after (from 50 to 250 ms, red) the M1 activity. Data are aligned to reach onset and gray shade denotes 50% interval of the distribution of reach offset. Asterisk indicates a significant difference from the shuffled data (p < 0.05 with Bonferroni correction, paired t test) before (from −200 to 0 ms relative to reach onset, dashed lines) or during t(from 0 to 500 ms, dashed lines) he movement epoch. Shaded area, SEM.

Our model predicts that, if this negative peak in correlation reflects online feedback processing, then it should only appear during the reaching movement. We tested this prediction by examining how the positive and negative correlations changed before and during movement (Fig. 6C). Effectively, this was done by averaging the correlations along vertical strips (double-sided arrow) from 50 to 250 ms (future, red area) and −200 to 0 ms (past, blue area). Figure 6D highlights that the positive correlation with future LatVel was observed both before and during reaching compared with chance levels (−200 to 0 ms: t₍₁₇₃₀₎ = 8.98, p < 0.001; 0 to 500 ms: t₍₁₇₃₀₎ = 9.54, p < 0.001, paired t test; Fig. 6D, left, red). In contrast, the negative correlation with past LatVel was only observed during reaching (−200 to 0 ms: t₍₁₇₃₀₎ = 0.287, p = 0.774; 0 to 500 ms: t₍₁₇₃₀₎ = −4.46, p < 0.001, paired t test; Fig. 6D, left, blue). For FwdVel, there was a small phasic increase in the correlation between ortho-PD and future hand velocity before reach onset (−200 to 0 ms: t₍₁₇₃₀₎ = 2.83, p = 0.005; Fig. 6D, right, red), but this correlation disappeared after reach onset.

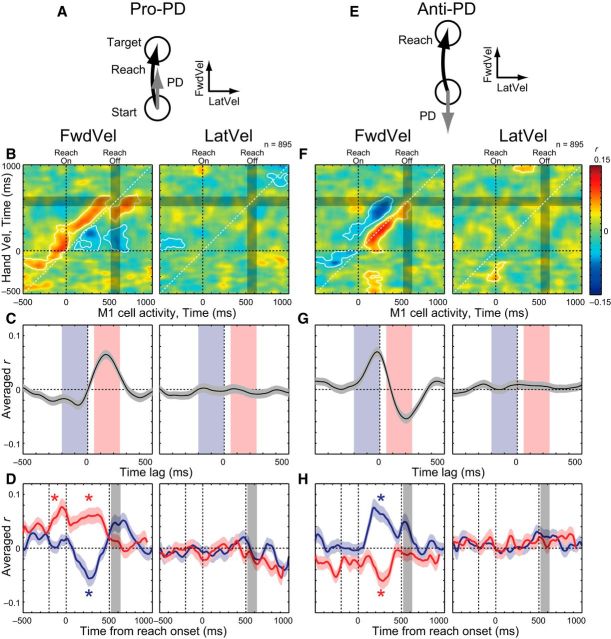
We also examined how M1 activity correlated with online adjustments in the direction to the target (Fig. 7). For this analysis, we calculated correlations between FwdVel and M1 activity for the pro-PD and anti-PD groups. In the pro-PD group, M1 activity was positively correlated with FwdVel in the near future and negatively correlated in the near past (Fig. 7B, left). In addition, there was no correlation with LatVel during movement (Fig. 7B, right). When we analyzed the time lag of the correlation peaks, the pro-PD group showed positive correlation with FwdVel at 140 ms in the future and negative correlation with FwdVel at 75 ms in the past (Fig. 7C, left). Further, the positive correlation with future FwdVel was observed both before and during reaching (−200 to 0 ms: t₍₈₉₄₎ = 5.58, p < 0.001; 0 to 500 ms: t₍₈₉₄₎ = 7.44, p < 0.001, paired t test; Fig. 7D, left, red), whereas the negative correlation with past FwdVel was only observed during reaching (−200 to 0 ms: t₍₈₉₄₎ = 0.892, p = 0.373; 0 to 500 ms: t₍₈₉₄₎ = −2.97, p = 0.003, paired t test; Fig. 7D, left, blue). The M1 activity in this pro-PD group showed minimal correlations with LatVel (Fig. 7B–D, right).

Figure 7.

M1-Vel correlations during pro- and anti-PD reaching. A, Schema about the PD and hand velocities. B, M1-Vel correlation maps for pro-PD reaching: FwdVel (left) and LatVel (right). Same format as Figure 5B. C, D, Averaged intertrial correlation. Same format as Figure 6, B and D. E–H, M1-Vel correlation maps for anti-PD reaching. Same format as A–D.

In the anti-PD group, M1 activity showed similar intertrial correlations with hand velocities as observed for the pro-PD group, but in the opposite polarity: negative correlation with future hand motion and positive correlation with past hand motion (Fig. 7F, left). When we examined the time lag of the correlations (Fig. 7G, left), the most negative correlation with FwdVel was at 205 ms in the future and the positive correlation with FwdVel was at 20 ms in the past. When we looked at the temporal change of the intertrial correlations, the negative and positive correlations were observed only after movement onset (−200 to 0 ms: t₍₈₉₄₎ = −2.26, p = 0.024; 0 to 500 ms: t₍₈₉₄₎ = −4.37, p < 0.001; blue, −200 to 0 ms: t₍₈₉₄₎ = −0.093, p = 0.926; 0 to 500 ms: t₍₈₉₄₎ = 5.28, p < 0.001, paired t test; Fig. 7H, left, red). Again, the M1 activity in this group does not show systematic correlations with LatVel (Fig. 7F–H, right). These results demonstrate that M1 activity is also correlated with past and future hand motions in pro- and anti-PD reaching when the movement is in the neuron's PD.

Partial correlation analysis

Our intertrial correlation analyses highlight three types of correlations: (1) negative correlations between early and late hand velocities with ∼250 ms time lag, (2) positive correlations between M1 neural activity and future hand velocity in neuron's PD with ∼160 ms time lag, and (3) negative correlations between M1 neural activity and past hand velocity in its PD with ∼90 ms time lag. These three correlations raise a question as to whether correlation between M1 activity and past hand velocity is simply a spurious byproduct resulting from the other two correlations. To exclude this possibility, we examined partial correlations between M1 activity and hand velocity while controlling for the effects of future hand velocity (r_xy|z; Fig. 8A). Figure 8B shows the partial correlation map between M1 activity and LatVel in the ortho-PD group after removing the effect of LatVel 250 ms in the future. This time lag between future and past hand motion was chosen based on the largest negative correlation between early and late LatVel (τ1 + τ2 = 250 ms; Fig. 3A, arrow). The partial correlation map clearly demonstrates the negative correlation with past hand motion was preserved even after removing the effect of future hand motion. This result indicates that M1 activity has a negative correlation with past hand motion that is not accounted for by the linear correlation with future hand motion. Similarly, the partial correlation map when controlling for past LatVel (r_xz|y) showed a significant positive correlation with future hand motion (Fig. 8C,D).

Figure 8.

Partial correlation between M1 activity and hand velocity. A, Schema showing partial correlation analysis. B, Partial correlation map (r_xy|z) between M1 activity and LatVel with controlling the effect of future hand velocity in ortho-PD group. Same format as Figure 5B. White contours indicate the area where r_xy|z was significantly different from the chance level (p < 0.05 with cluster size correction, paired t test). C, D, Partial correlation map (r_xz|y) between M1 activity and LatVel with controlling the effect of past hand velocity. Same format as A and B.

Mutual information analysis

Our analysis suggests M1 activity is correlated with hand motion in the near future and in the near past. In contrast, the analysis in Mulliken et al. (2008) suggested neural activity in the parietal reach region (PRR) encodes the current state of movement because they found a maximum mutual information between PRR activity and hand motion with minimal time lag. From these observations, they suggested that PRR was involved in a forward model for online sensorimotor control. However, they calculated mutual information between neural activity and hand kinematics in the middle of reaching. Philip et al. (2013) applied the same mutual information analysis to M1 activity and suggested that most neurons in M1 and parietal cortex similarly encode the current state of movement, rather than the future or past movements, as suggested by our analyses above.

We examined our dataset using the same approach as Mulliken et al. (2008) based on mutual information rather than calculating correlation coefficients. Our initial analysis looked at the middle of movement (200–300 ms after reach onset) following Mulliken et al. (2008). In this case, we also found, on average, a zero lag between the peak of the mutual information between neural activities and hand motion, replicating Philip et al. (2013) (Fig. 9A,B).

Figure 9.

Mutual information between M1 activity and hand velocity. A, Normalized mutual information between M1 neuron activity and hand velocity for the example neuron shown in Figure 4 (m5–b022). Hand velocity was projected to the neuron's PD (PDVel). Positive and negative lag indicates firing activity has information about future and past hand velocity, respectively. Crosshair indicates peak and its time lag. B, Histogram of peak lag time for mutual information between M1 activity and PDVel (443 neurons). Horizontal bars beneath the x-axis indicate the approximate lag time ranges for sensory feedback (black), forward estimate (gray), and motor command (black) representations. C, Averaged PDVel across all trials included for this analysis (27,286 trials). Solid line and shade indicates mean ± SD, respectively. Gray rectangle indicates the analytical time window when lag time is zero. D, Averaged PDVel and different analytical time windows. Gray rectangles indicate time windows. Scale bar, 10 cm/s. E, Histogram of peak lag time for mutual information between M1 activity and PDVel. Same format as B.

However, the middle of the movement happens to be the time when there is maximal variability in hand motion. Figure 9C displays the average hand velocity projected along each neuron's PD across all directions: the mean (solid line) is almost zero during movement as reaching trials were averaged across all directions, whereas the SD of hand velocity is maximal at the middle of movement. This was also the time when mutual information between neural activity and hand motion was maximal (Mulliken et al., 2008; Philip et al., 2013).

We investigated whether the selection of a mid-movement time epoch influenced the peak lags for the mutual information by shifting the epoch from 200 ms before to 200 ms after the middle of movement (Fig. 9D). We found that this shift had a substantial impact on the results such that an early epoch had maximal mutual information with hand velocity ∼200 ms in the future (Fig. 9E, top) and a late epoch had maximal mutual information with the hand velocity ∼200 ms in the past (Fig. 9E, bottom). This indicates that mutual information was always aligned with the middle of movement when the variability in hand velocity was maximal, with the time lag varying considerably dependent on time window selected. Therefore, the mutual information analysis used in these studies was not suitable to identify the temporal relationship between neural activity and hand motion.

Discussion

Intertrial variability reflects a feedback process during reaching

Previous studies have shown that initial movement variability is uncorrelated with endpoint variability (Messier and Kalaska, 1999; Todorov and Jordan, 2002; van Beers et al., 2004; Nashed et al., 2012), suggesting that deviations in hand motion at the beginning of the movement are compensated for later in the movement. However, one possibility is that this pattern of limb motion is entirely generated by a feedforward or preprogrammed process. Many studies highlight that hand trajectories are relatively straight, but also possess slight curvatures in the trajectory of the hand to a spatial goal (Morasso, 1981; Flash and Hogan, 1985; Uno et al., 1989; Wolpert et al., 1994; Osu et al., 1997; van Beers et al., 2004; Nashed et al., 2012). Interestingly, some feedforward control models predict hand trajectories that are slightly curved for certain target locations in human subjects (Uno et al., 1989; Osu et al., 1997). These studies suggested that the curved trajectory was a result of the optimization of intrinsic parameters (e.g., minimizing torque change) and thus preprogrammed.

There are several reasons why we think the trial-to-trial variability of hand motion reflects a feedback process. First, these feedforward theories explain why the “average” hand trajectories are slightly curved, but not why trial-to-trial variability should be correlated between initial and later hand trajectory across trials (Fig. 2). If these trial-to-trial variations are also preprogrammed, then this suggests that subjects are changing their optimization criteria (i.e., cost function) on a trial-to-trial basis.

A simpler explanation is that the temporal correlation for hand motion is the signature of a feedback controller. A broad range of studies have highlighted how rapid goal-directed corrections are generated by the motor system following mechanical disturbances of the limb (Crevecoeur et al., 2012, 2013; Nashed et al., 2012, 2014) or shifts in visual feedback of hand motion (Brenner and Smeets, 2003; Saunders and Knill, 2003; Franklin and Wolpert, 2008; Dimitriou et al., 2013; Franklin et al., 2014). These corrections consider a variety of factors such as target shape (Nashed et al., 2012; Crevecoeur et al., 2013) or the presence of obstacles (Nashed et al., 2014). Further, corrective responses can be observed even for very small disturbances that approach the range of variability observed during unperturbed reaching (Crevecoeur et al., 2012). We suggest that a similar process generates online compensation for errors or variability generated by the motor system itself, resulting in a negative correlation for trial-to-trial variability between initial and later hand motion.

Role of M1 in online control of movement

Our results demonstrate that M1 activity is correlated with hand velocity in the near future both before and during reaching (Figs. 6D, 7D). This suggests that M1 neurons provide both initiation and a continuous control signal related to limb motion. This result is consistent with previous studies demonstrating that the population vector from M1 activity predicts the instantaneous direction and speed of the averaged hand motion of the monkey's arm ∼100–160 ms later (Georgopoulos et al., 1988; Moran and Schwartz, 1999a,b), as well as muscle activity with a ∼50 ms time lag (Morrow and Miller, 2003). We extend this by demonstrating neural variability around the mean pattern also correlates with future variability in hand motion. We found peak latencies of 140–165 ms for both the ortho-PD and pro-PD groups, which would be expected due to transmission time and muscle force development leading to movement. As for the positive correlation well before reach onset (200 ms or more before reach onset; Figs. 5B, 6D), it is likely that the correlation reflects postural control rather than motor preparation for a forthcoming movement because our task was a reaction time task and it did not have an instructed delay period. Furthermore, the M1 activity was correlated with hand motion before movement onset, but not after it. Note that, although we used hand motion to explain M1 activity, we are not suggesting M1 activity represents hand motion in external space (Scott et al., 2001). In theory, we could perform the same correlation analysis with other motor parameters that are more similar to spatiotemporal features of muscle activity, such as joint torques, or even correlate to electromyographic activity itself. Comparison of intertrial correlation between these parameters should be a focus for future studies.

Role of M1 in online feedback control of movement

Our key observation is that M1 activity is negatively correlated with past hand motion as well as positively correlated with future hand motion during reaching (Figs. 5B, 7B). Importantly, our partial correlation analysis demonstrated that the negative correlation with past hand motion was not generated by a spurious correlation between M1 activity and future hand motion and vice versa (Fig. 8). This result strongly suggests that M1 activity is modulated based on feedback from the limb, which leads to corrections in future hand motion.

There are two possible mechanisms for how M1 reflects variability of past hand motion: internal feedback or sensory feedback. Internal feedback of motor commands could be used to estimate the motion of the limb to overcome time delays associated with sensory feedback (Wolpert et al., 1998). Such a forward internal model could estimate limb motion with very little delay. However, the peak latency between M1 and past hand motion is ∼75–90 ms for the pro-PD and ortho-PD groups (Figs. 6B, 7C). Therefore, it is unlikely that this internal feedback is the main source of the negative correlation with past hand motion. The more feasible mechanism is that the correlation was generated by sensory feedback from the limb. Previous studies have shown neural activity in M1 responds in as little as 20 ms to a mechanical disturbance, although the onset times span a range up to 100 ms or more (Herter et al., 2009). Further, the influence of limb mechanics first emerges at ∼50 ms and peaks at ∼100 ms in M1 following mechanical disturbances (Pruszynski et al., 2011). These latencies are similar to the peak latency of the negative correlation between M1 activity and past hand motion (75–90 ms; Figs. 6B, 7C). Therefore, our negative correlation between M1 and past hand motion is likely mediated largely from sensory feedback from the limb rather than internal feedback.

It is notable that the anti-PD group also displayed reciprocal correlations with past and future hand motions, but the peak latency was different from the other groups (205 ms in future and 20 ms in past hand motion; Fig. 7G). In addition, the anti-PD group did not display premovement correlations with future hand motion (Fig. 7H). Why the latencies for anti-PD group were different is not clear, but it might be related to the fact that neurons with PDs opposite to the direction of reaching often decrease their firing activity and sometimes become silent. This nonlinearity might impact the correlational analyses used in this study.

A previous study suggested that M1 activity encoded the present hand motion using mutual information analysis (Philip et al., 2013). However, our mutual information analysis demonstrates that the lag between M1 activity and hand motion systematically shifted based on the time window used in the analysis (Fig. 9). This suggests that the time lag obtained from mutual information analysis does not provide an accurate measure of temporal links between M1 activity and body motion, but instead reflects the fact that the variance of hand kinematics is largest at midreach. Suggestions that PRR specifies the present hand position should also be reexamined because their selected time window was again centered on the midway point of the movement (Mulliken et al., 2008). Note that this does not mean that mutual information is always unsuitable to examine neural encoding of movement. In theory, mutual information provides a more general measure than linear correlation analysis and we could compute a similar correlation map with mutual information. However, because of its non-negativity, it cannot provide a polarity of correlation (i.e., positive and negative) that is critical for our study.

The present results also provide an explanation for previous observations that M1 codes fragments of movements termed “pathlets” (Hatsopoulos et al., 2007). Strikingly, these pathlets demonstrated spatially complex and temporally extensive profiles. The extracted pathlets often spanned from recent past to the near future relative to the neuron activity and the direction of the trajectory often dramatically changed during the time window. Pruszynski et al. (2010) demonstrated that muscle activity also showed similar complex tuning of hand kinematics, suggesting a peripheral source for the spatiotemporal features of pathlets. Our results provide further explanation as to why M1 neurons display pathlets spanning both future and past limb motion. Specifically, the present study demonstrated there are correlations with past and future hand motions in M1 and, critically, their polarity was opposite (i.e., negative–positive or positive–negative). This would lead to pathlets that include motion in one direction for the recent past and in the opposite direction for the near future, as is commonly observed (Hatsopoulos et al., 2007; Pruszynski et al., 2010).

One limitation of the present correlation analyses is that they assume a linear relationship between M1 activity and hand motion. There are, of course, many nonlinearities in the musculoskeletal system and likely many associated with neural dynamics in M1 (Churchland et al., 2012; Russo et al., 2018). Although the time between M1 activity and hand motion is relatively short, which helps to reduce the impact of these nonlinearities, it is possible that they could influence the correlational analyses in this study. Future studies could examine the potential influence of these nonlinear effects using artificial neural networks that control a mechanically realistic model of the limb (Lillicrap and Scott, 2013).