Abstract
Human metacognition, or the capacity to introspect on one's own mental states, has been mostly characterized through confidence reports in visual tasks. A pressing question is to what extent results from visual studies generalize to other domains. Answering this question allows determining whether metacognition operates through shared, supramodal mechanisms or through idiosyncratic, modality-specific mechanisms. Here, we report three new lines of evidence for decisional and postdecisional mechanisms arguing for the supramodality of metacognition. First, metacognitive efficiency correlated among auditory, tactile, visual, and audiovisual tasks. Second, confidence in an audiovisual task was best modeled using supramodal formats based on integrated representations of auditory and visual signals. Third, confidence in correct responses involved similar electrophysiological markers for visual and audiovisual tasks that are associated with motor preparation preceding the perceptual judgment. We conclude that the supramodality of metacognition relies on supramodal confidence estimates and decisional signals that are shared across sensory modalities.
SIGNIFICANCE STATEMENT Metacognitive monitoring is the capacity to access, report, and regulate one's own mental states. In perception, this allows rating our confidence in what we have seen, heard, or touched. Although metacognitive monitoring can operate on different cognitive domains, we ignore whether it involves a single supramodal mechanism common to multiple cognitive domains or modality-specific mechanisms idiosyncratic to each domain. Here, we bring evidence in favor of the supramodality hypothesis by showing that participants with high metacognitive performance in one modality are likely to perform well in other modalities. Based on computational modeling and electrophysiology, we propose that supramodality can be explained by the existence of supramodal confidence estimates and by the influence of decisional cues on confidence estimates.
Keywords: audiovisual, confidence, EEG, metacognition, signal detection theory, supramodality
Introduction
Humans have the capacity to access and report the contents of their own mental states, including percepts, emotions, and memories. In neuroscience, the reflexive nature of cognition is now the object of research under the broad scope of the term “metacognition” (Koriat, 2007; Fleming et al., 2012). A widely used method to study metacognition is to have observers do a challenging task (first-order task), followed by a confidence judgment regarding their own task performance (second-order task; see Fig. 1, left). In this operationalization, metacognitive accuracy can be quantified as the correspondence between subjective confidence judgments and objective task performance. Although some progress has been made regarding the statistical analysis of confidence judgments (Galvin et al., 2003; Maniscalco and Lau, 2012; Barrett et al., 2013) and more evidence has been gathered regarding the brain areas involved in metacognitive monitoring (Grimaldi et al., 2015), the core properties and underlying mechanisms of metacognition remain largely unknown. One of the central questions is whether, and to what extent, metacognitive monitoring should be considered supramodal: is the computation of confidence fully independent of the perceptual signal (i.e., supramodality) or does it also involve signal-specific components? According to the supramodality hypothesis, metacognition would have a quasihomuncular status, the monitoring of all perceptual processes being operated through a single shared mechanism. Instead, modality-specific metacognition would involve a distributed network of monitoring processes that are specific for each sensory modality. The involvement of supramodal, prefrontal brain regions during confidence judgments first suggested that metacognition is partly governed by supramodal rules (Fleming et al., 2010; Yokoyama et al., 2010; Rahnev et al., 2015). At the behavioral level, this is supported by the fact that metacognitive performance (Song et al., 2011), and confidence estimates (de Gardelle and Mamassian, 2014; Rahnev et al., 2015) correlate across subjects between two different visual tasks, as well as between a visual and an auditory task (de Gardelle et al., 2016). However, the supramodality of metacognition is challenged by the report of weak or null correlations between metacognitive performance across different tasks involving vision, audition, and memory (Ais et al., 2016). Beyond sensory modalities, metacognitive judgments across cognitive domains were shown to involve distinct brain regions, notably, frontal areas for perception and precuneus for memory (McCurdy et al., 2013). Supporting this view, patients with lesions to the anterior prefrontal cortex were shown to have a selective deficit in metacognition for visual perception, but not memory (Fleming et al., 2014). This anatomo-functional distinction across cognitive domains is further supported by the fact that meditation training improves metacognition for memory, but not for vision (Baird et al., 2014). Compared with previous work, the present study sheds new light on the issue of supramodality by comparing metacognitive monitoring of stimuli from distinct sensory modalities but during closely matched first-order tasks. At the behavioral level, we first investigated the commonalities and specificities of metacognition across sensory domains including touch, a sensory modality that has been neglected so far. We examined correlations between metacognitive performance during a visual, auditory, and tactile discrimination task (Experiment 1). Next, extending our paradigm to conditions of audiovisual stimulation, we quantified for the first time the links between unimodal and multimodal metacognition (Deroy et al., 2016) and assessed through computational modeling how multimodal confidence estimates are built (Experiment 2). This allowed us to assess whether metacognition is supramodal because of a generic format of confidence. Finally, we investigated the neural mechanisms of unimodal and multimodal metacognition and repeated Experiment 2 while recording 64-channel electroencephalography (EEG, Experiment 3). This allowed us to identify neural markers with high temporal resolution, focusing on those preceding the response in the first-order task [eventrelated potentials (ERPs), alpha suppression] to assess whether metacognition is supramodal because of the presence of decisional cues. The present data reveal correlations in metacognitive behavioral efficiencies across different unimodal and bimodal perception; computational evidence for integrative, supramodal representations during audiovisual confidence estimates; and the presence of similar neural markers of supramodal metacognition preceding the first-order task. Altogether, these behavioral, computational, and neural findings provide nonmutually exclusive mechanisms explaining the supramodality of metacognition during human perception.
Figure 1.
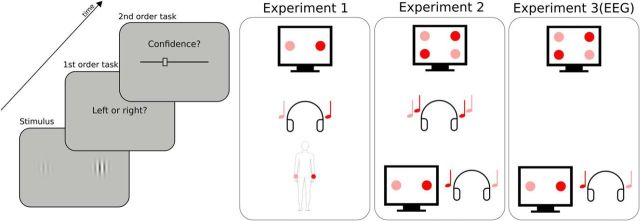
Experimental procedure. Participants had to perform a perceptual task on a stimulus (first-order task) and then indicate their confidence in their response by placing a cursor on a visual analog scale (second-order task). The types of stimuli and first-order task varied across conditions and experiments, as represented schematically on the right. In Experiment 1, a pair of two images, sounds, or tactile vibrations was presented on each trial. The stimuli of each pair were lateralized and differed in intensity (here, high intensity is depicted in red, low intensity in pink). The first-order task was to indicate whether the most intense stimulus was located on the right (as depicted here) or left side. In Experiment 2, either two pairs of two images (unimodal visual condition), two sounds (unimodal auditory condition), or one pair of two images with one pair of two sounds (bimodal audiovisual condition) were presented on each trial. The first-order task was to indicate whether the most intense stimulus of each pair were both on the same side (congruent trial) or each on a different side (incongruent trial, as depicted here). Experiment 3 was a replication of Experiment 2 including EEG recordings, focusing on the unimodal visual condition and the bimodal audiovisual condition. The order of conditions within each experiment was counterbalanced across participants.
Materials and Methods
Participants.
A total of 50 participants (Experiment 1: 15 including 8 females, mean age = 23.2 years, SD = 8.3 years; Experiment 2: 15 including 5 females, mean age = 21.3 years, SD = 2.6 years; Experiment 3: 20 including 6 females, mean age = 24.6 years, SD = 4.3 years) from the student population at the Swiss Federal Institute of Technology (EPFL) took part in this study in exchange for monetary compensation (20 CHF per hour). All participants were right-handed, had normal hearing and normal or corrected-to-normal vision, and no psychiatric or neurological history. They were naive to the purpose of the study and gave informed consent in accordance with institutional guidelines and the Declaration of Helsinki. The data from two participants were not analyzed (one in Experiment 1 due to a technical issue with the tactile device and one from Experiment 2 because the participant could not perform the auditory task).
Stimuli.
All stimuli were prepared and presented using the Psychophysics toolbox (Pelli, 1997; Brainard, 1997, Kleiner et al., 2007; RRID:SCR_002881) in Matlab (Mathworks; RRID:SCR_001622). Auditory stimuli consisted of either an 1100 Hz sinusoidal (high-pitched “beep” sound) or a 200 Hz sawtooth function (low-pitched “buzz” sound) played through headphones in stereo for 250 ms with a sampling rate of 44,100 Hz. The loudness of one of the two stimuli was manipulated to control for task performance and the other stimulus remained constant. In phase 1, the initial inter-ear intensity difference was 50% and increased (decreased) by 1% after each incorrect (two correct) answers. The initial difference and step size were adapted based on individual performance. The initial difference in phase 2 was based on the results from phase 1 and the step size remained constant. In the auditory condition of Experiment 2, both sounds were played simultaneously in both ears and were distinguished by their timbre. When necessary, a correction of hearing imbalance was performed before the experiment to avoid response biases.
Tactile stimuli were delivered to the palmar side of each wrist by a custom-made vibratory device using coin permanent-magnetic motors (9000 rpm maximal rotation speed, 9.8 N bracket deflection strength, 55 Hz maximal vibration frequency, 22 m/s2 acceleration, 30 ms delay after current onset) controlled by a Leonardo Arduino board through pulse width modulation. Task difficulty was determined by the difference in current sent to each motor and one motor always received the same current. In phase 1, the initial interwrist difference was 40% and increased (decreased) by 2% after each incorrect (two correct) answers. The initial difference and step size were adapted individually based on performance. A correction of tactile imbalance due to a difference of pressure between the vibrator and the wrist was performed before the experiment to avoid response biases. The initial difference in phase 2 was determined by the final difference from phase 1. The step size for the stimulus staircase remained constant for both phases.
Visual stimuli consisted in pairs of two 5° × 5° Gabor patches (5 cycles/°, 11° center-to-center distance). When only one pair of visual stimuli was presented (visual condition of Experiment 1, audiovisual condition of Experiments 2 and 3), it was centered vertically on the screen. When two pairs were presented (visual condition of Experiment 2 and 3), each pair was presented 5.5° above or below the vertical center of the screen. Visual contrast of one Gabor of the pair was manipulated, whereas the other always remained at constant contrast. The staircase procedure started with a difference of contrast between Gabor patches of 40% and an increment (decrement) of 2.5% after one incorrect (two correct) answers.
General procedure.
All three experiments were divided into two main phases. The first phase aimed at defining the participant's threshold during a perceptual task using a one-up/two-down staircase procedure (Levitt, 1971). In Experiment 1, participants indicated which of two stimuli presented to the right or left ear (auditory condition), wrist (tactile condition), or visual field (visual condition) was the most salient. Saliency corresponded respectively to auditory loudness, tactile force, and visual contrast (see below for details). In Experiment 2, participants indicated whether the two most salient stimuli of two simultaneous pairs were presented to the same or different ear (auditory condition), visual field (visual condition), or if the side of the most salient auditory stimulus corresponded to the side of the most salient visual one (audiovisual condition). Stimuli were presented simultaneously for 250 ms. All staircases included a total of 80 trials and lasted ∼5 min. All thresholds were defined as the average stimulus intensity during the last 25 trials of the staircase procedure. All staircases were visually inspected and restarted in case no convergence occurred by the end of the 80 trials (i.e., succession of multiple up/down reversals). The initial stimulation parameters in the audiovisual condition of Experiments 2 and 3 were determined by a unimodal staircase procedure applied successively to the auditory and visual condition.
In the second phase, participants did the same perceptual task with an initial stimulus intensity given by the final value in the staircase conducted in phase 1. As in phase 1, stimuli in phase 2 were controlled with one-up/two-down staircase procedure to keep task performance ∼71% throughout, thus accounting for training or fatigue effects. This ensured a constant level of task difficulty, which is crucial to quantify metacognitive accuracy precisely across conditions and is a standard approach (Fleming et al., 2010, McCurdy et al., 2013; Ais et al., 2016). Immediately after providing their response on the perceptual task, participants reported their confidence on their preceding response on a visual analog scale using a mouse with their right hand. The left and right end of the scale were labeled “very unsure” and “very sure,” respectively, and participants were asked to report their confidence as precisely as possible trying to use the whole scale range. A cursor slid over the analog scale automatically after mouse movements and participants clicked the left mouse button to indicate their confidence. Participants could click the right button instead to indicate when they had made a trivial mistake (e.g., pressed the wrong button, obvious lapses of attention), which allowed us to exclude these trials from the analysis. During a training phase of 10 trials, the cursor changed color after participants clicked to provide their answer to the perceptual task. The cursor turned green after correct responses and red after incorrect responses. No feedback was provided after the training phase. In the audiovisual condition of Experiments 2 and 3, auditory and visual stimuli intensities were yoked so that a correct (incorrect) answer on the bimodal stimulus led to an increase (decrease) in the stimulus intensity in both modalities. Each condition included a total of 400 trials divided into five blocks. Trials were interspaced with a random interval lasting between 0.5 and 1.5 s drawn from a uniform distribution. The three conditions (two in Experiment 3) were run successively in a counterbalanced order. One entire experimental session lasted ∼3 h.
Behavioral analysis.
The first 50 trials of each condition were excluded from analysis because they contained large variations of perceptual signal. Only trials with reaction times <3 s for the type 1 task and type 2 task were kept (corresponding to an exclusion of 22.2% of trials in Experiment 1 and 12.6% in Experiment 2). In Experiment 3, we used a more lenient superior cutoff of 5 s, resulting in 3.7% excluded trials because many trials had to be removed due to artifacts in the EEG signal. Meta-d′ (Maniscalco and Lau, 2012) was computed with MATLAB (The MathWorks; RRID:SCR_001622), with confidence binned into six quantiles per participant and per condition. All other behavioral analyses were performed with R (2016; RRID:SCR_001905), using type 3 ANOVAs with Greenhouse–Geisser correction (afex package: Singmann et al., 2017) and null effect estimates using Bayes factors with a Cauchy prior of medium width (scale = 0.71; BayesFactor package: Morey et al., 2015). Correlations in metacognitive efficiencies across senses were quantified by R2 adjusted for the number of-dependent variables relative to the number of data points. The overlap between confidence and reaction times probability density functions after correct and incorrect responses was estimated as the area defined by the x-axis and the lower of the two densities at each point in x (Overlap package: Ridout and Linkie, 2009). The package ggplot2 (Wickham, 2009; RRID:SCR_014601) was used for graphical representations.
Preprocessing of EEG data.
Continuous EEG was acquired at 1024 Hz with a 64-channels Biosemi ActiveTwo system referenced to the common mode sense-driven right leg ground (CMS-DRL). Signal preprocessing was performed using custom MATLAB (The MathWorks; RRID:SCR_001622) scripts using functions from the EEGLAB (version 13.5.4; Delorme and Makeig, 2004; RRID:SCR_007292), Adjust (Mognon et al., 2011; RRID:SCR_009526) and Sasica toolboxes (Chaumon et al., 2015). The signal was first downsampled to 512 Hz and band-pass filtered between 1 and 45 Hz (Hamming windowed-sinc finite impulse response filter). After visual inspection, artifact-contaminated electrodes were removed for each participant, corresponding to 3.4% of total data. Epoching was performed at type 1 response onset. For each epoch, the signal from each electrode was centered to zero and average referenced. After visual inspection and rejection of epochs containing artifactual signal (3.9% of total data, SD = 2.2%), independent component analysis (Makeig et al., 1996) was applied to individual datasets, followed by a semiautomatic detection of artifactual components based on measures of autocorrelation, correlation with vertical and horizontal EOG electrodes, focal channel topography, and generic discontinuity (Chaumon et al., 2015). Automatic detection was validated by visually inspecting the first 15 component scalp map and power spectra. After artifact rejection, epochs with amplitude changes of ±100 μV DC offset were excluded (2.9% of epochs, SD = 3.1%), and the artifact-contaminated electrodes were interpolated using spherical splines (Perrin et al., 1989).
Statistical analyses of EEG data.
After preprocessing, analyses were performed using custom MATLAB scripts using functions from the EEGLAB (Delorme and Makeig, 2004; RRID:SCR_007292) and Fieldtrip toolboxes (Oostenveld et al., 2011; RRID:SCR_004849). Event-related potentials were centered on zero. Time–frequency analysis was performed using Morlet wavelets (3 cycles) focusing on the 8–12 Hz band. Voltage amplitude and alpha power were averaged within 50 ms time windows and analyzed with linear mixed-effects models (lme4 and lmerTest packages; Bates et al., 2014; Kuznetsova et al., 2014). This method allowed analyzing single trial data with no averaging across condition or participants and no discretization of confidence ratings (Bagiella, Sloan, and Heitjan, 2000). Models were performed on each latency and electrode for individual trials, including raw confidence rating and condition (i.e., visual vs audiovisual) as fixed effects and random intercepts for subjects. Random slopes could not be included in the models because they induced convergence failures (i.e., we used parsimonious instead of maximal models; Bates et al., 2015). Significance of fixed effects was estimated using Satterthwaite's approximation for degrees of freedom of F statistics. Statistical significance for ERPs and alpha power within the ROI was assessed after correction for false discovery rate. Topographic analyses were exploratory and significance was considered for p < 0.001 without correcting for multiple comparisons.
Signal-detection theory (SDT) models of behavior.
The models assume that, on each trial, two internal signals are generated, {X1, X2}, and then combined into a bivariate normal. Because X1 and X2 are independent, the covariance matrix is diagonal. The marginal distributions of the bivariate normal corresponded to one of the stimuli pairs in each condition. Each pair can be described as R (or L) if the strongest stimulus in the pair is the right (or left) one. The bivariate distribution was parametrically defined with an arbitrary mean with | μ | = (1, 1) (μ = 1 in cases of R stimuli and μ = −1 in cases of L stimuli) and two SDs σ1, σ2. Therefore, the four probability densities can be expressed as a function of the internal signal strength X and its distribution parameters μ and σ as follows:
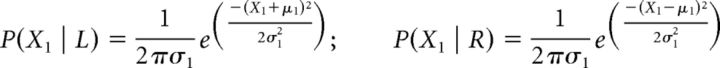 |
 |
For each set of four stimuli presented in every trial of Experiment 2, congruent pairs correspond to either LL or RR stimuli, whereas incongruent correspond to LR or RL stimuli.
Decision rule: type 1 task.
In the model, the type 1 congruency decision depends on the log-likelihood ratio as follows:
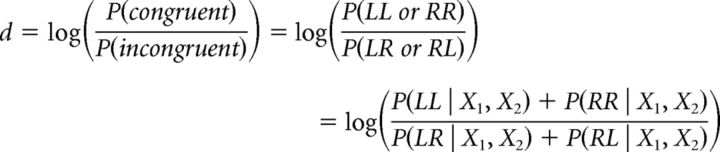 |
Applying Bayes' rule and given that X1, X2 are independent, then:
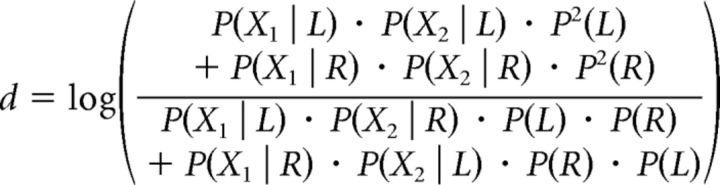 |
and assuming equal priors P(R) = P(L), then:
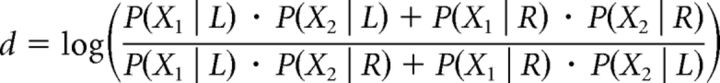 |
If d > 0, then the response given is “congruent,” whereas if d < 0, the response is “incongruent.” The values of (X1, X2), corresponding to d = 0, where the congruent and incongruent stimuli are equally likely, should satisfy the following relation:
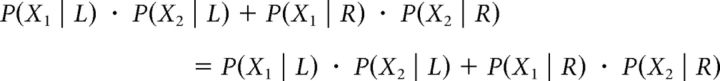 |
The solution to this relation should then satisfy the following:
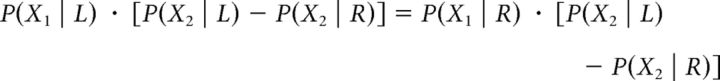 |
and, trivially for an ideal observer, possible solutions for the type 1 decision are given by the following:
Therefore, the internal response space (X1, X2) is divided in four quadrants such that an ideal observer will respond “congruent” if X1 and X2 are both greater than zero or both lower than zero. If X1 and X2 have different signs, the response will be incongruent.
Confidence judgment: type 2 task.
All models assume that confidence in each trial is proportional to the likelihood of having given a correct answer as follows:
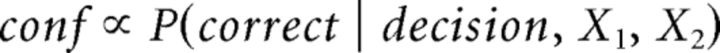 |
If a response is “congruent,” then a participant's confidence in that response is as follows:
The values of confidence in this case correspond to the top-right and bottom-left quadrants in the 2D SDT model. The two remaining quadrants correspond to trials in which the response was “incongruent” and are symmetrical to the former relative to the decision axes.
Again, applying Bayes' rule and assuming that confidence in the unimodal condition is calculated on the basis of the joint distribution and hence P(X1, X2 | RR) = P(X1 | R) · P(X2 | R), it follows that:
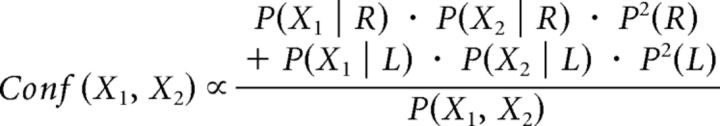 |
Assuming equal priors P(L) = P(R) and given that P(X1) = P(X1 | R) + P(X1 | L) and P(X2) = P(X2 | R) + P(X2 | L), then the expression above can be rewritten as follows:
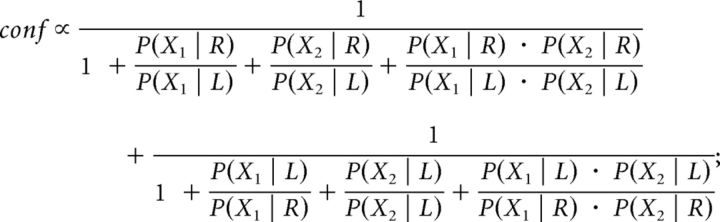 |
Assuming bivariate normal distributions of the internal signals (as detailed above) and after simplification, it can be shown that:
 |
Modeling strategy.
The modeling included two phases. In the first phase, we obtained the parameter values that best explained the unimodal data. In the second phase, behavioral data in the bimodal condition were predicted by combining the parameter values obtained in phase 1 according to different models. The predictions of these models were compared using Bayes Information Criterion (BIC) and relative BIC weights (see below).
Phase 1: fits to the unimodal conditions.
The behavioral data for each participant were summarized in eight different categories: those trials in which confidence was higher/lower than the median confidence value for each participant, for correct/incorrect type 1 response, for congruent/incongruent stimuli (i.e., 2 confidence bins × 2 accuracies × 2 conditions). We summarize these data in the vector containing the number of trials for each category nobs. In the context of SDT, two parameters are enough to determine fully the expected probability densities pexp of these eight response types: the internal noise (σ) and confidence criterion (c). We defined the best-fitting model parameters as those that maximized the likelihood of the observed data. More specifically, we randomly sampled the parameter space using a simulated annealing procedure (using the custom function anneal, which implements the method presented by Kirkpatrick et al., 1983) and used maximum likelihood to obtain two parameter values. The best fit (the point of maximum likelihood) was defined as the set of values for pexp that minimized the negative log-likelihood nL of the data as follows:
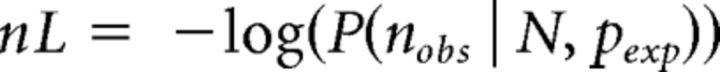 |
Where P is the multinomial distribution with parameters nobs = (n1, …, n8), N = Σ (n1, …, n8), and Pexp = (P1, …, P8), with the superindices corresponding to each of the 8 possible categories as follows:
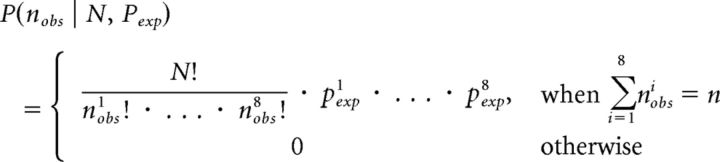 |
In the unimodal conditions, σ1 and σ2 correspond to each of the stimuli pairs of the same modality and were therefore constrained to be equal. The parameter c determined the type-2 criterion above which a decision was associated with high confidence ratings.
The model relied on three assumptions: first, it assumed equal priors for all possible stimuli. Second, type 1 decisions were assumed to be unbiased and optimal. Third, as noted above, confidence was defined as proportional to the likelihood of having given a correct answer given the type 1 decision and the internal signal for each stimuli pair. We argue that the second assumption of equality for σ1 and σ2 is a reasonable one in the unimodal visual case in which the two stimuli pairs differed only on their vertical position (but did not differ in their distance from the vertical midline). This assumption, however, is less clearly valid in the unimodal auditory condition, in which the two pairs of stimuli were different (a sinewave “beep” vs a sawtooth “buzz”). To estimate the model fits in the unimodal condition, R2 values for the correlation between observed and modeled response rates pooled for all participants were obtained. The model was flexible enough to fit the different behavioral patterns of most participants and the model fits obtained for the unimodal auditory condition were comparable to those in the unimodal visual condition (see Results).
Phase 2: predictions of the bimodal condition.
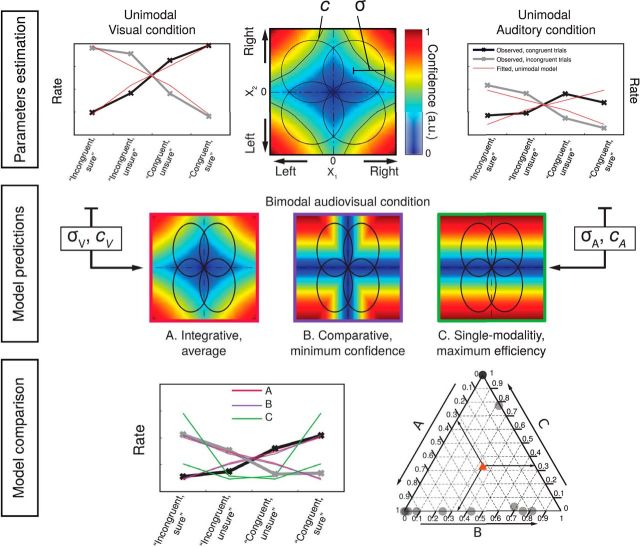
Once the σ and c parameters were estimated from the unimodal data for each participant, they were then combined under different models to estimate the predictions of the data in the audiovisual condition. Note that, with this procedure and unlike the fits to the unimodal conditions, the data used to estimate the model parameters were different from those on which the model fits were compared. In the bimodal condition and in contrast to the unimodal ones, σ1 and σ2 corresponded to the internal noise for the visual and auditory signal, respectively, and were allowed to vary independently. Here, X1, X2 are the internal responses generated by each pair of stimuli of the visual and auditory modality respectively. Because confidence was binned into “high” and “low” based on individual median splits, the criterion value was a critical factor determining model fits. Models were grouped into three families to compare them systematically. The family of integrative models echoes the single-modality model and represents the highest degree of integration: here, confidence is computed on the basis of the joint distribution of the auditory and visual modalities (see Fig. 4). Within this family, the average model considers one value of σ for each modality and takes a criterion resulting from the mean of the two modalities estimated. The derivation and expression of confidence in the integrative models is equal to that of the unimodal model, described in detail above.
Figure 4.
Top row, Parameter estimation in the unimodal visual and unimodal auditory conditions. In the middle panel, circles represent the partially overlapping bivariate internal signal distributions for each of the stimulus combinations, represented at a fixed density contour. The top right quadrant corresponds to congruent stimuli, in which the stimuli in each pair were stronger on the right side. The colors represent the predicted confidence, normalized to the interval (0,1) for every combination of internal signal strength for each stimulus pair (X1, X2). Parameters for internal noise (σ) and criterion (c) were defined for each participant based on the fitting of response rates (“congruent”/“incongruent” and “sure”/“unsure” based on a median split of confidence ratings) in the unimodal visual (left) and auditory (right) conditions. The thick black and gray lines correspond, respectively, to observed responses in congruent and incongruent trials for a representative participant. The red lines represent the response rates predicted by the model with fitted parameters. Middle row: Model predictions. Modeling of bimodal data based on the combination of cA, cV, and σA, σV, according to integrative (A, in blue), comparative (B, in red), and single-modality (C, in green) rules. Note that for models A and B, confidence increases with increasing internal signal level in both modalities, whereas in the single-modality model C, confidence depends on the signal strength of only one modality. Bottom row, Model comparison for the audiovisual condition. Left, Fit of response rates in the audiovisual condition for a representative participant according to model A (blue), B (red), or C (green). Right, Individual BIC weights for the three model fits. The arrows show how to read the plot from an arbitrary data point in the diagram, indicated with a red triangle. Consider that the sum of the BICw for all models A–C amounts to 1 for each participant. To estimate the relative BICw of each model for any given participant, use the lines parallel to the vertex labeled 1 for that model. The intersection between the line parallel to the vertex and the triangle edge corresponding to the model indicates the BICw.
The family of comparative models (see Fig. 4) assumes that confidence can only be computed separately for each modality and combined into a single summary measure in a second step. Within this family, the minimum-confidence model takes the minimum of the two independent confidence estimates as a summary statistic. After a very similar derivation as for the integrative models, here confidence can be expressed as follows:
 |
Finally, the family of single-modality models (see Fig. 4) assumes that confidence varies with the internal signal strength of a single modality and therefore supposes no integration of information at the second-order level. Within this family, the maximum efficiency model computes confidence on the basis of the modality with the best metacognitive efficiency alone as follows:
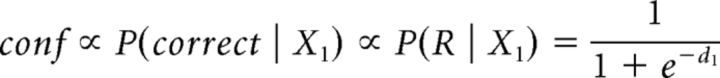 |
where modality 1 had the best metacognitive efficiency for this participant.
Model fits.
Single-modality models were assessed by calculating the percentage of variance explained for the data from the unimodal conditions. First, the nlme package in R (Pinheiro and Bates, 2010) was used to estimate the predictive power of the models while allowing for random intercepts for each participant. Then, goodness-of-fit was estimated with R2 using the piecewiseSEM package (Lefcheck, 2016). BIC values were then calculated to compare the different models while accounting for differences in their number of parameters. BIC weights for the model fits to the bimodal condition were estimated following Burnham and Anderson (2002) and as in Solovey et al. (2015). By definition, the BIC weight for model i can be expressed as follows:
 |
where BICk is the BIC for model k and BICmin is the lowest BIC corresponding to the best model out of those considered.
Results
Experiment 1
We first compared metacognitive performance across the visual, auditory, and tactile modalities. Participants were presented with a pair of simultaneous stimuli at a right and left location and asked to indicate which of the two stimuli had the highest intensity (Fig. 1, right). In this way, the first-order task consisted in a two-alternative forced choice on visual, auditory, or tactile intensity (i.e., respectively contrast, loudness, or force). After each choice, participants reported their confidence on their previous response (second-order task; Fig. 1, left). The main goal of this experiment was to test the hypothesis that metacognitive efficiency would correlate positively between sensory modalities, suggesting a common underlying mechanism. We first report general results of type 1 and type-2 performances and then turn to the central question of correlations between sensory modalities.
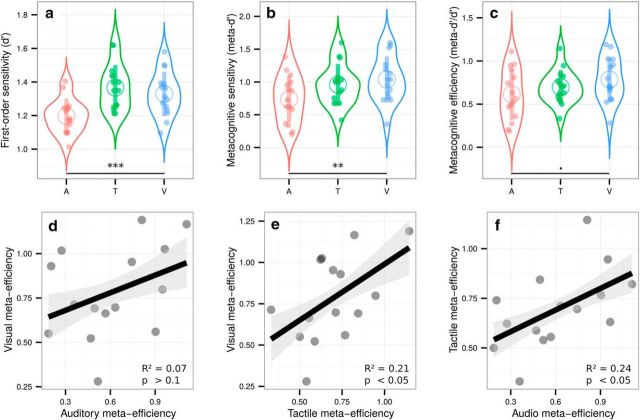
We aimed to equate first-order performance in the three modalities using a one-up/two-down staircase procedure (Levitt, 1971). Although this approach prevented large interindividual variations, some small but significant differences in d′ (i.e., first-order sensitivity) across modalities subsisted, as revealed by a one-way ANOVA (F(1.92,26.90) = 8.76, p < 0.001, ηp2 = 0.38; Fig. 2a). First-order sensitivity was lower in the auditory condition [mean d′ = 1.20 ± 0.05, 95% confidence interval (CI)] compared with the tactile (mean d′ = 1.37 ± 0.07, p = 0.002) and visual (mean d′ = 1.33 ± 0.07, p = 0.004) (Fig. 2a) conditions. No effect of condition on response criterion was found (F(1.96,27.47) = 0.30, p = 0.74, ηp2 = 0.02). The difference in first-order sensitivity is likely due to the difficulty of setting perceptual thresholds with adaptive staircase procedures. Importantly, however, it did not prevent us from comparing metacognitive performance across senses because the metrics of metacognitive performance that we used are independent of first-order sensitivity. As reported previously (Ais et al., 2016), average confidence ratings correlated between the auditory and visual conditions (adjusted R2 = 0.26, p = 0.03), between the tactile and visual conditions (adjusted R2 = 0.55, p = 0.001), and between the auditory and tactile conditions (adjusted R2 = 0.51, p = 0.002). Metacognitive sensitivity was estimated with meta-d′, a response-bias free measure of how well confidence estimates track performance on the first-order task (Maniscalco and Lau, 2012). A one-way ANOVA on meta-d′ revealed a main effect of condition (F(1.93,25.60) = 5.92, p = 0.009, ηp2 = 0.30; Fig. 2b). To further explore this main effect and to rule out the possibility that it stemmed from differences at the first-order level, we normalized metacognitive sensitivity by first-order sensitivity (i.e., meta-d′/d′) to obtain a pure index of metacognitive performance called metacognitive efficiency. Only a trend for a main effect of condition was found (F(1.76,24.61) = 3.16, p = 0.07, ηp2 = 0.18; Fig. 2c), revealing higher metacognitive efficiency in the visual (mean ratio = 0.78 ± 0.13) versus auditory domain (mean meta-d′/d′ ratio = 0.61 ± 0.15; paired t test: p = 0.049). The difference in metacognitive efficiency between the visual and the tactile conditions (mean ratio = 0.70 ± 0.10) did not reach significance (paired t test: p = 0.16, Bayes factor = 0.65).
Figure 2.
Top, Violin plots representing first-order sensitivity (a: d′), metacognitive sensitivity (b: meta-d′), and metacognitive efficiency (c: meta-d′/d′) in the auditory (A, in red), tactile (T, in green), and visual modalities (V, in blue). Full dots represent individual data points. Empty circles represent average estimates. Error bars indicate SD. The results show that, independently of first-order performance, metacognitive efficiency is higher in vision compared with audition. Bottom, Correlations between individual metacognitive efficiencies in the visual and auditory conditions (d), visual and tactile conditions (e), and tactile and auditory conditions (f). The results show that metacognitive efficiency correlates across sensory modalities, providing evidence in favor of the supramodality hypothesis. **p < 0.01, ***p < 0.001, •p < 0.1.
We then turned to our main experimental question. We found positive correlations between metacognitive efficiency in the visual and tactile conditions (adjusted R2 = 0.21, p = 0.047; Fig. 2e) and in the auditory and tactile conditions (adjusted R2 = 0.24, p = 0.038; Fig. 2f). The data were inconclusive regarding the correlation between the visual and auditory condition (adjusted R2 = 0.07, p = 0.17, Bayes factor = 0.86; Fig. 2d). These results reveal shared variance among auditory, tactile, and visual metacognition, consistent with the supramodality hypothesis. Moreover, the absence of any correlation between first-order sensitivity and metacognitive efficiency in any of the conditions (all adjusted R2 < 0; all p-values >0.19) rules out the possibility that such supramodality during the second-order task was confounded with first-order performance. Finally, no effect of condition on type 1 reaction times (F(1.78,24.96) = 0.28, p = 0.73, ηp2 = 0.02) or type 2 reaction times (F(1.77,24.84) = 1.77, p = 0.39, ηp2 = 0.06) was found.
Experiment 2
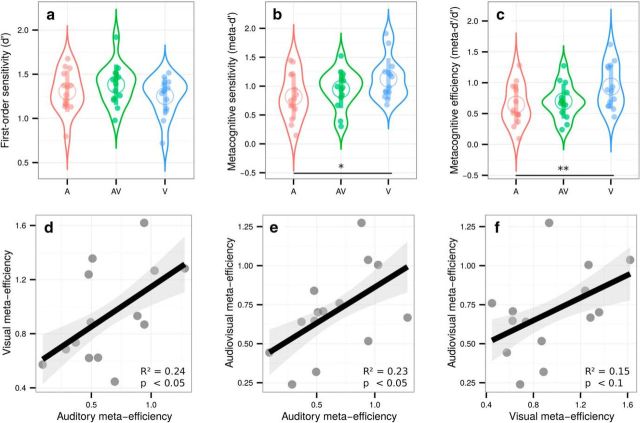
Experiment 1 revealed correlational evidence for the supramodality of perceptual metacognition across three modalities. A previous study (McCurdy et al., 2013), however, dissociated brain activity related to metacognitive accuracy in vision versus memory despite clear correlations at the behavioral level. Therefore, correlations between modalities are compelling, but not sufficient to support the supramodality hypothesis. We therefore put the evidence of Experiment 1 to a stricter test in Experiment 2 by comparing metacognitive efficiency for unimodal versus bimodal, audiovisual stimuli. We reasoned that, if metacognitive monitoring operates independently from the nature of sensory signals from which confidence is inferred, then confidence estimates should be as accurate when made on unimodal or bimodal signals. In contrast, if metacognition operated separately in each sensory modality, then one would expect that metacognitive efficiency for bimodal stimuli would only be as high as the minimal metacognitive efficiency for unimodal stimuli. Beyond these comparisons, the supramodality hypothesis also implies the existence of correlations between unimodal and bimodal metacognitive efficiencies. Participants performed three different perceptual tasks, all consisting of a congruency judgment between two pairs of stimuli (Fig. 1, right). In the unimodal visual condition, participants indicated whether the Gabor patches with the strongest contrast within each pair were situated on the same or different side of the screen. In the unimodal auditory condition, they indicated whether the loudest sounds of each pair were played in the same ear or in two different ears. In the bimodal audiovisual condition, participants indicated whether the side corresponding to the most contrasted Gabor patch of the visual pair corresponded with the side of the loudest sound of the auditory pair. Importantly, congruency judgments required that participants responded on the basis of the two presented modalities. The staircase procedure minimized variations in first-order sensitivity, such that sensitivity in the auditory (mean d′ = 1.31 ± 0.12), audiovisual (mean d′ = 1.38 ± 0.12), and visual conditions (mean d′ = 1.25 ± 0.11) were similar (Fig. 3a, F(1.75,22.80) = 2.12, p = 0.15, ηp2 = 0.14). No evidence of multisensory integration was found at the first-order level because the perceptual thresholds determined by the staircase procedure were not lower in the bimodal versus unimodal condition (p = 0.17). This is likely due to the task at hand involving a congruency judgment. As in Experiment 1, no effect of condition on response criterion was found (F(1.87,24.27) = 2.12, p = 0.14, ηp2 = 0.14). No effect of condition on average confidence was found (F(1.76,24.64) = 0.91, p = 0.40, ηp2 = 0.06) and average confidence ratings correlated between the auditory and audiovisual conditions (adjusted R2 = 0.56, p = 0.001) and between the visual and audiovisual conditions (adjusted R2 = 0.38, p = 0.01) and a trend was found between the auditory and visual conditions (adjusted R2 = 0.12, p = 0.11). A significant main effect of condition on type 1 reaction times (F(1.66,21.53) = 18.05, p < 0.001, ηp2 = 0.58) revealed faster responses in the visual (1.30 ± 0.10 s) compared with the auditory (1.47 ± 0.13 s) and audiovisual task (1.68 ± 0.11 s). No difference was found for type 2 reaction times (F(1.82,23.62) = 1.69, p = 0.21, ηp2 = 0.11). A main effect of condition for both metacognitive sensitivity (meta-d′: F(1.98,25.79) = 4.67, p = 0.02, ηp2 = 0.26) and metacognitive efficiency (ratio meta-d′/d′: F(1.95,25.40) = 6.63, p = 0.005, ηp2 = 0.34; Fig. 3b,c, respectively) was found. Pairwise comparisons revealed higher metacognitive efficiency in the visual (mean ratio = 0.94 ± 0.19) versus auditory (mean meta-d′/d′ ratio = 0.65 ± 0.17; paired t test: p = 0.005) and audiovisual domains (mean meta-d′/d′ ratio = 0.70 ± 0.15; paired t test: p = 0.02). Because auditory and audiovisual metacognitive efficiencies were not different (p = 0.5, Bayes factor = 0.38), the differences in metacognitive efficiency are likely to stem from differences between auditory and visual metacognition, as found in Experiment 1. Therefore, the fact that metacognitive efficiency is similar in the audiovisual and auditory tasks implies that the resolution of confidence estimates in the bimodal condition is as good as that in the more difficult unimodal condition (in this case, auditory) despite its requiring the analysis of two sources of information.
Figure 3.
Top, Violin plots representing first-order sensitivity (a: d′), metacognitive sensitivity (b: meta-d′), and metacognitive efficiency (c: meta-d′/d′) in the auditory (A, in red), audiovisual (AV, in green), and visual (V, in blue) modalities. Full dots represent individual data points. Empty circles represent average estimates. Error bars indicate SD. The results show that, independently of first-order performance, metacognitive efficiency is better for visual stimuli versus auditory or audiovisual stimuli, but not poorer for audiovisual versus auditory stimuli. Bottom, Correlations between individual metacognitive efficiencies in the visual and auditory conditions (d), audiovisual and auditory conditions (e), and audiovisual and visual conditions (f). The results show that metacognitive efficiency correlates between unimodal and bimodal perceptual tasks in favor of the supramodality hypothesis. *p < 0.05, **p < 0.01.
Crucially, we found correlations between metacognitive efficiency in the auditory and visual conditions (adjusted R2 = 0.24, p = 0.043; Fig. 3d); more importantly, we also found correlations between metacognitive efficiency in the auditory and audiovisual conditions (adjusted R2 = 0.23, p = 0.046; Fig. 3e) and a trend between metacognitive efficiency in the visual and audiovisual conditions (adjusted R2 = 0.15, p = 0.097; Fig. 3f). This contrasted with no correlations between first-order sensitivity and metacognitive efficiency in any of the conditions (all R2 < 0.06; all p > 0.19) except in the visual condition, in which high d′ was predictive of low meta-d′/d′ values (R2 = 0.39, p = 0.01). The absence of such correlations in most conditions makes it unlikely that relations in metacognitive efficiency were driven by similarities in terms of first-order performance. In addition to the equivalence between the resolution of unimodal and bimodal confidence estimates, the correlations in metacognitive efficiency between unimodal and bimodal conditions suggest that metacognitive monitoring for unimodal versus bimodal signals involves shared mechanisms (i.e., supramodality).
Computational models of confidence estimates for bimodal signals
Using the data from Experiment 2, we next sought to reveal potential mechanisms underlying the computation of confidence in the bimodal condition. For this, we first modeled the proportion of trials corresponding to high versus low confidence in correct versus incorrect type 1 responses in the unimodal auditory and unimodal visual conditions separately. Each condition was represented by a 2D SDT model with standard assumptions and only 2 free parameters per participant, internal noise σ and confidence criterion c (Fig. 4 and Materials and Methods). This simple model accounted for more than half the total variance in participants' proportion of responses, both in the unimodal visual (R2 = 0.68) and unimodal auditory conditions (R2 = 0.57). We then combined the fitted parameter values under different rules to estimate and compare their fits with the audiovisual data. All models assume that the visual and auditory stimuli did not interact, which is supported by the fact that perceptual thresholds determined by the staircase procedure were not lower in the bimodal vs unimodal conditions. Note that with this procedure, and unlike the fits to the unimodal conditions, the data used to estimate the model parameters were different from those on which the model fits were compared. We evaluated different models systematically by grouping them into three families varying in degree of supramodality. We present here the best model from each family (Fig. 4) and all computed models in SI. The integrative model echoes the unimodal models and represents the highest degree of integration: here, confidence is computed on the basis of the joint distribution of the auditory and visual modalities. The comparative model assumes that confidence is computed separately for each modality and in a second step combined into a single summary measure (in particular, the minimum of the two estimates, see Materials and Methods for other measures). The single-modality model assumes that confidence varies with the internal signal strength of a single modality and therefore supposes no integration of information at the second-order level. We compared these different models by calculating their respective BIC weights (BICw: Burnham and Anderson, 2002; Solovey et al., 2015), which quantify the relative evidence in favor of a model in relation to all other models considered.
By examining individual BICw in a ternary plot (Fig. 4), we found that the best model for most participants was either the integrative or the comparative model, whereas the BICw for the single-domain model was equal to 0. However, the single-modality model is also plausible because it does predict the responses of four participants better than any of the other two models. The reason that our models could not distinguish clearly between the integrative model and the comparative model may be due to the fact that differences in intensity between the left and right stimuli of the auditory and visual pairs were yoked: the staircase procedure that we used controlled both pairs simultaneously, increasing (decreasing) the difference between the left and right stimuli in both modalities after an incorrect (two correct) response. As a result, we sampled values from a single diagonal in the space of stimulus intensities, which limits the modeling results. In future studies, nonyoked stimuli pairs could be used—albeit at the cost of a longer experimental session—to explore wider sections of the landscape of confidence as a function of internal signal to better test the likelihood of the models studied here.
Together, these computational results suggest that most participants computed confidence in the bimodal task by using information from the two modalities under a supramodal format that is independent of the sensory modality, in agreement with the first mechanism for supramodal metacognition we introduced. We conclude that the confidence reports for audiovisual signals arise either from the joint distribution of the auditory and visual signals (integrative model) or are computed separately for distinct modalities and then combined into a single supramodal summary statistic (comparative model). These two models indicate that metacognition may be supramodal because monitoring operates on supramodal confidence estimates computed with an identical format or neural code across different tasks or sensory modalities. We later refer to this as the first mechanism for supramodal metacognition. In addition, metacognition may be supramodal in case nonperceptual cues drive the computation of confidence estimates (mechanism 2). Among them, likely candidates are decisional cues such as reaction times during the first-order task because they are present no matter the sensory modality at play and are thought to play an important role for confidence estimates (Yeung and Summerfield, 2012). We next sought to determine whether metacognition was supramodal due to the influence of decisional cues that are shared between sensory modalities (mechanism 2).
Our modeling results suggest that confidence estimates are encoded in a supramodal format compatible with the supramodality hypothesis for metacognition. Notably, however, apparent supramodality in metacognition could arise in case nonperceptual signals are taken as inputs for the computation of confidence. In models implying a decisional locus for metacognition (Yeung and Summerfield, 2012), stimulus-independent cues such as reaction times during the first-order task take part in the computation of confidence estimates. This is supported empirically by a recent study showing that confidence in correct responses is decreased in case response-specific representations encoded in the premotor cortex are disrupted by transcranial magnetic stimulation (Fleming et al., 2015). In the present study, decisional parameters were shared across sensory modalities because participants used a keyboard with their left hand to perform the first-order task for all tasks. To extend our modeling results and to assess whether supramodality in metacognition also involves a decisional locus (mechanism 2 discussed above), we examined how participants used their reaction times to infer confidence in different conditions. Specifically, we quantified the overlap of first-order reaction times distributions corresponding to correct versus incorrect responses as a summary statistic representing how reaction times differ between correct and incorrect trials. We measured how reaction time overlap correlated with the overlap of confidence ratings after correct versus incorrect first-order responses, which is a summary statistic analogous to ROC-based methods typically used to quantify metacognitive sensitivity with discrete confidence scales (Fleming and Lau, 2014). If confidence involves a decisional locus, then one would expect a correlation between confidence overlap and reaction time overlap so that participants with the smallest confidence overlap (i.e., highest metacognitive sensitivity) are the ones with the smallest reaction times overlap (i.e., distinct reaction times in correct vs incorrect responses). Interestingly in Experiment 1, the correlation strength mirrored the difference in metacognitive efficiency that we found between sensory modalities: higher correlations were found in the visual domain (adjusted R2 = 0.54, p = 0.002; average metacognitive efficiency = 0.78 ± 0.13) compared with the tactile (adjusted R2 = 0.26, p = 0.03; average metacognitive efficiency = 0.70 ± 0.10) and auditory (adjusted R2 = −0.06, p = 0.70; average metacognitive efficiency = 0.61 ± 0.15) domains. This suggests that decisional parameters such as reaction times in correct versus incorrect trials may inform metacognitive monitoring and may be used differently depending on the sensory modality with a bigger role in visual than in tactile and auditory tasks. These results are consistent with second-order models of confidence estimation (Fleming and Daw, 2017) and support empirical results showing better metacognitive performance when confidence is reported after versus before the first-order task (Siedlecka et al., 2016) or better metacognitive performance for informative versus noninformative action during the first-order task (Kvam et al., 2015). Importantly, although such correlations between reaction time overlap and confidence overlap would be expected in experiments containing a mixture of very easy and very difficult trials, the correlations in the visual and tactile modalities reported above persisted even after the variance of perceptual evidence was taken into account using multiple regressions. This result rules out the possibility that these correlations are explained by variance in task difficulty. This pattern of results was not found in Experiment 2 (i.e., no correlation between reaction times and confidence overlaps; all R2 < 0.16, all p > 0.1), but replicated in Experiment 3 as further detailed below.
Experiment 3
The aim of Experiment 3 was threefold. First and foremost, we sought for the first time to document the potential common and distinct neural mechanisms underlying unimodal and bimodal metacognition. After the link between reaction times and metacognitive efficiency uncovered in Experiment 1, we expected to find supramodal neural markers of metacognition preceding the first-order task, as quantified by the amplitude of ERPs and in alpha suppression over the sensorimotor cortex before key press (Pfurtscheller and Lopes da Silva, 1999). Second, we aimed at replicating the behavioral results from Experiment 2, especially the correlation between visual and audiovisual metacognitive efficiency. Third, we aimed at estimating the correlations between confidence and reaction times overlap on a new group of participants. Therefore, we tested participants on these two conditions only.
Behavioral data
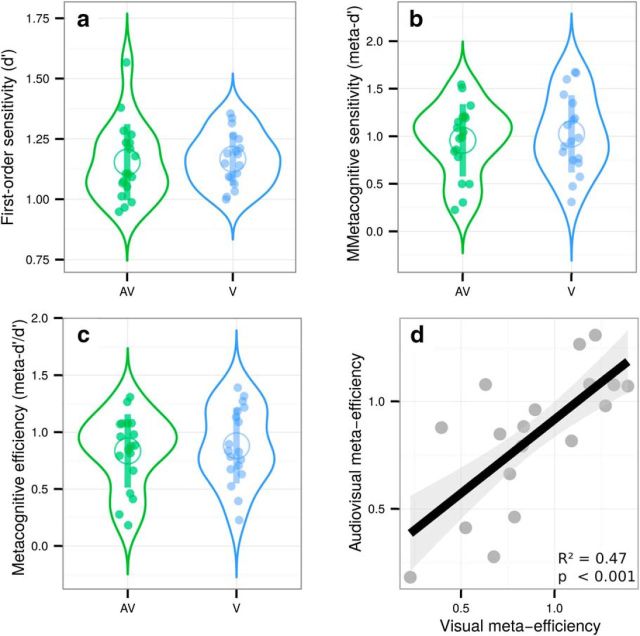
The staircase procedure minimized variations in first-order sensitivity (t(17) = 0.3, p = 0.76, d = 0.07) such that sensitivity in the audiovisual (mean d′ = 1.15 ± 0.07) and visual conditions (mean d′ = 1.17 ± 0.05) were similar. Contrary to what was found in Experiments 1 and 2, the response criterion varied across conditions (t(17) = 4.33, p < 0.001, d = 0.63), with a tendency to respond “congruent” more pronounced in the audiovisual (mean criterion = 0.27 ± 0.12) versus visual condition (mean criterion = −0.02 ± 0.15). This effect was unexpected, but did not preclude us from running subsequent analyses dealing with metacognitive sensitivity. We found no effect of condition on average confidence (t(17) = 0.56, p = 0.14, d = 0.08). Average confidence ratings correlated between the visual and audiovisual conditions (adjusted R2 = 0.65, p < 0.001). No difference in metacognitive sensitivity was found between conditions (t(17) = 0.78, p = 0.44, d = 0.09) or efficiency (t(17) = 0.78, p = 0.44, d = 0.08). Crucially, we replicated our main results from Experiment 2 because we found a positive significant correlation between relative metacognitive accuracy in the audiovisual and visual conditions (adjusted R2 = 0.47, p < 0.001) and no correlation between first-order sensitivity and metacognitive efficiency in either condition (both R2 < 0.01; both p-values >0.3; Fig. 5). Regarding the decisional locus of metacognition, Experiment 3 confirmed the results of Experiment 1: reaction time and confidence overlaps correlated more in the visual condition (adjusted R2 = 0.41, p = 0.003) than in the audiovisual condition (adjusted R2 = −0.05, p = 0.70), suggesting that decisional parameters such as reaction times may inform metacognitive monitoring, although differently between the visual and audiovisual conditions. Altogether, these behavioral results from three experiments with different subject samples confirm the existence of shared variance in metacognitive efficiency between unimodal and bimodal conditions and do not support major group differences between them. Further, they support the role of decisional factors such as reaction time estimates, as predicted when considering a decisional locus for metacognition.
Figure 5.
Violin plots representing first-order sensitivity (a: d′), metacognitive sensitivity (b: meta-d′), and metacognitive efficiency (c: meta-d′/d′) in the audiovisual (AV, in green) and visual conditions (V, in blue). Full dots represent individual data points. Empty circles represent average estimates. Error bars indicate SD. The results show no difference between visual and audiovisual metacognitive efficiency. d, Correlation between individual metacognitive efficiencies in the audiovisual and visual conditions.
EEG data
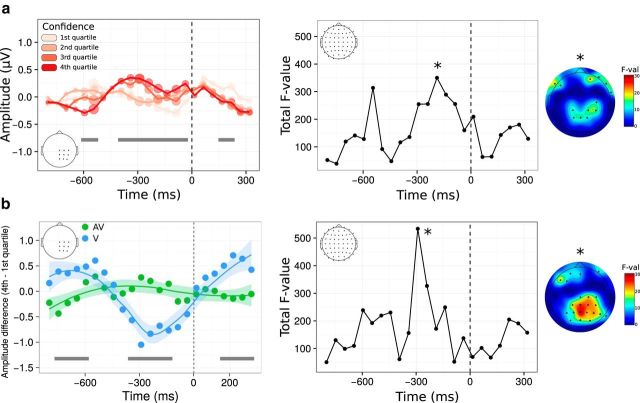
Next, we explored the neural bases of visual and audiovisual metacognition, focusing on the decisional locus of confidence by measuring ERPs locked to the type 1 response. This response-locked analysis took into account the differences in type 1 reaction times between the visual and audiovisual tasks (562 ms shorter in the visual condition on average: t(17) = 6.30, p < 0.001). Because we showed that decisional parameters such as reaction times inform metacognitive monitoring, this analysis was performed on a set of scalp electrodes over the right sensorimotor cortex that included the left hand representation with which participants performed the first-order task (see Boldt and Yeung, 2015 for findings showing that parietal scalp regions also correlate with confidence before response). Incorrect type 1 responses were not analyzed because the lower bound of the confidence scale that we used corresponded to a “pure guess” and therefore did not allow disentangling detected versus undetected errors. For each trial, we extracted the ERP amplitude time locked to the onset of correct type 1 responses averaged within 50 ms time windows. For each time window and each electrode, we assessed how ERP amplitude changed as a function of confidence using linear mixed models with condition as a fixed effect (visual vs audiovisual) and random intercepts for subjects (see Materials and Methods for details). This analysis allowed us to assess where and when ERP amplitudes associated with the type 1 response were predictive of confidence ratings given during the type-2 response. Main effects correspond to similar modulations of ERP amplitudes by confidence in the visual and audiovisual condition (i.e., supramodality hypothesis), whereas interaction effects correspond to different amplitude modulations in the visual versus audiovisual conditions. A first main effect of confidence was found early before the type 1 response, underlying a negative relationship between ERP amplitude and confidence (−600 to −550 ms; p < 0.05, FDR corrected; Fig. 6a, left, shows the grand average between the visual and audiovisual condition). A second main effect of confidence peaked at −300 ms (−400 to −100 ms; p < 0.05, FDR corrected), so trials with high confidence reached maximal amplitude 300 ms before key press. These two effects are characterized by an inversion of polarity from an early negative to a late-positive relationship, which has been linked to selective response activation processes (i.e., lateralized readiness potentials; for review, see Eimer and Coles, 2003; for previous results in metamemory, see Buján et al. (2009)). Therefore, the present data show that sensorimotor ERP also contribute to metacognition because they showed a relationship with confidence both in the audiovisual and visual conditions. Confidence modulated the amplitude and not the onset latency of the ERP, which suggests that the timing of response selection itself does not depend on confidence. We complemented this ROI analysis by exploring the relation between confidence and ERP amplitude for all recorded electrodes (Fig. 6a, right). This revealed that the later effect 300 ms before key press was centered on centroparietal regions (i.e., including our ROI; p < 0.001), as well as more frontal electrodes, potentially consistent with several fMRI studies reporting the role of the prefrontal cortex for metacognition (Fleming et al., 2010; Yokoyama et al., 2010; McCurdy et al., 2013; for review, see Grimaldi et al., 2015). The linear mixed-model analysis also revealed significant interactions, indicating that the modulation of ERP amplitude as a function of confidence was significantly stronger in the visual condition, with, again, one early (−750 to −600 ms) and one late component (−350 to −150 ms; Fig. 6b, left). Topographical analysis of these interactions implicated frontal and parietooccipital electrodes. These results at the neural level are consistent with our behavioral data because we found that reaction times have more influence on the computation of confidence in the visual compared with the audiovisual condition.
Figure 6.
Voltage amplitude time locked to correct type 1 responses as a function of confidence. a, Left, Time course of the main effect of confidence within a predefined ROI. Although raw confidence ratings were used for the statistical analysis, they are depicted here as binned into four quartiles, from quartile 1 corresponding to trials with the 25% lowest confidence ratings (light pink) to quartile 4 corresponding to trials with the 25% highest confidence ratings (dark red). The size of each circle along the amplitude line is proportional to the corresponding F-value from mixed model analyses within 50 ms windows. Right, Same analysis as shown in a on the left on the whole scalp. The plot represents the time course of the summed F-value over 64 electrodes for the main effect of confidence. The topography where a maximum F-value is reached (*) is shown next to each plot. b. Left, Time course of the interaction between confidence and condition following a linear mixed-model analysis within the same ROI as in a. Although raw confidence ratings were used for the statistical analysis, the plot represents the difference in voltage amplitude between trials in the fourth versus first confidence quartile. Right, Same analysis as shown in b on the left on the whole scalp, with corresponding topography. In all plots, gray bars correspond to significant main effects (a) or interactions (b), with p < 0.05 FDR corrected. Significant effects on topographies are highlighted with black stars (p < 0.001, uncorrected).
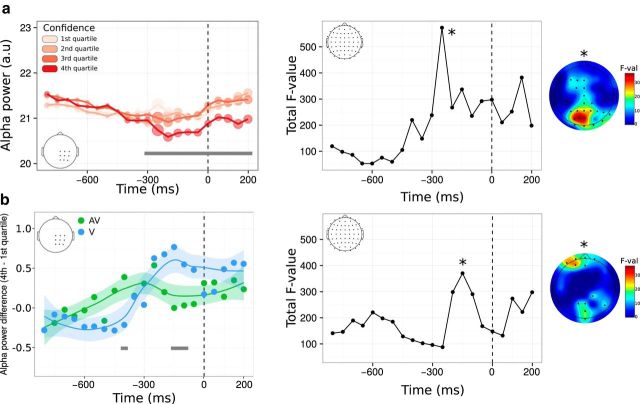
Complementary to ERP amplitude, we also analyzed oscillatory alpha power (i.e., premovement related desynchronization) as a signature of motor preparation (Pfurtscheller and Lopes da Silva, 1999). Results of the linear mixed-model analysis revealed a sustained main effect of confidence starting 300 ms before key press and continuing until 200 ms after the type 1 response (p < 0.05 FDR corrected) showing a negative relationship between confidence and alpha power (i.e., alpha suppression; Fig. 7a, left). Contrary to what we found in the amplitude domain, the main effect of confidence on alpha power was found even after a first-order response was provided. Likewise, the topographical analysis revealed a different anatomical localization than the effect that we found in the amplitude domain, with more posterior, parietooccipital electrodes involved. This suggests that alpha suppression before type 1 response varies as a function of confidence nondifferentially in both the audiovisual and visual conditions. The linear mixed-model analysis also revealed a main effect of condition, with higher alpha power in the visual versus audiovisual condition (Fig. 7b, left). This could be related to the fact that the audiovisual task was judged more demanding by participants, as reflected by their longer type 1 reaction times. Finally, significant interactions between confidence and condition were found, with topographical locations predominantly within frontal electrodes. The main effects of confidence on voltage amplitude and alpha power reveal some of the markers validating the supramodality hypothesis at a decisional locus. These are likely to be part of a bigger set of neural mechanisms operating at a decisional, but also postdecisional, locus that was not explored here (Pleskac and Busemeyer, 2010). The existence of significant interactions reveals that some domain-specific mechanisms are also at play during metacognition, which accounts for the unexplained variance when correlating metacognitive efficiencies across modalities at the behavioral level.
Figure 7.
Alpha power time locked to correct type 1 responses as a function of confidence. a, Left, Time course of the main effect of confidence within a predefined ROI. Although raw confidence ratings were used for the statistical analysis, they are depicted here as binned into four quartiles, from quartile 1 corresponding to trials with the 25% lowest confidence ratings (light pink) to quartile 4 corresponding to trials with the 25% highest confidence ratings (dark red). The size of each circle along the alpha power line is proportional to the corresponding F-value from mixed-model analyses within 50 ms windows. Right, Same analysis shown in a on the left on the whole scalp. The plot represents the time course of the summed F-value over 64 electrodes for the main effect of confidence. The topography where a maximum F-value is reached (*) is shown next to each plot. b, Left, Time course of the interaction between confidence and condition following a linear mixed-model analysis within the same ROI as in a. Although raw confidence ratings were used for the statistical analysis, the plot represents the difference in voltage amplitude between trials in the fourth versus first confidence quartile. Right, Same analysis as shown in b on the left on the whole scalp, with corresponding topography. In all plots, gray bars correspond to significant main effects (a) or interactions (b), with p < 0.05 FDR-corrected. Significant effects on topographies are highlighted with black stars (p < 0.001, uncorrected).
Discussion
Is perceptual metacognition supramodal, with a common mechanism for distinct sensory modalities, or is it modality-specific, with idiosyncratic mechanisms for each sensory modality? As of today, this issue remains unsettled because the vast majority of experiments on metacognitive perception only involved the visual modality (but see de Gardelle et al., 2016; Ais et al., 2016). In vision, Song et al. (2011) found that approximately half of the variance in metacognitive sensitivity during a contrast discrimination task was explained by metacognitive sensitivity in an orientation discrimination task, suggesting some level of generality within vision. Likewise, approximately one-fourth of the variance in metacognitive sensitivity during a contrast discrimination task was explained by metacognitive sensitivity during a memory task involving words presented visually (McCurdy et al., 2013). Here, we extend these studies by assessing the generality of metacognition across three sensory modalities and conjunctions of two sensory modalities. In Experiment 1, we tested participants in three different conditions that required discriminating the side on which visual, auditory, or tactile stimuli was most salient. We found positive correlations between metacognitive efficiency across sensory modalities and ruled out the possibility that these correlations stemmed from differences in first-order performances (Maniscalco and Lau, 2012). These results extend previous reports (Ais et al., 2016; de Gardelle et al., 2016) showing similarities between auditory and visual metacognition to auditory, tactile, and visual laterality discrimination tasks and therefore support the existence of a common mechanism underlying metacognitive judgments in three distinct sensory modalities.
In Experiment 2, we further extended these results to a different task and also generalized them to bimodal stimuli (Deroy et al., 2016). First, using a first-order task that required congruency rather than laterality judgments, we found again that metacognitive efficiency for auditory stimuli correlated with metacognitive efficiency for visual stimuli. Second, we designed a new condition in which participants had to perform congruency judgments on bimodal, audiovisual signals that required information from both modalities to be taken into account. Three further observations from these conditions support the notion of supramodality in perceptual metacognition. First, we observed that metacognitive efficiency in the audiovisual condition was indistinguishable from that in the unimodal auditory condition, suggesting that the computation of joint confidence is not only possible, but can also occur at no additional behavioral cost. These results confirm and extend those of Experiment 1 in a different task and with different participants and further suggest that performing confidence estimates during a bimodal task was not more difficult than doing so during the hardest unimodal task (in this case, auditory) despite its requiring the computation of confidence across two perceptual domains. We take this as evidence in support of supramodality in perceptual metacognition. Second, we found a positive and significant correlation in metacognitive efficiency between the auditory and audiovisual conditions and a trend between the visual and audiovisual conditions, later replicated in Experiment 3. As in Experiment 1, these results cannot be explained by confounding correlations with first-order performance. We take this as another indication that common mechanisms underlie confidence computations for perceptual tasks on unimodal and bimodal stimuli. Although the reported correlations involved a rather low number of participants and were arguably sensitive to outliers (McCurdy et al., 2013), we note that they were replicated several times under different conditions and tasks in different groups of participants, which is likely in <1% of cases under the null hypothesis (binomial test). In addition, qualitatively similar correlations were obtained when metacognitive performance was quantified by the area under the type 2 receiving operative curve and by the slope of a logistic regression between type 1 accuracy and confidence.
The next piece of evidence in favor of supramodal metacognition goes beyond correlational evidence and provides new insights regarding the mechanisms involved in confidence estimates when the signal extends across two sensory modalities. Using a modeling approach, we found that data in the audiovisual condition could be predicted by models that computed confidence with a supramodal format either based on the joint information from a bimodal audiovisual (integrative model) representation or on the comparison between unimodal visual and auditory representations (comparative model). Although these two models have distinct properties, they both involve supramodal confidence estimates with identical neural codes across different sensory modalities. Therefore, although we could not distinguish which of the two models was most representative of behavioral data at the group level, they are both evidence in favor of the first mechanism that we introduced, according to which metacognition is supramodal because monitoring operates on supramodal confidence estimates.
Finally, we assessed in Experiment 3 whether supramodal metacognition could arise due to the second mechanism that we introduced, according to which supramodality is driven by the influence of nonperceptual, decisional signals during the computation of confidence estimates. For this purpose, we replicated correlations in metacognitive efficiency between the visual and audiovisual conditions while examining the neural mechanisms of visual and audiovisual metacognition preceding the perceptual judgment (i.e., at a decisional level). In a response-locked analysis with confidence and condition as within-subject factors, we found that confidence preceding the type 1 response was reflected in ERP amplitude and alpha power (main effect) within an ROI that included the parietal and sensorimotor cortex corresponding to the hand used for the type 1 task, as well as more frontal sites. Before discussing the main effects of confidence, we note that the analysis also revealed interactions between confidence and condition, revealing that idiosyncratic mechanisms are also at play during the metacognitive monitoring of visual versus audiovisual signals and that modulations of ERP and alpha power as a function of confidence were overall greater in the visual versus audiovisual condition. Regarding the main effects, we found an inversion ERP polarity over left sensorimotor regions, suggesting a link between confidence and selective response activation, so that trials with high confidence in a correct response were associated with stronger motor preparation (Eimer and Coles, 2003; Buján et al., 2009). Regarding oscillatory power, we found relative alpha desynchronization in occipitoparietal regions, which has been shown to reflect the level of cortical activity and is held to correlate with processing enhancement (Pfurtscheller, 1992). At the cognitive level, alpha suppression is thought to instantiate attentional gating so that distracting information is suppressed (Pfurtscheller and Lopes da Silva, 1999; Foxe and Snyder, 2011; Klimesch, 2012). Indeed, higher alpha power has been shown in cortical areas responsible for processing potentially distracting information, both in the visual and audiovisual modalities (Foxe et al., 1998). More recently, prestimulus alpha power over sensorimotor areas was found to be negatively correlated with confidence (Baumgarten et al., 2016; Samaha et al., 2016) or attentional ratings during tactile discrimination (Whitmarsh et al., 2017). Although these effects are usually observed before the onset of an anticipated stimulus, we observed them before the type 1 response, suggesting that low confidence in correct responses could be due to the effect of inattention to common properties of first-order task execution such as motor preparation or reaction time (stimulus locked-analyses that are not reported here revealed no effect of confidence before stimulus onset). This is compatible with a recent study showing that transcranial magnetic stimulation over the premotor cortex before or after a visual first-order task disrupts subsequent confidence judgments (Fleming et al., 2015).
The finding of lower alpha power with confidence in correct responses is compatible with the observation that participants with more distinct reaction times between correct and incorrect responses had better metacognitive efficiency, as revealed by the correlation between confidence and reaction times overlaps after correct versus incorrect responses. Therefore, attention to motor task execution may feed into the computation of confidence estimates in a way that is independent of the sensory modality involved, thereby providing a potential decisional mechanism for supramodal metacognition. In Experiment 1, we also found that confidence and reaction times overlap were more correlated in the visual condition compared with the tactile, auditory, or audiovisual conditions. Based on these results, we speculate that decisional parameters are associated with processes related to movement preparation and inform metacognitive monitoring. Our EEG results and the correlations between reaction time and confidence overlaps suggest that decisional parameters may have a stronger weight in the visual than in the other modalities, which could explain the relative superiority of visual metacognition over other senses. We argue that this decisional mechanism in metacognition is compatible with the supramodality hypothesis, in addition to the supramodal computation of confidence supported by our behavioral and modeling results. Our analysis focusing on the alpha band to uncover the role of decisional cues on confidence estimates is not exhaustive and other frequencies might contribute to confidence estimates equally between sensory domains (e.g., the theta band; Wokke et al., 2017).
Altogether, our results highlight two nonmutually exclusive mechanisms for the finding of correlated metacognitive efficiencies across auditory, tactile, visual, and audiovisual domains. First, our modeling work showed that confidence estimates during an audiovisual congruency task have a supramodal format after computations on the joint distribution or on the comparisons of the auditory and visual signals. Therefore, metacognition may be supramodal because of supramodal formats of confidence estimates. Second, our electrophysiological results revealed that increased confidence in a visual or audiovisual task coincided with the amplitude of ERP and decreased alpha power before type 1 response, suggesting that decisional cues may be a determinant of metacognitive monitoring. Therefore, metacognition may be supramodal, not only because confidence estimates are supramodal by nature, but also because they may be informed by decisional and movement preparatory signals that are shared across modalities.
Notes
Note Added in Proof: The author contributions were incorrectly listed in the Early Release version published September 15, 2017. The author contributions have now been corrected. Also note, Complementary results, raw behavioral data, and modeling scripts are available here: https://osf.io/x2jws. This material has not been peer reviewed.
Footnotes
N.F. was a Swiss Federal Institute of Technology fellow cofunded by Marie Skłodowska-Curie. O.B. is supported by the Bertarelli Foundation, the Swiss National Science Foundation, and the European Science Foundation. We thank Shruti Nanivadekar and Michael Stettler for help with data collection.
References
- Ais J, Zylberberg A, Barttfeld P, Sigman M (2016) Individual consistency in the accuracy and distribution of confidence judgments. Cognition 146:377–386. 10.1016/j.cognition.2015.10.006 [DOI] [PubMed] [Google Scholar]
- Bagiella E, Sloan RP, Heitjan DF (2000) Mixed-effects models in psychophysiology. Psychophysiology 37:13–20. 10.1111/1469-8986.3710013 [DOI] [PubMed] [Google Scholar]
- Baird B, Mrazek MD, Phillips DT, Schooler JW (2014) Domain-specific enhancement of metacognitive ability following meditation training. J Exp Psychol Gen 143:1972–1979. 10.1037/a0036882 [DOI] [PubMed] [Google Scholar]
- Barrett AB, Dienes Z, Seth AK (2013) Measures of metacognition on signal-detection theoretic models. Psychol Methods 18:535–552. 10.1037/a0033268 [DOI] [PubMed] [Google Scholar]
- Bates DM, Kliegl R, Vasishth S, Baayen H (2015) Parsimonious mixed models. arXiv preprint arXiv:150 604967:1–27. [Google Scholar]
- Bates D, Maechler M, Bolker B, Walker S (2014) lme4: linear mixed-effects models using S4 classes. R package version 1.1–6. R. [Google Scholar]
- Baumgarten TJ, Schnitzler A, Lange J (2016) Prestimulus alpha power influences tactile temporal perceptual discrimination and confidence in decisions. Cereb Cortex 26:891–903. 10.1093/cercor/bhu247 [DOI] [PubMed] [Google Scholar]
- Boldt A, Yeung N (2015) Shared neural markers of decision confidence and error detection. J Neurosci 35:3478–3484. 10.1523/JNEUROSCI.0797-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. (1997) The Psychophysics Toolbox. Spat Vis 10:433–436. 10.1163/156856897X00357 [DOI] [PubMed] [Google Scholar]
- Buján A, Lindín M, Díaz F (2009) Movement related cortical potentials in a face naming task: Influence of the tip-of-the-tongue state. Int J Psychophysiol 72:235–245. 10.1016/j.ijpsycho.2008.12.012 [DOI] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR (2003) Model selection and multimodel inference: a practical information-theoretic approach. Berlin: Springer Science & Business Media. [Google Scholar]
- Chaumon M, Bishop DV, Busch NA (2015) A practical guide to the selection of independent components of the electroencephalogram for artifact correction. J Neurosci Methods 250:47–63. 10.1016/j.jneumeth.2015.02.025 [DOI] [PubMed] [Google Scholar]
- de Gardelle V, Mamassian P (2014) Does confidence use a common currency across two visual tasks? Psychol Sci 25:1286–1288. 10.1177/0956797614528956 [DOI] [PubMed] [Google Scholar]
- de Gardelle V, Le Corre F, Mamassian P (2016) Confidence as a common currency between vision and audition. PLoS One 11:e0147901. 10.1371/journal.pone.0147901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A, Makeig S (2004) EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods 134:9–21. 10.1016/j.jneumeth.2003.10.009 [DOI] [PubMed] [Google Scholar]
- Deroy O, Spence C, Noppeney U (2016) Metacognition in multisensory perception. Trends Cogn Sci 20:736–747. 10.1016/j.tics.2016.08.006 [DOI] [PubMed] [Google Scholar]
- Eimer M, Coles MGH (2003) The lateralized readiness potential as an on-line measure of central response activation processes. Behavior Research Methods, Instruments, & Computers 30:146–156. [Google Scholar]
- Fleming SM, Daw ND (2017) Self-evaluation of decision-making: a general Bayesian framework for metacognitive computation. Psychol Rev 124:91–114. 10.1037/rev0000045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming SM, Lau HC (2014) How to measure metacognition. Front Hum Neurosci 8:443. 10.3389/fnhum.2014.00443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming SM, Weil RS, Nagy Z, Dolan RJ, Rees G (2010) Relating introspective accuracy to individual differences in brain structure. Science 329:1541–1543. 10.1126/science.1191883 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming SM, Ryu J, Golfinos JG, Blackmon KE (2014) Domain-specific impairment in metacognitive accuracy following anterior prefrontal lesions. Brain 137:2811–2822. 10.1093/brain/awu221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming SM, Maniscalco B, Ko Y, Amendi N, Ro T, Lau H (2015) Action-specific disruption of perceptual confidence. Psychol Sci 26:89–98. 10.1177/0956797614557697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming SM, Dolan RJ, Frith CD (2012) Metacognition: computation, biology and function. Philos Trans R Soc Lond B Biol Sci 367:1280–1286. 10.1098/rstb.2012.0021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foxe JJ, Snyder AC (2011) The role of alpha-band brain oscillations as a sensory suppression mechanism during selective attention. Front Psychol 2:154. 10.3389/fpsyg.2011.00154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foxe JJ, Simpson GV, Ahlfors SP (1998) Parieto-occipital approximately 10 Hz activity reflects anticipatory state of visual attention mechanisms. Neuroreport 9:3929–3933. 10.1097/00001756-199812010-00030 [DOI] [PubMed] [Google Scholar]
- Galvin SJ, Podd JV, Drga V, Whitmore J (2003) Type 2 tasks in the theory of signal detectability: discrimination between correct and incorrect decisions. Psychon Bull Rev 10:843–876. 10.3758/BF03196546 [DOI] [PubMed] [Google Scholar]
- Grimaldi P, Lau H, Basso MA (2015) There are things that we know that we know, and there are things that we do not know we do not know: confidence in decision-making. Neurosci Biobehav Rev 55:88–97. 10.1016/j.neubiorev.2015.04.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick S, Gelatt CD Jr, Vecchi MP (1983) Optimization by simulated annealing. Science 220:671–680. 10.1126/science.220.4598.671 [DOI] [PubMed] [Google Scholar]
- Kleiner M, Brainard D, Pelli D, Ingling A, Murray R, Broussard C (2007) What's new in Psychtoolbox-3. Perception 36:1. [Google Scholar]
- Klimesch W. (2012) Alpha-band oscillations, attention, and controlled access to stored information. Trends Cogn Sci 16:606–617. 10.1016/j.tics.2012.10.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koriat A. (2007) Metacognition and consciousness. In: The Cambridge handbook of consciousness (Zelazo PD, Moscovitch M, Thompson E, eds.) pp. 289–325. New York, NY: Cambridge University Press. [Google Scholar]
- Kuznetsova A, Brockhoff PB, Christensen HB (2014) lmerTest: Tests for random and fixed effects for linear mixed effect models (lmer objects of lme4 package). R package version:R package version 2.0–6. [Google Scholar]
- Kvam PD, Pleskac TJ, Yu S, Busemeyer JR (2015) Interference effects of choice on confidence: Quantum characteristics of evidence accumulation. Proc Natl Acad Sci U S A 112:10645–10650. 10.1073/pnas.1500688112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefcheck JS. (2016) piecewiseSEM: Piecewise structural equation modelling in r for ecology, evolution, and systematics. Methods in Ecology and Evolution 7:573–579. 10.1111/2041-210X.12512 [DOI] [Google Scholar]
- Levitt H. (1971) Transformed up-down methods in psychoacoustics. J Acoust Soc Am 49:467+. 10.1121/1.1912375 [DOI] [PubMed] [Google Scholar]
- Makeig S, Bell AJ, Jung T., Sejnowski TJ (1996) Independent component analysis of electroencephalographic data. In: Advances in neural information processing systems. pp. 145–151. [Google Scholar]
- Maniscalco B, Lau H (2012) A signal detection theoretic approach for estimating metacognitive sensitivity from confidence ratings. Conscious Cogn 21:422–430. 10.1016/j.concog.2011.09.021 [DOI] [PubMed] [Google Scholar]
- McCurdy LY, Maniscalco B, Metcalfe J, Liu KY, de Lange FP, Lau H (2013) Anatomical coupling between distinct metacognitive systems for memory and visual perception. J Neurosci 33:1897–1906. 10.1523/JNEUROSCI.1890-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mognon A, Jovicich J, Bruzzone L, Buiatti M (2011) ADJUST: an automatic EEG artifact detector based on the joint use of spatial and temporal features. Psychophysiology 48:229–240. 10.1111/j.1469-8986.2010.01061.x [DOI] [PubMed] [Google Scholar]
- Morey R, Rouder J, Jamil T (2015) BayesFactor: computation of bayes factors for common designs. R package version 0.9.12–2. Available at: https://CRAN.Rproject.org/package=BayesFactor.
- Oostenveld R, Fries P, Maris E, Schoffelen JM (2011) FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput Intell Neurosci 2011:156869. 10.1155/2011/156869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelli DG. (1997) The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis 10:437–442. 10.1163/156856897X00366 [DOI] [PubMed] [Google Scholar]
- Perrin F, Pernier J, Bertrand O, Echallier JF (1989) Spherical splines for scalp potential and current density mapping. Electroencephalogr Clin Neurophysiol 72:184–187. 10.1016/0013-4694(89)90180-6 [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G. (1992) Event-related synchronization (ERS): an electrophysiological correlate of cortical areas at rest. Electroencephalogr Clin Neurophysiol 83:62–69. 10.1016/0013-4694(92)90133-3 [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Lopes da Silva FH (1999) Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol 110:1842–1857. 10.1016/S1388-2457(99)00141-8 [DOI] [PubMed] [Google Scholar]
- Pinheiro JC, Bates DM (2010) The NLME package. October. [Google Scholar]
- Pleskac TJ, Busemeyer JR (2010) Two-stage dynamic signal detection: a theory of choice, decision time, and confidence. Psychol Rev 117:864–901. 10.1037/a0019737 [DOI] [PubMed] [Google Scholar]
- Rahnev D, Koizumi A, McCurdy LY, D'Esposito M, Lau H (2015) Confidence leak in perceptual decision making. Psychol Sci 26:1664–1680. 10.1177/0956797615595037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridout MS, Linkie M (2009) Estimating overlap of daily activity patterns from camera trap data. J Agric Biol Environ Stat 14:322–337. 10.1198/jabes.2009.08038 [DOI] [Google Scholar]
- Samaha J, Iemi L, Postle BR (2017) Prestimulus alpha-band power biases visual discrimination confidence, but not accuracy. Conscious Cogn 54:47–55. 10.1016/j.concog.2017.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siedlecka M, Paulewicz B, Wierzchoń M (2016) But I was so sure! Metacognitive judgments are less accurate given prospectively than retrospectively. Front Psychol 7:218. 10.3389/fpsyg.2016.00218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singmann H, Bolker B, Westfall J Aust F (2017) afex: analysis of factorial experiments. R package version 0.18–0. Available at: https://CRAN.Rproject.org/package=afex.
- Solovey G, Graney GG, Lau H (2015) A decisional account of subjective inflation of visual perception at the periphery. Atten Percept Psychophys 77:258–271. 10.3758/s13414-014-0769-1 [DOI] [PubMed] [Google Scholar]
- Song C, Kanai R, Fleming SM, Weil RS, Schwarzkopf DS, Rees G (2011) Relating interindividual differences in metacognitive performance on different perceptual tasks. Conscious Cogn 20:1787–1792. 10.1016/j.concog.2010.12.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitmarsh S, Oostenveld R, Almeida R, Lundqvist D (2017) Metacognition of attention during tactile discrimination. Neuroimage 147:121–129. 10.1016/j.neuroimage.2016.11.070 [DOI] [PubMed] [Google Scholar]
- Wickham H. (2009) ggplot2: elegant graphics for data analysis. New York: Springer-Verlag. [Google Scholar]
- Wokke ME, Cleeremans A, Ridderinkhof KR (2017) Sure I'm sure: prefrontal oscillations support metacognitive monitoring of decision making. J Neurosci 37:781–789. 10.1523/JNEUROSCI.1612-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeung N, Summerfield C (2012) Metacognition in human decision-making: confidence and error monitoring. Philosophical transactions of the Royal Society of London Series B, Biological sciences 367:1310–1321. 10.1098/rstb.2011.0416 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yokoyama O, Miura N, Watanabe J, Takemoto A, Uchida S, Sugiura M, Horie K, Sato S, Kawashima R, Nakamura K (2010) Right frontopolar cortex activity correlates with reliability of retrospective rating of confidence in short-term recognition memory performance. Neurosci Res 68:199–206. 10.1016/j.neures.2010.07.2041 [DOI] [PubMed] [Google Scholar]