Temporal Response Properties of Accessory Olfactory Bulb Neurons: Limitations and Opportunities for Decoding

Abstract

The vomeronasal system (VNS) is a major vertebrate chemosensory system that functions in parallel to the main olfactory system (MOS). Despite many similarities, the two systems dramatically differ in the temporal domain. While MOS responses are governed by breathing and follow a subsecond temporal scale, VNS responses are uncoupled from breathing and evolve over seconds. This suggests that the contribution of response dynamics to stimulus information will differ between these systems. While temporal dynamics in the MOS are widely investigated, similar analyses in the accessory olfactory bulb (AOB) are lacking. Here, we have addressed this issue using controlled stimulus delivery to the vomeronasal organ of male and female mice. We first analyzed the temporal properties of AOB projection neurons and demonstrated that neurons display prolonged, variable, and neuron-specific characteristics. We then analyzed various decoding schemes using AOB population responses. We showed that compared with the simplest scheme (i.e., integration of spike counts over the entire response period), the division of this period into smaller temporal bins actually yields poorer decoding accuracy. However, optimal classification accuracy can be achieved well before the end of the response period by integrating spike counts within temporally defined windows. Since VNS stimulus uptake is variable, we analyzed decoding using limited information about stimulus uptake time, and showed that with enough neurons, such time-invariant decoding is feasible. Finally, we conducted simulations that demonstrated that, unlike the main olfactory bulb, the temporal features of AOB neurons disfavor decoding with high temporal accuracy, and, rather, support decoding without precise knowledge of stimulus uptake time.

SIGNIFICANCE STATEMENT A key goal in sensory system research is to identify which metrics of neuronal activity are relevant for decoding stimulus features. Here, we describe the first systematic analysis of temporal coding in the vomeronasal system (VNS), a chemosensory system devoted to socially relevant cues. Compared with the main olfactory system, timescales of VNS function are inherently slower and variable. Using various analyses of real and simulated data, we show that the consideration of response times relative to stimulus uptake can aid the decoding of stimulus information from neuronal activity. However, response properties of accessory olfactory bulb neurons favor decoding schemes that do not rely on the precise timing of stimulus uptake. Such schemes are consistent with the variable nature of VNS stimulus uptake.

Introduction

Most vertebrates have two major olfactory systems, which are known as the main olfactory system (MOS), and the vomeronasal system (VNS; Kepecs et al., 2006; Spehr et al., 2006). One prominent difference between them concerns stimulus delivery, a process that determines the dynamics of stimulus-induced neuronal responses. In the MOS, odorants reach sensory neurons via an ongoing cycle of sniffing, which rapidly draws odorants across the epithelium within tens of milliseconds (Wachowiak, 2011). In contrast, VNS stimulus uptake requires active suction by the sympathetically controlled vomeronasal organ (VNO) whose unitary uptake event evolves over seconds (Meredith and O'Connell, 1979). Furthermore, the physical path that fluid-soluble vomeronasal stimuli must traverse from nostril to VNO duct is more intricate than that of volatiles to the nasal epithelium (Wöhrmann-Repenning, 1984). Together, these factors suggest that neuronal dynamics in central VNS structures will be considerably slower and more variable than their MOS counterparts.

Indeed, recordings in the accessory olfactory bulb (AOB) reveal prolonged stimulus-induced responses (Luo et al., 2003; Hendrickson et al., 2008; Ben-Shaul et al., 2010; Bergan et al., 2014; Zylbertal et al., 2015), which are consistent with a role for the VNS in controlling endocrine processes and global behavioral states. This is in striking contrast to the MOS, where neuronal responses can occur within individual sniff cycles, resulting in temporal scales of tenths or even hundredths of seconds (Cury and Uchida, 2010; Shusterman et al., 2011).

In the main olfactory bulb (MOB), the fine temporal structure of responses with respect to sniffing markedly aids stimulus decoding (Giraudet et al., 2002; Laurent, 2002; Bathellier et al., 2008; Cury and Uchida, 2010; Dhawale et al., 2010; Shusterman et al., 2011; Smear et al., 2011; Friedrich, 2013; Wilson, 2013; Uchida et al., 2014; Sirotin et al., 2015), demonstrating that temporal dynamics are informative about stimulus features. However, the capacity of the temporal structure of AOB responses to convey stimulus information has not been systematically investigated. Indeed, quantification of stimulus-induced VNS activity mainly involved averaging over extended temporal windows spanning up to tens of seconds (Luo et al., 2003; Ben-Shaul et al., 2010; Arnson and Holy, 2013; Tolokh et al., 2013; Bergan et al., 2014; Cichy et al., 2015; Kahan and Ben-Shaul, 2016). However, the VNS clearly also plays a role in behavioral processes that evolve over seconds (Leypold et al., 2002; Stowers et al., 2002; Isogai et al., 2011; Wu et al., 2014). Since in freely behaving animals, instances of stimulus uptake are concealed from the experimenter, a systematic analysis of the temporal dynamics of AOB mitral-tufted cells requires controlled stimulus delivery. Furthermore, because the dynamics of VNO pumping are key determinants of temporal response features, addressing this issue requires functional VNO suction.

The general motivation for this study was to understand whether, and how, information about stimulus identity is represented in the temporal dynamics of AOB responses. Our first goal was to characterize the temporal features of AOB responses and to determine whether they are associated with particular neurons, particular stimuli, or with their combinations. The second goal was to identify the temporal windows in which AOB responses are most informative with respect to stimulus properties. Third, we sought to understand whether consideration of finer temporal structure improves the ability to decode stimulus information from AOB neuronal activity. To these ends, we used controlled stimulus delivery to the intact VNO in anesthetized mice while recording extracellular neuronal activity of AOB mitral-tufted cells.

We demonstrated that although consideration of stimulus delivery timing aids decoding in the AOB, incorporation of fine temporal resolutions is not as beneficial as it is in the MOB. Testing various decoding schemes on real and simulated data, we determined that AOB neuronal responses do not benefit from decoding with high temporal accuracy, and only marginally from using precise information about stimulus onset. Instead, AOB physiology is compatible with decoding with coarser temporal windows, even without precise knowledge of stimulus uptake time.

Materials and Methods

Mice

All procedures were approved by the ethical committee of the Hebrew University Medical School. The dataset includes recordings from 34 adult (8- to 12-week-old) BALB/C male and female mice. Stimuli were collected from adult (8- to 12-week-old) male and female mice of the BALB/C and C57BL/6 strains. All mice were purchased from Harlan Laboratories.

Stimuli

For stimulus collection, mice were gently held over a plastic sheet until they urinated. The urine was transferred to a plastic tube with a micropipette and then flash frozen in liquid nitrogen and subsequently stored at −80°C. All dilutions were made with Ringer's solution. Our analyses are based on two datasets. Dataset 1 was used for all classification analyses (see Figs. 5, 6, 7, 8) and for the analysis of multiple factor ANOVA (see Table 2). It included nine different stimuli, which comprised mixtures of male, female, and predator stimuli each at 1:100, 1:30, and 1:10 dilutions in Ringer's solution. Male and female mixtures included stimuli from the BALB/C and C57BL/6 strains. Predator mixtures included bobcat, fox, lion, and wolf urine purchased from PredatorPee. Dataset 2 included individual male samples, a mix of castrated male urine, and mixtures of female urine stimuli. These samples were collected from BALB/C and C57BL/6 mice, and were diluted 1:10. In addition, dataset 2 included another group of urine stimuli from females at two estrus stages (estrus and nonestrus) in various dilutions (1:1, 1:10, 1:33, 1:100, 1:300). The last group included neurons that were also analyzed in the study by Kahan and Ben-Shaul (2016).

Figure 5.

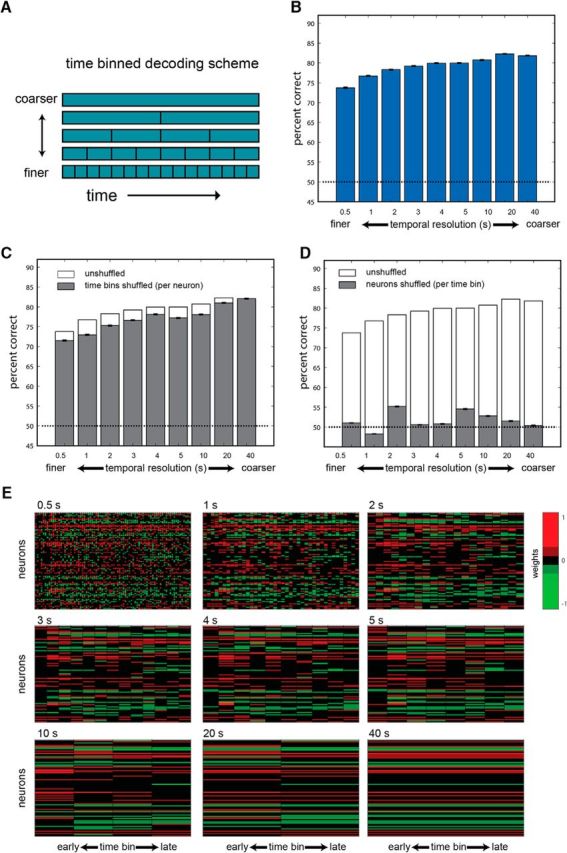
Time-binned classification. A, Time-binned decoding scheme. In this scheme, the entire 40 s period is divided into contiguous bins of a given size. B, Performance of classifiers at various temporal resolutions. Bars represent the averaged performance across the three possible discriminations and 1000 instantiations of each classifier. Error bars show the SEM. C, Performance following shuffling of the temporal order of the data (while keeping the identity of neurons intact) in the training and testing sets. For comparison, the nonshuffled performance is indicated by the empty bars. D, Performance following shuffling data across neurons in both the training and the test set, while keeping the temporal order intact. Chance performance (50%) in all plots is represented by the broken dashed line. E, Classifier weights associated with each of the temporal resolutions. Weights are normalized to scale between −1 and 1. Each of the nine panels corresponds to one of the nine resolutions, as indicated above the matrix. In all matrices, rows represent neurons and columns represent time bins. The number of columns thus varies as a function of the resolution. For example, the 0.5 s resolution includes 80 columns, while the 40 s resolution includes a single time bin.

Figure 6.

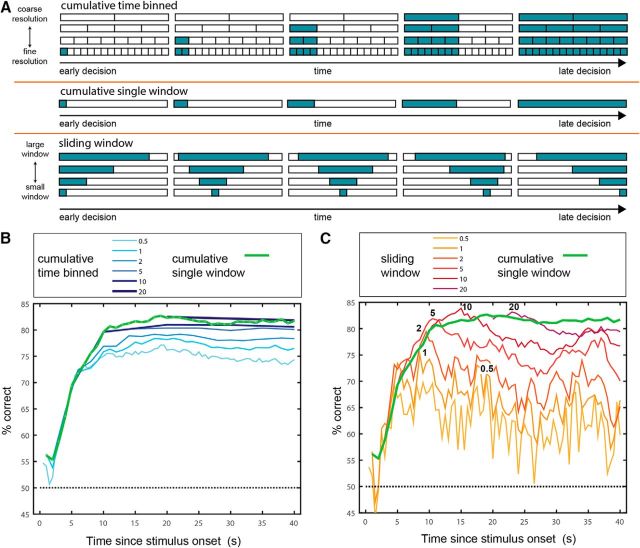
Classifier performance as a function of time and temporal resolution. A, Schematic of the three classification schemes shown in this figure. In the cumulative time-binned scheme, classification at time t is based on counts in contiguous time bins. In the cumulative single-window scheme, classification is based on spike counts in one temporal window starting at time 0. The window is increased in steps of 1 s. Under the sliding window scheme, classification is based on a single temporal window with a given duration. The window is slid across the entire period at steps of 0.5 s. Under all schemes, the decision time associated with each window is the time by which it ends. B, Performance of cumulative binned classifiers of different resolutions as a function of time. Note that at any given time t, only classifiers with resolutions finer than t can provide classification. For example, the first time point for the classifier operating at a temporal resolution of 10 s occurs at 10 s. Performance of the cumulative single-window classifier is shown in green. C, Performance of sliding window classifiers of different widow sizes as a function of time. Numbers in black indicate the times of peak performance for each resolution. Performance of the cumulative single-window classifier is shown in green.

Figure 7.

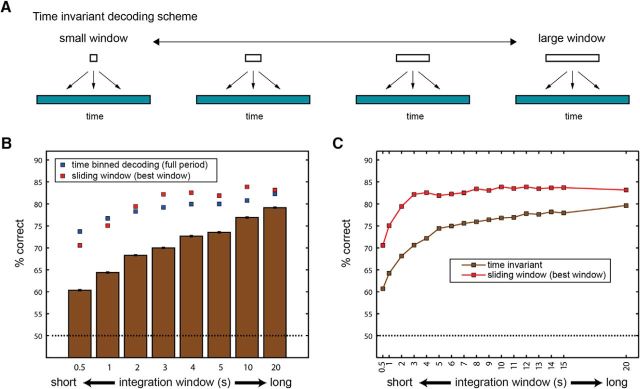
Performance of time-invariant classifiers. A, Schematic of time-invariant classification. In this scheme, classifiers receive data from a single window of a given duration, sampled at any time period during the 40 s poststimulus period. B, Bars show performance of the time-invariant classifiers for various window durations. Blue squares denote performance with the time-binned decoding scheme, at the same resolution. Red squares denote the performance achieved with the best sliding window of the same duration. C, Performance for time-invariant and sliding window classifiers as a function of integration window size, shown for more window durations.

Figure 8.

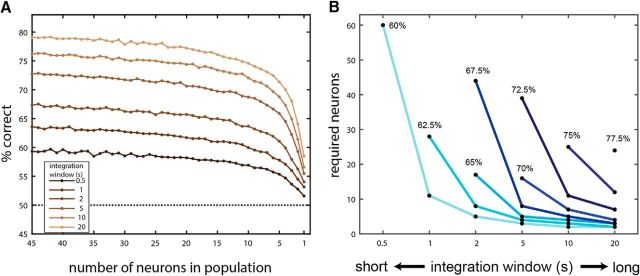
Time-invariant classifiers require neuronal populations. A, Performance of time-invariant classifiers as a function of window size (different traces) and the number of neurons in the population. The horizontal axis is truncated at 45 neurons because performance does not improve much with additional neurons. B, Tradeoffs among integration window size, performance, and number of neurons. Each trace (or point, in the case of 77.5%) corresponds to a certain classifier performance level. The key feature evident in these traces is that for any given performance, classifiers operating on smaller windows require more neurons.

Table 2.

Statistical tests of factors determining temporal feature distributions

	t10	tpeak	t50	t90	Asymmetry	Width	ΔR
One-way (neuron ID)	0	0	0	0	0.0001	0	0
Three-way
Neuron ID	4.7 × 10−6	0	0	0	0.024	0	0
Dilution	1	0.99	1	0.57	1	1	0.09
Stimulus	0.047	1	0.7	0.37	1	0.99	0.9

One-way: p-values with one-way non-parametric ANOVA (Kruskal-Wallis test) with neuron identity as factor. N = 1973 trials from 192 single neurons. Three-way: p-values with neuron identity, dilution and stimulus as main factors (anovan MATLAB function). N = 1033 trials from 102 neurons. All p-values are shown after adjustment for multiple comparisons using the Dunn-Sidak correction (which shifts all p-values closer to 1). Values lower than 10⁻¹⁰ are rounded to 0. Values higher than 0.995 are rounded to 1.

Experimental design

Surgical preparation.

Anesthesia was induced with an intraperitoneal injection of a ketamine-xylazine mix (10 mg/kg xylazine and 100 mg/kg ketamine) or 3% isoflurane mixed with oxygen gas in an anesthesia chamber. After placing the mouse on a stereotaxic stage, anesthesia was maintained with ∼1% isoflurane and monitored using a heart rate monitor and by testing the foot withdrawal reflex. The experimental procedures were described in detail recently (Yoles-Frenkel et al., 2017). Briefly, a tracheotomy was performed with a polyethylene tube, and a cuff electrode was placed around the sympathetic nerve trunk. Incisions were closed with veterinary glue (Vetbond, 3M), after which the mouse was placed in a custom-built stereotaxic apparatus.

Electrode targeting.

A craniotomy was made immediately rostral to the rhinal sinus, the dura was removed around the penetration site, and electrodes were advanced into the AOB at an angle of ∼30° with a manual micromanipulator (model MM-33, Sutter Instrument) or electronic micromanipulator (model MP-285 Sutter Instrument). All recordings were made with 32-channel probes (A4×8-5 mm-100-200-177-A32 or A4×8-5 mm-50-200-177-A32 configurations; NeuroNexus). Before recordings, electrodes were dipped in fluorescent dye (DiI, Invitrogen) to allow subsequent confirmation of electrode placement within the AOB external cell layer, which contains the mitral-tufted cells (Larriva-Sahd, 2008). It should be noted that, as in all extracellular recordings, it is impossible to confirm that recorded neurons were mitral-tufted cells. However, our accumulated experience over many recording sessions and subsequent histological analysis indicates that when electrodes are not within the external cell layer of the AOB (but rather in the granule cell layer or the glomerular layer), baseline activity is virtually absent, and there are no neuronal responses to VNO stimulus delivery. Thus, we are certain that our neuronal sample is predominated by principal neurons within the external (mitral-tufted) cell layer of the AOB.

Stimulus delivery.

In each trial, 2 μl of the stimulus were applied directly into the nostril (stimulus application). After a delay of 20 s, a square-wave stimulation train (duration, 1.6 s; current, ±120 μA; frequency, 30 Hz) was delivered through the sympathetic nerve trunk (SNT) cuff electrode to induce VNO pumping and stimulus entry to the VNO lumen (SNT stimulation). Throughout the manuscript, we refer to the start of the stimulation train as time 0. Following another delay of 40 s, the nasal cavity and VNO were flushed with 1–2 ml of Ringer's solution, which flowed from the nostril into the nasal cavity and drained via the nasopalatine duct using a solenoid-controlled suction tube. The flushing procedure was 50 s long and included a single sympathetic trunk stimulation to facilitate stimulus elimination from the VNO lumen. In each session, 9–12 different stimuli were presented in a pseudorandom order, typically five times each. The experiments were sequenced and controlled using programs custom-written in MATLAB (MathWorks).

Basic data processing.

Neuronal data were recorded using either a TDT system (RZ2 processor, PZ2 preamplifier, and RA16CH head-stage amplifiers, Tucker-Davis Technologies) or an INTAN board (RHD2000 V1, Intan Technologies) integrated with a data acquisition board (USB-6343, National Instruments). Signals were sampled at 25 kHz and bandpass filtered (300–5000 Hz). Spike waveforms were extracted using custom-written MATLAB code. Spikes were sorted automatically using KlustaKwik (Harris et al., 2000) and then manually verified and adjusted using Klusters (Hazan et al., 2006). Spike clusters were evaluated by their spike shapes, projection on principal component space (calculated for each session individually), and autocorrelation functions. A spike cluster was designated as a single unit if it showed a distinct spike shape, was fully separable from both the origin (noise) and other clusters along at least one principal component projection, and if the interspike interval histogram demonstrated a clear trough around time 0 of at least 10 ms. Clusters not meeting these criteria were designated as multiunits and were excluded from the present analyses.

Statistical analysis

All data analyses and visualizations were performed with custom-written MATLAB programs. MATLAB-created images (*.fig file) were then saved in EPS format and graphically processed in Adobe Illustrator for improved visualization.

Selection of units for analysis.

We have previously described our observation that in some cases, stimulus application is sufficient to induce a neuronal response before sympathetic nerve trunk stimulation (Ben-Shaul et al., 2010; Yoles-Frenkel et al., 2017). While such stimulus application-locked responses present genuine VNO-mediated AOB responses, they are excluded from the present analysis, because their onset is not marked by a definite trigger, as is the case with SNT stimulation responses. Thus, to be included in the analysis, single neurons had to exhibit significant stimulation-locked responses without significant application-locked responses to at least one of the tested stimuli. A stimulation-locked response is considered significant if the distribution of single-trial firing rates (typically, five single-trial values for each stimulus), quantified for 20 s following VNO stimulation, is significantly different from the distribution of the prestimulus firing rate of the same neuron. An application-locked response is considered significant if the distribution of single-trial firing rates, quantified for 20 s following stimulus application, is significantly different from the distribution of the prestimulus firing rate of the same neuron. The prestimulus firing rate distribution is evaluated during the 15 s period before stimulus application, pooled across all trials of all stimuli for the neuron in question. The response of a neuron to a given stimulus is considered significant if these distributions differ at the p < 0.05 significance level, determined using a nonparametric ANOVA (MATLAB Kruskalwallis function). For analyses of decoders (see Figs. 5, 6, 7, 8), we included neurons that showed a significant stimulation-locked response to at least one of the stimuli and no application-locked responses to any of the stimuli. Once a neuron was included, all individual trials for all stimuli were used for the decoding analysis.

Definition of temporal features.

All temporal features were derived after binning spike times (0.2 s bins) and smoothing (with triangular window with an area of 1 and a base of 2.8 s). Time 0 is defined as the beginning of the sympathetic nerve trunk stimulation. For these analyses, all measures were defined with respect to a 40 s window following time 0. The parameters 10% time (t₁₀), 50% time (t₅₀), and 90% time (t₉₀) are defined as the time by which the corresponding percentage of spikes has occurred. Peak time (t_peak) is defined as the time of occurrence of the highest peak in firing rate in the window.

Width is defined as follows: 75% time − 25% time.

Asymmetry is defined as follows:

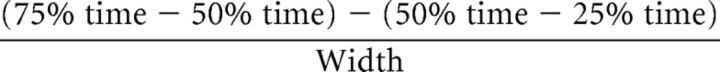Firing rate modulation (ΔR) was defined on a trial-by-trial basis as the difference between the average firing rate in a 40 s window after SNT stimulation and the firing rate during the 15 s window before stimulus application (i.e., the baseline firing rate). Since the temporal features defined here apply to rate elevations, this analysis was applied only to responses associated with rate elevations, but not to responses of rate suppression (measured relative to baseline). The analysis of temporal features (Fig. 1) was applied to neurons from datasets 1 and 2.

Figure 1.

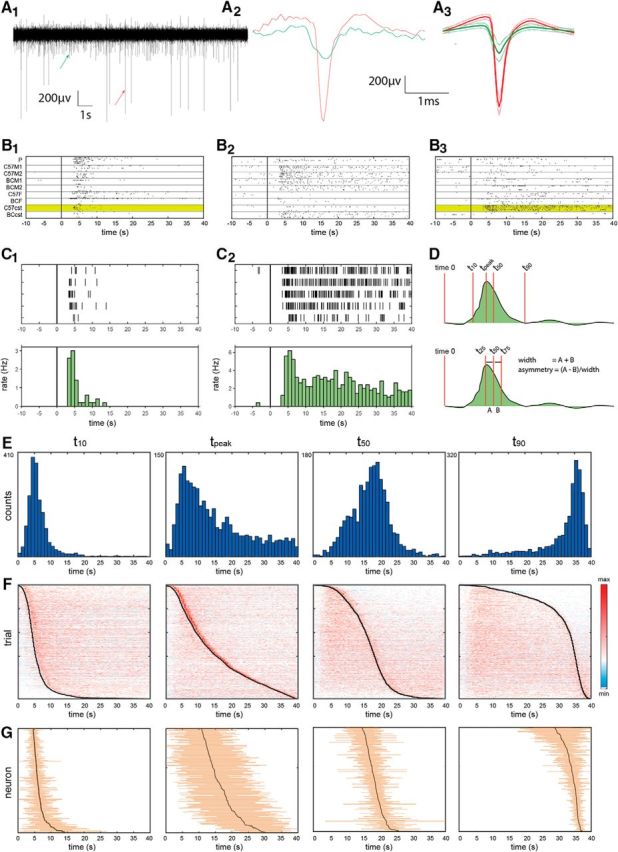
Temporal response properties of AOB neurons. A₁, Segment from a band-passed electrode trace. A₂, A₃, Arrows show individual spikes, highlighted in A₂, the mean and SD of the spike shapes of these units are shown A₃. Note that only the larger of these two units was designated as a single unit and is thus included in our analysis. B₁–B₃, Examples of responses of three simultaneously recorded neurons. Each panel shows raster displays of stimulus-evoked spiking. Time 0 corresponds to sympathetic nerve trunk stimulation. Within each panel, the trials are partitioned according to the stimulus, as indicated on the left of B₁. P, Predator urine. C57M1 and C57M2: urine from two different C57BL/6 male individuals, BCM1, and BCM2: urine from two different BALB/C male individuals, C57F and BCF: urine mixes from BALB/C and C57BL/6 females, respectively. C57cst and BCcst: urine mixes from castrated C57BL/6 and BALB/C males, respectively. All stimuli are diluted 1:10 in Ringer's solution. Each stimulus was presented five times (except predator urine, which was presented here six times) in a randomly interleaved presentation order. C₁, C₂, Detailed view of the responses highlighted in B₁ and B₃.Top, Raster displays. Bottom, firing rates in 1 s time bins. D, Schematic of temporal parameter definitions. For example, the values (mean ± SD) for the response shown in C₁ are as follows: t₁₀, 3.8 ± 0.5 s; t₅₀, 5.0 ± 0.5 s; t₉₀, 9.9 ± 2.0 s; t_peak, 4.7 ± 0.7 s; width, 2.2 ± 0.9 s; asymmetry, 0.3 ± 0.2. Values for the response shown in C₂ are as follows: t₁₀, 5.7 ± 0.4 s; t₅₀, 17.4 ± 2.3 s; t₉₀, 34.3 ± 1.3 s; t_peak, 5.7 ± 0.7 s; width, 16.1 ± 1.7 s; asymmetry, −0.02 ± 0.1. E, Histograms of temporal parameters across the entire population of single trials (N = 1973). Numbers to the left of each panel indicate the upper vertical limit. F, Normalized responses in all single trials, sorted according to the parameter indicated in E above. G, Mean and SDs of temporal parameter values for individual neurons (N = 192), sorted according to their mean value. Note that since different individual neurons may respond to a different number of stimuli, the total number of trials included in this display is not identical for all neurons.

Statistical analysis of temporal features.

To test whether temporal feature distributions are neuron specific, we applied a nonparametric ANOVA (Kruskal–Wallis test) with neuron identity as a major factor. Testing the effects of multiple factors (i.e., stimulus and dilution) was not possible across the entire set of responses since not all neurons were tested with the same set of stimuli. We therefore focused on dataset 1, which consists of neurons that were tested with the same set of stimuli, allowing us to apply a three-way ANOVA for assessing the three main effects of neuron, stimulus, and dilution (MATLAB anovan function). Assessing interactions between factors was also not possible since most neurons did not respond to all stimulus/dilution combinations.

To compare temporal parameter distributions of a given neuron across stimuli, we considered neurons that exhibited significant responses to more than a single stimulus. We then compared, for each neuron, all pairs of effective stimuli. For each stimulus pair, the associated distributions were compared with a Wilcoxon rank-sum test (MATLAB ranksum function). Then, we calculated the probability to obtain the observed number of significantly different comparisons (at the p < 0.01 level) under the null hypothesis according to which of the temporal response features of a given neuron are not affected by stimulus identity. This probability can be derived from the binomial probability function (MATLAB binocdf function) with p = 0.01 and N being the number of comparisons.

In a related analysis, we confined the comparison to pairs of qualitatively distinct stimuli. In this case, responses were compared only if they were elicited by stimuli from distinct sources (i.e., we did not compare stimulus pairs that were both from male urine, both from female urine, or both from predator urine, even if they were at different dilutions or from different strains). All p values reported in Table 2 and Table 3 were adjusted for multiple comparisons using the Dunn–Sidak correction. Specifically, the adjusted p value is given by the following: 1 − (1 − p′)^m, where p′ is the original (nonadjusted) p value, and m is the number of comparisons. Since the individual temporal features are not entirely independent, this correction results in a conservative test.

Table 3.

Statistical analysis of differences in temporal parameter distributions

	t10	tpeak	t50	t90	Asymmetry	Width	ΔR
Same neuron different stimuli (N = 460)	0.2% (1)	0.65% (1)	0% (1)	1.5% (0.5)	0.65% (1)	0.65% (1)	2.4% (0.02)
Same neuron qualitatively different stimuli (N = 268)	0.4% (1)	0% (1)	0% (1)	1.9% (0.3)	0.4% (1)	0.75% (0.99)	2.6% (0.04)
Different neurons (N = 18,336)	6.3% (0)	5.7% (0)	12% (0)	11.8% (0)	2.9% (0)	9.6% (0)	15.3% (0)

Percentage of cases in which the null hypothesis (of equal distribution) is rejected at the 0.01 level (Wilcoxon rank sum test). Values in parenthesis show the probability to obtain (at least) the observed number of significantly different cases after adjustment for multiple comparisons (Dunn-Sidak correction). Values below 10⁻¹⁰ are rounded to 0. Values above 0.995 are rounded to 1.

Same neurons different stimuli: comparison of significant responses (of the same neuron) to two stimuli that differ in either dilution or source (or both). Same neurons qualitatively different stimuli: responses of individual neurons to stimuli from different sources. Different neurons: responses of different neurons to different stimuli (regardless of stimulus dilution or source).

Analysis of correlations between simultaneously recorded neurons.

This analysis was designed to evaluate trial-to-trial correlations in temporal parameter values of simultaneously recorded neurons. To this end, we calculated the correlation coefficients between response parameters of all pairs of simultaneously recorded units that showed a significant response to a given stimulus. For each temporal parameter, we calculated all pairwise correlation coefficients between trial-to-trial values of the two neurons in the pair. We used a two-sided Wilcoxon signed rank test-to-test whether the median value of the population of these correlation coefficients is significantly different from 0. As an additional test of significance, we derived a bootstrapped distribution of correlation coefficients, by repeatedly (100 times) shuffling trial order for each neuron pair. The distribution of real (nonshuffled) correlation coefficients was then compared with the bootstrapped distribution using a two-sided Wilcoxon rank-sum test.

Analysis of stimulus detection and discrimination for various window sizes.

We define stimulus detection as the ability to distinguish stimulus-evoked firing rates from baseline firing rates. Stimulus discrimination is defined as the ability to distinguish firing rates evoked by different stimuli. This analysis was based on the auROC metric (area under the receiver operating curve). The ROC is defined with respect to two firing rate distributions and is the relationship between the true-positive rate and the false-positive rate as the discrimination threshold is changed (Fawcett, 2006). The area of the ROC was calculated, and the auROC score was defined as follows: area − 0.5. Thus, the absolute value of the auROC score can range between 0 (indistinguishable distributions) and 0.5 (perfectly distinguishable distributions). The auROC analysis was performed with stimulus-evoked firing rates in various temporal windows (Fig. 2A). Specifically, temporal windows ranged in duration from 0.5 to 40 s (with 1 s increments for windows between 1 and 40 s), and in latency from 0 to 39.5 s (at 0.5 s increments). As in all other analyses, time 0 corresponds to sympathetic nerve trunk stimulation.

Figure 2.

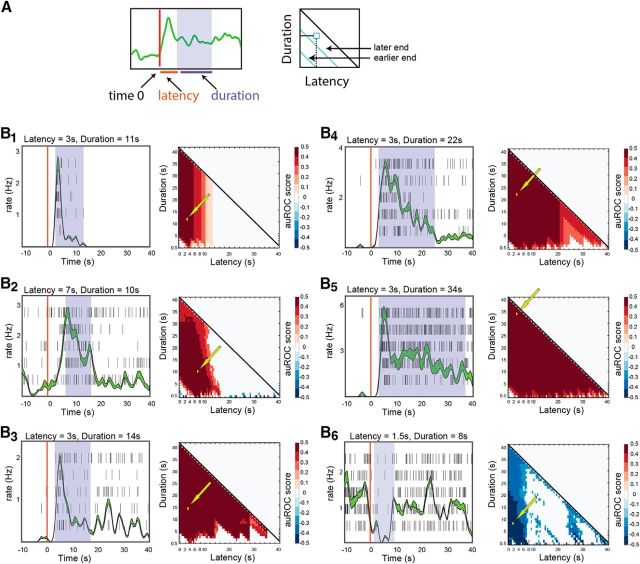
Analysis of stimulus detection for individual neuron–stimulus combinations. A, Schematic illustrating the definition of latency and duration of temporal windows for analysis. The scheme also shows how latency and duration are mapped on the auROC matrix. Each pixel in the matrix shows the auROC score associated with a particular latency and duration of the response of the neuron to one stimulus, compared with baseline. For example, the bottom row of each matrix represents 0.5 s windows at various latencies from stimulus onset, while the leftmost column represents windows starting at time 0, increasing in duration in 0.5 s steps. B₁–B₆, Examples of auROC analysis for individual neurons. Each panel shows a raster plot and a peristimulus rate histogram (lines represent SE boundaries) on the left and the auROC matrix on the right. The shaded regions shown over each of the raster displays indicate one (arbitrarily selected) window providing optimal discrimination. These windows are also indicated by the arrows over the corresponding matrices. Time 0 (vertical red lines) corresponds to the onset of stimulus delivery. The following stimuli were presented in each of the examples: B₁, C57BL/6 castrated male urine mix (diluted 1:10); B₂, C57BL/6 estrus female urine mix (diluted 1:33); B₃, castrated BALB/C male urine mix (diluted 1:10); B₄, castrated C57BL/6 male urine mix (diluted 1:10); B₅, C57BL/6 castrated male urine mix (diluted 1:10); B₆, mix of C57BL/6 and BALB/C male urine (diluted 1:10).

For the analysis of stimulus detection, one sample consisted of firing rate distributions of a given neuron to a given stimulus (across all repeated presentations), while the other sample consisted of baseline firing rates of that same neuron across all trials of all stimuli (during the 15 s period before stimulus application). For analysis of stimulus discrimination, the two samples corresponded to the firing rate distributions following SNT stimulation for each of the two distinct stimuli. To compare stimulus detection associated with rate elevations and rate suppressions across the population (Fig. 3A,B), for each neuron–stimulus combination, we separated temporal windows with positive auROC scores (representing rate elevations relative to baseline) from windows with negative auROC scores (representing rate suppression relative to baseline).

Figure 3.

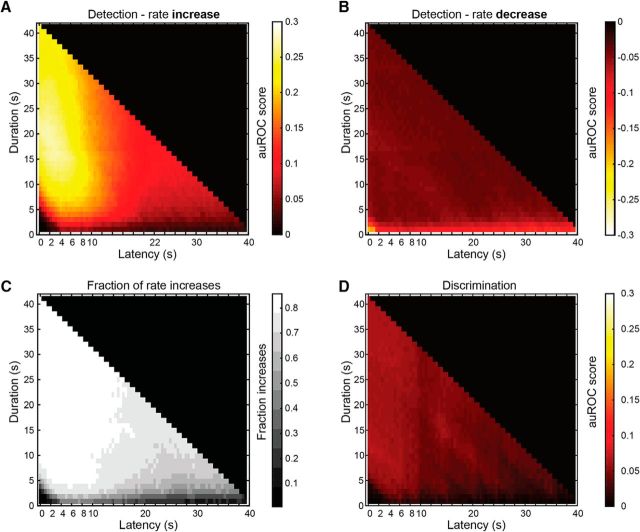
Optimal detection and discrimination windows across the population of neuron–stimulus pairs. A, Averaged auROC scores for all responses with positive auROC scores (i.e., response firing rates are higher than the baseline counts). B, Averaged auROC scores for cases of negative auROC scores (i.e., response counts are lower than the baseline counts). C, Fraction of responses with rate increases, in each window. D, Average auROC matrix for discrimination among stimuli.

To verify the statistical significance of auROC scores, for each score we recalculated auROC scores after randomly mixing data from the two groups (baseline vs response for detection, and response to stimulus 1 vs response to stimulus 2 for discrimination). For each neuron–stimulus combination and each duration–latency combination, shuffling was repeated 100 times. Positive auROC scores were considered significant if they were in the top 2.5% of shuffled auROC scores. Negative auROC scores were considered significant if they were in the bottom 2.5% of shuffled auROC scores. Only significant auROC scores were considered (nonsignificant scores were set to 0). Thus, any nonzero auROC score in the matrices shown in Figures 2 and 3 is significant according to this criterion.

Classification/decoding analyses.

All functions for the classification analysis were custom written in MATLAB. Although we implemented several different classification schemes, all were based on the same linear approach applied in our previous work (Kahan and Ben-Shaul, 2016). The classifier was implemented with the perceptron MATLAB function (neural networks toolbox, R2017b; http://www.mathworks.com/help/nnet/ref/perceptron.html), which is described in http://www.mathworks.com/help/nnet/ug/perceptron-neural-networks.html. The perceptron function was called with default parameters, with the exclusion of the sample selection parameter during training, for which we used the trainr function.

Classification analysis was applied to dataset 1 (see definitions above) since it includes neurons that were tested with the same stimulus set. In all analyses, we show the averaged results over multiple realizations of the classification process. Furthermore, classifier results represent averages across all three pairwise discriminations, namely, male versus female, male versus predator, and female versus predator. Finally, all three dilutions of each stimulus were pooled together (Fig. 4A), thus requiring the classifiers to overcome stimulus–intensity-related variability (Kahan and Ben-Shaul, 2016). As each stimulus was presented five times at each of three dilutions, our dataset contains 15 repeated presentations of each stimulus. In the few cases in which a stimulus was presented only four times (1%), the fifth trial was randomly selected from the set of four. When stimuli were presented six times (4%), one trial was randomly left out.

Figure 4.

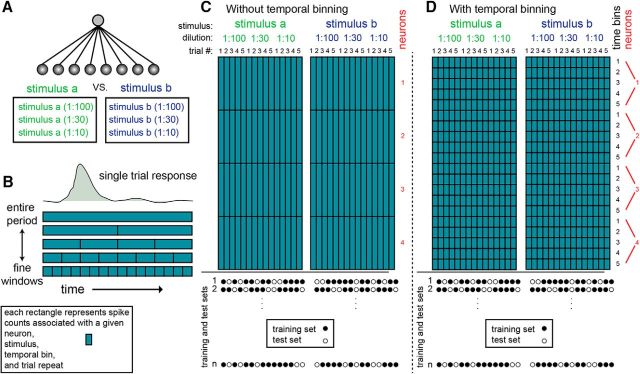
Explanation of the basic classification procedure. A, All classifiers considered here discriminate among two different stimuli, each of which can be presented at one of three different dilutions. Thus, classifiers must overcome not only trial-to-trial variability, but also variability associated with stimulus intensity. Spheres at the bottom represent inputs for the classifiers. Each input corresponds to a given temporal window from a given neuron. For classifiers operating on a coarse timescale, the response of each neuron is represented by a single input. However, if responses are partitioned into multiple time bins, then each neuron contributes multiple inputs to the classifier. Thus, classifiers operating on finer temporal scales are associated with more inputs and weights. Lines represent classifier weights assigned during training. B, Response of a single neuron to a single stimulus presentation can be described in various temporal resolutions. In the top row, the entire postpresentation period is described as a single number (which is the average firing rate across the long window). Lower rows depict increasingly finer temporal resolutions. In these cases, individual trials are described as a sequence of firing rate values within smaller windows. C, D, Representation of the dataset without and with temporal binning. Each small rectangle represents spike counts associated with a particular neuron, stimulus, trial, and time period. The two rectangles represent data matrices associated with each of two stimuli. The difference between C and D is the extent of binning (a single time bin in C and five time bins in D). In both panels, the number of neurons shown is four. The circles at the bottom show examples of division of the dataset into training and test sets. One thousand such random divisions were made, and each was classified separately.

Training and testing samples, denoted here as population response vectors (PRVs), were generated by a random selection of single trial responses from each of the neurons (Fig. 4). The structure of the dataset used for classification is shown in Figure 4, C (without temporal binning) and D (with temporal binning). In these panels, each square in the matrix denotes one data point containing spike counts associated with a certain stimulus, dilution, neuron, and temporal window (relative to stimulus onset). Although the details vary for different decoding schemes, in all cases we used a training set of 20 trials and a test set of 10 trials (as mentioned above, there are 15 trials associated with each stimulus, and thus 30 for each pairwise comparison). Each classification was repeated 1000 times, each time using a different random division of trials to the training and testing set, with the constraint that the 20 training-set trials comprised 10 trials from each stimulus, and the 10 test set trials similarly contained five trials from each stimulus. This sampling procedure can give rise to ∼9 × 10⁶ combinations of training and testing sets, given by ${\left(\frac{15!}{10!\left(15-10\right)!}\right)}^2$, since in each repeat, 10 trials to stimulus a are chosen for the training set, while, independently, 10 trials for stimulus b are chosen (Fig. 4C,D, bottom). For the shuffling analysis shown in Figure 5C, all time bins (from a given neuron in a given trial) were randomly shuffled before defining the training and testing sets. This procedure abolishes any consistency in temporal structure across trials, but maintains the identity of neurons. For the analysis in Figure 5D, a similar procedure was applied, except that values were shuffled between neurons, while keeping the identity of time points. This procedure amounts to abolishing the distinctions between neurons. In a similar analysis (mentioned in the text, but not shown), the shuffling was applied to the testing set only, while keeping the training set unperturbed.

For the analysis of time-invariant classifiers (see Figs. 7, 8), each PRV included responses of all neurons from a single time window. For this decoding scheme, a single time window is selected for the entire population for each of the trials, and each trial is represented only once in the training and test sets. This procedure ensures that there are no overlaps whatsoever between the training set and the testing set. More specifically, the training and test sets cannot include data from even partially overlapping windows of the same trial. Note that here, a training set of 20 greatly undersamples the total number of possible values (for each stimulus, there are 15 values for each of the trials, multiplied by the number of distinct windows). The unit removal analysis (see Fig. 8) was conducted as described by Kahan and Ben-Shaul (2016). Briefly, each iteration was initiated with all neurons, and then in each iteration, the unit assigned with the smallest (absolute) weight was removed from the analysis. As with other analyses, this entire procedure was repeated 1000 times.

The time-binned analysis was also conducted with nonlinear classifiers (support vector machines with quadratic kernels, using the MATLAB functions svmtrain and svmclassify). Those comparisons showed similar trends observed with our linear classifiers. The nonlinear classifiers generally performed poorer than linear classifiers, likely due to their increased ability to overfit the training set data at finer temporal resolutions. Here, we focused our analyses on linear classifiers, as they allow direct identification of the influence of individual neurons according the weights assigned to them during training. We note that all our conclusions involve relative, rather than absolute, classifier performance, and are thus independent of the specifics of the decoding procedure.

Generation of simulated neuronal data.

Simulated data were generated using custom-written MATLAB code. Here, we provide only a brief description of the simulation approach. See the GitHub repository (https://github.com/yorambenshaul/neuronal_response_simulator) for the code and for more detailed documentation.

The simulations generate neuronal populations, which are defined by responses to two stimuli (stimulus a and stimulus b). More specifically, each population is defined by a range of starting times, a range of response durations, and a range of response magnitudes to each of the two stimuli. In practice, latencies, durations, and response magnitudes for stimulus b are defined relative to stimulus a. Each trial is realized as a binary process with a probability of spiking at each time bin given by its baseline or response rate and the bin size. In addition, neurons may be associated with trial-to-trial variability (jitter) in response time (in either latency and/or duration). Importantly, even without temporal jitter, responses are defined probabilistically, and thus there will also be trial-to-trial variability in the timing of individual simulated spikes. Naturally, the variability will be higher if the jitter will be larger than 0, since the underlying response functions will also vary temporally.

Once a population is thus defined (graphically via the interface), it is possible to view response realizations (shown as raster displays and peristimulus time histograms) and metrics of response discriminability (using the sensitivity score - d′, auROC scores, or differences in spike counts). Furthermore, it is possible to apply further analyses on the simulated activity. Here, we have implemented the very same analyses on real and simulated data. For all scenarios analyzed here, the number of neurons in the population was set at 10, the baseline firing rate was set to 2 Hz, and 15 trials were generated for each neuron–stimulus combination. Each trial lasted 20 s.

Each of the panels (Fig. 9B–G) represents a different family of scenarios. Each trace in each of the plots in these panels represents one particular scenario. Importantly, because scenarios are often defined probabilistically (i.e., by specifying a range of values), for each scenario we sampled 10 different populations, each of which was classified 100 times repeatedly. Thus, each single data point in each trace of Figure 9 represents 1000 individual classification iterations (10 populations × 100 repeated iterations of each).

Figure 9.

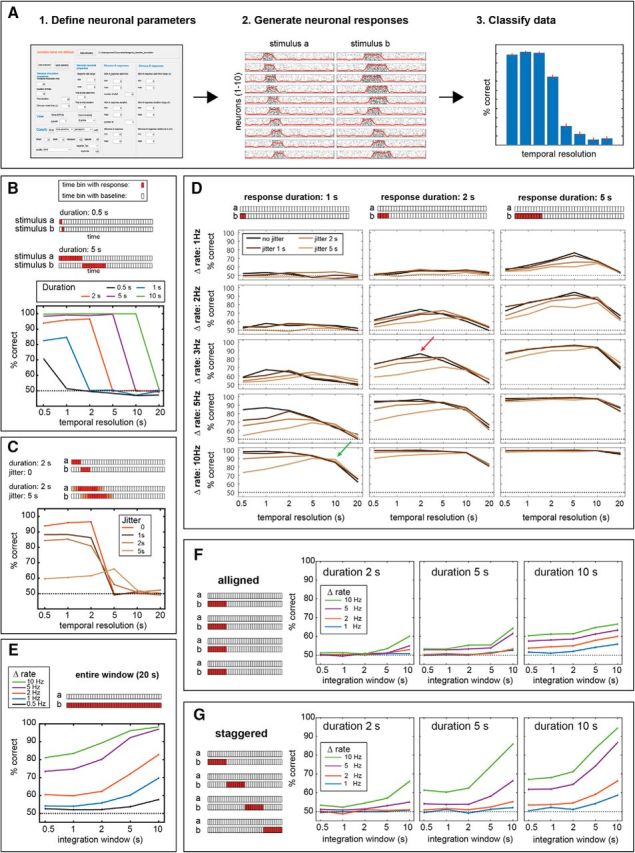
Temporal decoding of simulated data. A, Schematic description of the simulation process, showing the simulator interface, simulated response generated by it, and the results of classification using these responses. B, Time-binned classification using neuronal responses with different temporal profiles for each of two different stimuli. Each trace corresponds to a different response duration, two of which (0.5 and 5 s) are shown schematically in the panel. These schematics represent the responses of one neuron to two different stimuli (a and b). Each rectangle corresponds to one time bin of 0.5 s. Red squares indicate epochs of elevated firing rates. In all traces, each data point represents the averaged performance upon repeated classification (for details, see Materials and Methods). Note that while all schemes show the responses of only one neuron, all populations comprised 10 neurons. C, As in B, for a response duration of 2 s, with various degrees of single-trial response onset time jitter. Lighter shades in the schematic indicate epochs that are affected by temporal jitter. D, Time-binned classification on temporally defined neuronal responses. See text for reference to green and red arrows. Different panels correspond to response durations (columns) and magnitudes (rows). Within each panel, different traces correspond to different jitter values. E, Time-invariant classification of responses spanning the entire analyzed duration. Different traces correspond to different firing rates. F, Time-invariant classification on a population of neurons (only 4 of 10 are shown), with responses aligned to stimulus onset. Different panels correspond to different response durations, and within each panel, different traces correspond to different response rates. G, Time-invariant decoding on a population of responses that differ in their onset times. As in F, different panels correspond to different durations and different traces correspond to different rate changes. See Materials and Methods and the text for further details.

In the first family of scenarios (see Fig. 9B), the responses of each neuron to the two stimuli differ in timing, but not in magnitude. In these scenarios, response rates are 4 Hz for both stimuli. The response onset to stimulus b begins exactly when the response to stimulus a ends. For example, for a response duration of 2 s, the response to stimulus a will take place during seconds 0–2, while the response to stimulus b will take place in seconds 2–4. In this family of scenarios, all 10 neurons in the population shared the same response definitions.

In the second family of scenarios (see Fig. 9C), we focused on the 2 s duration from the first set of scenarios and added various degrees of jitter to the response onset time. For example, a jitter of 5 s implies that the start time of responses to stimulus a will vary between 0 and 5 (with corresponding response end times between 2 and 7 s). The start time of responses to stimulus b will vary between 2 and 7 s (with corresponding response ends between 4 and 9 s).

In all other scenarios, responses to the two stimuli differed in magnitude but not in timing. For simplicity, in these scenarios, responses to stimulus a were set to 0 (i.e., the response to stimulus a was identical to the baseline rate of 2 Hz). In the scenarios shown in Figure 9D, populations differed in response rate, duration, and jitter. Response rates of individual neurons in the population were specified using a range. For example, a rate of 5 Hz implies that the response of each neuron was drawn (uniformly) from the interval 0–5 Hz above baseline rate. The response magnitude of each neuron (to stimulus b) was drawn only once and then applied to all trials.

For time-invariant classification, we first created scenarios with prolonged responses that spanned the entire 20 s poststimulus period (see Fig. 9E). Here too, the response to stimulus a was set at 0 (i.e., equal to baseline), while response magnitudes to stimulus b were randomly chosen from a specified range (uniformly).

To examine time-invariant classification on populations with shorter durations, we implemented two classes of scenarios. In the first (see Fig. 9F), the responses of neurons in the population were aligned to the beginning of the trial. In the other, the response start times of individual neurons were distributed to span the entire 20 s period (see Fig. 9G).

Results

Temporal profiles of AOB responses

We began our analysis by examining single-trial response profiles of AOB neurons. Our dataset for this analysis includes 1973 single trials from 192 neurons (391 neuron–stimulus pairs) collected during 57 recording sessions from 34 mice. Figure 1A shows an example of high-pass filtered raw electrode data and spike shapes that were extracted from it. Figure 1B shows examples of responses from three simultaneously recorded neurons to a set of nine stimuli. The examples demonstrate the variability in responses between trials, across stimuli for a given neuron, and across neurons. Figure 1C shows expanded views of the raster displays and peristimulus time histograms of the responses of two of these neurons to one of the stimuli (Fig. 1B, yellow highlights). One feature that is common to both examples and was also observed earlier (Ben-Shaul et al., 2010), is the delayed response onset on the order of 3 s. We note that time 0 corresponds to the beginning of sympathetic nerve trunk stimulation. Thus, the ∼3 s delay observed here sets an upper limit on the interval between VNO suction and the initiation of the neuronal response. Examination of the two responses also reveals a major difference between the two examples. Namely, one (Fig. 1C₁) is considerably briefer than the other (Fig. 1C₂), which does not fully return to baseline even after the 40 s poststimulus period. At least in these examples, comparison of single-trial responses within and across neurons suggests that individual neurons display characteristic temporal dynamics that do not considerably vary across different stimuli.

To quantitatively compare response dynamics across trials, stimuli, and neurons, it is necessary to parameterize the temporal evolution of the responses. To this end, we defined several temporal parameters (t₁₀, t₅₀, t₉₀, t_peak, width, and asymmetry), which are shown schematically in Figure 1D (for details, see Materials and Methods). While the selection of these specific parameters is inevitably arbitrary, together they capture key features of the responses. For example, whereas the time of the peak response is similar for both cases in Figure 1, C₁ and C₂ (t_peak: Fig. 1C₁, 4.7 ± 0.7 s; Fig. 1C₂, 5.7 ± 0.7 s, mean ± SD across trials), the time by which half of the spikes have occurred (t₅₀: Fig. 1C₁, 5.0 ± 0.5 s; Fig. 1C₂, 17.4 ± 2.3 s), and the response width (width: Fig. 1C₁, 2.2 ± 0.9 s; Fig. 1C₂, 16.1 ± 1.7 s) are markedly different (Fig. 1, complete list of temporal parameters for these examples in the legend). Key statistics of the distributions of these parameters across the population of responses are given in Table 1.

Table 1.

Key statistics of temporal parameters

	t10	tpeak	t50	t90	Asymmetry	Width
Mean ± SD	6.1 ± 3.7	14.8 ± 10.1	17.2 ± 5.7	31.8 ± 7.4	0.08 ± 0.3	15.7 ± 6.3
SEM	0.08	0.23	0.13	0.17	0.007	0.14
Median	5.2	11.8	17.6	34.6	0.08	17
Mode (1 s bins)	4	5	19	35	0	19

All values are in seconds. N = 1973 single trial responses. SD: standard deviation. SEM: standard error of the mean.

The histograms in Figure 1E show the distributions of four of these parameters for all single trials (only significant neuron–stimulus pairs are included; see Materials and Methods). Figure 1F shows all single trials sorted according to these parameters. Examination of these distributions highlights one of the most distinctive characteristics of AOB responses: their prolonged temporal evolution. Specifically, responses to a single VNO uptake episode, the unitary sampling event in the VNS, may develop over seconds and even tens of seconds (Fig. 1E,F). For comparison, in the MOS, where the unitary sampling event is the sniff, responses evolve within tens of milliseconds (Shusterman et al., 2011). Another prominent feature of AOB responses is the variability of single-trial responses, as revealed by the broad distribution of each of the temporal parameters (Fig. 1E,F).

Variability of single-trial responses

Next, we studied the variability of single-trial responses. The pattern of variability is significant, as it can fundamentally limit the decoding schemes that can be applied to derive stimulus information. For example, if response dynamics are entirely random across trials, there is little to be gained by considering fine temporal structure. Alternatively, if individual neurons reveal consistent and reliable differences for different stimuli, consideration of fine temporal structure can be highly informative, as it is in the MOS.

We first assessed the variability associated with individual neurons by plotting their mean parameter values and their SDs (Fig. 1G). Examination of the SDs in Figure 1G shows that different neurons exhibit varying degrees of response variability. Although the variability within neurons is substantial, examination of the mean and SD ranges across neurons suggests that different neurons are associated with distinct temporal parameter distributions (Fig. 1G). To test this hypothesis, we performed a one-way nonparametric ANOVA (Kruskal–Wallis test), challenging the hypothesis that parameter distributions are identical for all neurons in the population. In addition to the temporal parameters, we also tested ΔR (calculated over the 40 s following stimulus onset). Across all parameters tested, and after correcting for multiple comparisons (see Materials and Methods), p values for the rejection of the null hypotheses were extremely low [Table 2, one-way, neuron identity (ID)], indicating unequivocally that different neurons are indeed associated with distinct temporal characteristics.

Next, we expanded the analysis to test whether temporal parameter values can be attributed to particular stimuli or dilutions (i.e., intensities). To this end, we considered a subset of neurons (N = 102, dataset 1; see Materials and Methods) that were all tested with the same stimulus set: male, female, and predator urine at three different dilutions (1:100, 1:30, 1:10). This dataset allowed us to compare the effects of neuron, dilution, and stimulus on the temporal profiles of responses. A three-way ANOVA using these factors was conducted on all temporal parameters as well as on ΔR. The analysis (Table 2, three way, neuron ID), confirmed that neuron identity was a highly significant factor for all temporal parameters. In contrast, the only significant effect of the factors dilution and stimulus was a small effect of stimulus identity on the parameter t₁₀. In addition, the analysis showed that different neurons were associated with significantly different ΔR values (Table 2, neuron ID). After correcting for multiple comparisons, neither stimulus nor dilution had a significant main effect on firing rates. Together, the results shown in Table 2 clearly indicate a strong effect of neuron identity on temporal response features.

Temporal response features of individual neurons are largely stimulus independent

The previous analyses (Table 2) revealed that stimulus identity and dilution do not exert a consistent effect on temporal response profiles across the population of neurons. However, this does not rule out the possibility that temporal response profiles of individual neurons are stimulus dependent. This is the case in the main olfactory system, where fine (subsniff) temporal features of individual neurons depend on the presented stimulus (Cury and Uchida, 2010; Shusterman et al., 2011; Gschwend et al., 2012). To test whether this is the case in the AOB, we focused on neurons that showed a significant response to two or more stimuli and conducted pairwise comparisons of temporal parameter distributions associated with pairs of stimuli (Wilcoxon rank-sum test). We then counted the number of comparisons that yielded statistically significant differences (p < 0.01) and applied the binomial distribution to determine whether the number of such cases exceeded that expected by chance.

The results of this analysis indicate that none of the six temporal parameters differed in a larger number of cases than expected by chance (Table 3, same neuron, different stimuli). The outcome was essentially identical when we limited the analysis to pairs of stimuli from distinct sources (Table 3, same neuron, qualitatively different stimuli). For comparison, when the same analysis was applied to pairs of responses from distinct neurons, the number of significant p values far exceeded that expected by chance for all temporal parameters (Table 3, different neurons). Notably, differences in firing rate modulations were prominent among distinct neurons and also, though to a lesser extent, between pairs of stimuli for individual neurons.

In conclusion, although our analysis does not rule out the existence of stimulus-dependent temporal profiles, it does indicate that temporal response profile variability between neurons far exceeds that between stimuli for a given neuron. Thus, we conclude that while AOB neurons often display stimulus-dependent firing rate changes, stimulus-specific temporal response profiles are rare.

Optimal windows for stimulus detection and discrimination

The temporal parameters describing individual responses (t₁₀, t₅₀, t₉₀, t_peak, width, and asymmetry) provide a useful metric to characterize and detect differences between responses, but not for decoding neuronal activity. Indeed, most of these features cannot be determined in real time since they require knowledge of the time by which the response has ended. For rate-based decoding, whether at fine or coarse temporal resolutions, optimal epochs for stimulus detection and discrimination are dictated by the temporally evolving spike rates. More specifically, the relevant metrics are signal magnitudes and their variability, compared with baseline rates (for stimulus detection) and to responses elicited by other stimuli (for stimulus discrimination).

To assess which temporal windows are most informative, we measured the discriminability of firing rate distributions (stimulus-induced vs prestimulus baseline activity) in windows of varying latencies and durations (Fig. 2A) using the auROC, a common approach to characterize discriminability between two distributions (Fawcett, 2006). auROC scores of −0.5 or 0.5 indicate perfect discrimination, whereas a score of 0 indicates that the two distributions cannot be discriminated (see Materials and Methods). The sign of the auROC score is determined by whether the firing rates associated with the stimulus are smaller (negative auROC) or larger (positive auROC) than the baseline distribution. In our analysis, window durations were varied from 0.5 to 40 s (with 1 s increments for windows between 1 and 40 s), while latencies were varied from 0 to 39.5 s (at 0.5 s increments). As in the above analyses, time 0 corresponds to stimulation of the sympathetic nerve trunk. Only auROC scores that were determined to be significant are shown in this analysis (see Materials and Methods).

Figure 2B shows auROC scores for individual neuron–stimulus combinations (Fig. 2B₁,B₅ show the same cases shown in Fig. 1C). Each example includes the responses of a neuron to five repeated presentations of a given stimulus (left), and the corresponding matrix of auROC scores (right). Except for the last example (Fig. 2B₆), which shows a rate suppression response, all other examples are of rate elevations. Matrix pixels represent stimulus versus baseline auROC scores in specific latency–duration windows. Thus, pixels along lines parallel to the main diagonal (Fig. 2A, cyan lines) correspond to windows that end at the same time. In each of the cases in Figure 2B, one individual window, selected among those providing optimal detection, is indicated on the matrix (yellow arrows) and on the corresponding raster display (blue shading).

Examination of the individual examples shows that, generally, there is a range of temporal windows that allow reliable discrimination between baseline and response distributions. This is expressed by the continuous blocks with high discriminability scores in the latency–duration space (Fig. 2B₁–B₅). Although the regions associated with high detection scores are not identical for all cases, the analysis confirms that long-duration windows (e.g., 30–40 s), as used in our previous analyses (Ben-Shaul et al., 2010; Kahan and Ben-Shaul, 2016), generally provide good detection scores. The obvious drawback of long windows is the latency by which detection can be achieved. Thus, if the premium is on achieving rapid decision, the best windows are those that are close to the origin (Fig. 2A).

Optimal windows for detection and discrimination across the population of neurons

Going beyond specific examples, we examined the average detection and discrimination performance as a function of window latency and duration. We stress that in this analysis, we are still studying detection and discrimination performances of individual neurons. Thus, the results in this section represent averages of individual cases such as are shown in Figure 2B (across 510 neuron–stimulus pairs from 252 neurons). To compare detection associated with rate increases to that associated with rate decreases (relative to baseline), we separated the analysis of these two response types. The results for rate increases are shown in Figure 3A, where auROC scores can range between 0 (no ability to discriminate) and 0.5 (perfect discrimination). Examination of Figure 3A indicates that, on average, the best windows are those that begin around stimulus onset and range between 15 and 30 s in duration. This indicates that while very long duration windows (e.g., 30–40 s) provide near-optimal detection performance, considerably briefer windows can also suffice. Nevertheless, there are constraints on the minimal window duration, as windows terminating before 5 s following stimulus onset provide very poor performance. This is expected since at this delay, most responses have only begun (Fig. 1). Generally, very brief windows (∼1 s) are not associated with high detection scores.

The analysis of rate decreases is shown in Figure 3B. Note that the color scale has been reversed to allow comparison with detection using rate increases (Fig. 3A). Comparison of panels A and B in Figure 3 shows that at virtually any window, rate increases provide better detection than is possible with rate decreases. The exceptions are the very brief windows associated with rate decreases, which are due to the nonnegligible number of short epochs lacking any spike counts. Figure 3C shows, for each temporal window, the fraction of responses in which the auROC score was positive (i.e., response rates were higher than baseline rates). Clearly, with the exception of the very brief windows, the large majority of windows was strongly dominated by rate increases. Thus, stimulus detection by AOB activity is much more effective using rate increases compared with rate decreases, and is consistent with the very low baseline rates of AOB neurons (Luo et al., 2003; Ben-Shaul et al., 2010). We note that the patterns evident in the leftmost columns of Figure 3A are remarkably similar to those in the study by Luo et al. (2003, their Fig. 2B), which shows the population level profiles of increased firing rate responses in freely exploring mice.

We next characterized the optimal epochs for discriminating between two stimuli. The results of this analysis are shown in Figure 3D. The analysis includes all cases of individual neurons that exhibited a significant response to multiple stimuli (N = 597 pairs, from 115 neurons). Unlike the case of stimulus detection, here the designation of the reference and the signal distribution is arbitrary, and it is thus irrelevant to distinguish between rate increases and decreases. Comparison of Figure 3A,B with Figure 3D indicates that auROC scores for stimulus discrimination are considerably lower than those for stimulus detection. This is expected since stimulus-evoked firing rates are generally more distinct from baseline activity than they are from responses to other stimuli. As with stimulus detection, discrimination among stimuli is poor at very brief windows and at short durations relative to stimulus onset.

Fine temporal resolution does not improve decoding

In the previous sections, we examined individual neurons separately. However, as we and others have shown (Tolokh et al., 2013; Kahan and Ben-Shaul, 2016), decoding of natural stimulus information from AOB activity is best achieved with a population code. Thus, we next tested whether consideration of fine temporal structure aids the decoding of stimulus identity from ensembles of AOB neurons. For this analysis, we used a population of 84 neurons (recorded during 21 sessions, from 13 BALB/C male mice, 1–12 units in each session). We presented three stimuli (male, female, and predator urine) at three different dilutions (1:100, 1:30, and 1:10). Classifiers are confronted with the task of distinguishing between two different stimuli. This is analogous to the task of discrimination (Fig. 3D). Complicating the task of the classifiers, each stimulus could be randomly selected from one of the three different dilutions (Fig. 4A), reflecting the realistic scenario in which stimuli must be recognized and discriminated over a range of dilutions (Ben-Shaul, 2015).

To quantify the benefits afforded by considering temporal structure, we compared the performance of linear decoders (perceptrons) with access to neuronal responses at varying temporal resolutions (Fig. 4B). We state at the outset that we are not suggesting that decoding of AOB activity is actually realized by a linear classifier. However, such classifiers allow quantification of the decoding capacity of the population as a function of temporal resolution and the number of neurons, and thus provide very useful analytical tools.

At the coarsest resolution (Fig. 4C), the response of each neuron is characterized by a single value, which is the mean firing rate in the 40 s poststimulus epoch. In this scenario, a classifier receives a total of 84 inputs, one from each of the neurons in the population. At finer resolutions, the poststimulus period is divided into several temporal bins (Fig. 4D). At the finest resolution, the poststimulus period is divided into 0.5 s bins, so that each classifier receives 80 inputs (40/0.5) from each of the neurons. Every classifier is trained to discriminate one pair of stimuli from another (male vs female urine, female vs predator urine, or male vs predator urine). Classifiers were trained and tested with random single-trial PRVs. In all our analyses, the training set comprises 20 PRVs (10 from each stimulus), while the test set includes 10 PRVs (five from each stimulus). To account for variability in the selection of the training and testing sets and in the training procedure itself, each classification is conducted 1000 times. Finally, for each temporal resolution, classifier performance is averaged across the three pairwise classifications (male vs female, female vs predator, and male vs predator). Thus, the performance of classifiers is reported as an average across repetitions and across the three comparisons.

In our first classification scheme, we used the entire 40 s window and partitioned it into temporal bins of various sizes. We denoted this scheme as time-binned decoding (Fig. 5A). Classification performance under this scheme for various temporal resolutions is shown in Figure 5B. This analysis shows that although there was a slight increase in performance from a 40 s period (i.e., one window) to a 20 s resolution (i.e., two windows), consideration of finer temporal resolution generally leads to decreased classifier performance. This result may seem surprising given that classifiers operating at finer resolutions include all the information present in coarser resolutions. In other words, fine-resolution classifiers could simply disregard fine temporal structure by summing spike counts from multiple windows. However, the drop in performance occurs because spike count variability in smaller windows is higher, thus limiting the ability of the classifier to learn and generalize. Similar trends were observed with a nonlinear classifier (support vector machines with a quadratic kernel). Thus, the drop at higher resolutions is not a peculiarity of linear decoders. We note that the general features in Figure 5B are also apparent in each of the three pairwise comparisons, and even when making direct comparisons between stimuli without pooling across dilutions (data not shown).

The effect of overtraining on small windows does not rule out the possibility that classifiers can nevertheless exploit the temporal structure in the data. To test this, we eliminated the temporal structure in the data by shuffling data from different time points before training and testing. Only time bins from a given neuron and trial were shuffled with each other, so that neuron identity was not affected by shuffling. This manipulation led to a clear, but modest decrease in performance (Fig. 5C). Shuffling the test set only (after training with unshuffled data) led to a very similar decrease in performance (data not shown). These analyses indicate that classifiers can indeed use temporal information in the data, but that the benefits are minor. In contrast, when shuffling is applied to different neurons (while keeping the temporal identity unchanged), performance falls nearly to chance levels (Fig. 5D), indicating that classifiers indeed rely on the differences between individual neurons to distinguish among the stimuli. When neuron identity is shuffled only in the test set (data not shown), performance falls exactly to chance levels.

Classifier weights assigned to each input (defined by the neuron and the time since stimulus onset) are shown in Figure 5E. Each image corresponds to one temporal resolution, while across all resolutions, rows represent neurons. The weights shown here were derived by averaging weights across 100 repeated classifications (weight distributions were highly correlated among different classification repeats; data not shown). Comparison of the different plots shows a similarity in the weights assigned to a given neuron under various resolutions. Inspection of the weights assigned at higher resolutions shows that for many (but not all) individual neurons, similar weights are assigned across multiple time bins.

An important technical issue in our recordings is that the neuronal population used for classification analysis is a “virtual population,” with data pooled across different sessions (see Materials and Methods). This implies that if the trial-to-trial variability in response features is correlated across neurons, then pooling responses from different sessions can overestimate the degree of temporal jitter between neurons. This will (negatively) affect all our decoding schemes (Figs. 5, 6, 7, 8), which rely on simultaneous sampling of neuronal activity. Yet, decoding with finer resolutions will be effected to a larger extent than decoding with coarser resolutions. To assess the potential effect of this limitation, we analyzed the correlations between temporal properties of simultaneously recorded neurons. Our analysis indicates that although the median values of the pairwise correlation coefficients are often significantly larger than 0 (and also larger that in shuffled data; see Materials and Methods), the deviations from 0 are small (Table 4). For example, the highest median value of the correlations is for the t₉₀ parameter, which assumes a value of 0.129. We also note that in all our analyses, activity that was recorded simultaneously was kept together in the PRVs. Thus, we conclude that our recordings and analysis may to some extent underrepresent the benefits of decoding using fine temporal resolution, but if so, this is a minor effect.

Table 4.

Trial-to-trial correlation of temporal response parameters of simultaneously recorded neurons

	t10	tpeak	t50	t90	Asymmetry	Width
Median different from zero? (p value)	0.061	0.0004	4.11E-05	0.0004	0.041	0.613
Median different from shuffled distribution? (p value)	0.054	0.0002	7.16E-06	0.0002	0.024	0.638
Median correlation coefficient	0.066	0.114	0.156	0.129	0.075	0.061

Trial to trial correlations among temporal parameters of simultaneously recorded neurons in data set 1.

Evolution of classifier performance with time

Regardless of their temporal resolution, the classifiers considered above sample activity over the entire 40 s poststimulus period. This is clearly a very long time period, even for a sensory system that is not designed to mediate rapid responses. This suggests another potential benefit of using finer temporal resolutions, which, despite their lower performance, could provide classification at earlier time points. We therefore next studied how classification performance evolves with time.

We begin with a scheme that we denote as cumulative time-binned classification (Fig. 6A). Results of classification using this scheme, as a function of time, for different temporal resolutions, are shown in Figure 6B. Across all temporal resolutions, the first 10–15 s mark a rapid rise in classification performance, after which it remains relatively stable, with a mild drop in some cases. This indicates that the later 20 s period is considerably less informative than the first 20 s period. Note that the performance of each classifier at the last time point (40 s), converges with that obtained in the time-binned scheme (Fig. 5B). Consistent with Figure 5B, here too, at all time points, larger windows outperform finer windows. This last observation suggests that at any given time point, it may be most advantageous to simply consider a single integration window starting at time 0.

To test this prediction, we next applied a decoding scheme, denoted as the cumulative single window (Fig. 6A), in which at any given time point, classifiers receive the total spike count up to that time. Thus, all temporal windows begin at time 0, increase in 1 s increments, and end at 40 s. As shown in Figure 6B, at virtually any given time point, classification using the cumulative single-window scheme outperforms that obtained with time-binned classification. As with time-binned classification, also under the cumulative single-window scheme, it is advantageous to sum spike counts up to 10–15 s, but further integration does not provide additional improvement in classification.

Under the cumulative single-window scheme, at any given time, values reflect the entire period starting at time 0. However, specific windows not starting at time 0 may potentially yield even better performance. To test this, we applied yet another decoding scheme in which classifiers have access to spike counts in single sliding windows of various durations (Fig. 6A). The performance of these sliding window classifiers, for various window lengths, is shown in Figure 6C. The analysis shows that some sliding windows yield better classification than possible using the cumulative single-window scheme. The highest performance achieved with this scheme (∼84%) is associated with a window of 10 s, which ends at 15 s following stimulus onset. Thus, specific integration windows that do not begin with stimulus onset provide an improvement, albeit modest, over classifiers that begin integration at the time of stimulus onset.

An important observation regarding the sliding window classifiers, especially those using larger integration windows, is that they achieve well above chance classification performance during the entire 40 s window. However, even for a given integration window size, different time points may be associated with different classifiers (i.e., different weights). Thus, to exploit the sliding window scheme across the entire 40 s duration requires dedicated classifiers for each time lag. This does not seem like an economic or efficient approach for decoding stimulus information, and this led us to consider yet another decoding scheme.

Time-invariant stimulus classification

We next investigated the performance of classifiers when the requirement of knowing the exact time of stimulus delivery is relaxed. Specifically, we considered an extreme scenario, in which decoders have access to a single time window of fixed duration, sampled at any arbitrary time within the entire 40 s period following stimulus delivery. This time-invariant decoding scheme is shown in Figure 7A. We note that the selection of the PRVs ensures that there is no overlap whatsoever between windows in the training and test set (see Materials and Methods).

The performance of classifiers as a function of the integration window duration is shown in Figure 7B, which illustrates that longer integration windows provide higher classification performance. The decline in the performance of classifiers with smaller windows is due to the fact that these are associated with more variability. Not only are firing rate estimates more variable within small windows, but there are also more small windows than there are large windows. Figure 7B also shows, for comparison, the performance achieved under the time-binned scheme at a resolution corresponding to the integration window (blue squares). In addition, the best classification performance achieved using sliding window of the same size is shown (Fig. 7B, red squares).

A more detailed comparison between the time-invariant and the sliding window schemes can be seen in Figure 7C, which shows the performance of both types of classifiers, for various integration window durations, over a linear horizontal (time) axis. Comparison of the sliding window and the time-invariant classifiers highlights the advantage that can be gained by consideration of stimulus onset time. Figure 7C also shows the diminishing benefits of both classification schemes as the integration window is increased. Specifically, for time-invariant decoding, there is a clear benefit to increase windows to about 5 s, with a continuing, but modest, benefit at longer durations. For the sliding window classification, it is advantageous to increase the window to ∼4 s, but subsequent increases provide only a small, if any, benefit in performance.

Classification depends on a population of neurons

Thus far, all classifiers, and the time-invariant classifiers in particular, had access to the entire population of neurons in the dataset (N = 84). This choice was based on the implicit assumption that decoding requires a population code. To test this assumption directly, we next analyzed the dependence of the time-invariant classifiers on the number of polled neurons. Specifically, we sequentially removed individual neurons from the classifier, until only one remained. At each cycle, the neuron to which the classifier assigned the smallest (absolute) weight was removed (Kahan and Ben-Shaul, 2016), so that only the most informative neurons remained in later cycles.

The results of this analysis, across various integration window durations, are shown in Figure 8A. The maximal values, attained with all neurons, are by design equivalent to those shown in Figure 7B (brown bars). Across all window lengths, performance rapidly decreases as the number of neurons falls below a certain value. The tradeoffs among integration window duration, population size, and classifier performance are shown in Figure 8B. The traces show that for any given performance criterion, the number of required neurons increases as the integration window size is decreased. Thus, we conclude that rapid and accurate time-invariant discrimination requires the integration of information across ensembles of AOB neurons.

Analysis of the features that influence performance of temporal decoding schemes

Classification performance under the various decoding schemes analyzed here ultimately depends on the response properties of the heterogeneous AOB population sampled. To gain insight about the essential response features that determine classifier performance, we simulated various scenarios of neuronal activity and used the fake data from these simulations to classify neuronal activity. Importantly, the classifier-generated data were subjected to the very same analysis functions applied to the data from the AOB. The MATLAB-based simulator can be used to generate a wide range of scenarios and to analyze them. The software and documentation is available at (https://github.com/yorambenshaul/neuronal_response_simulator). See also Materials and Methods for details on the scenarios simulated here.

The simulator produces single trial responses of a population of neurons to two different stimuli (Fig. 9A). Each neuron within the population is characterized by a baseline firing rate and the response to each of two stimuli. Spontaneous activity rates in all simulations are 2 Hz. The response is a constant firing rate change during a single temporally defined window, and the entire poststimulus period is 20 s long. Neuronal responses to the two stimuli may differ in their rate, their timing, or in both aspects. In addition, single-trial responses may be associated with trial-to-trial variability (jitter) in onset time and duration. Although the simulated responses and the neuronal populations are much simpler than those of real neurons, they already give rise to a huge number of scenarios and conditions. Here, we focus our analysis on two key classification schemes explored here, namely, the time-binned (Fig. 5) and the time-invariant (Fig. 7) schemes.

We began with a family of scenarios in which the responses of each neuron to the two stimuli differs in timing, but not in magnitude. Thus, the expected number of action potentials generated by each neuron during the entire (20 s) response period is identical for both stimuli. A schematic representation of such responses, for two different response durations (0.5 and 5 s) is shown in Figure 9B. The schemes only depict the responses of one neuron in the population, but in all simulations, populations comprise 10 different neurons. For this analysis, response rates were set to 4 Hz. The results of time-binned classification on responses generated by this scenario are shown in Figure 9B, with individual traces representing different response durations. Several observations can be made from this analysis. First, for all scenarios, there is a certain temporal resolution below which only chance-level performance is possible. This is because at low resolutions, the responses to the two stimuli, which differ only in time course, are indistinguishable. Expectedly, the resolution that allows above-chance classification performance matches the duration of the responses, with briefer responses requiring higher resolutions. Second, longer response durations allow better classification performance. This is because the total number of spikes that distinguish responses from each other, and from baseline activity, is higher with longer windows. Finally, the optimal resolution for each case matches the response duration. This is because this specific resolution allows sampling activity from the entire response period, without any baseline activity, thus providing the best ratio between signal (response) and noise (baseline).

In all the scenarios explored in Figure 9B, responses had a definite onset time and duration (although spike timing, as dictated by the underlying rate functions, did vary across trials). To explore the effect of trial-to-trial variability in response onset, we focused on one response duration (2 s) and introduced various degrees of jitter. Timing jitter was introduced by specifying response onset times as an interval, rather than a single definite time (response durations were kept identical across all trials). A schematic illustration of the effect of applying a 5 s onset time jitter on 2 s responses is shown in Figure 9C. As can be seen from the individual traces in Figure 9C, temporal jitter clearly impairs classifier performance. This is because with higher jitter, spike count distributions in any given temporal window are more variable. Together, the analyses shown in Figure 9, B and C, in which responses to the two stimuli differ only their time course (but not rates), highlight the benefits of matching the temporal resolution to the duration of the responses.

We next considered another set of scenarios, in which responses to the two stimuli share the same temporal dynamics, but rates may differ (Fig. 9D). To successfully distinguish among stimuli, a classifier must therefore detect rate changes within a confined temporal window. In terms of response magnitude, the key values in these scenarios are the differences of the two responses from each other, and of both, from the baseline rate. For simplicity, we defined the responses to stimulus a as zero (i.e., no firing rate change from the baseline rate), and we varied both the duration and the magnitude of the response to stimulus b. Under these conditions, stimulus discrimination is equivalent to stimulus detection. The results of the classification are shown in Figure 9D, where each column corresponds to a certain response duration, and each row corresponds to a given response magnitude. Thus, each of the 15 panels in Figure 9D shows results for one specific duration/magnitude combination. See Materials and Methods for the definition of response magnitudes in this and subsequent scenarios. Finally, each panel contains four different traces, which corresponds to different trial-to-trial temporal jitters (in the response onset time to stimulus b). Examination of these panels shows that, as expected, at any a given response magnitude, longer responses yield better classification, simply because they result in more spikes and hence higher discriminability. The same reasoning explains the improved performance with higher response magnitudes, at any given response duration. As in Figure 9B and C, inspection of Figure 9D reveals that each response duration is associated with an optimal temporal window for classification. Without temporal jitter (Fig. 9D, black traces in each panel), this resolution matches the response duration (Fig. 9D, red arrow for one example). However, when jitter is introduced, the optimal resolution shifts to coarser windows (Fig. 9D, green arrow for one example). The same effect can also be seen in Figure 9C. Thus, in addition to confirming the expected beneficial effects of increasing response duration and magnitude, these simulations demonstrate that temporal jitter has two effects. First, it generally impairs classifier performance. Second, it shifts optimal resolutions to coarser values.

Next, we explored the performance of time-invariant classifiers. We began with what appeared to be the most favorable conditions for time-invariant decoding, namely, uniform responses that span the entire 20 s period (Fig. 9E). Each of the traces in Figure 9E shows the performance of time-invariant classifiers on data from populations with different response magnitudes. As expected, at any given integration window, higher response rates yield better classification. Furthermore, as observed with real AOB data, for each population, longer integration windows provide better classification. Note that the maximal integration window is 10 s, as time-invariant classification is applicable only to intervals that are smaller than the entire 20 s response period.

Finally, we evaluated time-invariant decoding on data from populations with less prolonged responses. For each response duration (2, 5, and 10 s), we distinguished between two cases. In one (Fig. 9F), the responses of all neurons in the population were aligned to the same time. In the other (Fig. 9G), response start times were staggered to span the entire 20 s response period. For each duration, we examined four different response magnitudes. The results of time-invariant classification on these analyses indicate that longer integration windows, higher rates, and longer response durations, result in higher classification performance. These findings are not surprising, as each of these factors acts to enhance the differences between responses to the two stimuli. However, the difference between classification with the aligned (Fig. 9F) and the staggered (Fig. 9G) populations is perhaps less obvious. Comparison of these two classes of scenarios reveals that even when the total number of spikes is kept constant, staggered responses provide higher classification performance. This is because they effectively distribute the information about stimulus identity over the entire response window, highlighting the benefits that can be gained by populations with heterogeneous (in this case temporal) response properties.

Viewed together, these simulations provide important insights regarding the optimal schemes for decoding activity of AOB neurons. Our analysis of response properties of individual neurons (Table 3) indicated that, unlike the scenario examined in Figure 9B, temporal response dynamics of AOB neurons are not stimulus dependent. Furthermore, we have shown that responses are often prolonged and associated with high trial-to-trial variability (Fig. 1G). Combined with previous studies showing the low rates of AOB mitral-tufted cell responses (typically <10 Hz; Hendrickson et al., 2008; Ben-Shaul et al., 2010), these features reduce the benefits of considering finer resolutions and favor coarser temporal windows for classification. Finally, the observation that response times of individual neurons are variable and often prolonged (Fig. 1C₂), is consistent with the feasibility of a time-invariant decoding scheme.

Discussion

In this manuscript, we analyzed the temporal response properties of AOB mitral-tufted cells. We showed that temporal response features are neuron specific, variable on a trial-by-trial basis, and, for individual neurons, weakly dependent on stimulus properties. Examining several decoding schemes, we first showed that partitioning the entire poststimulus period into finer windows yields reduced performance. Next, using single integration windows of various durations and onset times after stimulus uptake, we find that optimal classification can be achieved within 10–15 s after stimulus onset. Since such classification requires knowledge of stimulus onset times, and because VNO uptake is inherently variable, we investigated decoding schemes without information about stimulation timing. While inferior to classification using temporally defined windows, such time-invariant decoding provides above-chance performance with windows as brief as 0.5 s. Finally, we conducted simulations to identify the key response features that affect classification under various decoding schemes. These simulations confirm that the sluggish and variable responses of AOB neurons do not favor decoding using fine temporal windows. However, the heterogeneous and prolonged nature of AOB responses is consistent with the time-invariant decoding schemes. Consequently, while consideration of fine temporal structure markedly improves stimulus decoding using mitral-tufted cell responses in the MOB (Chaput, 1986; Cury and Uchida, 2010; Shusterman et al., 2011; Smear et al., 2011), this is not the case in the AOB.

Temporal and physiological differences between the MOS and VNS

Why are AOB dynamics so slow? Assuming that fast and temporally reliable responses are costly (Sterling and Laughlin, 2015), the question actually is: “why should they be any faster?” Ultimately, the dynamics of any sensory system depend on the physical nature of the detected stimulus (Dusenbery, 1992). In “conventional” olfaction, the transmission of chemosensory information requires the transport of molecules from source to receiver via diffusion or flow, and is thus slower and less spatiotemporally predictable than the transmission of auditory or visual information (Bradbury and Vehrencamp, 2011). These features favor long sampling times and explain the slow rates of chemosensory information transmission compared with auditory and visual channels (Perge et al., 2012). Gustatory system response dynamics (Moran and Katz, 2014) are generally slower than in the MOS, but faster than in the VNS, potentially reflecting the need to rapidly identify harmful stimuli.

In mice and likely other rodents, the VNS is associated with sensation of other organisms (Isogai et al., 2011). This can be accomplished via either the detection of deposited secretions or direct interaction with other individuals. Although direct contact with the substrate reduces the variability associated with transfer of molecules via air, temporal dynamics do not provide information about the stimulus itself, whether a secretion or another individual. This is in contrast to auditory and visual signals, and even to MOS-based olfaction, which can be used for tracking (Dusenbery, 1992).

Another unique aspect of VNS function is stimulus uptake. In the MOS, stimulus sampling is coupled to breathing and can thus reach frequencies of 10 Hz (Wachowiak, 2011), dictating the dynamics of sensory representations in this system (Spors et al., 2006). The situation in the VNS differs in several ways. First, before reaching the VNO duct, dissolved stimuli must traverse the nasal cavity, a process that can impose temporal delays and variability. Then, VNO suction itself is a slow process operating over seconds (Meredith and O'Connell, 1979; Meredith, 1994). Finally, once stimuli reach the VNO duct opening, the strength and time course of suction may depend on blood pressure and sympathetic tone, factors that can further affect the amount and time course of stimulus actually reaching sensory neurons.

Considering the costs of transmission with high rates (Sterling and Laughlin, 2015), these limitations in early sensory processing disfavor fast VNS dynamics in the brain. Notably, temporal differences between the MOS and the VNS are not limited to stimulus uptake, but also involve the intrinsic physiological properties of neurons. For example, vomeronasal sensory neurons show highly variable spontaneous activity, further limiting the reliability of information transmission (Arnson and Holy, 2011). Furthermore, firing rates of AOB mitral-tufted cells are considerably lower than their MOB counterparts (Luo et al., 2003). This is significant since rapid responses are necessary for conveying fast temporal dynamics. Finally, the physiological time constants of AOB neurons are considerably slower than their MOB counterparts (Zibman et al., 2011; Shpak et al., 2012; Zylbertal et al., 2015). Notably, the intrinsically slow temporal course of AOB mitral-tufted cells can be viewed as an adaptation aimed to compensate for the uncertainty in stimulus uptake (Fig. 9C,D). Thus, the slow dynamics of AOB mitral-tufted cells could effectively implement a “smoothed” representation of the sensory stimulus. It would be interesting to know whether VNS dynamics in other species, such as snakes, that use the VNS for tracking prey (Halpern and Kubie, 1980) are faster than those observed in mice.

Implications for decoding stimulus information from AOB activity

In our previous analyses, we quantified neuronal responses over prolonged (40 s) windows after stimulus onset (Kahan and Ben-Shaul, 2016). Our present analysis shows that in terms of classification accuracy, partitioning the poststimulus period into smaller time bins does not provide a benefit. However, in terms of decision time, prolonged windows are disadvantageous. Indeed, similar classification performance can be achieved considerably earlier (∼10 s) using a single integration window starting at stimulus onset. A further, albeit minor, improvement is obtained with shorter windows beginning with some delay after stimulus onset.

It may come as a surprise that temporal binning does not improve decoding. After all, fine-binned data are at least as informative as nonbinned data, and finer resolutions could allow adjustment of classifier weights (Fig. 5E) for each neuron to match its optimal temporal decoding window (Fig. 2). That such improvement is not observed here indicates that spike counts of AOB neurons, with their low rates and variable timing, are not sufficiently reliable to allow accurate classifier performance within small temporal bins. Indeed, our analyses indicate that abolishing temporal structure leads to only a minor decrement in performance. Notably, the limitation of using small-duration windows is not due to the specific classifiers used here, as the application of nonlinear classifiers (support vector machines with quadratic Kernels; data not shown) results in even poorer performance (likely due to the enhanced ability of such classifiers to overfit the training set).

Although we highlighted the variable nature of stimulus uptake, it may well be that downstream recipients of AOB activity have reliable information about stimulus timing. One possibility is via an “efferent copy” of the pumping signal. Another option is that stimulus-induced neuronal activity will in itself signal the onset of sensory activity. This could be read out by the summed activity of large populations, perhaps of nonselectively responding units, or alternatively, by local field potentials patterns (Leszkowicz et al., 2012; Tendler and Wagner, 2015; Pardo-Bellver et al., 2017). Recently, ultra-slow AOB oscillations were described by us and others (Gorin et al., 2016; Zylbertal et al., 2017). However, the typically slow time course and neuron-specific nature of these oscillations render them less appropriate for providing information about stimulus uptake.

The variable nature of stimulus onset, and the minor decrements following temporal shuffling of the data, led us to propose and test the feasibility of time-invariant classifiers, which do not rely on knowledge of exact stimulus onset time. Although such time-invariant decoders achieve lower performance than temporally sensitive decoders, they are simple (requiring only one input from each neuron) and can achieve above-chance performance within windows as brief as 0.5 s. Furthermore, their strong dependence on the number of neurons in the population implies that considerable improvement in classification accuracy and decision time could be gained by incorporating more neurons. Previous work by others (Tolokh et al., 2013), and by us (Kahan and Ben-Shaul, 2016), indicates that population-level decoding of AOB activity is necessary for overcoming multiple sources of stimulus-associated variability. Here, we extend this notion and suggest that population-level decoding can also overcome variability resulting from the unique mode of VNS stimulus uptake.

While we explored various decoding schemes, we clearly cannot determine which of these is actually implemented in the mouse brain. Indeed, different downstream recipients of AOB activity may use distinct decoding schemes, depending on which functions they control. Likewise, AOB neurons with different response properties may be read by distinct targets. For example, faster-responding neurons may be more appropriate for rapid decoding using short windows, and perhaps for mediating behavioral responses occurring over seconds (Stowers et al., 2002), while prolonged responses may be appropriate for controlling slower endocrinological processes (Bruce, 1959). The AOB may include functionally distinct populations of AOB neurons, with characteristic temporal features. Although our recordings do not distinguish between different AOB populations (e.g., those sampling from the anterior vs the posterior AOB), future studies could reveal whether particular subpopulations display characteristic response dynamics. Determining how information is actually decoded is a challenging goal, which might be addressed by combining artificial stimulation of AOB neurons with behavioral analyses.