The Neural Correlates of Hierarchical Predictions for Perceptual Decisions

Abstract

Sensory information is inherently noisy, sparse, and ambiguous. In contrast, visual experience is usually clear, detailed, and stable. Bayesian theories of perception resolve this discrepancy by assuming that prior knowledge about the causes underlying sensory stimulation actively shapes perceptual decisions. The CNS is believed to entertain a generative model aligned to dynamic changes in the hierarchical states of our volatile sensory environment. Here, we used model-based fMRI to study the neural correlates of the dynamic updating of hierarchically structured predictions in male and female human observers. We devised a crossmodal associative learning task with covertly interspersed ambiguous trials in which participants engaged in hierarchical learning based on changing contingencies between auditory cues and visual targets. By inverting a Bayesian model of perceptual inference, we estimated individual hierarchical predictions, which significantly biased perceptual decisions under ambiguity. Although “high-level” predictions about the cue–target contingency correlated with activity in supramodal regions such as orbitofrontal cortex and hippocampus, dynamic “low-level” predictions about the conditional target probabilities were associated with activity in retinotopic visual cortex. Our results suggest that our CNS updates distinct representations of hierarchical predictions that continuously affect perceptual decisions in a dynamically changing environment.

SIGNIFICANCE STATEMENT Bayesian theories posit that our brain entertains a generative model to provide hierarchical predictions regarding the causes of sensory information. Here, we use behavioral modeling and fMRI to study the neural underpinnings of such hierarchical predictions. We show that “high-level” predictions about the strength of dynamic cue–target contingencies during crossmodal associative learning correlate with activity in orbitofrontal cortex and the hippocampus, whereas “low-level” conditional target probabilities were reflected in retinotopic visual cortex. Our findings empirically corroborate theorizations on the role of hierarchical predictions in visual perception and contribute substantially to a longstanding debate on the link between sensory predictions and orbitofrontal or hippocampal activity. Our work fundamentally advances the mechanistic understanding of perceptual inference in the human brain.

Introduction

When dealing with complex and volatile environments, agents are faced with uncertainties introduced by imprecise sensory signals (“perceptual uncertainty”), the known stochasticity of predictive relationships within a stable environment (“expected uncertainty”), or changes in the statistical properties of the environment that compromise predictions based on previous experience (“unexpected uncertainty”; Yu and Dayan (2005)).

To make adaptive inferences about the causes of uncertain information, the brain recurs to learned predictions, which are thought to match the hierarchical structure of the world (Friston, 2005). For instance, when estimating the flight trajectory of the shuttlecock during a badminton match, the current shuttlecock position depends on previous shuttlecock positions and this dependence of current on previous positions in turn depends on the current wind situation. Sensory signals indicating the current shuttlecock position may be noisy (e.g., due to partial occlusion), resulting in “perceptual uncertainty”. Furthermore, expected uncertainty arises from the known irregularity of the shuttlecock trajectory within stable wind conditions, whereas unexpected uncertainty results from changes in wind conditions that affect the relation between successive shuttlecock positions. To deal with these uncertainties, a badminton player cannot only rely on sensory signals generated by the shuttlecock, but also requires a “high-level” prediction about the likely shuttlecock trajectory given the current wind condition, which he or she can then use to generate a “low-level” prediction about the current shuttlecock position based on previous positions. Here, we investigated how such hierarchically related predictions are updated and maintained in the brain.

Hierarchical predictions can be elegantly formalized by Bayesian predictive coding. Bayesian theories propose that our brain entertains a predictive model of the environment, enabling inference and learning under uncertainty (Knill and Pouget, 2004; Yu and Dayan, 2005; Behrens et al., 2007; Hohwy et al., 2008; Nassar et al., 2010; Payzan-LeNestour et al., 2013). These perspectives are tightly related to hierarchical predictive coding schemes (Rao and Ballard, 1999; Lee and Mumford, 2003), which assume that predictions are serially implemented across hierarchical levels and that prediction errors are generated in cases of mismatch between predictions and incoming signals. Please note that, here, we do not use the term “predictive coding” in its narrow sense for the specific instantiation of top-down predictions proposed by Rao and Ballard (1999), but in its broader sense referring to hierarchical predictive models aiming at the minimization of prediction errors (Clark, 2013) or free energy (Friston, 2005).

To investigate the neural implementation of hierarchical predictions, we devised a crossmodal associative learning task (Fig. 1, Schmack et al. (2016)) in which participants made inferences about volatile cue–target associations. In brief, we presented participants with flashing dot quartets that elicited the perception of either clockwise (CW) or counterclockwise (CCW) tilt motion. These dot quartets were preceded by auditory cues that probabilistically predicted the tilt direction of the upcoming visual target. Over time, observers learned the relation between auditory and visual stimuli, whereas cue–target contingencies changed unpredictably at times unknown to the participants. Crucially, perceptually ambiguous dot quartets equally compatible with CW and CCW tilt were covertly interspersed in the sequence of visual stimulation. In relation to the example of the badminton match, the CW or CCW tilting dot quartet (i.e., the visual target stimulus) corresponds to the current shuttlecock position. The auditory cue in our experiment corresponds to the current wind condition in the badminton example. That is, by introducing changes in cue–target association, our paradigm induces varying degrees of predictability of the visual target given the cue, akin to changes in predictability of the shuttlecock position due to changing wind conditions. Moreover, perceptual uncertainty is introduced by the use of ambiguous visual stimuli, akin to perceptual uncertainty caused by, for example, temporary partial occlusion of the shuttlecock.

Figure 1.

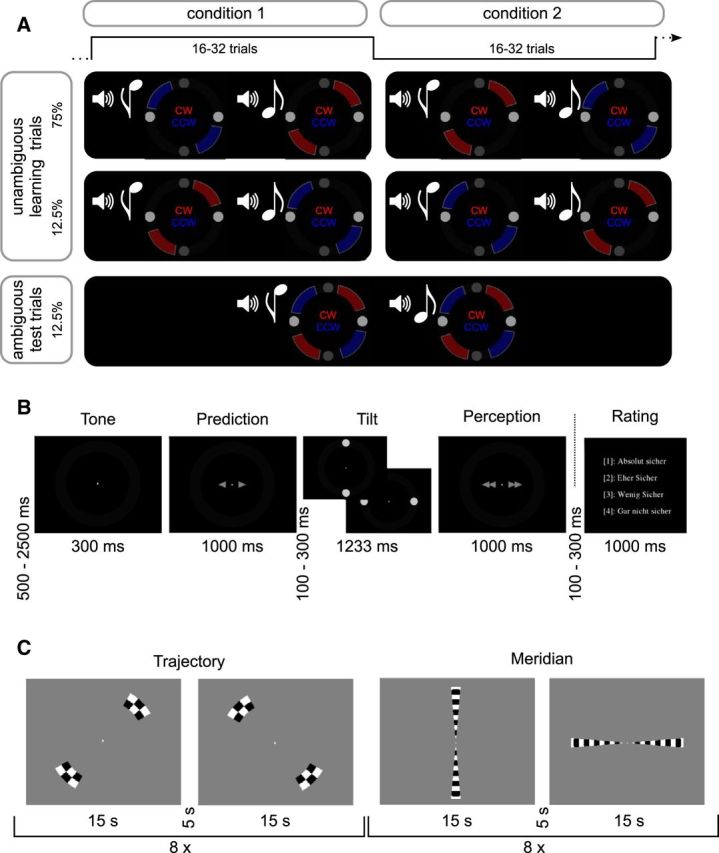
A, Experimental paradigm. In this experiment, we coupled CW (motion trajectory highlighted in red) or CCW (motion trajectory highlighted in blue) tilting dot pairs (visual targets) with high or low tones (auditory cues), which were predictive of the upcoming visual stimulus at a contingency of 75%. Importantly, the association between tones and visual stimuli reversed unpredictably for the participants every 16–32 trials. Furthermore, 12.5% of tilting dot pairs were ambiguous with regard to the perceived direction of tilt. Such test trials enabled us to quantify the influence of predictions formed during crossmodal associative learning on visual perception. B, Trial structure: Main experiment. After presentation of a high (576 Hz) or low pitch (352 Hz) auditory cue, participants indicated their predicted tilting direction. After presentation of the visual target (which could be either unambiguous or ambiguous), participants reported their perception. In an additional perceptual rating experiment, this sequence was followed by a rating on the certainty associated with the perceptual response. C, Trial structure: Localizer. At the end of the fMRI experiment, we conducted localizer sessions mapping the meridians and the dot trajectories of CW and CCW tilt, respectively. Checkerboards were flickered in the respective areas eight times for 15 s in alternation while participants performed a challenging change detection task at fixation.

We used computational modeling in a Bayesian framework (Mathys et al., 2014a) to estimate hierarchically related predictions on a trial-by-trial basis. Correlating these trialwise estimates with fMRI time courses allowed us to dissociate the neural correlates of “high-level” predictions regarding the coupling of tones and visual stimuli from “low-level” predictions regarding the probability of binary perceptual outcomes.

Materials and Methods

Participants

Twenty-five participants took part in the experiment, which was conducted with informed written consent and approved by the local ethics committee. One participant had to be excluded because of not following the experimental instructions correctly. A second participant was excluded due to excessive movement inside the scanner (5 mm maximum average translational movement across runs. All remaining participants (N = 23, age 19–34 years, mean 25.6 years, 14 female) had normal or corrected-to-normal vision and no prior psychiatric or neurological medical history.

Experimental procedures

Main experiment.

In this fMRI experiment, we aimed at disentangling the neural representations of continuously updated hierarchical predictions. To this end, participants performed an associative reversal learning task (Fig. 1A) similar to Schmack et al. (2016), which induced changing expectations about visual stimuli. High or low tones were coupled with subsequently presented CW or CCW tilting dot pairs, which could be either unambiguous or ambiguous with regard to the direction of tilt. On unambiguous trials, tilt direction was determined by a motion streak, yielding a clear impression of the corresponding movement. The association of tones with tilting directions was probabilistic (75% correct and 12.5% incorrect associations with 12.5% ambiguous trials, see below) with contingencies changing unpredictably every 16–32 trials. Ambiguous trials used the phenomenon of apparent motion (Muckli et al., 2005; Sterzer et al., 2006; Sterzer and Kleinschmidt, 2007) to induce the percept of tilting movement and were covertly interspersed in the experimental sequence (12.5% of all trials). Here, the motion streak was omitted and the physical visual stimulus was hence uninformative with regard to the direction of tilt.

During the main experiment, participants completed a total of 576 trials, which were divided into 9 individual runs of varying length with a medium duration of ∼9 min. Visual and auditory stimuli were produced using MATLAB 2014b (The MathWorks) and Psychophysics Toolbox 3. Frames were projected at 60 Hz using a Sanyo LCD projector (resolution 1024 × 768 pixels) on a screen placed at 60 cm viewing distance at the Trim Trio Siemens 3T fMRI scanner's bore.

Auditory stimuli were presented binaurally at −15 dB (relative to maximum intensity) using MRI-compatible headphones powered by MR-ConFon hardware. At the beginning of every trial (Fig. 1B), a high (576 Hz) or low (352 Hz) tone was presented for a total of 300 ms. Immediately afterwards, participants indicated their prediction about whether the upcoming visual stimulus would tilt CW or CCW by pressing a left or right button on a standard MRI button box using the index and middle fingers of their right hand. The prediction screen was displayed for 1 s and consisted of 2 single arrows (displayed at 2.05° eccentricity right and left of fixation and turning from white to red after the response). The offset between the prediction screen and the onset of the visual stimuli was jittered between 100 and 300 ms (mean offset: 200 ms). Visual stimuli consisted of two light-gray dots of 1.2° diameter presented simultaneously at an eccentricity of 4.01° on the vertical (starting position) or horizontal (final position) meridian. The circumference of the tilting movement was depicted by a dark-gray circular streak of 1.2° width, which was displayed throughout the trial. Starting and final dot positions were presented for 600 ms, separated by trajectories of 33 ms duration.

On unambiguous trials, the tilting direction was defined by motion streaks (upper right and lower left quadrant for CW tilt, upper left and lower right for CCW tilt). On ambiguous trials, no motion streak was presented and visual stimuli were compatible with CW and CCW tilt. Immediately after presentation of the visual stimulus, participants reported their perception by pressing a left or right button using the index and middle finger of their right hand. The video response screen consisted of two double arrows (displayed at 2.05° eccentricity right and left of fixation and turning from white to red after response) and was presented for 1 s. Trials were separated by fixation intervals jittered between 0.5 and 2.5 s (mean fixation interval: 1.5 s) and amounted to a mean duration of 5.25 s each.

Perceptual rating.

Subsequent to the main experiment, we aimed at assessing the perceptual quality of ambiguous and unambiguous trials in an additional perceptual rating experiment, which was performed during the anatomical scan. Here, trial structure was identical to the main experiment. However, the video response screen was followed by a confidence rating (offset to perceptual response jittered between 100 and 300 ms, mean offset: 200 ms), which displayed a 4-point scale where 1 = very sure, 2 = rather sure, 3 = rather unsure, and 4 = very unsure with regard to the visual percept for a total of 1 s. Participants reported their rating using the index, middle, ring and little finger of the right hand. The selected rating turned from white to red after response. In total, participants rated their perceptual confidence for a total of 60 trials.

Localizer.

Given that the binary perceptual outcomes of the visual target were spatially separated, our design enabled us to investigate how activity in retinotopic stimulus representations in primary visual cortex would relate to predictive processes evoked during the main experiment. To identify voxels corresponding to CW or CCW tilt, we conducted two localizer scans (Fig. 1C) at the end of experimental session. The first localizer was designed to map the dot trajectories. Black-and-white checkerboards covering the circular dot trajectories from the main experiment were flickered at a frequency of 8 Hz in each visual field quadrant, but did not cover the starting and final position of the dot pairs. Specifically, the upper right and lower left (CW tilt) as well as the upper left and lower right quadrant (CCW tilt) were flickered in alternating sequence for 15 s each for a total of 8 repetitions separated by 5 s of fixation.

The second localizer was conducted with identical temporal structure, but mapped the vertical and horizontal meridian spanning over starting and final dot positions. For both localizers, checkerboards were scaled by the cortical magnification factor and participants performed a fixation task, responding to color changes in the fixation dot (alternating between white and red in unpredictable intervals) with their right index finger.

Behavioral analysis

The behavioral analysis outlined here is directed at the influence of the current cue–target association on perceptual decisions under ambiguity. In previous work using a similar experimental design with a different visual stimulus (Schmack et al., 2016), we found that in addition to a main effect of “associative learning,” perceptual history also had an influence on perceptual decisions under ambiguity in the form of “priming” and “sensory memory.” Whereas “priming” refers to the influence of the immediately preceding trial on the current trial, the term “sensory memory” (Pearson and Brascamp, 2008) is defined by the influence of the preceding ambiguous trial on the current ambiguous trial and therefore acts over longer timescales. In our current work, we used an optimized experimental design with a different visual stimulus that we expected to maximize the effect of associative learning while minimizing the effects of perceptual history. Nevertheless, in our behavioral analyses, we considered not only the main effect of associative learning but also the effects of priming and sensory memory to account for variance of no interest caused by perceptual history.

Conventional analysis.

To establish that prior predictions acquired during the course of the experiment biased perceptual decision under ambiguity, we performed a series of conventional behavioral analyses, which furthermore served as a validation for our inverted Bayesian model (see below). Our central interest was in the effect of learned tone–target associations on perceptual decisions under ambiguity. We therefore calculated the proportion of ambiguous percepts congruent to the currently prevalent hidden contingency (associative learning) averaged across runs and participants. Given our previous findings suggesting additional effects of perceptual history on perceptual decisions under ambiguity, we further quantified the proportion of trials perceived in congruence with the preceding unambiguous trial (priming) or the preceding ambiguous trial (sensory memory; Schmack et al., 2016).

We further investigated the effectiveness of the disambiguation by calculating the proportion of unambiguous trials perceived according to the disambiguation and averaged across runs and participants.

To assess the results from our perceptual rating experiment, we calculated the proportion of trials rated as 1 = very sure, 2 = rather sure, 3 = rather unsure, and 4 = very unsure for unambiguous and ambiguous trials separately and averaged across participants. To assess a potential mediation of the effect of predictions on perceptual decision under ambiguity by perceptual uncertainty, we conducted an across-participants correlation between average perceptual ratings and the proportion of ambiguous trials perceived according to the current cue–target contingency.

Finally, correlating the metrics for the strength of the impact of learned associations on perceptual decisions under ambiguity between conventional and model-based behavioral analyses allowed us to validate our Bayesian modeling approach.

Bayesian modeling.

To investigate the neural correlates of hierarchical predictions, we adopted a Bayesian modeling approach (implemented previously in Schmack et al., 2016), which allows for the estimation of individual trial-by-trial model quantities such as the dynamic and continuously updated “high-level” prediction about the association between auditory cues and visual target or the inferred “low-level” conditional probability of a binary visual outcome given a specific auditory cue.

Our model, which is defined in detail in the section “Mathematical model description,” frames perception as an inferential processes in which perceptual decisions are based on posterior distributions. According to Bayes' rule, such posterior distributions are derived from likelihood distributions representing the sensory evidence, and prior distributions, which, in the context of this experiment, can be used to formalize expectations about perceptual outcomes.

Crucially, here, we were interested in such perceptual expectations or priors that are formed by associative learning; that is, the subjects' continuously updated inference on the probabilistic coupling between tones and visual stimuli (please note that this is not equivalent to the hidden contingency used for conventional analysis, which is in principle unknown to the participant). As indicated by our previous work (Schmack et al., 2016), perception might be further influenced by priors that are derived from perceptual history: priming (the influence of a visual percept on the subsequent trial) and sensory memory (the influence of the visual percept in an ambiguous trial on the subsequent ambiguous trial). Inclusion of these priors based on perceptual history into a model helps to explain away additional variance of no interest. Please note that the factors of associative learning and priming constitute potential priors for perceptual decisions on all trials regardless of ambiguity, whereas sensory memory is defined as a prior for perceptual decisions under ambiguity only.

All of these priors (associative learning, priming, and sensory memory) can be modeled by Gaussian probability distributions, which are defined by their respective mean and precision (the inverse of variance). Importantly, the precision term represents the impact of a prior on the posterior distribution and thus relates to its influence on visual perception.

In the analysis presented here, we fitted our model on two behavioral responses given by our participants: The prediction of upcoming tilting direction y_prediction (which we hypothesized to depend on the conditional probability of tilting direction given the tone as expressed by the prior distribution “associative learning”) and the perceived tilting direction y_perception (which we reasoned to be based on a specific combination of the prior distributions “associative learning”, “priming”, “sensory memory”, and the likelihood-weight “disambiguation”). Therefore, our model is divided into two interacting parts: a “contingency” model, which was built to model the inferred association between tones and CW or CCW tilt and used to extract “high-level” model quantities, and a “perceptual” model, which was designed to predict the participants' perceptual choices and enabled us to assess “low-level” model quantities.

To determine which factors drive perceptual predictions relevant for perceptual decisions under ambiguity, we used Bayesian model selection. In addition to the factor “associative learning”, which we were interested in primarily, we considered the additional factors “priming and sensory memory” to allow for models that account for the variance caused by perceptual history. We constructed behavioral models incorporating all combinations of the prior distributions “associative learning” (A), “priming” (P), and “sensory memory” (S), whereas all models considered incorporated the distribution “disambiguation”, which adjusts the weight of the fixed bimodal likelihood. This yielded a total of eight behavioral models to be compared (A-P-S-, A-P-S+, A-P+S-, A-P+S+, A+P-S-, A+P-S+, A+P+S-, A+P+S+), which were optimized for the prediction of both behavioral responses using a free energy minimization approach. This allowed us to compare the behavioral models using random effects Bayesian model selection (Stephan et al., 2009). We used a version of the hierarchical Gaussian filter for binary inputs (Mathys et al., 2014a, 2014b), as implemented in the HGF 4.0 toolbox (distributed within the TAPAS toolbox translationalneuromodeling.org/tapas/), for model optimization and SPM12 (http://www.fil.ion.ucl.ac.uk/spm/) for model selection.

After identifying the optimal model using Bayesian model selection, we analyzed its posterior parameters using classical frequentist statistics and extracted model quantities for model-based fMRI. To test for a relation between fMRI activity and “high-level” predictions, we extracted the absolute cross-model prediction μ̂₂ from the contingency model. To account for additional variance in the BOLD signal, we further extracted the precision of the absolute cross-model prediction π̂₂ and the precision-weighted crossmodal prediction error |ϵ₂| from the contingency model.

To investigate the relationship between fMRI activity and “low-level” predictive processes, we assessed the dynamic stimulus-specific prediction μ_a (i.e., the inferred conditional probability of CW tilt given the tone) and its analog 1 − μ_a (i.e., the inferred conditional probability of CCW tilt given the tone) from the perceptual model. To capture additional variance in the recorded BOLD signal, we furthermore extracted the following model quantities from the perceptual model: the posterior probability of CW tilt P(θ₁) and CCW tilt P(θ₀), the choice prediction error ε_choice and the perceptual prediction error |δ_q|.

Please see the section “Mathematical model description” for a detailed definition of our modeling procedures. Figure 2A provides a graphical illustration of the modeling approach. We provide exemplary time courses for “high-” and “low-level” model quantities in Figure 2B. Table 1 provides a summary of model quantities and model parameters, including prior mean and variance for inversion as well as average posterior parameter estimates across participants.

Figure 2.

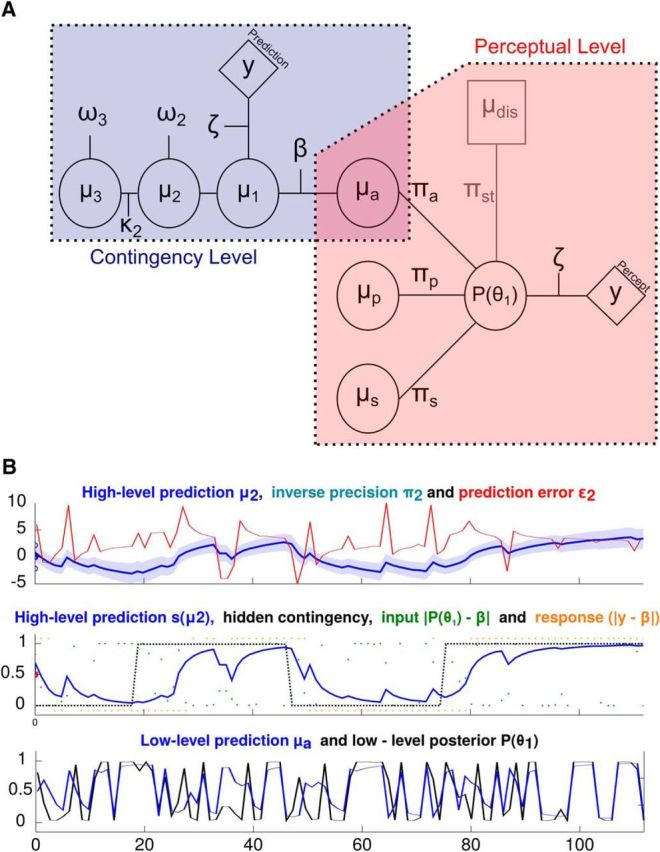
Hierarchical Gaussian filter. A, The behavioral model consists of a standard hierarchical Gaussian filter for binary perceptual outcomes (contingency level), representing the inferred association between tones and tilting directions during the experiment. This part of the model is coupled to the perceptual level, which determines the influence of prior predictions derived from previous cue–target associations as well as priming and sensory memory on perceptual decisions. B, Exemplary model quantities for one individual participant and run. The top displays the time course of the “high-level” prediction μ₂, its variance (i.e., the inverse precision π₂) as well as the precision-weighted “high-level” prediction error ε₂. The middle panel shows the sigmoid transform of the “high-level” prediction s(μ₂), the time course of the underlying contingency (black dotted line) as well as inputs and responses (both transformed on the level of the contingency between auditory cues and visual targets). The bottom displays the “low-level” conditional probability of CW tilt (in blue) as well as the “low-level” posterior probability of CW tilt (in black).

Table 1.

Summary of model parameters and quantities

	Name	Explanation	Inversion
Sensory Stimulation	μdis	Mean of sensory stimulation
	β	High- or low-pitch tone
Responses	yprediction	Binary prediction
	yperception	Binary perceptual decision
Model Parameters			Prior mean	Prior variance	Posterior
Perceptual Model	πa	Associative precision	0.5	1	1.6052 ± 0.0456
	πp	Priming precision	0.5	1	0 ± 0
	πs	Sensory memory precision	0.5	1	0.6138 ± 0.0511
	πdis	Disambiguation precision	1.5	0	1.5 ± 0
Contingency Model	ω2	Learning rate of 2nd level	−1.28	1	−0.0483 ± 0.0713
	ω3	Learning rate of 3rd level	−6.14	1	−6.6800 ± 0.0469
	κ2	Coupling strength between 3rd and 2nd level	1	0	1 ± 0
	μ2/30	Initial mean of 2nd/3rd level	0/1	0/0	0/1
	σ20	Initial variance of 2nd level	4.6413	1	4.5739 ± 0.0536
	σ30	Initial variance of 3rd level	4	1	3.3315 ± 0.0536
Response Mapping	ζ	Inverse decision temperature (response model)	1	0	1
Selected Model Quantities
Predicted Responses	ŷprediction	Model prediction on yprediction
	ŷperception	Model prediction on yperception
Perceptual Model	μa	Inferred conditional probability of CW-tilt (“low-level” prediction)
	δq	Perceptual prediction error
	ϵchoice	Choice prediction error
	P(θ1)	Posterior probability of perceiving CW-tilt
Contingency Model	μ̂2 and π̂2	Prior mean (“high-level” prediction) and precision of 2nd level
	ϵ2	Precision-weighted (“high-level”) contingency prediction error

Table 2.

Model-based fMRI Results with thresholds p < 0.05, FWE, for $\left|\widehat{{\mu }_2}\right|$ and p < 0.001, uncorr., for μ_a

|μ̂2|
Region	Hem.	x	y	z	T	Region	Hem.	x	y	z	T
Mid. Orbital Gy.	R	6	40	−10	11.04	Post. Hippocampus	R	10	−40	5	7.65
Mid. Orbital Gy.	L	−4	50	−8	11.44	Post. Hippocampus	L	−7	−42	5	8.70
Caudate Nucleus	L	−7	18	−8	9.06	Precuneus	R	8	−50	8	6.49
Insula	R	43	−12	5	11.01	Precuneus	L	−4	−54	12	9.04
Precentral Gy.	R	16	−24	78	9.61	Postcentral Gy.	R	48	−12	35	6.50
Post. med. frontal Gy.	R	10	−17	78	7.95	Postcentral Gy.	L	−20	−30	72	7.05

μa
Region	Hem.	x	y	z	T	Region	Hem.	x	y	z	T
Rolandic Operculum	L	−60	3	5	4.47	Inf. Temporal Gy.	L	−42	−62	−10	3.70
Inf. Occipital Gy.	L	−42	−70	−8	3.79	Caudate Nucleus	L	−14	6	15	4.29
Inf. Frontal Gy.	R	48	38	0	3.89	Caudate Nucleus	R	18	−17	20	4.27

Table 3.

Explorative model-based fMRI Results. Statistical thresholds are p < 0.05 FWE for the regressors “Tone”, “Tile”, $\left|\widehat{{\mu }_2}\right|$, |δ_q| and |ϵ₂| as well as p < 0.001 uncorr. for the remaining regressors

Tilt						Tone
Region	Hem.	x	y	z	T	Region	Hem.	x	y	z	T
Inf. Occipital Gy.	R	38	−74	−12	12.30	Sup. Temporal Gy.	R	53	−14	0	14.29
Inf. Occipital Gy.	L	−37	−84	−5	11.75	Sup.Temporal Gy.	L	−60	−42	15	12.06
Mid. Occipital Gy.	R	30	−92	0	12.60	Cerebelum (VI)	R	33	−62	−28	12.54
Mid. Occipital Gy.	L	−22	−97	−2	11.49	Cerebelum (VI)	L	−30	−67	−28	9.20
Fusiform Gy.	R	30	−72	−18	12.81	Thalamus	R	8	−12	2	8.64
Fusiform Gy.	L	−32	−77	−18	15.10	Thalamus	L	−7	−17	0	9.82
Lingual Gy.	R	23	−90	−5	14.45	Post. med. frontal Gy.	R	8	23	52	7.47
hMTI+/V5	R	50	−70	5	12.29	Post. med. frontal Gy.	L	−7	3	55	7.28
						Precentral	L	−37	−17	55	7.78
						Insula	R	30	23	−2	7.06

$\left|\widehat{{\mu }_2}\right|$
Region	Hem.	x	y	z	T	Region	Hem.	x	y	z	T
Heschls Gy.	R	43	−22	8	7.65	Insula	L	−44	0	−2	6.52
Heschls Gy.	L	−37	−27	10	6.48	Postcentral Gy.	R	23	−37	72	7.11

|δq|						|ϵ2|
Region	Hem.	x	y	z	T	Region	Hem.	x	y	z	T
Insula	L	−32	26	5	8.29	Precentral Gy.	R	46	6	28	7.89
Mid. Temporal Gy.	L	−50	−60	2	6.93
Precentral Gy.	R	46	6	28	7.89	Inf. Parietal Lob.	R	46	−50	50	7.31
Inf. Parietal Lob.	L	−40	−80	22	7.54	Inf. Parietal Lob.	L	−50	−47	55	7.02
Insula	L	−32	26	5	5.81	Sup. Parietal Lob.	R	6	−67	48	6.48
Inf. Frontal Gy.	L	−47	16	30	5.20	Caudate Nucleus	R	13	0	20	5.25

ϵchoice						P(θ = 1)
Region	Hem.	x	y	z	T	Region	Hem.	x	y	z	T
Inf. Occipital Gy.	L	−42	−77	−10	5.25	Sup. Occipital Gy.	R	20	−97	28	4.21
		-				Posterior-medial frontal Gy.	L	−12	18	60	4.55

Mathematical model description

Here, we applied a Bayesian modeling approach to assess the continuous updating of predictions about the causes of sensory input and their impact on perceptual decisions under ambiguity. We devised a model that was inverted on two behavioral responses given by the participants: The prediction of upcoming tilting direction y_prediction and the perceived tilting direction y_perception. With this, we inferred on model parameters that govern the updates in model quantities belonging to two different interacting parts of our model: A “contingency” model dealing with the inferred contingencies between concurring auditory and visual stimuli and a “perceptual” model, which integrates different sources of prior and likelihood information to predict individual perceptual choices.

Perceptual model.

At each time point t, the two alternative visual percepts are predicted on the basis of a posterior probability distribution over θ:

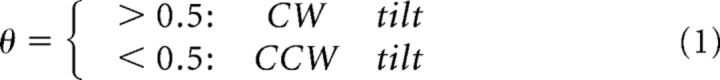Participants responded with button presses indicating the current visual percept as follows:

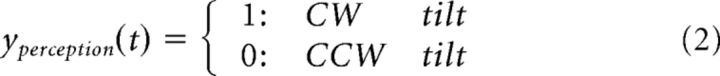Based on previous work (Schmack et al., 2016), we formalized a number of prior distributions that could influence on participants' perception, considering separate contributions of priming, sensory memory, and associative learning. The latter was driven by the co-ocurrence of the direction of tilt (see above) and the pitch of the preceding tone, which was defined as follows:

To map the dynamic inference on the contingency between tones β and perceived direction of tilt y, we constructed a three-level hierarchical Gaussian filter (Mathys et al. (2014b), see below for details), which received the conjunction of tone and posterior probability of tilt direction as input. From here, we extracted first level prediction μ̂₁(t), which represents the inferred contingency over tones and rotations. This was transformed into the conditional probability of CW tilt given the tone as follows:

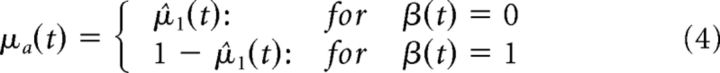This defines the mean of the prior distribution “associative learning” (associative learning ∼𝒩(μ_a, π_a⁻¹)), while π_a represents its precision. Please note that the conditional probability of CCW tilt is given by 1 − μ_a. We refer to these model quantities as “low-level perceptual predictions”.

Likewise, the mean of the prior distribution “priming” (priming ∼ 𝒩(μ_p, π_p⁻¹)) in trial t was defined by the visual percept in the preceding trial:

The mean of the prior distribution “sensory memory” (sensory memory ∼ 𝒩(μ_s, π_s⁻¹)) in trial t was defined by the visual percept in the preceding ambiguous trial t_a:

In addition to these prior distributions, we defined the disambiguation (i.e., the presence of motion streaks along the trajectory of tilt) by means of the likelihood weight “disambiguation” (disambiguation ∼ 𝒩(μ_dis, π_dis⁻¹)) in trial t:

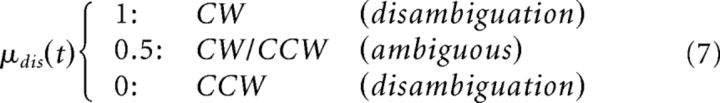To predict the perceptual outcomes, we derived the posterior distribution with respect to CW or CCW tilt from the model. This distribution results from a weighting of a bimodal likelihood distribution by a combination of prior distributions such as “associative learning”, “priming”, “sensory memory”, as well as the likelihood weight “disambiguation”.

For a specific combination of these prior distributions, a joint prior distribution with mean μ_m and variance π_m can be calculated by adding up the means of influencing factors relative to their respective precision:

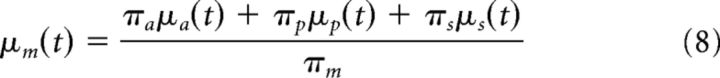This joint prior distribution (described by μ_m and π_m) as well as the disambiguation (defined by μ_dis and π_dis) is used to adjust the density ratio of the posterior for the two peak locations θ₀ = 0 and θ₁ = 1:

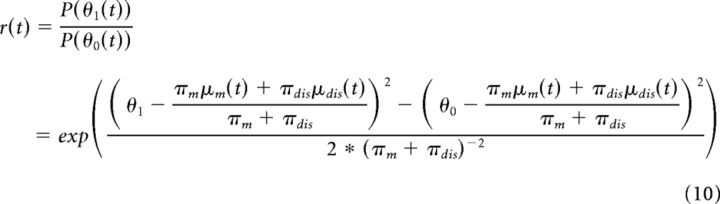P(θ₁) denotes the posterior probability of CW tilt. Therefore, 1 − P(θ₁) represents the posterior probability of CCW tilt. For simplicity, we refer to P(θ₁) and P(θ₀) as “low-level” posteriors.”

The model prediction ŷ_Perception on the participants percept is given by applying a unit sigmoid function with inverse decision temperature ζ = 1 to P(θ₁):

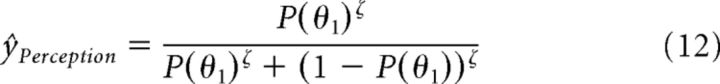From here, we extracted a “perceptual prediction error”, which was given by:

In addition, we defined a “choice prediction error”, which was obtained by subtracting the inferred conditional probability of CW tilt given the tone (i.e., μ_a) from the actual perceptual outcome y_perception:

Contingency model.

To extract the inferred trial-by-trial prediction $\widehat{{\mu }_1}\left(t\right)$, we used a version of the three-level hierarchical Gaussian filter (Mathys et al., 2011). The input to the HGF modeling the inferred contingency between auditory and visual stimuli was defined by the following:

Please note that, due to the lack of a stereodisparity cue in ambiguous trials, P(θ₁(t)) is closer to 0 or 1 on unambiguous trials. Therefore, updates in the inferred contingency are smaller in ambiguous cases and the HGF implemented here specifically takes differences in perceptual certainty between ambiguous and unambiguous trials into account.

Likewise, the participants' prediction was defined as follows:

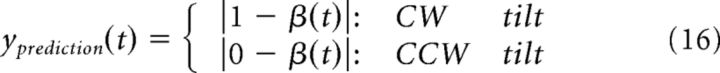The posterior of the first level μ₁(t) is set to be equal to Input(t):

The second-level prediction of the HGF models the tendency of the first level toward μ₁(t) = 1 and is given by the following:

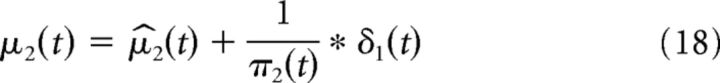Please note that we refer to the strength of the second-level prediction $\left|\widehat{{\mu }_2}\left(t\right)\right|$ as the crossmodal or “high-level” prediction. The precision of the second-level prediction evolves according to the following:

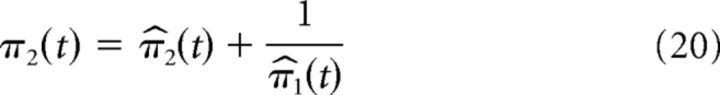The first-level prediction $\widehat{{\mu }_1}$ is defined by a logistic sigmoid transform of the second-level prediction μ₂ as follows:

The difference between the first level prediction μ₁ (t) and first-level posterior μ₁(t) yields a prediction error δ₁(t) as follows:

Crucially, δ₁(t) is combined with the second level precision Π₂, yielding the precision-weighted “high-level” prediction error ε₂(t), which updates second-level prediction μ̂₂(t) as follows:

The precision of the prediction on the first and second level evolve according to the following:

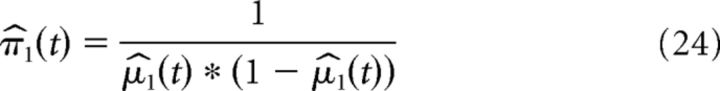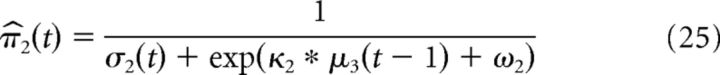The volatility prediction error δ₂ governs the update to the third level of the HGF and is given by the following:

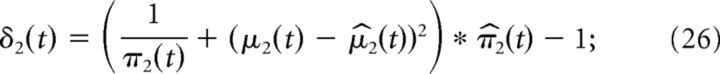The third-level prediction $\widehat{{\mu }_3}\left(t\right)$ and its precision $\widehat{{\pi }_3}\left(t\right)$ are defined by the following:

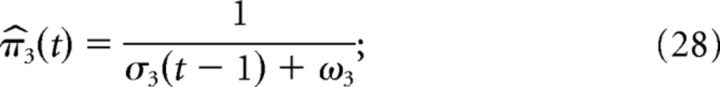Finally, the third level posterior μ₃(t) and its precision π₃(t) are given by the following:

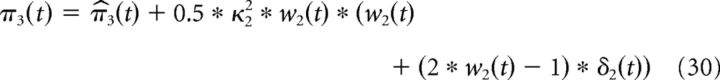The model prediction ŷ_Prediction on the participants' predicted tilting direction of the upcoming visual stimulus is given by applying a unit sigmoid function with inverse decision temperature ζ = 1 to $\widehat{{\mu }_1}$ as follows:

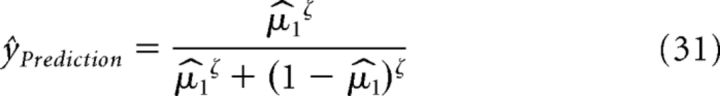Finally, combining the two log-likelihoods of ŷ_Prediction and ŷ_Perception given the actual responses y_Prediction and y_Perception yields the modeling cost. From here, the precision of the prior distributions can be optimized via the minimization of free energy (which represents a lower bound on the log-likelihood) with regard to the predicted responses.

As an optimization algorithm, we chose the quasi-Newton Broyden-Fletcher-Goldfarb-Shanno minimization (as implemented in the HGF 4.0 toolbox). To assess the evidence for existence of the prior distributions “associative learning”, “priming” and “sensory memory”, their precisions were either estimated as free parameters in the perceptual model or fixed to zero (thereby effectively removing a prior distribution from the model). The precision of the prior distribution “disambiguation” was always estimated as a fixed parameter; therefore, this yielded 2³ = 8 models.

The prior distributions for π_a, π_p, and π_s had a mean of 0.5 and a variance of 1 when the corresponding parameter was estimated and π_a, π_p, and π_s were set to 0 when they were not estimated. π_dis was fixed to 1.5. Parameters from the HGF were defined as follows: μ₂, 0 = 0; μ₃, 0 = 1; σ₂, 1 = log(4.6413); σ₃, 1 = log(4); κ₂, 0 = 1; ω₂, 1 = −1.28; ω₃, 1 = −6.14; ζ, 0 = 1. Indices denote the level of the HGF.

Model inversion was performed separately for each run of the experiment and estimated models were compared using Bayesian model selection (fixed effects on the subject level and random effects on the group level) as implemented in SPM12. From the winning model, we extracted posterior parameters and averaged across runs and participants.

fMRI

Acquisition and preprocessing.

We recorded BOLD images by T2-weighted gradient-echo echoplanar imaging (TR 2500 ms, TE 25 ms, voxel size 2.5 × 2.5 × 2.5 mm) on a 3T MRI scanner (Tim Trio; Siemens). The number of volumes amounted to ∼1330 volumes for the main experiment and 220 volumes for the localizers. We used a T1-weighted MPRAGE sequence (voxel size 1 × 1 × 1 mm) to acquire anatomical images. Image preprocessing (slice timing with reference to the middle slice, standard realignment, coregistration, normalization to MNI stereotactic space using unified segmentation, spatial smoothing with 8 mm full-width at half-maximum isotropic Gaussian kernel) was performed with SPM12 (http://www.fil.ion.ucl.ac.uk/spm/software/spm12).

General linear models (GLMs)

Whole-brain analysis.

To probe the potential neural correlates of predictive processes in the main experiment, we conducted a model-based fMRI approach using model quantities from the inverted behavioral model. Here, we aimed at disentangling the neural representation of the crossmodal “high-level” prediction $\left|\widehat{{\mu }_2}\right|$ from the “low-level” prediction μ_a. In addition, we considered a number of model-based regressors of no interest.

The “high-level” prediction $\left|\widehat{{\mu }_2}\right|$ describes the individual participants' estimate in the predictive strength of the auditory cue with regard to the visual target on a trial-by-trial basis. Due to changes in the contingencies between auditory cues and visual targets at time points unknown to the participants, such estimates in the predictive strength varied during the course of the experiment. Importantly, this quantity is orthogonal to the specific direction being predicted at a given trial.

In turn, the “low-level” prediction μ_a describes the inferred conditional probability of CW tilt given the tone, which ranges from 0 to 1. Its computation is contingent on the participants current estimate for the “high-level” prediction, whereas the two entities $\left|\widehat{{\mu }_2}\right|$ and μ_a are orthogonal to each other. This is because the conditional probabilities are defined on a stimulus-level (with regard to CW and CCW tilt), whereas the “high-level” prediction describe the strength of the overall contingencies. Importantly, because the conditional probabilities sum up to 1, the conditional probability of CCW tilt is given by 1 − μ_a.

Next to these quantities of interest, we considered a number of regressors to account for additional variance of no interest. Here, we included $\widehat{{\pi }_2}$, which represents the precision of the “high-level” prediction $\widehat{{\mu }_2}$ and describes how persistent a participant's belief in the audiovisual contingency is over time as well as in the light of potentially contradictory evidence. Furthermore, we took the absolute precision-weighted prediction error |ϵ₂| into account, which describes the update in the “high-level” prediction $\widehat{{\mu }_2}$. It is larger for unexpected visual stimuli and for situations in which the participant has an imprecise belief about the current cue–target contingency. On the level of the visual stimuli, in turn, we considered the “low-level” prediction error ε_choice, which is given by the difference between the actual visual outcome and the conditional probability of CW tilt. We also considered the “low-level” posterior probability of CW tilt P(θ₁), which results from the integration of the visual stimulation and the prior predictions (i.e., “associative learning”, “priming”, “sensory memory”). This entity predicts visual perception on a trial-by-trial basis. Last, we considered the remaining evidence for the alternative visual percept in the posterior distribution as the perceptual prediction error δ_q (for an in-depth discussion of the quantity, see also Weilnhammer et al., 2017).

The GLM contained the regressors tone and tilt, which were represented by stick functions and temporally aligned to the presentation of the auditory cue and to the onset of the tilting movement (regardless of direction or ambiguity).

Furthermore, the tone regressor was parametrically modulated by our two model quantities of interest: the crossmodal “high-level” prediction $\left|\widehat{{\mu }_2}\right|$ as well as the “low-level” prediction μ_a (i.e., the inferred conditional probability of CW tilt given the tone). To account for additional variance, we included the precision of the “high-level” prediction $\widehat{{\pi }_2}$ as a further regressor.

The tilt regressor, in turn, accounted for additional variance and was modulated by the “high-level” prediction error |ϵ₂| as well as the “low-level” perceptual posterior P(θ₁(t)), the “low-level” choice prediction error ε_choice, and the absolute perceptual prediction error |δ_q|. All model trajectories were extracted separately for each experimental run from the winning model of our Bayesian model comparison.

Regressors were convolved with the canonical hemodynamic response function as implemented in SPM12. Please note that the regressors of interest $\widehat{{\mu }_2}$ and μ_a were placed at the last positions of the design matrix. To ensure that our design was able to segregate between regressors of interest and regressors of no interest, we computed the colinearity between the SPM regressors and averaged across participants. The highest values of colinearity for the cue-related regressor of interest $\widehat{{\mu }_2}$ (i.e., the “high-level” prediction) with target-related regressors were 0.50 ± 0.02 for the “high-level” prediction error ε₂ and 0.4414 ± 0.03 for the perceptual prediction error δ_q. The highest values of collinearity for the cue-related regressor of interest μ_a (i.e., the “low-level” prediction) with target-related regressors were 0.57 ± 0.02 for the “low-level” prediction error ε_choice and 0.46 ± 0.04 for the perceptual posterior P(θ₁).

We added six rigid-body realignment parameters as nuisance covariates and applied high-pass filtering at 1/128 Hz. We estimated single-participant statistical parametric maps and created contrast images which were entered into voxelwise one-sample t tests at the group level. Anatomic labeling of cluster peaks was performed using the SPM Anatomy Toolbox Version 1.7b. We assessed our data across the whole brain reporting voxels surviving FWE correction at p < 0.05.

ROI analysis.

We hypothesized that the “low-level” conditional stimulus probabilities would correlate with BOLD activity in retinotopic representations of the motion trajectories during CW and CCW tilt in primary visual cortex across all trials. To test this idea, we defined the correlates of the trajectories of CW and CCW tilt (which are highlighted in red and blue in Fig. 1A) by intersecting contrast images obtained from both the localizer and the main experiment:

From the localizer experiment, we estimated single-participant GLMs that contained box-car regressors representing the presentation of checkerboards over the upper-right and lower-left trajectories for CW tilt and lower-right and upper-right quadrant for CCW tilt and computed statistical parametric maps as well as contrast images for “CW tilt > CCW tilt” (and vice versa), thresholded at p < 0.05, uncorrected.

To only select voxels that were highly specific for CW and CCW tilt in the main experiment, we estimated a second set of single-subject GLMs from the main experiment, containing CW and CCW tilt for ambiguous and unambiguous trials separately, and computed single subject parametric maps as well as contrast images for “CW tilt > CCW tilt” (and vice versa) for unambiguous trials only, thresholded at p < 0.05, uncorrected. Please note that these contrasts are orthogonal to all predictive factors and are thus apt for the definition of functional ROIs (see also Friston et al., 2010).

ROIs were then defined by intersecting the respective contrast images for “CW tilt > CCW tilt” and “CCW tilt > CW tilt”. Parameter estimation was performed using MARSBAR (marsbar.sourceforge.net/) with a design identical to whole-brain analyses. Specifically, we investigated the correlation of activity in retinotopic representations of the motion trajectories on all trials with the “low-level” prediction of tilt direction μ_a (i.e., the conditional probability of CW tilt given the tone) and 1 − μ_a (i.e., the conditional probability of CCW tilt given the tone). Please note that the design matrix contained information about the posterior P(θ₁) and thus the actual sensory information. Therefore, any correlation between the BOLD signal and μ_a and 1 − μ_a will be due to variance that is explained by “low-level” predictions independently of the sensory stimulation per se.

Results

Behavioral analysis

Conventional analysis

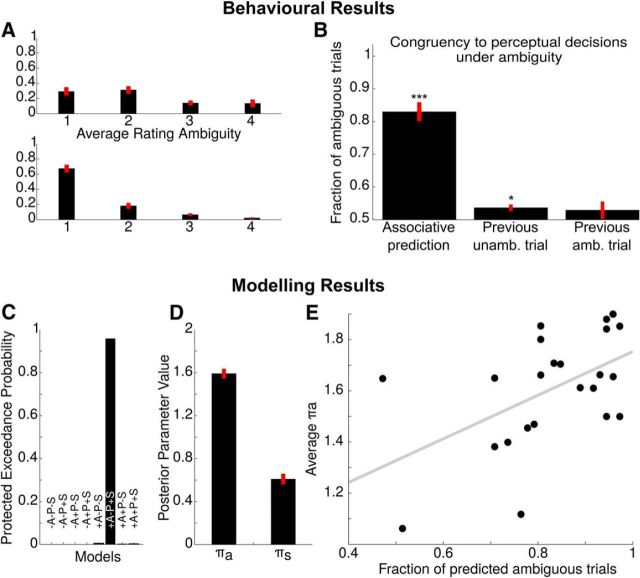
Assessing the potential effect of crossmodal predictions on perceptual decisions under ambiguity, we found that 82.61 ± 3.87% of all ambiguous trials were perceived according to the currently prevalent hidden contingency (p < 10⁻⁵, T = 11.4494, one-sided test). The effect of priming on ambiguous trials (53.62 ± 0.98%; p = 0.0013, T = 3.6858) was substantially smaller, whereas conventional analyses discarded a significant impact of sensory memory on perceptual responses under ambiguity (52.90 ± 2.59%; p = 0.2757, T = 1.1178, Fig. 3B). As expected, 97.46 ± 0.62% of all unambiguous trials were perceived according to the disambiguation.

Figure 3.

Behavioral analysis. A, Perceptual rating. Participants tended to report a higher perceptual certainty at disambiguated trials (bottom) compared with ambiguous trials (top). B, Conventional analyses. Here, we show the proportion of ambiguous trials perceived according to the current hidden contingency (associative learning, p < 10⁻⁵, T = 11.4494, one-sided test), the preceding unambiguous trial (priming, p = 0.0013, T = 3.6858, one-sided ttest) and preceding ambiguous trial (sensory memory, p = 0.2757, T = 1.1178). Overall, the current cue–target association most strongly affected perceptual decisions under ambiguity, whereas the effect of priming was much smaller and conventional statistics discarded a significant impact of sensory memory. C, Bayesian model comparison. Random effects Bayesian model selection indicated that the model incorporating the factors “associative learning” (+A) and “sensory memory” (+S) best explained the behavioral data collected in this experiment at a protected exceedance probability of 97.77%. This is reflected by the Bayesian model family comparison shown in the inset (A+ 99.99%, P + 2.93%, S+ 94.86% exceedance probabilities). D, Posterior model parameters extracted from the winning model of our Bayesian model comparison. In analogy to conventional analysis of the contributing factors, we found a stronger influence of “associative learning” (as expressed by π_a) than for “sensory memory” (π_s). “Priming” (π_p) is not displayed because it was not part of the winning model. E, Correlation between conventional metrics and inverted model quantities. The fraction of ambiguous trials perceived according to the currently prevalent hidden contingency was highly correlated with π_a (ρ = 0.5208, p < 0.0108, Pearson correlation), indicating successful model inversion. *p < 0.05, ***p < 0.001.

We proceeded by evaluating a potential mediating role of perceptual uncertainty for the influence of associative learning on perceptual decisions under ambiguity. Here, our rating experiment indicated that the majority of unambiguous trials (67.20 ± 5.09%) elicited very clear motion percepts. Such very clear motion percepts were less frequent for ambiguous trials (31.59 ± 6.00%; Fig. 3A). There was no significant across-subject correlation between the average perceptual certainty at ambiguous trials and the proportion of ambiguous trials perceived according to the currently prevalent hidden contingency (ρ = 0.1238, p = 0.5735).

In brief, conventional analyses indicated that the crossmodal associations significantly affected perceptual decisions under ambiguity, whereas we could not observe a relation between the strength of this effect and perceptual uncertainty.

Bayesian modeling

To infer the participants' trial-by-trial prediction about the crossmodal association and to quantify its impact for perceptual decisions under ambiguity, we conducted a Bayesian modeling approach. First, we used Bayesian model selection between models incorporating all combinations of the factors “associative learning”, “priming”, and “sensory memory” to establish which factors were likely to affect visual perception.

Random effects Bayesian model comparison indicated evidence for an influence of the factors “associative learning” and “sensory memory” by identifying model 6 as a clear winning model at an protected exceedance probability of 97.77% (Fig. 3C). This is also reflected by model family comparison, which yielded clear evidence for a contribution of the factors “associative learning” (exceedance probability for associative learning models: 99.99%) and “sensory memory” (exceedance probability for sensory memory models: 94.86%), while rejecting a significant influence of priming on perceptual decisions (exceedance probability for priming models: 2.93%).

To assess the winning model on a parameter level, we extracted posterior model parameters from the perceptual model and averaged across runs and participants (Fig. 3D). Consistent with conventional analyses of the contributing factors, the effect (i.e., precision) of associative learning on visual outcomes (1.5862 ± 0.0607) was enhanced compared with sensory memory (0.6612 ± 0.0708; Fig. 3D).

Bayesian model comparison and posterior parameter estimates paralleled the results from conventional analysis by showing that the learned crossmodal association was most influential in biasing perceptual decisions at ambiguous trials, whereas the effects of perceptual history (sensory memory and priming) were estimated to be much smaller or negligible.

As an indication of successful inversion of our Bayesian model, π_a (as the metric for the strength of the impact of crossmodal associations on ambiguous trials) was highly correlated with the proportion of ambiguous trials perceived according to the currently prevalent hidden contingency (ρ = 0.5208, p < 0.0108; Fig. 3E). In analogy to conventional analyses, we did not observe a significant correlation between posterior HGF parameters describing the strength of the influence of associative learning on perceptual outcomes (i.e., π_a) with perceptual certainty at ambiguous trials as indicated by the independent perceptual rating experiment (ρ = –0.0184, p = 0.9338). With this, we corroborated a significant impact of predictions on perceptual decisions regardless of perceptual uncertainty and ensured successful inversion of our model.

In brief, our behavioral analysis indicate a major influence of predictions driven by crossmodal associative learning next to a minor influence by predictions derived from perceptual history such as sensory memory and priming.

fMRI

GLMs

Whole-brain analysis.

Having identified the optimal behavioral model, we aimed at identifying the neural correlates of “high-level” versus “low-level” predictions while considering additional model quantities as regressors of no interest. Because these entities served as parametric modulators for the onsets of the auditory cue and the visual target, respectively, we first mapped the contrasts “tone > baseline” and “tilt > baseline”. As expected, “tone > baseline” yielded significant clusters in bilateral superior temporal gyrus, cerebellum, and thalamus as well as bilateral posterior medial frontal gyrus, left precentral gyrus, and insula, whereas the contrast “tilt > baseline” showed significant activations in bilateral inferior and middle occipital gyrus, right inferior temporal gyrus (V5/hMT+), bilateral putamen, and right lingual gyrus, as well as bilateral fusiform gyrus (FWE, p < 0.05).

For the main focus of whole-brain analysis, we found that the “high-level” cross modal prediction $\left|\widehat{{\mu }_2}\right|$ correlated with activity in supramodal brain regions such as bilateral middle orbital gyrus, bilateral rolandic operculum, bilateral Heschl's gyrus, right superior medial frontal gyrus, left caudate nucleus, bilateral postcentral gyrus, right precentral gyrus and right insula. Moreover, $\left|\widehat{{\mu }_2}\right|$ was also associated with activity in bilateral posterior hippocampus at the intersection to the precuneus and bilateral precuneus (Fig. 4A, p < 0.05 FWE).

Figure 4.

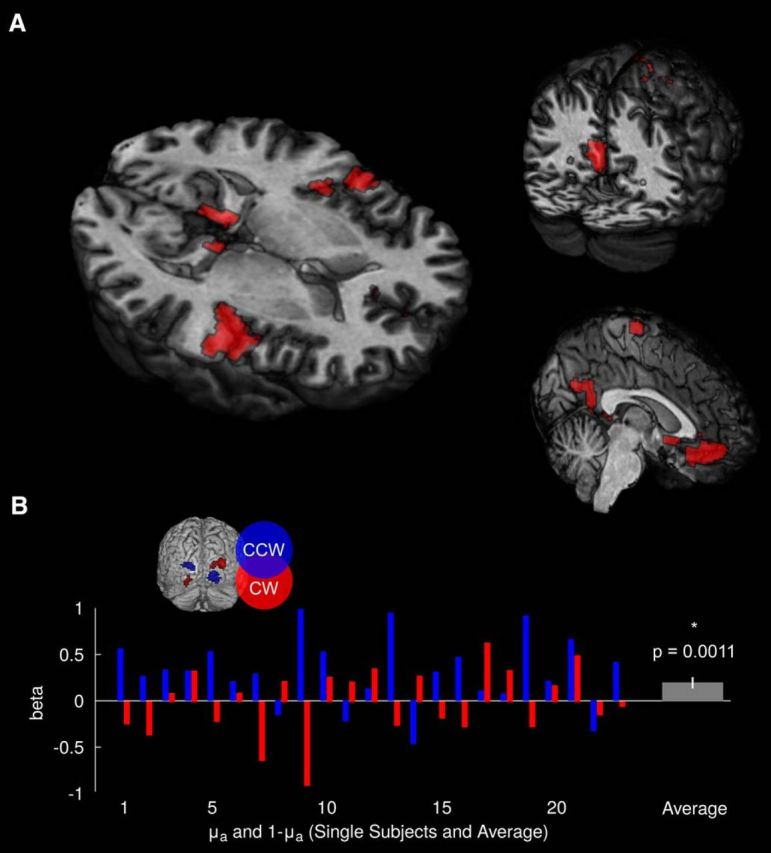
Imaging analyses. A, Whole-brain results. The time course of the “high-level” prediction about the cue–target contingency correlated with activity in bilateral medial orbital gyrus, posterior hippocampus at the intersection to the precuneus, precuneus, postcentral gyrus, as well as right insula, precentral gyrus, posterior medial frontal gyrus, and left caudate nucleus (p < 0.05, FWE). B, ROI-based analysis. Activity in retinotopic representation of the visual targets (i.e., the tilt trajectories for CW an CCW tilt) was related to the inferred conditional probability of CW (μ_a) and CCW (1 − μ_a) at the time of cue onset (p = 0.0011, t₍₂₃₎ = 3.7585, one-sided t test).

In contrast, “low-level” predictions (i.e., μ_a) were not significantly related to activity in any region of the brain when applying the same rigorous threshold (p < 0.05, FWE). However, consistent with the results of the ROI analyses described below, “low-level” predictions as expressed by μ_a correlated with activity in occipital cortex at a more liberal statistical threshold (p < 0.001, uncorrected).

The remaining parametric regressors (π̂₂, |ϵ₂|, ε_choice, |δ_q| and P(θ₁)) were added to the GLM to account for additional variance in the BOLD signal and corroborated previous neuroimaging results. The stability of the “high-level” prediction $\widehat{{\pi }_2}$, which determines how stable a given “high-level” prediction is over time, correlated with activity right Heschl's gyrus as well as left insula and right postcentral gyrus (p < 0.05, FWE). Further explorative analyses indicated that the “high-level” precision-weighted contingency prediction errors (|ϵ₂|) correlated with activity in posterior medial frontal cortex, right middle frontal gyrus, inferior parietal lobulus, left insula, and right caudate nucleus (p < 0.05, FWE), which overlaps with results from Iglesias et al. (2013).

In turn, “low-level” perceptual prediction errors (|δ_q|) were associated with BOLD activity in areas such as left insula, right precentral gyrus, and left middle temporal gyrus (p < 0.05, FWE), which is consistent with results from Weilnhammer et al. (2017). As expected, “low-level” choice prediction errors (ε_choice) and the posterior probability of CW tilt P(θ₁) were associated with activity in occipital cortex.

ROI-based analysis.

We furthermore examined how BOLD responses in retinotopic representations of motion trajectories of CW and CCW tilt across all trials would relate to conditional probabilities of the visual targets as defined by the inverted behavioral model. To account for interindividual variability in the retinotopic organization of visual cortex, our approach was based on ROIs that were functionally defined for each individual. As predicted, we found that the “low-level” prediction parametrized by the conditional probabilities of CW tilt μ_a and CCW tilt 1 − μ_a were significantly correlated with BOLD time courses in voxels corresponding to the respective trajectories of CW and CCW tilt (p = 0.0011, t₍₂₃₎ = 3.7585, one-sided one-sample t test).

The “high-level” prediction $\left|\widehat{{\mu }_2}\right|$ was not related to BOLD time courses in retinotopic stimulus representations. In an explorative analysis, we found that the posterior probabilities of CW tilt P(θ₁) and CCW tilt P(θ₀) = 1 − P(θ₁) were related to activity in voxels corresponding to the respective trajectories of CW and CCW tilt (p < 10⁻⁷, t₍₁₄₎ = 9.0292, two-sided one-sample t test). This result is expected given that this posterior also contains information of the sensory stimulation per se (CW tilt or CCW tilt). When assessing the remaining parameters of our GLM as a negative control, we did not find any significant correlation to retinotopic BOLD data for the choice prediction error ε_choice, the absolute perceptual prediction error |δ_q|, or the absolute “high-level” prediction error |ϵ₂|.

In sum, ROI-based analyses indicated that primary visual cortex implements “low-level” predictions encoding conditional visual stimulus probabilities as opposed to “high-level” predictions encoding crossmodal cue–stimulus associations.

Discussion

In this work, we studied the neural correlates of dynamically updated prior predictions and their effect on perceptual decisions in a crossmodal associative learning experiment. Crucially, this task required participants to engage in hierarchical learning to represent both the dynamically changing strength of cue–target associations as well as conditional target probabilities given a specific cue. Due to the existence of covertly interspersed ambiguous trials, our paradigm enabled us to study processes involved in perceptual inference with regard to the combination of sensory information with conditional target probabilities and prior influences from perceptual history such as priming and sensory memory. Thereby, our paradigm afforded the dissociation between “high-level” predictions about the strength of cue–target associations and “low-level” predictions about both the conditional probability of the binary visual outcome.

Conventional and model-based behavioral analyses indicated that participants successfully engaged in hierarchical associative learning. Here, perceptual decisions under ambiguity were strongly biased by changing cue–target associations. This is consistent with our previous results from an analogous behavioral experiment using ambiguous structure-from-motion spheres (Schmack et al., 2016). Both in the current and in the previous study, individual perceptual uncertainty ratings of ambiguous stimuli were not correlated to the size of the impact introduced by crossmodal associative learning. To our minds, this is most likely because the ambiguous trials elicited bistable perception while participants did not have metacognitive access to the ambiguity of the visual stimuli.

However, there is an ongoing debate about the interaction of bistable perception and perceptual uncertainty (Knapen et al., 2011). Strikingly, in the current version of the experiment using ambiguous apparent motion stimuli, the impact of associative learning was substantially greater than in our previous study using ambiguous spheres (Schmack et al., 2016). This intended difference might arise because the stimulus interpretations induced by apparent motion in our present experiment were characterized by lower perceptual certainty compared with ambiguous spheres and might thus be more susceptible to prior predictions. We believe that future studies are needed to investigate how perceptual decisions under ambiguity and their modulation by prior predictions might interact with differing levels of perceptual uncertainty.

Although conventional statistics did not show evidence for a significant contribution of sensory memory to perceptual decisions under ambiguity, the winning model from Bayesian model comparison statistics incorporated a minor impact of the factor sensory memory. This discrepancy is most likely to be caused by differences in the statistical approaches. In Bayesian analysis, the factor sensory memory is embedded within a generative model and evaluated in terms of protected exceedance probability, whereas conventional statistics look at all factors in isolation.

Importantly, our model-based fMRI results indicate that “high-level” predictions are related to activity in supra-modal brain areas such as middle orbital gyrus, insula, posterior medial frontal gyrus, postcentral gyrus, as well as the posterior hippocampus extending into the precuneus. These findings suggest that activity in such regions tracks an individual participant's trial-by-trial belief in the strength of the cue–target association. In the context of the present experiment, our results suggest that activity in these brain areas may determine the stability over time of learned associations between auditory cues and visual targets.

Therefore, increased activity in these areas reflects a currently strong “high-level” prediction. In this case, the participant strongly relies on past experiences for the prediction of future outcomes. Furthermore, an unexpected visual outcome is rather attributed to the inherent stochasticity of the experiment, that is, expected uncertainty, and has therefore relatively little effect on the currently assumed cue–outcome contingency. In contrast, decreased activity in these brain areas reflects a currently weak “high-level” prediction. In this case, the participant is unsure about the prevalent cue–outcome contingency and therefore only weakly relies on past experiences for the prediction of future outcomes. Furthermore, unexpected visual outcomes have a relatively strong affect the assumed cue–target contingency.

In more general terms, our results suggest that activity in regions such as middle orbital gyrus, insula, posterior medial frontal gyrus, postcentral gyrus, and posterior hippocampus encode the strength of an agents belief in the statistical dependencies within the environment. With regard to the example of a badminton game, this would translate to how strongly the current wind condition is believed to be stable and therefore taken into account when estimating the trajectory of the shuttlecock.

The encoding of the “high-level” prediction in these regions is consistent with results from closely related experiments on unexpected and expected uncertainty (Payzan-LeNestour et al., 2013). Here, the probability of a change in the statistical properties of the experimental environment (i.e., the negative “high-level” prediction) was negatively correlated with activity in left insula, bilateral postcentral gyrus, left hippocampus, as well as posterior cingulate cortex and left middle temporal gyrus. Furthermore, placebo experiments related activity in orbitofrontal cortex to the build-up and maintenance of predictions regarding sensory outcomes (Petrovic et al., 2002; Wager et al., 2004). Finally, a recent experiment using behavioral modeling and muscimol inactivation in rats has revealed a potential implication of both the orbitofrontal cortex as well as the dorsal hippocampus in model-based planning (Miller et al., 2017). This is interesting because behavior associated with model-based planning relates to relying on a “high-level” prediction about the statistical properties of the environment.

Another important functional aspect of brain areas coding for the “high-level” prediction could be the instantiation of the effect of predictions on sensory processing through feedback processes. Consistent with our results, regions in the orbitofrontal cortex have repeatedly been discussed as mediators for the effect of predictions on sensory processing (Bar et al., 2006; Kveraga et al., 2007; Summerfield and Koechlin, 2008). Moreover, studies on the role of predictions for perceptual inference in healthy participants and patients with paranoid schizophrenia have highlighted the impact of feedback processes from orbitofrontal cortex to sensory areas on the modulation of perceptual decisions under ambiguity by prior knowledge (Schmack et al., 2013, 2017).

In contrast to “high-level” predictions about the strength of the association between cue and target, “low-level” predictions about the conditional probabilities of binary perceptual outcomes at the time of cue presentation were reflected by retinotopic representations of the visual stimulus. This finding provides a potential neural correlate for the influence of predictions on perceptual decisions. One might speculate that this phenomenon is mediated by similar feedback mechanisms as those involved in spatial- or feature-based attention, which are known to modulate brain activity in primary visual cortex (Gandhi et al., 1999; Posner and Gilbert, 1999).

In relation to work by Iglesias et al. (2013), who focused on hierarchical precision-weighted prediction errors, our study extends these findings by looking more closely at the neural correlates of hierarchical predictions, which are key elements of hierarchical predictive coding schemes. The computation of conditional target probabilities represented in primary visual cortex is contingent on the inferred cue–target association reflected by activity in regions such as the orbitofrontal cortex, hippocampus, and precuneus. This suggests an interplay between “high-level” and “low-level” regions in human cortex via feedback connections, which might mediate the influence of prior knowledge on perceptual decisions. Therefore, the aforementioned regions and the effective connectivity between them will be interesting targets for the investigation of aberrant predictive processes in neuropsychiatric disorders such as schizophrenia (Adams et al., 2013; Powers et al., 2017).

Together, our results suggest that observers flexibly use dynamic predictions derived from hierarchical associative learning adapted to a volatile environment to perform perceptual inference. Our imaging analyses indicate that “high-level” predictions about cue–target associations are represented in supramodal brain regions such as orbitofrontal cortex and hippocampus, whereas “low-level” conditional target probabilities are associated with activity in primary visual areas, providing a potential neural correlate for the influence of prior knowledge on perceptual decisions.