Rhythm and Synchrony in a Cortical Network Model

Abstract

We studied mechanisms for cortical gamma-band activity in the cerebral cortex and identified neurobiological factors that affect such activity. This was done by analyzing the behavior of a previously developed, data-driven, large-scale network model that simulated many visual functions of monkey V1 cortex (Chariker et al., 2016). Gamma activity was an emergent property of the model. The model's gamma activity, like that of the real cortex, was (1) episodic, (2) variable in frequency and phase, and (3) graded in power with stimulus variables like orientation. The spike firing of the model's neuronal population was only partially synchronous during multiple firing events (MFEs) that occurred at gamma rates. Detailed analysis of the model's MFEs showed that gamma-band activity was multidimensional in its sources. Most spikes were evoked by excitatory inputs. A large fraction of these inputs came from recurrent excitation within the local circuit, but feedforward and feedback excitation also contributed, either through direct pulsing or by raising the overall baseline. Inhibition was responsible for ending MFEs, but disinhibition led directly to only a small minority of the synchronized spikes. As a potential explanation for the wide range of gamma characteristics observed in different parts of cortex, we found that the relative rise times of AMPA and GABA synaptic conductances have a strong effect on the degree of synchrony in gamma.

SIGNIFICANCE STATEMENT Canonical computations used throughout the cerebral cortex are performed in primary visual cortex (V1). Providing theoretical mechanisms for these computations will advance understanding of computation throughout cortex. We studied one dynamical feature, gamma-band rhythms, in a large-scale, data-driven, computational model of monkey V1. Our most significant conclusion is that the sources of gamma band activity are multidimensional. A second major finding is that the relative rise times of excitatory and inhibitory synaptic potentials have strong effects on spike synchrony and peak gamma band power. Insight gained from studying our V1 model can shed light on the functions of other cortical regions.

Introduction

Because it is found all over the cerebral cortex and is associated with important cortical functions and also malfunctions, gamma-band activity is of continuing interest in neuroscience (Wang, 2010; Buzsáki and Wang, 2012; Cardin, 2016). Cortical gamma-band activity is often measured in the local field potential (LFP). When cortex is idling, LFP fluctuations are apparently random with a 1/f power spectral density (PSD) (Pesaran et al., 2002; Henrie and Shapley, 2005; Jia et al., 2011). However, when cortex is activated by a stimulus or task, usually the PSD of the LFP fluctuations develops a bump in the gamma-band between 30 and 80 Hz (Eckhorn et al., 1988; Buzsáki et al., 2003). Gamma activity usually wanders in phase and frequency (Bragin et al., 1995; Livingstone, 1996; Womelsdorf et al., 2007; Xing et al., 2012). Therefore, the PSD of gamma is a broad spectral bump not a narrow line, in primate primary visual cortex (V1) (Eckhorn et al., 1988; Ray and Maunsell, 2010; Jia et al., 2011) and in rodent hippocampus (Montgomery et al., 2008). Gamma is episodic not continuous; there are bursts of gamma interrupted by quiescent periods (Burns et al., 2011; Xing et al., 2012; Burke et al., 2015; Cardin, 2016). Gamma-band activity can be graded. Gamma power, and the sharpness of its tuning in frequency, can be modulated by bottom-up, feedforward input, as in visual input to the V1 cortex, where gamma characteristics are known to depend on orientation (Gray and Singer, 1989; Frien et al., 2000; Volgushev et al., 2002; Kayser and König, 2004), contrast (Henrie and Shapley, 2005), and size of visual stimuli (Ray and Maunsell, 2010). Gamma-band activity also can be modulated by top-down influence. Increased gamma power, for example, has been observed in cortical area V4 when attention increases (Fries et al., 2001; Womelsdorf et al., 2007). Explaining such diverse data about gamma requires a new theoretical understanding of how gamma is generated (cf. Cardin, 2016; Sohal, 2016).

Given all the interest in gamma band rhythms, we revisit the theoretical question of how gamma is produced and offer a new concept of what causes cortical synchrony and gamma band peaks. The main idea is that multiple sources of synaptic drive interact to produce gamma's diverse properties. Model simulations showed that the delicate temporal balance between recurrent excitation and local circuit inhibition that produces synchronous spike firing is an important component, as suggested by Rangan and Young (2013), and consistent with the observations of Okun and Lampl (2008) on the close tracking of E and I currents in time. Pulses of feedforward and feedback excitation also influence synchronous cortical spiking in the gamma-band by altering momentarily the cell's operating point; such modulation could explain both attention's top-down effect, and sensory drive's bottom-up induction of gamma-band synchrony. Finally, we found that synchronous spiking depends on cellular biophysics, including the rise and decay times of synaptic excitatory and inhibitory conductances. Their effects on synaptic rise times, coupled with recurrent excitation, could help to explain the efficacy of learning or drugs in changing gamma.

The new explanation offered here was found through analysis of cortical activity with a large-scale, data-driven model of macaque V1 (Chariker et al., 2016). For brevity, we will refer to the model as the “CSY model”. The CSY model was developed to explain population distributions of firing rates and feature selectivities in V1; its architecture was based on neuroanatomy and it simulates the visual properties of V1 very well. When the CSY model was visually driven, gamma-band activity emerged in the model's spiking activity as it does in V1. The realism of the CSY model offers a better window into gamma-band activity in the real cortex than was available previously. Because there is similarity of circuitry in different cortical regions, and gamma-band activity is ubiquitous, we believe that the findings of this paper probably will apply throughout cerebral cortex, far beyond the specific model used.

Materials and Methods

The CSY model

The CSY model (Chariker et al., 2016) is a realistic, conductance-based model of layer 4Cα, the input layer in the Magnocellular pathway, of the macaque V1 cortex. This model is realistic in the sense that as much neuroanatomy was incorporated into the network architecture as possible. Model parameters were chosen to conform to firing rates of real cortex under a variety of conditions. The model's outputs replicated data of many visual properties, including orientation and spatial frequency selectivity, bimodal distribution of simple and complex cells, diversity of neuronal responses, intracellular dynamics, and, most relevant to the present study, gamma-band rhythms. We refer the reader to Chariker et al. (2016) for details, recalling here only some basic facts. The main components of the CSY model are (1) a 9-hypercolumn sheet of layer 4Cα of the V1 cortex, located at ∼5 degrees eccentricity, (2) two sheets of LGN cells (left and right eye) that project to this region of cortex, and (3) outputs of layer 6 to layer 4Cα providing “feedback” to layer 4Cα.

Layer 4Cα in the model consisted of ∼4000 cells per hypercolumn of which 75% are excitatory (E) and 25% inhibitory (I). The peak probability of connection between E- and E-cells was ∼15%. Peak probabilities of E-I, I-E, and I-I were ∼60% (Holmgren et al., 2003; Oswald and Reyes, 2011). Connectivity was assumed to be isotropic, and the probability of connection declined with distance consistent with data on local circuitry (Oswald and Reyes, 2011). Following Connolly and van Essen (1984) and Silveira and Perry (1991), we assumed that the receptive fields of ∼10 LGN cells, 5 ON and 5 OFF, occupy each region corresponding to a hypercolumn. Layer 6 was modeled as a network driven by independent sources. This network produced a constant firing rate, which we modified (through spike duplication and deletion) to achieve firing rates that matched data on layer 6 outputs. The model of layer 6 used in the present paper is an improvement over that in (Chariker et al., 2016) in that the baseline firing rate was higher, resulting in less synchronized projections that resembled experimental data better (Ringach et al., 2002; Xing et al., 2012).

Individual cells in layer 4Cα were modeled as leaky integrate-and-fire (LIF) neurons. That is, the membrane potential v of a neuron of type σ = E or I was governed by the LIF equation:

Normalized voltage units were used. The membrane potential v was driven toward its spike firing threshold V_th = 1. At threshold, a spike was fired and v was reset to the resting potential V_rest = 0. Membrane capacitance was normalized to 1. Therefore, conductance was proportional to the inverse of the membrane time constant and has the same units, sec⁻¹. A normalized conductance of 1000 s⁻¹ was equivalent to ∼20 nS. Membrane current was conductance scaled by the difference between membrane potential and the reversal potential for the particular conductance channel. The currents also were calculated in normalized units where, for current, sec⁻¹ is equivalent to 300 pA. In the LIF equation, t was in seconds, the leakage conductance g_R,σ was set to 50 s⁻¹ for σ = E and 1.33 × 50 s⁻¹ for σ = I (Beierlein et al., 2003). g_E(t) and g_I(t) were the E- and I-conductances of the neuron in question at time t; their time evolutions are described below. Finally, V_E and V_I were E- and I-reversal potentials, which in normalized coordinates are 14/3 and −2/3, respectively.

The evolution of g_I(t), the I-conductance in a neuron of type σ = E or I, is given by the following:

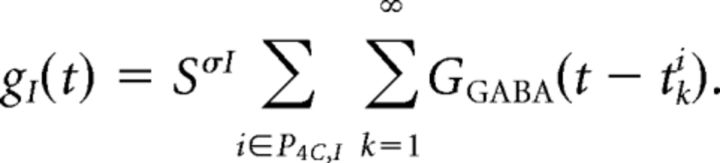Here S^σI is the synaptic weight, or the constant describing the change in I-conductance in the neuron in question upon receiving synaptic input from an inhibitory neuron. The first summation in the equation for g_I(t) is over all I-neurons in P_4C,I, defined to be the set of all I-neurons in layer 4Cα that synapse on this neuron. The second summation is over the spikes fired by neuron i. Specifically, tⁱ_k is the time of the kth spike fired by neuron i, and G_GABA (s) describes the time course of I-conductance for a neuron when a spike is fired by a presynaptic I-neuron at time s = 0.

The E-conductance g_E(t) was defined similarly to g_I(t) except that it was the sum of four terms, describing synaptic conductances coming from (1) LGN, (2) E-neurons from within layer 4Cα, (3) E-neurons from layer 6, and (4) neuromodulatory influences from the rest of the brain or body. Each term has its own synaptic weight: S^σ,LGN for (1), S^σE for (2), S₆^σE for (3) etc. Details about excitatory synaptic conductances were provided previously (Chariker et al., 2016).

The procedure for determining the many parameters needed to define the CSY model was systematic and data-driven. Complete details about parameter determination were described previously (Chariker et al., 2016, in Materials and Methods).

In the present model, the time courses G_AMPA(t) and G_GABA(t) were different from those in our previous work (Chariker et al., 2016), which used the same conductance time courses as in Tao et al. (2004). Here the rise times were faster and more consistent with data (Nusser et al., 2001; Atallah and Scanziani, 2009; Oswald and Reyes, 2011). The function G_AMPA(t) [resp. G_GABA(t)] was defined to be the difference of two exponentials, i.e.:

We refer to τ_rise^AMPA as the rise time of AMPA, and τ_decay^AMPA as its decay time. I-conductance time courses were defined similarly, with τ_rise^GABA and τ_decay^GABA as rise and decay times. In the simulations in this paper we used τ_rise^AMPA = τ_rise^GABA = 0.5 ms, τ_decay^AMPA = 2 ms and τ_decay^GABA = 5 ms; see Figure 6 for a depiction of the time courses used.

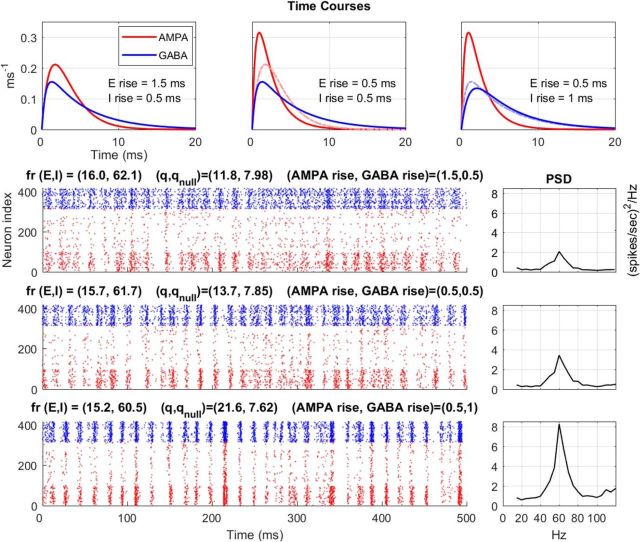
Figure 6.

Conductance dynamics effects on synchrony and PSD in model cortex. In the top row are drawn the relative rise times of E (AMPA) and I (GABA) conductances in three different regimes, three different cortical states as it were. Below the conductance plots are three rows of rasters with their corresponding PSDs. The left, middle, and right conductance plots correspond to the top, middle, and bottom rasters, respectively. Each raster depicts the spiking of 400 neurons within an orientation domain when the model cortex is stimulated by a drifting grating in the optimal orientation for the domain. As before, red dots stand for E-cell spikes; blue dots stand for I-cell spikes. Vertical axis of the raster is cell index. Above each raster are written the mean firing rates for E- and I-cells, and the synchrony measures (q values; see Materials and Methods) for each condition. What are varied from raster to raster are the rise times of E and I; all other parameters are identical. The middle raster is for the CSY model; its rise times for both E and I are 0.5 ms. Compared with the middle row, E rise time in the top row is slowed down by 1 ms, and I rise time in the bottom row is slowed down by 0.5 ms. These small differences in rise times (dashed lines in each conductance plot showing what was changed from the previous one) led to the marked changes in synchrony and sizes of PSD peaks. The synchrony index ratio (q/q_null) for each of the three rasters was 1.47 ± 0.01, 1.77 ± 0.02, and 2.87 ± 0.03, respectively, from top to bottom. The PSD peaks had standard deviations, respectively, from top to bottom of ±0.09, 0.14, and 0.46 (spikes/s)²/Hz.

As in Chariker et al. (2016), to test the model we used as visual stimuli sine gratings of high contrast, drifting at a rate of 4 Hz, similar to stimuli used in many experimental studies of V1 function. Each simulation was the model's response to 5 s of grating stimulation.

Two important features of the present version of the CSY model were that (1) its neuronal activity was driven by dynamical interactions among neurons that were not prescribed by transducer functions, and (2) it was driven more by corticocortical input than by feedforward input from LGN (Douglas and Martin, 2004; Angelucci and Sainsbury, 2006); only ∼10% of excitatory current received by an E-neuron came from LGN.

Analytical tools

Fourier PSD.

The power spectrum (more technically the power spectral density (PSD)) is a measure of the variance in a signal as a function of frequency; it is the Fourier transform of the signal's autocorrelation function (Wiener, 1933). In the case of neuronal populations, the signal is the spike density (SD): the sum of all spikes in the population that occur in the time bin (t, t+Δt), as a function of running time, t. In this paper, we used time bins Δt of width 2.5 ms to compute SD. The PSD was then computed using overlapping windows of 200 ms. Three to four seconds of data were used for each PSD computation (note similar plots by Geisler et al., 2005). The PSD of summed spikes was computed as follows: consider a patch of cortex consisting of N neurons. For a fixed time interval (0, T), which we divide into time bins B_n = [(n−1)Δt, nΔt], n = 1,2, …, the SD u_n per neuron in B_n is given by u_n = m_n/(NΔt) where m_n is the total number of spikes fired in B_n. The discrete Fourier transform of {u_n} on (0, T) is then given by the following:

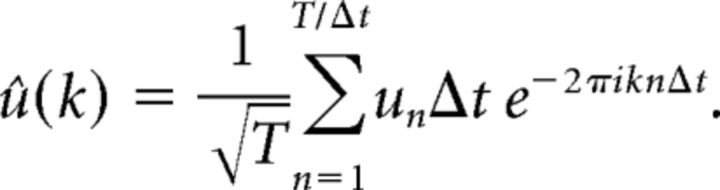The “power” concentrated at frequency k is defined to be |û(k)|², and this quantity as a function of k is called the PSD.

For the PSDs computed in this paper, we used T = 0.2 s, Δt = 0.0025 s. PSD plots were obtained as averages over sliding windows of length T with starting times increasing in increments of 0.0025 s, i.e., we treated the spike densities as a stochastic process which we sampled on time intervals (0, T), (0.0025, T+0.0025), (0.005, T+0.005), … over 3–4 s, then averaged the PSDs of the samples (cf. Jenkins and Watts, 1968).

Spike synchrony index.

We found that gamma-band activity was evident in population spike trains as rhythmic clustering of spikes in synchronous packets across the population of model neurons (Fig. 1A). In model regimes that simulated the real cortex, synchrony was only partial: although there was a tendency for neurons to spike in clusters, such clusters seldom involved large fractions of the local population. It is necessary, therefore, to have a quantitative measure to differentiate between the various degrees of synchrony. PSD captures more the presence of periodicity than synchrony. To capture directly the degree of synchrony, we developed the following quantity called spike synchrony index (SSI):

Figure 1.

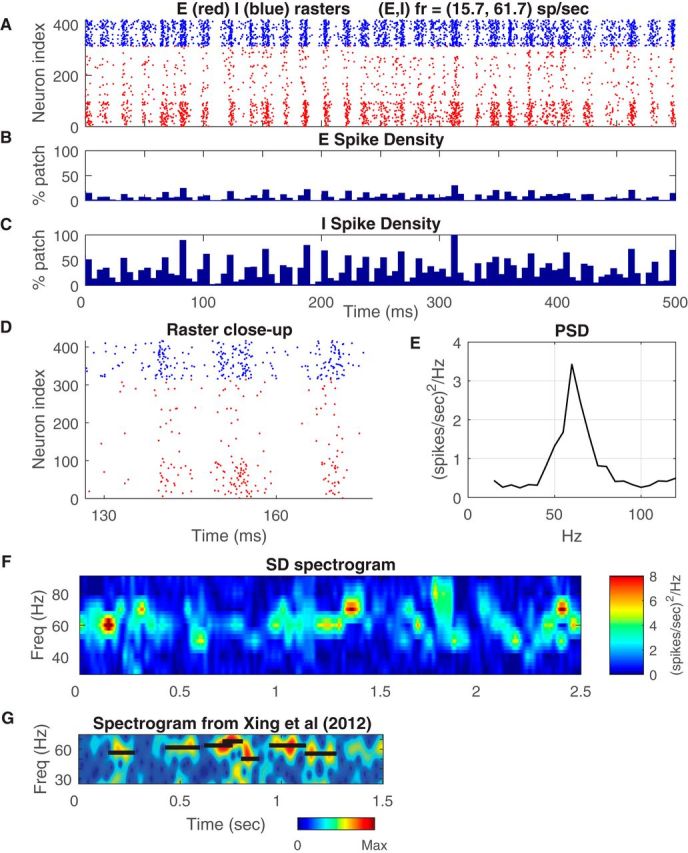
Dynamics of local population in the CSY model. A, Rasters of spikes of cells in a patch of 400 E- and I-cells in the vertical-preferring domain of a cortical hypercolumn. These are spike time rasters during stimulation by an optimal (vertical) grating, drifting at 4 Hz (250 ms period). The x-axis is time; y-axis is neuron index within the patch. E-cell spikes are red dots, sorted by decreasing number of LGN inputs: the cells near the bottom are likely complex; I-cell spikes are blue dots. B, SD of the E population as a function of time, shown in 5 ms windows. Vertical scale is the fraction of the total number of cells in the patch spiking in that window. C, Corresponding SD plot of the I population. D, Magnified view of the raster in A. SSI/SSI_null for this population ∼1.8 ± 0.01. E, PSD of the SD of the E-cells in A, indicating broadband fluctuations with a peak in the gamma-band at ∼60 Hz. At peak, the standard deviation of the PSD was ± 0.14 (spikes/s)² /Hz. F, Time-frequency analysis of SD. PSD of SD calculated within sliding windows of 200 ms, for the same data as in A. G, Similar time-frequency analysis of LFP data of response to a high contrast drifting grating in awake macaque V1 (Xing et al., 2012). The black horizontal bars mark the peak frequency and the duration of each LFP gamma band burst as calculated by Xing et al. (2012).

Fix a window of length w ms (we found that w between 2 and 8 ms is optimal for viewing rhythms in the gamma-band). If a spike is fired at time t, we computed the following:

Suppose the total number of neurons in the local population was N. Then for w small enough, we assumed that n(t)/N is the fraction of the population firing “at roughly the same time”, and defined SSI of the system to be the average of n(t)/N, the average being taken over all spikes. We averaged this quantity over all spikes (and not over all time bins) because synchrony is about coactivation, and to capture coactivation, one is interested in the level of activity in the population when a spike is fired.

Thus, if a system fired only full population spikes, and w was chosen so that they all fell within a single window length, then SSI = 1, the maximum possible value for SSI. The smaller the SSI, the less synchronous the spike firing of the system. For systems in which SSI is far <1, it is illuminating to ask how far the system is from a “null model”, defined to be a model in which spikes occur independently and randomly in time, in a Poisson point process. To that end, we defined the SSI_null of a model to be the SSI of the null model with the same firing rate, i.e., for a system with a mean spike rate of r spikes/s per neuron, SSI_null = r × w/1000 where w is the time window (in ms) used in the computation of SSI. Thus, the closer the SSI/SSI_null ratio was to 1, the more randomly timed the spike firing was.

We will sometimes use the more compact notation “q” and “q_null”, defined to be 100 × SSI and 100 × SSI_null, respectively, so that q = 16 means that on average 16% of the population is activated when one neuron spikes. In this paper the calculation of SSI used window size w = 5 ms, which we found to be optimal after trying larger and smaller windows.

There are obvious conceptual similarities between SSI and notions such as spike field coherence (SFC) (Fries, 2005; Chalk et al., 2010), and paired correlations (e.g., Smith et al., 2013). SSI differs from SFC because it is concerned with spike-spike synchrony. It differs from pairwise correlation in its emphasis on population activity: SSI measures how the spike firing of a neuron is correlated to that of its entire local population because that is what synchrony is about.

Statistical analyses of model simulations.

The reliability of the estimates of SSI, PSD, and the population analysis in Figure 5 was tested by running fifty repeats of the model's response with different random seeds. The random seeds determined the values used to set the following randomized parameters in the CSY model (Chariker et al., 2016): variability in synaptic coupling between cells, the times of ambient kicks, the random component of the input current to LGN cells, the timing of layer 6 feedback, the initial membrane voltage at the start of a run. Average and SD of model results were calculated over the 50 repeats. Error bars are shown for statistics involving individual behaviors of samples of neurons as in Figure 2H. For time averages of population statistics that are expected to converge to their theoretical means by the Ergodic theorem upon adequate sampling, we have included error bounds (±1 standard deviation) to indicate the degree of convergence in the figure legends for Figures 1E, 3B, 5, and 6.

Figure 5.

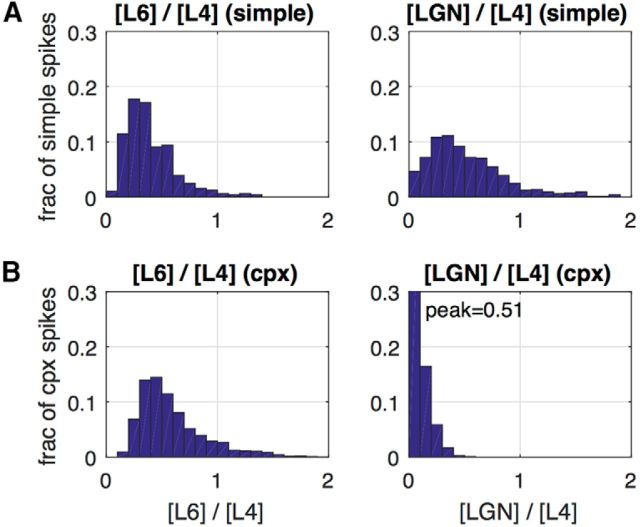
Contributions of different sources of excitatory current to spike-firing in model E-cells; population histograms. Components of excitatory current in the 5 ms interval preceding each spike. A, Simple cells. B, Complex cells. Left, The distribution of the ratio of layer 6 to layer 4 current across the population of neurons in the E-cell population. Plotted is the fraction of spikes with a particular layer 6–layer 4 ratio. The mean value for simple E-cells of the L6/L4 distribution was 0.41 ± 0.02. For complex cells, the mean L6–L4 ratio was 0.59 ± 0.02. Right, The distribution of the ratio of LGN to layer 4 current across the population of neurons in the E-cell population. Plotted is the fraction of spikes with a particular LGN–layer 4 ratio. For simple cells, the mean LGN–L4 ratio was 0.59 ± 0.03, whereas for complex cells it was 0.08 ± 0.003.

Figure 2.

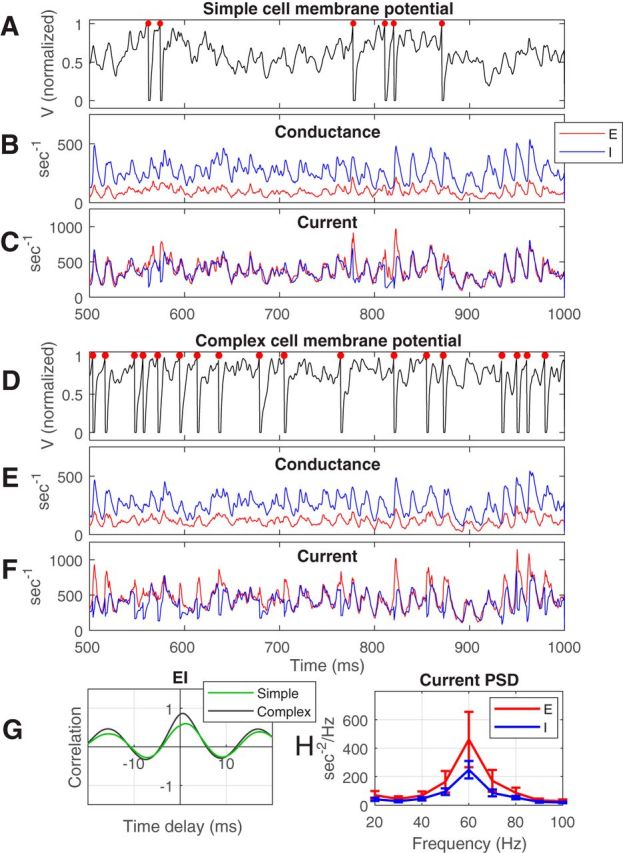
Intracellular voltages and conductances of visually driven E- and I-cells in the CSY model. A, Membrane potential of a model simple cell that is part of the population in Figure 1A, driven by an optimal stimulus. B, C, Membrane conductance and currents, respectively, for the same simple cell. D–F, Corresponding plots (voltage, conductance, current) for a complex E-cell. E-conductance is drawn in red and I-conductance in blue. Notice that E- and I-currents are almost balanced almost all the time. G, Cross-correlation between the E- and I-currents in F and C, respectively. H, Average PSD of the E and I currents of 32 randomly chosen simple cells and 32 complex cells in the same population as in Figure 1A. PSDs were computed for each cell and the PSDs were averaged. Error bars mark 1 standard deviation.

Figure 3.

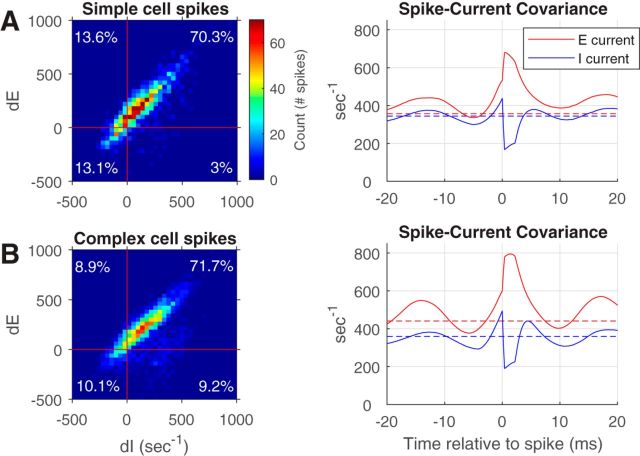
2-D histograms and spike-current cross-covariances for simple and complex E-cells. A, Left, 2-D histogram of the change in the E- and I-currents in the 5 ms preceding a spike for randomly chosen simple cells in a local population. The percentage of spikes with dE and dI both positive preceding a spike is indicated in the top right corner as 70.3%. The percentage of spikes that had dE and dI both negative preceding a spike is written in the bottom left corner as 13.1%. Right, Spike-current covariance for the same simple cell population confirms that the average E-current and I-current were both increasing before the occurrence of a spike. A and B, Dashed horizontal lines are plots of the spike-current covariance when spike times are placed randomly in time; they indicate a baseline for the covariance. The abrupt jump up in E-current and the abrupt downswing in I-current at t = 0 in the spike-current covariance plots is a consequence of the integrate-and-fire mechanism used in the model. After a spike, the membrane potential is reset to 0, suddenly changing the driving force for E- and I-current. B, These are the corresponding plots for a population of complex cells. The maximum standard deviation of the covariances was ±40 s⁻¹.

Results

Three groups of results will be presented.

The first group (Figs. 1, 2) consists of more detailed documentation of the gamma-band activity in the CSY model than in our previous work (Chariker et al., 2016). Here we present analysis of the model's (1) synchronous spike firing in local populations, and (2) fluctuations in the synaptic conductances, currents, and membrane potentials of model neurons.

The second group of results (Figs. 3–5) is an in-depth analysis of the mechanism for spike firing in gamma band activity. We review some previously proposed mechanisms and examined their validity, as well as the possibility of new mechanisms, using the CSY model. Here is where we found the multidimensional nature of cortical gamma band activity.

The third group of results (Fig. 6) is about our new observation that partial spike-synchrony in local populations depends on cellular biophysics and how this dependence can be explained by the dynamics of interactions in the CSY model.

Emergent gamma-band spiking in the CSY model

Gamma-band activity is generated in many different recurrent models as has been documented in the literature (Brunel and Wang, 2003; Rangan and Young, 2013; Chariker and Young, 2015). Unlike these earlier models, the CSY model was designed to simulate V1 in a realistic manner. We studied how gamma-band activity was generated in the CSY model to learn what factors led to the properties of gamma activity in the real cortex. Gamma-band activity in the CSY model was observable as clustering of spikes in raster plots of population spike activity. Figure 1A is a plot of spike rasters for 300+ E-neurons and ∼100 I-neurons in one orientation domain of the CSY model. These are rasters of driven activity; neurons were responding to a visual stimulus in the form of a sinusoidal grating drifting at a rate of 4 Hz.

There were clearly identifiable “spiking events”, characterized by brief durations of synchronized spiking across the population, as evidenced by the vertical bands in the raster plot (Fig. 1A). Rangan and Young (2013) called spike clusters like these MFEs. The rate of occurrence of MFEs is in the gamma-band of frequencies. Observe that E- and I-neurons (colored red and blue, respectively) tended to spike together and roughly synchronously in MFEs. We will analyze this partially synchronous firing in detail below, but wish to be clear from the start that there was nothing in the design of the model or in the visual stimulus that instructed E- and I-neurons to coordinate their spike firing in the manner shown. Therefore, MFEs occurring at frequencies in the gamma-band were emergent phenomena.

Layer 4Cα neurons have the same range of orientation selectivity as neurons in other layers of macaque V1 (Livingstone and Hubel, 1984; Ringach et al., 2002). The grating used as a visual stimulus in the model simulations was chosen to have an orientation that was aligned with the population's preferred orientation, and it was a high-contrast grating, so that it produced a large visual response. Gamma-band activity in V1 (Gray and Singer, 1989; Frien et al., 2000; Volgushev et al., 2002; Kayser and König, 2004) and in the CSY model (Chariker et al., 2016) was orientation-selective.

The spike clustering illustrated in Figure 1A is what we mean by population synchrony of spike firing. It should not be confused with what others have termed “the synchronous state” (Brunel and Hakim, 1999; Brunel, 2000). We used the term “synchrony” to mean coordinated spike firing in MFEs that is not necessarily periodic; our use of the term synchrony is similar to how it has been used by many others: Gray and Singer (1989), White et al. (1998), Fries et al. (2001), Börgers and Kopell (2003), and Martin and Schröder (2016).

Spike density

The fraction of the neuronal population that participated in each MFE is a crucial characteristic that differentiates between models. Raster plots like Figure 1A with over 400 neurons can be misleading: they may give the impression that the entire population was spiking in synchrony when only a small fraction of the population was. Therefore, to get a quantitative estimate of synchrony, we calculated the spike density (SD), the fraction of the population of neurons that fired spikes within a narrow bin of time. SD, expressed as a percentage of the population active within 5 ms windows, is plotted in Figure 1B for E-cells, and in Figure 1C for I-cells (other authors have referred to measures proportional to the SD as “the population firing rate”; Geisler et al., 2005). The SD reveals that the fraction of E-cells that participated in any one MFE seldom exceeded 0.2 (Fig. 1B). Although MFEs for the I-cell population are larger, most of them were not close to being full population spikes (Fig. 1C). Partial synchrony can explain what has been reported about the real cortex, that gamma-band activity can be observed in multiunit spike activity but rarely in single-unit spike activity (Zeitler et al., 2006). Many LFP data obtained in experiments on the cortex indicate that the spike synchrony associated with gamma-band activity is only partial (Eckhorn et al., 1988; Henrie and Shapley, 2005; Zeitler et al., 2006; Ray and Maunsell, 2010; Jia et al., 2011). Such partial synchrony has been observed also in other network models (Brunel and Wang, 2003; Geisler et al., 2005).

To help the reader interpret Figure 1A–C, 1D depicts a zoomed-in raster plot of the spikes in a 40 ms time interval from the raster in 1A. In the zoomed-in raster, you can see that the 300 excitatory neurons in the population did not all fire synchronously during an MFE. Consistent with the SD plots of Figure 1, B and C, only a fraction fired in any one MFE. The SDs in Figure 1B, C, and the zoomed-in view of the spike rasters in 1D are support for the statement that there was only partial synchrony in the CSY model.

Spike synchrony index

In Materials and Methods, we introduced a measure of spike synchrony in a population of spiking neurons, namely the spike synchrony index (SSI). SSI is defined as the fraction of the population that spiked within a brief window centered at each spike, averaged over all spikes. For the E-cell population in the model under the conditions of the experiment in Figure 1A, SSI = 0.138, so on average slightly <14% of E-cells in the population fired together. To gauge the amount of accidental synchrony caused by spike coincidences that occur by chance, we calculated SSI_null, the SSI of a population of independent Poisson pulse trains with the same mean spike rate as the population under study (see Materials and Methods). In the E-cell population in Figure 1, SSI_null = 0.078, so the amount of synchrony over that caused by chance, {SSI/SSI_null}, was 1.77 ± 0.02. In the I-cell population, {SSI/SSI_null} was approximately the same as for E-cells, ∼1.8 ± 0.02.

To gauge the meaning of {SSI/SSI_null}, consider two extreme scenarios. A population of Poisson pulse trains must have {SSI/SSI_null} = 1, which is the lower bound of {SSI/SSI_null}. To get the upper bound we consider total synchrony, i.e., population spikes. If all MFEs were population spikes in which 100% of cells fired together, then SSI = 1, and {SSI/SSI_null} depends on spike rate and window size. We used window size = 5 ms throughout. In the simulations shown, the average response rate was 16 spikes/s. Therefore SSI_null = 16 × 0.005 = 0.08. Then {SSI/SSI_null} = 1/0.08 = 12.5 for population spikes with the mean rate of the simulated cortex. Therefore, the model's {SSI/SSI_null} = 1.77 indicates that the E-cell population in the CSY model was significantly more synchronous than a population of randomly spiking neurons but much less synchronous than a network firing population spikes.

Power spectral density

Gamma-band activity has often been analyzed by studying the power spectrum of neuronal population activity. The plot in Figure 1E is an illustration of the PSD of the spiking activity of E-cells in the CSY model (see Materials and Methods, Analytical Tools). The PSD had a broad peak centered on 60 Hz. Note that the PSD plotted in Figure 1E (and later in other figures) is that of spike rate and not of LFP, which is known to contain large low-frequency components in addition to a gamma peak (Pesaran et al., 2002; Henrie and Shapley, 2005; Jia et al., 2011). The breadth of the gamma-band peak in the model's PSD resembled what is observed in V1 LFP data (Henrie and Shapley, 2005; Jia et al., 2011; among others). The breadth of the peak can be quantified by its half-width at half-height, which in Figure 1E is ∼20 Hz. This is similar to the observed breadth of gamma band peaks in published V1 data (Henrie and Shapley, 2005; Jia et al., 2011). The peak's breadth was consistent with the fact that frequency and phase of gamma-band fluctuations were not constant over time, as in LFP data (Livingstone, 1996; Burns et al., 2010, 2011; Jia et al., 2011; Xing et al., 2012; Burke et al., 2015).

In the Introduction it was noted that gamma-band activity in V1 (and other cortical areas) is episodic and bursty, and that frequency and phase of gamma-band fluctuations were not constant over time. The SD plots in Figure 1, B and C, support the statement that gamma-band activity is episodic in the CSY model. Further proof was obtained by time-frequency analysis of the SD plots, by computing the PSD over a 200 ms window every 2.5 ms. The spectrogram was smoothed by averaging each time bin with the 8 adjacent earlier and later time bins (±20 ms) and by plotting the smoothed spectra versus time as a spectrogram as was done previously for the LFP (Burns et al., 2011; Xing et al., 2012). A representative spectrogram of the CSY model's SD is plotted in Figure 1F, and it offers a vivid illustration of amplitude and frequency variability that has been observed in V1 spectrograms, with bursts of high amplitude gamma interrupted by periods of lower amplitude, and variability in the locus in frequency of highest amplitude. The similarity of the model's spectrogram with data can be seen by comparing the model's spectrogram in Figure 1F with a spectrogram of LFP data (Xing et al., 2012) from macaque V1 cortex, in Figure 1G. Data and model agree that gamma activity is episodic (cf. Cardin, 2016).

It is worth stating that the CSY model was not tuned to produce gamma band activity, but rather gamma was an emergent property of the model. Chariker and Young, (2015) demonstrated in detail and explicitly that many different parameter choices in recurrent networks produce gamma band activity. Synchronous firing in the gamma band range in the CSY model relied on our use of biophysical time constants but was not caused by the tuning of parameters in a narrow range.

Membrane conductance, currents, and spike firing in model simple and complex cells

In the CSY model, as in other conductance-based neural models, intracellular conductances and currents determined the membrane potential and spike firing. Figure 2 describes the intracellular dynamics for a simple E-cell (A–C) and a complex E-cell (D–F) from the population of neurons represented in Figure 1. We present model data separately for simple and complex excitatory cells because the simple/complex dichotomy is of functional importance for the visual cortex (Hubel and Wiesel, 1962; De Valois et al., 1982) and because simple and complex cells have different spike firing patterns. Spiking in simple cells in the CSY model followed more faithfully the luminance variation in the visual image, whereas spiking in model complex cells was increased but not modulated much or at all by the passage of the bars in gratings, as in the real cortex (Maffei and Fiorentini, 1973; De Valois et al., 1982). The CSY model produced simple and complex cells because of differential amounts of connectivity to LGN feedforward inputs (Chariker et al., 2016).

Dynamics of membrane potentials, currents, and conductances

One crucial prediction of the CSY model is that E- and I-conductances and currents should covary in detail in time. Figure 2 shows the waveforms of membrane potentials, conductances, and currents in two representative model neurons over the same stretch of time during a period of visual stimulation. E-conductance (red) describes the summed excitatory synaptic drive from all E-synapses on the neurons, whereas I-conductance (blue) is the summed inhibitory synaptic bombardment (Fig. 2B,E). I-conductance was significantly larger than E-conductance, but both conductances had very similar temporal structure in each neuron.

The membrane potentials, currents, and conductances were related to gamma-band activity in the spike rasters (Fig. 1A). The time series of the currents in Figure 2C, F together with the PSD of the currents in Figure 2H show that (1) membrane current fluctuations were in the gamma-band, (2) the membrane potentials rose and fell in irregular ways, and (3) there were more peaks in the membrane potentials than there were spikes. As expected from the LIF equations that govern the time evolution of membrane potentials in neurons in the CSY model (see Materials and Methods), spike firing was controlled by the difference of E- and I-currents. Spikes occurred when the E-current into the cell exceeded the I-current by a certain amount (Fig. 2: compare A and C, D and F). The results in Figure 2 could only have been obtained in a conductance-based model like CSY; rate-based models could not reveal the links between network dynamics and intracellular conductances and currents.

Cross-correlation between E- and I-currents

To obtain a quantitative estimate of the covariation of E- and I-currents in the CSY model, we calculated the cross-correlation between E- and I-currents:

where < … > means average over time, and σ_E and σ_I are the standard deviations of the E- and I-currents. The results (Fig. 2G) indicated that fluctuations of E- and I-currents were approximately simultaneous, with a 0 time offset for the simple cell and with E-current arriving slightly ahead of I-current for the complex cell; the offset is small compared with the breadth of the cross-correlations.

The incoming currents to a cell, which can be seen as a summary of the spike firing activity in the local population, showed much stronger gamma-band characteristics than the spiking patterns of individual cells (Fig. 2). That is the reason we characterized the model spiking behavior in terms of population measures of spike firing like SD, and population measures of synchrony like SSI rather than simulating and analyzing pairwise correlations that are known to be weak in the cortex (Smith et al., 2013) as expected theoretically (Renart et al., 2010). The CSY model's result, that gamma-band rhythms were produced collectively in local populations but were not readily apparent by examining one or even a few neurons at a time, is consistent with cortical data (Fries et al., 2001; Zeitler et al., 2006) and with other theory papers (Brunel and Wang, 2003; Geisler et al., 2005; Rangan and Young, 2013; Chariker et al., 2016).

Previously proposed mechanisms for gamma-band activity

To facilitate the mechanistic explanations of the model results in Figures 1 and 2, we first recall some previous theories of gamma-band phenomena. A number of models of gamma-band activity exist in the literature. A long but incomplete list includes Leung (1982); Traub et al. (1996); Wang and Buzsáki (1996); Ermentrout and Kopell (1998); White et al. (1998); Brunel and Hakim (1999); Traub et al. (1999); Whittington et al. (2000); Tiesinga et al. (2001); Börgers and Kopell (2003); Brunel and Wang (2003); Rangan and Young (2013); Chariker and Young (2015); and Börgers (2017). From this by no means exhaustive list (for review, see Wang, 2010) we compare and contrast two main proposed explanations for how gamma-band activity comes about. One is the PING mechanism of Whittington et al. (2000) and Börgers (2017), and the other is what we call the REI (recurrent excitation inhibition mechanism) for MFEs (Rangan and Young, 2013).

PING

PING was originally proposed as a mechanism for periodic neuronal oscillations in hippocampus; it is often cited as a mechanism for gamma-band activity in cortex. The idea is as follows: E-neurons in a local population are driven by a steady external current, leading to a population spike. The E-population spike causes an I-population spike, which suppresses the E-neurons. When the suppression is lifted, the external current again drives the E-neurons to a population spike and the cycle is repeated. A simple schematic is as follows:

The REI mechanism

We have coined the term REI (recurrent excitation inhibition) for the dynamical mechanism that was proposed by Rangan and Young (2013) and elaborated on by Chariker and Young (2015). The main ideas of REI, which are applicable to any local population of E- and I-neurons that have many recurrent connections, are summarized in the flowchart below.

Rangan and Young (2013) proposed that a multiple firing event (MFE) in a population of spike trains is typically precipitated by the crossing of threshold by one or more E-neurons, as a result of the excitatory drive they receive together with normal fluctuations in membrane potential. These crossings produce some amount of recurrent excitation in the local E-population, and this may or may not lead to more substantial excitatory firing through recurrent excitation. The excitation produced raises the membrane potentials of E- and I-neurons alike. For some brief moments, the balance of intracellular currents in both E- and I-neurons is tilted toward excitation, leading possibly to the firing of more spikes and the generation of a partially synchronous event, an MFE. Then GABA release caused by spike firing in I-cells eventually catches up, and tilts the balance toward inhibitory currents. I-cells being quite densely connected to both E- and I-cells, this leads to hyperpolarization of membrane potentials for a large fraction of the local population, and a period of quiescence. Then the decay of inhibition and continued (mostly feedforward and feedback) excitatory drive return the network to a state where, through stimulation or by chance, another MFE is initiated. The decay time of GABA-A conductance together with the time it takes E-cells to depolarize cause the frequency of occurrence of MFEs to be in the gamma range.

The stability of the REI mechanism hence gamma-band activity with respect to parameter perturbations was first reported by Rangan and Young (2013), who studied a semirealistic model of layer 2/3 of V1. The phenomenon was subsequently studied systematically by Chariker and Young (2015) where the authors investigated both the frequency and the size of the population participating in spiking events in gamma activity using a local population of a few hundred E and I integrate-and-fire neurons with connectivity similar to that of the CSY model; the drive was Poisson. They demonstrated the robustness of gamma rhythms by varying the balance between the E and I populations (at times by as much as a factor of two), the strength of the drive, and decay times of E and I conductances. They found that even as gamma characteristics varied, the presence of a rhythm persisted.

PING versus REI

The most salient differences between PING and REI are (1) MFEs caused by REI typically involve only partial activation of the E- and I-populations; they are not population spikes; (2) in REI, spiking in the E- and I-populations is roughly simultaneous, whereas in PING they are offset in time; and (3) spiking in REI is preceded by recurrent excitation, whereas in PING, it follows disinhibition.

With respect to point (1), the results in Figure 1 imply that population synchrony is only partial in the CSY model. In this respect, the model's output is closer to REI than to PING. Partial synchrony is what happens in the real cortex (Cardin, 2016). With respect to point (2) the correlation of E- and I-synaptic currents in Figure 2G showed that the E- and I-populations produced synaptic currents that were roughly simultaneous, again consistent with REI and also with the data of Okun and Lampl (2008). Below we report on an investigation into point (3).

Analysis of spike-generation in the CSY model

Events leading to spike firing: a close-up look

First, we address the crucial question (3), whether spike firing in gamma activity is caused more by excitation or by disinhibition. We examined thousands of spikes generated by the CSY model in a local population during optimal visual stimulation, and plotted 2-D histograms (Fig. 3, left) of how many spikes had particular values of dE and dI current during the 5 ms preceding each spike (using the convention that both E and I currents are positive, and dE > 0 means E-current rose in the 5 ms before the spike). We also did the same analysis for the 3 ms preceding a spike and the results were very similar. By far the largest percentage of spikes had dE and dI > 0 (top right quadrant), consistent with the behavior of an REI mechanism. The fact that the percentage in the bottom left quadrant, where dE and dI both were negative, was so low suggests that spikes rarely occurred when inhibition was decreasing, i.e., by a disinhibitory mechanism. If a spiking neuron receives no synaptic input in the 5 ms before the time of the spike recorded, both dE and dI will be negative due to decay of synaptic conductance, yet a majority of the spikes occurred when dE and dI are both positive, supporting our contention that most spikes in MFEs occurred because of recurrent excitation and a much smaller, though non-zero, fraction occurred because of disinhibition.

Another way to study what caused synchronous spikes is to calculate spike-current covariance. Spike-current covariance was calculated as the spike-triggered average current:

where t_i is the time of the ith spike, and < > means the average over spikes. The range of τ was −20 to 20 ms; negative τ means time before a spike, and positive τ is after a spike. We calculated spike-current covariance during MFEs, for simple and complex excitatory cells (Fig. 3, right) in the visually driven patch of cortex illustrated in Figure 1, averaged over those spikes that occurred within an MFE. The results in Figure 3 further confirm that spikes occurred on average when excitatory current was increasing, i.e., that excitation caused most spikes. The E-current on average was increasing in the 5 ms (−5 to 0 ms) before a spike occurred. The minor but non-zero effect of disinhibition is obscured in the covariances plotted in Figure 3 because covariance reports the average result, and, on average, spikes occurred because of increased excitation. It is important to notice that I-current was, on average, also increasing before a spike occurrence, in a way that was highly correlated with the excitatory current, as predicted by the REI mechanism and opposite to what PING predicts.

Sources of synaptic excitation triggering spikes

We analyze next the composition of the Excitatory current during the 5 ms before a spike, dividing the current sources into “recurrent”, meaning coming from within layer 4Cα, “LGN”, referring to the feedforward input received by a neuron, and “feedback”, referring to the current from layer 6.

In Figure 4, we analyze model data in a representative simple E-cell (Fig. 4B) and complex E-cell (Fig. 4C). In Fig. 4, B and C, the bottom shows a decomposition of the E-current that enters the cell in a 250 ms stretch into 4Cα, LGN, and feedback. The top shows the total E-synaptic current in red, the I-current in blue, and spikes are indicated by black arrows.

Figure 4.

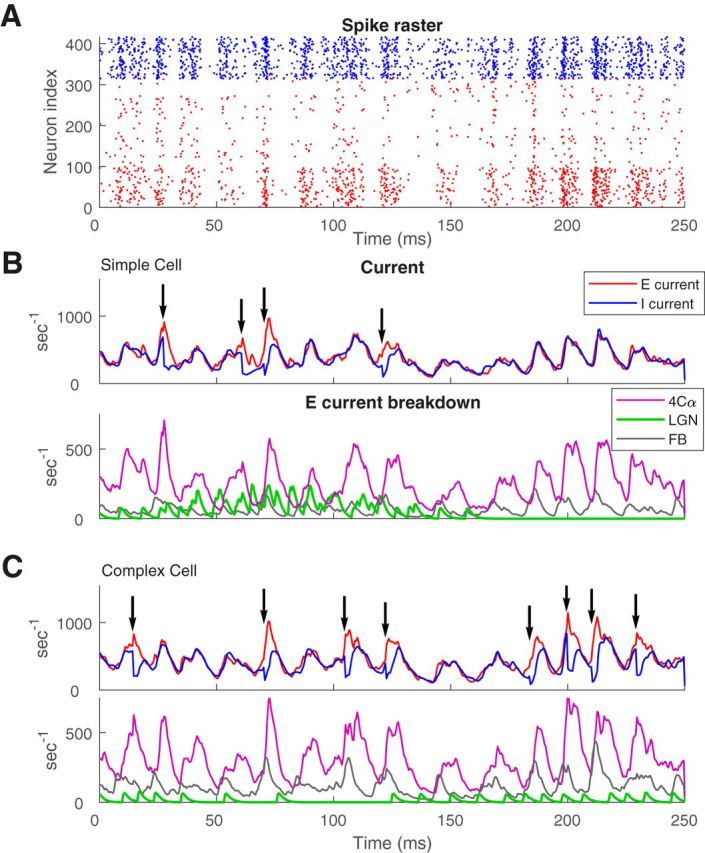
Contributions of different sources of excitatory current to spike-firing in two example model E-cells. A, The raster of spikes shown in Figure 1A is replotted here to compare with intracellular currents in model cells. B, Simple cell, and C, complex cell. Top, E-current (red) and I-current (blue) plotted versus time during the same time interval as the spike-firings in the raster. Spike occurrences are indicated by the arrows. E- and I-currents are closely balanced at most times; the exceptions are when E-current exceeds I-current and these are times when spikes are fired. Bottom, The E-current is dissected into its components: recurrent layer 4C excitation (purple), LGN drive (green), and layer 6 feedback (gray).

For both simple and complex cells, recurrent excitation was the largest component of the excitatory current (Fig. 4B,C, bottom). This property of the model was dictated by data about the number of excitatory connections from each source, the strength of synaptic coupling, and the (measured) firing rates of neurons in layer 4Cα, in LGN, and in layer 6.

However, the dominance of recurrent excitation was not the entire explanation for the semisynchronous spiking. Examining the different sources of excitation in the bottom of Figure 4, B and C, we found that LGN and feedback both had powerful influence on spike firing. In the simple cell (Fig. 4B), spiking had a strong tendency to occur during the stimulus phase when all LGN neurons projecting to the V1 cell were activated. Sometimes an LGN spike led directly to a cortical spike, but mostly it was the overall elevation of total LGN-driven E-current that enhanced spiking. In the complex cell, increasing feedback excitation often was associated with spike timing as one can see by examining the timing of spikes and of pulses of feedback excitation. There was great diversity in spiking characteristics of cells, e.g., some systematically fired earlier than others within most MFEs, but the effects of LGN and feedback on the generation of MFEs seemed incontrovertible in the many plots similar to those in Figure 4, B and C, that we examined. To document the diverse influences of synaptic excitation on synchronous spike firing we compiled the population statistics shown in Figure 5.

To quantify the sources of input currents, we computed the ratio of L6 to L4 excitatory synaptic current, and also LGN to L4, over 5 ms intervals before a spike. The distributions of these ratios, collected over many thousands of spikes from dozens of neurons, are depicted in Figure 5. The mean value for simple E-cells of the L6/L4 distribution was 0.41. For complex cells, the mean L6/L4 ratio was 0.59. For simple cells, the mean LGN/L4 ratio was 0.59, whereas for complex cells it was 0.08. Therefore, the contribution of LGN to spiking in simple cells, as well as those from L6 to both simple and complex cells, were a large fraction of, but less than, that of the synaptic current caused by other E-cells within layer 4Cα. For simple cells, LGN and layer 6 contributed roughly equally, though the influence of LGN was more localized in time because of temporal modulation of LGN input by the visual stimulus.

Cellular biophysics and synchrony in cortical populations

The detailed analysis of synaptic currents and spike timing above points naturally to the hypothesis that conductance time courses, which control the durations and magnitudes of EPSCs and IPSCs, will have a direct effect on excitatory-inhibitory interaction, and that in turn will impact in a predictable way the degree of synchrony and peak frequency of the rhythm. Indeed gamma characteristics are known to change with the state of cortex. It was observed in several previous models of gamma activity (Whittington et al., 2000; Tiesinga et al., 2001; Brunel and Wang, 2003) that lengthening the time course of decay of the IPSC leads to a lower peak frequency of gamma-band rhythm, and the same holds true in the CSY model (data not shown). Such changes in synaptic persistence may be important in anesthetic effects on brain state as has been hypothesized by others (McCarthy et al., 2012). In addition, we have observed that the peak gamma frequency is affected by several other factors in the CSY model, such as the operating points of the E and I-cells, the amount of ambient excitation that reflects neuromodulation, and the temporal frequency of pulses of feedback excitation from layer 6. Our pilot studies of this subject have shown that what determines the peak gamma frequency and also the degree of synchrony of the gamma band activity in a realistic setting is quite complicated and is beyond the scope of the present paper. What we were able to model and analyze was the strong effect of E- and I-synaptic rise times on gamma band synchrony, as follows.

Relative rise times of E- and I-conductances

In the CSY model, the time course of E (respectively, I) conductance was defined to be the difference of two exponentials defined in terms of its rise and decay times (see Materials and Methods). Here we present a novel observation on how the degree of synchrony depends sensitively on the relative rise times of E- and I-conductances. We first describe the observation, and then explain it in terms of REI.

Three different regimes are shown in Figure 6. Time courses for the conductances of the three regimes, G_AMPA(t) and G_GABA(t), each of which were normalized to have integral equal to 1, are shown in the top row of the figure; below that spike rasters are plotted with the PSD for each raster plotted to its right. The three regimes depicted in Figure 6 differed only in the relative rise times of E- and I-conductances; all other parameters were identical. The middle raster was produced using parameters from the CSY model: rise times for both AMPA and GABA were 0.5 ms, decay time for AMPA was 2 ms and decay time for GABA was longer, at 5 ms. The top raster differs from the middle one only in that its AMPA rise time was increased to 1.5 ms. The bottom raster differed from the middle one in that its GABA rise time was increased to 1 ms.

All three regimes had similar firing rates (between 15 and 16 spikes/s), but the heights of their PSD peaks differed markedly, by a factor of 4 from top to bottom. The synchrony quotients q/q_null (see Materials and Methods) also differed: they were 1.47 ± 0.01, 1.77 ± 0.02, and 2.87 ± 0.03 in the top, middle, and bottom rows, respectively, confirming the visual impression of an increase in the degree of synchrony as the ratio of the rise times for inhibition versus excitation increased from 0.33 (top) to 1.0 (middle) to 2.0 (bottom). The large changes, in PSD peak height and in q/q_null, between the middle and bottom panels is a striking result because the only difference between the results in these two rows was a 0.5 ms difference in rise time of the GABA conductance. As can be seen from the synaptic conductance waveforms above the rasters, the difference between the middle and right waveform plots are perceptible but not large, yet the regime depicted in the bottom raster (corresponding to the conductance waveform plot on the right) produced much more synchronized spike patterns than in the middle raster.

We now offer an explanation for the results in Figure 6 in terms of the REI mechanism. Recall that the formation of MFEs is precipitated by the crossing of threshold by E- and I-neurons, caused either by normal fluctuations or by excitatory input from outside of the local population, i.e., from feedforward or feedback pulses. How large the MFE, as measured by, for instance, how many E-neurons cross threshold during the spiking event, depends to some degree on chance, such as whether the postsynaptic E-neurons are close to spiking threshold, as well as on the nature of the external drives. But since the bulk of the current is from recurrent excitation (Fig. 4), a very important factor is how quickly the I-neurons step in to curb the MFE. This is key to understanding why synchrony depends sensitively on relative rise times in E- and I-conductances.

When E-conductance rose slowly relative to I-conductance as in the top raster of Figure 6, I-cells intervened quickly to disrupt the formation of large MFEs. As a result, MFEs tended to be small, that is, spike patterns tended to be diffused. But, when I-rise time was slower, as in the bottom raster of Figure 6, it allowed a larger number of E-neurons to participate in MFEs. The strong excitation in this case led also to the spiking of a larger number of I-neurons. Because the number of I-neurons that spiked is large, the suppressive effect was strong, leading to a “gap” of ∼10 ms during which there was little spiking of any kind. The highly concerted excitation together with the subsequent “gap” produced the highly synchronous spiking seen in the bottom raster.

The explanation offered for the strong effect of relative conductance rise times underscores how delicate the interplay is between E- and I-neurons in the “push-and-pull” (or hyperpolarization-depolarization) that results in gamma rhythms. Very small changes in timing can affect the characteristics of the rhythms produced. We hypothesize that cellular biophysics that affects synaptic rise times causes some of the changes in PSD observed in experiments, and present this as a testable prediction of our model.

Discussion

This paper is a study of gamma-band activity in a previously constructed model of the monkey V1 cortex: the CSY model. This study offered a window into what gamma-band activity is like in a model that emulates cortical function, while numerical simulations allowed us to dissect the phenomena observed in ways not possible in the laboratory.

Gamma activity as by-product of neuronal processes and indicators of local cortical states

The microstructure of recurrent networks with opposing actions of excitatory and inhibitory currents has to generate rhythms, via REI and other mechanisms revealed in the course of our analysis (Rangan and Young, 2013; Chariker and Young, 2015; see Results). The operating point of cortical cells, and the time courses of AMPA and GABA synaptic conductances, cause the rhythms to occur in the gamma range. We propose therefore that gamma rhythms are byproducts of natural neuronal processes rather than mechanisms designed for specific roles. One should expect to find gamma-band fluctuations throughout cortex (Pesaran et al., 2002; Khawaja et al., 2009; Buzsáki, 2011), where similar local E-I circuitries are present and neurons have similar operating points.

Gamma-band activity as observed in experiments refers to a rich collection of rhythmic behaviors with diverse properties. In the CSY model as in V1 data, gamma characteristics change with stimulus contrast (background vs driven activity) and with stimulus features (Chariker et al., 2016). Here we pointed out gamma's dependence on cellular biophysics, using as an example the relative rise times of E- and I-conductances. Since cellular biophysics can be affected by disease or drugs, and by other factors that influence cortical state (such as attention), our results imply that gamma characteristics are a gauge of local circuit activity.

Mechanisms for the generation of gamma rhythms

Based on our results with the CSY model, we concluded that the mechanisms for producing gamma-band activity in cortex are heterogeneous and multidimensional.

For definiteness, we focused on two previously proposed mechanisms, PING (Traub et al., 1999; Whittington et al., 2000; Tiesinga et al., 2001; Börgers and Kopell, 2003; Börgers, 2017), and REI (Rangan and Young, 2013; Chariker and Young, 2015).

While both PING and REI involve the same excitation-suppression ideas, the two mechanisms are substantially different (see Results). Our analysis found the mechanism for gamma-band activity in the CSY model to be much more aligned with the REI mechanism, which is also in agreement with the description of intracellular events described by Atallah and Scanziani (2009) and Salkoff et al. (2015), among others. MFEs in the CSY model involved only small fractions of the population (Fig. 1B,C). Gamma-band fluctuations in spike density were broad-band in frequency (Fig. 1E), i.e., not periodic. Most significantly, in the CSY model, a large majority of the spikes occurred when both E- and I-currents were on the rise, i.e., they were caused by excitation rather than disinhibition (Figs. 3, 4).

REI, however, was not the whole story (Figs. 4, 5). We found that feedforward excitation from LGN and feedback pulses from layer 6 played a significant role in the formation of MFEs, not just through the currents they provided but also through their timing. To a lesser extent, disinhibition played a role as well (Fig. 3). The mechanisms for generating gamma rhythms in the CSY model truly were multidimensional.

Our results should be contrasted with those of Brunel and Wang, 2003 and Geisler et al. (2005). Though we all studied gamma-band rhythms in networks of spiking E- and I-neurons, there is very little overlap between their results and ours. Under the assumption that the network's population firing rate was a periodic oscillation plus noise, Brunel and colleagues focused on the period of the oscillation; mechanisms were not considered. Our primary goal was to explain the mechanisms that lead to the emergence of not really periodic gamma rhythms in the real cortex.

Other mechanisms that affect gamma-band activity not discussed in this paper include the role of inhibitory neurons, only one type of which, the parvalbumin (PV) basket cells, was modeled in CSY; this was a simplification based on the data of Defelipe et al. (1999), who reported that almost all inhibitory neurons in macaque layer 4Cα were PV interneurons. Recent work on mouse V1 also stressed the role of PV interneurons (Chen et al., 2017). Others have found that long-distance modulation of gamma band activity in upper layers of mouse V1 was influenced strongly by the activity of SOM inhibitory interneurons that mediate spatial-contextual effects on gamma in layer 2/3 neurons (Veit et al., 2017), findings that support our proposal that the sources of gamma-band activity are multidimensional.

Another simplification in the CSY model is that we have not treated explicitly synaptic facilitation or depression. The model's behavior with this simplifying approximation captured many of the features of gamma band activity observed in experiments at high contrast as presented in this paper. However, the extension of the model to explain a wider range of phenomena may require the use of synaptic dynamics; this is an area we plan to explore.

Two novel observations: corollaries of the spike-generation analysis

We believe the following two observations are of independent interest for general theories of the brain. They are not directly connected to gamma-band activity but were spinoffs of our analysis of spike-firing mechanisms in the CSY model.

Balancing of E- and I-currents

In the CSY model, E- and I-currents fluctuated together (Fig. 2C,F,G) resembling the remarkable experimental data obtained by Okun and Lampl (2008). Indeed, the model's currents were very precisely balanced most of the time. When they were not in balance and E > I, a spike often resulted. The difference between E- and I-currents was correlated to the firing rate of the neuron (though the dependence was not linear, as timing also mattered). As can be seen in Figures 2C and 4B, E- and I-currents were very much balanced most of the time in simple cells; instances of imbalance occurred more frequently in complex cells (Figs. 2F, 4C), and even more frequently in I-cells (data not shown), causing I-cells to spike at much higher rates than E-cells as is the case in V1 cortex.

In theoretical neuroscience, there is the very well known idea of a balanced state, referring in general to the balancing of E- and I-currents within local populations and over time (van Vreeswijk and Sompolinsky, 1996). This idea is often imposed on reduced models such as rate models through the choice of parameters. We point out two important differences between this classical theory and our new findings. First, the balancing of E- and I-currents in the CSY model was an emergent property. It was not imposed. Rather, balance emerged when the model was benchmarked to emulate the performance (firing rates, tuning selectivity) and the detailed anatomy of real V1. Second, the balancing in the CSY model was of a much more precise nature. It did not just happen on average but was maintained, by the system itself, moment by moment. Spikes occurred only when there were large enough deviations from E-I balance.

The (unreasonable) effectiveness of external inputs

“External sources” here refers not to outside of the brain but outside of the local circuitry. In the CSY model, when optimally driven, neurons in 4Cα received on average only ∼10% of their E-current from LGN (more for simple cells than for complex cells), and only ∼20% of their inputs from layer 6 (more for complex cells than for simple cells, to maintain a higher firing rate for complex cells as demanded by data). Yet from Figure 5A, we see that during the 5 ms before a cortical spike, the percentage of current from LGN was considerably >10% in most simple cells. And in Figure 5B the percentage of layer 6 current that preceded a spike was >20% in most complex cells. These results prove that external sources of current were more effective in causing spike-firing than their time-averaged percentages would indicate.

We offer the following mechanistic explanation. In the case of LGN spikes, even though its average percentage was small, LGN synaptic current was concentrated to half of the cycle (of the grating drift rate). That most of the spikes from simple cells occur during the active phase of their LGN afferents is strong indication that this extra amount of current caused the membrane potential to sit closer to spike-firing threshold during this part of the cycle, making it easier for the membrane potential to cross threshold (Figs. 2, 4B). As for the effects of layer 6 spikes, while E- and I-neurons in the local population in 4Cα were involved in the waves of polarization-depolarization caused by REI within their recurrent circuit, the arrival times of layer 6 external pulses were not tied to the rhythms in 4Cα, and such pulses arriving at opportune times were more effective in setting off MFEs than their mean current would indicate.