Decorrelated Input Dissociates Narrow Band γ Power and BOLD in Human Visual Cortex

Abstract

Although fMRI using the BOLD contrast is widely used for noninvasively mapping hemodynamic brain activity in humans, its exact link to underlying neural processing is poorly understood. Whereas some studies have reported that BOLD signals measured in visual cortex are tightly linked to neural activity in the narrow band γ (NBG) range, others have found a weak correlation between the two. To elucidate the mechanisms behind these conflicting findings, we hypothesized that BOLD reflects the strength of synaptic inputs to cortex, whereas NBG is more dependent on how well these inputs are correlated. To test this, we measured NBG, BOLD, and cerebral blood flow responses to stimuli that either correlate or decorrelate neural activity in human visual cortex. Next, we simulated a recurrent network model of excitatory and inhibitory neurons that reproduced in detail the experimental NBG and BOLD data. Results show that the visually evoked BOLD response was solely predicted by the sum of local inputs, whereas NBG was critically dependent on how well these inputs were correlated. In summary, the NBG-BOLD relationship strongly depends on the nature of sensory input to cortex: stimuli that increase the number of correlated inputs to visual cortex will increase NBG and BOLD in a similar manner, whereas stimuli that increase the number of decorrelated inputs will dissociate the two. The NBG-BOLD relationship is therefore not fixed but is rather highly dependent on input correlations that are both stimulus- and state-dependent.

SIGNIFICANCE STATEMENT It is widely believed that γ oscillations in cortex are tightly linked to local hemodynamic activity. Here, we present experimental evidence showing how a stimulus can increase local blood flow to the brain despite suppressing γ power. Moreover, using a sophisticated model of cortical neurons, it is proposed that this occurs when synaptic input to cortex is strong yet decorrelated. Because input correlations are largely determined by the state of the brain, our results demonstrate that the relationship between γ and local hemodynamics is not fixed, but rather context dependent. This likely explains why certain neurodevelopmental disorders are characterized by weak γ activity despite showing normal blood flow.

Introduction

fMRI using the BOLD contrast has become the de facto imaging modality for measuring human brain function (Friston, 2009), although its exact relationship with underlying neural activity as measured with local field potentials (LFP) and EEG is unclear. A general assumption is that the stimulus-evoked BOLD and EEG response better reflects the input and local processing of cortical neurons rather than their spiking output (Logothetis, 2008; Whittingstall and Logothetis, 2009; Buzsáki et al., 2012). As a result, changes in the magnitude of a stimulus-evoked BOLD response should be approximately proportional to changes observed in the EEG. Support for this comes from studies showing that the amplitude of both BOLD and EEG/LFP narrow band γ band (NBG) potentials increases in a similar fashion with stimulus contrast (Niessing et al., 2005; Koch et al., 2009), possibly due to the high-energy demand of initiating and maintaining γ oscillations (Galow et al., 2014). However, other studies in humans have shown that BOLD responses in visual cortex are insensitive to large changes in NBG (Muthukumaraswamy and Singh, 2009; Swettenham et al., 2013) and that certain types of visual stimuli (e.g., noise patterns) do not elicit NBG (Hermes et al., 2015) despite being clearly perceivable to the subject and yielding a robust hemodynamic response (Grill-Spector et al., 1998; Kayser et al., 2004). This raises the question of why might certain stimuli comodulate NBG and BOLD in a similar fashion while others dissociate them (Bartolo et al., 2011).

EEG integrates the electrical activity over several millions of neurons. As a result, the magnitude of the response is highly dependent on the degree to which inputs to neurons are correlated (Lindén et al., 2011; Reimann et al., 2013; Musall et al., 2014). This is especially important when interpreting NBG given that the frequency and amplitude of γ oscillations depend on the interaction between excitatory (E) and inhibitory (I) neurons (Atallah and Scanziani, 2009). When inputs are spatially decorrelated (i.e., inputs to different cells are of different strengths), the E-I balance becomes locally perturbed yielding a wide range of oscillation frequencies across the population (Wang and Buzsáki, 1996; Buzsáki and Wang, 2012), which, when spatially integrated (as scalp EEG does), results in a broad EEG spectral profile without a prominent γ peak. Therefore, the lack of a stimulus-induced NBG response may not reflect a lack of input to neurons, but rather a lack of correlated input. The BOLD response, on the other hand, is thought to reflect the metabolic burden associated with integrating and processing synaptic inputs (Logothetis, 2008), although whether or not BOLD is altered by changes in input correlations is largely unexplored.

Assuming that BOLD and NBG are separately dependent on input strength and correlation, respectively, we here hypothesized that stimuli that increase the correlated drive to visual cortex will increase NBG and BOLD in a similar manner, whereas stimuli that solely alter input correlations will dissociate the two. To test this, subjects viewed a grating with three different levels of Michelson contrast and spatial randomization, the latter of which has been shown to decorrelate V1 neurons (Zhou et al., 2008) without altering their overall output rates (Jia et al., 2013), thus making it an ideal stimulus for testing this hypothesis. We then combined the stimulus-evoked NBG, BOLD, and cerebral blood flow (CBF) responses with the output from a model E-I circuit fed with the same stimuli. The results show that NBG is more dependent on input correlations, whereas BOLD better represents the net sum of inputs, regardless whether they are correlated or not. This demonstrates that NBG is not an accurate marker of BOLD, and explains why certain stimuli can elicit large BOLD/CBF responses despite yielding little to no NBG.

Materials and Methods

Subjects and stimuli.

The study was conducted over separate EEG, fMRI, and arterial spin labeling (ASL) sessions. A total of 22 subjects participated in the study (9 female, no psychiatric or neurologic symptoms at the time of scanning or in the past, corrected to normal vision) according to the guidelines of the Internal Review Board of the Centre Hospitalier Universitaire de Sherbrooke. All stimuli were generated using Psychophysics Toolbox (Brainard, 1997) and presented on a gray background with luminance equal to the mean luminance of the stimulus (see Fig. 1a, top). The parameters of the unperturbed grating are as follows: a spatial frequency of 3 cycles/degree, a temporal frequency of 6 cycles/s, drifting from right to left within a 7 degree circular aperture placed in the center of the subject's visual field. The Michelson contrast (MC) was adjusted (100%, 33%, and 5%) by narrowing the luminance range of the unperturbed grating while keeping mean luminance constant and equal to the background luminance. Spatial randomization (SR) of the unperturbed grating was accomplished by spatial swapping of grating patches (Zhou et al., 2008). Briefly, grating patches (0.15 × 0.15°) were randomly selected and swapped with other randomly selected regions, until a desired percentage of the grating was randomized (for this study, SR levels were 10% and 60%) without changing MC (Sun et al., 2015).

Figure 1.

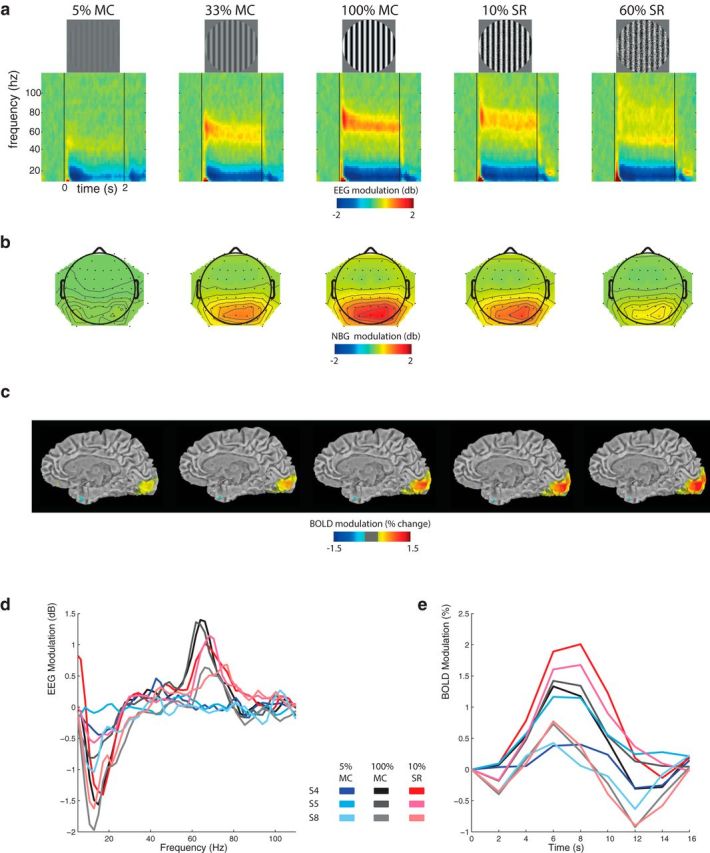
Qualitative overview of EEG and BOLD responses to visual stimulation. Five visual stimulus types: from left to right, 5% MC, 33% MC, 100% MC, 10% SR, and 60% SR and corresponding group-average (n = 22) of the (a) EEG time frequency decomposition, (b) NBG (60–70 Hz) scalp topography, and (c) BOLD response maps overlaid on a T1-weighted anatomical template (for visual purposes only, values <±0.5% are masked out). Both NBG and BOLD tend to increase with MC but become dissociated with SR. Examples of stimulus-evoked (d) EEG and (e) V1 BOLD signals from 3 subjects and stimulus conditions. The same trend is observed for both “strong” (Subjects S4 and S5) and “weak” (Subject S8) NBG responders.

fMRI acquisition and analysis.

Whole-brain volumes were acquired on a 3T MRI scanner (Ingenia, Philips Healthcare) using a 32 channel head coil for reception and the following parameters: TR/TE = 2000/30 ms, flip angle = 70°, FOV = 224 × 224 × 136.5 mm and voxel size = 3.5 mm isotropic. Stimuli were projected from an MRI-compatible monitor (resolution = 800 × 600 pixels, frame rate = 75 Hz) to a mirror positioned above the subject's face. Stimulus presentation was divided into 9 separate 8.5 min acquisition intervals, with acquisition halting for ∼1 min between intervals to converse with the subject. A T1-weighted 3D gradient-echo image (TR/TE = 7.9/3.5 ms, flip angle = 8°, FOV = 240 × 240 × 150 mm, voxel size = 1 mm isotropic) was acquired following the fMRI acquisition. Stimuli were presented at a rate of one stimulus per 16 s in which the grating was present for 2 s. Each of the five stimuli types was presented 5 times per 8.5 min interval in a pseudo-random order, for a total of 270 presentations (45 per stimulus type). Subjects were instructed to maintain fixation on a central crosshair for the duration of each 8.5 min interval and withhold blinks from periods during or directly following the stimulus presentation, as indicated by the color of the central fixation point (red for periods −4:10 s relative to stimulus onset, black for periods later than 10 s following stimulus onset). All fMRI processing was done using AFNI (Cox, 1996), FSL (Jenkinson et al., 2012), and custom written MATLAB (The MathWorks) scripts. fMRI images were motion corrected (Jenkinson et al., 2002) for both intrascan and interscan movements. Images were then concatenated across the 9 sessions, and independent component analysis (ICA) using MELODIC (Beckmann and Smith, 2004) was used to generate 150 ICs. The time course from each component was correlated with a stimulus-convolved (using default values in spm_hrf.m) response, and components with a robust and statistically significant (r > 0.25, which corresponds to p < 0.00001, Bonferroni corrected) correlation were selected for further analysis and averaged (typically 1–3 components per subject). This correlation threshold was selected as it resulted in ICA weight maps constrained to gray matter near the occipital pole of all subjects. Stimulus-related BOLD magnitude was calculated on a single-trial basis at each time point from 0 to 16 s relative to stimulus onset by subtraction of the baseline (t = 0 s) from the value at that point. To create group-average maps and perform voxel-based analysis, images were nonlinearly warped to a standardized atlas (MNI 152) using ANTS (Avants et al., 2011).

CBF acquisition and analysis.

Eight subjects who participated in the fMRI experiment also participated in an ASL experiment. To measure CBF, a 20 s on-off block design was used, over 3 stimulus types (5% MC, 100% MC, 60% SR) using sequentially interleaved CBF and BOLD acquisitions where three 8.5 min CBF blocks were interleaved with three 8.5 min BOLD acquisitions, for an experiment lasting 50 min. To estimate relative CBF changes, a pCASL sequence with background suppression was used with a labeling slab at the base of the cerebellum. Imaging was performed with a label duration of 1650 ms and postlabel delay of 1600 ms, using a 2D multislice EPI readout with TR/TE of 4000/14 ms. Eighteen contiguous 4-mm-thick slices were acquired with 3 × 3 mm in-plane resolution and an axial FOV of 240 × 240 mm. At each time point, the labeled image was subtracted from the control image, yielding an effective temporal resolution of 8000 ms. Sixty label/control pairs were acquired. Each subject's ASL and BOLD volumes were registered to the first volume from the first BOLD scan after applying motion correction to all BOLD images. Functional ROIs were defined separately for BOLD and ASL experiments by correlation using the standard HRF-convolution approach. To ensure that the BOLD-ASL comparison was not biased by ROI size/location, the two correlation maps (one for ASL, one for BOLD) were averaged, and a single ROI was created for both modalities by thresholding the averaged maps at r > 0.35. BOLD and ASL time series were then averaged across voxels within this ROI, and baseline normalized by the averaged 8 s preceding the stimulus onset. This correlation coefficient threshold was slightly higher than for the BOLD only experiment (r > 0.25) due to the longer stimulation/rest periods used in the CBF acquisition. Stimulus-induced changes were defined as (stimulus − baseline)/baseline for BOLD, and stimulus/baseline for ASL, giving the percentage change and fractional change, respectively. ICA was not used in the analysis of the ASL/BOLD data because BOLD percentage change must be in a prespecified range (typically between 1% and 10%) for realistic cerebral metabolic rate of oxygen (CMRO₂) estimation via the Davis model (Davis et al., 1998), and percentage change values from ICA time courses were well outside this range.

EEG acquisition and analysis.

Scalp signals were acquired on a 64 channel EEG system (Brain Products). Subjects were comfortably seated in a standard office chair as stimuli were presented on a CRT monitor (resolution = 800 × 600 pixels, frame rate = 85 Hz). The stimulus presentation sessions were of similar length to the BOLD sessions, with stimulus presentation broken up into nine separate 8.5 min intervals, halting acquisition for ∼1 min between intervals to converse with the subject and verify signal quality. The stimuli were presented at a rate of 1 stimulus every 5 s, and each of the 6 stimulus types was presented 135 times in a pseudo-random fashion, for a total of 810 trials per subject. Each trial began with a fixation point color change from black to red, followed 0.5–1 s later (pseudo-random jitter) by stimulus onset. The drifting grating was visible for 2 s as in the fMRI experiment, and subjects were instructed to maintain fixation for an additional 0.5 s following stimulus offset before the crosshair changed back from red to black, commencing the 2 s rest period. Each 8.5 min acquisition interval contained five 8 s rest periods, spaced every 2 min, during which subjects were permitted to blink repeatedly and make small postural adjustments in an effort to confine large scale myogenic activity to times during which the stimulus was not being presented. All EEG data processing was done using eeglab (Delorme and Makeig, 2004) version 10.0 and custom-built MATLAB scripts. Datasets were down sampled to 256 Hz, and electrodes with poor signal (defined as those where: zscore (sum(abs(diff(channel time series))) >2.5) were interpolated. EEG sessions were concatenated into a continuous 90 min dataset, bandpass filtered between 1 and 120 Hz, and decomposed using ICA. A novel method of automatic ICA component selection was devised to isolate specific neural components: First, a template neuronal response function (NRF) was defined by filtering scalp space posterior electrodes (all PO, P, and O sites) in the 10–25 Hz and 40–110 Hz range and taking the grand average across all subjects (this range was chosen as it encompassed most significant stimulus-induced activity). This yielded two template time courses: one for the lower and one for the higher frequencies. ICA components were then filtered in the same two frequency ranges and rectified. The rectified, filtered time series of each component was epoched and correlated on a single-trial basis with an NRF in the same frequency range. Components were then sorted according to their correlation (Pearson's r) with the NRF, and the top 2 components from each subject were selected. Visual inspection of these components revealed that their weight maps were always restricted to the occipital lobe electrodes, thus reducing the contribution of eye movements to the data (Onton and Makeig, 2009; Hipp and Siegel, 2013). Stimulus trials were then epoched from [−0.85:2.85 s] relative to stimulus onset, and baseline-corrected event-related spectral perturbation was estimated in single trials and averaged across the top two components. EEG modulation at each frequency was averaged over the [500–2000 ms] time range.

Model network.

The model used corresponds to a spiking Wilson-Cowan network of γ activity (Brunel and Wang, 2003; Wallace et al., 2011; Jadi and Sejnowski, 2014). The network consists of interconnected populations of excitatory and inhibitory Poisson neurons with binary states: when a neuron j is active at time t, its spiking activity X^j(t) is set to 1, and set to 0 otherwise. The neurons' individual firing rates obey r_e,i^j = β_e,i^jf(u_e,i^j), for some gain β and where f is the neurons response function. The membrane potential proxies u_e,i^j obey the set of dynamical equations as follows:

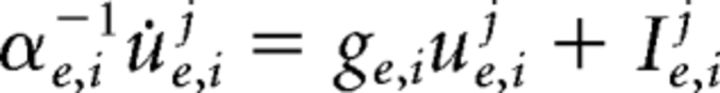The presynaptic excitatory and inhibitory inputs correspond to sums of afferent, recurrent, and feedback contributions as follows:

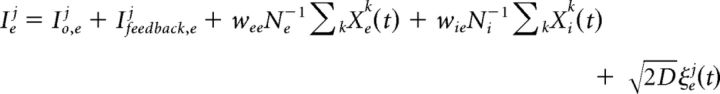and

where the w_nm are synaptic weights, I_o,{e,i}^j are bias currents, and ξ_e,i^j(t) are independent, zero-mean white noise processes. Excitatory neurons are further driven by a feedback input I_feedback,e^j = GN_e⁻²∑_kX_e^j(t)X_e^k(t), through which coincident spiking triggers an inhibitory feedback response. The network is sparse with connection probability 0.8; inhibitory synapses can reach out to all neurons, whereas excitatory synapses are only permitted to connect to the 50 closest neighbors. Model parameter values are listed in Table 1. The network global EEG signal was computed using a weighted average of the individual potentials as follows:

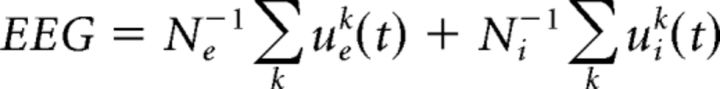To simulate the effects of MC, excitatory neurons were subjected to an additional contrast-dependent input C^j. For a chosen level of spatial randomization SR = [0, 1], a number SR · N_e of excitatory neurons had their contrast dependent input perturbed by some random amount; that is, C^j = C_mean + η_SR^j, where η_SR^j are zero mean random perturbations representing localized random changes in contrast. Yet, throughout, the network average contrast-dependent input remained constant; that is, < C_j > = C_mean. For clarity, we refer to input contrast-dependent changes (MC) and input correlation-dependent changes (SR) as I_m and I_sc, respectively. In this respect, a low I_sc value reflects the scenario whereby cortical neurons receive different input strengths: spatially decorrelated input (as opposed to different input timings, i.e., desynchronized input, which was not studied here). This approach was meant to reproduce the so-called “dark dominance” of V1 neurons whose response to dark stimuli (on gray background) is relatively larger than to white stimuli compared with corresponding onset latency differences (Yeh et al., 2009; Xing et al., 2010, 2014).

Table 1.

Model parameters used for simulations

Symbol	Definition	Value
Ne	No. of excitatory neurons	800
Ni	No. of inhibitory neurons	200
p	Connection probability	0.8
f	Response function	(1 + exp[−ϵμ])−1
ϵ	Response gain	25
βe	Firing rate gain of excitatory cells	1 s−1
βi	Firing rate gain of inhibitory cells	2 s−1
αe	Membrane time scale of excitatory population	10 ms
αi	Membrane time scale of inhibitory population	5 ms
ge	Excitatory membrane leak constant	−0.65
gi	Inhibitory membrane leak constant	−0.65
wee	Synaptic gain e → e	26.0
wei	Synaptic gain e → i	26.0
wie	Synaptic gain i → e	−32.0
wii	Synaptic gain i → i	−1.5
G	Feedback gain	−5
Io,e	Bias potential excitatory cells	0.0
Io,i	Bias potential inhibitory cells	−0.2
D	Noise intensity	0.0015

Model validation.

In total, we simulated a total of 2450 possible (I_m, I_sc) combinations, each yielding a distinct EEG signal. From this, we only focused on the simulated signals that best matched the experimental EEG data in each of the 5 stimulus conditions. To do so, a two-step approach was used: First, the power spectrum of each simulated EEG signal was correlated with each of the 5 experimental EEG power spectra shown in Figure 2a, b, and only the top 2% were retained (representing ∼13 [I_m, I_sc] combinations per stimulus condition). Although this first step ensured that only simulated data with spectral peaks matching the experimental data were kept, it did not ensure that their amplitudes necessarily matched those observed across stimulus conditions. For this, we used a second step whereby the mean power in the NBG (60–70 Hz) range was computed and only the simulated NBG values falling within 1 SD of the experimental data were retained. In summary, this two-step procedure ensured that the only (I_m, I_sc) combinations kept for further analysis closely matched the experimental data in both spectral shape and amplitude.

Figure 2.

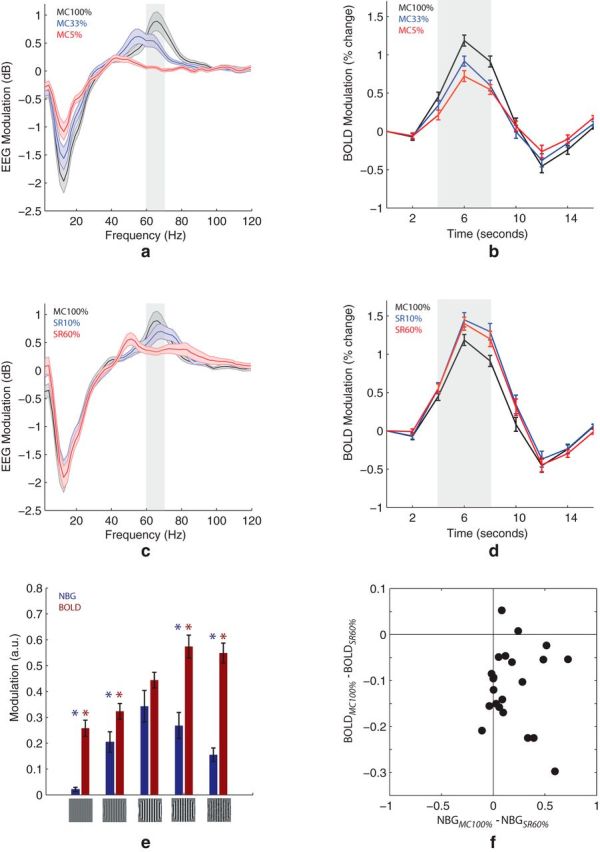
Quantitative analysis of EEG and BOLD responses to MC and SR. Group-average (n = 22) EEG and BOLD modulation for different MC (a, b) and SR (c, d) levels. a, c, Highlighted area represents the represents the frequency range (60–70 Hz) where EEG modulation is statistically significant (p < 0.05, FDR) in both MC and SR conditions. e, Summary of NBG and BOLD response magnitude (averaged within highlighted areas in a–d across all stimulus types). *Significant difference (p < 0.01) relative to 100% MC. Error bars indicate SEM. f, Each dot indicates the mean NBG and BOLD modulation at SR 60% (relative to MC 100%) from a single participant (22 subjects in total). Subject-to-subject variations in NBG and BOLD were not significantly correlated (p > 0.05).

GLM analysis.

To quantify the contributions of I_m and I_sc to the experimental data, both were used as regressors in a GLM as follows:

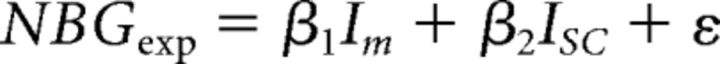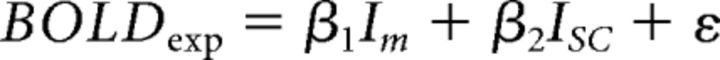where NBG_exp and BOLD_exp represent the group-average experimental values, whereas I_m and I_sc represent the simulation values. This was performed in two steps: First, the average (I_m, I_sc) values were used and the goodness of fit (R²) was computed. Next, all possible (I_m, I_sc) combinations were used, yielding several R² values per stimulus condition. This process was repeated after randomly shuffling the experimental and simulated data.

Statistical procedures.

All error bars indicate SEM. Statistical significance of differences between stimulus types in single subjects was assessed with the independent-samples two-tailed t test (MATLAB's ttest2). Statistical significance of difference between stimuli types in group-averaged data was assessed with the paired-sample two-tailed t test (MATLAB's ttest).

Results

NBG and BOLD responses to changes in MC and SR

A qualitative overview of the group-average EEG and BOLD results is shown in Figure 1. Presentation of a high-contrast grating (Fig. 1a, middle) induced a sustained increase in NBG power over posterior/occipital electrodes (Fig. 1b, middle) as well as a BOLD signal increase within striate cortex (Fig. 1c, middle). To quantify this, statistical analysis of the EEG spectral profile revealed that only a narrow band of frequencies in the γ range (60–71 Hz) were significantly modulated in both MC and SR stimulus conditions (p < 0.05, FDR). This band is highlighted in Figure 2a, c; and for the remainder of this work, NBG refers to the average power in the 60–71 Hz range. As expected, decreasing the gratings MC significantly decreased both NBG power (Fig. 2a) and BOLD response magnitude in primary visual cortex (Fig. 2b). On the other hand, perturbing the grating spatial structure (SR) decreased NBG power (Fig. 2c) but slightly increased the BOLD response (Fig. 2d). In summary, these results show that NBG and BOLD are associated during changes in MC, although dissociated during changes in SR (Fig. 2e). The latter was also evident in single-subject analysis (Fig. 2f).

Decoupling of NBG and energy metabolism

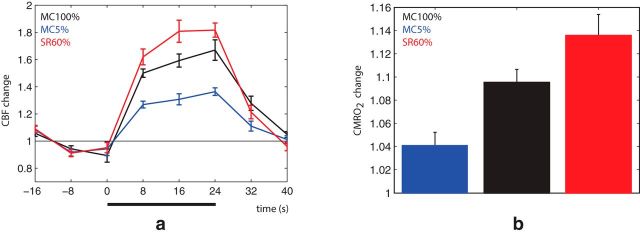
The above results clearly demonstrate that SR suppresses NBG despite increasing BOLD. This suggests that stimuli that yield weak NBG responses may nonetheless be highly metabolically expensive. To confirm this, we used ASL to measure CBF and estimate cerebral metabolic rate of oxygen (CMRO₂) at 5% MC, 100% MC, and 60% SR. These results were in agreement with the BOLD results, demonstrating that SR indeed substantially increased both CBF and CMRO₂ (Fig. 3a,b) despite suppressing NBG.

Figure 3.

Control CBF and CMRO₂ measurements. Group-average (n = 8) BOLD, CBF, and CMRO₂ results. a, Like BOLD, 60% SR (red curve) yielded a stronger CBF response compared with 100% MC (black curve) and 5% MC (blue curve). b, CMRO₂ estimation based on the Davis model using M = 0.1, α = 0.25, and β = 1.5.

Modeling the NBG-BOLD relationship

When reducing MC, NBG power and peak frequency decreased in a similar fashion (Figs. 1, 2a). On the other hand, SR appeared to suppress NBG while broadening its spectral profile (Figs. 1, 2b). This strongly suggests that the NBG results obtained during MC and SR are mediated by different neural mechanisms. To test this, we simulated the effects of MC and SR on NBG by varying both the magnitude (I_m) and spatial correlation (I_sc) of synaptic inputs to a network of cortical neurons (see Materials and Methods; Fig. 4a,b; Table 1). As expected (see Materials and Methods), the simulated NBG (NBG_sim) matched in detail the experimental NBG (NBG_exp; Fig. 4c), demonstrating that the (I_m, I_sc) values used in the simulation (Fig. 4d) faithfully reproduced the experimental EEG data. With increasing MC, both I_m and I_sc increased (Fig. 4d). However, when SR was increased, I_m continued to increase, whereas I_sc was significantly suppressed. This is because NBG_exp was not only weak during SR, but also spectrally broad, as is typically observed during periods of strong, asynchronous input (Miller et al., 2009). Across all five stimulus conditions, NBG_exp better followed I_sc, whereas the experimental BOLD results (BOLD_exp) better tracked I_m. To quantify this, both I_m and I_sc were used as regressors in a GLM. The GLM reproduced both NBG_exp and BOLD_exp (Fig. 4e), although with different contributions from I_m and I_sc. Again, NBG_exp was more dependent on I_sc whereas BOLD_exp was dominated by I_m (Fig. 4f) and F testing further showed that the I_sc regressor added significant information to the NBG_exp (p = 0.03) but not the BOLD_exp (p = 0.71). In summary, these modeling results reveal two important aspects regarding the experimental NBG and BOLD data: First, they confirm that NBG is more sensitive to changes in I_sc, whereas BOLD is more sensitive to changes in I_m. Second, they indicate that MC and SR are indeed mediated by different neural mechanisms: Increasing MC increases the number of correlated inputs to visual cortex, whereas increasing SR increases the number of decorrelated inputs. As a result, the NBG-BOLD association during MC can be attributed to an increase in correlated drive, whereas their dissociation during SR is due to an increase in decorrelated drive.

Figure 4.

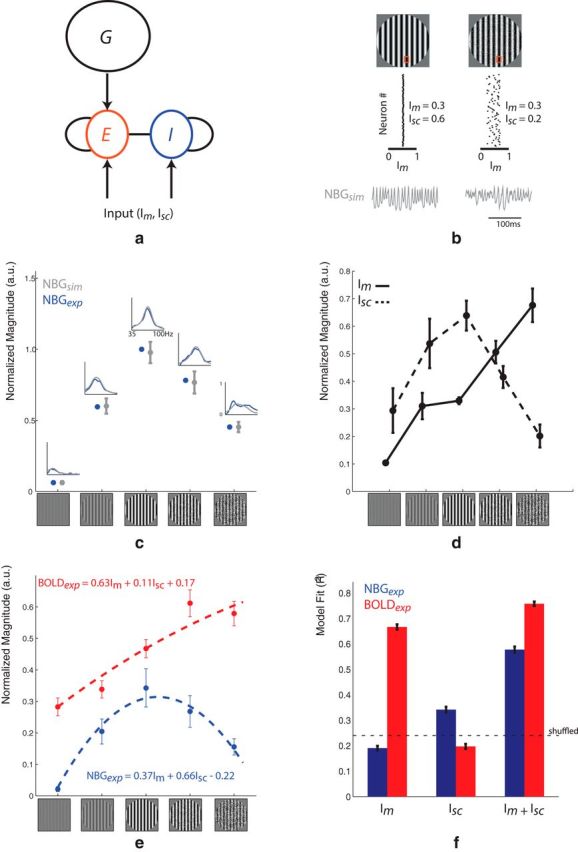
Simulations of NBG as a function of input magnitude (I_m) and spatial correlation (I_sc). a, The network consists of reciprocally connected excitatory (E) and inhibitory (I) spiking neurons driven by inputs with different levels of magnitude (I_m) and spatial correlations (I_sc). A feedback pathway (G), representing recurrent inputs from higher cortical areas, further shapes the responses of the excitatory population. b, An example simulated EEG response to different (I_m, I_sc) combinations. Red squares represent a patch of neurons receiving spatially correlated (e.g., MC 100%) or decorrelated (e.g., SR 10%) input. Gray time courses represent the corresponding simulated EEG signal. For MC 100% (left), input is strong (average I_m = 0.3) and spatially correlated (I_sc = 0.6), thus yielding a robust and sustained NBG response (NBG_sim). However, when input strength is left unchanged (average I_m = 0.3) although input correlations are reduced (I_sc = 0.2), NBG_sim is suppressed, similar to that observed during SR 10%. c, Summary of the simulated data used in this study. For each stimulus condition, the spectral profile of the simulated EEG signal (gray line) and corresponding average power in the 60–70 Hz range (gray dots) closely match the experimental observations (NBG_exp). d, I_m and I_sc values underlying the NBG_sim results shown in c. The SR 10% and SR 60% are best characterized as an increase in decorrelated inputs relative to MC 100%. e, Fit of NBG_exp and BOLD_exp data using I_m and I_sc as regressors in a GLM. f, Quantitative summary of GLM fits (R²). Dashed line indicates the mean R² value obtained when using shuffled data. The NBG_exp fit is increased when adding I_sc in the GLM, whereas the same has little effect on the BOLD_exp fit.

Cortical origin of NBG-BOLD dissociation

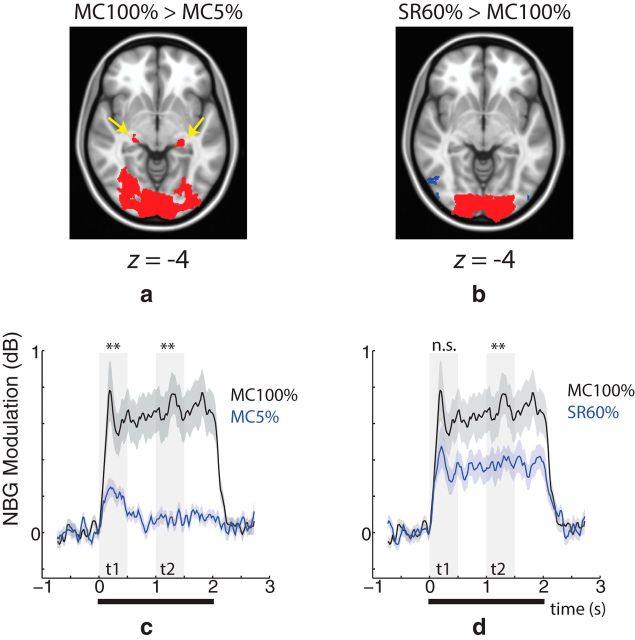
The modeling results presented thus far suggest that SR boosts the number of decorrelated inputs to primary visual cortex. In an attempt to localize the origin of these additional inputs, we compared whole-brain BOLD responses during MC 100% with MC 5% (Fig. 5a). Voxelwise statistical testing revealed that the BOLD response in voxels covering a large swath of the visual cortex and lateral geniculate nucleus (LGN) was stronger during MC 100% (p ≪ 0.01, cluster corrected). When comparing MC 100% and SR 60%, on the other hand, no differences in LGN were detected despite large differences in visual cortex (Fig. 5b). To explore this further, we next examined the temporal profile of the NBG response in the same conditions. Compared with MC 100%, MC 5% was smaller in both the early (0–400 ms) and late (1000–1400 ms) phases of the NBG response (Fig. 5c). Conversely, SR 60% was smaller only in the late phase (Fig. 5d). Together, the spatial and temporal analysis of the BOLD and NBG response, respectively, suggests that the boost of inputs to V1 observed during SR cannot be solely due to increased activation of early thalamocortical circuits.

Figure 5.

Spatial and temporal analysis of BOLD and NBG responses, respectively. Spatial analysis of BOLD response magnitude for (a) MC 100% > MC 5% and (b) SR 60% > MC 100% (n = 22). In both cases, red areas represent areas where the effect was statistically significant (p ≪ 0.01, cluster corrected for a minimum 200 voxels). Compared with MC 5%, MC 100% yields a stronger BOLD response near LGN (yellow arrow), whereas no differences are observed during SR 60%. A slight decrease in extrastriate cortex was observed during SR 60% (blue voxels). c, During MC 100% (black curve), NBG (averaged over group) was significantly stronger than MC 5% (blue curve) in both the early (t1: 0–0.4 s) and late (t2: 1.0–1.4 s) phases of the response (transparent gray bars). d, On the other hand, compared with SR 60%, only the late phase of the NBG response is significantly different. **p < 0.01. Thick black line indicates the period when the visual stimulus was presented.

Discussion

Studies in animal models have reported a tight link between γ-band LFP and BOLD signals (Logothetis, 2002; Shmuel et al., 2006; Goense and Logothetis, 2008; Maier et al., 2008; Magri et al., 2012), particularly in the NBG range (Niessing et al., 2005). In this study, we sought to identify the neural mechanisms underlying NBG and BOLD responses in human visual cortex. The main findings are twofold: First, we show that certain stimuli can substantially increase BOLD and metabolic activity in visual cortex despite almost completely suppressing NBG. Second, we show that NBG is critically dependent on synaptic input correlations, whereas BOLD magnitude better reflects the net sum of these inputs, regardless whether they are correlated or not. These results show that NBG and BOLD are sensitive to entirely different aspects of synaptic input and, as a result, can easily be dissociated.

Experimental results

When increasing stimulus contrast (condition MC), NBG and BOLD responses were tightly linked, although on the other hand, increasing stimulus spatial randomization (condition SR) suppressed NBG despite further increasing BOLD, CBF, and CMRO₂. This provides, to our knowledge, the first evidence demonstrating how stimulus manipulations that progressively reduce NBG can also increase regional CBF and energy metabolism in the same subjects. Importantly, the NBG responses (magnitude and peak frequency) described here are similar to those reported in anesthetized macaque V1 using the same stimulus (Jia et al., 2013), indicating that our results cannot be explained by artifacts associated with eye movements (Yuval-Greenberg et al., 2008; Winawer et al., 2015). In summary, the experimental results confirm that neuronal processes that actively suppress NBG are highly metabolically demanding. In the following section, we describe the characteristics of these mechanisms.

Modeling results

The main goal of this study was to explain how a clear and perceivable stimulus can elicit a large vascular response while almost completely suppressing NBG oscillations in visual cortex. For this, we simulated how changes in input strength and spatial correlation to a population of cortical neurons affect NBG and BOLD activity. These results showed that the NBG response across all stimuli could be modeled as a linear combination of both input strength and correlation, with the latter being the better predictor. Specifically, increasing MC increased the number of correlated inputs, whereas increases in SR increased the number of spatially decorrelated inputs to visual cortex. The weak NBG response observed during SR is thus likely due to the fact that strong, heterogeneous drive to neurons induces frequency dispersion across the population (Wang and Buzsáki, 1996; Buzsáki and Wang, 2012), which, when spatially integrated (as scalp EEG does), results in a broad EEG spectral profile without a prominent γ peak (as observed during SR). This provides further evidence that the absence of a strong NBG peak in humans does not necessarily imply a lack of input to visual cortex, but rather a lack of correlated input. This is similar to studies showing that the spatial reach of the LFP is largely determined by the correlation rather than the strength of synaptic input (Lindén et al., 2011) and that NBG is a poor predictor of spiking (Ray and Maunsell, 2011; Jia et al., 2013).

The BOLD results, on the other hand, were almost entirely explained by the overall strength of input to visual cortex, regardless whether it was correlated or not. This is due to the fact that integrating synaptic inputs is an energetically expensive process (Harris et al., 2012; Niven, 2016) requiring subsequent vessel dilation to increase CBF. Moreover, the SR levels used in our study have been shown to have little to no effect on V1 spike rates (Zhou et al., 2008; Jia et al., 2013), reinforcing the notion that BOLD is more dependent on the input and local processing of neurons rather than their output. However, it should be noted that a recent study also showed that SR of natural scenes does not modulate spiking in anesthesized mice, although it strongly increases it in the awake state (Froudarakis et al., 2014), perhaps due to increased input from higher visual areas. As our measurements were made in alert humans, we therefore cannot rule out that the BOLD increase observed during SR is related to both synaptic input and spiking output. Future experiments comparing neural and vascular based measures in anesthetized and behaving animals are needed to further investigate this.

Overall, our study demonstrates that stimuli and/or cognitive tasks that increase the correlated drive to cortex will enhance NBG and BOLD in a relatively similar manner, whereas those that increase the number of decorrelated inputs will dissociate the two. As the level of synaptic input correlations can change depending on the stimulus and state of the brain, we conclude that the NBG-BOLD relationship is not a static or fixed quantity, and we urge caution when interpreting neurovascular coupling in humans (Nunez and Silberstein, 2000).

Decorrelated input to cortex: effects of low- versus high-level processing

A significant finding from our study is that SR increases the decorrelated drive to visual cortex. But what is the source of this additional input? We speculate that it is not purely thalamic in origin because our fMRI results showed that SR had no significant effect on thalamic BOLD responses and NBG differences associated with SR were most prominent in the late phase of the stimulus response. Together, these findings point to SR having a stronger effect on corticocortical rather than early thalamocortical processing, although the reasons for this are unclear. One possibility that SR increases the subject's attentional focus, which in turn recruits higher-visual areas that send strong, desynchronized feedback input to V1 (Murray et al., 2002), thus increasing its local metabolic burden while suppressing NBG. This would agree with studies showing how increasing attentional load reduces NBG and spike correlations while increasing BOLD in V1 (Chalk et al., 2010; Watanabe et al., 2011; Herrero et al., 2013). Given all of these previous results, visual stimuli that amplify the V1 BOLD response while actively suppressing NBG likely reflect changes in neuromodulatory feedback from higher visual areas rather than changes in feedforward thalamic input. This may also in part explain why certain neurodevelopmental disorders are characterized by reduced NBG despite showing essentially normal or even increased hemodynamic responsiveness to basic visual stimulation (Hadjikhani et al., 2004; Snijders et al., 2013; Schwarzkopf et al., 2014).

Distinct role of NBG versus α/β activity

Rather than using a traditional γ range, we focused on a narrow band of frequencies as they were the only ones significantly modulated in both stimulus conditions. Aside from NBG, however, other frequency ranges are likely also involved in regulating BOLD in other brain regions. In our study, α/β oscillations were strongly modulated by MC, though not SR. This is similar to the BOLD responses observed in LGN, suggesting that α/β and NBG may represent distinct channels of thalamocortical signal propagation (Schmiedt et al., 2014; van Kerkoerle et al., 2014; Bastos et al., 2015). Furthermore, our results indicate that SR also increased broadband (40–120 Hz) EEG power in a manner similar to BOLD, although this effect did not reach statistical significance, nor was this observed in our modeling results (data not shown). Further improvements in EEG denoising or modifications to our model (Miller et al., 2009) may help better assess the potential link between broadband EEG and BOLD (Winawer et al., 2013). Our results therefore further support the view that the BOLD response cannot be exclusively tied to a single, narrow EEG frequency range (Kilner et al., 2005; Magri et al., 2012).

In conclusion, in this study, we show that the NBG-BOLD relationship is variable because of their respective sensitivities to vastly different aspects of cortical input: the magnitude of an evoked-BOLD response is best predicted by the sum of incoming synaptic inputs, whereas NBG magnitude is more dependent on the correlation of these inputs. This provides new insights as to why certain stimuli, cognitive tasks, and brain disorders can be characterized by weak NBG yet robust BOLD activity. We suggest that future experiments purposely designed to dissociate EEG and BOLD will be useful in isolating the role input correlations play on cognitive processing.