Linear Summation of Repulsive and Attractive Serial Dependencies: Orientation and Motion Dependencies Sum in Motion Perception

Abstract

Recent work from several groups has shown that perception of various visual attributes in human observers at a given moment is biased toward what was recently seen. This positive serial dependency is a kind of temporal averaging that exploits short-term correlations in visual scenes to reduce noise and stabilize perception. To date, this stabilizing “continuity field” has been demonstrated on stable visual attributes such as orientation and face identity, yet it would be counterproductive to apply it to dynamic attributes in which change sensitivity is needed. Here, we tested this using motion direction discrimination and predict a negative perceptual dependency: a contrastive relationship that enhances sensitivity to change. Surprisingly, our data showed a cubic-like pattern of dependencies with positive and negative components. By interleaving various stimulus combinations, we separated the components and isolated a positive perceptual dependency for motion and a negative dependency for orientation. A weighted linear sum of the separate dependencies described the original cubic pattern well. The positive dependency for motion shows an integrative perceptual effect and was unexpected, although it is consistent with work on motion priming. These findings suggest that a perception-stabilizing continuity field occurs pervasively, occurring even when it obscures sensitivity to dynamic stimuli.

SIGNIFICANCE STATEMENT Recent studies show that visual perception at a given moment is not entirely veridical, but rather biased toward recently seen stimuli: a positive serial dependency. This temporal smoothing process helps perceptual continuity by preserving stable aspects of the visual scene over time, yet, for dynamic stimuli, temporal smoothing would blur dynamics and reduce sensitivity to change. We tested whether this process is selective for stable attributes by examining dependencies in motion perception. We found a clear positive dependency for motion, suggesting that positive perceptual dependencies are pervasive. We also found a concurrent negative (contrastive) dependency for orientation. Both dependencies combined linearly to determine perception, showing that the brain can calculate contrastive and integrative dependencies simultaneously from recent stimulus history when making perceptual decisions.

Introduction

Many aspects of our visual environment are stable and predictable, with significant correlations existing over the short-term (Dong and Atick, 1995). The visual system could capitalize on this temporal continuity by integrating information over short periods to average out noisy fluctuations due to factors such as eye movements, shadows, and occlusion and thus improve the signal-to-noise ratio and perceptual stability. Several recent studies have found evidence consistent with this so-called “continuity field” (Fischer and Whitney, 2014) by showing serial dependencies in perception for various visual features and attributes such as orientation (Fischer and Whitney, 2014), numerosity (Cicchini et al., 2014), and aspects of face processing including identity (Fritsche et al., 2017), attractiveness (Taubert et al., 2016), and gender (Taubert et al., 2016). These studies present sequences of brief stimuli to observers and find that perception on a given trial is biased toward the previously presented stimulus (i.e., a positive serial dependency). Positive perceptual dependencies are assimilative and are thus consistent with a temporal integration or averaging process. Complementing these behavioral findings, a recent fMRI study examined serial dependence in perceived orientation and found that orientation responses in V1 on a given trial were biased toward the previously presented orientation (St John-Saaltink et al., 2016), tying the perceptual dependency to early cortical activity.

Most demonstrations of positive perceptual dependency have used stable features or attributes such as visual orientation or the identity or gender of a face image. Shaping present perception by the recent past is a kind of temporal integration that would be beneficial for the stable attributes in a visual scene but would not be effective for attributes that are fundamentally dynamic. Serial dependency studies have not examined whether motion perception shows a positive dependency, but as a dynamic attribute, it would be counterproductive and reduce sensitivity to change. Indeed, negative dependencies are well known in motion perception and occur after exposure to sustained motion in the form of repulsive motion aftereffects (Alais et al., 2005; Anstis et al., 1998; Wohlgemuth, 1911). Even very brief adaptation periods (i.e., subsecond durations, similar to the brief exposures common in serial dependency studies) are sufficient to elicit repulsive motion aftereffects (Glasser et al., 2011; Kanai and Verstraten, 2005). The nature of a repulsive effect is a contrastive relationship that serves to enhance sensitivity to change. In contrast, a positive dependency effectively smears perception over time and thus reduces sensitivity to change. Here, we investigate serial dependencies in motion perception using direction discrimination and predict a negative perceptual dependency because this is the optimal strategy for change sensitivity.

Materials and Methods

Ethics statement.

The experiment was approved by the Human Research Ethics Committee of the University of Sydney. The experimental procedure conformed to the Declaration of Helsinki and participants gave informed consent before commencing the experiment.

Participants.

All participants were naive to the aims of the experiments, had normal or corrected-to-normal vision, and were paid $AU20 for participating. Ten subjects (6 female, 4 male) participated in Experiment 1, 10 in Experiment 2 (4 female, 6 male), 10 in Experiment 3 (4 female, 6 male), and 9 (6 female, 3 male) in Experiment 4.

Apparatus.

The experiment was conducted in a dark room where participants were seated at a desk facing a matte white PVC projector screen (Epson ELP-SC21B, 1771 × 996 mm) from a distance of 171 cm. A PROPixx DLP color projector (VPixx Technologies) was located in front of the participant just below the line of sight and cast a viewable image area of 129 × 72 cm (43 × 24° of visual angle) at a native resolution of 1920 × 1080 pixels at 120 Hz. The projector was connected via a DataPixx2 display driver and controlled using software written in MATLAB 2014a (The MathWorks) using the PsychophysicsToolbox extensions (Brainard, 1997; Pelli, 1997) and running on an Apple Mac Pro computer. The projector was set to operate in quadrant mode, which displayed images with a resolution of 960 × 540 pixels at a frame rate of 480 Hz. The projector's luminance output was linearized.

Stimuli.

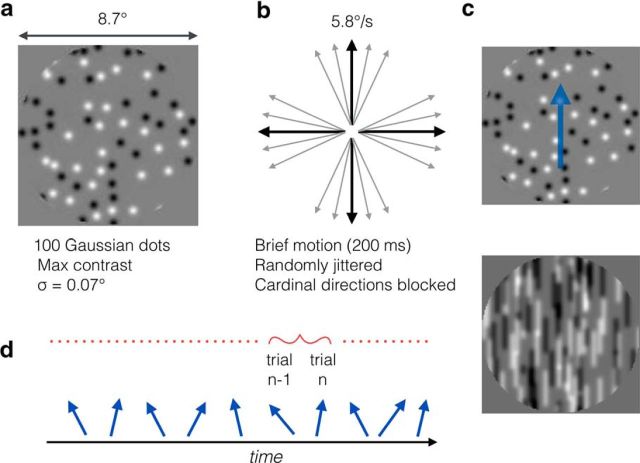
In all experiments, the motion stimuli were arrays of 100 dark and light Gaussian profile luminance blobs (Fig. 1) distributed over a mean luminance background (76.3 cd/m²). The Gaussian blobs had a SD of 0.07° of visual angle (1.5 pixels) and blob locations were determined randomly apart from the constraint that two blobs could not overlap. To achieve this, the spatial extent of the Gaussian blobs was truncated at 3.2 SDs. Using this definition, when creating the random blob arrays, any blob that overlapped with a neighboring blob was redrawn randomly until this constraint was satisfied. 50% of the blobs were black (minimum luminance: 0.2 cd/m²) and 50% white (maximum luminance: 152.9 cd/m²) and the Gaussian luminance profiles were defined with 12-bit contrast resolution. The blob array had a central fixation cross, was contained within a circular aperture with a diameter of 8.7° of visual angle, and the array translated rigidly at a speed of 5.7°/s. All stimulus presentations were 200 ms in duration, during which the blob array translated through 96 video frames (480 Hz frame rate) with a step size of 0.28 pixels per frame. This produced a trajectory length of 27 pixels, accumulating at 13.5 pixels per 100 ms. This rate of movement is sufficient to produce salient streaks because Geisler (1999) determined that the critical length for an effective motion streak was twice the blob width (defined as ±2 SDs) per 100 ms.

Figure 1.

Methods and stimuli used in these experiments. a, Motion stimuli were 100 Gaussian profile luminance blobs at maximum contrast, with 50 having positive and 50 having negative contrast. b, Blobs translated rigidly for 200 ms in a direction that was jittered around a cardinal direction. Cardinal directions were blocked and presented in random order and jitter around the cardinal was randomly sampled from a set of directions: ±1.5°, ±3°, ±6°, ±12°, ±24°, and ±48° (Experiments 2, 3, and 4), or 0°, ±1.5°, ±3°, ±6°, ±12°, and ±24° (Experiment 1). c, Due to temporal integration, fast-moving random-dot patterns leave oriented trails that can be encoded by orientation-selective mechanisms. In this example, a translating random-dot pattern has been linearly integrated over 100 ms. The summed motion frames take on a streaky appearance with a clear but slightly noisy orientation along the motion trajectory. d, Intertrial data analysis. On each trial, participants judged if the direction was clockwise or anticlockwise of the cardinal direction. For every trial in the sequence, the response to a given trial n was binned into a category determined by the direction presented in the preceding trial n − 1.

In Experiments 3 and 4, grating stimuli were interleaved with the motion trials. Gratings had the same size as the dot array (filling the circular aperture) and had maximum contrast and a spatial frequency of 1.8 cycles per degree. In Experiment 3 the grating was static and, in Experiment 4, the grating translated at the same speed as the dot array (5.7°/s).

Design and procedure.

Participants were presented for 200 ms with various motion directions drawn randomly from a set of predefined directions. For Experiment 1, the directions were as follows: 0°, ±1.5°, ±3°, ±6°, ±12°, and ±24° and for Experiments 2, 3, and 4, the directions were as follows: ±1.5°, ±3°, ±6°, ±12°, ±24°, and ±48° Clockwise angles are positive and anticlockwise angles are negative and all sets of directions were centered on one of the cardinal axes within a block of trials. After each motion presentation, participants made an unspeeded response indicating whether the motion was clockwise or anticlockwise of the cardinal axis using a ResponsePixx hand-held response box (VPixx Technologies) and no feedback was given. The interval between trials was determined by the observer's response time (group mean response times were on the order of 650–750 ms across the four experiments) plus a fixed delay of 150 ms, making an average intertrial interval (ITI) of ∼850 ms. In Experiment 1, each of the 11 directions was measured 33 times in a session (363 trials) and eight sessions were conducted: two for each cardinal direction of up, down, left, right.

For analysis, the data from each cardinal direction were rotated into a common directional reference and pooled (in total, 2904 trials per subject). In Experiments 2, 3 and 4, each of the 12 directions was measured 24 times in a session (288 trials) and 8 sessions were conducted (2304 trials per subject). In Experiment 2, within each block, upward and downward motions were presented in alternation from trial to trial, with the start direction counterbalanced over blocks. Similar to Experiment 1, on any given trial the upward (or downward) direction varied randomly around the cardinal. Each of the 12 directions was therefore tested 96 times for the upward motion and 96 times for downward. Data from downward trials were rotated by 180° and pooled with the upward trials for analysis. In Experiment 3, subjects completed five blocks of 288 trials. All trials were upward motion, randomly varying around the cardinal. Within each block, the upward dot motion was alternated from trial to trial with an upwardly moving (i.e., horizontally oriented) grating, with the starting stimulus (grating or dots) counterbalanced over blocks. Subjects therefore completed 60 trials of each direction for the dot stimulus and 60 trials of each direction for the grating. In Experiment 4, trials cycled through a four-trial sequence: upward motion, static vertical grating, downward motion, and static vertical grating. On any trial, the motion direction or orientation varied randomly around vertical among the 12 directions. For each block, the direction of the first motion (upward or downward) was determined randomly. Subjects completed eight blocks of 288 trials. Participants completed each session in ∼7–8 min (9–10 min for Experiment 1) and were given rest periods between sessions for as long as required.

When direction discrimination data were plotted and fitted with a psychometric function, the mean of each subject's function tended to be slightly offset from 0° (Fig. 2a). This is likely due to variability among participants in subjective vertical and to other fixed sources such as a slightly tilted table or monitor stand adding a small, nonzero value to the motion directions. This meant that, when the data were subdivided into bins based on the preceding direction and refitted with psychometric functions, as in Figure 2b, there was both an effect of preceding direction on current direction perception (lateral separation between the functions) and a global horizontal shift added to all functions due to the nonzero subjective vertical. For this reason, before plotting the points of subjective equality (PSEs) from the functions in Figure 2b, the subjective vertical error for each subject was subtracted from their PSEs before plotting the PSEs as a function of preceding direction (Fig. 2c). The data in Figures 2c, 3, 4a, 5a, and 6 have all been corrected for subjective vertical in this way. These corrections were small (1°, on average) but served to align the data into a common reference frame. Importantly, this correction does not alter the pattern of PSE changes dependent on the preceding direction because it is an offset applied to the whole pattern of PSEs.

Figure 2.

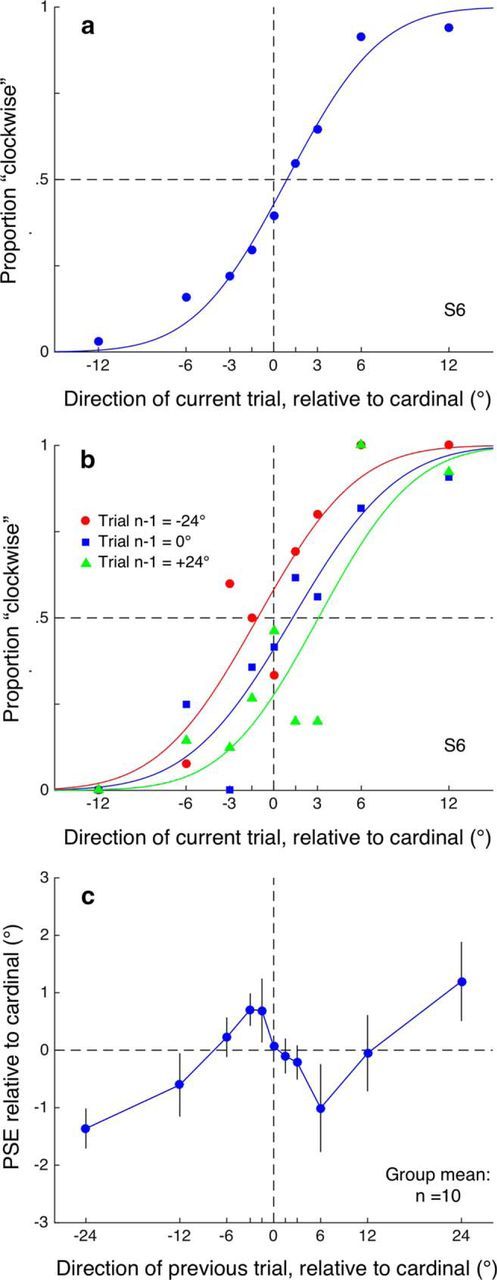
Results from Experiment 1. a, Data from a single participant in Experiment 1 plotting a psychometric function obtained by pooling all trials by direction and fitting a cumulative Gaussian to the data. This is the classical approach to analyzing perceptual discrimination data and the point of subjective equality PSE (given by parameter μ) and function width (σ) are the parameters of interest. Here, the observer's perceptual bias is very small (error from true cardinal is only 0.90°) and the discrimination threshold (5.03°) shows good precision for motion discrimination. b, Intertrial analysis. Instead of pooling all responses into a single function, each response is binned into one of 11 categories depending on the direction presented on the preceding trial. Separate psychometric functions are then fitted for each of the 11 preceding directions. As shown for one observer for several levels of preceding direction (−24°, 0°, and 24°), the horizontal position of the psychometric functions varied systematically with the preceding trial's direction, indicating a sequential dependency. This dependency, typical of all observers, would tend to broaden discrimination functions calculated in the traditional manner by conflating laterally shifted functions. In all subsequent plots, only the PSEs are shown, plotted as a function of the preceding trial's direction. c, Group mean data from Experiment 1 plotting the PSE (indicating the subjective cardinal, the direction where motions are equally judged leftward or rightward of the cardinal) as a function of the preceding trial's direction. Error bars indicate ±1 SEM.

Figure 3.

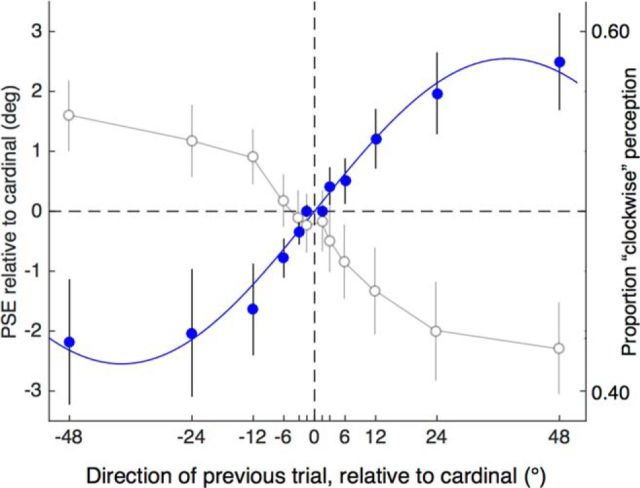
Group mean data from Experiment 2. Filled symbols plot the PSE for direction discrimination as a function of the preceding trial's motion direction. These data were obtained with translating dots that alternated in direction between up and down, canceling motion adaptation between trials but not orientation adaptation. The results show a strong positive relationship for between PSE and the preceding trial's direction attributable to the orientation component. The continuous line shows the best-fitting sinusoidal function with the following parameters: amplitude = 2.55°, peak = 37.8°, and r² = 0.99. Open symbols relate to the second y-axis and show mean proportion of “perceived clockwise” responses and thus reflect the observers' perception. Each data point is the mean of all points on the psychometric function that was calculated for each preceding direction. The proportion of clockwise perception and PSE location exhibit an inverse relationship, illustrating that the positive PSE function is a negative one in perceptual terms: a repulsion effect or negative dependency. Error bars indicate ±1 SEM.

Figure 4.

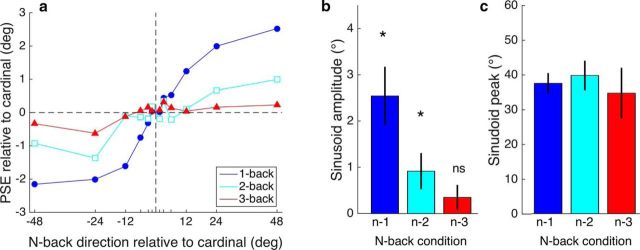
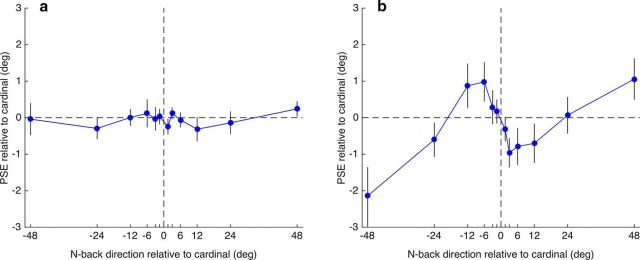
Group mean data from Experiment 2. a, PSE for direction discrimination as a function of the n-back trial's motion direction. The PSE shifts for the one-back direction are compared with PSEs for two-back and three-back directions. b, Data for each n-back level in a were fitted with a sinusoid function (as in Fig. 3). The amplitudes of the best-fitting functions show a strong decline to near-zero amplitude at the three-back level. Asterisks show a significant difference from zero on a one-tailed t test (α = 0.05). c, Peak of the best-fitting sinusoid is very similar across the three n-back levels. Error bars indicate ±1 SE of measurement.

Figure 5.

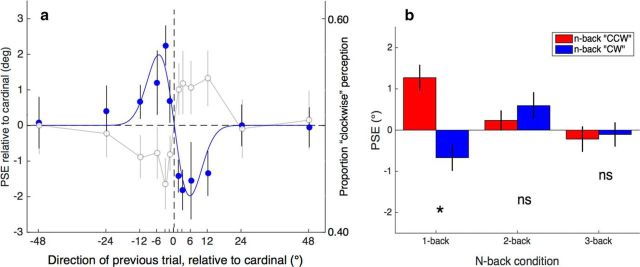
Group mean data from Experiment 3. a, Filled symbols plot the PSE for direction discrimination as a function of the n-back trial's motion direction. These data were obtained with translating dots alternating from trial to trial with a translating grating to isolate the intertrial motion component. The results show a strong repulsive effect on PSE (cf. Fig. 3). The continuous line shows the best-fitting Gaussian first derivative with the following parameters: SD = 5.44, amplitude = 3.31, and r² = 0.87. Open symbols show mean proportion of “perceived clockwise” responses (second y-axis). Each data point is the mean of all points on the psychometric function that was calculated for each preceding direction. The two curves illustrate that the positive PSE function is a negative one in perceptual terms: a perceptual attraction effect or positive dependency. b, As for the intertrial orientation component (Fig. 4), the amplitude of the intertrial motion component declines as the n-back level increases. Red columns show the mean PSE for all counterclockwise n-back directions and blue columns show the mean PSE for all clockwise n-back directions. Only the one-back direction had a significant effect on mean PSE. Asterisks show a significant difference between n-back directions on a two-tailed t test (α = 0.05). Error bars indicate ±1 SEM.

Figure 6.

Group mean data from Experiment 4. a, Results of the first analysis examining the intertrial effect between a motion stimulus moving along a vertical trajectory and a subsequent vertical grating. The PSE for orientation discrimination is shown as a function of the previous trial's motion direction. None of the data points is significantly different from zero, indicating that adaptation to orientation signals from rapid motion stimuli does not transfer to static oriented stimuli. b, Results of the second analysis examining the intertrial effect between a vertical grating and a subsequent motion stimulus moving along a vertical trajectory. The PSE for direction discrimination is shown as a function of the previous trial's orientation and exhibits a strong cubic trend, as observed in Experiment 1, indicating that adaptation to static oriented stimuli strongly influences the perceived direction of rapid motion stimuli. Error bars indicate ±1 SEM.

Results

Experiment 1

In the first experiment, we presented brief motion stimuli randomly jittered in direction around a cardinal direction to look for sequential dependencies in motion direction discrimination. The classical approach to analyzing perceptual discrimination data is to group all trials by direction and fit a psychometric function (Fig. 2a) to calculate the PSE (indicating the perceptual bias) and the function's width (indicating the discrimination threshold). This approach obscures any sequential dependencies between trials. Our intertrial analysis involves binning each response into one of 11 categories depending on the preceding trial's direction and fitting psychometric functions separately to each bin (Fig. 2b). If there were no dependency on the previous trial, then all functions would overlay each other and estimate the same PSE. This is clearly not the case in Figure 2b, indicating that a sequential dependency does exist because the perceived direction is contingent upon the motion direction in the preceding trial. To summarize the intertrial dependency, the PSEs from each of the 11 psychometric functions can be plotted as a function of the preceding trial's direction, as in Figure 2c, which shows group mean data. A one-way repeated-measures ANOVA on the PSEs showed a significant effect of preceding direction (F_(10,90) = 2.271, p = 0.02). The pattern of data was further explored in trend analyses, which indicated a significant cubic trend (F_(1,9) = 17.315, p = 0.002), with no linear (F_(1,9) = 0.531, p = 0.485) or quadratic (F_(1,9) = 1.028, p = 0.337) trends.

The results of Experiment 1 show a clear sequential dependency in that the PSE for motion discrimination around a cardinal direction was contingent upon the motion direction presented in the preceding trial. As has been observed recently for a number of stimuli in the visual, auditory, and audiovisual domains (Alais et al., 2015; Fischer and Whitney, 2014; Fritsche et al., 2017; Van der Burg et al., 2013, 2015), sequential dependencies often occur between sequences of brief stimulus presentations such that perception on a given trial is biased by the previous trial. The effect may be positive, with perception attracted toward the previous stimulus (Fischer and Whitney, 2014; Fritsche et al., 2017), or negative (Alais et al., 2015; Harvey et al., 2014; Van der Burg et al., 2013, 2015), which is more typical of repulsive aftereffects after sustained adaptation to attributes such as motion and orientation (Gibson and Radner, 1937; O'Toole and Wenderoth, 1977). Here, the significant cubic trend plotted in Figure 2c suggests that both positive and negative dependencies co-occurred in our stimuli. The PSE shifted away from the preceding direction if that direction was close to the cardinal and shifted toward the preceding direction if it was far from the cardinal. This particular pattern of sequential dependencies with both attractive and repulsive components was not expected and, to our knowledge, has never been shown before.

The cubic pattern of PSE shifts caused by the preceding motion direction might be related to the fact that the fast-moving dot patterns that we used contain components of both motion and orientation (i.e., motion streaks; Geisler, 1999). It is already known that intertrial dependencies from sequences of Gabor stimuli varying in orientation are attractive (Fischer and Whitney, 2014). However, it is not known whether sequences of motion stimuli varying in direction would exhibit an attractive or repulsive pattern. The aim of the next two experiments is to reveal these two components separately using a new “stimulus-interleaving” approach designed to annul one component to reveal the other component. First, in Experiment 2, we will use the same translating dot stimuli and motion direction discrimination task, but we will interleave upward and downward motions on alternating trials to annul the motion component to reveal the orientation component.

Experiment 2

In this experiment, we will present the same brief motion stimuli randomly varying in direction as in Experiment 1. The key difference is that, here, upward and downward motions will be interleaved with the aim of decoupling the motion and orientation signals to reveal sign of the intertrial dependency for orientation effect. The rationale is that alternating upward and downward motion should nullify motion adaptation between successive trials and cancel the intertrial effect due to motion adaptation. In contrast, alternating upward/downward motion should not affect orientation adaptation from trial to trial because opposed motion directions will produce streaks with the same orientation. With the motion component nulled, we will reveal the pattern of PSE shifts as a function of angle that is linked to the orientation dependency.

Figure 3 shows the results from Experiment 2, plotting the group average shift in motion direction PSE (solid symbols) as a function of the preceding motion's direction. A one-way repeated-measures ANOVA on the PSEs showed a significant effect of preceding direction (F_(11,99) = 6.107, p < 0.0001). The pattern of data was further explored in trend analyses, which indicated a significant linear trend (F_(1,9) = 7.553, p = 0.023), but no quadratic trend (F_(1,9) = 0.015, p = 0.708) or cubic trend (F_(1,9) = 1.128, p = 0.316). More theoretically relevant to an angular orientation effect, the data are very well described by a sinusoidal function (r² = 0.99) with an amplitude of 2.55° and peak (i.e., one-quarter of the wavelength) at 37.8°.

As expected, nulling the motion component with alternating up/down motion revealed a single pattern of PSE shifts attributable to the intertrial orientation dependency. The pattern of PSE shifts is a positive function of the preceding trial's direction, suggesting that this orientation component accounts for the positive-going tails of the cubic function plotted in Figure 2c. As shown in Figure 4a, the group mean PSE shifts as a function of the n-back trial direction are most pronounced for the one-back direction (solid blue symbols). There is a similar but weaker sigmoidal pattern of PSE shifts evident for the two-back direction, but the pattern is absent for the three-back data. This pattern of reducing PSE shifts as the n-back trial increases is summarized in Figure 4b, where the amplitudes of the best-fitting sinusoids to the data in Figure 4a are plotted. The amplitude of the two-back condition was significantly greater than zero but the three-back amplitude was not.

Our results are notable for two reasons. First, we obtain an orientation effect without asking subjects to make any orientation judgements: they simply discriminated motion direction. Second, we get the orientation effect without any orientation apparent in the stimulus. This orientation signature is consistent with streaks from fast-moving objects being encoded by orientation mechanisms (Geisler, 1999). Even though motions streaks are not usually perceived in rapid motion, their existence is predicted because neurons do not provide instantaneous responses but rather a time-averaged response. Here, we have revealed an orientation signature in a motion stimulus using a motion task rather than an orientation task.

The results in Figure 3 (filled symbols) show a clear positive pattern of PSE shifts as a function of angle. This means that psychometric functions moved to the right as the preceding direction moved farther clockwise (Fig. 2c). However, the serial dependencies for orientation reported by Fischer and Whitney (2014) were obtained by measuring perception directly (subjects rotated a line to match their perceived orientation). The difference between measuring perception directly and measuring the location of a psychometric function (i.e., PSE) is critical because they are inversely related. The open symbols in Figure 3 make this clear by showing the average proportion of “clockwise” judgements for the psychometric functions associated with each preceding direction. The average proportion of clockwise percepts declines because, as a psychometric function moves rightward, it will have more values at floor level and fewer at the ceiling. Plotting the data in terms of perception rather than PSE highlights their inverse relationship and shows that the sequential dependency that we obtained for orientation is a perceptual repulsion effect and thus has the opposite sign to that found by Fischer and Whitney (2014).

The tuning of the serial dependency that we report for orientation differs from Fischer and Whitney's (2014) report in two further ways: the amplitude of our effect is smaller and its orientation bandwidth is broader. Stimulus differences may explain these discrepancies. First, the larger amplitude of their effect is probably due to the longer exposure duration used in their experiment (500 vs 200 ms). The size of adaptation effects generally increases monotonically over time and is largely saturated after several tens of seconds (Greenlee and Magnussen, 1987; Hershenson, 1989; Keck and Pentz, 1977). A similar time/magnitude relationship likely exists with rapid intertrial adaptation and our adaptation duration being 2.5 times shorter would inevitably produce a smaller effect. The second difference between our findings is that our orientation effect is more broadly tuned than Fischer and Whitney's, peaking at 38°, whereas theirs peaks at 28°. This is likely due to the orientation component of our stimulus being broader than theirs. The broad orientation content of our stimulus is evident in the summed motion frames shown in Figure 1c (bottom), which clearly has a noisier orientation content than a Gaussian windowed sine wave grating as used by Fischer and Whitney. The tuning of Fischer and Whitney's intertrial orientation effect is rather broad to begin with, peaking at 28° (broader than typical tunings of the tilt illusion and aftereffect, which peak at 15–20°; Gibson and Radner, 1937; O'Toole and Wenderoth, 1977; Wenderoth and Johnstone, 1988), and a stimulus with noisy orientation content would be expected to produce an even broader tuning.

Figure 4 shows that the intertrial orientation effect is short lived and does not persist beyond two trials. How long the intertrial effect lasts will partly depend on stimulus parameters (such as stimulus duration and ITI). Although we found a two-back effect, but no significant three-back effect, Fischer and Whitney's (2014) effects were significant for the two-back and three-back cases. This is consistent with the point made above about our shorter durations producing a weaker effect because recovery time from adaptation is proportional to adaptation duration (Greenlee and Magnussen, 1987; Hershenson, 1989; Hoffmann et al., 1999) and Fischer and Whitney's duration was 2.5 times as long as ours (500 vs 200 ms). The other factor determining the short-term nature of intertrial adaptation is that, in the two-back case, the one-back stimulus is completely independent of the current trial and two-back trial. This means that, over the course of the experiment, the average orientation of the one-back stimulus is 0°, which effectively reduces the orientation difference between the preceding two trials and the current trial. The intertrial adaptation effect is therefore inevitably reduced in the two-back case and even more so in the three-back case.

As the results of Experiment 2 show, alternating upward and downward motion trials effectively isolated an orientation component in our stimulus by nulling the motion component. From the orientation results, we can predict the shape of the motion component by subtracting the sigmoidal orientation effect (Fig. 3) from the cubic pattern of Experiment 1 (Fig. 2). Qualitatively, this subtraction predicts a repulsive pattern of motion PSEs as a function of preceding direction (see also Fig. 7a,b). That is, the predicted pattern is positive PSEs after negative directions on trial n − 1 and negative PSEs after positive directions on trial n − 1. We test this prediction in Experiment 3.

Figure 7.

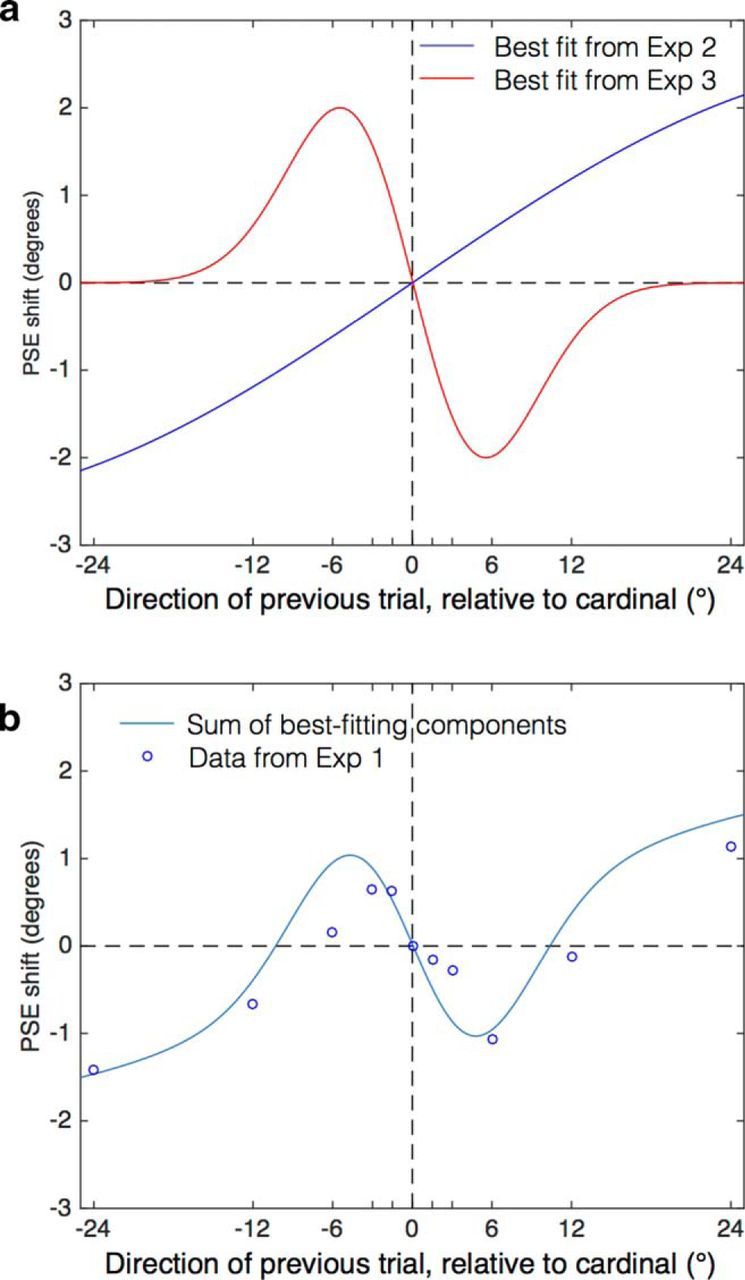
a, Best-fitting sinusoidal function from Experiment 2 overlaid with the best-fitting Gaussian first-derivative from Experiment 3. These functions illustrate the orientation and motion components, respectively, of the rapidly translating dot stimuli. b, Data points showing the results of Experiment 1. The continuous line is the sum of the two components from a, which produces a cubic function that captures the pattern of the data. The data are well described by combining the components with a single free parameter: an amplitude weight that is applied to both components. Here, an amplitude of 0.57 is shown and provides a good fit to the data (r² = 0.85).

Experiment 3

The aim of Experiment 3 is to cancel the orientation component of the cubic intertrial dependency reported in Figure 2 to reveal the motion component. To do this, we used a similar interleaving approach to that used in Experiment 2. We presented translating dot stimuli randomly varying in direction around the cardinal direction in alternation with a translating grating varying around the same cardinal direction. The key is that a moving grating has an orientation orthogonal to its motion direction, whereas translating dots leave motion streaks aligned with the motion direction. This means that there will always be motion present from one trial to the next that are approximately aligned, but the orientations are orthogonal from trial to trial, ensuring that there is no intertrial orientation adaptation. This manipulation should reveal the intertrial motion effect without any orientation component. Qualitatively, this predicts a negative pattern of PSE shifts as a function of preceding direction (see Fig. 7a,b), in contrast to the positive PSE dependency seen for orientation.

Figure 5a shows the results from Experiment 3, plotting the group average shift in motion direction PSE as a function of the preceding motion's direction. A one-way repeated-measures ANOVA on the PSEs showed a significant effect of preceding direction (F_(11,99) = 3.223, p = 0.0009). The pattern of data was further explored in trend analyses, which indicated a significant cubic trend (F_(1,9) = 8.941, p = 0.015), but no linear trend (F_(1,9) = 2.818, p = 0.128) or quadratic trend (F_(1,9) = 0.370, p = 0.558). More theoretically relevant than the cubic trend, the data are very well described (r² = 0.87) by a two-parameter Gaussian first-derivative function. With the mean assumed to be zero and no baseline offset, the best-fitting SD (σ) was 5.44° and amplitude was 3.31°. Figure 5b summarizes the effect for one-, two-, and three-back analyses, comparing the mean PSE of all counterclockwise n-back directions (red columns) with the mean of all clockwise n-back directions (blue columns). Only the one-back analysis showed a significant difference (two-tailed t test, p < 0.05) between mean clockwise versus counterclockwise PSE.

The aim of Experiment 3 was to test the prediction that the intertrial adaptation effect for the motion component would show a negative pattern of PSE shifts. The prediction was based on the assumption that the cubic pattern of data obtained in Experiment 1 (Fig. 2) was due to the rapidly translating dot stimulus containing both motion and oriented streak components. With the data from Experiment 2 showing a clear positive shift in PSEs (Fig. 3), the prediction was that Experiment 3 would show a negative pattern of PSE shifts, reflecting the difference between the data patterns in Figures 2 and 3. The results from Experiment 3 confirm this prediction: the data in Figure 5 show that interleaving grating motion and translating dots produces a clear negative pattern of PSE shifts as a function of the preceding trial's direction. That is, PSEs are positive after a negative direction on trial n − 1 and are negative after a positive direction on trial n − 1.

The notable feature of the repulsive function in Figure 5a is how narrow it is compared with those reported in other studies (Kohn and Movshon, 2004; Levinson and Sekuler, 1976; Schrater and Simoncelli, 1998). The likely reason for this is the concentration of sampled directions close to the mean direction of zero in our study. Although we randomly interleaved directions between +48° and −48°, they were concentrated near zero so that half of the trials (±6, ±3, and ±1.5°) were very close to the mean direction of 0° and would have fallen within the bandwidth of a single motion filter. This would result in very strong adaptation of that channel rather than a wider spread of adaptation if a linear separation of directions were used, and the stronger the attenuation of one channel relative to its neighbors, the narrower is the first-derivative tuning function (see Discussion).

Experiment 4

Experiment 4 interleaves static gratings varying randomly in orientation around vertical with translating dot motion also varying randomly around vertical to examine interactions between orientation generated by motion streaks and orientation from static gratings. Consecutive motion trials (i.e., every second trial) alternate between up and down directions. Assuming an oriented streak component in the fast dot motions, this design will ensure that there is an orientation component on every trial, which should produce an attractive pattern of PSE shifts as seen in Experiment 2. Moreover, this design allows two informative analyses to be compared. First, trials in which motion is preceded by a grating will reveal the effect of static orientation on motion-generated orientation and, second, trials in which a grating was preceded by motion will reveal the effect of motion-generated orientation on static orientation. According to the model outlined by Geisler (1999), these conditions should be equivalent because early orientation filters were proposed to encode both kinds of orientation signal.

Because motion and grating stimuli were interleaved in strict alternation, we conducted two analyses. The first analysis reveals the effect of orientation from motion streaks on a subsequent stationary grating (because motion was always the first stimulus) by calculating the one-back effect between even trials and the preceding trial (i.e., gratings preceded by motion). The second analysis reveals the effect of orientation from static gratings on a subsequent motion stimulus by calculating the one-back effect between odd trials and the preceding trial (i.e., motion preceded by gratings). The interactions between the motion and grating stimuli were very similar regardless of whether the motion was upward or downward, so the four-trial sequence (upward, grating, downward, and grating) was pooled into a two-trial sequence (motion and grating) for the purposes of analysis.

Figure 6a shows the results of the first analysis (the effect of orientation from motion on a static grating's orientation), plotting the group average shift in orientation PSE as a function of the preceding motion's direction. Although we predicted an attractive pattern of PSE shifts similar to that seen in Experiment 2 (Fig. 3), it is clear that this is not the case. A one-way repeated-measures ANOVA on the PSEs confirmed that the effect of preceding direction was not significant (F_(11,88) = 0.904, p = 0.54).

The results of the second analysis (the effect of a static grating's orientation on motion direction) are shown in Figure 6b, plotting the group average shift in motion PSE as a function of the preceding grating's orientation. This analysis reveals a similar cubic function to that seen in Experiment 1 (Fig. 2c). A one-way repeated-measures ANOVA on the PSEs showed a significant effect of preceding orientation (F_(11,88) = 2.532, p = 0.008). The pattern of data was further explored in trend analyses, which, as in Experiment 1, indicated no linear trend (F_(1,8) = 0.365. p = 0.563) or quadratic trend (F_(1,8) = 0.731 p = 0.417), but a significant cubic trend (F_(1,8) = 16.383, p = 0.004).

The prediction for Experiment 4 was for an attractive pattern of PSE shifts, similar to that seen in Figure 3, arising from the fact that each trial contains orientation information, whether from a motion streak or a static grating. The results, however, reveal a curious asymmetry. The first analysis showed orientation signals generated by rapid motion do not influence static orientation perception (Fig. 6a), yet the second analysis shows that static orientation does influence rapid motion perception. It is clear that intertrial dependencies occur between static orientations (Fischer and Whitney, 2014) and between orientations generated by rapid motion (Experiment 2, described above). However, by interleaving motion and orientation in this experiment, we have revealed a clear asymmetry. We suggest that a possible explanation for this is that there are separate mechanisms for orientation originating from static form and for orientation arising from rapid motion, with a simple asymmetry in signal flow: the static orientation mechanism can input to a subsequent (or parallel) motion orientation stage, but orientation signals encoded at the motion stage cannot feed back to (or feed across to) the static orientation stage. Observations consistent with this view come from a temporal frequency-masking study using contrast modulating gratings. The study found that, at high temporal frequencies (such as present in any image that moves fast enough to produce motion streaks), modulating gratings strongly suppressed target gratings of any orientation (Cass and Alais, 2006).

Discussion

Here, we studied sequential dependencies for motion discrimination in brief, random-dot patterns varying in direction over trials. Contrary to predictions, results showed a positive perceptual dependency for motion perception and, unexpectedly, we found a second perceptual dependency linked to orientation exhibiting a negative dependency. Both dependencies occurred simultaneously in our motion discrimination task (Experiment 1), but were separable with appropriate interleaving of stimuli. Experiment 2 nulled intertrial motion adaptation to reveal the orientation component and found a strong positive pattern of PSE shifts, a negative perceptual dependency, over preceding trial direction, an effect that we attribute to adaptation from oriented motion streaks (Geisler, 1999). Experiment 3 eliminated the orientation component between trials to reveal a narrow, negative pattern of PSE shifts over preceding trial direction (positive perceptual dependency), an effect consistent with motion priming. A weighted sum of the separately isolated orientation and motion components from Experiments 2 and 3 produced a cubic function (Fig. 7b) similar to the data from Experiment 1 and consistent with motion and orientation components in translating dot patterns summing to shape current motion perception in terms of the previous stimulus. Another recent study showed that opposed serial dependencies can arise from different attributes of a single stimulus (Taubert et al., 2016), although in that study, subjects responded explicitly to two attributes. In our study, we show that two dependencies can arise from responses to a single stimulus attribute.

Experiment 2 interleaved upward and downward motions to null motion adaptation between trials and reveal the orientation effect. The negative perceptual dependency for orientation (Fig. 3) is a repulsive effect like the tilt aftereffect (TAE; Gibson and Radner, 1937), in which exposure to an adapting orientation makes neighboring orientations appear tilted further away. The TAE will occur even after very brief presentations such as used here (Dickinson et al., 2012; Sekuler and Littlejohn, 1974; Suzuki, 2001). The standard TAE explanation is that adaptation reduces the response of neurons selective for the adapter, causing the population's peak output for neighboring orientations to occur further from the adapted orientation (Clifford et al., 2000). We propose that our repulsive perceptual effect for orientation is a TAE arising from oriented motion streaks (Geisler, 1999). This contrasts with a recent study reporting an attractive dependency for orientation (Fischer and Whitney, 2014), although a recent study comparing the type of response task used may explain this. In two experiments with very similar parameters and procedures, Fritsche et al. (2017) showed that the sign of the serial dependency for orientation is task dependent, with comparative judgments (e.g., a two-alternative forced-choice: 2AFC) producing repulsion and direct perceptual reports such as the method of adjustment producing repulsion (Fritsche et al., 2017). Although ours was a single-interval task, it was inherently a comparative task because subjects were discriminating the stimuli against a subjective cardinal direction.

Experiment 3 eliminated the orientation component between trials to isolate the motion effect and found a negative pattern of PSE shifts, a positive perceptual dependency (Fig. 4). This new finding for motion extends recent reports of positive serial dependencies for orientation (Fischer and Whitney, 2014), face identity (Liberman et al., 2014), face attractiveness (Taubert et al., 2016), and face gender (Taubert et al., 2016). This positive dependency is consistent with motion priming, an effect in which a brief priming motion preceding an ambiguous motion biases perceived direction toward the primed direction (Kanai and Verstraten, 2005; Pinkus and Pantle, 1997), and also with Fischer and Whitney's notion of a continuity field, which averages recent stimulus history to stabilize perception. More generally, it is consistent with accounts in terms of Kalman filtering and predictive coding frameworks (Cicchini et al., 2014).

On Fritsche et al.'s (2017) account, positive sequential dependencies are due to decision-level factors and working memory effects as stimulus representations are retained while subjects reproduce their percept. The negative dependency revealed by the 2AFC task reflects sensory-level factors. The two opposed dependencies that we found map well onto this framework. Rapidly translating dots are known to produce orientation effects in perceptual and neural responses (Apthorp and Alais, 2009; Apthorp et al., 2013; Geisler et al., 2001) thought to arise from temporal integration in orientation-selective neurons smearing the stimulus into oriented motion streaks. Although orientation effects from motion are easy to demonstrate (Apthorp et al., 2010; Burr and Ross, 2002; Edwards and Crane, 2007), the streaks themselves are not perceived at moderate speeds such as used here. Therefore, the only aspect of our stimulus that was consciously available at the decision level was the motion attribute and this produced a positive dependency, whereas the orientation component was not consciously available and produced a negative dependency. This fits with Fritsche et al.'s (2017) task-based distinction and with findings that TAEs arise at early cortical levels and do not require the tilt adapter to be perceived (Apthorp et al., 2009; Blake and Fox, 1974; Wade and Wenderoth, 1978).

Two notable features in our data are the very narrow motion tuning (Fig. 5) and the very broad orientation tuning (Fig. 3). We attribute the broad orientation tuning (the sinusoidal function peaks at 37°; Fig. 3) to the broad orientation spectrum of the temporally summed random-dot motion images (Apthorp et al., 2011) relative to sinusoidal gratings. Studies using gratings show much narrower orientation tunings (15–20°; Clifford, 2002; Gibson and Radner, 1937; O'Toole and Wenderoth, 1977; Wenderoth and Johnstone, 1988). The very narrow motion tuning (Fig. 5) may result from the clustering of motion directions around the cardinal. Half our trials were within ±6° of the cardinal and this bias may have led to stronger motion priming among filters coding the cardinal direction than the more oblique directions. Within a standard multichannel motion model, and assuming that priming is due to boosted gain in a given channel, our center-biased directions would produce a stronger gain near the cardinal direction and a narrower repulsion function than if the priming gain were centrally concentrated. Adding to this, the directional tuning of monkey MT cells become narrower after motion adaptation in the preferred direction (Kohn and Movshon, 2004), an effect that would manifest mostly around the cardinal in our experiment.

In Experiment 4, we alternated trials of rapid-dot motion with static gratings oriented along the motion trajectory to test whether grating and motion components would interact. Although we did find an interaction, it was asymmetrical: static orientation influenced motion direction, but motion-defined orientation did not alter static orientation. Indeed, PSE shifts for orientation are strikingly absent in Figure 6a. Geisler's (1999) original proposal was that signals from orientation-tuned simple cells were multiplied in V1 with complex cells signaling direction. Given our strong asymmetry, we suggest either that the early orientation/motion combination in Geisler's (1999) original proposal is strictly a one-way process with orientation feeding into motion but not vice versa or that the process happens at sequential levels with orientation from static form preceding orientation from motion, with the latter not feeding back to static orientation mechanisms. The first possibility is a simple modification of Geisler's model, whereas the second is a significant change to its architecture. Consistent with the second possibility, Tang et al. (2015) very recently reported a similar orientation/motion asymmetry. Based on psychophysical evidence, they concluded that orientation precedes motion and suggested that orientation extracted in V1 provides a gain-modulating signal to MT motion units, boosting gain for the motion trajectory to narrow the motion system's output.

Another factor relevant to the orientation asymmetry is that temporal integration estimates for suprathreshold global motion stimuli are much longer than those for simpler motion stimuli. Estimated integration periods are typically in the range of 100–200 ms (Baker and Braddick, 1985; Burr, 1981; McKee and Welch, 1985; Morgan and Ward, 1980; Snowden and Braddick, 1991), yet increase markedly for global motion stimuli such as biological motion (2000 ms; Neri et al., 1998) and optic flow (3000 ms; Burr and Santoro, 2001). Two studies examining integration times for translating random-dot patterns found integration periods of 700 ms (Neri et al., 1998) and 500 ms (Watamaniuk and Sekuler, 1992), the latter study being highly relevant because its direction discrimination task is similar to the present study. These studies imply that motion streaks may be longer than indicated by the convolution of a random-dot image by models of early temporal impulse response functions (Manahilov et al., 2003), which produce rather short streaks (see Fig. 5 of Alais et al., 2011). Also relevant is a study showing that temporal integration of parallel contours in relatively large stimuli such as those used here has a long integration period and probably occurs in area V4 (Aspell et al., 2006). Because there are strong interconnections between V4 and MT (Maunsell and van Essen, 1983; Ungerleider and Desimone, 1986), globally integrated streak contours at the level of V4 could provide motion trajectory input to MT and explain the asymmetrical influence of orientation on motion.