Sensory Flow as a Basis for a Novel Distance Cue in Freely Behaving Electric Fish

Abstract

The sensory input that an animal receives is directly linked to its motor activity. Behavior thus enables animals to influence their sensory input, a concept referred to as active sensing. How such behavior can serve as a scaffold for generating sensory information is of general scientific interest. In this article, we investigate how behavior can shape sensory information by using some unique features of the sensorimotor system of the weakly electric fish. Based on quantitative behavioral characterizations and computational reconstruction of sensory input, we show how electrosensory flow is actively created during highly patterned, spontaneous behavior in Gnathonemus petersii. The spatiotemporal structure of the sensory input provides information for the computation of a novel distance cue, which allows for a continuous estimation of distance. This has significant advantages over previously known nondynamic distance estimators as determined from electric image blur. Our investigation of the sensorimotor interactions in pulsatile electrolocation shows, for the first time, that the electrosensory flow contains behaviorally relevant information accessible only through active behavior. As patterned sensory behaviors are a shared feature of (active) sensory systems, our results have general implications for the understanding of (active) sensing, with the proposed sensory flow-based measure being potentially pertinent to a broad range of sensory modalities.

SIGNIFICANCE STATEMENT Acquisition of sensory information depends on motion, as either an animal or its sensors move. Behavior can thus actively influence the sensory flow; and in this way, behavior can be seen as a manifestation of the brain's integrative functions. The properties of the active pulsatile electrolocation system in Gnathonemus petersii allow for the sensory input to be computationally reconstructed, enabling us to link the informational content of spatiotemporal sensory dynamics to behavior. Our study reveals a novel sensory cue for estimating depth that is actively generated by the fishes' behavior. The physical and behavioral similarities between electrolocation and other active sensory systems suggest that this may be a mechanism shared by (active) sensory systems.

Introduction

In the great majority of cases, sensing is an active process during which some form of sensor or body movement is used to shape sensory input (Poincaré, 1902; Bajcsy, 1988). The use of internal models enables animals to predict the sensory consequences of their motor action (Sperry, 1950; von Holst and Mittelstaedt, 1950; Blakemore et al., 1998; Körding and Wolpert, 2004); motion thus serves as a tool to actively shape sensory input. Shaping the sensory input through motion either allows the extraction of specific features of sensory input or changing the statistics of the sensory input to align it with the tuning properties of neurons (Kern et al., 2005; Rucci et al., 2007; Ahissar, 2008; Gordon et al., 2011; Jung et al., 2011; Clarke et al., 2015). The former reveals specific features that cannot be sensed if an animal behaves differently, and the latter matches input properties to the sensitivity of the neuronal substrate. This motor aspect of sensing is crucial for the flexibility and adaptability of sensing (Schnitzler, 1973; Metzner et al., 2002; Towal and Hartmann, 2006; Diamond et al., 2008; Schroeder et al., 2010; Wachowiak, 2011; Braun et al., 2012; Arkley et al., 2014), and is often performed by highly specialized patterns of movement (i.e., “active sensing strategies”) (Hofmann et al., 2013b; Anderson and Perona, 2014) that can be interpreted as an externalization of the brain's integrative functions. Here we investigate the spatiotemporal dynamics of behaviorally generated sensory input and how this sensorimotor interaction allows for the extraction of behaviorally relevant information in the weakly electric fish Gnathonemus petersii.

These fish sense their surroundings by emitting brief (≤500 μs) biphasic electric signals (electric organ discharge [EOD]) (Machin and Lissmann, 1958; Harder et al., 1964) that build up a 3D electric field around the animals' body. Perturbations to this field caused by nearby objects lead to alterations in the pattern of transcutaneous currents, termed the “electric image” (EI) (Rasnow, 1996; Caputi and Budelli, 1998; Rother et al., 2003). This pattern is sensed with an array of electroreceptors distributed in the animals' skin (Harder, 1968; Bacelo et al., 2008). EOD emission is volitionally controlled in a task-dependent manner (Post and von der Emde, 1999; Caputi et al., 2003; Jun et al., 2016), which highlights the importance of timing during electrosensory acquisition and allows for the “when” in sampling experimentally to be precisely determined. At the same time, the near-range nature of active electrolocation (Knudsen, 1975; Snyder et al., 2007) provides access to the specifics of the sensory environment that are being sampled (i.e., the “what”). Even though it is possible to precisely determine these key features of sensing in electrolocation, the spatiotemporal features or the behavioral context of electrosensory input has yet only rarely been addressed (Nelson and MacIver, 1999; MacIver et al., 2001; Babineau et al., 2007; Fotowat et al., 2013).

Here we study motor behavior and its sensory corollaries by computationally reconstructing the sensory input for a large dataset of quantitatively characterized sequences of sensory behavior. In our analysis, we consider both spatial and temporal aspects of the sensory input and investigate the following: (1) how the sensory flow is shaped by the animal's behavior; and (2) how coherent motor and electromotor behavior aids in sensing through the generation of dynamic sensory input that contains information not available through less-structured behavior. Our study thus begins to uncover the role of sensory flow in active electroreception in G. petersii and provides evidence for the importance of timing and structured motor patterns in (active) sensing in general.

Materials and Methods

In this study, we combined a quantitative behavioral characterization of spontaneous electrolocation behavior with a biophysical model for the calculation of EIs with the aim of reconstructing the spatial and temporal dynamics of the electrosensory input.

For statistical tests, the data were tested for normality (Lillifors test), after which appropriate parametric or nonparametric tests were conducted. Data collection, analysis, and visualization were performed with MATLAB (version R2011b; RRID: SCR_001622) routines.

Behavior: animals.

G. petersii (N = 11; 11 ± 2 cm, fish of unspecified sex) were obtained from a commercial fish dealer and housed separately in individual tanks prior data acquisition with a water conductivity of 100 ± 10 μS/cm. At 24 h before beginning the experiment, the fish were transferred to the experimental tank for acclimatization. All experimental procedures were performed at a water conductivity of 100 ± 10 μS/cm.

Video recordings.

The results presented in this study are based on the quantitative characterizations of electrolocation behavior published in an earlier study (Hofmann et al., 2014). In brief, we videotaped (AVT Marlin F-033B, Stemmer Imaging, 656 × 494 pixels, 12 bit, maximal frame rate 78 Hz) the spontaneous behavior of solitary fish in a shallow water (6 ± 0.5 cm) tank (80 × 80 cm), with different metal cubes (1, 8, or 27 cm³) being temporarily introduced in the center of the tank. Recordings were performed under IR illumination (880 nm) to rule out the possibility of visually guided behaviors (Ciali et al., 1997). Image acquisition was frame-locked to the EOD (recorded with a custom-built electrode array and amplifier) so that one video image was acquired for each EOD.

Video tracking.

Position, orientation, and posture of the animal were then determined from the video data collected during the experiment. The animals' center of mass was ascertained by using a background subtraction approach with subsequent thresholding. The animal's posture was obtained by applying a third-order polynomial fit through the midline of the body (see Fig. 1E, inset, red dotted line). This fit was restricted in length according to the size of each individual. Head and tail points were determined based on the spindle-like shape of the fish's body, with the head being closer to the body's center of mass. The cubes were tracked similarly to the animal in each single frame of the videos. For all behavioral data, the term “distance” always refers to the relationship between the animal's head and the object's center of mass. From the tracked positions of the animals, we determined the kinematics (i.e., thrust, slip, and yaw), which we used for classifying the behavior.

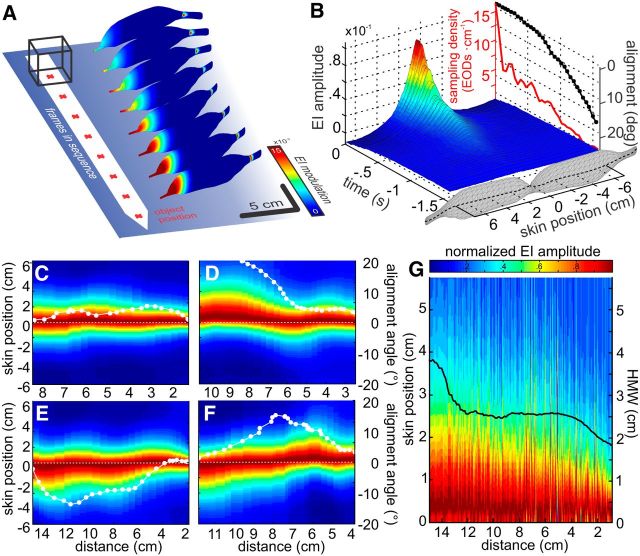
Figure 1.

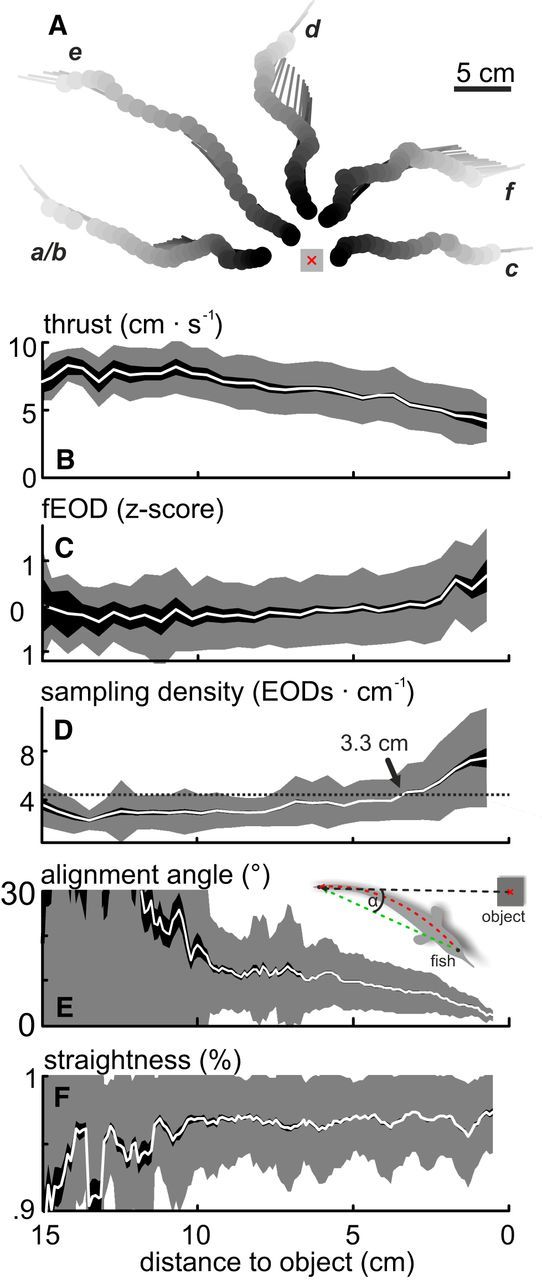
Object approach behavior. A, Example trajectories of the “object approach behavior.” Top view, Filled dots and lines indicate head position and body orientation at the time of EOD emission, respectively. Gray shading represents the temporal order within each sequence. The object was an 8 cm³ metal cube (gray scheme, red crosshair represents center of mass). Letters indicate individual trajectories that are used in Figure 2. B–D, Average sampling behavior during the approach. Top to bottom, Parameters shown are as follows: thrust (B), EOD frequency (C; values were z-scored for individual recording sessions), and sampling density (D). Whereas thrust decreased steadily with increasing proximity to the object, EOD frequency increased. The sampling density reflects the number of EODs emitted per centimeter traveled. Sampling density increased with increasing proximity to the object and was significantly elevated from baseline at a distance of 3.3 cm (dotted line and arrow). These data are pooled for approaches to different object sizes because no significant differences were found (see also Materials and Methods). E, F, Average of postural parameters of the approach behavior. Parameters shown are as follows: body-object alignment (E) and straightness of the body (F). Alignment increased (decreasing values) while the overall body curvature was reduced with increasing proximity to the object (F). E, Inset: Scheme of how the alignment angle (α) and the straightness were obtained (see Materials and Methods). B–F, Mean (white line) ± SEM (dark shading) and standard deviation (light shading) as calculated from pooled data of all “object approach” sequences (N = 235, 11 fish).

Behavioral classification.

We classified the behavior based on clustering algorithms (Braun et al., 2010; Geurten et al., 2010). Kinematics were separated with a hierarchical clustering followed by a k-means based classification. These clusters are referred to as “kinematic prototypes.” The transition probabilities between kinematic prototypes were analyzed to find recurring patterns (for details, see Hofmann et al., 2014). We focused on one specific pattern, the “object approach behavior.” The frequency of this pattern was increased in presence of an object in the tank, indicating that it was clearly related to electric sensing.

Model.

The electrosensory input was calculated for each emitted EOD (i.e., each recorded image) with a computational model developed by Rother and Budelli (Rother et al., 2003) using the boundary element method (Bacher, 1983; Hunter and Pullan, 1997; Assad et al., 1999). This procedure first sets up the geometric relationship between the fish's body and a given object (the electric scene), which then is used to calculate the transdermal current on the surface of the body. The model output was experimentally corroborated by physiological recordings in previous studies (Sanguinetti-Scheck et al., 2011; Hofmann et al., 2013a). A more thorough description of the model was given by Pedraja et al. (2014).

Electric scene reconstruction.

Electric scenes are defined by the geometric relationship between the animal and the cube. The animal was reconstructed in 3D using 50 ellipses to form a cross section of the fish along defined points of its body axis. The connections between 835 nodes located on the ellipses were used to generate the tessellation that represents the surface of the animal. Size and location of the ellipses were scaled to match the length of each individual fish and were subsequently fitted frame by frame to the posture extracted from the videos. Whereas the modeling was calculated in three dimensions, the information used to set up the scene was 2D only. For modeling purposes, pitch, roll, and elevation were not included. The variability of electric images is therefore likely underestimated in our study.

Boundary element method model.

The electric organ was simulated by a local dipole in the tail of the body model. With this, the electric field was simulated and geometric reconstruction was used to calculate the transcutaneous distribution of the current. This procedure was performed twice: once without any object present (basal condition) and once with presence of an object (object-perturbed condition). This enabled us to estimate the perturbing effect of the object and calculate the EI over the whole surface of the body (see Analysis). The simulation results were assessed along a linear transect (sampling equator), which ran along the frontal 70% of both sides of the body model, crossing the head in the nasal region (see also scheme in Fig. 2B). This reduced the data dimensionality while enabling us to reliably estimate the sensory input, particularly for the foveal head region of the fish. The absolute spatial resolution of the sampling equator differed depending on body position and animal size (the number of nodes used in the body model was constant regardless of fish size). For a fish of 10 cm in length, the average resolution along the sampling equator was 8.6 nodes/cm, with an increased resolution in the head region (17 nodes/cm for the region ± 1.5 cm from the tip or the head).

Figure 2.

Spatiotemporal electrosensory flow during naturalistic behavior. A, Electric images for every second frame of the final 16 EODs of an individual approach. Images are shown with a frame-by-frame lateral offset from the object. Red crosshairs represent object center of mass. B, Spatiotemporal representation of the EI (as calculated in Eq. 2) for the sequence shown in A. The spatial domain is represented on the x-axis. Skin position is calculated along a sampling equator along the fish body that is indicated by the black dotted line in the fish schemes: positive x-values indicate positions on the left side of the body, whereas negative values indicate positions on the right side. The discontinuous temporal domain is shown on the y-axis. Sampling density (red line) increased, whereas the alignment angle between body and object decreased steadily (black line). This was a consistent pattern (Fig. 1D, E). C–F, EI sequences plotted as a function of object distance for four approaches. y-axis indicates the skin position of the EI along the sampling equator (see B). Individual electric images along this equator were normalized to their peak value and then plotted as a function of object-distance (x-axes). White lines indicate the body-object alignment for the individual sequences (see right-hand y-axes). White dots indicate where an EOD was emitted. G, Normalized and stacked EIs from all EODs (n = 2388) emitted during all approaches toward the 8 cm³ cube. Each normalized EI was arranged such that its peak is located on the right side of the animals' body, the side being shown here. Following this, EIs were ordered as a function of distance to the cube, leading to a cumulative figure showing how the sensory input changed with nearness to the cube. The peaks of electric images became more focused on the head (skin position = 0) with nearness to the cube; likewise, the average half-maximum width (black line) decreased. This illustrates a gradual focusing of the EI on the head region. The trajectories used for visualization in this figure are marked with their respective panel letter in Figure 1A.

The procedures described above were performed for all trajectories of “object approach behavior” (N = 235, 5079 frames). Our modifications to the EI modeling advanced the model to a level in which the calculation of sensory input for experimentally observed behavior can be performed on a large scale.

Analysis: behavior.

To quantify the straightness of the fish body, the ratio of the Euclidian distance between the head and tail (see Fig. 1E, inset, green dotted line) to the length of the animal was used. The latter was taken from a polynomial fit to the animals' midline (red dotted line). The ratio of straightness is limited to the range between 0 and 1, with smaller values representing stronger curvature of the animal's body.

The animal's alignment to the object was determined as the angle between the vector connecting head and tail position and the vector connecting tail position with the object's center (see Fig. 1E, inset, green and black dotted line).

The EOD frequency was calculated as the inverse of the interframe interval. The EOD frequency was z-scored for each experimental session (i.e., per experimental session) to account for individual changes in basal EOD frequency as follows:

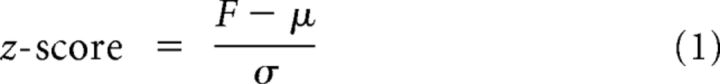with EOD frequency F, its arithmetic mean (μ), and standard deviation (σ) computed anew for each recording session.

The sampling density (SD) was determined as the number of EODs emitted per distance traveled. Object independent SD (baseline) was determined by averaging all data at distances >7.5 cm from the object. SD values exceeding a threshold (arithmetic mean of object-independent SD plus one standard deviation) were considered to be significantly elevated from baseline (see Fig. 1D, horizontal dashed line). The SD tended to increase at higher distances for larger objects. However, when fitting the data of individual-approach sequences with power-law fits, the parameters were not significantly different between object sizes (Kruskal–Wallis test; scaling: χ² = 0.43, F = 0.31, df = 2, p = 0.73; exponents: χ² = 5.83, F = 3.12, df = 2, p = 0.052; shift: χ² = 1.79, F = 0.89, df = 2, p = 0.41). Consequently, the behavioral data are shown pooled across differently sized objects. We obtained the coefficient of determination by linearly correlating the EOD frequency and the thrust with the SD. This was used as a measure to quantify how much variance in the SD is explained by the EOD frequency or thrust (variance-accounted-for [VAF]). The variability of this measurement was estimated via bootstrapping (200 repetitions, based on randomly discarding 25% of the full dataset).

EI analysis.

The EI at a given spatial position (x) along the sampling equator was calculated as the object-perturbed potential relative to the unperturbed condition as follows:

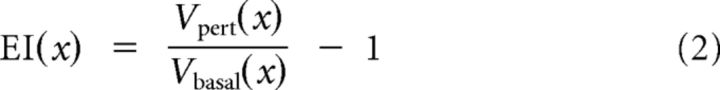where, V_pert(x) is the voltage measured in the perturbed condition, and V_basal(x) is the voltage measured in the unperturbed condition at a given skin position x. Unmodulated EIs thus have a value of zero.

EI amplitude was characterized as the root mean square (RMS) of the EI as follows:

with N being the number of nodes along the sampling equator. This operation integrates the spatial amplitude pattern of the EI into a single mean perturbation, thereby removing spatial information from the EI.

The slope-to-amplitude ratio (SAR) (von der Emde et al., 1998) was calculated by dividing the peak amplitude in the EI by the maximum slope in the EI. In the original study, this was done for EIs measured at the trunk of the animal's body. In our study, the EIs span bilaterally across the head of the animal. This enables two “maximum slopes” in the image to be determined, one on each side of the body. We found that always using the smaller of the two maximum slopes for the SAR calculation resulted in less variability (note that the larger slope yielded qualitatively comparable results). In earlier characterizations of the relation between SAR and distance, the SAR was fitted with exponential functions over a limited range of object distances. For our data, evaluating the r² values of a linear fit in log/log space indicated that a power-law relation was closer to the data, which we consequently used in our analysis.

The temporal resolution of the discontinuous sampling of G. petersii is directly linked to the sampling interval. Electrosensory information thus is only available to the fish when EODs are emitted. Accordingly, we calculated all dynamic measures based on the change of given parameters between successive EODs. For example, the electrosensory flow between two consecutive EIs was calculated as follows:

where the index i represents the index of the EI analyzed. ΔRMS_i is the difference between two EODs, as defined in Equation 3. As this finite spatial difference depends on the animal's sampling behavior (probing its surroundings at an irregular pace), the electrosensory flow during a given trajectory can thus be regarded as a variable spatial derivative of the electric field, and we will use this term in the following analysis. The relative gradient (RG) was calculated by normalizing the ΔRMS_i by the product of the change in position (ΔPos_i) and the EI amplitude (RMS_i):

Receiver operating characteristic (ROC) analysis.

Object detection and distance-discrimination performance, based on either the SAR or the RG, were compared using an ROC analysis. This was independently conducted for both SAR and RG using histograms (bin width 1 cm) of the SAR or RG values at distance intervals (step size 0.2 cm) relative to the object. The histograms at 10.5 cm distance served as the reference point to which all data at closer distances were compared. Sensitivity was estimated based on the area under the determined ROC curve and was considered to enable a significant detection of the objects when it exceeded 70%.

To determine the distance discrimination capability of either the SAR or the RG, the procedure described above was repeated using each histogram once as a reference. The relative distances where the sensitivity reached 70% served to indicate distance-discrimination performance: the just-noticeable-difference distance (JND). The variability of these data were estimated by bootstrapping (200 repetitions, based on randomly discarding 50% of the full dataset).

Results

Object-approach behavior

The object-approach behavior of G. petersii is kinematically defined by a pattern of prototypical movements (Hofmann et al., 2014). This spontaneous behavior is observed when animals advance to novel objects (i.e., the behavior is goal directed and involves changes of the sampling behavior that depend on the distance to an object). We analyze the sensorimotor consequences of this patterned behavior (see randomly chosen examples in Fig. 1A). Characteristic for this approach is a reduction in the average thrust (Fig. 1B), which is accompanied by an increase in the EOD frequency (Fig. 1C). We calculated the resolution of sensory sampling as the number of EODs emitted per distance traveled. This SD increased nonlinearly toward the object (Fig. 1D), significantly exceeding the baseline SD once fish were within 3.3 cm of the cube (Fig. 1D, black dotted line and black arrow). A comparison of the SD observed for approaches to objects of different size showed that the SD tends to increase earlier for larger objects. This trend was not significant and we thus pooled the behavioral data (see Materials and Methods). SD depends on changes of EOD frequency and thrust; and to address which of the two behaviors is predominantly used to modulate the SD, the VAF was calculated. This calculation showed that, on average, thrust contributed more to the SD than the EOD frequency (VAF thrust: 0.449 ± 0.015, VAF EOD frequency: 0.328 ± 0.024; mean ± range; ANOVA; F = 5.4 × 10⁴; df = 1; p = 0). This finding is comparable with data from a pulsatile Gymnotid fish (Gymnotus sp., Jun, 2014), suggesting that the resolution of sensory sampling is dominated by controlling thrust in both groups of electric fish.

The gradual changes of the sampling density and thrust during the approach-behavior were accompanied by adaptations in postural behavior: the alignment between the animals' direction and the objects' position gradually increased (i.e., decreasing relative angle between animal and object, Fig. 1E), and the curvature of the animals' body decreased (Fig. 1F).

Sensory flow during object-approach behavior

To quantify the sensory corollaries of the sensory and motor behavior, simultaneous measurement of the local electric field amplitude at each of the thousands of electroreceptors would be required for every instance of sampling. Because this is not technically possible at present, we refined and adapted a computational model (Rother et al., 2003; Rother, 2003) to calculate the spatially distributed sensory input for each EOD (Fig. 2A). These modeled electric images give us access to both the static and dynamic information available from the sensory input: while the spatial aspects of the 2D current distribution over the animals' skin at each EOD represent the present electrosensory scene, the change between successive scenes conveys spatiotemporal information. This change, subsequently referred to as electrosensory flow, depends both on the timing of sampling as well as the movement of the animal.

The electrosensory flow encountered during natural behavior is complex, as it reflects the temporal evolution of the spatially varying pattern of current densities along the skin of the fish (Fig. 2A). We reduced its dimensionality by evaluating the EIs along a sampling equator (Fig. 2B; black dotted line on fish schemes; see also Materials and Methods). During the approach shown in Figure 2A, B, the electromotor behavior changed analogously to the change in the pooled data (Fig. 2B, side plots: SD (red) and alignment angle (black)). The EI amplitude increased nonlinearly, associated with a gradual shift of the EI peak toward the head region of the animal (Fig. 2B, main plot). This centering of the EI peak on the foveal regions of the head was consistently observed during the final phase of the approaches (see examples in Fig. 2C–F). In Figure 2C–F, the data are plotted as a function of distance to the cube to simplify comparability between the individual sequences. At the same time, the fish increasingly aligned themselves with the cube (see superimposed white lines, alignment angle decreased on average; compare Fig. 1E). In Figure 2G, all 2388 EIs of approaches to an 8 cm³ cube were normalized and stacked such that the maximum EI always is shown to the left. As a consequence of this alignment, the EI peak (i.e., center) was gradually shifted onto the center of the head (0 cm skin position of the y-axis, see Fig. 2G), where it became more focused with increasing proximity (i.e., the contrast increased). This is quantitatively depicted by the decreasing half-maximum width (Fig. 2G, black line).

These results suggest that the strategy by which fish localize and reach targets increases the EI intensity from EOD to EOD while simultaneously reorienting to gradually move the EI peak onto the head region.

Does natural behavior influence spatial EI cues?

When approaching an unknown object, estimating one's relative distance is crucial in performing distance-dependent actions, such as collision avoidance or stopping the approach at an appropriate stage (e.g., to inspect the object; see Discussion). In active electroreception, unlike the visual sense, depth must be determined from image blur (Lewis and Maler, 2002). The SAR is a measure of this blur and conveys object-size invariant information about distance (von der Emde et al., 1998).

An analysis of the suitability of the SAR for distance estimation in naturalistic behavior has not previously been performed or published. Accordingly, we examined whether the SAR as well as a related parameter (half-maximum width of EIs; data not shown) can provide a distance cue under naturalistic and hence noisy conditions (Fig. 3A). The data of approaches toward cubes of different sizes did indeed show considerable overlap, and fitting data from individual approaches proved the datasets to be inseparable (Fig. 3A, insets; Kruskal–Wallis, p > 0.07) and thus size invariant. The SAR thus provides distance information, even for the strongly curved head region that appears to be the foveal region in terms of receptor density (Bacelo et al., 2008).

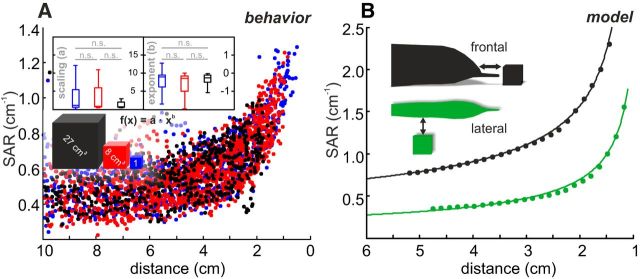
Figure 3.

Distance estimation based on spatial SAR. A, SAR for all EIs as a function of distance to the metal object (0 = center of the object). Blue represents 1 cm³ cube. Red represents 8 cm³ cube. Black represents 27 cm³ cube. SAR increased with nearness to the object. The data were compared by fitting power-law functions to the SAR values of individual approach trajectories. Inset, Box-and-whisker plots for axis shift and exponents of the individual functions. These distributions were inseparable (Kruskal–Wallis test; shift: χ² = 5.2, F = 2.6, df = 2, p = 0.08; exponents: χ² = 2.1, F = 1.0, df = 2, p = 0.36), confirming that the SAR provides a size invariant measure of object distance. B, Modeled SAR-distance functions for a cube (8 cm³) calculated for the head region (black) and the trunk (green). Exponents and offsets of the data differed for the different body regions, showing a potential weakness if animals were to rely on the SAR metric only.

Under natural conditions, the SAR is highly variable (Fig. 3A). To a large extent, this is due to the dependency of the EIs on the animals' posture. It is further increased because EIs (and hence the SAR) depend on the part where they occur on the fish's body (Fig. 3B) (Pusch et al., 2008; Hofmann et al., 2013a). Finally, the number of electroreceptors (per mm²) varies considerably for different body regions (Harder, 1968; Bacelo et al., 2008), which directly affects the accuracy by with which an animal could resolve SAR spatially. For these reasons, spatial metrics provide, at best, a crude estimation of distance during dynamic behavior. We hypothesized that the temporal electrosensory input dynamics might offer alternative, potentially more reliable cues for distance estimation that could eliminate the need to integrate the sensory input of the spatially distributed electroreceptors.

Distance estimation based on electrosensory flow

Given the spherical dissipation of the electric field emitted, the fish should experience an EI amplitude that is inversely proportional to the fourth power of distance (d⁻⁴) (Rasnow, 1996; Sicardi et al., 2000; Chen et al., 2005; Nelson and MacIver, 2006) and scale with the size of the object being approached. Indeed, the EI amplitude in our data were well approximated by power-law fits with exponents of −4 and scaling factors that were object size-dependent (Fig. 4A). The closer the animal gets to the object, the steeper the increase in the EI amplitude. In the following, we use the RMS as a measure of amplitude; however similar results were obtained when using the EI maximum. The electrosensory flow (i.e., the rate of change of the sensory input from one EOD to the next) allows for the extraction of a novel distance metric that we subsequently refer to as the relative gradient. In contrast to geometric analyses of EIs as required for the SAR, the parameters that are necessary to obtain this electric flow-based measure are readily available from the sensory input.

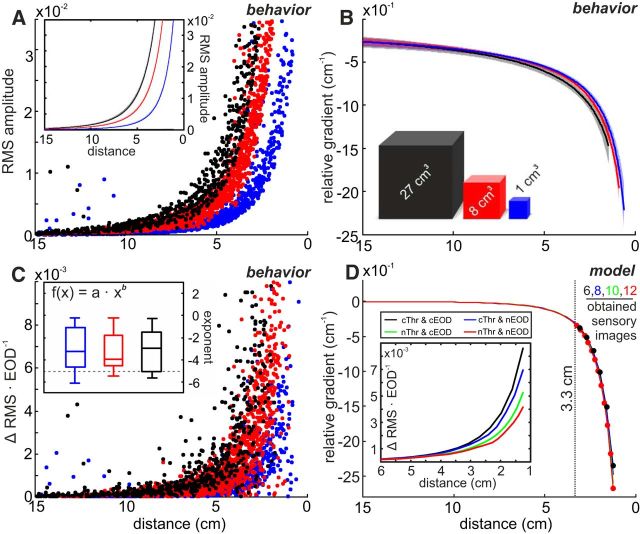
Figure 4.

Electrosensory flow allows distance estimation. A, Electric image amplitude (RMS, see Eq. 3) as a function of distance for the three different object sizes (0 = center of objects). The EI amplitude increased following a power law with an exponent of −4. Inset, Power-law fits to the data with CIs. B, Relative gradient (fit with CIs) as a function of distance. Data of individual sequences were inseparable between cube sizes (Kruskal–Wallis test; scaling: χ² = 1.0, F = 0.5, df = 2, p = 0.49; exponent: χ² = 0.3, F = 0.2, df = 2, p = 0.85), indicating that the relative gradient provides a size invariant estimate of the distance to objects. C, Electrosensory flow calculated for the behavioral data, plotted as a function of distance to the object at the present EOD. The flow is calculated as the absolute change of the EI RMS amplitude between successive EODs. Inset, Distribution of the power-law exponents obtained from the fits of the electrosensory flow of individual approach sequences. For the great majority of sequences (87%), exponents were >−5 (i.e., first derivative of field, horizontal dashed line), indicating that the patterned behavior actively reduces the magnitude of the electrosensory flow. The distributions of fit parameters were inseparable between cube sizes (Kruskal–Wallis test; shift: χ² = 1.8, F = 0.9, df = 2, p = 0.41; exponent: χ² = 0.2, F = 0.1, df = 2, p = 0.93). D, Effect of different modeled sampling behaviors on the RG and electrosensory flow. Different sampling results in different slopes of the electrosensory flow (inset), whereas the relative gradient is not affected (main panel). However, the number of EIs obtained is doubled from constant to naturalistic behavior. cThr, Constant thrust; nThr, naturalistic thrust; cEOD, constant EOD frequency; nEOD, naturalistic EOD frequency. For naturalistic values, we used the population means (Fig. 1B, C).

The relative gradient can be obtained by normalizing the change in the EI amplitude (e.g., ΔRMS) by the product of the distance traveled between two EODs and the current EI amplitude. Dividing the ΔRMS by the distance traveled yields the spatial derivative of the electric field. Dividing by the current EI amplitude implies dividing the power law relation of the field amplitude by its first derivative, resulting in a quotient that is proportional to 1/d. Accordingly, the spatial derivative that initially depends on both the objects' electrical properties and the animals' behavior is turned into an is object-size invariant measurement that only scales with distance (Fig. 4B). The relative gradient overlaps considerably (Fig. 4B) for the approaches to differently sized cubes (Fig. 4B), and individual approaches were indeed indistinguishable across cube sizes (Kruskal–Wallis, p > 0.49).

In order for this metric to be derived, an animal should continuously decrease its distance to a target, as this allows the change in distance to the object from the distance traveled to be inferred. This is in agreement with the postural adaptions described above.

A second aspect of the animals' behavior that contributes to the RG is the adaptation of the sampling density, which increases the closer the proximity to the object (similar to the ΔRMS). Constant sampling during the approach would result in the electrosensory flow being equal to the first derivative of the electric field (power law to the power of −5). For natural sampling, however, we found that the steepness of the flow is decreased (Fig. 4C, inset, distribution of exponents; dashed line representing expected value from constant behavior; exponents were indistinguishable between cube sizes, Kruskal–Wallis, p > 0.41). This indicates that the animals dynamically increase their sampling rate as they approach an object, thereby accounting for the steep increase in the rate of change in the sensory input.

How the different components of the sampling behavior influence the resolution of the relative gradient was further investigated by modeling approaches along simplified linear trajectories to the same object with different SDs (Fig. 4D). As expected, different sampling densities reduced the electric flow to different degrees (Fig. 4D, inset), but this did not affect the relative gradient (Fig. 4D, main panel). Notably, the number of samples that an animal would obtain at close distance was effectively doubled for natural sampling behavior (Fig. 4D, red dots; 12 EI samples at distances <3.3 cm) as opposed to nonadapted behavior (Fig. 4D, black dots; 6 EI samples). Assuming that fish use this novel metric, the natural approach behavior would result in self-generated electrosensory flow, which allows for precise estimation of relative distance to the object using an electrosensory flow based measure, such as the relative gradient.

As shown by our behavioral data, the RG was found to be object-size invariant. We additionally tested whether the relative gradient is invariant to shape and material using simulated straight approaches toward objects (Fig. 5). These simulations further confirmed that the relative gradient conveys unequivocal information of the distance to the target (i.e., it is size, shape, and material invariant). Furthermore, the relative gradient is largely independent of the body position from which it is obtained (Fig. 6).

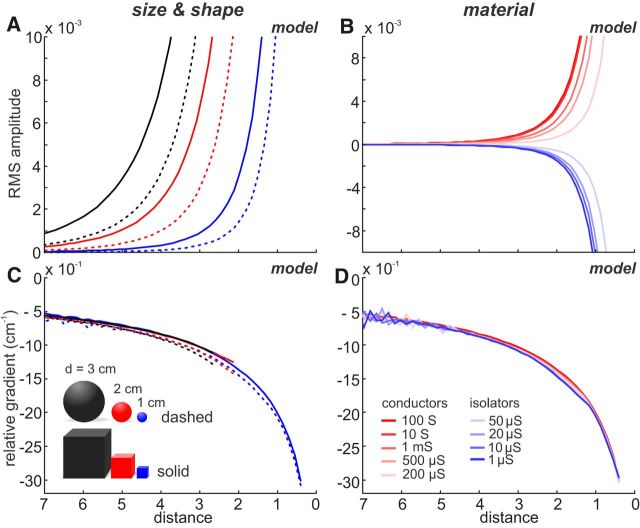
Figure 5.

The relative gradient is invariant to object size, shape, and material. A, B, The effect of object properties on the sensory input (RMS amplitude; see Eq. 3) was modeled based on a linear trajectory with a constant sampling density. Thus, differences in the data solely depend on object properties. We simulated an approach toward objects that differed in size (d = 1, 2, or 3 cm) and shape (sphere or cube) (A) or conductivity (B). C, D, Relative gradient for the data of A, B. Although the amplitude functions differ with size and shape (A) or material (B), the relative gradient overlaps, indicating that it is invariant to these object parameters. A–D, Solid lines indicate data for cubes. Dashed lines indicate spheres. B, D, Data are based on a cube of fixed size (d = 1 cm) and different conductivity (see color code). The water conductivity in all cases was 100 μS, and conductive versus nonconductive objects are shown in red and blue, respectively.

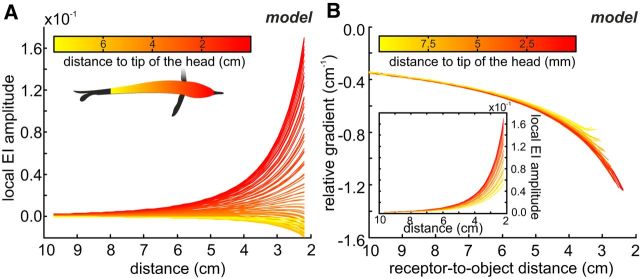
Figure 6.

Body position invariance of the relative gradient metric. A, Local EI amplitude (see Eq. 2) at distinct body positions as a function of object distance. The data were obtained by simulating a straight approach to a metal cube (8 cm³) and fitting power-law functions to the EI amplitudes obtained at different positions along the sampling equator (see color code). Depending on the position on the body, EI amplitude either increased (in the head region and in close vicinity; red colors) or decreased (lateral body regions; yellow colors) with increasing proximity to the object. B, Relative gradient calculated for a subset of the data shown in A (inset). Thrust was assumed to be constant in our simulation, and the distance to the cube was separately calculated for each position on the skin. The strong overlap of the data shows that this metric is only weakly influenced by the body position. For a comparison of the RG and SAR for distance estimation, see Figure 7.

We further compared the object detection and distance discrimination capability of the relative gradient (Fig. 7A) to that of the SAR (Fig. 7B). Object detection based on the relative gradient (6 cm distance) outperformed object detection based on the SAR (3 cm distance, compare Fig. 7C, red and blue). The relative gradient-based JND (the capability to discriminate distances) was consistently better up to distances of ∼5 cm (Fig. 7D).

Figure 7.

Distance estimation based on electrosensory flow versus single EI cues (SAR). A, RG as a function of object distance. B, SAR as a function of object distance. A, B, Data indicate standard deviation (shaded area), SEM (solid area), and the arithmetic mean (black line) of all approaches pooled. C, Object detection for RG (red) and SAR (blue). Data were calculated by comparing a reference distribution of the behavioral values at high distance (10.5 cm) to all closer distributions, taking the area under the ROC curve as a measure of sensitivity. A threshold of 70% was defined as detection, which is achieved at 6 cm distance for the RG and at 3 cm distance for the SAR, showing a higher sensitivity for the RG. D, Distance discriminability of the two measures was quantified by the JND. The JND was lower for the RG compared with the SAR for all distances >5 cm, indicating a better distance resolution when relying on the RG at high distances.

In summary, our analysis of the sensory corollaries of approach behavior revealed that weakly electric fish dynamically reposition their body with respect to the target. This would enable them to obtain a sensory-flow based object-invariant distance cue. Whereas the specific kinematic adjustments described here are of high importance for the extraction of this cue, our findings are also likely applicable to other active and nonactive sampling sensory modalities in similar behavioral contexts.

Discussion

An animals' behavior is inherently influenced by the sensory input it receives, which enables this input to be actively shaped through behavior. The characterization of such potentially purposeful-sensing behaviors with respect to their effect on the sensory input is a powerful step toward better understanding the brains' sensory-motor integrative functions.

Recurring patterns of behavior are well suited for researching how sensory input is shaped. We thus focused on “object approach behavior” of Gnathonemus, combining a quantitative behavioral characterization (Hofmann et al., 2014) with a computational reconstruction of electric images (Rother et al., 2003). This enabled us to analyze the sensory flow linked to this specific behavior, thereby extending previous studies on the topic (Nelson and MacIver, 1999; MacIver et al., 2001; Hofmann et al., 2013a). Using these techniques, we investigated sensorimotor coupling and its contribution to sensing in a large dataset.

The approach toward novel objects is characterized by a dynamic adjustment of the motor and sampling behavior. The general challenge in estimating the distance to unknown objects is comparable to many visually guided behaviors, such as landing, navigation, and prey-capture behavior in insects (Kirchner and Srinivasan, 1989; Kral and Poteser, 1997; van Breugel et al., 2014), or control of locomotion in mammals (Sun et al., 1992; Warren et al., 2001). A unifying theme in these examples is that the sensory dynamics (the optic flow) (Lee, 1980; Koenderink, 1986) are actively shaped by the animals to aid in the acquisition of information.

In our experiment, the fish had no knowledge of the precise spatial layout of the sensory scene. The distance-dependent changes in the electromotor and kinematic behavior must therefore be based on the sensory input. Continuous gradual alignment to the object can be achieved following two simple heuristic rules by which the animal aims to (1) move the peak of the EI toward the head and (2) increase the overall EI amplitude from one sampling step to the next. Although not necessarily optimal in a Bayesian sense, such reactive behavior would enable fast and efficient navigation. Alternatively, or in addition to these heuristics, internal or forward models would also allow the environment to be predicted by integrating past sensory input. In this sense, object-approach behavior may be regarded as a form of sensory hypothesis testing (Gregory, 1980): the motor activity follows the sensory input and is chosen to optimally disambiguate the mismatch between the sensory feedback and the previous prediction of the world (Loeb and Fishel, 2014).

Weakly electric pulsatile fish have control over the sensory flow in two ways: motor behavior and the timing of EOD emissions. Both modulate the SD as shown by the VAF analysis. SD increased with proximity to the object, resulting in a reduction of the electrosensory flow compared with a constant sampling density (Fig. 4C). It is likely that this reflects the reactive effort of the animal to accurately sample the electric field, including the proposed distance metrics. Similar context-dependent adjustments in the spatiotemporal sampling resolution are known from other discontinuously sampling systems, such as echolocation in bats or sniffing and whisking in rodents (Ghose and Moss, 2006; Schroeder et al., 2010). Future high-resolution recordings of similar behavior are necessary to resolve whether the SD increase differs for different object sizes, as this trend was not significant in our dataset. Both of these results can be taken as further evidence of the above-stated claim that the increased sampling density is based on sensory input, and thus reactive.

To navigate toward an object, information on distance is needed to mediate changes in electromotor behaviors (e.g., Fig. 1) (Toerring and Belbenoit, 1979; Toerring and Moller, 1984; Hofmann et al., 2014). Estimating the distance is also essential for the formation and use of cognitive maps of space, and fish are known to rely on such representations of space (Braithwaite and de Perera, 2006; Jun et al., 2016). Several metrics have been proposed to extract distance, including the SAR (von der Emde et al., 1998) and the half-maximum width of electric images (Lewis and Maler, 2001; Chen et al., 2005), the temporal SAR (Sim and Kim, 2012; Hofmann et al., 2013a), and the “slope-ratio” (Sim and Kim, 2011). Of those, SAR and half-maximum width can potentially be useful to analyze the sensory input during the “object approach behavior.” They both require an analysis of the spatial properties of static electric images and provide noisy distance estimates that surpass the noise-level from only 3 cm onwards (see ROC analysis; Fig. 7). This noise is partially reafferent noise due to the animals' movements (Engelmann et al., 2008; Sawtell and Williams, 2008). The increasingly straight posture in vicinity to the objects (Fig. 1F) might reflect the active effort of the animals to reduce this noise (Nelson and MacIver, 1999; MacIver et al., 2001; Fotowat et al., 2013). A substantial weakness of these metrics was revealed from our analyses with the finding that they change with the location of the EIs on the animals' body, resulting in inaccurate or at least ambiguous result in the estimation of distance (Fig. 3B).

We argue that incorporating the spatiotemporal dynamics, as shown for the relative gradient, may help to overcome several of the above limitations. This lends support to earlier theoretical work, which suggests that the information embedded in the electric flow could exceed that of a static sensory scene analysis (Babineau et al., 2007; Hofmann et al., 2013a).

To make use of this self-generated distance information, animals require knowledge about the change in the EI amplitude between consecutive EODs, and then normalize this ratio with respect to the current EI amplitude. Unlike the absolute amplitude, the relative change is invariant with respect to object size, shape, and material. This is the case because sensory input is defined through its relation to the EI amplitude. This is shared by all sensory systems that actively generate energy for sensing, whereas other sensory systems, such as vision, lack this type of frame of reference, and most optic flow based mechanisms can only yield relative estimations of distance (but see van Breugel et al., 2014).

The relative gradient can be estimated based on local sensory input (Fig. 6), whereas spatial measures depend on a sufficiently detailed representation of EIs over the animals' skin. Furthermore, detection sensitivity and discriminability of the relative gradient were better than that of the SAR (Fig. 7). To determine the relative gradient, information on the current and recent electric image amplitude, as well as the speed, are required. These parameters are readily available: (1) EI amplitude is an essential parameter used in electric image analysis and was shown to be of behavioral relevance (von der Emde et al., 1998); (2) the change in EI amplitude is likely a key parameter encoded by the medullary electrosensory lateral line lobe, which is known to extract information based on a neuronal comparison between present and past sensory information (Sawtell et al., 2005); and (3) the distance traveled between successive EIs is equal to the product of thrust and inter-EOD interval; both are under control by the animal and may be accessible through proprioceptive signals. The mechanosensory lateral line could potentially provide a direct measure of the external flow speed, and thus of the fish's velocity (Chagnaud et al., 2008; Salumäe and Kruusmaa, 2013). The postural and kinematic adjustments during the approach (Fig. 1E,F) allow for the change in the animals' position to be directly inferred and can be used to compute the relative gradient.

Further studies are necessary to determine whether and how animals use such sensory flow measures to navigate their environment. In active electrolocation, this may be addressed in experiments using electrosensory illusions to manipulate animals' behavior. A remaining key question is whether electric flow is decoded in the electrosensory pathway, and if so, where this takes place. Using closed-loop electrophysiological methods (i.e., recording from sensory neurons while stimulating with mimics of naturalistic object-animal trajectories, or recording freely moving animals together with the modeling procedure used here) should yield novel insights into fundamental concepts of sensory-motor interaction and its integration in the CNS.