Synchronous Infra-Slow Bursting in the Mouse Accessory Olfactory Bulb Emerge from Interplay between Intrinsic Neuronal Dynamics and Network Connectivity

Abstract

Rhythmic neuronal activity of multiple frequency bands has been described in many brain areas and attributed to numerous brain functions. Among these, little is known about the mechanism and role of infra-slow oscillations, which have been demonstrated recently in the mouse accessory olfactory bulb (AOB). Along with prolonged responses to stimuli and distinct network connectivity, they inexplicably affect the AOB processing of social relevant stimuli. Here, we show that assemblies of AOB mitral cells are synchronized by lateral interactions through chemical and electrical synapses. Using a network model, we demonstrate that the synchronous oscillations in these assemblies emerge from interplay between intrinsic membrane properties and network connectivity. As a consequence, the AOB network topology, in which each mitral cell receives input from multiple glomeruli, enables integration of chemosensory stimuli over extended time scales by interglomerular synchrony of infra-slow bursting. These results provide a possible functional significance for the distinct AOB physiology and topology. Beyond the AOB, this study presents a general model for synchronous infra-slow bursting in neuronal networks.

SIGNIFICANCE STATEMENT Infra-slow rhythmic neuronal activity with a very long (>10 s) duration has been described in many brain areas, but little is known about the role of this activity and the mechanisms that produce it. Here, we combine experimental and computational methods to show that synchronous infra-slow bursting activity in mitral cells of the mouse accessory olfactory bulb (AOB) emerges from interplay between intracellular dynamics and network connectivity. In this novel mechanism, slow intracellular Na⁺ dynamics endow AOB mitral cells with a weak tendency to burst, which is further enhanced and stabilized by chemical and electrical synapses between them. Combined with the unique topology of the AOB network, infra-slow bursting enables integration and binding of multiple chemosensory stimuli over a prolonged time scale.

Introduction

Synchronous rhythmic activity of neurons, also termed neuronal oscillation, is fundamental to brain function. Indeed, synchronous rhythmic activity has been documented in almost all brain structures and has been implicated in virtually all brain functions (Ward, 2003; Lakatos et al., 2008). Synchronous rhythmic activity is known to occur at a wide range of frequencies. Some examples include the gamma (25–100 Hz) and theta- (4–12 Hz) bands, which have been implicated in various cognitive functions (Buzsáki and Draguhn, 2004), including social interactions (Tendler and Wagner, 2015), and the delta-band (<4 Hz), which dominates brain activity during sleep (Steriade et al., 1993). Synchronous activity reaching the lowest range of frequencies (<0.1 Hz) characterizes brain centers that control basic functions such as respiration (Rybak et al., 2014). The suggested mechanisms underlying brain rhythmicity range from network dynamics, in which excitatory and inhibitory synaptic interactions among neurons can lead to stable oscillations (Marder and Bucher, 2001; Bartos et al., 2007), to intrinsic cellular properties, in which complex interactions between voltage- and ion-dependent channels can produce rhythmic activity (Hughes et al., 2002; Cressman et al., 2009).

Here, we focused on synchronous rhythmic activity with unusually slow pace (“infra-slow,” meaning one cycle in several tens of seconds), which have been demonstrated recently in the projection neurons of the accessory olfactory bulb (AOB), the AOB mitral cells. (Zylbertal et al., 2012; Vargas-Barroso et al., 2015; Gorin et al., 2016). The olfactory sense plays a central role in mammalian social interactions, which depend heavily on the exchange of chemosensory stimuli detected and processed by both the main olfactory system and the accessory olfactory system (AOS). The principles of information processing in the early stages of the main olfactory system, the main olfactory epithelium (MOE) and the main olfactory bulb (MOB), are well documented (Schoppa and Urban, 2003). In contrast, those characterizing the parallel pathway of the AOS, from the vomeronasal organ (VNO) to the AOB, remain elusive.

One distinction of the AOB is its network topology. In contrast to the “labeled lines” characterizing the wiring between the MOE and MOB, the connectivity between the VNO and AOB seems to be much more complex (Dulac and Torello, 2003; Luo et al., 2003). Each population of VNO sensory neurons, all expressing the same vomeronasal receptor, innervates multiple (up to 30) AOB glomeruli (Belluscio et al., 1999). Moreover, each mitral cell sends dendritic tufts to multiple spatially dispersed glomeruli. In some cases, these glomeruli seem to be innervated by VNO neurons expressing the same receptor (homotypic mitral cell; Del Punta et al., 2002), whereas in others, each of these glomeruli seems to be innervated by VNO neurons expressing a distinct receptor (heterotypic mitral cells; Dulac and Wagner, 2006).

Another prominent feature of information processing in the AOB seems to be integration and processing of sensory information over prolonged time scales (Luo et al., 2003). For example, AOB mitral cells are capable of responding to transient stimuli with prolonged firing independently of network connectivity (Shpak et al., 2012). We have demonstrated previously that these extended epochs of persistent firing reflect a slow interplay between dendritic Na⁺ and Ca²⁺ extrusion mechanisms (Zylbertal et al., 2015). This slow interplay dictates extremely prolonged dynamics of Na⁺ and Ca²⁺ concentrations in the dendrites of AOB mitral cells.

Here, we examined the infra-slow bursting activity in the AOB in light of the slow dynamics of AOB mitral cell responses to transient stimuli and the unique network topology of the AOB. We used a combination of experimental methods (whole-cell patch recording, Ca²⁺ imaging, and optogenetics) and computational modeling to show that synchronous infra-slow bursting emerges from the interplay between intrinsic properties and network connectivity of the AOB mitral cells, which form “group pacemakers” (Rekling and Feldman, 1998). Finally, we show that, given the unique connectivity of the AOB, these dynamics enable a novel form of long-term sensory integration, thus providing a possible functional significance for synchronous infra-slow bursting in the AOB.

Materials and Methods

Animals.

C57BL/6J (RRID:IMSR_JAX:000664), Thy1:GCaMP6 (Dana et al., 2014, RRID:IMSR_JAX:025393), and Tbet:cre x Ai32 (Haddad et al., 2013, RRID:IMSR_JAX:024507, RRID:IMSR_JAX:012569) male mice were maintained in the specific-pathogen-free mouse facility of the Hebrew University of Jerusalem under veterinary supervision according to National Institutes of Health standards, with food and water ad libitum and lights on from 7:00 A.M. to 7:00 P.M. Eight- to 20-week-old mice (25–35 g) were held in groups of 5–10 mice per cage. All experiments were approved by the Animal Care and Use Committee of the Hebrew University (permit number NS-12-13310-4). Mice were anesthetized (pentobarbitone, 60 mg/kg) and killed by cervical dislocation.

Slice preparation.

Olfactory bulbs were dissected into a physiological solution containing the following (in mm): 125 NaCl, 25 NaHCO₃, 5 glucose, 3 KCl, 2 CaCl₂, 1.3 NaH₂PO₄, and 1 MgCl₂, oxygenated by bubbling through a 95% O₂ and 5% CO₂ mixture, pH 7.4, 36°C. Parasagittal olfactory bulb slices, 300–400 μm thick, were prepared and equilibrated for 0.5–3 h in the same solution at physiological temperature (Huang and Uusisaari, 2013).

For electrophysiological recordings and imaging, slices were submerged in oxygenated physiological solution (identical to above) at room temperature in a recording chamber and perfused at a constant rate of 5–7 ml/min. To test the effect of Ca²⁺ removal, an equimolar amount of MgCl₂ was used instead of CaCl₂. Where indicated, gabazine (10 μm; Tocris Bioscience), 6,7-dinitroquinoxaline-2,3-dione (DNQX, 20 μm; Sigma-Aldrich), (2R)-amino-5-phosphonovaleric acid (AP5, 80 μm; Sigma-Aldrich), and carbenoxolone (100 μm; Sigma-Aldrich) were added to the bath solution to block GABA_A receptors, AMPA receptors, NMDA receptors, or gap junctions, respectively.

Electrophysiology.

For whole-cell recordings, we used an Olympus BX61WIF microscope equipped with a motorized stage and manipulators (Luigs & Neumann), pulse generator (Master8; A.M.P.I.), and a MultiClamp 700B amplifier (Molecular Devices).

Mitral cells were visualized using infrared differential interference contrast video microscopy via a 40× water-immersion objective. Mitral cells were identified by the location of the cell body on the ventral side of the external plexiform layer of the AOB. Whole-cell recordings were performed using borosilicate pipettes filled with standard intracellular recording solution containing the following (in mm): 130 K-gluconate, 10 Na-gluconate, 10 HEPES, 10 phosphocreatine, 4 MgATP, 0.3 NaGTP, and 4 NaCl, pH 7.25 with KOH, 5–12 MΩ. Seal resistance was at least 2 GΩ and typically 5–10 GΩ.

All amplified signals were digitized at 2–20 kHz using a National Instruments board and homemade software written in LabVIEW (National Instruments; RRID:SCR_014325).

Two-photon imaging.

Slices were stained by Oregon Green BAPTA-1 AM (Invitrogen). A 4 mm dye stock solution was prepared using 20% Pluronic F-127 in DMSO. Slices were placed in a culture insert (Millicell-CM filter inserts, pore size 0.4 μm, diameter 30 mm; Merck) with 2 ml of ACSF containing a 20 μm concentration of the dye. The insert was placed for incubation in oxygenated ACSF maintained at 36°C for 50 min and the stained slices were later returned to regular ACSF.

Imaging was done using an FV1200 MP laser scanning microscope (BX61W1 configuration; Olympus) with an XLPlan N 25× objective lens and Mai Tai DeepSee laser source (Spectra-Physics) equipped with an ACSF perfusion system. The rate of scanning was 1–2 Hz, capturing a single focal depth and a field of ∼0.5 × 0.5 mm at 512 × 512 pixel resolution. The images were low-pass filtered and mitral cells were identified manually based on shape and location. Image analysis and ROI selection was done using FiJi (Schindelin et al., 2012; RRID:SCR_002285). The effects of slow changes in absolute fluorescence (due to bleaching and focal plane drift) were discarded by dividing the fluorescence time series by the low-pass-filtered signal of the same time series.

Local afferent stimulation was applied by a microelectrode AC amplifier (Model 1800; A-M Systems) unit coupled to a theta electrode (a bipolar micropipette pulled from a tubing with a θ-like cross-section) positioned in the glomerular layer (burst duration: 4 s, pulse duration: 1 ms, interpulse duration: 0.1 s, amplitude: 60 V).

Wide-field calcium imaging.

Thy1:GCaMP6 mice were used for wide-field imaging. Fluorescence signals were recorded using a high-speed camera (MiCAM Ultima; Brainvision).

Detailed computational model.

The computational model was constructed using the NEURON simulation environment with Python (Hines and Carnevale, 1997; Hines et al., 2009; RRID:SCR_005393, RRID:SCR_008394). The building block of the model was the conductance-based mitral cell model that we constructed previously based on the cell's response to short stimulus (Zylbertal et al., 2015). Morphological variation among individual cells was achieved by randomly setting the length and surface area of each cellular compartment in the range of −50% to +50% relative to the original value.

Modeling a glomerulus with N cells was done by creating N variable cells and the following interaction among them. First, each cell was connected to the remaining N-1 cells by a gap junction with conductance of 0.17 nS located in the dendritic tuft. The cell leak conductance was slightly reduced to compensate for the extra gap junction conductance (Amsalem et al., 2016). Then, each cell was connected to all N cells (including to itself) by excitatory synapses (weight = 10 pS, delay = 1 ms, tau = 1 s, reversal potential = 0) and inhibitory synapses (weight = 19 pS, delay = 10 ms, tau = 1 s, reversal potential = −65 mV). The indirect nature of the inhibitory interactions is reflected by the long delay. Cells that were shared with a second glomerulus similarly interacted with all of its cells via their second dendritic tuft. The model code is available online at: https://senselab.med.yale.edu/ModelDB/showModel.cshtml?model=207695.

Minimal abstract model.

The minimal model is based on simplified single-compartment Hodgkin–Huxley (HH) formalism (Eq. 1–8) (Butera et al., 1999), with the addition of Ca²⁺ conductance (Eq. 9–10), Ca²⁺ and Na⁺ accumulation (Eq. 11–12), Ca²⁺-dependent conductance (I_CAN, Eq. 13–14), and Na⁺-dependent outward current (I_pump, Eq. 15).

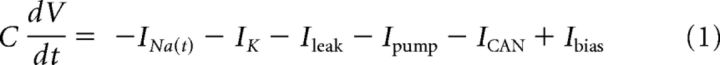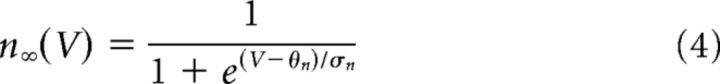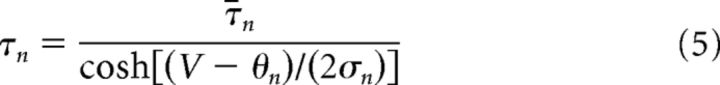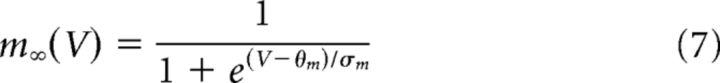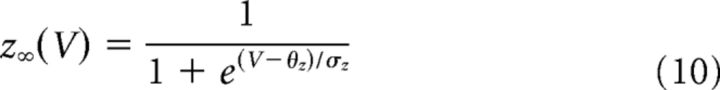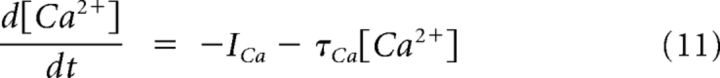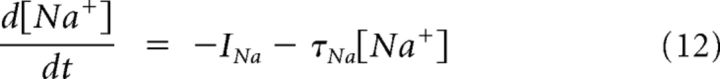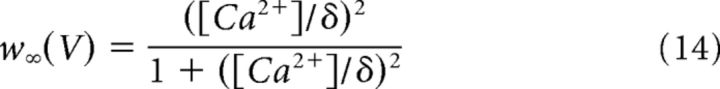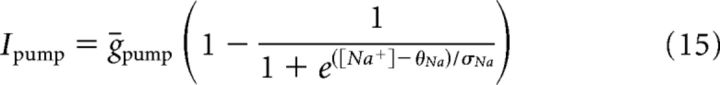Fixed parameter values are shown in Table 1.

Table 1.

Fixed parameter values

C	21 pF	ḡCa	0.05 nS
ḡK	11.2 nS	ECa	130 mV
EK	−85 mV	θz	−30 mV
θn	−29 mV	σz	−6 mV
σn	−4 mV	τCa	500 ms
¯τn	10 ms	τNa	40 s
ḡNa	28 nS	ḡCAN	0.7 nS
ENa	50 mV	ECAN	10 mV
θm	−34 mV	δ	100 pC
σm	−5 mV	ḡpump	15 nS
gleak	2.8 nS	θNa	0.33 μC
Eleak	−65 mV	σNa	0.017 μC

Network feedback was simulated by a feedback current calculated by leaky integration of spikes (detected by zero crossings of the membrane potential) as follows:

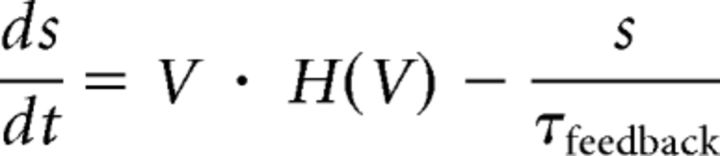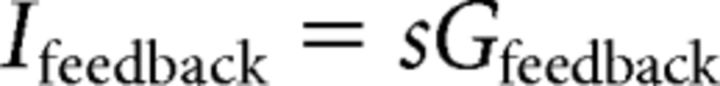Where H(V) is the Heaviside step function, G_feedback is the feedback gain and τ_feedback = 50 ms.

Data analysis.

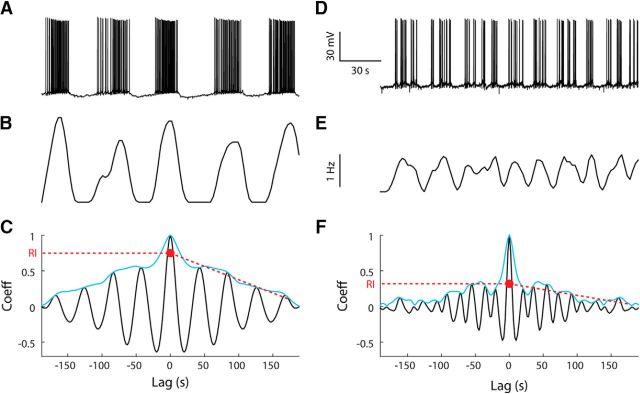
We calculated the rhythmicity index (RI) of a signal (either of a firing time histogram or fluorescence time course) by fitting a line to the top envelope (Hilbert transform power function) of the normalized autocorrelation function of that signal starting from a lag of +20 s. The RI is the intercept of this line at zero lag (Fig. 1C,F). The autocorrelation function of a perfectly rhythmic signal has a linearly decaying envelope starting from the central peak, so its RI would be 1. In other cases, the fitted line will intercept with the zero lag line below the central peak, resulting in a lower RI. An RI of zero was assigned in cases of very slow-changing signal (prominent frequency of less than two cycles per recording window).

Figure 1.

AOB mitral cells exhibit infra-slow bursting. A, Voltage recording from an AOB mitral cell showing highly rhythmic bursting. B, Smoothed time histogram (2 s bins) of the firing shown in A. C, Autocorrelation function of the histogram shown in B demonstrating the method of RI extraction (red) based on the envelope (blue, Hilbert transform power function) of the autocorrelation function. D–F, Similar to A–C but applied for a recording from a less rhythmic mitral cell.

We assessed the bursting frequency of each cell by the peak location of the fluorescence time series power spectral density (Burg's method).

We defined synchronous assemblies by clustering cells into groups in which each cell is highly correlated (correlation coefficient >0.6) with at least one more cell. The correlation coefficient was defined as the maximal value of the normalized unbiased cross-correlation function in the range of −15 to +15 s lag, thus allowing cells having coherent signals with phase difference to be regarded as synchronous. Notably, we did not require each cell in the assembly to be correlated with all of the remaining cells.

Five hundred surrogate populations of neurons were constructed to assess the probability of getting the measured proportion of synchronous rhythmic cells by chance. Each of these populations was constructed based on the observed population, along with its division into separate slices. This was done by randomizing the phases of all frequencies of each fluorescence signal (uniform distribution, [−π, π]) and transforming it back to the time domain, leaving the power spectra intact.

The population synchrony index was defined as the sum of the squares of assembly sizes divided by the total population size squared. This definition results in a higher value for a population with a small number of large assemblies relative to a population with large number of small assemblies.

Results

Assemblies of AOB mitral cells exhibit spontaneous synchronous infra-slow bursting activity

As shown by us (Zylbertal et al., 2012) and others (Vargas-Barroso et al., 2015; Gorin et al., 2016), AOB mitral cells tend to fire periodic bursts of action potentials at an interval of 20–30 s, corresponding to a rate of 0.03–0.05 Hz. Figure 1A shows an example of such bursting activity, with a mean interburst interval of 18.5 s and a mean burst duration of 19.0 s. To quantify the regularity of bursting, we calculated the time histogram of firing (Fig. 1B) and the autocorrelation function of the time histogram (Fig. 1C). We defined an RI based on extrapolating the envelop of the autocorrelation function (Fig. 1C, red; Materials and Methods), which in this example reaches a value of 0.76. However, such high rhythmicity was encountered only in some neurons; others exhibited a lower level of rhythmicity (e.g., see Fig. 1D–F, in which an RI of 0.35 was calculated). A recently published detailed description of the spontaneous activity of AOB mitral cells, including the heterogeneity in their bursting, demonstrated variable rhythmic activity in 63% of the neurons and suggested that interdependent conductances underlie this behavior (Gorin et al., 2016).

An alternative attractive possibility to explain the observed oscillations is that network connectivity supports and stabilizes the tendency of single cells for bursting. In that case, we expect that connected cells will show correlated (synchronous) bursting activity. To examine this possibility, we focused our experiments on simultaneously recording bursting activity in populations of AOB mitral cells using Ca²⁺ imaging.

Two-photon Ca²⁺ imaging of AOB slices incubated in the calcium indicator dye OGB-1 AM is exemplified in Figure 2A, demonstrating numerous stained neurons. The changes in fluorescence of two neurons are shown in Figure 2B as continuous fluorescence waveforms (top) and as a color-coded raster plot (bottom). These recordings demonstrate clear periodic changes with an RI of 0.57 and 0.53, resembling the periodic bursting recorded intracellularly (Fig. 1A). Notably, the activity in these two neurons was highly correlated, as revealed by the cross-correlation analysis (Fig. 2C), demonstrating a high degree of in-phase periodic synchrony.

Figure 2.

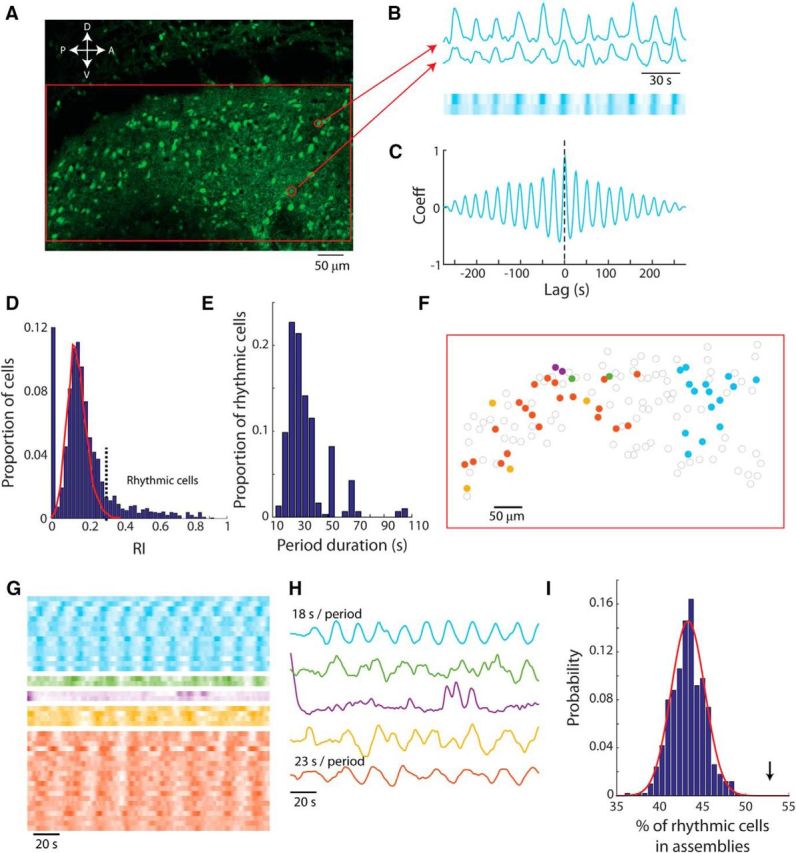
Synchronous rhythmic bursting in mitral cell assemblies is revealed by two-photon imaging. A, Image of AOB slice incubated with OGB-1 AM showing the area mapped in E (red rectangle). White arrows denote tissue orientation (A, anterior; P, posterior; D, dorsal; and V, ventral). B, Fluorescence intensity of two example cells from A shown as a waveform (top) and raster plot in which color intensity denotes fluorescence intensity (bottom). C, Cross-correlation function based on the signals of the two cells shown in B. D, Distribution of RIs in all observed cells from 21 slices (blue bars) and distribution of RIs in a simulated population of random signals (red line). E, Distribution of period duration in all rhythmic cells (n = 304). F, Map of the detected mitral cells in the slice shown in A in which synchronous cells are similarly colored. Noncolored cells are not synchronous and may be rhythmic, not rhythmic, or not active. G, Calcium indicator fluorescence displayed in raster plot (as in B) for all the cells marked in F clustered to synchronous assemblies and ordered by relative phase within each assembly. H, Average fluorescence in each assembly calculated after eliminating phase differences between cells. The period durations of two rhythmic assemblies are presented above their traces. I, Histogram of the probability of rhythmic cells to belong to a synchronous assembly as calculated in 500 resampled populations (blue bars) and the fitted normal distribution (red line). The arrow indicates the value calculated based on experimental results.

The distribution of RI values of all cells observed in the 21 AOB slices examined is positively skewed (Fig. 2D). Calculating the RIs of randomly generated signals (Gaussian white noise, low-pass filtered in the same manner as the data) yields a bell-shaped distribution (Fig. 2D, red line). Based on the difference between the observed and simulated distributions, we defined signals with an RI >0.3 as being rhythmic.

Such rhythmic signals were observed to a varying degree in all 21 AOB slices examined, where it was found in 13% of all encountered cells (304 of 2331 cells). The period duration measured in all rhythmic neurons was mainly in the range of 15–40 s (34 ± 15 s, mean ± SD; Fig. 2E).

The synchronous activity shown in Figure 2B is far from being anecdotal. In fact, 53% of all rhythmic cells were synchronous with at least one other cell, forming synchronous cellular assemblies. We defined such assemblies as groups of cells in which the activity of each cell is highly correlated (correlation coefficient >0.6, allowing 15 s lag) with at least one other cell (see Materials and Methods). It should be noted that the observed size of an assembly is bound to be an underestimate due to the likelihood that more assembly members are left undetected by the limited field of view and restricted focal depth of the two-photon imaging.

Using this definition, we detected in the example shown in Figure 2A five assemblies that showed limited spatial organization covering an area of up to 0.2 × 0.2 mm (Fig. 2F). The activity in these assemblies is shown in Figure 2G as a raster plot of each cell in the assembly (matching colors) and the average activity within an assembly is shown in Figure 2H. Nonrhythmic cell assemblies were also detected, usually based on one or few isolated synchronous bursts of activity (Fig. 2G,H, purple). Overall, 61 assemblies were observed in 21 slices recorded in control conditions (observed assembly size: 4.97 ± 0.99 cells, mean ± SEM; median: 2 cells).

These results suggest that the rhythmic bursting of AOB mitral cells should be examined in the context of the AOB network connectivity. This connectivity may either participate solely in burst synchronization or contribute also to burst production and stabilization.

This conclusion is further supported by the observation that rhythmic cells tended to belong to synchronous assemblies more than predicted by chance. This was tested by constructing 500 surrogate slice populations based on randomizing the phases of the observed fluorescence signals while keeping the power spectrum intact (see Materials and Methods). Among the surrogate populations, the proportion of rhythmic cells that belonged to synchronous assemblies was normally distributed (mean: 43%, SD: 2%; Fig. 2I). Based on this distribution, the probability of getting the measured value (53%; Fig. 2I, arrow) or higher by chance is 9 × 10⁻⁷.

Electrical coupling and chemical connections between mitral cells play a role in maintaining their synchrony

One simple possible mechanism for synchrony within cellular assemblies is reciprocal chemical synapses between mitral cells, most likely located at their dendritic tufts, as was shown for MOB mitral cells (Urban and Sakmann, 2002; Christie and Westbrook, 2006). To examine this possibility, we perfused AOB slices with a mixture of synaptic blockers (20 μm DNQX, 80 μm AP5, and 10 μm gabazine), thus shutting down activity of ionotropic glutamate and GABA_A receptors. As exemplified in Figure 3A, even under these conditions, several synchronous assemblies were readily detected (Fig. 3A, top), for some of which both the raster plot (Fig. 3A, middle) and the average activity show rhythmicity as well as synchrony. To estimate synchrony in each slice, we used a synchrony index based on the ratio of the sum of assembly sizes to total cell count in the slice (Materials and Methods). Analysis of the activity in 13 slices (Fig. 3B) revealed that, whereas synaptic blockers could have a considerable effect on the activity in a given slice, on average, only a moderate increase in period duration (t test, p = 0.052) and no significant change in synchrony (t test, p = 0.1) were observed.

Figure 3.

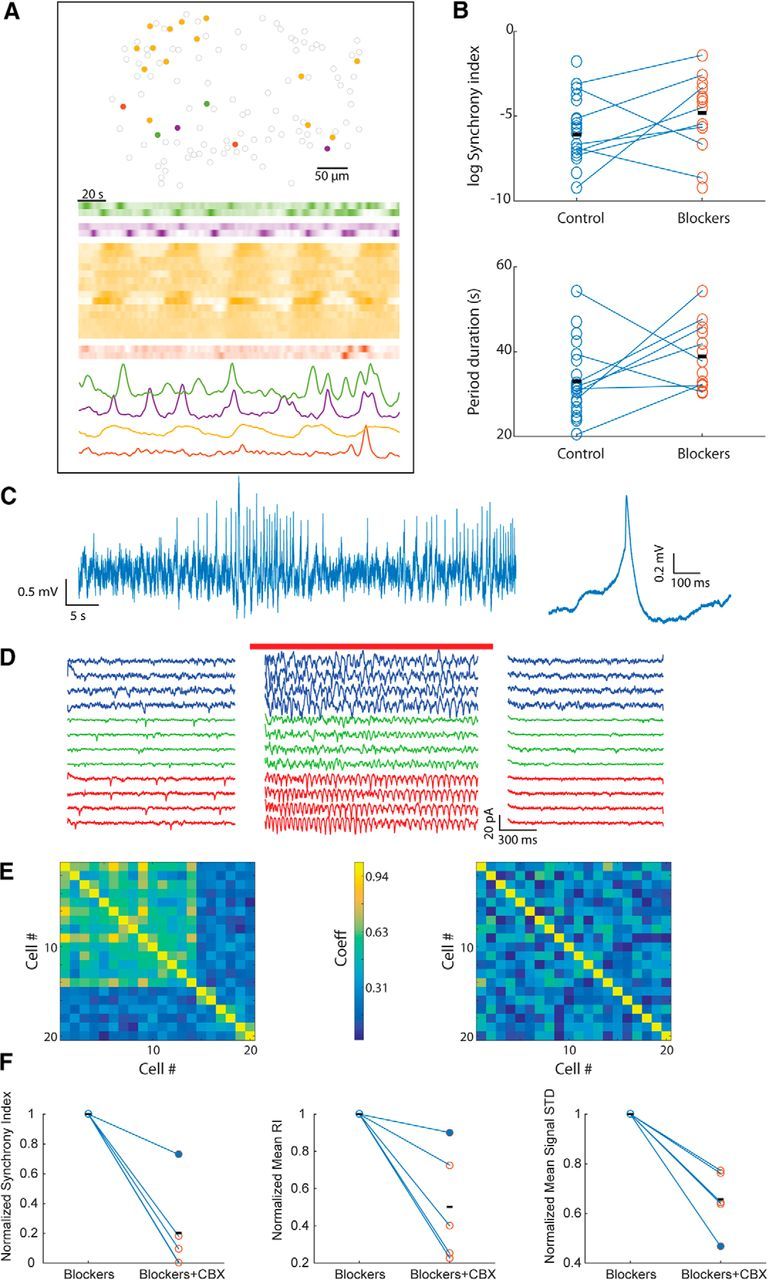
Both chemical and electrical synapses mediate synchrony and support rhythmicity in mitral cell assemblies. A, Map of assemblies of synchronous cells (top), calcium indicator fluorescence of the cells in these assemblies (middle), and the average fluorescence of the cells in each assembly (bottom traces) in a slice incubated with blockers of chemical synaptic transmission. B, Effect of synaptic blockers on the synchrony index (log scale, top) and the average period duration (bottom) in multiple AOB slices (n = 21 control, n = 13 blockers). C, Spontaneous spikelets recorded intracellularly from a mitral cell (left) and their average waveform (right). Note the biphasic appearance of the waveform. D, Voltage-clamp recordings from three mitral cells (denoted by red, green, and blue) before, during, and after optogenetic stimulation of the entire slice (red bar) in the presence of chemical synaptic blockers (DC changes and resulting artifacts are removed). E, Correlation matrix of the fluorescence signal of the cells from the assemblies marked in A before (left) and after (right) CBX application. F, Normalized slice synchrony index (left), mean RI (middle), and mean signal SD (right) in five slices from four different animals before and after CBX application. Filled circles represent the slice shown in E.

Because synchrony between mitral cells was not abolished by blocking chemical synapses, we hypothesized that electrical coupling between the cells may be involved. Notably, AOB mitral cells were shown to express various members of the connexin family, which form the gap junctions mediating neuronal electrical coupling (Zhang and Restrepo, 2003; Degen et al., 2004; Zhang, 2011). Indeed, whole-cell recordings from AOB mitral cells (Fig. 3C, left) revealed spontaneous fast depolarization events (“spikelets”) that seemed to be organized in bursts resembling the bursting activity described above. Furthermore, averaging these events (Fig. 3C, right) revealed a biphasic potential with a fast depolarizing phase followed by pronounced hyperpolarization, a hallmark of action potentials transmitted through gap junctions (Valiante et al., 1995).

If these spikelets reflect action potentials in electrically coupled cells, then elevating the population firing rate in an AOB slice should increase the frequency of such events. This was examined in slices derived from transgenic mice expressing the optogenetic neuronal activator channelrhodopsin-2 in AOB mitral cells under the Tbet promoter (Haddad et al., 2013). Global illumination of the slice by blue light in the presence of synaptic blockers markedly and reliably increased the frequency of recorded spikelets (Fig. 3D). These findings strongly support the existence of electrical coupling between AOB mitral cells, as shown previously for MOB mitral cells (Christie et al., 2005; Christie and Westbrook, 2006; Maher et al., 2009).

To assess the role of electrical coupling in the synchrony of bursting in AOB mitral cells, we perfused AOB slices in which the synchrony persisted in the presence of chemical synaptic blockers (Fig. 3A) with carbenoxolone (CBX, 100 μm), a gap junction blocker. As exemplified in Figure 3E, while in the presence of only chemical synaptic blockers, robust synchronous bursting with high intercellular cross-correlation was readily recorded (Fig. 3E, left), the addition of CBX dramatically reduced both the rhythmicity (p = 1.9 · 10⁻⁶, paired t test, n = 116 cells) and cross-correlation of the calcium signals in the slice (Fig. 3E, right; all 31 pairs with correlation coefficient >0.6 became less correlated, with their mean ± SEM correlation coefficient reduced from 0.68 ± 0.02 to 0.31 ± 0.03).

These results were repeated in all slices treated with CBX (5 slices from 4 animals), in which the slice synchrony index, mean rhythmicity, and mean signal SD (a measure of activity) were all reduced (Fig. 3F, p = 0.03 for each metric, single-tailed Wilcoxon signed-rank test). Therefore, electrical coupling between AOB mitral cells seems to allow synchronization of their bursting even during blockade of chemical synapses.

Cellular infra-slow bursting activity is predicted by an AOB mitral cell model and enhanced by feedback

To further explore the mechanisms that produce the infra-slow bursting and the role of network connectivity in it, we referred to a realistic model of an AOB mitral cell that we presented in a recent study (Zylbertal et al., 2015). This model, which was constructed to examine mechanisms of persistent firing activity, was tightly constrained by measurement of the cells' electric and Ca²⁺ responses to multiple types of transient stimuli. The single-cell model, which was trained to reproduce persistent responses, includes several slow opposing processes that might lead to generation of oscillatory firing behavior. In particular, the accumulation of [Na⁺]_i during firing increases the outward current through the Na⁺–K⁺ pump (Pulver and Griffith, 2010) and hyperpolarizes the Na⁺ reversal potential. These two processes gradually lead to hyperpolarization of the membrane potential and thus to the cessation of firing.

We examined this possibility by studying the model response to a long (4 s) train of action potentials. As shown in Figure 4A (top trace), the model indeed produces ongoing bursting activity with interburst interval of 3 s, a burst duration of 3.7 s, and an RI of 0.75. However, this bursting activity is extremely fragile, as demonstrated by adding a realistic noisy current (Fig. 4A, middle trace) or changing the stimulus duration to 4.5 s (Fig. 4A, bottom trace). Both procedures significantly reduced the rhythmicity of the response, as quantified by its RI (shown below each trace).

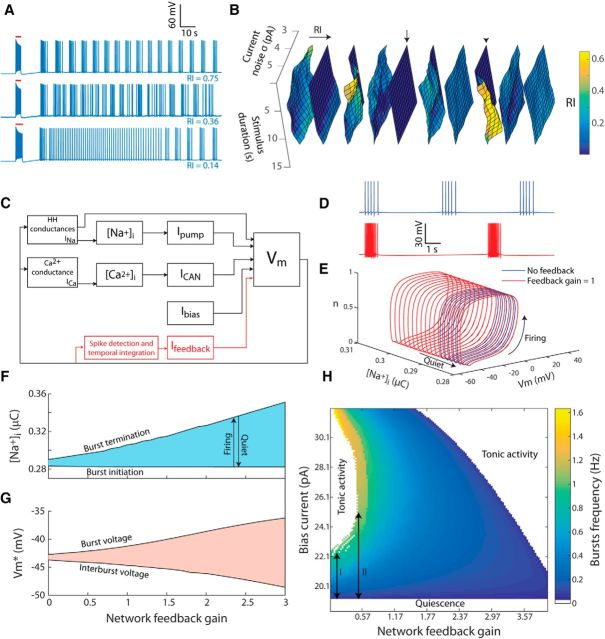
Figure 4.

Infra-slow bursting activity is predicted by an AOB mitral cell model and enhanced by feedback. A, Top, Bursting activity is reproduced in the mitral cell model using noise-free model and a carefully adjusted stimulus (red bar). Middle, Bursting in the same cell is markedly reduced by injecting current white noise. Bottom, Bursting is also reduced when stimulus duration was increased by 1 s. B, RI of the firing of a single cell (with 10 random morphology variations) stimulated by a transient stimulus with varying duration (x-axis) in the presence of current Gaussian noise with varying SD (y-axis). Arrow and arrowhead mark examples of a cell showing no rhythmicity and a cell showing rhythmicity in certain conditions, respectively. C, Diagram of the minimal abstract model containing HH-style spiking mechanism, Ca²⁺ conductance, Ca²⁺-dependent conductance (I_CAN), and Na⁺-dependent outward current (I_pump). An optional “synaptic” feedback mechanism is outlined in red. D, Membrane potential resulting from running the minimal model without feedback (blue) and with a unitary gain feedback (red). E, Results of running the minimal model without feedback (blue) and with a unitary gain feedback (red) shown in phase space projection of the membrane potential (V_m), the Na⁺ concentration ([Na⁺]_i), and the inactivation gating variable (n). Arrows mark the quiescence and firing epochs. F, Critical [Na⁺]_i resulting in bifurcation that initiates and terminates each burst as a function of the feedback gain. G, Mean voltage during bursts and the interburst voltage as a function of the feedback gain. H, Map of the bursting properties as a function of the feedback gain (x-axis) and the bias current (y-axis) showing the occurrence and frequency of bursting. As apparent, introducing feedback increases the range of bias currents that result in bursting (cf. I and II).

The ability of the model to produce bursting activity depends not only on the stimulus duration and noise level, but also on the precise morphological structure of the model neuron. This is demonstrated in Figure 4B, where the RI of 10 morphologically different modeled cells was calculated while varying the noise level and stimulus duration. As apparent, the rhythmicity in a given condition was highly sensitive to morphological variations. For example, in one cell (arrow), no rhythmic activity was produced in any tested parameter combinations, whereas in another cell (arrowhead), rhythmic activity was produced in the condition of low current noise.

To investigate how this model produces infra-slow bursting and what causes its susceptibility to perturbations, we developed a minimal abstract model that contains the core elements of the detailed model (Fig. 4C, black; see Materials and Methods). In brief, it is a “point neuron” containing simplified HH-style Na⁺, K⁺, and leak conductances, along with a Ca²⁺ conductance, Ca²⁺-dependent nonspecific cationic conductance (I_CAN) and a Na⁺-dependent outward current (I_pump). When applying a positive DC (bias) current in the range of ∼19–21 pA, this minimal model produces bursting (Fig. 4D, blue). The rhythmic transitions between spiking and quiescence can be understood by considering the slow Na⁺ concentration variable as fixed relative to the fast components (fast subsystem; Izhikevich, 2007). When the fast subsystem is spiking, it follows a stable limit cycle. As the Na⁺ concentration reaches a critical level, the fast subsystem undergoes a bifurcation that produces a stable fixed point instead of the limit cycle, resulting in quiescent epoch (Fig. 4E, straight arrow). Na⁺ then slowly declines up to a critical level when the limit cycle is created again (Fig. 4E, curved arrow) as a result of another bifurcation. This outcome, however, only appears in a narrow range of bias current values (19–21 pA) and is highly susceptible to noise because the difference in mean voltage between the spiking and quiescence regimes is ∼1 mV.

To better understand how network feedback may enhance rhythmic bursting, we introduced a feedback current to the minimal model, calculated by integrating the output spikes (Fig. 4C, red). The extra inward current enabled the model to keep firing even in the presence of strong outward pump current, pushing the bifurcation point that terminates the burst to a higher level of Na⁺ concentration (Fig. 4D,E, red). The relationship between the feedback gain and the critical Na⁺ levels and membrane potentials for burst initiation and termination is described in Figure 4, F and G. As apparent, terminating the bursts with higher Na⁺ level increased the duration of quiescence between the bursts during which the Na⁺ level gradually declines. In addition, the feedback increased the voltage difference between the firing and quiescence periods (Fig. 4G), making the model much more resistant to noise. Running the minimal model with multiple combinations of bias current and network feedback gain showed how these two parameters affect both the induction of bursts and bursting frequency (Fig. 4H). Notably, at very low feedback gains (Fig. 4H, “I”) the range of bias currents allowing bursting is very narrow (19–21 pA), making the model highly sensitive to stimulus properties. When the feedback gain is increased (Fig. 4H, “II”), this range widens dramatically. At a given bias current, the bursting frequency decreases with an increase in the network feedback gain.

In conclusion, the features of the AOB mitral cell model bear the potential to produce infra-slow bursting. However, their high sensitivity to perturbations limits their tendency for rhythmic activity and makes them unlikely to account by themselves for the experimentally observed phenomenon (Fig. 1A and Gorin et al., 2016). Our minimal model predicts that network feedback might enhance the tendency of single cells for bursting activity (Fig. 4). Indeed, the experimental results show that bursting is synchronous across cellular assemblies (Fig. 2) and that this synchronization and the rhythmic bursting are reduced by blocking network connectivity (Fig. 3E,F).

Clustering of AOB mitral cells into a glomerular module stabilizes their tendency for infra-slow bursting

To study how AOB network interactions might stabilize the single-cell tendency for bursting, we constructed a realistic computational model of an AOB glomerulus in which interactions take place between the dendritic tufts of multiple mitral cells. These interactions, namely direct synaptic excitation by dendritic glutamate release (Castro and Urban, 2009), electrical coupling, and indirect synaptic inhibition, link each mitral cell to the rest of the cells that project to the same glomerulus (Fig. 5A). Each neuron in the glomerulus is simulated using our previously described detailed mitral cell model, with random variations in morphology (see Materials and Methods).

Figure 5.

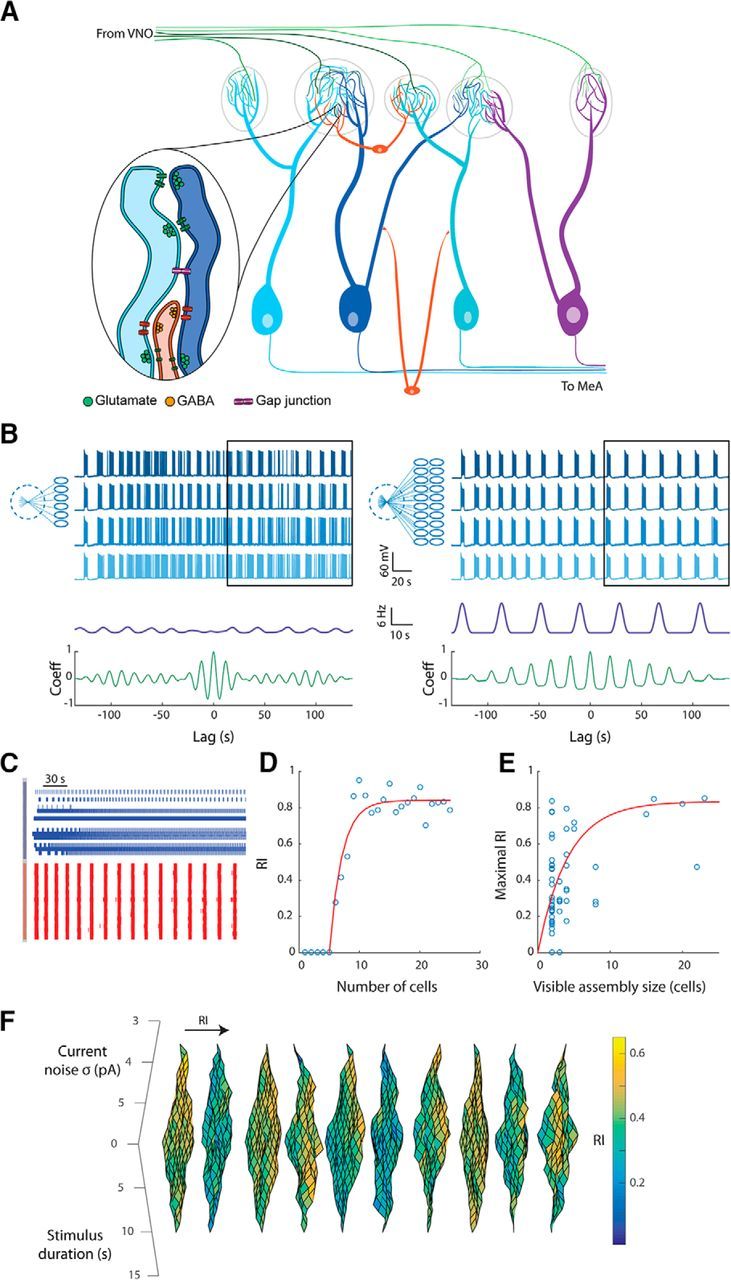
Robust, synchronous, infra-slow bursting activity is predicted to emerge at the network level. A, Schematic illustration of the AOB network showing the afferent fibers from the VNO (green), mitral cells (cyan, blue, purple), and inhibitory interneurons (orange). Magnification of the putative intraglomerulus synaptic connectivity used in the network simulation is shown in the inset, demonstrating direct synaptic excitation, indirect synaptic inhibition, and electrical coupling. B, Examples of simulating the glomeruli of six cells (left) and 20 cells (right), both with random morphological variation and white noise current injection. The blue traces show the voltage responses of four representative cells to a 4 s stimulus. Population firing time histogram during the period denoted by black box (purple) and autocorrelation function of the time histogram (green) both demonstrate stronger rhythmicity in the 20 cells glomerulus. C, Blue, Raster plot showing the firing of 20 unconnected morphologically distinct model cells without noise as a response to a stimulus (gray bar). Red, Response of the same 20 cells when connected by glomerular interactions. D, RI, calculated from the population firing, as a function of the number of cells showing monotonic increase. An exponential curve (red line) was fitted to the data. E, Same as in C but for the experimental observation in AOB slices showing the maximal RI within each assembly as a function of observed assembly size. F, RI values of the firing of a randomly chosen cell from a 30-cell glomerulus stimulated with a transient stimulus with varying duration (x-axis) in the presence of current Gaussian noise with varying SD (y-axis). Each of the 10 surfaces shows the results of simulating a glomerulus comprising a different set of 30 cells with random morphological variations. Note the difference from the similar analysis of 10 unconnected cells shown in Figure 4B.

Synchronous bursting activity was initiated by a global stimulation of the glomerulus, simulating an afferent input, while Gaussian current noise was added to each cell. The results indicate that, as predicted by the minimal model (Fig. 4), the bursting rhythmicity is enhanced with the increase in the number of mitral cells assembled in a given glomerulus (member cells). This is demonstrated in Figure 5B by comparing a glomerulus with six member cells (Fig. 5B, left) with a glomerulus with 20 member cells (Fig. 5B, right). Examining the membrane potential of four representative cells from each glomerulus (Fig. 5B, blue traces) reveals that, after the direct response to the stimulus, the cells of both glomeruli shift to bursting activity. The rhythmicity of this bursting is demonstrated by the population firing time histogram during the period denoted by a rectangle (Fig. 5B, purple), and is further reflected by the autocorrelation function of the time histogram (Fig. 5B, green). The latter shows that the RI increases from 0.12 in the 6-cell glomerulus to 0.76 in the 20-cell glomerulus. As also predicted by the minimal model (Fig. 4D–H), increasing the network feedback (by increasing the number of member cells in the glomerulus) evidently increases the bursting period duration.

The resulting rhythmic behavior in the model glomerulus is not merely an amplification of the rhythmic properties of individual cells. The raster plot in Figure 5C (blue) shows the firing response of 20 noiseless unconnected model cells to stimulation (Fig. 5C, gray bar). Because the cells are not identical, they display a wide range of responses; some do not fire beyond the duration of the stimulus, some switch to tonic firing, and others switch to bursting activity with varying period duration. Figure 5C (red) shows the response of the same 20 cells when they are connected by glomerular interactions. The resulting activity does not resemble any of the responses of the individual cells, but rather demonstrates a highly correlated rhythmic bursting in all member cells.

To quantify the relationship between the number of member cells and the rhythmicity of the neurons in a glomerulus, we calculated the RI of the population activity in the simulated glomerulus while increasing the number of member cells. The results shown in Figure 5D indicate that a positive relationship between the number of cells in the glomerulus and the RI of their firing is expected (Spearman's ρ = 0.57, p = 2.7 · 10⁻³). Consistent with this prediction of the model, a similar relationship was found experimentally. Analysis of all observed assemblies revealed that larger assemblies were associated with a higher RI (Fig. 5E, Spearman's ρ = 0.48, p = 9.1 · 10⁻⁵). It should be noted that the large scattering of the experimental results is most likely due to underrepresentation of the total assembly size.

Notably, the lateral interactions among mitral cells in the glomerular model stabilize their bursting activity and render it insensitive to noise level, stimulus duration, or morphological variations. This is exemplified in Figure 5F, which depicts the RI (color coded) of a randomly chosen cell from a 30-cell glomerulus as a function of the SD of the Gaussian noise and the stimulus duration (10 trials, each with different morphological variations). As apparent, relatively high average RI values are predicted in most of the parameter space, as opposed to the behavior of the single cell model depicted in Figure 4B.

In conclusion, both the computational simulations and the experimental observations suggest that the network interactions among mitral cells boost and stabilize their tendency for rhythmic bursting activity.

Computational glomerulus model predicts several properties of the synchronous bursting activity in the AOB network

To further examine the synchronous bursting mechanism, we tested several more predictions made by the computational glomerulus model against experimental observations.

First, we examined the response of a model glomerulus comprising 20 cells to a stimulus delivered to all of the member cells while they were bursting. As shown in Figure 6A, such stimulus (gray bar) affects the bursting activity in two ways. First, the intraburst firing frequency of subsequent bursts got lower compared with prestimulus bursts; second, the subsequent bursts are delayed relatively to the expected activity without the external stimulus. Both effects stem from the significant increase in [Na⁺]_i in all cellular compartments of all member cells due to the external stimulus.

Figure 6.

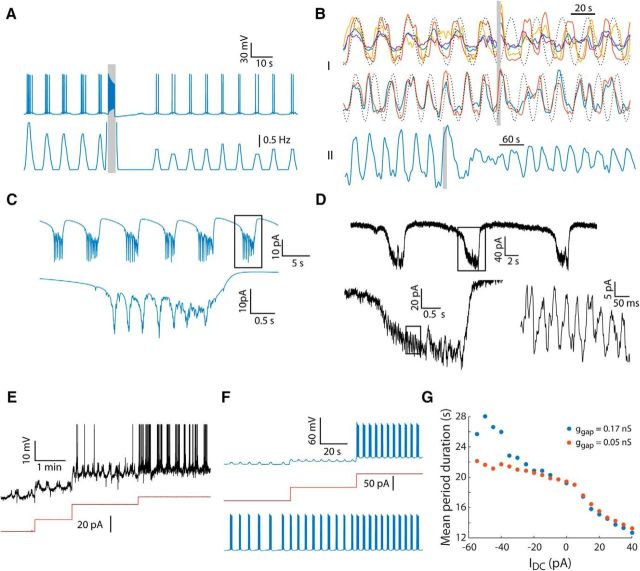
Model glomerulus predicting multiple experimental observations. A, Simulating an afferent stimulus in a 20-cell glomerulus showing membrane potential of a representative cell (top) and its firing histogram (bottom). Synchronous rhythmic bursting was induced by a first stimulus (data not shown), whereas the second stimulus (gray line) was given during synchronous bursting, showing the resulting phase delay and reduction in intraburst firing frequency. B, “I,” Fluorescence of four cells that form one assembly (top) and another two cells that form a second assembly in the same slice (bottom). Local electrical stimulation (gray bar) evoked an immediate response followed by a marked delay, as indicated by the dotted line that shows sinusoidal functions that approximately follow the fluorescence before the stimulation and predicts the expected activity without stimulation. “II,” Fluorescence of a different cell that shows a marked reduction in the amplitude of the rhythmic activity after the stimulation (gray bar). C, Current in a simulated mitral cell belonging to a 35-cell glomerulus clamped to −70 mV in the absence of chemical synaptic transmission showing rhythmic episodes of inward current (top) composed of summation of unitary events (bottom). D, Current recorded experimentally in a mitral cell after blocking synaptic transmission by substitution of extracellular Ca²⁺ with Mg²⁺ showing similar results in terms of both the rhythmic episodes and the unitary events. E, Whole-cell recording of an AOB mitral cell (black) during injection of hyperpolarizing current steps (red). F, Simulated injection of hyperpolarizing DC current to a member cell from a 20-cell glomerulus. In the injected cell (top), prevention of action potentials by hyperpolarization revealed rhythmic subthreshold events of which the period duration increased with further hyperpolarization. The similar change in activity in another cell from the same glomerulus (bottom) shows that this effect is a network property. G, Period duration of synchronous bursting in a model 20-cell glomerulus as a function of the DC current injected to a single cell, when 0.17 nS (blue) or 0.05 nS (orange) were used as gap junction conductance.

We examined this prediction experimentally by delivering local afferent stimulus to the glomerular layer during two-photon Ca²⁺ imaging (see Materials and Methods). The results of such stimulus indeed confirm the model prediction (Fig. 6B). First, as exemplified in Figure 6B (“I”) for two assemblies from the same slice after the stimulus (gray bar), the activity resumes with a significant phase delay relative to the expected activity represented by the dashed line (p = 2.4 × 10⁻⁴, Wilcoxon signed-rank test, n = 13 cells, cells that changed the bursting frequency were excluded). Second, the amplitude of bursts after the stimulus was indeed reduced (Fig. 6B, “II,” p = 5.3 × 10⁻⁶, one-tailed paired t test, n = 21 cells, comparing signal variance before and after the stimulus), an effect mostly prominent in cells with relatively strong transient responses.

Second, the model glomerulus accurately predicts membrane currents measured experimentally during bursting activity. As shown in Figure 6C, a simulated voltage clamp of one cell out of a 35-cell glomerulus (in the absence of chemical synapses) results in rhythmic episodes of inward current, each composed of a slow inward current component with superimposed fast events (spikelets; Fig. 6C, bottom). A similar result, in terms of both slow and fast time scale, was obtained experimentally (Fig. 6D) in voltage-clamp conditions and synaptic blockade (by replacing the extracellular Ca²⁺ with Mg²⁺).

Finally, we examine the model response to DC current injection. In their recent study, Gorin et al. (2016) showed that DC current injection into a recorded cell alters the period duration of the bursting, an observation interpreted as an evidence for cell-autonomous rhythmogenesis. We encountered similar results while injecting hyperpolarizing DC current (Fig. 6E, red line) during whole-cell recordings: infra-slow, subthreshold voltage oscillations in which the period duration increases with stronger negative current injection were readily observed. We simulated this experiment in a 20-cell glomerulus examining the voltage response of a single neuron to DC current (Fig. 6F, top blue and red line, respectively). As apparent, the hyperpolarizing current eliminated the spiking activity in the injected cell and increased the period duration of the underlying depolarizing events. Although a single cell was hyperpolarized directly by the current injection, the period duration of the entire population was affected via the spread of the injected current through gap junctions, as demonstrated by the increase in period duration of another cell of the simulated glomerulus (Fig. 6F, bottom). We tested this effect systematically by simulating a range of DC current values in two different gap junction conductance values: 0.17 and 0.05 nS (Fig. 6G). As shown, beyond a certain threshold, the effect of the simulated DC current injection is stronger when the gap junction conductance is larger.

We conclude that the change in period duration upon DC current injection in itself does not imply a predominantly cell-autonomous rhythmogenesis, but may be explained by the spread of the injected current to coupled cells.

GABA_A-mediated inhibition within the AOB network controls the extent of interglomerular synchrony

A commonly proposed mechanism for neuronal population bursting relies on reciprocal excitatory–inhibitory or inhibitory–inhibitory connectivity within the network (Marder and Bucher, 2001; Bartos et al., 2007). We therefore aimed to examine the contribution of GABA_A-mediated inhibition in the AOB network to the synchronous bursting.

Using gabazine (1–20 μm) to block GABA_A-mediated inhibitory synaptic transmission led to a drastic increase of the level of synchrony among mitral cells, usually up to complete synchrony of the entire population in a given field of view. Consistent with previous studies (Gorin et al., 2016), GABA_A blocker application led to a shift to full synchrony of rhythmic activity in five of five cases (see below) and such global synchrony was evident in every slice pretreated with GABA_A blockers (n > 20). For example, in the case shown in Figure 7, A and B, gabazine application changed the map of synchronized neurons from six small assemblies to one global assembly encompassing most of the neuronal population. Along with the increase in synchrony, GABA_A blockade caused a significant increase in synchronous bursting period duration (Fig. 7C), usually up to 150–300 s per cycle, as well as to an increase in the amplitude of the fluorescence signal.

Figure 7.

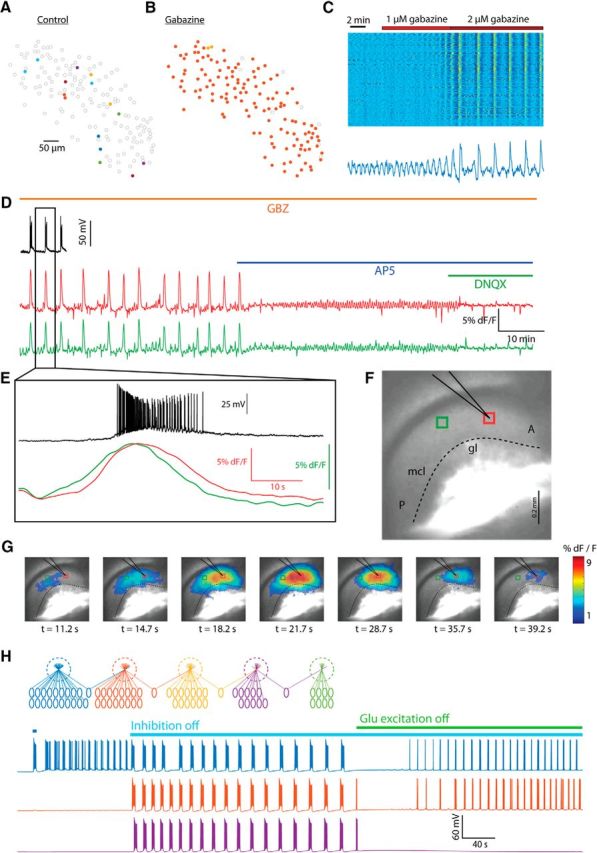
Inhibitory interactions determine the size of assemblies and the extent of rhythmicity and restrict interglomerular burst propagation. A, Map of an AOB slice in control conditions showing seven assemblies (color coded) of correlated activity. B, Map of the same slice after gabazine application showing global synchrony. C, Top, Raster plot of the fluorescence of cells from the slice shown in A and B before and during gabazine application (red bar). Note the emergent of global synchronous rhythmicity. Bottom, Example of the fluorescence recorded from a single cell bursting under control conditions demonstrating an increase in amplitude and interburst interval in the presence of gabazine. D–G, Wide-field imaging of an AOB slice in which GCaMP6 is expressed in mitral cells in the presence of gabazine. D, Simultaneous recording of electrical activity (black trace) and fluorescence changes in a two ROIs marked in E with corresponding colors. APV (blue bar) and DNQX (green bar) were added sequentially. E, Magnification of a single event marked in D, showing the temporal relationship among the signals. F, Photomicrograph of the imaged area, showing the locations of the recording pipette (black) and the ROIs (red and green squares). mcl, Mitral cell layer; gl, glomerular layer; P, posterior; A, anterior). G, Time-lapse imaging of the propagation of the burst of activity shown in E. H, Reproducing the blockers' effects in a network of five glomeruli of different sizes, in which pairs of “adjacent” glomeruli share mitral cells. Electrical activity of representative cells from the three glomeruli is shown in matching colors. The blue glomerulus was stimulated (blue bar) to initiate synchronous bursting activity that spread to adjacent glomeruli upon blockade of synaptic inhibition (cyan bar). After blockade of synaptic excitation (green bar), modified synchronous bursting activity continues in some of the glomeruli.

This global synchrony under GABA_A blockade allowed the examination of the rhythmic activity using wide-field calcium imaging. An example is shown in Figure 7, D–G, where a slice from a mouse genetically expressing the calcium indicator GCaMP6 under regulation of the Thy1 promoter was used (Dana et al., 2014). The voltage recording from a single mitral cell is shown in Figure 7D (black trace), along with the average fluorescence signals simultaneously recorded from two ROIs (Fig. 7F), one containing the recorded cell (red in Fig. 7D,F) and the other located in a more posterior region (green in Fig. 7D,F). Blocking NMDA receptors using AP5 (Fig. 7D,F, blue bar) decreased the amplitude of the fluorescence signal and increased the frequency of the rhythmic activity. With further blockade of AMPA receptor-mediated excitatory transmission (DNQX; Fig. 7D,F, green bar), the rhythmic activity disappeared, most likely due to a reduction in synchrony below the level detectable by wide-field imaging. This observation shows that, indeed, chemical excitatory interactions are a part of the system of lateral interactions that mediate synchrony in the AOB network.

A close examination of single events (Fig. 7E; marked by a rectangle in Fig. 7D) shows a phase difference between the calcium signals in the two ROIs, indicating that the activity propagates in space. Indeed, a time lapse of the fluorescence shown in Figure 7G demonstrates that the activity propagates in a posterior to anterior direction at a speed of ∼0.07 mm/s.

To simulate such behavior, the model had to be expanded to include multiple glomeruli. This was done by constructing several model glomeruli with varying number of cells (Fig. 7H, top), where some cells interact with more than one glomerulus (heterotypic cells), a well known feature of AOB network topology (Takami and Graziadei, 1991). Although the degree of interglomerular interaction in the AOB is most likely even greater, we chose a conservative approach in which one cell from each glomerulus interacts with the cells from the next glomerulus. Applying a transient stimulus to one of the glomeruli results in synchronous bursting activity in this particular glomerulus (Fig. 7H, blue line) without propagation to adjacent glomeruli. Blocking inhibitory transmission (Fig. 7H, cyan bar) results in interglomerular synchrony of bursting, along with an increase in period duration, burst duration, and intraburst frequency, all of which show similarity to the experimental findings (Fig. 7A–C). Subsequent blockade of excitatory synaptic transmission (Fig. 7H, green bar) decreases the period duration and burst duration in some glomeruli (Fig. 7H, blue and orange lines), whereas blocking bursting in others (Fig. 7H, purple line; cf. Fig. 7D). This is in agreement with the notion that excitatory glutematergic transmission increases the network feedback, thus contributing to the modulation of the synchronous bursting but not necessary for its production.

These results not only further confirm the validity of our model, but also demonstrate the possibility of interglomerular synchrony in the context of the unique topology of the AOB (where each mitral cell innervates several glomeruli) and the role of lateral inhibition in controlling it. Contrary to the suggested role of inhibitory connectivity in the production of network oscillations in other systems, in the novel mechanism presented here, we propose that inhibition limits the extent of synchronous bursting rather than promoting it.

Novel mode of long-term sensory input integration emerges from the proposed mechanism of synchronous bursting in AOB glomeruli

To further examine the role of the AOB unique network topology in sensory information processing, we examined the response of a model network to asynchronous stimulation of several glomeruli. The network was composed of four glomeruli with varying number of cells, with one heterotypic cell shared between each pair of glomeruli, thus creating two assemblies (Fig. 8A). As demonstrated by the raster plot shown in Figure 8B, cells in each glomerulus start bursting only when their own glomerulus was stimulated (Fig. 8B, colored arrows). However, when both glomeruli in each assembly were stimulated at distinct time points, their activity became synchronous within 10–40 s. This is clearly demonstrated by the population firing time histogram of each assembly (Fig. 8C, top, solid lines), showing peaks of correlated firing across the two glomeruli comprising each assembly. This synchronization is not a result of the exact timing of stimuli because it was not observed in a similar simulation where no shared cells connected between the glomeruli (Fig. 8C, bottom, dotted lines).

Figure 8.

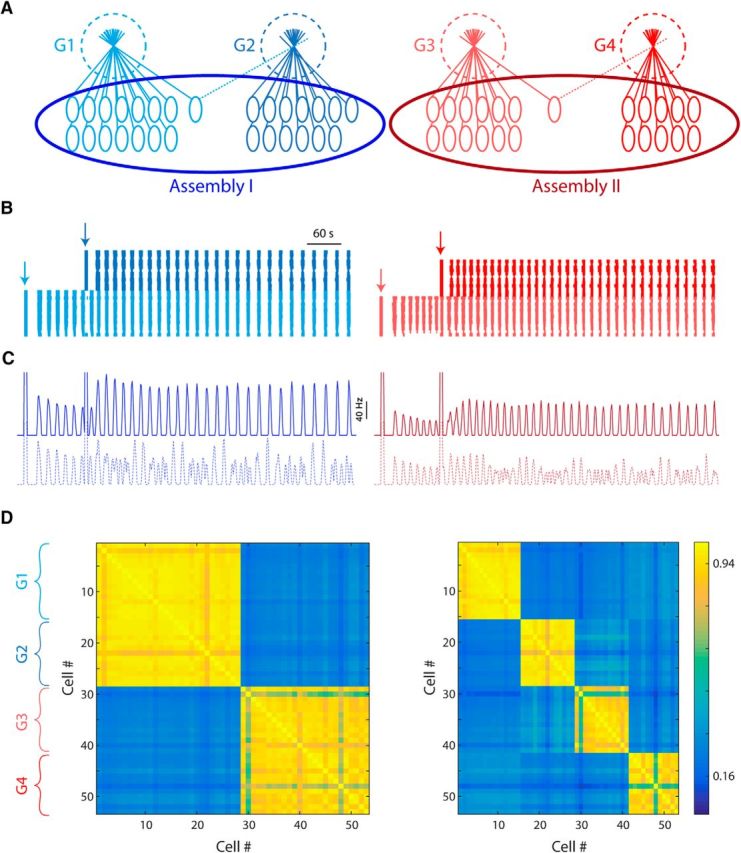
Interglomerular interactions enable integration of inputs over extended time scales. A, Network topology used in the simulation, containing four glomeruli of 15, 13, 13, and 12 member cells. Each pair form an assembly via one shared cell that project dendrites to both glomeruli. The lateral excitation and inhibition weights are slightly different in each assembly. B, Raster plot showing the firing of the cells from assembly I (left) and assembly II (right) color coded to match the glomeruli. Times of stimulation of each glomerulus are denoted by vertical arrows. C, Population firing time histogram for each glomerulus in the original topology (top, solid lines) and in the absence of shared cells (bottom, dotted lines). D, Correlation matrix of the entire population, ordered by glomeruli, in the original topology (left) and in the absence of shared cells (right). Note that correlated activity between the glomeruli of each assembly occurs only when shared cells are present and it is independent of the time of stimulation.

This effect is further demonstrated by the cross-correlation matrix among the 53 cells that comprise the network. When shared cells are present (Fig. 8D, left), each pair of connected glomeruli indeed function as a synchronous assembly with all member cells burst uniformly. However, no correlation exists between the two assemblies. When shared cells are absent (Fig. 8D, right), the synchrony between glomeruli disappears and each glomerulus functions as a distinct entity.

Therefore, the synchronous infra-slow bursting activity in the AOB enables the AOB network to integrate distinct inputs that arrive to different glomeruli at different moments in time. Each subsequent input may add glomeruli to the “orchestra” of bursting glomeruli, thus increasing the probability of superthreshold input to the AOB target neurons. Notably, as shown above, the amount of such interglomerular synchrony can be regulated locally by lateral inhibition in the AOB.

Discussion

In this study, we combined electrophysiological recordings, calcium imaging, optogenetics, and computational modeling to investigate the mechanism of synchronous infra-slow bursting activity exhibited by AOB mitral cells and its consequences for sensory information processing. Our computational modeling results show that weak tendency for bursting activity is predicted by the intrinsic properties of AOB mitral cells and that this tendency is predicted to be facilitated and amplified by network feedback. Our experimental results confirm that synchronous infra-slow rhythmic bursting is an emergent property of the AOB neuronal network. Specifically, this activity relies on the interplay between the cellular properties of AOB mitral cells and the AOB network connectivity composed of both lateral chemical synapses (excitatory and inhibitory) and electrical coupling through gap junctions.

Generation of synchronous infra-slow bursting activity

It has been suggested recently (Gorin et al., 2016) that infra-slow bursting is the product of the interplay between two distinct populations of AOB mitral cells: intrinsic pacemakers and entrained neurons. We could not find evidence for a dichotomous division of AOB mitral cells into pacemaker and entrained cells and our results indicate that such division is not needed to account for the observed activity. Rather, it seems that AOB mitral cells lie on a continuous spectrum of tendency to burst and the observed activity is an emergent network property creating a “group pacemaker” (Rekling and Feldman, 1998). This is a common theoretical concept in many systems of coupled oscillators, in which the intrinsic tendency of the individual component to oscillate is stabilized and amplified by the coupling among them (Smale, 1976; Manor et al., 1997; Pogromsky and Nijmeijer, 2001).

The tendency of AOB mitral cells to produce infra-slow oscillations reflects slow intracellular dynamics that we characterized in a previous study (Zylbertal et al., 2015), in which we focused on the persistent response of these cells to transient stimuli. Specifically, these dynamics include a slow hyperpolarizing current mediated by the Na⁺–K⁺ pump, the activity of which is accelerated after stimulation due to the significant Na⁺ influx during the initial firing response. In addition, the increase in [Na⁺]_i causes a reduction of leak Na⁺ influx, thus further hyperpolarizing the cell. A prerequisite for such dynamics is a dendritic voltage-gated Na⁺ conductance that generates, during each action potential, an Na⁺ reservoir without proximity to a diffusion sink.

These processes underlie an adaptation current, an activity-dependent current that slowly leads to firing termination. In dynamical systems terms, this current forms a slow subsystem alongside the fast subsystem that underlies the firing activity. Such fast–slow dynamics are a prerequisite for rhythmic bursting (Izhikevich, 2007) and are readily reproduced in a minimal model containing only an HH-style firing mechanism, Ca²⁺ conductance, Ca²⁺-dependent conductance, and Na⁺-dependent outward current. This cellular tendency, however, must be enhanced and stabilized by the lateral electrical and chemical synapses among mitral cells in the AOB network. As shown using this minimal model (Fig. 4C–H), any type of abstract feedback mechanism may fulfill this requirement. Indeed, some cells having a particular morphology and certain makeup of membrane mechanisms may produce precise rhythmic infra-slow bursting even in isolation, although this bursting is highly sensitive to variations in intrinsic parameters. These cells, however, seem to represent an extreme case rather than form a well defined population and their existence in the network is not a prerequisite for synchronous bursting activity.

It should be emphasized that the model cell used here for reproducing infra-slow rhythmic bursting in AOB mitral cells was developed to account for a totally different phenomenon: the cells' prolonged response to transient stimuli (Zylbertal et al., 2015). It is remarkable that, without any modifications or adjustments, this model can also account for the synchronous infra-slow bursting activity once it is embedded in the AOB local circuitry.

The role of dynamic ionic concentrations in the production of slow bursting activity has been studied previously mostly in the pre-Bötzinger complex that generates the respiratory rhythm using both computational (Cressman et al., 2009; Barreto and Cressman, 2011; Krishnan and Bazhenov, 2011; Rybak et al., 2014) and experimental methods (Krey et al., 2010). These studies have shown that a model of the pre-Bötzinger network produces synchronous bursting in a large region of parameter space without requiring persistent Na⁺ current or Ca²⁺-dependent cation current. Similarly to our findings, this behavior was possible only when taking network connectivity into account. Notably, the region of parameter space that enabled synchronous bursting in the pre-Bötzinger network became even larger when additional cellular mechanisms, such as persistent Na⁺ conductance, were incorporated. These relationships between the distinct mechanisms seem to apply to the AOB as well. Our results indicate that network interactions combined with the intracellular properties are sufficient to produce synchronous infra-slow bursting. The additional conductances shown by Gorin et al. (2016) are likely to take part in shaping and stabilizing the synchronous bursting activity in the AOB. Therefore, similarly to the model of the pre-Bötzinger network, our suggested model fulfills the principle of homeostatic architecture of neuronal networks, which combines compensatory intrinsic and connectivity properties to preserve the network function throughout a wide space of possible parameters (Marder and Goaillard, 2006; Grashow et al., 2010).

Chemical and electrical synaptic interactions within the AOB glomerular networks

Several lines of evidence indicate the existence of gap junctions and electrical coupling between AOB mitral cells. Various types of connexins, the gap junction proteins, are expressed in the AOB (Zhang and Restrepo, 2003; Degen et al., 2004; Zhang, 2011), whereas we recorded spontaneous and optogenetically evoked spikelets from AOB mitral cells in the presence of synaptic blockers (Fig. 3C,D). Because synchrony and rhythmicity persisted in AOB slices even after the blockade of chemical synapses (by either synaptic blockers or removal of extracellular Ca²⁺), it is reasonable to assume that network feedback is maintained in these conditions by electrical coupling. This assumption is further supported by the results obtained using CBX, a gap junction blocker (Fig. 3E,F). Notably, electrical coupling between mitral cells innervating the same glomerulus was shown to synchronize spiking activity in the MOB (Christie et al., 2005; O'Connor et al., 2012).

Although rhythmicity persisted in the presence of synaptic blockers, synaptic transmission does play a major role in shaping the burst duration, the intraburst firing rate, and the bursting period duration. Indeed, selective blockade of inhibitory connections increased the synchrony and lowered the frequency of the infra-slow activity. Blocking excitatory transmission with intact inhibition resulted in either increase or decrease in synchrony. Given that excitatory synaptic blockade also blocks the input to inhibitory interneurons (Urban and Castro, 2005), such mixed effects are expected due to the variability in the initial excitation/inhibition ratio in a given slice.

Therefore, our results suggest that electrical and chemical synapses between AOB mitral cells work in synergy to produce synchronous activity (Christie and Westbrook, 2006). According to our model, electrical synapses mediate the initial local synchrony among cells projecting to a common glomerulus, leading to a sufficient level of intraglomerular glutamate release, which in turn amplifies the synchronized spiking activity.

Possible functional role for the infra-slow rhythmicity

Here, we presented a novel computational model of the AOB network, which includes multiple glomeruli arranged in several assemblies. This model suggests, for the first time, a specific role for the unique connectivity within the AOB in sensory information processing (see the introduction). According to our model, stimulating a particular glomerulus elicits synchronous rhythmic bursting activity in all its mitral cells. Asynchronous stimulation of several glomeruli caused a prolonged synchronous bursting activity, which achieved synchrony between these glomeruli only if heterotypic cells were shared between them (Fig. 8). Therefore, the splitting of the VNO input to multiple glomeruli may enable the emergence of multiple synchronous AOB subnetworks that separately integrate and bind partially overlapping inputs, which are reflected by their synchronous bursting over prolonged time scales. Such subnetworks are predetermined by the connectivity of AOB heterotypic mitral cells and are regulated dynamically by the local inhibitory network, which is controlled by top-down innervation. The extended time window of integration may, for example, support a prolonged sampling and binding of chemosensory stimuli before a decision on a behavioral outcome. Such a scenario seems to take place during social investigation of a conspecific, in which different sets of cues are detected in sequences of repeated sampling of the facial and ano-genital areas (Luo et al., 2003). Per our hypothesis, in such a scenario, only specific combinations of cues derived from these different sources would result in widespread synchronous bursting sufficient to drive amygdalar target neurons and thus to evoke a certain social behavior.

In their groundbreaking study, Luo et al. (2003) recorded single-unit activity from AOB mitral cells during spontaneous investigation of social stimuli. They demonstrated highly oscillatory firing responses of these cells that were extended for tens of seconds after a bout of social investigation. Accordingly, we previously showed that AOB mitral cells are endowed with intrinsic membrane mechanisms that allow persistent firing responses, lasting tens of seconds, to transient stimuli (Shpak et al., 2012; Zylbertal et al., 2015). Our current work, consistent with recent studies by others (Vargas-Barroso et al., 2015; Gorin et al., 2016), demonstrates that these cells also exhibit prolonged periods of infra-slow rhythmic bursting, which may be elicited and modulated by arriving inputs. Moreover, we show that this activity may be used, in combination with the unique connectivity characterizing the AOB, to integrate sensory information over an unusually extended time window. Altogether, these studies strongly suggest that the AOS processes sensory information using much slower time scales than most other sensory systems. These slow time scales may fit the involvement of this system in regulating emotional and hormonal states that are known to characterize various types of social behavior.