Abstract
Categorization involves organizing perceptual information so as to maximize differences along dimensions that predict class membership while minimizing differences along dimensions that do not. In the current experiment, we investigated how neural representations reflecting learned category structure vary according to generalization demands. We asked male and female human participants to switch between two rules when determining whether stimuli should be considered members of a single known category. When categorizing according to the “strict” rule, participants were required to limit generalization to make fine-grained distinctions between stimuli and the category prototype. When categorizing according to the “lax” rule, participants were required to generalize category knowledge to highly atypical category members. As expected, frontoparietal regions were primarily sensitive to decisional demands (i.e., the distance of each stimulus from the active category boundary), whereas occipitotemporal representations were primarily sensitive to stimulus typicality (i.e., the similarity between each exemplar and the category prototype). Interestingly, occipitotemporal representations of stimulus typicality differed between rules. While decoding models were able to predict unseen data when trained and tested on the same rule, they were unable to do so when trained and tested on different rules. We additionally found that the discriminability of the multivariate signal negatively covaried with distance from the active category boundary. Thus, whereas many accounts of occipitotemporal cortex emphasize its important role in transforming visual information to accentuate learned category structure, our results highlight the flexible nature of these representations with regards to transient decisional demands.
SIGNIFICANCE STATEMENT Occipitotemporal representations are known to reflect category structure and are often assumed to be largely invariant with regards to transient decisional demands. We found that representations of equivalent stimuli differed between strict and lax generalization rules, and that the discriminability of these representations increased as distance from abstract category boundaries decreased. Our results therefore indicate that occipitotemporal representations are flexibly modulated by abstract decisional factors.
Keywords: category learning, classification learning, fMRI, intraparietal sulcus
Introduction
Organisms must be able to flexibly adjust the degree of generalization applied to category knowledge to accomplish different goals (Norman and O'Reilly, 2003; Roy et al., 2010; Seger and Miller, 2010; Chumbley et al., 2012; Collins and Frank, 2013). For instance, when using a vending machine, it may be necessary to use a strict generalization threshold to distinguish “dimes” from “non-dimes,” but when cleaning out your desk, it may be necessary to use a more lenient threshold to distinguish “coins” from “non-coins.” In the present study, we sought to investigate how perceptual representations differ between generalization strategies. We did so by having participants learn and apply multiple generalization thresholds during the performance of an A/notA categorization task (see Fig. 1), in which behavioral performance typically varies according to the degree of perceptual similarity between visual stimuli and a prototype, and in which knowledge is often difficult to verbalize.
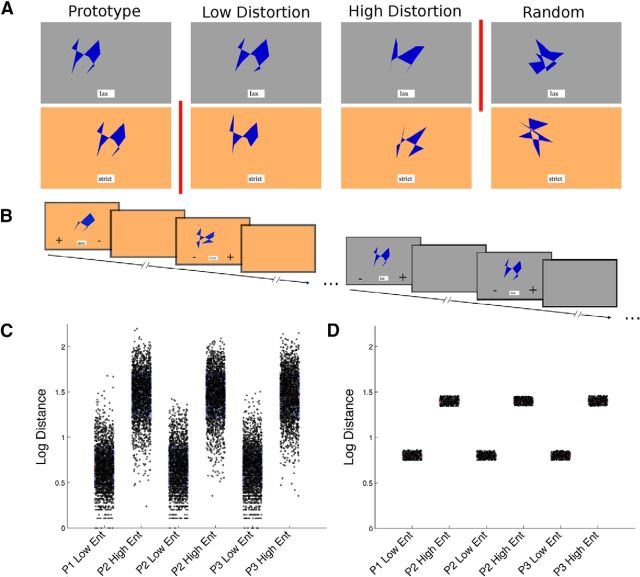
Figure 1.
A, Participants categorized dot-prototype stimuli at four levels of distortion, according to two decision rules (indicated by red vertical lines). In the lax condition (top, gray), participants had to categorize all prototype distortions as category members, excluding only random stimuli. In the strict condition (bottom, orange), participants had to categorize only the prototype stimuli as category members, excluding all other stimuli. This design dissociates perceptual generalization (distance from the prototype) from distance from category boundary. When the strict bound was in play, the random stimuli were farthest from the categorization boundary, whereas when the lax bound was in play, the prototype stimuli were farthest from the boundary. Each of the four distortion levels neighbored one of the decision boundaries: the prototype and low distortion stimuli were closest to the strict bound, whereas the high distortion and random stimuli were closest to the lax bound. The position of each stimulus on the screen was spatially jittered in the x and y planes, and the mapping between background color and categorization rule was randomized between participants. B, On each trial, participants saw a stimulus, a cue at the bottom of the screen indicating the current rule, and two response-location cues (“+,” which indicated a stimulus belonged “inside the category”; and “−,” which indicated “outside of the category”), which were pseudo-randomly assigned to the left versus right bottom corners of the screen on each trial. C, We first generated 2000 stimuli for each of the three category prototypes (P1, P2, and P3) at two entropy levels (low: 3.5 bits per dot, and high: 6.5 bits per dot). y axis: Log Euclidean distance from the prototype. D, To control the visual similarity between stimuli of different distortion levels, we included only the 300 exemplars closest to a specific distance from each prototype at each distortion level. Through pilot testing, we adjusted this distance to minimize behavioral differences between tasks. The random exemplars (data not shown) were created without consideration of their distance from the prototype.
Although A/notA tasks superficially resemble A/B categorization tasks (in which participants categorize stimuli into two categories), neurobiological differences have been observed between them. For instance, although deficits in A/B performance are observed in healthy aging and in neuropsychological disorders affecting the hippocampus, A/notA categorization is typically preserved (Knowlton and Squire, 1993; Zaki, 2003; Bozoki et al., 2006; Glass et al., 2012). Additionally, whereas A/B tasks tend to elicit activity in frontoparietal and hippocampal regions (Seger et al., 2000; Zeithamova et al., 2008), A/notA tasks tend to elicit activity in visual cortices and in the basal ganglia (Reber et al., 1998, 2003; Aizenstein et al., 2000; Summerfield and Koechlin, 2008; Zeithamova et al., 2008). Regions associated with A/notA categorization thus closely resemble those associated with perceptual priming and repetition suppression (Wiggs and Martin, 1998; Koutstaal et al., 2001; Henson, 2003), as well as the theorized neurobiological substrate of the perceptual representation system (Schacter, 1990; Reber and Squire, 1999; Ashby and O'Brien, 2005; Casale and Ashby, 2008).
In typical instantiations of the A/notA task, participants learn to apply a single generalization threshold (but see Nosofsky et al., 2012), and so neural signals reflecting representational factors (Strange et al., 2005; Seger et al., 2011, 2015; Davis et al., 2014), which vary with distance from the prototype, and decisional factors (Grinband et al., 2006; Kayser et al., 2010; White et al., 2012), which vary with distance from the category boundary, are confounded, in that decisional difficulty increases with distance from the category prototype. In the current experiment, participants categorized filled dot prototype stimuli as category members or nonmembers according to “strict” and “lax” generalization rules (see Fig. 1). For the lax rule, participants used a lenient criterion that allowed all stimuli formed as distortions of the prototype into the category while excluding random exemplars. For the strict rule, participants used a strict criterion which allowed only the prototype stimulus into the category while excluding all other exemplars (both low- and high level distortions and randomly formed stimuli). The two rules allowed us to differentiate effects associated with distance from the prototype, from effects associated with distance from the bound. This allowed us to differentiate representational factors from decisional factors and to investigate whether category representations vary according to generalization demands.
Materials and Methods
Participants
Eighteen participants (age 20.7 ± 2.5 years; mean ± SD; 10 female) were recruited from the undergraduate population at South China Normal University. All were paid for their participation and met criteria for MR scanning. Two participants were excluded for excessive motion during the scan (>2 mm in any of the ordinal directions, or 2 degrees pitch, roll, or yaw), resulting in a total of 16 participants included in the final analyses.
Stimuli
We generated “filled” dot-prototype stimuli at four levels of distortion (Fig. 1). This approach of making complex polygons from dot patterns has been used successfully in previous category learning studies (Posner and Keele, 1968; Homa et al., 1981; Smith et al., 2005). Three stimulus sets based on a different prototype were constructed, and each subject learned one of these randomly assigned sets. Prototypes were formed from nine points, or dots, pseudo-randomly assigned to locations within a 23 × 23 grid. To increase visual salience, the nine dots were connected with lines, and the resultant shape was then filled with solid blue color. We designed the distorted exemplars according to a well-established procedure (Posner et al., 1967; Smith and Minda, 2001), which allowed us to create a large number of unique exemplars. After defining the category prototypes, this involved perturbing the locations of the dots by first identifying 12 “rings” surrounding each dot. Each ring was comprised of the cells surrounding the previous ring; therefore, the dot itself comprised a single cell, the adjacent ring comprised 8 cells, and the outermost ring comprised 88 cells. Although a dot had equal probability of moving to any cell within each ring, the probability of a dot moving to a ring decreased with distance from its original position. Using this framework, the uncertainty of the dot positions of a particular stimulus, s, can be defined according to its entropy, H as follows:
where K is the number of cells that a point could be located and pk is the probability that a point is within a particular cell, k.
We first generated 2000 exemplars at each entropy level: low distortion exemplars were created with 3.5 bits per dot, high distortion exemplars were created with 6.5 bits per dot, and random exemplars were generated without regards to the template, so as to be perceptually distinct. Thus, if we describe the prototype as a point in 18-dimensional space, through this procedure, we produced three stimulus “clouds” surrounding this point, such that average Euclidean distance moved per dot per stimulus increased from the low distortion to the high distortion stimulus set, and from high distortion set to random stimulus set, but such that there was considerable variance within each set (Fig. 1C). An attractive characteristic of dot prototype stimuli is that the psychological distance, dψ, between stimuli has been shown to follow a logarithmic function of the average Euclidean distance moved by each dot (Posner et al., 1967; Smith and Minda, 2001):
where d(prototype, exemplar) represents the average Euclidean distance moved per dot between an exemplar and the prototype. To reduce the variance within each stimulus set, we selected 300 exemplars from the low uncertainty stimulus set and 300 stimuli from the high uncertainty stimulus set that fell closest to a specific distance from the prototype (Fig. 1D), and we selected 300 random stimuli that were farther from the prototype than the farthest high distortion exemplar. Through pilot testing, we adjusted these distances to minimize differences in behavioral performance (accuracy and reaction time) between the two rules. As there was greater variability within the random stimulus set, to accurately model effects associated with these stimuli, we used Equation 2 to parametrically define stimulus distances in the neuroimaging models used for voxel selection. To estimate the location of each decision bound, we calculated the point midway between the clusters closest to it (i.e., for the strict rule, the optimal category boundary lay midway between the prototype and the mean of the low distortion exemplars; for the lax rule, it lay midway between the means of the high-entropy and random exemplars).
Procedure
Training session.
Participants were told that there would be two different conditions, strict and lax, and that each would be indicated by an instruction cue and a distinctive background color. They were further told that, in the strict condition, they should be careful to exclude any stimuli that might not be members. In the lax condition, they should try not to miss any potential category members and only exclude stimuli that were unrelated to the category. During the fMRI study, participants were given written instructions in English and spoken instructions in Mandarin Chinese. All participants had studied English previously; however, Chinese-speaking research assistants discussed the instructions with participants in Chinese and answered any questions before beginning testing procedures to ensure comprehension. After instructions, participants learned to categorize by these rules through trial and error. On each trial, the active rule was indicated by an instructional cue presented below the stimulus. During pilot testing in the United States, the instructional cues were the words: “strict” and “lax.” However, as the final fMRI experiment took place in China, the equivalent Chinese characters were used instead: strict: 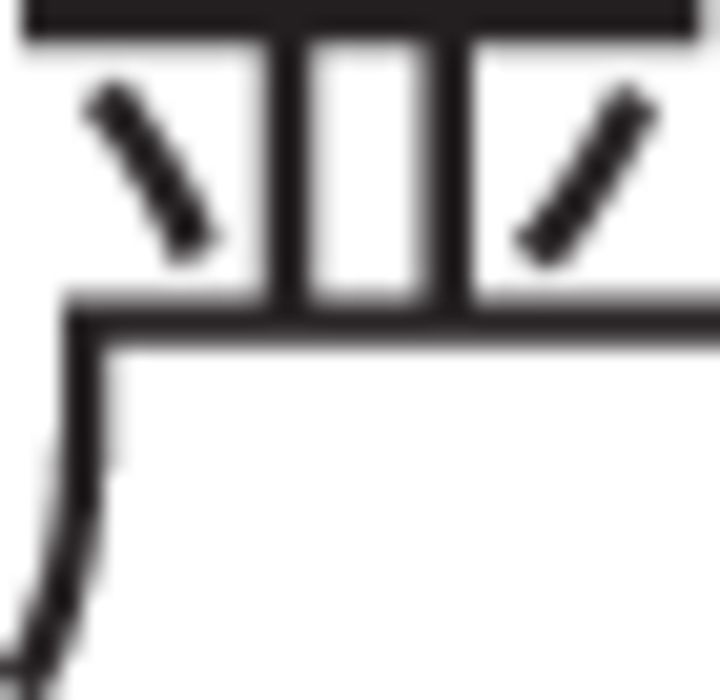 (pinyin transliteration: yan, tone2) and lax
(pinyin transliteration: yan, tone2) and lax 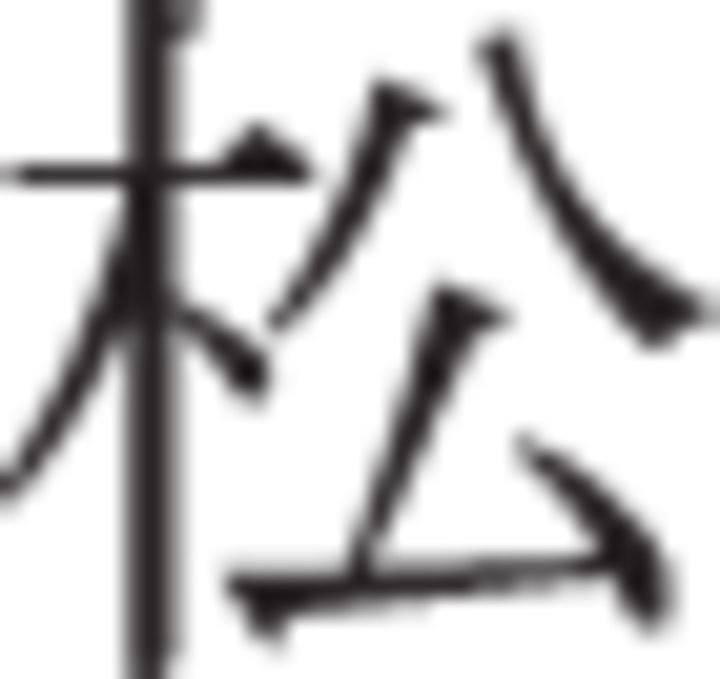 (pinyin transliteration: song, tone1). To mitigate the possibility that participants might not notice switches between cues, each rule was also indicated by the background color of the screen (orange or gray). To avoid possible visual confounds associated with background color, the mapping between rule and color was counterbalanced across participants.
(pinyin transliteration: song, tone1). To mitigate the possibility that participants might not notice switches between cues, each rule was also indicated by the background color of the screen (orange or gray). To avoid possible visual confounds associated with background color, the mapping between rule and color was counterbalanced across participants.
To avoid confounding motor response with decision (member or nonmember), we cued participants as to which hand response to use for each response on each trial. Each stimulus display included two response cues: a “+” and a “−” in the lower left and right corners. The “+” indicated that a stimulus was a category member, whereas the “−” indicated that a stimulus was a category nonmember. The locations of the “+” and “−” signs were randomized on each trial but were counterbalanced across rules, distortion levels, and categories. During training, the word “Correct!” was shown for 0.75 s in green font, following correct responses. Following incorrect responses, the word “Wrong” was shown for 0.75 s in red font. If no response was made within the 2.25 s response window, the words “Too slow” were displayed in black font. No feedback was provided in the scanner.
During training, a greater number of stimuli near the category boundaries were included so that participants could efficiently gain experience with the category boundaries associated with each rule. Thus, while the probability of category member versus nonmember was held at 50% for each rule, when learning the strict rule, there were three low distortion exemplars for every high distortion or random exemplar; and when learning the lax rule, there were three high distortion stimuli for every low distortion or prototype exemplar. During scanning, we adjusted the proportion of stimuli within each distortion level so that, for each rule, we could have the same number of trials within each distortion level. This altered the proportion of stimuli belonging within the category for each rule but was necessary to compare representations of stimulus distortion between rules.
So that we could unpredictably switch between rules in the scanner (to mitigate effects associated with anticipation of rule switches and to be able to directly compare rules), we adopted a training protocol that encouraged participants to frequently switch between rules. Participants trained on five alternating task blocks. In each block, participants trained until reaching a 90% accuracy criterion over k trials on each task. After each successful block, k decreased by 5 trials; so while participants had to complete (at least) 26 trials in the first block, they only had to complete 6 trials in the final block if they were 100% accurate. The criterion window was reset after [k + 5] trials; and if participants failed to achieve the accuracy criterion within this window, they had to complete at least another k trials. After completing the initial training, participants completed a brief task (100 trials), which included temporal jitter and excluded feedback, so as to be as similar as possible to the actual scanner task.
Scanning session.
Participants performed the task during four 10 min scanner runs. Each participant performed 368 trials in total. To mitigate effects associated with the prediction of impending rule switches, participants switched unpredictably between rules every 4, 6, 8, or 10 trials. The trial format was identical to training, except feedback was not included (to isolate representations associated with stimulus and response). The intertrial interval was jittered according to a positively skewed geometric distribution ranging from 2.25 to 9.75 s (mean 4.06 s). The efficiency of the design was optimized using custom software. Participants made responses via magnet compatible response boxes with fingers of their right and left hands.
Image acquisition
Images were obtained with a 3.0 tesla MRI scanner (Siemens Tim Trio) at the Brain Imaging Center at South China Normal University. The scanner was equipped with a 12-channel head coil. Structural images were collected using a T1-weighted MP-RAGE sequence (256 × 256 matrix; FOV, 256 mm; 192 1 mm slices). Each scanning session included four 10 min functional runs, each of which involved the collection of 400 whole-brain volumes. Functional images were reconstructed from 25 axial oblique slices obtained using a T2*-weighted 2D echoplanar sequence (repetition time, 1500 ms; echo time, 30 ms; flip angle, 76; FOV, 220 mm; 64 × 64 matrix; 4.5-mm-thick slices). The first three volumes, which were collected before the magnetic field reached a steady state, were discarded.
Neuroimaging analyses
Preprocessing.
Preprocessing was implemented using SPM12 (version 6470), and for both the univariate and multivariate analyses consisted of slice time correction to the middle slice, motion correction, and coregistration. While the multivariate pattern analyses (MVPA) were based on the unsmoothed images in each participant's native space, the functional images were additionally warped to MNI space (using the deformation fields derived from the anatomical segmentation), and smoothed with a 6 mm FWHM Gaussian kernel for univariate analyses and for group-level MVPA. Time-series were filtered using a 128 s high-pass filter.
Univariate analyses.
We modeled each event with its precise duration (stimulus onset to response and simultaneous stimulus offset), an approach that is known to be more sensitive to events with variable durations than constant epoch or variable amplitude impulse models (Grinband et al., 2008). In addition, as mismodeling of the HRF can bias estimates of HRF amplitude, we modeled the HRF with a double-gamma HRF function and included both the temporal and dispersion derivatives in the first-level design matrices. We combined this information using a low-dimensional parameterization, which allows separately estimating the amplitude, time-to-peak, and width of the hemodynamic response for each voxel, condition, and subject (Wager et al., 2005). We did not find differences in the time-to-peak or width parameters between conditions, and thus report only analyses related to the amplitude of the HRF. To minimize effects associated with differences in behavioral strategy, univariate statistical analyses were limited to correct trials (defined as being in concordance with the current decision bound). To control the familywise error rate at the group level, we estimated the null distribution by randomly flipping the signs associated with the subject-level contrast maps 10,000 times (Eklund et al., 2014, 2016) using the BROCCOLI software package. For the univariate analyses, we used a cluster-based threshold (initial cluster-forming threshold: p < 0.001, q < 0.05). For the MVPA, the familywise error rate was corrected at the voxel level (minimum threshold: p < 0.01).
Multivariate analyses.
We first used the least-squares separate procedure (Mumford et al., 2012) to obtain individual trial β- and t-statistic images. Unlike the univariate analyses, we did not exclude incorrect trials, and we included an equal number of trials for each distortion level within each rule. We mitigated effects associated with reaction times through a two step procedure (Todd et al., 2013). We first modeled each event with a duration equal to the reaction time before convolution with the HRF, which has the effect of minimizing effects of systematic mismodeling, and thus mitigating confounds associated with reaction times in MVPA. We then used regression to remove the effect of reaction time from the least-squares separate statistical maps before analysis. We additionally repeated the analysis illustrated in Figure 6E after removing the minimum number of trials, such that the mean reaction time was either equal between rules for each distortion level or switched direction from the original results; this yielded the same qualitative pattern of results and confirmed that the effects were not driven by differences in reaction time.
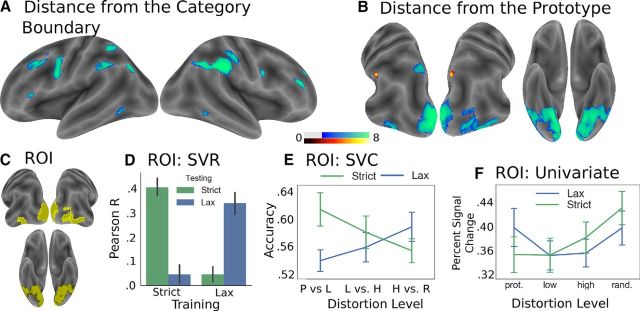
Figure 6.
MVPA. A, Regions representing distance from the category boundary (familywise error rate corrected at the voxel level, p < 0.001). B, Regions representing distance from the prototype (familywise error rate corrected at the voxel level, p < 0.01). Warm colors represent ROIs that were significant under only the strict rule. Cool colors represent voxels that were significant under both rules. C, The occipitotemporal ROI referred to by D–F. D, Within this ROI, distortion level could be decoded significantly more accurately when the model was trained (x axis) and tested (bar color) on the same rule than when it was trained and tested on different rules. E, For each rule, classification accuracy (of neighboring stimulus distortion levels) decreased with distance from the category boundary. y axis: classification accuracy. x axis: P, Prototype; L, low distortion; H, high distortion; R, random. F, The univariate pattern of the occipitotemporal ROI. This pattern is similar to that shown in Figure 4, indicating that the multivariate analysis did not select voxels with radically different univariate response properties. Error bars indicate SEM.
To identify neighborhoods of voxels representing distance from the prototype or distance from the decision bound, we used a searchlight approach (sphere radius 10 mm) (Kriegeskorte et al., 2006), in conjunction with linear support vector regression (SVR). We implemented the searchlight using custom code based on the Nilearn python package (Abraham et al., 2014) and implemented the SVR analysis using the SciKit-Learn machine learning package for python (Pedregosa et al., 2011), setting the SVR penalty parameter, C, to 0.01 based on the results from a separate dataset. We used a fourfold cross-validated approach in which we repeatedly trained the model on 3 of the 4 runs, and tested the accuracy of the model on the held-out data (each time holding out data from a different scanner run). For group-level analyses, we Fisher z-transformed the Pearson correlation values, smoothed the resultant maps with a 6 mm FWHM Gaussian kernel, and then performed a permutation test (10,000 sign-flips of the individual subject z-statistic maps), controlling the familywise error rate at the voxel level.
We performed additional permutation tests to confirm that we could decode information from the individual ROIs (Etzel et al., 2013) and to test specific hypotheses about the nature of the representation. Although the details of the specific tests are described with the results (below), each permutation test involved using a support vector machine (with C = 0.01) in conjunction with the same fourfold, leave-one-run-out cross-validation procedure used in the searchlight analysis. We compared the predictive accuracy of the support vector machine to that of a null distribution, which was estimated by repeating the analysis 500 times, each time permuting the labels of the training (but not the test) data. We then transformed the resultant p values to z scores and performed a single-sample t test to estimate statistical significance at the group level.
Results
Behavioral results
We examined performance across the strict and lax rules, with the stimuli associated with each rule considered in relation to its respective boundary (three levels: close, middle, and far; Fig. 2A) and to stimulus distance in perceptual space independent of categorization rule (four levels: prototype, low distortion, high distortion, and random; Fig. 2B). A 2 × 3 repeated-measures ANOVA with factors of rule (strict and lax) and distance from the category boundary (close, middle, and far) indicated that subjects had a difference in accuracy between the two rules (percentage correct for the strict condition 95 ± 5%; percentage correct for the lax condition 90 ± 10%) (F(1,15) = 4.7, p = 0.05, η2 = 0.24). Accuracy increased with distance from the decision boundary (F(1.25,18.75) = 39.06, p < 0.01, η2 = 0.72). The interaction between rule and boundary distance was not significant (F(1.31,19.76) = 1.71, p = 0.21, η2 = 0.1). A 2 × 4 repeated-measures ANOVA with factors of rule condition (strict and lax) and stimulus distortion level (prototype, low, high, and random) further indicated that accuracy differed depending on stimulus distortion level (F(3,45) = 6.21, p < 0.01, η2 = 0.29).
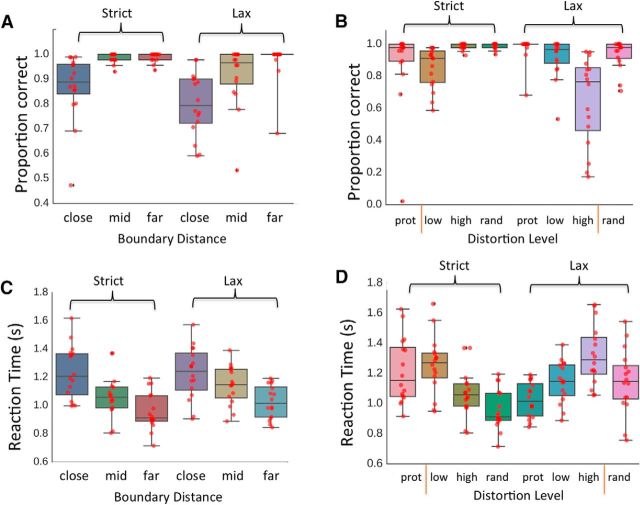
Figure 2.
Accuracy (top) and reaction time (bottom) results. A, C, Independent variable of boundary distance within the strict and lax conditions. B, D, Independent variable of stimulus distortion level within the strict and lax conditions. Vertical red bars represent the trained decision bound in each condition (as in Fig. 1A). Red dots represent individual participant means. Shaded rectangles represent middle quartiles. Interior horizontal line indicates the mean. Error bars indicate the range of the distribution within 1.5 × the interquartile range. mid, Middle boundary distance; prot, prototype; low, low distortion; high, high distortion; rand, random stimuli.
A visual inspection of Figure 2B indicates that the difference between strict and lax rule performance was likely due to high distortion stimuli in the lax condition. An examination of the individual subject means reveals large individual differences. Nine subjects maintained high levels of accuracy (≥80%), but 3 subjects performed near 50% (indicating random accuracy) and an additional 4 subjects performed at below 40% accuracy, consistently judging high distortion stimuli as out of the category rather than in the category. This pattern can be interpreted as these 4 subjects shifting to categorizing using a decision boundary that fell between the low and high distortion stimuli rather than the trained boundary between the high distortion and random stimuli; this boundary change was likely enabled by the lack of corrective feedback during the testing phase in the scanner. As we were interested in whether the boundary setting influenced the neural expression of perceptual information, we did not discard data from these participants but instead conducted post hoc analyses to investigate the effect. We did not find effects associated with these participants (or with idiosyncratic variation in behavioral performance across the group as a whole), and so do not discuss these results further, and did not exclude these participants from the analyses.
To investigate effects associated with reaction time, we conducted two repeated-measures ANOVAs. In the first, we binned trials according to their distortion level, resulting in a 2 × 4 repeated-measures ANOVA with factors of rule condition (strict and lax) and stimulus distortion level (prototype, low, high, and random). In the second, we binned trials based on distance from the active category boundary, resulting in a 2 × 3 repeated-measures ANOVA with factors of rule (strict and lax) and distance from the category boundary (close, middle, and far). To correct for violations of sphericity, we report Greenhouse-Geisser–adjusted degrees of freedom where appropriate. We conducted post hoc Tukey HSD tests where relevant. In the first ANOVA examining stimulus distortion, we found that the main effect of rule was not significant (F(1,15) = 1.89, p = 0.2, η2 = 0.11). The effect of distortion level was significant (F(2.02,30.3) = 15.1, p < 0.01, η2 = 0.5), such that reaction times were faster for the prototype (1.12 ± 0.2) and for random exemplars (1.05 ± 0.2) than for the low distortion (1.2 ± 0.18; prototype vs low distortion: t = −3.11, p(Tukey) = 0.02, low distortion vs random: t = 5.84, p(Tukey) < 0.01) and high distortion stimuli (1.19 ± 0.22; prototype vs high distortion: t = −2.87, p(Tukey) = 0.03, high distortion vs random: t = 5.6, p(Tukey) < 0.01). The interaction between rule and distortion level was also significant (F(2.08,31.25) = 27.15, p < 0.01, η2 = 0.64), such that reaction times tended to be slower for distortion levels neighboring the active category boundary.
In the second repeated-measures ANOVA, examining distance from the active category boundary, the main effect of rule was again not significant (F(1,15) = 3.93, p = 0.07, η2 = 0.21). The main effect of distance from the category boundary was significant (F(1.3,19.46) = 49.8, p < 0.01, η2 = 0.77), such that reaction times decreased with distance from the boundary (low distance: 1.23 ± 0.19; medium distance: 1.11 ± 0.15; high distance: 0.99 ± 0.13). Tukey's HSD tests indicated a significant difference between low and medium distance stimuli (t = 5.2, p(Tukey) < 0.01) and a significant difference between medium and high-distance stimuli (t = 0.98, p(Tukey) < 0.01). The interaction between rule and distance was not significant (F(1.54,23.1) = 2.3, p = 0.14, η2 = 0.13).
Neuroimaging results
Distance from decision boundary
To investigate decision processes common to both categorization rules, we investigated parametric contrasts for the effects associated with distance from the strict and lax category boundaries. Increasing distance from the categorical boundary is sometimes termed “decisional confidence” (e.g., Sanders et al., 2016; Braunlich and Seger, 2016) as it positively covaries with behavioral accuracy. It should be noted, however, that this normative estimate of decisional confidence differs from subjective estimates of confidence, which are sensitive to additional sources of bias and noise and which may involve separate representations and/or neural systems (Paul et al., 2015).
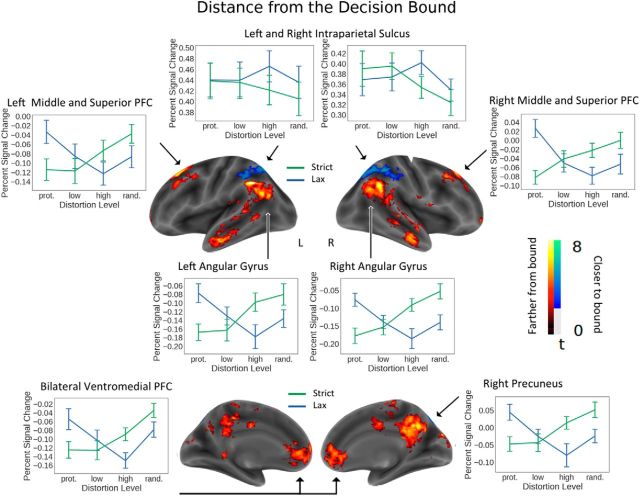
As shown in Figure 3 and Table 1, decisional confidence was associated with lateral inferior parietal activity extending from the angular gyri to the temporal-parietal junction and superior temporal gyri. Medial frontoparietal activity was found across the cuneus and posterior cingulate and the ventromedial prefrontal cortex. In addition, activity extended along the bilateral superior and middle temporal gyri, similar to that which has been reported in previous categorization studies (Zeithamova et al., 2008; Paul et al., 2015). Decisional uncertainty was associated with activity within bilateral clusters along the intraparietal sulcus immediately superior to the regions associated with decisional confidence. Counter to our predictions, we did not find that regions of the “salience” network (anterior cingulate and frontal operculum/anterior insula) covaried with conflict (e.g., Seger et al., 2015). To investigate this effect, we performed an exploratory analysis at a lower statistical threshold and found that these regions showed subthreshold patterns corresponding to our prediction.
Figure 3.
Regions sensitive to distance from the decision bound across strict and lax trials. Warm colors represent increasing distance (i.e., increasing decisional confidence). Cool colors represent decreasing distance (i.e., increasing decisional uncertainty). y axes indicate mean percentage signal change. x axes indicate distortion level. Separate lines indicate decision rule: blue represents lax; green represents strict. Error bars indicate SEM.
Table 1.
Parametric modulators: distance from the bound and distance from the prototypea
| Region | Size | x | y | z |
|---|---|---|---|---|
| Increase with distance from decision bound | ||||
| L angular gyrus | 2296 | −50 | −52 | 46 |
| L middle temporal gyrus | −60 | −10 | −20 | |
| R superior temporal gyrus | −40 | −32 | 22 | |
| R angular gyrus | 2686 | 58 | −50 | 32 |
| R middle temporal gyrus | 60 | −12 | −24 | |
| R superior temporal gyrus | 54 | −32 | 2 | |
| B cuneus | 4092 | 8 | −74 | 28 |
| B posterior cingulate | 0 | −38 | 30 | |
| B supplementary motor area | 4 | −20 | 64 | |
| L superior and middle frontal gyri | 1017 | −20 | 24 | 42 |
| B ventromedial frontal cortex | 1824 | 4 | 37 | 2 |
| R superior and middle frontal gyri | 749 | 24 | 28 | 42 |
| Decrease with distance from decision bound | ||||
| L intraparietal sulcus | 708 | −44 | −40 | 46 |
| L intraparietal sulcus, superior parietal | −18 | −68 | 54 | |
| L intraparietal sulcus, superior parietal | 1125 | 20 | −70 | 48 |
| L intraparietal sulcus, supramarginal | 32 | −40 | 42 | |
| Increase with distance from prototype | ||||
| R lingual and fusiform gyri | 442 | 26 | −62 | −6 |
| L lingual and fusiform gyri | 550 | −28 | −58 | −14 |
| Decrease with distance from prototype | ||||
| No activated clusters |
aModel-based univariate results for correct trials only. The familywise error rate for each contrast was controlled at the cluster level using a nonparametric permutation testing approach (initial cluster-forming threshold: p < 0.001, q < 0.05).
To further explore the direction of these effects, we examined the percentage signal change within each of these regions across the four levels of distortion and two rule conditions (strict and lax). To avoid circular analyses, these data were not subjected to nonorthogonal post hoc statistical tests. As can be seen in Figure 3, the intraparietal sulci (greater activity closer to the bound) exhibited an expected pattern: for the strict rule, activity was greatest for the prototype and low distortion stimuli adjacent to the strict decision bound, and lowest for the random stimuli furthest from the decision bound. In contrast, for lax stimuli, activity was greatest for the high distortion stimuli near the bound, and lower for the prototype and low distortion stimuli further from the bound. In the lax condition, activity for the random stimuli was lower than for the high distortion stimuli; this could be due to the greater variability within the random stimuli in regard to distance from the prototype. Regions identified as having activity increasing with distance from the category bound (middle and superior frontal gyri, angular gyri, ventromedial prefrontal, and precuneus) overall showed the expected pattern that was opposite to that found for the intraparietal sulcus: greater activity for the high and random stimuli when using the strict rule and greater activity for prototype stimuli when using the lax rule.
Distance from the prototype
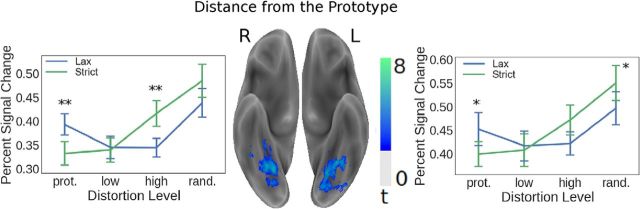
As shown in Figure 4, activity in the inferior temporal regions, including the bilateral lingual and fusiform gyri, covaried with distance from the prototype. Although these voxels were selected based on this effect, visual inspection of the plots suggested an interaction between rule and distortion level. We therefore conducted a post hoc analysis (Friston et al., 2006; Kriegeskorte et al., 2009), which was orthogonal to the contrast used for voxel selection. A repeated-measures ANOVA indicated that the interaction was significant for both the left (F(3,45) = 9.48, p < 0.01, η2 = 0.39) and right (F(3,45) = 11.76, p < 0.01, η2 = 0.44) fusiform gyri, suggesting that the visual characteristics of the stimuli were processed differently between categorization rules. Post hoc t tests (FDR corrected p values) (Benjamini and Hochberg, 1995) indicated that, for the left fusiform, the amplitude of the response significantly differed between rules for the prototype (t(15) = 2.97, p = 0.01, d = 0.74, CI = [0.02, 0.09]), and for the random exemplars (t(15) = −2.97, p = 0.02, d = −0.74, CI = [−0.09, −0.02]), but did not differ for the low distortion exemplars (t(15) = 0.47, p = 0.65) or for the high distortion exemplars (t(15) = −1.92, p = 0.1). For the right fusiform, the amplitude significantly differed between rules for the prototype (t(15) = 3.38, p < 0.01, d = 0.84, CI = [0.02, 0.1]), and for the high distortion exemplars (t(15) = −3.42, p < 0.01, d = −0.85, CI = [−0.12, −0.03]), but not for the random exemplars (t(15) = −2.26, p = 0.05) or the low distortion exemplars (t(15) = 0.3, p = 0.77).
Figure 4.
Distance from the prototype. Activity within bilateral inferior temporal lobe regions neighboring the mid-fusiform sulci positively covaried with distance from the prototype. Although the ROIs were selected based on their sensitivity to stimulus distortion, a post hoc analysis indicated a significant interaction between distortion level and rule. Significant pairwise t tests: **p < 0.01 (FDR-corrected); *p < 0.05. Error bars indicate SEM.
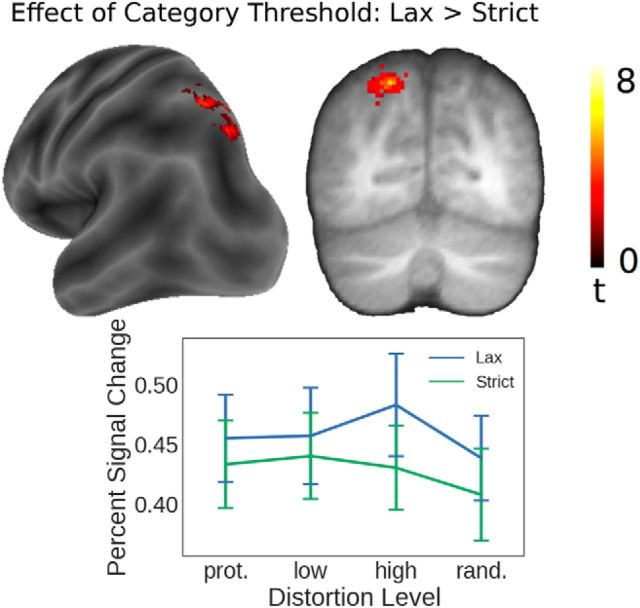
Strict versus lax
To compare differences between the rules, we compared all correct lax trials with all correct strict trials (regardless of their distances from the category boundary or from the prototype). We found that a region in superior bank of the posterior intraparietal sulcus (Fig. 5; spatial extent 305 voxels, coordinates of voxel with maximal t value: x = −18, y = −70, z = 52) showed greater activity when subjects categorized according to the lax categorization rule than according to the strict categorization rule. No regions showed greater activity for the strict rule than for the lax rule.
Figure 5.
Categorization rule. Regions of the medial bank of the left posterior intraparietal sulcus showed greater activity during categorization according to the “lax” rule than the “strict” rule. Error bars indicate SEM.
MVPA
To investigate multivariate representations associated with decisional and perceptual factors, we conducted several multivariate pattern analyses. We first used SVR, in conjunction with a searchlight approach (described above) to localize neighborhoods of voxels representing relevant information. We were able to decode information related to distance from the decision bound from several frontoparietal regions, including bilateral superior and inferior parietal regions (neighboring the intraparietal sulcus), and right middle frontal cortex (illustrated in Fig. 6A; Table 2). Representations associated with distance from the prototype (illustrated in Fig. 6B; Table 2) were primarily restricted to visual regions (bilateral lingual gyri and ventral temporal lobe extending to the calcarine sulcus and extrastriate cortex), and small bilateral regions of the superior parietal lobe/precuneus, which overlapped both with regions representing distance from the decision bound (Fig. 3) and with the contrast of lax > strict (Fig. 5). For each resultant ROI, we then performed permutation tests (as described above) to confirm that information was represented at the ROI level (rather than only at the searchlight level) (Etzel et al., 2013), and to confirm the representations were decodable within each rule. To perform the permutation tests, we trained each model using trials from both rules, but, for each cross-validation fold, tested the model separately for each rule. This allowed us to train the model using as much data as possible, but then test each rule separately. The statistical maps shown in Figure 6 and Table 2 include only ROIs that were significant for these ROI level permutation tests, and are color-coded to indicate association with rule. Finally, to investigate whether the rules might be represented differently within subregions of the occipitotemporal ROI, we conducted a searchlight analysis, in which we sought to decode distortion level separately for each rule. As we did not find notable regional differences between rules, we will not discuss this analysis further.
Table 2.
MVPA: distortion and decision boundary distancea
| Region | Size of cluster (voxels) | x | y | z | Ruleb |
|---|---|---|---|---|---|
| Distortion | |||||
| B occipital, lingual gyri, inferior temporal | 8408 | −12 | −98 | 12 | B |
| L superior parietal/precuneus | 361 | −10 | −70 | 58 | B |
| L inferior parietal | 76 | −58 | −32 | 42 | S |
| R superior parietal/precuneus | 116 | 12 | −76 | 52 | S |
| L inferior frontal gyrus | 27 | −42 | 6 | 28 | S |
| Boundary distance | |||||
| B intraparietal sulcus, lateral parietal | 5701 | 56 | −46 | 46 | B |
| 12 | −76 | 52 | |||
| −38 | −74 | 40 | |||
| L middle frontal/precentral | 786 | −50 | 8 | 38 | B |
| L lateral occipital/inferior temporal | 246 | −52 | −70 | −4 | B |
| R middle frontal | 343 | 28 | 40 | 26 | B |
| L inferior frontal | 53 | −54 | 28 | 6 | B |
| R inferior temporal | 40 | 54 | −54 | −12 | B |
| R precentral gyrus | 40 | 44 | 6 | 32 | B |
aSearchlight results using a 10 mm searchlight radius. Linear SVR was used to identify regions sensitive to stimulus distortion (familywise error rate corrected at the voxel level: p < 0.001) and distance from the decision boundary (familywise error rate corrected at the voxel level: p < 0.01) across categorization rules. The familywise error rate was controlled using a nonparametric permutation approach. For each ROI, we additionally conducted permutation tests for each rule separately to confirm the generality of the decoded representations. ROIs that were not significant for at least one rule were removed from the map. MNI coordinates (x, y, z) of cluster voxel with highest t value.
bWhether the ROI was significant for both rules (B) or the strict rule only (S); no ROIs were significant for only the lax rule.
We additionally investigated whether stimulus distortion was represented in the same way between the two rules. If occipitotemporal category representations differed between the strict and lax rules, we would predict that a support vector machine trained on one rule would have difficulty making predictions concerning the other rule. To test this hypothesis, we conducted four separate SVR analyses (C = 0.01, with fourfold, leave-one-run-out cross-validation). On each cross-validation fold, we trained the model on one rule and then tested it on held-out trials associated with either the same rule or the other rule. As illustrated in Figure 6D, this allowed us to investigate how the performance of the model varied according to how it was trained. For each analysis, we Fisher z-transformed the resultant Pearson correlation values, and then performed a paired-samples t test. When trained on the strict rule, the model performed significantly better when tested on the strict rule than the lax rule (t(15) = 5.1, p < 0.01, d = 1.27, CI = [0.21, 0.5]). When trained on the lax rule, the model performed significantly better when tested on the lax rule than on the strict rule (t(15) = 4.49, p < 0.01, d = 1.12, CI = [0.16, 0.43]). The models also only performed significantly above chance when trained and tested on the same rule (trained and tested on the strict rule: t(15) = 10.13, p < 0.01, d = 2.53, CI = [0.32, 0.49]; trained and tested on the lax rule: t(15) = 7.74, p < 0.01, d = 1.94, CI = [0.25, 0.44]) than when trained and tested on different rules (trained on the strict rule and tested on the lax rule: t(15) = 1.15, p = 0.27; trained on the lax rule and tested on the strict rule: t(15) = 1.47, p = 0.16). These findings suggest that stimulus distortion was represented differently between the two rules.
To investigate whether this effect was driven by distance from the active category boundary, or existed across all levels of stimulus distortion, we sought to distinguish neighboring distortion levels for each rule separately (Fig. 6E). To do so, we used a linear support vector classifier (C = 0.01) in conjunction with a fourfold, leave-one-run-out, cross-validation procedure. First, for each pairwise test (prototype vs low distortion exemplars, low distortion exemplars vs high distortion exemplars, and high distortion exemplars vs random stimuli), we performed a permutation test (as described in Materials and Methods) to determine whether each model could successfully classify neighboring distortion levels. We found that we were able to differentiate between neighboring distortion levels for both the strict (prototype vs low distortion: t(15) = 5.75, p < 0.01, d = 1.44, CI(z statistic) = [1.11, 2.41]; low distortion vs high distortion: t(15) = 3.84, p < 0.01, d = 0.96, CI(z statistic) = [0.58, 2.02]; high distortion vs random exemplars: t(15) = 3.82, p < 0.01, d = 0.95, CI(z statistic) = [0.42, 1.47]) and for the lax rule (prototype vs low distortion: t(15) = 3.12, p < 0.01, d = 0.83, CI(z statistic) = [0.28, 1.28], low distortion vs high distortion: t(15) = 3.41, p < 0.01, d = 0.85, CI(z statistic) = [0.4, 1.75], high distortion vs random exemplars: t(15) = 4.86, p < 0.01, d = 1.22, CI(z statistic) = [0.86, 2.21]). To determine whether the classification accuracy of neighboring distortion levels interacted with generalization rule, we conducted a repeated-measures ANOVA with rule, distortion level, and the interaction between rule and distortion level as factors. We found that the interaction between rule and distortion level was significant (F(2,30) = 4.95, p = 0.01, η2 = 0.25), but the main effects of rule (F(1,15) = 1.59, p = 0.23, η2 = 0.1) and distortion level (F(2,30) = 0.06, p = 0.94) were not. These findings indicate that the discriminability of stimulus distortion negatively covaried with distance from the active category boundary.
Discussion
We investigated how perceptual representations interacted with top-down factors in a task requiring switches between “strict” and “lax” generalization thresholds. When categorizing according to the strict rule, participants had to notice fine-grained differences between low distortion exemplars and the category prototype; and when categorizing according to the lax rule, they had to generalize knowledge to atypical category members. Behavioral differences between rules were minimized through pilot experiments on separate participants, and equivalent stimulus distributions were used for each task.
Activity within primary and higher-order visual cortices covaried with increasing stimulus distortion, whereas activity within frontoparietal and dorsal attention networks covaried with decisional demands (distance from the active category boundary). This pattern can be broadly interpreted as reflecting neural separation of functionally independent processes, with higher-order visual cortex transforming stimulus attributes into an abstract representation of stimulus typicality (i.e., distance from the category prototype), and frontoparietal and dorsal attention networks applying this visual information flexibly, according to current task goals (Gold and Shadlen, 2007; Jiang et al., 2007; Li et al., 2009; McKee et al., 2014). However, regions that were most sensitive to stimulus distortion (occipitotemporal cortex) were also sensitive to differences between the categorization rules (Figs. 5, 6D, 6E), and regions that were strongly sensitive to decisional factors (precuneus and superior parietal) were also sensitive to stimulus distortion (Fig. 6B). Interestingly, the slope of the line relating distance from the prototype to univariate amplitude was steeper under the strict rule than the lax rule (Figs. 4, 6F); activity for the prototype was lower under the strict rule than the lax rule, and activity for the highly distorted and random exemplars was greater under the lax rule than the strict rule. This suggests that distance from the active category boundary influenced perceptual processing. The MVPA results support this interpretation, as representations of stimulus distortion differed between rules (Fig. 6D), and the discriminability of this information negatively covaried with distance from the active category boundary; this means that perceptual attributes of stimuli near the active category boundary were more easily differentiated than attributes belonging to stimuli far from the boundary (Fig. 6E).
Contemporary accounts of occipitotemporal function tend to emphasize its important role in the transformation of high-dimensional perceptual information into a lower-dimensional abstract space, where representations are robust to various sources of perceptual variance (e.g., partial occlusion and changes in position and size) and where decision-relevant information can be easily integrated by downstream neurons. For instance, feedforward neural networks (Riesenhuber and Poggio, 1999; Khaligh-Razavi and Kriegeskorte, 2014; Yamins et al., 2014; Güçlü and van Gerven, 2015) support this kind of abstraction via a hierarchical architecture where receptive field sizes increase across successive layers. Within this framework, switches between strict and lax generalization thresholds can be implemented in abstract space by adjusting the threshold of an output unit tuned to the category prototype, and perceptual representations within lower hierarchical layers could thus remain largely insensitive to transient generalization demands.
In biological visual systems, feedback projections from higher-order brain regions play an important role in optimizing sensory computations during transient decisional context (Reynolds and Chelazzi, 2004; Gilbert and Li, 2013; Lehky and Tanaka, 2016). Attention, for instance, is known to improve neural sensitivity to attended stimuli in extrastriate and inferior temporal cortices (Moran and Desimone, 1985; Reynolds et al., 2000; Zhang et al., 2011), and inferior temporal representations in both primate (Sigala and Logothetis, 2002; Freedman et al., 2003; Meyers et al., 2008) and human (Li et al., 2007) similarly covary with their behavioral significance. With regards to the current experiment, one possibility is that top-down signals may have supported a mnemonic representation of the prototype, against which incoming sensory information could be compared (Summerfield et al., 2006; Sugase-Miyamoto et al., 2008; Myers et al., 2015). Within the predictive coding framework (Rao and Ballard, 1999; Friston, 2005; Rao, 2005), similar signals represent contextually sensitive predictions for activity within lower hierarchical levels and only unpredicted information is propagated to higher-order brain regions. This reduces the transfer of redundant information and provides an important learning signal to higher-order regions. Additionally, as the univariate signal can be conceptualized as reflecting the difference between the expected (statistically, the category centroid/prototype was the most-likely percept) and the observed stimuli (Murray et al., 2002; Summerfield et al., 2008; Auksztulewicz and Friston, 2016), the predictive coding framework provides a compelling account for the typicality-driven effect illustrated in Figures 4 and 6F (Vuilleumier et al., 2002; Chouinard et al., 2008).
Although top-down anticipatory signals can support the transformation of high-dimensional sensory information into a lower-dimensional space, where decision-relevant information can be easily integrated by downstream neurons (Sugase-Miyamoto et al., 2008; Myers et al., 2015), they do not easily account for the observed differences between rules. As differences in psychological representation can alter neural similarity gradients (Davis and Poldrack, 2014), and as the strict rule required participants to notice fine-grained perceptual details, but the lax rule did not, one possibility is that the prototype may have been represented with greater mnemonic precision (Ma et al., 2014) under the strict rule. This would predict that occipitotemporal representations should be more sensitive to stimulus distortion under the strict rule than the lax rule. Although we did find that the slope of the line relating distance from the prototype to univariate amplitude was steeper under the strict rule (Figs. 4, 6F), this hypothesis provides an incomplete account of our results, as distortion level could be decoded from each rule separately (Fig. 6D), and the discriminability of this information increased as distance from the active category boundary decreased (Fig. 6E).
As the stimuli used in the current study were selected from spheres surrounding the category prototype, it was impossible to perform the task by learning simple linear or unidimensional category boundaries in perceptual space. Instead, participants were required to compare incoming sensory information with a mnemonic representation of the prototype, and to place category boundaries within this abstract similarity space. As the discriminability of stimulus distortion negatively covaried with distance from the active category boundary, our findings imply that perceptual processes were influenced by decisional uncertainty. Our findings are therefore consistent with theories wherein low level sensory processes first convey coarse resolution information and fine-grained perceptual processes are then guided by top-down attentional signals (e.g., Hochstein and Ahissar, 2002). They are also consistent with Bayesian frameworks wherein perceptual processing can be described as a series of mutually informative interactions between top-down and bottom-up signals (Lee and Mumford, 2003; Friston, 2005), and with experimental results indicating that the time course of neural representation often proceeds from coarse-to-fine resolution (Sugase et al., 1999; Hegdé, 2008; Goffaux et al., 2011). Although trial-wise effects reflecting ad hoc decisional factors may be present in many neuroimaging results, it should be noted that not all category structures influence perceptual representation (Folstein et al., 2012); and we encourage the reader to be cautious when interpreting the results of any single fMRI study, particularly when sample size is small.
Although previous studies of A/notA categorization focused on low level occipital regions (Reber et al., 1998; Aizenstein et al., 2000) (e.g., V1 and V2), we identified univariate signals related to distance from the prototype in the bilateral fusiform. Our approach, however, differed in several ways: we used polygonal stimuli rather than dot patterns, primarily parametric analyses (tracking distance from the prototype, and distance from the category boundary) rather than analyses based on pairwise contrasts between conditions, supervised training via trial and error rather than observation (unsupervised learning), and used a longer training period. Because discriminability of relevant stimulus dimensions may emerge with category training (Folstein et al., 2013), this last factor may have been particularly important.
In conclusion, category learning allows us to make sense of the external world by assigning common meaning to perceptually distinct stimuli. Frontoparietal regions represent abstract category signals more strongly, but representations within sensory cortices are also modulated by these factors (Freedman et al., 2003; Meyers et al., 2008). Neural representations of perceptual dimensions that predict category membership are often more discriminable than dimensions that do not (Sigala and Logothetis, 2002; Li et al., 2007; De Baene et al., 2008; Folstein et al., 2013). Similarly, category training selectively facilitates perceptual discrimination of behaviorally relevant dimensions (Goldstone, 1994; Op de Beeck et al., 2003; Gureckis and Goldstone, 2008; Folstein et al., 2012), particularly for perceptual values neighboring active category boundaries (Goldstone et al., 1996). Thus, categorization is often described as “stretching” perceptual space to accentuate differences between categories while “compressing” perceptual space to minimize differences within categories.
Instead of investigating how occipitotemporal representations were modulated by differences in category structure, we investigated how they were modulated by differences in generalization strategy. We found that representations of equivalent stimuli differed between “strict” and “lax” generalization rules, and that the discriminability of stimulus distortion negatively covaried with distance from the active category boundary. Thus, occipitotemporal representations were sensitive not only to learned category structure, but were flexibly modulated via interactions with abstract decisional factors. This implies that decisional uncertainty can “stretch” occipitotemporal representations to improve classification of stimuli neighboring abstract category boundaries.
Footnotes
This work was supported by South China Normal University, the Chang Jiang Scholars Program of the Ministry of Education, the State Administration of Foreign Experts Affairs, Key Institute of Humanities and Social Sciences, Ministry of Education 16JJD880025, and the National Natural Science Foundation of China 31371050. We thank Professor Lei Mo for helpful advice; Alex Forseth, Sam Carr, and Lauren Hartsough for contributions to task development and piloting; and Wenliang Lu, Peiwen Xiang, and Quiying Liu for collecting fMRI data.
The authors declare no competing financial interests.
References
- Abraham A, Pedregosa F, Eickenberg M, Gervais P, Mueller A, Kossaifi J, Varoquaux G (2014) Machine learning for neuroimaging with Scikit-Learn. Front Neuroinform 8:1–15. 10.3389/fninf.2014.00014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aizenstein HJ, MacDonald AW, Stenger VA, Nebes RD, Larson JK, Ursu S, Carter CS (2000) Complementary category learning systems identified using event-related functional MRI. J Cogn Neurosci 12:977–987. 10.1162/08989290051137512 [DOI] [PubMed] [Google Scholar]
- Ashby FG, O'Brien JB (2005) Category learning and multiple memory systems. Trends Cogn Sci 9:83–89. 10.1016/j.tics.2004.12.003 [DOI] [PubMed] [Google Scholar]
- Auksztulewicz R, Friston K (2016) Repetition suppression and its contextual determinants in predictive coding. Cortex 80:125–140. 10.1016/j.cortex.2015.11.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc B 57:289–300. [Google Scholar]
- Bozoki A, Grossman M, Smith EE (2006) Can patients with Alzheimer's disease learn a category implicitly? Neuropsychologia 44:816–827. 10.1016/j.neuropsychologia.2005.08.001 [DOI] [PubMed] [Google Scholar]
- Braunlich K, Seger CA (2016) Categorical evidence, confidence, and urgency during probabilistic categorization. Neuroimage 125:941–952. 10.1016/j.neuroimage.2015.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casale MB, Ashby FG (2008) A role for the perceptual representation memory system in category learning. Percept Psychophys 70:983–999. 10.3758/PP.70.6.983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chouinard PA, Morrissey BF, Köhler S, Goodale MA (2008) Repetition suppression in occipital-temporal visual areas is modulated by physical rather than semantic features of objects. Neuroimage 41:130–144. 10.1016/j.neuroimage.2008.02.011 [DOI] [PubMed] [Google Scholar]
- Chumbley JR, Flandin G, Bach DR, Daunizeau J, Fehr E, Dolan RJ, Friston KJ (2012) Learning and generalization under ambiguity: an fMRI study. PLoS Comput Biol 8:e1002346. 10.1371/journal.pcbi.1002346 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins AG, Frank MJ (2013) Cognitive control over learning: creating, clustering, and generalizing task-set structure. Psychol Rev 120:190–229. 10.1037/a0030852 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis T, Poldrack RA (2014) Quantifying the internal structure of categories using a neural typicality measure. Cereb Cortex 24:1720–1737. 10.1093/cercor/bht014 [DOI] [PubMed] [Google Scholar]
- Davis T, Love BC, Preston AR (2012) Striatal and hippocampal entropy and recognition signals in category learning: simultaneous processes revealed by model-based fMRI. J Exp Psychol Learn Mem Cogn 38:821–839. 10.1037/a0027865 [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Baene W, Ons B, Wagemans J, Vogels R (2008) Effects of category learning on the stimulus selectivity of macaque inferior temporal neurons. Learn Mem 15:717–727. 10.1101/lm.1040508 [DOI] [PubMed] [Google Scholar]
- Eklund A, Dufort P, Villani M, Laconte S (2014) BROCCOLI: Software for fast fMRI analysis on many-core CPUs and GPUs. Front Neuroinform 8:24. 10.3389/fninf.2014.00024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eklund A, Nichols TE, Knutsson H (2016) Cluster failure: why fMRI inferences for spatial extent have inflated false-positive rates. Proc Natl Acad Sci U S A 113:7900–7905. 10.1073/pnas.1602413113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Etzel JA, Zacks JM, Braver TS (2013) Searchlight analysis: promise, pitfalls, and potential. Neuroimage 78C:261–269. 10.1016/j.neuroimage.2013.03.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Folstein JR, Gauthier I, Palmeri TJ (2012) How category learning affects object representations: not all morphspaces stretch alike. J Exp Psychol Learn Mem Cogn 38:807–820. 10.1037/a0025836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Folstein JR, Palmeri TJ, Gauthier I (2013) Category learning increases discriminability of relevant object dimensions in visual cortex. Cereb Cortex 23:814–823. 10.1093/cercor/bhs067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman DJ, Riesenhuber M, Poggio T, Miller EK (2003) A comparison of primate prefrontal and inferior temporal cortices during visual categorization. J Neurosci 23:5235–5246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ. (2005) A theory of cortical responses. Philos Trans R Soc B 360:815–836. 10.1098/rstb.2005.1622 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Rotshtein P, Geng JJ, Sterzer P, Henson RN (2006) A critique of functional localisers. Neuroimage 30:1077–1087. 10.1016/j.neuroimage.2005.08.012 [DOI] [PubMed] [Google Scholar]
- Gilbert CD, Li W (2013) Top-down influences on visual processing. Nat Rev Neurosci 14:350–363. 10.1038/nrn3476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glass BD, Chotibut T, Pacheco J, Schnyer DM, Maddox WT (2012) Normal aging and the dissociable prototype learning systems. Psychol Aging 27:120–128. 10.1037/a0024971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goffaux V, Peters J, Haubrechts J, Schiltz C, Jansma B, Goebel R (2011) From coarse to fine? Spatial and temporal dynamics of cortical face processing. Cereb Cortex 21:467–476. 10.1093/cercor/bhq112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN (2007) The neural basis of decision making. Annu Rev Neurosci 30:535–574. 10.1146/annurev.neuro.29.051605.113038 [DOI] [PubMed] [Google Scholar]
- Goldstone R. (1994) Influences of categorization on perceptual discrimination. J Exp Psychol Gen 123:178–200. 10.1037/0096-3445.123.2.178 [DOI] [PubMed] [Google Scholar]
- Goldstone RL, Steyvers M, Larimer K (1996) Categorical perception of novel dimensions. In: Proceedings of the eighteenth annual conference of the Cognitive Science Society, pp 243–248. [Google Scholar]
- Grinband J, Hirsch J, Ferrera VP (2006) A neural representation of categorization uncertainty in the human brain. Neuron 49:757–763. 10.1016/j.neuron.2006.01.032 [DOI] [PubMed] [Google Scholar]
- Grinband J, Wager TD, Lindquist M, Ferrera VP, Hirsch J (2008) Detection of time-varying signals in event-related fMRI designs. Neuroimage 43:509–520. 10.1016/j.neuroimage.2008.07.065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Güçlü U, van Gerven MA (2015) Deep neural networks reveal a gradient in the complexity of neural representations across the ventral stream. J Neurosci 35:10005–10014. 10.1523/JNEUROSCI.5023-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gureckis TM, Goldstone RL (2008) The effect of the internal structure of categories on perception. Proceedings of the 30th Annual Conference of the Cognitive Science Society, pp 1876–1881. [Google Scholar]
- Hegdé J. (2008) Time course of visual perception: coarse-to-fine processing and beyond. Prog Neurobiol 84:405–439. 10.1016/j.pneurobio.2007.09.001 [DOI] [PubMed] [Google Scholar]
- Henson RN. (2003) Neuroimaging studies of priming. Prog Neurobiol 70:53–81. 10.1016/S0301-0082(03)00086-8 [DOI] [PubMed] [Google Scholar]
- Hochstein S, Ahissar M (2002) View from the top: hierarchies and reverse hierarchies in the visual system. Neuron 36:791–804. 10.1016/S0896-6273(02)01091-7 [DOI] [PubMed] [Google Scholar]
- Homa D, Sterling S, Trepel L (1981) Limitations of exemplar-based generalization and the abstraction of categorical information. J Exp Psychol Hum Learn Mem 7:418–439. 10.1037/0278-7393.7.6.418 [DOI] [PubMed] [Google Scholar]
- Jiang X, Bradley E, Rini RA, Zeffiro T, VanMeter J, Riesenhuber M (2007) Categorization training results in shape- and category-selective human neural plasticity. Neuron 53:891–903. 10.1016/j.neuron.2007.02.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kayser AS, Buchsbaum BR, Erickson DT, D'Esposito M (2010) The functional anatomy of a perceptual decision in the human brain. J Neurophysiol 103:1179–1194. 10.1152/jn.00364.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khaligh-Razavi SM, Kriegeskorte N (2014) Deep supervised, but not unsupervised, models may explain IT cortical representation. PLoS Comput Biol 10:e1003915. 10.1371/journal.pcbi.1003915 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knowlton BJ, Squire LR (1993) The learning of categories: parallel brain systems for item memory and category knowledge. Science 262:1747–1749. 10.1126/science.8259522 [DOI] [PubMed] [Google Scholar]
- Koutstaal W, Wagner AD, Rotte M, Maril A, Buckner RL, Schacter DL (2001) Perceptual specificity in visual object priming: functional magnetic resonance imaging evidence for a laterality difference in fusiform cortex. Neuropsychologia 39:184–199. 10.1016/S0028-3932(00)00087-7 [DOI] [PubMed] [Google Scholar]
- Kriegeskorte N, Goebel R, Bandettini P (2006) Information-based functional brain mapping. Proc Natl Acad Sci U S A 103:3863–3868. 10.1073/pnas.0600244103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Simmons WK, Bellgowan PS, Baker CI (2009) Circular analysis in systems neuroscience: the dangers of double dipping. Nat Neurosci 12:535–540. 10.1038/nn.2303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee TS, Mumford D (2003) Hierarchical Bayesian inference in the visual cortex. J Opt Soc Am A Opt Image Sci Vis 20:1434–1448. 10.1364/JOSAA.20.001434 [DOI] [PubMed] [Google Scholar]
- Lehky SR, Tanaka K (2016) Neural representation for object recognition in inferotemporal cortex. Curr Opin Neurobiol 37:23–35. 10.1016/j.conb.2015.12.001 [DOI] [PubMed] [Google Scholar]
- Li S, Ostwald D, Giese M, Kourtzi Z (2007) Flexible coding for categorical decisions in the human brain. J Neurosci 27:12321–12330. 10.1523/JNEUROSCI.3795-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S, Mayhew SD, Kourtzi Z (2009) Learning shapes the representation of behavioral choice in the human brain. Neuron 62:441–452. 10.1016/j.neuron.2009.03.016 [DOI] [PubMed] [Google Scholar]
- Ma WJ, Husain M, Bays PM (2014) Changing concepts of working memory. Nat Neurosci 17:347–356. 10.1038/nn.3655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKee JL, Riesenhuber M, Miller EK, Freedman DJ (2014) Task dependence of visual and category representations in prefrontal and inferior temporal cortices. J Neurosci 34:16065–16075. 10.1523/JNEUROSCI.1660-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyers EM, Freedman DJ, Kreiman G, Miller EK, Poggio T (2008) Dynamic population coding of category information in inferior temporal and prefrontal cortex. J Neurophysiol 100:1407–1419. 10.1152/jn.90248.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran J, Desimone R (1985) Selective attention gates visual processing in the extrastriate cortex. Science 229:782–784. 10.1126/science.4023713 [DOI] [PubMed] [Google Scholar]
- Mumford JA, Turner BO, Ashby FG, Poldrack RA (2012) Deconvolving BOLD activation in event-related designs for multivoxel pattern classification analyses. Neuroimage 59:2636–2643. 10.1016/j.neuroimage.2011.08.076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray SO, Kersten D, Olshausen BA, Schrater P, Woods DL (2002) Shape perception reduces activity in human primary visual cortex. Proc Natl Acad Sci U S A 99:15164–15169. 10.1073/pnas.192579399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers NE, Rohenkohl G, Wyart V, Woolrich MW, Nobre AC, Stokes MG (2015) Testing sensory evidence against mnemonic templates. eLife 4:1–25. 10.7554/eLife.09000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman KA, O'Reilly RC (2003) Modeling hippocampal and neocortical contributions to recognition memory: a complementary-learning-systems approach. Psychol Rev 110:611–646. 10.1037/0033-295X.110.4.611 [DOI] [PubMed] [Google Scholar]
- Nosofsky RM, Little DR, James TW (2012) Activation in the neural network responsible for categorization and recognition reflects parameter changes. Proc Natl Acad Sci U S A 109:333–338. 10.1073/pnas.1111304109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Op de Beeck H, Wagemans J, Vogels R (2003) The effect of category learning on the representation of shape: dimensions can be biased but not differentiated. J Exp Psychol Gen 132:491–511. 10.1037/0096-3445.132.4.491 [DOI] [PubMed] [Google Scholar]
- Paul EJ, Smith JD, Valentin VV, Turner BO, Barbey AK, Ashby FG (2015) Neural networks underlying the metacognitive uncertainty response. Cortex 71:306–322. 10.1016/j.cortex.2015.07.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Vanderplas J (2011) Scikit-learn: machine learning in Python. J Machine Learn Res 12:2825–2830. [Google Scholar]
- Posner MI, Goldsmith R, Welton KE Jr (1967) Perceived distance and the classification of distorted patterns. J Exp Psychol 73:28–38. 10.1037/h0024135 [DOI] [PubMed] [Google Scholar]
- Posner MI, Keele SW (1968) On the genesis of abstract ideas. J Exp Psychol 77:353–363. 10.1037/h0025953 [DOI] [PubMed] [Google Scholar]
- Rao RP. (2005) Bayesian inference and attentional modulation in the visual cortex. Neuroreport 16:1843–1848. 10.1097/01.wnr.0000183900.92901.fc [DOI] [PubMed] [Google Scholar]
- Rao RP, Ballard DH (1999) Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat Neurosci 2:79–87. 10.1038/4580 [DOI] [PubMed] [Google Scholar]
- Reber PJ, Squire LR (1999) Intact learning of artificial grammars and intact category learning by patients with Parkinson's disease. Behav Neurosci 113:235–242. 10.1037/0735-7044.113.2.235 [DOI] [PubMed] [Google Scholar]
- Reber PJ, Stark CE, Squire LR (1998) Contrasting cortical activity associated with category memory and recognition memory. Learn Mem 5:420–428. [PMC free article] [PubMed] [Google Scholar]
- Reber PJ, Gitelman DR, Parrish TB, Mesulam MM (2003) Dissociating explicit and implicit category knowledge with fMRI. J Cogn Neurosci 15:574–583. 10.1162/089892903321662958 [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Chelazzi L (2004) Attentional modulation of visual processing. Annu Rev Neurosci 27:611–647. 10.1146/annurev.neuro.26.041002.131039 [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Pasternak T, Desimone R (2000) Attention increases sensitivity of V4 neurons. Neuron 26:703–714. 10.1016/S0896-6273(00)81206-4 [DOI] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T (1999) Hierarchical models of object recognition in cortex. Nat Neurosci 2:1019–1025. 10.1038/14819 [DOI] [PubMed] [Google Scholar]
- Roy JE, Riesenhuber M, Poggio T, Miller EK (2010) Prefrontal cortex activity during flexible categorization. J Neurosci 30:8519–8528. 10.1523/JNEUROSCI.4837-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders JI, Hangya B, Kepecs A (2016) Signatures of a statistical computation in the human sense of confidence. Neuron 90:499–506. 10.1016/j.neuron.2016.03.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schacter D. (1990) Perceptual representation systems and implicit memory systems. Ann N Y Acad Sci 608:543–571. 10.1111/j.1749-6632.1990.tb48909.x [DOI] [PubMed] [Google Scholar]
- Seger CA, Miller EK (2010) Category learning in the brain. Annu Rev Neurosci 33:203–219. 10.1146/annurev.neuro.051508.135546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seger CA, Poldrack RA, Prabhakaran V, Zhao M, Glover GH, Gabrieli JD (2000) Hemispheric asymmetries and individual differences in visual concept learning as measured by functional MRI. Neuropsychologia 38:1316–1324. 10.1016/S0028-3932(00)00014-2 [DOI] [PubMed] [Google Scholar]
- Seger CA, Dennison CS, Lopez-Paniagua D, Peterson EJ, Roark AA (2011) Dissociating hippocampal and basal ganglia contributions to category learning using stimulus novelty and subjective judgments. Neuroimage 55:1739–1753. 10.1016/j.neuroimage.2011.01.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seger CA, Braunlich K, Wehe HS, Liu Z (2015) Generalization in category learning: the roles of representational and decisional uncertainty. J Neurosci 35:8802–8812. 10.1523/JNEUROSCI.0654-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigala N, Logothetis NK (2002) Visual categorization shapes feature selectivity in the primate temporal cortex. Nature 415:318–320. 10.1038/415318a [DOI] [PubMed] [Google Scholar]
- Smith JD, Minda JP (2001) Journey to the center of the category: the dissociation in amnesia between categorization and recognition. J Exp Psychol Learn Mem Cogn 27:984–1002. 10.1037/0278-7393.27.4.984 [DOI] [PubMed] [Google Scholar]
- Smith JD, Redford JS, Gent LC, Washburn DA (2005) Visual search and the collapse of categorization. J Exp Psychol Gen 134:443–460. 10.1037/0096-3445.134.4.443 [DOI] [PubMed] [Google Scholar]
- Strange BA, Duggins A, Penny W, Dolan RJ, Friston KJ (2005) Information theory, novelty and hippocampal responses: unpredicted or unpredictable? Neural Netw 18:225–230. 10.1016/j.neunet.2004.12.004 [DOI] [PubMed] [Google Scholar]
- Sugase Y, Yamane S, Ueno S, Kawano K (1999) Global and fine information coded by single neurons in the temporal visual cortex. Nature 400:869–873. 10.1038/23703 [DOI] [PubMed] [Google Scholar]
- Sugase-Miyamoto Y, Liu Z, Wiener MC, Optican LM, Richmond BJ (2008) Short-term memory trace in rapidly adapting synapses of inferior temporal cortex. PLoS Comput Biol 4:e1000073. 10.1371/journal.pcbi.1000073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Summerfield C, Koechlin E (2008) A neural representation of prior information during perceptual inference. Neuron 59:336–347. 10.1016/j.neuron.2008.05.021 [DOI] [PubMed] [Google Scholar]
- Summerfield C, Egner T, Greene M, Koechlin E, Mangels J, Hirsch J (2006) Predictive codes for forthcoming perception in the frontal cortex. Science 314:1311–1314. 10.1126/science.1132028 [DOI] [PubMed] [Google Scholar]
- Summerfield C, Trittschuh EH, Monti JM, Mesulam MM, Egner T (2008) Neural repetition suppression reflects fulfilled perceptual expectations. Nat Neurosci 11:1004–1006. 10.1038/nn.2163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd MT, Nystrom LE, Cohen JD (2013) Confounds in multivariate pattern analysis: theory and rule representation case study. Neuroimage 77:157–165. 10.1016/j.neuroimage.2013.03.039 [DOI] [PubMed] [Google Scholar]
- Vuilleumier P, Henson RN, Driver J, Dolan RJ (2002) Multiple levels of visual object constancy revealed by event-related fMRI of repetition priming. Nat Neurosci 5:491–499. 10.1038/nn839 [DOI] [PubMed] [Google Scholar]
- Wager TD, Vazquez A, Hernandez L, Noll DC (2005) Accounting for nonlinear BOLD effects in fMRI: parameter estimates and a model for prediction in rapid event-related studies. Neuroimage 25:206–218. 10.1016/j.neuroimage.2004.11.008 [DOI] [PubMed] [Google Scholar]
- White CN, Mumford JA, Poldrack RA (2012) Perceptual criteria in the human brain. J Neurosci 32:16716–16724. 10.1523/JNEUROSCI.1744-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiggs CL, Martin A (1998) Properties and mechanics of perceptual priming. Curr Opin Neurobiol 8:227–233. 10.1016/S0959-4388(98)80144-X [DOI] [PubMed] [Google Scholar]
- Yamins DL, Hong H, Cadieu CF, Solomon EA, Seibert D, DiCarlo JJ (2014) Performance-optimized hierarchical models predict neural responses in higher visual cortex. Proc Natl Acad Sci U S A 111:8619–8624. 10.1073/pnas.1403112111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaki SR, Nosofsky RM, Jessup NM, Unverzagt FW (2003) Categorization and recognition performance of a memory-impaired group: evidence for single-system models. J Int Neuropsychol Soc 9:394–406. 10.1017/S1355617703930050 [DOI] [PubMed] [Google Scholar]
- Zeithamova D, Maddox WT, Schnyer DM (2008) Dissociable prototype learning systems: evidence from brain imaging and behavior. J Neurosci 28:13194–13201. 10.1523/JNEUROSCI.2915-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Meyers EM, Bichot NP, Serre T, Poggio TA, Desimone R (2011) Object decoding with attention in inferior temporal cortex. Proc Natl Acad Sci U S A 108:8850–8855. 10.1073/pnas.1100999108 [DOI] [PMC free article] [PubMed] [Google Scholar]