Mesoscale Mapping of Mouse Cortex Reveals Frequency-Dependent Cycling between Distinct Macroscale Functional Modules

Abstract

Connectivity mapping based on resting-state activity in mice has revealed functional motifs of correlated activity. However, the rules by which motifs organize into larger functional modules that lead to hemisphere wide spatial-temporal activity sequences is not clear. We explore cortical activity parcellation in head-fixed, quiet awake GCaMP6 mice from both sexes by using mesoscopic calcium imaging. Spectral decomposition of spontaneous cortical activity revealed the presence of two dominant frequency modes (<1 and ∼3 Hz), each of them associated with a unique spatial signature of cortical macro-parcellation not predicted by classical cytoarchitectonic definitions of cortical areas. Based on assessment of 0.1–1 Hz activity, we define two macro-organizing principles: the first being a rotating polymodal-association pinwheel structure around which activity flows sequentially from visual to barrel then to hindlimb somatosensory; the second principle is correlated activity symmetry planes that exist on many levels within a single domain such as intrahemispheric reflections of sensory and motor cortices. In contrast, higher frequency activity >1 Hz yielded two larger clusters of coactivated areas with an enlarged default mode network-like posterior region. We suggest that the apparent constrained structure for intra-areal cortical activity flow could be exploited in future efforts to normalize activity in diseases of the nervous system.

SIGNIFICANCE STATEMENT Increasingly, functional connectivity mapping of spontaneous activity is being used to reveal the organization of the brain. However, because the brain operates across multiple space and time domains a more detailed understanding of this organization is necessary. We used in vivo wide-field calcium imaging of the indicator GCaMP6 in head-fixed, awake mice to characterize the organization of spontaneous cortical activity at different spatiotemporal scales. Correlation analysis defines the presence of two to three superclusters of activity that span traditionally defined functional territories and were frequency dependent. This work helps define the rules for how different cortical areas interact in time and space. We provide a framework necessary for future studies that explore functional reorganization of brain circuits in disease models.

Introduction

Mapping functional connectivity in mouse cortex from resting-state activity can be performed using diverse mesoscopic imaging modalities such as wide-field calcium, voltage-sensitive dye, laser-speckle contrast, intrinsic signal, optoacoustic imaging, or fMRI, and mostly performed under anesthesia (White et al., 2011; Bero et al., 2012; Guevara et al., 2013a,b; Guilfoyle et al., 2013; Mohajerani et al., 2013; Bauer et al., 2014; Mechling et al., 2014; Nasiriavanaki et al., 2014; Vanni and Murphy, 2014; Bergonzi et al., 2015; Liska et al., 2015; Matsui et al., 2016; Xie et al., 2016). Using these approaches it is possible to reveal correlated signals spanning distant brain regions defining functional modules (White et al., 2011; Mohajerani et al., 2013; Vanni and Murphy, 2014). Moreover, these patterns of connectivity were observed over a wide range of frequency bands of cortical oscillation and animal state (Mohajerani et al., 2013; Chan et al., 2015). However, the dynamic behavior of these functional modules, as well as the spatial organization of intrinsic connections at a finer spatial scale, have been relatively underexplored. Although the general pattern of correlation does not change between major behavioral state transitions, such as awake and anesthetized states (Mohajerani et al., 2013; Silasi et al., 2016), the higher inhibitory processing observed during awake states (Haider et al., 2013) could drive modifications that affect parcellation of these functional modules over different frequencies of ongoing activity.

To visualize how the cortex is functionally organized, parcellation methods need to be applied at different spatial and temporal scales in awake mice. Because of the lack of sensitivity of previous methods (such as intrinsic imaging; White et al., 2011) and the inability of small-molecule voltage-sensitive dyes to record awake mice longitudinally, mesoscopic functional imaging approaches using genetically engineered calcium indicators represent an ideally suited imaging paradigm to address this challenge (Vanni and Murphy, 2014; Kim et al., 2016; Ma et al., 2016; Sofroniew et al., 2016; Wekselblatt et al., 2016; Zhuang et al., 2017). Recently, advances have been made in wide-field imaging with the development of highly sensitive, genetically-encoded reporters of neuronal activity expressed in transgenic mice (Chen et al., 2013; Madisen et al., 2015). In addition to having higher amplitude signals that allow for more reliability in parcellation, these new models also permit cell-type-specific expression of activity sensors and can be combined with chronic imaging window implants allowing repeated recordings from awake animals (Silasi et al., 2016).

In the present study, wide-field fluorescent imaging of spontaneous activity was performed in awake, head-fixed mice expressing GCaMP6. Spectral analysis of superficial cortical activity revealed the presence of two frequency modes: a low-frequency mode encompassing activity <1 Hz and a higher frequency mode at 3 Hz. The low-frequency mode was associated with three main functional modules corresponding to cortical territories associated with major mouse behavioral functions: (1) vision and navigation, (2) locomotion, and (3) orofacial processing. In contrast, the higher-frequency mode segregated the cortex in two modules, one lateral and one medial, and could correspond to default mode network landmarks described using fMRI in humans as well as in rodents (Lu et al., 2012). These patterns were very consistent, and the boundary regions separating clusters appear to function as polymodal hubs. Moreover, within each of these clusters, a clear topography of connections between distant regions could be characterized.

Materials and Methods

Mice

All procedures were approved by the University of British Columbia Animal Care Committee and conformed to the Canadian Council on Animal Care and Use guidelines. Transgenic GCaMP6 mice (n = 14, 8 males, 6 females) were produced by crossing Emx1-cre (B6.129S2-Emx1^tm1(cre)Krj/J, Jax #005628), CaMK2-tTA (B6.Cg-Tg(Camk2a-tTA)1Mmay/DboJ, Jax #007004), and TITL-GCaMP6s (Ai94; B6.Cg-Igs7^{tm94.1(tetO-GCaMP6s)Hze}/J, Jax #024104) strains (Madisen et al., 2015). The presence of GCaMP expression was determined by genotyping each animal before each surgical procedure with PCR amplification. This crossing is expected to produce a stable expression of GCaMP6s (Tian et al., 2009; Chen et al., 2013) specifically within all excitatory neurons across all layers of the cortex (Vanni and Murphy, 2014).

Surgical procedure

For chronic window implantation, animals were anesthetized with isoflurane (2% in pure O₂) and body temperature was maintained at 37°C using a feedback-regulated heating pad monitored by a rectal thermometer. Mice received an intramuscular injection of 40 μl of dexamethasone (2 mg/ml) and a 0.5 ml subcutaneous injection of a saline solution containing buprenorphine (2 μg/ml), atropine (3 μg/ml), and glucose (20 mm), and were placed in a stereotaxic frame. After locally anesthetizing the scalp with lidocaine (0.1 ml, 0.2%), the skin covering the skull was removed and replaced by transparent dental cement and a glass coverslip (Hira et al., 2009; Guo et al., 2014; Silasi et al., 2016). A metal screw was attached to the chamber for future head fixation during recordings. At the end of the procedure, the animal received a second subcutaneous injection of saline (0.5 ml) with 20 mm of glucose and recovered in a warmed cage in pure O₂ for 30 min. This giant window was designed to permit head-fixation of the mice and allowed recording of wide-field fluorescence in a region covering an ∼8.6 mm diameter of field of view on anesthetized animals as well as in quiet awake states or during active performance of a task. Furthermore, this imaging window implant facilitated longitudinal, repeated imaging sessions from mice extending several months. This strategy contributes to better reliability of measures as well as the monitoring of brain function or photo-activation during training or plasticity (Guo et al., 2014; Vanni and Murphy, 2014; Silasi et al., 2016).

Calcium imaging recordings

As in previous studies, in vivo single-wavelength fluorescence wide-field imaging was performed using one camera collecting green fluorescence under single-photon blue excitation light (Shibuki et al., 2003; Coutinho et al., 2004; Murakami et al., 2004, 2015; Husson et al., 2007; Bouchard et al., 2009; Andermann et al., 2011; Ackman et al., 2012; Grienberger et al., 2012; Stroh et al., 2013; Ma et al., 2014; Vanni and Murphy, 2014; Vazquez et al., 2014; Busche et al., 2015; Daniel et al., 2015; Storace et al., 2015; Matsui et al., 2016; Xie et al., 2016; Xiao et al., 2017). Although the depth of focus is large (∼1 mm; Lim et al., 2012), in blue/green wavelengths, this approach is expected to mostly record fluorescence signals from superficial cortical layers (Ma et al., 2016; Wekselblatt et al., 2016). Although we concede that deeper layers may show unique maps a recent study combining mesoscopic calcium imaging and single-unit multichannel laminar electrodes showed high similarity maps across different cortical depths (Xiao et al., 2017).

For recordings, the heads of awake mice were stabilized by attaching a skull-mounted screw to a pole mounted on a baseplate while the body was resting inside a Plexiglas tube (Fig. 1A,B). Mice were placed in a sensory-isolated enclosed imaging recording chamber that is kept dark and has been insulated with acoustic foam to further reduce ambient sounds. From our observations of behavioral imaging of the mice (under infrared illumination), once habituated, the mice do not exhibit much active behavior. Images of the cortical surface were recorded through a pair of back-to-back photographic lenses (tandem lens pair: focal length 50 mm, f = 1.4; focal length 35 mm, f = 2; optical magnification: 1.43×, working distance: 35 mm) coupled to a 1M60 Pantera CCD camera (Dalsa). Calcium indicators were excited with blue-light-emitting diodes (Luxeon, 470 nm) with bandpass filters (467–499 nm). Emission fluorescence was filtered using a 510–550 nm bandpass filter. 12 bit images were collected at 30 Hz temporal resolution (33.3 ms exposure time using XCAP imaging software. Each of the 14 mice were recorded every day, 3–18 times in total (average: 7.7 ± 1.3×) for 5 min in darkness and silence.

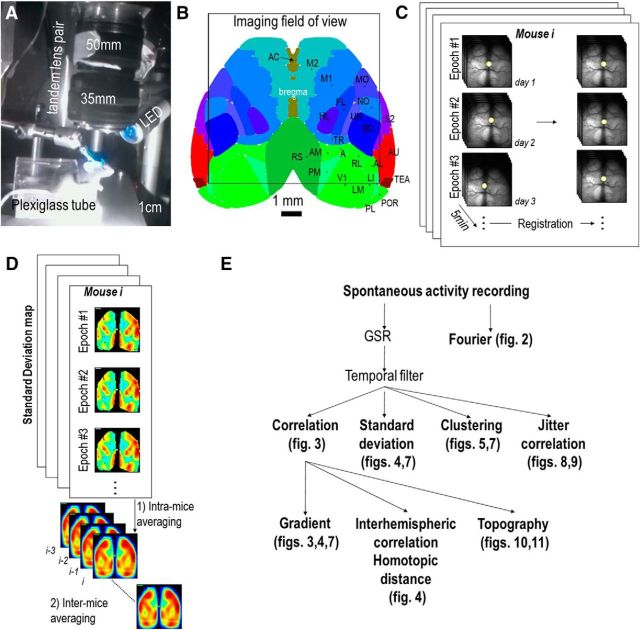
Figure 1.

General design of the experiment. A, Picture of the setup showing the mouse head-fixation system, the LED, and the tandem lens macroscope. The recording chamber was illuminated with an infrared LED that allowed simultaneous acquisition of behavioral video of the mouse in darkness and silence with a second camera. B, Allen Institute Atlas (http://brain-map.org) of the brain regions recorded through the chronic window (black square). M1 and M2, Primary and secondary motor areas, respectively; MO, mouth; NO, nose; TR, trunk; S1, primary somatosensory area; S2, supplemental or secondary somatosensory area; A, anterior or also called posterior partial association areas: PTLp or pTA; AL, anterolateral; AM, anteromedial; LM, lateralmedial; LI, lateralintermediate; PL, posterolateral; PM, posteromedial; POR, postrhinal; RL, rostrolateral regions of the extrastriate visual areas, respectively; AU, primary auditory area; AC, anterior cingulate areas; and TEA, temporal association. C, Each of the 14 mice were recorded for a total of 3–18 sessions on consecutive days for 5 min epochs and each individual sequence was registered by evaluating the spatial shift (X, Y) and rotation relative to the first recording (Materials and Methods). D, Then any the results of subsequent analysis (SD in the example) were averaged between epochs before being compared between mice. E, Each epoch was Fourier transformed or preprocessed to perform different mapping procedures: correlation mapping without or with jitter, clustering, or SD. Correlation maps were then used to create gradient, interhemispheric/homotopic, and topographic maps (Materials and Methods).

Image processing of calcium signals

Data import.

All data were imported and analyzed with MATLAB (Mathworks). When multiple epochs of recordings were performed from one mouse (Fig. 1C), each individual sequence was registered by evaluating the spatial shift (X, Y) and rotation relative to the first recording using autocorrelation (Murphy et al., 2016). Then any result of subsequent analysis (such as Fourier, correlation, SD, gradient, parcellation maps, etc.) were averaged between epochs before being averaged and compared between mice (Fig. 1D,E).

Spectral analysis.

To explore the spectral distribution of calcium signals, the Fourier transform was processed on each pixel individually (Vanni et al., 2010a,b). To better appreciate the spatial pattern at each frequency, the amplitude of power maps of each frequency was scaled from 0 to 1 (divided by the maximum amplitude). The brain activity associated with one specific frequency band was measured by averaging the power amplitude of Fourier within a frequency window. Alternatively, to calculate the optimal frequency of each pixel, the frequency associated with the peak values was determined (frequency having the highest power amplitude; Fig. 2E). These analysis were performed on the full 5 min duration of each recordings as well as individual 1 min segments to control for stability during the epoch (Fig. 2D,F).

Figure 2.

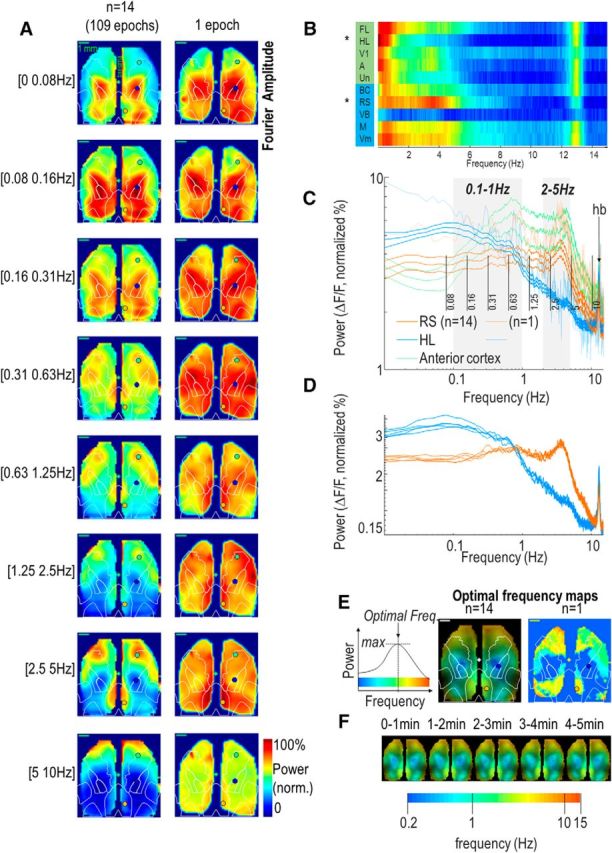
Spatial and spectral distribution of the brain activity. A, Normalized power frequency maps of spontaneous brain activity in eight different frequency bands (0–10 Hz) defined as a function of a log scale and computed from a single epoch (right) and from the averaged activity from 14 mice (left, combining 109 epochs in total). Overlaid on maps in white are positions of M1, HL, FL, BC, V1, and RS brain regions from the atlas information in Figure 1C. The blue, orange, and green points indicate the three 1 × 1 pixel ROIs quantified in C. Green plus sign denotes the position of the bregma. B, Average power spectra of brain activity from 10 different ROIs (right hemisphere: BC, FL, HL regions of the primary somatosensory area calculated from an average between the value of the Allen Institute Atlas: RS, V1, VB, A, M, Vm, Un) during a 5 min recording period (from normalized power maps; Materials and Methods). Spectra were classified in two groups by using k-means clustering (blue and green boxes in background). C, Average power spectra of the brain activity within right RS (orange), HL (blue), and anterior cortex areas (green; mean ± SEM, n = 14). No difference was observed in power amplitude between the anterior region and RS for both frequency bands (0.41 ± 0.04 vs 0.39 ± 0.03, unpaired t test, p = 0.604 and 0.4 ± 0.04 vs 0.39 ± 0.03, p = 0.747 for 0.1–1 and 2–5 Hz, respectively). Dimmer orange and blue colored curves: power spectra of the individual epoch shown in A (right). Dashed gray regions are the low (0.1–1 Hz) and high-frequency domains (2–5 Hz) used for later figures and vertical black lines indicate the boundaries of the different frequency bands used for A. hb, Heartbeat artifact; peak = 762 ± 8 bpm (n = 14). D, Average power spectra of the brain activity within right RS and HL areas from five successive 1 min periods. E, Average (center) and individual (right) optimal frequency map during 5 min (in colored log scale; Materials and Methods) normalized by the magnitude power of Fourier transform (luminance). The left diagram presents how the optimal frequency is evaluated from the power as a function of frequency. F, Average optimal frequency map normalized during five successive periods of 1 min.

Temporal filtering, correlation and SD maps.

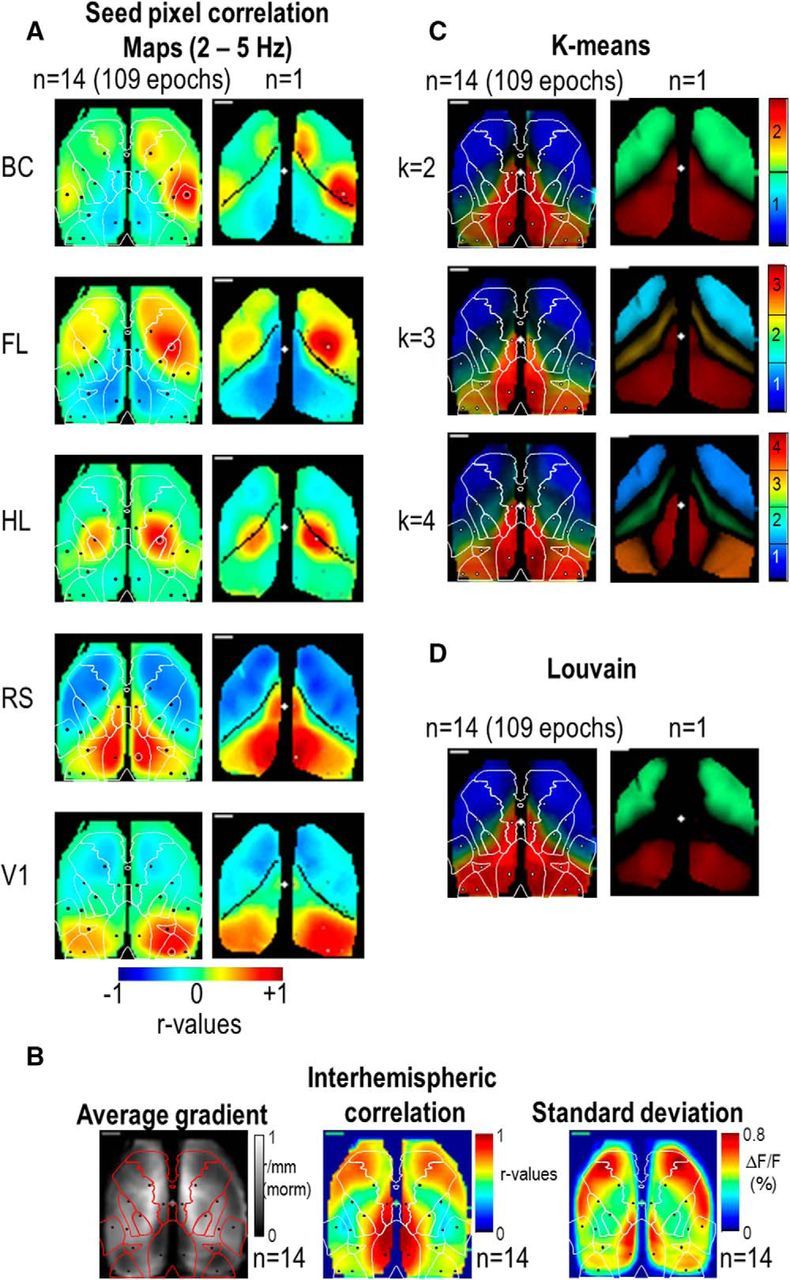
To remove the contribution of global brain fluctuations and illumination noise affecting cortical parcellation, the average activity of the cortex (within a masked region) was subtracted from the signal of each pixel (Fox et al., 2009; Vanni and Murphy, 2014; Abbas Farishta et al., 2015). Spontaneous activity recording sequences were then temporally pass-band filtered (0.1–1 or 2–5 Hz). Seed-pixel correlation maps were created wherein the cross-correlation coefficient r values between the temporal profiles of one selected pixel and all others were calculated over 5 min (White et al., 2011; Mohajerani et al., 2013; Vanni and Murphy, 2014). Seed-pixel correlation maps were limited to 10 seed locations for each cortical hemisphere (20 in total; Fig. 3A, black points): BC, Barrel field; FL, forelimb; and HL, hindlimb regions of the primary somatosensory area; RS, retrosplenial area; V1 and VB, primary monocular and binocular visual area; A, anterior visual area; M, motor area; Vm, visuomotor area; and Un, unassigned multimodal region. Their locations were defined according to the Allen Institute Atlas (i.e., barycenter of each region, http://brain-map.org) and previous studies (Vanni and Murphy, 2014) and were chosen to represent a wide distribution of cortical territories (3 somatosensory, 2 visual, 2 motor, and 3 associative). By picking up the correlation r values in of each of these regions and for each of the seed-pixel correlation map, it was possible to generate correlation matrices (Fig. 3B1). Because of some variability in the imaging window placement can exist, some ROIs may have not been processed for all the mice and were not included. To better visualize the connectivity matrix, indices were reordered by putting high r values closer to the diagonal (reorderMAT function from brain connectivity toolbox: https://sites.google.com/site/bctnet; Fig. 3B2). To measure the spatial rate of change of the correlation r values the local 2D gradients vector strength were calculated for each pixel of each correlation map (Fig. 3C; Cohen et al., 2008; Vanni and Casanova, 2013; Wig et al., 2014a,b). To control for the potential impact of image processing on the analyses of seed-pixel mapping, processing steps involving average activity subtraction, temporal pass-band filtering and correlation maps were also implemented on synthetic data created by scrambling the phase spectrum of original data while keeping the same amplitude spectrum to conserve a similar spatial coherence.

Figure 3.

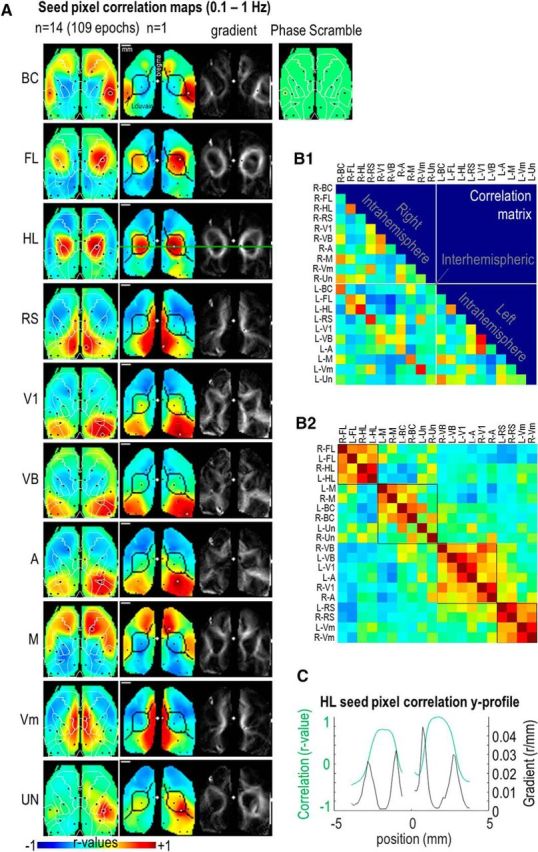
Correlation mapping at low-frequency mode (0.1–1 Hz). A, Seed-pixel correlation maps derived from low-frequency mode of activity (0.1–1 Hz). First column: averaged data from 14 mice combining 109× 5 min epochs in total, second column, same example used in the previous Figure 2). The white lines denote the landmarks of M1, HL, FL, BC, V1, and RS regions. The black points indicate all the seed locations explored (Fig. 2), whereas the white circle indicates the current seed location. The black lines indicate the boundaries of the clusters using Louvain parcellation (Fig. 5). Third column: spatial gradient of the corresponding correlation maps (second column). Green line in the HL map (third line): profile used in C to compare correlation r values and its spatial gradient. White plus sign denotes the position of the bregma. Last column of the first line: phase scramble data (Materials and Methods). B1, Matrix of correlation of signals between different pairs of seed locations. Same scale as in A. B2, Same values as in B1 but reordered by putting high r values closer to the diagonal. C, Profile of correlation (green line) and spatial gradient of the correlation (black line) for the green line presented in A (HL seed).

To evaluate the blood volume contribution to map, we did multiple measurements of green reflectance and fluorescence in two mice by alternating the collection of frames under blue LED illumination (GCaMP fluorescence) and green LED illumination (reflectance) every 6.67 ms (150 Hz frame rate; Wekselblatt et al., 2016). The green reflectance was then used to normalize the fluorescence (corrected green fluorescence) by subtracting the fractional changes (ΔF/F).

Contralateral and ipsilateral connections.

To evaluate the strength of interhemispheric correlation at each pixel of the cortex, we calculated the highest r value measured within the contralateral hemisphere for each pixel of the ipsilateral cortex (Fig. 4B). Using the same data, we also estimated the “error” of homotopic connections relative the axis of symmetry between both hemispheres: for each pixel, the distance (white arrow) between the location of the pixel with the highest r value within contralateral hemisphere (blue cross) and the expected mirrored position of the ipsilateral seed of the ipsilateral hemisphere (black cross) was used to generate a map of homotopic distance. To quantify the long-range topography of connections we generated maps revealing the number of islands of high correlation associated with each seed-pixel correlation map (Fig. 10A). Basically, this evaluated for each pixel (each seed-pixel correlation map) the number of spatial domains of high correlation within the same hemisphere by measuring the maximum number of domains for binary maps generated with different r values' threshold. To spatially explore the cortical brain activity fluctuation, the SD of calcium signal was also calculated for each pixel.

Figure 4.

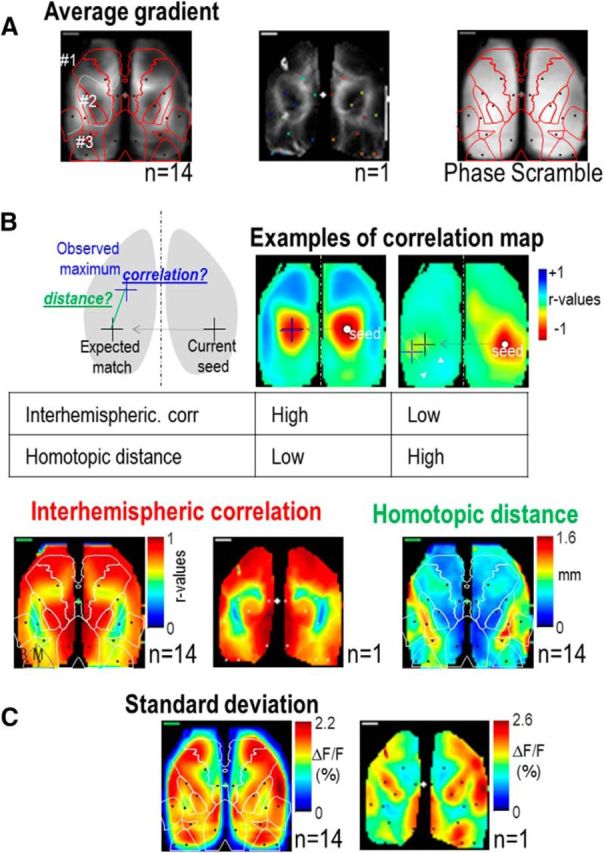
Gradient, interhemispheric connectivity and SD for low-frequency mode. A, Average gradient of correlation map for all pixels averaged between mice (left; n = 14) and for one single epoch (middle). Right, Average gradient of correlation map from phase scramble data. Brain region landmarks, as in Figure 2A, are denoted by red lines here. Dashed white lines illustrate the boundaries of identified Clusters 1, 2, and 3. Black and colored points indicate the seed-pixel locations. B, Top, Diagram of the method used to estimate the interhemispheric correlation and homotopic distance values for each seed. Bottom: Interhemispheric correlation map (Materials and Methods) averaged (left) and for one single epoch (middle). Black dotted lines highlight the location of binocular and monocular visual cortex (B, M). Right, Average homotopic distance map between the maximum locus of correlation in opposite hemisphere and the expected mirrored position of the maximum. C, SD map of cortical activity averaged (left) and for one single epoch (right).

Figure 10.

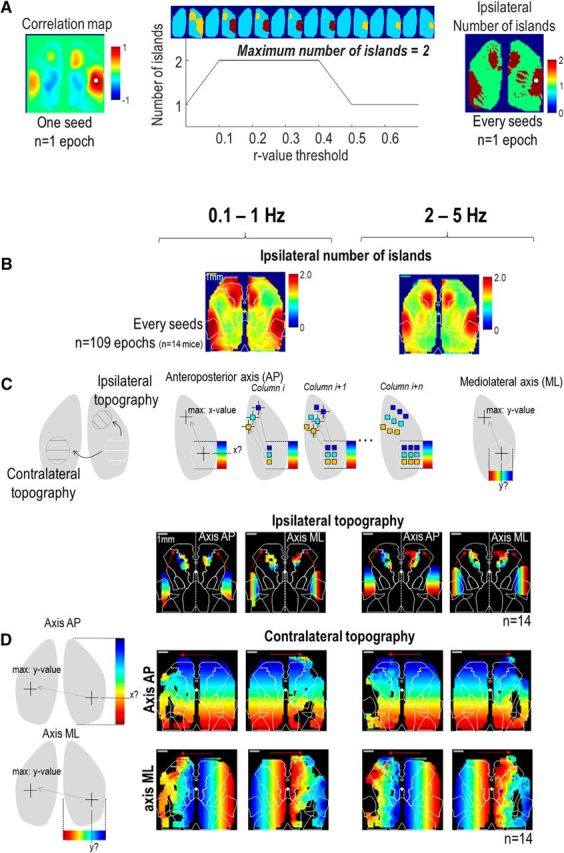
Topography of connections observed at both frequency bands. A, Description of the method used to calculate the number of ipsilateral islands: for each seed-pixel correlation map (i.e., for every pixel), the number of individual regions of high correlation was determined. To evaluate this number, the correlation map was thresholded with different r values and the number of regions was estimated. In the example, we choose an example for a seed into barrel cortex showing a clear remote correlation into motor cortex. When the r values threshold is too low, the counting cannot discriminate barrel and motor cortex, when it is too high, it only thresholds the barrel cortex. In an intermediate range of r values, it is possible to count two regions. Accordingly to the color code, red values represent seed locations associated with correlation maps having two individual islands or high correlation within the same hemisphere while green values were associated with the existence of one single region of correlated activity. B, Average number of island (NI) of high correlation maps within the ipsilateral hemisphere associated with each seed pixel for 0.1–1 (left) and 2–5 Hz (right) bands. These maps were calculated from correlation maps of individual epochs and then averaged across the 14 mice. C, Top, Description of the method used to evaluate the topography. For each seed, we identify the location of the maximum correlation in remote region and attributed to this pixel location the x or y value of the seed to make maps in anteroposterior and mediolateral axis, respectively. Bottom, Location of the maximum ipsilateral correlation for seeds located within lateral island with NI > 1.7 and 1.4 for 0.1–1 (left) and 2–5 Hz (right) bands, respectively (ipsilateral topography; see Materials and Methods) using the average correlation maps from every mice (n = 14, 109 epochs). D, Location of the maximum contralateral correlation (contralateral topography; Materials and Methods). Red arrows: tail-end of red arrows indicate the region/hemisphere of the seed locations tested and the tip of arrows indicate the corresponding location of maximum correlation in the remote region/hemisphere.

Cortical parcellation.

The spatial parcellation of functional activity was investigated with different approaches (Fig. 5): (1) By calculating the correlation between each pixel, the pairwise distance vector between the N × N pairs of pixels was used to generate hierarchical cluster tree with linkage algorithm using Euclidean distances as well as cluster indexation at different hierarchical stage (pdist, linkage, dendrogram, and cluster MATLAB functions; White et al., 2011). (2) Alternatively, another method was used in complement to the correlation clustering. Thus, k-means algorithm was used to create a partition of the n pixel signals into k clusters (k-means). (3) As both of these previous methods are dependent on a predetermined parameter setting, the number of clusters, a third method was also used in parallel: the Louvain method for community detection was used to extract communities from the N pixels (community_louvain from the brain connectivity toolbox: https://sites.google.com/site/bctnet; Blondel et al., 2008; Rubinov and Sporns, 2010; Newman, 2011). For each of these methods, the Silhouette coefficient was calculated for each pixel to evaluate the accuracy of the classification (silhouette MATLAB functions).

Figure 5.

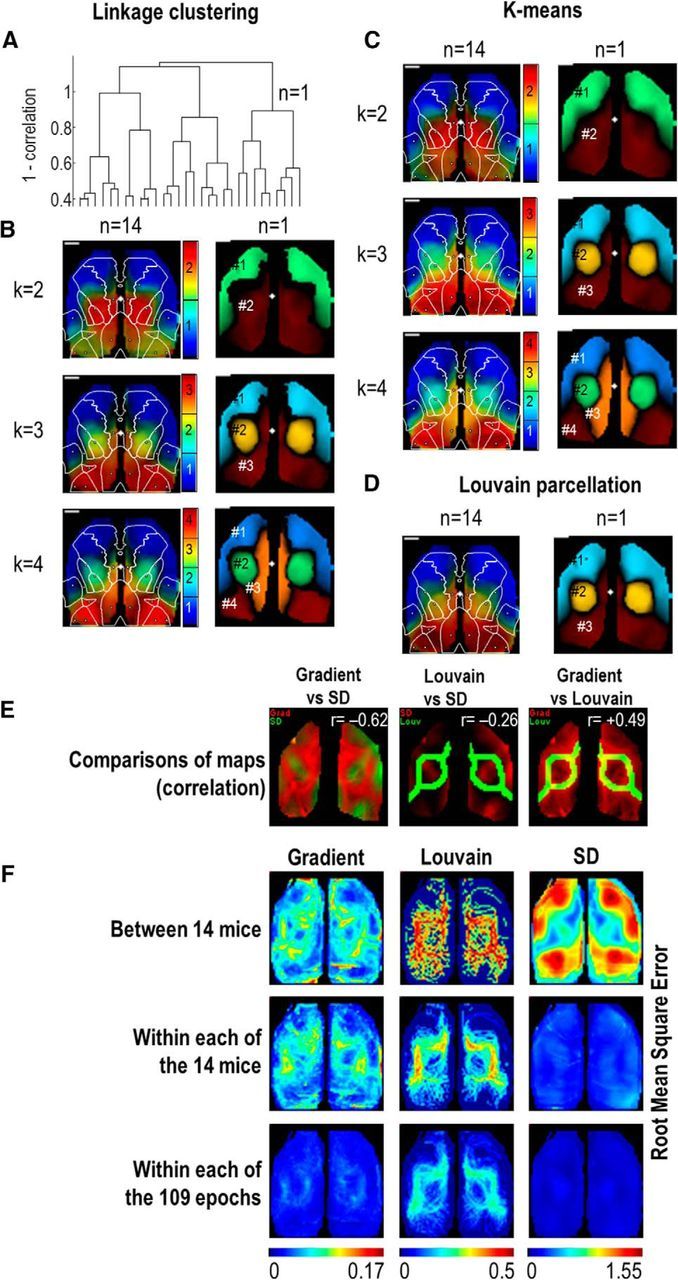
Functional clustering for low-frequency mode. A, Dendrogram of correlation between clusters in one single epoch (same example presented in previous figures). B, Brain parcellation in 2, 3, or 4 clusters according to the correlation (linkage) averaged (left; n = 14) and from the example described previously (right). The colors indicate the cluster index, whereas the luminance is the accuracy of the clustering (silhouette value). C, Same as B but using k-means parcellation. D, Brain parcellation using community structure clustering (Louvain). E, Example of merging between Gradient, SD maps, and Louvain boundaries. The correlation between the two examples maps are shown in the respective top right corner of the images. Average correlation between gradient and SD maps: r = −0.53 ± 0.03 (one-sample t test for the hypothesis that the data are centered to 0: p < 0.001), gradient and Louvain: r = +0.54 ± 0.02 (p < 0.001), SD and Louvain: r = −0.28 ± 0.02 (p < 0.001). Not shown; Interhemispheric correlation and gradient: r = −0.47 ± 0.04 (p < 0.001), SD: r = +0.28 ± 0.05 (p < 0.001), and Louvain: r = −0.43 ± 0.02 (p < 0.001). F, Average RMS (root means square) of gradient, Louvain, and SD maps (Materials and Methods) between mice (first line), between each epoch of the same mouse (second line), and between two periods of the same epoch (third line).

Comparison of maps.

For each epoch, the similarity of patterns between blood vessel pattern (spatially high-passed at >2 mm to avoid uneven illumination), gradient, SD, and Louvain maps were compared by computing the spatial cross-correlation between pairs of maps comprising each combination of analysis modality (Figs. 5E, 6). In the case of Louvain maps, the edges of the map were processed with a Sobel filter and used for comparison. To quantify the variability of gradient, SD, and Louvain maps during and across epochs in each mouse, as well as between mice, two methods were used. (1) Distribution of cross-correlation r values between each pairs of maps of the same modality was performed for the first and second half part of each epoch or between each epoch of each mouse or between each epoch of different mice. (2) Alternatively, to evaluate the spatial location of the variability, maps of each modality were z-transformed by computing the root means square error (RMS) at each pixel (Fig. 5F).

Figure 6.

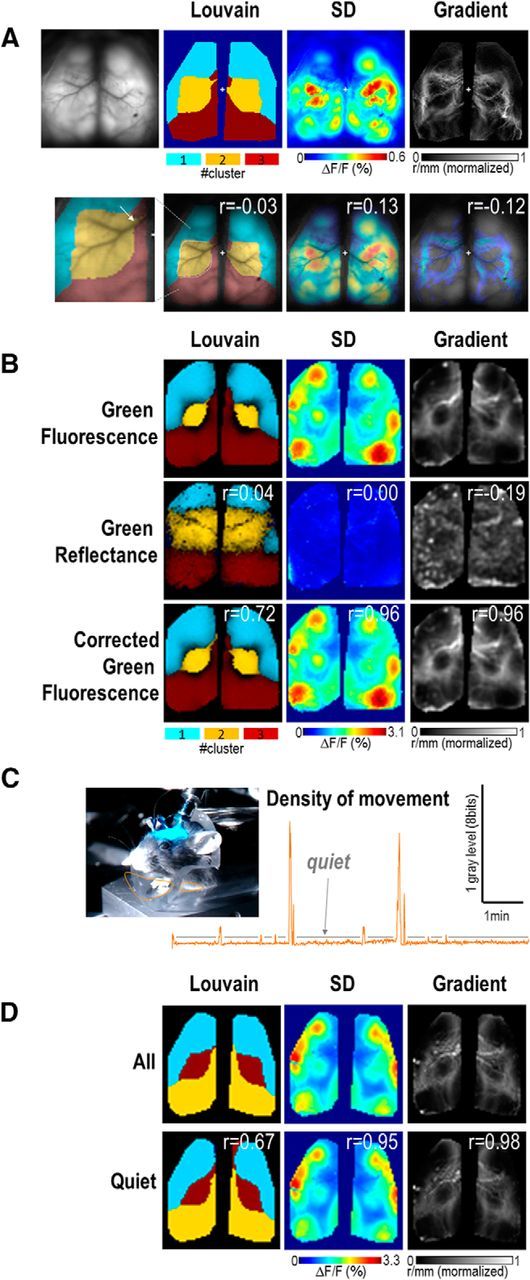
A, Top, Blood vessel pattern (raw green fluorescence), Louvain parcellation, SD, and Gradient maps calculated from another example (bandpass: 0.1–1 Hz). Bottom: Same maps but overlaid by the blood vessel pattern and showing the r values of cross-correlation between each of these map with the blood vessel pattern. Although some degree of correlation exists between vascular landmarks (white arrow), they did not correspond to the majority of the functional boundaries observed (dotted white line). This can explain the low r values observed between blood vessel pattern and Louvain [r = −0.03 ± 0.01 vs −0.01 ± 0.01 (for shuffled mice blood vessel pattern, Materials and Methods), paired t test: p = 0.04, n = 14], SD (0.20 ± 0.03 vs 0.05 ± 0.02, p < 0.001) and gradient (−0.14 ± 0.02 vs −0.02 ± 0.01, p < 0.001). B, Louvain parcellation, SD, and gradient maps calculated from an independent set of experiment where the green reflectance was acquired in parallel with green fluorescence to investigate the contribution of blood volume artifacts (Materials and Methods). The third line shows the mapping on corrected green fluorescence. r Values of cross-correlation between uncorrected green fluorescence and corrected green fluorescence or green reflectance are shown in the top right of each image. A strong similarity in mapping was observed between uncorrected and corrected green fluorescence (r = 0.69 ± 0.03, 0.92 ± 0.03 and 0.93 ± 0.01, n = 15, for comparison between Louvain, SD, and gradient maps, respectively) in contrast to the comparison between green fluorescence and reflectance (0.08 ± 0.02, 0.03 ± 0.03, and 0.27 ± 0.03). C, One frame of the video capture of the mouse behavior recorded in parallel of the cortical activity. Orange boundaries delimit regions where the density of movement was calculated. Graph: profile of the density of movement as a function of time. Gray bars are the periods of quietness. D, Louvain parcellation, SD, and Gradient maps calculated from the full sequence of spontaneous activity (first line) and the concatenation of periods of quietness (second line). r Values of cross-correlation between maps from full and quiet periods are shown in the top right of the image.

Temporal dynamics.

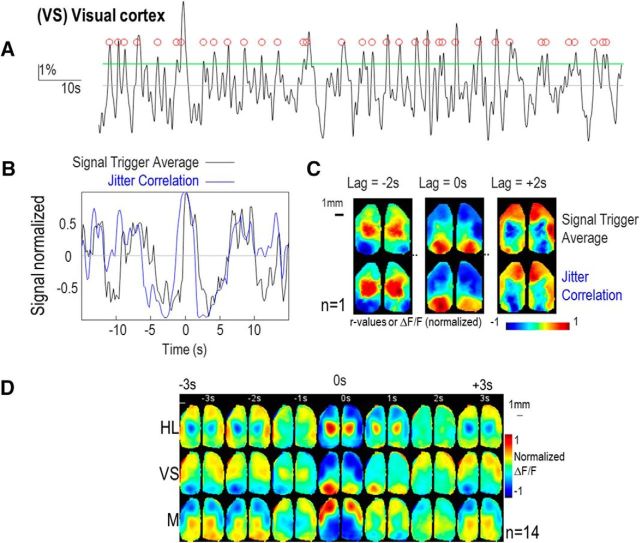
To explore the temporal dynamics of cortical activity, two methods were used: (1) spike-triggered averaging and (2) jittered correlation. For spike-triggered averaging, cortical activity was analyzed in different seeds by calculating the median and SD (σ). Calcium activity that exceeded a threshold (median + σ) was considered as a “calcium spike”. Then, similar to Xiao et al. (2017), the calcium activity in a window of ±15 s around each spike was averaged for each pixel to create an average sequence of cortical activity associated with a “calcium spike” in each of the selected seeds (Fig. 8A–C). Alternatively, jittered correlation was used to explore the temporal dynamics of cortical activity by correlating the signal recorded in each selected seed location, to signals of all other pixels using seed-pixel correlation by incorporating a varying time lag (Fig. 9A). Matrices of correlation maps as a function of the jitter were generated and used to reveal the cortical sequence of activity. The frequency of the oscillation was calculated by performing the Fourier transform on correlation values versus jitter at the seed location. Then, for each pixel, the phase and magnitude of Fourier transform of correlation values at this frequency was used to create maps of jitter dynamics (Fig. 9B).

Figure 8.

Cortical dynamics of clustered activity using spike-triggered averaging. A, Cortical activity for seeds in left posterior visual cortex (intermediate location between RS and V1: VS) for the frequency band 0.1–1 Hz and for a single epoch. Green lines: threshold value corresponding to median + σ. Red circles: calcium spikes corresponding to events that exceeded the threshold. B, Black curves: profile of spike-triggered averaging of the normalized fluorescence change in VS. Blue curves: profile of the normalized correlation value as a function of the jitter. C, Comparison of the cortical dynamic between spikes triggered averaging (top) and jittered correlation (bottom, normalized between −1 to 1) for three different lags: −2, 0, and +2 s. D, Spike-triggered average frames normalized between −1 to 1 and averaged (n = 14) for seeds located in three different ROIs: HL, VS, and M.

Figure 9.

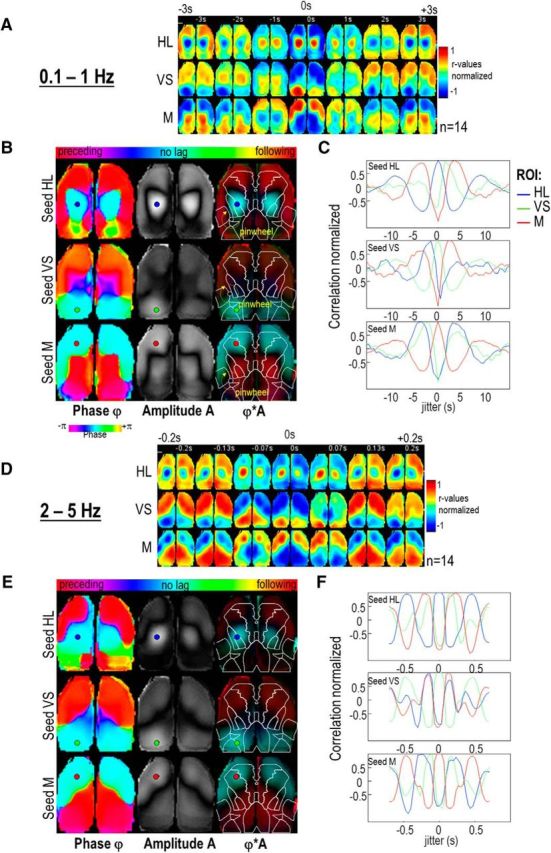
Cortical dynamics of clustered activity using jitter correlation. A, Seed-pixel correlation-maps normalized between −1 to 1 and averaged (n = 14) for seeds in left HL, VS, and M and incorporating temporal jitters ranging from ±3 s (jittered correlation sequence) for the frequency band 0.1–1 Hz. B, Jitter Phase maps (first column, range: ±4.3 s), amplitude (second column) and combination of both (third column) of the jitter correlation map oscillations for seeds in HL, VS, and M (indicated by the colored circles). Cyan color corresponds to ϕ = 0, whereas orange/green colors (ϕ < 0) indicate preceding correlation and blue/purple colors (ϕ > 0) indicate following correlation. The yellow dotted circular arrows indicate the clockwise pinwheels within left hemisphere. C, Profile of the normalized correlation values within 3 regions of interest (ROI) (HL, VS, and M, in blue, green, and red, respectively) as a function of the jitter and the three seeds. Jittered correlation map corresponding to the maximum correlation coefficient value of each ROI are indicated by the colored dotted boxes in A. D–F, Same as A–C but for the frequency band 2–5 Hz (range: ±0.2 s).

Topography.

Topography was explored on individual epochs as well as on average correlation maps from every mouse: for analysis of average correlation maps, the computation was restricted to pixels having an average number of islands >1.7 and 1.4 (for low and high-frequency, respectively; Contralateral and ipsilateral connections). The location of the maximum correlation within the remote island of the same hemisphere was calculated to generate topographic ipsilateral maps in the mediolateral and caudorostral axis (Fig. 10C): then, the x_s (or y_s) values of the seed was attributed to the location (I(x_m,y_m)) of the maximum (color map). In a similar way, for every pixel, the location of the maximum correlation within the opposite hemisphere was calculated to generate topographic contralateral maps in the mediolateral and caudorostral axis (Fig. 10D).

To create topographic maps from individual epochs, correlation maps were generated for seed pixels equally spaced and ordered to a line. Then, for each seed-pixel correlation map series, the Fourier transform was computed for each pixel (Fig. 11A). The resultant extracted phase and amplitude information at the first harmonic (1/number of seed) were then used to infer the topography (Kalatsky and Stryker, 2003; Groleau et al., 2014; Abbas Farishta et al., 2015; Garrett et al., 2017; Zhuang et al., 2017).

Figure 11.

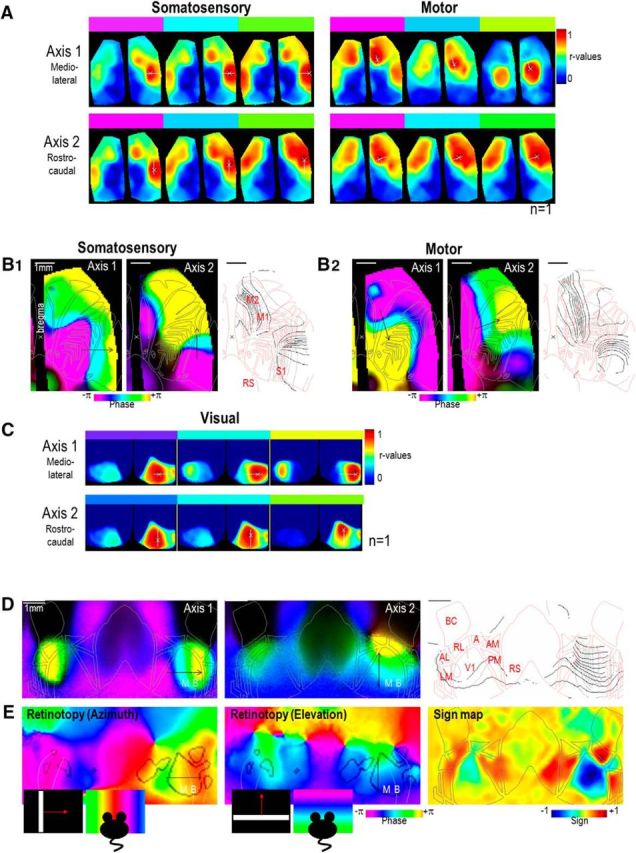
Example of topography of connections. A, correlation maps calculated for nearby seed pixels (white cross) within somatosensory and motor cortex in two orthogonal directions (axes 1 and 2, white lines). These data are from one epoch. B1, Left and Middle, Phase of Fourier map calculated from the sequence of correlation maps presented in A (from seeds within somatosensory cortex; Materials and Methods). Right, Gradients of phases from both axes (axis 1: gray; axis 2: black) overlaid with the cortical areas (red). B2, Same as B1 but for seeds within motor cortex. Phase indicated by color bar positioned above corresponding correlation maps in A. Black arrows indicate the position and direction of movement of the seed location. C, Correlation maps calculated for nearby seed pixels within V1 in two orthogonal directions (axes 1 and 2). These data are from another single epoch. D, Phase of Fourier maps calculated from the sequence of correlation maps presented in C. White dotted line represent the limit between binocular (B) and monocular zone (M). E, Phase of visual responses for bars moving periodically in the azimuth and elevation axis (Fourier retinotopic map (phase and amplitude; Materials and Methods). These data are from another single epoch with visual stimulation on the same mouse. Right, Sign map showing the mirrored gradient of phase (Materials and Methods).

Retinotopy.

In a subset of experiments, sensory stimulation was performed to investigate topography (Fig. 11E). To perform retinotopic mapping, 5 min of visual stimuli were generated using Psychtoolbox and presented on a LCD screen placed 19 cm in front of the mouse's eyes. A continuous stimulation paradigm was used where black and white bars were periodically moving at 0.2 Hz horizontally or vertically over a gray background to generate elevation and azimuth maps, respectively (Kalatsky and Stryker, 2003; Groleau et al., 2014; Abbas Farishta et al., 2015; Zhuang et al., 2017). Similar to spontaneous activity presented previously, the signal of each pixel was decomposed by Fourier transform to obtain phase and magnitude matrices. Then, the phase values at the stimulus frequency were used to determine retinotopic maps along the elevation and azimuth independently. Sign maps were used to functionally delimit each visual area based on the reversion of the gradient of phase and was computed by measuring for each pixel the sine of the difference between gradients of azimuth and elevation from the retinotopic maps (Sereno et al., 1995; Garrett et al., 2014; Zhuang et al., 2017).

Experimental design and statistical analysis

One-hundred and nine epochs were recorded across 14 mice. Analyses were performed between periods from the same epoch, between epochs in one mouse or between mice. Any results of analysis were averaged between epochs before being averaged and compared between mice. Statistical tests were performed using unpaired t test and one-sample t test for the hypothesis that the data are centered to zero by using the Statistical and Machine Learning Toolbox of MATLAB. Unimodal normal distribution of the was tested using one-sample Kolmogorov–Smirnov test.

Results

The spectral and spatial decomposition of spontaneous brain activity revealed two operating modes

Mice were implanted with a chronic window covering most of the bilateral dorsal cortex including prefrontal, sensorimotor and visual regions (Fig. 1B). Using this preparation, spontaneous activity was collected in quiet awake mice during 5 min epochs. To increase statistical power and to ensure functional connectivity measures were robust we collected and assessed spontaneous activity from 109 imaging sessions across n = 14 Ai-94 GCaMP6s mice (Materials and Methods). To identify specific temporal and spatial signatures of brain activity, the Fourier transform was computed on each pixel to present the spatial distribution of different brain oscillations for different frequency bands (Fig. 2A). The average power spectrum of activity was also presented for different regions of interest (Fig. 2B) showing the presence of two spectral structures: one associated with low-frequency components (<1 Hz, well represented by HL), and a second associated with the presence of a higher-frequency component (between 1 and 5 Hz, well represented by RS). The distribution of the power within the dorsal cortex showed a unimodal normal distribution of the activity (one-sample Kolmogorov–Smirnov test: p = 0.675 and p = 0.352 for low- and high-frequency bands, respectively, n = 109 epochs). Quantification of power measured from right RS and HL (Fig. 2C) showed that, whereas no difference was observed in 0.1–1 Hz frequency band between HL and RS (0.44 ± 0.02 vs 0.39 ± 0.03%, respectively, unpaired t test: p = 0.202, n = 14), RS exhibited significantly more power than HL within the 2–5 Hz higher frequency band (0.23 ± 0.01 vs 0.39 ± 0.03%, unpaired t test: p < 0.001). To measure the frequency distribution of discrete regions more precisely, the frequency associated with the highest signal was determined for each pixel of the cortex (Fig. 2E, optimal frequency). Consistent with spectral measurements, operating frequency was lower in HL than RS (0.11 ± 0.25 vs 2.43 ± 0.33 Hz, unpaired t test: p < 0.001). By subdividing the brain activity of each 5 min epoch into five 1 min segments, it was observed that the spectral distribution and optimal frequency was constant for the duration of the recording (Fig. 2D,F). In conclusion, the spatial and spectral decomposition of signal clearly revealed the presence of two main modes of activity: one, located in the center of the dorsal region including HL, was mostly associated with slow components <1 Hz (low-frequency mode, 0.1–1 Hz) and a second one located in the medial posterior regions, including the RS and lateral cortex, was more clearly associated with faster components (within 2–5 Hz window and beyond: high-frequency mode). Given this spectral separation of spontaneous brain activity into low- and high-frequency modes, the parcellation of cortical signal was further explored for these two frequency bands.

Low-frequency activity was associated with parcellation in three main clusters of brain activity within dorsal cortex

Functional connectivity was first explored within the low-frequency band (0.1–1 Hz) by computing seed-pixel correlation maps and a region-by-region comparison correlation matrix (Fig. 3A,B). Similarly to previous studies using GCaMP3, iGluSnFR, voltage-sensitive dye, or intrinsic optical imaging (White et al., 2011; Mohajerani et al., 2013; Vanni and Murphy, 2014; Chan et al., 2015; Xie et al., 2016), consistent patterns of functional connectivity were observed including strong correlation between homotopic regions as well as between distant locations within the same hemisphere such as between BC and motor cortex. By reorganizing the matrix (Fig. 3B1) to have the highest r values closer to the diagonal, it was possible to observe multiple groups of highly correlated regions (Materials and Methods; Fig. 3B2): (1) FL and HL; (2) BC, M, and Un; (3) visual regions: V1, VB, and A; and (4) medial regions: RS and Vm. All of these correlated clusters also exhibited strong contribution of interhemispheric connection between homotopic regions. This gross parcellation is consistent with higher resolution parcellation described later in the current studies (Fig. 5). The absence of observed patterns when processing synthetic data created by scrambled phase spectrum (Materials and Methods) confirmed the neuronal specificity of mapping (Fig. 3A, first line). For each seed location examined, the regions of high correlation (r > 0.5, orange-red colors) encompassed several mm² and, outside of this region, r values rapidly fell <0 in less than a millimeter (Fig. 3C). To evaluate the extent of highly correlated regions, spatial gradients of correlation were computed and showed that boundaries of highly correlated regions were very stable when seed-pixel positions were moved to different locations within the same domain (Fig. 3A, last column).

This generated reliable averaged gradient maps between mice (Fig. 4A) delimiting three main bilateral territories: a first one (Cluster 1) encompassing most of M2, the lateral part of M1 and BC, MO, and NO regions of the somatosensory areas; a second territory (Cluster 2), including the medial part of M2 and limb region of the somatosensory area (HL and FL), and a third one (Cluster 3), including visual and RS areas. Except at the boundaries between Clusters 1 and 2, as well as within monocular visual cortex, the strength and mirroring accuracy of interhemispheric connectivity was high (r = 0.62 ± 0.03, n = 10 vs 0.74 ± 0.04, n = 8, unpaired t test: p = 0.02 between V1 and VB, monocular and binocular region of the visual cortex, respectively. 0.81 ± 0.02, n = 14 vs 0.41 ± 0.05, n = 14, unpaired t test: p < 0.001 between HL and the Un; Fig. 4B). To identify the regional distribution of cortical activity, the SD of spontaneous activity was processed for each pixel and the resulting maps clearly showed domains of high activity delimited by “valleys” which overlap with the location of high gradients (Figs. 4C, 5E).

To further explore the parcellation of cortex into functional clusters, complementary methods of classification based on the similarity of signal time series were used. First, correlations were calculated between all pairs of pixels to generate dendrogram trees classifying each group of pixels (Fig. 5A,B). Thus, at each step, it was possible to show the spatial pattern of parcellation with the clear limits of each functional cluster. Parcellation was also processed using k-means clustering classifying pixels in K groups based on their similarity (Fig. 5C). One limitation of both of these parcellation approaches is the subjectivity of the threshold that has to be established to parcellate the brain into a discrete number of functional modules. To objectively define the number of clusters, community structure algorithms were also used: Louvain parcellation applied to the same data were able to define the spatial pattern of 2.89 ± 0.04 clusters (n = 14; Fig. 5D). Using this latter approach and consistent with previous observations from gradient maps of correlation (Fig. 4A), three functional modules were observed: the first two encompassed the sensorimotor region (1: orofacial regions; 2: limb regions), whereas the third one was associated with medial posterior areas (3: visual cortex and RS). In agreement with previous studies (Mohajerani et al., 2010; White et al., 2011; Sforazzini et al., 2014), strong interhemispheric correspondence was observed (correlation of patterns between both hemispheres: r = 0.44 ± 0.05, 0.59 ± 0.04 and 0.46 ± 0.04 for gradient, SD, and Louvain boundaries maps, respectively; for all, p < 0.001, one-sample t test for the hypothesis that the data are centered to 0) as well as consistent patterns between Louvain boundaries and gradient or SD maps (Fig. 5E). For each mouse, the patterns were more consistent within one epoch than between epochs from different days [correlation of maps: gradient r = 0.89 ± 0.02 (n = 14) vs 0.69 ± 0.01 (n = 513 pairs, unpaired t test, p < 0.001); SD: 0.91 ± 0.01 vs 0.73 ± 0.01 (p = 0.002); and Louvain 0.64 ± 0.04 vs 0.44 ± 0.01 (unpaired t test, p < 0.001)]. Although conserved, a weaker consistency of pattern was observed between animals (gradient: r = 0.32 ± 0.00, SD: 0.25 ± 0.00, Louvain: 0.18 ± 0.00, n = 5373 pairs, all unpaired t test, p < 0.001). Similarly, average RMS maps (Materials and Methods) showed more differences between animals than with different epochs within the same individual animal or from two periods of the same epoch (Fig. 5F): RMS between animals: 0.062 ± 0.005, 0.226 ± 0.01 and 0.761 ± 0.152 n = 14 (for gradient, Louvain, and SD, respectively) versus within different epoch of one animal: 0.054 ± 0.004, 0.15 ± 0.006, 0.237 ± 0.029, n = 14 (unpaired t test, p = 0.173, p < 0.001 and p = 0.002). A similar trend was observed for the RMS within different epoch of one animal and different period of one epoch (0.02 ± 0.001, 0.103 ± 0.002, 0.089 ± 0.005, n = 109, unpaired t test, for all: p < 0.001).

For each mouse, the surface blood vessel patterns were compared with the corresponding Louvain clustering, gradient, and SD maps and were found not to impact parcellation (Fig. 6A). To evaluate the potential the contribution of blood volume changes on our measurements of green fluorescence, we also measured the green reflectance changes in parallel (Materials and Methods; Wekselblatt et al., 2016). The reflected signal was then used to correct the green fluorescence, but ultimately did not show any significant impact on mapping consistent with our previous work (Xiao et al., 2017). These control experiments support the idea that, given a large amplitude of calcium signals green fluorescence was minimally affected by blood artifacts within the frequency bands of our experiments (Fig. 6B). This can be observed by the smaller amplitude of reflected green signals compared with fluorescence (Fig. 6B, compare SD map of reflectance and fluorescence).

The contribution of sensory driven cortical activity produced by movement was assessed by associating video capture of body movement with brain calcium activity similarly to our recent work (Xiao et al., 2017). Periods of escape-like behavior or grooming and their associated body and limb movements were rare, but were easily identified by selecting regions of interest on limbs and quantifying the density of movement corresponding to the average pixel value changes (absolute) within the region of interest and for each frame (Fig. 6C, orange region). Cortical mapping was then processed and compared between periods of quietness (concatenated sessions without limb movements) with full periods of spontaneous activity (including periods of movements) and did not show differences (cross-correlation of maps: r = 0.96 ± 0.02, 0.99 ± 0.01, and 0.77 ± 0.05 for gradient, SD, and Louvain boundaries maps, respectively, n = 10; for all p < 0.001, one-sample t test for the hypothesis that the data are centered to 0; Fig. 6D).

The bimodal parcellation observed at higher frequency may be associated with a default mode-network structure

Using the same dataset, cortical parcellation was also explored within spontaneous activity associated with the higher frequency mode (2–5 Hz). Seed-pixel correlation mapping was performed and showed that the connectivity between BC and motor cortex was preserved (Fig. 7A; r = 0.38 ± 0.06 vs 0.46 ± 0.07 for high- and low-frequency mode activity, respectively, unpaired t test: p = 0.441, n = 14). At a higher frequency, a reduction of the anticorrelated relationship for connectivity between HL and both motor cortex and BC was observed (0.01 ± 0.07 vs −0.22 ± 0.05, unpaired t test: p = 0.012 and 0.11 ± 0.05 vs −0.34 ± 0.07, p < 0.001, for high- and low-frequency mode activity, respectively). These results may suggest that the cluster of the somatosensory cortex associated with limb functions (previous Cluster 2) is no longer independent and is now more co-associated with Cluster 1 which includes the BC and motor cortex. This was confirmed by cortical parcellation as well as gradient mapping (Fig. 7B–D) showing the presence of mostly two main clusters: a lateral/anterior cluster that encompasses all the somatosensorimotor areas recorded, and a second cluster, more medial/posterior that encompasses visual cortex as well as RS. Interestingly, a subset of experiments, performed under light isoflurane anesthesia (1.2%), revealed a similar pattern that was independent of the frequency mode investigated (0.1–1 or 2–5 Hz, data not shown). These results suggest then the unique arrangement of cortical activity observed in awake mice at low-frequency (0.1–1 Hz), whereas higher-frequency (2–5 Hz) could be more influenced by the default mode pattern of cortical processing.

Figure 7.

Cortical parcellation based on correlation at higher frequency mode (2–5 Hz). A, Seed-pixel correlation maps for higher frequency mode of activity (2–5 Hz) in one single epoch (right; same example used in previous Figs. 2–5) and averaged from 14 mice (left). Overlaid on maps in white are positions of M1, HL, FL, BC, V1, and RS brain regions. The black lines indicate the boundaries of the clusters using Louvain parcellation in D. B, Average gradient, interhemispheric, and SD maps from 14 mice. C, Brain parcellation in 2, 3, or 4 clusters using k-means clustering averaged (left; n = 14) and from one single epoch (right). D, Brain parcellation using community structure clustering (Louvain).

Jitter correlation reveals a programmed sequence of cortical clustered activity

Several lines of investigation revealed that the low-frequency mode of spontaneous activity (0.1–1 Hz) can be parcellated into three consistent clusters within the dorsal cortex. To establish whether the relative activation of each of these clusters was random or sequential, the dynamics of activity was examined using temporal analysis. As shown in the example in Figure 8A the cortical activity in a seeds located in the intermediate location between left RS and V1 (VS) was measured and showed the presence of calcium spikes that were identified by applying a threshold (red circle; Materials and Methods). We then averaged the temporal profile of cortical activity associated with each spike (spike-triggered averaging; Fig. 8B,C). In this example from one epoch, we observed that the activity in VS was preceded by activity within bilateral HL regions and was followed by activity within a bilateral anterior cluster including M and BC. Spike-triggered averaging was then generated for each epochs and then averaged between mice and for three different seeds in HL, VS, and M and showed that the cortical dynamic described was robust enough to still be present (Fig. 8D, second line). A similar corresponding spatiotemporal profile of activity was observed for seeds in HL (first line) and M (third line): HL was preceded by activity in BC and M and followed by VS, whereas M was preceded by activity in VS and followed by HL.

However, variability of the calcium-signal amplitude between mice and epochs could have impacted the average. Moreover, this trigger average method depends on a threshold value which can also be dependent on the variability of amplitude and signal-to-noise ratio. We therefore used a parallel method to explore the sequence of clustered cortical activation based on jittered analysis: basically, the correlation of activity within the seed locations was compared with the activity measured from all other pixels and incorporated a temporal jitter extending ±15 s in 0.5 s steps (Materials and Methods; in Figs. 8B,C, blue curves and lower montage, Fig. 9A). Using this approach, it was possible to identify the active network preceding (high correlation for jitters <0 s) and following (>0 s) the activity for each seed location similar to the cortical activity preceding and following each identified spike. This analysis clearly confirmed that the activity of HL was correlated with preceding activity within a bilateral anterior cluster including M and BC and was followed by a bilateral posterior cluster activity including VS and so on (Fig. 9C, red and green curves of seed HL). A similar spatiotemporal profile of activity was observed for seeds in VS and M. Although a cyclic pattern of activity could be identified, the relative delay of activation between clusters can be then calculated at the frequency of the oscillation: for each pixel the Fourier phase of the jittered correlation maps sequence was computed to generate a Fourier map of the temporal dynamics (Materials and Methods; Fig. 9B). This approach clearly revealed a circular sequence of correlation activating in cyclic order of HL, followed by VS, followed by M (and BC), and so on, looping at 0.12 ± 0.00 Hz (n = 14) around a polymodal pinwheel axis located within the unassigned region of somatosensory cortex between the multimodal area A (also called the pTA), BC, and FL.

Although only two main clusters were identified from the higher frequency mode (2–5 Hz), the temporal dynamics of activity was also examined using jittered analysis (Fig. 9D–F). In contrast to the looping structure observed previously, a bimodal dynamic between lateral-anterior and medial-posterior clusters was observed oscillating at 2.61 ± 0.10 Hz (n = 14), particularly apparent for seeds located within VS or M. In conclusion, two modes of spatiotemporal dynamic appeared to coexist within dorsal cortex: (1) a slow one, activating in sequence the locomotion, visual, and orofacial regions around a polymodal pinwheel every ∼8 s; and (2) a fast one, encompassing alternating lateral and medial region activation every ∼0.4 s.

Within the somatosensory motor and visual clusters, a highly preserved topography of connections can be revealed

Although spontaneous cortical activity can be parcellated in a limited number of clusters at a large hemisphere-wide scale, a finer level of functional organization was investigated by exploring the preserved topography of connections between multiple regions of each functional cluster. Seed-pixel correlation maps already revealed the presence of ipsilateral islands of correlated activity between barrel and motor cortex at low and high frequencies (Figs. 3A and 7A, seeds in the BC and M). By calculating the number of ipsilateral islands observed for each correlation map of each hemisphere, ipsilateral Number of Island maps were created from activity of the two frequency bands previously explored (Materials and Methods; Fig. 10A,B). As indicated by the color map, red values represent seed locations that were associated with correlation maps having two individual islands of high correlation within the same hemisphere (seed in barrel cortex evoking a remote island of high correlation in motor cortex), whereas green values were associated with the existence of one single large region of correlated activity. This clearly confirmed the existence of robust remote islands of correlation between sensory and motor cortex that were present in both frequency modes.

The arrangement of locations of highest ipsilateral correlation was then calculated for differing seed locations along the caudorostral and medial-lateral axes within lateral region of the barrel cortex associated with high average number of island values (Fig. 10C, ipsilateral topographic map). For clarity, we mapped mediolateral and anteroposterior axes independently (Materials and Methods). For each seed, we identified the location of the maximum correlation in remote region and attributed to this pixel location the x or y value of the seed to make maps in the two axes, respectively (Materials and Methods). This showed the presence of a highly arranged topography of connections between sensory and motor cortex. The arrangement of locations of highest contralateral correlation was also calculated for every seed location in the opposite hemisphere (Fig. 10D, contralateral topographic map) and also revealed a very well preserved topography of connections between homotopic locations of both hemispheres, except for the polymodal regions previously described. This interhemispheric pattern is consistent with the correlation maps already presented in Figure 3A (compare Un seeds with every other) as well as the weaker and less resolved interhemispheric connections between polymodal regions at the border of visual and somatosensory cortex (Fig. 4B). Therefore, the intra and interhemispheric topographic mapping performed here on a broad spectral band of spontaneous activity from all mice, revealed a very well preserved pattern mirroring functional domains between multiple regions.

To explore the topography of connections between sensory and motor cortex in greater detail, seed-pixel correlation maps calculated for nearby seed pixels were generated for single epochs after bandpass filtering at 0.1–1 Hz. Seed-pixel locations were systematically varied along a line (Fig. 11A, white line) and showed that the centers of remote islands of correlations moved accordingly to the seed-pixel locations. For sensory cortex, correlation maps were generated for different seed locations along the mediolateral (Axis 1) and caudorostral axes (Axis 2). This clearly revealed that within the same hemisphere, remote islands of high correlation were found within motor cortex of both hemispheres. These correlation maps were used to calculate the topographic map using Fourier analysis (Materials and Methods), matching each local and remote location accordingly to a color code (Fig. 11B) and showed a highly preserved arrangement of connections between sensory cortex and primary and secondary motor cortex. Reciprocally, correlation maps were generated for different seed locations along two different axes within motor cortex and revealed consistent mutual results. Together, these results revealed axes of symmetries in posterolateral axis mirroring the maps between areas S1 and M1, M1, and M2 but also, in some experimental conditions S1 and S2 (data not shown).

Topographic mapping was also applied to visual cortex regrouping the primary visual area (V1) and its surrounding extrastriate areas (AL, LM, AM, PM, etc.), themselves, receiving projections from V1 (Wang and Burkhalter, 2007; Marshel et al., 2011). Correlation and topographic maps were generated for different seed locations along the mediolateral and caudorostral axis within visual cortex (Fig. 11C,D). Remote islands of high correlation were found in the opposite hemisphere when seed pixels were located within the binocular zone and near the boundary of V1 and AL/LM (Fig. 11D, yellow regions). When seed pixels were moved in V1 toward the midline, this interhemispheric connectivity disappeared and remote islands of correlation were instead observed within ipsilateral AL/LM (Fig. 11D, blue/purple regions). When seed pixels were moved along the caudorostral axis within V1, islands of high correlation within AL and LM were also observed to move correspondingly. These functional landmarks based on spontaneous activity were confirmed by sensory mapping using visual stimulation. Sweeping vertical and horizontal bars were presented periodically within the mouse's visual field, and the cortical retinotopy along the azimuth and elevation axis was mapped (Fig. 11E; Materials and Methods). Consistent with previous work (Marshel et al., 2011; Garrett et al., 2014; Carandini et al., 2015), this mapping revealed that the mirrored gradient of phases observed between V1 and LM/AM in the azimuth axis using retinotopic stimulation (Fig. 11D, green to red and reciprocally) and could also be observed using spontaneous activity in the same mouse when not visually stimulated using time locked retinotopic stimulation.

Discussion

Clusters of synchronized activity can coexist within cortex. In the present study, the spatial organization of these clusters and their topography was explored using mesoscopic calcium imaging in the superficial cortex of awake mice. Multiple approaches of parcellation were applied and revealed the presence of two to three major clusters of correlated activity that were frequency dependent and delimited by stable boundaries corresponding to locations of multimodal activity. Within these functional domains, multiple remote islands of correlated activity derived from seed-pixel correlation maps were observed and, by moving the location of seed pixels, the topography of long range connections within somatosensorimotor as well as visual cortex were clearly revealed. These results showed that within mouse cortex, several functional modules run in parallel and that the classical cytoarchitectonic boundaries of cortical areas are not the only constraint for clustering.

The dorsal mesoscopic network is parcellated in three main functional clusters

With the development of new tools, cortical mapping can now be performed at different spatial scales and using multiple functional modalities (Pollock et al., 2014; Hawrylycz et al., 2016). One obvious example is the major advances made during the last decade on macroscopic human brain functional connectivity mapping using resting-state spontaneous activity in fMRI (Fox and Raichle, 2007). More recently, these approaches have been applied to mouse models with success (van Meer et al., 2010; Jonckers et al., 2011; Guilfoyle et al., 2013; Mechling et al., 2014; Nasrallah et al., 2014; Sforazzini et al., 2014; Liska et al., 2015; Zerbi et al., 2015). However, weak signal and low spatial resolution are the two main limiting factors when using fMRI on mice. Moreover, the fundamental interpretation of spontaneous BOLD signals as a neural activity correlate is not entirely clear (Chen-Bee et al., 2007; Logothetis, 2008). In parallel to the MRI approach, different in vivo functional optical methods also measuring intrinsic signals were used to map mesoscopic neural circuits in mouse cortex (White et al., 2011; Bero et al., 2012; Guevara et al., 2013a,b; Bauer et al., 2014; Liao et al., 2014; Nasiriavanaki et al., 2014; Bergonzi et al., 2015). These approaches confirms that, although a dense pattern of direct and indirect interconnections exist between different areas (Oh et al., 2014; Zingg et al., 2014; Hintiryan et al., 2016), the functional processing operated in these different cortical territories is specialized. Now, the recent development of transgenic mice expressing supersensitive indicators, such as GCaMP6, have opened new opportunities and was used in the present study (Chen et al., 2013; Madisen et al., 2015) to explore neural circuits at different scales (Issa et al., 2014).

By calculating correlation of spontaneous activity signals between pixels of the cortex, functional domains of correlated activity were observed and revealed sharp transitions of correlation between them. These high rates of spatial changes were used to calculate correlation gradients (Cohen et al., 2008; Wig et al., 2014a) and revealed that, within the low-frequency band (<1 Hz), stable boundaries separate three functional domains encompassing different cortical areas associated with specific behaviors such as vision and navigation, locomotion and orofacial motility (Fig. 12). This boundary detection was confirmed by using parcellation methods classifying groups of pixels according to the similarity of their signal (Blondel et al., 2008; Rubinov and Sporns, 2010; Newman, 2011; White et al., 2011) and identified clusters that corresponded exceptionally well with one another and across methodological approaches, similar to previous studies performed on human subjects using fMRI (Power et al., 2011; Yeo et al., 2011). Resultantly, the boundaries between clusters were located in unsynchronized regions associated with low SD values of spontaneous calcium fluctuation and may correspond to high-level hub areas computing multimodal information such as the visuotactile region of the mouse cortex (Olcese et al., 2013), which could correspond to the pinwheel locus revealed by jitter analysis in the present study. Because of the uniformity of low-frequency activity between recordings, this observed clustering is expected to be minimally influenced by a sporadic epileptic phenotype that some transgenic lines expressing GCaMP can exhibit (Steinmetz et al., 2017).

Figure 12.

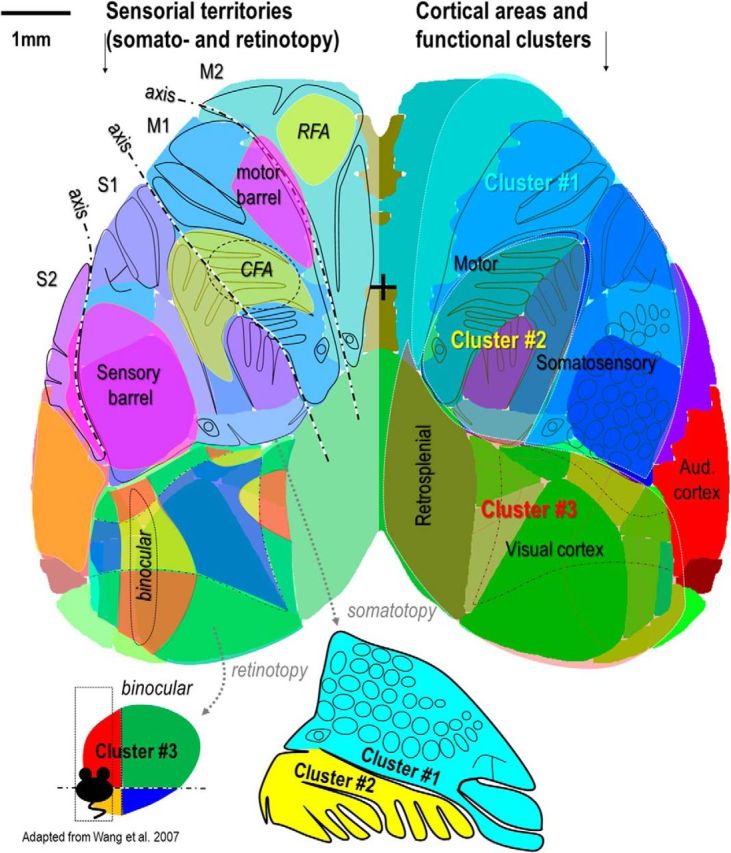
Multiple levels of mapping based on spontaneous activity. Right hemisphere, The thee functional clusters overlaid on the area boundaries from Allen Institute Atlas. Left hemisphere, Highlight of the somatotopy within sensory and primary and secondary motor cortex (related to mouse homoculus below) as well as retinotopy within visual cortex (related to the 4 visual quadrants below, the binocular zone is indicated by black dotted line). Putative caudal forelimb area (CFA) and rostral forelimb area (RFA) locations are shown in yellow, sensory and motor barrel region are shown in purple.

Another exclusive characteristic highlighted by the present study is the change of cortical parcellation observed in the higher frequency band (2–5 Hz). In contrast to the low-frequency mode, this activity segregated into two functional modules, a lateral module and a medial module, and appears consistent with previous studies using anatomical tracing and fMRI in rodents and could correspond to the delimitation of the default mode network initially described in humans (Raichle et al., 2001; Stafford et al., 2014; Zingg et al., 2014; Bota et al., 2015; Li et al., 2015; Liska et al., 2015; Rubinov et al., 2015; van den Heuvel et al., 2016).

Does fine scale topography of connections influence computational processing?

Although at a wider spatial scale, boundaries of functional domains could be revealed, inside each of these functional domains, the topography of long range connections could also be mapped at a finer scale of parcellation. Within somatosensorimotor cortex, the functional connections clearly showed the topography of reciprocal connections between S1, M1, S2, and M2 areas together within same hemisphere, but also between hemispheres (Fig. 12). These results are consistent with spontaneous activity and sensory and anatomical mapping showing a preserved topography of the somatotopy in BCS1 and BCM1 in rodent cortex (Ferezou et al., 2007; Aronoff et al., 2010; Mao et al., 2011; Hooks et al., 2013) as well as for sensory and motor cortex in human and nonhuman primates (Brock et al., 2013; Wang et al., 2013; Zeharia et al., 2015). Using resting-state spontaneous activity fMRI, consistent results were also observed in primate and human (Power et al., 2011; Yeo et al., 2011; Wang et al., 2013).

Within visual cortex, located in the posterior part of cortex, several islands of correlation were also observed and revealed the topography of connections between V1 and extrastriate areas consistent with previous studies (Wang and Burkhalter, 2007; Marshel et al., 2011; Polack and Contreras, 2012; Garrett et al., 2014). Clear interhemispheric topographic connections were also observed when seed pixels were placed in the transition zone between V1 and LM within the binocular zone wherein a larger number of interhemispheric connections can be found (Vanni et al., 2010a). Thus, by using spontaneous activity mapping approaches, this work revealed axes of symmetries between different adjacent visual areas, similar to those revealed by retinotopic mapping in human and other animal models (DeYoe et al., 1996; Engel et al., 1997; Vanni et al., 2010b, 2015; Marshel et al., 2011; Garrett et al., 2014, 2017; Zhuang et al., 2017).

Topography and functional domain boundaries are the strongest rules of the functional parcellation: is the concept of “cortical area” obsolete?

Within cortex, neighboring neurons generally share similar functional properties and this organization is assumed to be a strategy to optimize computation (Kaas, 1997). By using mesoscopic calcium imaging, several levels of cortical functional organization have been revealed. At higher levels of parcellation, functional modules presenting strong specificity of neuronal activity have been defined, whereas at a lower level, the topography between brain regions of each functional module has been mapped. Interestingly, whatever the level of parcellation, the boundaries of clusters generally did not entirely correspond to cytoarchitectonic cortical area boundaries, consistent with previous reports in humans (Wig et al., 2014). Thus, the concept of cortical area should be revisited to take into account the fact that multiple cortical areas could be involved in a variety of functions. For example, in mouse, the pair of S1 and M1 territories are involved in whisking exploration (Ferezou et al., 2007). Thus, the strong difference in motor and cognitive processing involved in these two different behavioral activities could have a significant impact on cortical parcellation, much more than architectonic divisions alone.

From mouse to human cortex parcellation

By using multiple functional parcellation approaches, two or three functional territories of strongly correlated activity, depending on the frequency mode of activity, were found in the mouse dorsal cortex. In contrast, many more patterns have been revealed in human studies by using fMRI resting-state functional connectivity (Power et al., 2011, 2014; Yeo et al., 2011; Wig et al., 2014). Although some similar modules could be observed between these two experimental approaches, direct correlates must be interpreted carefully. The human brain and behavior are expected to be more complex and could be at the origin of the larger number of functional modules defined. However, optical access was restricted to the dorsal cortex in our experimental preparation; a large portion of ventromedial cortex was not imaged and could be the main limiting factor of the number of clusters found. Although, full-brain functional parcellation using fMRI resting-state functional connectivity in mouse also defined a larger number of functional clusters (Jonckers et al., 2011; Mechling et al., 2014; Sforazzini et al., 2014; Liska et al., 2015).

Thus, by exploring different spatial and temporal levels of mesoscopic mapping, several imbricated levels of parcellation and topography were defined. Beyond the basic description of mouse cortex functional organization, this work also opens new possibilities in the exploration of neural circuits by using an animal model offering quantitative behavior assay as well as multiple brain disease models.