Place and Grid Cells in a Loop: Implications for Memory Function and Spatial Coding

Abstract

Place cells in the hippocampus and grid cells in the medial entorhinal cortex have different codes for space. However, how one code relates to the other is ill understood. Based on the anatomy of the entorhinal-hippocampal circuitry, we constructed a model of place and grid cells organized in a loop to investigate their mutual influence in the establishment of their codes for space. Using computer simulations, we first replicated experiments in rats that measured place and grid cell activity in different environments, and then assessed which features of the model account for different phenomena observed in neurophysiological data, such as pattern completion and pattern separation, global and rate remapping of place cells, and realignment of grid cells. We found that (1) the interaction between grid and place cells converges quickly; (2) the spatial code of place cells does not require, but is altered by, grid cell input; (3) plasticity in sensory inputs to place cells is key for pattern completion but not pattern separation; (4) grid realignment can be explained in terms of place cell remapping as opposed to the other way around; (5) the switch between global and rate remapping is self-organized; and (6) grid cell input to place cells helps stabilize their code under noisy and/or inconsistent sensory input. We conclude that the hippocampus-entorhinal circuit uses the mutual interaction of place and grid cells to encode the surrounding environment and propose a theory on how such interdependence underlies the formation and use of the cognitive map.

SIGNIFICANCE STATEMENT The mammalian brain implements a positional system with two key pieces: place and grid cells. To gain insight into the dynamics of place and grid cell interaction, we built a computational model with the two cell types organized in a loop. The proposed model accounts for differences in how place and grid cells represent different environments and provides a new interpretation in which place and grid cells mutually interact to form a coupled code for space.

Introduction

Place cells in the hippocampus (O'Keefe and Dostrovsky, 1971) and grid cells in the medial entorhinal cortex (MEC; Hafting et al., 2005) differentially encode the current position of the animal. Place cells are only active when the animal is in a restricted part of the environment, known as place field. Although small environment changes have no or little effect on place fields (pattern completion), larger changes may lead to pattern separation in which place fields either move to unpredictable new positions (global remapping; Muller and Kubie, 1987; Quirk et al., 1990; Leutgeb et al., 2004, 2005b; Wills et al., 2005) or remain at the same position but with altered firing rate (rate remapping; Leutgeb et al., 2005b, 2007; Leutgeb and Leutgeb, 2007). On the other hand, grid cells have many place fields organized in a regular triangular pattern that covers the whole environment. The distance between place fields of the same grid cell is constant across different environments, but their specific locations change (grid realignment; Fyhn et al., 2007; Leutgeb et al., 2007). The spatial codes of place and grid cells are interdependent; for instance, grid realignment co-occurs with global remapping but not rate remapping (Fyhn et al., 2007; Colgin et al., 2010). However, how the spatial codes of place and grid cells relate to each other is not fully understood.

Available anatomical and neurophysiological data may provide the necessary pieces for completing the puzzle of how place and grid cell codes interact: the hippocampus and the entorhinal cortex are organized in a loop (Tamamaki and Nojyo, 1995; Tamamaki, 1997; Johnston and Amaral, 1998; Witter et al., 2014); place cells develop before grid cells (Langston et al., 2010; Wills et al., 2010) and do not require grid cells to form place fields (Koenig et al., 2011; Hales et al., 2014); place cells increase firing stability with age much more gradually than the abrupt time course of grid cell maturation, and peak place field stability coincides with the maturation of grid cells (Muessig et al., 2015); place cells can globally remap when grid cells are impaired by septal inactivation (Brandon et al., 2014); and exhibit pattern completion and separation even before grid cells have matured (Muessig et al., 2016); the triangular regularity of grid cells vanishes if inputs from place cell are removed (Bonnevie et al., 2013). Altogether, the evidence suggests that the spatial code of place and grid cells are complementary (Bush et al., 2014).

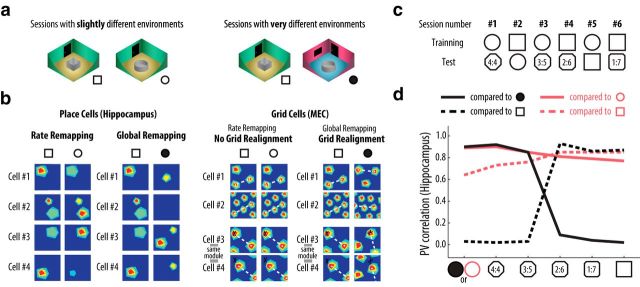
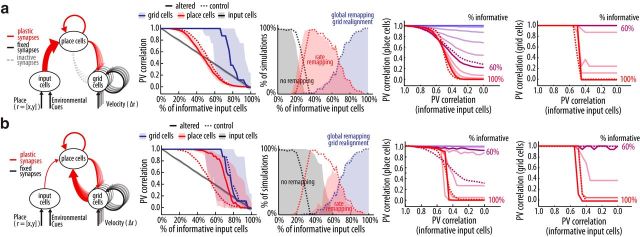
In this study, we sought to understand how all these pieces come together with a model with place and grid cells organized in a loop. To that end, we used the model to simulate experiments in which animals were trained and tested in different environments (Leutgeb et al., 2005a, 2007; Wills et al., 2005; Leutgeb and Leutgeb, 2007; Colgin et al., 2010; Lu et al., 2013). In these experiments, the animals are first familiarized to two environment setups with a controllable number of shared landmarks (training sessions); later, electrophysiological data are recorded as the animals revisit the initial setups (test sessions). Depending on whether the initial setups are slightly or very different (Fig. 1a), one can observe, respectively, rate remapping without grid realignment or global remapping with grid realignment (Fig. 1b). During the test sessions of some experiments, the environment can be configured in intermediate setups (Fig. 1c) to probe for pattern completion and separation (Fig. 1d).

Figure 1.

Place cell remapping and grid cell realignment. a, In experiments that evoke remapping, animals are familiarized to slightly different or very different environment setups (Leutgeb et al., 2005b). b, Schematic of place and grid cell rate maps for conditions with rate and global remapping of place cells. Grid cell realignment only occurs in conditions leading to place cell global remapping (Fyhn et al., 2007). c, Protocol for morphing experiments. During training sessions, the animals explore the two extreme setups in alternated sessions. Later, during test sessions, the animals explore variable setups in a random order. d, PV correlation curve for hippocampal ensemble activity for rate (red) and global remapping (black) experiments, shown as reference to round (solid line) and square shaped wall (dashed line). Adapted from Colgin et al., (2010). PV correlation measures the similarity in ensemble neuronal activity between different experimental conditions.

The questions we intended to answer are as follows: (1) Does a model with grid and place cells organized in a loop support multiple memory-related phenomena such as representation accuracy, pattern completion, pattern separation, rate and global remapping and grid realignment? (2) Which features are essential for any/all these processes? (3) How does grid realignment relate to place cell remapping and what determines whether rate or global remapping occurs? (4) What is the role of grid cells in the representation of different environments? By answering these questions, our work provides insight into the computational principles governing the spatial codes of place and grid cells.

Materials and Methods

All codes were written in Python and can be obtained on request from the authors.

Virtual environment.

An environment is defined by a discrete Cartesian subspace (a set of 4 × 4 bins) and a context value (s, 0 ≤ s ≤ 1). The granularity of the representation was selected such that each spatial bin, also referred to as “position” or “location”, corresponds to an area of 400 cm² in the original morphing experiment (arena size of 80 × 80 cm), which is smaller than the average place field size (∼900 cm²; Leutgeb et al., 2007; average size computed by de Almeida et al., 2009a). The use of a coarse grain dramatically reduces the computational cost of the simulations but still allows the use of standard rate map analyses. The context value encodes the environment setup used in the experiment. For example, in the morphing experiment, we define s = 0.0 for the circle environment, s = 1.0 for the square environment, and s = 0.5 for the environment in-between. Thus, although we mention square and round environments in the text to use the same nomenclature as the experimental reference, all environments are implemented as a square grid of bins.

Emulation of experiments with environmental modifications.

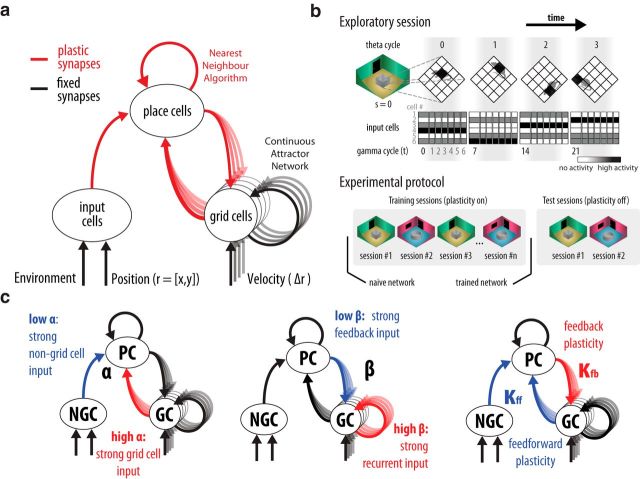
Simulated experiments mimicry actual protocols applied to rats. We define an experiment as a sequence of sessions simulated in order. Each session corresponds to the trial in which a rat can freely explore one environment. For each session, we define a context value (s) that encodes the environment setup and a sequence of visited positions (a “trajectory”). Each set of seven gamma cycles (1 theta cycle, see below) is associated with one fixed position. The trajectories are implemented as random permutations of all possible positions, such that each spatial bin is visited at least once. Thus, the animal can move from one position to any other in the arena in the next theta cycle; the instantaneous velocity (v) is the resultant vector from the subtraction between the current and the previous positions. Context values in different sessions emulate environment modifications in studies with rats. The synaptic weights are randomly initialized before the experiment as described below (naive network). In the training sessions of the experiment, multiple sessions are simulated with alternating context values (s = 0 or 1). During the training sessions, the synaptic weight can be modified (see learning rules in the Grid cells and Place cells subsections). The synaptic weights are maintained from one session to the other. During the test sessions, the synaptic weights are fixed. The analysis was performed on data acquired during test sessions. In experiments designed to study the dynamics of model convergence (Figs. 3, 4), all training and test sessions used the same fixed position. Training and test sessions were intercalated to evaluate the effect of learning on network activity. In these experiments, the network was trained with either one (s = 0; Figs. 3, 4a) or two context values (s = 0 and s = 1; Fig. 4b) and tested with the full range of values (s = 0 to 1). In exploration experiments (Figs. 5–9), 12 training sessions of different trajectories with five visits to each position and with alternate context values (s = 0 and s = 1) were simulated before the test sessions. In the network of Figure 8a, 60 training sessions of trajectories with one visit to each position were simulated. In morphing experiments, intermediate context values (0 ≤ s ≤ 1) were used to emulate the modification of the walls in test sessions.

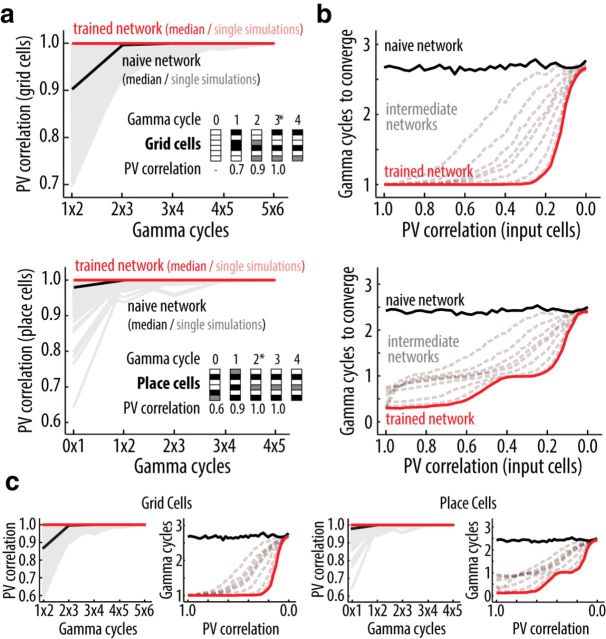
Figure 3.

Network convergence within one theta cycle. a, Average correlation between the patterns of ensemble activity (PVs) of grid (top) and place cells (bottom) in two subsequent gamma cycles. Median (solid lines) and single simulations (shaded lines) results shown for naive (black) and trained networks (red). Network activity is stable when the PV correlation between subsequent gamma cycles is >0.99. Insets, Color-coded PVs for a sample of six cells across different gamma cycles, along with corresponding cycle-to-cycle PV correlations. *Indicates the gamma cycle in which the network converged. Note that grid cells in the first cycle are silent since the place cell input from the previous cycle is not defined. b, Average number of gamma cycles required for grid (top) and place cell (bottom) network convergence as a function of the PV correlation between the input patterns of training and test sessions. Results shown for naive (solid black line, 0 training sessions), intermediate [dashed gray lines, (2, 5, 10, 20, 30, 40) training sessions], and trained (solid red line, 50 training sessions) networks. c, as in a and b, but for simulations performed with the alternative model.

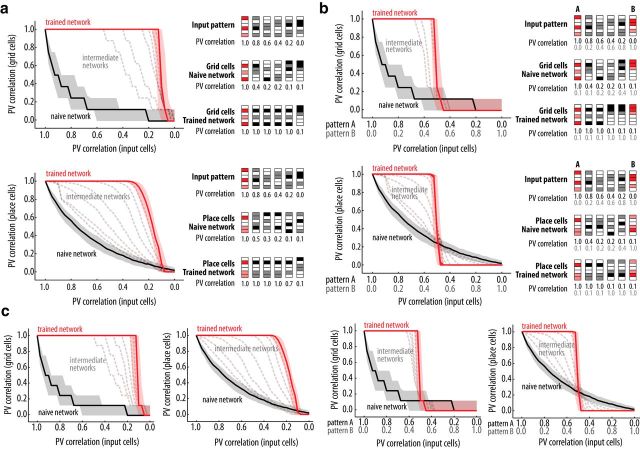
Figure 4.

Rapid pattern completion and attractor dynamics in place and grid cell network. a, b, PV correlation (median and interquartile range) of converged grid (top) and place cell (bottom) patterns within the first theta cycle as a function of the similarity between input patterns. Right, Color-coded PVs for a sample of input and grid/place cells with varying input patterns. a, Network trained with one input pattern. b, Network trained with two input patterns. For grid and place cells, PV correlation computed between the converged pattern and the activity pattern obtained with the training input (shown in red). Results shown for naive (solid black line, 0 training sessions), intermediate [dashed gray lines, (2, 5, 10, 20, 30, 40) training sessions], and trained (solid red line, 50 training sessions) networks. c, as in a and b, but for simulations performed with the alternative model.

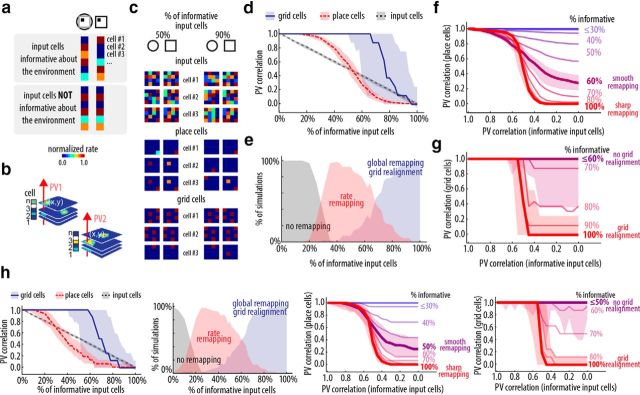
Figure 5.

Global remapping and grid realignment in a bidirectional place and grid cell network. a, Representation of the activity of input cells in different environments (left and right, color-coded vectors). Input cells informative about the environment change their firing rates (top), whereas noninformative input cells do not (bottom). b, Scheme showing two PVs built from the tiling of rate maps. c, Sample rate maps from input, place, and grid cells in two environment conditions (square and round) and different percentages (50% and 90%) of input cells that are informative about the environment. d, Average PV correlation of place (dashed red), grid (solid blue), and input cells (dashed gray) between the two environments as a function of the number of input cells which are environment-informative. Line represents median, shaded area is the interdecile range of values for 64 runs. e, Percentage of simulations that resulted in no remapping, rate remapping, or global remapping depending on how environment-informative the input was. f, g, PV correlation curves of place (f) and grid cells (g) in the morphing experiment. Results shown as a function of the PV correlation of informative input cells. Different colors depict results for varying percentage of input cells which are informative about the environment (coded from red, high informative, to blue, low informative). Line represents median; shaded area is the interdecile range of values for 64 runs shown for 60% and 100% informative inputs. Network parameters are α = 0.1, β = 0.7, κ_fb = 0.5, κ_ff = 0.01. h, as in d–g, but for simulations performed with the alternative model.

Figure 9.

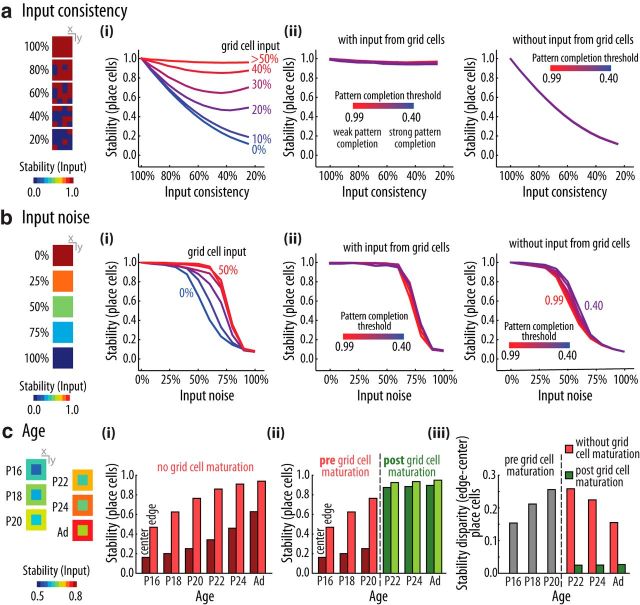
Effect of grid cell input on the stability of place cell representation. a, b, Place cell stability across multiple explorations of the same environment with different levels of (a) input consistency and (b) input noise. Place cell stability was defined as the average PV correlation of place cell rate maps (n = 64 sessions; see Material and Methods). Input consistency is the percentage of positions in which input cells have the same pattern of activity upon different visits to the position. Input noise is defined as the percentage of input cells that have random activity regardless of the position. Leftmost panels illustrate different levels of input consistency and input noise by means of the spatial map of the stability of input cells, defined as the average PV correlation of input cells for each position. Right, Place cell stability for networks with (ai, bi) variable strength of grid cell input, color coded from blue (no grid cell input) to red (strong grid cell input); and (aii, bii) variable threshold for the pattern completion algorithm in place cell activity, color coded from red (weak pattern completion; γ = 0.99) to blue (strong pattern completion; γ = 0.40), and shown for strong (40%, left) and no (0%, right) grid cell input to place cells. c, The leftmost panel shows the spatial stability of input cells depending on age, simulated as a reduction of input noise. For all ages, input noise in the center was higher than in the edge of the arena. Right, Place cell stability separately for center and edge for networks (ci) without grid cell input and (cii) with grid cell input only after P20. The disparity between edge and center stability is also shown (ciii).

Figure 8.

Effects of session length and plasticity in the feedback synapses on place cell remapping and grid realignment. Left, Variations of the model described in Figure 2, as follows: a, the training sessions are shortened by a factor of 5 and run five times more, such that the total length of training is unchanged; b, plasticity in the feedback synapses from place to grid cells is five times weaker (κ_fb = 0.1). Second to fifth panels as in Figure 5d–g. Results of the control network (Fig. 5) are reproduced as dashed lines; in the fourth and fifth panels, only PV curves for 60% and 100% informative inputs of the control network are shown.

Simulation of ensemble neural activity.

Input, place, and grid cells are modeled as rate-based neurons. The set of firing rates (i.e., the ensemble activity) is computed iteratively. Each iteration cycle t is assumed to correspond to one gamma cycle; the assumption of a time resolution of one gamma period (10–25 ms) was motivated by the use of a competitive 10%-max winner-take-all mechanism to select which cells fire (see below), which was postulated to occur within a gamma cycle (de Almeida et al., 2009b). A theta cycle is defined as a sequence of seven gamma cycles to reflect the ratio between theta and gamma frequencies (∼8 Hz and ∼40–100 Hz, respectively); however, using a lower number of gamma cycles per theta leads to similar results because network convergence occurs within two to four gamma cycles (see Fig. 3). The ensemble neural activity computed in a gamma cycle is used as input in the computation of the ensemble activity in the next gamma cycle. In brief, the ensemble activity of input cells is defined based on the current position and context; the ensemble activity of grid and place cells is computed applying a population-wide competition over the integrated input (de Almeida et al., 2009b).

Input cells.

Input cells (n_input = 500 cells) are informative about the current position and context and are the only source of context information in the model. The firing rate of each cell i, A_input (i, r, s), is set at the beginning of each theta cycle and remains constant in all nested gamma cycles within the theta cycle. A_input (i, r, 0) and A_input (i, r, 1) are independently defined for each cell and position as the product of two uniform random variables on (0,1) to produce a left-skewed distribution of firing rate values (for a discussion about the non-Gaussian distribution of firing rates, see Roxin et al., 2011); A_input (i, r, s) = A_input (i, r, 0) if s < c(i), otherwise A_input (i, r, s) = A_input (i, r, 1), where the context transition value (c(i)) is randomly defined for each cell from a uniform distribution on (0, 1). A subset of the input cells is made uninformative about the context by setting A_input (i, r, 0) = A_input (i, r, 1) at every position. The percentage of input cells that are informative about context is a free parameter in the simulations. The ensemble activity vector of the input cells at a given gamma cycle is also referred to as the input pattern.

Grid cells.

To implement the observed discretization of the entorhinal grid map, in which cells are clustered into modules of the same grid spacing (Stensola et al., 2012), we simulated eight modules of grid cells organized in an N × N square lattice. Each module is implemented as an independent continuous attractor network with recurrent connections (see below) such that the grid spacing of its grid cells is fixed and determined by the number of cells in the module (Guanella et al., 2007). To achieve the observed grid scaling of ∼√2 between modules (Stensola et al., 2012), the side of the square lattice is increased by two cells; namely, the eight modules respectively have 2 × 2, 4 × 4, 6 × 6, 8 × 8, 10 × 10, 12 × 12, 14 × 14, and 16 × 16 cells, totaling n_grid = 816 cells.

The activity of grid cells A_grid(i, t) at each gamma cycle t is computed from the integrated input following a competitive 10%-max winner-take-all mechanism (de Almeida et al., 2009a,b) effective over each module:

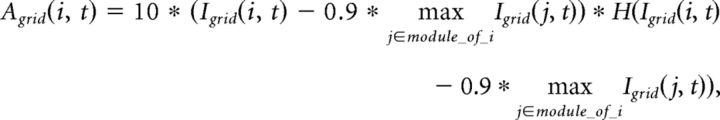where I_grid(i, t) is the integrated input of grid cell i at cycle t and H(.) is a Heaviside function. I_grid(i, t) is determined by a convex sum of the feedback drive from the place cells, I_grid^place, and the recurrent drive from the module of grid cells, I_grid^grid:

where the free parameter β balances the influence from recurrent and feedback inputs. I_grid^place(i, t) at gamma cycle t is computed as follows:

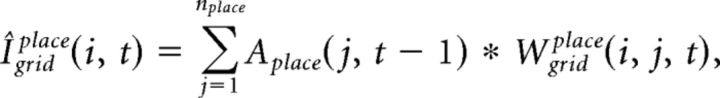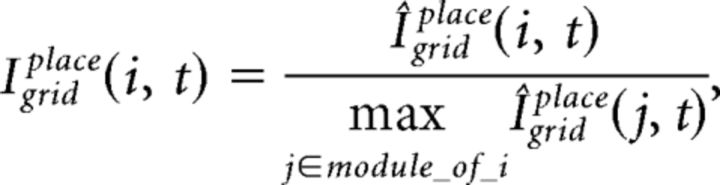where n_place is the number of place cells and A_place(j, t − 1) is the activity of place cell j at gamma cycle t − 1 (see below), and W_grid^place(i, j, t) is the synaptic weight from place cell j to grid cell i at t. I_grid^grid(i, t) at gamma cycle t is computed as follows:

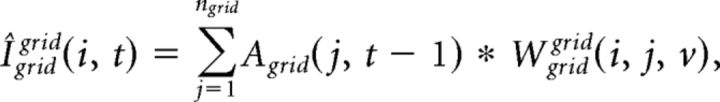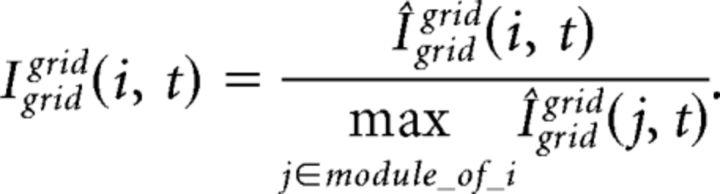Where W_grid^grid(i, j, v) is the synaptic weight from grid cell j to grid cell i at velocity v.

The synaptic weight matrix, W_grid^place, is initialized with random values from a log-normal distribution with mean = 0.0 and σ = 1.0. These synapses are plastic and their weights change every gamma cycle with a learning rate κ_fb (0.5, if not mentioned):

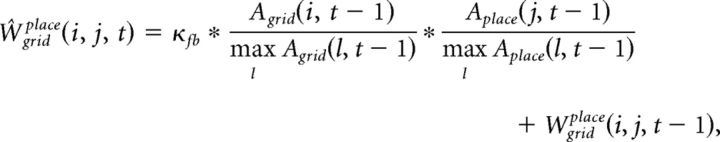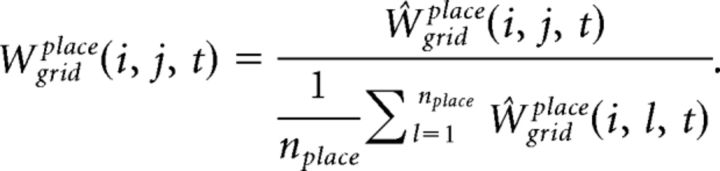The synaptic weight matrix, W_grid^grid, is fixed for each velocity v and set in such a way that the connectivity within modules of grid cells has a twisted torus topology, as described by Guanella et al. (2007). In brief, W_grid^grid(i, j, v) = 1 if cell i is connected with cell j for the velocity v and W_grid^grid(i, j, 0) = 0 otherwise. Cells from the same module are organized in an N × N square lattice such that neighboring cells code for neighboring positions. Cells in one boundary of the lattice relate with cells in the other boundary as if the lattice was tiled.

Place cells (original model).

The activity of place cells (n_place = 5000 cells) at a gamma cycle t is first computed from the integrated input following a competitive 10%-max winner-take-all mechanism over the pool of cells:

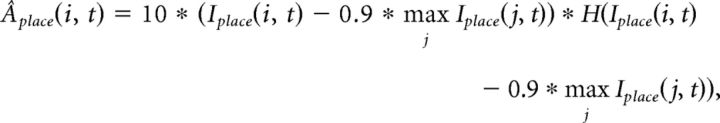where I_place(i, t) is the integrated input of place cell i at cycle t and H(.) is a Heaviside function. Thus, according to this rule, a place cell is active in a given gamma cycle if its integrated input is within 10% of the integrated input of the place cell with maximal input (de Almeida et al., 2009b). Next, a pattern completion procedure adapted from Rennó-Costa et al. (2014) is used to compare the current ensemble activity with previously stored patterns. Thus, we do not explicitly model the connectivity among place cells, but we model an equivalent stereotyped pattern completion mechanism. If the highest correlation between the vector Â_place(t) = [Â_place(1, t), …, Â_place(n_place, t)] and the previously stored patterns of activity is below a threshold value γ (0.8, if not mentioned), then Â_place(t) is incorporated into the memory as a new pattern. Otherwise, A_place(t) is set as follows:

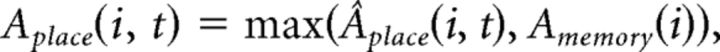where A_memory is the pattern with the highest correlation with Â_place(t).

The integrated input of place cells, I_place, is determined by a convex sum of the feedforward drive from grid cells, I_place^grid, and from input cells, I_place^input:

where the free parameter α balances the influence from grid and input cells. I_place^grid(i, t) and I_place^input(i, t) at every gamma cycle t is computed as follows:

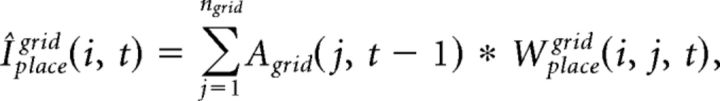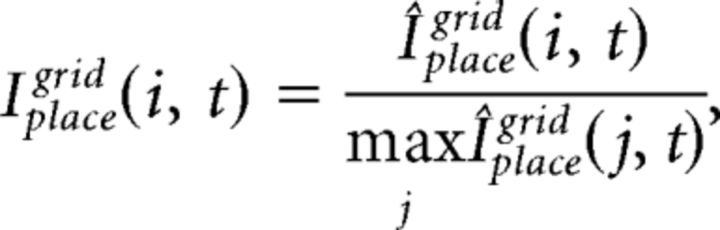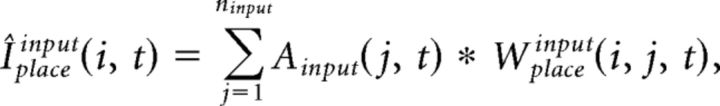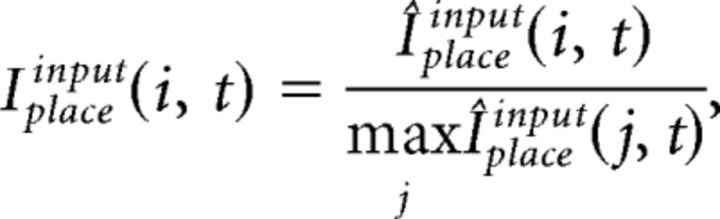where W_place^grid(i, j, t) is the synaptic weight from grid cell j to place cell i at t, and W_place^input(i, j, t) is the synaptic weight for input cell j to place cell i at t.

The synaptic weight matrices W_place^grid(i, j, t) and W_place^input(i, j, t) are initialized with random values from a log-normal distribution with mean = 0.0 and σ = 1.0. These synapses are plastic and their weights change every gamma cycle with learning rate κ_ff (0.01, if not mentioned):

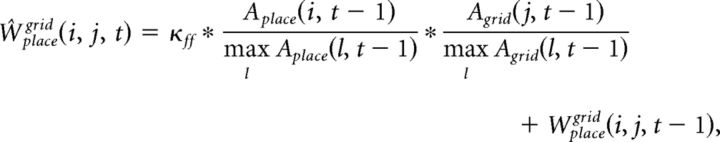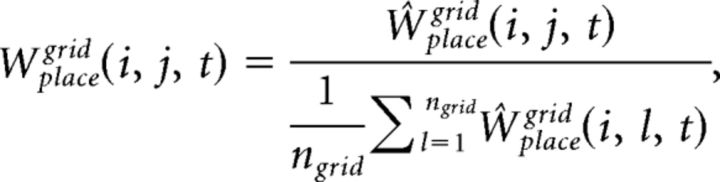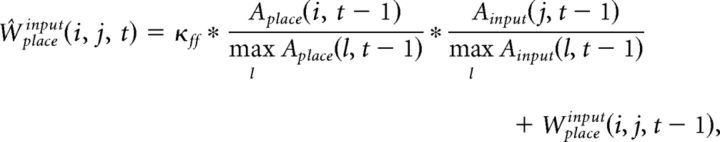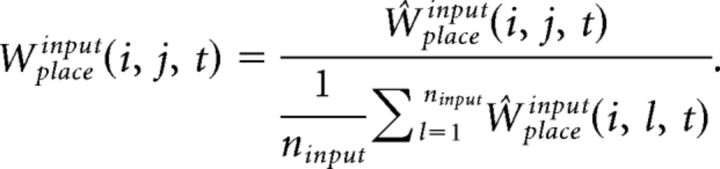Place cells (alternative model).

To determine whether the results of the original model could be due to the different implementations of the recurrent connections within the place and the grid cell networks, we also run simulations in an alternative model in which the recurrent input from place cells, I_place^place, takes part in their integrated input, I_place:

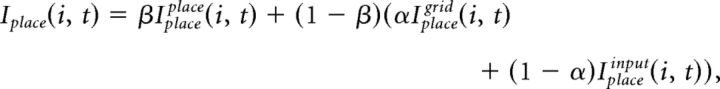where the free parameter β balances the influence from the recurrent inputs and has the same value as the one used for the grid cell network.

The activity of place cells (n_place = 5000 cells) at a gamma cycle t is computed as in the original model:

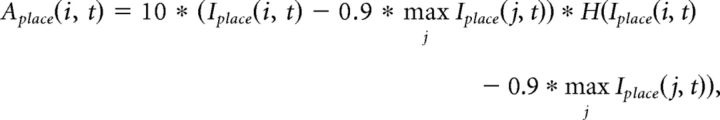and, also as in the original model, if the maximum correlation between the population vector of the computed activity of place cells, A_place(t), and all stored patterns is below a threshold value (0.8, if not mentioned), A_place(t) is incorporated into the memory as a new pattern.

The recurrent input I_place^place(i, t) is defined based on the population vector of place cell activity in the previous gamma cycle, A_place(t − 1), such that A_place(t − 1), such that I_place^place(i, t) = 0 for every place cell if A_place(t − 1) was not stored in memory; otherwise, I_place^place(i, t) = max(A_place(i, t − 1), A_memory(i)), where A_memory is the stored pattern with the highest correlation with A_place(t − 1).

Experimental design and statistical analysis.

The correlation of the population vectors (PVs) in different conditions was used to assess the level of change in the ensemble activity (Leutgeb et al., 2007). In Figure 3, we computed the PV correlation between two subsequent gamma cycles. In this case, network convergence is defined as PV correlation >0.99. In other figures, we computed the PV correlation of the last gamma cycle in the same position (r) between different contexts (s). To assess whether the hexagonal grid pattern is present in the rate map of grid cells, we measured the maximum PV correlation between the grid cell rate map and all possible hexagonal templates of the same scale of the grid cell module under analysis. A PV correlation >0.95 indicated a match between the grid cell rate map and a precise hexagonal pattern. The grid firing pattern was considered present if all grid cells had a match with a precise hexagonal pattern. Place cells were considered active if their firing rate was non-zero positive in at least one spatial bin. For each cell, the number of place fields is the number of spatial bins with non-zero positive rate values. The population of place cells was considered to have a regular number of place fields if the average number of place fields of active cells was between 1 and 1.5.

Motivated by the fact that the spatial stability of place cell firing depends on age and specific location (Muessig et al., 2015), we evaluated how the amount of noise in the sensory input may influence place cell stability. The noise level of a spatial position refers to a specific percentage of input cells that have activity values randomly defined at each visit to the position. We performed three kinds of experiments to evaluate place cell stability: (1) variations in “input consistency” (see Fig. 9a): in these simulations, the noise level was either 0% or 100% at each position, and we varied the ratio of noisy/non-noisy positions (the first position of the trajectory was always non-noisy); (2) variations in “input noise” (see Fig. 9b): in these simulations, the noise level was uniform across all positions and varied from 0% to 100%; and (3) variations in “age” (see Fig. 9c): in these simulations, the noise levels linearly decreased with age, from 40% to 20% at the edge of the arena, and from 50% to 30% at the center. We assessed the stability of place cell activity across multiple simulations (n = 64) of trained networks under the same experimental condition. For each position, we first computed the average PV correlation over all pairwise combinations of the different simulations. Place cell stability was then measured as the average PV correlation over either all positions (see Fig. 9a,b) or restricted to edge/center positions (see Fig. 9c).

Results

We incorporated a feedback loop to a hippocampal-entorhinal circuitry model (Fig. 2a; see Material and Methods) and investigated with computer simulations whether the resulting dynamics accounts for changes in spatial firing patterns of grid and place cells upon environmental modifications (Leutgeb et al., 2005b, 2007; Wills et al., 2005; Fyhn et al., 2007; Colgin et al., 2010; Fig. 1). The simulations mimicked the experimental protocols, thus allowing for direct comparisons. These experiments had training sessions in which animals were familiarized to two environment setups, and test sessions in which neurophysiological data were recorded. In the simulation, an exploratory session was implemented by establishing a trajectory (a sequence of positions) and a context value related to the environment setup (Fig. 2b). Position and context were encoded in the activity of input cells [i.e., cells that provide input to place cells such as lateral entorhinal cortex (LEC) and MEC non-grid cells], and the ensemble activity of place and grid cells was computed for the specific location defined in the trajectory. We implemented both training and test sessions. The initial network with the synaptic weights initialized randomly is denoted as a naive network. Training sessions include multiple experimental sessions with alternated context values and synapses modeled as plastic. The network after the training sessions is denoted as a trained network. As in experimental studies (Leutgeb et al., 2007), the similarity of the ensemble activity of grid and place cells was analyzed using the correlation of population vectors (PV, an array of firing rates indexed by cell number) across conditions. Simulated data used in the analysis were collected during the test sessions.

Figure 2.

Model of place and grid cell network with bidirectional connectivity. a, Circles denote neuronal populations. Arrows represent synaptic connections. Synapses are either fixed (black) or plastic (red). Place cells recurrent collaterals are modeled implicitly by a pattern completion process like a nearest neighbor algorithm which requires learning (Rennó-Costa et al., 2014). Place cell population adapted from Rennó-Costa et al. (2010, 2014; n = 5000 neurons). Grid cells recurrent collaterals are fixed and implement a continuous attractor network model as by Guanella et al. (2007; n = 816 neurons). Input cell population as by Rennó-Costa et al. (2010; n = 500 neurons). b, The experiment comprises the simulation of sequential sessions divided into training and test sessions. Each session has a characteristic context value (s) and a trajectory of position values (r). The rat stays at a position for a theta cycle (or 7 gamma cycles). The activity of input cells is determined in each gamma cycle based on the position and context values. The naive network is the network prior the training sessions whereas the trained network is the network after the training sessions. Analyses are performed on data collected during the test sessions. c, Model parameters. α denotes connection strength from grid to place cells normalized by the overall feedforward connection strength reaching the place cells $\left(\alpha =\frac{\text{GC}\to \text{PC}}{\text{GC}\to \text{PC}+\text{NGC}\to \text{PC}}\right)$. β denotes the normalized strength of the recurrent connections among grid cells in relation to the feedback connection strength from place to grid cells $\left(\beta =\frac{\text{GC}\to \text{GC}}{\text{GC}\to \text{GC}+\text{PC}\to \text{GC}}\right)$. κ_fb and κ_ff denote learning rate for the feedback and feedforward synapses, respectively. NGC, Non-grid cells (input cells); PC, place cells; GC, grid cells. Default parameters: α = 0.1; β = 0.7; κ_fb = 0.5; κ_ff = 0.01.

Ensemble activity of grid and place cells was computed as follows: place cells compete to determine which cells fire (de Almeida et al., 2009b) based on the rapid integration of the projections from input and grid cells. Importantly, the dynamics of local competition is assumed to occur at every gamma cycle (de Almeida et al., 2009b), which delimits the time resolution of the simulation (∼20 ms). Place cells are subject to a pattern completion process emulating the effect imposed by the recurrent collaterals that is equivalent to a nearest neighbor algorithm (Rennó-Costa et al., 2014). Place cells' recurrent collaterals are not modeled explicitly and are separated from the competition process. This model choice was motivated by the fact that they have transmission time much shorter than a gamma period (Miles, 1990; Guzman et al., 2016); moreover, given the fast monosynaptic transmission among recurrent place cells, in the model the hippocampal pattern completion process was assumed to be effective within the same gamma cycle. Grid cells compete with similar mechanisms of the place cells but based on the rapid integration of the projections from place cells and recurrent connections from other grid cells. Recurrent grid cell connections are hardwired to form independent modules of velocity-driven continuous attractor networks (Guanella et al., 2007). Contrarily to the place cells recurrent network, we chose to model the grid cell attractor network explicitly and effective in the next gamma cycle. This model choice was based on the assumption of disynaptic communication between grid cells (Couey et al., 2013; Pastoll et al., 2013), but we note that the experimental evidence for this is controversial (Fuchs et al., 2016).

Synapses connecting different neuronal groups (grid cells, place cells, and input cells) are subject to Hebbian-like plasticity. The main parameters of the model (Fig. 2c) are the relative input strength from grid cells and input cells to place cells, the relative input strength from recurrent grid cells and place cells to grid cells, whether the incoming synapses of place cells or grid cells are plastic, and the threshold for intrahippocampal pattern completion. As default values, we consider plasticity enabled in all synapses and stronger recurrence input than place cell input to grid cells, a condition necessary for the emergence of grid firing pattern in our model. Grid to place cell input corresponded to 10% of all place cell input because grid cells are ∼20% of MEC cells (Zhang et al., 2013) and MEC and LEC projection targets at hippocampal dendrites are about the same size (Hama et al., 1989).

Of note, to check whether the results could be due to different choices of the time scale of hippocampal and entorhinal recurrence, we also simulated an alternative model in which the recurrent place cell activity is fed back in the next gamma cycle, as implemented for the grid cells (see Material and Methods).

Network dynamics within a theta cycle

Before simulating the exploration sessions, we evaluated whether the rapid dynamics of the model is compatible with the time characteristic of the hippocampal neurophysiology. Compatibility cannot be taken as granted because the feedback loop from place to grid cells leads to intrinsic iterative dynamics, i.e., the activity pattern at a given time depends on its past, contrasting with feedforward models where the activity pattern is completely determined by the concurrent input. For this reason, feedback models can produce complex and unpredictable behavior; it is therefore important to evaluate whether model dynamics is bounded. Specifically, because the representation of the current position happens within a theta cycle (Sanders et al., 2015), the ensemble activity of place and grid cells should stabilize in a few gamma cycles (in our model a theta cycle is defined to occur every 7 gamma cycles). We thus analyzed how the ensemble activity of grid and place cells evolves in the first gamma cycles of environment exploration. We observed that the ensemble activity converges to a steady pattern within a few gamma cycles, after which the same subset of neurons is active in subsequent cycles (Fig. 3a). This occurs for naive and trained networks (naive networks use the initial synaptic weights before training session whereas trained networks had the synaptic weights modified by learning in previous explorations; see Material and Methods), although convergence is faster for the trained network (average of 2.7 gamma cycles for naive and 1 gamma cycle for trained network). We also evaluated whether using a different input pattern from the one used during training (reference pattern) affects network convergence. In trained networks, the time for convergence is only affected when the input pattern substantially differs from the reference pattern (PV correlation <0.3; Fig. 3b). As PV correlation between input patterns decreases to zero, convergence time increases but stays well within a theta cycle, approaching the time required for the naive network (∼2.7 gamma cycles). Similar results were obtained with the alternative model (Fig. 3c). Thus, the network is capable of rapidly achieving stable activity states upon changes in the input pattern, which is to say that the network promptly codes for changes in episodic variables such as the current position.

Rapid pattern completion and attractor dynamics in place and grid cell network

We next asked whether the changes in the input pattern not only affect convergence time but also influence the steady-state pattern of grid and place cell activity within a theta cycle. Given that the switch between neural representations is theta-frequency paced (Jezek et al., 2011), the converged pattern of grid and place cell activity within a theta cycle should already reflect properties observed in remapping experiments. First, when trained with different environments, for mild changes in the environment, the activity of place and grid cells is unaffected (Wills et al., 2005; Colgin et al., 2010). Second, for extensive changes in the environment, place cells globally remap and grid cells realign. Third, when morphing from one environment to another, actual place cells may abruptly shift between representations (Wills et al., 2005; Colgin et al., 2010).

In our simulations, although the naive network exhibits drastic changes of the grid and place cell patterns for small variations in the input, they are invariant in the trained network (Fig. 4), which is in accordance with the first property above. Moreover, consistent with the second property, the grid and place cell patterns of the trained network are only affected when the input pattern markedly differs from the reference pattern (Fig. 4a). This effect, known as pattern completion, shows that after training the mapping of the input pattern into a pattern of grid cell activity follows attractor dynamics. Thus, long-term plasticity in the feedforward synapses from the entorhinal cortex to the hippocampus and in the feedback synapses from place cells to grid cells seem to be sufficient for the development of attractor dynamics in both place and grid cells. Finally, to test for the third property, we trained the network with two different reference patterns (A and B) and then tested intermediate input patterns. Consistent with experimental results (Wills et al., 2005; Colgin et al., 2010), we observed an abrupt switch of the grid and place cell patterns when the input pattern was an even mixture of the two reference patterns (Fig. 4b). The same observation holds for the alternative model (Fig. 4c).

Rate remapping, global remapping, and grid realignment

The results above indicate that the converged pattern of grid and place cell activity already reflects properties of remapping experiments at the very first theta cycle. It remains to be shown whether ensemble activity of place and grid cells quantitatively accounts for experimental data (Fig. 1) across a full environment exploration (i.e., across several theta cycles). We constructed rate maps from the ensemble activity obtained with the emulation of experiments that induce hippocampal remapping (Leutgeb et al., 2005b, 2007; Wills et al., 2005; Fyhn et al., 2007; Colgin et al., 2010). The simulated grid and place cells exhibited characteristic features prior and after learning, such as limited number of place fields (∼96% of active place cells had 1 place field, and ∼4% had 2 place fields; after learning, active place cells at each environment corresponded to ∼5% of hippocampal neurons) as well as presence of a triangular firing pattern for grid cells. However, with the naive network, the alignment of grid cells changed depending on the initial position of the trajectory (average PV correlation of 0.17 considering 64 trajectories). With the trained network, the alignment of grid cells was stable.

Notably, a key variable determining grid realignment and global remapping was the amount of environment information in the input cells, defined as the percentage of cells that exhibit differential firing depending on the environment (Fig. 5a). We defined rate remapping as a drop in the PV correlation (to <0.95) of the place cells (Fig. 5b) but not in the PV correlation of the grid cells (Leutgeb et al., 2005b, 2007). Global remapping and grid realignment were characterized by a reduction of the PV correlation for both place and grid cells. We observed rate or global remapping depending on the percentage of environment-informative input cells (Fig. 5c,d). Rate remapping occurs for conditions with low to moderate percentage of environment-informative input cells, whereas global remapping takes place when the percentage of input cells informative about the environment is higher than a threshold (∼65%; Fig. 5e). The threshold varied depending on initial conditions (i.e., input patterns and synaptic weights), which is in accordance with the fact that global remapping is not consistently evoked by subtle changes in the environment (Wills et al., 2005; Fyhn et al., 2007; Leutgeb et al., 2007; Colgin et al., 2010), whereas it is reliably induced by extensive changes in the environment (Leutgeb et al., 2005b; Fyhn et al., 2007; Colgin et al., 2010).

Sharp transition of hippocampal ensemble activity in the morphing experiment

We also analyzed ensemble activity in protocols involving full exploration of intermediate configurations of the reference environments through morphing of the arena (Wills et al., 2005; Leutgeb et al., 2007; Colgin et al., 2010). These experiments were designed to verify whether hippocampal-entorhinal network activity exhibits attractor dynamics identified in auto-associative memory systems (Hopfield, 1982; McNaughton and Morris, 1987; de Almeida et al., 2007). As in experimental data (Colgin et al., 2010), when morphing through environments, we observed a sharp transition in the place cell PV correlation curve in conditions that induced global remapping (>60% of informative input cells) or a smooth transition otherwise (Fig. 5f). Importantly, the sharp transition in the pattern of place cell activity co-occurs with a sharp transition in the pattern of grid cell activity (Fig. 5g). Of note, for all simulation protocols we found no qualitative difference with the alternative model (Fig. 5h).

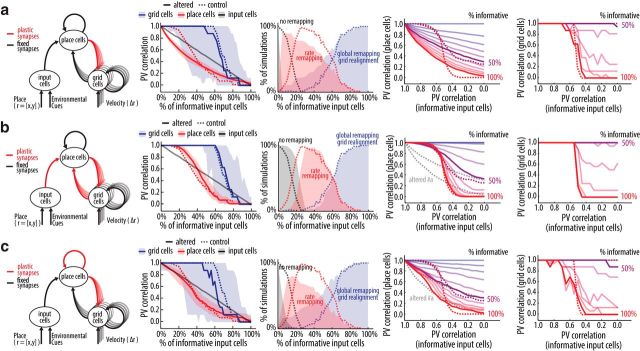
We next evaluated which features of the model were determinant for the appearance of the sharp transition of hippocampal ensemble activity in the morphing experiment. We first considered the hypothetical experiment in which hippocampal plasticity is impaired (both for synapses from the entorhinal cortex and for its recurrent collaterals; the latter is equivalent to having no intrahippocampal pattern completion). Depending on the percentage of informative input cells, global remapping with grid realignment could still be observed, but the sharp transition in the morphing experiment vanished (Fig. 6a). We next evaluated the effect of plasticity on each pathway separately. With plasticity in the input synapses and without intrahippocampal pattern completion, the sharp transition in the morphing experiment became once again apparent (Fig. 6b). On the other hand, the network still exhibited a smooth transition when programmed without plasticity in the input synapses but with the pattern completion algorithm effective in place cells (data not shown). Interestingly, enhancing the strength of intrahippocampal pattern completion (by reducing its threshold to γ = 0.4) led to a change in the place cell PV correlation curve that did not match the sharp transition seen in the standard network but resembled the CA3 PV correlation curve observed experimentally (Fig. 6c; Leutgeb et al., 2007; Rennó-Costa et al., 2014).

Figure 6.

Effects of hippocampal plasticity on place cell remapping and grid realignment. Left, Variations of the model described in Figure 2, as follows: a, feedforward synapses from input and grid cells to place cells are not plastic and intrahippocampal pattern completion is off; b, intrahippocampal pattern completion is off; c, feedforward synapses from input and grid cells to place cells are not plastic and the threshold for intrahippocampal pattern completion is low (γ = 0.4). Second to fifth panels as in Figure 5d–g. Results of the control network (Fig. 5) are reproduced as dashed lines; in the fourth and fifth panels, only PV curves for 60% and 100% informative inputs of the control network are shown; in the fourth panels of b and c, the PV curves for 60% and 100% informative inputs of a are also shown as gray dashed lines.

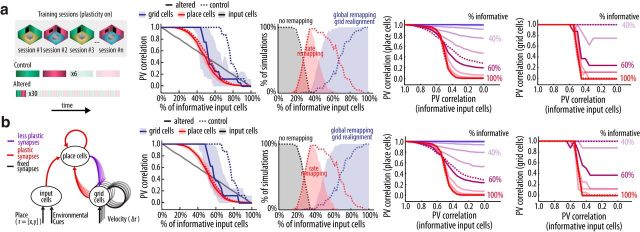
Place cells do not require grid cells to remap

We next evaluated whether the model captures the observation that place cells do not require grid cell input to remap and display pattern completion (Brandon et al., 2014; Muessig et al., 2016). We reran the previous simulations but without the synapses from the grid cells to the place cells (Fig. 7a). The removal of the grid cell input did not alter the basic characteristics of the place cells such as the number of place fields and invariability of the ensemble activity to the trajectory. Global remapping and grid realignment with a sharp transition in the morphing experiment was also observed without grid cell input (Fig. 7a, second to fifth panels). Moreover, for the experimental conditions in which the input was less informative about the environment, place cells remapped with a smooth transition but grid cells did not realign, which is characteristic of rate remapping. Despite exhibiting qualitatively similar results without grid cell inputs, however, the PV correlation curves of place cells were quantitatively different from those of the control network, indicating that the grid cell input influences associative properties of place cells.

Figure 7.

Effects of the relative strength of grid cell input on place cell remapping and grid realignment. Left, Variations of the model described in Figure 2, as follows: a, grid cell input to place cells is set to 0% of the overall input strength; b, grid cell input to place cells is set to 40% of the overall input strength. Second to fifth panels as in Figure 5d–g. Results of the control network (Fig. 5) are reproduced as dashed lines; in the fourth and fifth panels, only PV curves for 60% and 100% informative inputs of the control network are shown.

LEC impairment reduces rate remapping

LEC lesions have been previously shown to reduce rate remapping (Lu et al., 2013). In our model, removing the LEC input is equivalent to reducing the strength of the non-grid cell input to place cells. In such a scenario, which in the model is equivalent to enhancing the relative input strength from grid cells to place cells, we found that place cell rate remapping occurred in most of the simulations in a narrower range of informative input cells, from 20 to 90% (Fig. 5d) to 40–90% (Fig. 7b, third panel). Thus, although rate remapping could still be observed, our model predicts that it would be more difficult to induce experimentally because for a wide range of input changes (20–40%) rate remapping occurred in control networks but not in networks lacking LEC inputs.

Session length influences grid realignment

Different studies have found that the same level of place cell PV correlation (∼0.2) can be observed along with either rate (Leutgeb et al., 2005a) or global remapping (Colgin et al., 2010). We evaluated if the length of exploration sessions affects whether the network displays rate or global remapping. To that end, we reduced the length of the trajectory in training sessions by a factor of five while keeping the total training time unchanged by running five times more sessions. We found that such modification had little effect on place cell PV correlations but strongly affected how grid cells encoded different environments (Fig. 8a, second panel). Namely, the minimal percentage of informative input cells leading to grid realignment as the most likely outcome decreased from ∼70% in the control network to ∼50% in the modified network (Fig. 8a, third panel). These results indicate that either global or rate remapping can be observed for the same level of place cell PV correlation depending on session length during training. For instance, note that at 60% informative input cells, place cell PV correlation is <0.3 both in the control and in the modified network, which respectively exhibit rate and global remapping (Fig. 8a, fourth and fifth panels). Of note, reducing the learning rate of the feedback connection from place to grid cells by a factor of five leads to similar results (Fig. 8b).

Grid cells enhance robustness of place cell representation of space

Having shown that place cells do not need grid cells to represent different environments, we next sought to understand the functional role of these incoming connections to the place cells. Grid cells have already been implicated in other phenomena such as path planning (Kubie and Fenton, 2012; Bush et al., 2015) and mind-travel (Hasselmo, 2009; Sanders et al., 2015). For this purpose, the theoretical ability of grid cells to implement path integration (McNaughton et al., 2006) might be the means for place cells to deal with incomplete, ambiguous, and noisy sensory input. The few models that considered both pathways that interconnect grid and place cells focused on the possible role of the loop in the stabilization of the grid cells (Guanella et al., 2007; Samu et al., 2009), but they provide little insight into the implications of the loop in the activity of place cells regarding features such as pattern completion and remapping. We studied how robust is the place cell representation upon changes in the information content of the sensory input. Specifically, we tested conditions in which the positional information in sensory inputs was either inconsistent or noisy. Sensory information at a given position was considered consistent when the same set of input cells was active/inactive in different explorations of the same environment. Input consistency refers to the percentage of positions with consistent sensory information (Fig. 9a); input noise refers to the percentage of input cells that exhibit random activity regardless of the position (Fig. 9b).

Without grid cell inputs, we found that the place cell representation is highly susceptible to a reduction in the percentage of positions with consistent sensory information; on the other hand, increasing the strength of the input from grid cells allowed for stable place cell representation even when the input consistency was as low as 20% (Fig. 9ai). This result suggests that preweanling pups have lower place field stability in the center than in the border of the arena (Muessig et al., 2015) due to lower sensorial information in the center compared with the border (Solstad et al., 2008) along with the lack of mature grid cells. We also found that grid cells enhanced the robustness of place cell representation to noisy inputs (Fig. 9bi), modeled as random activity in a percentage of input cells. Therefore, a mechanism by which the relative strength of the inputs to place cells varies depending on the reliability of the sensory input can enhance the stability of the spatial representation. Finally, we found that the pattern completion algorithm acting on the place cells did not prevent the reduction in place cell stability upon changes in input consistency (Fig. 9aii), but slightly increased robustness to noisy inputs (Fig. 9bii).

In face of these results, we next sought to simulate the observations that (1) the spatial stability of the place cell representation gradually increases with age and is initially higher at the edge of the arena, and (2) that the maturation of grid cells coincides with the age in which the representation of the center and the edge of the arena are similarly stable (Muessig et al., 2015). As shown in Figure 9c, these findings could be replicated by assuming that the input noise decreases with development (Verschure et al., 2006), and is always higher in the center of the arena where border cell information is not available (Solstad et al., 2008; Bjerknes et al., 2014). We found that the enhancement of place cell stability promoted by grid cell inputs (Fig. 9a) can compensate for the edge-center difference in input noise (Fig. 9c).

Discussion

Here we show that a model with place and grid cells organized in a loop can account for rate and global remapping of place cells and realignment of grid cells. Contrary to the previous notion that grid realignment causes global remapping, in our model the place cell input to grid cells induces grid realignment during global remapping, and not the other way around. This is somewhat expected from model design because the grid cell input to place cells is weak when compared with the non-grid cell input (10% vs 90% of inputs, respectively). Indeed, in our model, place cells can natively represent different environments without the need of grid cell input, as in models devised before grid cells were discovered (Burgess and O'Keefe, 1996; Redish, 1999; Hartley et al., 2000; Arleo et al., 2001). Although grid cells do not seem to be necessary for the remapping phenomena, they influence the associative properties of place cells, as inferred by the changes in place cell PV correlation curves in the morphing experiment (Fig. 7). Moreover, the grid cells seem to stabilize the place cell code upon noise/inconsistent inputs (Fig. 9). In all, our work suggests that place cells do not inherit positional information from grid cells, but instead interact with them to build a unified representation.

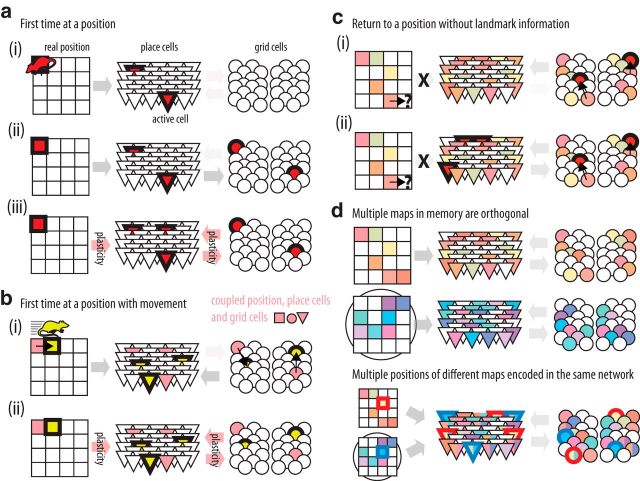
Our model provides a detailed picture of how the hippocampus-entorhinal circuit could establish the cognitive map (Fig. 10). In brief, the flow of information originates in neurons of the entorhinal cortex other than grid cells that are informative about the environment (Fig. 10a). The sensory inputs reverberate through the place and grid cell loop, converging into a stable network state with a specific grid cell alignment. This state is memorized through Hebbian plasticity in the bidirectional connections between the hippocampus and the entorhinal cortex in two steps: (1) the development of a place cell representation through plasticity in the feedforward synapses from non-grid cells to place cells; and (2) the formation of an integrated code through plasticity in the place-to-grid and grid-to-place cell synapses. The network can switch to another activity state by using either allothetic information such as environmental cues from the non-grid cells or idiothetic information such as velocity signals that impinge on the grid cell modules (Fig. 10b; McNaughton et al., 2006; Kropff et al., 2015). The link between different stored representations indexed by the idiothetic information implements a map that could underlie navigational computation such as path integration and trajectory planning (Kubie and Fenton, 2012; Bush et al., 2015). In this sense, although place cells appear before grid cells during development (Langston et al., 2010), it would only be after grid cells mature (Muessig et al., 2015) that the animal should be able to use the map to navigate. The map is reloaded from the recall of any of its positions through the perception of sensory anchors such as visual landmarks (Pérez-Escobar et al., 2016). Once the start point of path integration is set (and thus, the grid alignment), all positions are reachable through the modulation of grid cells by idiothetic information (Fig. 10c), and/or through changes in allothetic inputs from non-grid cells. As similar positions from different environments are stored with uncorrelated patterns of grid cell activity, multiple maps can be stored without interference (Fig. 10d; Redish, 1999).

Figure 10.

Model of the establishment of grid and place cell spatial codes. Illustration of the activity of place (triangles) and grid cells (circles) in relation to animal position (squares). Active cells are shown with solid color and bold border. Coupled cells are shown with the same color. a, Once the animal is at a position for the first time (ai) sensory information reaches the hippocampus, activating a random set of place cells; (aii) the activity of place cells is projected to the medial entorhinal cortex, activating a random set of grid cells at different modules. Such process sets activity bumps in the continuous attractor network of each module; (aiii) place and grid cells interact and converge to a stable set of active cells. The link between active place cells and sensory landmarks is enhanced by plasticity in the input synapses. Active place and grid cells become coupled by plasticity in the bidirectional connections. b, Once the animal moves (bi) new sensory landmarks change the activity of input cells; and the bump of activity within grid cell modules changes with speed, activating a new set of grid cells. A new set of place cells is activated based on the activity of both input and grid cells. bii, As before, grid and place cell activity converges and plasticity links sensory landmarks to place cells and couples active place and grid cells. c, If the animal returns to a known position but landmark information is unavailable (ci) the information about the movement (speed) will determine the set of active grid cells. cii, Because grid and place cells are coupled, active grid cells will recall the correct place cells for that location. d, As the animal moves, the cognitive map is updated by storing each position in the network through the procedures described in a and b. Different environments can be stored with orthogonal maps since different ensembles of place cells are active at each position and because each map has a different grid alignment. Once the animal is repositioned at a known environment, the activity state of place and grid cells is recalled from the landmark information.

The formation of the cognitive map as described above has two core mechanisms. One is the emergence of neural representations that are episode specific, where an episode is regarded as a position in each context. The second is the anchoring of the internal navigation framework to the neural representations of the same context. Our simulations indicate that grid cells are essential for the latter but not the former. Indeed, place cells form place fields in the absence of grid cell input (Brandon et al., 2014), a fact reproduced by our model. Also, global remapping is observed even in the absence of grid cell input (Brandon et al., 2014; Muessig et al., 2016), another fact reproduced by our model (Fig. 7a). Thus, the role of grid cells in establishing the cognitive map would not be the formation of place fields, but to provide a computational scheme that rapidly aligns the place fields to a navigation framework. Such functionality also has an impact on the robustness of the spatial representation, as indicated by the increase in place field stability after the grid cell network has matured (Fig. 9; Muessig et al., 2015).

In our simulations, plasticity in the synaptic inputs to the hippocampus and in its recurrent collaterals is not required for establishing different maps in different environments. However, blocking plasticity in the synaptic inputs to the hippocampus leads to no sharp transition in place cell activity during the morphing experiment (Fig. 6). In this case, as the network does not form stable representations, there is no attractor dynamics. Consistently, long-term stabilization of CA1 place fields requires protein synthesis in the hippocampus (Agnihotri et al., 2004; Renaudineau et al., 2009). Importantly, in our model, strong intrahippocampal pattern completion alters the representation transition in the morphing experiment, which becomes more similar to the one observed during rate than global remapping (Rennó-Costa et al., 2014; Solstad et al., 2014).

Thus, our model predicts that impairing plasticity in the recurrent CA3 synapses should have no effect in the morphing experiment under conditions that promote global remapping, but may affect the PV correlation curve under rate remapping protocols. However, it should be noted that such prediction may be a consequence of our model design. Namely, the implementation of the intrahippocampal pattern completion algorithm in our model is assumed to occur within a gamma cycle and was not explicitly modeled. It is possible that explicitly modeling the CA3 recurrent synapses leads to different results. Moreover, we cannot discard a possible role of pattern completion in other intrahippocampal loops such as the CA3 backprojection to the DG (Scharfman, 2007), which were not considered in this model. In any case, our results shed light on the discussion of whether the origin of attractor dynamics in the morphing paradigm is due to auto-associative properties of the CA3 region or resides in the path integrator system (Colgin et al., 2010). Here we show that the bidirectional connection between the hippocampus and the entorhinal cortex is able to implement an attractor dynamics that leads to a sharp transition in simulated morphing experiments without the need of CA3 recurrent collaterals (implemented in our model as pattern completion algorithm in the hippocampus; Fig. 7).

There are, thus, two concurrent sites for attractor dynamics in the hippocampal formation: although the broad memory system of the entorhinal-hippocampal loop can encode different spatial contexts (such as different environments), as revealed by the sharp transition during global remapping, the narrow memory system in the CA3 can encode different non-spatial aspects within the same spatial context, as revealed by the smooth nonlinear transition during rate remapping (Leutgeb et al., 2007). Therefore, our results add the notion that the brain may implement attractor networks in multiple scales, allowing the construction of stable memories with different levels of detail, from general contexts (in the hippocampal-entorhinal loop) to specific episodes (in the CA3 recurrent collaterals). The timescale of attractor convergence is compatible with theta oscillations organizing local computation in gamma cycles (Mizuseki et al., 2009). The retrieval of stored grid and place cell patterns take a few gamma cycles (Figs. 3, 4); thus a map can be recalled in the broad attractor as rapidly as a theta cycle (Jezek et al., 2011). Yet, convergence in the narrow attractor in the CA3 is even faster, occurring in the time scale of a single gamma cycle (Rennó-Costa et al., 2014).

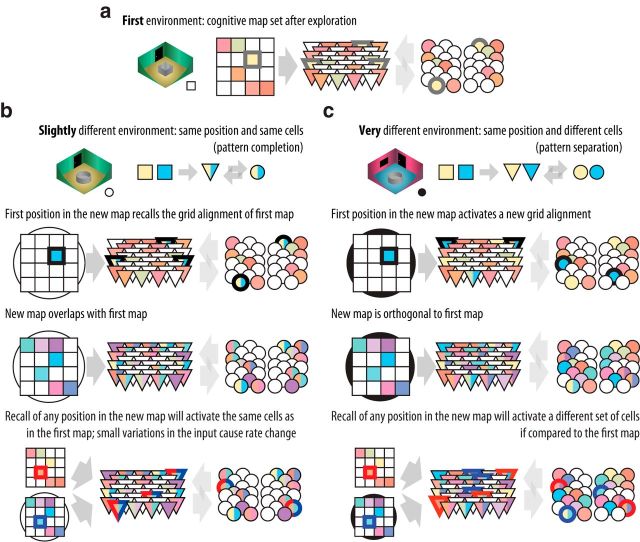
The results of remapping and morphing experiments can be understood with the notion of two attractor networks. When changes in the environment are mild (Leutgeb et al., 2007), the pattern of activity in the entorhinal-hippocampal loop converges to the same broad attractor. In this case, there is no grid realignment as the grid cells converge to the same pattern (Fig. 11b). Yet, the activity of hippocampal neurons in the narrow attractor network converges to a different state and rate remapping is observed. No sharp transition is expected for mild changes due to the characteristics of the narrow attractor network in the CA3 (Rennó-Costa et al., 2014). For substantial changes in the environment (Wills et al., 2005), activity in the entorhinal-hippocampal loop converges to a different broad attractor depending on which environment the animal is placed in, and a sharp transition in network activity is expected as the environment is morphed. In this case, grid realignment and global remapping occur (Fig. 11c). As attractors are self-organized, the interaction between sensory inputs and the initial state of the network determines how two environments are classified, with no requirement for an explicit external signal.

Figure 11.

Mechanisms of rate and global remapping. Illustrations as Figure 10. a, For a first environment, after exploration the cognitive map is set as described in Figure 10. b, In a new and slightly different environment, sensory inputs for the same position are similar and encoded by the same cells (pattern completion). Once the animal is in this new environment, the same place and grid cells are activated as in the first environment. The construction of the map will follow the procedure described in Figure 10, leading to overlapping maps. Once both maps as established, the same set of place and grid cells will be active at the same position regardless of the environment. In this case, rate remapping will be observed since small variations of sensory inputs are reflected in the spike rate of the place cells. c, In a new and very different environment, sensory inputs for the same position are different and encoded by different cells (pattern separation). Once the animal is in this new environment, a different set of place and grid cells is activated in relation to the first environment. The construction of the map will follow the procedure described in Figure 10, leading to orthogonal maps. Once both maps are established, different sets of place and grid cells will be active depending on the environment. In this case, global remapping and grid realignment will be observed.

In summary, our model suggests that the loop between grid and place cells accounts for important phenomena of pattern completion and separation, global remapping and grid realignment, rate remapping, and spatial representation accuracy. These results help to bridge the gap between the roles of sensory stimuli and path integration in the establishment of a compromise representation of the environment. Our results imply that place cells do not necessarily inherit positional information from grid cells, as place cells can display global and rate remapping considering only inputs from non-grid cells in the entorhinal cortex. However, our model indicates that the grid cell input organizes the place cell space code in a predefined grid space that gives support to general computations applied over positional information such as path integration (McNaughton et al., 2006), path completion and disambiguation (Brown et al., 2010), and trajectory planning during mental simulation (Bellmund et al., 2016). Therefore, although grid cells are not necessary to build basic representations of the space, they help to establish robust spatial representations aligned to a computational framework that underlies the operation of the cognitive map.