Information-Theoretic Evidence for Predictive Coding in the Face-Processing System

Abstract

Predictive coding suggests that the brain infers the causes of its sensations by combining sensory evidence with internal predictions based on available prior knowledge. However, the neurophysiological correlates of (pre)activated prior knowledge serving these predictions are still unknown. Based on the idea that such preactivated prior knowledge must be maintained until needed, we measured the amount of maintained information in neural signals via the active information storage (AIS) measure. AIS was calculated on whole-brain beamformer-reconstructed source time courses from MEG recordings of 52 human subjects during the baseline of a Mooney face/house detection task. Preactivation of prior knowledge for faces showed as α-band-related and β-band-related AIS increases in content-specific areas; these AIS increases were behaviorally relevant in the brain's fusiform face area. Further, AIS allowed decoding of the cued category on a trial-by-trial basis. Our results support accounts indicating that activated prior knowledge and the corresponding predictions are signaled in low-frequency activity (<30 Hz).

SIGNIFICANCE STATEMENT Our perception is not only determined by the information our eyes/retina and other sensory organs receive from the outside world, but strongly depends also on information already present in our brains, such as prior knowledge about specific situations or objects. A currently popular theory in neuroscience, predictive coding theory, suggests that this prior knowledge is used by the brain to form internal predictions about upcoming sensory information. However, neurophysiological evidence for this hypothesis is rare, mostly because this kind of evidence requires strong a priori assumptions about the specific predictions the brain makes and the brain areas involved. Using a novel, assumption-free approach, we find that face-related prior knowledge and the derived predictions are represented in low-frequency brain activity.

Introduction

In the last decade, predictive coding theory has become a dominant paradigm to organize behavioral and neurophysiological findings into a coherent theory of brain function (George and Hawkins, 2009; Friston, 2010; Huang and Rao, 2011; Clark, 2013; Hohwy, 2013). Predictive coding theory proposes that the brain constantly makes inferences about the state of the outside world. This is supposed to be accomplished using prior knowledge to build hierarchical internal predictions, which are compared with incoming information to continuously adapt these internal models (Mumford, 1992; Rao and Ballard, 1999; Friston, 2005, 2010).

The postulated use of predictions for inference requires several preparatory steps. First, task-relevant prior knowledge passively stored in synaptic weights needs to be transferred into activated prior knowledge, i.e., information stored in neural activity (for an explanation of the distinction between active and passive storage, see Zipser et al., 1993). Subsequently, (pre)activated prior knowledge needs to be maintained until needed and transferred as a prediction in a top-down direction to a lower cortical area, where it will be matched with incoming information (Mumford, 1992; Friston, 2005, 2010).

With respect to the neural correlates of activated prior knowledge and predictions, we know that the prediction of specific features or object categories increases fMRI BOLD activity in the brain region where the feature or category is usually processed (Puri et al., 2009; Esterman and Yantis, 2010; Kok et al., 2014). However, little is known about how the maintenance of preactivated prior knowledge and the corresponding transfer of predictions are actually implemented in neural activity proper.

As a first step toward resolving this issue, a microcircuit theory of predictive coding has been put forward. According to this theory, internal predictions are processed in deep cortical layers, where they are maintained and then retrieved via low-frequency neural activity (<30 Hz) along descending fiber systems (Bastos et al., 2012).

This theory is in line with findings showing a spectral predominance of low-frequency neural activity in deep cortical layers (Buffalo et al., 2011), as well as physiological findings linking feedback connections to α/β-frequency channels in monkeys (Bastos et al., 2015) and humans (Michalareas et al., 2016).

Recently, neurophysiological studies have supported this microcircuit theory of predictive coding by showing the predictability of events to be associated with neural power in α (Bauer et al., 2014; Sedley et al., 2016) or β frequencies (van Pelt et al., 2016).

However, representation and signaling of preactivated prior knowledge serving predictions has been difficult to investigate with classical analysis methods. One reason is that classical analysis methods require a priori assumptions about which predictions specific brain areas are going to make, assumptions that might be very challenging to make beyond early sensory cortices and for complex experimental designs (Wibral et al., 2014). Moreover, classical analysis methods do not allow to reliably quantify the amount of preactivated prior knowledge for predictions. For example, diminished neural activity measured by fMRI or MEG/EEG may still come with less or more information being maintained in these signals. To overcome these problems, we studied the maintenance and signaling of preactivated prior knowledge for predictions using the information-theoretic measures of active information storage (AIS; Lizier et al., 2012; Gómez et al., 2014) and transfer entropy (TE; Schreiber, 2000; Vicente et al., 2011). AIS measures the amount of information in the future of a process predicted by its past (predictable information), while TE measures the amount of directed information transfer between two processes (see Materials and Methods).

Using these information-theoretic measures, we investigated the preactivation of prior knowledge for face predictions in neural source activity reconstructed from MEG recordings of 52 human subjects. To induce the preactivation of face-related prior knowledge, subjects were instructed to detect faces in two-tone stimuli (Mooney and Ferguson, 1951; Cavanagh, 1991).

Materials and Methods

Basic concept and testable hypotheses.

To study the neural correlates of preactivated prior knowledge for face predictions, we used the information-theoretic measures AIS and TE, measuring predictable information (Lizier et al., 2012) and information transfer (Schreiber, 2000; Vicente et al., 2011), respectively.

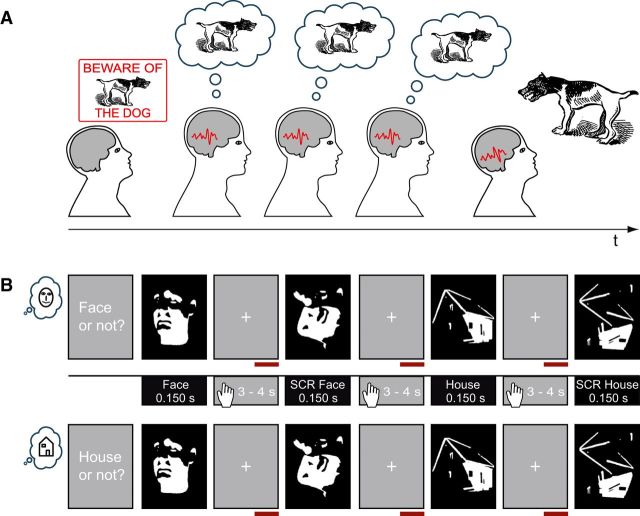
The use of AIS and TE in our study is based on the following rationale. Since the brain will usually not know exactly when a prediction will be needed, it will maintain activated prior knowledge related to the content of the prediction. If there is a reliable neural code that maps between content and neural activity, maintained activated prior knowledge must be represented as maintained information content in neural signals, measurable by AIS (Fig. 1A).

Figure 1.

Central idea of the study and experimental design. A, Typically, preactivated prior knowledge related to the content of a prediction must be maintained as the brain will not know exactly when it will be needed. If there is a reliable neural code that maps between content and neural activity, maintained activated prior knowledge should lead to brain signals that are themselves predictable over time (here the brain signals are depicted as identical, although the relation between past and future will almost certainly be much more complicated). B, Exemplary stimulus presentation in Face blocks (top) and in House blocks (bottom). Face and House icons on the left indicate Face and House blocks, respectively. Middle, Depiction of stimulus categories and timing. The beginning of the response time window is indicated by the hand icon. Red horizontal bars mark the analysis interval. Figure elements obtained from OpenCliparts Library (http://www.openclipart.org) and modified.

Importantly, we do not suggest that predictable information in neural signals as measured by AIS measures the predictability of external events. Rather, we suggest that AIS can be used as a measure to detect increased predictable information in specific brain areas. This predictable information is bound to rise (Fig. 1A) when prior knowledge is preactivated based on perceptual demands and thereby becomes available for predictions.

Further, predictions based on prior knowledge are supposed to be transferred to hierarchically lower brain areas, where they can be matched with incoming information. This information transfer thus must be measurable via TE.

From this basic concept we derived five testable hypotheses about AIS and TE in the predictive coding framework. First, when activated prior knowledge is maintained, predictable information as measured by AIS is supposed to be high in brain areas specific to the content of the predictions. Second, if the microcircuit theory of predictive coding is correct, maintenance of preactivated prior knowledge should be reflected in α/β frequencies, i.e., predictable information and α/β power should correlate. Third, if maintenance of relevant prior knowledge is reflected by predictable information on a trial-by-trial basis, the content of predictions should also be decodable from AIS information on a trial-by-trial basis. Fourth, information transfer related to predictions (i.e., signaling of preactivated prior knowledge measured by TE) should occur in a top-down direction from brain areas showing increased predictable information, and should be reflected in α/β-band Granger causality. Fifth, as predictions based on preactivated prior knowledge are known to facilitate performance, predictable information is supposed to correlate with behavioral parameters, if it reflects the relevant preactivated prior knowledge.

Subjects.

Fifty-seven subjects participated in the MEG experiment. Five of these subjects had to be excluded due to excessive movements, technical problems, or unavailability of anatomical scans. Fifty-two subjects remained for the analysis (average age: 24.8 years; SD, 2.8 years; 23 males). Each subject gave written informed consent before the beginning of the experiment and was paid €10 per hour for participation. The local ethics committee (Johann Wolfgang Goethe University clinics, Frankfurt, Germany) approved of the experimental procedure. All subjects had normal or corrected-to-normal visual acuity and were right-handed according to the Edinburgh Handedness Inventory scale (Oldfield, 1971). The large sample size was chosen to reduce the risk of false positives, as suggested by Button et al. (2013).

Stimuli and stimulus presentation.

Photographs of faces and houses were transformed into two-tone (black and white) images known as Mooney stimuli (Mooney and Ferguson, 1951). Mooney stimuli were used based on the rationale that recognition of two-tone stimuli cannot be accomplished without relying on prior knowledge from previous experience, as is evident, for example, from the late onset of two-tone image recognition capabilities during development (>4 years of age; Mooney, 1957) and from theoretical considerations (Kemelmacher-Shlizerman et al., 2008).

To increase task difficulty, in addition to Mooney faces and houses, scrambled stimuli (SCR) were created from each of the resulting Mooney faces and Mooney houses by displacing the white or black patches within the given background. Thereby all low-level information was maintained but the configuration of the face or house was destroyed. Examples of the stimuli can be seen in Figure 1B.

All stimuli were resized to a resolution of 591 × 754 pixels. Stimulus manipulations were performed with the program GIMP (GNU Image Manipulation Program, 2.4, Free Software Foundation).

A projector with a refresh rate of 60 Hz (resolution, 1024 × 768 pixels) was used to display the stimuli at the center of a translucent screen (background set to gray, 145 cd/m²). Stimulus presentation during the experiment was controlled using the Presentation software package (Version 9.90, Neurobehavioral Systems).

The experiment consisted of eight blocks of 7 min each. In each block, 120 stimuli were presented (30 Mooney faces, 30 Mooney houses, 30 SCR faces, 30 SCR houses) in a randomized order. Stimuli were presented for 150 ms with a vertical visual angle of 24.1° and a horizontal visual angle of 18.8°. The intertrial interval between stimulus presentations was randomly jittered from 3 to 4 s (in steps of 100 ms).

Task and instructions.

Subjects performed a detection task for faces or houses (Fig. 1B). Each of the eight experimental blocks started with the presentation of a written instruction; four of the experimental blocks started with the instruction “Face or not?” while the other four experimental blocks started with the instruction “House or not?”. The former are referred to as “Face blocks” and the latter as “House blocks”. Face and House blocks were presented in alternating order. The same blocks of stimuli were presented as Face blocks for half of the subjects, while for the other half of the subjects these experimental blocks appeared as House blocks and vice versa. This way, the initial block was alternated between subjects (i.e., half of the subjects started with Face blocks and the other half with House blocks). Importantly, as the blocks contained the same face, house, SCR face, and SCR house stimuli, the only difference between Face and House blocks was in the subjects' instruction.

To avoid accidental serial effects, the order of blocks was reversed for half of the subjects. Subjects responded by pressing one of two buttons directly after stimulus presentation. The button assignment for a “Face” or “No-Face” response in Face blocks and “House” or “No-House” in House blocks was counterbalanced across subjects (n = 26 right index finger for Face response).

Between stimulus presentations, subjects were instructed to fixate a white cross on the center of the gray screen. Further, they were instructed to maintain fixation during the whole block and to avoid any movement during the acquisition session. Before data acquisition, subjects performed Face and House test blocks of 2 min with stimuli not used during the actual task. During the test blocks, subjects received feedback on whether their response was correct or not. No feedback was provided during the actual task.

Data acquisition.

MEG data acquisition was performed in line with recently published guidelines for MEG recordings (Gross et al., 2013). MEG signals were recorded using a whole-head system (Omega 2005, VSM MedTech.) with 275 channels. The signals were recorded continuously at a sampling rate of 1200 Hz in a synthetic third-order gradiometer configuration and were filtered on-line with 300 Hz low-pass and 0.1 Hz high-pass fourth-order Butterworth filters.

Each subject's head position relative to the gradiometer array was recorded continuously using three localization coils, one at the nasion and the other two located 1 cm anterior to the left and right tragus on the nasion–tragus plane for 43 of the subjects and at the left and right ear canal for nine of the subjects.

For artifact detection, the horizontal and vertical electrooculogram (EOG) was recorded via four electrodes; two were placed distal to the outer canthi of the left and right eye (for horizontal eye movements) and the other two were placed above and below the right eye (for vertical eye movements and blinks). In addition, an electrocardiogram (ECG) was recorded with two electrodes placed at the left and right collar bones of the subject. The impedance of each electrode was kept <15 kΩ.

Structural magnetic resonance (MR) images were obtained with either a 3T Siemens Allegra or a Trio scanner (Siemens Medical Solutions) using a standard T1 sequence (3-D magnetization-prepared rapid-acquisition gradient echo sequence, 176 slices, 1 × 1 × 1 mm voxel size). For the structural scans, vitamin E pills were placed at the former positions of the MEG localization coils for coregistration of MEG data and MR images.

Behavioral responses were recorded using a fiberoptic response pad (Lumitouch Control Response System, Photon Control) in combination with the Presentation software (Version 9.90, Neurobehavioral Systems).

Statistical analysis of behavioral data.

Responses were classified as correct or incorrect based on the subject's first answer. For hit-rate analysis, the accuracy for each condition was calculated. For reaction-time analysis, only correct responses were considered.

Post hoc Wilcoxon signed-rank tests were performed on hit rates as well as reaction times. To account for multiple testing, Bonferroni's correction was applied (uncorrected α = 0.05).

MEG data preprocessing.

MEG data analysis was performed with Matlab (RRID:nlx_153890; Matlab 2012b, Mathworks) using the open-source Matlab toolbox Fieldtrip (Version 2013 11-11; RRID:nlx_143928; Oostenveld et al., 2011) and custom Matlab scripts.

Only trials with correct behavioral responses were taken into account for MEG data analysis. The focus of data analysis was on the prestimulus intervals from 1 to 0.050 s before stimulus onset. Trials containing sensor jump artifacts or muscle artifacts were rejected using automatic FieldTrip artifact-rejection routines. Line noise was removed using a discrete Fourier transform filter at 50, 100, and 150 Hz. In addition, independent component analysis (ICA; Makeig et al., 1996) was performed using the extended infomax (runica) algorithm implemented in fieldtrip/EEGLAB. ICA components strongly correlated with EOG and ECG channels were removed from the data. Finally, data were visually inspected for residual artifacts.

To minimize movement-related errors, the mean head position over all experimental blocks was determined for each subject. Only trials in which the head position did not deviate >5 mm from the mean head position were considered for further analysis.

Because artifact rejection and trial rejection based on the head position may result in different trial numbers for Face and House blocks, the minimum number of trials across Face and House blocks was selected randomly after trial rejection from the available trials in each block (stratification).

Sensor level spectral analysis.

Spectral analysis at the sensor level was performed to determine the subdivision of the power spectrum in frequency bands (Brodski et al., 2015). As we aimed to identify frequency bands based on stimulus-related increases or decreases, respectively, new data segments were cut from −0.35 to −0.05 s before stimulus onset for the time interval of “baseline” and from 0.05 to 0.35 s after stimulus onset for the interval of “task.” Before spectral transformation, a single Hanning taper was applied to the data. The spectral transformation was calculated in an interval from 4 to 150 Hz using a fast Fourier approach. Average spectra of task and baseline periods were contrasted over subjects using a dependent-sample permutation t metric with a cluster-based correction method (Maris and Oostenveld, 2007) to account for multiple comparisons. Adjacent samples whose t values exceeded a threshold corresponding to an uncorrected α level of 0.05 were defined as clusters. The resulting cluster sizes were then tested against the distribution of cluster sizes obtained from 1000 permuted datasets (i.e., labels “task” and “baseline” were randomly reassigned within each of the subjects). Cluster sizes larger than the 95th percentile of the cluster sizes in the permuted datasets were defined as significant.

Source grid creation.

To create individual source grids, we transformed the anatomical MR images to a standard T1 MNI template from the SPM8 toolbox (http://www.fil.ion.ucl.ac.uk/spm) and obtained an individual transformation matrix for each subject. We then warped a regular 3-D dipole grid based on the standard T1 template (15 mm spacing resulted in 478 grid locations) with the inverse of each subject's transformation matrix, to obtain an individual dipole grid for each subject in subject space. This way, each specific grid point was located at the same brain area for each subject, which allowed us to perform source analysis with individual head models as well as multisubject statistics for all grid locations. Lead fields at those grid locations were computed for the individual subjects with a realistic single-shell forward model (Nolte, 2003) accounting for the effects of the ICA component removal in preprocessing.

Source time course reconstruction.

To enable a whole-brain analysis of AIS, we reconstructed the source time courses for all 478 source grid locations.

For source time course reconstruction, we calculated a time-domain beamformer filter [linear constrained minimum variance (LCMV); Van Veen et al., 1997] based on broadband-filtered data (8 Hz high pass, 150 Hz low pass) from the prestimulus interval (−1 to −0.050 s) of Face blocks as well as House blocks (use of common filters; Gross et al., 2013).

For each source location, three orthogonal filters were computed (x, y, z direction). To obtain the source time courses, the broadly filtered raw data were projected through the LCMV filters, resulting in three time courses per location. We performed on these source time courses a singular value decomposition to obtain the time course in the direction of the dominant dipole orientation. The source time course in the direction of the dominant dipole orientation was used for calculation of AIS.

Definition of AIS.

We assume that the reconstructed source time courses for each brain location can be treated as realizations {x₁, …, x_t, …, x_N} of a random process X = {X₁, …, X_t, …, X_N}, which consists of a collection of random variables, X_t, ordered by some integer t. AIS then describes how much of the information the next time step t of the process is predictable from its immediate past state (Lizier et al., 2012). This is defined as the mutual information (Eq. 1) A_x = ${\lim }_{k\to \infty }I\left(X_{t-1}^k;X_t\right)={\lim }_{k\to \infty }{\displaystyle {\sum }_{x_t,x_{t-1}^k}p\left(x_t,x_{t-1}^k\right)\log \frac{p\left(x_{t-1}^k,x_t\right)}{p\left(x_{t-1}^k\right)p\left(x_t\right)}}$, where I is the mutual information and p(.) are the variables' probability density functions. Variable X_t−1^k describes the past state of X as a collection of past random variables X_t−1^k = {X_t−1, …, X_{t−1−(k*τ)}}, where k is the embedding dimension (i.e., the number of time steps used in the collection) and τ the embedding delay between these time steps. For practical purposes, k has to be set to a finite value k_max, such that the history before time point t − k_max * τ does (statistically) not further improve the prediction of X_t from its past (Lizier et al., 2012).

Predictable information as measured by AIS indicates that a signal is both rich in information and predictable at the same time. Note that neither a constant signal (predictable but low information content) nor a memory-less stochastic process (high information content but unpredictable) will exhibit high AIS values. In other words, a neural process with high AIS must visit many different possible states (rich dynamics); yet visit these states in a predictable manner with minimal branching of its trajectory (this is the meaning of the log ratio of Eq. 1). As such, AIS is a general measure of information that is maintained in a process, and could here reflect any form of memory based on neural activity. AIS is linked specifically to activated prior knowledge in our study via the experimental manipulation that alternately activates face-specific or house-specific prior knowledge, and via an investigation of the difference in AIS between the two conditions.

Analysis of predictable information using AIS.

The history dimension (k_max; range, 3–6) and optimal embedding delay parameter (τ; range, 0.2 to 0.5 in units of the autocorrelation decay time) was determined for each source location separately using Ragwitz's criterion (Ragwitz and Kantz, 2002), as implemented in the TRENTOOL toolbox (Lindner et al., 2011). To avoid a bias in estimated values based on different history dimensions, we chose the maximal history dimension across Face and House blocks for each source location (median k_max over source locations and subjects, 4).

The actual spacing between the time points in the history was the median across trials of the output of Ragwitz's criterion for the embedding delay τ (Lindner et al., 2011).

Based on the assumption of stationarity in the prestimulus interval, AIS was computed on the embedded data across all available time points and trials. This was done separately for each source location and condition in every subject.

Computation of AIS was performed using the Java Information Dynamics Toolkit (Lizier, 2014). A minimum of 68,400 samples entered the AIS analysis for each subject, block type, and source location (minimum of 57 trials; ∼1 s time interval; sampling rate, 1200 Hz). AIS was estimated with four nearest neighbors in the joint embedding space using the Kraskov–Stoegbauer–Grassberger (KSG) estimator (Kraskov et al., 2004; algorithm 1), as implemented in the open source Java Information Dynamics Toolkit (JIDT; Lizier, 2014).

Computation of AIS was performed at the Center for Scientific Computing Frankfurt, using the high-performance computing Cluster FUCHS (https://csc.uni-frankfurt.de/index.php?id=4), which enabled the computationally demanding calculation of AIS for the whole brain across all subjects as well as Face and House blocks (478 × 52 × 2 = 49,712 computations of AIS).

AIS statistics.

To determine the source locations in which AIS values were increased when subjects held face information in memory, a within-subject permutation t metric was computed. Here, AIS values for each source location across all subjects were contrasted for Face blocks and House blocks. The permutation test was chosen as the distribution of AIS values is unknown and not assumed to be Gaussian. To account for multiple comparisons across the 478 source locations, a cluster-based correction method (Maris and Oostenveld, 2007) was used. Clusters were defined as adjacent voxels whose t values exceeded a critical threshold corresponding to an uncorrected α level of 0.01. In the randomization procedure, labels of Face block and House block data were randomly reassigned within each subject. Cluster sizes were tested against the distribution of cluster sizes obtained from 5000 permuted datasets. Cluster values larger than the 95th percentile of the distribution of cluster sizes obtained for the permuted datasets were considered significant.

Correlation analysis of spectral properties and AIS.

We investigated the relationship of spectral power in the prestimulus interval and AIS values on the single-trial level. Before calculation of single-trial spectral power, a single Hanning taper was applied to each prestimulus epoch. Then, single-trial spectra were computed with the fast Fourier approach, averaged over all epochs, and subdivided in the predefined frequency bands for each subject. Next, Spearman's ρ was computed for correlation of the median single-trial spectral power in the predefined frequency bands with the single-trial AIS values to obtain individual correlation values. Median correlation values over both block types were computed for each subject. To test the significance of the correlation analysis, the epochs were randomly permuted 5000 times for each subject and correlation was recalculated also for the permuted datasets. For each subject, an original correlation value >99.99997% (or <99.99997%; threshold Bonferroni's correction adjusted for the 52 * 5 * 6 multiple comparisons) of the correlation values obtained for the permuted datasets was considered significant. At the second level, we used a binomial test to assess whether the number of subjects showing significant correlations (for one source and frequency range) could be explained by chance. Median correlation values over subjects and their significance based on the binomial test are reported.

We also calculated a correlation of two t-value maps: (1) the mean AIS contrast and (2) a mean power contrast. For both t-value maps, the dependent samples t-metric Face blocks vs House blocks was computed over all 52 subjects and all 478 source locations inside the brain. For the power t-value map, source power in the α-frequency (8–14 Hz) and β-frequency (14–32 Hz) band was reconstructed with the DICS (dynamic imaging of coherent sources; Gross et al., 2001) algorithm as implemented in the FieldTrip toolbox using real valued filter coefficients only (Grützner et al., 2010).

Correlation analysis of reaction times and AIS.

Last, we assessed the relationship of AIS values and reaction times for each subject. To this end, before the correlation analysis, mean reaction times and mean AIS values in the brain areas of interest for Face and House blocks for each subject were subtracted from each other. This made it possible to account for different behavioral speeds among subjects. The correlation of the difference in AIS values and the difference in reaction times was calculated via Spearman skipped correlations using the Robust Correlation Toolbox (Pernet et al., 2012). To calculate skipped correlations, bivariate outliers must be identified and removed (Rousseeuw, 1984; Rousseeuw and Driessen, 1999; Verboven and Hubert, 2005). This can provide a more robust measure, which has been recommended for brain–behavior correlation analyses (Rousselet and Pernet, 2012). The uncorrected α level was set to 0.05. For each correlation, bootstrap confidence intervals (CIs) were computed based on 1000 resamples. To account for multiple comparisons across brain areas, bootstrap CIs were adjusted using Bonferroni's correction. If the adjusted CI did not encompass 0, the correlation was considered significant.

Decoding analysis.

To investigate whether prediction content (i.e., Face or House block) can be decoded from individual trial AIS values, we applied a multivariate analysis using support vector machines (SVMs) with the libsvm toolbox (Chang and Lin, 2011; available at http://www.csie.ntu.edu.tw/∼cjlin/libsvm). For each subject, the linear SVM classifier was trained using 70% randomly chosen trials as training data. However, the training data always contained the same number of trials for Face and House blocks, respectively. Parameters for the SVMs were optimized in a threefold cross-validation procedure for the training data only. Subsequently, the classifier was tested using the data from the remaining 30% of the trials with the best parameters obtained from the training procedure, thereby ensuring strict separation of training and testing data (Nowotny, 2014).

This procedure was repeated 10 times. We report the median accuracy value for each subject. To test the significance of the median accuracy value, for each subject the labels of Face blocks and House blocks were randomly permuted 500 times for each of the 10 training and testing sets and the median over the 10 accuracy values was calculated also for the permuted datasets. A median accuracy value of >99.999% (threshold Bonferroni's correction adjusted for the 52 multiple comparisons) of the median accuracy values obtained for the permuted datasets was considered to be significant, corresponding to an uncorrected α level of 0.05.

Definition of TE (and Granger analysis).

TE (Schreiber, 2000) was applied to investigate the information transfer between the brain areas identified with AIS analysis. For links with significant information transfer, we studied post hoc the spectral fingerprints of these links using spectral Granger analysis (Granger, 1969).

Both, TE and Granger analysis are implementations of Wiener's principle (Wiener, 1956), which can be summarized as follows: if the prediction of the future of one-time series X can be improved compared with predicting it from the past of X alone by adding information from the past of another time series Y, then information is transferred from Y to X.

TE is an information-theoretic, model-free implementation of Wiener's principle and can be used, in contrast to Granger analysis, to study linear as well as nonlinear interactions (Chang and Lin, 2011) and was previously applied to broadband MEG source data (Wibral et al., 2011). TE is defined as a conditional mutual information as follows (Eq. 2):

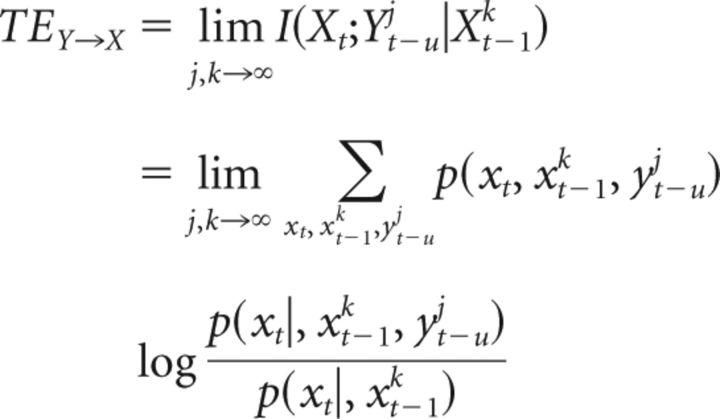where X_t describes the future of the target time series X, X_t−1^k describes the past state of X, and Y_t−u^j describes the past state of the source time series Y. As for the calculation of AIS, past states are defined as collections of past random variables with number of time steps j and k and a delay τ. The parameter u accounts for a physical delay between processes Y and X (Wibral et al., 2013) and can be optimized by finding the maximum TE over a range of assumed values for u.

Analysis of information transfer using TE and Granger causality analysis.

We performed TE analysis with the open-source Matlab toolbox TRENTOOL (Lindner et al., 2011), which implements the KSG estimator (Kraskov et al., 2004; Frenzel and Pompe, 2007; Gómez-Herrero et al., 2015) for TE estimation. We used ensemble estimation (Wollstadt et al., 2014; Gómez-Herrero et al., 2015), which estimates TE from data pooled over trials to obtain more data and hence more robust TE estimates. Additionally, we used Faes's correction method to account for volume conduction (Faes et al., 2013).

In the TE analysis, we used the same time intervals (prestimulus) and embedding parameters as for AIS analysis. TE values for Face blocks and House blocks were contrasted using a dependent-sample permutation t metric for statistical analysis across subjects. In the statistical analysis, Bonferroni's correction was used to account for multiple comparisons across links (uncorrected α level, 0.05). As for AIS, the history dimension for the past states was set to finite values; we here set j_max = k_max and used the values obtained during AIS estimation for the target time series of each signal combination.

For the significant TE links, we computed post hoc nonparametric bivariate Granger causality analysis in the frequency domain (Dhamala et al., 2008). Using the nonparametric variant of Granger causality analysis avoids choosing an autoregressive model order, which may easily introduce a bias. In the nonparametric approach, Granger causality is computed from a factorization of the spectral density matrix, which is based on the direct Fourier transform of the time series data (Dhamala et al., 2008). The Wilson algorithm was used for factorization (Wilson, 1972). A spectral resolution of 2 Hz and a spectral smoothing of 5 Hz were used for spectral transformation using the multitaper approach (Percival and Walden, 1993; nine Slepian tapers). We were interested in the differences among Granger spectral fingerprints in Face and House blocks. However, we also wanted to make sure that the Granger values for these differences significantly differed from noise. For that reason, we created two additional “random” conditions by permuting the trials for the Face block and the House block condition for each source separately. Two types of statistical comparisons were performed for the frequency range between 8 and 150 Hz and each of the significant TE links: (1) Granger values in Face blocks were contrasted with Granger values in House blocks using a dependent-samples permutation t metric; (2) Granger values in Face blocks/House blocks were contrasted with the random Face block condition/random House block condition using another dependent-samples permutation t metric. For the first test, a cluster correction was used to account for multiple comparisons across frequency (Maris and Oostenveld, 2007). Adjacent samples with uncorrected p values of <0.01 were considered clusters. Five thousand permutations were performed and the α value was set at 0.05. Frequency intervals in the Face block versus House block comparison were only considered significant if all included frequencies also reached significance in the comparison with the random conditions using a Bonferroni's correction. Last, Bonferroni's correction was also applied to account for multiple comparisons across links.

Results

Behavioral results

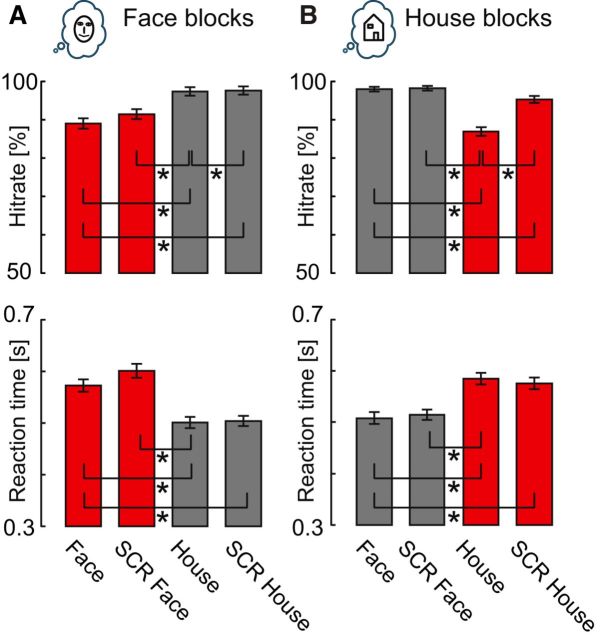
We found no differences between Face blocks and House blocks for hit rates (average hit rate: Face blocks, 93.9%; House blocks, 94.6%; Wilcoxon signed-rank test p = 0.57) and reaction times of correct responses (average mean reaction times: Face blocks, 0.545 s; House blocks 0.546 s; Wilcoxon signed-rank test p = 0.85). For both block types, subjects showed decreased hit rates and increased reactions times for the instructed intact stimulus (i.e., face in Face blocks and house in House blocks) compared with the noninstructed intact stimulus (house in Face blocks and face in House blocks), as the instructed intact stimuli had to be distinguished from a similar distractor (SCR stimuli; Fig. 2). Also, slower reaction times were found for the instructed intact stimulus versus the noninstructed SCR stimulus for both block types. Moreover, for both block types, subjects showed lower hit rates for houses than SCR houses (Fig. 2).

Figure 2.

Behavioral results. A, B, Depiction of hit rates and reaction times of correct responses for (A) Face blocks and (B) House blocks. Equivalent conditions in different block types are marked in red and gray, respectively. Asterisks indicate significant differences based on Wilcoxon signed-rank tests within block type (n = 52; Bonferroni's correction for multiple comparisons). Error bars indicate SE.

Definition of frequency bands

Following the same approach as Brodski and colleagues (2015), we defined frequency bands for subsequent neural analysis based on the significant clusters of a task versus baseline contrast at the MEG sensor level. This analysis was based on the spectra of all conditions for both block types and revealed one positive cluster with task-related increases in activity and one negative cluster with task-related decreases in activity (Fig. 3). Based on the spectral profile of the two significant clusters, the following six frequency bands were defined for further analysis: (1) 8–14 Hz (α); (2) 14–32 Hz (β); (3) 32–50 Hz (low γ), (4) 50–60 Hz (mid-γ), (5) 60–100 Hz (high γ), and (6) 100–150 Hz (very high γ).

Figure 3.

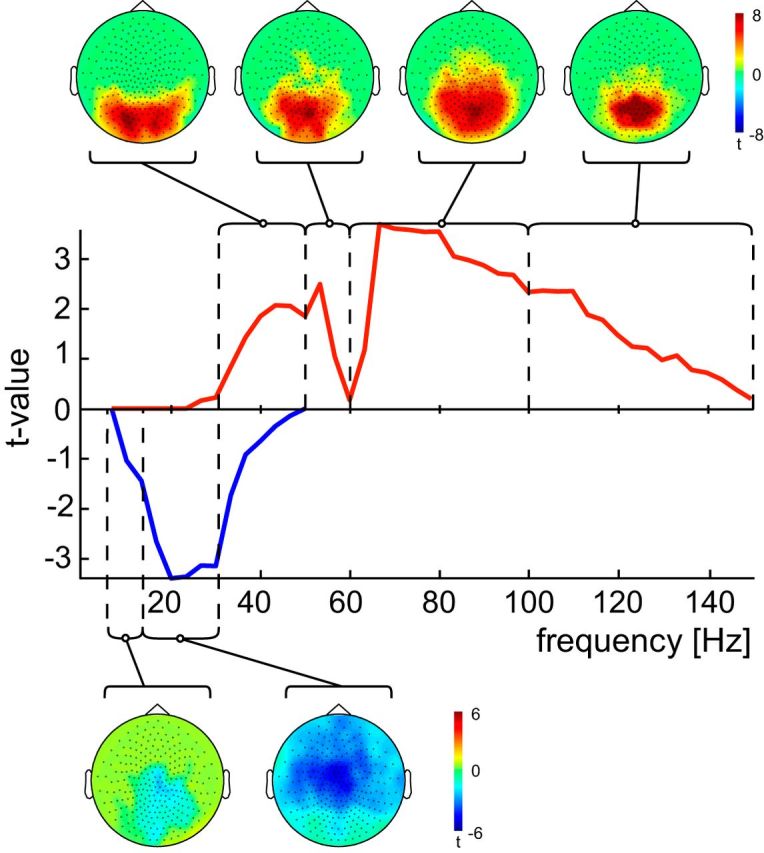
Sensor-level frequency analysis: defining frequency bands. Middle, Power spectra for all significant clusters (one positive and one negative cluster) at the sensor level (permutation t metric, contrast [0.05 0.35 s] vs [−0.35 −0.05 s] around stimulus onset, t values masked by p < 0.05, cluster correction, n = 52). Frequency analysis at the sensor level was calculated using both block types jointly. Task-related increases in power are shown in red (positive cluster) and task-related decreases in blue (negative cluster). Black dashed lines frame the identified frequency ranges. Top and bottom, Topographical plots of the task-related increases (top) or decreases (bottom) for each defined frequency range.

Analysis of predictable information

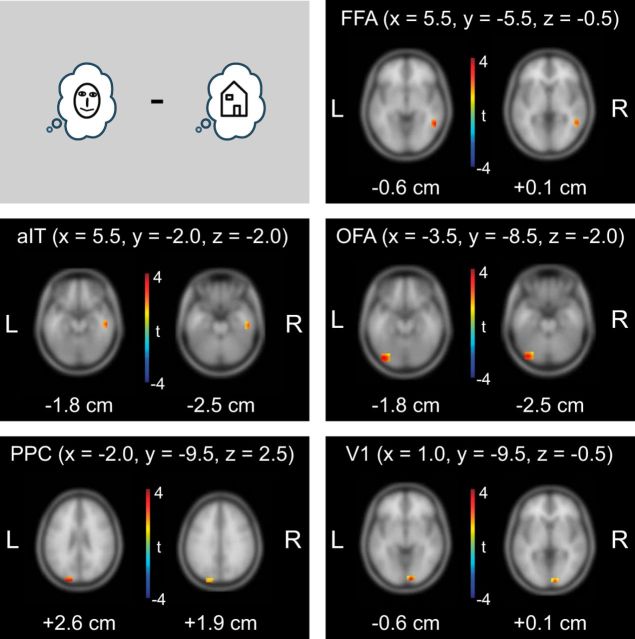
Statistical comparisons of AIS values between Face blocks and House blocks in the prestimulus interval revealed increased AIS values for Face blocks in clusters in the fusiform face area (FFA), anterior inferior temporal cortex (aIT), occipital face area (OFA), posterior parietal cortex (PPC), and primary visual cortex (V1; Fig. 4). We referred to these five brain areas as the “face-prediction network” and subjected it to further analyses. In contrast to this finding of a face-prediction network, we did not find brain areas showing significantly higher AIS values in House blocks compared with Face blocks. This is similar to frequently cited previous studies that failed to find prediction effects for houses in the brain in contrast to faces (Summerfield et al., 2006a, 2006b; Trapp et al., 2016).

Figure 4.

Statistical analysis of predictable information (measured by AIS) at the MEG source level. Results of whole-brain dependent samples permutation t metric contrasting Face blocks and House blocks (n = 52, t values masked by p < 0.05, cluster correction). Peak voxel coordinates in MNI space are shown at the top for each brain location; z values are displayed below each brain slice.

Correlation of single-trial power and single-trial predictable information

To investigate the neurophysiological correlates of activated prior knowledge identified via AIS analysis, we conducted a correlation analysis of single-trial power in distinct frequency bands with single-trial AIS. Correlation analysis revealed significant positive correlations in the α-frequency and β-frequency bands (Table 1). This means that α-band and β-band activity is the most likely carrier of activated prior knowledge. Additionally, for two of the brain areas, we also found a weak negative correlation of single-trial very high γ power and AIS. However, the tiny effect size of the very high γ correlation questions the relevance of this effect. We will therefore only discuss the findings in the α and β band.

Table 1.

Correlation of single-trial power and single-trial predictable information (measured by AIS) in the face-prediction network

	ρ Value
	FFA	aIT	V1	OFA	PPC
α (8–14 Hz)	0.46*	0.46*	0.49*	0.47*	0.47*
β (14–32 Hz)	0.33*	0.34*	0.31*	0.33*	0.3*
Low γ (32–50 Hz)	0.07	0.07	0.08	0.07	0.09
Mid-γ (50–60 Hz)	0.03	0.01	0.02	0.02	0.04
High γ (60–100 Hz)	−0.007	−0.02	0.01	0.003	0.05
Very high γ (100–150 Hz)	−0.13	−0.16*	−0.12	−0.13*	−0.11

*Significant, based on binomial test.

While we found a significant correlation of single-trial power and predictable information in the α and β band, the contrast map based on mean beamformer reconstructed source power over all source grid points for Face and House blocks (t values obtained from dependent sample t metric over all 52 subjects) did not correlate with the mean AIS contrast map for both α and β power (α ρ = 0.043, p = 0.33; β ρ = 0.05, p = 0.21; Fig. 5). This suggests that AIS analysis provides additional information not directly provided by a spectral analysis. In other words, while AIS seems to be carried by α/β-band activity, not all α/β-band activity contributes to AIS.

Figure 5.

Correlation of predictable information contrast maps and source power contrast maps. A, Illustration of the t-value maps of the dependent samples t metric for the Face-block versus House-block contrast (n = 52, no correction) on the cortical surface. B, Scatter plots of the relationship of the α/β contrast and the AIS contrast. Each dot represents a source location within the brain. Spearman correlation values are displayed at the top right corner of each plot (n = 478). Linear regression lines are included in gray (solid).

Decoding prediction content from single-trial AIS values

To study whether face or house predictions can be decoded from AIS values of the face-prediction network on a trial-by-trial basis, SVMs were used (Chang and Lin, 2011). Cross-validated decoding performance reached ≤65.2% (mean performance, 53.5%; SD, 3.9% over subjects). When Bonferroni's correction was applied for the high number of subjects tested (n = 52), performance was still significantly better for 22 of 52 subjects than for permuted datasets (p < 0.05/52). Note, that this fraction is much higher than would have been expected by chance (p = 1.1 × 10⁻⁵², binomial test).

Analysis of information transfer

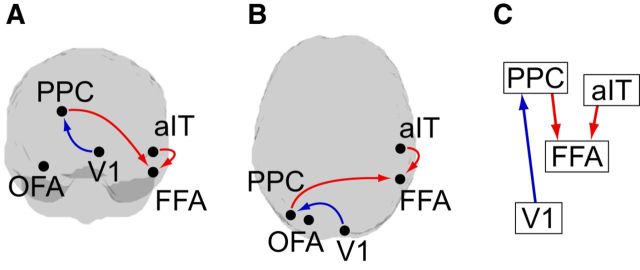
To understand how activated prior knowledge is communicated within the cortical hierarchy, we assessed the information transfer within the face-prediction network in the prestimulus interval by estimating TE (Schreiber, 2000) on source time courses for Face blocks and House blocks, respectively. Statistical analysis revealed significantly increased information transfer for Face blocks from aIT to FFA (p = 0.0001, Bonferroni's correction) and from PPC to FFA (p = 0.0014, Bonferroni's correction). For House blocks, information transfer was increased compared with Face blocks from brain area V1 to PPC (p = 0.0014, Bonferroni's correction; Fig. 6).

Figure 6.

Analysis of information transfer in the prestimulus interval. Results of dependent sample permutation t tests on TE values (Face blocks vs House blocks, n = 52, p < 0.05, Bonferroni's correction). Red arrows indicate increased information transfer for Face blocks; blue arrows indicate increased information transfer for House blocks. A–C, Illustration of the resulting network in (A) a view of the back of the brain, (B) a view of the top of the brain, and (C) depiction of the network hierarchy (based on the hierarchy by Zhen et al., 2013; Michalareas et al., 2016).

Post hoc frequency-resolved Granger causality analysis did not reveal any significant effects.

Correlation of predictable information and reaction times

To study the association of predictable information and behavior, we correlated the per-subject difference of AIS values between Face blocks and House blocks with the per-subject difference in reaction times. This analysis was performed for FFA, aIT, and PPC, three brain areas that, according to our findings, showed an increase of information transfer during Face blocks. For these brain areas, we tested the hypothesis that predictable information for Face blocks was associated with performance, i.e., reaction times during Face blocks. Negative correlation values were found for all three brain areas. However, only brain area FFA reached significance when correcting for multiple comparisons (Fig. 7; FFA robust Spearman's ρ, −0.41; robust CI after correcting for multiple comparisons, [−0.68 −0.066]; aIT robust Spearman's ρ, −0.12; CI, [−0.4554 0.245]; PPC robust Spearman's ρ, −0.21; CI, [−0.5480 0.1178]).

Figure 7.

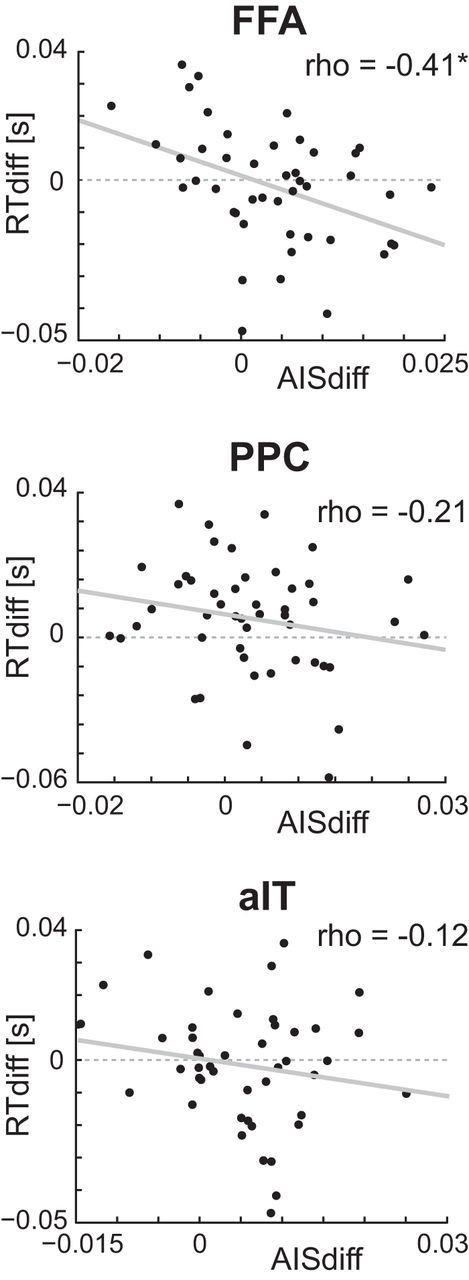
Correlation analysis for predictable information and reaction times. Scatter plots displaying the (skipped) correlation of per-subject AIS difference values (Face blocks − House blocks) with per-subject reaction time difference values (Face blocks − House blocks). Robust Spearman correlation values are displayed at the top right corner of each plot. Asterisks indicate significant correlation, using Bonferroni's correction of bootstrap CIs. Linear regression lines are included in gray (solid).

Discussion

We tested the hypothesis that the neural correlates of prior knowledge activated for use as an internal prediction must show up as predictable information in the neural signals carrying that activated prior knowledge. This hypothesis is based on the rationale that the content of activated prior knowledge must be maintained until the knowledge or the prediction derived from it is used. The fact that activated prior knowledge has a specific content then mandates that increases in predictable information should be found in brain areas specific to processing the respective content. This is indeed what we found when investigating the activation of prior knowledge about faces during face-detection blocks. In these blocks, predictable information was selectively enhanced in a network of well known face-processing areas. In these areas, prediction content was decodable from the predictable information on a trial-by-trial basis and increased predictable information was related to improved task performance in brain area FFA. Given this established link between the activation of prior knowledge and predictable information, we then tested current neurophysiological accounts of predictive coding suggesting that activated prior knowledge should be represented in deep cortical layers and at α-band or β-band frequencies and should be communicated as a prediction along descending fiber pathways (Bastos et al., 2012). Indeed, predictable information within the network of brain areas related to activated prior knowledge of faces was associated with α-band and β-band frequencies and information transfer within this network was increased in a top-down direction, in accordance with the theory.

We will next discuss our findings with respect to their implications for current theories of predictive coding.

Activated prior knowledge for faces shows up as predictable information in content-specific areas

We found increased predictable information as reflected by increased AIS values in Face blocks in the prestimulus interval in the FFA, OFA, aIT, PPC, and V1. Out of these five brain areas FFA, OFA, and aIT are well known for playing a major role in face processing (Kanwisher et al., 1997; Kriegeskorte et al., 2007; Tsao et al., 2008; Pitcher et al., 2011).

It might seem surprising that predictable information for Face blocks was not increased within the superior temporal sulcus (STS), a brain area that has been recently identified as a key region for the prediction of face identities in a face-identity recognition task (Apps and Tsakiris, 2013). This finding may be explained by the specific role of the STS in face processing: mainly processing facial identities and emotional expressions (Winston et al., 2004; Fox et al., 2009). In contrast, the STS may play a lesser role in the pure face-detection task of our design, where neither identities nor emotional expressions were of relevance.

In addition to increased predictable information in well known face-processing areas, we also found increased predictable information in Face blocks in the PPC. We consider the increase in predictable information in the PPC also as content-specific, because regions in the PPC have been recently linked to high-level visual processing of objects, like faces (Pashkam and Xu, 2014), and activation of the PPC has been repeatedly observed during the recognition of Mooney faces by us and others (Dolan et al., 1997; Grützner et al., 2010; Brodski et al., 2015).

In sum, our finding of increased predictable information for Face blocks in the FFA, OFA, aIT, and PPC confirms our hypothesis that activation of face prior knowledge elevates predictable information in content-specific areas. Additionally, our results suggest that predictable information in content-specific areas is associated with the corresponding prediction on a trial-by-trial basis, by decoding the anticipated category (Face or House block) from trial-by-trial AIS values at the face-prediction areas.

However, while we found increased predictable information in content-specific areas for Face blocks, we did not find brain areas showing increased predictable information for House blocks. Similarly, Summerfield and colleagues (2006a) observed in a face/house discrimination task increased activation in the FFA, when a house was misperceived as a face, but failed to see increased activation in the parahippocampal place area (PPA), a scene/house-responsive region, when a face was misperceived as a house. The authors suggest that this might be related to the fact that the PPA is less subject to top-down information than the FFA because faces have more regular features potentially useful for top-down mechanisms than the natural scenes that the PPA usually responds to. Additionally, because of their strong social relevance (Farah et al., 1995), faces capture a disproportionate amount of attention (Vuilleumier and Schwartz, 2001). Thus, also face predictions/templates may be prioritized compared with other templates (e.g., for houses; Puri et al., 2009; Esterman and Yantis, 2010; Van Belle et al., 2010).

Maintenance of activated prior knowledge about faces is reflected by increased α/β power

We found a positive single-trial correlation of AIS with α/β power for all face-prediction areas. This finding supports the assumption that the maintenance of activated prior knowledge as indexed by AIS is related to α and β frequencies.

Mayer and colleagues (2016) recently showed, in findings consistent with ours, that activation of prior knowledge about previously seen letters is associated with increased power in α frequencies in the prestimulus interval. Also, Sedley and colleagues (2016) observed that the update of predictions, which also requires access to maintained activated knowledge, is associated with increased power in β frequencies.

Extending these previous findings, we are the first to report that single-trial low-frequency activity strongly correlates with the momentary amount of activated prior knowledge in content-specific brain areas. Specifically, our results demonstrate that the current amount of activated prior knowledge usable as predictions for face detection is associated with neural activity in the α-frequency and β-frequency range, supporting the hypothesis of a popular microcircuit theory of predictive coding (Bastos et al., 2012).

Face predictions are transferred in a top-down manner

In Face blocks we observed increased information transfer to the FFA from the aIT as well as from the PPC, both areas located higher in the processing hierarchy than the FFA (Zhen et al., 2013; Michalareas et al., 2016). Thus, the FFA seems to serve as a convergence center where information from higher cortical areas is transferred to prepare for rapid face detection.

Closely related to our findings Esterman and Yantis (2010) observed that anticipation effects for faces in the FFA (and houses in the PPA) were associated with increased activity in a posterior IPS region (part of the PPC) extending to the occipital junction. However, to our knowledge our study is the first to report face-related anticipatory top-down information transfer from the PPC and aIT to the FFA.

Top-down information transfer in face-processing regions in a preparatory interval before face detection is in general supportive of the predictive coding account (Mumford, 1992; Rao and Ballard, 1999; Friston, 2005, 2010), which suggests a top-down propagation of predictions. This top-down information transfer of predictions is probably associated with a low-frequency channel (Bastos et al., 2012), in contrast to the bottom-up propagation of prediction errors, which has been linked to a high-frequency channel (Bastos et al., 2012, Brodski et al., 2015). The spectral dissociation between the transfer of predictions and of prediction-error frequencies is in line with physiological findings in monkeys and humans (Bastos et al., 2015; Michalareas et al., 2016) and received recent support from an MEG study investigating the (spectrally resolved) information transfer during the prediction of causal events (van Pelt et al., 2016). Our spectrally resolved Granger causality analysis did not contradict this view, yet results failed to reach statistical significance.

In addition to the two top-down links showing increased information transfer for Face blocks, we observed a bottom-up link from V1 to the PPC with increased information transfer for House blocks. As we did not find a prediction network for houses and our analysis was thus only performed in the brain areas of the face-prediction network, one can only speculate on the function of this bottom-up information transfer. It is possible that it indicates that house detection was rather performed in a bottom-up manner, for instance by first identifying low-level features that distinguish houses from their scrambled counterparts.

Preactivation of prior knowledge about faces facilitates performance

Across subjects we found elevated predictable information in the FFA in Face blocks in contrast to House blocks to be associated with shorter reaction times for Face blocks compared with House blocks. This suggests that preactivation of prior knowledge, especially about faces in the FFA, facilitates processing and speeds up face detection, as also suggested by FFA effects in previous fMRI studies (Puri et al., 2009; Esterman and Yantis, 2010). Our study is, however, the first to demonstrate that the size of the facilitatory effect on perceptual performance depends on the quantity of activated prior knowledge for faces in the FFA, measurable as the difference in AIS between Face and House block for each subject. Differential size of the faciliatory effect among subjects and the associated differences in the quantity of activated prior knowledge in the FFA may be related to the differential ability in maintaining an object-specific representation (Ranganath et al., 2004).