Effector-Invariant Movement Encoding in the Human Motor System

Abstract

Ipsilateral motor areas of cerebral cortex are active during arm movements and even reliably predict movement direction. Is coding similar during ipsilateral and contralateral movements? If so, is it in extrinsic (world-centered) or intrinsic (joint-configuration) coordinates? We addressed these questions by examining the similarity of multivoxel fMRI patterns in visuomotor cortical regions during unilateral reaching movements with both arms. The results of three complementary analyses revealed that fMRI response patterns were similar across right and left arm movements to identical targets (extrinsic coordinates) in visual cortices, and across movements with equivalent joint-angles (intrinsic coordinates) in motor cortices. We interpret this as evidence for the existence of distributed neural populations in multiple motor system areas that encode ipsilateral and contralateral movements in a similar manner: according to their intrinsic/joint coordinates.

SIGNIFICANCE STATEMENT Cortical motor control exhibits clear lateralization: each hemisphere controls the motor output of the contralateral body. Nevertheless, neural populations in ipsilateral areas across the visuomotor hierarchy are active during unilateral movements. We show that fMRI response patterns in the motor cortices are similar for both arms if the movement direction is mirror-reversed across the midline. This suggests that in both ipsilateral and contralateral motor cortices, neural populations have effector-invariant coding of movements in intrinsic coordinates. This not only affects our understanding of motor control, it may serve in the development of brain machine interfaces that also use ipsilateral neural activity.

Introduction

Cortical motor control exhibits clear lateralization where each hemisphere mainly controls the motor output of the contralateral side of the body as demonstrated by the lateralization of cortical connectivity with the muscles (Penfield and Boldrey, 1937). Nevertheless, neural populations in ipsilateral motor areas are active during unilateral movements and exhibit reliable directional selectivity during reaching movements to peripheral targets (Donchin et al., 1998; Cisek et al., 2003). Neurons in the primary motor cortex (M1) can even represent ipsilateral limb position continuously (Ganguly et al., 2009). This directional selectivity during movements of the ipsilateral arm is not limited to the primary motor cortex but distributed across multiple cortical areas involved in movement planning and execution, as was shown in humans using fMRI (Fabbri et al., 2010; Haar et al., 2015). It is still unclear to what extent the representation of hand movement is similar for ipsilateral and contralateral movements in cortical visuomotor brain areas.

Ipsilateral arm movement directions have been decoded in humans using different techniques including EEG (Bundy et al., 2012), electrocorticograph(ECoG; Hotson et al., 2014), and fMRI (Fabbri et al., 2010; Haar et al., 2015). However, neural representations of contralateral and ipsilateral movements are not often compared. We tested whether the directional selectivity of fMRI activity patterns during reaching movements with the two arms suggests an effector-invariant representation of movement. Such effector-invariant representation may be in extrinsic (world) coordinates or in intrinsic (muscles and joints) coordinates, or in a mixture of the two. In a previous study (Haar et al., 2015), we showed that changing the relationship of arm movement and cursor movement does not affect movement representation in motor cortices. This “motor oriented” representation might suggest that motor cortices represent movements in an intrinsic/joint coordinate system. However, previous work on bilateral representation in individual motor cortical neurons gives a mixed picture. Some neurons in M1 show similar directional tuning bilaterally in extrinsic coordinates, others show similar tuning in intrinsic coordinates, and others show no similarity in either coordinate system (Steinberg et al., 2002; Cisek et al., 2003). We consider the possibility that an fMRI exploration of bilateral tuning in M1 would provide a more consistent picture. When comparing patterns of motor cortical activation across movements of the two arms, we can specifically isolate the effector-invariant aspects of representation. This could help clarify which neural population is dominant in effector-invariant representation in motor cortices.

In the current study, we recorded fMRI responses of healthy human subjects as they made slice (out-and-back) reaching movements to four peripheral targets using either the right or left arm. We then used pattern classification techniques to determine whether it was possible to decode movement direction from the fMRI response patterns in each of several visual and motor cortical areas when examining ipsilateral or contralateral movements separately. In agreement with previous studies (Fabbri et al., 2010; Haar et al., 2015), we were able to decode the direction of movements performed by contralateral or ipsilateral arm with above chance accuracy. Next, we trained a classifier to distinguish between fMRI responses of movements to different targets when performed by one arm and tested its decoding ability using fMRI responses of movements made by the other arm. We performed this analysis once with movements defined according to their extrinsic target locations (i.e., real-world coordinates) and again with movements defined according to their intrinsic, joint-angle coordinates. This initial approach is the most widely used in the multivoxel pattern analysis (MVPA) literature. However, it does not address the possibility that effector-invariant representation combines intrinsic and extrinsic components. Therefore, we also applied pattern-component modeling analysis and a geometrical analysis of the voxel-by-voxel fMRI patterns to further examine similarities across contralateral and ipsilateral movements when defined in extrinsic or intrinsic coordinates.

Materials and Methods

Subjects.

The data analyzed in the current study was collected during a previous study (Haar et al., 2017). Thirty-two right-handed volunteers with normal or corrected-to-normal visual acuity [15 women and 17 men, aged 22–36 (25.6 ± 2.5)] participated in the study. The Soroka Medical Center Internal Review Board approved the experimental procedures and written informed consent was obtained from each subject. The sample size was selected so that the t test effect size of 0.5 would have power >1 − β = 0.85 (one-tailed test), with α set to 0.05. According to G*Power (Faul et al., 2009), the required minimum sample size is 31.

Experimental setup and design.

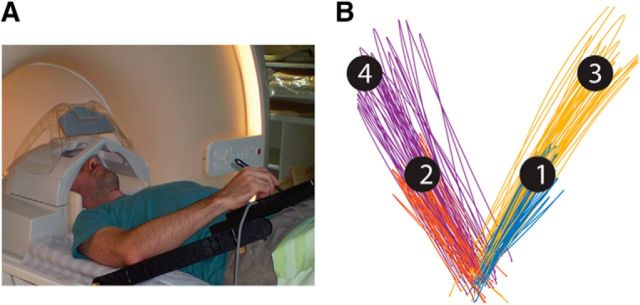
Subjects lay in the scanner bore and viewed a back-projected screen through an angled mirror, which prevented any visual feedback of their arm and hand. An MRI-compatible digitizing tablet (Hybridmojo) was placed over the subject's waist and used to track their arm movements (Fig. 1A). Subjects performed slice (out-and-back) reaching movements from a central target to four peripheral targets differing in their directions and extents (Fig. 1B) and did not receive any visual feedback of their arm location during movement. The directions were ±45° and the extents were 7 and 13 cm. Each trial started with the presentation of a peripheral target for 1 s. Four seconds after the target disappeared, the central target changed from red to green, indicating that the movement should be performed by moving the stylus pen on the tablet. Subjects had 1 s to complete the movement after which the center target turned red and remained red for the entire intertrial interval (ITI), which lasted 6 s. There was no post-trial visual feedback or knowledge-of-results. All subjects performed three experimental runs with each arm, each lasted 9 min and contained 11 movements to each of the four targets. The experiment started with three runs of the left (nondominant) arm, followed by three runs of the right (dominant) arm. Between the sets the experimenter helped the subject to move the stylus from his left hand to his right hand without moving his head and body. Before the scan, the subjects trained on the task to get familiar with the tablet and the task rule (wait for the go cue), and to get comfortable with moving a stylus pen on a tablet with their left (non-dominant).

Figure 1.

A, Experimental setup. B, Representative example of movement paths of one subject with his right arm to the different targets. Movement paths are color coded according to their target.

Movement recording.

Kinematic data were recorded at 200 Hz. Trials with a reaction time of >1 s, trials with a movement angle error >22.5° (at peak velocity or end point), and trials with movement length that was <50% or >200% of the target distance were discarded from further analysis. Trials containing correction movements (i.e., velocity profiles with more than 2 peaks) were also removed. Additionally, to avoid classification biases due to uneven number of trials, in each pair of targets (long and short) we removed the trials with the highest angular errors from the target that had more trials, to force even number of trials. On average ∼8% (SD 3%) of the trials were discarded for each subject. There was no significant difference in the number of discarded trials between the two arms.

MRI acquisition and preprocessing.

Imaging was performed using a Philips Ingenia 3T MRI scanner located at the Ben-Gurion University Brain Imaging Research Center. The scanner was equipped with a 32-channel head coil, which was used for RF transmit and receive. Blood oxygenation level-dependent (BOLD) contrast was obtained using a T2*-sensitive echo planar imaging pulse sequence (TR = 2000 ms; TE = 35 ms; FA = 90°; 28 slices; voxel size: 2.6 × 2.6 × 3 mm and, with 0.6 mm gap). Anatomical volumes were acquired with a T1-weighted sagittal sequence (TR = 8.165 ms; TE = 3.74 ms; FA = 8°; voxel size: 1 × 1 × 1 mm).

MRI data were preprocessed with the FreeSurfer software package (http://surfer.nmr.mgh.harvard.edu; Fischl, 2012) and FsFast (FreeSurfer Functional Analysis Stream). Briefly, this process includes removal of non-brain tissue and segmentation of subcortical, gray, and white matters based on image intensity. Individual brains were registered to a spherical atlas, which used individual cortical folding patterns to match brain geometry across subjects. Each brain was then parcellated into 148 cortical regions-of-interest (ROIs) using the Destrieux anatomical atlas (Destrieux et al., 2010). Functional scans were subjected to motion correction, slice-timing correction, and temporal high-pass filtering with a cutoff frequency of two cycles per scan. Functional scans were registered to the high-resolution anatomical volume. No additional spatial smoothing was performed. Preprocessed data were imported into MATLAB (R2015a, MathWorks), and all further analysis was performed using custom software written in MATLAB.

Identification of ROI.

Visual and motor ROIs were defined a priori according to a combination of anatomical and functional criteria in the native space of each subject. We identified seven commonly reported visual, visuomotor, and motor ROIs (Gallivan et al., 2011; Vesia and Crawford, 2012; Barany et al., 2014; Haar et al., 2015) by selecting 150 continuous functional voxels with the strongest activation during movements of the contralateral arm to the four targets. The ROIs were located in the following anatomical areas: early visual cortex (Vis), occipital pole and calcarine sulcus; superior parieto-occipital cortex (SPOC), superior portion of the parieto-occipital sulcus; inferior parietal lobule (IPL), dorsal portion of the angular gyrus and the middle segment of the intraparietal sulcus; superior parietal lobule (SPL), anterior portion of the superior parietal lobule, superior to the IPS and slightly posterior to the postcentral sulcus; M1, anterior bank of the central sulcus in the hand knob area; dorsal premotor cortex (PMd), junction of superior frontal sulcus and precentral sulcus; supplementary motor area (SMA), medial wall of the superior frontal gyrus, anterior to the central sulcus, posterior to the vertical projection of the anterior commissure. The averaged centers across subjects of all ROIs are listed in Table 1.

Table 1.

Mean ROI MNI coordinates

ROI name	MNI coordinates
	x	y	z
L Vis	−17	−94	−1
R Vis	17	−88	3
L SPOC	−14	−59	22
R SPOC	17	−57	22
L IPL	−29	−46	49
R IPL	35	−47	45
L SPL	−28	−36	55
R SPL	32	−34	52
L M1	−27	−23	58
R M1	29	−20	55
L PMd	−25	−11	54
R PMd	26	−6	50
L SMA	−5	−15	57
R SMA	8	−13	63

We defined eight additional ROIs outside the brain (1 ROI in each corner of the scanned volume). These ROIs were used in control analyses to assess measurement noise during the scan of each subject.

Time course analysis.

To ensure that our fMRI patterns were not generated by head motion, respiration, and blood flow artifacts, we removed the following components from the fMRI time course of each cortical voxel, through linear regression: (1) six head motion parameters obtained by rigid body correction of head motion (3 translations and 3 rotations), (2) fMRI time course from the lateral ventricles, and (3) the mean fMRI signal of the entire cortex (i.e., global component). Last, we normalized the time course of each voxel to present signal change.

MVPA.

We first estimated the response amplitude for movement execution of each voxel in each trial using a general linear model (GLM) analysis where the GLM contained a row for every time-point and a column for every trial. Each column contained a delta function at time of the go cue (movement onset), which was convolved with a canonical hemodynamic response function. The response amplitude associated with each trial (i.e., β value) was estimated using multiple regression and the statistical significance of the response amplitude was estimated by computing its t statistic. Voxel-by-voxel t values of each trial formed a multidimensional vector with the number of dimensions equal to the number of voxels in the ROI. t Value rather than β value vectors were used in all classification analyses to suppress the contribution of voxels with large trial-by-trial variability (Misaki et al., 2010). Next, we deducted the mean from the voxel-by-voxel fMRI response pattern of each trial, to remove possible effect of the changes in overall activation, which could reflect uninteresting vascular dynamics of large-vessels, which do not encode the task (O'Herron et al., 2016).

We performed the classification analyses using a multiclass linear discriminant analysis (LDA) classifier implemented in MATLAB's statistics toolbox. We trained each of the classifiers to identify the movement direction of each trial according to the voxel-by-voxel fMRI patterns in each ROI. We first performed this analysis within arm (i.e., using movements of the same arm) using a “leave-one-out” validation scheme. This included training the classifier using all but one of the accurate trials, and then assessing the accuracy of the classifier by decoding the movement direction of the remaining trial. We repeated this process while leaving-out each of the trials and then estimated the overall decoding accuracy by computing the proportion of accurately decoded trials for each arm in each ROI. We then performed cross-decoding, between-arms, where we trained the classifier on all trials performed with one arm and tested it while decoding the movement direction in all trials performed with the other arm. Decoding accuracy was estimated as the proportion of trials that were accurately decoded. The number of trials used to train each of the classifiers was balanced across targets to prevent classification bias toward over-represented targets.

To assess statistical significance of decoding accuracy in both within and between arms analyses, we performed a randomization test, which was identical to the classification analysis described above except that we randomly shuffled the movement labels before training the classifier. We ran this analysis 2000 times, on each we randomly choose 32 subjects (with repetitions) and for each subject separately we reshuffled the movement labels each time, and then computed the mean across subjects in each iteration. The mean decoding accuracy across subjects was considered significantly larger than chance if it exceeded the 97.5th percentile of the null/chance distribution for each ROI. Accordingly, all statistical tests used in all graphs and all analyses are based on the permutation tests and not on theoretical chance levels. We used the false discovery rate (FDR) correction (Benjamini and Hochberg, 1995; Yekutieli and Benjamini, 1999) to correct for the multiple comparisons across ROIs.

Searchlight analysis.

We used a searchlight analysis (Kriegeskorte et al., 2006) to map classifier decoding accuracies across the entire brain. Clusters of 27 functional voxels were defined by creating a volumetric cube with an edge length of 3 voxels around each gray matter voxel. An LDA classification analysis was performed for each cluster as described above such that each gray matter voxel was associated with a decoding accuracy value yielding a decoding accuracy map. The searchlight analysis was performed in the native space of each subject. Decoding accuracy maps of all subjects were transformed to a standard cortical surface using FreeSurfer and a t test was used to determine whether each vertex (distributed points along the cortical surface from which FreeSurfer is sampling the fMRI data) exhibited significant above-chance decoding accuracies across subjects. We used FDR correction to correct for the multiple comparisons across vertices (Storey, 2002).

Correlations between patterns.

Another way to characterize the similarity of fMRI activity patterns in different behavioral conditions has been through the analysis of the covariance of the patterns (using pattern component modeling; Diedrichsen et al., 2011). By analyzing the covariance matrix, the high dimensionality of the problem of comparing patterns (where dimensionality is in the hundreds) is reduced to the much lower dimensionality of the size of the covariance matrix (whose dimensionality is generally <20). In addition, this approach allows simultaneous effector-invariant representation in both extrinsic and intrinsic coordinates in a single ROI. This approach has already been used to test for effector-independent representations of finger tapping sequence (Wiestler et al., 2014). In brief, the approach treats every aspect of the movement as a “component” that will contribute to the overall pattern of activity. In our study, we included components for the two different arms and also for each of the four different targets during movements of each arm. Thus, there were a total of 10 components. These components are then used as a random effect in a linear regression. This means that the regression estimates the covariance matrix of each pattern expression rather than estimating the pattern itself. The size of the covariance of different components expresses the similarity in the patterns that are expressed during trials in which that component appears. This allows us to estimate the degree of extrinsic effector-independent representation with the covariance between components representing movements to the same target with the different arms. We can, at the same time, measure the degree of intrinsic effector-independent representation with the covariance between components representing movements with the different arms to mirror-symmetric targets. The strength of this approach is that it allows estimating these two different covariances simultaneously whereas the previous approaches essentially classified each ROI as either extrinsic or intrinsic.

Distances between patterns.

In an attempt to get a lo-dimensional representation of the distance between patterns, we projected the multidimensional fMRI pattern on a single dimension-of-interest (see Fig. 6A). The single dimension was the one that connects the mean patterns of two movements performed with the same arm to different targets. By projecting the mean patterns of the movements with the other arm to these same targets we were able to localize them on this single dimension. We scaled this one-dimensional representation so that the distance between the two right arm movements would be one, and averaged this unidimensional projection across subjects. We compared these results relative to these of a null dataset. For the null dataset we generated triplets of random vectors with the same number of dimensions as the original data (150 voxels) from a multivariate normal distribution, and projected the third on the single dimension connecting the other two. We repeated this once for each subject (32 times) and averaged the projections over the subjects to get an average projection. This whole process was repeated 1000 times to get a distribution of the average projection for null data. We compered the actual mean projections to the 95% HDI of the null data mean projections (see Fig. 6B, red patch).

Figure 6.

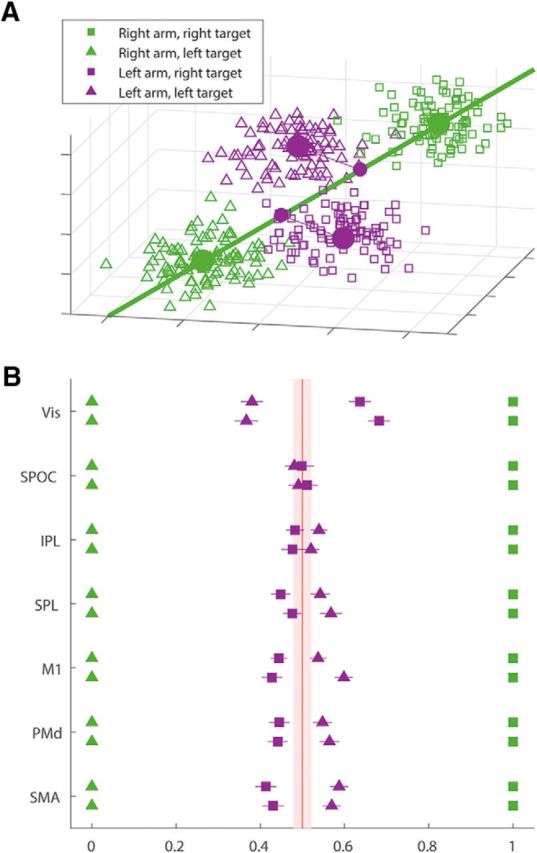
Spatial relation between fMRI patterns. A, 3D simulation of the multidimensional projections: each square/triangle represents the 3 voxel fMRI pattern of a single trial (which is a simplification of the 150 voxels patterns in the data). The squares are trials to the right target and the triangles are trials to the left target, both are color coded for the moving arm (green, right arm; purple, left arm). The large dots represent the mean fMRI pattern across all trials performed with the same arm to each target. The green line is the dimension-of-interest in this space: the dimension that connects the two mean patterns of right arm movements. On this line we project the mean patterns of the left arm movements. The small purple dots are the projections of the left arm movements' patterns on the dimension-of-interest. In this example, the projections suggest an intrinsic/joint representation as the projection of the mean pattern of left arm movements to the right target (purple squares) is close to the mean pattern of right arm movements to the left target (green triangles). B, Distances between fMRI patterns: the mean fMRI response patterns of left arm movements to each target in each ROI was projected onto the difference vector between the two mean patterns of right arm movements. The distance matrix of each subject was normalized so that the distance between the right arm patterns is fixed to one. Each dot represents the mean across subjects of the unidimensional projection (color code and marker types are the same as in A), and the lines represent SEM. For each ROI the top row is the left hemisphere ROI and the bottom one is the right hemisphere. The light red patch is 95% HDI of null data.

Results

Thirty-two right-handed volunteers lay in the MRI scanner bore and performed slice (out-and-back) reaching movements from a central target to four peripheral targets in two different directions and to two different distances (Fig. 1).

Decoding movement direction

We assessed the decoding accuracy of movement directions, during movement execution, in each of seven visuomotor brain regions, in each hemisphere (Fig. 2). These were defined according to anatomical constraints and functional responses in each subject separately (see Materials and Methods). In the first analysis, we evaluated the decoding accuracy within each arm. LDA classifiers identified movement direction according to the voxel-by-voxel response patterns of single trials, and we assessed decoding accuracy using a leave-one-out validation scheme. We used a randomization analysis to determine statistical significance and then applied an FDR correction to address the multiple comparisons problem (see Materials and Methods). Our analysis classified long and short movements separately. Although the decoding accuracies were a bit higher for the longer movements, the results were almost identical for the two sets of movement types, suggesting high reproducibility. We present results averaged across the two different movement lengths. All results are presented with FDR-corrected significance.

Figure 2.

ROIs. Cortical areas that exhibited strong responses during right (A) and left (B) arm movements are shown in red/orange. Results calculated across all subjects (random-effects GLM) and displayed on inflated hemispheres of a template brain. The general locations of the selected ROIs are indicated, but actual ROIs were anatomically and functionally defined in each subject.

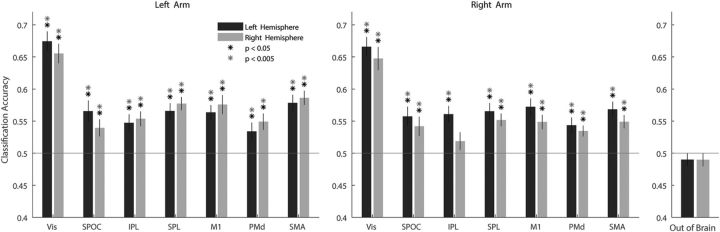
The mean decoding accuracies were significantly above chance level (50%) in both hemispheres while making movements with either arm (Fig. 3). Vis showed the highest decoding accuracies (>64%, p < 0.001), whereas all other ROIs showed relatively similar values (>54%, p < 0.001) with the only exceptions the PMd during ipsilateral arm movements (>53%, p < 0.005), and right IPL during ipsilateral movement, which was the only region not to show significant decoding (52%, p = 0.18). A two-tailed Student's t test found no significant differences in the decoding accuracy between the right and the left arm (p > 0.25), nor between the ipsilateral and the contralateral ROIs in any of the regions (p > 0.43). However, we note that visual cortical areas (Vis and SPOC) showed slightly better decoding for the dominant, left hemisphere, whereas motor cortical areas (SPL, M1, PMd, and SMA) showed slightly better decoding for the contralateral hemisphere. In any case, our results showed that directional selectivity was clearly apparent in the voxel-by-voxel fMRI patterns of multiple visual and motor system areas both for contralateral and ipsilateral movements. Control regions outside of the brain showed chance classification for both right and left arm movements.

Figure 3.

Within arm decoding. Mean decoding accuracies across subjects for each of the arms separately using a leave-one-out validation scheme (left hemisphere ROIs in black, right hemisphere ROIs in gray). Solid red line indicates chance level (50%, 2 movement directions). Error bars indicate SEM across subjects. Asterisks indicate significant above-chance decoding accuracies (randomization test, FDR-corrected for multiple comparisons).

Decoding movement direction across arms

The bilateral robustness of directional selectivity throughout the visuomotor hierarchy, demonstrated by the within arm decoding, led us to ask whether some directional selectivity reflected an effector-invariant movement representation. We tested this using cross-decoding. We tested whether a classifier for fMRI patterns trained to identify movement direction using trials performed with one arm would be able to decode movement direction from the trials performed with the other arm. We present cross-decoding accuracies averaged across both arms and both target distances. Successful cross-decoding in a particular ROI suggests that some of the fMRI activity in that ROI represents the movement in the same way during movements of either arm. Figure 4A illustrates two decoding possibilities: movements could have similar representation when they are in the same direction in space (extrinsic coordinate representation) or when they involve movement of the same right/left arm joints and are, therefore, in mirror-symmetric directions in space (intrinsic/joint coordinate representation).

Figure 4.

Between arms decoding. A, Illustration of the possible pairs of movement with both arms that may share similar fMRI representations. On the right with a light blue background, movements to different spatial targets using similar joint configuration, which suggest representation in intrinsic/joint coordinates. On the left with a light red background, movements to the same spatial target using different joint configuration, which suggest representation in extrinsic coordinates. B, Mean decoding accuracies between arms across subjects in the ROIs of the both hemispheres (left hemisphere in black, and right hemisphere in gray) and outside the brain. Bars going to the right (light blue background) are for decoding in intrinsic/joint coordinates, and bars going to the left (light red background) are for decoding in extrinsic coordinates. Error bars indicate SEM across subjects. Asterisks indicate significant above-chance decoding accuracies (FDR-corrected for multiple comparisons). C, Whole-brain searchlight analysis between arms. For each cluster of vertices the classifier was trained on trials performed with one arm and tested on trials performed with the other arm. Cortical vertices with between arms decoding accuracies that were significantly above chance across subjects in intrinsic/joint coordinates (blue, p < 0.05, FDR-corrected) or in extrinsic coordinates (red, p < 0.01, FDR-corrected) are marked on inflated hemispheres of a template brain.

Response patterns in visual brain areas were accurately decoded in extrinsic coordinates, whereas response patterns in some motor brain were accurately decoded in intrinsic coordinates (Fig. 4B). Decoding accuracies in extrinsic coordinates were significantly above chance levels only in the visual cortex bilaterally (>60%, p < 0.001). Decoding accuracies in intrinsic coordinates were significantly above chance levels in M1 bilaterally (>53%, p < 0.001), SMA bilaterally (>54%, p < 0.001), left PMd (53%, p < 0.001), right PMd (52%, p < 0.002), left SPL (52%, p < 0.005), and right SPL (53%, p < 0.001). SPOC and IPL showed chance classification in both hemispheres (p > 0.35). Control regions outside of the brain also showed chance decoding.

These cross-decoding results showed reproducibility across the two hemispheres, across the different combinations of training and testing arm, and across the two different sets of movements to the long and the short targets. All these different cross-decoding results showed no significant statistical differences (two-sample t tests across all pairs, p > 0.36), demonstrating the robustness of the results.

Searchlight decoding

We used a whole-brain searchlight analysis (Kriegeskorte et al., 2006) to assess effector-invariant directional selectivity across the entire cortical surface without restricting the analysis to a priori ROIs. We defined volumetric searchlight cubes across the cortical gray matter, and for each cube we performed between-arm cross-decoding (training the classifier on one arm and then decoding trials from the other arm) as described above in the ROI analysis. A t test across subjects, followed by FDR correction, assessed decoding accuracy significance in each voxel (see Materials and Methods).

The searchlight map in both hemispheres was remarkably similar and shows complementary results to those described in the ROI analysis (Fig. 4C). Significant effector-invariant decoding in intrinsic coordinates was evident in M1, PMd, SMA, and SPL in both hemispheres, whereas significant decoding in extrinsic coordinates was evident only in the visual cortex. These results validate the ROI results using far smaller clusters of voxels for the classification and decoding procedures. Although there was significant decoding in intrinsic coordinates in the superior postcentral sulcus (which overlapped with the ROI defined for SPL), no other effector-invariant decoding was apparent in the posterior parietal cortex (PPC). This can suggest either that there is no effector-invariant representation of movement in the parietal cortex or that there are effector-invariant representations in both intrinsic and extrinsic coordinate frames that combine in a manner that prevents decoding.

Correlations between patterns

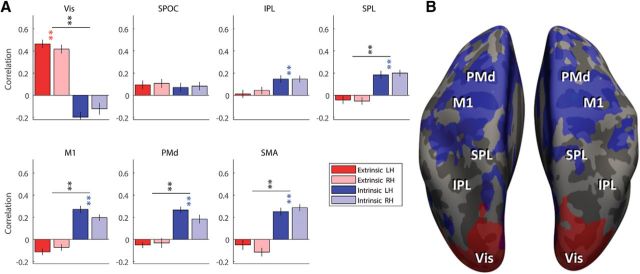
To address the possibility of effector-invariant representations in both intrinsic and extrinsic coordinate in the same region, we extend the analysis following the logic of Wiestler et al. (2014). Their approach hypothesizes that the patterns associated with movement can be decomposed into arm-related components and movement-specific components. Rather than identifying these components, they estimate their covariance matrix using pattern-component modeling (Diedrichsen et al., 2011). Following this approach (see Materials and Methods), we can estimate the correlation between the movement-specific components; i.e., what proportion of the informative, movement-specific pattern was shared between the two arms in extrinsic and/or in intrinsic coordinates.

In the cross-correlation analysis each trial is classified to one target or the other, and as a result the bars (Fig. 4B) can only go to one direction or the other (extrinsic/intrinsic). On the other hand, the pattern component analysis allows each region to have significant correlations in both extrinsic and intrinsic coordinates. In this approach we calculate the correlation between the component of moving one arm to one target, to the two components of moving the other arm to the two different targets, and get two independent correlation coefficients. Thus, in Figure 5A the red (extrinsic) and blue (intrinsic) bars can go up simultaneously. Similarly, in the surficial correlation map (Fig. 5B) the same region can be both extrinsic and intrinsic (red and blue combine as purple). Nevertheless, the results showed that this does not happen. The visual cortex showed strong and significant correlations in extrinsic coordinates (r > 0.4, p < 0.001) and M1, PMd, SMA, and SPL, showed strong and significant correlations in intrinsic/joint coordinates (r > 0.18, p < 0.001; Fig. 5A). This analysis did reveal that IPL also had significant representation in intrinsic coordinates (r > 0.14, p < 0.005). However, it was not significantly greater than the extrinsic representation, as revealed in pattern component correlations. This may explain why the classification approach above failed to uncover this representation.

Figure 5.

Correlation analysis between arm. A, Corrected correlation coefficients were computed using pattern component modeling for each ROI in extrinsic (red) and intrinsic/joint (blue) coordinates for the left (dark red/blue) and right (light red/blue) hemisphere. Colored asterisks indicate correlations that are significantly >0; black asterisks indicate significant difference between the intrinsic and extrinsic correlations. **p < 0.001,*p < 0.01. LH, Left hemisphere; RH, right hemisphere. B, Map of correlation of the pattern components in extrinsic coordinates (red) and intrinsic/joint coordinates (blue), thresholded at r > 0.15.

These results were reproduced in a searchlight analysis, where we ran the same analysis on a volumetric cube shifted across the cortical gray matter. On the surface (Fig. 5B) one can see clearly how the extrinsic correlations are limited to the occipital cortex, and see the spread of the intrinsic correlations across the frontal and posterior parietal cortex.

Distances between patterns

Last, we developed a geometrical analysis to represent the relation between the movement patterns spatially. The aim of this additional analysis is to get a low-dimensional representation of the distance between fMRI patterns of the different movements to facilitate spatial visualization. Figure 6 shows the actual distances between the patterns of the different movements. This complements the MVPA methods by presenting the raw data after a simple projection onto the dimension-of-interest. We calculated the mean fMRI pattern across all trials performed with the same arm to each target and interpreted this pattern as a point in a multidimensional space where each dimension represents activity of a single voxel. In this space, we used, as a reference, the vector connecting movements to two different targets with the right arm (Fig. 6A). We asked where along this vector the two movements of the left are located. Thus, we projected the patterns associated with the left arm onto the vector defined by movements of the right arm. This allowed us to ask to which right arm movement pattern each left arm movement pattern was closest. To allow comparison across subjects, we normalized the distances between patterns by the size of the reference vector.

Figure 6B presents the normalized distances between patterns in each of the ROIs, compared with the 95% HDI of randomly generated patterns. In visual cortices, patterns of movements of the two arms to the same target were closer than patterns of movements to opposite targets (t test on the distances between the projections, p < 10e−10). In motor cortices, the opposite was the case. fMRI patterns of movements with the right or left arm to mirror-symmetric targets were closer to each other (p < 10e−5). In the intermediate visuomotor regions in parietal cortex, the fMRI patterns of the projections of the two left arm movements were relatively similar to each other and were within the range of the distribution of the randomly generated patterns.

Control for kinematic differences

All the results above are based on the assumption that movements to different directions have similar kinematics. Otherwise, the decoding we do may be influenced by these kinematics and not only by the direction. Indeed, movements to the ipsilateral target are somewhat longer and faster than movements to the contralateral target (Fig. 7). To ensure that those kinematic differences did not impact our results we tested for a possible correlation between the kinematic differences and the decoding accuracies across subjects. There was no such correlation in any of the ROIs (r < 0.15, p > 0.1 uncorrected). In an additional control analysis, we reran the cross-decoding analysis only on the subjects that do not show consistency across arms (movements to the ipsilateral target are longer and faster only in one arm but not it the other, or in none of the arms). In this case, if the decoding on the training data are based on the kinematics and not the direction it should produce no cross-decoding to the other arm where there is no kinematic difference between the movement directions. These cross-decoding results were similar to the ones reported in Figure 4 (i.e., all motor cortices significantly decode movement direction across arms in intrinsic/joint coordinates), suggesting that we do classify the difference in the direction and not in the extent or the velocity.

Figure 7.

Kinematic differences. Left (A) and right (B) arm movement extents are presented for the movements to the ipsilateral targets (x-axis) versus the contralateral targets (y-axis), for the short (light gray) and long (dark gray) movements. Each dot is the median extent of movements to the target by a subject; the plus is the 50% confidence interval across trials. C, The difference in movement extents between the ipsilateral and the contralateral targets for the right arm (x-axis) versus the left arm (y-axis). The color code is the same as in A and B.

Discussion

It is well established that motor brain areas are active during ipsilateral arm movements and even exhibit reliable directional selectivity (Donchin et al., 1998; Cisek et al., 2003; Fabbri et al., 2010; Haar et al., 2015). Here we tested whether the expression of this directional selectivity in patterns of fMRI activation is similar across ipsilateral and contralateral arm movements and revealed effector-invariant representation in cortex. We further asked whether effector-invariant representation is primarily expressed in an intrinsic or extrinsic coordinate frame. Our results reveal that ipsilateral and contralateral movements involving symmetric joint configurations are encoded in a similar manner by neural populations in the motor cortices (M1, PMd, SMA, and SPL). This is evidence for effector-invariant encoding of movements in intrinsic/joint coordinates. Effector-invariant representation of movement in M1 suggests that the two M1s receive a common drive. This common drive may explain the pathology of mirror movements in joint coordinates (Tsuboi et al., 2010; Ruddy and Carson, 2013).

Clinical studies suggest an important role for ipsilateral activity in the recovery of motor function (Bradnam et al., 2013). After unilateral damage to a sensorimotor area, the brain activity on the side ipsilateral to the paralyzed limb increases to compensate (Johansen-Berg et al., 2002). In fact, recent work uses ipsilateral motor activity to develop brain machine interfaces (BMIs) for patients with unilateral damage (Bundy et al., 2012; Hotson et al., 2014). Our results suggest specific constraints on the decoding mechanisms used in ipsilateral BMIs, which may facilitate the use of BMIs in controlling ipsilateral movements following contralateral damage.

Single-cell recordings during arm reaching movements in monkeys also show directional tuning across the motor cortices for both contralateral and ipsilateral movements (Donchin et al., 1998; Cisek et al., 2003). At the level of individual neurons, comparing representation for movements of the two arms is complicated by the fact that the tuning of many neurons changes over the course of the trial (from planning to execution; Cisek et al., 2003). In addition, a key finding is that the difference in the directional tuning of a neuron to the two arms is not consistent across M1 neurons (Steinberg et al., 2002; Cisek et al., 2003). These findings can be explained by the fact that different neurons in M1 encode direction in different coordinate systems (Wu and Hatsopoulos, 2006). Although the picture at the single neuron level may be complicated, a recent study asked a similar question at the ensemble level of M1 neurons (Ganguly et al., 2009). That study, which compared activity of the two cortices during right arm movements, found that both contralateral and ipsilateral ensemble activities were more strongly correlated with angular joint kinematics than end-point hand coordinates. Although this work was done only on right arm movements, and therefore did not compare the activity and selectivity of the same ensemble of neurons while moving the two arms, these results are consistent with our finding that effector-invariant representation in M1 is in intrinsic/joint coordinates.

Importantly, motor cortex represents distal hand movements in anatomical areas distinct from those used for proximal arm movements. Similar representational divisions have been demonstrated in monkeys (Kwan et al., 1978; Park et al., 2001) and humans (Meier et al., 2008). The coordinate systems of representation are also different. M1 representation of distal movements is dominated by extrinsic representation (Kakei et al., 1999), whereas the proximal representation is more mixed (Wu and Hatsopoulos, 2006).

In the PMd, neural recordings suggest that the preferred directions of neurons that are tuned with both arms are similar between arms (in extrinsic coordinates), but this was mostly true before trial onset. During movement, most PMd cells that stay tuned with both arms show varying directional differences of tuning between the arms (Cisek et al., 2003). Like in M1, this diversity may be the expression of neurons encoding in different coordinate systems (Wu and Hatsopoulos, 2007). Our experiment was not designed to isolate preparatory from movement related activity. As a result, we did not explore PMd activity specifically in the pre-movement period.

In the parietal cortex we did not find effector-invariant representation of movement in any of the analyses we ran (except from the primary somatosensory area, which overlapped with the ROI defined for SPL). This can be explained by the role of the parietal cortex in sensorimotor mapping (Buneo and Andersen, 2006; Tanaka et al., 2009; Bernier and Grafton, 2010; Haar et al., 2015), because the transformation between the extrinsic visual coordinates to the intrinsic motor coordinates is effector-specific. Therefore, although single neurons in the parietal cortex may decode movement in an effector-invariant manner in one coordinate system or the other, the area as a whole seems to decode movement in an effector-specific manner.

Although the current study focused on proximal arm movements (shoulder and elbow), similar results were shown in distal finger movements. Recent fMRI studies have suggested that finger movements with right and left hands exhibit hand-invariant representations in M1, PMd, SMA, and SPL when examined in intrinsic coordinates (Diedrichsen et al., 2013). Interestingly, finger sequence movements also suggested intrinsic representations in M1, whereas patterns associated with sequence-specific movements in the PMd suggested both intrinsic and extrinsic representation (Wiestler et al., 2014). Such a combination of coordinate frames in the PMd is not apparent in our results (Fig. 5). This difference in representation in PMd may suggest real differences in the ipsilateral neural representation of finger and arm movements. This goes in line with previous findings demonstrating that ipsilateral distal movements activate only secondary motor areas and deactivate M1, whereas ipsilateral proximal movements do activate M1 bilaterally (Nirkko et al., 2001).

When comparing our study with those on distal representation, it is striking that decoding levels in our study are lower than those in the earlier ones. This is not surprising. fMRI can be used to produced detailed digit maps, with physically adjacent digits represented next to each other (Siero et al., 2014; Ejaz et al., 2015) even following amputation of the limb (Kikkert et al., 2016). Directional selectivity of the arm on the other hand, shows no clear spatial topography in fMRI and therefore relatively low decoding levels (Gallivan et al., 2011; Haar et al., 2015; Gertz et al., 2017).

A recent study (Gallivan et al., 2013) classified reaching movements and grasping movements in the two hands. The study compared reach and grasp movements with similar arm trajectories but different action-goals (reach vs grasp). They found, as we did, bilateral decoding in many motor areas. However, their pattern of effector-invariant representation was different from ours. They found effector-invariant representation in PPC and PMd but not in the primary sensory and motor cortices; we found effector-invariant representation in all frontal motor cortices, but not in PPC. These differences apparently result from differences between the two tasks. Their analysis shows that reach representation in the two hands are more similar than reach representation and grasp representation. Our results do not contradict this. Rather, we compare representation of reach in different directions and compare the similarity of representation between directions. At this level of analysis, the representation task, which includes grasp representation, is much more distal than our task. As discussed above, the distal and proximal movement systems are quite different, and it is not necessarily surprising that the results are not the same. Together with our results, we hypothesize that motor cortices contain an effector-invariant representation of the movement trajectory (in intrinsic coordinates) whereas the parietal cortex contains an effector-invariant representation of action goals. The PMd may contain effector-invariant representations of both trajectory and goal in extrinsic coordinates as well.

Conclusions

The current findings deepen our understanding of effector-invariant encoding of arm movement trajectory across the human cortex. They highlight the existence of such encoding across the motor cortices in intrinsic/joint coordinates. Together with previous studies that made similar maps for action goals (Gallivan et al., 2013) and for finger movements (Diedrichsen et al., 2013; Wiestler et al., 2014), our results offer a coherent picture of effector-invariant representations across cortex. Although this is of central importance to our understanding of motor control, it may also be useful in the development of BMIs based on ipsilateral activity.