Interlayer Repulsion of Retinal Ganglion Cell Mosaics Regulates Spatial Organization of Functional Maps in the Visual Cortex

Abstract

In higher mammals, orientation tuning of neurons is organized into a quasi-periodic pattern in the primary visual cortex. Our previous model studies suggested that the topography of cortical orientation maps may originate from moiré interference of ON and OFF retinal ganglion cell (RGC) mosaics, but did not account for how the consistent spatial period of maps could be achieved. Here we address this issue with two crucial findings on the development of RGC mosaics: first, homotypic local repulsion between RGCs can develop a long-range hexagonal periodicity. Second, heterotypic interaction restrains the alignment of ON and OFF mosaics, and generates a periodic interference pattern map with consistent spatial frequency. To validate our model, we quantitatively analyzed the RGC mosaics in cat data, and confirmed that the observed retinal mosaics showed evidence of heterotypic interactions, contrary to the previous view that ON and OFF mosaics are developed independently.

SIGNIFICANCE STATEMENT Orientation map is one of the most studied functional maps in the brain, but it has remained unanswered how the consistent spatial periodicity of maps could be developed. In the current study, we address this issue with our developmental model for the retinal origin of orientation map. We showed that local repulsive interactions between retinal ganglion cells (RGCs) can develop a hexagonal periodicity in the RGC mosaics and restrict the alignment between ON and OFF mosaics, so that they generate a periodic pattern with consistent spatial frequency for both the RGC mosaics and the cortical orientation maps. Our results demonstrate that the organization of functional maps in visual cortex, including its structural consistency, may be constrained by a retinal blueprint.

Introduction

In the primary visual cortex (V1) of higher mammals, the spatial distribution of orientation preference across the cortical surface is arranged quasi-periodically, ending in an organized orientation map (Blasdel and Salama, 1986; Ts'o et al., 1990; Bonhoeffer and Grinvald, 1993). It is not completely understood how such periodic organization is initially developed (Purves et al., 1992; Horton and Adams, 2005; Van Hooser, 2007), but clues are found in how the segregation between ON and OFF subregions in the cortical receptive field is developed to originate the orientation tuning in a single V1 neuron (Hubel and Wiesel, 1959; DeAngelis et al., 1995; Reid and Alonso, 1995). In the classical view, it is suggested that a V1 neuron selectively samples feedforward inputs from thalamic neurons to generate an orientation-tuned receptive field (Hubel and Wiesel, 1962).

However, experimental observations have suggested that the orientation tuning in V1 might be determined by the spatial distribution of thalamic afferents. Orientation tuning of V1 neurons was well predicted by the local average of thalamic ON and OFF receptive fields (Jin et al., 2008, 2011; Wang et al., 2015). Also, the topography of functional maps in V1 is strongly correlated to the spatial distribution of thalamic afferents (Kremkow et al., 2016; Lee et al., 2016). These results may reconfirm the earlier observations that the preferred orientation of a V1 neuron remains consistent without recurrent cortical activity, when the thalamic afferents are the only input provided (Ferster et al., 1996; Chung and Ferster, 1998; Lien and Scanziani, 2013). These observations altogether indicate that the topography of cortical orientation maps may be initially seeded by the spatial distribution of ON and OFF thalamic inputs before the postnatal refinement (Chapman et al., 1996; Crair et al., 1998; Fig. 1A).

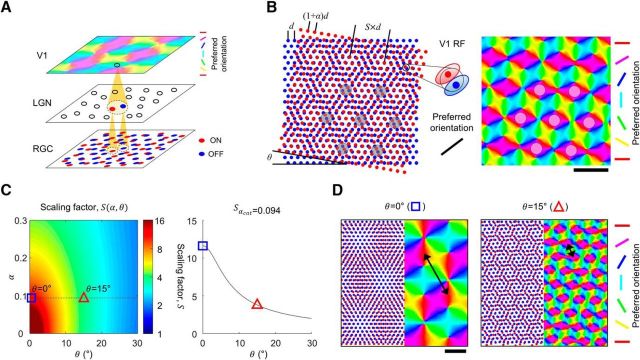
Figure 1.

Retinal origin of cortical orientation map and its variation of spatial organization. A, Developmental model of orientation map as feedforward projection of ON and OFF retinal mosaics. Receptive field of a V1 neuron is organized from the local projection of ON and OFF retinal mosaics. B, The period of the retinal moiré interference pattern (scaling factor, S) is a function of the lattice spacing ratio (α) and the alignment angle (θ) between ON and OFF RGC mosaics. Orientation tuning of a V1 cell is decided from the local structure of ON and OFF RGC mosaics with feedforward wiring, thus the periodic retinal interference pattern seeds a cortical orientation map. Scale bar, S. C, Left, scaling factor S as a function of α and θ. Right, variation in the calculated value of S, when α is fixed to 0.094 as estimated from cat data (Zhan and Troy, 2000). D, Sample orientation maps developed by moiré interference of RGC mosaics for α = 0.094. Spatial period of maps appear to vary significantly for different value of θ Left, S = 11.7 of developed map for θ = 0°. Right, S = 3.8 for θ = 15°. Black arrows indicate spatial period of maps. Scale bar, 5d.

Given this, how can the spatial distribution of thalamic afferents be organized in a quasi-periodic manner, as observed in the orientation map? Considering that neurons in lateral geniculate nucleus (LGN) relay the receptive field of the retinal ganglion cells (RGCs; Usrey et al., 1999), the statistical wiring model (Ringach, 2004, 2007) suggests that V1 receptive field structure may be constrained by the spatial organization of ON- and OFF-center receptive fields of RGCs (Soodak, 1987). Based on this notion, a theoretical model (Paik and Ringach, 2011, 2012) proposes that moiré interference between the hexagonal lattice of ON- and OFF-center RGC generates a quasi-periodic pattern that can seed the topography of an orientation map at an early stage of development (Fig. 1B).

However, the model did not state explicitly how the consistent spatial periodicity of maps within a species could be achieved (Obermayer and Blasdel, 1993; Blasdel et al., 1995). According to the model, the spatial periodicity of an interference pattern depends on two parameters; the lattice distance ratio (α) and the alignment angle (θ) between the two lattice patterns (Fig. 1B). The value of α can be restricted by the cell densities of ON and OFF hexagonal mosaics, but θ also needs to be restricted to a small range to achieve consistent spatial periodicity (Fig. 1C). Thus, it must be explained how θ is restricted during development (Fig. 1D).

Here, we demonstrate that local repulsive interactions between RGCs can restrict θ, and achieve a consistent spatial periodicity in the retinal moiré interference pattern and the cortical orientation map. Using our model simulations, we tested the effect of repulsive interactions between nearby RGCs that induced gradual shifts of cell positions. We first observed that homotypic (ON-to-ON or OFF-to-OFF) interactions could induce a long-range hexagonal organization in each type of RGC mosaic (Wässle et al., 1981a), and that the presence of heterotypic (ON-to-OFF) interactions plays an important role in regulating θ. Then, to validate our model, we quantitatively analyzed the structure of the RGC mosaics observed in cat data, and found evidence that the heterotypic repulsive interaction is in effect during the development, contrary to the notion from previous research (Eglen et al., 2005).

Materials and Methods

Experimental design and statistical analysis.

Local repulsive interaction F between nearby cells was designed as a function of distance r between the centers of dendritic fields to induce a gradual shift of cell position (Fig. 2A). To simulate the development of RGC mosaics, particularly focusing on the effect of local repulsive interactions, we implemented a simplified model (Fig. 2B). Initially, cells are randomly distributed and then a repulsive force, F, between any pair of two RGCs modulates the position of cells in the mosaic (Fig. 2C). We assumed that (1) F increases as two cells approach and (2) that the somas of two cells should not overlap during the developmental process (Ringach, 2007). Considering the physical definition of potential energy, F was assumed to have the form 1/r² and the diameter of the soma (s) was assumed to be 0.17d (Wässle et al., 1981a; Rapaport and Stone, 1983), where the unit distance d is the theoretically estimated lattice distance of mosaics with ideal hexagonal structure assumed (Fig. 2B). Then, for a given unit distance d, the equation of F is given as follows:

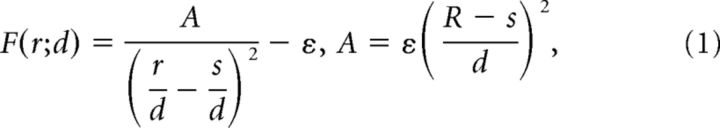where A is a coefficient for calibration of the strength and the interaction distance R. ε Is a fixed constant set to 0.01 for making the interaction disappear at r = R, so F(R) = 0.

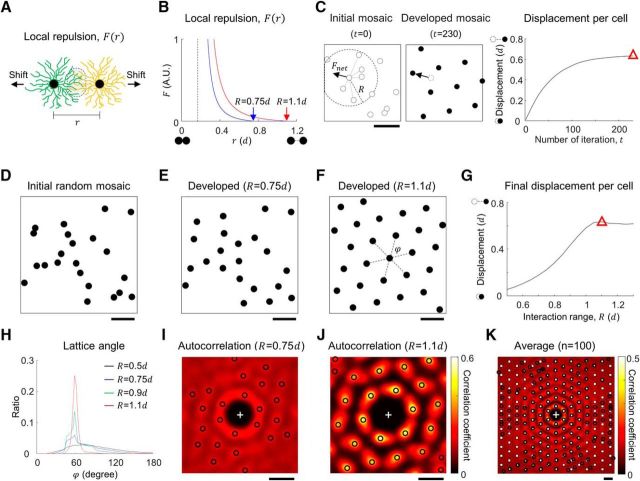
Figure 2.

Local repulsive interaction can develop hexagonal patterns in a monotypic cell mosaic. A, Model of local repulsion. Repulsive interaction between dendritic fields of nearby RGCs induces a gradual shift of each cell. B, Modeled repulsive interaction function that regulates the development of mosaic structure. Magnitude of the interaction force F is a function of distance between the cells (r). F is set to diverge to avoid soma overlap and the dashed line indicates the soma diameter, 0.17d, where d is cell distance in the ideal hexagonal lattice. Red and blue curves show different choice of interaction distance R (red and blue arrows). C, Left, Example of initial cell mosaic. Net repulsion for a cell determines the direction of gradual shift at each iteration. Middle, Developed mosaic and black arrow indicates displacement of a cell from the initial location. Right, Average displacement of a cell during the development for R = 1.1d. The amount of displacement converges as the distribution of cells in the mosaic approaches equilibrium. Red triangle indicates the final state of the simulation. D, For the initial retinal mosaics, cells were sequentially distributed at a random location to avoid soma overlap. E, F, Developed cell mosaics. E, R = 0.75d, F, R = 1.1d. G, Average displacement in the developed mosaic for different R. If R is much smaller than 1d, the amount of cell shift is not enough to induce regular packing of mosaics. The displacement increases as R increases, and when R > 1d, cells are orderly packed and the displacement does not increase any more, even for larger R. Red triangle indicates the displacement in the developed mosaic at R = 1.1d as in C. H, Distribution of lattice angles (ϕ) of simulated mosaic developed with various R. When R is sufficiently large (>∼0.8d) histogram of ϕ peaked at 60°, implying a hexagonal mosaic structure. I, J, 2D autocorrelation of each cell mosaic for investigation of spatial periodicity: the peak at the origin was removed for better presentation of first-order peaks. Black circles indicate the significant local peaks (p < 0.05; see Materials and Methods for details). I, R = 0.75d; autocorrelation peaks show weak periodicity of mosaic lattice. J, R = 1.1d; autocorrelation peaks show strong hexagonal periodicity of developed mosaic. K, Average of aligned autocorrelation of 100 mosaics developed when R = 1.1d. Black circles indicate significant peaks (p < 0.05; see Materials and Method for details) and white solid squares indicate the expected peak position for perfect hexagonal lattice. Note that higher-order peaks suggest that a local repulsive interaction could generate a long-range hexagonal lattice pattern of mosaics. Scale bars: C–F, I–K, 1d.

Considering the slight difference between cell densities of ON and OFF RGCs, each homotypic interaction (F_ON and F_OFF) was defined based on the lattice distance (d_ON and d_OFF) as F_ON = F(r;d_ON) and F_OFF = F(r;d_OFF). From the mosaic in the animal data (Zhan and Troy, 2000), the relationship between d_ON and d_OFF was estimated as d_ON = 1.094 × d_OFF, so α = $\frac{d_{ON}}{d_{OFF}}$ − 1 = 9.4%. Heterotypic interaction (F_ONOFF) was defined by the average of F_ON and F_OFF for a given cell distance r as F_ONOFF = F(r; d_ONOFF), where d_ONOFF = $\frac{d_{ON}+d_{OFF}}{2}$ = 1.05d_OFF.

For each iteration of mosaic development simulation, the actual shift of a cell was decided by the net force F⃗_net, the summation of all local repulsive interactions that the cell receives. To avoid any unrealistic oscillatory movement, spatial shifts of the cells were modeled to occur by a unit distance, and only when the net force exceeded a threshold at each iteration. If F⃗_net exceeded the threshold (10⁻⁴), the cell was shifted by 0.01d in the direction of F⃗_net. Otherwise, the cell maintained its location. The simulation was terminated when <0.5% of cells moved at each iteration.

All simulations and statistical tests were performed using MATLAB R2016b. Bootstrap and Wilcoxon rank sum test were performed: bootstrap was used to define the significant peaks in 2D autocorrelation of the cell mosaics (see subsections below for details).

Autocorrelation of cell mosaics.

Autocorrelation of a single mosaic was calculated as a smoothed 2D autocorrelogram, which revealed the relative distribution between every pair of cells. Autocorrelations were smoothed with a Gaussian kernel of SD 0.15d. The value of correlation was normalized so that the self-correlation peak at the center becomes unity, and the center peak was removed after normalization. The significance of a local peak was verified by bootstrap test: the magnitude of a peak was compared with those in the autocorrelations of control mosaics where the y-coordinates of cell positions were shuffled among the cells. To calculate the averaged autocorrelation, each single autocorrelation was rotated so that the strongest peak was aligned in the +y-axis (Paik and Ringach, 2011). The significance of local peaks was verified by bootstrap test similarly as above, but the control was obtained by calculating the average of randomly rotated autocorrelations.

Estimation of intermosaic distance between ON and OFF RGC mosaics.

Based on the observation that the dendritic fields of ON and OFF RGCs are not developed in the same plane, but in separate layers in the inner plexiform layer (IPL), we estimated the ON and OFF intermosaic distance in two steps: estimating the width of the IPL and the depth difference between ON and OFF RGC mosaics in IPL. The IPL width was estimated to be 45.6 μm in the cross-sectional image of the retina (Kolb, 1979), and the depth difference between ON and OFF layers was 55.6% of the IPL (Balasubramanian and Sterling, 2009). Considering the unit lattice distance in the OFF RGC mosaic (d) was assumed to be 102 μm, the intermosaic distance between ON and OFF RGC mosaics was estimated to be 45.6 μm × 55.6% × (d/102 μm) = 0.248d.

Estimating angle alignment between simulated ON and OFF mosaics.

The angle alignment between simulated ON and OFF mosaics was estimated by matching 2D autocorrelation between the mosaics. Autocorrelation of OFF mosaics was enlarged (increasing α) and rotated (varying θ) to find the condition at which the similarity to autocorrelation of ON mosaics was maximized. Similarity between autocorrelation was measured by the dot product between the 2D correlation plots within 1.25d from the origin. In this step, each single autocorrelation was smoothed by a Gaussian kernel with a SD of 0.26d, for better estimation of peak positions.

Calculation of repulsive energy for a spatial shift of one mosaic.

The energy map was calculated to measure the variation of energy state between heterotypic cell pairs when one mosaic is intentionally shifted. When an ON and OFF cell pair induces repulsive interaction, the repulsive energy (E) is derived from the repulsive force:

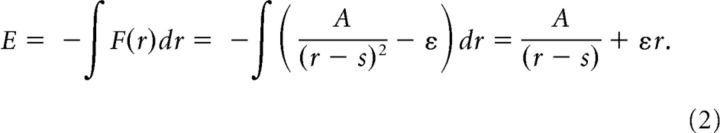First, the heterotypic energy per ON cell was recorded at the origin of the energy map. For all the other points of the map, the OFF mosaic was intentionally shifted by the spatial vector to the point and the energy per cell was measured in the area of overlap between ON and the shifted OFF mosaic.

Results

Homotypic local repulsive interaction as the developmental mechanism of hexagonal RGC mosaics

Regarding the development of orderly retinal mosaics, it has been reported that somas (Wässle et al., 1981a; Zhan and Troy, 2000), dendritic fields (Wässle et al., 1981b), and receptive fields (Gauthier et al., 2009) of one class of RGC are distributed in a quasi-uniform manner across retinal surfaces in adult mammals. This uniform coverage was thought to evolve as a consequence of repulsive interactions between the dendrites of densely located neighboring cells during development to avoid overlap between the functional territory of each cell (Parrish et al., 2007; Grueber and Sagasti, 2010; Zipursky and Grueber, 2013; Lefebvre et al., 2015). This leads their dendritic fields to develop in directions opposite from neighboring cells and results in the shifting of their functional territories to minimize overlap, implying the critical role of the repulsive interaction between nearby cells to develop orderly spatial patterns mosaics. If a local repulsive interaction between neighboring cells can induce gradual shifts of RGC dendritic fields across retinal surfaces (Fig. 2A), this may modulate the spatial organization of RGC mosaics. Here we assumed that this local interaction between dendrites of neighboring cells may develop the quasi-regular hexagonal distribution of dendritic fields observed in RGC mosaics data (Wässle et al., 1981a) and tested the hypothesis by simulating the development of RGC mosaics.

We first investigated whether a local repulsive interaction between cells of the same type (homotypic interaction) could develop a hexagonal pattern in the RGC mosaics (Fig. 2C), which is a necessary condition to achieve moiré interference (Wässle et al., 1981a; Gauthier et al., 2009; Paik and Ringach, 2011). In this case, we simulated an arbitrary monotypic mosaic that could be either an ON or an OFF mosaic. From the initial condition where the dendritic fields were randomly distributed (Fig. 2D), homotypic repulsive interaction gradually rearranged the center of dendritic fields, and could generate a quasi-regular structure of a developed dendritic field mosaic (Fig. 2E,F). When the interaction distance R was smaller than 1d, dendritic fields were spread to some degree but could not tile the mosaic regularly enough to generate a long-range lattice pattern (Fig. 2E,I). However, when the range of interaction was sufficiently large (R > 1d), we could observe a salient pattern of hexagonal lattice in the developed cell mosaics (Fig. 2F,J). Our results suggest that the local interaction range is a critical factor in the development of regularly structured mosaics (Fig. 2G).

To quantify the lattice pattern developed, we examined the distribution of the lattice angle (ϕ) between neighboring cells (Boots, 1974; Muir et al., 2011; Fig. 2F, black dash lines). As the interaction distance R increased, the peaks at 60° became stronger, confirming the hexagonal structure of the mosaics (Fig. 2H). In addition, we examined the distribution of peaks in the autocorrelation of mosaics (Fig. 2I,J, black circles). At R = 0.75d, autocorrelation peaks show weak periodicity in the mosaic lattice (Fig. 2I), but when R = 1.1d, the angular locations of the local peaks relative to the strongest peak (0°) in the individual mosaics were within ±5° of the multiple of 60° in all trials of the simulation (Fig. 2J). We also found that this hexagonal pattern was not limited to local mosaic structure, but also had long-range order (Fig. 2K). When the local repulsive interaction range was sufficiently large (R > 1d), higher-order peaks (up to 6th–7th order) were observed in the autocorrelation of mosaics (Fig. 2K, black circles). In addition, the positions of the peaks up to fourth order were matched to those mathematically calculated from an ideal hexagonal lattice (Fig. 2K, solid white squares). Our results suggest that a local repulsive interaction between RGCs may generate a long-range hexagonal lattice pattern of ON and OFF mosaics.

Repulsive interactions between heterotypic RGCs

The superposition of hexagonal ON and OFF RGC mosaics induced by homotypic interaction could produce a periodic moiré interference, as suggested in previous model studies (Paik and Ringach, 2011, 2012). However, there is no guarantee of a consistent spatial periodicity of an interference pattern (Obermayer and Blasdel, 1993; Blasdel et al., 1995), unless the alignment angle (θ) between the two mosaics is restricted to a small range. This restricted alignment between two mosaics might not be achieved when ON and OFF RGC mosaics are developed independently as suggested previously (Eglen et al., 2005; Hore et al., 2012). Instead, we assumed that heterotypic interaction between the ON and OFF RGC mosaics might also be in effect during retinal development, and that this could restrict the alignment angle.

It has been observed that the dendritic fields of ON and OFF RGCs occupy different tissue planes in the IPL (Balasubramanian and Sterling, 2009; Fig. 3A). The interlayer distance (d_m) between the two types of planes guarantees that ON and OFF RGCs are at least d_m away from each other. This implies that the actual distance of a heterotypic RGC pair must be greater than the distance previously estimated from the 2D data where ON and OFF RGCs are assumed to be on the same plane (Wässle et al., 1981a; Eglen et al., 2005; Ringach, 2007). Furthermore, the growth of RGC dendritic fields is not isotropic but is largely on the plane of each layer (Famiglietti et al., 1977), indicating that the repulsive interaction of dendritic fields between heterotypic RGCs may have smaller effect than that between homotypic RGCs. For these reasons, the influence of heterotypic repulsive interaction might not have been observed to be as significant as the homotypic ones (Wässle et al., 1981a).

Figure 3.

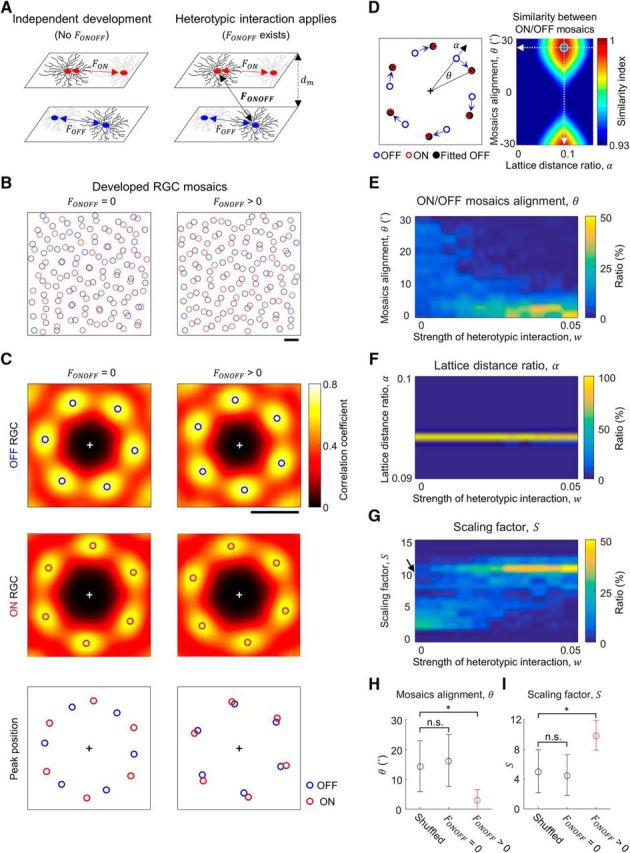
Heterotypic interaction can restrict the angle alignment (θ) between ON and OFF mosaics. A, Model mosaics separated by interlayer distance d_m = 0.25d (Famiglietti et al., 1977; Kolb, 1979), with and without heterotypic interaction (F_ONOFF). When F_ONOFF exists, a cell receives both homotypic and heterotypic interactions. B, Simulated mosaics developed with (right; w = 0.01), and without (left; w = 0) repulsive interaction, F_ONOFF, from an identical set of initial mosaic structures. C, Top and middle, 2D autocorrelations of developed mosaics in B. The local peaks (open circles) show hexagonal patterns. Bottom, The peak locations in B were plotted together (red and blue open circles). D, To find the relative lattice distance (α) and the alignment angle (θ) between ON and OFF mosaics, autocorrelation of the OFF mosaic was expanded and rotated (black solid circles) to match the autocorrelation of the ON mosaic. From various sets of interference parameters, α and θ were estimated by the set that maximizes the similarity between ON and OFF mosaics. White dashed lines indicate the estimated α and θ. E, Estimated θ from 100 ON and OFF mosaic pairs for different degrees of heterotypic interaction, F_ONOFF. When F_ONOFF is absent (w = 0), θ is randomly distributed. As w increased, distribution of θ appear to be limited to small angles. F, Estimated α from 100 ON and OFF mosaic pairs as in E. As w increased, α was maintained at near the mathematically calculated value (α = 0.094) from the density of ON and OFF cells in hexagonal lattice. G, Scaling factor (S) estimated from E and F. As w increases, value of S is kept consistent. The black arrow indicates the expected scaling factor (S = 10.4) in the theoretical model (Paik and Ringach, 2011). H, Observed θ from the developed mosaics (w = 0 and 0.04) and the control with randomly aligned mosaics (Wilcoxon rank sum test; *p < 10⁻²¹; n.s., p = 0.28). I, Estimated scaling factor (Wilcoxon rank sum test; *p < 10⁻²¹; n.s., p = 0.27). H, I, Error bars indicate SD. Scale bars: B–C, 1d.

Heterotypic interaction restricts alignment between mosaics

As with the model of single-type RGC mosaic development, we implemented both homotypic (Eglen et al., 2005) and heterotypic repulsive interactions in our model simulations of ON and OFF RGC development (Fig. 3A). We modulated the strength of heterotypic interaction (F_ONOFF) by introducing the weight term w, to indicate the relative strength compared with that of homotypic interaction. Based on the experimental observations, we set interlayer distance at 0.25d, where d is the expected average lattice distance in simulated OFF mosaics (Famiglietti et al., 1977; Kolb, 1979). The ratio between the expected lattice distances of simulated ON and OFF mosaics (1 + α) was set to 1.094, based on animal data (Zhan and Troy, 2000).

In the mosaics developed in the absence of heterotypic interaction F_ONOFF (termed simulated control mosaics; Fig. 3B, left), we observed hexagonal patterns from the angular distribution of local peaks in the autocorrelation (Fig. 3C, left), similar to the result in Figure 2J. Here, the alignment between ON and OFF hexagonal patterns appeared independent (Fig. 3C, left, bottom). On the other hand, we observed that a certain level of heterotypic interaction could affect the alignment between the mosaics without interrupting the development of the hexagonal pattern in each mosaic. In the presence of F_ONOFF (termed simulated model mosaics; Fig. 3B, right), each of the simulated mosaics still showed a hexagonal pattern (Fig. 3C, right), but the alignment between ON and OFF hexagonal patterns appeared restricted, and different from that developed without F_ONOFF (Fig. 3C, right, bottom).

To further investigate the influence of F_ONOFF, we measured the angular alignment between simulated ON and OFF mosaics for different w. We estimated the relative ratio of lattice distance (α) and the alignment angle (θ) between ON and OFF mosaics, by searching the amount of rotation and linear expansion of the autocorrelation of the OFF mosaic that maximizes the similarity to the autocorrelation of ON mosaic (Fig. 3D). We found that θ was restricted to small angles as w increased (Fig. 3E). On the other hand, α was maintained at near the expected level in the model (0.094; Fig. 3F). This is because α is mostly constrained by the ratio between the cell densities. Consequently, the scaling factor S, which is the spatial period of the moiré interference pattern, could be computed based on the obtained θ and α (Paik and Ringach, 2011). As w increased, the computed scaling factor was also restricted within a narrow range around the expected level of the scaling factor (S = 10.4; Fig. 3G, black arrow; Paik and Ringach, 2011). When the heterotypic interaction was sufficiently large (w > 0.02), we confirmed that the obtained θ and the estimated scaling factor S were significantly different from those of the control where ON and OFF mosaics were randomly aligned (*p < 10⁻²¹, Wilcoxon rank sum test; Fig. 3H,I), whereas they were not distinguishable from the control for w = 0. Considering that the absence of the heterotypic interaction (w = 0) resulted in a failure to restrict the scaling factor to a small range, these results suggest that the heterotypic interaction in RGC mosaics could be the key factor in achieving consistent spatial periodicity in the interference pattern within a species.

Validation of heterotypic interaction in observed RGC mosaics

Next, to validate the central prediction of our model about the presence of the heterotypic interaction, we tried to estimate the influence of the heterotypic interaction during development using experimental data. The typical approaches for measuring interactions between two cell mosaics are 2D cross-correlograms (Ringach, 2007) or 1D density recovery profiles (Rodieck, 1991; Eglen et al., 2005). However, these methods only focus on the spatial distribution relative to neighboring cells, rather than the relationship at whole-mosaic scale. Thus, to investigate the effect of heterotypic interaction at the whole-mosaic scale, we conducted an analysis of the repulsive energy in each pair of ON and OFF RGCs, using simulated mosaics and measured mosaic data from animal experiments (soma: Wässle et al., 1981a, Zhan and Troy, 2000; receptive field: Gauthier et al., 2009; Fig. 4). Although our developmental model is for the spatial distribution of dendritic fields, we assumed that this model could also be applied to the mosaic structure of a cell body and receptive field, because it was reported that all three of them are spatially clustered on the retinal surface (Brown et al., 2000). Thus, the influence of the heterotypic interaction between dendrites can also be estimated in receptive field and soma mosaics data.

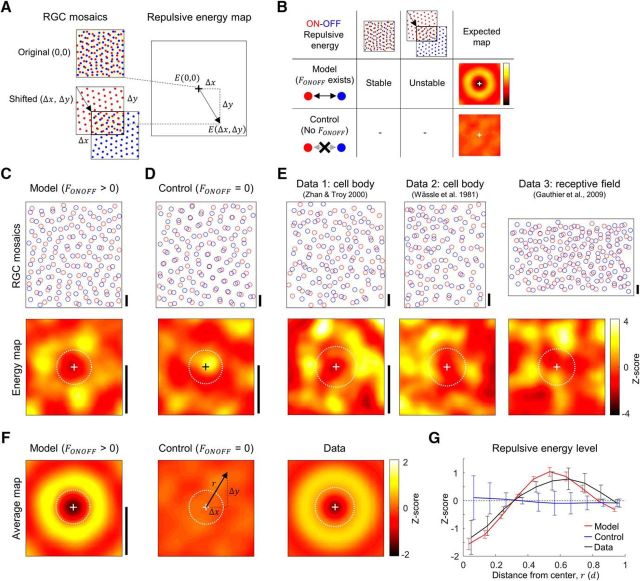
Figure 4.

Observed evidence of heterotypic interactions in animal data. A, A repulsive energy map was plotted from the estimation of heterotypic repulsive energy of each cell pair in overlapped regions of ON and OFF mosaics for each amount of spatial shifts of OFF mosaics. B, A theoretical model predicts that the energy map will have a local minimum at the origin. If a repulsive interaction exists during development then ON and OFF RGC locations would be modulated to reduce total repulsive energy. The energy map will have a high energy band around the origin, because the intentional shift of OFF mosaic will increase the repulsive energy level, compared with the stable state at the origin. This pattern will not appear if ON and OFF mosaics were developed independently (simulated control, F_ONOFF = 0). C–E, Sample ON and OFF mosaics and their energy map. Scale bar, 1d, expected hexagonal lattice distance in OFF mosaics. White dashed circles indicate the average heterotypic nearest neighbor distance. C, Simulated model mosaics (F_ONOFF > 0). D, Simulated control mosaics (F_ONOFF = 0). E, Three experimental data: Data 1 and Data 2 are cell body mosaics from Zhan and Troy (2000) and Wässle et al. (1981a), and Data 3 are receptive field mosaics from Gauthier et al. (2009). F, Averaged energy map. Left and middle, Average from 100 simulated ON/OFF mosaic pairs. Simulated model mosaics show a local minimum at the origin and a high energy band around it, whereas simulated control mosaics do not show the pattern. Right, Averaged energy map was achieved from the summation of energy maps rotated by 0–360°, with 10° intervals. Note a local minimum at the origin and a high energy band around it, as in the simulated model result. Scale bar, 1d. G, The average of energy level in the radial direction show a local minimum at the origin and a high-energy band around it, both in the simulated model and the animal data. Error bars indicate SD.

As two cells shift away from each other, repulsive energy between the cells would decrease, resulting in a more stable state of the cell pair. Thus, if heterotypic repulsive interaction exists during the development of RGC mosaics, regardless its strength, the structure of ON and OFF mosaics will be modulated in a way that heterotypic repulsive energy is reduced. Therefore, by examining whether the heterotypic repulsive energy of RGC mosaics is minimized in the animal data, we could investigate whether the actual organization of the RGC mosaic is consistent with our model with heterotypic interaction.

Under this condition, if either an ON or an OFF RGC mosaic developed with heterotypic interaction is shifted a bit in any direction, the repulsive energy per cell within the areas of overlap of ON and OFF mosaics will increase compared with the original state (Fig. 4A). On the other hand, ON and OFF mosaics developed without heterotypic repulsive interactions will not show this pattern of energy change (Fig. 4B). To validate this hypothesis, we examined the repulsive energy, while we varied the amount of spatial shift of an OFF mosaic in all directions in both simulated and observed mosaics (Fig. 4C–E).

In the simulated mosaic developed with heterotypic interaction, the energy map had a local minimum at the origin, and a band of a higher energy level around it (Fig. 4F, left). In contrast, this pattern was not observed in the energy map of simulated control mosaics developed with no heterotypic interaction (Fig. 4F, middle). Notably, the energy maps estimated from the RGC mosaics observed in animal studies (Wässle et al., 1981a; Zhan and Troy, 2000; Gauthier et al., 2009) showed a local minimum at the origin and a higher energy band around it (Fig. 4F, right), similar to that from the model simulation. To analyze this energy distribution quantitatively, we investigated the radial distribution of energy by averaging the map in polar coordinates (Fig. 4G). In both the model simulation and the animal data, the energy maps showed local minima at the origin and the energy levels off the origin were higher than those in annuli close to the origin, implying that the original RGC mosaics were in stable energy states in terms of ON-OFF RGC repulsive energy (Fig. 4G). Our results suggest that the observed RGC mosaics in animal data show the vestige of heterotypic interaction during RGC development.

Development of hexagonal pattern does not require a particular form of the repulsive interaction

Although the dendritic maturation of RGC could be affected by various factors (such as stimulus-dependent synaptic activity; Tian, 2011), it has been observed that RGC mosaics can develop without visual experience (Anishchenko et al., 2010). This implies that a simple intercellular interaction in the retina may be sufficient to originate orderly functional structure across retinal surfaces. Our model provides a simple explanation of this retinal interaction between neighboring cells during retinal development. In previous studies, it was argued that molecular mechanisms caused avoidance between dendrites of other cells in the retina (Zipursky and Grueber, 2013; Lefebvre et al., 2015), but it is worth pointing out that our current result is valid as long as both homotypic and heterotypic repulsive interactions exist, regardless of the underlying mechanism. Considering that the exact form of local interaction in retinal mosaics has not been measured, we performed additional simulation for different forms of interaction (Fig. 5A), just in case the form of interaction (∝1/r² in the main simulation) substantially affected our conclusion. As long as the interaction distance is sufficient to tile the mosaic (R = 1.1d), all the forms of interaction reproduced regular and hexagonal mosaic structures (Fig. 5B,C), consistent with the results in Figure 2. Probably, observations of the retinal mosaic structure during each developmental stage could provide direct evidence of details in our model.

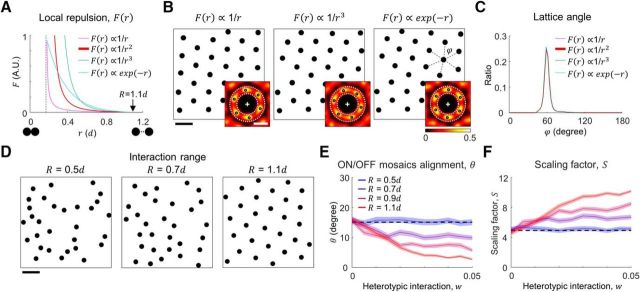
Figure 5.

Consistency of simulation results with different forms of repulsive function and spatial noise in mosaics. A, Repulsive interaction function defined by the different forms of decaying functions: 1/r, 1/r² (used in the main simulation), 1/r³, and exp(−r). All the functions become 0 at r = 1.1d. B, Cell mosaics developed by different interactions in A, from the same initial condition. Inset is the autocorrelation of each mosaic. Although the angular location of local peaks can vary, the hexagonal pattern is maintained across the interaction functions. Only local peaks of significance p < 0.05 were selected, compared with N = 100 autocorrelations of control mosaics where y positions of cells were shuffled. Scale bar, 1d. C, Distribution of lattice angles (ϕ) in the developed cell mosaic. In all cases, strong hexagonal peaks were observed at 60°. D, Sample mosaics developed by the original interaction form for different interaction range, R. As R declines, a less-orderly mosaic develops. Scale bar, 1d. E, Distribution of estimated θ for mosaics of different interaction ranges. With R = 0.5R, the distribution of the angle does not change as w increases, whereas the alignment angle is restricted to small angles with R ≥ 0.7d. Black dashed line indicates the average of 10,000 randomly selected angles between 0 and 30°. F, The scaling factor estimated from the fitted parameters α and θ. For R ≥ 0.7d, the scaling factor increases as the heterotypic interaction becomes stronger. Black dashed line indicates S = 4.9, for randomly aligned mosaics as a control. E, F, Shaded regions indicate SE (N = 100).

Alignment between mosaics was kept even with noisy mosaics

One might argue that the simulated mosaics developed in our model have a much more regular organization of the lattice pattern than what is observed in the animal data (Wässle et al., 1981a; Zhan and Troy, 2000). Here, we intended to focus on illustration of the mechanism by which local RGC repulsive interaction could develop long-range order in the ON and OFF mosaics, and also regulate the alignment between them (see Discussion). For this reason, the simulation parameters were chosen to best describe the hexagonal lattice structure of mosaics and the alignment angle of mosaics (R = 1.1d). However, we confirmed that the suggested mechanism also worked under noisy conditions of mosaics by modulating the regularity of the mosaic structure with the interaction range R (Fig. 2E,F; Fig. 5D). We observed that the alignment of ON and OFF simulated mosaics and the computed scaling factor were still restricted (Fig. 5E,F) when we reduced interaction range R to produce much less orderly mosaics, consistent with the results in Figure 3E–G. This result suggests that our theoretical model is also applicable to more realistic parameter conditions.

Limitation in observing periodicity at long range in measured mosaics

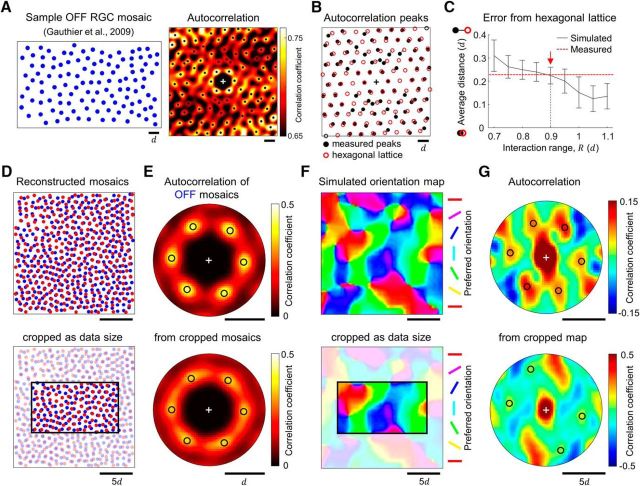
One may argue that the simplest way to validate our model is to observe the moiré patterns of ON and OFF RGC in the measured mosaics. However, an analytical limitation arises from the size of the measured retinal patches, which is, at most, ∼1 mm² including only ∼100 cells for a single type of RGC. This may not be sufficiently large to investigate the emergence of interference pattern between mosaics. To address this issue, we reconstructed a larger mosaic with a level of long-range order similar to that of the measured mosaic and examined whether the size of the mosaic could affect the observation of the interference pattern.

As represented in our previous work (Paik and Ringach, 2011), our analysis of the autocorrelation of a measured RGC mosaic revealed the hexagonal arrangement of first-order peaks and many other higher-order peaks (Fig. 6A). For quantitative analysis of the hexagonal arrangement at long range in the measured RGC mosaics, we found that the spatial distribution of these higher-order peaks are well fitted to a hexagonal lattice up to fifth to sixth order, which is the limit of analysis with the given size of measured mosaic (Fig. 6B). However, considering that the expected period of the interference pattern in RGC mosaics is larger than this (Paik and Ringach, 2011), the available range of local peaks may not be large enough to reveal a complete period of the interference pattern.

Figure 6.

Observed RGC mosaics can develop interference patterns, depending on the size of the mosaics. A, Hexagonal arrangement of RGC in the experimental data. Left, Receptive fields mosaics of OFF RGCs from Gauthier et al. (2009). Right, Autocorrelation of the mosaic shows a hexagonal arrangement of first-order peaks and the presence of higher-order peaks. B, The distribution of local peaks in the autocorrelation is compared with that of an ideal hexagonal lattice, implying the periodicity at long range in the measured mosaic. Black solid circles indicate the local peaks in A and red open circles indicate the fitted hexagonal lattice. C, The average distance between the observed peak and the nearest ideal peaks in the autocorrelation (error distance) of our simulated mosaics (w = 0). Red dashed line indicates the average error distance in the experimental data in B. When the interaction range R = 0.9d (red arrow), the simulated mosaics show level of error distance similar to that of the measured mosaics. D–G, Top, Analysis of the reconstructed mosaics. Bottom, Analysis of a local patch of the reconstructed mosaics cropped to the same size as the measured mosaics in A. D, The sample model mosaics developed with R = 0.9d as the condition for data reconstruction. Black rectangle indicates the size of the measured mosaics in A. E, Autocorrelation of the reconstructed OFF mosaics in D. The hexagonal arrangement of the first-order peaks is also maintained in the analysis of the cropped mosaic. F, Orientation map simulated from the reconstructed mosaics in D. G, Autocorrelation of the orientation maps in F. Note that reconstructed mosaics could reproduce an orientation map and an interference pattern with hexagonal periodicity (top), but it may not be clearly observed in the analysis of the small retinal mosaic currently available in the data (bottom).

Thus, for further validation of our prediction, we generated large mosaics with level of long-range periodicity equivalent to that of the measured mosaics from the parameter search (Fig. 6C). We searched model parameters where simulated mosaics and measured mosaics had the same level of error distance from an ideal hexagonal lattice. Note that as the parameter R increases, the developed mosaic becomes more hexagonal (Fig. 2H); so the error distance decreases (Fig. 6C). Then, we observed that the mosaics simulated with repulsion range R = 0.9d represented a level of long-range hexagonal periodicity similar to that of the measured mosaics (Fig. 6C, red arrow). We used this condition to reconstruct large mosaics in Figure 6D and further examined whether the reconstructed large mosaics could reproduce an interference pattern that could seed an orientation map. In the autocorrelation analysis of each mosaic structure, not only the whole reconstructed mosaics but also the cropped mosaics showed a hexagonal arrangement of first-order peaks (Fig. 6E). This implies that both sizes of mosaics show hexagonal lattice patterns, as in Figure 6A.

Next, with reconstructed ON and OFF mosaics in (Fig. 6D), we simulated orientation maps using the statistical wiring model (Fig. 6F; Paik and Ringach, 2011). If ON and OFF mosaics reproduce an interference pattern at long-range, the resulting orientation map must show a hexagonal structure, as predicted by the moiré pattern. As expected, the interference pattern between the largely reconstructed mosaics seeded a hexagonal structure in the orientation map (Fig. 6G, top). However, we also observed that a small part of the reconstructed mosaics that were cropped to the same size as the measured mosaics could not clearly show hexagonal periodicity of a reconstructed orientation map (Fig. 6G, bottom). This implies that among mosaics, sufficient size is necessary for a direct estimation of the long-range periodicity, and that the observation of the interference pattern at long range might not be guaranteed from currently available size of measured mosaics. Thus, our analysis provides a vestige of the long-range periodicity in the measured mosaics (Fig. 6A,B), but it remains to be investigated further when larger patches of retinal mosaics could be obtained experimentally.

Discussion

How is the consistent spatial periodicity of an orientation map retained within a species? In the present study, we proposed a developmental model of RGC mosaics to provide an answer to this fundamental question by addressing a scenario with both homotypic and heterotypic interactions. We first showed that a local repulsive interaction between same-type (homotypic) RGCs developed a long-range hexagonal pattern in ON and OFF simulated mosaics. Then we showed that the relatively weak interaction between ON and OFF (heterotypic) RGCs constrains the alignment angle between the two mosaics, even though it is not strong enough to significantly modulate the structure of the mosaic of the other type. This restricted alignment between mosaics induces a consistent periodicity of retinal moiré interference patterns that will seed a cortical orientation map. Last, in the analysis of the observed RGC mosaics of the experimental data, we found evidence of heterotypic interaction that supports our model prediction. This suggests that both homotypic and heterotypic retinal interactions may be crucial to the organization of functional architecture in the retina, which would initiate the functional architectures in V1 (Soodak, 1987; Ringach, 2004, 2007, Paik and Ringach, 2011, 2012).

Because the quasi-uniform tiling of a retinal cell mosaic has been observed (Wässle et al., 1981a), the developmental origin of this regular spacing has been studied in some molecular-biological and genetic studies (Lin et al., 2004; Zipursky and Grueber, 2013; Lefebvre et al., 2015). In particular, Eglen et al. (2005) suggested a mathematical model for the developmental process of the regularly structured retinal mosaic. The developmental mechanism implemented in this study was based on the pairwise interaction point process (PIPP), where cells were created or removed by conceptual birth-and-death steps. In the PIPP model, each RGC is repeatedly removed and relocated to random positions until all the positions of cells are accepted by a process of stochastic interaction. Consequently, the PIPP model could not generate a hexagonal pattern in mosaics, leading to the conclusion that local interaction between nearby RGCs does not reproduce a hexagonal pattern (Hore et al., 2012). However, the PIPP process did not consider the actual process of development, where cells are not really created and removed every time. The model did not address the possibility that the position of RGCs are gradually modulated by repulsive interactions so that they might generate a well packed organization of dendritic fields and receptive fields as observed (Gauthier et al., 2009). In our present study, instead of the conceptual birth-and-death steps, we introduced a more biologically plausible mechanism based on the observed pattern of dendritic field growth. Our developmental mechanism allowed a continuous change of dendritic field area, which enabled close-packing of cells into a hexagonal lattice pattern. Furthermore, our simulation showed that the closely packed local hexagonal lattice could generate a long-range order of lattice (Wässle et al., 1981a,b; Zhan and Troy, 2000; Gauthier et al., 2009).

In the aspect of the role of heterotypic interaction, in a previous study, it was assumed that ON and OFF RGC mosaics develop independently (Eglen et al., 2005). Based on the analysis whether a density of one type of cell is dependent on the position of the other types of cells, the researchers concluded that the distribution of the cells was uniform, implying that the location of an RGC does not provide any information about the location of other types of cells. However, the authors neglected the chance that relatively weak heterotypic interactions between ON and OFF RGCs exist. Indeed, an analysis in the study above showed that there was a weak spatial dependency between the ON and OFF cells (Eglen et al., 2005, their Fig. 1). Because the dendritic fields of ON and OFF RGCs occupy different tissue planes (Balasubramanian and Sterling, 2009), the actual distance of a heterotypic RGC pair could be larger than what is measured in previous 2D data, where ON and OFF RGCs were assumed to be in the same plane (Wässle et al., 1981a; Eglen et al., 2005; Ringach, 2007). Thus, the repulsive interaction between heterotypic RGCs may not appear as significant as that between homotypic RGCs.

For better realization of a biologically plausible model, we may implement some additional factors in a future model that we did not apply to the current model for the convenience of theoretical argument. For example, variation in the spatial aspect ratio of receptive fields (Suematsu et al., 2013) implies the elliptic and anisotropic development of RGC dendritic fields, and this may develop more realistic and noisy structure of RGC mosaics. Thus, it remains to be determined how much the restricted alignment between the mosaics can be maintained by local repulsion under noisy conditions. Because our model predicts that the orderly structure of RGC mosaics is necessary for the development of orientation maps, it can be also tested whether incomplete tiling of RGCs induces abnormal development of the cortical map. Controlled experiments on the abnormal development of RGC mosaics, such as in mutant animals with the shrinkage of repulsion between RGC dendrites (Parrish et al., 2007; Grueber and Sagasti, 2010; Zipursky and Grueber, 2013; Lefebvre et al., 2015) might give an answer to this argument. To validate our model prediction further, more precise investigation is needed about what is required in the feedforward and recurrent circuits to seed quasi-regular orientation maps from the simulated mosaics. For example, the convergence of retinogeniculate (Usrey et al., 1999) and thalamocortical (Reid and Alonso, 1995; Jin et al., 2011) feedforward connections need to be examined carefully because they significantly affect the receptive field structure and orientation tuning developed in V1 neurons.

Considering the comparable retinal organization between higher mammals and rodents, one might argue why the orientation preference is arranged randomly in rodent V1, termed a salt-and-pepper map, if the structure of the orientation map is already seeded in the retinal mosaics. To address this issue, we can argue two aspects. First, experimental data suggest that the composition of retinal cells in rodents has greater variation than that in higher mammals. In the statistics of RGC spacing, the nearest-neighbor distance in a single type of RGC widely varies across animals and even sometimes the number of ON cells in a retinal patch is greater than that of OFF cells (Anishchenko et al., 2010), although more OFF cells are measured in most experiments in higher mammals (Wässle et al., 1981a; Zhan and Troy, 2000; for review, see Balasubramanian and Sterling, 2009). Second, more importantly, the structure of feedforward projection through the visual pathway seems to be different between rodents and primates. Retinogeniculate connection in higher mammals is almost one-to-one so the structure of a single LGN receptive field has a shape similar to that of a single RGC (Usrey et al., 1999). However, in rodents, recent tracing techniques revealed that the network of retinogeniculate connection is much more complex, so that a single LGN neuron receives input from a number of different types of RGCs (Morgan et al., 2016). We expected that the characteristics of feedforward convergence would be a crucial factor in determining the structure of cortical receptive fields and their spatial organization, so that even different types of orientation map could be seeded even from an identical set of retinal mosaics. Further tracing experiments may reveal the structural difference in visual systems of rodents and higher mammals and explain the origin of the diversity of orientation maps across species.

Note that the present scope of the model is limited to explaining how the cortical map structure is initially organized by the retinal origin (Paik and Ringach, 2011). For the complete comprehension of the visual cortical functions (Lien and Scanziani, 2013; Reinhold et al., 2015), the postnatal activity-dependent development of recurrent cortical circuits should be taken into account to explain observations such as the cortical responses for multiple orientations (Basole et al., 2003; Koch et al., 2016) or the matching process between orientation maps through two eyes (Crair et al., 1998).

It is worth pointing out that the basic concept of our model is connected to other disciplines that also investigate the spatial distribution of particles or their local interaction. In solid-state physics, the hexagonal arrangement of atoms has been widely observed to maximize the volume of the virtual spheres between atoms when they are closely-packed in a limited space (Ashcroft and Mermin, 1976; Kittel, 2005), supporting that the hexagonal arrangement would be an efficient strategy for uniform tiling of cells. In physical chemistry, the role of local interaction between nearby particles were extensively discussed in phase transition (Blundell and Blundell, 2009; Ivancevic and Ivancevic, 2014). These previous studies in various disciplines suggest the crucial role of local interaction in the organization of regular spacing of particles.

Overall, our results suggest that local repulsive interactions in retinal development may be crucial to the development of the orderly structure of retinal mosaics, and also to the consistent organization of functional architectures in the visual cortex.