Neural Representations of Hierarchical Rule Sets: The Human Control System Represents Rules Irrespective of the Hierarchical Level to Which They Belong

Abstract

Humans use rules to organize their actions to achieve specific goals. Although simple rules that link a sensory stimulus to one response may suffice in some situations, often, the application of multiple, hierarchically organized rules is required. Recent theories suggest that progressively higher level rules are encoded along an anterior-to-posterior gradient within PFC. Although some evidence supports the existence of such a functional gradient, other studies argue for a lesser degree of specialization within PFC. We used fMRI to investigate whether rules at different hierarchical levels are represented at distinct locations in the brain or encoded by a single system. Thirty-seven male and female participants represented and applied hierarchical rule sets containing one lower-level stimulus–response rule and one higher-level selection rule. We used multivariate pattern analysis to investigate directly the representation of rules at each hierarchical level in absence of information about rules from other levels or other task-related information, thus providing a clear identification of low- and high-level rule representations. We could decode low- and high-level rules from local patterns of brain activity within a wide frontoparietal network. However, no significant difference existed between regions encoding representations of rules from both levels except for precentral gyrus, which represented only low-level rule information. Our findings show that the brain represents conditional rules regardless of their level in the explored hierarchy, so the human control system did not organize task representation according to this dimension. Our paradigm represents a promising approach to identifying critical principles that shape this control system.

SIGNIFICANCE STATEMENT Several recent studies investigating the organization of the human control system propose that rules at different control levels are organized along an anterior-to-posterior gradient within PFC. In this study, we used multivariate pattern analysis to explore independently the representation of formally identical conditional rules belonging to different levels of a cognitive hierarchy and provide for the first time a clear identification of low- and high-level rule representations. We found no major spatial differences between regions encoding rules from different hierarchical levels. This suggests that the human brain does not use levels in the investigated hierarchy as a topographical organization principle to represent rules controlling our behavior. Our paradigm represents a promising approach to identifying which principles are critical.

Introduction

Humans rely on different types of rules to define complex plans and orchestrate their actions to achieve specific goals (Bunge and Wallis, 2008). In some situations, rules linking actions to specific stimuli (e.g., “if the phone rings, answer it”) may suffice. However, more complex situations may require the application of hierarchical rule sets. Hierarchical rule sets contain rules within a cognitive hierarchy in which higher-level rules influence the application of lower-level rules; for instance, higher-level rules may define in which context it is appropriate to apply lower-level rules. In the example above, a higher-level rule may make answering the phone inappropriate if it rings while one is in a meeting.

Previous studies have demonstrated the involvement of a wide frontoparietal network in simple rule representation and application in both monkeys (White and Wise, 1999; Wallis and Miller, 2003; Stoet and Snyder, 2004; Genovesio et al., 2005; Buschman et al., 2012) and humans (Bunge et al., 2002; Brass and von Cramon, 2004; Schumacher et al., 2007; Woolgar et al., 2011; Reverberi et al., 2012a; Baggio et al., 2016). Recent research has focused on a possible functional specialization of this network, especially within PFC. Several theories propose an anterior-to-posterior gradient within PFC. Gradient theories state that rules from lower levels are represented by more posterior PFC regions, whereas progressively higher level rules reside in increasingly anterior PFC regions (Fuster, 2000; Petrides, 2005; Koechlin and Summerfield, 2007; Badre, 2008; Botvinick, 2008; Christoff et al., 2009; O'Reilly, 2010). Some experimental work supports the existence of such a gradient (Koechlin et al., 2003; Badre and D'Esposito, 2007; Nee and Brown, 2012). Other studies argue against strong, location-specific specialization, claiming that the same parietal and prefrontal regions are involved in a wide variety of cognitive tasks and proposing a single general “multiple-demand network” (MDN) instead (Duncan, 2006; Fedorenko et al., 2013).

Gradient theories also make claims about how the brain represents rule hierarchies. For example, one hypothesis states that PFC implements a “representational hierarchy” (Badre, 2008) with distinct regions representing rules depending on their hierarchical level and not just contributing differentially to their application. Evidence for a gradient in PFC derives mainly from studies collapsing rule representation and application (Koechlin et al., 2003; Badre and D'Esposito, 2007). However, neural activity during rule application does not reflect only rule representation, but also additional cognitive processes necessary to perform the task (stimulus evaluation, motor activity, etc.).

Recent advances in analysis techniques allow access to contents of current mental states (Kamitani and Tong, 2005; Haynes and Rees, 2006; Kriegeskorte et al., 2006; Norman et al., 2006), making it possible to explore the structure of brain representations. For example, multivariate pattern analysis (MVPA) exploits local patterns of brain activity to identify neural representations of experimental factors (e.g., rules), so it is suitable for investigating rule representations. However, most previous studies that assessed rule representations using MVPA typically did not investigate different hierarchical levels (Reverberi et al., 2012a). Further, the two studies that did assess hierarchical rule representations have limitations either because both low and high hierarchical levels were manipulated simultaneously, thus preventing the independent exploration of each level (Nee and Brown, 2012), or because higher- and lower-order information was conveyed in different ways (Reverberi et al., 2012b), thus collapsing the information format with hierarchy.

In the present study, we investigate how the brain represents a type of hierarchical rule sets (see “Relation with other paradigms and theories” section) by testing whether rules at different levels are represented in distinct brain regions or if they are encoded by one common system. To accomplish this goal, we devised a paradigm allowing for the following: (1) exploring the representation of rules at each level of a cognitive hierarchy in the absence of information about rules from other levels or other, potentially confounding, task-related information; (2) assessing rule representations directly with MVPA; and (3) minimizing differences between rule representations by conveying information with formally identical IF-THEN rules.

Materials and Methods

Participants

The general experiment setup follows our previous work (Reverberi et al., 2012a, 2012b). Overall, 54 participants underwent the training procedure (see “Experimental procedure” section). Fifteen of these were excluded during the training because of poor performance at the task (accuracy < 0.80); the remaining 39 participants took part in the fMRI study. All people participated in the experiment in exchange for monetary payment. Participants were right-handed (score > 50 on the Edinburgh Handedness Inventory; Oldfield, 1971) native German speakers, had normal or corrected-to-normal vision, no self-reported neurological or psychiatric history, and no anatomical brain abnormalities. Data from 2 of these 39 participants were discarded before data analysis because of poor performance at the task (accuracy < 0.80) in the fMRI session. The mean age of the remaining participants (N = 37, 24 females and 13 males) was 24.6 years (range: 19–31). Instructions and all study materials were provided in German. The ethics committee of the Humboldt University of Berlin approved the study. All participants gave written informed consent.

Experimental stimuli

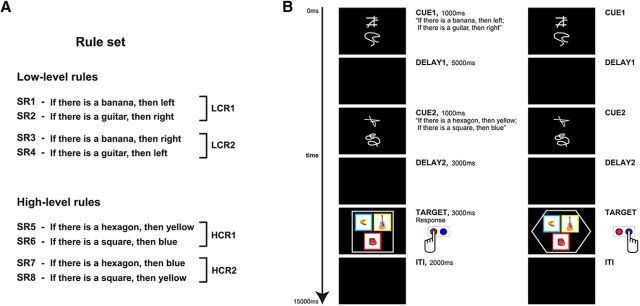
Participants were required to retrieve, maintain, and apply sets of conditional rules to different target stimuli (Fig. 1). Each rule set consisted of two compound rules from a two-level cognitive hierarchy (Fig. 1A): one “low”-level compound rule (LCR) and one “high”-level compound rule (HCR). Each compound rule consisted of two single rules. All single rules had the same logical form. They were all conditionals: “If you see X, then Y” (abbreviated “X → Y” below). The LCR consisted of two “simple stimulus–response associations” (Bunge and Wallis, 2008) that assigned button presses to target images (i.e., the rules defined a “direct sensorimotor mapping”; Petrides, 2005). An example of an LCR is as follows: “If you see a banana, then press left; If you see a guitar, then press right.” The HCR consisted of two individual rules defining the background color of the pictures that should be considered relevant for LCR (i.e., rules that “regulate the allocation of attention and therefore selection based on conditional operations”; Petrides, 2005), thus determining when the low-level rules should be evaluated (i.e., HCRs were “rules that govern rules”; Badre, 2013). For example, an HCR is as follows: “If you see a square, then consider only blue pictures; if you see a hexagon, then consider only yellow pictures.” A hierarchical rule set is thus established in that “the outcome of a decision at one level guides the appropriate action at the next level down” (Crittenden and Duncan, 2014). For the main analyses, two LCRs (LCR1 and LCR2) and two HCRs (HCR1 and HCR2) were used (Fig. 1A, Table 1). The two compound rules from the same level always contained the same targets (e.g., for the LCRs: banana, guitar) and responses (left, right) and only differed in how the individual rules connected targets and responses (e.g., LCR1: “banana → left; guitar → right,” LCR2: banana → right; guitar → left”; the same applies to HCR1 and HCR2). This arrangement prevents that differences between the triggers (e.g., “banana” vs “guitar”) or the responses (“left” vs “right”) can be exploited by the classifiers in the MVPA analyses. The same reasoning also applies for high-level rules. On each trial, one LCR and one HCR were active. Therefore, an example for a complete hierarchical rule set on one single trial would be as follows: LCR: “banana → left; guitar → right;” and HCR: “square → blue; hexagon → yellow.”

Figure 1.

Schema of the experimental paradigm. A, From eight different single conditional rules (SR1–SR8), four compound experimental rules were produced: LCR1 and LCR2 or HCR1 and HCR2. B, Timeline of the experiment. At the beginning of each trial, a pair of cues was presented, indicating which LCR (or HCR) had to be applied in the current trial. After a delay of 5 s, another pair of cues specifying which HCR (or LCR) was active for the current trial was shown. A second delay of 3 s followed the second cue presentation and then the target screen was presented. Participants had to apply the active rules to the target stimuli and derive as fast as possible the appropriate response(s). After the target screen and before the beginning of the consecutive trial, a blank screen was presented for ∼2 s (intertrial interval, ITI; see “Experimental stimuli” section for details). In the first example (left), the figure in the target is a square; then, only the blue pictures are relevant. The only picture with a blue background is the banana; then, the correct response is to press the left button. In the second example (right), the shape in the target is a hexagon, so yellow pictures are relevant. The only yellow picture is the guitar; then, the correct response is a right button press.

Table 1.

Types of compound rules used during fMRI scanning

	Low level	High level
Experimental trials
Rule 1	LCR1 (SR1, SR2)	HCR1 (SR5, SR6)
Rule 2	LCR2 (SR3, SR4)	HCR2 (SR7, SR8)
Unbalanced catch trials
Rule 3	LCR3 (SR1, SR3)	HCR3 (SR5, SR7)
Rule 4	LCR4 (SR1, SR4)	HCR4 (SR5, SR8)
Rule 5	LCR5 (SR2, SR3)	HCR5 (SR6, SR7)
Rule 6	LCR6 (SR2, SR4)	HCR6 (SR6, SR8)

For each different rule (e.g., Rule 1), the compound rule (e.g., LCR1) and the composing single rules (e.g., SR1 and SR2, in parentheses; see Fig. 1A) are reported for the corresponding level (low or high) and for both experimental trials and unbalanced catch trials.

Rules were instructed by visual cues. Before the fMRI experiment, participants learned 16 abstract visual cues, two visually unrelated cues for each of the eight individual single rules (SR1-8 in Fig. 1A). Participants learned the associations between cues and rules in a separate training session (see “Experimental procedure” section). The associations between cues and rules were randomized across participants so that each participant learned different cue–rule associations.

The target screen displayed three pictures surrounded by a shape (square, hexagon, circle, or star); each picture was presented on a colored background (Fig. 1B, yellow, blue, green, or red). Target pictures were 3D colored pictures of four different objects: banana, guitar, car, and chair (courtesy of Michael J. Tarr, Carnegie Mellon University). To prevent confounding effects due to the specific object, shape, or color, we used different pairs of objects, shapes, and colors to define the rules for different participants; the other objects, shapes, and colors were not relevant for the participants. Specifically, participants were assigned randomly to two groups. LCRs always used responses left and right but different target objects: either banana and guitar (group 1) or chair and car (group 2). HCRs used hexagon and square (group 1) or circle and star (group 2) as target figures and yellow and blue (group 1) or green and red (group 2) as relevant colors. During the target phase, participants had to apply both the low- and the high-level compound rule and derive the correct response. When the shape on the target screen matched one of the shapes of the HCR, participants had to apply the LCR only to the objects with the background color specified by the HCR (e.g., LCR: “banana → left; guitar → right”; HCR: “square → blue; hexagon → yellow”; the target displays a square and thus the LCR has to be applied only to bananas and guitars with a blue background color) and to press the appropriate key(s). If the shape did not match any of the shapes in the HCR, then participants had to apply the LCR to every relevant object regardless of its background color. The experiment was implemented and administered with MATLAB (The MathWorks) using the Cogent 2000 toolbox (Functional Imaging Laboratory and Institute of Cognitive Neuroscience, University College London).

Figure 1B shows a typical trial. Each trial started with a first cue screen (cue 1) displaying a pair of cues for 1 s at the center of the screen, one above the other. After cue 1, a delay period of 5 s followed (delay 1) and then a second cue screen (cue 2) was presented that displayed another pair of cues for 1 s. After a second delay period of 3 s (delay 2), the target screen was shown for 3 s. This showed three pictures on colored background embedded in one shape. The cues informed participants about which rules had to be applied in the current trial. The cues in each cue screen always instructed rules of the same level (low or high). In half of the trials, the LCR was instructed (during cue 1) before the HCR (during cue 2); in the remaining half, the HCR was instructed before the LCR. Therefore, only LCR or HCR information was available in delay 1. Because this was the task phase that we were interested in, we used a delay of several seconds to capture the signal of interest and prevent it to overlap with signal related to subsequent task phases. We did not further increase the delay with time jittering to ensure a sufficient number of repetitions of the experimental conditions within each run without making the experiment duration excessive.

When the target screen appeared, participants had to apply both the LCR and the HCR. Participants had to check whether the shape in the target matched one of the shapes in the active HCR; if so, the LCRs had to be applied only to the pictures with the appropriate background color, otherwise to all pictures. Participants then had to apply the LCR to all selected pictures and to press all the key(s) triggered by the LCR. Multiple responses were possible and participants could press the appropriate keys in any order (e.g., if two items required a “left” response and one item a “right” response, the responses “left, left, right,” or “left, right, left,” or “right, left, left” were correct). Participants had to respond as quickly as possible by pressing buttons with either their left or their right index fingers. Given the active rules and the target shown on a particular trial, four different outcomes were possible: Participants had to apply (1) both low- and high-level rules when a relevant shape was present and the background of a target object matched the color in the rule (hereafter: “Both”); (2) only the low-level compound rule when the shape did not match a high-level rule but at least one of the objects matched a low-level rule (“OnlyLCR”); (3) only the high-level rule when the shape was relevant but either the background color of none of the pictures was appropriate or the object(s) with the matching color did not trigger the LCR (“OnlyHCR”); or (4) none of the rules, when both the shape was irrelevant and the objects did not trigger the LCR (“None”). When it was not possible to apply the LCR (OnlyHCR and None conditions), participants had to explicitly press a “no response” button by using the right middle finger.

In addition to standard experimental trials, catch trials were interspersed throughout the standard trials. We used two different types of catch trials: trials with shorter delays and trials with an “unbalanced” combination of composing rules. In short catch trials, both delay 1 and delay 2 lasted only 2 s. This forced participants to immediately retrieve and represent the rule set. In catch trials with unbalanced combinations (Table 1), the composing rules shared either the triggering condition (object or shape) or the response (motor response or color). For example, both individual rules of the compound rule “if there is a banana, then left; if there is a banana, then right” share the object “banana.” Unbalanced rule combinations enforced participants to retrieve the rules of both cues that were shown and thus prevented them from applying shortcuts to only represent one single rule and then derive the other rule at the target screen.

Rationale behind the experimental paradigm

The experimental paradigm has been explicitly designed to achieve two important goals: (1) assess “pure” representations of high- and low-level rules when information about the other level is absent, thus allowing for (2) evaluating the difference between rule representations of the two levels. To achieve these goals, in our task, the first cue instructed either a low- or a high-level rule equally often, so that only one compound rule had to be maintained during delay 1; moreover, we used two different rules for each level in the hierarchy. Therefore, we could decode the identity of a compound rule by classifying the two rules from the same hierarchical level (e.g., low level) using data from the subset of trials in which a rule from this level was maintained during delay 1. Finally, because low- and high-level rules were represented during delay 1 in distinct trials, we could also compare representations of rules from the two levels in the hierarchy in this time window. However, because only rules from one level are represented during delay 1, our paradigm does not allow for exploring the representation of hierarchical rule sets that simultaneously contain low- and high-level rules.

Relation with other paradigms and theories

Above, we explained why the HCRs in our paradigm could be considered at a higher hierarchical level than our LCRs. However, several theories exist that differ in the general principles defining a hierarchy. To allow a clear interpretation of our study, we detail explicitly the relation of our LCRs and HCRs with major theories in the field and compare them with paradigms of previous empirical studies.

Hierarchical relation can be defined by the level of abstraction of the involved operations (Petrides, 2005). This applies directly to our rules: LCRs define “a direct sensorimotor mapping,” whereas HCRs regulate “selection based on conditional operations” (Petrides, 2005). Our hierarchy also fits to definitions that use the abstraction level of the policies to be implemented. For example, “a simple rule linking a stimulus and a response is a first order policy,” as our LCRs, whereas rules “adding additional contingencies,” as our HCRs, result “in more abstract policy” (Badre and D'Esposito, 2009). In addition, “the depth of the decision tree remaining to be traversed from any branch point to reach a response determines the order of policy abstraction” (Badre, 2013), so our experimental paradigm instantiates a second-order hierarchy because it has two decision points. Conversely, it should be considered that HCRs do not select among multiple first-order rule sets, as is often the case for the higher-level rules in representational hierarchies. Instead, HCRs modify the triggering conditions of LCRs. Therefore, if one would rely strictly on this requirement, then HCRs should not be considered a more abstract policy. Furthermore, hierarchical relation can be defined by temporal abstraction (Koechlin et al., 2003). In a temporal hierarchy, control signals may be defined as either being “related to the immediate context in which the stimulus occurs” or being traceable to a past event (episodic control) defining an “episode in which a new set of rules apply” (Koechlin and Summerfield, 2007). In our paradigm, both the HCRs and the LCRs pertain to the immediate context, so the rules in our experiment do not differ in the temporal dimension of the episodic control. Finally, hierarchies have been also defined as structures comprising multiple levels maintaining asymmetrical relations; that is, structures in which information at higher levels influences operations at lower levels more than vice versa (Badre, 2008; Botvinick, 2008). From this point of view, the rule sets that we use in our experimental paradigm hold a clear hierarchical relation because HCRs modify the implementation of LCRs but not vice versa.

In addition to theoretical considerations, our hierarchy implementation is similar to the operationalization of representational hierarchies in other classic experimental paradigms. For example, in the feature experiment of Badre and D'Esposito (2007), the low-level rules may be seen as rules prescribing a left response when a condition is present and a right response when it is absent, whereas the high-level policy is a rule specifying which condition is relevant. Therefore, the higher-level rule modifies only the triggering conditions of the lower level rules that remain identical across all conditions of the experiment; similarly, our HCR modifies the triggering conditions of the active LCR.

Experimental procedure

During fMRI scanning, participants performed 300 trials divided into six runs. In each run, 50 trials were administered in a pseudorandom order: 40 experimental trials, four short catch trials, and six catch trials with an unbalanced combination of rules. The intertrial interval was around 2 s (range 1.5–3.5 s). The whole fMRI experiment lasted ∼73 min.

Participants underwent two training sessions scheduled on separate days at most 3 d before scanning. On the first day of training, participants learnt the cue–rule associations; on the second day, they practiced the experimental task and received feedback on their accuracy on each trial. Overall, the training procedure lasted ∼2.5 h (mean duration on day 1 = 68 min; mean duration on day 2 = 84 min). Only participants who reached a high accuracy (at least 12 correct responses in the last 15 trials) were allowed to the fMRI session. Overall, 15 participants were excluded during the training.

Directly before scanning, participants performed a “refresher session” of ∼10 min to ensure that they remembered the cue–rule associations. In the scanner, participants additionally performed five experimental trials to get used to the scanner environment before the experiment started (these data were not analyzed). After scanning, a questionnaire was administered to investigate whether participants used strategies to perform the task and, if so, which strategies they had adopted.

Image acquisition

fMRI data were collected using a 3 T Siemens Trio scanner equipped with a 12-channel head coil. In each of the six scanning runs, we acquired 376 T2*-weighted volumes in descending order using gradient-echo echoplanar imaging sequences. The images were composed of 33 slices (3 mm thick) separated by a gap of 0.75 mm. Imaging parameters were as follows: TR 2000 ms, TE 30 ms, FA 78°, matrix size 64 × 64, and FOV 192 mm × 192 mm, thus yielding an in-plane voxel resolution of 3 mm³, resulting in a voxel size of 3 mm × 3 mm × 3.75 mm. A T1-weighted anatomical dataset and magnetic field mapping images were also acquired. Imaging parameters for the anatomical scan were as follows: TR 1900 ms, TE 2.52 ms, FA 9°, matrix size 256 × 256 × 192, FOV 256 mm × 256 mm × 192 mm, 192 slices (1 mm thick), and resolution 1 mm × 1 mm × 1 mm. For the field maps, the parameters were the following: TR 400 ms, TE 5.19 ms and 7.65 ms, FA 60°, matrix size 64 × 64, FOV 192 mm × 192 mm, 33 slices (3 mm thick), and resolution 3 mm × 3 mm.

Experimental design and statistical analysis

Behavioral analyses

We performed linear mixed-effect model (LMM) analyses to assess the effect of multiple task variables on reaction time (RT) and accuracy measures (see “Behavioral results” section for details about each single analysis). All LMM analyses were performed using R 3.1.0 (The R Foundation for Statistical Computing, Vienna, Austria, 2014) and the lme4 package (Bates et al., 2015) for LMM analyses (Baayen et al., 2008). We preferred this approach over repeated-measures ANOVA, which is typically used for within-subject designs, because LMMs take into account not only the subject variability in overall mean responses, but also individual subject sensitivity to different experimental conditions. Therefore, they constitute a more powerful tool with which to detect effects of interest than repeated-measures ANOVA (Barr et al., 2013).

Preprocessing and first-level analyses

fMRI data were preprocessed and analyzed using SPM8 (Wellcome Trust Centre for Neuroimaging, Institute of Neurology, University College London). Images were realigned and slice-time corrected. Low-frequency noise was removed using a high-pass filter with a cutoff period of 128 s (Worsley and Friston, 1995) and an autoregressive AR model was fit to the residuals to allow for temporal autocorrelations (Friston et al., 2002). The images were neither spatially smoothed nor normalized to preserve fine-grained patterns of brain activity.

Two independent GLMs were setup to estimate runwise correlation coefficients from the realigned and slice-time corrected images: model 1 to decode the identity of the LCRs and model 2 to decode the identity of the HCRs. Each model comprised two conditions corresponding to the two pairs of rules: LCR1 and LCR2 for model 1 and HCR1 and HCR2 for model 2 (e.g., for LCRs, the two conditions in model 1 were LCR1: “banana → left; guitar → right” and LCR2: “banana → right; guitar → left”). We used two independent models to prevent any potential interaction between the two rule levels. Because we were only interested in differences between rule representations during the delay period independent of any specific assumption on HRF shape or onsets and durations of mental processes during that time, we applied a finite impulse response (FIR) model (Henson, 2004) to allow for flexible modeling of the BOLD time course. Each condition was modeled using 8 consecutive FIR time bins of 2 s each (total FIR model length 16 s). The time vectors of all regressors were defined using cue 1 onset times. Only experimental trials with a correct response were used to estimate the parameters (i.e., both incorrect and catch trials were excluded). Each first-level model resulted in 96 (8 FIR bins × 2 conditions × 6 runs) individual first-level regressor images per participant. Note that creating one regressor for each individual rule and detecting differences between rules from the same level and then comparing these results between levels differs from the standard procedure for univariate fMRI analysis, which creates one regressor for all rules from a specific level and then contrasts these regressors directly to test for differences between levels.

Representation of low- and high-level rules (whole-brain)

We used MVPA with a searchlight approach (Kriegeskorte et al., 2006; Haynes et al., 2007) to identify which brain regions represent low-level rules when information about high-level rules is absent and vice versa. Two independent decoding analyses were implemented: the first analysis aimed at identifying brain regions containing specific information about low-level compound rules in the absence of high-level rules and the second one aimed at identifying brain regions encoding high-level compound rules in the absence of low-level rules. The first analysis decoded between LCR1 and LCR2 and the second analysis between HCR1 and HCR2 (Fig. 2A). Note that this procedure differs from standard univariate experiments, which do not contrast brain responses elicited by different individual rules within each level to identify level-specific regions, but instead contrast brain responses to all rules from one level against a baseline condition.

Figure 2.

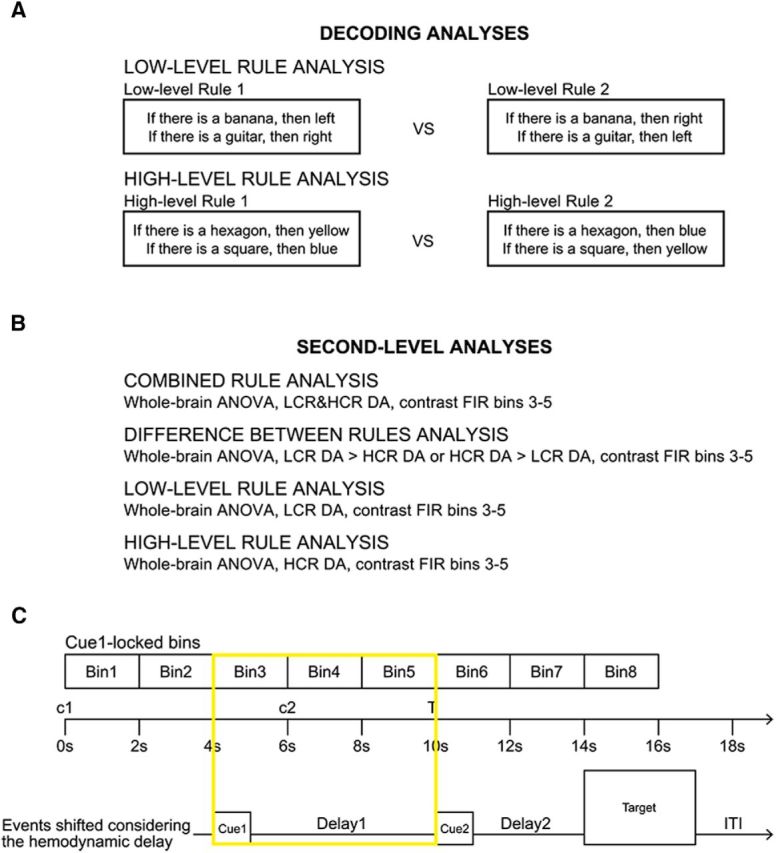
Analysis methods. A, Schema of the decoding analyses. The two decoding analyses for rule identity on either low- or high-level rules are explained. Both analyses decode between two compound rules of the same level. Each compound rule contains the same basic elements (banana, guitar, left, and right for the LCRs and hexagon, square, blue, and yellow for the HCRs); thus, the only difference between the two compound rules contrasted in each analysis is the link between the elements in the rules. B, Schema of the second-level ANOVA analyses. Four second-level ANOVAs are explained: (1) the analysis to identify regions encoding rule identity regardless of the type of rule (see results in Fig. 4A), (2) the analysis to identify regions where one type of rule was encoded better than the other (see results in Fig. 4B), (3) the analysis to identify regions encoding low-level rule information (see results in Fig. 4C), and (4) the analysis to identify regions encoding high-level rule information (see results in Fig. 4D). C, FIR model for the analyses performed on fMRI data from delay 1. Each FIR model consisted of eight time bins lasting 2 s each to model the whole trial duration. The first cue (c1) was presented at the beginning of each trial (onset 0 s), followed by a delay of 5 s (onset 1 s), a second cue (c2, onset 6 s), a second delay (onset 7 s), the target (T, onset 10 s), and the intertrial interval (ITI, about 2 s). To account for the temporal delay of the BOLD signal, we considered the time bins 3–5 because time bin 3 was the earliest that could reflect cue-related activity, as shown by the timeline representing the events shifted by the first two volumes. In this model, cue 1 presentation corresponded to the first second of time bin 3, whereas delay 1 coincided with time bins 3, 4, and 5. DA = decoding accuracy.

In general, cross-validated searchlight decoding is a spatially unbiased method to test for localized information throughout the brain. Specifically, it tests whether information is present in a local sphere around each voxel that allows for distinguishing two different task conditions from activity patterns of voxels within that sphere. The following procedure has been performed for each of the two models, for each participant, and for each FIR bin. For each voxel v_i in the brain, within the searchlight sphere (here: radius = 4 voxels) around that voxel v_i, the parameter estimates of all six runs were extracted for the two experimental conditions to be compared (model 1: LCR1 vs LCR2; model 2: HCR1 vs HCR2). The extracted parameters form a pattern vector for each condition and each run, yielding a total of 12 vectors (6 runs × 2 conditions) for each participant in each of the two analyses. The vectors were repeatedly assigned to independent training and test sets to avoid overfitting (Mitchell, 1997) using a 6-fold leave-one-run-out cross-validation procedure in which in each fold the data of one run was left out as test set once and the remaining data constituted the training set. A linear support vector classifier (Müller et al., 2001; Cox and Savoy, 2003) with fixed regularization parameter C = 1 was trained to distinguish between the two conditions using only the data from the training dataset. The classifier was then applied to the left-out test set. Classification accuracy was calculated as number of correct classifications divided by number of all classifications across all cross-validation folds. The resulting classification accuracy of each searchlight analysis around voxel v_i was stored in a new full-brain image to voxel v_i, resulting in one accuracy map for each participant for each FIR bin for each analysis. The cross-validated accuracies in this map serve as a measure of how well the classifiers discriminated between the experimental conditions based on the multivariate signal in each sphere v_i. Note that these maps do not quantify activity differences between a condition of interest versus a baseline condition or activity differences between different hierarchical levels (as in standard univariate analysis), but assess how well different rules from the same level can be distinguished by using local patterns of activation. Decoding analyses were performed using The Decoding Toolbox (TDT) (Hebart et al., 2014).

For each participant, the resulting 16 accuracy maps (2 conditions × 8 bins) were normalized to MNI space using the parameters calculated during preprocessing and then submitted to second-level ANOVAs to test at the group level in which brain regions the decoding accuracies were significantly above chance level (50% for the present analyses) across participants. A decoding accuracy significantly above chance level implies that the patterns of brain activity in the sphere v_i contain information about the relevant experimental condition; that is, which specific rule (LCR1 or LCR2, HCR1 or HCR2) had been represented by a participant. Because only rules from the same hierarchical level were contrasted, differences between either rule levels or general processes that were specific to one or the other level could not systematically influence the results. We tested for the presence of information in the FIR time bins from 3 to 5, corresponding to the time window from 4 to 10 s after cue 1 onset. Taking into account the ∼4 s delay of the hemodynamic response, this interval includes only activity related to cue 1 and delay 1 (Fig. 2C). A one-factorial ANOVA was calculated for each model (model 1 for LCRs or model 2 for HCRs; Fig. 2B) including the accuracy maps from all participants for each of the 8 FIR time bins as individual levels of the same factor (i.e., FIR bin). A contrast c = ⅓ × [0 0 1 1 1 0 0 0] was calculated to test for the presence of information in the relevant time window. Nonsphericity correction (Friston, 2003; Henson and Penny, 2003) was used to correct for temporal correlation effects between time bins. The described procedure has two advantages. First, performing individual decoding analyses for each time bin and then submitting the results as single levels of an ANOVA allows for slight differences in rule encoding between different time points and thus for some temporal flexibility in representations. The only requirement for this analysis is that activity patterns differ between conditions within each FIR bin. Second, including time bins before and after the critical time window improves the estimation of the error variance (i.e., improves the sensitivity of the statistical test) and allows for performing further quality checks on the response around the target time window.

Finally, statistical images were assessed for cluster-wise significance at α = 0.05 corrected for multiple comparisons using FWE correction at cluster level (Friston, 1997; see also Flandin and Friston, 2017). We used a cluster-defining single-voxel threshold of p = 0.001, following recent recommendations (Woo et al., 2014) to minimize the peril of inflated FWE rates (Eklund et al., 2016). Note also that FWE_c p-values for all significant clusters in the analyses are far below α = 0.05. This procedure resulted in two maps indicating where in the brain information about either individual LCRs or individual HCRs could be distinguished above chance level from local patterns of brain activity (i.e., where the BOLD signal contains information about the specific rule stored in working memory).

We only analyzed brain data from delay 1 to achieve a pure observation of low- and high-level rule representations because a single compound rule from only one level (either an LCR or an HCR) was recalled and maintained during this time window. We could not use brain data from delay 2 because it contained both low- and high-level information, the short duration of delay 2 did not allow us to isolate brain responses from later phases within the same trial, and brain activity during delay 2 might additionally reflect rule integration processes. For similar reasons, we did not analyze brain activity during target presentation; many additional cognitive processes were involved when applying both rules to the target stimuli.

Testing for differences between LCR and HCR representations (whole-brain)

The analyses described in the “Representation of low- and high-level rules (whole-brain)” section identified which regions in the brain represent LCR (or HCR) information. The results, however, are not suitable to test for location-specific differences between LCR and HCR representations (“the difference between “significant” and “not significant” is not itself statistically significant”; Gelman and Stern, 2006). To assess spatial differences in decoding accuracies, we performed an ANOVA that contrasted the LCR and HCR identity decoding analyses described in the “Representation of low- and high-level rules (whole-brain)” section (i.e., LCR and HCR identity decoding) in a single test analogous to the procedure described above. Specifically, we used all decoding accuracy maps from all time bins of the LCR and HCR decoding analyses for all participants, yielding one ANOVA with 16 levels (Fig. 2B): Levels 1–8 included the data for the 8 time bins of the LCR analysis and levels 9–16 the data for the 8 time bins of the HCR analysis. We then tested whether decoding accuracies were significantly higher for LCRs than for HCRs and vice versa during the relevant time span 4–10 s after cue 1 onset (FIR bins 3–5). We used a contrast vector c = ⅓ × [0 0 1 1 1 0 0 0 0 0 −1 −1 −1 0 0 0] to test for LCR > HCR and c = ⅓ × [0 0 −1 −1 −1 0 0 0 0 0 1 1 1 0 0 0] to test for HCR > LCR. As described in the “Representation of low- and high-level rules (whole-brain)” section, data from all FIR time bins were used to increase sensitivity through a more stable variance estimate and nonsphericity correction was used to account for correlations between all levels. This procedure resulted in two brain maps containing locations with significantly higher decoding accuracies for LCRs than HCRs or significantly higher decoding accuracies for HCRs than LCRs.

It is important to emphasize that we did not compare the univariate or multivariate activation signal of LCRs versus HCRs directly. Therefore, for example, we did not use a multivariate classifier to assess whether patterns of activation can discriminate between “If you see a banana, then press left” (an LCR) and “If you see a square, then consider only blue images” (an HCR). In fact, this direct comparison would have likely collapsed information related to our specific research question (rule representation) with other irrelevant sources of information such as the representation of a motor act (only present in LCRs) or the representation of a color (only present in HCRs). To avoid this risk, we first applied MVPA analyses to alternative rules at the same hierarchical level (LCR1 vs LCR2 and HCR1 vs HCR2), which are composed of the same “basic ingredients”: same motor acts, same images, same colors, and same figures. This allowed us to obtain clean maps of the brain regions specifically representing rule information at each hierarchical level (see also Reverberi et al., 2012a, 2012b for a similar analysis strategy). We then contrasted these maps to test at the group level whether and where these information distribution maps are significantly different.

Comparing accuracies from different analyses might be problematic because the relation between information content and decoding accuracy values may also depend on parameters not related to information representation, such as the number of training examples or the cross-validation scheme. This is why we took special care to make the accuracy maps from low- and high-level decoding analyses directly comparable by using the following measures: (1) the same number of trials, (2) the same analysis pipeline (preprocessing, parameter estimation, decoding analysis), (3) an identical trial structure, and (4) the exact same task that participants performed in both conditions.

Testing for overlap between LCR and HCR representations (ROI and whole-brain)

We used ROI analyses to test whether the significant clusters from the decoding analysis for one rule level would also contain information about the other rule level (i.e., whether the significant clusters from the LCR analysis would also contain HCR information and vice versa). ROI analyses are useful because they improve statistical sensitivity compared with the whole-brain analyses since they define a more specific hypothesis (presence of information at a specific location) and thus require less multiple-comparisons correction. Therefore, ROI analyses can detect the presence of information in regions that the whole-brain analysis might have missed. The implemented ROI analyses are not circular because the analyses used to define the ROIs and those used to perform the tests are independent (the LCR and HCR analyses relied on different, mutually exclusive trials). In contrast, using the previously described ROI analyses to test for significant differences between LCR and HCR information would be circular because the data of one condition in each analysis would have also been used to define the ROIs and thus the analyses would have no longer been independent (Kriegeskorte et al., 2009). Therefore, the ROI analyses are only suitable to test for overlap of information (i.e., to test whether regions contain information about both rule levels), whereas the whole-brain contrast analysis can test for information differences. In Figure 4, we only present accuracy estimates of the respective other hierarchical level (i.e., mean HCR decoding accuracy for each LCR cluster in Fig. 4C and mean LCR decoding accuracy for each HCR cluster in Fig. 4D), but not the accuracies from the ROI defining condition (i.e., mean LCR decoding accuracy for each LCR cluster in Fig. 4C and mean HCR decoding accuracy for each HCR cluster in Fig. 4D) to avoid presenting circular data.

Figure 4.

Neuroimaging results. A, Main effect of compound rule encoding: regions encoding which compound rule is currently active regardless of its hierarchical level. Brain regions representing rule identity were VLPFC, SPL and IPL, premotor cortex, postcentral gyrus and PrCG, and MOG. The effect in VLPFC is not driven only by LCR information despite the fact that the HCR whole-brain analysis (D, left) did not detect information in VLPFC. In fact, the ROI analysis in the significant LCR clusters demonstrates significant decoding accuracy for HCRs in VLPFC (C, right). B, Significant differences between LCR and HCR encoding: regions where decoding accuracies were different for LCRs and HCRs, whole-brain analysis. In PrCG (green) decoding accuracies were significantly higher for LCRs compared with HCRs. The barplot on the right shows the mean decoding accuracy for either LCRs or HCRs within this region. C, Results of the whole-brain decoding analysis for LCR identity. Brain regions encoding information about low-level rules (in pink) were VLPFC, PC, SPL, IPL, cerebellum, and MOG. The barplot on the right shows the mean decoding accuracy for HCRs in the LCR ROIs (yellow bars). D, Results of the whole-brain decoding analysis for HCR identity. Brain regions containing information on high-level rules (in yellow) were SPL, PC, IPL, and MTG. The HCR whole-brain decoding analysis was not significant in VLPFC (green circle). However, HCR information was detectable in this region when a more sensitive ROI-based approach was used (sixth bar in the bar plot in C and see text section “Overlap between LCR and HCR representations”). The barplot on the right represents the mean decoding accuracy for LCRs in the HCR ROIs (pink bars). The results of the ROI analyses (barplots in C and D) confirmed that information about LCRs was present in all HCR ROIs and that HCR information was present in all LCR ROIs except cerebellum. Color scales represent t-values for the group-level statistics. Error bars indicate SEM. rMOG = right MOG; lMOG = left MOG; Cer = cerebellum. *p < 0.05; **p < 0.01; ***p < 0.001.

We used the MarsBaR toolbox (Brett et al., 2002) to extract the mean decoding accuracies within all voxels of each HCR (or LCR) ROI (Fig. 4C,D, Table 2) from the LCR (or HCR) searchlight accuracy maps obtained from the analyses described in the “Representation of low- and high-level rules (whole-brain)” section and then tested whether they were significantly higher than chance. The same ANOVA setup as in those whole-brain searchlight analyses was used, again considering the time span 4–10 s after cue 1 onset (FIR bins 3–5).

Table 2.

Results of the whole-brain decoding analyses for low- and high-level rules

Anatomical region	Cluster size (k)	p (FWEc)	x	y	z	Accuracy at t-peak (%)	Average cluster accuracy	Main BAs
LCRs
SPL/PrCG	2447	<0.001	45	−19	49	61.6	57.6	7, 40
			48	−28	55	61.3
			48	−28	46	61.1
MOG	762	<0.001	−36	−85	−8	58.3	56.3	18, 19
			−36	−94	4	57.6
			−33	−64	−23	57.6
IPL	495	<0.001	−51	−7	22	58.6	56.5	40
			−42	−34	61	57.2
			−48	−49	58	57.2
MOG	176	<0.001	36	−91	10	58.5	56.4	18, 19
			36	−88	19	58.5
			27	−88	10	56.9
PC	160	<0.001	−9	−58	52	57.8	56.2	7
			−30	−91	28	56.1
			−12	−73	64	53.8
VLPFC	127	<0.001	48	44	1	57.5	56.3	46, 47
			39	50	−8	57.5
			51	47	16	54.0
Cerebellum	64	0.003	−9	−61	−8	57.2	56.2
			3	−64	−11	56.8
			−12	−67	−14	56.6
HCRs
SPL/angular gyrus	591	<0.001	33	−67	49	59.6	56.3	7, 40
			27	−67	40	58.3
			21	−73	58	57.5
MTG	463	<0.001	−48	−58	−11	59.4	56.4	37
			−48	−67	−8	58.8
			−54	−55	−2	58.5
PC	307	<0.001	−27	−76	31	60.1	56.3	7
			−30	−67	43	57.0
			−33	−70	55	56.7
IPL	113	<0.001	−48	−37	40	57.2	55.8	40
			−45	−37	49	56.7
			−57	−37	43	56.4

Brain regions with decoding accuracies significantly higher than chance (50%) are reported for both LCR and HCR analyses. x, y, and z coordinates are in MNI-template space and the selection of cluster maxima follows the conventions of SPM8. The reported p-values refer to cluster-level inference and are FWE corrected for multiple comparisons at the cluster-level (FWE_c). We report the decoding accuracy of the searchlight at each t-peak and the average decoding accuracy over all searchlights within each cluster. The main Brodmann's areas (BAs) are also provided for each cluster.

Finally, we assessed which brain areas contained information about rule identity regardless of the rule level. By using the same combined whole-brain ANOVA analysis described in the “Testing for differences between LCR and HCR representations (whole-brain)” section, we tested in which regions in the brain the decoding accuracies were significantly higher than chance level regardless of the hierarchical level of the rules between which the classification was performed. We used the contrast vector c = $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.$ × [0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 0] (Fig. 2B). In other words, we tested where in the brain the average decoding accuracy across rule types was higher than chance.

Testing for the presence of LCR and HCR information in PFC regions reported in previous studies supporting either gradient or MDN theories

We performed additional ROI analyses to explore whether and where LCRs and HCRs are encoded in PFC regions previously reported in studies on cognitive control supporting either gradient (Koechlin et al., 2000, 2003; Badre and D'Esposito, 2007) or MDN (Fedorenko et al., 2013) theories. First, we considered PFC regions for which a hierarchy-specific role has been proposed: dorsal premotor (PMd), pre-PMd, lateral PFC (LPFC), and frontopolar cortex (FPC). Two separate sets of ROIs were defined: set 1 (Badre and D'Esposito, 2007), including the four PFC regions (i.e., PMd, pre-PMd, LPFC, and FPC) in both the left and the right hemisphere (because no region on the right hemisphere was reported in that study, we used the inverse x-coordinate to define the right hemisphere ROIs), and set 2 (Koechlin et al., 2003), considering the same PFC regions (for FPC, we referred to Koechlin et al., 2000) in both hemispheres. All ROIs were defined as spheres centered on the relevant coordinates with radius = 12 mm to match the size of the searchlight sphere and make the results comparable. Then, we considered PFC regions of the MDN for which a lesser degree of specialization has been advocated: anterior and posterior inferior frontal sulcus (aIFS and pIFS, respectively), anterior insula/frontal operculum (AI/FO), inferior frontal junction (IFJ), premotor cortex (PM), and anterior cingulate cortex/presupplementary motor area (ACC/pre-SMA; we omit this region from the analysis involving an “hemisphere” factor because it lays perfectly in the medial aspect of the brain and thus is not lateralized). We extracted the MDN regions from the activation map of Fedorenko and colleagues (2013) available at imaging.mrc-cbu.cam.ac.uk/imaging/MDsystem to define a third set of ROIs.

We tested for the presence of either LCR or HCR information in the regions of the three sets, as well as for differences between the two hierarchical levels. In contrast to the ROI analyses in the “Testing for overlap between LCR and HCR representations (ROI and whole-brain)” section, in this case, a direct comparison between LCRs and HCRs is appropriate because the ROIs considered here were defined using previous independent studies. For each participant and for each of the 26 ROIs (4 PFC regions × 2 hemispheres for sets 1 and 2 and 5 PFC regions × 2 hemispheres for set 3), we extracted the mean decoding accuracy for both the LCR and the HCR decoding analyses within all voxels of the ROI in the time window of interest (i.e., 4–10 s after cue 1 onset). These values were entered in a 3-factorial (4 ROIs × 2 hemispheres × 2 decoding analyses for set 1 and 2 and 5 ROIs × 2 hemispheres × 2 decoding analysis for set 3) repeated-measures ANOVA. A separate ANOVA was performed for each set using R 3.1.0.

Behavioral control analyses

A recent study (Todd et al., 2013) hypothesized that successful decoding of rule identity from fMRI data could be explained by differences in RTs or related factors such as difficulty. To test directly whether individual differences in RT could explain the neuroimaging results, we performed two control analyses (we have already used the same analysis to test this hypothesis in previous work before Todd et al. critique; Reverberi et al., 2012b; see also Görgen et al., 2017). First, we tested whether the RTs of the two LCRs (or two HCRs) allowed us to correctly classify compound rules. Therefore, we performed the same analyses that we did on fMRI data but we used RTs as evidence. Second, to make the analyses directly comparable to that in Reverberi and colleagues (2012b), we investigated whether RT differences could explain the fMRI results. Therefore, we correlated RT differences to fMRI accuracies to determine whether participants with larger RT differences between rules also showed higher fMRI decoding accuracies for these rules.

Decoding compound rules using RTs.

To test whether the two LCRs (or HCRs) can be distinguished using RT, we performed two cross-validated decoding analyses on RTs for each participant, one for LCRs and one for HCRs, and then tested across participants whether RT could predict LCR (or HCR) identity above chance. For this purpose, we used the same analysis pipeline that we used for fMRI data: For each participant, we calculated the average RT for each run and condition from trials that contained LCRs (or HCRs) in the first delay period (delay 1) using the same trials that were also used for the fMRI analysis (to parallel the creation of β estimates from the fMRI data). We used the resulting 12 average RT values (six per condition) to perform leave-one-run-out cross-validated decodings between the two LCRs (or HCRs). We then tested whether the LCRs (or HCRs) could be predicted better than chance using a t test on the 37 participants' individual decoding accuracies.

Relation between RT decoding performance and fMRI decoding performance.

The ability of RTs to predict LCRs (or HCRs) across individuals does not automatically imply that RTs also explain fMRI decoding performance or have the same underlying cause. We tested directly whether RT differences could explain the fMRI decoding results by correlating participants' fMRI decoding performance with two behavioral measures: the individual RT-decoding performance and the absolute RT differences between the two conditions (as in Reverberi et al., 2012b). These correlation analyses were performed for each significant cluster of the main fMRI analyses by correlating LCR fMRI accuracies to LCR RT measures and HCR fMRI accuracies to HCR RT measures.

Bayesian correlation analyses.

We calculated Bayes factors for all correlation analyses with the Bayesian correlation analysis implemented in JASP (the JASP Team, Amsterdam, The Netherlands, 2017; version 0.8.2) using a “noninformative,” one-sided flat prior for H1 (i.e., the JASP default, Ly et al., 2016). Bayes factors allow robustness checks for null hypotheses under the given assumptions by quantifying the likelihood of H0 over H1 (Jeffreys, 1961; Kass and Raftery, 1995; Dienes, 2014; Jarosz and Wiley, 2014; Lee and Wagenmakers, 2014). Two Bayes factors are typically calculated: BF₁₀ and BF₀₁. BF₁₀ states how more likely H1 is than H0 and BF₀₁ (i.e., 1/BF₁₀) states how more likely H0 is than H1. Therefore, a Bayes factor of 1 means that both hypotheses are equally likely, whereas a Bayes factor larger than 1 provides evidence for the respective first hypothesis (i.e., H1 for BF₁₀, H0 for BF₀₁) and a Bayes factor smaller than 1 favors the respective second hypothesis. Two scales are commonly used to interpret how much evidence a given Bayes factor provides: the (Jeffreys, 1961), with updated terminology by Lee and Wagenmakers (2014), and a scale by Kass and Raftery (1995). Following Lee and Wagenmakers (2014), we consider Bayes factors < 3 as “anecdotal” evidence, Bayes factors > 3 as “moderate” evidence, and Bayes factors > 10 as “strong” evidence.

Results

Behavioral results

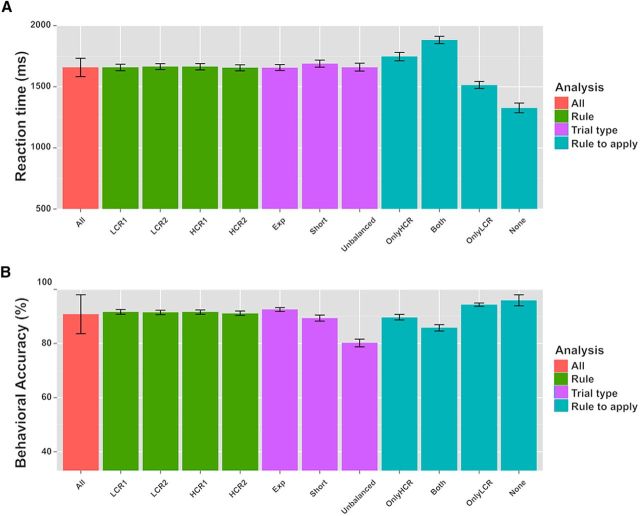
During scanning, participants were highly accurate in applying the rules. Responses to experimental trials were correct on average in 92.6% (SD = 4.5%) of the trials (Fig. 3). Because up to three button presses were required, left and right buttons could be pressed in any order and pressing the “no response button” and not responding at all were also possible responses; the chance level for normal trials was 1/11 = 9.09% (chance level for all trials was even lower, i.e., 3.45%, see below). Participants responded quickly: the first button was pressed in about half of the total time allowed for responding (3 s). Mean RT (here calculated as the latency for the first button press) for the experimental trials was 1656.9 ms (SD = 148.1 ms).

Figure 3.

Behavioral results (LMM). Plots of the mean response RTs (A) and accuracies (% of correct responses; B) for different trials. All: average across all trial types. LCR1 and LCR2: low-level compound rules 1 and 2; HCR1 and HCR2: high-level compound rules 1 and 2. Exp: Experimental trials; Short: catch trials with delay 1 and delay 2 lasting 2 s; Unbalanced: catch trials with unbalanced combinations of rules. OnlyHCR: Only the HCR applies; OnlyLCR: only the LCR applies; Both: both rules apply; None: neither the LCR nor the HCR applies. See text sections “Experimental stimuli” and “Behavioral results” for a detailed description of the different conditions. Error bars indicate SEM.

To assess potential differences in difficulty between the rules, we extracted all trials in which participants were required to apply a specific experimental compound rule and compared the relative mean accuracies and RTs. We performed LMM analyses of the relation between either RT or accuracy and the specific rule. As fixed effect, we introduced compound rule identity into the model and intercepts for participants as random effects to allow for subject variability in mean responses. P-values were calculated with likelihood ratio tests of the full model with the effect of interest against the model without that effect (Barr et al., 2013). No effect of the specific compound rule on either RT or accuracy was found (χ₍₃₎² = 2.05, p = 0.56, and χ₍₃₎² = 1.44, p = 0.70, respectively).

Two types of catch trials were used in the experiment to ensure that participants readily represented the complete rule sets upon cue presentation. As in normal trials, participants were very fast and accurate in catch trials, showing that they were performing the task as requested. In catch trials with unbalanced combinations of rules, the average accuracy was 80.2% (SD = 8.8%) and the mean RT was 1660.1 ms (SD = 196.7 ms). In short catch trials, participants had a mean accuracy of 89.4% (SD = 6.9%) and an average RT of 1688.9 ms (SD = 176.4 ms). The accuracy of both types of catch trials was again highly above chance level, which was for most catch trials again 1/11 = 9.09% (like in normal trials) or even lower for catch trials with unbalanced LCR combinations in which both individual rules contained the same triggering stimulus (e.g., “banana → left; banana → right”). These trials could require up to six responses (if all target images matched the rules; here, if three bananas were shown), so the chance level drops to 1/29 = 3.45% for these trials. To assess the presence of differences in RT and accuracy between the different types of trials, we performed LMM analyses of the relation between either RT or accuracy and the type of trial. As fixed effect, we introduced trial type into the model. As random effects, we considered intercepts and random slopes for each participant, thus allowing for intersubject variability both in mean responses and in sensitivity to different rule types. The effect of trial type on RT was not significant (χ₍₂₎² = 3.30, p = 0.19); in contrast, the effect of trial type on accuracy was significant (χ₍₂₎² = 45.1, p < 0.001). Post hoc tests using the Tukey's HSD method revealed that accuracy in experimental trials was significantly higher than either in catch trials with unbalanced rule combinations (p < 0.001) or in short trials (p = 0.006).

To evaluate possible differences between diverse response outcomes, we also analyzed RTs and accuracies for four different response classes depending on whether the target images matched the LCR or the HCR (see “Experimental stimuli” section): (1) both the LCR and the HCR applied to the target (“Both”); (2) only the LCR applied (“OnlyLCR”); (3) only the HCR applied (“OnlyHCR”); or (4) neither the LCR nor the HCR applied (“None”) (see Fig. 3 for mean RTs and accuracies for each condition). In general, we found that the fewer rules to apply, the faster and the more accurate the responses. We performed LMM analyses of the relation between either RT or accuracy and the combinations of rules to apply. As a fixed effect, we added the combination of to-be-applied rules to the model. As random effects, we considered intercepts for participants, as well as by-participant random slopes to account also for differences between participants in their susceptibility to the experimental factor. The effect of the combination of rules to be applied on both RT and accuracy was significant (χ₍₃₎² = 78.38, p < 0.001 and χ₍₃₎² = 41.22, p < 0.001, respectively). Post hoc tests using the Tukey's HSD method showed a significant difference in RTs between conditions for all the pairwise comparisons (all p < 0.001); accuracies were significantly different between the conditions in which the HCR had to be applied (either alone or together with the LCR) and the conditions in which it had not (i.e., only the LCR or neither of the rules applied; all p < 0.01). These differences were expected because the application of HCRs required additional cognitive operations such as selective attention and response inhibition. Together, these results further demonstrate that participants performed the task as requested.

Neuroimaging results

Neural representations of low- and high-level rules

The central research question of this study was where and how the brain represents low- and high-level rules, specifically in the absence of information about the alternative level. To answer this question, we performed MVPA decoding analyses to identify brain regions that contained information on either low- (i.e., LCR) or high- (i.e., HCR) compound rules using data from a time period (cue 1 and delay 1 in Fig. 1B) in which participants were maintaining only one compound rule (either LCR or HCR). Note that this period is also long before task execution, so information about the target stimuli could not interfere.

We first used whole-brain searchlight analyses that test for local activity patterns that can distinguish between rules from the same level (i.e., either LCR or HCR rules). This analysis is comparable to a conventional (mass-)univariate analysis in the respect that it is a spatially unbiased and locally resolved test. As described in the Materials and Methods, this analysis tests for information about individual rules within one hierarchical level (e.g., LCR1 vs LCR2) to reveal rule-specific differences in brain activity independent of any other potential level-specific effect.

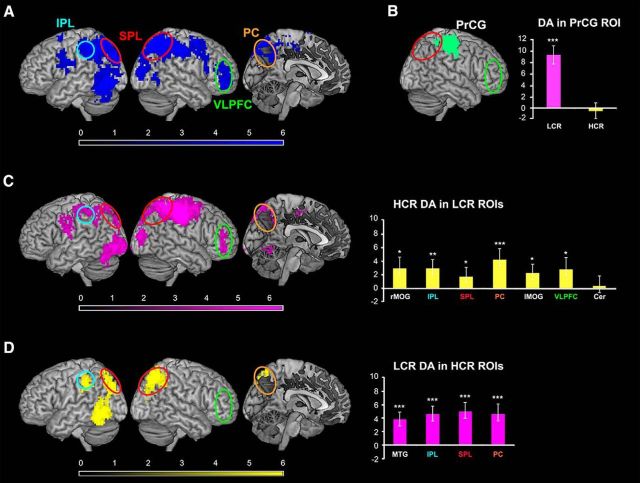
The results of the whole-brain analyses are shown in Figure 4, C and D, and in Table 2 (all p < 0.05 FWE corrected at the cluster level, p < 0.001 at the single-voxel level, voxel extent threshold = 64 voxels). The identity of the LCRs could be decoded from right superior parietal lobule (SPL, mainly BA 7/40), right ventrolateral PFC (VLPFC, mainly BA 47), left inferior parietal lobule (IPL, mainly BA 40), left precuneus (PC, BA 7), left cerebellum, and bilaterally in middle occipital gyrus (MOG, mainly BA 19). During the same time window (cue 1 and delay 1), information on HCR identity was decoded in right SPL (BA 7/40), in left IPL (BA 40), left PC (BA 7), and left middle temporal gyrus (MTG, BA 37).

Differences between LCR and HCR representations

Next, we tested for spatial differences in decoding accuracies between LCRs and HCRs across the brain. Decoding accuracies were significantly higher for LCRs than HCRs only in right precentral gyrus (PrCG); an additional ROI analysis did not show any presence of HCR information in this region (Fig. 4B). HCR accuracies were not significantly higher than LCR accuracies in any region. Importantly, these whole-brain analyses showed no statistically significant difference in decoding accuracy between LCRs and HCRs in VLPFC.

Overlap between LCR and HCR representations

To further assess whether the regions where we could decode either LCRs or HCRs encoded also information about rules from the other hierarchical level, we performed a set of ROI analyses. This additional test is important because, whereas the whole-brain analyses can detect regions containing information anywhere in the brain without any a priori assumptions, they also have a lower sensitivity given the required multiple comparison correction. Restricting the location to a smaller area strongly increases the sensitivity of the analysis and is thus useful to test which regions contain both LCR and HCR representations. These analyses are not circular because the trials used to define the ROIs are independent from the trials used to perform the tests. In contrast, testing the same conditions that had been used to define the ROIs or comparing LCR versus HCR decoding accuracies would be circular. Therefore, we only report the results for the respective other condition in Figure 4, C and D (bar plots).

Information about LCRs was present in all four brain regions that were found to encode HCR information in the whole-brain analysis. Similarly, for all LCR ROIs, the mean decoding accuracy for HCRs was significantly higher than chance level, except in cerebellum (p = 0.43).

Finally, we assessed which brain regions encoded information about rule identity regardless of the hierarchical level. We could decode rule information with accuracy significantly higher than chance in a wide frontoparietal network (Fig. 4A, Table 3) comprising SPL (BA 7), IPL (BA 40), MOG (BA 19), right VLPFC (BA 46/47), postcentral gyrus and PrCG (BA 6/4), and premotor cortex (BA 6).

Table 3.

Results of the whole-brain decoding analysis for rule identity irrespective of the hierarchical level

Anatomical region	Cluster size (k)	p (FWEc)	x	y	z	Accuracy at t-peak (%)	Average cluster accuracy	Main BAs
SPL and IPL/MOG	6264	<0.001	33	−58	52	57.9	54.9	7, 40, 19
			48	−52	58	57.7
			−48	−70	−8	57.5
Inferior and middle frontal gyrus	346	<0.001	48	47	−5	55.9	54.3	47, 46
			45	44	−20	55.0
			45	53	−11	54.3
PrCG and postcentral gyrus	182	<0.001	−60	−1	34	55.5	54.6	4, 6
			−51	−4	25	55.5
			−57	−16	28	55.3
Premotor cortex	71	0.001	−18	5	73	54.3	54.6	6
			−27	5	61	54.3
			−18	8	61	54.3

Brain regions with decoding accuracies significantly higher than chance for rule identity irrespective of the hierarchical level are reported (i.e., results from the whole-brain ANOVA in text section entitled “Testing for overlap between LCR and HCR representations (ROI and whole-brain)”; see also Fig. 4A). Coordinates, p-values, and decoding accuracies are as in Table 2.

Comparison with results from previous studies

In contrast to previous studies investigating the hierarchy-based segregation of information within PFC, we found no difference between LCRs and HCRs (except in the PrCG). Moreover, whole-brain analyses failed to detect information on rules in many of the regions previously reported to perform hierarchy-specific computations (Koechlin et al., 2000, 2003; Badre and D'Esposito, 2007), as well as in some regions of the MDN argued to represent rule information in a less specialized fashion (Fedorenko et al., 2013). To better assess the role of those regions in our task, we performed ROI analyses at the specific locations that had been reported in these studies.

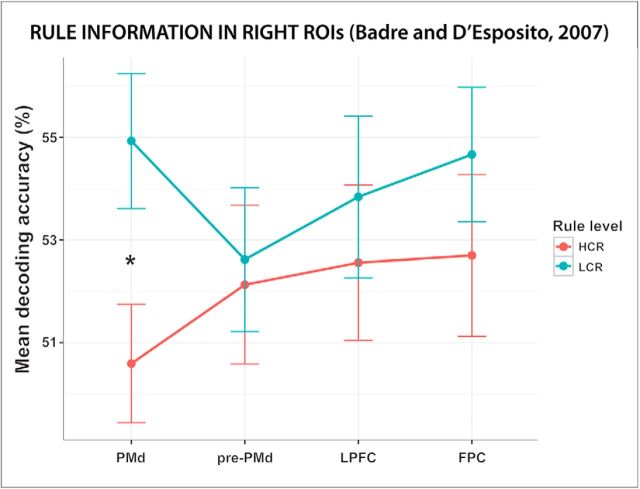
The ANOVA analysis performed using the ROIs from set 1 (Badre and D'Esposito, 2007) showed a significant effect of hemisphere (F_(1,36) = 6.66, p = 0.014, η_g² = 0.005). Decoding accuracies of the ROIs in the right hemisphere were higher than those of the ROIs in the left one. The intercept term was also significant (F_(1,36) = 4006, p < 0.001, η_g² = 0.975), indicating that the mean decoding accuracy over the whole PFC network was higher than chance. Importantly, there was no effect of either ROI or rule level (p = 0.84 and p = 0.30, respectively) and no interaction effect of these two factors (p = 0.23), indicating that decoding accuracies for LCRs and HCRs in the different PFC regions did not differ (Fig. 5). To further assess the presence and distribution of LCR and HCR information in each ROI, we performed multiple one-sample and paired t tests (we report only results significant at p < 0.05, uncorrected). LCR information was present in all regions except the left pre-PMd cortex (p = 0.16); HCR information was present in left pre-PMd ROI and in right LPFC and FPC ROIs. The difference between LCR and HCR decoding accuracies was significant only in the right PMd ROI (t_(70.8) = 2.48, p = 0.01, d = 0.575), where the mean decoding accuracy was higher for LCRs than for HCRs.

Figure 5.

Rule information in PFC regions reported in a previous study on hierarchical rule representation. The plot shows the mean decoding accuracy in the four ROIs in the right hemisphere of set 1 (Badre and D'Esposito, 2007). The average decoding accuracy in these regions is displayed separately for LCRs and HCRs. Error bars indicate SEM. PMd = Premotor dorsal; pre-PMd = pre-premotor dorsal. *Significant difference (p < 0.05) between LCR and HCR decoding accuracies.

The ANOVA analysis performed including the ROIs from set 2 (Koechlin et al., 2000, 2003) showed no significant main effect of any factor or any interaction effect. The intercept term was significant (F_(1,36) = 10675, p < 0.001, η_g² = 0.977), indicating a mean decoding accuracy significantly higher than chance and thus the encoding of rule information in the network of PFC regions. The results of t tests similar to those performed for the ROIs in set 1 showed the presence of LCR information in both the left and the right PMd ROIs and in the right LPFC ROI; HCR information was encoded by the left pre-PMd cortex. The LCR and HCR decoding accuracies differed significantly only in the right PMd ROI (t_(68.6) = 1.96, p = 0.03, d = 0.456), where the mean decoding accuracy for LCRs was higher than for HCRs.

The ANOVA analysis performed using the ROIs from set 3 (Fedorenko et al., 2013) showed neither a significant main effect of any factor nor interaction effects. Once again, the intercept term was significant (F_(1,36) = 3561, p < 0.001, η_g² = 0.972), indicating a mean decoding accuracy significantly higher than chance and thus revealing rule information encoding in the network of PFC regions. Results of t tests similar to those performed for the ROIs in sets 1 and 2 revealed the presence of LCR information in the right aIFS and pIFS ROIs and in the IFJ and PM ROIs on both hemispheres; HCR information was present in left IFJ and PM cortex. LCR and HCR decoding accuracies did not differ significantly in any of the regions of set 3.

To summarize, these analyses show that information about both LCRs and HCRs was present in the network of PFC regions previously reported to perform hierarchy-specific computations, as well as within the MDN. Moreover, these analyses show no difference between LCRs and HCRs in any node of the two networks except in the right PMd cortex. This area corresponds approximately to the region where we found higher decoding accuracy for LCRs than for HCRs in the present study (i.e., PrCG; see Fig. 4B).

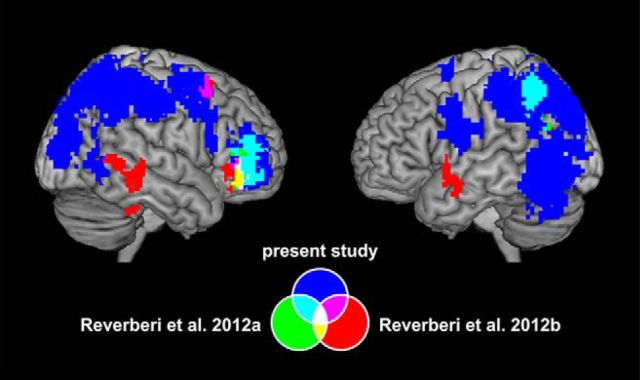
Moreover, we compared the results of the present study with the findings of previous MVPA studies on rule representation from our group (Fig. 6). The accuracy map (Fig. 6, blue) from the combined ANOVA analysis on rule identity was compared with the accuracy maps from the analysis on compound rule identity in Reverberi and colleagues (2012a, 2012b) (in Fig. 6, the regions are shown in green and red, respectively). In those studies, MVPA was used to identify neural representations of conditional compound rules similar to our LCRs and HCRs. Reverberi and colleagues (2012a) used compound conditional rules linking a specific category to a motor response (e.g., “if face then left; if house then right”); Reverberi and colleagues (2012b) used compound conditional rules that linked a particular category with a letter that indicated the motor response depending on its position on the screen (e.g., “if furniture then A; if transport then B”). The clusters in the right VLPFC (BA 47) found in all the three studies overlap (overlaps are shown in cyan, yellow, magenta, and white in Fig. 6). The clusters in the left IPL (BA 40) in the present study and in Reverberi and colleagues (2012a) are also overlapping (region in cyan on the map on the right in Fig. 6).

Figure 6.

Comparison with regions encoding compound conditional rule identity in previous MVPA studies. Results of analyses decoding rule identity from the present study (in blue) and two previous MVPA studies on rule representation (from Reverberi and colleagues 2012a, in green, and from Reverberi and colleagues 2012b, in red) are depicted. The clusters in right VLPFC encoding compound rule identity in the present study, in Reverberi and colleagues (2012a), and in Reverberi and colleagues (2012b) overlap (yellow, cyan, magenta, and white areas). Additional overlap (cyan area on the map on the right) exists between the clusters in parietal cortex from the present study and from Reverberi and colleagues (2012a).

The comparison identified VLPFC as the only brain region encoding compound rule information across all three studies. Therefore, we conducted additional analyses to explore the distribution of information in this region. We performed ROI analyses similar to those described in the “Testing for overlap between LCR and HCR representations (ROI and whole-brain)” section; we used the VLPFC clusters (in inferior frontal gyrus, BA 47) from the two previous studies referred above as ROIs to test for the presence of information about LCRs and HCRs. The results of these analyses confirmed that the average decoding accuracy for both LCRs and HCRs was significantly higher than chance in the VLPFC regions from both previous studies (all p < 0.05, corrected), with no significant difference between LCR and HCR decoding accuracies (p = 0.09 for the region in Reverberi and colleagues 2012a and p = 0.21 for the region in Reverberi and colleagues 2012b).

RT decoding and correlation between RT measures and fMRI results

Recently, Todd and colleagues (2013) hypothesized that decoding of rule identity from fMRI data could be caused by differences in RT (or related factors such as difficulty). To test this hypothesis, we assessed whether RT within participants contained information about the two LCRs (or HCRs) by conducting cross-validated decoding between the two LCRs (or HCRs) on RT data. We found that, in general, RTs predicted LCR (mean decoding accuracy = 57.88%, 95% confidence interval [CI₉₅] = 52.8–63.0%; t₍₃₆₎ = 3.15, p = 0.003, d = 1.05) and HCR (mean decoding accuracy = 57.43%, CI₉₅ = 51.8–63.0%; t₍₃₆₎ = 2.69, p = 0.01, d = 0.90) better than chance.

However, differences in RT do not imply that they also underlie fMRI decoding or have a shared common cause. This is particularly true in our experiment, in which the task phase that we explored is seconds before the phase in which rules are applied and RT measured. Therefore, we tested this possibility directly by correlating RT accuracies (and absolute differences in RT) to the fMRI accuracies of all significant ROIs (see also Reverberi et al., 2012b). The results clearly contradict the hypothesis that RT differences underlie fMRI rule decoding both for LCRs and HCRs (Table 4). No correlation was significant at α = 0.05 after multiple-comparisons correction either for correlations with RT decoding accuracies or for absolute RT differences. Without correction, only one correlation analysis (of the 22 tests performed) was significant at the standard α-level of α = 0.05, but here the correlations between RT and fMRI accuracies were even negative (PrCG/SPL, ρ = −0.36, p = 0.03; IPL, ρ = −0.31, p = 0.07), meaning that participants with higher accuracies in fMRI decoding had lower accuracies in RT decoding. If RT effects indeed underlie fMRI decoding, then correlations between the two should be positive; that is, participants with higher fMRI accuracies should also show higher RT accuracies. Therefore, these results contradict the hypothesis that RT differences underlie fMRI decoding between rules in our experiment. Given that null findings provide limited evidence, we performed additional analyses to further assess the relation between RT differences and fMRI decoding performance. For this, we calculated Bayes factors for the correlation analyses and added a regressor of no interest to the second-level analyses that contrasts the LCR and HCR decoding accuracies.

Table 4.

Correlations between RT analyses and fMRI decoding

	DART			|ΔRT|			x	y	z
	p	ρ	BF0+	p	ρ	BF0+
LCR ROIs
MOG	0.28	0.18	2.43	0.22	0.20	1.09	−36	−85	−8
VLPFC	0.89	−0.02	3.46	0.97	−0.01	8.72	48	44	1
SPL/PrCG	0.03*	−0.36*	12.74S	0.22	−0.21	10.87S	45	−19	49
Cerebellum	0.73	−0.06	8.54	0.32	−0.17	10.39S	−9	−61	−8
PC	0.45	−0.13	5.26	0.68	−0.07	5.43	−9	−58	52
MOG	0.66	−0.08	7.49	0.90	−0.02	4.17	36	−91	10
IPL	0.07T	−0.31T	9.78	0.63	−0.08	7.71	−51	−7	22
HCR ROIs
SPL/angular gyrus	0.39	−0.15	4.81	0.27	−0.18	7.88	33	−67	49
PC	0.29	−0.18	4.11	0.19	−0.22	6.62	−27	−76	31
IPL	0.63	−0.08	5.54	0.95	−0.01	7.79	−48	−37	40
MTG	0.51	−0.11	4.35	0.78	−0.05	6.07	−48	−58	−11

P-value and correlation coefficient (ρ) of rank–order correlation analyses between decoding accuracies on RT (DA_RT)/absolute RT differences ( ΔRT ) of low-level compound rules (LCRs) and high-level compound rules (HCRs) correlated to fMRI decoding accuracies of all significant ROIs (mean fMRI decoding accuracy across FIR bins 3–5). No correlation survived multiple-comparisons correction. The only correlations with p < 0.10 (LCR DA_RT in SPL/PrCG and IPL) even showed a negative correlation, meaning that better decoding accuracies on RTs correlated with worse decoding accuracies on neural data. Bayes factors (BF₀₊) for H0 over H1 (H0: no correlation between the measure and the fMRI decoding accuracy; H1: positive correlation between the two measures) for Pearson's correlation coefficients are also reported. Values of BF₀₊ > 10 indicate strong evidence for H0, values > 3 denote moderate evidence, whereas values > 1 indicate anecdotal evidence for H0. BF₀₊ for all correlations indicate moderate evidence for H0, except for MOG, where BF₀₊ shows anecdotal evidence for H0 and SPL/PrCG, where it indicates strong evidence in favor of H0. Together, these results speak against the hypothesis that differences in RT cause fMRI decoding results (or have a common underlying cause). ROI names and x, y, and z coordinates are as in Table 2.

*Significant at p < 0.05, uncorrected; T superscript indicates trend (0.05 < p < 0.10, uncorrected); S superscript indicates strong evidence for H0.

First, we performed one-sided tests for positive correlations between RT measures and fMRI decoding accuracies (H0: no correlation between the two measures, H1: flat “noninformative” prior for positive correlation values). The results are shown in Table 4. We calculated Pearson and Kendall rank correlation coefficients (Kendall coefficients are not shown in Table 4). Nearly all correlations between decoding on RTs and fMRI decoding accuracies provide at least moderate evidence for H0 (i.e., all BF₀₊ > 3). Correlation in PrCG provides even strong evidence for H0 (BF₀₊ > 10), whereas correlation in MOG shows only anecdotal evidence for H0 (BF₀₊ > 1). Similarly, most correlations between average RT differences and fMRI decoding accuracies also provide moderate evidence for H0. PrCG and cerebellum provide strong evidence for H0 (BF₀₊ > 10), whereas MOG again shows only anecdotal evidence (BF₀₊ > 1). No result indicated evidence for a positive correlation (i.e., H1). Together, these results demonstrate that the observed null correlations are informative and reasonably robust.

Finally, we recomputed the second-level analysis testing for differences in decoding accuracy between LCRs and HCRs by adding a regressor of no interest that accounts for individual subject RT decoding accuracy effects. If fMRI decoding results depended on RT differences, then adding the RT covariate should remove fMRI results. The results confirm our initial main results: only PrCG shows decoding accuracies significantly higher for LCRs than HCRs and no decoding accuracies significantly higher for HCRs than LCRs are present anywhere in the brain, as in the original analysis without the regressor of no interest.

Discussion

In this study, we investigated how and where the human brain represents rules at different hierarchical levels. First, we found that both low- and high-level rules can be decoded from local patterns of brain activity. Second, information about both levels is present across frontal and parietal brain regions. Third, the brain regions encoding active rules in general did not differ between high and low hierarchical levels, except for motor and premotor cortex. Our study differs from previous work on hierarchical rule sets (Koechlin et al., 2003; Badre and D'Esposito, 2007; Nee and Brown, 2012) in three important aspects: (1) we focused on the pure representation of low- and high-level rules; (2) we investigated each rule level in isolation from other task-related information; and (3) we minimized potential aspecific differences by conveying information at all hierarchical levels with formally identical IF-THEN rules. Most previous studies analyzed brain activity during rule application, making a clean separation between rule representations and rule application difficult (e.g., preparation vs execution; Grafton and Hamilton, 2007). Our results address both the neural representations of hierarchical rule sets and the organization of the human control system.

Rules are represented regardless of their hierarchical level

The first aim of this study was to locate neural representations of rules from different levels within a cognitive hierarchy. Both LCRs and HCRs could be decoded from brain activity patterns within a network comprising mainly parietal (SPL, IPL, and PC) and frontal (VLPFC) brain regions. These results replicate previous findings from our group showing that lateral parietal regions and VLPFC represent conditional rules (Fig. 6) and extend them to rules at a higher hierarchical level. In particular, VLPFC represented the identity of conditional rules in all three studies. This result agrees with evidence that VLPFC is involved in task–rule retrieval and maintenance (Sakai and Passingham, 2003; Rowe et al., 2008; Bengtsson et al., 2009). VLPFC has been related to the use of both bivalent stimuli (Crone et al., 2006) and conditional rules (Bunge, 2004; Reverberi et al., 2012a, 2012b). In all of these experiments, the stimulus–response associations were variable, so the same stimuli required different responses depending on the rule active on a specific trial. Despite our LCRs and HCRs belonged to different hierarchical levels, they were both conditional rules linking a condition to its consequence (either a button press or a relevance shift) and were both represented in VLPFC. This suggests that VLPFC flexibly represents conditional associations regardless of their hierarchical level. This high flexibility, however, does not imply that any task-relevant information would be represented in VLPFC; for example, the information on which rule should be applied first is not encoded in VLPFC (Reverberi et al., 2012b).

Beyond VLPFC, parietal cortex has been repeatedly implicated in rule retrieval and maintenance (Bunge et al., 2003; Bode and Haynes, 2009; Reverberi et al., 2012a). We found that SPL, IPL, and PC encoded information about both LCRs and HCRs, suggesting that these regions are involved in rule representation independent of their hierarchical level. This result is consistent with a recent meta-analysis (Niendam et al., 2012) showing that these parietal regions are consistently activated across studies using different tasks involving cognitive control (see also Wisniewski et al., 2015).

We found few brain regions that specifically encoded rules from one hierarchical level: right PrCG and cerebellum encoded only information about LCRs. A potential explanation for the difference in PrCG is that this region encodes the link between stimuli and motor responses, which were only present in LCRs. Similarly, a main function of the cerebellum is motor control (It̄o, 1984), which LCRs, but not HCRs, required. Therefore, we speculate that the differences we found between LCRs and HCRs might be explained by the different consequences that they produced.

The second goal of the study was to delineate how rules at different hierarchical levels are represented in the brain. We found that regions within the frontoparietal control network encode both the LCRs and the HCRs. Explicitly testing for differences in decoding accuracies between LCRs and HCRs in the PFC regions of the MDN, as well as in regions previously reported to perform hierarchy-specific computations, revealed differences only in premotor cortex, suggesting that, in almost all of these regions, rule information is encoded regardless of hierarchical level during maintenance.

Why did we not find a gradient in PFC whereas previous studies did? We propose a number of possible explanations. First, most evidence in favor of the existence of a functional gradient in PFC comes from studies that analyzed brain activity during rule implementation, thus collapsing rule representation and application. The required processing of rule and stimuli during execution makes it difficult to distinguish processing from representations of specific content (Wood and Grafman, 2003). Therefore, differences in results with previous studies may reflect different cognitive processes underlying rule application and representation (Toni et al., 1999; Sigala et al., 2008). To permit a separation and to identify specifically neural representations of hierarchical rules, we applied MVPA to fMRI data from a time window before task execution so that processing could not interfere with the analysis. Second, multiple principles defining rule hierarchies exist (see “Experimental stimuli” section). Our experiment does not explore hierarchies based on temporal abstraction but those relying on policy abstraction (but see “Experimental stimuli” section for more conservative definitions of policy abstraction) and asymmetrical relations. Therefore, although our results suggest that hierarchical relations and policy abstraction (as defined in the present study) are not sufficient to elicit gradients in PFC, they do not exclude that other types of hierarchical relations (e.g., temporal) might induce PFC gradients. Third, the only previous study using MVPA to investigate hierarchical rule set representations (Nee and Brown, 2012) manipulated both the low and the high hierarchical levels simultaneously (in the “early delay”, conditions differ for both the context that is relevant to determine the target response and the stimulus that is associated with the target response). This feature prevents the exploration of each level representation independently. However, it also induces the representation of the whole hierarchical rule set and not just of a specific component (i.e., either only high- or only low-level rules) as in our paradigm. This hints at the possibility that the simultaneous representation of the full hierarchical rule set is critical to inducing the involvement of more anterior PFC regions, whereas the representation of only one level of the hierarchy, even the higher one, is not.

Organization of the human control system

This study explored two questions relevant for the current debate on the organization of the human control system: (1) whether rules from different hierarchical levels are encoded by a single general system or represented at different locations and, if so, whether specialized regions segregate along an anterior-to posterior gradient (Christoff and Gabrieli, 2000; Fuster, 2000; Koechlin and Summerfield, 2007; Badre and D'Esposito, 2009); and (2) how rule information is distributed across the brain.

Gradient theories defining hierarchies based on either policy abstraction or asymmetrical relations (see “Experimental stimuli” section) predict that higher-level rules (HCRs) should be represented more anterior within PFC compared with lower level rules (LCRs). In contrast, theories claiming that a single network encodes task rules (Dehaene and Naccache, 2001; Duncan, 2001) predict no differences between HCRs and LCRs, with information from both rule levels represented within the network. We found neither prefrontal nor parietal regions specifically encoding one hierarchical level. Therefore, the hierarchy relation explored in this study did not generate an anatomo-functional gradient, as some gradient theories would have predicted. However, our results are not fully consistent with accounts proposing a single network for task coding. Information distribution in our study partly differs from that proposed within the MDN theory (Duncan, 2006) because only some MDN regions represent our rules (but consider Harding et al., 2015; Woolgar et al., 2016). Moreover, brain regions critical for encoding hierarchical rule sets (e.g., VLPFC) lie outside the MDN as described currently (Fedorenko et al., 2013; but see Woolgar et al., 2016).

Overall, our results suggest that the brain represents all conditional rules in the same way regardless of their position in the investigated cognitive hierarchy. This implies that the human brain did not use this dimension as an organizational principle for building task representations. This does not mean that cognitive control and its neural basis are functionally homogeneous or exclude that gradients might emerge when different types of hierarchical relations are considered. Other studies have shown functional dissociations within the control network for different features; for example, signals related to the immediate versus past context (Koechlin et al., 2003; Nee and D'Esposito, 2016), rule identity and order (Reverberi et al., 2012b) or the type of logical relation (Baggio et al., 2016). Our research approach is useful in investigating which dimensions are relevant in shaping the human control system and thus is promising to unravel its neurophysiological architecture.