Edge-Related Activity Is Not Necessary to Explain Orientation Decoding in Human Visual Cortex

Abstract

Multivariate pattern analysis is a powerful technique; however, a significant theoretical limitation in neuroscience is the ambiguity in interpreting the source of decodable information used by classifiers. This is exemplified by the continued controversy over the source of orientation decoding from fMRI responses in human V1. Recently Carlson (2014) identified a potential source of decodable information by modeling voxel responses based on the Hubel and Wiesel (1972) ice-cube model of visual cortex. The model revealed that activity associated with the edges of gratings covaries with orientation and could potentially be used to discriminate orientation. Here we empirically evaluate whether “edge-related activity” underlies orientation decoding from patterns of BOLD response in human V1. First, we systematically mapped classifier performance as a function of stimulus location using population receptive field modeling to isolate each voxel's overlap with a large annular grating stimulus. Orientation was decodable across the stimulus; however, peak decoding performance occurred for voxels with receptive fields closer to the fovea and overlapping with the inner edge. Critically, we did not observe the expected second peak in decoding performance at the outer stimulus edge as predicted by the edge account. Second, we evaluated whether voxels that contribute most to classifier performance have receptive fields that cluster in cortical regions corresponding to the retinotopic location of the stimulus edge. Instead, we find the distribution of highly weighted voxels to be approximately random, with a modest bias toward more foveal voxels. Our results demonstrate that edge-related activity is likely not necessary for orientation decoding.

SIGNIFICANCE STATEMENT A significant theoretical limitation of multivariate pattern analysis in neuroscience is the ambiguity in interpreting the source of decodable information used by classifiers. For example, orientation can be decoded from BOLD activation patterns in human V1, even though orientation columns are at a finer spatial scale than 3T fMRI. Consequently, the source of decodable information remains controversial. Here we test the proposal that information related to the stimulus edges underlies orientation decoding. We map voxel population receptive fields in V1 and evaluate orientation decoding performance as a function of stimulus location in retinotopic cortex. We find orientation is decodable from voxels whose receptive fields do not overlap with the stimulus edges, suggesting edge-related activity does not substantially drive orientation decoding.

Introduction

Orientation decoding in human visual cortex has become the test case for determining the source of decodable information in neuroimaging studies employing multivariate pattern analysis (MVPA). Although MVPA is highly influential, a significant drawback of the sensitivity of classification techniques is that the source of decodable information used by the classifier is ambiguous (Bartels et al., 2008; Op de Beeck, 2010a; Naselaris and Kay, 2015). The initial demonstrations of orientation decoding from patterns of BOLD activity in human V1 a decade ago were significant (Haynes and Rees, 2005; Kamitani and Tong, 2005), as these studies were conducted at the resolution of 3T fMRI, a coarser spatial scale than orientation hypercolumns, now known to be observable at 7T (Yacoub et al., 2008). Consequently, it was suggested that MVPA conferred hyperacuity to fMRI, allowing fine-scale orientation information to be detected at a subvoxel resolution (Boynton, 2005; Kamitani and Tong, 2005). Since then, the issue of whether hyperacuity is attainable from MVPA has inspired significant debate (Mannion et al., 2009; Op de Beeck, 2010a, b; Swisher et al., 2010; Chaimow et al., 2011; Clifford et al., 2011; Freeman et al., 2011, 2013; Alink et al., 2013; Carlson, 2014; Carlson and Wardle, 2015; Clifford and Mannion, 2015; Maloney, 2015; Pratte et al., 2016). As orientation processing in early visual cortex is well understood from neurophysiology (Hubel and Wiesel, 1963, 1972), it is the ideal domain for testing empirical approaches to elucidating the source of decodable information.

The principal alternative to the hyperacuity explanation of orientation decoding is the coarse scale map account (Freeman et al., 2011, 2013), which suggests that coarse-scale biases in orientation preference existing at the level of retinotopic maps are sufficient for orientation decoding (Furmanski and Engel, 2000; Sasaki et al., 2006). Originally, it was proposed that the coarse-scale biases primarily arose from the radial bias (Freeman et al., 2011); however, decoding of radially balanced spiral stimuli in V1 (Mannion et al., 2009; Seymour et al., 2010; Alink et al., 2013) and a reexamination of the methods used to support this claim (Pratte et al., 2016) suggest that biases in voxel responses produced by the radial bias are not necessary for orientation decoding. Importantly, Freeman et al. (2013) later demonstrated that coarse scale biases that do not arise from the radial bias support orientation decoding. Although there is substantial evidence for a role of coarse-scale biases, the question of whether there is a contribution from information at the columnar level is still actively debated (e.g., Op de Beeck, 2010a; Freeman et al., 2013; Carlson and Wardle, 2015; Pratte et al., 2016) and has recently been extended from fMRI to MEG (Cichy et al., 2015; Stokes et al., 2015; Wardle et al., 2016).

Recently, a third potential source of decodable information from fMRI was identified by modeling the responses of voxels in V1 to gratings of different orientations (Carlson, 2014). Carlson (2014) demonstrated that a “perfect cube model” based on Hubel and Wiesel's ice cube model of visual cortex (Hubel and Wiesel, 1963, 1972) produces characteristic activity at the stimulus edges. As the edge-related activity covaries with orientation, it could potentially be used by classifiers to recover stimulus orientation from patterns of BOLD activation in V1. In contrast to both the hyperacuity and coarse-scale map accounts, edge-related activity does not require an underlying biased representation of orientation at any spatial scale. The potential contribution of edge-related activity to orientation decoding has not yet been empirically tested with fMRI. Here we use population receptive field (pRF) modeling (Dumoulin and Wandell, 2008) to map decoding performance as a function of retinotopic stimulus location in V1. If edge-related activity substantially drives orientation decoding, the highest decoding performance is expected from voxels with pRFs overlapping with the stimulus edges. Further, we apply a transformation to classifier weights (Haufe et al., 2014) to evaluate whether voxels with pRFs overlapping with the stimulus edges contribute most to orientation decoding (Fig. 1C).

Figure 1.

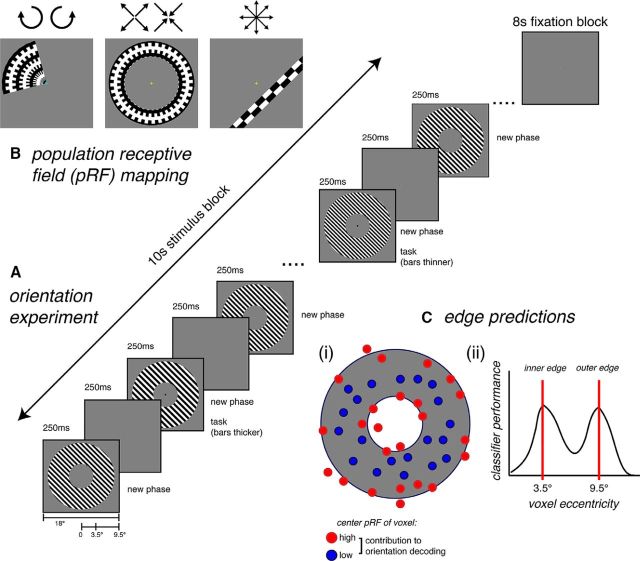
Stimuli and fMRI experimental design for (A) the orientation experiment and (B) the pRF mapping sessions. C, Predicted pattern of data if edge-related activity substantially contributes to orientation decoding. Ci, When all voxels are available for classification, voxels with pRFs located at the stimulus edges should contribute more to orientation decoding than voxels with pRFs corresponding to the middle of the stimulus. Cii, When voxels are binned by pRF eccentricity before classification, higher classification performance is expected for bins with voxel eccentricities centered near the stimulus edges (at 3.5° and 9.5°).

Materials and Methods

Subjects.

Four subjects (2 female authors: S2, S3; two naive: 1 male and 1 female) participated in two scanning sessions on separate days: one orientation experiment session and one pRF mapping session. Each subject completed 10 fMRI runs for the orientation experiment (8 experimental, 2 stimulus localizer runs) and 10–12 fMRI runs for the pRF mapping session.

MRI acquisition.

MRI data were acquired with a 3T Siemens Verio MRI scanner at Macquarie Medical Imaging, Macquarie University Hospital. A high-resolution (1 × 1 × 1 mm) T1-weighted 3D whole-brain structural MRI scan was collected for each participant at the start of each session to align the fMRI data between sessions. Functional scans were acquired with a 2D T2*-weighted EPI acquisition sequence: TR = 2.5 s; TE = 32 ms; FA = 80°; voxel size = 2 × 2 × 2 mm, in plane matrix size = 120 × 120. A partial volume containing 33 slices was collected oriented parallel to the calcarine sulcus.

Orientation experiment.

Stimulus presentation was controlled using MATLAB with functions from the Psychtoolbox (Brainard, 1997; Pelli, 1997; Kleiner et al., 2007). The stimulus was a large (19° diameter) 1 cycle/° square wave grating annulus centered on fixation (3.5°–9.5° eccentricity), presented on a mid-gray background (Fig. 1A). A sharp edge was used as this is predicted to produce the strongest magnitude of edge-related activity (Carlson, 2014). The grating was presented at six orientations (15°–165° in 30° steps) in a block design. Each 10 s stimulus block was followed by an 8 s fixation block. All six orientations were presented once in random order before repeating each in a new random sequence for a total of four times per orientation; in total, 24 blocks occurred per run.

During each block, the stimulus cycled on-off at a rate of 4 Hz, with changes in phase synchronized with each stimulus onset to avoid apparent motion artifacts (Kamitani and Tong, 2005). Within each orientation block, 20 unique phases were presented in random order for 250 ms each (Fig. 1A). Subjects fixated on a central fixation bull's-eye (0.4° diameter), and the task was to monitor the stripe thickness of the grating, which changed twice per block (similar to Kamitani and Tong, 2005). The timing of the task was signaled by the fixation bull's-eye turning black for the duration of the spatial frequency change (250 ms). In each block, the grating reduced in spatial frequency by 0.2° for one phase change and increased by 0.2° for another phase change, with the order randomized across blocks. One task trial occurred in the first 5 s of the block and the other in the last 5 s of the block, with the timing jittered across blocks to maintain attention throughout each block. On each trial, subjects responded whether the bars appeared thinner or thicker by pressing the appropriate response button (left or right).

Localizer runs consisted of four black-and-white checkerboard annuli corresponding to the entire stimulus (2.5°–10.5° eccentricity), inside edge (2.5°–4.5°), middle (5.5°–7.5°), and outside edge (8.5°–10.5°) of the annulus. Stimuli were presented in blocks of 16 s interspersed with 8 s fixation blocks after each stimulus appeared once. Subjects passively maintained central fixation during the localizer runs and did not perform a task. Data from the full-sized stimulus localizer were used to define the ROI for the stimulated region of retinotopic V1. The data collected for the other three localizer stimuli were not used. In later analyses (see Figs. 2B, 4B, 5B), ROIs corresponding to different stimulus locations [inner edge, middle (no edges), outer edge] were defined precisely by using each voxel's fitted pRF.

Figure 2.

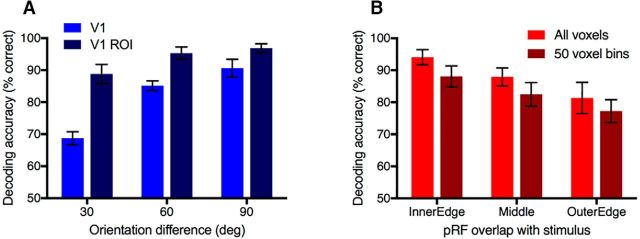
Orientation decoding accuracy, averaged across all 4 subjects and 15 orientation pairs. Chance performance is 50%. Error bars indicate between-subjects SEM. A, Decoding accuracy for V1 and the V1 ROI defined as the subset of V1 voxels responsive to the stimulus location (for voxel counts, see Table 1) used in all subsequent analyses. B, Orientation decoding as a function of the stimulus region (stimulus edges or middle of grating). Because of the cortical magnification factor, the number of voxels in each ROI falls off systematically from the inner to outer stimulus edge. To equate ROI size, 50 voxels were resampled from each ROI 100 times to compare decoding performance for equal ROI sizes (dark red bars).

Figure 4.

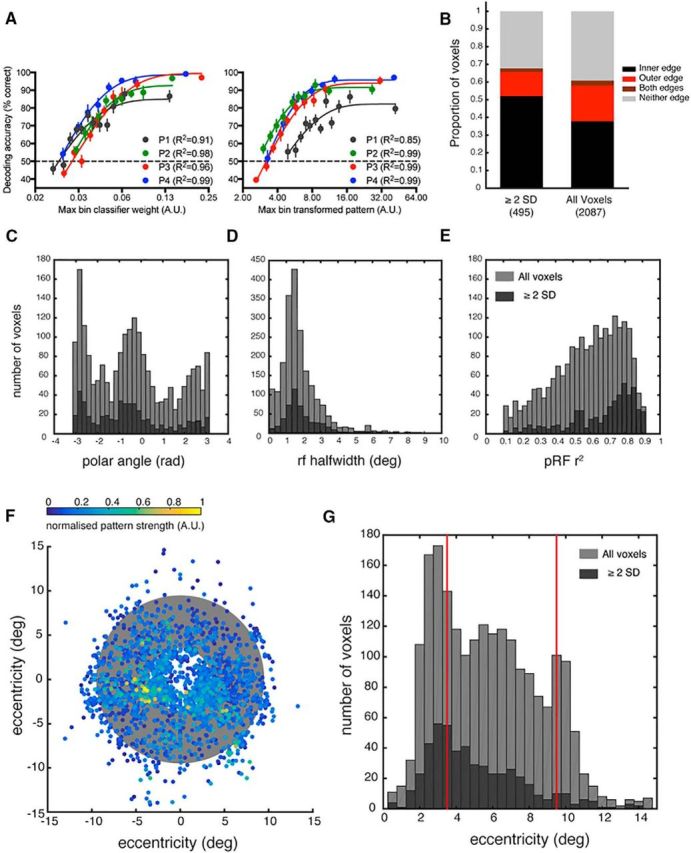
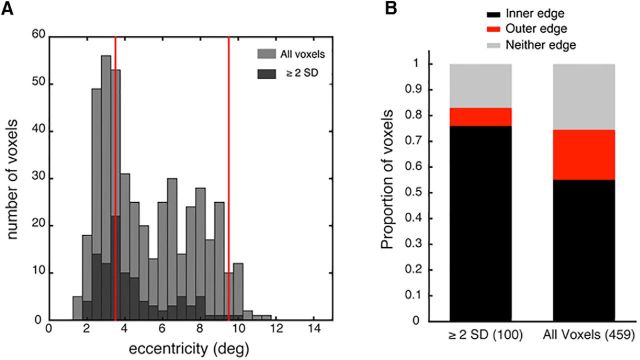
Distribution of voxels driving orientation classification performance, including all voxels from the 4 subjects. A, Decoding performance as a function of raw classifier weight (left) and transformed classifier pattern (right). Bin size = 50 voxels. Weights and patterns are derived from prior classification with all voxels. Voxels not fitting into the final (low weight) full-sized bin are discarded from the analysis. B, Proportion of voxels with pRFs overlapping with the stimulus edges, defined as a function of pRF eccentricity and half-width at half-height. Voxels with transformed patterns ≥2 SDs above the mean are classed as high performing voxels for classification. C–E, Histograms comparing the distributions of polar angle, pRF size (HWHM), or pRF goodness of fit of all voxels (light gray) versus those whose contribution to classifier performance was ≥2 SDs above the mean for at least 1 of the 15 orientation classification pairs (dark gray). F, Center of each voxel's pRF. Color represents relative contribution to classification performance across all 15 orientation classification pairs. Gray annulus indicates the stimulus location. G, Histogram comparing the distributions of eccentricity for all voxels (light gray) versus the eccentricity of voxels whose contribution to classifier performance was ≥2 SDs above the mean for at least 1 of the 15 orientation classification pairs (dark gray). Red lines indicate the stimulus edges at 3.5° and 9.5°.

Figure 5.

Distribution of voxels with population receptive fields between 1.5–2° half-width at half maximum (HWHM). All voxels in this pRF size range are included for all subjects. Voxels with transformed patterns ≥2 standard deviations above the mean are classed as high performing voxels for orientation classification. A, Histogram comparing the distributions of eccentricity for all voxels (light grey) within the selected pRF size range (1.5–2° HWHM) versus the eccentricity of voxels in this range whose contribution to classifier performance was ≥2 standard deviations above the mean for at least one of the 15 orientation classification pairs (dark grey). Red lines mark the stimulus edges at 3.5 and 9.5°. B, Proportion of voxels in the selected size range (1.5–2° HWHM) with population receptive fields overlapping with the stimulus edges, defined as a function of pRF eccentricity and half width at half height.

pRF mapping.

pRF mapping was conducted using MATLAB and MGL software (http://gru.stanford.edu/doku.php/mgl/overview) for stimulus presentation and mrTools software for pRF model fitting and analysis (http://gru.stanford.edu/doku.php/mrTools/overview). pRF mapping stimuli (Fig. 1B) consisted of clockwise rotating wedges (2 runs), counterclockwise rotating wedges (2 runs), expanding (1–2 runs) and contracting (1–2 runs) rings, and bars that swept across the visual field in 8 different directions (4 runs). All stimuli were composed from high-contrast dynamic black-and-white stimuli to stimulate early visual cortex. Observers fixated on a cyan central fixation cross while completing a 2AFC fixation task, which required judging in which of two intervals the fixation cross appeared dimmer by pressing a key on the response pad. The fixation cross turned yellow to indicate when a response was required. The brightness of the fixation cross was controlled using a staircase to maintain task difficulty across the experimental session. pRFs were fit to each voxel using the Nelder-Mead algorithm and the Gaussian-hdr pRF model as implemented in mrTools, which produces a fitted eccentricity, polar Angle, and rfHalfWidth for each individual voxel in addition to fitting the hemodynamic response function. Voxels with poor pRF fits (4%–6% ROI voxels per subject) defined as r² < 0.1, rfHalfWifth < 0, or eccentricity >15° were removed from further analysis (total of 26–35 voxels per subject; Table 1).

Table 1.

Final ROI size in voxels for each subject^a

Subject	V1 size	ROI size	Discarded voxels	Missing values
P1	1310	618	27 (4.2%)	5
P2	1567	553	35 (6.0%)	5
P3	1375	520	35 (6.3%)	3
P4	1744	412	26 (5.9%)	3

^aThe ROI used for all subsequent analyses was the intersection ROI (restricted to the voxels within V1 that correspond to the retinotopic representation of the stimulus). Additionally, a small percentage of voxels with poor pRF fits were discarded from the ROI and further analysis. Missing values are voxels that were not assigned a weight by the SVM during classification analysis and thus returned an NaN.

Preprocessing.

Minimal preprocessing was applied to the MRI data using SPM8. For each observer, fMRI data from both orientation and pRF mapping sessions were motion corrected, slice-time corrected, and coregistered to a common space (the structural scan from the pRF session for each subject). No normalization or spatial smoothing was applied, and all analyses were conducted in the native brain space of each subject.

Region of interest (ROI) definition.

V1 was defined from each observer's individual anatomy using the method described in Benson et al. (2012). First, cortical reconstruction was performed in Freesurfer 5.3 (http://surfer.nmr.mgh.harvard.edu/) from the high-resolution structural MRI for each subject. Next, the cortical surface templates from Benson et al. (2012) were registered to each subject's inflated cortical surface to define V1 from each individual subject's surface topology. Benson et al. (2012) reported that the precision of this method in defining the retinotopic organization of V1 is equivalent to a 10 min scanning session of standard phase-encoded retinotopic mapping for eccentricity and a 25 min session for polar angle. We used the template to define the boundaries of V1 and pRF mapping to precisely measure each voxel's polar angle and eccentricity within V1. The region of V1 corresponding to the retinotopic representation of the stimulus was functionally defined in mrTools by including all voxels within the borders of V1 that were significant in a stimulus>fixation contrast within a GLM (FWE-corrected, p < 0.05). This resulted in an intersection ROI that included only voxels that were both inside the boundaries of V1 and significantly activated by the functional stimulus localizer. Finally, voxels with poor pRF fits as defined above (4%–6% ROI voxels per subject) were removed from the ROI before further analysis (Table 1).

Orientation decoding.

The functional data from the orientation experiment were entered into a GLM in SPM8 with a separate regressor for each orientation per experimental run to produce separate parameter estimates for each orientation condition in each run. Fixation blocks were not included in the model but provided an implicit baseline. Decoding of orientation was performed using a linear SVM as implemented in the Decoding Toolbox (Hebart et al., 2014) with standard leave-one-run-out cross validation in a pairwise classification analysis. The classifier was trained and tested on the parameter estimates (β weights) from the GLM analysis corresponding to one estimate per run for each of the 6 orientation conditions.

Classifier weights and activation patterns.

To estimate the contribution of each individual voxel to orientation decoding, we transformed the weights into “activation patterns” using the method described by Haufe et al. (2014) and implemented in the Decoding Toolbox (Hebart et al., 2014). For N voxels, A is a vector of transformed activation patterns of length N where X is the fMRI data (N × M observations) and w is a vector of classifier weights of length N (Eq. 1) as follows:

Raw classifier weights are not directly interpretable as providing stimulus-relevant classification information because a high weight may signal either a high level of information about the stimulus, or high utility in suppressing noise for the classifier (Haufe et al., 2014). Each pairwise classification of orientation produces a weight for each voxel and a corresponding activation pattern for every iteration of leave-one-run-out cross-validation. To produce a single weight (and activation pattern) value for each voxel and orientation pair, we repeated classification without cross validation. In the subsequent analyses, voxels scoring ≥2 SDs above the mean (absolute value) in the transformed “activation pattern” for at least 1 of the 15 orientation pairs were considered to be high performing voxels in their contribution to orientation decoding. For each voxel, the activation patterns and raw classifier weights were linked to the pRF fits using custom-made scripts.

Results

Orientation decoding as a function of stimulus location

First, we confirmed that stimulus orientation could be decoded from V1 (Fig. 2A). Overall orientation classification performance was high across subjects. Classifier accuracy appears higher for the ROI constructed from a subset of retinotopic voxels in V1 (V1 ROI) than when all voxels in V1 were available for classification, even though the V1 ROI only contained approximately one-third of all V1 voxels (Table 1). As one ROI (V1 ROI) is a subset of the other (V1), the data were not independent and were analyzed in a separate repeated-measures ANOVA for each ROI as a function of orientation difference. For both ROIs, there was a significant main effect of orientation difference on classification performance (V1: F_(2,6) = 20.116, p < 0.01; V1 ROI: F_(2,6) = 12.873, p < 0.01). Significant linear trends indicate that decoding accuracy increased as a function of orientation difference (V1: F_(1,3) = 20.835, p < 0.05; V1 ROI: F_(1,3) = 11.864, p < 0.05). These results replicate previous observations of an increase in classifier accuracy in V1 with increasing orientation difference (Kamitani and Tong, 2005) and also the predictions of the ice cube model (Carlson, 2014). All subsequent analyses use the V1 ROI.

To examine whether orientation decoding differed between voxels corresponding to the stimulus edges or the middle of the grating, we classified each voxel's receptive field as overlapping with the inner or outer edge, or the middle of the stimulus, based on their fitted pRFs. Voxels not fitting into one of these categories were discarded from this analysis. We constructed new ROIs from these groups to examine decoding performance as a function of stimulus location (Fig. 2B). Data are analyzed in a repeated-measures ANOVA. Orientation decoding was high across the stimulus; however, classifier performance decreased with increasing distance from the fovea (inner edge), and there was a main effect of pRF location (F_(2,6) = 16.161, p < 0.01). Because of cortical magnification, ROIs corresponding to the inner edge (nearer the fovea) contained more voxels than ROIs corresponding to the outer edge (by a factor of 1.2–2.3 across subjects). To equate ROI size, we created new ROIs for each category and subject by resampling voxels in 50 voxel bins 100 times (with replacement across permutations) and performing the decoding analysis on the resampled bins. Classifier performance was lower for the resampled 50 voxel ROIs than when all voxels in each group were used. However, the significant main effect of pRF location remained (F_(2,6) = 57.153, p < 0.001) and decoding decreased with increasing distance from the inner edge, demonstrating that this effect is robust to ROI size.

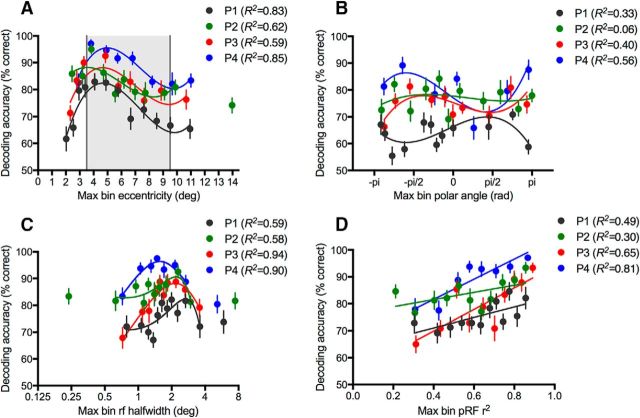
To further examine the relationship between decoding performance and stimulus location, we systematically created multiple new ROIs by binning voxels according to the fitted pRF parameters of eccentricity (Fig. 3A), polar angle (Fig. 3B), and pRF size (Fig. 3C). There is a consistent relationship between decoding accuracy and voxel eccentricity across all subjects; performance increases toward the inner stimulus edge and falls off around the middle of the stimulus at ∼6° eccentricity (Fig. 3A). Importantly, decoding performance does not rise again to coincide with the outer edge of the stimulus, as would be expected if edge-related activity (Carlson, 2014) had a significant impact on decoding performance (compare Fig. 1C). In contrast to eccentricity, systematic variation in decoding performance is not observed as a function of polar angle (Fig. 3B). For consistency, we fitted a cubic polynomial to the data for polar angle (as for eccentricity and pRF size); however, in this case, the fits are generally poor. Decoding peaks for pRF sizes ∼1.5°–2° half-width at half-maximum (HWHM), which is likely to relate to the 1 c/° spatial frequency of the stimulus. Voxel preference for spatial frequency varies as a function of eccentricity (Tootell et al., 1998), and as receptive field size increases with eccentricity (Smith et al., 2001), it is likely that the receptive field size of a voxel is related to its spatial frequency preference.

Figure 3.

Decoding tuning curves. Orientation decoding by binned pRF values (bin size = 50 voxels); individual data shown for all four subjects. x-axis indicates the maximum value of each parameter per bin. Leftover ROI voxels not fitting into the highest 50 voxel bin are discarded from this analysis. Chance classification performance is 50%. Decoding accuracy is shown as a function of voxel population receptive field parameters. A, Eccentricity. Shaded region represents stimulus area. B, Polar angle. C, Receptive field size (half-width at half-height). D, Goodness of fit for the pRF Gaussian-hdr model. Best fitting cubic polynomials (A–C) and straight lines (D) are plotted, fitted to the individual data with weighted least-squares. Individual outlier bins with maximum eccentricities exceeding 13° (A) or pRF sizes outside the range 0.5°–4° HWHM (C) are discarded from the curve fitting. Error bars indicate within-subjects SEM of decoding performance across the 15 unique orientation pairs for each 50 voxel bin.

In addition to binning by the fitted pRF parameters, we examined the relationship between decoding performance and goodness-of fit (r²) for the pRF model (Fig. 3D). Decoding accuracy was high even for bins with the lowest values of r², confirming that our inclusion of only voxels with pRF fits reaching above r² = 0.1 was an appropriate cutoff for the analysis. The strong relationship between decoding accuracy and pRF goodness of fit is notable as the data for pRF fitting and orientation decoding were collected on separate days. A likely explanation for the relationship between decoding performance and goodness of fit is simply that voxels with higher functional signal-to-noise will tend to have both better pRF fits and more stimulus-related information. Alternatively, it is possible that voxels with poorer pRF fits are broadly tuned both for spatial location and the visual features of the dynamic checkerboard stimuli used in the pRF mapping sessions. If this is the case, a voxel with low selectivity to these spatial properties is also likely to have low orientation specificity, which may explain the positive relationship between goodness of fit of the pRF model and orientation decoding performance.

pRF distribution of high performing voxels

Decoding performance as a function of voxel eccentricity suggests that voxels with pRFs overlapping with the stimulus closer to the fovea perform better in orientation decoding than more peripheral voxels, regardless of whether these voxels overlap with the stimulus edges (Fig. 2A). To assess the relative contribution of voxels to classification of the orientation of a large grating stimulus when all voxels are available, we used the method of Haufe et al. (2014) to transform the classifier weights into interpretable activation patterns and examine the pRF distribution of voxels that disproportionately drive classification.

First, to evaluate the relationship between the transformed patterns and decoding performance, we compared decoding performance as a function of raw classifier weight and transformed activation pattern (Fig. 4A). Weights were obtained by using all voxels for classification; voxels were then rebinned in sets of 50 voxels according to their weight to assess the relationship with decoding performance. As expected, classifier accuracy increased systematically with increases in binned classifier weight, confirming that voxels assigned a high raw weight in SVM classification with a full set of voxels performed well in decoding when only a much smaller subset of voxels were available. Decoding performance increased exponentially with increasing raw classifier weight (all R² > 0.91). Critically, the relationship between voxel weights prescribed by the classifier and decoding performance held when these weights were transformed into activation patterns (Haufe et al., 2014) and the voxels were rebinned, confirming that the activation patterns relate to classifier performance as strongly as the raw weights (Fig. 4B). The majority of voxels in each ordered bin were different after transforming the weights into activation patterns (76%–100% across subjects and binned ROIs), demonstrating that the transformation substantially changed which voxels were assigned a high weight. These results justify the use of transformed activation patterns as an estimate of voxel's contribution to classification performance.

Next, we identified the high performing voxels, defined as those with a transformed pattern (absolute value) ≥ 2 SD above the mean on at least 1 of 15 orientation classifications. A clear prediction from the edge model of orientation decoding is that high performing voxels will be clustered around the stimulus edges (Fig. 1C). We observed that high performing voxels were disproportionately more likely to have pRFs overlapping with the inner edge and less likely to overlap with the outer edge, compared with the entire voxel pRF distribution (Fig. 4B). Regardless of pRF size, high performing voxels were more likely to have an eccentricity preference near the inner edge than the outer edge. Examination of the eccentricity distributions (Fig. 4G) suggests that high performing voxels are a random subset of the overall voxel distribution. The second peak in the voxel distribution ∼10° is likely due to a small proportion of erroneous pRF fits corresponding to the screen edge as fits are less accurate for voxels with receptive fields near the border of the stimulated area (Lee et al., 2013). However, this second peak is not present in the high performing voxel distribution, inconsistent with the predictions of the edge model of orientation decoding. The center of each voxel's receptive field is plotted in Figure 4F, weighted by its contribution to all 15 pairwise orientation classifications. Highly weighted voxels tend to be clustered near the inner (but not outer) edge of the stimulus.

As decoding performance varied as a function of pRF size (Fig. 3C) and receptive field size in V1 is known to increase with eccentricity (Gattass et al., 1987; Smith et al., 2001; Dumoulin and Wandell, 2008), we repeated the analysis of high performing voxels while holding receptive field size constant. We selected voxels with pRF sizes between 1.5° and 2° HWHM (459 of 2087 voxels) as this size range corresponded to higher decoding performance when voxels were binned by pRF size (Fig. 3C) and is within the peak of the pRF size distribution of all voxels (Fig. 4D). We repeated the classification analysis with this subset of voxels of the same pRF size, obtaining a new weight and transformed pattern (Haufe et al., 2014) for each voxel. Consistent with the full analysis, we found that, when pRF size was held constant, highly weighted voxels tended to have eccentricities corresponding to the inner edge and area of the stimulus nearest the fovea (Fig. 5A) and pRFs that overlapped with the inner edge (Fig. 5B). This suggests that it is proximity to the fovea or inner edge of the annulus that is important, rather than pRF size.

Although the above analysis suggests that pRF size does not account for the observed relationship between eccentricity and decoding performance, it is difficult to account for all possible effects of cortical magnification in these analyses. We used a resampling approach to equate the number of voxels in ROIs regardless of their eccentricity (Fig. 2B). This analysis showed that the higher performance of the classifier for voxels corresponding to the inner edge (rather than middle or outer edge) is robust, even when ROI size is equated in the number of voxels. However, each voxel has a cortical magnification factor and voxels closer to the occipital pole (i.e., more foveal) will contain more detailed spatial information than more anterior voxels. Our finding across repeated analyses that voxels nearer the fovea have higher decoding performance is consistent with some contribution from cortical magnification.

In summary, neither the observed relationship between decoding with eccentricity (Fig. 3A) nor the pRF distribution of highly performing voxels (Fig. 4B–D) is wholly consistent with our predictions based on the edge model (Fig. 1C). We expected two peaks in decoding performance, corresponding to each stimulus edge. Instead, voxels that overlap with the stimulus closer to the fovea appear to drive classification disproportionately more than voxels with more peripheral pRFs. Notably, decoding performance is still superior for voxels nearer the fovea and inner regions of the stimulus when ROI size (Fig. 3A) and pRF size (Fig. 5) are equated. Although the strong performance of inner edge voxels is partially consistent with a contribution from edge-related activity, cortical magnification appears to contribute more strongly to decoding performance as there is no corresponding peak in performance associated with the outer stimulus edge. Further, decoding of orientation is possible across the visual field, even in regions of the stimulus where the voxel pRFs do not contain either stimulus edge (Fig. 2B). As we did not find the predicted relationship between voxel eccentricity and contribution to orientation classification, we also checked the relationship between high performing voxels and their polar angle (Fig. 4C), pRF size (Fig. 4D), and goodness of fit for the pRF model (Fig. 4E). Overall, the distribution of high performing voxels appears consistent with a random selection of voxels from the entire distribution of available voxels, with no obvious bias in the location or properties of their pRFs. However, when only some voxels are available for classification, clear differences in decoding performance emerge as a function of eccentricity (Fig. 3A), pRF size (Fig. 3C), and pRF goodness of fit (Fig. 3D). There was also evidence for higher decoding performance for voxels overlapping with the inner edge (Fig. 2B), and inner edge voxels tend to contribute disproportionately to classification when all voxels are available (Fig. 4B).

Discussion

Recent modeling of voxel responses in V1 identified a new possible source of decodable information localized to the stimulus edges that was suggested to contribute to orientation decoding (Carlson, 2014). Here we applied pRF mapping to test two straightforward predictions of the edge model of orientation decoding. First, we examined orientation decoding as a function of stimulus location by grouping voxels as a function of their pRF parameters. We found that orientation was decodable from voxels with receptive fields overlapping with any region of a large grating stimulus, even if they did not overlap with the edges. Voxels with eccentricities closer to the fovea or inner edge of the stimulus tended to have higher decoding accuracies; however, there was not a similar increase in performance for voxels corresponding to the more peripheral outer stimulus edge as predicted if edge-related activity substantially drives orientation decoding. Second, when all voxels were available for decoding, voxels with pRFs corresponding to more foveal regions of the stimulus tended to have higher transformed patterns (Haufe et al., 2014) than peripheral voxels, indicative of a stronger contribution to decoding performance. However, voxels with a strong contribution to decoding performance did not cluster at the stimulus edges, as would be predicted if edge-related activity was a dominant factor in orientation decoding. Overall, orientation decoding was significant across all regions of the stimulus and was not mediated by the presence of an edge.

Although our data show clearly that edge-related activity (Carlson, 2014) is not necessary for orientation decoding, we are unable to evaluate the more challenging question of whether edge-related activity is sufficient for orientation decoding. The high performance of voxels corresponding to the inner edge is consistent with a contribution from both cortical magnification and edge-related activity. However, the contribution from cortical magnification is much stronger than any contribution from edge-related activity, as the falloff in decoding performance tracks the falloff in cortical magnification with eccentricity and there is no second rise in decoding at the outer stimulus edge. As the edge model (Carlson, 2014) does not include cortical magnification, it is unclear how the two factors would interact. Inner edge voxels remained the strongest classifiers of orientation, even after accounting for differences in ROI size and pRF size as a function of eccentricity. It is not possible to empirically isolate edge-related activity from other potential sources of decodable information as even at the stimulus edges, multiple sources of potential decodable information may be present. Thus, we cannot rule out the possibility here that edge-related activity may contribute to orientation decoding. Nevertheless, it is clear that edge-related activity is not required to explain previous reports of orientation decoding (Haynes and Reese, 2005; Kamitani and Tong, 2005) as our data show that orientation decoding is possible across a large annular grating, even from voxels that do not overlap with the stimulus edges.

The observation that orientation is decodable from voxels whose pRFs exclude the stimulus edges is consistent with more subtle findings in the literature. Notably, Kamitani and Tong (2005) used a stimulus localizer that was smaller than the oriented gratings, excluding 0.5° from the inner edge and 1° from the outer edge. Although this method would not reliably exclude all voxels overlapping with the stimulus edges to the same degree as pRF mapping, their finding of orientation decoding with this localizer is consistent with our result of significant orientation decoding for voxels with receptive fields overlapping with the middle of the stimulus. Additionally, orientation maps in V1 for annular gratings with blurred edges are consistent with the maps observed for gratings with visible edges (Freeman et al., 2011), suggesting that activity related to the stimulus edges does not modulate the orientation-related responses in V1 detectable with fMRI. Further, orientation information is observed across retinotopic cortex (Pratte et al., 2016), rather than localized at regions of cortex representing eccentricities corresponding to the stimulus edges. Together with our systematic mapping of decodability across the visual field, these data suggest that edge-related activity is not solely driving orientation decoding from patterns of BOLD activation in human visual cortex.

A consistent feature of our results is that decoding performance is stronger for voxels closer to the fovea than for more peripheral voxels, even when differences in voxel numbers due to cortical magnification are accounted for. There are several possible reasons for this. It may be that these voxels have better signal because the central area of the visual field has higher acuity than the periphery. Alternatively, there may be an effect of attention differentially modulating the response of voxels based on their visual field location. Although the stimulus was a large annular grating, subjects maintained central fixation in the middle of the annulus while completing a task judging small changes in stripe thickness of the grating. We selected this task because it seemed easier to perform while maintaining central fixation and attending to the whole grating; however, it is possible that subjects were attending more to the part of the stimulus located near fixation than peripheral regions. Attention has a strong modulatory effect on the BOLD response in V1 (Brefczynski and DeYoe, 1999; Gandhi et al., 1999; Somers et al., 1999); thus, if observers distributed attention unevenly across the stimulus, this may be reflected in differences in signal and hence decodability as a function of voxel eccentricity (Jehee et al., 2011). However, all orientation decoding experiments would be susceptible to similar subtle biases in spatial attention, and we based our stimulus, design, and task closely on previous studies (Kamitani and Tong, 2005; Freeman et al., 2011, 2013).

Overall, our analysis using the method of Haufe et al. (2014) to transform classifier weights into interpretable activation patterns suggests a high degree of randomness in the retinotopic location of voxels driving orientation classification of a large annular grating. Similarly, Seymour et al. (2010) found that highly weighted voxels for decoding the orientation, color, and conjunction of color and orientation for spiral gratings were randomly distributed across retinotopic cortex, without any clear clustering based on corresponding visual field location. Although these were untransformed classifier weights before the methodological development introduced by Haufe et al. (2014), and some highly weighted voxels would reflect utility in suppressing noise rather than information about the stimulus classes, their result is consistent with ours using different methods. We found that, when all voxels were available for classification, highly weighted voxels defined using the weight transformation of Haufe et al. (2014) had pRF properties generally consistent with a random subset of the overall pRF distribution, although there was a bias for voxels with pRFs overlapping with the inner stimulus edge. Importantly, we confirmed that the bias for inner edge voxels to be highly weighted remained after controlling for pRF size. These results may be a consequence of voxels with pRFs overlapping with the most foveal portion of the stimulus having better signal-to-noise (whether from better acuity nearer the fovea, effects of attention, or both), which introduces a slight bias into the otherwise randomly distributed selection of voxels that contribute most to orientation classification.

Although our data do not directly inform the ongoing controversy about whether MVPA confers hyperacuity in both fMRI (Kamitani and Tong, 2005; compare Op de Beeck, 2010a) and MEG (Cichy et al., 2015; Stokes et al., 2015; compare Wardle et al., 2016), they do emphasize the difficulty of empirically excluding potential sources of decodable information. Modeling approaches that consider MR-specific factors such as aliasing and the effect of draining veins on the feasibility of decoding from the columnar level offer a valuable complement to experimental methods (e.g., Chaimow et al., 2011). Our results show that edge-related activity is not necessary for orientation decoding; however, it remains an open question whether edge-related activity contributes to orientation decoding. Similarly, it is challenging to provide positive empirical evidence for hyperacuity. Instead, evidence in favor of hyperacuity is sometimes concluded on the basis of ruling out other potential sources of decodable information (Kamitani and Tong, 2005; Cichy et al., 2015; Stokes et al., 2015). However, hyperacuity cannot serve as a “null hypothesis” when attempting to identify sources of decodable information as it is empirically challenging to isolate any particular source of decodable information. To date, the controversy over the source of information underlying orientation decoding in V1 has produced a rich debate highlighting the challenges of interpreting MVPA results in neuroscience. The exquisite sensitivity of MVPA analysis is accompanied by substantial obstacles in interpretation which require careful consideration if neuroscience is to continue to benefit from the application of these powerful methods (Bartels et al., 2008; de-Wit et al., 2016; Ritchie et al., 2017).