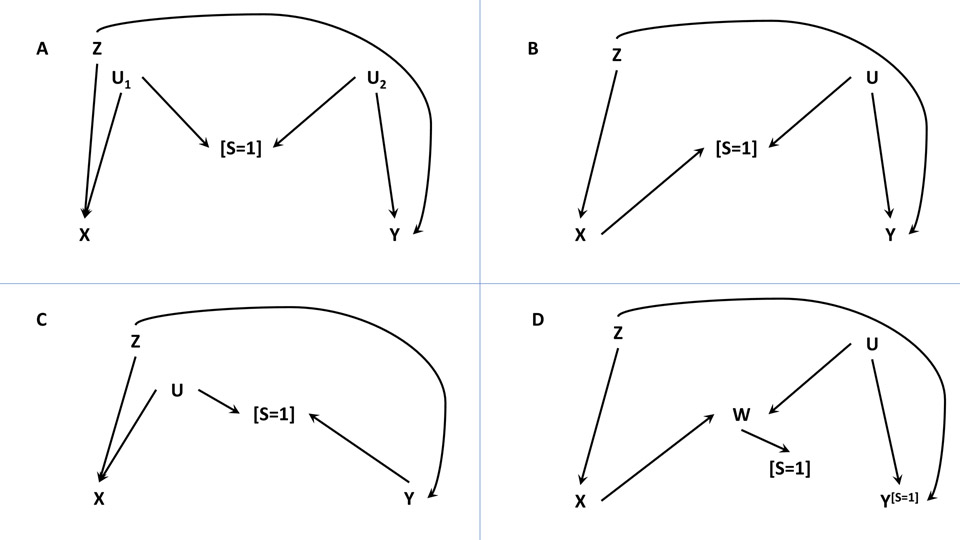
FIGURE 1:
Directed acyclic graphs (DAGs) depicting typical causal scenarios where selection bias can potentially occur (DAGs A-C in particular). X represents the exposure, Y the outcome, Z the measured confounder(s), S the selection (where S = 1 means selected into the study sample), U the unmeasured covariate(s) or confounder(s), and W is a consequence of X that is associated with Y. In all DAGs, X does not cause Y, but they will become non-causally associated if selecting on S = 1. In DAGs A to C, Y is not independent of S conditional on measured variables X and Z; in DAG D, Y is independent of S given X, Z and W. (A) This DAG denotes a selection bias structure, called the M-bias, due to two open backdoors between the selection node S and exposure X and the outcome Y; conditioning on the collider S opens up the path X←U1→[S=1]←U2→Y leading to a type of collider-stratification bias commonly referred to as M-bias. (B) This DAG looks like that in A except X causes S here; conditioning on the collider S opens up the path X→[S=1]←U→Y. (C) Again, this DAG resembles the one in A except Y causes S here; conditioning on the collider S opens up the path X←U→[S=1]←Y leading to selection bias in the effect of X on Y. (D) This DAG is the same as the one in B except W replaces S as the collider between X and Y in the path X→W←U→Y, and W causes S; conditioning on S would appear to induce selection bias between X and Y in the path X→[W]←U→Y because conditioning on the consequence of a collider also leads to collider-stratification bias; nonetheless, the effect of X on Y can still be estimated without selection bias if all variables except Y are fully observed prior to selection and Y is only observed among S=1 (hence, the Y[S=1] notation).