Optimization and Evaluation of the Site-Identification by Ligand Competitive Saturation (SILCS) as a Tool for Target-Based Ligand Optimization.

Abstract

Chemical fragment cosolvent sampling techniques have become a versatile tool in ligand-protein binding prediction. Site-Identification by Ligand Competitive Saturation (SILCS) is one such method that maps the distribution of chemical fragments on a protein as free energy fields called FragMaps. Ligands are then simulated via Monte Carlo techniques in the field of the FragMaps (SILCS-MC) to predict their binding conformations and relative affinities for the target protein. Application of SILCS-MC using a number of different scoring schemes and MC sampling protocols against multiple protein targets was undertaken to evaluate and optimize the predictive capability of the method. Seven protein targets and 551 ligands with broad chemical variability were used to evaluate and optimize the model to maximize Pearson’s correlation coefficient, Pearlman’s Predictive Index, correct relative binding affinity and root mean square error versus the absolute experimental binding affinities. Across the protein-ligand sets, the relative affinities of the ligands were predicted correctly an average of 69 % of the time for the highest overall SILCS protocol. Training the FragMap weighting factors using a Bayesian machine learning (ML) algorithm led to an increase to an average 75 % relative correct affinity predictions. Furthermore, once the optimal protocol is identified for a specific protein-ligand system average predictabilities of 76 % are achieved. The ML algorithm is successful with small training sets of data (30 or more compounds) due to the use of physically correct FragMap weights as priors. Notably, the 76 % correct relative prediction rate is similar to or better than free energy perturbation methods that are significantly computationally more expensive than SILCS. The results further support the utility of SILCS as a powerful and computationally accessible tool to support lead optimization and development in drug discovery.

Graphical Abstract

Introduction

The goal of computer-aided drug design (CADD) is to facilitate design both qualitatively and quantitatively. Qualitative design involves visual inspection while quantitative efforts include predicting the binding pose of small molecules on a protein or other target along with their associated absolute or relative binding affinities. The range of approaches used in quantitative CADD is quite large, including simple estimates of the interaction energy, the linear interaction energy approach,¹ continuum solvation models such as Poisson Boltzmann and Generalized Born² and Free Energy Perturbation methods.^{3, 4}

A more recent class of CADD approaches are the cosolvent simulation methods.^5–9 In this approach the target macromolecule is simulated in an aqueous environment that includes a probe molecule, referred to as the cosolvent, that is representative of common functional group types. Binding sites for the functional groups on the macromolecule are identified as zones that the probe molecule occupies with a high probability in the simulation. Observing the occupancy of probe molecules near a protein, relative to bulk conditions, provides information about the affinity between the probe molecules and the protein sites. Because the probe molecules must compete with water for occupancy of the space, the occupancy pattern of the probe molecules contains desolvation contributions as well as information on interactions of the functional group with the target macromolecule.

SILCS is a cosolvent sampling method that simultaneously includes multiple probe molecules in the simulation system along with water, thereby allowing for information on the binding pattern of a range of functional groups with the target to be determined.^{8, 10–13} Functional group probability distributions obtained from the SILCS calculations are normalized for the concentration of the group in bulk solution and the normalized probabilities of the probe atoms converted into free energy binding maps (FragMaps) through a Boltzmann inversion of the probabilities. The resulting FragMaps are of utility for both qualitative and quantitative CADD. Visualization of the FragMaps reveals both favorable and unfavorable regions for the different functional groups allowing for determination of regions where modifications of ligands can lead to improved affinity or where small molecules may bind as in fragment-based drug design. Quantitatively, the FragMaps may be used for rapid posing in the field of the FragMaps along with estimation of ligand binding affinities, as described below.

While the original SILCS approach was based on molecular dynamics (MD) simulations,¹⁰ this was found to be limiting in the context of macromolecules with deep or totally occluded pockets as well as regions were charged functional groups bind favorably.¹⁴ To overcome this, Grand-Canonical (GC) simulation methods ^{15, 16, 17–19} were extended to a hybrid oscillating μ_ex Grand Canonical Monte Carlo-Molecular Dynamics (GCMC-MD) approach ¹⁴ that was shown to enhance sampling of ions and probe molecules around macromolecules.^{12, 20} Oscillating μ_ex GCMC improves the sampling of the probe molecules throughout the system by inserting and deleting probe molecules and water in the simulation system as well as applying translations, rotations, and torsional rotations. The inclusion of MD allows for additional conformational sampling of the probe molecules and water and, importantly, incorporates protein flexibility into the sampling regimen, thereby allowing the probe molecules and water to sample regions “under” the traditional solvent accessible surface ²¹ of the protein or target macromolecule. Calculation of the SILCS FragMaps using this approach is computationally demanding, typically requiring that the SILCS GCMC-MD simulations involve an iterative GCMC-MD approach of 10 × 100 ns of MD (see below). However, once completed and the SILCS FragMaps generated, they are of utility for a variety of analyses and calculations including pharmacophore screening,^{22, 23} ligand docking,^{8, 11, 13} database screening,¹² identification of cryptic or occluded ligand binding sites,¹² including allosteric binding sites,^{24, 25}, for determination of protein-protein interactions²⁶ as well as lead compound optimization.^25–29

In this study, we focus on the use of SILCS for the quantitative prediction of ligand binding poses and relative binding affinities in the context of lead compound optimization. MC techniques have been used in the past for CADD, where the interactions between the target protein and ligand are directly calculated.^30–33 When used in conjunction with the SILCS FragMaps, MC sampling of the ligand conformation and orientation is done in the field of the maps, referred to as SILCS-MC. Thus, in SILCS-MC the ligand explores its conformational space on the free energy surface defined by the precomputed FragMaps along with the SILCS exclusion map, which represents the forbidden region of the protein not sampled by the probe molecules or water non-hydrogen atoms during the SILCS GCMC-MD simulation. The combination of the SILCS FragMaps and exclusion map yields a 3D representation of the target protein that accounts for the interaction free energy of functional group-protein interactions, protein flexibility, and both protein and functional-group desolvation contributions. As the SILCS FragMaps and exclusion map are precomputed, SILCS-MC is computationally inexpensive allowing for larger numbers of ligands to be posed and energetically evaluated, a process that includes many independent cycles of SILCS-MC for each ligand to identify a minimum free energy binding pose and estimate its binding affinity (see below).

When performing SILCS-MC, along with the intramolecular energy, poses are modulated by the overlap of atoms in the ligand with the SILCS FragMaps and penalized by overlap of the ligand atoms with exclusion maps. Accordingly, it is necessary to map the atoms in each ligand to a corresponding FragMap, while the overlap of any atom with the exclusion map yields a large unfavorable energy penalty. The overlap of an atom with a specific FragMap allows for the assignment of a free energy score to each atom in the ligand, termed the grid free energy (GFE).¹³ The sum of the atomic GFE scores, which may include contributions from the SILCS exclusion map, yields the Ligand GFE (LGFE) that is the basis of the Metropolis criteria in the MC sampling. The assignment of the atoms to FragMaps is based on an atom classification scheme (ACS) as described below.

The present study investigates the impact of the ACS as well as variations in the MC sampling approach on the ability to predict the relative and absolute affinities in the context of ligand optimization. This included the utility of the inclusion of SILCS FragMaps on halogenated functional groups on ligand posing and scoring. Seven protein targets from eight sets of ligand-protein complexes that includes 551 ligands served as a rich experimental data pool of diverse targets and ligands for the study. The data sets were selected based on the availability of a sufficient number of ligand-protein crystal structures to allow for initial placement of the ligands in the ligand binding pocket (LBP) and we note that in all cases all the ligands presented in each original study were used. The results indicate an ACS and SILCS-MC sampling protocol that yields the best overall agreement with the experimental data for all the data sets while simultaneously showing that the optimal protocol is system dependent. In addition, the SILCS FragMap method is extended by applying a Bayesian Markov-Chain Monte Carlo machine learning (ML) method that allows for reweighting of the FragMaps leading to improved predictability of the method once a small training set of ligands is available. The results are encouraging because the final correct relative affinity score across eight sets of ligands is 76 %. This value is comparable to more expensive FEP methods which scored 78% on average using enhanced sampling³⁴ and 70% on average without enhanced sampling and with an alternate different force field.³⁵ Furthermore, in those studies, across eight sets of ligands 173 out of 372 ligands were removed without explanation versus the inclusion of all ligands from the experimental studies included in the present work.

Methods

SILCS simulations, FragMap generation and SILCS-MC calculations were performed using the MolCal program (SilcsBio, LLC).^{8, 11} GCMC calculations were performed using code developed in-house¹⁴ and MD calculations were performed in GROMACS 2018.1.³⁶ The empirical force field for the proteins was the additive CHARMM36 model ^{37, 38} and the probe and ligand molecules were generated and the parameters assigned using the CHARMM General Force Field (CGenFF) and the CGenFF program,^39–41 including the updated halogen parameters.⁴² The CHARMM TIP3P model was used for water.^{43, 44} The simulation box size extended 15 Å beyond the proteins and was defined by periodic boundary conditions. GCMC simulations used a cutoff distance of 12 Å with non-bond lists updated every 1,000 MC steps. For the MD simulations all covalent bonds with hydrogen atoms were constrained using the LINCS algorithm ⁴⁵ with an integration time step of 2 fs. Long-range electrostatic interactions were handled with the particle-mesh Ewald method⁴⁶ with a real space cutoff of 8 Å, maximum grid spacing κ = 0.12 nm with a 4th-order spline. A force-switching function⁴⁷ was applied to the Lennard-Jones interactions from 5 to 8 Å, and isotropic long-range dispersion corrections⁴⁸ were applied to the energy and pressure for Lennard-Jones interactions beyond the 8 Å cutoff length.

The SILCS GCMC-MD protocol is a loop of 200,000 GCMC steps followed by 1 ns of MD simulation cycles that allow water and probe (or solute) molecules to access the environment around the protein including regions under the protein solvent accessible surface.¹² Ten independent instances, J, of the protocol are run to obtain converged SILCS FragMaps. Variations in the protocol have been introduced in this study as described below. Determination of convergence of the FragMaps is performed by calculating the overlap of the FragMaps based on instances J = 1–5 and 6–10. In the present study, the overlap coefficients were at minimum 0.74 or higher, indicating satisfactory convergence of the FragMaps on all the studied systems.

SILCS GCMC-MD simulations were initiated from the X-ray crystal structures listed below with all non-protein ligands, cofactors, and waters removed. In addition to the previously published protocol, the side chain conformations of solvent accessible residues were varied prior to initiation of the 10 SILCS simulations. Solvent accessible surface area (SASA) of each sidechain is calculated using the GROMACS utility gmx sasa.⁴⁹ Residues with SASA greater than 0.005 nm² are identified as solvent accessible. For each of the 10 simulations, the χ₁ dihedral for each of these solvent accessible residues is rotated in 36 degrees increments. For example, for simulation 1, χ₁ of the residue is set to 0°, in simulation 2 χ₁ is set to 36°, in simulation 3 χ₁ is set to 72° and so on. This process is repeated for all the solvent accessible residues thereby enabling exploration of greater conformational space than otherwise when initiating all the 10 simulations with the same crystallographic starting conformation as performed previously.²² While setting χ₁ to the above values may lead to steric clashes of side chains with neighboring residues, subsequent minimization and equilibration (described below) relaxes the steric clashes yielding reasonable, diverse starting conformations thereby facilitating sampling during the SILCS simulation. See Figure S1 in the Supporting Information for an example of side chain starting configurations using LYS 238 on the protein MCL1.

The ten protein starting conformations are then solvated by water at 55 M and the probe molecules at an approximate concentration of 0.25 M. Each of these solvated systems are minimized using the steepest descent (SD) algorithm for 5,000 steps. These minimized systems are then equilibrated in GROMACS using MD for 100 ps to 298 K using the velocity rescaling thermostat and Berendsen barostat⁵⁰ to allow for initial relaxation of the system volume. The seed used for velocity assignment is randomized across the ten runs. Each of these equilibrated systems are then subjected to 25 X 200,000 step GCMC cycles to redistribute the water and probe solutes in the presence of the protein targeting concentrations of 55 and 0.25 M for the water and probes, respectively. This process involves initially deleting all water and solute molecules in a rectangular subvolume (see following paragraph) with that region refilled during the subsequent 25 X 200,000 step GCMC cycles. The final atomic coordinates of each cycle served as the initial coordinates of a subsequent cycle following adjustment of the excess chemical potential, μ_ex, of the probe molecules.¹⁴ A production run of 100 cycles of GCMC/MD follows. In each of these cycles, after 200,000 GCMC steps, a 5,000 step SD minimization and a 100 ps MD equilibration is performed. This is followed by 1 ns of production MD with Cα protein atoms restrained with a harmonic restraint of 0.12 kcal/mol/Ų. While not addressed in the present study, specific cases, such as in a target with a segment of a loop in the binding site, may benefit from lower or no restraint forces on selected Cα atoms. MD was performed in the NPT ensemble with Nosé-Hoover temperature control^{51, 52} and Parinello-Rahman pressure control.⁵³ The timestep was 2 fs and atomic positions of all atoms were saved every 10 ps.

The GCMC portion of each GCMC/MD cycles involves 200,000 attempted moves. The possible moves include insertions, deletions, translations, rotations, and dihedral rotations. In GCMC the probe molecules and water are exchanged between a gas phase reservoir and an active subvolume of the simulation system. The active subvolume is the rectangular volume that contains the protein that is defined by a 15 Å margin between edges of the full simulation system and the active GCMC subvolume. Insertions and deletions in the subvolume were driven by the excess chemical potential μ_ex. The μ_ex was adjusted every 3 cycles in response to the probe concentration in the subvolume.¹⁴ The probabilities of these moves as governed by the Metropolis criteria ⁵⁴ are

$$\begin{gathered} {\text{P}}_{\text{insert}}=\min \left(1,{\text{f}}_{\text{n}}/\left(\text{n}+1\right)\exp \left(\text{B}-\beta \mathrm{\Delta }\text{E}\right)\right) \\ {\text{P}}_{\text{delete}}=\min \left(1,\text{n/}\left({\text{f}}_{\text{n}-1}\right)\exp \left(\text{B}-\beta \mathrm{\Delta }\text{E}\right)\right) \\ {\text{P}}_{\text{trans/rot/dihed}}=\min \left(1,\exp \left(\beta \mathrm{\Delta }\text{E}\right)\right) \end{gathered}$$ Eq. 1

where $B=\beta {\mu }_{\text{ex}}+\ln \overline{n},\overline{n}=\overline{\rho v}$, μ_ex is the excess chemical potential, $\overline{n}$ is the expected number of molecules, $\overline{\rho }$ is the density, $\overline{v}$ is the volume of system A, f_n is the fractional volume of the subspace where the insertion attempts are made, ∆E is the change in energy due to a move, β is 1/k_BT, k_B is the Boltzmann constant, and T is temperature (300 K in the present study). Through the GCMC simulation, the volume of the simulation system A and the total number of particles between the system A and its reservoir are fixed.

SILCS FragMaps are obtained using the 1-ns MD trajectories across the 100 cycles and across the 10 systems (1 μs cumulative MD time) using snapshots saved every 10 ps. These are based on probability distributions of selected probe molecule atoms and of the water oxygens generated by binning into 1×1×1 Å cubic volume elements (voxels) and calculating the local voxel occupancy of each FragMap atom type over the GCMC-MD cycles. The probability distributions are then normalized and converted to grid free energies, GFEs, as described in the following section.

Estimation of Ligand Binding Affinities using the Ligand Grid Free Energies

As previously described, estimation of relative binding affinities using the SILCS FragMaps is performed by converting the probe atom solute occupancies into free energies based on a Boltzmann transformation. This is performed by taking the occupancies (or probabilities) of the 1 ų cubic voxels by the respective probe solute atoms or water oxygens, occ_xyz, followed by normalization with respect to the number of snapshots from the SILCS simulations, the probabilities or occupancies in the bulk (i.e., absence of the target protein), occ_bulk,xyz, and the number of atoms in the solutes used to define a given FragMap type, n_atoms. This normalization and conversion of the FragMaps to yield their corresponding grid free energies, GFE_xyz, is performed using equation 2:

$${\text{GFE}}_{\text{xyz}}=\left(-\text{RT}\right)*\ln \left({\text{occ}}_{\text{xyz}}/\left({\text{n}}_{\text{atoms}}*{\text{occ}}_{\text{bulk,xyz}}\right)\right)$$ Eq. 2

Normalization by n_atoms accounts for the covalent connectivity of the probe molecules such that when one voxel is occupied, then n_atom voxels will simultaneously be occupied. Only non-hydrogen atoms are considered. This yields probe-based FragMap GFEs that represent the energy of an entire functional group occupying the region visualized in the FragMaps (e.g. benzene or propane). However, when calculating the LGFE scores the atom-based GFE energy is required which is based on

$${\text{GFE}}_{\text{xyz,MC}}=\left(-{\text{RT/n}}_{\text{atoms}}\right)*\ln \left({\text{occ}}_{\text{xyz}}/\left({\text{n}}_{\text{atoms}}*{\text{occ}}_{\text{bulk,xyz}}\right)\right)$$ Eq. 3.

that accounts for the probe molecules containing multiple atoms representing a specific type of functional group (e.g., the 6 aromatic carbons in benzene). This represents conversion from a probe molecule-based concentration to an atom-based concentration. In practice, the SILCS FragMap GFEs are initially calculated using Equation 2 and stored for visualization (i.e. GFE_xyz). When performing SILCS-MC calculations the GFEs are based on equation 3 (i.e. GFE_xyz,MC). The GFE_xyz,MC scores of classified atoms in each molecule are summed to yield the LGFE scores.¹³ This process may be performed with functional group specific atoms as well as with generic FragMaps (GENN, GENA, GEND, GEHC) that include contributions from multiple, related functional groups, with the scaling values for these used in equation 3 given below. An improved normalization of the SILCS FragMaps and scaling of the GFE scores was implemented in the present study yielding LGFE scores that are more consistent with experimental binding affinities.

Finally, it should be noted that when calculating a binding affinity in the context of the LGFE score there is a RTln(1/n_atoms) offset that is associated with the free ligand concentration/volume as described in previous studies.^{14, 55, 56} In practice this correction is divided by n_atom of the probe molecule to yield an effective correction that can be added to the LGFE for the corresponding atom types. However, as this correction is small and the same for all the probes it has not been applied in the present study.

An important aspect of the calculation of the GFE_xyz values is the bulk occupancy (or concentration), occ_{bulk_xyz}, of the probe molecules in the simulation systems as these values are required to normalize the GFE_xyz values (Eq. 2 and 3). When the systems are initially set up the number of each probe molecule added to the simulation is adjusted to yield a target concentration of 0.25 M and the assumption to date has been to use that target concentration of 0.25 M as occ_{bulk_xyz}. However, in practice the concentration of the solutes varies from the target concentration due to challenges in calculating the true volume of the aqueous solution due to the presence of the protein, and bilayer when appropriate, in the simulations system as well as fully converging to the targeted solute concentrations. To overcome this the concentration of the solutes can be calculated from the SILCS simulations by counting the actual number of solutes in the systems and obtaining the average over all 10 simulations. These values may then be used with i) the total simulation system volume or ii) the total number of water molecules in the system to calculate the solute concentrations. Approach ii) simply involves assuming a concentration of 55 M for water and determining the concentration of the solutes based on their relative number to that of water. For example, if there is 1 solute molecule for every 55 waters then the concentration of the solute is 1 M.

LGFE Scoring

Ligand atoms were classified into FragMap types based on the ACS described below. For each classified atom in a ligand its coordinates (x_i, y_i, z_i) are assigned to the appropriate voxel from which a score equal to the GFE value of the corresponding FragMap type f, ${\text{GFE}}_{\text{xi,yi,zi,}}^{\text{f}}$, is obtained. The single atom GFE contributions are capped at 3.0 kcal/mol for consistency due to the maximum ${\text{GFE}}_{\text{xi,yi,zi,}}^{\text{f}}$ values varying for each specific FragMap and simulation system with those values all being in the vicinity of 3.0 kcal/mol. The final LGFE is the sum of the atomic GFE values for the classified ligand atoms. Also, it should be emphasized that the LGFE scores are a simple sum of the GFE contributions of selected atoms and do not account for the covalent connectivity of the functional groups in the ligands. Accordingly, once the SILCS FragMaps are available, calculation of the LGFE score for a given ligand orientation is virtually instantaneous allowing the LGFE scores to be used in MC sampling of ligand conformation and orientation. We note that inspection of the GFE scores of the individual ligand atoms indicates the contribution of that atom to the overall LGFE representing useful information for ligand design. For example, the contributions may indicate the scaffolding elements in a ligand versus those that are driving ligand binding.

Atom Classification Schemes and FragMap Scaling

The original ACS used for previous SILCS studies,^{8, 11, 12, 27} referred to as Generic 2016 (G16) in the present work, was based on the following functional group definitions in the absence of the normalizations presented in equations 2 and 3. This included assigning the probe atoms to the following FragMap types; generic nonpolar (GENN, benzene and propane carbons, also referred to as apolar), generic acceptor (GENA, formamide acceptor O, acetaldehyde acceptor O, imidazole acceptor N and methanol acceptor O), generic donor (GEND: formamide donor N, imidazole donor N and methanol donor O), methylammonium nitrogen (MAMN), or acetate oxygen (ACEO). With this approach the contribution of each atom in the respective classifications were all weighted equally, with a value of 1, when calculating the GFE_xyx,MC and LGFE scores; the 1/n_atoms prefactor in equation 3 was not applied to scale the voxel GFE_xyzs. The result of this scheme yielded highly favorable LGFE values that are significantly more favorable then experimental binding free energies. This approach corresponds to applying a solute based GFE normalization to all classified atoms in each ligand, thereby overestimating the favorable LGFE scores. Most notably, this leads to the GENN FragMap contributions being significantly overestimated. For example, the binding affinity of small fragments, such as benzene will typically have dissociation constants, K_d, of 10 to 0.1 mM,^{57, 58} which corresponds to binding free energy of −2.8 to −5.4 kcal/mol, respectively, based on the van’t Hoff equations, ΔG = RTln(K_d), where R is the Boltzmann constant, T is the temperature of 298 K and K_d is the dissociation constant. However, when applying the solute based GFE_xyz FragMaps to benzene and assuming a value of −1.2 kcal/mol (i.e., ~2kT) the free energy of binding is −7.2 kcal/mol, corresponding to a K_d of ~5 μM. When applying this to larger ligands that may contain 20 or more aromatic or aliphatic atoms LGFE scores of −30 kcal/mol or more are obtained. While the LGFE scores are not directly analogous to binding affinities as various terms are omitted (e.g., the configurational entropy loss associated with the covalent connection of a full ligand versus the solute-based functional groups) it is still desirable for these scores to be consistent with anticipated binding affinities. In addition, proper treatment of the GFE_xyz contributions to the LGFE scores assures that the balance of the contributions of the different types of functional group types is more accurate during ligand posing during SILCS-MC sampling.

Further improvements in the ACS developed for this study involved changes to avoid overcounting of the number of atoms contributing to functional groups. This is exemplified above for benzene, leading to the use of GFE_xyz,MC from equation 3 when calculating LGFE scores. The scaling factors used in the 2018 ACS are shown in Table 1. Beyond benzene and propane, where n_atoms = 6 and 3, respectively, this overcounting is also relevant to charged and polar groups. The importance of this is seen in the handling of phosphate oxygens. If the negative FragMaps are calculated based on the two oxygens of acetate, then the presence of 4 oxygens in anionic phosphate will lead to the contribution of the single negative charge actually being twice that of a single negatively charged acetate. To overcome this the acetate carbon was used for scoring in conjunction with the phosphate phosphorus atom. Sulfates are treated similarly while functional groups such as in phenolate, methoxide and methylthiolate use the respective O or S atoms with the acetate C GFE_xyz,MC FragMaps. With positively charged groups such as imidazolium, guanidinium and amidine where there are 2 or 3 nitrogens on a positively charged moiety, a central carbon (e.g., guanidinium carbon (MAMC)) is used for scoring. MAMN is still used for protonated amines. This approach is also used for neutral species such as alcohols and aldehydes where the functional group contains both a donor and acceptor. To account for this the methanol oxygen (MEOO) and acetaldehyde C (AALC) atoms were used for scoring. Similarly, based on imidazole an atom type of carbons in heterocycles, GEHC, was defined.

Table 1.

Atoms defining the FragMaps and associated scale factors used to calculate the ligand grid free energy (LGFE) scores.

SILCS type	Scaling Factor (1/natom)	1st atom type	2nd atom type	3rd atom type
BENC	0.167	6 C on benzene
PRPC	0.333	3 C on propane
ACEO	0.500	2 O on acetate
ACEC	1.000	C on acetate
GENN	0.333	3 C on propane	6 C on Benzene
GENN/BENC	0.167	6 C on benzene
GENN/PRPC	0.333	3 C on propane
GEND	0.500	N(H) on imidazole	N on formamide
GENA	0.333	O on formamide	O on acetaldehyde	N on imidazole
GEHC	0.333	3 C on imidazole
MEOO	1	O on methanol
FORN	1	N on formamide
FORO	1	O on formamide
MAMN	1	N on methylammonium
MAMC	1	C on methylammonium
AALO	1	O on acetaldehyde
AALC	1	C(=O) on acetaldehyde
IMIN	1	N on imidazole
IMINH	1	N(H) on imidazole

A second change was more judicious choices with respect to the contribution of carbons adjacent to polar functional groups to the LGFE. For example, with small solutes such as methanol and acetaldehyde the solute concentration will be equivalent to the atom concentration for the single atom in the system used to define the FragMaps. With methanol, this leads to the methyl carbon contribution being ignored while with acetaldehyde the methyl carbon and the carbonyl oxygen are ignored. This definition of the FragMaps also takes into account that both methanol and acetaldehyde can act as both hydrogen bond donors and acceptors. Similarly, the methyl groups in methylammonium and acetate are ignored. This approach is then extended to large ligands when doing LGFE calculations such that atoms adjacent to the atoms defining FragMaps are assigned as non-classified (NCLA) such that these atoms do not make contributions to the LGFE scores.

Based on the considerations discussed above several variations of the ACS and scaling schemes were tested in the present study. These are summarized below. Common to all of the ACS but used to varying degrees are the following generic types: GENN, nonpolar (or apolar) based on benzene and propane carbons; GEND, hydrogen bond donors based on formamide N and imidazole N(H); GENA, hydrogen bond acceptors based on formamide O, acetaldehyde O and imidazole N; and GEHC, heterocycle carbons based on imidazole carbons. Also, in the standard maps halogens are treated as GENA, due to recent studies in our laboratory indicating their favorable interactions with hydrogen bond donors,⁵⁹ with the exception of FETX and the aliphatic chlorine and bromine containing groups which are treated using PRPC. If desired users may treat all halogens as nonpolar GENN by assigning that type in the classification file. Moreover, the negatively charged groups are treated based on the acetate C (ACEC) FragMaps and the positively charged groups based on the methylammonium C (MAMC) or N (MAMN) FragMaps, as described above. In addition to the 2018 ACS listed below, the previously used ACS based on generic atom types without 1/n_atom scaling, G16,¹³ was included to allow for the new ACS to be compared to that used in previous studies.

Generic Apolar Standard 2018 (GAS18):

Nonpolar (e.g., apolar) benzene and propane carbons are used to define the GENN FragMaps. However, when used for GFE_xyx,MC there are separate classifications for benzene carbon (BRBC) and propane carbon (PRPC) which are assigned to GENN maps and scaled as 0.167 and 0.333, respectively. Use of the term “Apolar” in the name of this ACS is to differentiate it from the previous use of nonpolar for GENN where both benzene and propane were grouped together.

Specific Standard 2018 (SS18):

Specific FragMaps are used for the majority of atom types, though some generic types used for selected atoms including GEHC for heterocycle carbons and GENA for ether or furan oxygens. Specific FragMaps include benzene carbons (BENC), propane carbons (PRPC), formamide nitrogen (FORN), imidazole protonated nitrogen (IMIH), imidazole acceptor nitrogen (IMIN), formamide oxygen (FORO), acetaldehyde oxygen (AALO) for carbonyl oxygens, with the exception of aldehydes where the acetaldehyde carbon (AALC) was used to account for both the donor and acceptor characteristics of this functional group, as is also done for alcohol groups based on the methanol oxygen (MEOO) FragMaps. In addition, the charged FragMaps in Table 1 are included.

Halogen Maps:

The generic and specific schemes described above can be extended to include the treatment of halogens as well as ether oxygens. Halogens in drug design have been explored in other cosolvent studies.^{9, 60} Explicit maps for fluoroethane fluorine (FETX), trifluoroethane carbon (TFEC), fluorobenzene fluorine (FLBX), chloroethane chlorine (CLEX), chlorobenzene chlorine (CLBX), bromobenzene bromine (BRBX), and dimethyl ether oxygen (DMEO) were used to supplement the generic and specific standard ACS described above. With bromobenzene and chlorobenzene the halogen atoms have lone pair particles to reproduce the σ-holes and improve halogen bonding as implemented as part of the improved treatment of halogens in CGenFF.⁴² The DMEO oxygens FragMaps are used explicitly for the specific classification or included in the generic GENA maps. The FragMaps for these atoms are generated by a completely new suite of “halogen” probes called SILCS-X that also include methanol to have a common functional group between the standard SILCS and SILCS-X sets. Otherwise the simulation protocol is identical to that described above. The ACS that include the SILCS-X FragMaps are indicated by a X in the classification acronyms. Trifluoromethyl groups are treated based on the trifluoroethane carbon (TFEC) while in trichloro- and tribromomethyl groups the carbons are NCLA and the contribution is based on the aliphatic chlorine (CLEX).

SILCS-MC Protocol

Ligand binding poses are predicted using Metropolis MC sampling of the ligands in the “field” of the GFE_xyz,MC FragMaps.⁸ SILCS-MC calculations involved subjecting the ligand to rotational, translational and intramolecular dihedral degrees of freedom, with the latter restricted to rotatable bonds. The rotatable bonds are automatically detected based on the topology of the molecule based on the CGenFF program. All acyclic non-terminal bonds are considered rotatable supplemented by hydroxyl and sulfhydryl groups. The intramolecular energies were comprised of dihedral, van der Waals (vdW) and electrostatic terms. Due to the absence of protein and solvent during these simulations a distance dependent dielectric (=4|r|) was used to evaluate the intramolecular electrostatics. The Metropolis MC is evaluated as follows

$${\text{E = E}}_{\text{vdw,intra}}+{\text{E}}_{\text{elec,intra}}+{\text{E}}_{\text{dihe,intra}}+\text{LGFE}$$ Eq. 4

where the acceptance of MC moves is then determined by the Metropolis Criteria:

$${\text{P}}_{\text{move}}=\min \left(1,\text{exp}\left(-\beta \mathrm{\Delta }\text{E}\right)\right)$$ Eq. 5

where β=1/k_BT and E is defined on Eq. 4. The simulated temperature T is 300 K for the normal MC sampling. For MC-based simulated annealing (SA) the temperature is ramped from 300 K to 0 K over the course of the SA steps. As the temperature decreases, it becomes less likely that MC moves with unfavorable energy changes are accepted, which makes the final pose more likely to assume a pose corresponding to the lowest LGFE score on the local free energy surface.

In all SILCS-MC protocols the ligand molecule is (i) energy minimized for 10,000 steps of Broyden–Fletcher–Goldfarb–Shanno minimization with a gradient tolerance of 3×10⁻⁸ kcal/mol/Å and a function tolerance of 10⁻⁴ in the context of Cartesian coordinates using the full CGenFF potential energy function, (ii) given an initial orientation in the FragMaps, (iii) sampled by MC in the FragMaps for some number of attempted moves, n_MC, where the moves include molecular translations and rotations, and dihedral rotations of rotatable bonds with a magnitude between zero and a maximum size (dX,dθ,dφ), respectively, and (iv) subjected to SA into a local minimum free energy pose in the FragMaps for some number of steps, n_SA, with maximum step sizes of dX_SA,dθ_SA, and dφ_SA. Steps (i) to (iv) comprise one cycle of SILCS-MC. Multiple independent cycles are performed for each ligand to more rigorously explore the binding orientation of the ligand to identify the optimal free energy minimum. It should be emphasized that the FragMaps represent free energy distributions of the different functional groups such that the MC sampling is designed to identify the lowest free energy orientation of the ligand rather than generate an ensemble of conformations from which a free energy of binding is calculated.

Several SILCS-MC protocols were applied in the present study: Local, Long-Local and Exhaustive. Local sampling effectively relaxes the ligand pose to identify a local free energy minimum while exhaustive sampling allows for extensive pose generation in the LBP. In all cases a protocol for each ligand involved a specified number of cycles in five parallel runs using the following procedure: (1) Number of cycles: the Local protocol includes 10 cycles in each of the five parallel runs. The Long-Local and Exhaustive protocols include 50 cycles in each of the five parallel runs; if the lowest 3 LGFE scores in each run are within 0.5 kcal/mol the run is terminated. If that criteria is not met additional cycles are run until this convergence criteria is achieved up to a maximum of 250 cycles in each run. (2) Number and size of attempted moves as shown in Table 2. (3) Initial placement of a ligand: in Local and Long-Local protocols the initial placement of ligands is based on a known, user assigned orientation (e.g., based on a crystallographic structure) while in the Exhaustive protocol the ligand is placed randomly within a sphere defined by a user assigned position and ligand placement radius (r_LP) with the ligand subjected to one randomly selected rotatable bond rotated by a random value (−180<φ<180) followed by a random rigid molecular translation and rotation with the final ligand center of mass being in the defined sphere. The placement radii, r_LP, are 1, 2, 5, 10, and 15 Å. Details of the three MC protocols are described in Table 2.

Table 2.

Description of Local, Long-Local, and Exhaustive SILCS-MC sampling protocols.

MC protocol	Initial ligand placement	nCY	nMC	dX	dθ	dφ	nSA	dXSA	dθSA	dφSA
Local	aligned	10	100	0.5	15	45	1000	0.2	9	9
Long-Local	aligned	250	10,000	1	180	180	40,000	0.2	9	9
Exhaustive	random	250	10,000	1	180	180	40,000	0.2	9	9

Target and Ligand Sets

Seven proteins were used as they represent well studied proteins of various biological functions for which experimental data on a significant number of ligands is available. For each of the cited studies all available ligands were included in the present study yielding a total of 551 ligands over the 7 proteins. In the case of MCL1 two independent ligand sets were available from Friberg et al. ⁶¹ and from Fletcher and coworkers²⁹ and treated independently, yielding a total of 8 data sets. The affinity values of some ligands in each set were weaker than the limit of detection. In the cases of these compounds we used the limit as the affinity value. See Table S1 in the Supplementary Information for more details. The proteins and specific protein databank (PDB) files⁶² used include three from the Drug Design Data Resource challenge (See supporting information Table S1) including Farnesoid X receptor (FXR) apo structure 1dvwb,⁶³ tRNA m1G37 methyltransferase enzyme TrmD (TRMD) PDB entry 4ypw,⁶⁴ and heat shock protein 90 (HSP90) PDB entry 2jjc.⁶⁵ Additional proteins include mouse double minute 2 homolog (HDM2) PDB entry 4jv7,⁶⁶ Myeloid Cell Leukemia 1 (MCL1) PDB entry 4hw3,⁶¹ p38α Mitogen-Activated Protein Kinase (p38) PDB entry 3fly, ⁶⁷ and tyrosine kinase 2 (TYK2) PDB entry 4gih. ⁶⁸

Ligand preparation

Ligands included in the study were prepared as follows. For the Local and Long-Local SILCS-MC calculations the protein structure of the protein-ligand cocrystal structures were aligned to the protein structure used in the SILCS GCMC-MD calculations to obtain the starting ligand orientation for the SILCS-MC protocols. The HDM2,⁶⁶ MCL1-Friberg,⁶¹ MCL1-Fletcher,²⁹ p38,⁶⁷ and TYK2⁶⁸ ligand structures were built by manually adjusting the aligned crystal structure with the maximum common substructure (MCS) to the ligand in MOE (Chemical Computing Group). The authors of the FXR⁶³ and HSP90⁶⁵ sets provided SMILES for the ligands, therefore we built the ligand structures by generating structure files in MOE and aligning them to the respective crystal structure with the Open3D Align implementation in RDKIT.⁶⁹ MCS was determined with the RDKIT DiceSimilarity function. The TRMD set was composed entirely of ligand cocrystal structures. The sphere positions used for the Exhaustive searches were determined using the center of mass of one crystal ligand structure for each target: FXR, 1btoj; HDM2, 4jwr; HSP90, 2jjc; MLC1, 4hw3; P38, 3FLN; TRMD, 4ypw; TYK2, 4gfo.

The FXR, HDM2, and TYK2 sets contained some affinity values for a racemic mixture of many of the ligands. A single stereoisomer is often responsible for most of the binding. Accordingly, for all racemates both stereoisomers of the ligands were built and run in SILCS-MC with the Local protocol and GAS18 atom classification. The stereoisomers with the more favorable LGFE score was chosen as the representative structure for that ligand. For FXR ligand racemates with cocrystal structures the stereoisomer in the crystal structures were used.

Evaluation of the accuracy of the predictions

Correlation analysis between the calculated and experimental data was performed in two ways. The Pearson’s correlation coefficient (R) is the most well-known descriptor of the quality of a linear fit and was included in this study. In addition, the predictive indices (PI) for ligand scoring were calculated.⁷⁰ PI is a correlation that ranges between 1 for 100% true predictions and −1 for 100% false predictions. It is weighted by the difference between experimental binding energies based on the premise that two ligands with a large difference should be easier to capture a true positive or true negative result, such that the correlation is dominated by the rank ordering rather than the calculated values themselves. In order to show the overall quality of both the R and PI correlation scores 8-set-average correlation scores associated with the 8 ligand sets are reported; <R>₈ and <PI>₈, respectively

In the context of a drug design project it is desirable to obtain knowledge of whether a ligand modification will increase or decrease activity, information that the medicinal chemist may find useful in the context of a go/no-go decision. This type of analysis has been previously reported in the evaluation of the SILCS and single-step free energy perturbation methodologies.¹¹ To this end we calculated the sum of true positive and true negative comparisons, which is referred to as the percent correct rate (PC) for each ligand. In the manuscript PC values are presented interchangeably as the actual percentage or the associated fraction (e.g., 70.2% or 0.702). When comparing one ligand to another, a true positive (TP) result is achieved when the second ligand is predicted to have a higher affinity than the reference ligand and the prediction agrees with experiment. Similarly, a true negative (TN) result is achieved when the second ligand is predicted to have lower affinity and that prediction agrees with experiment. In the course of lead optimization with a predictive tool the percent correct rate should be maximal. However, when calculating the PC, the result is dependent on the compound selected as the reference for the relative affinity calculation of the remaining compounds in a data set. The variation of the calculated PC values for different targets as a function of the experimental affinity of the reference ligand is shown in supporting information Figures S2 and S3. Notably, the highest PC values are typically obtained when ligands with the highest or lowest affinities are selected as the reference, with the results fluctuating about a constant value for the intermediate affinity compounds. Notably, this trend is consistent for the different targets studied. Such a result is not unexpected as, when the ligand affinity is at an extreme, the probability that the other ligands will bind with systematically more or less favorable affinity will likely be higher than for ligands of intermediate affinity. Accordingly, in the present study the reported PC values are the average over the percent correct with each ligand in the data set selected as reference (<PC>_S). The expectation value of <PC>_S for a large set of random data is 50%. While the majority of analysis was based on the R, PI and <PC>_S values, an additional descriptor was the root-mean-square error (RMSE) based on the difference between the ligand LGFE and experimental ∆G_bind values for all the ligands in each set. For all the metrics, the 8-set averages over all, <R>₈, <PI>₈, <<PC>_S>₈ and <RMSE>₈ were calculated.

Bayesian Machine Learning FragMap Reweighting

Reweighting was done using a Bayesian Markov-Chain Monte Carlo-Simulated Annealing (MCSA) approach using the SILCS FragMaps as the priors. The initial temperature is set to 500 K and is reduced by an adjustable factor after a selected number of steps (set to 0.75 and 1600 steps, respectively, for the current study) during the calculation. The parameter space is the weighting (or scaling) factor for each FragMap type (Table 1), which directly adjusts the GFE contribution of each of the classified atoms in the ligands in the set. It was found necessary to establish predefined upper and lower boundaries which are set to be double and half of the initial FragMap weight (i.e., 2 and 0.5 assuming a weight of 1.0) to avoid overfitting. The initial weights (i.e., Scale factors) for the FragMap types are in Table 1. A flat potential is applied with no penalty for parameters within the boundaries with a penalty of 1000 applied to the error function if parameters are beyond the upper and lower boundaries.

In the optimization, each of the parameters is initially varied by a predefined increment (0.01 in the current study) that is randomized at each MC step. The parameters are accepted based on the Metropolis criteria⁵⁴ [Eq. 5] where E in this case is the difference between the new and old error function values (R, <PC>_S or RMSE). During MCSA the parameter increments are adjusted to achieve a 50% acceptance ratio. Each MCSA run is considered as converged if the difference between the error function value of the current and last optimum point was less than 0.001 or if the parameter increment is less than 0.0005. An optimum point is defined as a parameter set that will give the lowest error function up to the current running step. Here we considered three types of error functions consistent with the accuracy metrics: R, <PC>_S, and the RMSE between the predicted LGFE scores and the experimental binding free energies. The method has been implemented into an in-house code written in FORTRAN.

The Bayesian ML FragMap reweighting approach was applied individually to each of the eight sets of ligands. Training was performed initially using the posed structures from the GAX18 and SX18 Exhaustive r_LP = 10 Å protocols. The effort involved k-fold cross-validation on the ligands, where k = 5. For each target-ligand set, we randomly filled five validation sets of approximately equal number with ligands. The FragMap scaling values were trained on the 80% of the ligands in the set (the training set) to give new weighting factors for each FragMap, with the remaining 20% of the compounds left as the validation set. After optimization of the weighting factors on the training set the entire target-ligand set (training + validation compounds) was re-run in SILCS-MC for each of the k sets and the resulting error function determined. The reweighting procedure was also applied without k-fold cross-validation such that 100% of the ligands in the target-ligand set were used as the training set and then subsequently re-run via SILCS-MC to see how the models improved.

Results and Discussion

SILCS simulations were performed on seven protein structures from which the SILCS FragMaps were generated for the entire protein structures. Two separate ligand data sets were used with MCL1, yielding a total of 8 target-ligand data sets. The FragMaps were based on fifteen representative solutes with different chemical functionalities. Eight of the solutes were members of the standard SILCS fragment set as used previously, including benzene, propane, acetaldehyde, methanol, formamide, imidazole, acetate, and methylammonium.^{8, 71} Motivated by the widespread presence and importance of halogen atoms in drug candidates⁵⁹ a halogen-based probe mixture, termed SILCS-X, was developed. This mixture included chloroethane, fluoroethane, trifluoroethane, bromobenzene, fluorobenzene, and chlorobenzene. The bromobenzene and chlorobenzene atoms have a lone pair particle to reproduce the σ-holes and improve halogen bonding, consistent with new halogen parameters in CHARMM. ⁴² Dimethylether was included in SILCS-X to improve explicit treatment of ether oxygens and methanol was common to both sets. When combining the standard SILCS and SILCS-X probe sets the methanol MEOO FragMaps were recalculated using the combined probability distributions.

From the SILCS simulations the FragMaps in terms of GFE scores according to Equation 2 are generated. An important step in this process is the normalization based on the concentration of the probe molecules in the bulk. In practice, the bulk concentration is that of the probe molecules in the full SILCS simulation system. When performing the oscillating μ_ex GCMC simulations, a concentration of 0.25 M is targeted. However, the exact concentration of the solutes is based on the effective volume accessible to the probe molecules and water, a value that is complicated by the presence of the highly anisotropic protein in the simulation system. Accordingly, we calculated the bulk concentration using three methods. The first simply used a value of 0.25 M based on that targeted in the GCMC simulations. The second was based on the average number of the individual probe molecules over the GCMC-MD simulations in the average volume of the simulation system. The third approach counted the number of each probe molecule relative to the number of water molecules with that ratio used to calculate the probe concentration assuming a water concentration of 55 M. When the three normalization schemes are applied, that which gives the most representative concentration of the probe molecules will yield a distribution of GFE scores of 0.0 kcal/mol. The value of 0.0 kcal/mol assumes that the solutes are effectively in a bulk aqueous environment. The GFE histograms for this analysis are shown in Figure S4 in the Supporting Information for p38 MAP kinase. The assumption of a bulk concentration of 0.25 M leads to systematically too favorable GFE distributions, due to the actual probe molecule concentrations being below 0.25 M in the simulation systems. Concentration determination procedures 2 and 3 both lead to maxima in the distributions close to zero. Method 3, based on the relative number of probe molecules to water molecules, was used to determine the concentration for the remainder of the systems.

SILCS-MC method validation

Three SILCS-MC sampling protocols for ligand posing were developed (Table 2) and tested to identify that, which in combination with the ACS, yields the best agreement with the relative experimental binding affinities based on three criteria; Pearson’s R (R), the predictive index (PI) and the percent correct (PC). In the Local SILCS-MC protocol, which was initiated from atomic coordinates of the ligands corresponding to that identified in crystallographic structures, the MC moves were designed to only sample the local orientation and conformation of the ligand. The Long-Local protocol used the same starting orientations combined with more rigorous MC sampling to more robustly sample the FragMap free energy surface in the region of the initial binding orientations of the ligands. The Exhaustive protocol was intended to explore the conformational space of the ligands in the FragMaps in the LBP to a substantially greater degree than the Local protocols without any knowledge of the initial orientation by inserting the ligand in random orientations and conformations in the LBP. The use of different initial poses allows the ligand to sample a wider range of the free energy surface to identify the binding pose with the most favorable LGFE. Five ACSs, G16, SS18, SX18, GAS18, and GAX18 were tested with the Local and Exhaustive r_LP = 1 Å SILCS-MC methods. The previous G16 ACS was among the worst or next to worst performers of the five ACS (Table 3). Notably, the G16 set yields average LGFE scores that are systematically much more favorable than the new 18 ACS sets. For example, the average LGFE score over all 551 ligands was −28.4 and −6.5 kcal/mol for the GS16 and GAS18 ACS, respectively, for Exhaustive r_LP = 1 Å. In the MCL1-Fletcher and MCL1-Friberg target-ligand sets, where APOLAR Fragmaps extensively cover the LBP, the average LGFE score over all 118 ligands was −37.9 versus −7.7 kcal/mol, respectively. This result clearly points to the inherent overestimation of the LGFE using the previous ACS associated with the lack of accounting for the conversion from solute-based to atom-based GFE scoring as presented in Equation 3. This issue along with the poorer predictability of G16 versus the new 18 ACSs lead to the G16 scoring regimen not being considered further.

Table 3.

8-set-average correlation scores for the SILCS-MC sampling protocol/ACS combinations. The G16 ACS was only tested with the Local and Exhaustive r_LP = 1 Å SILCS-MC protocol. Standard errors are reported in Table S2 of the supporting information.

Protocol	ACS	<R>8	<PI>8	<<PC>S>8
Local	G16	0.32	0.32	0.60
Local	SS18	0.39	0.39	0.63
Local	SX18	0.38	0.40	0.64
Local	GAS18	0.43	0.43	0.64
Local	GAX18	0.37	0.40	0.63
Long Local	SS18	0.37	0.37	0.62
Long Local	SX18	0.41	0.42	0.64
Long Local	GAS18	0.40	0.41	0.64
Long Local	GAX18	0.42	0.43	0.65
Exhaustive rLP = 1 Å	G16	0.41	0.39	0.63
Exhaustive rLP = 1 Å	SS18	0.42	0.39	0.63
Exhaustive rLP = 1 Å	SX18	0.39	0.36	0.62
Exhaustive rLP = 1 Å	GAS18	0.44	0.40	0.63
Exhaustive rLP = 1 Å	GAX18	0.44	0.43	0.65
Exhaustive rLP = 2 Å	SS18	0.36	0.36	0.61
Exhaustive rLP = 2 Å	SX18	0.43	0.42	0.63
Exhaustive rLP = 2 Å	GAS18	0.46	0.43	0.64
Exhaustive rLP = 2 Å	GAX18	0.48	0.48	0.67
Exhaustive rLP = 5 Å	SS18	0.42	0.40	0.63
Exhaustive rLP = 5 Å	SX18	0.44	0.41	0.63
Exhaustive rLP = 5 Å	GAS18	0.49	0.48	0.66
Exhaustive rLP = 5 Å	GAX18	0.50	0.50	0.68
Exhaustive rLP = 10 Å	SS18	0.41	0.40	0.63
Exhaustive rLP = 10 Å	SX18	0.45	0.42	0.64
Exhaustive rLP = 10 Å	GAS18	0.50	0.48	0.66
Exhaustive rLP = 10 Å	GAX18	0.54	0.54	0.69

Comparisons were next made of the Local versus Long-Local sampling protocols. For the SS18, SX18 and GAS18 sets the predictability of the two protocols were similar. However, with the GAX18 ACS, the Long-Local sampling leads to overall improved predictability versus Local. This result suggests that the presence of halogens may require additional sampling to identify the appropriate free energy pose in the field of the FragMaps. We note that the initial orientations for the local sampling protocols include ligands whose chemical structure is similar to that of a “parent” ligand directly subjected to crystallographic analysis with those ligand orientations being based on that parent ligand. Such ligands, which represent small modifications from the parent ligand such as those encountered in ligand optimization, may be expected to undergo rearrangements in the LPB which is suggested to be more important in the case of halogenated species, leading to the improved predictability with Long-Local over Local sampling protocols.

While ligand optimization often is initiated with a known bound orientation, as is necessary for FEP methods, more extensive ligand orientations may occur than that accessible to the local protocols. In addition, inclusion of more extensive chemical modifications as well as new chemical scaffolds require more exhaustive sampling of both the ligand orientation and conformation. Accordingly, the SILCS-MC Exhaustive protocol was developed. With the Exhaustive protocol a relatively large region of the LBP is sampled, which may be controlled by the user assigned “center” of the LBP as well as the radius of the sphere, r_LP, into which initial ligand placement is performed. As the center of the LBP in this study was based on the crystallographic position of known ligands, analysis focused on the impact of r_LP on the prediction quality. The r_LP values used were 1, 2, 5, 10, and 15 Å. Use of a larger radius gives the ligand a more diverse set of starting positions that may allow the ligand to orient in the LBP in more favorable free energy conformations. The results for this analysis are included in Table 3. In general, the predictability tends to increase as r_LP increases, with a maximum approached at r_LP = 10 Å, with only modest gains achieved from r_LP = 10 to 15 Å. In addition, upon increasing r_LP from 10 to 15 Å a number of ligands start to sample regions significant beyond the LBP (see below).

Notably the use of Exhaustive over Local searching generally leads to improvements in the predictability. In addition, the inclusion of the halogen FragMaps generally lead to similar or improved predictability over that standard FragMaps alone. Such a result is expected given the significant number of halogens, as well as ether oxygens in the validation set ligands (Table S1 of the supporting information). Based on the analysis of the 8-set averages, the present analysis indicates that the use of exhaustive sampling with a r_LP = 10 Å using the extended set of FragMaps that include those for halogens as well as ester oxygens to give the best overall agreement with the experimental relative free energies of binding. In addition, the generic maps (e.g., GAX18) gives systematically improved results over the specific FragMap sets (e.g., SX18). However, variation in the predictability for the different sampling and ACS are observed for the different sets as overviewed in Table 4 and Tables S4 to S11 for the individual data sets. This variability indicates the importance of user input in selecting the most suitable sampling protocol for a given system.

Table 4.

Summary of the top scoring sampling protocols and ACS for the 8 datasets studied. With P38 Goldstein and TRMD-GSK different sampling protocol/ACS combinations yielded specific top scoring metrics.

System	Sampling Protocol	ACS	R	PI	<PC>S
FXR-GSK	Exhaustive rLP = 15 Å	GAX18	0.60	0.61	0.71
HDM2-Turiso	Exhaustive rLP = 10 Å	GAS18	0.64	0.63	0.72
HSP90-Abbvie	Local	GAX18	0.30	0.35	0.63
MCL1-Fletcher	Exhaustive rLP = 5 Å	GAX18	0.85	0.83	0.82
MCL1-Friberg	Exhaustive rLP = 10 Å	GAX18	0.87	0.87	0.84
P38 Goldstein	Exhaustive rLP = 10 Å	GAX18	0.51
	Exhaustive rLP = 15 Å	SX18		0.54	0.70
TRMD-GSK	Local	GAX18		0.58	0.69
	Exhaustive rLP = 15 Å	GAX18	0.63
TYK2 Liang	Local	SS18	0.67	0.69	0.71

Ligand conformation and orientation

Beyond improved predictability it is important to understand the impact of the different sampling protocols on the final orientations of the ligands, including the extent that the Exhaustive protocol samples the LBP and beyond. This analysis was performed by determining the atomic root mean squared distance (<RMSD>_L) and center of mass difference (<COMD>_L) of the final ligand orientations relative to their initial, crystal structure-derived orientations. The results were then averaged over the 551 ligands with the results presented in Table S3 and Figure 1. As expected Local sampling leads to small changes where the <COMD>_L value are just above 1 Å with the <RMSD>_L value being 2.0 Å. Interestingly, the additional sampling in Long-Local leads to the expected increase in <RMSD>_L vs. Local to a value of 4.0 but the <COMD>_L value decreased to 0.9 Å, indicating that the ligands are reorienting and undergoing conformational changes in the LBP, but are not shifting from their local assigned positions. However, when analyzing the different datasets there is no clear improvement with Long-Local with respect to the predictability, further indicating the system dependent nature of the method.

Figure 1.

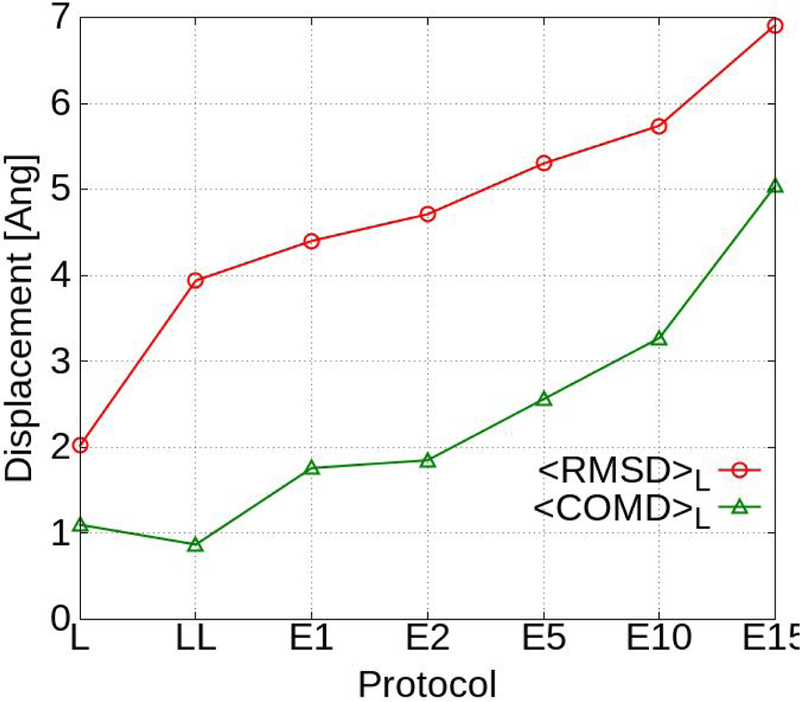
<RMSD>_L and <COMD>_L for GAX18 averaged over all 551 ligands.

Going from the local sampling SILCS-MC protocols to the Exhaustive protocol leads to the expected larger reorientation and shifts in the ligand positions in the LBP. The larger search radii lead to increases in the changes in the orientations of the ligands with respect to both the <RMSD>_L and <COMD>_L values as shown in Table S3 and Figure 1. The <RMSD>_L and <COMD>_L increase approximately monotonically with r_LP from 1 to 10 Å. At r_LP = 10 the <RMSD>_L is relatively large assuming a value of 5.7 Å but the <COMD>_L is only slightly larger than 3 Å indicating that the ligands are predominantly still located in the LBP though they have undergone significant reorientation and conformational changes. However, upon going from r_LP = 10 to 15 Å the <RMSD>_L and <COMD>_L increase by 20% and 54% respectively, indicating that in a number of cases the ligands are no longer in the LBP.

Specific cases where the set-average <RMSD>_S and <COMD>_S increase dramatically include FXR, HSP90, TRMD, and P38 when the radius is increased from r_LP = 10 to r_LP = 15 Å. Examples are shown in Figure 2 and Figures S5 and S6 in the Supporting information. The minimum LGFE poses of all ligands in the FXR, HSP90 and TRMD sets are overlaid in these figures. With the Local (panel A) and Exhaustive r_LP = 1 Å (panel B) SILCS-MC method the ligands are all in the LBP. With r_LP = 10 Å (panel C) the ligands remain in the LBP, though larger shifts from the starting conformations are present. However, many of the ligands with r_LP = 15 Å (panel D) have clearly found more remote binding orientations beyond the LBP. In the FXR set with r_LP = 10 Å there was only one ligand, FXR-Roche-009–1sjpr with COMD > 11 Å, and this minimum energy pose remained partially within the LBP. When the r_LP was increased to 15 Å the result was 10 ligands with COMD > 14 Å and their locations are clearly visible in Figure 2D. For HSP90, there were 54 out of 180 ligands with COMD > 14 Å with r_LP = 15 Å. In the TRMD set for r_LP = 10 Å the maximum COMD was 2.81 Å, and for r_LP = 15 Å there were 6 ligands with COMD > 12 Å. These results and the generally improved predictability of r_LP = 10 over r_LP = 15 Å indicates this search radius to lead to improved sampling of the ligands while maintaining the ligands in the LBP. Distributions for RMSD and COMD for all 551 ligands with local and exhaustive protocols with GAX18 ACS are shown in Figure S7 in the Supporting information. A marked increase in large displacement values is clearly visible when comparing the results of r_LP = 15 Å to any other protocol.

Figure 2.

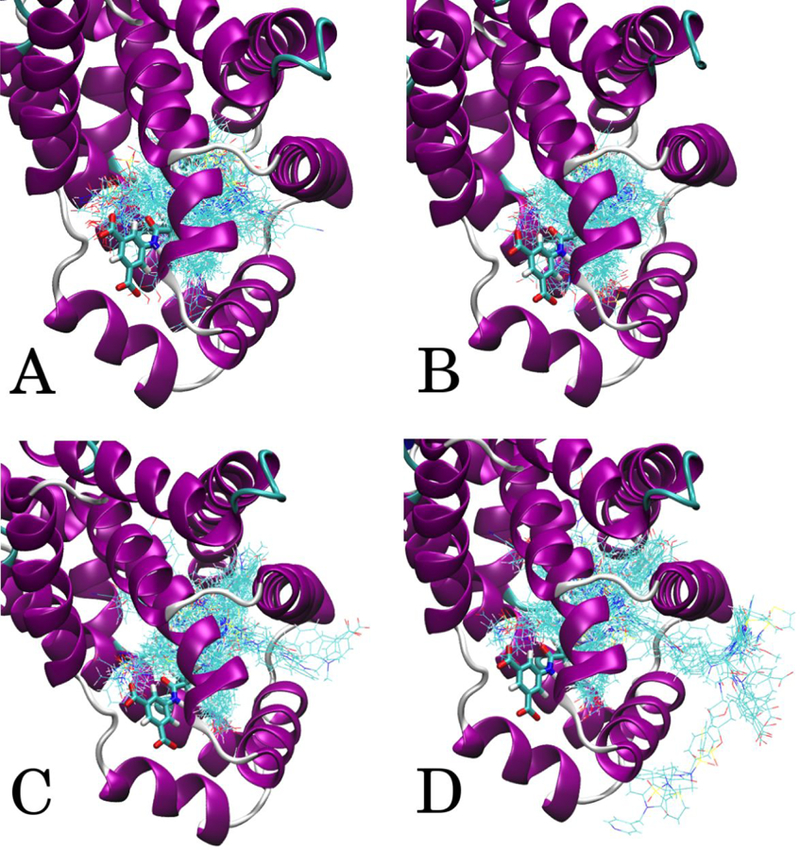
FXR ligand minimum conformations from GAX18 ACS. A) Local protocol, B) Exhaustive r_LP = 1 Å, C) Exhaustive r_LP = 10 Å, D) Exhaustive r_LP = 15 Å. The crystallographic position of ligand FXR-Roche-033–1fggu is shown in thick stick representation to indicate the LBP location.

As an example of the impact of the use of larger r_LP values (e.g., 10 vs. 1 or 2 Å) in the Exhaustive protocol on ligand orientations we analyzed a ligand from the MCL1-Fletcher set. The MCL1-Fletcher ligands were built in MOE based on aligning the fused ring structures to the MCL1-Friberg cocrystal structures 4hw2 and 4hw3.⁶¹ The sphere positions used for Exhaustive searches were based on the center of mass of the 4hw3 crystal structure ligand, MCL1-Friberg-60. In Figure 3 the minimum conformations for ligand MCL1-Fletcher-32 for Exhaustive r_LP = 1 Å and r_LP = 10 Å are shown. The ligand in both cases is located in the same region of the LBP, but the orientations are significantly different with the COMD value being 2.81 Å and the RMSD between the orientations being 5.70 Å with the LGFE equal to −8.58 and −10.85 kcal/mol for r_LP = 1 Å and r_LP = 10 Å, respectively. In the r_LP = 10 Å case (panel b) the oxygen atom of the hydroxyl group on the naphthalene ring is interacting with the MEOO FragMap adjacent to ARG263 with a GFE of −0.85 kcal/mol, the sulfone oxygens are able to access a GENA FragMap achieving GFEs of −0.31 and −0.25 kcal/mol, and the nitrogen adjacent to the sulfone group accesses the GEND FragMap achieving a GFE of −0.42 kcal/mol. In the r_LP = 1 Å case (a) those GFE values are −0.35, +0.07, +0.43, and +0.31 kcal/mol, respectively. The acetate carbon in the protocols are in virtually the same position in the most favorable part of the ACEC FragMap; the distance between them is 0.524 Å and their GFE scores are both −2.64 kcal/mol. In both protocols, they are responsible for the largest negative contributions to the LGFE. Thus, the results indicate how the use of a wider search radius in the exhaustive sampling protocol can allow for lower LGFE conformations to be attained while the ligand is still maintained in the LBP. In the case of MCL1 with the Fletcher set of ligands for which no crystallographic orientation of any of the ligands is available, the enhanced searching yielded ligands orientations significantly different in the binding site than that assigned based on an analogous ligand as seen in Figure S8 in the Supporting Information that shows histogram of the RMSD for the entire MCL1-Fletcher set. Importantly, these orientations yield improved agreement with experiment, suggesting them to be the more relevant orientations.

Figure 3.

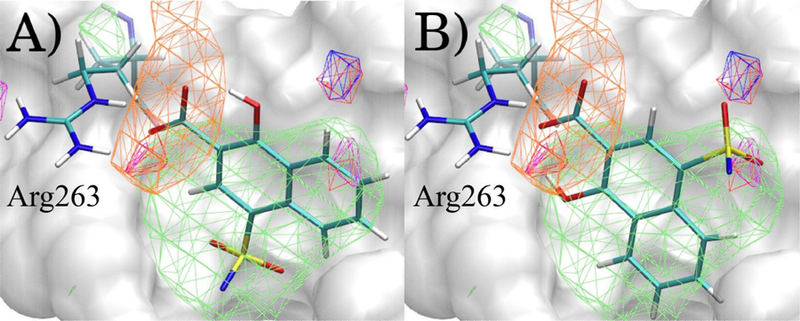
Minimum LGFE conformations of Ligand MCL1-Fletcher-32 after A) Exhaustive r_LP = 1 Å B) Exhaustive r_LP = 10 Å with the GAH18 ACS. FragMaps at contours GFExyz = −1.2 kcal/mol for GENN (green), ACEC (orange), MEOO (red), GENA (blue), GEND (magenta). The ligand atoms attached to the sulfone nitrogen are not shown for clarity and the location of Arginine 263 in MCL1 is shown.

Comparison of LGFE scores to experimental binding free energies

Optimization of the ACS as part of the present study was motivated by the need to obtain LGFE values more consistent with experimental ligand binding free energies, ΔG_bind. LGFE scores do not directly correspond to binding affinities due to the omission of contributions associated with covalent linking the functional groups into full ligands, configurational entropy and other terms.⁷² However, the LGFE values should approximate experimental ΔG_bind as the individual functional groups binding strengths do correspond to the experimental regimen and, as such, the proper balance of their contributions to the LGFE will contribute to improved ligand posing. A comparison between experimental ΔG_bind and predicted LGFE scores is shown in Figure 4 based on the GAX18 Exhaustive r_LP = 10 Å SILCS-MC. Over all 551 ligands the results are scattered around the x = y line. Interestingly, the ligand-target sets occupy different regions. The set-average value <LGFE-ΔG_bind>_S is given in the last column of Table 5. HDM2, MCL1-Fletcher, and MCL1-Friberg have the most favorable LGFE scores relative to ΔG_bind. FXR, HSP90, P38, and TYK2 are distributed approximately at the y=x line. If not for the nonbinding compounds (Table S1), HSP90 and TYK2 would be farther above the line, with averages of +1.00 and +1.21 kcal/mol. Thus, while system-dependent shifts in the LGFE scores relative to the experimental ΔG_bind values are present, the current ACS yield LGFE values that are consistent with their experimental counterparts.

Figure 4.

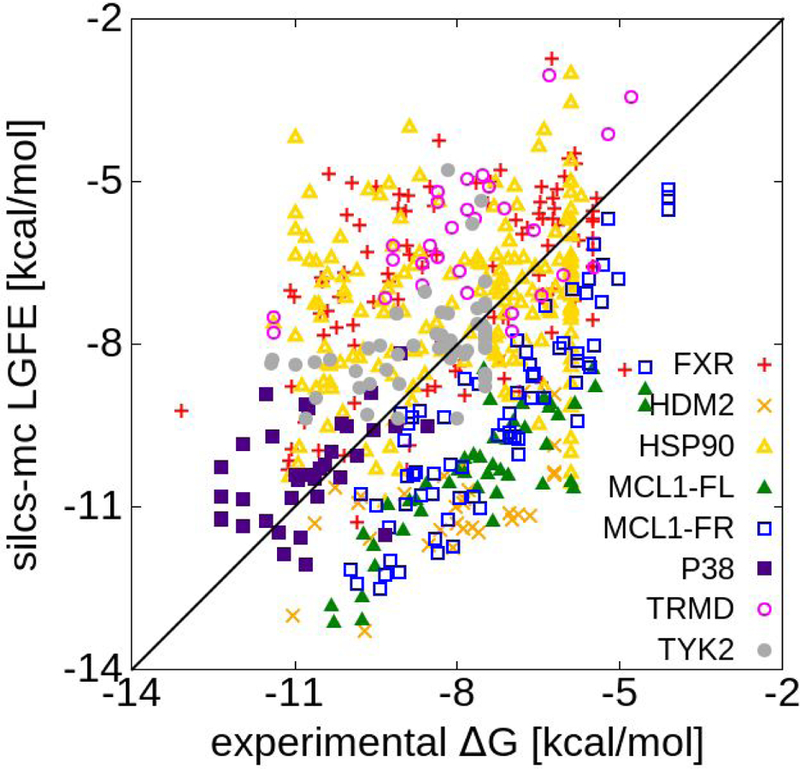
Correlation between ΔG_bind experimental data and predicted LGFE scores and for all eight sets using the GASH18 ACS and Exhaustive rLP = 10 Å protocol.

Table 5.

Average target-ligand displacement information for each data set with the GAX18 Exhaustive r _LP = 10 Å protocol. Average <LGFE-ΔG_bind>_S is given in kcal/mol. The displacement values are reported in Å.

Target	Dataset	R	PI	<PC>S	<RMSD>S	<COMD>S	<LGFE-ΔGbind>S
FXR	Roche	0.44	0.42	0.64	7.39	5.03	1.22
HDM2	Turiso	0.55	0.50	0.68	4.50	1.94	−2.87
HSP90	Abbvie	0.20	0.20	0.57	5.22	2.64	0.67
MCL1	Fletcher	0.83	0.82	0.81	6.02	2.63	−2.82
MCL1	Friberg	0.87	0.87	0.84	3.55	2.13	−2.04
P38	Goldstein	0.51	0.50	0.68	10.36	7.31	0.36
TRMD	GSK	0.51	0.47	0.65	2.62	1.63	1.75
TYK2	Liang	0.39	0.51	0.63	6.51	3.22	0.59

Details on the Individual Protein and Ligand Data Sets:

The predictability results for the eight individual systems are presented in Table S4–S11 of the supporting information and summarized in Table 4, which shows the top ACS/sampling for each set. In Table 5, the results using the GAX18 ACS Exhaustive r_LP = 10 Å protocol are presented. The variability of the top protocols for the different data sets is evident. This speaks to the inherent challenge in computer-aided drug design of applying standardized methods to a wide range of systems. While in the present study the GAX18 ACS Exhaustive r_LP = 10 Å protocol is overall the best, significant variability is present. Specific details associated with the individual systems are presented in the following paragraphs.

The highest scores for the FXR set were with GAX18 r_LP = 15 Å. Due to a number of ligand poses outside the binding pocket (Figure 2) for r_LP = 15 Å, the preferred protocol is r_LP = 10 Å, which produced the second highest overall predictability scores (Table S4). Inclusion of the halogen FragMaps improved the predictive ability better than with any other ligand set. For example, for r_LP = 10 Å the <PC>_S improves by 0.135 and 0.104 when comparing GAX18 and SX18 with their corresponding standard probe ACSs, respectively. This is consistent with the significant number of halogenated compounds (72 out of 102) in that set (Table S1).

The highest scores for HDM2 were in the r_LP = 10 Å protocol with the GAS18 ACS (Table S5). While for the majority of the studied systems the halogen ACSs have better correlation scores than the standard ACSs, with HDM2 with many sampling protocols the opposite is true. The lower predictability in the absence of the halogen FragMaps is particularly interesting for the HDM2 set because every ligand in the set contains halogen atoms plus there are DMEO-classified atoms in 31 out of 32 ligands. Analysis of the predictability as a function of r_LP shows higher values with the halogen containing FragMaps for 1 and 2 Å while lower values occur with the larger values of r_LP (Table S5). This suggests that the halogen FragMaps may be leading to a decrease in the quality of the ligand poses when an extensive range of conformational sampling is allowed despite the more extensive sampling leading to improve predictability. Recent developments to improve the modeling of halogen-protein geometries in the CGenFF/CHARMM36m force field⁷³ may lead to improvements in this system as well as the other systems when halogens are considered explicitly.

With HSP90 the predictability scores were typically low (Table S6). The highest scores were in the local protocol with the GAX18 ACS with a significant decrease when Exhaustive sampling is used. The generally low predictability may be attributed to a wide diversity of ligand chemical scaffolds, speaking to the challenge of accurately ranking diverse ligands.

The highest scores for MCL1-Friberg were in the Exhaustive r_LP = 10 Å protocol with the GAX18 protocol (Table S7). The MCL1-Friberg set was the highest scoring set, which we attribute to the congeneric nature of the compounds. MCL1-Fletcher was also a high scoring set (Table S8). Interestingly, the targets occupy different regions of the RMSE plot in Figure 4. The two MCL1 sets overlap due to similar FragMap interactions, although the binding poses are different (Table 5). The Friberg set has high scores for every protocol, whereas predictive ability in the Fletcher set becomes comparable only after a large r_LP allows the reorientation of the binding poses described above (Figure 3). This indicates the importance of allowing reorientation of ligands especially in cases where the bound orientation of any of the ligands in the set has not been determined.

With P38 the entire set of ligands contains DMEO-classified atoms. Consistent with this, the highest predictability scores are found in ACS including the halogen FragMaps (Table S9), although with different sampling protocols improvements did not always occur with the halogen containing ACS. With Exhaustive r_LP = 15 Å the specific halogen, SX18, FragMaps yields the highest predictability for PI and PC while r_LP = 10 Å GAX18 yields the top R. These results indicate that the inclusion of the ether containing probe and the resulting ether FragMaps yields an increase in the predictability of the model.

In the TRMD set the highest scores were with the Local protocol for PI and PC with the GAX18 ACS with the highest R value obtained with Exhaustive r_LP = 15 Å and GAX18 (Table S10). However, with GAX18 the local protocol yield R = 0.604 vs. 0.633 for Exhaustive r_LP = 15 Å. The high predictability of the Local protocol indicates that the starting confirmations accurately represent the binding space of the ligands in the LBP. This is suggested to be associated with the authors releasing cocrystal structures for each of the 29 ligands in this set.

The TYK2 set also contains all halogenated ligands. As with HDM2 the FragMaps containing halogens are not the most predictable, with Local SS18 giving the best predictability although the decrease in predictability with SX18 is relatively small (Table S11). This success of the Local protocol appears to be due to the availability of a crystallographic structure of one ligand with the remaining ligands being structurally similar to that in the experimental structure. The success of the Local protocol suggests that the chemical modifications to the ligands do not significantly alter the binding poses relative to the crystal orientation of the parent ligand. The decrease in predictability with the halogen FragMaps may indicate that the halogen FragMaps may be leading to limitations in posing when using the Local protocol. Future studies using improvements in the halogen-protein force field may address this issue.

FragMap Reweighting Using Machine Learning

Physics-based approaches in ligand development offer the advantage that a priori knowledge of the ligands and their activities is not required to make useful predictions concerning both the identity of novel ligands for a target or ligand modifications to improve ligand affinity. The SILCS methodology falls into this category as only the structure of the target protein or other macromolecule is required, as is common to all target-based ligand design approaches including FEP, PB or GB/MMSA, LIE or other docking methods. And as has been shown above the SILCS approach allows for reasonable correlations to be achieved for different targets, with predictability as determined by the PC metric being competitive with much more computationally demanding methods, such as FEP, consistent with previous reports. ¹¹ However, once experimental data is available on a collection of ligands, with SILCS that information may be exploited to facilitate the ligand development process as long performed in the context of Quantitative-structure activity relationship (QSAR) and related methods.^74–76

More recently, advances in ML technologies have greatly increased the potential utility of QSAR-based approached. Indeed, ML technologies such as Support Vector Machine ⁷⁷, Random Forest,⁷⁸ and Neural Networks ⁷⁹ have been used in drug development for close to 20 years, especially in the area of absorption disposition, metabolism, excretion and toxicity (ADMET) predictions.^{80, 81} While such approaches are powerful, ML technologies typically require significant amounts of input data to train the high dimensional non-linear nets that many ML approaches use,^{82, 83} thereby limiting their utility in drug design during early parts of a ligand optimization project. An alternative to this is a Bayesian-type approach where the presence of a high-quality prior has the potential to yield predictive models without large amounts of training data. In the present study, this strategy is applied taking advantage of the SILCS FragMaps representing priors that may simply be reweighted targeting experimental ligand data sets of the size used in the present study. This represents the use of complex predictors that require less training data for model development versus simple predictors, like chemical structure, that require a lot of training data. SILCS FragMaps are indeed complex predictors which are based on functional group probability distributions collected during extensive SILCS GCMC-MD simulations.

In the present ML approach, we apply Bayesian Markov Chain Monte Carlo sampling to optimize the scaling factors associated with the different SILCS FragMaps that are the basis of the GFE and LGFE scores used for ligand posing and ranking (Table 1). This represents, in the case of the SILCS FragMaps, 10 to 20 scaling factors that require reweighting. Specifically, the number of scaling factors that need reweighting for the different ACS are GAS18=10, GAX=16, SS18=13 and SX18=20. However, the actual number of FragMap scale factors for which reweighting is required is based on the FragMap types represented in the ligands in the training set. For example, with the halogens, aliphatic F and Cl FragMaps are available; however, these classifications are often not present in a set of ligands as the halogens are typically located on aromatic groups. While the scale factors for such maps are not optimized during ML it needs to be emphasized that they are included unmodified when the ML revised SILCS FragMaps are applied such that additional ligands that include previously not represented FragMap types are modelled at a high level of accuracy. Indeed, the ease of the Bayesian MC optimization approach allows the model to be readily updated as new experimental data is obtained.

Evaluation of the ML approach applied k-fold validation with k = 5 initiated from the final GAX18 and SX18 Exhaustive r_LP=10 Å models for the 8 data sets. Reweighting was performed individually targeting the PC, R and RMSE metrics. Inclusion of RMSE was performed to determine if the reweighting approach would improve the agreement between the LGFE scores and the absolute binding affinities, while still yielding a predictable model. Initial application of the reweighting approach lacked bounds on the weighting factors yielding extreme deviations in the LGFE scores from experimental binding free energies when the R or PC metrics were targeted (Figure S9 of the supporting information). This represents severe over training associated with extreme rewkjjeighting which substantially compromise the physical meaning of the maps. Accordingly, the remaining results were based on the use of upper and lower bounds on the scaling factor as described in the methods. After reweighting based on the training set, the full set of ligands for each target were run in SILCS-MC and the average of the metrics over the five k-fold validation sets were determined: <<PC>_S>₅, <R>₅, and <RMSE>₅. We define a significant difference between the original metric and average metric over the 5-fold sets to be an improvement of more than one standard deviation.

The <<PC>_S>₅ of the full ligand sets for GAX18 are shown in Figure 5. Results are presented for the original scaling along with those following ML targeting the PC, R or RMSE metrics. When targeting the <PC>_S or R metrics, the <<PC>_S>₅ is always significantly improved by the reweighting. When targeting the RMSE, the <<PC>_S>₅ was significantly improved only for the FXR, HDM2, HSP90, TRMD and TYK2 sets. This indicates that the specific metric being targeted in the ML, not unexpectedly, impacts the improvements in the predictability of the model with respect to the different metrics.

Figure 5.

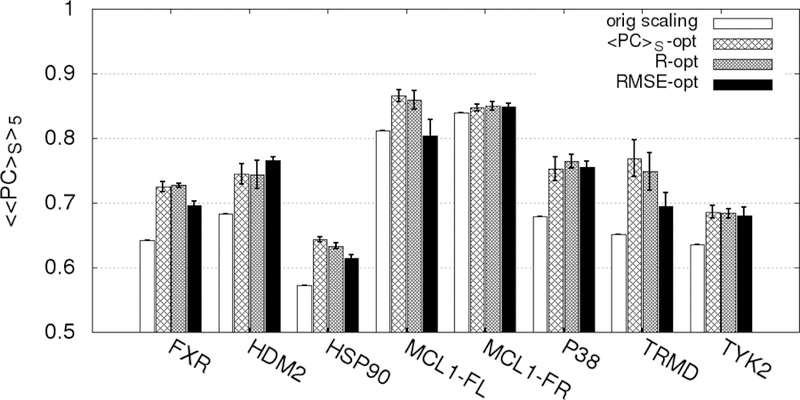
Percent correct average values <<PC>_S>₅ for each target-ligand set before and after rescaling using the ML algorithm in 5-fold cross-validation for the GAX18 ACS. The PC-opt, RMSE-opt, and R-opt bars are the correlation scores for the entire set (training + validation) targeting the respective metrics averaged across the 5 training-validation set pairs. The magnitude of the error bars are one standard deviation of the 5 <PC>_S values for each correlation.

To further investigate the impact of the metric targeted in the ML reweighting on the improvement in the metrics themselves analysis was done on R and RMSE. The results are shown in Figure 6 and 7, respectively. As may be seen in Figure 6 the <R>₅ values are always improved when R was targeted. When <PC>_S was targeted, all the R values except for MCL1-Friberg were significantly improved. However, when RMSE was targeted MCL1-Fletcher and MCL1-Friberg failed to improve.

Figure 6.

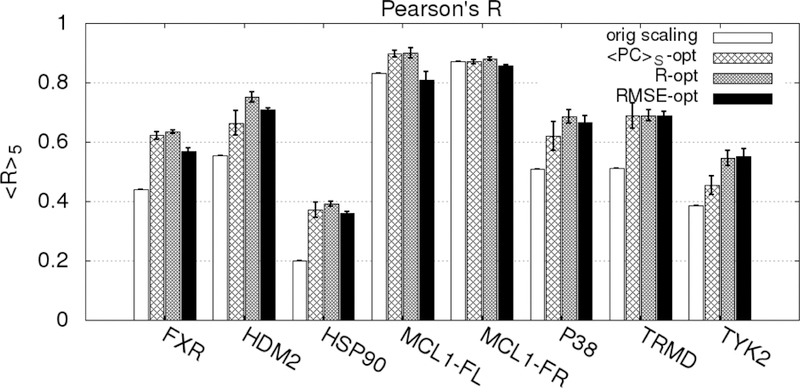
Pearson’s R average values <R>₅ for each target-ligand set before and after rescaling using the ML algorithm in 5-fold cross-validation for the GAX18 ACS. The PC, RMSE, and R-opt bars are the correlation scores for the entire set (training + validation) targeting the respective metrics averaged across the 5 training-validation set pairs. The error bars are one standard deviation of the 5 R values.

Figure 7.

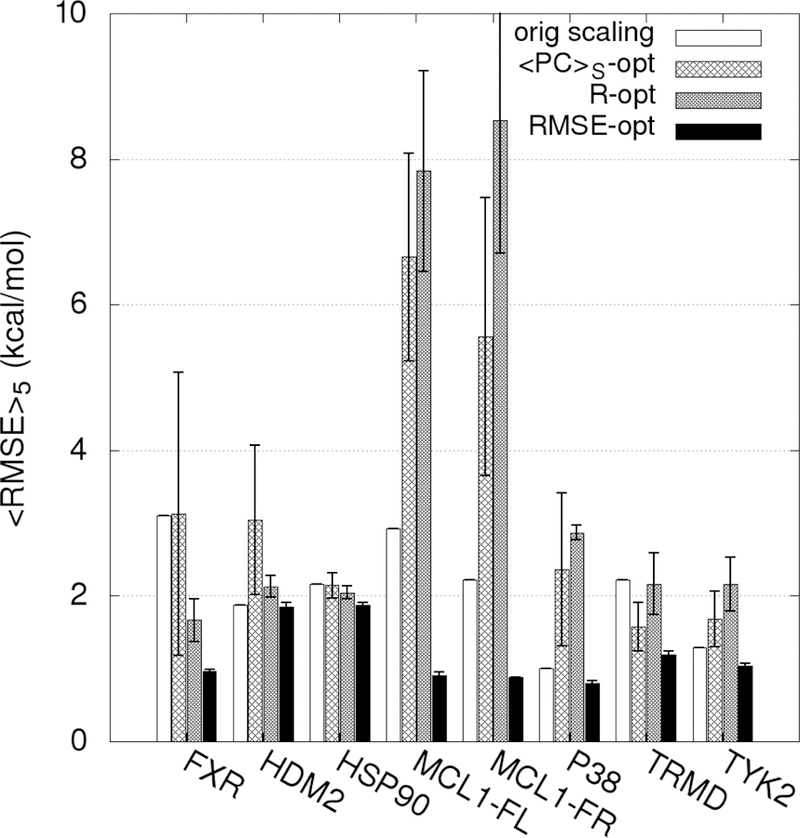
RMSE average values <RMSE>₅ for each target-ligand set before and after rescaling using the ML algorithm in 5-fold cross-validation for the GAX18 ACS. The PC-opt, RMSE-opt, and R-opt bars are the correlation scores for the entire set (training + validation) averaged across the 5 training-validation set pairs.

A significantly different pattern is obtained with respect to the impact of ML on the optimized RMSE values. Typically, when PC or R are targeted there is a large degradation in the <RMSE>₅ values (Figure 7) in contrast to typically small improvements in PC and R when RMSE is targeted (Figures 5 and 6). However, there is significant improvement in RMSE when RMSE is targeted (Figure 7).

Similar analysis to that in Figures 6, 7 and 8 for the SX18 ACS is presented in Figures S10, S11 and S12 of the supporting information. The trends are generally the same as with the GAX18 analysis. Targeting R or PC leads to improvement in each metric, while only small improvements in RMSE are obtained. Targeting RMSE leads to significant improvements in RMSE itself while R and PC typically get worse. Thus, reweighting the FragMaps to improve the agreement of the LGFE with the absolute values of the experimental binding free energies by targeting RMSE does not improve the correlation of the relative LGFE scores with the experimental data. When R or PC are targeted there are small improvements in the RMSE, though the extent of the improvements is substantially less then when RMSE itself is targeted. Targeting either R or PC typically leads to improvements in both R and PC, as expected as both metrics are primarily dictated by the relative binding affinities of the ligands in the individual target sets. These results indicate that when applying the ML approach, targeting R and PC is preferable when the goal is to improve the predictability of the model, with PC preferred as this metric is of the greatest utility when make go, no go decisions in the context of the ligand optimization campaign.

A summary of the average percent correct across all 8 target-ligand sets, <<<PC>_S>₅>₈, is presented in Table 6. For GAX18 r_LP = 10 Å the average PC was 68.8% with the original weighting, while a value of 63.8% was obtained with SX18 r_LP = 10 Å. With the GAX18 ACS, use of either the PC or R metric led to an improvement of 6% to values of 75%. With the specific SX18 ACS improvement of about 10% occurred going from 64% to 74%. However, when the ML reweighting is performed targeting the RMSE metric the improvement in PC was decreased, consistent with the results above. The larger improvement is the SX18 PC values is suggested to be associated with the greater number of FragMaps available for reweighting versus GAX18, though the lower PC values based on the original weights may contribute.

Table 6.

Average percent correct scores from the 5-fold k validation across the eight ligand sets when targeting the different metrics for the ML reweighting protocol

Objective function	<<<PC>S>5>8, GAX18	<<<PC>S>5>8, SX18
original weights	0.69	0.64
<PC>S	0.75	0.74
R	0.75	0.75
RMSE	0.73	0.72

Considering the individual data sets, analysis of Figures 6 and 7 indicate that the amount of improvement by ML is impacted by the initial predictability of the original SILCS FragMaps. For example, small improvements occur with the both MCL1 sets, which had R and PC values of greater than 0.8. The HDM2, HSP90 and TRMD sets showed significant improvements of 6.2, 7.1 and 12.1%, respectively, for PC when the PC metric was targeted (Figure 5). Interestingly, the size of the training set does not appear to be important as the HDM2 and TRMD sets contain 32 and 29 ligands, being the smallest sets studied, while the HSP90 set has 180 ligands, representing the largest set.

Conclusions and outlook

Through extensive simulations of a chemical library of 551 ligands broken down into eight sets that targeted seven proteins, we have optimized and evaluated the SILCS-MC methodology. The protocol makes use of a new normalization that accounts for the concentration of the probe atoms in the simulation system and scaling of the FragMap GFE values based on the number of probe atoms contributing to each FragMap. Scaling of the FragMap GFE values is required to properly treat solute- versus atom-based concentrations when using the atom-based GFE scores to calculate the full ligand LGFE scores. These improvements lead to better agreement between absolute ligand LGFE scores and experimental ΔG_bind values, though it is again emphasized that the LGFE values do not directly represent ΔG_bind due to the omission of a number of terms such as the energetic costs of covalently linking the functional groups into the full ligands, intramolecular distortion associated with binding and others.⁷²

The ACS-protocol pair that yielded the highest 8-set-average overall correlation score was GAX18 Exhaustive r_LP = 10 Å, which yielded correct predictions for 68.8% of ligand pairs. The GAX18 protocol includes specific FragMaps for halogen atoms and contributions of ether oxygens to the GENA FragMaps from a new probe suite called SILCS-X that was introduced in this study. In six out of eight systems, the SILCS-X FragMaps increased the predictive ability of SILCS-MC. Thus, building on previous studies that include halogen containing species in cosolvent simulations,^{9, 60} the present results further show that the inclusion of specific information on halogenated functional groups leads to improved predictability.

Concerning the MC sampling protocol, the Exhaustive r_LP = 10 Å method initiates ligands in random orientations within 10 Å of the binding pocket. The protocol involves many independent MC runs combined with a convergence criteria to assure that the free energy landscape of the LBP as defined by the FragMaps is well explored by the ligands. The general improvements over Exhaustive sampling with small radii indicates the importance of sampling a range of possible conformations. Importantly, usage of r_LP = 10 Å still maintains the ligands in the LBP. An important consideration when applying exhaustive sampling is assuring that the ligands are sampling the targeted LBP, as it may be anticipated that in some systems ligands may sample beyond the LBP with r_LP = 10 Å.

While overall the Exhaustive r_LP = 10 Å approach is best, there are clear exceptions. For example, improved predictability using the Local protocol occurs with the HSP90, TRMD and TYK2 sets. This appears to be due to these ligand sets being dominated by a congeneric series of compounds for which a good starting orientation of the parent ligand is available. In such cases the Local sampling protocol would be the best to use, versus the use of the Exhaustive r_LP=10 Å protocol when more diverse ligands and less well-defined starting orientations of the ligands are available.

The final section of the paper applied a ML Bayesian Markov Chain Monte Carlo approach to optimize the SILCS FragMap scaling factors. Using cross validation, it is shown that the approach can lead to improved predictability for all the studied systems. Such a tool represents a useful extension of the SILCS approach as it allows for continuous improvements in the model even during the early stages of a drug discovery campaign when experimental data is only available on 10s of compounds. This is due to the use of the scaling factors of physically correct SILCS FragMaps as priors allowing for optimization with a small training set of compounds. Notably, the reweighted SILCS FragMaps are still physically interpretable, allowing for their use in both the qualitative and quantitative aspects of CADD. Future improvements in the reweighting procedure could be to focus on a subset the ligands for a given target, for example in sets like FXR and HSP90 with multiple ligand compound families.

The present results indicate the system specific nature of the use of SILCS FragMaps, a problem which is a general challenge to CADD. The results indicate that in cases where diverse ligands are being developed and/or there is low confidence in the bound orientations of the ligands being designed, then the GAX18 Exhaustive r_LR= 10 Å approach would initially be applied for prediction of compounds with improved activity. On the other hand, if the compounds being designed fall within a congeneric series and there is high confidence in the orientation of the ligands, then a local sampling protocol should initially be used for making prediction of compounds with improved activity. However, once an initial set of ligands has been developed and subjected to experimental analysis, then the ACS/sampling combination that yields the best predictability, PC, following ML training should be applied for the design of additional ligands. Indeed, when the top protocol for a given system is identified the average PC value is 72 % before ML training and 76% after ML training as shown in Table 7. Notably, the PC value of 76% is similar to the reported value of 78% of Wang et al.³⁴ and better than the value of 70% reported by Song et al.³⁵ In both of those studies FEP was used to predict affinities on 7 training sets on a total of 199 compounds out 372 compounds reported in the original literature, significantly lower that the number used in the present study that included all available compounds.

Table 7.

Percent correct, <PC>_S, for each set when the top Sampling/ACS protocol is identified for that set based on the available data following which the FragMap scaling factors are optimized using the presented machine learning protocol.

			SILCS Default FragMap Scoring	ML Reweighted FragMap Scoring
System	Sampling Protocol	ACS	<PC>S	<PC>S
FXR-GSK	Exhaustive rLP = 10 Å	GAX18	0.64	0.73
HDM2-Turiso	Exhaustive rLP = 10 Å	GAS18	0.72	0.75
HSP90-Abbvie	Local	GAX18	0.63	0.64
MCL1-Fletcher	Exhaustive rLP = 5 Å	GAX18	0.82	0.87
MCL1-Friberg	Exhaustive rLP = 10 Å	GAX18	0.84	0.85
P38 Goldstein	Exhaustive rLP = 10 Å	GAX18	0.68	0.78
TRMD-GSK	Local	GAX18	0.69	0.79
TYK2 Liang	Local	SS18	0.71	0.70
Average			0.72	0.76

Accordingly, application of the SILCS methodology allows for initial high quality predictions of relative ligands activities in the absence of any training data in a computationally accessible fashion, with significant improvements in the predictability of the method being accessible once even a small training set of data is available.