Honeybees use absolute rather than relative numerosity in number discrimination

Abstract

Various vertebrate species use relative numerosity judgements in comparative assessments of quantities for which they use larger/smaller relationships rather than absolute number. The numerical ability of honeybees shares basic properties with that of vertebrates but their use of absolute or relative numerosity has not been explored. We trained free-flying bees to choose variable images containing three dots; one group (‘larger’) was trained to discriminate 3 from 2, while another group (‘smaller’) was trained to discriminate 3 from 4. In both cases, numbers were kept constant but stimulus characteristics and position were varied from trial to trial. Bees were then tested with novel stimuli displaying the previously trained numerosity (3) versus a novel numerosity (4 for ‘larger’ and 2 for ‘smaller’). Both groups preferred the three-item stimulus, consistent with absolute numerosity. They also exhibited ratio-dependent discrimination of numbers, a property shared by vertebrates, as performance after 2 versus 3 was better than after 3 versus 4 training. Thus, bees differ from vertebrates in their use of absolute rather than of relative numerosity but they also have some numeric properties in common.

1. Introduction

The ability to discriminate between quantities has been documented in several vertebrate species, where it improves survival and reproductive success in various behavioural contexts [1–4]. Although the evolutionary origin of this capacity is a long-standing debate [4–8], studies using both training procedures and spontaneous choice tests [9] have demonstrated the existence of a shared system for representing quantities across vertebrate species. This system includes features such as a ratio-dependent discrimination of numerosities (i.e. accuracy decreases as the numerical ratio between the quantities to be discriminated increases in concordance with Weber's Law) [10–13] and a preference for the use of relative (select the larger/smaller number of items) rather than absolute numerosity (select a specific number of items) [14–16].

Relative numerosity has been studied using a protocol that yielded similar results in species as distant as humans and fish [16]. When subjects of both species were trained to select arrays containing 10 dots, either in 5 versus 10 (larger) or 10 versus 20 comparisons (smaller), they preferred subsequently a novel numerosity to the trained one (20 for ‘larger’ and 5 for ‘smaller’), based on a relative-numerosity rule.

Although research on quantitative abilities in animals has mainly focused on vertebrates, several studies have shown that invertebrate species can also estimate quantities. In particular, honeybees, with their remarkable cognitive abilities [17–19], have been the subject of various studies focusing on their sense of numerosity. Free-flying honeybees trained to forage at a feeder placed after a specific number of landmarks can use landmark number to decide where to land [20]. Also, in a delayed matching-to-sample protocol, bees choosing visual stimuli within a Y-maze were able to match stimuli based on number, irrespective of their shape, colour or spatial distribution [21]. The sense of numerosity of bees also includes the concept of zero (i.e. a quantity at the low end of a positive integer numerical continuum) [22], and even the capacity to perform basic addition and subtraction [23].

Here we studied if honeybees would follow a relative or an absolute numerosity judgement when confronted with a quantity discrimination task. We adapted a protocol used for fishes [14,16], and trained free-flying bees to select either the larger array (3) in a 2 versus 3 discrimination, or the smaller array (3) in a 3 versus 4 discrimination. In both cases, numbers were kept constant but stimulus characteristics and position were varied from trial to trial, in order to rule out the use of lower-order cues. Bees were then tested with the previously trained numerosity (3) versus a novel numerosity (4 or 2, respectively). Use of relative numerosity, as reported for humans and fish, predicts preference for 4 in the ‘larger’ group and for 2 for in the ‘smaller’ group; use of absolute numerosity predicts preference for 3 in both cases.

2. Methods

(a). Apparatus and stimuli

Twenty-four free-flying honeybee foragers (Apis mellifera) were individually marked and trained one at time to collect food (0.88 M sucrose solution) in a wooden Y-maze [24,25] (figure 1a). Further details on this set-up are available in the electronic supplementary material. Within the maze, bees had to learn to discriminate between two numerosities, one of which was rewarded with sucrose solution and the other punished with 60 mM quinine solution [26]. Reinforcing solutions were delivered in the centre of the back walls of the maze.

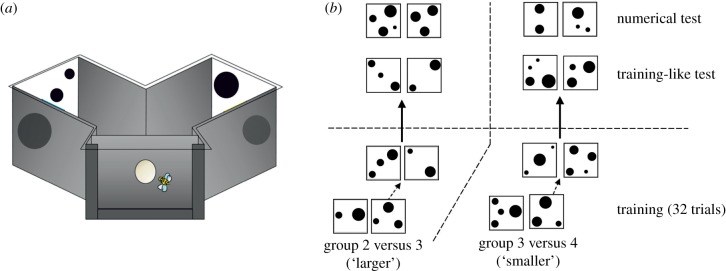
Figure 1.

(a) View of the Y-maze. The maze was covered by a UV-transparent Plexiglas ceiling, and had an entrance hole that allowed access to a decision chamber from where both numeric arrays were visible. (b) Examples of visual stimuli used during the training phase and the tests. The training phase consisted of 32 trials during which stimuli were varied from trial to trial, keeping the rewarded numerosity constant. The groups 2 versus 3 (larger) and 3 versus 4 (smaller) were always rewarded for choosing 3, irrespective of stimulus variation. After training, bees were subjected to two non-reinforced tests. In a training-like test, they had to choose between the numerosities experienced during training displayed through novel stimuli. In a numerical test, they were confronted with a novel situation in which the rewarded numerosity (3) was opposed to a novel one (4 for the ‘larger’ group, and 2 for the ‘smaller’ group). (Online version in colour.)

Stimuli consisted of groups of black dots on a white background (figure 1b). The size of the dots and their spatial distribution varied between trials to prevent bees learning non-numeric information. To exclude the possibility that bees could use the cumulative surface area of the dots of an array to estimate if it was larger or smaller [27], in half of the training stimuli the cumulative surface area was matched to 100%, whereas in the other half it was not controlled [14,28]. Furthermore, half of the stimuli were controlled for convex hull and the other half for density. Stimuli used in the test phase were all matched to 100% (for details see the electronic supplementary material).

(b). Training and test procedure

The experimental procedure consisted of a pre-training phase, in which all bees were familiarized with the Y-maze and the possibility of collecting sucrose solution therein in the absence of visual stimuli, a training phase and a test phase. For each bee, the three phases were completed in 1 day. During the training phase (figure 1b), two independent groups of individually marked bees were trained in parallel; one was trained to choose 3 in a 2 versus 3 (‘larger’ group; n = 12), while the other was trained to choose 3 in a 3 versus 4 discrimination (‘smaller’ group; n = 12). Each bee was trained during 32 consecutive visits to the maze. For both groups, only the stimulus displaying three dots was rewarded with sucrose solution, while the alternative stimulus provided quinine solution. Stimuli were presented in a pseudo-random sequence and the larger/smaller stimulus was never presented more than twice in a row on the same side (additional details on the training procedure can be found in the electronic supplementary material).

Once the bees completed the training phase, they were tested in two non-reinforced tests (figure 1b). Novel stimuli were presented during the tests. Each test lasted 45 s and was repeated twice. The left/right position of the stimuli was exchanged between repetitions to control for side biases. In the training-like test, bees were presented with the numerical discrimination experienced during training (either 2 versus 3 or 3 versus 4) but with novel item configurations never used during the training. In the numerical test, bees trained to discriminate between 2 versus 3 (‘larger’ group) were presented with 3 versus 4, whereas bees trained to discriminate 3 versus 4 (‘smaller’ group) were presented with 2 versus 3.

(c). Statistics

During the training, only the first choice (entering the maze arm displaying a given item array) was scored for statistical analyses. Training performances were consequently analysed using a generalized linear mixed model (GLMM, R 3.5.2, R Core Team, lme4 package). During the tests, we quantified the cumulative contacts of the bee with the surface of the two targets over the test length. The percentage of choices for each of the two test stimuli was then calculated. Performance during the tests was analysed in terms of the proportion of correct choices per test, producing a single value per bee to exclude pseudo-replication. A one-sample t-test was used to test if the proportion of correct choices was higher than the random value of 50%. The α-value was 0.05 in all cases. More details are available in the electronic supplementary material.

3. Results

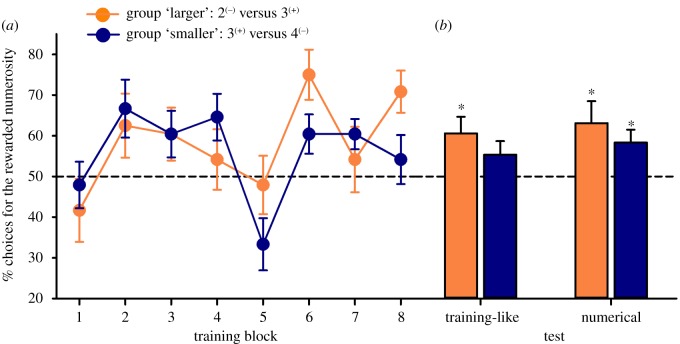
In the training phase (figure 2, left), no overall significant effect of learning (GLMM: Trial effect: ${\mathit{\Sigma }}_1^2=1047.1$, p = 0.19) was found. There was neither a significant group effect (${\mathit{\Sigma }}_1^2=1048.4$, p = 0.51) nor an interaction between training group and performance (Group*Trial: ${\mathit{\Sigma }}_1^2=1044.2$, p = 0.11). However, bees trained to discriminate 3 from 2 increased their correct choices from the first (42.7 ± 7.7% of correct choices; mean ± s.e.m.; figure 2a, left) to the last block of four trials (70.8 ± 5.2% of correct choices; two-sample t-test: t₁₁ = 3.19, p = 0.009; figure 2a, left). This was not the case for the group of bees trained to discriminate 3 from 4 (47.9 ± 5.7% versus 54.2 ± 6.0%; t₁₁ = 0.64, p = 0.54; figure 2a, left).

Figure 2.

Learning and test performance. (a) Learning curves of the groups 2 versus 3 (‘larger’; orange (light) symbols and bars) and 3 versus 4 (‘smaller’; blue (dark) symbols and bars), which were both rewarded for choosing 3. Data shown are means ± s.e.m. presented as blocks of four trials. Bees trained to discriminate 3 from 2 increased their correct choices from the first to the last block of four trials (two-sample t-test: t₁₁ = 3.19, p = 0.009). This was not the case for the group of bees trained to discriminate 3 from 4 (t₁₁ = 0.64, p = 0.54). (b) Performance during the learning test (same numerosities as those experienced during training but displayed through new stimuli) and the numerical test (the rewarded 3 numerosity versus 4 for the ‘larger’ group and versus 2 for the ‘smaller’ group). Data shown are means ± s.e.m. n.s.: non-significant; *p < 0.05. (Online version in colour.)

In the training-like test (figure 2b, right), bees trained with the 2 versus 3 discrimination preferred the trained numerosity (3) when the same discrimination was proposed using novel stimuli. Their preference (60.60 ± 4.07%; mean ± s.e.m.) was significantly different from a theoretical 50% choice performance (one-sample t-test; t₁₁ = 2.61, p = 0.02). In the case of bees trained with the 3 versus 4 discrimination, performance (55.36 ± 3.33%) did not reach significance in the training-like test when compared with a 50% value (t₁₁ = 1.61, p = 0.14).

In the numerical test (figure 2b), bees trained with the 2 versus 3 discrimination preferred significantly (63.10 ± 5.39%) the trained (3) to the larger numerosity (4) (t₁₁ = 2.43, p = 0.03), thus showing absolute number preference. Similarly, despite their performance in the training-like test, bees trained with the 3 versus 4 discrimination also preferred (58.37 ± 3.14%) the trained numerosity (3) to the smaller one (2) (t₁₁ = 2.67, p = 0.02), consistent with an absolute numerosity judgement.

4. Discussion

Our results show that bees, contrary to vertebrates [14], did not use a relative numerosity rule. Under our training conditions, they rather used an absolute numerosity rule, as in the numerical tests the two groups of bees always preferred stimuli displaying three items, irrespective of having been trained to choose the smaller or the larger item array. Importantly, our training procedure varied systematically the nature and position of numeric items and our stimuli were matched/randomized for lower-order cues so that learning involved the extraction of the numeric concept ‘three’ and thus required exact quantification. In classical studies on bee visual discrimination, pattern spatial frequency, i.e. the number of light/dark cycles per degree (c/deg) of visual angle, was said to play a role in the bees' choice [29]. Yet, later studies on higher-order visual learning in bees performed under similar conditions as our numerosity study (discrimination of multiple-item patterns presented vertically within identical Y-mazes) showed that bees do not rely on local-feature analyses allowing the computation of spatial frequency but rather on holistic views (e.g. [30]). Even if spatial frequency is influenced by the number of dots, its dependency on visual angle renders difficult determining if and when a flying bee uses it for discrimination, as visual angle varies not only with the distance to the target, but also with the yaw and tilt of the bee body, among other factors.

Our results are in apparent contradiction with a recent work showing that bees trained to solve numeric discriminations based on a ‘less-than’ rule transfer their choice to a no-stimulus situation when confronted with a single item, thus revealing the presence of a concept of zero [22]. In this case, bees used a relative numerosity strategy. Yet, the training procedure used in that work was different from the one used in our experiments. Numerosities were constantly varied during training, leaving only the ‘less-than’ rule as the single factor predicting reward [22]. On the contrary, we kept numerosity fixed during training. Numerosity was also maintained constant in a delayed-matching to sample protocol [21], which revealed the capacity of bees to match absolute number, irrespective of parameters such as shape, colour and position. In other words, if trained to do so, bees have the capacity to solve a problem using relative numerosity; yet, if their training does not promote this rule, and if numerosity remains constant, they use absolute numerosity. Thus, bees can use both absolute and relative numerosity and the strategy adopted may depend on parameters such as the difficulty of the discrimination or the training schedule used by the experimenter. In any case, the sense of numerosity of bees is highly plastic and adaptable to experimental conditions, a conclusion that applies to other forms of visual learning [31].

Our results showed that bees succeeded in achieving the 2 versus 3 discrimination but had more difficulties with the 3 versus 4 discrimination. Differences in the learning curves and the training-like test corresponding to the two types of discriminations support this conclusion. This difficulty could be explained by the fact that the 3 versus 4 discrimination hits the limit of numerosity (4) suggested by other works [21,32] and the difference of just one integer may have rendered this task complicated. A difference of one integer also exists for 2 versus 3 but the numeric ratio differed between the two discriminations: it was 0.66 for 2 versus 3 and 0.75 for 3 versus 4. This is consistent with a ratio-dependent discrimination of numerosities where accuracy decreases as the numerical ratio between the quantities to be discriminated increases [10–13,33]. Accordingly, when the 3 versus 4 group was confronted with the ‘easier’ 3 versus 2 discrimination (numerical test) they had no problems in preferring 3 to 2, despite the difficulties exhibited during the training. This underlines the difficulty of using this design to test additional discrimination pairs involving higher numerosities and for which the numerical ratio between quantities to be discriminated would be even larger (e.g. 0.8 for 4 versus 5). On the contrary, a 1 versus 2 discrimination would be easier (ratio 0.5), but the presence of a single item in one stimulus type would render it difficult to control for low-level cues such as convex hull or stimulus density in this experimental design.

The fact that bees seem to rely more on absolute rather than on relative numerosity after absolute conditioning suggests the existence of neurons dedicated to numbers, as found in corvids and primates [34–36]. The convergence between birds and primates indicates that circuits involved in processing numerosity may be evolutionarily conserved among vertebrates [37]. Although the brain of bees differs significantly from that of vertebrates, some higher-order areas could fulfil the characteristics required for numerosity representation. In particular, the central complex, a region of the insect brain receiving highly processed visual input, which is topologically ordered and involved in navigation, object recognition, path integration and short-term forms of visual memory [38], appears as an interesting candidate for visual number representation. Further studies should address the involvement of this and other structures of the bee brain in numerosity.

Ethics

French law does not require ethical approval for studies involving insects.

Data accessibility

Data available from the Dryad Digital Repository at: https://doi.org/10.5061/dryad.7rv4ct1 [39].

Authors' contributions

The experiments were designed by M.E.M.P., C.A., A.B. and M.G. They were conducted by M.B. who was supervised by M.E.M.P., C.A., A.B., A.A-W. and M.G. Analyses and figures were done by M.B., M.E.M.P., C.A, A.A-W. and M.G. The manuscript was written by M.B., M.E.M.P., C.A., A.B., A.A-W. and M.G. All authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

Funding was provided by the Centre National de la Recherche Scientifique, the Université de Toulouse and the Ministero dell'Istruzione, dell'Università e della Ricerca (MIUR; grant no. 2015FFATB7). M.G. thanks the Institut Universitaire de France for support.