An architectural understanding of natural sway frequencies in trees

Abstract

The relationship between form and function in trees is the subject of a longstanding debate in forest ecology and provides the basis for theories concerning forest ecosystem structure and metabolism. Trees interact with the wind in a dynamic manner and exhibit natural sway frequencies and damping processes that are important in understanding wind damage. Tree-wind dynamics are related to tree architecture, but this relationship is not well understood. We present a comprehensive view of natural sway frequencies in trees by compiling a dataset of field measurement spanning conifers and broadleaves, tropical and temperate forests. The field data show that a cantilever beam approximation adequately predicts the fundamental frequency of conifers, but not that of broadleaf trees. We also use structurally detailed tree dynamics simulations to test fundamental assumptions underpinning models of natural frequencies in trees. We model the dynamic properties of greater than 1000 trees using a finite-element approach based on accurate three-dimensional model trees derived from terrestrial laser scanning data. We show that (1) residual variation, the variation not explained by the cantilever beam approximation, in fundamental frequencies of broadleaf trees is driven by their architecture; (2) slender trees behave like a simple pendulum, with a single natural frequency dominating their motion, which makes them vulnerable to wind damage and (3) the presence of leaves decreases both the fundamental frequency and the damping ratio. These findings demonstrate the value of new three-dimensional measurements for understanding wind impacts on trees and suggest new directions for improving our understanding of tree dynamics from conifer plantations to natural forests.

1. Introduction

1.1. Natural frequencies and tree architecture

The dynamics of trees in the wind has interested observers for centuries, but detailed studies concerning the risk of wind damage are relatively recent [1,2]. All structures that can sway, such as trees in the wind, possess natural frequencies—characteristic shapes and speeds at which the motion is concentrated. The natural frequencies of a tree are related to its architecture [3,4] and they influence its response to wind loading [5], thus linking form and function. However, due to the difficulty of obtaining detailed information on tree architecture, this link has remained largely unexplored (although see [4]). Recently, terrestrial laser scanning (TLS) has revolutionized the mapping of tree architecture [6], paving the way for more detailed studies on this intriguing subject.

The lowest natural frequency, known as the fundamental frequency (f₀), is particularly relevant for wind damage risk. This is because wind energy is concentrated at low frequencies [7] and energy will be transferred from the wind to the tree more efficiently in trees with lower f₀, a phenomenon known as resonance [8–10]. Previous work found that the f₀ of 602 conifers in the UK and North America was accurately predicted by the cantilever beam approximation [8,9], which models the tree as a vertically oriented cylinder with uniform radius and material properties. According to this approximation, f₀ will decrease with increasing tree height, leading to an increased likelihood of resonant effects in taller trees. Importantly, no field study has yet recorded the moment a tree breaks or uproots due to wind loading [11] and the relevance of resonant effects in wind damage is the subject of ongoing debate in the literature [11–14].

Knowledge about the natural frequencies of a structure allows for a detailed model of that structure's dynamics under loading. In the case of conifer trees in the wind, data on f₀ provided the basis for an accurate model of tree motion under wind loading at the plot level [15]. This was possible because the dynamics of conifers are, in uniform plantations, dominated by f₀ due to their simple architecture. However, the dynamic properties of broadleaf trees are unlikely to follow these simple patterns, but rather consist of multiple significant natural frequencies and be dependent on tree architecture and the presence or the absence of leaves [3,16]. Trees with multiple significant natural modes can exhibit multiple resonance damping, a dynamic process whereby dangerous energy in the stem is dissipated by the movement of the branches [17,18]. The existence of this damping mechanism demonstrates the relationship between wind damage risk and tree architecture: trees with certain architectures will dissipate dangerous sway energy more efficiently and so reduce their risk of damage in storms. See Spatz & Theckes [17] for a review of multiple resonance damping (and the similar concepts of structural damping and damping by branching).

1.2. Objectives and structure of the paper

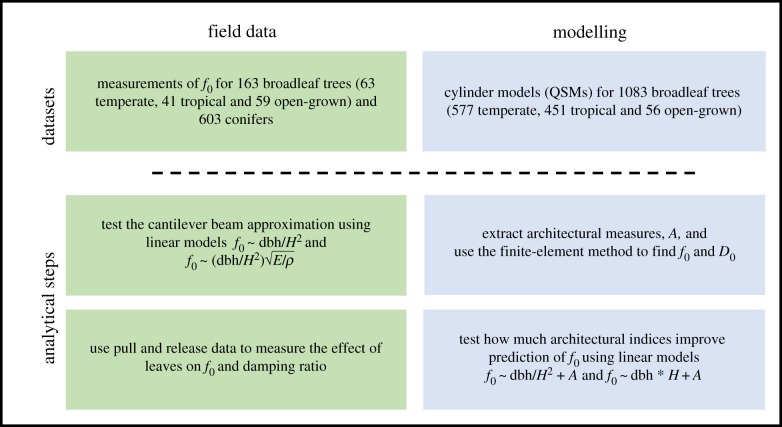
Our overall aim is to explore the relationship between tree architecture and the dynamics of trees in the wind, in particular their natural sway frequencies. We employ the cantilever beam approximation (equation (1.1)), appropriate to the simple architecture of many conifers, as a starting point and add additional terms to explain residual variation caused by the complexities of broadleaf trees (equation (1.1)). Our updated equation takes the form:

$$f_0\propto \left(\frac{\mathrm{dbh}}{H^2}\sqrt{\frac{E}{\rho }}\right)A\times L,$$ 1.1

where H is tree height and dbh is the diameter at breast height, measured at 1.3 m, and E/ρ is the ratio of green wood elasticity to density. The additional terms A and L represent the effect of tree architecture and leaves, as described below. In order to explore these additional terms, we:

• (1)Collate field data on f₀ for 163 broadleaf trees spanning open-grown conditions, tropical forests, temperate forests and a height range of 4.7–55.7 m (see electronic supplementary material, table S1 for a detailed overview). We then use this field data to test the applicability of the cantilever beam approximation to broadleaf trees. Architectural information was not collected in these studies and is immensely difficult to collect in the field.
• (2)Explore the range of tree architecture by bringing together TLS data for 1083 trees from previous studies spanning tropical and temperate forests, cities and parks (electronic supplementary material, table S1). We also test for covariance between these architectural indices, since they are used as explanatory variables in the next step.
• (3)Quantify the architectural term, A (equation (1.1)) in a model environment. We use finite-element analysis to simulate f₀ (figure 1) for each of the 1083 trees. We then test how well the cantilever beam approximation predicts the simulated f₀ and whether any residual variation can be explained by the architectural indices extracted in the previous step.
• (4)Calculate the dominance of the fundamental sway mode, D₀, based on the same finite-element simulations and test how it is related to tree architecture. D₀ is defined as the percentage of generalized mass contained in f₀. Trees with D₀ > 90% behave like a simple pendulum, with a single dominant sway mode, while lower D₀ values correspond to an increasing significance of higher order natural sway modes in the overall motion of the tree.
• (5)Use pull and release data to explore how leaves change f₀ and damping rates in deciduous broadleaf trees.

Figure 1.

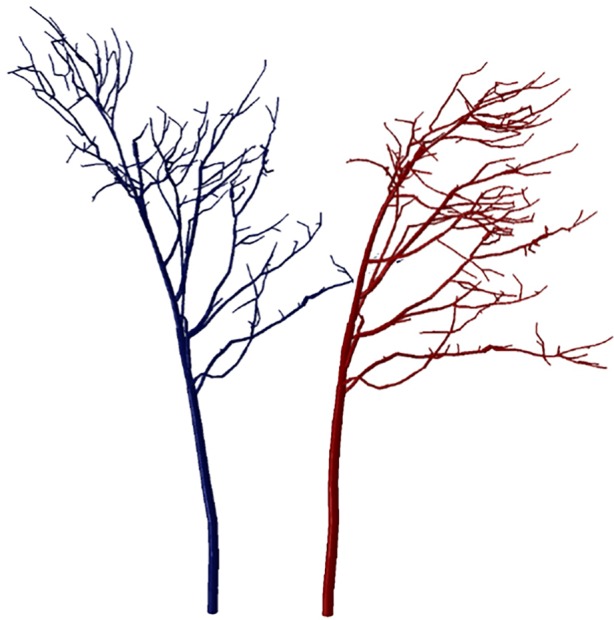
Simulated fundamental sway frequency of a tree. Finite-element simulation output showing the two extreme positions (blue and red) for a sycamore tree (Acer pseudoplatanus) swaying at its fundamental frequency, f₀ = 0.26 Hz. (Online version in colour.)

2. Material and methods

2.1. Analysis of field data

In order to extract field data on f₀, we measured wind-induced strain (extension/original length) following Moore et al. [19] for a period of eight months (spanning winter and summer) at 1.3 m height on the trunks of 18 trees (21 stems) in Wytham Woods, UK, and for five months on 20 trees in Danum Valley, Malaysia. We separated the strain data into hourly blocks and analysed them using a Welch's power spectral density function [20]. We smoothed the resulting spectra and extracted the peak frequencies. We then took the mean of all the hourly frequencies. We also collated data on the f₀ of trees from previous studies (see the electronic supplementary material, table S1 for an overview of field data). Fundamental frequency extraction from previous studies are described in the original publications [3,9,21–25].

To investigate the damping effect of leaves, we conducted pull and release tests on four trees (two Acer pseudoplatanus L., one Fraxinus excelsior L. and one Betula spp.) in Wytham Woods in February 2016 (leaf-off) and June 2016 (full-leaf), repeating the tests multiple times per tree in perpendicular directions. The trees behaved like damped harmonic oscillators and we therefore fit functions of the form

$$\epsilon ={\epsilon }_0{\mathrm{e}}^{-\mathrm{\lambda }t}\cos (2\pi f_{0}t+\theta ),$$ 2.1

to the data, where ɛ is strain, ɛ₀ is the initial strain, λ is the decay exponent, t is time and θ is the phase offset at time t = 0. The direct effect of damping on f₀ is given by

$$f_0^d=f_0^u\sqrt{1-{\left(\frac{\mathrm{\lambda }}{2\pi f_0^u}\right)}^2},$$ 2.2

where $f_0^d$ and $f_0^u$ are the damped and undamped fundamental frequencies, respectively.

2.2. Terrestrial laser scanning data and tree architectural indices

TLS data contains highly useful information on the three-dimensional structure of trees, but it is difficult to access directly from the point cloud. Therefore, quantitative structure models (QSMs), which are three-dimensional representations of the trees as a series of cylinders, are often fit to the raw TLS data [26]. We brought together 1083 QSMs from existing publications and ongoing projects [27–32]. In all cases, TLS data were collected with a Riegl VZ-400, but sampling details were study specific (see the electronic supplementary material, table S1 for details). We applied a simplification step in order to prepare the QSMs for finite-element analysis. This step removes QSM branches under 2 cm diameter and child branches whose diameter is less than 30% of its parent branch diameter, since they are error prone [33]. It also replaces each pair of neighbouring cylinders with a single cylinder with an increase their length to radius ratio and the mean orientation and radius of the original pair. This simplification was applied to remove most of the variation that arises from uncertainties in the cylinder fitting process for smaller branches. This level of simplification was chosen because the sensitivity of the architectural indices was relatively low (see electronic supplementary material, figures S6 and S7 for details). The following architectural indices, in addition to tree height and dbh, were extracted from the simplified QSMs:

• —Crown area—maximum ground area covered by the crown viewed from above. The crown is defined as all the cylinders with branching order greater than one, which is given by the QSM fitting software.
• —Crown aspect ratio—ratio of maximum crown width to crown height.
• —Crown volume ratio (CVR)—ratio of total woody volume to that in the crown. This is an inverse measure of how ‘top-heavy’ the tree is.
• —Crown volume asymmetry—the ratio of mean to maximum woody volume contained in each segment of crown. These segments were defined starting from the position of the base of the tree and summing the volume of cylinders in the crown between angles 0–45°, 46–90°, etc.
• —Path fraction—ratio of mean to maximum base-to-twig path length, this is considered a proxy for water use efficiency [34,35].
• —Mean branching angle—the average angle between two cylinders at each branching point.
• —Total volume—total volume of all the cylinders that make up the tree.

No validation of these architectural indices was possible since measuring tree architecture in the field is extremely slow and difficult. Indeed, it is exactly this difficulty that has hampered previous studies on tree architecture, which are now possible through TLS [6]. Previous work found that these QSMs are accurate enough to extract architecture information sufficient to identify species in a three-species environment [36]. Importantly, the TLS data quality differs systematically between study sites due to differences in forest structure [33]. Simple architectural indices such as crown area are likely to be robust, but more complex measures such as crown asymmetry may be less accurate in tall dense forests. A validation study of these, and other, TLS-derived architectural indices across different forest types would be highly valuable, albeit extremely time consuming.

2.3. Finite-element analysis

Finite-element analysis is a computational technique capable of simulating the dynamics of complex structures. It is the de facto investigation tool used to isolate mechanisms related to branched structures [11,18,37,38]. The QSMs were imported into Abaqus [39], with each cylinder represented as a beam. First, a gravitational force was applied to the trees, which caused a number of simulation failures due to poorly connected beams. This reduced the sample size from 577 to 568 for the temperate trees, 451 to 348 for the tropical trees and 56 to 52 for the open-grown trees. A subspace method [40] was employed to extract the natural frequencies and D₀ was calculated as the percentage of generalized mass contained in the f₀. This definition was chosen to give an indication of the significance of the fundamental mode in the overall motion of the tree. Other metrics, such as the distribution of modes in frequency space, could be used in future studies. See Jackson et al. [41] for a detailed description of the finite-element method applied to QSMs.

Due to the difficulty of co-locating TLS and census data, the species of trees represented by the QSMs were generally not determined in the original studies. Therefore, green wood density and elasticity were kept constant for all simulations at 800 kgm⁻³ and 9.5 GPa, respectively [42]. Our sensitivity analysis (electronic supplementary material, table S3) showed that this uncertainty is unlikely to affect our predictions of f₀. This is in agreement with Sellier & Fourcaud [4] who found that the effect of material properties on tree dynamics is likely to be secondary to that of tree architecture. Importantly, the same simplified model trees were used for the finite-element simulations and to extract the architectural indices, so our linear models predicting f₀ and D₀ from architecture are internally consistent.

2.4. Statistical analysis

For the field data, we tested linear regression models of the form f₀ = 1 + dbh/H² for each subset of trees (temperate forest, tropical forest, open-grown and conifer forest). For a subset of 40 broadleaf trees, those for which material properties information was available in Niklas & Spatz [42], we tested a linear model of the form $f_0=1+(\mathrm{dbh}/H^2)\sqrt{E/\rho }$ (this subset is indicated in electronic supplementary material, table S1 and the results are given in electronic supplementary material, table S2).

For the QSMs, for which we had both architectural information and simulated f₀ and D₀, we used linear models of the form f₀ = 1 + dbh/H² + (A₁ + A₂ + A₃) and f₀ = 1 + dbh/H² + dbh/H²: (A₁ + A₂ + A₃) to predict f₀ for each subset of trees, allowing the intercept to vary between subsets (linear models specified in Wilkinson notation). The same method was used for D₀ except that in this case H + dbh was the primary predictor variable. We used ordinary least-squares linear regression models for all the statistical analysis in this study. We ensured this method was appropriate by inspecting the residuals and testing robust regressions. The only problematic models were those for the open-grown trees, for which the result was highly dependent on the inclusion of 12 small trees. In these cases, we give both results and our conclusions are necessarily tentative where open-grown trees are concerned. In all cases, we selected the optimal model based on highest predictive power (adjusted R²) and lowest Akaike information criteria (AIC). See the electronic supplementary material, figures S1–4 for full details of the linear models and their outputs.

An overview of the workflow is given in figure 2.

Figure 2.

Workflow diagram. (Online version in colour.)

3. Results

3.1. Patterns in f₀ from field data

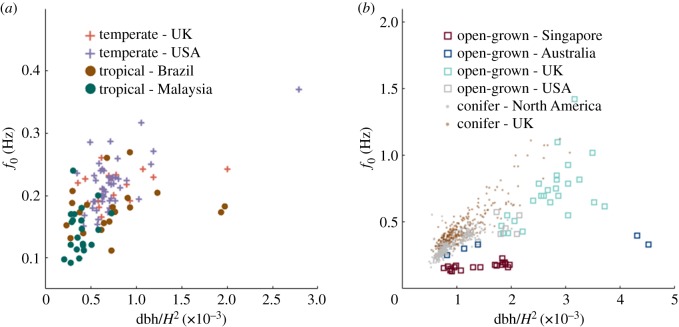
In this section, we test the applicability of the cantilever beam approximation to all of the field data on f₀. We find that f₀ is strongly related to dbh/H² for conifers, indicating that the cantilever beam approximation is accurate (see table 1 for fit statistics). This relationship is weaker for broadleaf trees (figure 3a) presumably due to their more varied architectures. This was expected, since trees with large branches clearly do not conform to the cantilever beam approximation. Differences between tropical and temperate forest broadleaf trees are not statistically robust in this limited sample. For a subset of 40 trees, we found that including material properties actually lowered the adjusted R² from 0.33 to 0.31 (see electronic supplementary material, table S2). This lack of explanatory power is likely due to the large range of inter- and intraspecific variation in material properties that is not accounted for in this simplistic approach [14,42]. Surprisingly, f₀ for open-grown broadleaf trees was well predicted by the cantilever beam approximation (table 1), even though these trees typically display the least ‘beam-like’ architecture. This is partly driven by the large range of f₀ and tree size in our open-grown tree sample. In addition, this high predictability could be due to a smaller range of architectures in open-grown trees.

Table 1.

Summary of linear models for f₀ and D₀. The entries are adjusted R²-values for ordinary least-squares linear regression models. In the case of f₀, the three architectural indices are CVR, crown asymmetry and aspect ratio. In the case of D₀, the two architectural indices are total tree volume and crown area. The numbers in parentheses for the open-grown trees correspond to the insets in figure 5, they demonstrate the sensitivity of linear models to outliers in this sample.

		field data		model results
		N	f0 ∝ dbh/H2	N	f0 ∝ dbh/H2	f0 ∝ dbh/H2 × (A1 + A2 + A2)	D0 ∝ H + dbh	D0 ∝ H + dbh+ A1 + A2
broadleaf	temperatea	63	0.32	568	0.42	0.83	0.09	0.12
	tropical	41	0.09	348	0.16	0.56	0.16	0.29
	open-grown	59	0.45	54 (42)	0.82 (0.18)	0.93 (0.42)	0.29	0.69
conifers		603	0.77	—	—		—	—
all trees		765	0.55	970	0.62	0.86	0.26	0.40

^aFor temperate deciduous trees, the field data were measured in full-leaf. All models are specified in Wilkinson notation. For details on linear model selection, see electronic supplementary material, figures S1–S4.

Figure 3.

Fundamental frequencies from field data. f₀ against dbh/H² for (a) broadleaf forest trees from temperate and tropical forests and (b) open-grown broadleaf trees and plantation conifers. Note the difference in axis ranges. (Online version in colour.)

3.2. Tree architecture

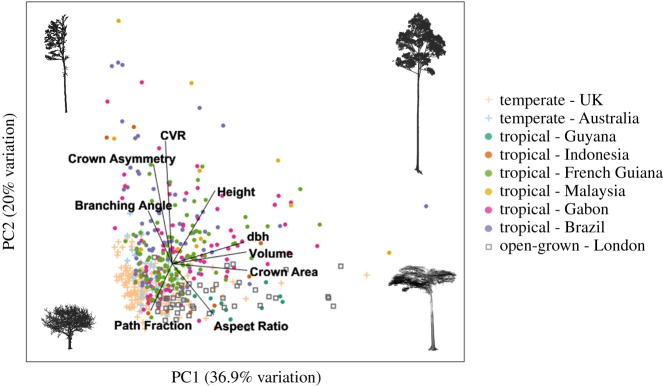
In this section, we explore our seven architectural indices using the TLS-derived QSMs collated from previous studies. Instantly apparent from figure 4 is the large range of architectural variation in the tropical trees, as compared to the temperate or open-grown trees. The primary axis of variation is driven by tree size: total volume, dbh and crown area are closely aligned and they account for much of the separation between the relatively small trees from a temperate forest in the UK and the large tropical trees. The second axis of variation is driven by crown properties, specifically the CVR and crown asymmetry. This suggests that some tropical trees have crowns that are both asymmetric and small relative to their stem, and that this does not occur in the open-grown trees in our sample. Instead, open-grown trees tend to have large, wide crowns and high path fractions. Correlations between architectural indices are given in the electronic supplementary material, figure S5 and the sensitivity of these architectural indices to simplification are given in electronic supplementary material, figures S6 and S7.

Figure 4.

Tree architectural indices. Principal component analysis of the architectural indices extracted from QSMs. Only trees with dbh > 30 cm were included in the analysis for clarity, but this did not substantially change the results. The overlaid images of trees are TLS point clouds which were selected as characteristic examples of the architecture expected at their position in the diagram. (Online version in colour.)

3.3. The effect of tree architecture on f₀

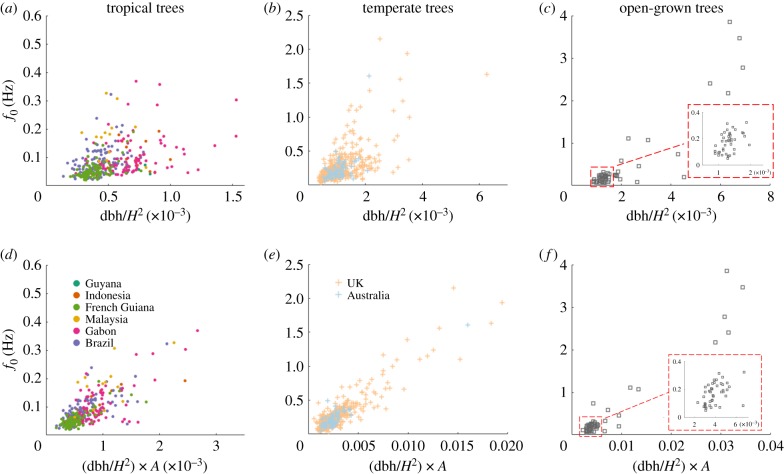
In this section, we use the 1083 TLS-derived QSMs to simulate f₀ and then test whether it is well modelled by the cantilever beam approximation, and whether the residual variation is driven by architecture. Across all the simulations, linear models showed that dbh/H² was positively correlated with f₀ meaning that slender trees tend to have low f₀. As in our field data, this relationship was weakest for the tropical trees (figure 4), presumably due to the higher range of architectures in this sample. The architectural term, A, improves f₀ predictability in all samples (figure 5). The predictability increased by approximately 40% in both temperate and tropical trees (table 1). Trees with large crown volume ratios tended to have lower f₀, while high crown asymmetry and aspect ratio were correlated with higher f₀ (see the electronic supplementary material, figure S2 for effect sizes). In this analysis we used the model with highest predictive power (adjusted R²) and lowest AIC (see electronic supplementary material, figure S1), which was a three-parameter model focusing on crown architecture. However, all of our architectural indices improved the predictability of f₀ to different extents and the key message is that any architectural information is useful when attempting to predict tree dynamics.

Figure 5.

Simulated fundamental frequencies. (a–c) Cantilever beam approximation predicting simulated f₀. (d–f) Predicting simulated f₀ using architectural information. Here A = (CVR + crown asymmetry + aspect ratio). Panels a,d are tropical forest trees, b,e are temperate forest trees and c,f are open-grown trees. The red-outlined insets in panels c,f give a closer view of the data near the origin, these sections correspond to the subsample for which summary statistics are given in parentheses in table 1. Note the difference in y-axis ranges.

3.4. Dominance of the fundamental sway mode

In this section, we explore the predictability of D₀, the dominance of the fundamental sway mode, based on simulations of the 1083 TLS-derived QSMs. Linear models showed that height and diameter explained 26% of the variation in D₀ across all QSMs (table 1). Taller trees tended to have higher D₀, while a larger dbh was associated with lower D₀ (electronic supplementary material, figure S4). This suggests that slender trees behave more like a simple pendulum, with the fundamental mode accounting for the majority of the motion. Architectural indices did not substantially improve our ability to predict of D₀, accounting for only 14% of the residual variation. Within our small subset of open-grown trees, it was possible to predict D₀ from tree height, dbh and total volume (table 1) but further open-grown tree data would be needed to robustly explore this relationship.

3.5. The effect of leaves

The swaying behaviour of deciduous trees changes as leaves fall in the autumn. We found that the mean f₀ increased by 19.4% in winter in Wytham Woods (figure 6). These changes are nearly uniform and can easily be parametrized. If we define L (equation (1.1)) as the increase of f₀ in winter, then L = 1.18 ± 0.12. We expect that the magnitude of this term will be influenced by total leaf biomass, which varies from site to site. For comparison with other forest plots, the leaf mass per unit ground area in Wytham Woods was measured to be 0.35 ± 0.02 kg m⁻² (dry weight) through direct measurement of cumulative autumn litterfall.

Figure 6.

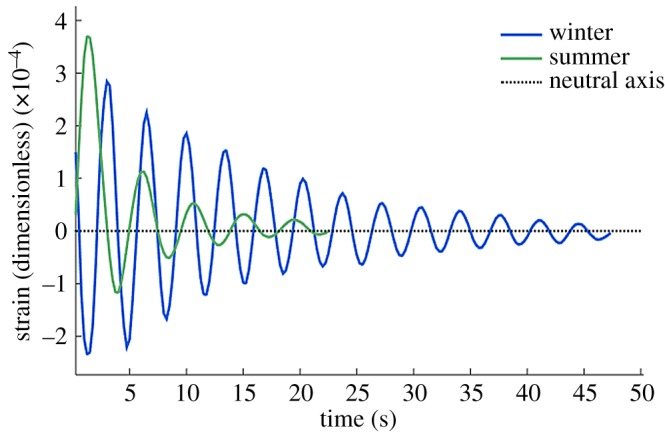
The effect of leaves on tree sway. Summer and winter pull and release test for a single sycamore tree in Wytham Woods, Oxford. (Online version in colour.)

Repeated pull and release tests on the same four trees in summer and winter determined the summer damping ratio to be 8.6 ± 2.2% and the winter damping ratio to be 3.9 ± 1.3%. If we assume that changes in temperature and air density do not have a significant effect on damping, we find that the leaves contributed a damping ratio 4.7 ± 2.5% or approximately half the full summer damping ratio. The direct effect of this damping on f₀ is less than 1% (equation (2.2)). This means that the change in f₀ is due to the mass of the leaves, not their aerodynamic drag.

4. Discussion

By using novel tools and sensors, particularly a large number of detailed three-dimensional measurements of individual tree structure across biomes, we have improved our understanding of the dynamic behaviour of broadleaf trees. In particular, we have introduced a new way to quantify the impact of tree architecture on natural frequencies. The improved predictability of f₀ is a step towards mechanistic modelling of wind damage for natural broadleaf forests, which plays a vital role in the terrestrial carbon cycle [43–45].

4.1. Tree architecture

We explored the range of tree architecture across 1083 broadleaf trees from tropical forests, temperate forests, parks and cities using QSMs based on TLS data. The primary axis of variation was driven by tree size and the secondary axis of variation by crown shape (figure 4). Interestingly, open-grown trees tended to cluster around high path fraction, the optimum architecture for hydraulic transport [35], as we would expect in the absence of competition for light or resources. More work is needed to validate these architectural measures and explore their sensitivity to TLS data processing parameters (see electronic supplementary material, figures S6 and S7).

4.2. Beyond the cantilever beam approximation

Most trees in our sample exhibited a clear f₀, which was related to dbh/H² as expected from the cantilever beam approximation (equation (1.1)). However, in the case of broadleaf trees, and especially tropical broadleaf trees, there was significant residual variation in f₀. This variation was not explained by material properties for a subset of 40 broadleaf trees. Moreover, our sensitivity analysis (electronic supplementary material, table S3) showed that variations in material properties are unlikely to explain this residual variation in general, since wood density and modulus of elasticity are strongly correlated [42]. Our modelling work shows that tree architectural information can increase the predictability of f₀ by approximately 40% for temperate and tropical forest broadleaf trees.

In deciduous forests, the presence of leaves caused an 18% increase in f₀ and a doubling of damping efficiency, which is similar to previous studies [22,46,47]. This increase in f₀ was due to the weight of the leaves, rather than the increased aerodynamic damping. Additionally, both water uptake and soil state can alter f₀ [22,25]. However, predicting leaf mass or volume of water uptake by the changes they cause in f₀ is difficult, since these changes are highly sensitive to their distribution within the tree.

The swaying behaviour of broadleaf trees in the wind may comprise more than a single significant natural frequency and we defined D₀, the dominance of the fundamental sway mode, to quantify this. D₀ can be thought of as an indication of the tractability of simpler (e.g. modal dynamics) modelling techniques [15] and as a proxy for the efficiency of multiple resonance damping [14]. Despite the fact that three-dimensional tree structure was fully mapped and specified in a virtual environment, we were not able to satisfactorily explain the resulting variation of D₀ using our architectural indices. This result suggests that D₀ is driven by finer scale properties, such as the presence of a single large branch, that are not captured by our tree-level architectural indices [48].

4.3. Implications and future directions

Tall, slender trees tended have lower f₀ and higher D₀, making them simultaneously easier to understand using a simple model [5] as well as potentially more vulnerable to wind damage. These tall trees store the majority of carbon in many tropical forests and have a high conservation value [49]. As a result, improved predictions of the likelihood of wind damage for tall tropical trees would be both tractable and highly valuable.

Overall, we have shown how detailed measurements of tree architecture gives us new insight into the dynamic properties of trees. Our work has quantified the relative importance of tree architectural indices in predicting natural frequencies, while also highlighting the greater challenge of developing a general model for energy dissipation in complex tree architectures. Our modelling approach, combining TLS data with finite-element analysis, could also be useful for valuable open-grown trees, to inform risk assessments and test proposed interventions in a virtual environment. With TLS-derived tree architectural information now becoming widely available, this is an area ripe for further inquiry.

Data accessibility

All field data collected for this study are available online (dois: 10.5285/533d87d3-48c1-4c6e-9f2f-fda273ab45bc; 657f420e-f956-4c33-b7d6-98c7a18aa07a). Field data from previous studies are available in the original publications. QSMs and software used to convert them to Abaqus input files are available online (http://doi.org/10.5281/zenodo.894543). Architectural indices were extracted in Matlab (https://github.com/TobyDJackson/TreeQSM_Architecture). An updated library for analysing tree structural information is also available in R (https://github.com/ashenkin/treestruct). Scripts used to create figures and run statistical analysis are available from the author on reasonable request.

Authors' contributions

T.J., A.S. and Y.M. wrote the manuscript. J.M., A.B., T.v.E., B.K., D.B. and K.J. provided field data. K.C., N.O., M.D., A.B., P.W., P.R., J.G.T.M., A.L., M.H. and R.C.G. were involved with TLS data collection and processing. A.S., Y.M., T.v.E., K.J., J.S. and T.F. provided valuable feedback and ideas at the early stages of this study.

Competing interests

The authors declare that they have no conflicts of interest.

Funding

This research was supported by an NERC studentship to T.J. (NE/L0021612/1). A.S. and Y.M. are supported by NERC grant no. NE/P012337/1 (to Y.M.) and Y.M. is also supported by the Frank Jackson Foundation. A.L., M.H. and J.G.T. are supported by CIFOR's Global Comparative Study on REDD+, and ERA-GAS NWO-3DforMod project 5160957540. M.D. was supported in part by NERC NCEO for travel and capital funding for lidar equipment, and NERC Standard grant nos. NE/N00373X/1 and NE/P011780/1. TLS data collection at Wytham Woods was funded through the Metrology for Earth Observation and Climate project (MetEOC-2), grant no. ENV55 within the European Metrology Research Programme (EMRP). The EMRP is jointly funded by the EMRP participating countries within EURAMET and the European Union.