A chordwise offset of the wing-pitch axis enhances rotational aerodynamic forces on insect wings: a numerical study

Abstract

Most flying animals produce aerodynamic forces by flapping their wings back and forth with a complex wingbeat pattern. The fluid dynamics that underlies this motion has been divided into separate aerodynamic mechanisms of which rotational lift, that results from fast wing pitch rotations, is particularly important for flight control and manoeuvrability. This rotational force mechanism has been modelled using Kutta–Joukowski theory, which combines the forward stroke motion of the wing with the fast pitch motion to compute forces. Recent studies, however, suggest that hovering insects can produce rotational forces at stroke reversal, without a forward motion of the wing. We have conducted a broad numerical parametric study over a range of wing morphologies and wing kinematics to show that rotational force production depends on two mechanisms: (i) conventional Kutta–Joukowski-based rotational forces and (ii) a rotational force mechanism that enables insects with an offset of the pitch axis relative to the wing's chordwise symmetry axis to generate rotational forces in the absence of forward wing motion. Because flying animals produce control actions frequently near stroke reversal, this pitch-axis-offset dependent aerodynamic mechanism may be particularly important for understanding control and manoeuvrability in natural flyers.

1. Introduction

Most flying animals flap their wings to produce the aerodynamic forces required for flight. These rapid oscillatory wing movements cause a complex unsteady airflow over the wing, resulting in unsteady aerodynamic force production. To explain how aerodynamic forces are related to the complex wing motion of flapping flight, distinct unsteady aerodynamic mechanisms have been defined and modelled [1]. Arguably the most important aerodynamic mechanisms currently identified for flapping flight are delayed stall and the linked leading-edge-vortex-based lift [2], rotational lift resulting from rapid wing pitch rotations [3], acceleration reaction forces or added mass forces [1], clap-and-fling [4], and wake capture [5].

Models of the separate unsteady aerodynamic mechanisms are often combined to form a single quasi-steady model, where the aerodynamic forces produced by a beating wing can be estimated as the sum of the forces resulting from the separate aerodynamic mechanisms [1]. For hovering fruit flies, a quasi-steady model based on only leading-edge-vortex-based forces and rotational forces predicts the total aerodynamic forces rather well, suggesting that these are two essential aerodynamic mechanisms [6,7].

The leading-edge-vortex-based forces scale with wing stroke rate and the angle-of-attack of the wing (figure 1a) [3]. Insect wings tend to operate at remarkably high angles-of-attack (of the order of 45°) [3], which results in high aerodynamic force production. The ability to operate at high angles-of-attack without stalling the airflow over the wing is linked to the presence of a leading-edge vortex on the wing [10], which is stabilized due the accelerations acting on the flow caused by the revolving wing movement [11]. Despite the importance of the revolving wing movement on force production, leading-edge-vortex-based forces are often called the translational forces [6,7]. Here, we will refrain from using this erroneous nomenclature, and call leading-edge-vortex-based forces the stroke-rate related forces.

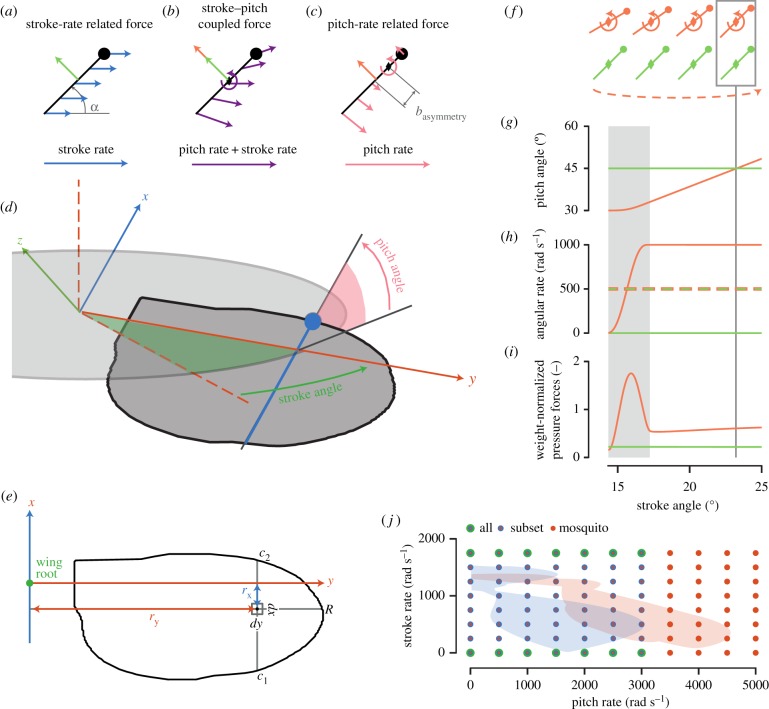
Figure 1.

(a–c) A two-dimensional schematic of the stroke-rate related force, the stroke–pitch coupled force, and the pitch-rate related force on a wing, respectively (equations (2.1) and (2.2)). The circle and diamond indicate the leading edge and pitch axis location, respectively. The green and orange arrows show stroke-rate related force and rotational force, respectively. (a) Blue arrows show wing velocity due to stroke movement. (b) Purple arrows show the wing-velocity distribution due to the combined stroke–pitch movement. (c) Pink arrows show the wing velocity due to the pitch movement; b_asymmetry is pitch asymmetry. (d) The fruit fly wing in the world reference frame, including the wing reference frame axes (attached to the wing), the stroke plane (in light grey), stroke angle, and pitch angle (angle between the stroke plane and the wing surface). (e) Wing geometry parameters for calculating the second-moment-of-area parameters S_xx, S_yy and S_x|x|. (f–i) The kinematics and forces used to estimate rotational force production, where data in orange are for the pitching wing, and the green data are of a non-pitching wing (ω_pitch = 0 rad s⁻¹); grey area is where the wing is still accelerating around its pitch axis; box with line indicates the stroke angle at which forces are extracted. (f) Schematic of the two wings; the curved dashed line indicates the direction of (revolving) stroke motion; (g) pitch angle versus stroke angle throughout the simulation, (h) pitch rate (solid) and stroke rate (dashed) versus stroke angle, and (i) forces normal to the wing surface versus stroke angle. (j) Parametric space of stroke rate and pitch rate for an average wingbeat of a hovering fruit fly (blue surface) [8] and of a hovering mosquito (red surface) [9]. Dots indicate the stroke rate and pitch rate of all simulations conducted with the mosquito wing (red dots), the fruit fly wing and the symmetric and most asymmetric elliptic wings (blue dots), and all eight tested wings (green dots). (Online version in colour.)

The second aerodynamic mechanism, the rotational force mechanism, is schematically represented in figure 1b,c. In flapping flight, an insect wing beats back and forth, and in order to keep a positive angle-of-attack during both the forward and backward stroke, the animal needs to rapidly pitch its wing up and down at stroke reversal (figure 1d). This rapid pitch rotation generates aerodynamic forces in addition to the stroke-rate related force mechanism described earlier [12–14], and adjusting the phase of the pitch movement relative to stroke reversal allows an animal to rapidly adjust this rotational aerodynamic force [3]. For this reason, it was suggested that rotational force production might be particularly important for flight control and manoeuvrability [3], which was confirmed in later studies [7,8,15].

The previously proposed rotational force mechanism in fruit flies is based on the Kramer effect and modelled using Kutta–Joukowski theory [13]. The Kramer effect describes the force production of an aerofoil that both translates and pitches up at the same time. The rotational velocity causes an increase in the circulation bound to the aerofoil, which causes an increase in force production on the translating wing. For hovering fruit flies, this Kutta–Joukowski based model predicts rotational forces rather well, but there are several issues associated with this approach.

Firstly, as described above, an insect wing in hovering flight does not produce a pure translating motion; the back and forth wing stroke movements are in fact rotational movements around the wing root. Secondly, the rotational force coefficient of the Kutta–Joukowski-based model remains depended on the wing-pitch rate and the chordwise location of the pitch axis [3,13]. By using an alternative force normalization, one may develop a rotational force model of which the coefficient is independent of wing-pitch rate and pitch-axis placement. Finally, the Kutta–Joukowski model predicts zero rotational force at zero stroke rate, which occurs at stroke reversal. In contrast, wing-pitch rates are highest during stroke reversal, and a recent study on the aerodynamics of mosquito flight showed that these insects produce relatively high aerodynamic forces near stroke reversal [16]. As these forces correlated strongly with wing-pitch rate, the authors suggested that mosquitoes produce these forces by using additional novel aerodynamic mechanisms called rotational drag and trailing-edge-vortex-based lift, by smart positioning of the wing pitch axis relative to the wing chord [16].

The model developed to predict the rotational drag forces works well when applied to a hovering hawkmoth [17]. However, the effect of the geometrical scaling on the rotational drag coefficient is not tested directly, as only a single wing was tested [17]. For example, the rotational drag model suggests that a fully symmetrical wing pitching about the symmetry axis would produce finite rotational drag. Such a wing would produce an aerodynamic torque about the pitch axis, but not a drag force because aerodynamic forces near the leading edge would be cancelled by equal and oppositely directed aerodynamic forces near the trailing edge.

Based on computational fluid dynamics (CFD) simulations with systematically varying wing morphology and wing movement kinematics, we tested how wing morphology and kinematics affect rotational force production. Using the outcomes, we propose an improved rotational force model. To isolate the rotational force mechanism from other aerodynamic mechanisms, such as the added mass, wake capture and leading-edge-vortex-based force mechanisms, we used a study design inspired by previous studies on the topic [3,13], where we simulated wings moving at constant stroke rates and pitch rates. But unlike these previous studies, we tested a range of wing shapes and kinematics that encompassed two extremes within the dipteran insect family, the fruit fly and the malaria mosquito. In addition, we simulated generic wing shapes and varied the kinematics in a systematic way. Together, these simulations led to the development of a new rotational force model that can predict rotational forces at stroke reversal due to an offset between the wing-pitch axis and the chordwise symmetry axis of the wing.

2. Methodology

We conducted a systematic CFD study within a parametric space based on eight different wing morphologies and a range of different kinematic parameters, using the IBAMR CFD solver based on the immersed boundary method [18]. See the Supplementary methods in the electronic supplementary material for more detail.

2.1. Wing morphology

To systematically test the effect of wing shape on rotational force production, we designed a set of six rigid elliptical wings with a systematically varying chordwise position of the pitch axis (figure 2a, right-hand side). Each generic elliptical wing had a span of 3 mm and maximum chord length of 1.3 mm; for the six wings, the rotational axis relative to the centre of the wing varied with a step size of 0.1 mm from 0 mm for the symmetric wing to 0.5 mm for the most asymmetric wing, that thus pitches around an axis close to the leading edge. Next to these six geometries, we tested both the wing geometry of a fruit fly Drosophila hydei [8] and a malaria mosquito Anopheles coluzzii [9]. Both wings were scaled to also have a wing span (from root to wing tip) of 3 mm, and the wing-pitch axis was set to go through the centre of the wing root (figure 2a).

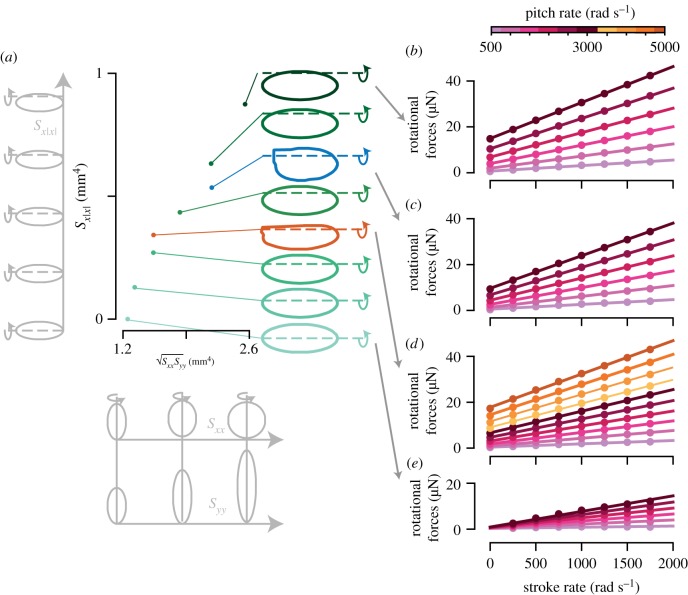
Figure 2.

(a) The geometry parameters, the stroke–pitch coupled second-moment-of-area √S_xxS_yy and the asymmetrical second-moment-of-area S_x|x| of the six elliptic wings (green), the fruit fly wing (blue), and the mosquito wing (red). In light-grey along the √S_xxS_yy-axis are examples of wings with both increasing S_xx and S_yy; in light-grey along the S_x|x|-axis is an example of wings with increasing S_x|x|. (b–e) The rotational forces (difference between total forces and stroke-rate related forces at an angle of attack of 45°) (ordinate) versus the stroke rate (abscissa) and pitch rate (colour-bar above (b)) for the most asymmetric elliptic wing, the fruit fly wing, the mosquito wing, and the symmetric wing, respectively. A linear function was fitted through the dataset at each simulated pitch rate. (Online version in colour.)

2.2. Kinematic design

The kinematics for these simulations were designed such that at a pitch angle of 45° the wing was moving at a constant pitch rate ω_pitch and stroke rate ω_stroke (figure 1f–h). At the point where the pitch angle is 45°, the forces were extracted. The extraction point was at a maximum stroke angle of 107°, to avoid wake interaction. As a consequence, at the point of extraction only the forces of two aerodynamic mechanisms are present: the stroke-rate related forces F_stroke and the rotational forces F_rotational. In line with previous studies into the rotational force mechanism [3,7], we estimated the rotational force (F_rotational) as the difference between the forces on a wing that is rapidly pitching up and the forces on the same wing with equal orientation, but with a zero pitch rate (figure 1i; electronic supplementary material, movie S1), as

$$F_{\mathrm{rotational}}=F_{\mathrm{total}}-F_{\mathrm{stroke}}.$$ 2.1

Here F_total is the total force on the wing with a pitch angle of 45° and moving with both a constant stroke rate and pitch rate, and F_stroke is the stroke-rate related force of a wing with a constant pitch angle of 45° and the same stroke rate. Also in line with previous studies [3], we assumed that rotational forces are the result of a pressure difference above and below the wing, and therefore we measured and modelled the rotational forces normal to the flat wing surface.

We performed these simulations for a range of constant pitch rates ω_pitch and stroke rates ω_stroke. The (ω_pitch, ω_stroke) parametric space was designed such that it spans the range of stroke rates and pitch rates employed by a fruit fly Drosophila hydei [15] and malaria mosquito Anopheles coluzzii [9] during hovering flight (figure 1j). The resulting simulations spanned a Reynolds-number range of 25–500 (equation (S1) in electronic supplementary material), which is representable for small to average-sized insects [3].

Our method implies that the rotational forces are not depending on the pitch angle. To test the validity of this assumption, we repeated all the simulations in the (ω_pitch, ω_stroke) parametric space of the most asymmetric elliptical wing, at a pitch angle of 30° and 60° (electronic supplementary material, figure S4).

2.3. Flow-field analysis

To study how changes in air movement and pressure distributions result in rotational forces, we visualized airflow dynamics at the wing surface and within two planes positioned perpendicular to the wing-pitch axis, placed at one-third and two-thirds of the wing span (i.e. y = 1 mm and 2 mm, respectively). On the wing surface, we visualized the pressure difference across the top and bottom surface of the wing, and within a selection of planes perpendicular to the wing-pitch axis we visualized the air-pressure distribution and distribution of the air-speed vectors.

2.4. Definition of our rotational model

We propose an aerodynamic rotational force model that captures the forces produced by an insect wing making simultaneous stroke and pitch movements, by combining a Kutta–Joukowski-based model [3] with the rotational drag model [17]. The Kutta–Joukowski-based model predicts forces based on stroke and pitch movement of the wing; therefore, we will call these forces the stroke–pitch coupled forces F_stroke-pitch. The rotational drag term is only dependent on the wing-pitch rate and therefore we will call these forces the pitch-rate related forces F_pitch [17]. Thus, the total rotational force is defined as

$$F_{\mathrm{rotational}}=F_{\mathrm{stroke}\text{-}\mathrm{pitch}}+F_{\mathrm{pitch}}.$$ 2.2

The stroke–pitch coupled force per unit span $F_{\mathrm{stroke}\text{-}\mathrm{pitch}}^{\mathrm{\prime }}$ can be modelled using Kutta–Joukowski theory [13] as (figure 1b)

$$F_{\mathrm{stroke}\text{-}\mathrm{pitch}}^{\mathrm{\prime }}=\rho U_{\mathrm{\infty }}\mathit{\Gamma },$$ 2.3

where U_∞ is the free-stream velocity and Γ is bound circulation caused by the rotational pitch movement [13]. The conventional rotational force model for insect wings expresses the bound circulation as a function of both pitch rate and a wing-geometry metric, and U_∞ was characterized using wing-tip speed [13]. But as discussed above, this model has the caveat that an insect wing has a rotational stroke movement rather than a purely translational movement. To solve this issue, we propose to model U_∞ as a function of ω_stroke and the second-moment-of-area S_yy, similar to the case of stroke-rate related forces [19]. Likewise, we propose to express the pitch-rate related bound circulation as a function of ω_pitch and the second-moment-of-area relative to the pitch axis S_xx. Thus, stroke–pitch coupled aerodynamic forces can be expressed based on Kutta–Joukowski theory (equation (2.3)) as

$$F_{\mathrm{stroke}\text{-}\mathrm{pitch}}=C_{F,\mathrm{stroke}\text{-}\mathrm{pitch}}\rho \sqrt{S_{xx}{S}_{yy}}{\omega }_{\mathrm{pitch}}{\omega }_{\mathrm{stroke}},$$ 2.4

where we call $\sqrt{S_{xx}{S}_{yy}}$ the pitch–stroke coupled second-moment-of-area, and C_{F,stroke-pitch} is the non-dimensional force coefficient for stroke–pitch coupled force production (figure 1b).

The second rotational force component (F_pitch, equation (2.2)) expresses the forces produced by a pitching wing in the absence of a stroke movement (figure 1c). Here, we suggest modelling these pitch-rate related forces similar to the rotational drag [17], but with a different geometrical scaling. We propose that the offset between the pitch axis and the chordwise centreline of the wing, called wing-pitch asymmetry (b_asymmetry, figure 1c), primarily affects the magnitude of pitch-rate related forces (figure 1c). The explanation of this is as follows. A fully symmetric wing, where the pitch axis is positioned at the wing centreline (figure 1b), will not produce a net aerodynamic force when only pitching up. In contrast, an asymmetric pitching wing, where the pitch axis is shifted towards the leading edge, will produce a net aerodynamic force due to the asymmetry in effective airspeed near the leading edge and trailing edge of the wing (figure 1c). The effect of pitch axis offset on the second-moment-of-area relative to the pitch axis can be quantified by the asymmetric second-moment-of-area defined as

$$S_{x|x|}={\int }_{c_1}^{c_2}x|x|\hspace{0.17em}\mathrm{d}A,$$ 2.5

where x is the chordwise wing axis, dA is an infinitesimal wing surface area, and c₁ and c₂ are the locations of the wing trailing edge and leading edge, relative to the pitch axis, respectively (figure 1e). Based on the here proposed scaling, we express pitch-rate related rotational aerodynamic forces as

$$F_{\mathrm{pitch}}=C_{F,\mathrm{pitch}}\rho S_{x|x|}{\omega }_{\mathrm{pitch}}^2,$$ 2.6

where C_F,pitch is the force coefficient for pitch-rate related force production. Note that equation (2.6) does not include the factor ½, because this results in the same scaling for F_pitch and F_stroke-pitch (equation (2.4)), with C_F,pitch and C_{F,stroke-pitch} as non-dimensional parameters, respectively.

3. Results

3.1. Numerical simulations

We performed numerical experiments for 312 combinations of stroke rate, pitch rate and wing geometry (figure 1j; electronic supplementary material, database S1). Each experiment took on average 25 000 time steps and the mesh size (after adaptive refinement) was on average four million cells. These simulations required 0.5 million CPU hours on our computer cluster with 176 CPUs.

3.2. Rotational force model

For our rotational force model, we focused on the forces normal to the wing surface, as we assumed rotational forces to primarily consist of pressure forces. We tested this assumption by comparing the normal and tangential components of the rotational forces. The tangential force component was 11% ± 6% (mean ± s.d.) of the total rotational forces, showing that tangential forces were small but not negligible. The full three-dimensional rotational forces for all simulations are provided in electronic supplementary material, database S1.

The rotational forces for all simulations of the most asymmetric elliptic wing, the fruit fly wing, the malaria mosquito wing, and the symmetric elliptic wing are shown in figure 2b–e, respectively. For each combination of pitch rate and wing type, the rotational force varies linearly with stroke rate, allowing a fit with the linear function F_rotational = A_strokeω_stroke + B_no-stroke, where A_stroke is the stroke-rate slope, and B_no-stroke is the intercept, i.e. the rotational force without a stroke rate.

The fits for the different wings and pitch rates, figure 2b–e shows that both the slope and intercept vary with pitch rate. Comparing this with our rotational model (equations (2.2)–(2.6)) suggests that slope of the fits (figure 2b–e) multiplied with the stroke rate are the stroke–pitch coupled forces (A_strokeω_stroke = F_stroke-pitch) and that the intercepts are the pitch-rate related forces B_no-stroke = F_pitch. Combining this with equations (2.4) and (2.6) results in

$$\begin{array}{cc}{A}_{\mathrm{stroke}}& =C_{F,\mathrm{stroke}\text{-}\mathrm{pitch}}\rho \sqrt{S_{xx}{S}_{yy}}{\omega }_{\mathrm{pitch}}\\ \mathrm{and}{B}_{\mathrm{no}\text{-}\mathrm{stroke}}& =C_{F,\mathrm{pitch}}\rho S_{x|x|}{\omega }_{\mathrm{pitch}}^2.\end{array}\}$$ 3.1

3.3. Stroke–pitch coupled rotational force model

We tested the relationship between F_stroke-pitch and both ω_pitch and $\sqrt{S_{xx}{S}_{yy}}$ in three consecutive steps (figure 3a–c). First, we tested how A_stroke varied with pitch rate (figure 3a), confirming that this relationship is also approximately linear, and can thus be expressed as

$$A_{\mathrm{stroke}}=A_{\mathrm{pitch}}{\omega }_{\mathrm{pitch}}.$$ 3.2

Figure 3.

Testing of the stroke–pitch coupled force model (a–c) and the pitch-rate related force model (e–g) using our CFD simulations. All data are colour-coded with wing geometry as defined in (d). (a) Stroke-rate slope of stroke–pitch coupled forces A_stroke (as defined by equation (3.1)) versus pitch rate for the eight wing geometries (colour coded). Linear functions were fitted through the data for each separate wing. (b) Pitch-rate slope for stroke–pitch coupled forces A_pitch (equation (3.2)) versus √S_xxS_yy, including a linear fit with intercept fixed at zero. (c) Normalized stroke–pitch coupled forces $F_{\mathrm{stroke}{\hspace{0.17em}}_{\text{-}}\mathrm{pitch}}^{\ast \ast }$ (equation (3.3)) versus pitch rate. The linear fit for each wing has a slope equal to its force coefficient C_{F,stroke-pitch} (equation (2.4)). (e) Pitch-rate related rotational forces F_pitch versus pitch rate, including quadratic fits. (f) Growth factor of these quadratic fits D_pitch (equation (3.4)) versus S_x|x|, including a linear fit. (g) Normalized pitch-rate related forces $F_{\mathrm{pitch}}^{\ast }$ (equation (3.5)) versus pitch rate. The growth factor of the quadratic fit for each wing equals its force coefficient, C_F,pitch (equation (2.6)). (Online version in colour.)

Here, A_pitch is the linear fit coefficient that quantifies the pitch-rate slope for stroke–pitch coupled forces. Secondly, we tested how A_pitch depends on wing geometry, expressed as $\sqrt{S_{xx}{S}_{yy}}$ (figure 3b). This test revealed that A_pitch scales approximately linearly with $\sqrt{S_{xx}{S}_{yy}}$, and that the intercept of the linear fit equals zero. Finally, to estimate the magnitude of the corresponding force coefficient C_{F,stroke-pitch}, we normalized the stroke–pitch coupled force as

$$F_{\mathrm{stroke}\text{-}\mathrm{pitch}}^{\ast \ast }=\frac{F_{\mathrm{stroke}\text{-}\mathrm{pitch}}}{\left(\sqrt{S_{xx}{S}_{yy}}{\omega }_{\mathrm{stroke}}\right)},$$ 3.3

and plotted this against ω_pitch for all our simulations (figure 3c). The linear fit for each wing geometry has a slope equal to C_{F,stroke-pitch}, which is similar among the eight tested wings (figure 3c). Thus, we estimated the stroke–pitch coupled force coefficient for all eight wing geometries combined as C_{F,stroke-pitch} = 2.08 ± 0.15 (mean ± s.d., n = 8).

3.4. Pitch-rate related rotational force model

We tested our pitch-rate related rotational force model using the same three-step approach as used for F_stroke-pitch scaling above (figure 3e–g). First, we tested how F_pitch (=B_no-stroke) varied with pitch rate for the different wings (figure 3e), confirming that F_pitch scales quadratically with pitch rate as

$$F_{\mathrm{pitch}}=D_{\mathrm{pitch}}{\omega }_{\mathrm{pitch}}^2,$$ 3.4

where D_pitch is the quadratic growth factor of pitch-rate related forces. The intercept is set to zero, because no rotational forces are produced by a non-moving wing (F_pitch = 0 N at ω_stroke = 0 rad s⁻¹ and ω_pitch = 0 rad s⁻¹). Secondly, we tested how D_pitch depends on the asymmetry of the wing, expressed by S_x|x|, showing that this relationship is linear (figure 3f). We have omitted the symmetric elliptic wing from this analysis, because for this wing F_pitch=0 N for all simulations with ω_stroke=0 rad s⁻¹ (figure 2e). Thirdly, to determine the magnitude of the pitch-rate related rotational force coefficient we normalized the pitch-rate related force with S_x|x| as

$$F_{\mathrm{pitch}}^{\ast }=\frac{F_{\mathrm{pitch}}}{S_{x|x|}},$$ 3.5

and plotted this against the pitch rate (figure 3g), for all simulations except those of the symmetric wing with S_x|x| = 0 m⁴. As expected, $F_{\mathrm{pitch}}^{\ast }$ scales quadratically with pitch rate, and thus we fitted quadratic functions through the data of each tested wing, where the quadratic growth factor of each fit equals C_F,pitch of that wing. The values of C_F,pitch of the different wings are similar, showing that the pitch-rate related rotational force coefficient is approximately independent of wing shape and kinematics. Therefore, we expressed this coefficient for the seven asymmetric wings combined as C_F,pitch = 2.08 ± 0.11 (n = 7).

3.5. The complete rotational force model

Surprisingly, C_F,pitch is nearly identical to C_{F,stroke-pitch} discussed in the previous section. In fact, the two coefficients are not significantly different from each other (paired t-test, t-value(degrees-of-freedom = 13) = −0.89, p-value = 0.41), and thus we suggest to use a single rotational force coefficient for both mechanisms, being C_F,rotational = 2.08 ± 0.13 (n = 15). This results in our new rotational force model for a generic insect wing that moves at both a constant stroke rate and pitch rate of

$$F_{\mathrm{rotational}}=C_{F,\mathrm{rotational}}\hspace{0.17em}\hspace{0.17em}\rho \left(\sqrt{S_{xx}{S}_{yy}}{\omega }_{\mathrm{stroke}}{\omega }_{\mathrm{pitch}}+S_{x|x|}{\omega }_{\mathrm{pitch}}^2\right).$$ 3.6

3.6. Effect of pitch angle on rotational force production

To test whether our rotational force model is independent of the pitch angle, we estimated the rotational force coefficient for the most asymmetric elliptical wing at pitch angles of both 30° and 60° (electronic supplementary material, figure S4). These coefficients were not significantly different from those of the 45° pitch angle simulations (C_F,pitch: independent t-test, t-value(5) = 2.28, p-value = 0.057; C_{F,stroke-pitch}: independent t-test, t-value(6) = 0.52, p-value = 0.62), showing that rotational force magnitude is not significantly dependent on pitch angle.

3.7. Aerodynamics of the combined stroke and pitch wing movement

The aerodynamic pressure forces produced by a wing moving with a combined stroke and pitch movement (F_total) act on the wing at its centre of pressure. The location of this centre of pressure is found by integrating the pressure distribution over the wing surface. We performed this analysis for the symmetric elliptic wing, the fruit fly wing, the mosquito wing, and the most asymmetric elliptic wings, moving with a stroke rate and pitch rate of both 1000 rad s⁻¹ (figure 4a–d, respectively). For all wings, the centre of pressure is located close to the chordwise centre of the wing, suggesting that it is nearly independent of the location of the pitch axis.

Figure 4.

The aerodynamics of the sub-set of four wings moving at a stroke rate and pitch rate of both 1000 rad s⁻¹. (a–d) Schematic of the aerofoil, where the dot indicates the leading edge and the diamond the rotation axis. Pink arrow illustrates the resultant force, F_total, blue arrow shows stroke direction, and green arrow indicates the direction of the wing pitch. The forces and their location were obtained by integration of the pressure differences across the wing surface. (e–h) The distribution of pressure differences across the wing surface. Dashed line indicates pitch-axis location; green and black lollipops indicate the location of the extraction planes shown in (i–l) and (m–p), respectively. (i–p) Pressure and flow field relative to the wing surface extracted from the planes indicated in (e–h). (Online version in colour.)

To illustrate the nature of the distribution of pressure differences, we show the pressure differences across the wing surfaces (figure 4e–h), and flow field and air pressures around the wings within two planes perpendicular to the pitch axis, at 1 mm and 2 mm from the root (figure 4i–l and figure 4m–p, respectively). These flow fields and air-pressure distributions are similar between all tested wing geometries: for all wings, the pressure differences across the wing surface is highest near the tip and leading edge of the wing (figure 4e–h), and along the complete lower side of each wing a high-pressure region is present (figure 4m–l). The magnitude of this high-pressure region is higher at the location 2 mm from the root (figure 4m–p) than at the 1 mm location (figure 4i–l). On the upper side of each wing, a low-pressure region is formed close to the leading edge, which coincides with the expected location of the leading-edge vortex. Both the low- and high-pressure regions intensify with increasing wing asymmetry, which is most apparent for the low-pressure region present near the trailing edge (figure 4i–p).

3.8. Aerodynamics of pitch-rate related rotational force production

The pitch-rate related aerodynamic forces on a wing (F_pitch, equation (2.6)) were isolated by analysing the simulations of wings moving only with a non-zero pitch rate (ω_stroke = 0 rad s⁻¹ and ω_pitch = 1000 rad s⁻¹, figure 5). We again analysed the results of the symmetric elliptic wing, the most asymmetric elliptic wing, the mosquito wing and the fruit fly wing. Comparing these results with those of the same wings moving with both a stroke and pitch movement (figure 4) highlights several interesting aspects.

Figure 5.

The aerodynamics of pitch-rate related force production by the sub-set of four wings moving at a pitch rate of 1000 rad s⁻¹ and a zero stroke rate. (a–d) Schematic of the aerofoil (dot indicates leading edge; diamond indicates rotation axis). Pink arrow indicates the pitch-rate related force F_pitch, and green arrow shows the direction of wing pitch. The forces and their location were obtained by integration of the pressure differences across the wing surface. (e–h) The distribution of pressure difference across the wing surface. Dashed line shows the pitch axis; black lollipop indicates the location of the extraction plane shown in (i–p). (i–p) Pressure and flow field in respectively the wing reference frame with subtraction of wing velocity (i–l) and the wing reference frame without subtraction of wing velocity (m–p). (Online version in colour.)

The centre of pressure of the pitch-rate related forces (F_pitch, figure 5a–d) lies closer to the trailing edge than that of the total aerodynamic force (F_total, figure 4a–d). For all wings, the distribution of the pressure difference across the wing surface does not vary along the span of the wing (figure 5e–h). In contrast, the pressure difference varies strongly in the chordwise direction, where it increases with the chordwise distance from the pitch axis. In front of the pitch axis (i.e. towards leading edge), these pressure differences are positive, whereas behind the pitch axis (i.e. towards the trailing edge) they are negative. Because negative pressure differences are associated with a positive force production, the wing area in front of the pitch axes contributes to negative pitch-rate related force production, and areas behind the pitch axis produce positive forces.

These dynamics explain why pitch-rate related aerodynamic forces increase with wing pitch asymmetry (as expressed by S_x|x|), and why the centre of pressure of F_pitch is located relatively close to the trailing edge (figure 5a–d): for the symmetric wing (S_x|x| = 0), the same amount of surface area is located in front and behind the pitch axis, and thus the positive and negative contributions to force production exactly balance each other (figure 5e), resulting in a zero net pitch-rate related force (figure 5a). For the asymmetric wings, the wing area behind the pitch axis is larger than the area in front of the pitch axis, resulting in a larger positive contribution to F_pitch near the trailing edge than the negative F_pitch production near the leading edge (figure 5b–d). As a result, the net pitch-rate related forces are positive and located behind the chordwise centre of the wing.

To illustrate the nature of these pressure differences across the wing surface, we show the flow field and air pressures around the wings within a plane perpendicular to the pitch axis and at 2 mm from the root of the wing for the four examined cases (figure 5i–p). The flow fields are shown in two reference frames, in the wing reference frame as defined above (figure 5i–l) and the wing reference frame without the subtraction of the wing velocity (figure 5m–p).

For the symmetric wing (figure 5i,m), the air pressure and flow fields are perfectly twofold rotational symmetric relative to the centre of the wing, explaining why no net pressure force is produced. For all asymmetric wings, there are large pressure variations near the trailing edge of the wing (figure 5j–l, n–p): underneath each wing there is a high-pressure region and above the wing a low-pressure region. Thus, the large pressure differences across the asymmetric wings, near the trailing edge, are due to both a high-pressure region below the wings and a low-pressure region above the wings.

To find the origin of the high-pressure region, we used the flow fields in the wing reference frame (figure 5j–l), showing that for all asymmetric wings, there is a stagnation point in the middle of the high-pressure region. To find the origin of the low-pressure region above the wing, we used the flow fields in the wing reference frame, but without subtracting of the wing velocity (figure 5m–p). These flow fields show that the air behind the stagnation point (towards the trailing edge) curls around the trailing edge, forming a vortex near the trailing edge on the top surface of the wing. The location of this trailing edge vortex coincides with a low-pressure region found above the wing near the trailing edge.

3.9. Aerodynamics of stroke–pitch coupled force production

Unlike for the pitch-rate related forces, there are no simulations at which only stroke–pitch coupled forces were produced. Therefore, to isolate the aerodynamics underlying the stroke–pitch coupled rotational forces (F_stroke-pitch) we used a method similar to the method for estimating rotational forces (equations (2.1) and (2.2)). When assuming that the pressure field around a wing that has a stroke and pitch movement (p_total) consists of the linear summation of the pressure field resulting from the stroke movement (p_stroke), the pitch movement (p_pitch) and the stroke–pitch coupling (p_stroke-pitch), then we can estimate p_stroke-pitch as

$$p_{\mathrm{stroke}\text{-}\mathrm{pitch}}=p_{\mathrm{total}}-p_{\mathrm{pitch}}-p_{\mathrm{stroke}},$$ 3.7

where the pressure fields p_total, p_pitch and p_stroke come from separate simulations.

We performed this analysis for the four wing geometries described earlier, moving at ω_stroke = 1000 rad s⁻¹ and ω_pitch = 1000 rad s⁻¹ (figure 6). Thus, to estimate p_stroke-pitch for a wing moving at ω_stroke = 1000 rad s⁻¹ and ω_pitch = 1000 rad s⁻¹, we subtracted both the pressure field p_stroke around a wing moving at ω_stroke = 1000 rad s⁻¹ and ω_pitch = 0 rad s⁻¹, and pressure field p_pitch of a wing moving at ω_stroke = 0 rad s⁻¹, ω_pitch = 1000 rad s⁻¹, from pressure field p_total around a wing moving at ω_stroke = 1000 rad s⁻¹ and ω_pitch = 1000 rad s⁻¹ (equation (3.7)). We did not apply this subtraction for the velocity field due to their nonlinear relation with the pressure field.

Figure 6.

The aerodynamics of stroke–pitch coupled force production by the sub-set of four wings moving at both pitch rates and stroke rates of 1000 rad s⁻¹. (a–d) Schematic of the aerofoil (dot indicates leading edge; diamond indicates rotation axis). Pink arrow indicates the resultant stroke–pitch coupled force F_stroke-pitch, and green arrow indicates the wing pitch direction. The forces and their location were obtained by integration of the pressure differences across the wing surface. (e–h) Distribution of pressure differences across the wing surface. Dashed line indicates the location of the pitch axis; green and black lollipops indicate the location of the extraction planes visualized in (i–l) and (m–p), respectively. (i–p) Pressure distributions throughout the planes defined in (e–h). All pressures were computed using equation (3.7). (Online version in colour.)

The comparison of the derived pressure fields that result in F_stroke-pitch (figure 6) with the pressure fields resulting in F_total and F_pitch (figures 4 and 5, respectively) highlights several interesting aspects. For all wings, both the magnitude and the location of F_stroke-pitch (figure 6a–d) lie in between those of F_total and F_pitch (figure 4a–d and figure 5a–d, respectively).

The pressure differences across the wing surface that causes F_stroke-pitch (figure 6e–h) are similarly distributed along the wing as for that of F_total (figure 4e–h), with a low-pressure region near the wing tip and trailing edge. Unlike for the F_total case, for F_stroke-pitch a secondary low-pressure is present close to the trailing edge at approximately two-thirds of the span (figure 6e–h).

The pressures in the two planes perpendicular to the pitch axis (figure 6i–p) reveal a high-pressure region at the bottom surface of all tested wings, which is slightly shifted towards the trailing edge. In the plane 1 mm from the wing root (figure 6i–l), a low-pressure region is distributed over a large area on top of each wing, whereas in the plane closer to the wing tip (2 mm from root) the low-pressure region is mostly concentrated near the leading edge. Particularly the intensity of the low-pressure region near the leading edge increases towards the wing tip (figure 6m–p), explaining the large pressure difference across the wing near the tip and leading edge.

4. Discussion

4.1. The rotational force model

In our study, we showed that the rotational aerodynamic force (F_rotational) produced by an insect wing moving at a constant stroke rate and pitch rate is composed of a pitch-rate related force component (F_pitch) and a stroke–pitch coupled force component (F_stroke-pitch) (equation (3.6)). The relation between F_rotational and the stroke rate, captured in the stroke–pitch coupled force component (F_stroke-pitch), is linear, which is in line with previous research [13]. Unlike these previous models, our stroke–pitch coupled force model explicitly quantifies the effect of wing morphology on stroke–pitch coupled force production.

Our pitch-rate related rotational force model is also similar to models described in previous studies [17,20]. But unlike these previous models, our model is able to accurately capture the effect of wing-pitch asymmetry on the pitch-rate related force, allowing us to show how flying insects can generate aerodynamic forces without making a stroke movement.

Our rotational model is based on CFD simulations on rigid insect wings and elliptical wings rotating at constant stroke rates and pitch rates. This approach isolates the rotational forces from the forces resulting from other aerodynamic mechanisms, which enabled us to model the rotational forces. This also removed the effect of the interaction between the rotational force mechanism and the other aerodynamic mechanism. Thus, how all these aerodynamic mechanisms interact remains an open question.

In addition, the proposed model assumes that the forces are all fully developed, while it is known that the flow over the wing needs time to develop [14], meaning that at rapid changing pitch rates the force estimates of our model might overestimate the forces found in real insects. We consider these transient effects part of a separate aerodynamic mechanism that should be investigated further in a future study.

Despite these limitations, our new rotational force model captures the full dynamics between rotational force production and wing morphology and motion, yet the model remains remarkable simple. Strikingly, the force coefficients of the stroke–pitch coupled force model and pitch-rate related force model do not differ significantly from each other, suggesting that both components form a single rotational mechanism (equation (3.6)).

4.2. Stroke–pitch coupled rotational forces

The stroke–pitch coupled rotational force model resembles the conventional rotational models based on Kutta–Joukowski theory [13,17], but we use a different geometrical scaling (equation (2.4)). After applying geometrical scaling, the previously defined conventional rotational lift model continues to show a dependency on wing pitch rate, as its force coefficient increases with pitch rate [13]. In contrast, our stroke–pitch coupled rotational force model removes the dependency of its force coefficient on the wing pitch rate completely (figure 3a–c).

In addition, due to the applied geometrical scaling (equation (2.4)), the coefficient of our stroke–pitch coupled rotational force model is also independent of wing geometry, at least for the eight tested wings (figure 3a–c), whereas for previous models this is ambiguous. This geometrical scaling shows equal effects of spanwise and chordwise wing size on force production, as shown by the equal contribution of S_yy and S_xx, respectively (equation (2.4)). This means that an insect wing with a large span (high aspect ratio) is equally able to generate pitch–stroke coupled rotational forces as an insect wing with a large chord width (low aspect ratio).

The distribution of the pressure differences across the wing surface that underlie the stroke–pitch coupled rotational forces also shows a dependence on both the span and the chord. This demonstrates the physical basis of the scaling used in our model: flapping-induced velocities further away from both the wing root and the pitch axis are higher, leading to larger pressure differences across the wing surface, which in turn leads to a larger net aerodynamic force.

4.3. Pitch-rate related rotational forces

Contrary to the stroke–pitch coupled forces, the pitch-rate related rotational forces are not dependent on the stroke rate, and can thus result in significant aerodynamic force production at stroke reversal of a beating insect wing. Such forces around stroke reversal were observed in flying mosquitoes, and ascribed to a new aerodynamic mechanism called rotational drag [16,17]. Our pitch-rate related rotational force model resembles the model previously developed for this rotational drag mechanism [17], but similar to the pitch–stroke coupled rotational force model, our geometrical scaling is crucially different. We have chosen a geometrical scaling that quantifies asymmetry in the wing, which is a vital basis for pitch-rate related rotational force production.

The geometrical scaling of our pitch-rate related rotational force model reveals that the offset of the pitch axis with respect to the wing symmetry axis determines the magnitude of the pitch-rate related rotational forces (figure 3e–g). Hence, a wing of which the pitch axis coincides with the symmetry axis cannot produce pitch-rate related forces, something that was not captured by previous models [3,17,20]. This suggests that an insect wing with a pitch axis located close to the chordwise symmetry axis cannot generate high forces around stroke reversal, using the rotational force mechanism.

The flow dynamics associated with pitch-rate related rotational force production shows that the low-pressure region is correlated to the presence of a trailing-edge vortex (figure 5). This trailing-edge vortex has been identified previously near the stroke reversal of a flapping mosquito wing, and which was proposed to result from wake capture [16]. In our study, wake capture was absent and we still found a trailing edge vortex; this suggests that the trailing edge vortex of the flapping mosquito wing might be related to rotational force production instead of wake capture.

4.4. Rotational forces in the fruit fly and malaria mosquito

Our rotational model is not a complete model for flapping insect flight because other important aerodynamic mechanisms such as added mass, wake capture, and stroke-based forces are not modelled. Therefore, a remaining question is: how important are the stroke–pitch coupled and pitch-rate related rotational forces for flying insects?

To investigate this, we applied our model to the full parametric space of stroke rates and pitch rates found within the wingbeat kinematics of a hovering fruit fly (figure 7a–d) [8] and a hovering malaria mosquito (figure 7e–h) [9]. Throughout each parametric space, we estimated the rotational forces F_stroke-pitch and F_pitch using our rotational force model (equation (3.6)), which we then normalized using the approximate body weight of these fruit flies and mosquitoes (mg, with mass m = 1 mg and gravitational acceleration g = 9.8 m s⁻²).

Figure 7.

Weight-normalized rotational forces throughout the parametric space of stroke rates and pitch rates, for the wingbeat of a hovering fruit fly (a–d) and a hovering malaria mosquito (e–h). The different components are: (a,e) weight-normalized stroke–pitch coupled rotational forces; (b,f) weight-normalized pitch-rate related forces; (c,g) weight-normalized total rotational forces; (d,h) percentage of pitch-rate related forces relative to the total rotational forces. All forces were estimated using our rotational force model (equation (3.6)). (Online version in colour.)

Both the stroke–pitch coupled rotational forces and pitch-rate related rotational forces were on average higher for the mosquito than for the fruit fly (figure 7), which is explained by the higher pitch rates throughout the mosquito wingbeat caused by the extremely high-frequency wingbeat (580 Hz for the mosquito compared to 190 Hz for the fruit fly) [8,9]. These results agree with previous studies that showed that high-frequency flappers rely more on rotational forces for weight support [16,21].

In contrast, our results suggest that the differences in rotational force production between the fruit fly and mosquito might be smaller than previously reported based on the wingbeat kinematics alone. The low aspect ratio wing of the fruit fly has a relatively high second-moment-of-area about the pitch axis, and as a result both$\sqrt{S_{xx}{S}_{yy}}$ and S_x|x| are higher for the fruit fly than for the mosquito (figure 2a). Hence, compared to the mosquito, the fruit fly has a wing shape that is better adapted for high rotational force production. This shows that to assess the relative contribution of rotational forces to total aerodynamic force production in flying insects, both wing kinematics and wing morphology should be considered. To maximize its rotational force production, an insect can employ a low-aspect-ratio wing in combination with high pitch rates and stroke rates. Furthermore, placing the pitch axis closer to the wing leading edge increases the asymmetric second-moment-of-area of the wing and consequently increases the pitch-rate related rotational forces.

For both the mosquito and fruit fly, pitch-rate related rotational forces dominate at low stroke rates, whereas at higher stroke rates the stroke–pitch coupled rotational forces are higher (figure 7d,h). This suggests that near stroke reversal our newly defined pitch-rate related rotational forces are the primary aerodynamic force mechanism at play. Several studies have shown that insects primarily use this phase of the wingbeat to produce aerodynamic roll and pitch torques for flight control [7], suggesting that the here-introduced pitch-rate related rotational forces might be relatively important for animal flight control and manoeuvrability.

The CFD simulations that we based our rotational lift model on encompass a Reynolds-number regime ranging from 25 to 500 (as defined by electronic supplementary material, equation (S1)). Most insects fly within this Reynolds-number range [3,22], suggesting that the model might be relevant for the majority of flying insects; more research is needed to test whether our model is also valid for natural flyers that operate at significantly higher Reynolds numbers, such as large insects, birds and bats.

Data accessibility

The datasets supporting this article are available in the electronic supplementary material, database S1.

Authors' contributions

W.G.v.V., J.L.v.L. and F.T.M. conceived and designed the study. W.G.v.V. developed the computational system, carried out the simulations, analysed the data and drafted the manuscript. F.T.M. provided the fruit fly and mosquito data, coordinated the study and helped to draft the manuscript. All authors contributed critically to writing the manuscript and gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

F.T.M. was supported by a grant from The Netherlands Organization for Scientific Research (NWO/VENI-863-14-007).