Challenges of biofilm control and utilization: lessons from mathematical modelling

Abstract

This article reviews modern applications of mathematical descriptions of biofilm formation. The focus is on theoretically obtained results which have implications for areas including the medical sector, food industry and wastewater treatment. Examples are given as to how models have contributed to the overall knowledge on biofilms and how they are used to predict biofilm behaviour. We conclude that the use of mathematical models of biofilms has demonstrated over the years the ability to significantly contribute to the vast field of biofilm research. Among other things, they have been used to test various hypotheses on the nature of interspecies interactions, viability of biofilm treatment methods or forces behind observed biofilm pattern formations. Mathematical models can also play a key role in future biofilm research. Many models nowadays are analysed through computer simulations and continue to improve along with computational capabilities. We predict that models will keep on providing answers to important challenges involving biofilm formation. However, further strengthening of the ties between various disciplines is necessary to fully use the tools of collective knowledge in tackling the biofilm phenomenon.

1. Introduction

It is estimated that bacteria and archaea constitute approximately half of all existing life on our planet [1]. It should thereby not come as a surprise that microbes have such a profound impact on our environment and our day to day lives. It is evident that the control and utilization of these tiny, ubiquitous organisms can generate huge leaps to advance human society, be it through introducing improvements in environmental protection [2], general health and well-being [3] or in various industries, e.g. food [4], energy [5], water treatment [6] or mining [7]. The immense complexity and diversity of the microbial world, and its sensitivity to environmental influences, physical or chemical alike, calls for a joining of forces between various science disciplines (for example biology, physics, mathematics, engineering or chemistry), to fully equip the research field with the necessary tools for solving the associated challenges [8–10].

Bacteria may either exist in a ‘free-floating’ planktonic state, or attached to a surface, forming biofilm communities [11]. There are substantial differences between these two modes of bacterial existence, chemical gradients and stress responses being only the tip of the iceberg [12]. In this review we will focus on the latter situation, i.e. bacteria growing in biofilms, although some comparisons to bacterial development in planktonic state will be included.

Biofilms can be defined as bacterial communities surrounded by polymeric matrices of extracellular matter and other associated products, most commonly attached to a surface or at an interface [13]. The biofilm matrix itself can be an immensely complicated environment, ranging from one strain and all its associated products to multiple species (for example oral biofilms can contain more than 500 species of bacteria [14]). Generally, the associated products include eDNA, proteins, polysaccharides and lysed cell debris, but the matrix can also contain enzymes, RNA and abiotic materials [1,15]. Furthermore, biofilm communities typically grow in complex environments such as soil; a highly heterogeneous and geometrically intricate landscape [16,17], which affects biological, ecological and physical processes in complicated ways.

Biofilm formation can be supported by virtually any nutrient sufficient environment, as is the case for general microbial growth [13]. The biofilm phenomenon poses a significant challenge to industries and to human health, as bacteria within a mature biofilm structure are better protected against harsh environmental conditions and antimicrobial agents as compared to planktonic cultures [13]. Indeed, such colonial growth can be seen as a strategy of unicellular organisms to gain the advantages that multi-cellular organisms have innately [18].

Biofilm control is of great importance to industries as their accumulation can cause significant economic losses, by causing, among other things, deterioration of equipment through inducing corrosion [19] or increasing fluid resistance [20]. Furthermore, biofilm contamination may affect chemical processes involved in production, thus making them less effective. This is particularly important in the energy and chemical industries [21]. Other noteworthy examples are the paper industry, where biofouling may have a detrimental effect on the quality of the final product, or the accumulation of biofilms below the waterline on the hulls of ships, which causes considerable losses for shipping industries by increasing drag, and what naturally follows, fuel consumption [21].

In contrast to generating losses, biofilm formation of some non-pathogenic bacteria can be used by industries, by e.g. inhibiting the growth of pathogens [22,23], preventing fungi-related food spoilage [24] or engineering biofuels [25,26]. Microbes have also been recognized as useful in the treatment of wastewater [27,28], cleaning up fuel spills [29], and even for their potential in generating electricity [5,10,30]. The list of associations between biofilms and industries goes on and on and it is therefore no wonder that these bacterial communities are of great interest from an economical perspective.

Apart from generating significant interest directly from businesses, there are also great health concerns associated with biofilm formation (which are also connected with economic factors, albeit indirectly) [31]. The problem is that there are innumerable species of human pathogens capable of forming biofilms, and many of these microbes, potentially dangerous to human health, are our constant co-habitants [32]. Microbial contamination in the food, agricultural or medical sectors calls for, among other control measures, detailed exploration of possible disinfection methods, employed to prevent human disease outbreaks and to reduce the amount of food waste. The quest to gain control over microorganisms is extremely difficult, as these organisms have many tools at their disposal which aid their survival and growth. Developing resistance to antimicrobials [33] and cooperation with other microbial species [34], by e.g. quorum sensing (QS) [35], are a few examples of such survival tools.

It has been repeatedly shown that bacteria in a sessile growth phase are much harder to control than the bacteria grown a free-floating state, and studies have been undertaken to understand what properties of biofilms give the bacteria embedded within a competitive edge against treatment [36]. Mathematical models have significantly contributed to the field of biofilm formation in at least two important ways. First, mathematical models help to understand the key mechanisms involved in biofilm formation. These include QS [37–43], effects of multi-species interactions [44–46], antimicrobial resistance [47] or the mechanical properties of the extracellular matrix (ECM) [48]. Second, mathematical models are routinely used to inform strategies to prevent or promote biofilm formation in specific situations relevant to, e.g., food and water security [27,49] or biofuel production [30,50].

In this review, we give a concise summary of the current stage of application of mathematical models of biofilms, providing arguments for the continuation and further strengthening interdisciplinary collaboration within the field. We emphasize the applications of the models rather than their mathematical intricacies which are covered by other reviews [1,51,52]. Section 2 describes results obtained from mathematical models used to understand key mechanisms for biofilm formation (see table 1 for a summary of the reviewed models and figure 1 for a schematic diagram of all sections discussed). The importance of mathematical modelling to address each of the selected topics is demonstrated by reviewing key findings based on state-of-the-art models that represent a substantial addition to the understanding gained through experimental approaches.

Table 1.

Summary of biofilm modelling work mentioned in this review.

author (date)	model description	organism	purpose
O. Wanner, S. Gujer (1986)	1D, continuum, deterministic	not specified	study of the competition between autotrophs and heterotrophs in a multispecies biofilm [45]
W. Nichols et al. (1989)	1D, continuum, deterministic	Pseudomonas aeruginosa	study of antibiotic penetration of biofilms of mucoid and non-mucoid strains [47]
E. Ben-Jacob et al. (1994)	2D, cellular automaton, stochastic	Bacillus subtilis	exploration of patterns of bacterial growth in various nutrient conditions [53]
O. Wanner, P. Reichert (1995)	1D, continuum, deterministic	not specified	extension of previous work [45]; general approach to modelling mixed species biofilms, exploring spatial profiles of chemical compounds and microbial organisms [54]
P. S. Stewart et al. (1996)	1D, continuum, deterministic	not specified	analysis of biocide action against biofilms [55]
C. Picioreanu et al. (2000)	2D, continuum, deterministic	not specified	study of the effect of biofilm surface roughness on the mass transport within the biofilm [56]
M. G. Dodds et al. (2000)	1D, continuum, deterministic	Pseudomonas aeruginosa	analysis of antimicrobial resistance mechanisms of biofilms [57]
J. Dockery, J. Keener (2001)	1D, continuum, deterministic	Pseudomonas aeruginosa	general analysis of the quorum sensing mechanism in biofilms [37]
D. L. Chopp et al. (2002)	1D, continuum, deterministic	Pseudomonas aeruginosa	prediction of acyl-HSL and oxygen concentration profiles within the biofilm and analysis of their effect on biofilm growth [58]
I. Chang et al. (2003)	3D, cellular automaton, stochastic	not specified	effect of transport limitation on microbial growth and biofilm structure [59]
K. Anguige et al. (2004)	1D, continuum	Pseudomonas aeruginosa	analysis of effects of quorum sensing inhibitors and antibiotics on the quorum sensing mechanism of biofilms [38]
C. Picioreanu et al. (2004)	2D/3D, individual-based	not specified	analysis of the effect of multidimensional gradients on multispecies biofilm development [60]
J. Xavier et al. (2004)	3D, individual-based	not specified	comparison of CLSM data to spatial structures of multispecies biofilms generated by the model [61]
J. Xavier et al. (2005)	3D, individual-based	not specified	introduction of a general framework for IBM modelling [62] and evaluating the efficiency of biofilm treatment by detachment promoting agents [63]
K. Anguige et al. (2005)	1D, continuum	Pseudomonas aeruginosa	quorum sensing inhibition [39]; extension of [38]
S. M. Hunt et al. (2005)	3D, cellular automaton	not specified	analysis of antimicrobial action on biofilms, which focused on the scope of substrate limitation contribution on antimicrobial resistance [64]
J. D. Chanbless (2006)	3D, hybrid differential-discrete cellular automaton, stochastic	not specified	exploration of four hypothetical mechanisms of antimicrobial resistance, i.e. poor antimicrobial penetration, stress response mechanism, physiological heterogeneity within the biofilm and persister cells [65]
A. K. Marcus et al. (2007)	1D, conduction-based, deterministic	not specified	modelling the electrochemical processes in microbial fuel cells biofilms with focus on factors affecting electron flow [30]
J. Xavier, K. Foster (2007)	2D, individual-based, deterministic	not specified	evolutionary outcomes of exopolymeric substances producers competing with non-producing individuals [46]
G. E. Kapellos (2007)	2D, hybrid differential-discrete cellular automaton, deterministic	not specified	analysis of biofilm growth dynamics in porous media; first modelling work to account for fluid flow through the biofilm [66]
F. Romero-Campero, M. Pérez-Jiménez (2008)	P-system	Vibrio fischeri	quorum sensing analysis using biochemical reaction networks [40]
J. Ward (2008)	1D, continuum, deterministic	not specified	investigation of anti-quorum sensing treatment of biofilms [39]
N. Jayasinghe, R. Mahadevan (2010)	1D, continuum model, combined with genome scale metabolism modelling	Geobacter sulfurreducens	analysis of the effect of maintenance energy requirements on maximum current production and thickness of biofilms in microbial fuel cells [10]
M. Frederick et al. (2011)	2D, continuum, stochastic	not specified	analysis of how quorum sensing controlled EPS production affects biofilm formation [42]
Z. Wang et al. (2011)	2D, cellular automaton, deterministic	Caldicellulosiruptfor obsidiansis, Clostridium thermocellum	study of cellulose degradation by biofilms in biofuel production [50,67]
L. Lardon et al. (2011)	2D, individual-based	not specified	introduction of a biofilm modelling platform for non-programmers; iDynoMiCS [68]
D. Rodriguez et al. (2012)	2D/3D, cellular automaton, stochastic	not specified	studying effects of surface roughness patterns on biofilm formation in the presence of flow [69]
M. Asally et al. (2012)	2D, hybrid differential-discrete cellular automaton, deterministic	Bacillus subtilis	theoretical analysis of mechanical forces behind emergent pattern formation of biofilms [70]
F. Pérez-Reche (2012)	3D, network, stochastic	not specified	analysis of network representation of soil samples with regards to potential microbial invasions [17]
R. Ferrier et al. (2013)	2D, individual-based, stochastic	Listeria monocytogenes	estimating counts of food spoilage organisms on the surface of cheese [49]
A. Ehret, M. Böl (2013)	3D, continuum, deterministic	Pseudomonas aeruginosa	study of mechanical role of EPS matrix on biofilms, representing the EPS matrix as a worm-like chain network [48]
S. Bottero et al. (2013)	2D, cellular automaton, stochastic	not specified	examination of factors influencing the development of flow paths in a biofilm formed in porous media [71]
W. Harcombe (2014)	2D, differential-discrete model, combined with genome scale metabolism modelling	Escherichia coli Salmonella enterica Methylobacterium extorquens	proposed a modelling framework for incorporating genomic scale information on the scale of microbial communities with the aim to predict the behaviour of multispecies consortia [72]
N. Jayasinghe et al. (2014)	1D, continuum model, combined with genome scale metabolism modelling	Geobacter sulfurreducens	metabolic modelling of spatial heterogeneity of biofilms in microbial fuel cells [73]
J. Cole et al. (2015)	3D, continuum model, combined with genome scale metabolism modelling	Escherichia coli	analysis of the effect of metabolic interactions within densely packed biofilm colonies, i.e. the relation between a cell's position within a colony and its metabolism [74]
B. Emerenini et al. (2015)	2D/3D, continuum, deterministic	not specified	analysis of biofilm detachment regulated by quorum sensing mechanism [43]
R. Bennett et al. (2016)	hydrodynamic, deterministic	Pseudomonas aeruginosa et al.	analysis of individual cells flagellar spinning movements on the surface in early biofilm development [75]
P. Phalak et al. (2016)	1D differential-discrete model combined with genome scale metabolism modelling	Pseudomonas aeruginosa, Staphylococcus aureus	role of metabolic factors on the spatial distribution of cells in a two species biofilm; the species were chosen for their common occurrence in chronic wound infections [76]
M. Azari et al. (2017)	activated sludge model	Candidatus brocadia et al.	wastewater treatment reactor study [27]
B. Né Dicte Martin et al. (2017)	2D, cellular automaton, stochastic	Streptococcus gordonii, Porphyromonas gingivalis	assessment of mixed species interactions in oral biofilms [44]
I. Tack et al. (2017)	2D, individual based, stochastic	Escherichia coli	analysis of the effect of various environmental factors on the biofilm morphology [77]
K. Coyte (2017)	2D, hydrodynamic, game theory	Escherichia coli	analysis of the relative success of microbial strategies in porous media for various flow conditions [78]
S. Stump et al. (2018)	2D, cellular automaton, stochastic	not specified	study of the competition between cooperators and cheaters within a microbial community [79]

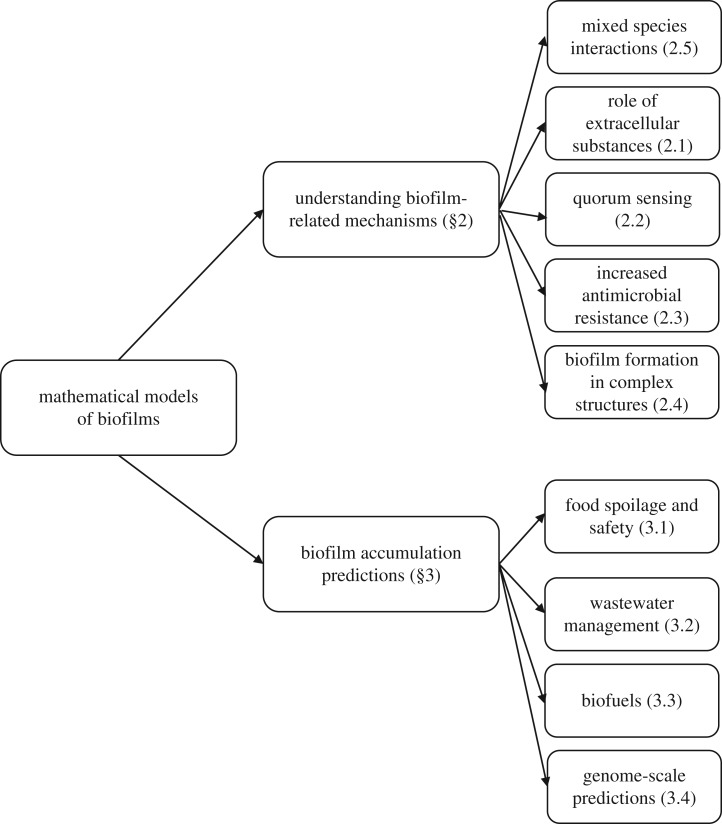
Figure 1.

Schematic diagram of the review. The biofilm models are categorized according to their purpose. Firstly, models that aimed to understand various biofilm formation mechanisms are discussed. We give examples of how mathematical modelling explained some observed phenomena arising from mixed species interactions, extracellular substances, quorum sensing mechanism, apparent antimicrobial resistance of biofilms and biofilm formation in complex structures. Secondly, attention is turned to the second type of biofilm model, which aim to predict levels of biofilm accumulation. These models are generally specific to a given area of interest. We give examples of applications of these predictive models in the food industry, wastewater management and in engineering biofuels.

2. Understanding biofilm-related mechanisms with mathematical models

Ever since the 1980s, efforts have been made to use mathematical descriptions to supplement experimental observations of biofilm communities. Many biofilm models have appeared since the initial efforts which considered one-dimensional, mono-species descriptions [80]. These have been extended to add more spatial dimensions, more bacterial species, or by analysing the effects of varying environmental properties such as temperature, pH, fluid flow or spatial constraints from rough surfaces or porous media. The biofilm models are either stochastic [49,59,68,69], taking into account a certain degree of randomness of biological processes, or deterministic [41,43,54], if the stochasticity analysis is not needed to answer a particular question. They can be individual-based [49,60–62,68,77], where each bacterial cell is considered as an entity, or mesoscopic [42,53,70], where an entity of interest is a whole colony or a microcolony of cells, and a single event may be for example population doubling. The models developed can focus on describing the biofilm at the scale of the whole population, or at the level of the individual cells, taking into account the details of cell structure and how it affects its behaviour [75]. The fact that different models have been developed to focus on different spatial and temporal scales reflects the inherent multi-scalar nature of the processes involved in biofilm formation [81,82].

Although biofilm models may significantly differ from each other, they also have many things in common. Fundamental processes such as attachment, microbial growth, nutrient uptake, cellular death, extracellular products generation, detachment and some chemical processes are usually introduced in some manner, albeit the methods used vary. For example, microbial growth in an individual-based model is introduced by a division of a cell with a set of rules governing the structural changes in the matrix following the introduction of a daughter cell. On the other hand, in models in which biomass is treated as a continuum, growth may be portrayed in terms of continuous biomass expansion and movement [1]. Furthermore, diffusion of chemical compounds is generally introduced by solving Fick's law, convection is often governed by Navier–Stokes equations for fluid flow or their approximations, and nutrient uptake and biomass growth implementation usually includes a form of Monod equation [51,52].

The following section presents examples in which mathematical modelling has proven instrumental to understand complex factors in biofilm growth whose elucidation using experimental methods remains a challenge. We will discuss the role of ECM and QS, the emergent antimicrobial resistance of biofilms and models which test viability of treatment methods, biofilm formation in complex structures and in mixed species biofilms. The list of topics presented here is by no means exhaustive. Due to the complexity of the field, we were forced to leave out many aspects, for example, the effect of motility of cells or factors influencing attachment (see, e.g. [75,83,84] for mathematical models incorporating some of these factors). We believe however, that the aspects we present give a taste of how mathematical modelling has been employed in biofilm research to this date.

2.1. Role of extracellular substances

The general role of the biofilm ECM is to hold the biofilm together and fix it in place, but it has also been reported to be used by cells as a nutrient source [1,15]. By keeping the cells closer together, accumulation of QS signalling molecules is more likely to occur, making communication mechanisms more effective [15]. Furthermore, the immobilizing properties of the ECM have the effect of keeping extracellular enzymes close to the cells and thus the ECM may act as an external digestive system [85]. Other fundamental roles include facilitating gene transfer [86] or inducing formation of complex, self-organized structures [70]. The ECM has also been reported to protect the biofilm cells from desiccation, biocides, antibiotics, heavy metals, UV light, host immune responses and protozoan grazers [85].

In individual based model (IbM) models, individual agents such as bacteria cells or exopolymeric substances (EPS) are treated as discrete entities, with specific properties assigned to them, such as their biomass, size and interactions with the environment. These agents are typically placed in continuous space, which is what puts IbM models apart from cellular automaton (CA) models, in which space is discretized in the form of a lattice [60].

A study using an IbM in three dimensions has been conducted to assess the potential of enzymic disruption of the ECM as a biofilm control strategy [62,63]. Prior to the theoretical study, the ability of NaOH to break down Staphylococcus epidermidis biofilms was confirmed experimentally, resulting in the need to identify factors affecting the efficiency of the treatment which could potentially be applicable for other bacterial species [87]. The simulations had two stages. In the first stage, a biofilm was developed without the presence of disruptive enzymes. Subsequently, after a simulation time of 60 days, the biofilm was treated with a chemical compromising the ECM matrix, along with activating flow in order to trigger the detachment effect of the weakened biofilm structure. The modelling study found that 99% of biofilm removal resulting from the treatment occurred quickly, i.e. within a couple of hours. However, it took much longer for the remaining biofilm to be removed, i.e. 94% of the total treatment time. Another interesting result obtained by the study was that the efficiency of the treatment in the simulations depended strongly on the ratios between the decay rate of the treatment substance in the biofilm, the rate at which the substance was able to compromise the ECM produced by the bacteria in question, and the rate at which the bacteria produced ECM. In some cases, the production of ECM was sufficient to counteract the effects of the treatment, resulting in persistence of the biofilm. The results of the study thus underlined the role of ECM material in biofilm prevalence, as well as provided possible reasoning behind differences in the relative success of biofilm treatment targeted at various bacterial strains.

The results of mathematical analysis of the role of ECM in protecting cells from antimicrobials will be discussed in later sections on antimicrobial resistance of biofilms. Now we introduce another modelling example, which analysed the influence of the ECM on the interactions between different species within the biofilm community [46]. This individual based modelling study of mixed species biofilms has challenged the common perception of EPS production within the ECM matrix as a purely cooperative behaviour. Computational analysis identified the potential evolutionary advantage of EPS production in terms of aiding the propagation of an individual's genes. The study considered two species, in all other aspects equal, except that one produced EPS and the other did not. The non-EPS producer grew faster, as it had more resources available to allocate for reproduction compared to the other species. Simulations of the competition between two species have shown that the outcome was strongly dependant on the ratio of EPS produced per biomass formed and the ratio between the density of the EPS to the biomass. In some cases, the non-producing species indeed had an advantage over the EPS producers. It is interesting, however, that the EPS producers were favoured when the density of the EPS was lower than the density of biomass, for a wide range of EPS production rates and diffusion coefficients of the growth-limiting compound. This extended to being able to ‘suffocate’ its rival with its generated product, while displacing the individuals of its species towards the top of the biofilm, where nutrients were more abundant. The authors of this study argued that considering EPS-producing behaviour solely as a group-benefiting sacrifice may be wrong, as this behaviour may be capable of causing a detrimental effect towards the neighbours of the producers.

2.2. Role of quorum sensing on biofilm formation

QS is a means of cell–cell communication using signal molecules (autoinducers), allowing bacteria to sense the changes in their environment and react appropriately by activating or inhibiting gene expression [88]. This phenomenon is thought to have a greater impact on bacterial communities in biofilms, as opposed to the planktonic phase, due to closer clustering of cells, which increases the number of signalling molecules in the external environment of the cells and may thus be a cause of increased QS associated gene expression [36]. The QS mechanism has been reported to greatly affect biofilm formation. It has been suggested to play a significant role in attachment of cells or their detachment. For example, disrupting the QS mechanism in P. aeruginosa biofilms has been observed to result in thinner biofilms [89]. The effect of QS on P. aeruginosa biofilms may well be a consequence of the fact that approximately 6% of all P. aeruginosa genes seem to be regulated by this communication mechanism [90].

Synthetic engineering of QS inhibitors (QSI) has been suggested as a possible solution to aid eradication of unwanted biofilms. It has been observed experimentally that supplementing tobramycin as an antibiotic treatment of P. aeruginosa biofilms with a garlic extract, a natural QSI, was successful in killing all biofilm cells, a result that was not obtained when using either one of the compounds alone. Interestingly, disrupting the growth of cells within biofilms through manipulating their QS mechanism is not solely a man-made concept. For example, it has been observed that inhibition of QS can be imposed on one bacterial species by another within a mixed species biofilm [91].

Several mathematical models have been developed over the years to describe the role of QS on biofilm communities [37,39–43,58,92]. For instance, the study in ref. [92] predicted a diminished role of the QS mechanism in a biofilm exposed to high flow rates, in agreement with experimental observations.

The factors that may influence the effectiveness of P. aeruginosa biofilm treatment by disrupting cell–cell communication were analysed in a theoretical study [39]. A critical biofilm depth was predicted, above which the treatment with QSI would not be successful. This is thought to be partly due to a predicted exponential increase of the successful concentrations of QSI, or for that matter, any kind of antimicrobial compound, with biofilm depth [39]. In contrast, in the case of planktonic cultures, the concentration of antimicrobials needed to eliminate the population of cells has been predicted by a previous theoretical study to increase linearly with the amount of treated biomass [38], which may be one of the direct causes of the difference in antimicrobial sensitivity between these two modes of bacterial growth.

In another application, a two-dimensional, deterministic model designed to study the QS mechanism has been proposed by Frederick et al. [42]. Specifically, it aimed to investigate whether the QS regulation of EPS production by cells may be beneficial compared to a non-regulated, steady extracellular excretion process. Cases when EPS could serve as a nutrient source and when it could not, were investigated separately under high and low nutrient conditions. It was found that upregulated EPS production does not provide an advantage in terms of achieving higher population numbers, when compared to steady, low EPS production. It may, however, increase the optical density of the biofilm and thus protect the cells from environmental stresses or trap nutrients and thus lead to out-competition of the low-EPS producing rivals in nutrient rich conditions, even though EPS production comes at a cost of slower growth [42].

2.3. Increased antimicrobial resistance

The structure and chemical composition of a mature biofilm provides a barrier which in many cases protects embedded cells from antimicrobials. This causes significant concern in the medical sector, among other industries [93]. Biofilm-caused infections often result in the development of chronic illnesses in patients, with available treatments inadequate in completely eradicating the bacteria within the biofilm. These can include foreign-body infections, e.g. biofilm formation on surgically inserted medical implants, or infections of regular tissue, e.g. lung tissue [36]. Chronic patients must often undergo constant, lifelong treatment with antibiotics in order to keep the biofilms at a manageable level. However, this solution, among other things, disrupts the normal gut flora which may cause further deterioration of the overall health of the patient and may as a consequence cause the emergence of bacterial infections resistant to all types of available antibiotics. This in turn renders further treatment even more challenging and ultimate eradication of the infection difficult [36]. Increased antimicrobial resistance of cells in biofilms is believed to be caused by many factors including, for example, increased levels of mutation in biofilms in comparison to their planktonic counterparts. This phenomenon in turn is believed to emerge due to increased cell–cell communication in the biofilm community, where cells are naturally bundled closer together than in the case of bacteria floating in a free planktonic state [36]. The increase in mutations can cause upregulation of genes responsible for production of enzymes which degrade antimicrobial agents, or increased activity of efflux pumps, which expel the antimicrobial agent out of the cell membrane, making the bacteria more tolerant to antibiotic exposure.

In addition to increase in mutations and its effects in increasing antimicrobial resistance, development of chemical gradients in the biofilm layers is also believed to contribute to the persistence of treated biofilms. The chemical gradients of nutrients and other substances within the biofilm structure cause the emergence of dormant cells in the layers of the biofilm where nutrients become limited, while the dividing cells occupy the outer layers, closer to the biofilm surface. Some commonly used antibiotics exclusively target either dormant or active cells which is why using only one type may not prove sufficient to kill all cells within the biofilm. However, applying both of those antibiotics at the same time seems to be able to overcome this particular problem. For example, synergistic treatment with ciprofloxacin and colistin have been observed to be successful in clinical trials on patients in the early stages of cystic fibrosis [36].

Another advantage gained by the cells from the structural properties of the biofilm matrix is that diffusion of antimicrobials through the matrix may be significantly delayed, or even inhibited due to the chemical composition of the matrix, by breaking down or trapping the antimicrobial compound before it reaches the cells within biofilm depths. Pre-treatment of the biofilm with enzymes degrading the biofilm matrix has been demonstrated to be a successful strategy by rendering the biofilm more susceptible to the application of antimicrobials in a study involving P. aeruginosa biofilms [36].

Numerous modelling efforts have been employed in order to address the challenge of biofilm treatment with antimicrobials [47,55,57,62,64,65,94], for example, a hybrid differential-discrete approach which tested four biofilm survival mechanisms separately (i.e. slow penetration, stress response, altered microenvironment and emergence of persisters). It was found by the study that the survival behaviours predicted by the simulations for each of the mechanisms were clearly distinct from each other. This result can be useful for determining the most dominant protection mechanism in an observed scenario and thus could prove informative in terms of choosing prospective disinfection strategies [65].

In another example, a continuous, diffusion-reaction, one-dimensional model, has been employed in order to predict antibiotic penetration into P. aeruginosa biofilms, in order to test the viability of antibiotic treatment for cystic fibrosis patients [47]. Tobramycin and cefsulodin were chosen as antimicrobial compounds, and a mucoid and non-mucoid version of the P. aeruginosa biofilm were modelled in the calculations, in order to assess how the physical barrier of mucus affects the resistance of the biofilm embedded bacteria to chemical treatment. Interestingly, the results pointed to the conclusion that even though the diffusion of the antibiotic was substantially delayed in the mucoid phenotype when compared to the non-mucoid phenotype, the penetration time difference was not significant enough to account for the reported antimicrobial resistance. That is, the time it took for the antibiotic concentrations to reach high levels at the base of a 100 µm thick biofilm was still well within the common treatment time of cystic fibrosis patients. Furthermore, even when accounting for adsorption of the antibiotic to the exopolysaccharide, the concentration of the antibiotic at the base of the biofilm was eventually able to reach the concentration at the substratum. In the light of these calculations, it was concluded that the exopolysaccharide itself should not be considered as a significant physical protection barrier for P. aeruginosa biofilms against antibiotics.

Another hypothesis tested in [47] was whether the effect of bacterial production of enzymes is sufficient to effectively break down the antimicrobial compound. Assuming the enzymatic breakdown of an antibiotic in the model led to a phenomenon in which the concentration of antibiotic at the base of the biofilm could not rise above a certain threshold, as the diffusing substance would be continuously removed by the cell-produced enzymes. Simultaneously, it was observed that bacterial cells exposed to cefsulodin grew very slowly, and thus it was hypothesized that slow growth may be another likely reason for increased tolerance of the bacteria. There may be many reasons for this phenomenon, for example, bacteria in a state of low metabolic activity may naturally allow less uptake of substances into the cells, therefore decreasing uptake of the toxin. Furthermore, low metabolic activity may be caused by upregulated production of toxin-degrading enzymes or upregulated activity of toxin-expelling efflux pumps. Results of experimental studies support the hypothesis that the concentration of biocides required for successful disinfection is much greater when applied to biofilms compared to planktonic cultures [95].

In another theoretical study, the efficiency of a biocide, benzalkonium chloride and peracetic acid, against P. aeruginosa biofilm was analysed [95]. When comparing the susceptibility of different strains of P. aeruginosa to benzalkonium chloride treatment, considerable differences have been found between the resistance of strains grown in biofilms (in contrast with planktonic cultures where no significant difference was found). In particular, the difference in the time it took for the antimicrobial activity to reach the depths of the biofilm cluster, and the resulting changes in the total inactivation rate of the bacterial cells, all seemed to confirm the crucial role of the ECM in determining disinfection efficiency. Moreover, it has been found that, in agreement with the modelling study, most cells within the biofilm have been deactivated during a short treatment time of 25 min, with few live cells remaining.

At present, biofilm treatment with enzymes is applied in industrial [96] and marine applications, and research is being undertaken to apply this strategy in the hospital setting with regards to development of antibacterial coatings for implants [36,97].

2.4. Biofilm formation in complex structures

Experiments and models often describe biofilm communities growing on relatively simple substrates (e.g. flat surfaces). However, extremely flat surfaces on, e.g., the micrometre scale are an exception only found in some artificial settings [69] and most natural biofilms grow on rugose surfaces or porous media. Indeed, most bacteria on the planet inhabit structurally complex environments such as oceans or soils [16,98].

The opacity of natural porous media makes it very challenging to study biofilm formation using only experiments. This fact has been recognized in e.g. predicting biofilm growth inside the cheese matrix, among other complex food structures [99] or questions regarding bacterial invasions of the gut [100]. Applications of mathematical modelling to understand microbial growth in porous media is still limited but we believe that mathematical models can significantly help understanding this phenomenon. A theoretical framework for generic biological invasions in porous media found that the shape, size and connectivity between pores within the medium plays a fundamental role in determining the extent of a potential microbial invasion [17]. In this study, the structural heterogeneity of the soil pore space was captured through a network description with edges and nodes representing channels and bifurcation points in the pore space, respectively. Biological invasions were numerically simulated as a stochastic epidemic spreading on the pore space network. Based on the topology of the networks of the porous medium, the authors argued that structural heterogeneity typically favours biological invasions. The growth of biofilms in porous media has recently been studied experimentally [101] and theoretically [66,71,78,102] but understanding is still limited due to the complexity of the problem. The difficulty of considering microbial accumulation in porous media is amplified by the fact that this network of flow channels is generally not static, i.e. various events, including microbial activities, lead to repeated clogging and unclogging of channels, formation of new channels, etc. [71]. An approach combining fluid dynamics with game theory and experimental techniques revealed that in porous media, relatively strong and weak flow conditions favour fast and slow growing microorganisms, respectively [78].

Mathematical models have also been applied to study the effect of heterogeneity of abiotic surfaces on biofilm formation [69,103–106]. Some of these studies use computer fluid dynamics (CFD) modelling which may be combined with reconstruction of specific surface topography by surface element integration (SEI) techniques, to assess the combined effect of flow and roughness patterns on biofilm accumulation [103,105]. These are highly advanced models, which can provide a detailed analysis of biofilm formation in a specific scenario. However, we discuss below in more detail results of a study that addressed the effect of surface roughness on biofilm formation with a cellular automaton, which we believe give a more general view of the problem [69]. In cellular automata, space is discretized into equally sized patches, forming a lattice. Each patch may contain several objects (e.g. cells, extracellular material, oxygen or nutrients in [69]) and rules are introduced as to how objects interact with each other and with their environment. Properties of both objects and the environment may be defined as required. The authors in ref. [69] argued that surface roughness may aid or inhibit biofilm formation when the flow of liquid above the biofilm is of considerable force, depending on the topography of the surface [69]. The study focused on roughness on the length scale of a bacterial cell, i.e. at around 1 μm. The motivation for studying surface roughness of such magnitude was to address biofilm growth on mechanically milled surfaces, as the effect of roughness patterns of these surfaces may be an important factor for industrial applications. The modelling study found that in the case when flow is an important factor, biofilms growing on flat surfaces are easily washed out. However, for otherwise identical environmental conditions, if blocks of size comparable to a single bacterium are fixed on the surface, the bacteria at the cracks between these blocks may become sheltered from the erosion effects of the flow, and are thus allowed to colonize, expand, and spread to downstream regions of the surface. This study found that one of the key factors determining whether roughness was beneficial to the development of the biofilm or not, was the spacing between the roughness blocks. If the spacing was too small, the resulting biofilms were flat, with less cells, as space for development was scarce; if the spacing was too large, the sheltering effect was insufficient to prevent flow-induced detachment. Furthermore, increasing the height of the blocks was also predicted to present a problem for the bacteria, as at sufficiently low niches nutrients could become limited, inhibiting biofilm development at the sheltered locations.

The results of the study discussed above provide a better understanding of how exactly some surface roughness patterns affect biofilm formation. In comparison, through experimental observations, it has been reported that when mimicking the conditions of a drinking water system, with flow adjusted to 10 cm s⁻¹, matt stainless steel accumulated a significantly greater number of microorganisms than electro-polished or bright annealed stainless steel [107]. A separate experimental study on 316 L stainless steel confirmed that bacteria may exhibit higher colonization levels at the cavities present on the unpolished metal surface [108]. Interestingly, although many experimental studies simply conclude that increased surface roughness seems to promote biofilm accumulation [107–110], when investigated more closely, the surface topography, i.e. the depth and size of the cavities on the surface, has been found to be of more importance [111–114]. The latter conclusions are supported by the modelling study of Rodriguez et al. [69].

It is worth noting that nowadays the engineering of surface coatings with topographies designed to reduce biofouling are extensively studied, as technological advances allow for creating topographies of exquisite detail [113–115]. In addition to the topography, other fundamental factors have to be taken into account in such designs. These include, but are not limited to, the surface free energy, wettability, elasticity and antimicrobial properties of the surface [114].

2.5. Mixed species interactions

A single species biofilm is in most cases a laboratory construct, as the natural environment is full of microbial life and growth of single species seldom occurs in isolation. It is therefore mixed-species biofilms that are mostly apparent in situ, and thus the study of inter-species interactions within a biofilm is of great importance in addressing the challenges associated with biofilm control. Studying the role of mixed species interactions on biofilm growth is experimentally challenging [44] and mathematical models can be of great help [44,46,60]. In particular, we describe two recent applications of mathematical models which reveal key mechanisms in biofilm communities involving multiple species.

Recently, a new 2D cellular automata (discrete space and time) model has been developed to study biofilm formation of two species of bacteria, Streptococcus gordonii and Porphyromonas gingivalis [44]. These two species have been identified as the leading causes of periodontitis, commonly referred to as gum infection, which can lead to tooth loss around the infected area. The study was performed to address the gaps in knowledge on the initial development of this two species biofilm, which follows after adhesion to periodontal tissues. Experiments informed by the model were performed to verify simulation outputs against observation. The model was designed to test whether the relationship between S. gordonii and P. gingivalis in the initial stages of biofilm development was independent, competitive or detrimental. The results of the simulations agreed with experimental observations only for the detrimental case, i.e. when it was assumed in the model that S. gordonii produces a compound that slows down the growth of P. gingivalis. This finding is in line with the fact that S. gordonii is known to be able to produce hydrogen peroxide, while P. gingivalis is known to be sensitive to this compound. Furthermore, it has been suggested by array analysis and reverse transcription PCR that oxidative stress response may be triggered in P. gingivalis in the presence of S. gordonii [116]. In summary, the model has been able to provide evidence for a detrimental effect of S. gordonii on the growth of P. gingivalis in a two-species biofilm, following adhesion.

In another recent example, a stochastic two-dimensional cellular automaton model was applied to study mutualism versus exploitation in a microbial context [79]. In particular, the study analysed potential mechanisms that could promote the success of bacteria producing nutrients for other organisms, over ‘cheating’ bacteria which did not produce any nutrients. The results of the contest between the two species exhibiting these distinct behaviours were mapped against the distance between the microbes and the distance at which the produced resources could reach other microbes. It was shown that, consistently, for high cell dispersal and high reach of the shared resource, cheaters had a competitive advantage, and after reaching a certain threshold for these parameters, extinction of the cooperators was predicted. It was reasoned that for these conditions, the cells were forced to interact with many random neighbours, thus making cooperators open to exploitation. In contrast, the case when both cell dispersal and reach of the resources were low, provided an opportunity for groups of cooperators to persist against the invasion of the cheaters. Interestingly, for intermediate conditions, i.e. high cell dispersal and low reach of the resource, or low cell dispersal and high reach of the resource, the cooperators also were found to persist. In the former case, it was found that the uncertainty of the interactions between neighbours harmed the exploiter, as it led to uncertainty of resources. In the latter case, the community exhibited self-organized pattern formation, in which cooperators organized themselves into stripes or spots. The conditions within these organized groups were such that they limited the growth of cheaters. It is noteworthy that such patterns are reminiscent of similar phenomena observed in biofilms.

3. Applications of mathematical models in predicting biofilm formation

Biofilm models have proliferated due to a need to answer particular questions stemming from areas where biofilm formation is a significant concern. Today, modern theoretical biofilm models are recognized for their ability to, among other things, analyse spatial interactions between organisms within a biofilm on an individual scale [117]. Other models may focus their analysis on predictions of biofilm formation in specific environments [10,26,27,32]. In the previous section, we have discussed the former, i.e. models developed in order to understand the role of various factors on biofilm formation. In this section, we will focus on the models which aim to predict accumulation of biofilms. For example, the output of such models may be a prediction of bacterial counts on a given surface [49], or a detailed biofilm composition in the studied environment [27].

3.1. Food spoilage and safety

It is recognized that food spoilage depends on factors such as storage conditions, initial unwanted microbial counts in the food and their properties, and finally, the properties of the food involved, such as its pH or moisture. Estimating the shelf life of food products has been aided by means of mathematical models developed as early as the nineteenth century [118,119], and the value of these microbial count models for the food industry is now widely appreciated at the product development stage [99].

Empirical models build on data obtained from storage trials are common among models employed to predict shelf life [120–122]. These models are characterized by a systematic experimental approach, in which the effect of a specific variable (e.g. temperature) on microbial growth is assessed. Data collection is followed by fitting experimental data with a theoretical curve in order to analyse the correlations between considered factors, formulate general hypotheses, and subsequently allow for making better predictions. One of the notable examples in this area is the work by Ratkowsky et al. [122], in which the authors proposed a general law governing the relationship between the temperature and growth rates of bacteria. The results of the Ratkowsky et al. study were found to fit experimental data better than what was predicted by Arrhenius Law [118,123] (this is a classical law describing the relation between chemical reaction rates and temperature). Furthermore, a slight modification of the Ratkowsky et al. model [122] was found to fit empirical data for a temperature dependency study of Lactobacillus plantarum growth [121]. Apart from temperature, other factors affecting growth have been empirically modelled, e.g. the effect of carbon dioxide on growth of Photobacterium phosphoreum and Shewanella putrefaciens [120].

More recently, predictive modelling has been employed to estimate bacterial growth in seafood, dairy, bakery, vegetable, meat products and other products, e.g. infant formula or acidified sauces [99]. For example, one of the recent approaches used an individual-based stochastic model, able to accurately predict Listeria monocytogenes counts on soft cheese [49]. The individual based approach, so far uncommon in the area of predicting the microbial shelf life of food products, was introduced in order to account for variability in the microenvironment of individual cells.

The area of predictive modelling for food safety is so vast that it is beyond the scope of this review to go into the amount of detail it deserves. For an extensive, recent evaluation of this particular topic, the reader is encouraged to turn to the book by Mahony & Seman [99].

It is noteworthy that apart from predicting growth of microorganisms during food storage, empirical mathematical modelling has also been applied to address other food safety concerns. For example, a relationship describing cross contamination of Escherichia coli and Listeria monocytogenes from slicer to deli meat has been proposed based on experimental data [124,125].

3.2. Wastewater management

The use of bacteria in the activated sludge (AS) process, designed to treat water systems, dates back over a hundred years and it is safe to say that this invention revolutionized wastewater management [126]. Computational modelling of microbial communities can contribute to engineering safe water treatment reactors by, for example, testing for mathematically plausible causes for the occurrence of some observed phenomenon. This may include testing the nature of interactions between microorganisms present in the reactor [27]. Such models aim to simulate a typical environment of a wastewater system, in order to predict the distribution and relative concentrations of various microorganisms and their effectiveness in water treatment.

Activated sludge model (ASM) is the name given to the specific type of a biofilm model designed to optimize the AS process. ASMs describe processes such as oxygen consumption, sludge production, nitrification and denitrification in the AS designed to treat water systems [127]. ASMs serve as a good example for specialized models that can be widely adopted in the field they are designed for [128]. These models can aid the daily operations of plants, as well as the development of plans for introducing modifications. Careful design and continuous improvement are fundamental in using ASMs as tools for the wastewater industry, as significant decisions with financial and environmental implications may be based on their predictions. With the incorporation of computational models into water treatment industry comes the necessity to develop stringent procedures for accurate software usage and interpretation of the model's outputs, a task that has been taken on by the International Water Association [129]. It was estimated that in 2009, the number of ASM users worldwide was between 3000 and 5000 and included university and public researchers, as well as private company employees [129].

The ASM1 model describes the water purification system by a series of processes that take place in the reactor. The processes are governed by substrate-dependant rates and by the stoichiometry of the occurring reactions in each process [128]. The rates of all processes are described by various equations; for example, growth of biomass is unsurprisingly modelled by use of Monod relationships [130]. The other processes modelled by ASM1 are the decay of biomass, ammonification of organic nitrogen and hydrolysis [128].

A very recent example of a biofilm model designed for wastewater management purposes was presented by Azari et al. [27]. The model had been developed with the aim of identifying the most important parameters affecting biofilm formation in an anammox reactor; a reactor engineered to remove ammonium from wastewater. The framework of the study was based on ASM1. It has been found by the model that biofilm formation and ammonium removal was most affected by the maximum specific growth rate of organisms and heterotrophic biomass yield. The levels of nitrogen compounds and biofilm composition predicted by the model were in good agreement with experimental findings, suggesting that the results obtained by the simulations were reliable [27].

3.3. Biofuels

With advancements in technology, energy consumption has been rapidly rising. The need to move from non-renewable energy sources such as fossil fuels, to sustainable solutions which rely on renewable energy sources, is apparent. Most people are aware of such solutions being applied in the form of harnessing solar, wind, geothermal or tidal energy. Surprisingly, it does not seem to be commonly known that microbes are also being used by the energy industry, for instance in engineering biofuels such as e.g. bioethanol, biodiesel or biohydrogen [131]. However, biofuels have been claimed to have the biggest potential for reducing CO₂ release into the atmosphere [26]. This is largely due to the fact that the demand for fuels makes up a majority of the overall demand for energy [132]. Biofuels can be produced by thermochemical means or by microbial fermentation [26]. In the latter case, degradation of biomass (e.g. cellulose) by microbes (e.g. yeast, bacteria or mould) is a key process in biofuel production [133]. Although there is already an established procedure for engineering biofuels, research is being undertaken to make this process more efficient [25,50]. The area of biofuels is a multifaceted one, as for instance complex chemical and biological reactions, as well as engineering solutions have to be designed and perfected for process optimization. Advanced technologies, e.g. genomics, have been identified to be fundamental for maximizing the efficiency of biofuel production methods [25]. Furthermore, given the undeniably immense global scale impact of the energy industry, the efforts for engineering biofuels should be done in close cooperation with environmental scientist [134]. One review on microalgal biofuels listed fundamental biology, systems biology, metabolic modelling, strain development, bioprocess engineering, integrated production chain and the whole system design, as areas that need to be included in the biofuel research portfolio. The biggest share of mathematical modelling in aiding biofuel production process engineering probably lies in metabolic modelling, which is a key part of the systems biology approach to metabolic engineering [135]. However, as such techniques are performed on the scale of genomes, rather than bacterial populations, these models are beyond the scope of this review. Although we have not found in the literature the link of population scale metabolic modelling to biofuel production, it should be noted that some recently published studies combined genome scale metabolic reconstructions with differential equations for the diffusion of metabolites, thus creating genome scale resolution models of biofilm populations [76].

There are not many papers available that explicitly link biofuels to biofilm formation, and this may be due to the fact that smaller scale modelling integrated in the system biology approach has been found more applicable for this field. We will presently discuss the results of a modelling study that did focus on population scale degradation of cellulose.

A cellular automaton model has been developed which is able to mimic experimentally observed structure of biofilms formed by Caldicellulosiruptor obsidiansis [67], and in a separate study, those formed by Caldicellulosiruptfor obsidiansis and Clostridium thermocellum on cellulose substrate [50]. In the latter study, the observed thickness of the biofilm was achieved in the simulation by incorporating a detachment mechanism, which was activated once the biofilm thickness approached an observed threshold. It is quite plausible that a colony that feeds on the substrate to which it adheres will exhibit such behaviour, as this allows detached cells to float towards areas where nutrients are unexploited, i.e. to the non-colonized areas of the substrate.

Analysis of both experimental and computational results obtained from the study published in [50] seemed to point to the conclusion that cellulose degradation was synchronous to biofilm formation of the particular species. Moreover, only cellulose areas to which bacterial cells were attached exhibited degradation and increasing number of planktonic cells in the culture did not produce a significant effect. In the light of the obtained results, the authors concluded that the process of cellulose degradation could theoretically be sped up by covering the cellulose substrate with a highly concentrated inoculum of cellulose-degrading cells [50].

3.4. Application of genome-scale reconstructions in biofilm modelling

With recent advancements in genomics, proteomics and metabolomics, there has been a rise in biofilm models that incorporate genome-scale data for obtaining more sophisticated predictions for microbial communities [10,72–74,76]. The aim of incorporation of genome scale data in biofilm modelling is to improve the quantitative understanding of spatial and temporal variation of the microenvironment of cells embedded within a biofilm, which is believed to have a critical impact on biofilm development [76]. A table of available genome-scale metabolic reconstructions which have been validated by experimental data can be accessed through the Systems Biology Research Group web page [136]. These reconstructions can be used to feed more information into biofilm models, e.g. the metabolic by-products, compound uptake fluxes, or the secretion of toxins and growth inhibitors of the documented strains. It has been suggested that the accuracy of predictions related to spatial partitioning of species within a mixed-species biofilm is enhanced by inclusion of the effect of metabolic factors [72,76].

The studies which explicitly coupled genomic scale data and biofilm modelling have targeted e.g. illness related biofilms [76] or microbial fuel cells biofilms [10,73]. In another study of this kind which focused on E. coli biofilms, it was suggested that a similar methodology may also be useful for models of tissues or tumours [74]. In essence, these studies incorporate differential equations for the diffusion of metabolites in population scale models, and they do seem promising in terms of improving prediction power of mathematical models of biofilms. For example, in a modelling study of E. coli colonies grown on glucose minimal agar, incorporation of data from E. coli metabolic reconstruction led to the discovery of a feature of E. coli colonies which has not been recognized previously. The study found that glucose and oxygen gradients within the colony gave rise to four distinctly spaced metabolic phenotypes, namely, rapidly growing cells at the bottom edge of the colony, where both glucose and oxygen concentrations were high, nearly dormant cells in the interior, where both glucose and oxygen levels were low, and two other subpopulations between which acetate cross-feeding was found to take place. The first subpopulation, located at the base of the agar, exhibited high glucose consumption and acetate production due to high glucose concentrations. The second subpopulation, located at the regime of high oxygen concentrations and low glucose concentrations, exhibited a phenotype that favoured acetate consumption. In terms of the predictive power of this modelling study, the height to width ratios of simulated colonies were in agreement with those of colonies grown experimentally [74].

4. Conclusion

Mathematics can be used to understand and exploit the world around us. Examples of mathematical models of biofilm formation presented in this review only scrape the surface of the vast number of models which have been developed, from their earliest descriptions until the present. We presented some examples of biofilm models which significantly advanced our understanding of biofilm communities and generated results applicable, for example, to medicine, the food industry, dentistry, water management and for engineering more environmentally friendly energy.

Although computational models have been found useful over the years in providing practical answers about microbial communities, they do all have considerable limitations. The fact that a model is necessarily a significant simplification of reality is both a handicap and a strength, depending on the point of view and application. Just as the biofilm field is complex, so is the branch of biofilm modelling. This creates obstacles between model development and applications, because if the model is to be trusted, it must be verifiable in a specific set-up for which it has been created. Furthermore, the wide use of any given model is difficult to achieve, as any model would have to go through modifications to become usable for another research problem. This requires understanding of the language in which the model source code was written, and a thorough grasp of the implemented processes. Luckily, when building a model to address a specific problem, one may build on the general rules adapted by existing models and choose suitable methods of implementation for the question that needs to be answered. For instance, empirical models give an idea of the relations between specific factors affecting biofilm formation, e.g. the relationship between temperature and growth rates. Although these are built on specific experimental results, as evidence of their reliability builds up, they become widely adapted, as has been the case with Monod growth equations, for example. Empirical modelling has been particularly favoured when estimating bacterial counts is the priority of the study, as is the case in e.g. developing food spoilage prevention methods. On the other hand, in studying the interactions between biofilm components on the scale of bacteria cells, the mechanisms of biofilm organization and structuring, or when considering structurally complex environments such as rough surfaces and porous media, spatial, individual based or cellular automaton models seem to be a suitable choice, as does the game theory approach. Furthermore, treating the biomass as a continuous, viscoelastic substance, may allow for applying mechanics laws in studying the material properties and behaviour of the biomass. Finally, for analysis of e.g. antimicrobial penetration of a biofilm, a one-dimensional model treating biomass as a continuum may be fitting for its purpose.

In their current form, mathematical models of biofilms can play a key role in addressing many important questions. For example, a proper combination of experimental and theoretical approaches will help understanding the behaviour of biofilm communities in some habitats that can be reasonably complex (e.g. through structural or chemical heterogeneity). Other questions will require holistic approaches accounting for biofilm formation at multiple scales, interactions between species and other factors. For instance, biofilms are likely to promote survival and persistence of pathogens in food-related environments [137]. In this context, biofilms can be regarded as just one element of a larger multifaceted problem involving domains ranging from the natural environment to food production factories and consumers. Integrating the key factors in a single framework to address biofilm-associated problems (e.g. risk assessment of food contamination), is a challenge that will necessarily involve mathematical modelling and data analysis combined with experimental approaches.

It seems that although great improvement has been seen over the years with regards to computational models of biofilm formation, with substantial useful information gathered from computational analysis, much work is yet to be done to bridge the gap between theoretical and practical aspects, in order to synergistically build a general set of principles by means of which microbial development can be understood. Although not an easy endeavour, it is a necessary next step to fully realize the potential of biofilm models in addressing new challenges associated with biofilm control and utilization. A relatively recent, however fast developing field of systems biology promises to provide such an integrated framework [138]. Systems biology has already been successful in engineering new solutions for e.g. biofuel or the pharmaceutical industry [139]. The idea behind this research field is to develop fine-detailed models of ecosystems which take advantage of the new advances in genome sequencing data collection [140]. Among a plethora of potential applications of this technology, when paired with advances in computing, it can lead to development of highly sophisticated biofilm models. The high resolution methodology of systems biology has already been to some extent applied at the scale of whole populations of bacteria cells, for example by combining genome-scale metabolic modelling techniques with partial differential equations to model the spatial distribution of metabolites within the biofilm [76]. The systems biology approach requires a high level of cooperation between various disciplines. In building such fine-resolution models, apart from biology, expertise in fields such as chemistry, physics, engineering and informatics may be necessary, depending on the research question. It is likely we will see more field-specialized biofilm models develop, as is the case with ASM models for wastewater management or shelf life prediction models. Before incorporating solutions to challenges of microbial control and utilization on a large scale, potential environmental concerns should be addressed, thus further widening the desirable network of collaboration in the biofilm research field. This sentiment has already been expressed by researchers in the biofuel field [134], however, it should extend to all areas capable of producing a large-scale impact on the environment.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by a scholarship grant from the School of Natural and Computing Sciences at the University of Aberdeen and the Faculty of Health Sciences at Curtin University.