Abstract
Agricultural losses to pests represent an important challenge in a global warming scenario. Intercropping is an alternative farming practice that promotes pest control without the use of chemical pesticides. Here, we develop a mathematical model to study epidemic spreading and control in intercropped agricultural fields as a sustainable pest management tool for agriculture. The model combines the movement of aphids transmitting a virus in an agricultural field, the spatial distribution of plants in the intercropped field and the presence of ‘trap crops’ in an epidemiological susceptible–infected–removed model. Using this model, we study several intercropping arrangements without and with trap crops and find a new intercropping arrangement that may improve significantly pest management in agricultural fields with respect to the commonly used intercrop systems.
Keywords: complex networks, plant infections, agriculture, aphid-borne virus transmission, intercropping, trap crops
1. Introduction
The sustainable intensification of agriculture is impera- tive for feeding a growing world population while minimizing its negative environmental impact. The world population will increase to between 9.6 and 12.3 billion in 2100 [1], and to feed these additional 2–4 billion people a duplication (100–110%) of crop production relative to its 2005 level is needed [2]. Today, 10% of ice-free land on Earth is used for crop cultivation [3], and returning half of Earth's terrestrial ecoregions to nature will mean global losses of 15–31% of cropland and of 3–29% of food calories [4]. Thus, increasing crop yield without extending the size of the cultivation areas and not intensifying the use of current technologies is a vital complex problem to be solved in the coming years. Agricultural yield is substantially reduced by pests [5–9], which cause losses of 10–16% of crop production [5–9], which may represent a real threat for entire world regions [10]. In addition to these scenarios, there is increasing concern that climate change could lead to increased plant damage from pests in future decades [11–16]. Bebber et al. [17] have demonstrated that pests and pathogens have shifted poleward by 2.7 ± 0.8 km yr−1 since 1960. This will produce a lower numerical response of biological control agents, which can be translated into higher probabilities of insect pest outbreaks. Deutsch et al. [18] estimated that global yield losses of rice, maize and wheat grains are projected to increase in the range of 10–25% per degree of global mean surface warming. Thus, in a projected scenario of a 2°C warmer climate the mean increases in yield losses owing only to pest pressure extend to 59, 92 and 62 metric megatons per year for wheat, rice and maize, respectively [18]. These losses cover most of the globe, as can be seen in fig. 2 in [18], but they are primarily centred in temperate regions.
From an agricultural point of view, a particularly important class of insect pests are the aphids (Aphididae) [19]. Aphids are by far the most important transmitters of plant viruses, being reported to transmit about 50% of insect-borne plant viruses (approx. 275 virus species). There are about 4700 aphids described, from which about 190 transmit plant viruses (see ch. 15 of [19]). From an economic point of view, this virus transmission by aphids represents global losses estimated at tens of millions to billions US dollars of yield loss per annum [20–22]. In the UK alone, the damage to cereals caused by aphids has been estimated to be around £60–120 million annually [23]. Thus, mathematical modelling is seen as an important tool to predict and mitigate the effects of viruses on agriculture [24,25].
Today, there are several alternative approaches to the sustainable intensification of agriculture based on agroecological and adaptive management techniques [26]. A recent report has shown that organic farming, for instance, promotes pest control [27]. An example is intercropping, consisting in growing two or more crops in the same field, which has proved to be important for pest control in several crops [28–30] (see electronic supplementary material, table S1). Intercropping has been known since the sixteenth to eighteenth centuries when Iroquoian farmers inter-planted the three sisters: corn, beans and squash [31]. Intercropping is known to reduce the levels of infestation by stemborers and increases insect pest parasitism [32]. These practices have been extended across the globe, as can be seen in fig. 1 of [30]. A meta-analysis of 552 experiments in 45 papers published between 1998 and 2008 showed that intercropping produces significant improvement for herbivore suppression, enemy enhancement and crop damage suppression [33] with respect to a monocrop. Brooker et al. [34] have concluded that intercropping ‘could be one route to delivering “sustainable intensification”’ of agriculture.' In the particular case of aphids, there are many reports on the successful use of intercropping strategies for controlling aphid-transmitted viral diseases [35–37]. In a recent review, a series of companion plants that could be potentially used in intercropping strategies for controlling aphids have been reported, together with several strategies for controlling aphid-produced diseases [38].
Here, we develop and implement a mathematical model that allows us to study intercropping as a sustainable pest management tool for agriculture. Our main goal is to investigate which are the best spatial arrangements for controlling aphid-transmitted viruses in agricultural scenarios by avoiding the propagation of aphids through the crop field. For this purpose, we combine the movement of aphids in the agricultural landscape [39–42] with the spatial distribution of plants in the intercropped field, in an epidemiological susceptible–infected–removed (SIR) [43] model. The model allows us to implement ‘trap crops’—plants which attract or detract insects to protect target crops [44–48]. Using this approach, we find that a new intercropping arrangement proposed here—particularly when combined with trap crops—can improve significantly pest management in agricultural fields with respect to the commonly used intercrop systems.
2. Theoretical methods
To develop the theoretical model used in this work, we made the following assumptions.
-
(1)
The infection is transmitted to plants by an aphid—a vector. That is, a susceptible plant receives the infection, e.g. a virus, from an infectious plant through a vector.
-
(2)
Recovered (removed) plants represent not only those that are dead but also those that are useless for commercial purposes, i.e. those that are so damaged they cannot be used for consumption.
-
(3)
The number of plants in the field is fixed.
-
(4)
When a susceptible vector is infected by a plant, there is a fixed time τ during which the infectious agent develops in the vector. At the end of this time, the vector can transmit the virus to a susceptible plant.
-
(5)
The number of infectious vectors is very large and at a given time t that number is proportional to I(t − τ).
These assumptions are an adaptation of the ones made by Cooke [49] for implementing a time delay SIR model to study vector-borne infection transmission to a given population. The corresponding equations are as follows:
| 2.1 |
where Si is the probability of plant i being susceptible to the infection, Ii is the probability of plant i being infective after having been infected by the disease and Ri is the probability of plant i being removed; β and μ are the birth and death rates of the disease, respectively, and j spans only those plants that are able to spread the disease by contact with plant i. Note that Si(t) + Ii(t) + Ri(t) = 1, and, consequently, . This model has been subsequently studied in the literature by several authors as a vector-borne disease transmission model (see for instance [50–53]). For other approaches to modelling vector-borne virus transmission on plants, see for instance [54].
Here, we generalize Cooke's model [49] in order to account for the probability that a vector hops not only to a neighbouring plant but also to a more distant one in the field:
| 2.2 |
| 2.3 |
| 2.4 |
where fij is a function of the ‘separation’ between plants i and j, and j spans to all the plants in the field. There are two possibilities to account for this separation between plants. The first is to consider the Euclidean distance between the corresponding two plants, i.e. , where xi and yi are the Cartesian coordinates of plant i in the plane. Note that this distance does not capture all the subtleties of the real separation between the plants as two plants can be of different height, and a third coordinate should be introduced. In this case, we can consider that the probability fij of moving from plant i to plant j is proportional to a certain function of this distance, e.g. decaying as a power law fij∝ρ−sij or decaying exponentially , where .
The second approach is to consider plant-to-plant separation in terms of the number of hops that an aphid needs to take to go from plant i to plant j using other intermediate plants. That is, let us consider that the aphid in question has an exploration radius equal to r. This means that if the aphid is on plant i it can hop directly to a plant which is at a distance less than r from i. In order to hop to a plant k separated by two radii from i it has to use two steps. That is, if we connect two plants by an edge if their geographical separation is ρij ≤ r, then the plant-to-plant (topological) separation dij is given by the number of edges in the shortest path connecting the two nodes in the resulting graph G = (V, E) with vertices V and edges E. In this case, we again can consider that the probability fij of moving from plant i to plant j is proportional to a certain function of this distance, e.g. decaying as a power law fij∝d−sij or decaying exponentially , where . Let us consider some of the potential differences between these two ways of accounting for the interplant separation.
(a). The rationale of the model: through-space versus plant-to-plant aphid mobility
From the complex movements that an aphid can display in a crop field (see [19, ch. 10], [55,56]), here we focus only on their exploratory movements within a crop field. These include mainly displacements to a neighbouring plant (primary movement) or a distant plant within the same field. We exclude here those unintentional movements of aphids such as the displacement by air currents that can transport them very long geographical distances. Thus, with this restriction in mind, we analyse the main differences in considering a model that includes the geographical or topological distance for epidemic transmission. In doing so, we have identified three main factors in favour of the use of topological interplant separation which are based on the main behavioural characteristics of aphids' exploratory movement within crop fields [57–60]. These three principles are the following: (i) first come first served, which essentially tells us that an aphid flying in one direction will land on the first available plant independently of the distance at which it is from its starting position; (ii) a bird in the hand is worth more than two in the bush, indicating that the probability that an aphid moves from plant i to another j decays with the number of other plants in the path between i and j; (iii) go back before it is too late, which indicates that an aphid flying in a direction without plants would prefer to return to its starting point. These principles are detailed in electronic supplementary material, Note 1.
(b). Susceptible–infected–removed model with topological distances
As a consequence of the previous hypothesis, we conclude that the use of the topological interplant separation is appropriate for our modelling purposes. Therefore, the SIR model of the field is expressed as [61]
| 2.5 |
| 2.6 |
| 2.7 |
where , d ≤ dmax, dmax is the diameter of the graph, i.e. the largest separation between two plants (in terms of steps), and the matrix Ad captures the (long-range) mobility of the pest between plants (figure 1).
Figure 1.
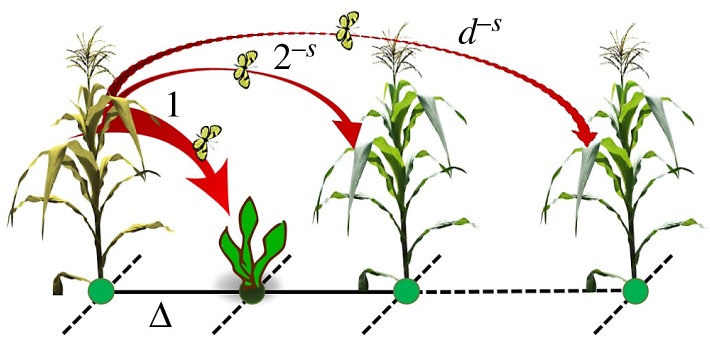
Inter-plants movements of an aphid in an agricultural plot with intercropping (see electronic supplementary material, Note 1). The hop of an aphid from an infected plant to a susceptible one separated by d steps is given by d−s (see electronic supplementary material, Notes 1 and 2). (Online version in colour.)
The d-path adjacency matrices Ad used in the current formulation are generalizations of the concept of the adjacency matrix. In electronic supplementary material, Note 2, we give a formal definition of them and an example (see also [62–64]). We will always consider a connected network here. Let dij = d be the shortest path distance between nodes i and j in network G. Then, the d-path adjacency matrix is defined by
| 2.8 |
We consider any 1 ≤ d ≤ dmax, where d = 1 provides the ‘classical’ adjacency matrix and where dmax is the diameter of the network. Then, we combine all the d-path adjacency matrices by using a transformation, such that
| 2.9 |
where s is an empirical parameter controlling insect mobility. The transformation in equation (2.9) is denoted as the Mellin d-path transformation. In this case, the entries of à are defined as follows:
| 2.10 |
Note that the transformed adjacency matrix à is symmetric in the case of undirected networks. Then, when the aphid has very poor mobility , all the entries of Ã, except those equal to 1, become 0, which indicates that the aphid can only perform hops to nearest neighbours. On the other hand, when the aphid has a very large mobility , every entry of à becomes 1, which means that the aphid can hop from one plant to another with equal probability independently of their separation in the field.
(c). Markovian formulation of the epidemiological model
Following the framework introduced in [65], we formulate a Markovian dynamics that, in principle, is valid for any epidemic prevalence. For that reason, hereafter, we restrict ourselves to this Markovian approach. Let pi(t) be the probability that a node i is infected at time t. Then, in the SIR model, the Markovian equations read as follows:
| 2.11 |
| 2.12 |
where ϱi(t) is the probability that node i is removed at time t. Note that the term 1 − pi(t) − ϱi(t) is just si(t), the probability that a node i is susceptible at time t. The expression for the infection probability qi(t − τ) is [61]
| 2.13 |
which represents the probability that, when node i is healthy at time t, it becomes infected at time t + 1. The expression qi is calculated as 1 minus the probability that the node i is not infected by any infectious contact. This last probability is the product over all the possible contacts of node i, considering that a node j transmits the disease to i with probability βÃijpj, after a delay time τ. Note that if node j is not connected to i (i.e. if dij > 1 and ), Ãij = 0, then the corresponding term in the product is equal to 1, since j cannot infect i regardless of its state, pj(t − τ).
We should note that this Markovian formulation holds for any disease incidence, while equations (2.5) and (2.6) are only valid when the disease prevalence is small. To explain this, take equation (2.13) for qi(t − τ) and consider that the prevalence is small, pi≪1 ∀i, and for this reason let us denote pi = xi. Then, the product in (2.13) transforms into: , the new expression for qi(t) in equation (2.11); passing from discrete to continuous time, we recover a similar expression to that in equation (2.6) for the evolution of the infected state of node i. For more details, the reader is referred to [66].
The rate of propagation of the aphid-borne viral infection across an agricultural field is defined here as
| 2.14 |
Finally, for the sake of simplicity, in this work, we suppose that the secondary crop of the intercropped systems is not susceptible to the disease and, consequently, its plants cannot become infected (i.e. pi = 0 for every plant i that belongs to the secondary crop). However, note that the presence of a secondary crop may modify the interactions between the plants of the main cultivar (i.e. dij and Ãij) and, consequently, their respective probabilities qi(t − τ). In the next section, we define the intercropping arrangements used in this work. In addition, the secondary crop can be used to implement ‘trap crops’, which may alter the mobility of an aphid, i.e. Ãij (see section 2d(iii)).
(d). Computational arrangements
(i). Intercropping arrangements
The intercropped systems considered here and shown in figure 2 are: strip intercropping, in which strips of the main cultivar are inserted between strips of the secondary crop; row intercropping, in which rows of the main and secondary crops are alternated one by one; column intercropping, the same as before but by columns instead of rows; chessboard intercropping, in which a plant of the main crop is inserted in the rows and columns between every two susceptible plants; patches intercropping, in which squared patches of the main crop are alternated with squared patches (of the same size) of the secondary crop; random intercropping, in which plants of the secondary crop are randomly inserted among those of the main crop. The first two intercropping arrangements—strips [48,67] and rows [68–70]—are frequently used in experimental designs and field applications. It is important to remark that, in all cases, we have considered exactly the same number of plants of the main crop such that the results obtained here are not due to size effects.
Figure 2.
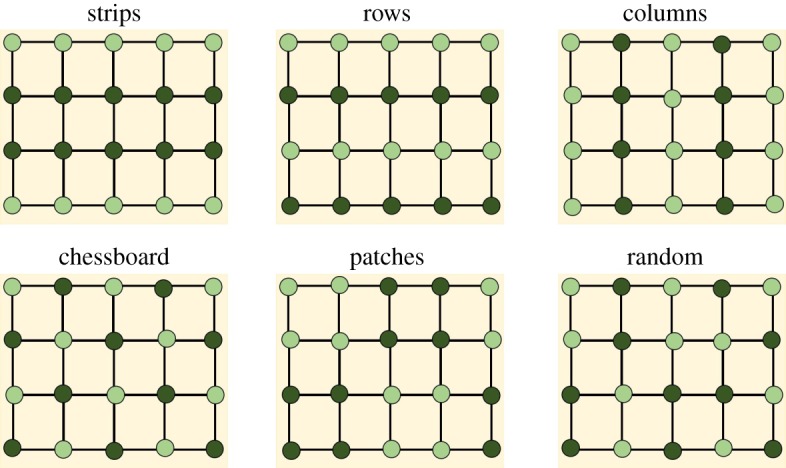
Intercrop arrangements. Different organizations of intercrops between two species studied in this work with r = Δ (see Network construction). Light green nodes represent the main crop and dark green nodes represent the secondary crop, which is considered to be not susceptible to the disease spreading on the field. In the case of trap crop strategies, the dark green nodes represent the plants with semiochemical activity to trap the pest to be controlled. The square lattices connecting the nodes correspond to the interconnection networks considered here. (Online version in colour.)
(ii). Network construction
Our arrangements consist of rectangular plots of lengths x = a and y = a−1. These plots guarantee that all simulations are carried out on fields of equal area. Rectangular plots have been shown—both theoretically and experimentally—to delay the propagation of epidemics more than square plots with the same area and density of plants [71]. We consider the distribution of a major crop intercropped with a secondary crop, which may or may not be a trap crop. In the intercropped field, we maintain a separation between plants equal to Δ (figure 3). In this case, the plant-to-plant connectivity, based on their separation, is represented by a squared partition of the plot. We simply normalize all the distances by dividing them by Δ. Then, two plants which are nearest neighbours are one step apart, a second nearest neighbour is two steps apart and so forth. In general, every plot consists of 20 rows and 50 columns. There is a plant at every intersection for a total of 1000 plants. As we have a unit rectangle with a = 1.6059, the value of Δ is 0.033, and we use a connection radius r = Δ, such that the plants are adjacent (connected in the network) only to those immediately to the left, right, up and down. In the case of the intercropped systems, we always replaced 500 plants of the main crop by the same number of plants of the secondary crop. In electronic supplementary material, Note 3, we analyse the case in which the separation between rows and columns in the plot is less than Δ, which is equivalent to considering the radius of the primary movement of the aphid equal to .
Figure 3.
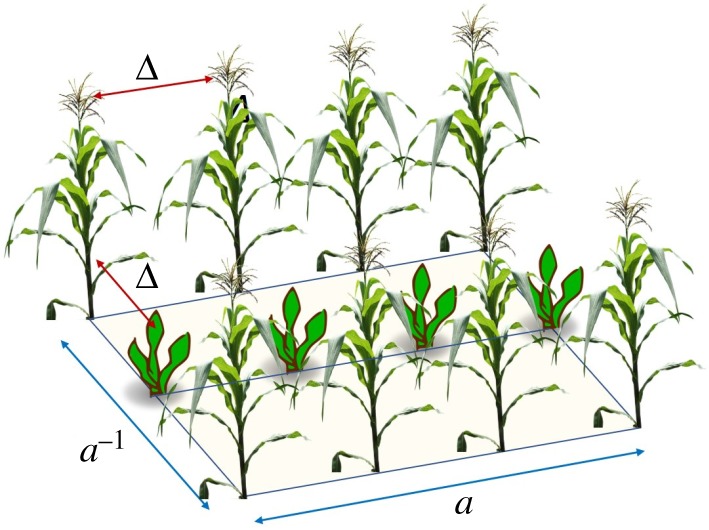
Schematic of the intercropping of two species in a rectangular plot of unit area and largest edge length a. The separation between plants is given by Δ. (Online version in colour.)
(iii). Implementation of the ‘trap crops’
Although trap crops can be formed either by ‘push’ crops or by a combination of ‘push–pull’ crops [44–47], here for modelling purposes we combine all the trap crop effects into a single one. Basically, we consider that the trap crop diminishes or completely avoids the propagation of a pest in a path beyond the place in which the trap is located. Consequently, if there is more than one trap in the path between two susceptible plants, we only consider the effect of one of them. An additive or multiplicative effect of the traps can be easily implemented using the current mathematical framework (see below), but it is not done here for the sake of simplicity. In this case, the secondary crop is located between the paths connecting the infected and the susceptible plants. Mathematically, let us consider two plants i1 and id+1, and the shortest path i1, i2, · s, id, id+1 of length d between them. To model trap crops, we modify the strength of the long-range mobility of the aphid between i1 and id+1 as follows:
| 2.15 |
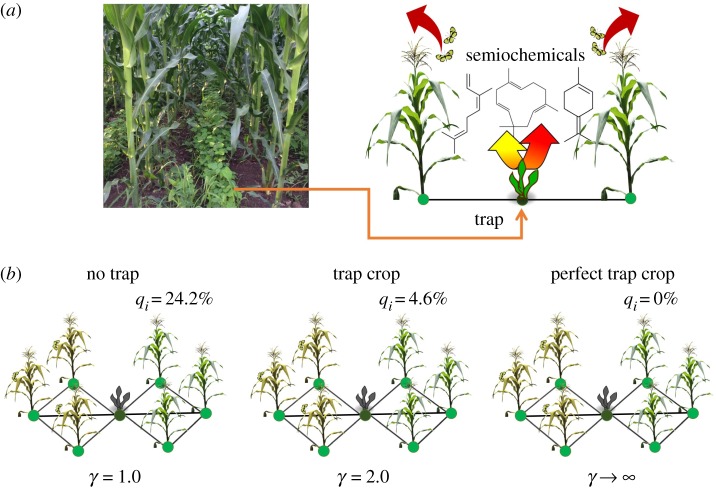
where γ≥1 is the trap strength. When γ = 1, there is no trap crop as we recover the original equation for the epidemic dynamics with long-range movements. On the other hand, when 1 < γ < ∞, movement of the aphid is reduced beyond the point at which the trap is located. For instance, when the trap crop is very effective, i.e. , the movement of the aphid from i1 to id+1 is completely interrupted, which means that the trap is perfect. In figure 4b, we illustrate the effects of a secondary crop in which we obtained the probability qi that the plants on the right-hand side are infected once the three plants on the left-hand side are infected by the pest. To do so, we suppose that pi = 0 for i spanning over the secondary crop and the plants of the main cultivar that are on the right-hand side of each arrangement, and pi = 1 otherwise. According to figure 4, the shortest path distance between the infected and the susceptible plants is always d = 2, and there is a secondary crop plant between them. Under these conditions, equation (2.13) reduces to qi = 1 − (1 − β2−sγ)3 for each plant on the right-hand side. Supposing τ = 0 (no delay), s = 2.5 (aphid with large mobility) and β = 0.5, when γ = 1 (no trap), the infectability of the susceptible plants is 24.2%, which represents the effects of an intercropped secondary species. However, when the strength of the trap is γ = 2, the probability that the susceptible plants are infected drops to less than 5%. This probability is reduced to 0% as γ is subsequently increased.
Figure 4.
(a) Intercropping with ‘push’ (or push–pull) strategies where semiochemicals [72,73] are released from trap crops (photograph courtesy of Rachel Monger (Immanuel International)). (b) Effects of the strength of the trap crop γ (small dark plants) on the probability of plants i becoming infected qi (see text for explanations) once the plants on the left of the figures are infected. (Online version in colour.)
(iv). Simulations
Using the Markovian formalism, i.e. equations (2.11)–(2.13), we perform 100 random realizations for each field arrangement, secondary crop (with or without trap) and aphid mobility (fast and slow). In each independent realization, the propagation is initialized by infecting randomly a single susceptible plant on the border of the field. Following [61], we set here μ = 0.5, since we are not trying to characterize any particular disease. For μ = 1, for instance, the recovery is too fast to see the spatial propagation and, conversely, in the case μ = 0 the dynamics would be an SI dynamics. We decided to aim our study between these two limiting cases.
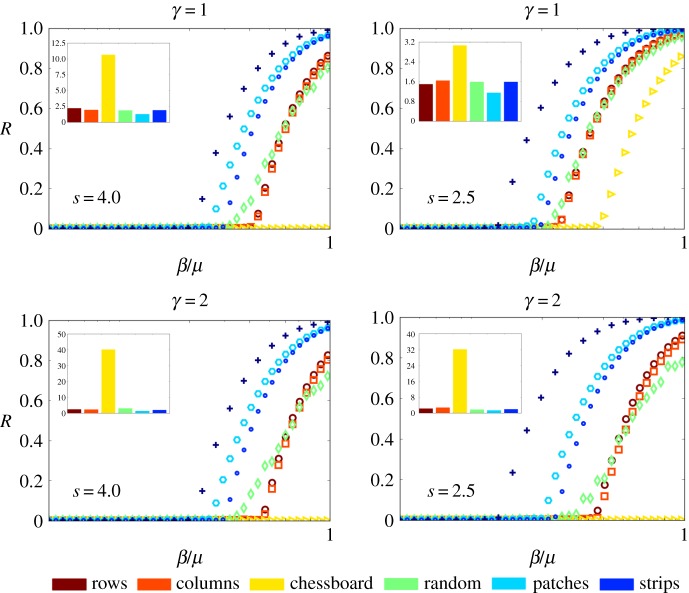
For the dynamics of the disease, we calculated the total amount of Markovian time t* in which the probability of being susceptible is higher than the probability of being removed (i.e. 1 − ϱi − pi > ϱi), for each plant of the main cultivar. To estimate the epidemic thresholds for a given value of γ, we calculated the average stationary fraction of removed plants (over 100 independent realizations), R(β, μ), for 50 logarithmically spaced values of β, between 0.02 and 1.0, when μ = 0.5, where , i spans over the plants of the main cultivar and Ni is the total number of plants in that crop. Then, using linear interpolation, we find the epidemic threshold τE in each field. We recall that the epidemic threshold is the smallest value of β/μ for each arrangement that satisfies the condition that R(β, μ) > 0. Visualization of the results in the form of rain clouds was performed using Matlab codes available from Allen et al. [74]
3. Results and discussion
(a). Influence of time delay
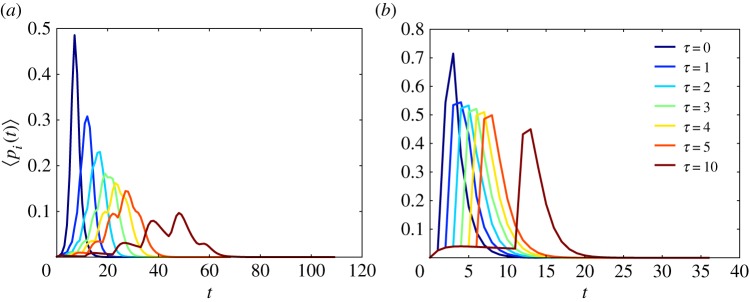
According to the results previously reported by Tchuenche & Nwagwo [52], the effects of the time delay τ are mainly observed at the initial times of the propagation dynamics and are focused on the population of susceptible plants. For a relatively large time, the evolutions of the SIR dynamics with and without time delay are almost indistinguishable (see fig. 2 in [52]). For instance, in figure 5, we can observe that the results without time delay, i.e. τ = 0, are qualitatively similar to those for τ = 1, with almost the same epidemic threshold and very similar shape of the propagation curves. We explore here the effects of τ on the epidemic dynamics when the vector mobility is incorporated into the model. Using the Markovian formulation described previously in equations (2.11)–(2.13), we obtained the evolution of the infected population of plants in a crop field consisting of a square lattice as described before for two different values of aphid mobility s in the Mellin-transformed Markovian SIR equations. The results are illustrated in figure 5, where we have used β = 0.5, μ = 0.5, r = Δ and s = 2.5 (figure 5a) and s = 1.0 (figure 5b). It can be seen that the inclusion of a time delay in the model means that the peak in the number of infected plants is displaced to longer times. For large aphid mobility (s = 1.0), it is observed that the shapes of the peaks of infection are very similar to each other for different values of time delay 0 ≤ τ ≤ 10. When the mobility of the aphids is relatively low (s = 2.5) the rate of propagation of the infection changes significantly for different values of τ, particularly for very large time delays. For instance, the values of the rate of propagation for a given time delay, v(τ), obtained from equation (2.14), are as follows: v(0) = 32.25, v(1) = 26.32, v(2) = 22.22, v(3) = 18.87, v(4) = 16.67, v(5) = 14.70, v(10) = 9.17. However, for the case of large aphid mobility these rates of propagation are not changed significantly with the time delay: v(0) = 43.48, v(1) = 40.00, v(2) = 38.46, v(3) = 35.71, v(4) = 34.48, v(5) = 33.33, v(10) = 27.78. That is, for relatively low time delays the results for disease propagation on plants are very similar to those without time delays. Also, when the aphid mobility is relatively large, the time delay does not significantly affect the propagation rate of the disease.
Figure 5.
Evolution of the number of infected plants in a square plot with varying time delays τ. The modelling is performed with β = 0.5, μ = 0.5, r = Δ and s = 2.5 (a) and s = 1.0 (b). (Online version in colour.)
As a consequence of the previous analysis and for the sake of keeping our model as simple as possible, we do not consider explicitly the time delay in further calculations in this work. The biological justification for this simplification is as follows. The interaction of the virus and aphid is controlled by the following phases (see ch. 15 of [19]): (i) acquisition, where the aphid takes up virions from an infected plant; (ii) retention, where the aphid carries the virions to specific sites; (iii) latency, which refers to the inability of an aphid to inoculate a virus immediately after acquisition; and (iv) inoculation, which is the release of retained virions into the tissues of a susceptible plant. There are three types of transmission of a virus to a plant (see ch. 15 of [19]). In non-persistent (NP) transmission, the acquisition and inoculation are very fast and require only a very brief stylet penetration, which takes less than 1 min. In this case, there is no latency period and the whole cycle of transmission can be completed within a few minutes. In semi-persistent (SP) transmission, the acquisition and inoculation require periods of about 15 min. In this case, there is no latency period either and the aphids retain the ability to inoculate for periods of up to 2 days following acquisition. Finally, in persistent (P) transmission, the virus acquisition requires a period between hours and days, there is a latency period and the retention is for days to weeks. From the about 270 viruses transmitted by aphids more than 200 are transmitted by NP transmission (see ch. 15 of [19]). The results to be considered here using an SIR model without time delays are then equivalent to a model of aphid-borne transmission of viruses to plants using either NP or SP transmission.
(b). Impact of intercrop arrangements on virus propagation
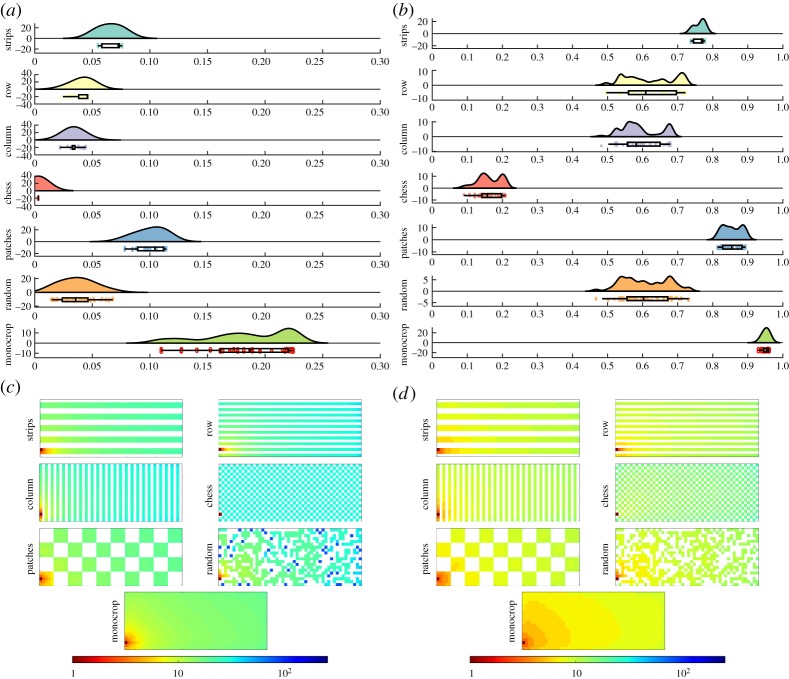
In figure 6, we illustrate the results of the simulations of the propagation of an aphid-borne virus in the six intercropped fields without traps (γ = 1.0) studied here as well as in a monocrop. In figure 6a, we show the results for an aphid with relatively low mobility (s = 4.0), and, in figure 6b, we give the same for a relatively high-mobility aphid (s = 2.5). To compare the dynamics of the different arrangements, firstly, we analyse their respective results before they reach equilibrium (t = 10). In the case in which s = 4.0 it is clear that the disease is propagated in a relatively slow fashion, and for t = 10 only 18.3% of plants are removed in the monocrop. As can be seen in this figure, all intercrop arrangements produce a significant decrease in the number of removed plants. The smallest decrease in the number of removed plants is observed for the patches configuration, in which the percentage of removed plants is 10.1%, followed by the strips configuration, with 6.6%. On the other hand, the most efficient arrangement is the chessboard one, which reduces the number of removed plants practically to zero (only 0.3% of removed plants).
Figure 6.
Aphid-borne virus propagation on intercropped fields without traps. Results of the simulations for SIR epidemics at t = 10 with r = Δ, β = 0.5, μ = 0.5 for different intercropping strategies without trap crops, i.e. the strength of the trap crop is γ = 1.0. Raincloud plots of the proportion of dead plants for a viral infection propagated by aphids: (a) aphid with reduced mobility (s = 4.0) and (b) with greater mobility (s = 2.5). The clouds show the kernel distribution of the proportion of dead plants for different realizations of the epidemics. Below, the raw data are plotted (the rain) together with their corresponding box and whisker plots. Illustration of the evolution of infection across fields with different intercropping systems: (c) aphid with reduced mobility (s = 4.0) and (d) with greater mobility (s = 2.5). In both panels, the time t* is given in a colour scale (see text), and the propagation is initialized by infecting the plant in the bottom-left corner of the plot. (Online version in colour.)
In figure 6b, we illustrate the results for the case in which the pest has relatively high mobility. Here, the picture observed is significantly different from the one in the previous case. First, the level of plants removed in the monocrop is 95.1%, indicating an almost complete destruction of the crop in a relatively short time (t = 10) when the pest is highly mobile. The range of amelioration of the infection across the fields is very wide here, ranging from a 10% decrease in removed plants observed for the patches arrangement (85.5% of removed plants) up to about an 80% decrease obtained with the chessboard arrangement (16.3% of removed plants). Note that the frequently used intercrop arrangement of strips produces, together with that of patches, the smallest improvement in the number of removed plants. Thus, although the results are quantitatively very different for the cases of low and high mobility of the aphid, they are qualitatively similar in identifying the worse arrangements (patches and strips) as well as the best one (chessboard). In both cases, the order of effectivity in reducing the impact of an aphid-borne virus propagation is: chessboard > columns > random > rows > strips > patches.
In figure 6c,d, we illustrate a snapshot of the aphid-borne propagation of a virus across the different intercropping systems with s = 4.0 and s = 2.5, respectively. In order to compare all the different arrangements, we always start the epidemic by infecting the same node, i.e. the one at the bottom-left corner of the field. The colours in the plots (see online version) represent the time t* in which the plant remains susceptible without becoming removed by the vector-borne virus disease. That is, a low value of this time indicates that the plant is removed relatively soon by the virus disease. In order to interpret quantitatively the results in these plots, we use the rate v of propagation of the aphid-borne virus previously defined in equation (2.14). It can be seen that in the monocrop the epidemic is propagated in a wave-like way, typical of diffusion processes. The values of v in the monocrop are 23.26 (s = 4.0) and 32.26 (s = 2.5). That is, when the aphid has relatively low mobility, there is an average infection rate of 23.26 plants per unit time. This rate is increased to 32.26 plants when the pest mobility is increased, owing to the fact that the aphids can now hop to wider regions of the plots. Characteristics of the wave-like propagation of the vector-borne virus are observed in all the intercrop arrangements studied. In the intercropped systems (without trap crops, γ = 1.0), the propagation rates of the virus are: for s = 4.0, chessboard (0.03) < random (5.46) < columns (7.35) = rows (7.35) < strips (10.0) < patches (11.36); for s = 2.5, chessboard (9.62) < random (12.19) < columns (13.16) = rows (13.16) < strips (14.70) < patches (15.62). In summary, the chessboard arrangement is significantly better at reducing the propagation of aphid-borne viruses in agricultural fields than the rest of the arrangements when there are no trap crops in the intercrop. The random arrangement also performs very well in terms of both the number of plants removed by the infection and the rate of propagation of the epidemic.
Finally, it is worth recalling that the prior results depend on the radius of primary dispersal of the aphid. See electronic supplementary material, Note 3, for the case when the separation between rows and columns is smaller than here and the pest can hop not only across the rows and columns but also diagonally between rows, i.e. when the radius for primary dispersal of the aphid is instead of r = Δ. When the pest mobility is relatively low (s = 4.0), the best arrangements are the rows and columns intercrops with about 10% of affected plants versus 78% affected plants in the monocrop for t = 10. However, when the pest has high mobility (s = 2.5), none of the intercropping systems is able to stop the propagation of the pest across the field, with percentages of affected plants similar to that in the monocrop (98.6%). An obvious measure to mitigate this problem is to increase the separation of the rows and columns in the crop field, or even—as shown in the experiments by Khan et al. [28]—to increase the separation between rows and keeping a smaller separation between columns.
(c). Impact of intercrops with a trap crop on aphid-borne virus propagation
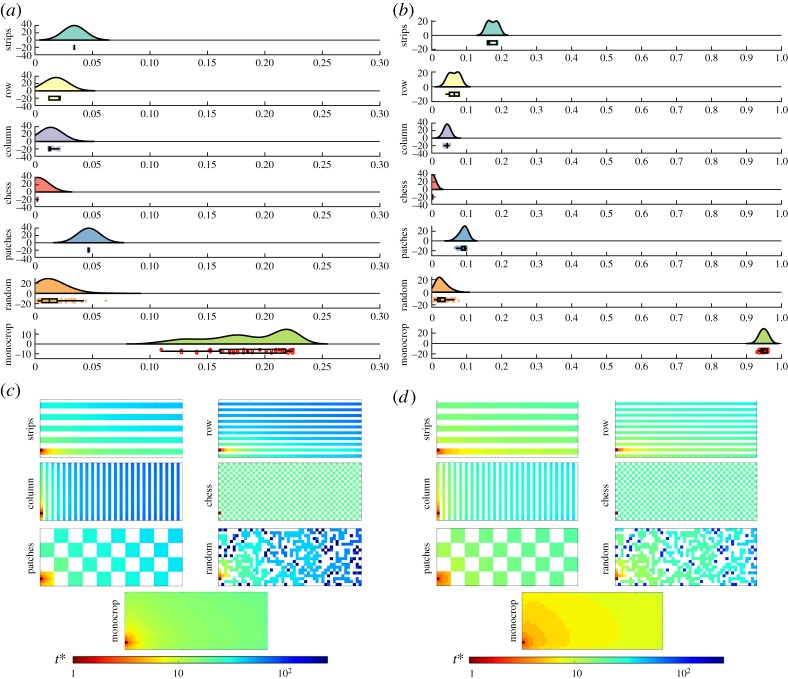
We now move to the analysis of the intercrop systems with trap crops. To have an idea of the many systems in which the current results can be applied the reader is referred to tables 1 and 2 in Hokkanen's paper [44], where many examples of one main crop intercropped with a trap crop are given. We consider here the existence of trap crops which are not perfect, i.e. they allow certain propagation of the aphid-borne viral infection (see electronic supplementary material, Note 4, for results with a perfect trap). Thus, we use γ = 2.0 and analyse the cases of relatively low (s = 4.0) and relatively high (s = 2.5) aphid mobility. In figure 7, we illustrate the results of our simulations for these systems using the different arrangements studied here. As can be seen for the case of relatively low mobility (s = 4.0), there is a significant reduction in the percentages of removed plants for all intercrop systems. The percentages of removed plants for each intercrop are: chessboard (0.2%), columns (1.4%), random (1.5%), rows (1.8%), strips (3.4%) and patches (4.7%). We remind the reader that the percentage of removed plants in the monocrop is 18.1%. When the pest has a relatively high mobility (s = 2.5), 95.1% of plants are removed in the monocrop, while in each of the intercrops they are: chessboard (0.2%), random (2.8%), columns (4.4%), rows (6.3%), patches (9.1%) and strips (17.4%). Note that here there are some important changes in the order of the arrangements in terms of their effectivity in reducing the propagation of the infection. When the aphid is of high mobility, the best arrangements are the chessboard and the random one. The worse arrangement, and the only one having more than 10% of removed plants, is the strip one. Also note that the percentage of removed plants in the chessboard arrangement is exactly the same for s = 2.5 and s = 4.0, indicating a high stability in the efficiency of this arrangement. It is important to remark one more time that these reductions in the number of removed plants are the consequence of the different topological patterns emerging from the intercrop arrangements. That is, these differences are not a dilution effect due to the fact that the number of susceptible and immune plants are kept the same in every arrangement.
Figure 7.
Aphid-borne virus propagation on intercropped fields with trap crops. Results of the simulations for SIR epidemics at t = 10 with r = Δ, β = 0.5, μ = 0.5 for different intercropping strategies with trap crops of strength γ = 2.0. Raincloud plots of the proportion of dead plants for a viral infection propagated by aphids: (a) aphid with reduced mobility (s = 4.0) and (b) with greater mobility (s = 2.5). The clouds show the kernel distribution of the proportion of dead plants for different realizations of the epidemics. Below, the raw data are plotted (the rain) together with their corresponding box and whisker plots. Illustration of the evolution of infection across fields with different intercropping systems: (c) aphid with reduced mobility (s = 4.0) and (d) with greater mobility (s = 2.5). In both panels, the time t* is given in a colour scale (see text), and the propagation is initialized by infecting the plant in the bottom-left corner of the plot. (Online version in colour.)
We now analyse the rate of propagation of the aphid-borne virus across the agricultural fields intercropped with a trap crop (figure 7c,d). The rate of propagation of the virus follows a different order from that of the case of intercrops without traps (γ = 1.0). That is, for s = 4.0, we find: chessboard (0.05) < random (1.67) < columns (4.59) < rows (4.67) < strips (7.04) < patches (7.94). For s = 2.5, chessboard (0.04) < random (4.18) < columns (7.58) < rows (8.06) < strips (10.87) < patches (11.63). Here, again there is a significantly high improvement, in terms of diminishing the impact and the rate of propagation of a virus across an agricultural field, when the chessboard arrangement is used. See electronic supplementary material, Note 3, for the case when the separation between rows and columns is smaller than here, i.e. when the radius for primary dispersal of the aphid is instead of r = Δ. These results agree with those previously reported using a different stochastic simulation model [75].
(d). Epidemic thresholds
Finally, we study the ratio β/μ, which drives the spreading of the disease. Depending on the infectious power of the aphid-borne virus there are two possible distinguishable phases for a given strength of the trap crop, γ, and of the pest mobility, s. The first one is an absorbing phase where the spreading of the virus is not efficient enough to reach a large fraction of the system and the propagation is absorbed, meaning that it does not progress across the field. The second phase is an active one, where the propagation of the virus reaches a macroscopic fraction of the agricultural field. The transition from the absorbing to the active phase strictly resembles a non-equilibrium second-order phase transition in statistical physics [76]. The critical value of this transition (β/μ)c = τ E is defined as the epidemic threshold. This term is also known as the basic reproduction number and it represents a threshold in the sense that below this point the propagation of the infection dies out and over it the propagation becomes an epidemic. We then investigated the epidemic threshold τE for the monocrop and the six intercrop arrangements without (γ = 1.0) and with a trap crop (γ = 2.0). We also considered, as before, two kinds of aphid, one with relatively low mobility (s = 4.0) and the other with higher mobility (s = 2.5). In figure 8, we summarize the results. Let us first consider the intercropped fields without trap crops (γ = 1.0). Then, when the pest has low mobility the epidemic threshold of the chessboard arrangement is more than 10 times higher than that of the monocrop. Notice that we have normalized all the bar plots in the insets of figure 8 by dividing the epidemic thresholds by that of the monocrop. Indeed, we have proved in electronic supplementary material, Note 5, that the chessboard arrangement can reach an infinitely large epidemic threshold if s is bounded and the trap crop has a very high strength. The rest of the arrangements have epidemic thresholds which are about twice that of the monocrop. When the aphid mobility increases, the epidemic thresholds logically drop, owing to the fact that it is easier for the pest to trigger the propagation of a virus across the field. In this case, the epidemic threshold of the chessboard arrangement is three times that of the monocrop, while the rest of the arrangements have values of about 1.5 times larger than that of the monocrop. When we incorporate trap crops (γ = 2.0) in the intercrop arrangements the changes in the epidemic threshold are very dramatic for the case of the chessboard arrangement. In this case, with low and high mobility, the epidemic thresholds are about 40 and 32 times higher than that of the monocrop, respectively. For the rest of the intercropped systems, the threshold increases by factors between 2 and 5. It is interesting that for the rest of the intercrop systems the ordering of the epidemic thresholds varies from one scenario to another. For instance, without a trap crop and with low mobility of the pest, the random arrangement is the second best, followed by the rows arrangement. However, if the aphid has larger mobility, the column arrangement is the second best followed by the rows one. When there are trap crops and low mobility of the pest, the rows arrangement is the second best followed by the columns one. If the mobility of the pest is higher then the column is the second best followed by the strips one. It is possible that the empirical observation that the rows and strips arrangements delay the propagation of an aphid-borne virus in a crop field has meant that these two arrangements have been the most widely used ones. However, in terms of (i) percentage of plants removed by the infection, (ii) rate of propagation of the aphid-borne virus across the field, and (iii) epidemic threshold, the chessboard arrangement introduced here is by far the most efficient intercrop arrangement without and with trap crops. In this respect our model agrees with previous results showing that the finer grained mixing of susceptible and resistant species impedes the propagation of diseases on plants [77–79]. However, as we have also shown in this work, when the radii of aphid movements increase, then other intercropping arrangements such as the column, rows and random are very efficient at stopping the propagation of diseases across a field.
Figure 8.
Epidemic thresholds for the propagation of aphid-borne viruses on intercropped fields. Effects of the strength of the trap crop γ and of the pest mobility s on the number of removed (dead) plants during the propagation of an aphid-borne virus infection across intercropped fields with r = Δ. The case for γ = 1 corresponds to no trap crop. The symbols used for each intercrop are: strips (small circles), rows (large circles), columns (squares), chessboard (triangles), patches (hexagons), random (diamonds) and monocrop (crosses). In the insets, we illustrate the normalized epidemic thresholds for each of the intercrop arrangements. The normalization is obtained by dividing every epidemic threshold by that of the monocrop in the corresponding system. The colour code for the insets is given at the bottom of the figure. In each inset, the columns are ordered as the labels of the legend. (Online version in colour.)
4. Conclusion
Here, we demonstrate, using intensive mathematical modelling, that the efficiency of intercropping arrangements can be improved dramatically in relation to the designs currently in use. We develop a mathematical framework that allows the effect of intercropping systems to be studied with and without ‘trap crops’. Our study shows that improving existing intercrop designs may decrease by up to 80% the number of plants affected by aphid-borne viruses, slow down the propagation of such aphid-borne viruses by a 300-fold factor and delay the triggering of these epidemics on plants by a 40-fold factor with respect to a monocrop. Indeed, our analytical and numerical findings show that the chessboard is the best arrangement when the pest can hop only across the rows and columns, but not diagonally between rows.
Supplementary Material
Acknowledgments
E.E. thanks inspirational encouragement from Consuelo Ramos-López who has used intercropping for more than 60 years.
Data accessibility
This article has no additional data.
Competing interests
We declare we have no competing interests.
Funding
A.A.-P. acknowledges the support of the Brazilian agency CNPq through grant no. 151466/2018-1.
References
- 1.Gerland P. et al. 2014. World population stabilization unlikely this century. Science 346, 234–237. ( 10.1126/science.1257469) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tilman D, Balzer C, Hill J, Befort BL. 2011. Global food demand and the sustainable intensification of agriculture. Proc. Natl Acad. Sci. USA 108, 20 260–20 264. ( 10.1073/pnas.1116437108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tubiello FN, Soussana JF, Howden SM. 2007. Crop and pasture response to climate change. Proc. Natl Acad. Sci. USA 104, 19 686–19 690. ( 10.1073/pnas.0701728104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mehrabi Z, Ellis EC, Ramankutty N. 2018. The challenge of feeding the world while conserving half the planet. Nat. Sust. 1, 409–412. ( 10.1038/s41893-018-0119-8) [DOI] [Google Scholar]
- 5.Oerke EC. 2006. Crop losses to pests. J. Agric. Sci. 144, 31–43. ( 10.1017/S0021859605005708) [DOI] [Google Scholar]
- 6.Strange RN, Scott PR. 2005. Plant disease: a threat to global food security. Annu. Rev. Phytopathol. 43, 83–116. ( 10.1146/annurev.phyto.43.113004.133839) [DOI] [PubMed] [Google Scholar]
- 7.Fisher MC, Henk DA, Briggs CJ, Brownstein JS, Madoff LC, McCraw SL, Gurr SJ. 2012. Emerging fungal threats to animal, plant and ecosystem health. Nature 484, 186–194. ( 10.1038/nature10947) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Flood J. 2010. The importance of plant health to food security. Food Secur. 2, 215–231. ( 10.1007/s12571-010-0072-5) [DOI] [Google Scholar]
- 9.Chakraborty S, Newton AC. 2011. Climate change, plant diseases and food security: an overview. Plant Pathol. 60, 2–14. ( 10.1111/j.1365-3059.2010.02411.x) [DOI] [Google Scholar]
- 10.Khan ZR, Pickett JA, van den Berg J, Wadhams LJ, Woodcock CM. 2000. Exploiting chemical ecology and species diversity: stem borer and striga control for maize and sorghum in Africa. Pest Manage. Sci. 56, 957–962. ( 10.1002/(ISSN)1526-4998) [DOI] [Google Scholar]
- 11.Bjorkman C, Niemela P (eds). 2015. Climate change and insect pests. Wallingford, UK: CABI. [Google Scholar]
- 12.Thomson LJ, Macfadyen S, Hoffmann AA. 2010. Predicting the effects of climate change on natural enemies of agricultural pests. Biol. Control 52, 296–306. ( 10.1016/j.biocontrol.2009.01.022) [DOI] [Google Scholar]
- 13.Howden SM, Soussana JF, Tubiello FN, Chhetri N, Dunlop M, Meinke H. 2007. Adapting agriculture to climate change. Proc. Natl Acad. Sci. USA 104, 19 691–19 696. ( 10.1073/pnas.0701890104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cannon RJ. 1998. The implications of predicted climate change for insect pests in the UK, with emphasis on non-indigenous species. Global Change Biol. 4, 785–796. ( 10.1046/j.1365-2486.1998.00190.x) [DOI] [Google Scholar]
- 15.Gu S, Han P, Ye Z, Perkins LE, Li J, Wang H, Zalucki M, Lu Z. 2018. Climate change favours a destructive agricultural pest in temperate regions: late spring cold matters. J. Pest Sci. 91, 1191–1198. ( 10.1007/s10340-018-1011-z) [DOI] [Google Scholar]
- 16.Rosenzweig C. et al. 2014. Assessing agricultural risks of climate change in the 21st century in a global gridded crop model intercomparison. Proc. Natl Acad. Sci USA 111, 3268–3273. ( 10.1073/pnas.1222463110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bebber DP, Ramotowski MA, Gurr SJ. 2013. Crop pests and pathogens move polewards in a warming world. Nat. Clim. Change 3, 985–988. ( 10.1038/nclimate1990) [DOI] [Google Scholar]
- 18.Deutsch CA, Tewksbury JJ, Tigchelaar M, Battisti DS, Merrill SC, Huey RB, Naylor RL. 2018. Increase in crop losses to insect pests in a warming climate. Science 361, 916–919. ( 10.1126/science.aat3466) [DOI] [PubMed] [Google Scholar]
- 19.Van Emden HF, Harrington R (eds). 2017. Aphids as crop pests. Wallingford, UK: CABI International. [Google Scholar]
- 20.Blackman RL, Eastop VF. 2000. Aphids on the world's crops: an identification and information guide, 2nd edn Chichester, UK: Wiley. [Google Scholar]
- 21.Kim CS, Schaible G, Garrett L, Lubowski R, Lee D. 2008. Economic impacts of the U.S. soybean aphid infestation: a multi-regional competitive dynamic analysis. Agric. Resour. Econ. Rev. 37, 227–242. ( 10.1017/S1068280500003026) [DOI] [Google Scholar]
- 22.Dedryver CA, Le Ralec A, Fabre F. 2010. The conflicting relationships between aphids and men: a review of aphid damage and control strategies. C. Rend. Biol. 333, 539–553. ( 10.1016/j.crvi.2010.03.009) [DOI] [PubMed] [Google Scholar]
- 23.Tatchell GM. 1989. An estimate of the potential economic losses to some crops due to aphids in Britain. Crop Protect. 8, 25–29. ( 10.1016/0261-2194(89)90095-1) [DOI] [Google Scholar]
- 24.Hilker FM. et al. 2017. Modeling virus coinfection to inform management of maize lethal necrosis in Kenya. Phytopathology 107, 1095–108. [DOI] [PubMed] [Google Scholar]
- 25.Jeger MJ, Thresh JM. 1993. Modelling reinfection of replanted cocoa by swollen shoot virus in pandemically diseased areas. J. Appl. Ecol. 1, 187–196. ( 10.2307/2404282) [DOI] [Google Scholar]
- 26.Wezel A, Casagrande M, Celette F, Vian JF, Ferrer A, Peigné J. 2014. Agroecological practices for sustainable agriculture. A review. Agron. Sustain. Dev. 34, 1–20. ( 10.1007/s13593-013-0180-7) [DOI] [Google Scholar]
- 27.Muneret L, Mitchell M, Seufert V, Aviron S, Djoudi EA, Pétillon J, Plantegenest M, Thiéry D, Rusch A. 2018. Evidence that organic farming promotes pest control. Nat. Sust. 1, 361–368. ( 10.1038/s41893-018-0102-4) [DOI] [Google Scholar]
- 28.Khan ZR, Pickett JA, Wadhams LJ, Hassanali A, Mideg CAO. 2006. Combined control of Striga hermonthica and stemborers by maize–Desmodium spp. intercrops. Crop Protect. 25, 989–995. ( 10.1016/j.cropro.2006.01.008) [DOI] [Google Scholar]
- 29.Smith HA, McSorley R. 2000. Intercropping and pest management: a review of major concepts. Am. Entomol. 46, 154–161. ( 10.1093/ae/46.3.154) [DOI] [Google Scholar]
- 30.Martin-Guay MO, Paquette A, Dupras J, Rivest D. 2018. The new green revolution: sustainable intensification of agriculture by intercropping. Sci. Total Environ. 615, 767–772. ( 10.1016/j.scitotenv.2017.10.024) [DOI] [PubMed] [Google Scholar]
- 31.Mt. Pleasant J, Burt RF. 2010. Estimating productivity of traditional Iroquoian cropping systems from field experiments and historical literature. J. Ethnobiol. 30, 52–79. ( 10.2993/0278-0771-30.1.52) [DOI] [Google Scholar]
- 32.Khan ZR. et al. 1997. Intercropping increases parasitism of pests. Nature 388, 631–632. ( 10.1038/41681) [DOI] [Google Scholar]
- 33.Letourneau DK. et al. 2011. Does plant diversity benefit agroecosystems? A synthetic review. Ecol. Appl. 21, 9–21. ( 10.1890/09-2026.1) [DOI] [PubMed] [Google Scholar]
- 34.Brooker RW. et al. 2015. Improving intercropping: a synthesis of research in agronomy, plant physiology and ecology. New Phytol. 206, 107–117. ( 10.1111/nph.13132) [DOI] [PubMed] [Google Scholar]
- 35.Brennan EB. 2016. Agronomy of strip intercropping broccoli with alyssum for biological control of aphids. Biol. Control 97, 109–119. ( 10.1016/j.biocontrol.2016.02.015) [DOI] [Google Scholar]
- 36.Xu Q, Hatt S, Lopes T, Zhang Y, Bodson B, Chen J, Francis F. 2018. A push–pull strategy to control aphids combines intercropping with semiochemical releases. J. Pest Sci. 91, 93–103. ( 10.1007/s10340-017-0888-2) [DOI] [Google Scholar]
- 37.Lai R, You M, Zhu C, Gu G, Lin Z, Liao L, Lin L, Zhong X. 2017. Myzus persicae and aphid-transmitted viral disease control via variety intercropping in flue-cured tobacco. Crop Protect. 100, 157–162. ( 10.1016/j.cropro.2017.06.021) [DOI] [Google Scholar]
- 38.Ben-Issa R, Gomez L, Gautier H. 2017. Companion plants for aphid pest management. Insects 8, 112 ( 10.3390/insects8040112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liebhold AM, Tobin PC. 2008. Population ecology of insect invasions and their management. Annu. Rev. Entomol. 53, 387–408. ( 10.1146/annurev.ento.52.110405.091401) [DOI] [PubMed] [Google Scholar]
- 40.Mazzi D, Dorn S. 2012. Movement of insect pests in agricultural landscapes. Annu. Appl. Biol. 160, 97–113. ( 10.1111/j.1744-7348.2012.00533.x) [DOI] [Google Scholar]
- 41.Schellhorn NA, Bianchi FJJA, Hsu CL. 2014. Movement of entomophagous arthropods in agricultural landscapes: links to pest suppression. Annu. Rev. Entomol. 59, 559–581. ( 10.1146/annurev-ento-011613-161952) [DOI] [PubMed] [Google Scholar]
- 42.Petrovskii S, Petrovskaya N, Bearup D. 2014. Multiscale approach to pest insect monitoring: random walks, pattern formation, synchronization, and networks. Phys. Life Rev. 11, 467–525. ( 10.1016/j.plrev.2014.02.001) [DOI] [PubMed] [Google Scholar]
- 43.Hethcote HW. 2000. The mathematics of infectious diseases. SIAM Rev. 42, 599–653. ( 10.1137/S0036144500371907) [DOI] [Google Scholar]
- 44.Hokkanen HM. 1991. Trap cropping in pest management. Annu. Rev. Entomol. 36, 119–138. ( 10.1146/annurev.en.36.010191.001003) [DOI] [PubMed] [Google Scholar]
- 45.Cook SM, Khan ZR, Pickett JA. 2007. The use of push-pull strategies in integrated pest management. Annu. Rev. Entomol. 52, 375–400. ( 10.1146/annurev.ento.52.110405.091407) [DOI] [PubMed] [Google Scholar]
- 46.Hassanali A, Herren H, Khan ZR, Pickett JA, Woodcock CM. 2008. Integrated pest management: the push–pull approach for controlling insect pests and weeds of cereals, and its potential for other agricultural systems including animal husbandry. Phil. Trans. R. Soc. B 363, 611–621. ( 10.1098/rstb.2007.2173) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pickett JA, Woodcock CM, Midega CA, Khan ZR. 2004. Push–pull farming systems. Curr. Opin. Biotech. 26, 125–132. ( 10.1016/j.copbio.2013.12.006) [DOI] [PubMed] [Google Scholar]
- 48.Xu Q, Hatt S, Lopes T, Zhang Y, Bodson B, Chen J, Francis F. 2018. A push–pull strategy to control aphids combines intercropping with semiochemical releases. J. Pest Sci. 91, 93–103. ( 10.1007/s10340-017-0888-2) [DOI] [Google Scholar]
- 49.Cooke KL. 1979. Stability analysis for a vectordisease model. Rocky Mount. J. Math. 9, 31–42. ( 10.1216/RMJ-1979-9-1-31) [DOI] [Google Scholar]
- 50.Di Liddo A. 1986. A SIR vector disease model with delay. Mat. Model 7, 793–802. ( 10.1016/0270-0255(86)90135-1) [DOI] [Google Scholar]
- 51.Xu R, Ma Z. 2011. Global dynamics of a vector disease model with saturation incidence and time delay. IMA J. Appl. Math. 76, 919–937. ( 10.1093/imamat/hxr013) [DOI] [Google Scholar]
- 52.Tchuenche JM, Nwangwo A. 2009. Local stability of an SIR epidemic model and effect of time delay. Math. Meth. Appl. Sci. 32, 2160–2175. ( 10.1002/mma.v32:16) [DOI] [Google Scholar]
- 53.Hamelin FM, Allen LJ, Prendeville HR, Hajimorad MR, Jeger MJ. 2016. The evolution of plant virus transmission pathways. J. Theor. Biol. 396, 75–89. ( 10.1016/j.jtbi.2016.02.017) [DOI] [PubMed] [Google Scholar]
- 54.Jeger MJ, Madden LV, van den Bosch F. 2018. Plant virus epidemiology: applications and prospects for mathematical modeling and analysis to improve understanding and disease control. Plant Dis. 108, 837–54. ( 10.1094/PDIS-04-17-0612-FE) [DOI] [PubMed] [Google Scholar]
- 55.Powell G, Tosh CR, Hardie J. 2006. Host plant selection by aphids: behavioral, evolutionary, and applied perspectives. Annu. Rev. Entomol. 51, 309–330. ( 10.1146/annurev.ento.51.110104.151107) [DOI] [PubMed] [Google Scholar]
- 56.Kring JB. 1972. Flight behavior of aphids. Annu. Rev. Entomol. 17, 461–492. ( 10.1146/annurev.en.17.010172.002333) [DOI] [Google Scholar]
- 57.Guerrieri E, Digilio MC. 2008. Aphid-plant interactions: a review. J. Plant Interact. 3, 223–232. ( 10.1080/17429140802567173) [DOI] [Google Scholar]
- 58.Diaz BM, Barrios L, Fereres A. 2012. Interplant movement and spatial distribution of alate and apterous morphs of Nasonovia ribisnigri (Homoptera: aphididae) on lettuce. Bull. Entomol. Res. 102, 406–414. ( 10.1017/S0007485311000745) [DOI] [PubMed] [Google Scholar]
- 59.Gottlieb D, Inbar M, Lombrozo R, Ben-Ari M. 2017. Lines, loops and spirals: an intraclonal continuum of host location behaviours in walking aphids. Anim. Behav. 128, 5–11. ( 10.1016/j.anbehav.2017.03.028) [DOI] [Google Scholar]
- 60.Gish M, Inbar M. 2006. Host location by apterous aphids after escape dropping from the plant. J. Insect Behav. 19, 143–153. ( 10.1007/s10905-005-9009-9) [DOI] [Google Scholar]
- 61.Arias JH, Gómez-Gardeñes J, Meloni S, Estrada E. 2018. Epidemics on plants: modeling long-range dispersal on spatially embedded networks. J. Theor. Biol. 453, 1–13. ( 10.1016/j.jtbi.2018.05.004) [DOI] [PubMed] [Google Scholar]
- 62.Estrada E. 2012. Path Laplacian matrices: introduction and application to the analysis of consensus in networks. Lin. Algebra Appl. 436, 3373–3391. ( 10.1016/j.laa.2011.11.032) [DOI] [Google Scholar]
- 63.Estrada E, Hameed E, Hatano N, Langer M. 2017. Path Laplacian operators and superdiffusive processes on graphs. I. One-dimensional case. Lin. Algebra Appl. 523, 307–34. ( 10.1016/j.laa.2017.02.027) [DOI] [Google Scholar]
- 64.Estrada E, Hameed E, Langer M, Puchalska A. 2018. Path Laplacian operators and superdiffusive processes on graphs. II. Two-dimensional lattice. Lin. Algebra Appl. 555, 373–97. ( 10.1016/j.laa.2018.06.026) [DOI] [Google Scholar]
- 65.Gómez S, Arenas A, Borge-Holthoefer J, Meloni S, Moreno Y. 2010. Discrete-time Markov chain approach to contact-based disease spreading in complex networks. EPL (Europhys. Lett.) 89, 38009 ( 10.1209/0295-5075/89/38009) [DOI] [Google Scholar]
- 66.Gómez S, Gómez-Gardeñes J, Moreno Y, Arenas A. 2011. Nonperturbative heterogeneous mean-field approach to epidemic spreading in complex networks. Phys. Rev. E 84, 036105 ( 10.1103/PhysRevE.84.036105) [DOI] [PubMed] [Google Scholar]
- 67.Tajmiri P, Fathi SAA, Golizadeh A, Nouri-Ganbalani G. 2017. Effect of strip-intercropping potato and annual alfalfa on populations of Leptinotarsa decemlineata Say and its predators. Int. J. Pest Manage. 63, 273–279. ( 10.1080/09670874.2016.1256513) [DOI] [Google Scholar]
- 68.Badenes-Perez FR, Shelton AM, Nault BA. 2005. Using yellow rocket as a trap crop for diamondback moth (Lepidoptera: Plutellidae). J. Econ. Entomol. 98, 884–890. ( 10.1603/0022-0493-98.3.884) [DOI] [PubMed] [Google Scholar]
- 69.Sheoran P, Sardana V, Singh S, Bhushan B. 2010. Bio-economic evaluation of rainfed maize (Zea mays)-based intercropping systems with blackgram (Vigna mungo) under different spatial arrangements. Indian J. Agric. Sci. 80, 244–247. [Google Scholar]
- 70.Moreira SL, Pires CV, Marcatti GE, Santos RHS, Imbuzeiro HMA, Fernandes RBA. 2018. Intercropping of coffee with the palm tree, macauba, can mitigate climate change effects. Agric. Forest Meteorol. 256, 379–390. ( 10.1016/j.agrformet.2018.03.026) [DOI] [Google Scholar]
- 71.Estrada E, Meloni S, Sheerin M, Moreno Y. 2016. Epidemic spreading in random rectangular networks. Phys. Rev. E 94, 052316 ( 10.1103/PhysRevE.94.052316) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Norin T. 2007. Semiochemicals for insect pest management. Pure Appl. Chem. 79, 2129–2136. ( 10.1351/pac200779122129) [DOI] [Google Scholar]
- 73.Pickett JA, Khan ZR. 2016. Plant volatile-mediated signalling and its application in agriculture: successes and challenges. New Phytol. 212, 856–870. ( 10.1111/nph.14274) [DOI] [PubMed] [Google Scholar]
- 74.Allen M, Poggiali D, Whitaker K, Marshall TR, Kievit R. 2018. Raincloud plots: a multi-platform tool for robust data visualization. PeerJ Preprints 6, e27137v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Banks JE, Ekbom B. 1999. Modelling herbivore movement and colonization: pest management potential of intercropping and trap cropping. Agric. Forest Entomol. 1, 165–170. ( 10.1046/j.1461-9563.1999.00022.x) [DOI] [Google Scholar]
- 76.Henkel M, Hinrichsen H, Lübeck S. 2008. Non-equilibrium phase transition: absorbing phase transitions. Dordrecht, The Netherlands: Springer Science. [Google Scholar]
- 77.Mundt CC, Leonard KJ, Thal WM, Fulton JH. 1986. Computerized simulation of crown rust epidemics in mixtures of immune and susceptible oat plants with different genotype unit areas and spatial distributions of initial disease. Phytopathology 76, 590–598. ( 10.1094/Phyto-76-590) [DOI] [Google Scholar]
- 78.Mundt CC, Brophy LS. 1988. Influence of number of host genotype units on the effectiveness of host mixtures for disease control: a modeling approach. Phytopathology 78, 1087–1094. ( 10.1094/Phyto-78-1087) [DOI] [Google Scholar]
- 79.Skelsey P, Rossing WA, Kessel GJ, Powell J, Van der Werf W. 2005. Influence of host diversity on development of epidemics: an evaluation and elaboration of mixture theory. Phytopathology 95, 328–338. ( 10.1094/PHYTO-95-0328) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This article has no additional data.