Predicting subcellular localization of multisite proteins using differently weighted multi-label k-nearest neighbors sets

Abstract

BACKGROUND:

For a protein to execute its function, ensuring its correct subcellular localization is essential. In addition to biological experiments, bioinformatics is widely used to predict and determine the subcellular localization of proteins. However, single-feature extraction methods cannot effectively handle the huge amount of data and multisite localization of proteins. Thus, we developed a pseudo amino acid composition (PseAAC) method and an entropy density technique to extract feature fusion information from subcellular multisite proteins.

OBJECTIVE:

Predicting multiplex protein subcellular localization and achieve high prediction accuracy.

METHOD:

To improve the efficiency of predicting multiplex protein subcellular localization, we used the multi-label k-nearest neighbors algorithm and assigned different weights to various attributes. The method was evaluated using several performance metrics with a dataset consisting of protein sequences with single-site and multisite subcellular localizations.

RESULTS:

Evaluation experiments showed that the proposed method significantly improves the optimal overall accuracy rate of multiplex protein subcellular localization.

CONCLUSION:

This method can help to more comprehensively predict protein subcellular localization toward better understanding protein function, thereby bridging the gap between theory and application toward improved identification and monitoring of drug targets.

1. Introduction

Proteins are more complex and diverse than the DNA sequence that generates them. As protein subcellular localization (PSL) is highly correlated with protein function, effective PSL prediction methods provide information for understanding protein functions that is essential for several research applications such as in molecular biology [1, 2], cell biology [3, 4], and neuroscience [5], as well as in clinical medicine [6, 7, 8]. The prediction and recognition of PSL using bioinformatics methods is one of the fundamental objectives of proteomics and cell biology [9], as PSL information is crucial for discovering protein functions toward helping to understand the complex cellular pathways involved in the process of biological regulation.

In recent decades, high-throughput molecular biology technologies have brought about exponential growth in the number of protein sequences identified. Considering the vast amount of molecular data now available and continuously accumulating, it is vital to develop a fast and available method for identifying the subcellular locations of their sequence information [10, 11, 12, 13]. The basic requirement for a cell to function normally is that the proteins operate in specific subcellular positions [14]. The main limitations of current methods of predicting PSL is that they cannot handle information on multiple proteins simultaneously. Thus, new prediction methods must be able to predict both single- and multiple-point PSLs.

Since a given feature extraction method and dataset will yield different results depending on the prediction algorithm applied, we here propose a new method for extracting protein subcellular information using a feature fusion technique. Feature extraction methods including the entropy density and pseudo amino acid composition (PseAAC) are typically used for protein coding. Considering these two feature extraction methods, we used the multi-label k-nearest neighbors (ML-KNN) algorithm and assigned diverse weights to various attributes for predicting multiplex PSL. We then evaluated the developed algorithms using a variety of well-established performance indexes.

2. Materials and method

2.1. Dataset

The dataset $S$ was used in the present study, which was applied for the Gpos-mPloc predictor as described previously [13]. The dataset consists of 519 different protein sequences, and each protein has one or many subcellular locations: four have two subcellular localizations and the remaining 515 have only one subcellular localization. No protein shows greater than 25% sequence consistency with other proteins. The dataset was downloaded from http://www.csbio.sjtu.edu.cn/bioinf/Gpos-multi/Data.htm (last accessed on April 30, 2018), which includes 174 protein sequences in the cell membrane, 18 protein sequences in the cell wall, 208 protein sequences in the cytoplasm, and 123 extracellular protein sequences.

2.2. Feature extraction

2.2.1. Entropy density

The entropy density was first introduced to represent DNA sequences and determine exons existing in gene sequences [15]. The Shannon entropy [16] is expressed as:

$$H(S)=-{\displaystyle \sum _{i=1}^{20}}{f}_i\log f_i\hspace{1em}i=1,2,3,\mathrm{\cdots },20$$ (1)

where $f_i(i=1,2,\mathrm{\dots },20)$ represent the normalized occurrence frequencies of the 20 amino acids that occur in protein $S$. Therefore, the entropy density function is defined as:

$$s_i(S)=-{\displaystyle \frac{1}{H(S)}}{f}_i\log f_i\hspace{1em}i=1,2,3,\mathrm{\dots },20$$ (2)

The sequence of protein $S$ is then represented as:

$$s(S)=(s_1(S),s_2(S),s_3(S),\mathrm{\dots },s_{20}(S))$$ (3)

Where $s_i(S)$ are the entropy values of the 20 amino acids in the protein sequence.

2.2.2. PseAAC

PseAAC was first developed to prevent the loss of hidden information in protein sequences and to provide a better expression of the initial information about AACs [17, 18, 19]. PseAAC reflects a protein expressed by generating 20 $+$$\lambda$ discrete numbers, and includes both the main features of the AAC and information beyond the AAC.

Suppose the protein molecule is represented by:

$$R_1{R}_2{R}_3{R}_4{R}_5\mathrm{\cdots }{R}_L$$ (4)

where $R_i(i=1,2,\mathrm{\cdots },L)$ indicates the amino acid residue located in area $L$. The protein sequence and other relevant information are also included in this expression. From the inherent nature of this representation, we can approximate the amino acid order information within a peptide chain sequence as a set of sequence order correlation factors, which can be expressed as:

$$\{\begin{array}{c}{\theta }_1={\displaystyle \frac{1}{L}}{\displaystyle \sum _{i=1}^{L-1}}\mathrm{\Theta }(R_i,R_{i+1})\hfill \\ {\theta }_2={\displaystyle \frac{1}{L}}{\displaystyle \sum _{i=1}^{L-2}}\mathrm{\Theta }(R_i,R_{i+2})\hfill \\ \mathrm{\cdots }\hfill \\ {\theta }_{\lambda }={\displaystyle \frac{1}{L}}{\displaystyle \sum _{i=1}^{L-\lambda }}\mathrm{\Theta }(R_i,R_{i+\lambda })\hfill \end{array},(\lambda <L)$$ (5)

$$\mathrm{\Theta }(R_i,R_j)={\displaystyle \frac{1}{3}}\left\{\begin{array}{c}{\left[H_1(R_j)-H_1(R_i)\right]}^2+{\left[H_2(R_j)-H_2(R_i)\right]}^2\hfill \\ +{\left[M(R_j)-M(R_i)\right]}^2\hfill \end{array}\right\}$$ (6)

where $H_1(R_i),H_2(R_i)$ and $M(R_i)$ denote the hydrophobicity, hydrophilicity, and the amino acid side-chain mass of $R_i$ ($i=1,2,\mathrm{\dots },L$), respectively. These values should first be transformed so that the average value of the coding sequence of the 20 amino acids is zero, and then substituted into Eq. (6). The transformations can be expressed as follows:

$$\{\begin{array}{c}{H}_1(R_i)={\displaystyle \frac{H_1^0(R_i)-\sum _{k=1}^{20}{H}_1^0(R_k)/20}{\sqrt{\sum _{\mu =1}^{20}{[H_1^0(R_{\mu })-\sum _{k=1}^{20}{H}_1^0(R_k)/20]}^2/20}}}\hfill \\ H_2(R_i)={\displaystyle \frac{H_2^0(R_i)-\sum _{k=1}^{20}{H}_2^0(R_k)/20}{\sqrt{\sum _{\mu =1}^{20}{[H_2^0(R_{\mu })-\sum _{k=1}^{20}{H}_2^0(R_k)/20]}^2/20}}}\hfill \\ M(R_i)={\displaystyle \frac{M(R_i)-\sum _{k=1}^{20}M(R_k)/20}{\sqrt{\sum _{\mu =1}^{20}{[M(R_{\mu })-\sum _{k=1}^{20}M(R_k)/20]}^2/20}}}\hfill \end{array}$$ (7)

In the classic 20-dimensional AAC, the sequence order-correlated factors in Eq. (5) are added to produce a PseAAC containing (20 $+$$\lambda$) units. That is, we can express the characterization of a protein sample $P$ as:

$$P={[p_1\mathrm{\cdots }{p}_{20}{p}_{20+1}\mathrm{\cdots }{p}_{20+\lambda }]}^T,(\lambda <L)$$ (8)

$$p_k=\{\begin{array}{cc}{\displaystyle \frac{f_k}{\sum _{i=1}^{20}{f}_i+\omega \sum _{j=1}^{\lambda }{\theta }_j}},\hfill & (1⩽k⩽20)\hfill \\ {\displaystyle \frac{\omega {\theta }_{k-20}}{\sum _{i=1}^{20}{f}_i+\omega \sum _{j=1}^{\lambda }{\theta }_j}},\hfill & (20+1⩽k⩽20+\lambda )\hfill \end{array}$$ (9)

where $f_i$ ($i=1,2,\mathrm{\dots },20$) indicate the normalized occurrence frequencies of the 20 amino acids in protein $P$, ${\theta }_j$ is the $j$-tier sequence-correlation factor of the proteins based on Eqs (5)–(7), and w is the weight of the sequence order effect. In Eqs (8) and (9), units 1–20 reflect the influence of the classical AAC, and the remaining units reflect the influence of the sequence order. The input of the algorithm combines these two feature extraction methods, which involves the simple addition of dimensions.

2.3. Algorithm

To guarantee the accuracy of PSL, a machine-learning algorithm must first be carefully designed. Although there are many algorithms available for predicting PSL, most of these focus only on a single subcellular location of a protein sequence, and cannot handle proteins located at multiple sites. With the increase in the discovery of multisite proteins, it is vital to obtain a fast and convenient method to recognize the subcellular location of proteins that do not have specific features. Here, we explored the use of the ML-KNN algorithm for this purpose, which is known to be beneficial for multi-label learning problems [20, 21, 22, 23]. In a test case $t$, ML-KNN should identify the $K$ nearest neighbors $N(t)$ within the training set. $H_1^l$ signifies that $t$ has label $l$, whereas $H_0^l$ signifies that $t$ does not have label $l$. Moreover, the event that exactly $j$ cases among the $K$ nearest neighbors of $t$ have label $l$ is denoted by $E_j^l$. Let $\overrightarrow{y}$ be the class vector of $x$. If $l\in Y$, then the l-th unit ${\overrightarrow{y}}_x(l)$ is 1; otherwise, it is 0. The expression of $N(x)$ is similar to $N(t)$. Therefore, according to the neighbor set of tags, the membership count vector can be expressed as:

$${\overrightarrow{C}}_x(l)={\displaystyle {\sum }_{a\in N(x)}}{\overrightarrow{y}}_a(l),l\in y$$ (10)

where ${\overrightarrow{C}}_x(l)$ represents the serial number of neighbors of $x$ at the l-th level.

Specifically, the prior probability of all labels is calculated based on whether they are training samples or test samples:

$$P(H_1^l)={\displaystyle \frac{s+\sum _{i=1}^m\overrightarrow{y_{x_i}(l)}}{s\times 2+m}}$$ (11)

$$P(H_0^l)=1-P(H_1^l)$$ (12)

Next, the Bayesian rule is used to compute the posterior probabilities:

$$P(E_j^l|H_1^l)={\displaystyle \frac{s+c[j]}{s\times (k+1)+\sum _{p=0}^{k}c[p]}}$$ (13)

$$P(E_j^l|H_0^l)={\displaystyle \frac{s+c^{\prime }[j]}{s\times (k+1)+\sum _{p=0}^k{c}^{\prime }[p]}}$$ (14)

where $c[j]$ is the number of instances in which there are exactly $j$ samples labeled $l$ within the $k$ nearest neighbors in the training set; $c^{\prime }[j]$ is similar to $c[j]$, except that $j$ denotes unlabeled samples.

Finally, we compute the maximum posterior probability using the following two equations:

$${\overrightarrow{y}}_t(l)=\arg \underset{b\in \{0,1\}}{\max }P(H_b^l)P(E_{{\overrightarrow{C}}_t(l)}^l|H_b^l)$$ (15)

$${\overrightarrow{r}}_t(l)={\displaystyle \frac{P(H_1^l)P(E_{{\overrightarrow{C}}_t(l)}^l|H_1^l)}{{\sum }_{b\in \{0,1\}}P(H_b^l)P(E_{{\overrightarrow{C}}_t(l)}^l|H_b^l)}}$$ (16)

However, the uneven features in the training set will lead to relatively low accuracy. Thus, we developed an improved algorithm to assign suitable weights to each attribute [24]. The weighting factors $w_t$ are defined as:

$$w_t={\displaystyle \frac{\log \left(a+\frac{\text{𝐴𝑣𝑔𝑁𝑢𝑚}}{\text{𝑁𝑢𝑚}(C_t)}\right)}{\log (a+1)}}(1<t<N)$$ (17)

$$a={\displaystyle \frac{\text{𝑀𝑎𝑥𝑁𝑢𝑚}}{\text{𝐴𝑣𝑔𝑁𝑢𝑚}}}$$ (18)

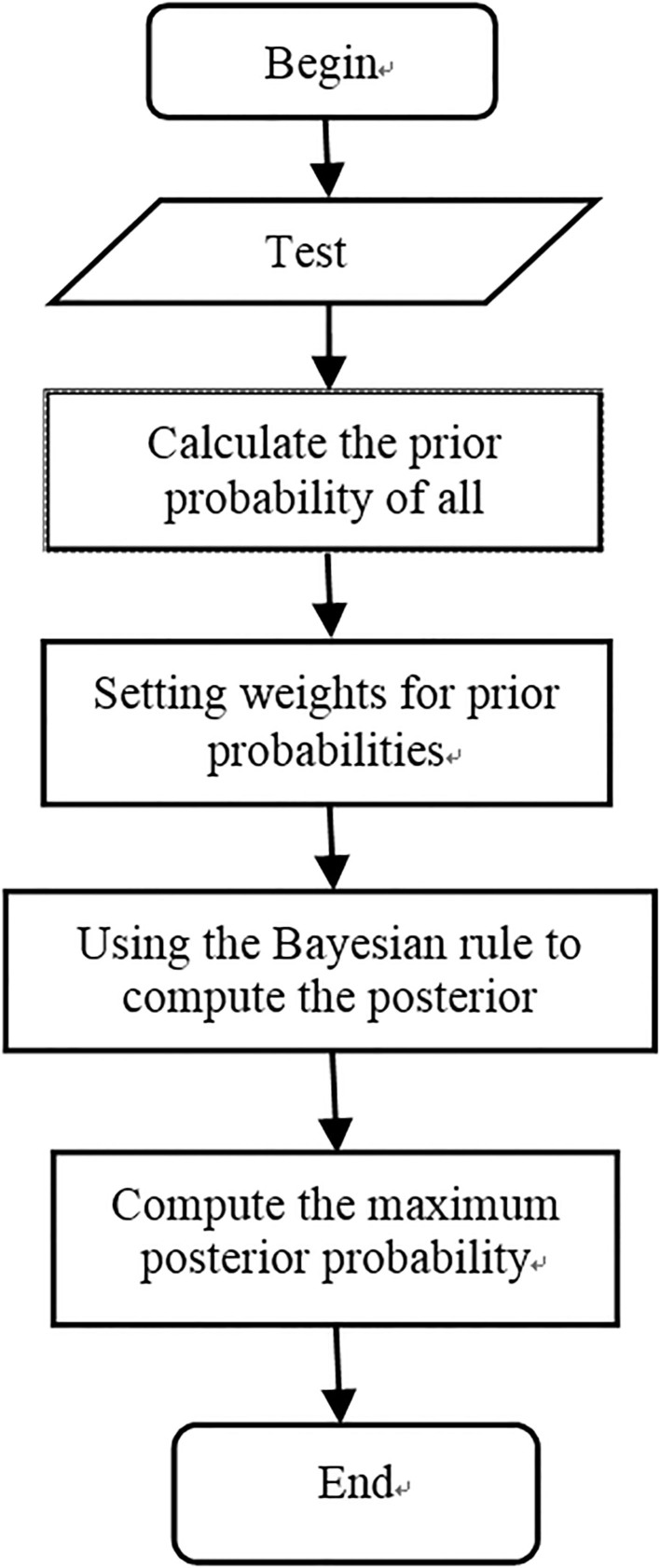
where AvgNum represents the average number of different categories of samples and $\text{𝑁𝑢𝑚}(C_t)$ represents the number of samples in class $C_t$. This novel ML-KNN method considering weighted prior probabilities was named wML-KNN. A flowchart of the prediction algorithm is shown in Fig. 1.

Figure 1.

Flowchart of the prediction algorithm.

2.4. Evaluation measures

The following multi-label evaluation indexes [25, 26] were applied to the multi-label test set $Z=\{(x_i,y_i)|1⩽i⩽p\}$: Hamming Loss, one-error, coverage, average recall, and absolute-true, described below in turn.

2.4.1. Hamming Loss

Hamming Loss is an indicator of the frequency with which an instance-label pair is wrong, expressed as:

$$\text{ℎ𝑙𝑜𝑠𝑠𝑍}(h)={\displaystyle \frac{1}{p}}{\displaystyle \sum _{i=1}^p}{\displaystyle \frac{1}{q}}\left|h(x_i)\mathrm{\Delta }{y}_i\right|$$ (19)

Where $p$ is the number of test samples, $h(x_i)$ is the predicted label, $y_i$ is the real label, $\mathrm{△}$ is the symmetry difference between two datasets, and $q$ is the number of labels. Thus, performance is inversely proportional to the value of $\text{ℎ𝑙𝑜𝑠𝑠𝑍}(h)$.

2.4.2. One-error

The one-error metric evaluates the maximum frequency of inappropriate labels for a given instance, expressed as:

$$\mathit{\text{one-errorZ}}(f)={\displaystyle \frac{1}{p}}{\displaystyle \sum _{i=1}^p}[\left[\arg \max f(x_i,y)\right]\notin y_i]$$ (20)

where $f$ is a real-valued function. For a case $x$ and corresponding label set $Yi$, a good learning process will output larger values for labels in $Yi$ than for labels that are not in $Yi$. The one-error evaluates the maximum frequency of inappropriate labels for an instance. Thus, performance is inversely proportional to the value of $\mathit{\text{one-errorZ}}(f)$.

2.4.3. Coverage

$$\text{cov }\text{𝑒𝑟𝑎𝑔𝑒𝑍}(f)={\displaystyle \frac{1}{p}}{\displaystyle \sum _{i=1}^p}\max {\text{𝑟𝑎𝑛𝑘}}_f(x_i,y)-1$$ (21)

The coverage averages the performance over all appropriate labels for a given instance. Thus, performance is inversely proportional to the value of $\text{𝑐𝑜𝑣𝑒𝑟𝑎𝑔𝑒𝑍}(f)$.

2.4.4. Average recall

$$\text{𝑎𝑣𝑔𝑟𝑒𝑐𝑍}(f)={\displaystyle \frac{1}{p}}{\displaystyle \sum _{i=1}^p}{\displaystyle \frac{\left|\left\{y^{\prime }\right|\text{𝑟𝑎𝑛𝑘𝑓}(x,y^{\prime })⩽\text{𝑟𝑎𝑛𝑘𝑓}(x_i,y),y^{\prime }\in y_i\}\right|}{\text{𝑟𝑎𝑛𝑘𝑓}(x_i,y)}}$$ (22)

The average recall is used to evaluate the mean value of labels that rank above specific values of $y\in Y$, which actually are in $Y$. Thus, pPerformance is proportional to the value of $\text{𝑎𝑣𝑔𝑟𝑒𝑐𝑍}(f)$.

2.4.5. Absolute-true

$$\mathit{\text{absolute-trueZ}}(h)={\displaystyle \frac{1}{p}}{\displaystyle \sum _{i=1}^p}[h(x_i)=y_i]$$ (23)

Absolute-true assesses the ratio of predicted labels that are the same as the actual label set. Thus, performance is proportional to the value of $\mathit{\text{absolute-trueZ}}(h)$.

3. Results

The feature extraction algorithm affects the final accuracy. In this study, the effect of using the entropy density and PseAAC feature extraction methods was examined. The ML-KNN and wML-KNN methods were both applied for comparison of results. The feature fusion method, with simple addition of dimensions, was also used. Overall, better results were obtained when $k=$ 1.

As shown in Tables 1 and 2, the entropy density and PseAAC feature extraction methods wML-KNN showed better performance than ML-KNN in each evaluation measurement. Moreover, the wML-KNN algorithm achieved better performance than ML-KNN for each evaluation criterion.

Table 1.

Results after applying entropy density to different algorithms

Evaluation criterion	Algorithm
	ML-KNN	wML-KNN
Hamming loss$\downarrow$	0.1783	0.0918
One-error$\downarrow$	0.3576	0.1855
Coverage$\downarrow$	0.6099	0.2333
Average recall$\uparrow$	0.7844	0.9018

“$\uparrow$” indicates that larger values provided better results, whereas “$\downarrow$” indicates that smaller values provided better results.

Table 2.

Results after applying PseAAC to different algorithms

Evaluation criterion	Algorithm
	ML-KNN	wML-KNN
Hamming loss$\downarrow$	0.1769	0.0798
One-error$\downarrow$	0.3595	0.1587
Coverage$\downarrow$	0.5946	0.2084
Average Recall$\uparrow$	0.7871	0.9149

“$\uparrow$” indicates that larger values provided better results, whereas “$\downarrow$” indicates that smaller values provided better results.

The comparative results presented in Tables 3 and 4 suggest that using wML-KNN increases the absolute-true rate by approximately 20%. Thus, the same feature extraction algorithm applied to the same dataset gives different results simply by including weight values within the ML-KNN algorithm. Similar changes in the absolute-true rate were observed with both feature extraction algorithms, indicating that the wML-KNN algorithm provides better prediction accuracy.

Table 3.

Comparative results of two different algorithms adopting the entropy density method

Algorithm	ML-KNN	wML-KNN
Absolute-true	62.72%	81.26%

Table 4.

Comparative results of two different algorithms adopting PseAAC

Algorithm	ML-KNN	wML-KNN
Absolute-true	62.52%	83.37%

4. Discussions

Previous PSL prediction studies largely focused on proteins with localization at a single site. Since the discovery of the phenomenon that several proteins have two or more subcellular sites, more attention has been paid to developing multisite subcellular localization prediction and related algorithms. As a multi-label learning method with good generalization ability, the ML-KNN algorithm achieved remarkable results in multisite subcellular localization prediction. Furthermore, using various feature extraction methods and adopting the wML-KNN prediction algorithm can achieve higher accuracy than reported in other studies. For example, using different fusion feature extraction methods, Qu et al. [13] adopted the ML-KNN algorithm to predict multisite subcellular localization in the Gpos-mploc protein dataset, and obtained the best overall accuracy rate of 66.1568%. Lin et al. [9] used ML-KNN as the prediction algorithm to predict a benchmark animal protein dataset and finally obtained an accuracy of 62.88%. Practically, one dataset often contains proteins with both single-site and multisite subcellular localizations. This imbalance in a dataset will inevitably influence the efficiency of the ML-KNN algorithm. Therefore, as an improved version of ML-KNN, we developed the wML-KNN algorithm to reduce the negative effects of this data imbalance in part and to achieve relatively higher prediction accuracy.

The ultimate purpose of studying multisite PSL is to understand a protein’s intrinsic function and obtain new insight into the nature of life. However, to date, the prediction of PSL has stagnated at the theoretical and experimental level. Despite the higher prediction accuracy obtained by adopting our proposed method, more research will be needed combining the results obtained in this study to link the theory to practice in this field. The following details should be considered as a preliminary analysis. First, more standardized protein datasets should be constructed to reduce the imbalance of data and the universality of related algorithms. Second, the entropy density and PseAAC are both effective local feature extraction methods. Thus, effective fusion methods of multiple features is expected to further improve the prediction accuracy. Moreover, the fusion of global and local protein physicochemical features, beyond information of the protein image, may bring breakthroughs in this field. Finally, just as important as the improvement of prediction accuracy described herein, it will be necessary to derive a plausible biological explanation for the results, which can facilitate application of the PSL theory into practice and should be a primary focus of the further work in this field.

Conflict of interest

The authors declare no conflict of interest, financial or otherwise.