Enhanced Diffusion of Catalytically Active Enzymes

Abstract

The past decade has seen an increasing number of investigations into enhanced diffusion of catalytically active enzymes. These studies suggested that enzymes are actively propelled as they catalyze reactions or bind with ligands (e.g., substrates or inhibitors). In this Outlook, we chronologically summarize and discuss the experimental observations and theoretical interpretations and emphasize the potential contradictions in these efforts. We point out that the existing multimeric forms of enzymes or isozymes may cause artifacts in measurements and that the conformational changes upon substrate binding are usually not sufficient to give rise to a diffusion enhancement greater than 30%. Therefore, more rigorous experiments and a more comprehensive theory are urgently needed to quantitatively validate and describe the enhanced enzyme diffusion.

Short abstract

Can enzymes diffuse faster during catalysis? We discuss current experimental observations and theoretical interpretations and highlight controversies and concerns that merit further consideration.

1. Introduction

Molecular motion is widely recognized as a key aspect of enzyme operation. Motions can range from small conformational changes regulating the active site in enzymes to the large conformational changes observed in motor proteins as they undergo their mechanochemical cycle. In myosins, kinesins, and dynein, a coupled interaction with cytoskeletal filaments translates conformational changes in the motor (an ATPase) into translation along the filament with step sizes exceeding 10 nm per cycle. However, a classic question in biophysics is if conformational changes can translate a protein in the absence of a filament: in other words, if a protein can “swim”. Purcell’s famous discussion of “Life at low Reynolds number” stresses that translation requires nonreciprocating motion (a simple back-and-forth will not do) and that once propulsion stops, the object stops (in far less than an Ångström).¹ The second point implies that the microscopic object translates at most as far as the stroke size of the motion. Due to the enzyme’s fast rotational diffusion, the individual “steps” occur in ever-changing directions at the rate of the catalytic events (typically 10–10 000 s^–1), giving the movement a diffusive character. Following Berg’s classic introduction “Random walks in Biology”,² the associated diffusion constant can be estimated as the square of the step size multiplied by the catalytic rate, yielding values consistently below 1 μm²/s. Given that the diffusion constant for passive diffusion of a protein ranges from 10 to 100 μm²/s and that the error of the measurement is typically close to 1 μm²/s, the added contribution of this catalysis-related “stepping” should be unmeasurably small.

However, during the past decade, several experiments have found that the diffusivity of enzymes increases during catalysis in a substrate-dependent manner by 30–80% above the diffusivity in the absence of substrate.³⁻⁶ These experiments have been conducted with different enzymes (catalase, urease, alkaline phosphatase, aldolase, etc.) using multiple experimental techniques (fluorescence correlation spectroscopy (FCS),^4,5 stimulated emission-depletion fluorescence correlation spectroscopy (STED-FCS),⁶ dynamic light scattering (DLS),⁷ and single molecular tracking⁸) by different laboratories and yielded the same surprising conclusion: catalytic events translate enzymes over distances exceeding their diameter, or as Jee et al.⁶ might summarize: “Enzymes leap!”.

Concurrently, the theoretical explanation of these observations has been hotly debated, with opinions ranging from an attribution of the observations to experimental artifacts⁹ or heating of the solution¹⁰ to the invocation of complex phenomena in fluid dynamics.¹¹ From our perspective, consensus has not been reached.

The matter is further complicated by the fact that the experimental observations are not all in agreement. Günther et al. recently summarized possible sources of artifacts in the widely employed FCS measurements and showed that these artifacts are present when F₁ATPase and alkaline phosphatase are studied with FCS.¹² Our own DLS measurements¹³ and pulsed field gradient nuclear magnetic resonance (PFG-NMR) measurements by Günther et al.¹⁴ of aldolase failed to detect enhanced diffusion in the presence of the substrate. These studies alert the community to potential problems with previous experiments.

Unexpected observations are the spice of science, and enhanced diffusion of enzymes is most unexpected. The observations point either to a gap in our understanding with potentially far ranging implications in biochemistry and biophysics or to a need for revisions in long established experimental protocols. Either way, past and future work advances science. In this review, we aim to chronologically summarize the experiments and theories on enhanced diffusion of enzymes which are interpreted as evidence of self-propulsion, and discuss the possible factors that may or may not cause the diffusion enhancement of enzymes during catalysis. We conclude that the current experimental and theoretical investigations are not sufficient to support the notion that enzymes can actively swim in substrate solution. For future studies, we suggest that the actual form of enzymes (e.g., isoenzymes, oligomeric/multimeric forms, aggregation states, etc.) should be fully characterized, that the effect of substrate binding on hydrodynamic radius should be quantified, and that steps should be taken to minimize confirmation bias such as conducting the experiments blinded.¹⁵

2. Experimental Observations

The discussion was initiated in 2010 by Sen and colleagues when they found that urease from Jack bean (Canavalia ensiformis) exhibited a 28% increase in its diffusion coefficient when substrate was added to the buffer solution, following a Michaelis–Menten-like dependence on the substrate concentration.⁴ These measurements were conducted with FCS experiments, a technique ideally suited to the determination of the diffusion coefficient of dilute, fluorescently labeled molecules.¹⁶ Subsequent publications by the Sen group found evidence of enhanced diffusion for fluorescently labeled urease and catalase in a microfluidic assay¹⁷ and for ruthenium-based Grubb’s catalysts in an NMR study.¹⁸

In the context of the earlier pioneering work of Sen and colleagues on the electrophoretic propulsion of catalytically active nanorods,¹⁹ this result appears as a logical extension of phoretic propulsion to the molecular scale. The team of Fischer demonstrated that metallic Janus nanoparticles (30 nm diameter) catalyzing the disproportionation of hydrogen peroxide exhibit enhanced diffusion of similar magnitude (∼30%).²⁰ Notably, the presence of the substrate for the platinum catalyst increased both the translational and rotational diffusion constants (up to 20% and up to 60%, respectively).

The findings by Sen et al. were echoed in 2014 by the high profile publication of the Bustamante team,⁵ which—using again FCS measurements—found similar enhancements (30–80%) in the diffusion constants of catalase, urease, and alkaline phosphatase, the enzymes catalyzing highly exothermic forward reactions. Triose phosphate isomerase, which catalyzes a slightly endothermic reaction, did not exhibit enhanced diffusion.⁵ In contrast, Leckie et al.²¹ tracked phosphatase–quantum dot conjugates and found enhanced diffusion only when the products of the enzymatic reaction are capable of fibrillar self-assembly.

The highlights of the year 2015 were three studies approaching enhanced diffusion from new angles. Ma et al. immobilized catalase, urease, and glucose oxidase on silica nanoparticles (400 nm diameter) and observed again an increase in the diffusion constant of 30–80%. Moreover, force measurements with optical tweezers demonstrated that the addition of substrate caused active motion against the trapping force.²² The team of Minteer employed Sen’s microfluidic technique to measure enhanced diffusion in an enzyme cascade and found 10-fold and 4-fold enhancements of the diffusion constants of mitochondrial malate dehydrogenase and citrate synthase, respectively.²³ The team of Tour showed that a light-activated molecular motor exhibits 26% enhancement in diffusion when spinning unidirectionally and 10% enhancement when rotating non-unidirectionally.²⁴ Given the rotational frequency of 2–3 MHz, this means that one rotation of a propeller less than 1 nm in length can propel the motor by 9 nm. Tour’s results thus directly connect enhanced diffusion to molecular motion but at the same time increase the mystery of the mechanism.

After a quiet 2016, 2017 brought a rash of new data related to enhanced diffusion. Illien et al. measured the substrate-dependent diffusion constant of aldolase using FCS and found that this endothermic and slow enzyme also exhibited a 30% increase in its diffusion constant at saturating substrate concentrations.²⁵ This result conflicts with any mechanism based on heat generation from the catalytic reaction. In contrast to the control experiments by the Sen group where inhibitors block enhanced diffusion,⁴ Illien et al. also found enhanced diffusion of aldolase in the presence of its inhibitor, implying that a catalytic reaction is not necessary. Zhao et al. used FCS to measure the diffusion constants of tracers in urease and aldolase solutions and found that the diffusion of dye molecules, nanospheres, and microspheres is enhanced in the presence of substrate by about 20%.²⁶ Jiang, Santiago, and Foord found that the frequency of collisions between catalase molecules and an electrode increased in the present of the hydrogen peroxide substrate and reproduced the earlier FCS measurements of enhanced diffusion of catalase.²⁷ Sun et al. tethered catalase to a supported lipid bilayer and found a doubling of the diffusion constant in the presence of hydrogen peroxide.²⁸ Finally, Granick and colleagues used STED-FCS to study urease and acetylcholinesterase and found that the reduced detection volume enabled by STED-FCS made the observation of “fast” events possible where the fluorescently labeled enzymes move ballistically through the observation volume. Great care was taken to align the visible and infrared laser so that the high intensity infrared laser does not exert optical forces on the enzymes.²⁹ The observed fast events only occur in the presence of substrate and are interpreted as direct and incontrovertible evidence of the previously inferred leaps of enzymes in connection with their catalytic process.^6,30 In the presence of high concentrations of inhibitors (>100 mM), enhanced diffusion is observed (a 40–50% enhancement rather than the 80% enhancement in the presence of 100 mM substrate), but ballistic motion is not observed.³⁰

While 2018 started with the first demonstration how the enhanced diffusion of enzyme-coated nanoparticles may deliver improvements in drug delivery,³¹ it ended with two reports outlining the potential for concern. First, Günther, Börsch, and Fischer outlined how artifacts in FCS experiments can affect measurements of the diffusion constant.¹² These artifacts include dissociation of multimeric enzymes, adsorption to surfaces, conformational changes, and fluorophore quenching. Apparent enhanced diffusion in FCS measurements of F₁-ATPase and alkaline phosphatase was traced back to dissociation and adsorption and to fluorescence quenching, respectively. Zhang et al. measured the diffusion constant of aldolase not with FCS but with DLS and found no change in the diffusion constant when substrate is added.¹³ A rejoinder to these concerns is the work by Xu, Ross, Valdez, and Sen, which is currently available as a preprint. Xu et al. followed the diffusive movement of single, fluorescently labeled urease molecules by particle tracking and found a 2-fold increase of the diffusion constant at saturating substrate concentrations.⁸ The enzymes are confined to the surface with highly viscous methylcellulose solution. It thus raises a concern if the enzymatic reaction could locally reduce the viscosity by changing the pH of the solution.³² Such a strategy has been utilized by bacterium Helicobacter pylori to move through the viscoelastic gastric mucus by producing urease³³ and has also been demonstrated with urease-coated magnetic micropropellers.³⁴ In addition, Mohajerani et al. found that noncatalytic substrate binding can enhance the diffusion of hexokinase (albeit to a lesser degree than catalytic binding in the presence of a cofactor) and that the inclusion of an enhanced diffusion term is required to model enzyme chemotaxis experiments.^35,36

What is the picture emerging from these data (Table 1 and Figure 1)? The majority of the involved researchers would answer the question if there is enhancement at all with a clear “yes”, despite the potential artifacts (some diffusion coefficients obtained from FCS measurements are significantly different from the reported values and classic predictions, Figure 1b) and the size of the effect being only 2–5 times the measurement error. Of course, if it would be easy to measure, it would have been found earlier. What the effect depends on is even less clear. The effect appears to follow the Michaelis–Menten kinetics of the enzyme, but the size of the effect appears to be independent of the turnover number and the molecular size. There is evidence for ballistic movement (“leaps”) for enzymes as well as catalytic particles. Enhanced diffusion of light-driven molecular rotors places the emphasis on mechanical movement rather than chemical effects, while the enhanced diffusion of tracer particles is familiar from the study of active suspensions.³⁷ The need for exothermicity is disputed.^5,25 Some studies, using the same system but different techniques, fail to find enhanced diffusion at all. Clearly, not all experimental observations can be correct, which makes the task of theoretical interpretation even more challenging.

Table 1. Experimental Reports of Enhanced Enzyme Diffusion.

enzyme	native form	Mw (kDa)	kcat (s–1)	D0 (μm2/s)	De,max (μm2/s)	D/D0	method	ref
urease (jack bean)	hexamer	544	2 × 104	31.8	40.6	1.28	FCS	(4, 5)
catalase (bovine liver)	tetramer	250	5.8 × 104	61a	79	1.3	FCS	(5)
alkaline phosphatase from bovine intestinal mucosa	dimer	160	1.4 × 104	NMb	NM	1.8	FCS	(5)
acetylcholinesterase (E. electricus)	four different forms	430 (8S), 780 (14S), 1100 (18S), 280 (11S)	NM	22	27	1.23	STED-FCS	(6)
hexokinase (Saccharomyces cerevisiae)	dimer	110	200	72.4c	106	1.46	FCS	(35, 36)
aldolase (rabbit muscle)	tetramer	158	5	42.6	56	1.31	FCS	(25)
α subunit of F1-ATPase	monomer	58.7		56.4	64.5	1.14	light scattering	(7)
F1-ATPase (Escherichia coli)	α3β3γδε complex	381d38	∼100d39	33	41	1.24	FCS	(40)

^aThe diffusion coefficient of catalase was measured to be 41 μm²/s by Sumner.⁴¹

^bNM: not mentioned.

^cThe diffusion coefficients of hexokinase monomer and dimer were measured to be 74.6 and 56.4 μm²/s, respectively.⁴²

^dData from a different reference.

Figure 1.

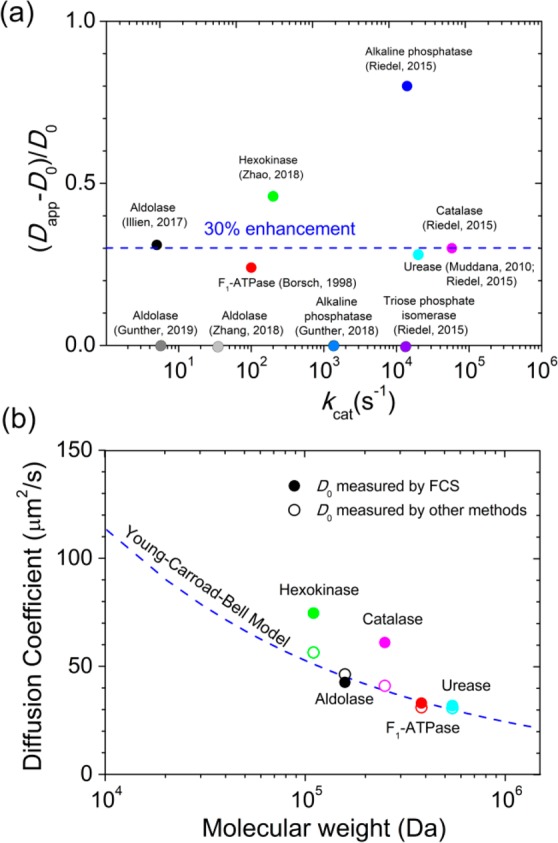
(a) Reported diffusivity enhancements of active enzymes as a function of turnover numbers. (b) Comparison of diffusion coefficients of free, inactive enzymes measured in FCS experiments and those measured by other methods. The predictions of diffusion coefficients based on the molecular weights were made according to the Young–Carroad–Bell model in aqueous solution at 20 °C (ref (43)). The diffusion coefficients of enzymes from FCS measurements (solid circles) can be found in Table 1; the reported diffusion coefficients from other methods (open circles) are hexokinase, 56.4 μm²/s, ref (42); aldolase, 46.3 μm²/s, ref (44); catalase, 41 μm²/s, ref (41); F₁-ATPase, 31 μm²/s, ref (45); and urease, 31 μm²/s, ref (46).

3. A Short Review of Diffusive Processes

Before we discuss the efforts to obtain a theoretical understanding of the phenomena, we believe it is helpful to briefly review diffusive processes. To quote Berg, “Diffusion is the random migration of molecules or small particles arising from motion due to thermal energy.”² Particles translate ballistically according to their thermal velocities until collisions with surrounding molecules and particles alter the velocity and direction of their motion. Due to the high density of fluids, collisions occur on a sub-Ångström scale.⁴⁷ The translational motion can be understood as a random walk of steps of size δ occurring at intervals τ resulting in a time-dependent increase in the mean square displacement described by a diffusion constant D = δ²/2τ. For the three-dimensional case, the average mean square displacement ⟨Δx²(t)⟩ increases with time t as

1

where the diffusion constant D is given by the Einstein–Smoluchowski–Sutherland relation:

2

with γ as the drag of the particle and k_B being the Boltzmann constant and T the temperature. The drag is given for, e.g., spherical particles by the Stokes equation as

3

with η as the viscosity of the fluid and r the radius of the particle. The drag depends only weakly on the shape of the particle if the volume is conserved.⁴⁸

Collisions also result in a diffusive rotational motion where the average of the square of the change in angular orientation evolves with time as

4

and the rotational diffusion constant D_r is given by

5

with f_r as the rotational drag of the particle. For a spherical particle, f_r = 8πηr³. Please note that the translational drag scales with the particle radius, whereas the rotational drag is proportional to the cube of the radius. This implies that the particle will have rotated on average about 50° in the time it has translated on average by its radius.

In water at 20 °C, the translational diffusion coefficient of an enzyme ranges from 10 to 100 μm²/s, whereas the rotational diffusion coefficient is on the order of 10⁴–10⁷ s^–1. These significantly increase with temperature because the viscosity of water decreases by about 2% for every 1 K temperature increase.

Another random walk process with a diffusion constant D′ simply adds to the mean square displacement if it is statistically independent from the first random walk, because the mixed terms average to zero over time. Movement with constant velocity v in a given direction (e.g., due to convection) scales quadratically with time, yielding for the total mean square displacement⁴⁹

6

Movement in a persistent random walk, where the particle moves with a constant velocity v but changes direction due to thermal forces, exhibits a decay in the correlation between the initial direction and the final direction. This exponential decrease in correlation can be characterized by a persistence length (L_p). Over distances below the persistence length, the movement appears directed, and over larger distances the movement appears diffusive with diffusion constant D = L_pv.⁵⁰

Experiments with the goal of identifying a new process responsible for an increase in the diffusion constant thus have to ensure that the temperature remains constant, that the particle shape is unchanged, and that directed motion is not misidentified as a contribution to diffusive motion.

For an enzyme with a relatively high turnover number of 10 000 s^–1, the catalytic events are separated in time by in average 100 μs. During this time, the enzyme will diffuse about 50 nm and completely randomize its orientation. If catalytic events lead to additional, nonthermal displacements of the enzyme, we can picture it as a sequence of displacements in random directions. Each displacement can result from a directed movement or a diffusive movement following a catalytic event, but they are not correlated with each other. To achieve a 30% enhancement of the diffusion constant, each displacement has to be larger than 20 nm, which is several times the enzyme diameter. Similar considerations apply to the faster but smaller rotary motors of Tour et al.²⁴ In contrast, an enzyme-covered microparticle (1 μm diameter, 10⁵ enzymes) exhibits a much larger number of catalytic events (10⁹ s^–1) and has a much smaller diffusion constant, requiring a displacement of less than an Ångström per catalytic event. The enhanced diffusion of enzyme-covered microparticles has been confirmed by optical microscopy by different groups,^22,51,52 but these examples cannot be evidence for the enhanced diffusion of enzymes due to the 4 orders of magnitude difference in relaxation time for a pushing event.

The fundamental theoretical challenge is thus to find an explanation how an enzyme could be propelled over many diameters in every catalytic event. Swimming at low Reynolds numbers is ruled out by Purcell’s argument (not because it is thermodynamically forbidden but because the magnitude of the potential effect is too small).¹ Ballistic motion is dampened after translation for sub-Ångström distances.^2,47 Finally, intermolecular interactions are short-range in typical buffers, where the Debye length (screening length) is less than 1 nm.

4. Theoretical Work

The backdrop to the discussion of enhanced diffusion in enzymes is the above-mentioned insights into motion at low Reynolds numbers¹ and the functioning of motor proteins.^2,53,54 In brief, molecular motion is always overdamped, meaning that the kinetic energy of a protein is dissipated into heat within less than an Ångström of movement. In motor proteins, directed molecular motion is generated by chemically controlled stepping between different conformational and binding states. Astumian stresses the importance of the proper application of thermodynamic principles, in particular the principle of microscopic reversibility, in the discussion of these molecular machines.⁵⁵ All-atom simulations of motor protein dynamics can now be performed over 40 μs and provide great detail about the conformational changes as the motor undergoes its chemical cycle.⁵⁶ Nothing fundamentally unexpected has been observed in these simulations.

Second, the pioneering work of Sen and colleagues on catalytic nanorods exhibiting active movement⁵⁷ published in 2006 gave rise to tremendous activity aimed at developing autonomous nano- and micromotors.⁵⁸⁻⁶⁰ At least conceptually, the propulsion mechanism is well-understood and believed to arise from different self-phoretic mechanisms.⁶¹ A body of theoretical work on the possible propulsion mechanism of catalytically active particles has emerged in this context.⁶²⁻⁶⁸

Golestanian was the first to mention enhanced diffusion of an individual enzyme in a theoretical work,⁶⁹ in the context of his elaboration of a minimal design for a molecular swimmer. While he concluded that conformational changes can indeed be exploited for swimming at velocities on the order of 100 nm/s for a swimmer resembling an enzyme, the rapid rotational diffusion of the enzyme (on a time scale of microseconds) would lead to diffusive motion with a vanishingly small diffusion constant.

The first full-fledged attempt to give an explanation for the observed enhanced diffusion was made by Riedel et al., who described a chemoacoustic effect where “the heat released during catalysis generates an asymmetric pressure wave that results in a differential stress at the protein–solvent interface that transiently displaces the centre-of-mass of the enzyme”.⁵ This, of course, is contrary to our understanding of the dynamics of intramolecular vibrational energy redistribution, where energy deposited in one degree of freedom is equilibrated between all other degrees of freedom of the molecule on a picosecond time scale rather than the other way around.^70,71 Moreover, to achieve ballistic motion over the required >10 nm, the model implicitly requires a fluid viscosity at least 100-fold less than the viscosity of water. These points are made with much more sophistication by Bai and Wolynes,⁹ who also suggested that the observed enhancement may be due to photophysical artifacts. This intuition was later supported by the experimental study of Günther, Börsch, and Fischer,¹² who could show that substrate-dependent quenching has been misinterpreted as enhanced diffusion of alkaline phosphatase by Riedel et al.

Golestanian responded to Riedel et al. by examining self-phoresis, the proposed chemoacoustic effect (assuming that it exists), and stochastic swimming for an enzyme in water and determined that all three mechanisms result in enhancements of the diffusion coefficient orders of magnitude smaller than the observed effect.¹⁰ However, using sophisticated theoretical approaches, Golestanian found that the exothermic reaction catalyzed by the enzyme can potentially heat the solution to a sufficient degree to lower the viscosity by 30% and thereby cause the enhancement of the diffusion constant. As described above, the required increase in temperature is 10–20 K, which—as Bustamante’s team quickly pointed out—is not achieved in typical FCS experiments and is ruled out by their control experiments.⁷²

Colberg and Kapral investigated Ångström-scale chemically self-propelled motors in a molecular dynamics simulation and found significant enhancements in their diffusivity when the motors are active due to microscopic equivalents of phoretic effects.⁷³ Unfortunately, the simulation is conducted in a fluid argon-like solvent rather than water, which makes it difficult to compare the result with an enzyme in water. A molecular dynamics simulation by Dennison, Kapral, and Stark was designed to explore the collective effects arising on molecular transport from catalytically driven conformational changes in enzymes,⁷⁴ similar to earlier work by Mikhailov and Kapral.⁷⁵ A 15% enhancement of the enzyme diffusion constant is found even for dilute enzymes, but it arises entirely from an assumed 50% uniaxial contraction of the enzyme following substrate binding. At high (>100 mg/mL) concentrations of enzyme, collective hydrodynamic effects further enhance diffusion.

Illien et al.²⁵ then elaborated a new mechanistic explanation for the enhanced diffusion, where they consider the enzyme aldolase as a dumbbell which changes its flexibility and shape upon substrate or inhibitor binding. While the aldolase is not a perfectly dumbbell-shaped enzyme, altered conformational fluctuations provide an alternative explanation of enhanced diffusion; we will discuss several clamp-shaped enzymes later in detail. This of course is not propulsion, but it explains the Michaelis–Menten-like dependence on substrate concentration and the independence of the effect of the turnover number.

However, Jee et al.—having experimentally observed enzyme leaps and not merely faster diffusion—defended enzyme propulsion with a new model.³⁰ According to this model, the enzyme is propelled by “an episodic catalytically driven boost ... whose amplitude f_B is constant during a boost time τ_B”. The boost enables the authors to nicely explain the data, for example, for their experiments with urease: “Specifically, the estimated force f_B ∼ 1 pN acts along a trajectory l_B ∼ 43 nm for a duration τ_B ∼ 6 μs, boosting the urease at a velocity v_B ∼ 7 nm/μs and dissipating an energy b ∼ 10 k_BT against the viscous drag, so the work required for the boost does not exceed the typical energy scales of enzymatic reactions.” The boost thus acts like the asymmetric pressure wave of Riedel et al. but is sustained for microseconds rather than pico- or nanoseconds and therefore conforms with the requirement for life at low Reynolds numbers. Unfortunately, the authors are unable to identify an interaction which would produce a boosting force of the required duration and interaction distance. The recent analysis by Feng and Gilson comes to the contrasting conclusion that the energy requirements for continuously “boosting” far exceed the free energy change of the enzymatic reaction.⁷⁶ Lauga has proposed that the constraints of Purcell’s scallop theorem could be circumvented if a swimmer undergoes reciprocal motions coupled with Brownian motion, resulting in enhanced diffusion of microparticles. However, such an effect cannot explain the enhanced diffusion of enzymes unless an enzyme can reciprocally swim with a velocity on the order of 10^–3 m/s, which again requires a reciprocal displacement of at least 100 nm per catalytic cycle.⁷⁷

5. Additional Considerations for the Interpretation of Enhanced Diffusion Experiments

Multimeric Forms of Enzymes and Isozymes Should Be Considered

The currently examined enzymes are all multimeric enzymes (Table 1). Since FCS measurements are often carried out with extremely diluted enzyme solutions (in a picomolar or nanomolar concentration range),⁷⁸ multimeric enzymes readily dissociate into subunits and thus give rise to apparently enhanced diffusion. For instance, the native form of hexokinase from Saccharomyces cerevisiae is a dimer, and its diffusion coefficient has been determined to be 56.4 μm²/s, while the measured diffusion coefficient in FCS experiments is 72.4 μm²/s, which more likely corresponds to its monomeric subunit.^36,42 The dissociation of the ε subunit of F₁-ATPase has been demonstrated to result in apparently enhanced diffusion in FCS experiments.¹² The diffusion coefficient of catalase from bovine liver measured in FCS experiments is also significantly greater than the previously reported value for unknown reasons (Figure 1b). The recent investigation by Xu et al. has shown that urease in the concentration ranges from 90 pM to 40 nM mainly consists of dimers and trimers.⁸ This suggests that the apparent diffusion may be a result of a combination of individual oligomers, each with distinct catalytic activity.

Another notable detail is that some commercially available enzyme products may be a mixture of isozymes that possess different molecular weights and catalytic activities; thus a complete characterization and separation are necessary before measuring the diffusion coefficients. For example, alkaline phosphatase from bovine intestinal mucosa provided by Sigma-Aldrich, used in Riedel’s research,⁵ contains at least three isoforms (according to the product information by Sigma). Acetylcholinesterase (AChE) from Electrophorus electricus used in Jee’s study⁶ is even more complicated. AChE isolated from extracts of the electric organ tissue of the electric eel contains three different forms containing a 50 nm tail structure with sedimentation coefficients of 8S, 14S, and 18S.^79,80 These species can be converted to an 11S form devoid of the tail by treatment with proteolytic enzymes or by autolysis. Although Sigma-Aldrich says the molecular weight is 230–260 or 280 kDa for two types of available products, it actually refers to the 11S form, a globular tetrameric enzyme composed of four equal subunits.⁸¹ If the AChE used by Jee et al. is purely the 11S form with M_w of 280 kDa, then the measured diffusion coefficient of 22 μm²/s is questionable because it is much smaller than that of the larger urease from Jack bean (31 μm²/s) with a molecular weight of 544 kDa. Therefore, the unexpected slow diffusion indicates that the sample contains a considerable amount of larger isozymes (with or without the long tail) or enzyme aggregates, and the enhanced diffusion may be a result of autolysis or dissociation.

Hydrodynamic Radius (R_h) Changes during Catalysis May Explain the Observed Enhanced Diffusion in Some Cases but Not in General

To validate if the changes in hydrodynamic radius can generally cause a 30–80% increase in the diffusivity of the enzymes, we tried to investigate how much the hydrodynamic radius can change upon forming an enzyme–substrate complex. In the past, many experiments have measured the changes in the radius of gyration (R_g) of an enzyme in the presence of its substrate. R_g is a measure of the compactness of a protein, which is defined as the root-mean-square distance of all atoms from the center of mass of a protein. Therefore, R_g more directly reflects the changes in protein conformation than R_h. Tyn and Gusek proposed a relation between the diffusion coefficient of proteins and R_g by adapting the Stokes–Einstein equation: D = 5.78 × 10^–8T/(ηR_g), where the constant has a dimension of (cm² cP Å)/(s K).⁸² It applies to a wide variety of proteins with good precision (87.4% of in total 198 experimental data fell into the ±20% accuracy range).

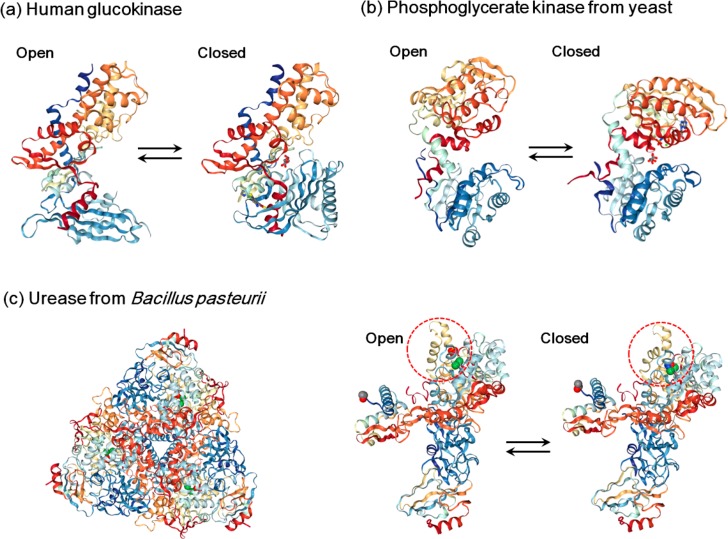
The radius of gyration of a protein can be measured by small-angle X-ray scattering (SAXRS) or small-angle neutron scattering (SANS). The measurements are usually carried out at room temperature with enzyme solutions at a concentration around 10 mg/mL in the presence or absence of substrates or ligands. Table 2 lists some examples of enzymes (or proteins) experiencing changes in R_g upon substrate (or ligand) binding. It suggests that the radius of gyration of enzymes can either decrease or increase upon substrate binding; most enzymes only undergo a change within 5%, and a few of them like the mitochondrial creatine kinase can change by 14%. Human glucokinase (also known as hexokinase IV) is a monomeric enzyme consisting of two domains. It undergoes significant conformational changes upon glucose binding by rotating the small domain (Figure 2a).⁸⁶ However, even such a large change in conformation only reduces the R_g by 6%. Hexokinase II from yeast shares a similarity with glucokinase in terms of their amino acid sequences and reaction mechanisms except that it is a dimeric enzyme.⁹² The degree of conformational changes induced by substrate binding of hexokinase is known to be slightly smaller than that of glucokinase.^85,93 Therefore, a 30% increase in diffusivity of hexokinase observed in FCS experiments is unlikely to originate from a reduced hydrodynamic radius. Phosphoglycerate kinase also experiences large conformational changes during the transition from an open state to a closed state, leading to a decrease in R_g within 5% (Figure 2b). Bowler estimated that the enzyme spends in average only 7% of its time in the closed state during a turnover cycle and remains in the open state for most of the time.⁹⁴ This effect further weakens the influence of substrate binding on the diffusion constants. The influence of conformational changes on diffusivity can also be assessed by molecular simulation. Echeverria et al. simulated the conformational dynamics of adenylate kinase, another clamp-shaped enzyme, in solution through a multiscale, coarse-grained model and also confirmed a less than 30% difference in diffusion coefficients between its fully closed state and open state.⁹⁵ Some enzymes with observed diffusion enhancements, such as catalase and urease, are roughly in globular shape and therefore are expected to experience an even smaller change in R_g compared with the clamp-shaped enzymes. For instance, the native form of urease from Bacillus pasteurii (UBP) is a heterotrimer of a complex of three subunits, (αβγ)₃ (Figure 2c). The active site is located on the α subunit, with two nickel ions incorporated. A helix–turn–helix motif serves as a flexible flap which can cover and expose the active site during catalysis, as shown in Figure 2c. Considering the large heterotrimer of the native urease, the conformational changes are subtle and should not make a big difference in the overall structure.⁹⁶ The construction of the active region is highly conserved and has been also found in other ureases such as urease from Jack bean and urease from Helicobacter pylori, and the flap structures perform the same function in these ureases.^97,98 Therefore, the enhanced diffusion of these enzymes cannot be solely ascribed to conformational changes.

Table 2. R_g Changes of Some Enzymes/Proteins upon Substrate Binding.

enzyme	Rg,free (Å)	substrate (or ligand)	Rg,bound (Å)	Rg,free/Rg,bound	ref
lobster arginine kinase	21.15 ± 0.15	arginine + Mg-ADP	19.95 ± 0.2	1.06	(83)
l-arabinose-binding protein	20.86 ± 0.21	l-arabinose	19.90 ± 0.21	1.05	(84)
yeast hexokinase (II isozyme, monomeric)	24.73 ± 0.19	glucose	23.78 ± 0.14	1.04	(85)
	24.73 ± 0.19	glucose 6-phosphate	23.48 ± 0.20	1.05	(85)
human glucokinase (hexokinase IV)	25.9	glucose + AMP-PNP	24.5	1.06	(86)
creaine kinase from mitochondria	55.6 ± 0.9	Mg-ATP	48.9 ± 0.5	1.14	(87)
	55.6 ± 0.9	creatine	55.1 ± 1.1	1.01	(87)
creaine kinase from muscle	28.0 ± 0.4	Mg-ATP	25.6 ± 0.4	1.09	(87)
	28.0 ± 0.4	creatine	28.3 ± 0.6	0.99	(87)
	28.0 ± 0.4	glucose 6-phosphate	23.48 ± 0.14	1.05	(87)
A1-ATPase from Methanosarcina mazei Gö1	50.2 ± 1	Mg-ADP	52.3 ± 1	0.96	(88)
	50.2 ± 1	Mg-ATP	51.4 ± 1	0.98	(88)
	50.2 ± 1	Mg-AMP-PNP	49.2 ± 1	1.02	(88)
rabbit muscle pyruvate kinase	39.7 ± 0.6	P-enolpyruvate	38.8 ± 0.6	1.02	(89)
	39.7 ± 0.6	l-phenylalanine (inhibitor)	40.6 ± 0.4	0.98	(89)
yeast malate synthase	39.6 ± 0.2	acetyl-CoA	38.1 ± 0.01	1.04	(90)
	39.6 ± 0.2	acetyl-CoA + pyruvate	38.0 ± 0.02	1.05	(90)
yeast phosphoglycerate kinase	23.34 ± 0.22	Mg-ATP + 3-phosphoglycerate	22.25 ± 0.26	1.05	(91)
	23.34 ± 0.22	Mg-ATP	22.76 ± 0.24	1.03	(91)
	23.34 ± 0.22	3-phosphoglycerate	23.04 ± 0.45	1.01	(91)

Figure 2.

Conformational changes of (a) human glucokinase, (b) phosphoglycerate kinase from yeast, and (c) urease from Bacillus pasteurii during the catalytic cycle. (a) For human glucokinase, the open conformation is shaped like a clamp with the active center at a groove (PDB entry 1 V4T). It closes upon glucose binding (PDB entry 1V4S). (b) Phosphoglycerate kinase from yeast possesses two lobes connected with a flexible hinge (open conformation, PDB entry 3PGK). The rotation of the hinge range brings the lobes closer, forming a closed conformation to initiate the reaction (closed conformation, PDB entry 1VPE). (c) Urease from Bacillus pasteurii is composed of a trimer of (αβγ)₃ with a 3-fold symmetry (left, PDB entry 2UBP); each (αβγ) heteropolymeric assembly is a functional unit, and the α subunit holds the active site where two nickel ions (shown as green spheres) are bound. A helix–turn–helix motif acts as a flap (red-dashed circle) which can regulate the open (PDB entry 2UBP) and closed (PDB entry 3UBP) conformations during catalysis.

Although the effect of conformational changes was invoked to explain the enhanced diffusion of aldolase (from rabbit muscle) observed in FCS experiments by Illien et al.,²⁵ it is not fully described which deformations or flexibility changes of the enzyme structure occur upon substrate binding and how much these alterations reduce the effective hydrodynamic radius. Aldolase is roughly a globular tetrameric protein with tight interactions at subunit interfaces,⁹⁹ and a 30% decrease in the hydrodynamic radius after substrate binding is difficult to envision. The recent DLS and PFG-NMR measurements, which found no measurable enhanced diffusion, align with the notion that the conformational changes upon substrate binding must be small.^13,14

6. Conclusion

Active motion induced by enzymatic reactions is one of the most fascinating phenomena in the field of active matters in the past decade and has attracted tremendous attention. However, the origin of the enhanced diffusion still remains controversial, and the existing observations are not sufficient to accept or refute if any enzyme can work as an active motor due to catalysis. In this Outlook, we reviewed the current experimental and theoretical investigations and pointed out the difficulties in forming a coherent understanding. We conclude that more sophisticated and rigorous experiments and a comprehensive theory are highly desired to advance our understanding of the role of catalytic reaction on the diffusion of enzyme. We suggest that further experiments should carefully identify the actual form of the enzymes present in the experiments and quantify the contribution of changes in effective hydrodynamic radius upon substrate binding. We look forward to more investigations aiming to reveal the underlying mechanism for the enhanced diffusion of active enzymes.

This work was financially supported by the Defense Threat Reduction Agency, under Grant HDTRA 1-14-1-0051 and the National Science Foundation, under Grant 1844149.

The authors declare no competing financial interest.