DukeSim: A realistic, rapid, and scanner-specific simulation framework in computed tomography

Abstract

The purpose of this study was to develop a CT simulation platform that is 1) compatible with voxel-based computational phantoms, 2) capable of modeling the geometry and physics of commercial CT scanners, and 3) computationally efficient. Such a simulation platform is designed to enable the virtual evaluation and optimization of CT protocols and parameters for achieving a targeted image quality while reducing radiation dose. Given a voxelized computational phantom and a parameter file describing the desired scanner and protocol, the developed platform DukeSim calculates projection images using a combination of ray-tracing and Monte Carlo techniques. DukeSim includes detailed models for the detector quantum efficiency, quantum and electronic noise, detector crosstalk, subsampling of the detector and focal spot areas, focal spot wobbling, and the bowtie filter. DukeSim was accelerated using GPU computing. The platform was validated using physical and computational versions of a phantom (Mercury phantom). Clinical and simulated CT scans of the phantom were acquired at multiple dose levels using a commercial CT scanner (Somatom Definition Flash; Siemens Healthcare). The real and simulated images were compared in terms of image contrast, noise magnitude, noise texture, and spatial resolution. The relative error between the clinical and simulated images was less than 1.4%, 0.5%, 2.6%, and 3%, for image contrast, noise magnitude, noise texture, and spatial resolution, respectively, demonstrating the high realism of DukeSim. The runtime, dependent on the imaging task and the hardware, was approximately 2–3 minutes per rotation in our study using a computer with 4 GPUs. DukeSim, when combined with realistic human phantoms, provides the necessary toolset with which to perform large-scale and realistic virtual clinical trials in a patient and scanner-specific manner.

I. Introduction

COMPUTED tomography (CT) has a significant role in the screening, diagnosis, and treatment of patients. As such, CT systems have been extensively advanced with the goal of better diagnostic accuracy and minimizing radiation burden. Conventionally, these new technologies are evaluated either using physical phantoms or patient images. Physical phantoms are too simplistic and generic, not representative of a human population, and thus have limited relevance to task-based or patient-specific assessments. Such limitations can be overcome by using patient images; however, patient images are ground truth limited, expensive, and sometimes ethically unattainable (e.g. in repetitive studies).

Virtual clinical trials (VCT) or in silico trials, defined as conducting clinical experiments using computer simulations, can overcome these challenges. In a virtual platform, the ground truth is fully known. Also, there is no need to use scanners or obtain Institutional Review Board (IRB) approvals, making the trials less expensive and much faster. Moreover, there is no ethical dilemma regarding the radiation risk in the design of a trial. The utility of a VCT, however, can be limited depending on the realism of its two main constituents: modeling of the patients and modeling of the imaging acquisition.

On the patient side, there have been extensive efforts in developing populations of anthropomorphic phantoms that model highly detailed organ anatomies [1]–[7] with intra-organ heterogeneities in the breast [8]–[12], lungs [13], [14], liver [15], and bones [16].

On the acquisition side, numerous CT simulators based on Monte Carlo (MC) methods have been developed, primarily for the purpose of dosimetric studies [17]–[20]. Although MC-based CT simulators are highly representative of the x-ray interaction process, they are slow in nature. Therefore, while these simulators are effective in estimating organ doses if one uses low-resolution phantoms (~5 mm voxel sizes), they are inefficient for generating realistic CT images of high-resolution phantoms (sub-millimeter voxel sizes) at a resolution necessary for realistic image quality assessments. This gets further challenging if one wishes to simulate imaging of a large population of phantoms.

To speed up the image generation process, alternative approaches such as GPU accelerated MC, ray-tracing, and hybrid (a combination of a ray-tracing and MC) simulators have been introduced [17], [21]–[26]. While successful in their applications, these simulators are limited for image quality VCTs for at least one of the following reasons: 1) compatibility with only surface-based phantoms which does not provide imaging of voxelized phantoms with intra-organ heterogeneities, 2) use of generalized scanner models which does not address the need for the evaluation of scanner-specific technologies in the clinic, and 3) being slow which makes them impractical for large-scale VCTs.

The purpose of this paper was to develop and validate a realistic CT simulation platform that is compatible with high-resolution 3D voxel-based computational phantoms, accounts for the geometry and physics of a given commercial CT scanner, and is computationally efficient. This platform enables the medical imaging community to virtually evaluate and optimize CT protocols and parameters for achieving targeted image quality while reducing radiation dose.

II. Methods

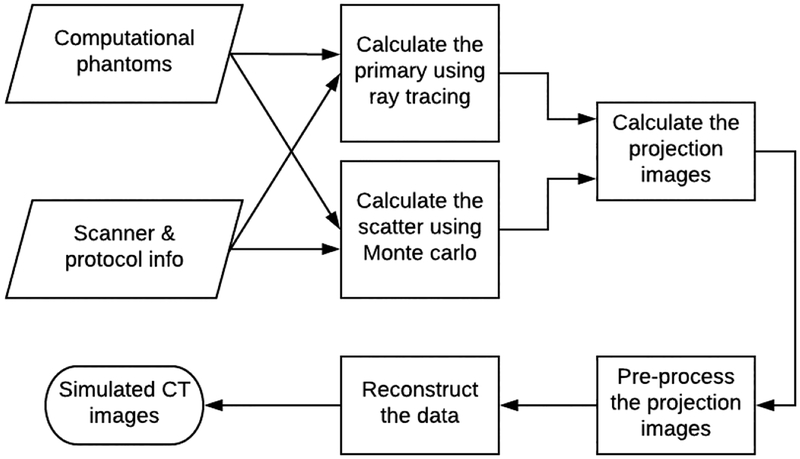
A simulation platform, called DukeSim, was developed to generate rapid, realistic, and scanner-specific CT images of voxelized computational phantoms. Given a computational phantom and a parameter file, DukeSim estimates the primary and scatter photons that hit the detector elements using ray-tracing and MC techniques, respectively. Combining these two signals while accounting for the physics of the detector elements, DukeSim computes the projection images and preprocesses them. The framework of DukeSim and an illustration of a VCT platform are shown in Fig. 1 and Fig. 2. The details are further explained in the following sub-sections.

Fig. 1.

The flowchart for DukeSim.

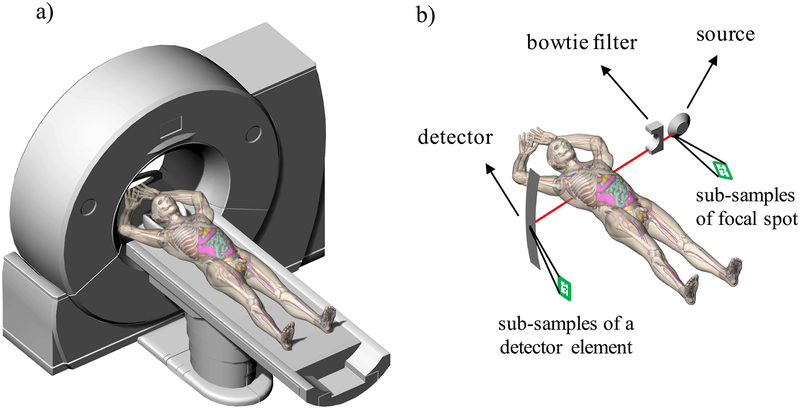
Fig. 2.

a) Illustration of a virtual clinical trial platform including a virtual scanner and a virtual patient. b) Illustration of the geometry of DukeSim.

A. Input Files

DukeSim runs with two inputs: a voxelized computational phantom and a parameter file containing information about the scanner and desired protocol. Within the parameter file, a user can define the source to detector distance, source to isocenter distance, number of projections per rotation, number of detector rows and channels, physical sizes of the detector elements and focal spot, detector offset, poly-energetic photon flux spectrum, tube current (mA), rotation speed, tube voltage (kV), beam collimation, focal spot periodic wobbles (also known as “Z” and “in-plane” flying focal spots), bowtie filter, and pitch (for helical scans).

B. Primary Signal

DukeSim has a ray-tracing module that tracks the primary photons from the focal spot, passing through the phantom and hitting the detector elements. For an energy-integrating detector element (i, j), at the projection angle α, the primary signal I is calculated as

$$I(i,j,\alpha )=\sum _E{N}_{i,j,a,E,dep}\cdot E\cdot R_E,$$ (1)

where E is the energy bin, R_E is the detector response (fraction of photons absorbed by the detector at energy bin E). This is estimated using MC simulations with the knowledge of detector properties [27], [28], considering the fluorescence and Compton events, the optical transport, their statistical properties, and the angle incident upon the detector surface. N_i,j,α,E,dep is the number of photons deposited in the detector at energy bin E, computed using the Beer-Lambert Law as [29]

$$N_{i,j,\alpha ,E,dep}=\frac{1}{K}\sum _{k=1}^{k=K}{N}_{i,j,\alpha ,E}\text{\hspace{0.17em}exp}\left(-{\sum }_m{\mu }_{m,E,k}{l}_{i,j,\alpha ,m,k}\right),$$ (2)

where N_i,j,α,E is the number of photons at energy bin E (post filtration by the bowtie filter), μ_m,E,k is the linear attenuation coefficient of the material m in the phantom (calculated from [30]) at energy bin E, l is the path length traversed by the source-to-detector ray through material m in the phantom, and k is an index for sampling the finite focal spot and detector element areas and K is the total number of these sub-samples. This sampling strategy, instead of modeling a pencil beam, was used to account for the finite sizes of the focal spot and detector elements and properly sample the phantom. To achieve this, the area of the detector and focal spot were uniformly divided (sub-sampled) into multiple smaller regions. The flying focal spot was modeled by wobbling the focal spot position periodically, as the source and the detector rotate around the phantom.

C. Scatter Signal

While ray-tracing is effective for modeling radiation transport of the primary beam, it does not account for scattered radiation. To simulate the scatter signal, a scanner-specific MC tool was developed based on the MC-GPU [17] framework. For accomplishing this, the MC-GPU code v1.3 [17] was modified and extended to incorporate a bowtie filter [31], curved energy-integrating detector model with energy response as described in the previous section, and anti-scatter grids. The anti-scatter grid was indirectly modeled using an angular acceptance distribution, which defines the probability of a photon at a certain incident angle passing through the anti-scatter grid without being absorbed. This angular distribution can be estimated using MC with the knowledge of the anti-scatter grid geometry and material for a given scanner.

The output from the MC tool includes a normalized scatter distribution, which incorporates scatter contribution from the Compton, Rayleigh, and multiple scatter processes. The simulated scattered radiation post patient is subject to statistical fluctuation due to the finite number of simulated histories. This can be remedied with a large number of histories, but that is computationally expensive. As scatter is expected to be a low frequency signal, the normalized scatter distribution was further smoothed using an optimized scatter kernel [32] (calculated using the same MC tool). The number of simulated histories and the smoothing kernel can be adjusted to account for higher frequency scatter components, in case a highly-attenuative object is present in the field of view (e.g., a pacemaker). The noise associated with primary and scatter signal is ascertained and incorporated in the noise simulation detailed below.

D. Projection Images

The total energy for each detector element is computed by summing the primary and scatter signals (I_t(i, j) = I_primary(i, j) + I_scatter (i, j)). To simulate the crosstalk, a percentage of the signal of the neighboring detector elements was added to each detector elements’ total signal. In other words:

$$I_t(i,j)=\sum _{a=-1}^{a=1}\sum _{b=-1}^{b=1}{w}_{a,b\cdot }{I}_t(i-a,j-b),$$ (3)

where the w_a,b are the neighboring crosstalk weight percentages which can be estimated using MC simulations [27] or measured experimentally [33]. To model the quantum noise and electronic noise components of the detector signal, a Gaussian random number generator [34] is used with the mean of μ_t = I_t and variance of ${\sigma }_t^2={\sum }_E\left(N_{E,dep}(primary)+N_{E,dep}(scatter)\right)\cdot {\sigma }_E^2+{\sigma }_{elec}^2,$ where ${\sigma }_E^2$ is the variance of the detector signal per input photon at the energy bin E (similar to R_E, ${\sigma }_E^2$ is also estimated based on the detector’s material and geometry [27], [28]), N_E,dep (primary) and N_E,dep (scatter) are the number of primary and scatter photons deposited in the detector at energy bin E, and ${\sigma }_{elec}^2$ is the variance associated with the electronic noise, measured in dark current. The choice of a Gaussian random number generator was based on the Central Limit Theorem.

Similar to how a clinical scanner outputs projection data, the final simulated projection image, S,is computed by normalizing the noisy detector energy signal with the air scan (I₀, the total unattenuated detector signal) using

$$S=-\text{ln}\left(\frac{Gaussian\left({\mu }_t,{\sigma }_t^2\right)}{I_0}\right).$$ (4)

The air scan, I₀, was estimated using Equations 1 and 2, where the material m was “air” and the path-length l was the source-to-detector distance. With this definition, I₀ is a function of N_i,j,α,E, i.e., the number of photons post filtration by the bowtie filter.

E. Pre-Processing

Following the standard data processing in CT systems, to suppress the effects of beam hardening, a 4^th order polynomial water correction was applied to the projection images [35]

$$S_{BHC}=\sum _{p=0}^{p=3}{a}_p(j,kVp).S^p,$$ (5)

where the coefficients a_p (a function of detector channel and the source tube voltage) were derived by applying a polynomial fit to a mono-energetic simulation of a detector signal attenuated by different thicknesses of water.

F. Computational Speed

Simulating realistic projection images of a computational phantom is computationally expensive considering the voxel size (sub-millimeter), number of projections per rotation (~1000–2500), scan range (multiple rotations per acquisition), number of detector elements (~25,000–50,000), poly-energetic nature of the spectrum and linear attenuation coefficients (~100–200 bins), and multiple samplings for finite focal spot and detector elements. The simulations were accelerated by: 1) programming in C++, 2) profiling the program, finding the bottle necks, and optimizing relevant functions, and 3) parallelizing the computations (using multiple GPUs). The simulations can be further accelerated using more advanced hardware (e.g., more memory and faster GPUs).

G. Verification and Validation

To ascertain the accuracy of a simulation tool, it is essential to subject it to verification and validation procedures. Verification answers the question of “did I build the thing, right?” [36] as intended, and validation answers the question of “did I build the right thing?” [36], ascertaining that the correct model was used.

For DukeSim, verification was performed by ascertaining that the program is functioning as per the “Methods” described in sub-sections “A” to “F”. This was done iteratively by 1) observing the intermediary and final outputs of the program under different settings (including the spectrum before and after the bowtie filter, projection images, and reconstructed images), 2) looking for unexpected results and any physical/geometrical artifacts, and 3) fixing them.

In the validation step, simulations and corresponding real experiments were performed, and the simulated and real CT images were compared in terms of image quality metrics. For this validation, a virtual model of the clinically-used Mercury phantom [37] was created. Real and simulated helical projection images of the Mercury phantom were acquired on a commercial scanner (Somatom Definition Flash; Siemens Healthcare) and DukeSim (based on the same scanner properties), respectively, under multiple X-ray flux levels (50, 150, and 300 mAs) at 120 kV and a pitch of 1.0. For the simulations, the exact geometry and physics for the specific scanner (provided by the manufacturer) were used. In these simulations, the geometry, focal spot size and positions, spectrum, shape and materials of the bowtie filter, anti-scatter grid angular acceptance distribution, neighboring cross-talk magnitudes were provided by the manufacturer. The variance of the electronic noise was based on a dark current measurement (variance of the detector signal where the beam was blocked using a lead shield). The focal spot and each detector element were uniformly sampled 4 and 5 times, respectively (total of 20 sub-samples per source-to-detector ray). This number of samples were empirically found to give results close to clinical data, with limited gain beyond.

To compare the realism of DukeSim projection data against actual CT systems, the real and simulated projection data were both reconstructed using a generic open-source reconstruction software, FreeCT [38], which is an implementation of weighted filtered backprojection reconstruction for helical fan-beam CT [39], [40]. All the projection images were reconstructed using FreeCT medium kernel with 0.6 mm slice thickness, 512 × 512 in-plane pixels, and 370 mm reconstruction field of view.

CT number values, noise magnitude, noise power spectrum (NPS), and modulation transfer function (MTF) were assessed as primary image quality metrics to compare the real and simulated images. The CT number accuracy was measured by selecting ROIs within the “Air” and “Water” inserts of the Mercury phantom images. The NPS measurements were performed by placing 8 squared ROIs (30 mm in radius) in 30 contiguous slices, with their centers uniformly distributed in a 40 mm distance from the center of the image, in the uniform regions of the phantom [41]. The noise magnitude was measured as the standard deviation in the same ROIs. The MTF was measured in the high contrast edges of the “Air” and “Bone” inserts in 30 contiguous slices using the algorithm discussed in [41]. Using this algorithm, circular ROIs (25.4 mm in radius) were placed in the center of the inserts. Edge-spread function (ESF, HU values as a function of distance from the center) was measured, binned, and averaged across all the ROIs. The binning and averaging were done to reduce the noise in the measurements. The Line-spread function (LSF) was calculated by taking the derivative of the ESF and finally, MTF was calculated by taking the Fourier transform of the LSF.

H. Pilot VCT

To demonstrate the utility of DukeSim in the context of performing realistic VCTs, we performed a pilot study to characterize the noise texture in CT images across different reconstruction algorithms.

A textured XCAT phantom [13], [14], [16] was imaged 50 times using DukeSim, based on the properties of a commercial scanner (Somatom Definition Flash; Siemens Healthcare) 120 kV and a pitch of 1.0. Projection images were reconstructed using a commercial reconstruction software (Siemens ReconCT) with filtered backprojection (FBP, kernel of B31f) and iterative (SAFIRE, kernel of I31f) algorithms. Here, the simulation being based on a specific clinical scanner and its commercial reconstruction software, enables us to fully replicate a clinical situation.

Each voxel in the reconstructed images were characterized as $\overline{I(x,y,z)}+N(x,y,z)$, where $\overline{I}$ is the averaged (noise-free) signal and N is the ensemble noise of the fifty measurements. For each reconstruction algorithm, a noise magnitude map was constructed by measuring the standard deviation of the ensemble noise across the fifty measurements. To compare the noise magnitude between the two reconstruction algorithms, a relative noise reduction map was calculated as

$${\sigma }_{reduction}(x,y,z)=\frac{{\sigma }_{FBP}(x,y,z)-{\sigma }_{IR}(x,y,z)}{{\sigma }_{FBP}(x,y,z)},$$ (6)

where x, y, z are voxel indices, and σ_{F B P} and σ_{I R} are the noise magnitudes for FBP and SAFIRE images. Moreover, for each reconstruction algorithm, NPS was measured in the lung regions (an organ that XCAT has a realistic model of heterogenous non-parenchyma and parenchyma structures) of the XCAT using

$$NPS(u,v)=A_{x,y}\cdot \left|\mathcal{F}\left[R_N(\mathrm{\Delta }x,\mathrm{\Delta }y)\right]\right|,$$ (7)

where u, v are spatial frequencies, A_x,y is the total area of a single pixel, $\mathcal{F}[.]$ is the Fourier transform operator, and R_N is the autocorrelation function of the ensemble noise N. This equation is valid under the assumption that the noise signal is wide sense stationary, which is not true for iterative images with a heterogenous background [42], [43]. Therefore, as proposed in [42], the noise signal for SAFIRE was divided into high and low noise magnitude regions, prior to the NPS calculations.

III. Results

A. Verification and Validation

Fig. 3 shows simulated CT images of a water phantom imaged with and without a bowtie filter, both reconstructed with and without our beam hardening correction algorithm. The results show that the beam hardening artifact, which is a function of spectrum and bowtie filter, was suppressed using our correction algorithm.

Fig. 3.

Simulated CT images of a water phantom. Images on the left were reconstructed without any beam hardening correction (BHC). Images on the right were reconstructed with BHC. The images on the first row were acquired without any bowtie filter, whereas the images on the second row were acquired using a Siemens “body” filter. The results show that our BHC was able to suppress the beam hardening artifact in both cases.

Fig. 4 shows real and simulated CT images of the Mercury phantom at three dose levels (50, 150, and 300 mAs). The realistic appearance of the simulated images can be seen as compared to the real ones. The contrast between the “Water” and “Air” inserts were 0.0188 ± 1.3e-05 mm²/g and 0.0191 ± 4.0e-05 mm²/g for the real and simulated images, respectively, showing a relative error of 1.4%.

Fig. 4.

Real (first row) and simulated (second row) images of a Mercury phantom at 50, 150, and 300 mAs, with the water inserts magnified, providing a closer look in the low contrast regions.

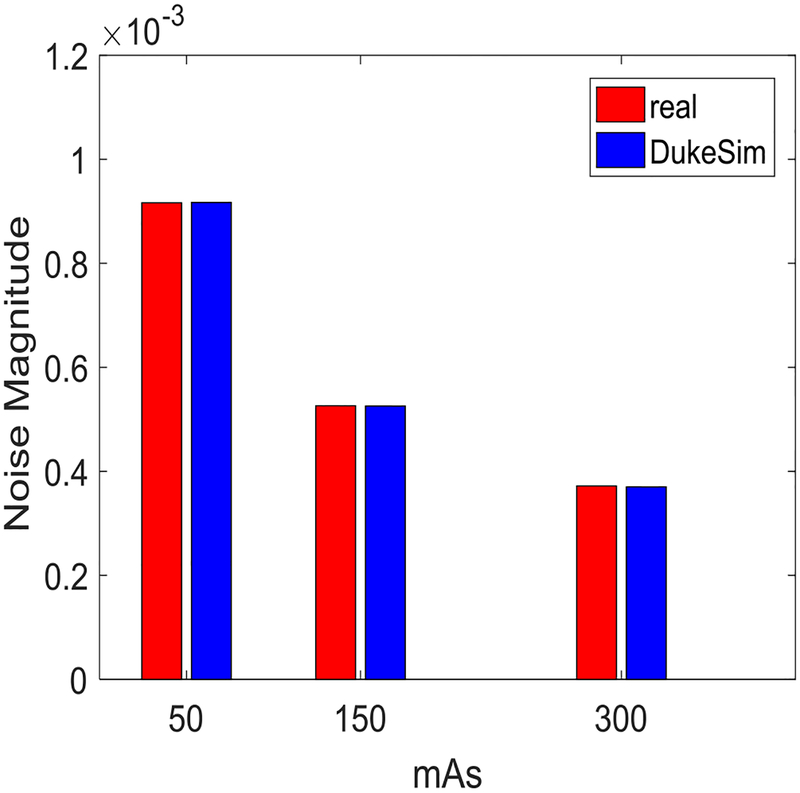
Fig. 5 shows the noise magnitude measured in the real and simulated images. The relative error was +0.07%, −0.11%, and −0.48% for 50 mAs, 150 mAs, and 300 mAs, respectively. Fig. 6 shows the NPS curves extracted from the real and simulated data for the three dose levels. In this Figure, to compare the shapes of the curves, the NPS measurements were normalized to have an area of one. The average and peak frequencies of the NPS curves, from both real and simulated images, are shown in Table 1. The relative error for the average and peak frequencies of the NPS curves were 2.49% and 2.57%, respectively. Overall, these results demonstrate that DukeSim is able to produce CT images with a noise magnitude and texture close to clinical scenario.

Fig. 5.

Noise magnitude measured in real and simulated Mercury phantom images at 50, 150, and 300 mAs.

Fig. 6.

Normalized noise power spectrum measured in real and simulated Mercury phantom images at 50, 150, and 300 mAs.

TABLE 1.

Average and Peak Frequencies of the NPS Curves in the Real (First Row) and Simulations (Second Row) at Multiple Dose Levels

		favg(mm−1)			fpeak(mm−1)
mAs	50	150	300	50	150	300
real	0.26	0.26	0.26	0.22	0.21	0.21
DukeSim	0.27	0.27	0.27	0.22	0.21	0.22

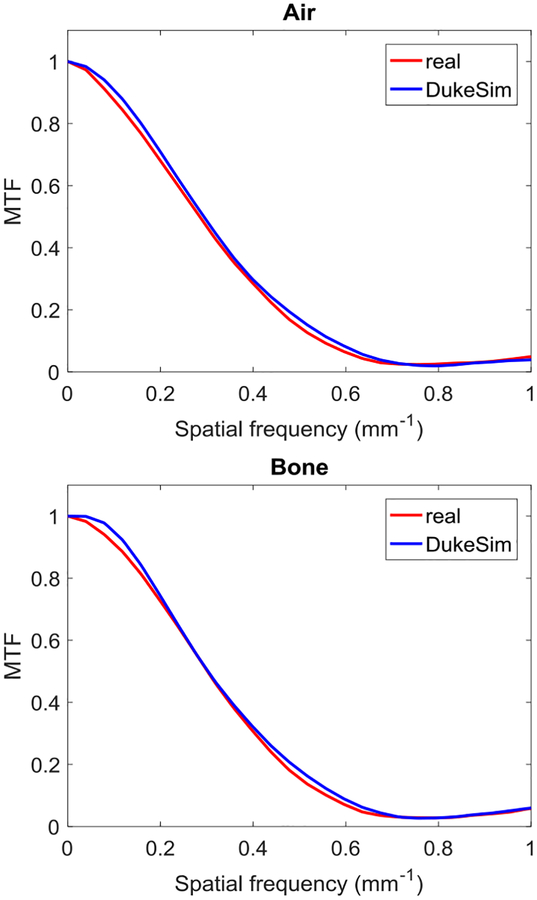
Fig. 7 displays the MTF curves measured in the “Air” and “Bone” inserts of the real and simulated images. For the Air insert, the cut off frequency at 50% (f₅₀) was 0.285 mm⁻¹ and 0.294 mm⁻¹ for the real and simulated images with a relative error of 3.1%. For the Bone insert, f₅₀ was 0.302 mm⁻¹ and 0.303 mm⁻¹ for the real and simulated images with a relative error of 0.4%. These MTF curves show that our simulated images have spatial resolution characteristics close to clinical CT images.

Fig. 7.

Modulation transfer functions measured in real and simulated Mercury phantom images.

B. Speed

All the simulations were run on a Linux machine with 64 GB of memory and four Nvidia Titan Xp GPUs. Running on four GPUs, for a phantom with 1900×1900×1000 voxels and a 0.25 mm isotropic voxel size, and a scan range of 115.2 mm (3 rotations with pitch of 1.0), it took approximately 2 minutes to obtain the scatter data (10^8 histories per projection and 10-degree angle increments), 3 minutes to calculate the intersected path lengths, and 4 minutes to calculate the final projection images (47104 detectors×6912 projection images). This speed efficiency enables large-scale VCTs in future studies.

C. Pilot VCT

Fig. 8 summarizes the noise study results. The noise maps showed the local stationarity of the FBP images and nonstationarity of the SAFIRE images, where the noise magnitude was higher in the high contrast regions. The noise reduction maps showed that while the noise magnitude was generally lower in SAFIRE images compared to FBP, it was higher in the edge voxels. This map also showed that the noise was 29% lower in SAFIRE images, lower than the expected decrease in uniform phantoms [42]. Moreover, the NPS peak frequency in the uniform regions of the SAFIRE images were lower than the FBP images, suggesting different noise correlations. These results are consistent with the previous experimental studies [42], [44] and suggest the utility of DukeSim and textured XCAT phantom for conducting large-scale realistic VCTs.

Fig. 8.

First row: simulated CT images reconstructed with FBP (left) and iterative (right) algorithms. Second row: voxel-based noise magnitude maps in FBP and iterative images measured by 50 repetitive image acquisitions. Results suggest that the noise is locally stationary in FBP images but not stationary in the iterative images. Third row: noise reduction maps on the left and NPS curves, measured in the lungs, on the right, demonstrating that iterative images have less noise in uniform regions but higher noise in the edge voxels. The peak frequency of the NPS corresponding to lower noise (uniform regions) were lower in comparison with FBP images.

IV. Discussion

Realistic VCTs enable comprehensive evaluation and optimization of CT imaging. Such studies need accurate, scanner-specific, and computationally efficient CT simulators. In this study, we developed and validated such a simulator that is compatible with high-resolution voxel-based computational phantoms and accounts for the physics and geometry of clinical scanners.

Our developed simulator, DukeSim, is a hybrid simulator that models the primary signal using ray-tracing methods and the scatter signal using MC simulations. Unique from the previously developed CT simulators, DukeSim models the detector quantum efficiency, quantum and electronic noise, focal spot wobbling, bowtie filter, detector cross talk, and finite distribution of the detector and focal spot areas. Moreover, on a Linux machine with 64 GB of memory and 4 Nvidia Titan Xp GPUs, DukeSim simulated a typical CT scan in several minutes, making it practical to run large-scale VCTs on high-resolution human models. Another advantage of our developed hybrid simulator is that it enables concurrent assessment of image quality and radiation dose (calculated from the MC simulator) which is essential for protocol optimization studies.

DukeSim was able to generate simulated CT images with image quality attributes of image contrast, noise magnitude, noise texture (NPS), and spatial resolution (MTF) similar to those from CT images of a specific clinical scanner in a simple cylindrical phantom. This validation is also a unique feature of the present study.

DukeSim can be used to study the effects of scanner parameters (mAs, kV, pitch, etc), scanner components (bowtie filter, anti-scatter grid, detector type, etc), and reconstruction algorithms on the ultimate image quality of a population of patients. The simulator is modular in the sense that its features can be used in various modes. For example, features such as noise modeling, polychromacity, scatter, and detector crosstalk can be included or excluded depending on the user’s preferences.

This study has some limitations. The validations were performed using a phantom with a simple geometry. The production of these phantoms is accurate, therefore, the differences between clinical data and simulated data are reflective of the simulation quality and not of any phantom production inaccuracies. Moreover, there are more established quantitative image quality metrics for these simplistic phantoms compared to anthropomorphic phantoms. Nevertheless, additional investigations are envisioned as future work using physical versions of the heterogenous XCAT phantoms, once available.

While it was out of the scope this study, DukeSim can also be extended to model other types of x-ray-based imaging systems such as radiography, tomosynthesis, mammography, and fluoroscopy. Also, beyond the primary and fundamental components of a CT acquisition which were incorporated in DukeSim, we envision to model other secondary effects such as detector noise correlations between neighboring detectors and more accurate models and sampling of the focal spot. Lastly, we envision to extend DukeSim to account for tube current modulation and to be capable of simulating dynamic (4D) computational phantoms, enabling VCT studies in the context of motion.

V. Conclusion

Modeling a realistic, rapid, and scanner-specific CT simulator is an essential step towards the goal of conducting virtual clinical trials. The developed CT simulator in this study, combined with realistic human models, would enable rigorous quantification and evaluation of CT scanners, not possible using ground truth-limited clinical trials or simplistic physical phantoms.