Localization of liver lesions in abdominal CT imaging: II. Mathematical model observer performance correlates with human observer performance for localization of liver lesions in abdominal CT imaging

Abstract

Determination of the effect of protocol modifications on diagnostic performance in CT with human observers is extremely time-consuming, limiting the applicability of such methods in routine clinical practice. In this work, we sought to determine whether a channelized Hotelling observer (CHO) could predict human observer performance for the task of liver lesion localization as background, reconstruction algorithm, dose, and lesion size were varied.

Liver lesions (5 mm, 7 mm, and 9 mm) were digitally inserted into the CT projection data of patients with normal livers and water phantoms. The projection data were reconstructed with filtered back projection (FBP) and iterative reconstruction (IR) algorithms for three dose levels: full dose (liver CTDIvol = 10.5 ± 8.5 mGy, water phantom CTDIvol = 9.6 ± 0.1 mGy) and simulated half and quarter doses. For each of 36 datasets (3 dose levels x 2 reconstruction algorithms × 2 backgrounds × 3 sizes), 66 signal-present and 34 signal-absent 2D images were extracted from the reconstructed volumes. Three medical physicists independently reviewed each dataset and noted the lesion location and a confidence score for each image. A CHO with Gabor channels was calculated to estimate the performance for each of the 36 localization tasks. The CHO performances, quantified using localization receiver operating characteristic (LROC) analysis, were compared to the human observer performances.

Performance values between human and model observers were highly correlated for equivalent parameters (same lesion size, dose, background, and reconstruction), with a Spearman’s correlation coefficient of 0.93 (95% CI: 0.82–0.98). CHO performance values for the uniform background were strongly correlated (ρ = 0.94, CI: 0.80–1.0) with the human observer performance values for the liver background.

Performance values between human observers and CHO were highly correlated as dose, reconstruction type and object size were varied for the task of localization of patient liver lesions in both uniform and liver backgrounds.

Introduction

The growth in computed tomography (CT) use in the United States in recent years, and subsequent increased concerns regarding potential cancer risk of radiation, has led to increased efforts to optimize CT acquisition and reconstruction protocols (Brenner and Hall 2007, Mettler et al 2008, AAPM CT Dose Summit 2010, Hendee et al 2010, IMV 2016). Traditionally, these studies are performed with human observers (i.e. radiologists) to ensure that protocol changes, such as reduced dose and different reconstruction algorithms, do not reduce the radiologists’ diagnostic performance in interpreting the images for evidence of disease, such as the presence or growth of liver lesions. However, the time requirements for human observer studies, as well as the number of human observers needed for generalizable results, preclude their widespread use for protocol optimization.

Model observers, which are mathematical models designed to make decisions on specific tasks based on statistical decision theory (Barrett et al 1993, Beutel et al 2000), have the potential to improve the efficiency of protocol optimization. The improved efficiency would allow for a greater number of variations in CT protocols to be assessed. The channelized Hotelling observer (CHO) has been used in previous studies and found to be a good representative of human observers in simple, uniform backgrounds (Barrett et al 1993, Leng et al 2013, Yu et al 2013, Zhang et al 2014). While Solomon et al and Xu et al have explored the effect of background on model observer performance, they did not correlate their findings to human observers (Xu et al 2015, Solomon et al 2016). Xu et al performed a lesion detection task comparing a CHO model observer’s performance across five doses with multiple filtered back projection (FBP) and iterative reconstruction (IR) parameters. Liver lesions of fixed size and contrast were digitally inserted into the XCAT phantom prior to reconstruction. The improvement of IR compared to FBP techniques was found to be dependent on the dose level; at 75% original dose, the performance improvement was statistically significant (p < 0.05).

Additionally, studies demonstrating the ability of CHO to predict human observer performance have been performed with artificial lesions with simple shapes, such as circles, while real lesions may be in irregular shapes (Leng et al 2013, Yu et al 2013, Zhang et al 2014). Our previous work measured diagnostic performance for low contrast object detection and localization in a uniform background (Leng et al 2013, Yu et al 2013). In the object detection task, cylindrical rods with contrast of – 15HU were imaged within a 36 × 25 cm² water phantom under 21 conditions (three sizes, two reconstructions, three dose levels). Four medical physicists performed 21 two-alternative forced choice (2AFC) trials to quantify the impact of FBP and IR on 2D (128 × 128 pixels) CT images with differing doses (Yu et al 2013). In the localization task, three medical physicists identified the presence (or absence) and location of a single lesion within 2D (128 × 128 pixels) CT images (Leng et al 2013). In this study, cylindrical rods once again were used to mimic –15 contrast lesions. Four doses and two size rods were used. Both studies found excellent correlation between the human observers and a CHO model observer. In the object detection task, the overall correlation coefficient was 0.986, and the object detection and localization task achieved a Spearman’s rank order correlation of 1.0. Both of these studies were limited by the use of a uniform water background, and cylindrical rods to mimic lesions. The object detection and localization task was limited also by the use of only a FBP algorithm (Leng et al 2013). In this work, we address these limitations by evaluating a CHO using actual patient liver lesions in the context of both uniform and anatomic backgrounds, and we address the limitations of Solomon et al and Xu et al by comparing the performance of CHO to that of human readers.

In Part I of this paper, we investigated human observer performance in the task of localization of low contrast, patient-derived liver lesions in uniform and liver parenchyma backgrounds. For Part II, we seek to determine whether the performances of CHO model observer and human observers are well correlated in both water and liver parenchyma backgrounds. We hypothesize that the CHO model observer can predict human observer performance for the detection of human liver lesions as background, reconstruction algorithm, dose, or lesion size are varied.

Methods and materials

For this study, human and model observers located multiple sizes of liver lesions in either liver or a uniform background in CT images reconstructed with different reconstruction algorithms at differing doses. The 36 datasets (2 reconstruction algorithms × 2 backgrounds × 3 doses × 3 sizes) of 100 36 pixel × 36 pixel regions of interest (ROIs) (66 lesion-present, 34 lesion-absent) described in Part I of this two-part manuscript was utilized for CHO model observer training and testing.

Human observer studies

Three medical physicists (SL, CF and LY) specialized in CT imaging independently reviewed the 36 datasets and identified the most likely location of the lesion within each ROI. Additionally, each reader was asked to assign a confidence score of a lesion’s presence for each ROI, with 1 indicating complete confidence the image did not contain a lesion and 10 indicating absolute confidence the image contained a lesion at the given location. These locations and scores were evaluated through multi-reader, multi-case (MRMC) nonparametric localization receiver operating characteristic (LROC) analysis to determine the area under the LROC curve (Az_LROC) for each set of conditions (Wunderlich and Noo 2012). For each of the 36 datasets, the average reader performances served as the reference standard to which our model observer performance was compared. More details of the human observer study are provide in Part I (Dilger et al 2019).

Model observer studies

Parameters

A CHO with Gabor filters was used in this study as the model observer due to its demonstrated good correlation with human performance results in a uniform background (Myers and Barrett 1987, Leng et al 2013, Yu et al 2013). The general form of the Gabor filter can be expressed as (Eckstein et al 2003):

$$U(x,y)=\exp \left[-4(\ln 2)\left({\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2\right)/{\omega }_s^2\right]\cdot \cos [2\pi f_c\left(\left(x-x_0\right)\cos \theta +\left(y-y_o\right)\sin \theta +\beta \right]$$ (1)

where f_c denotes the center frequency of the channel, is the channel width, the point (x₀, y₀) is the center of the channel, θ denotes the channel orientation, and β is a phase factor. While we implemented the same passbands and orientations as in Leng et al (2013) and Wunderlich and Noo (2008) (${\omega }_{\text{s}}=56.48$, 28.24, 14.12, and 7.06 pixels, f_c = 3/128, 3/64, 3/32, and 3/16 cycles/pixel,$\theta =0$, $2\pi /5$, $4\pi /5$, $6\pi /5$ and $8\pi /5$ ), we limited our filters to a single phase (β = 0), leading to a CHO with 20 channels.

Model observer training

Unlike in previous studies (Leng et al 2013, Yu et al 2013), the images within these datasets contained a non-zero background component. Therefore, a background dependent term (a DC component of 110 HU) was subtracted from every ROI prior to training or testing the model observer (Gifford et al 2005). An average signal-present image was generated by shifting the lesion in all 66 signal-present ROIs to the central pixel. This average signalpresent ROI was then shifted across the 36 × 36 image space to train each location. For each lesion location (x₀, y₀), the Gabor filters were computed, and the mean signal image (g_s) and the 330 signal-absent images for training (g_b) were channelized:

$${\overline{g}}_{sc}=U^T{\overline{g}}_s$$ (2)

$${\overline{g}}_{bc}=U^T{\overline{g}}_b$$ (3)

where${\overline{g}}_{sc}$ and${\overline{g}}_{bc}$ are the channel output of mean signal-present and signal-absent images, respectively. The CHO template for a lesion centered at (x₀, y₀) was computed by

$${\omega }_{CHO}=S_c^{-1}\left[{\overline{g}}_{sc}-{\overline{g}}_{bc}\right],$$ (4)

where S_c is the intraclass channel scatter matrix of the channel output covariance matrix for the 330 signal-absent images (K_bc),

$$S_c=K_{bc}=U^T{K}_{b}U.$$ (5)

Traditionally, the intraclass channel scatter matrix is the average of the covariance matrices for signal-present and signal-absent images (Leng et al 2013, Yu et al 2013). However, the covariance matrices are very similar between the signal-present and signal-absent images as the presence of signal had negligible effect on the covariance matrix calculation. Therefore, the intraclass channel scatter matrix can be calculated using the signal-absent image alone.

Model observer testing

Upon completion of training, CHO templates,${\omega }_{CHO}$, were available for lesions centered at every pixel location within the 36 × 36 ROIs. To localize the lesion within the ROIs, each CHO template was applied to each of the 100 ROIs (g_c) by means of the inner product to generate a response value,$\lambda$, for each location within the ROI:

$$\lambda \left(x_0,y_0\right)={\omega }_{CHO}^T\left(x_0,y_0\right)\cdot g_c.$$ (6)

The pixel location (x₀, y₀) corresponding to the maximum $\lambda$was selected as the probable lesion location and its corresponding $\lambda$value was used as the decision variable for this ROI.

For training and testing of the CHO, we performed two different methods and compared the performances in terms of Az_LROC. The first method is resubstitution, where the same signal-present images are used for training the CHO and estimating the performance. The second method was a separate training versus testing co hort where 26 randomly selected signal-present images were used for model training and the remaining 40 were used for testing. A Bland-Altman plot and linear fit were conducted to compare the performance metrics of the testing cases to determine if resubstitution was an adequate training and testing method.

Internal noise

In order to simulate the intra-observer variability present in human observers, internal noise was added to the decision variable$\lambda$. Gaussian noise with a mean of zero and a standard deviation proportional to the standard deviation of the decision variables from the signal-absent images $\left({\sigma }_{{\lambda }_b}\right)$ was added to the decision variables using the following equation:

$${\lambda }_{final}=\lambda +\alpha \times {\sigma }_{{\lambda }_b}\times \xi$$ (7)

where α is a weighing factor and$\xi$ is a random number from a Gaussian distribution N (0,1). The weighting factor was determined by adjusting α so the Az_LROC of the model observer matched the average Az_LROC of the human observers for a dataset with moderate performance (Az_LROC = 0.85 for the 7 mm lesion in liver background, reconstructed with IR at half-dose). The α values varied from 0 to 5 at 0.25 increments. The α value that generated the most similar Az_LROC for the model and human observer in this calibration dataset was selected and used for all 36 datasets. Thus, the internal noise added to the decision variables is dependent on the signal-absent images at a given dose and reconstruction setting and is intrinsically lesion dependent due to the influence of the CHO template, wcho, calculation in equation (4) and its use in the computation of the decision variable,$\lambda$, in equation (6).

LROC analysis for model observer

To convert the 100 decision variables,${\lambda }_{\text{final}}$, of each dataset to a summary performance metric, LROC analysis was performed. The LROC curve was determined by plotting the true positive localization fraction (TPLF) by the false positive fraction (FPF) as the threshold varied. True positive cases occurred when the decision variable of the signal-present image was higher than the threshold and the location was within the distance of one radius from the true lesion location. For the 5, 7, and 9 mm diameter lesions, this resulted in localization radii of 3, 5, and 6 pixels, respectively (pixel size ~0.75 mm). The Az_LRoc was calculated using a nonparametric procedure that has been utilized in previous studies (Popescu 2007, Wunderlich and Noo 2012, Leng et al 2013). To better estimate the model observer performance of each of the 36 datasets, the process of adding internal noise and LROC analysis was repeated 200 times, and the average and variance in Az_LROC was recorded.

Evaluation of model versus human observer performances

Comparison of performances between human and model observers occurred through visual and quantitative assessment. The Az_LROC values for the human and model observers were plotted for the different dose levels and lesion sizes, and compared between background type and reconstruction algorithm. A Bland-Altman plot to visualize the differences between the human and model observers across all datasets was also created.

For quantitative comparison, the Spearman’s rank order correlation between the Az_LROC for the average human and model observer performances was calculated. To determine the confidence interval for the correlation, bootstrap analysis with 1000 bootstraps was performed. Additionally, the root mean square error (RMSE) was computed between the human and model observers:

$$RMSE=\sqrt{\frac{1}{n}\mathrm{\Sigma }{\left(Y_1-Y_2\right)}^2}$$ (8)

where Y₁ is the average human observer performance of a particular dataset and Y₂ is the average model observer performance for the same dataset. The linear relationship between the model and human observers was also assessed for a slope of 1 and an intercept of 0, which indicates good one-to-one agreement between the observers.

Results

Comparison of training and testing schemas

The results of the two training schemas for the CHO—resubstitution and independent training and testing cohorts—are shown in figure 1. The average difference was 0.009 with a 95% confidence interval (95% CI) of [−0.002, 0.0198]; this average difference was not statistically different from 0 (p = 0.11). The greatest difference in Az_LROC was 0.098 and occurred for the 7 mm lesion in liver background at quarter dose with IR.

Figure 1.

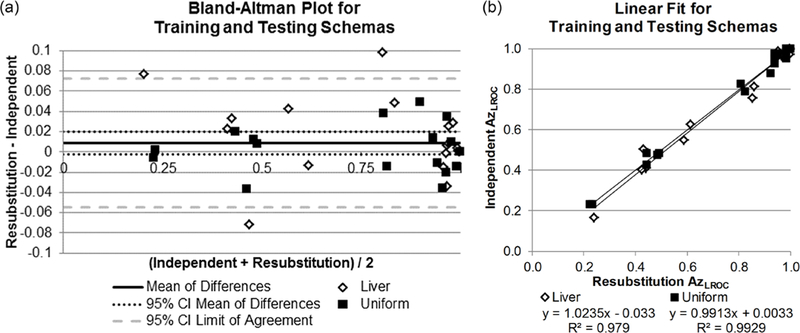
Comparison of the training and testing schemas, resubstitution and independent training and testing cohorts. (a) Bland-Altman plot of differences in performances between the two methods. The confidence interval of the mean contains 0 (no difference). (b) The linear relationship between resubstitution (x-axis) and independent training and testing cohorts (y-axis). Linear fits for both liver and uniform water backgrounds have slopes near 1, y-intercepts near 0, and R² values near 1, indicating good agreement between schemas.

The linear fit between the two schemas also indicated good agreement. The slope and intercept for the liver background were 1.024 (95% CI: 0.94, 1.10) and 0.033 (95% CI: −0.10, 0.03), respectively. Similarly, the slope and intercept for the uniform background were 0.99 (95% CI: 0.95, 1.04) and 0.003 (95% CI: −0.03, 0.04). Overall Spearman’s correlation coefficient was 0.91 (95% CI: 0.80, 0.98), and RMSE was 0.045 (95% CI: 0.036, 0.065). Based on the lack of statistical difference in the Bland-Altman plot and the indicators of good agreement from the linear fit analysis, resubstitution was determined to be a valid substitute for independent training and testing cohorts and was used for the remainder of the study.

Calibration of internal noise

Figure 2 shows the comparison of the average performance of human observers and the model observer for the calibration dataset (7 mm lesions in liver background images reconstructed at half dose with IR) at internal noise levels from 0–5. A model observer with an internal noise level of α = 1.75 was found to achieve the most similar performance as the human observer. This internal noise level was used in the model observer calculations for all 36 datasets, including both uniform and liver background.

Figure 2.

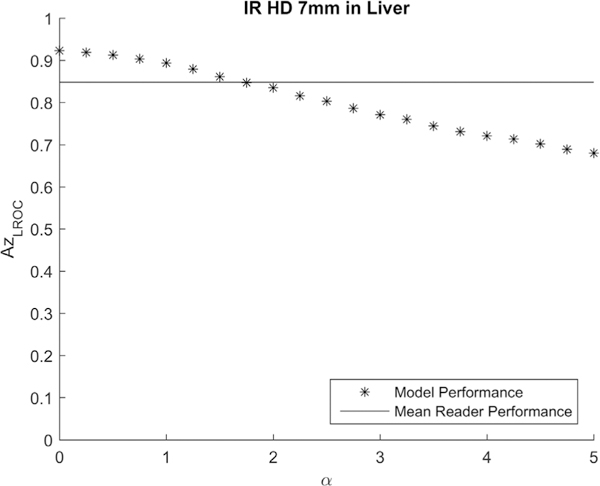
The calibration of internal noise was performed using the calibration dataset of 7 mm lesion in liver at half dose reconstructed with IR. The effect on LROC performance when different values of internal noise (α) were added to the model observer was compared with the mean human LROC performance (Az_LROC = 0.85). The final internal noise was determined to be 1.75.

Comparison of observer performances

All LROC performance results are summarized in figure 3, illustrating the comparison in performance values between human and model observers. As expected, the larger lesions were easier to localize than the smaller lesions (higher Az_LROC values), and the performance values increased as the dose level increased. There was evidence of a non-linear difference in performance between dose levels, with a larger difference occurring between the quarter and half dose images than between the half and full dose images. In general, the performances visually agreed well between human and model observers.

Figure 3.

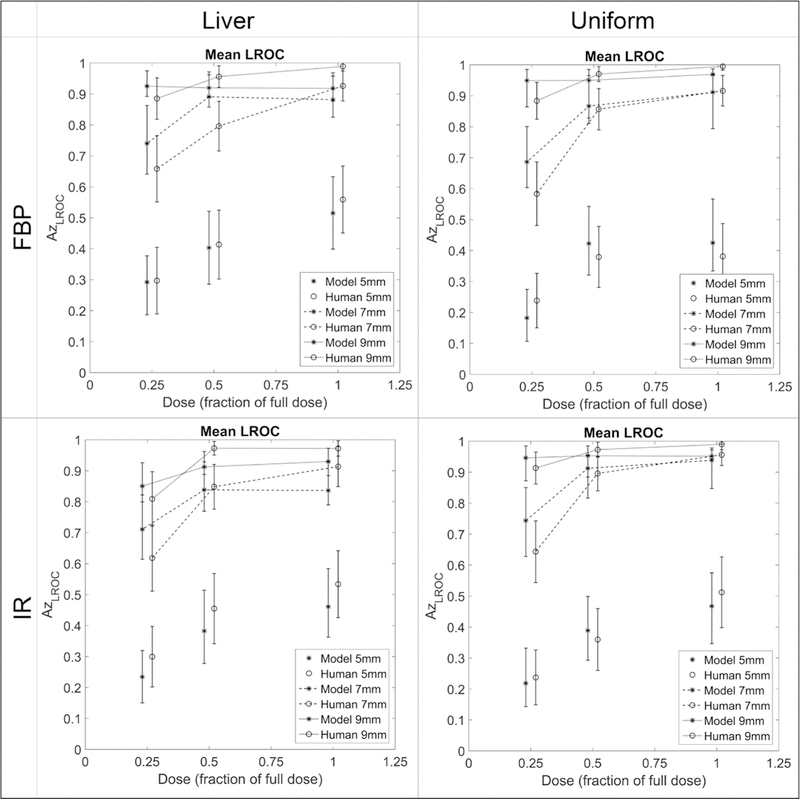
Average localization performances between model (stars) and human (connected circles) observers, separated by reconstruction algorithm and background and stratified by dose (x-axis). Error bars represent 95% confidence intervals.

The Bland-Altman plot in figure 4(a) further compares the performance differences between human and model observers. The average difference between LROC performances was –0.0017 ± 0.05, with a range of (–0.10, 0.08). The greatest differences in performance, Δ = –0.10, occurred for the 7 mm lesions in uniform background at quarter dose with either reconstruction algorithm. All differences fell within the limit of confidence (mean difference ± 1.96 * (standard deviation)), and the average difference was not statistically significantly different from zero with a 95% CI for the mean difference containing 0: (–0.02, 0.02), p = 0.85).

Figure 4.

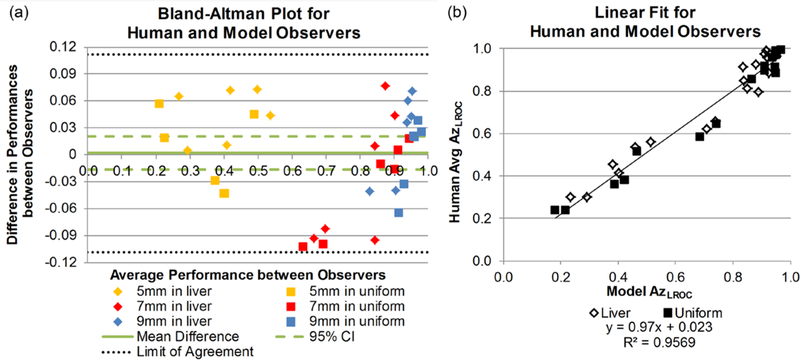
(a) Bland-Altman plot of LROC performance differences between human and model observers in the 36 localization tasks, separated by size and background. The solid line represents the mean difference in performance and the dashed lines illustrate the 95% confidence interval of the mean difference. The dotted lines represent the limits of agreement (±1.96 * standard deviation) around the mean difference; all data points lie within this range. (b) Linear fit between the model performance data and the average human observer performance data. Good agreement was seen between the observers, as indicated by a slope near 1 and a y-intercept near 0.

The human and model observer performances had a Spearman’s correlation coefficient of 0.93 (95% CI: 0.82, 0.98) and a RMSE of 0.076 (95% CI: 0.063, 0.089). For the linear relationship between the model and human observers (figure 4(b)), the slope was 0.97 (95% CI: 0.90, 1.04) and the intercept was 0.023 (95% CI: –0.03, 0.08) and indicated strong one-to-one agreement between observer types.

This one-to-one agreement was also present when looking within each background type. Within the liver background, the linear relationship was

$${\text{ Human}}_{liver}=0.95*{\text{ Model}}_{liver}+0.052$$ (9)

(95% CI for slope: 0.82, 1.07; 95% CI for intercept: –0.04, 0.14). For the uniform background, the linear relationship was

$${\text{ Human}}_{uniform}=0.99*{\text{ Model}}_{unifrm}-0.0043$$ (10)

(95% CI for slope: 0.90, 1.08; 95% CI for intercept: –0.072, 0.063). Spearman’s correlation was 0.89 (95% CI: 0.68, 0.98) for liver background and 0.95 (0.80, 1.00) for uniform background. The RMSEs for the two backgrounds were similar to the overall RMSE: 0.085 (95% CI: 0.069, 0.099) for liver and 0.066 (95% CI: 0.047, 0.091) for uniform background.

When the performances were separated by reconstruction algorithm, good agreement was maintained between the human and model observers. For FBP, the linear relationship was

$${\text{Human}}_{FBP}\text{=0}.\text{98*}Mode{l}_{FBP}\text{+0}.\text{0019}$$ (11)

with 95% CI of the slope and intercept being (0.88, 1.09) and (–0.08, 0.08), respectively. For the datasets that used IR, the slope was 0.96 (95% CI: 0.85, 1.06) and intercept of 0.04 (95% CI: –0.04, 0.12).

Comparison between model performance in uniform background and human performance in liver background

The final analysis explored whether the model observer trained with uniform background could be used to predict human observer performance with anatomical liver backgrounds. Figure 5(a) shows the Bland-Altman plot comparing the performances under these conditions. Compared to the previous Bland-Altman plot (figure 4(a)), greater variability was seen, with a larger standard deviation in differences (mean difference: 0.0011 ± 0.08). The greatest differences in performances occurred in two datasets; in the first, the model in uniform background underestimated human in liver performance of the 5 mm lesion at full dose with FBP by 0.13. The second dataset, 9 mm lesion at quarter dose with IR, resulted in the model in uniform background overestimated the performance of human readers in liver by 0.14. The RMSE was 0.11 (95% CI: 0.077, 0.13).

Figure 5.

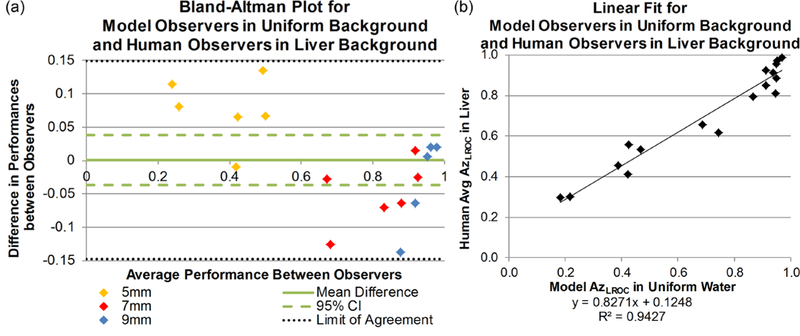
(a) Bland-Altman plot of LROC performance differences between human observers in liver background and model observers in uniform background, separated by size. The solid line represents the mean difference in performance and the dashed lines illustrate the 95% confidence interval of the mean difference. The dotted lines represent the limits of agreement (±1.96 * standard deviation) around the mean difference; all data points lie within this range. (b) Linear fit between the model performance data and the average human observer performance data. Slope and intercept do not achieve 1 and 0, respectively, and therefore do not demonstrate good one-to-one agreement.

The model observer performance in a uniform background was highly correlated to the human observers’ average performance in a liver background, with a Spearman’s correlation coefficient of0.95 (95% CI: 0.80, 1.00). The linear agreement between the two did not show a one-to-one agreement (figure 5(b)). The slope between the two models was 0.83 and the 95% confidence interval did not contain 1 (95% CI: 0.72, 0.94). Similarly, the intercept was 0.13 and the 95% confidence interval did not contain 0 (95% CI: 0.04, 0.21). However, this high level of correlation (0.95) indicates the linear relationship is a reliable conversion from model observer performance in a uniform background to human observer performance in liver parenchyma.

Discussion

In this study, we tested the capabilities of a CHO to imitate human observers in liver lesion localization. Three lesions sizes, three doses, and two reconstruction algorithms were explored for two different backgrounds between the two types of readers. We found excellent correlation and agreement between the model and human observers when comparing similar conditions–same background, reconstruction algorithm, dose, and lesion size. Finally, while not a one-to-one agreement, good correlation was found when determining whether the model observer in the uniform background could predict the human observers’ performances in the anatomical liver background.

This study also validated the use of resubstitution to generate the template images used for localization in the CHO. The resubstitution-derived performances were well correlated to the results of the independent training and testing schema, and, for both backgrounds, the confidence intervals for the slope and intercept describing the linear relationship between the two observers’ performances contained 1 and 0, respectively. The reduction of the number of Gabor channels likely contributed to the low amount of bias presented here. By reducing the number of channels to 20 (compared with previous work of 40 channels (Leng et al 2013)), we have reduced the number of images needed to train the model observer and maintain an accurate estimate of performance (Ma et al 2016).

While we found good correlation (ρ = 0.93) and similar Az_LROC performances between FBP and IR techniques in the model observers, this trend differed from Solomon et al’s recent work exploring the impact of the background on lesion detectability. Solomon showed statistically significant differences in detectability,$d^{\prime }$, between FBP and IR reconstructions (p = 0.02) (Solomon et al 2016). While the tasks differ (localization versus detectability), we do not observe an increase in performance with IR compared to FBP. For their work, thin-slice (0.6 mm) reconstructions at the highest level of SAFIRE (strength of 5) were used, whereas we used a clinical abdominal protocol (5 mm slices with medium IR strength of 3). It is likely the increased slice thickness and lower strength of SAFIRE reduced the performance differences seen in our comparison of reconstruction algorithms. These protocol differences also likely reduced the visual differences between the two backgrounds and could explain why we found fewer performance differences between a uniform and anatomical liver texture relative to Solomon’s findings.

Xu et al used an anatomy-simulating XCAT phantom (Xu et al 2015) in comparing FBP and IR. Similarly to our work, they did not find statistical differences in performance between FBP and IR at many dose levels, including full and half dose ($p⩾0.05$). At 75% of full dose did they find a statistical difference between FBP and IR (SAFIRE strength 5). In both Xu et al and Solomon et al, only model observer data were presented and there was no comparison to human observers (Xu et al 2015, Solomon et al 2016), whereas in this study we compared human reader and model observer performances in lesion localization.

A limitation of this study was the focus on hypodense liver lesions within liver parenchyma free of major vessels. These vessels were purposely avoided, both to remove human reader memory bias as the readers looked at different variations of the same images, as well as to create a random, nonuniform background for the model observers. The CHO has been designed for use on random, nonuniform backgrounds (Yao and Barrett 1992), however, vessels are nonrandom. Vessels are hyperdense relative to the parenchyma in contrast-enhanced images and are unlikely to be selected by the human observers when asked to localize a hypodense lesion, therefore, we felt their exclusion would have minimal effect on human observer performances. However, additional work in increasingly complex backgrounds is needed to determine whether our findings extend beyond isolated liver parenchyma. Finally, as discussed in Part I, this study is limited in scope to window level and window width of 40/400, the standard setting for abdominal CT imaging at many institutes.

Conclusion

In the task of hypodense lesion localization, model and human observer performance results are highly correlated, suggesting that future optimization studies could be carried out using highly-efficient model observers. Though not a one-to-one relationship, the strong correlation suggests the model in uniform water background could serve as a surrogate for human performance in anatomical liver background.

Abbreviations

CHO

Channelized Hotelling observer

CT

Computed tomography

FBP

Filtered back projection

IR

Iterative reconstruction

LROC

Localization receiver operating characteristic

SAFIRE

Sinogram affirmed iterative reconstruction

Az_LROC

Area under the LROC curve

ρ

Spearman correlation coefficient

CTDI_vol

Volume CT dose index

mGy

milliGrays

DICOM

Digital imaging and communications in medicine

ROI

Region of interest

MRMC

Multi-reader, multi-case

α

Weighting factor for internal noise

TPLF

True positive localization fraction

FPF

False positive fraction

ROC

Receiver operating characteristic

RMSE

Root mean square error

CI

Confidence interval

HO

Human observers

MO

Model observer