Abstract
Registering brain magnetic resonance imaging (MRI) scans containing pathologies is challenging primarily due to large deformations caused by the pathologies, leading to missing correspondences between scans. However, the registration task is important and directly related to personalized medicine, as registering between baseline pre-operative and post-recurrence scans may allow the evaluation of tumor infiltration and recurrence. While many registration methods exist, most of them do not specifically account for pathologies. Here, we propose a framework for the registration of longitudinal image-pairs of individual patients diagnosed with glioblastoma. Specifically, we present a combined image registration/reconstruction approach, which makes use of a patient-specific principal component analysis (PCA) model of image appearance to register baseline pre-operative and post-recurrence brain tumor scans. Our approach uses the post-recurrence scan to construct a patient-specific model, which then guides the registration of the pre-operative scan. Quantitative and qualitative evaluations of our framework on 10 patient image-pairs indicate that it provides excellent registration performance without requiring (1) any human intervention or (2) prior knowledge of tumor location, growth or appearance.
1. Introduction
Glioblastoma is the most common and aggressive malignant brain tumor that heavily and heterogeneously infiltrates surrounding tissue. This infiltration complicates treatment [1], as it is difficult to precisely localize the extent of infiltration. Considering that more than 80% of patients have a local tumor recurrence close to the initial resection cavity [2] (hence to the infiltrated brain tissue), we identify the need to accurately map correspondences between pre-operative (pre) and post-recurrence (post) brain tumor scans. Such registrations would support research into the early detection of tumor recurrence, e.g., enable the identification of subtle imaging phenotypic characteristics of tumor recurrence. Even though correspondences are established between longitudinal image-pairs, where scans are expected to be comparable (as they are of the same patient), registration is challenging due to there being two sources of image appearance changes: first, the pre scans contain tumors and mass effect deformations; second, the post scans typically contain tumor resection cavities (where the tumor used to be in the pre scan) and show signs of tumor infiltration and recurrence.
Registration in the presence of pathologies may employ cost function masking [3] to exclude regions without clear correspondences and hence avoid influencing the registration’s image similarity term. Alternatively, one could combine cost function masking with a model of infiltration and mass effect [4]. A joint segmentation-registration method has also been proposed [5,6], that incorporates a tumor growth model and that estimates a patient-specific atlas to guide the segmentation and registration, while using 4 MRI modalities. Building upon this and considering that both pre and post scans are of the same patient, Kwon et al. [7] proposed a framework to jointly segment and register the post to the pre scans. However, it may be challenging to estimate the deformations of pre scans with large tumors and post scans with large mass effect relaxation. In addition, these segmentation-registration approaches require manual interaction in the form of seed-points to initialize the growth model and to model the intensity distribution of each brain tissue across modalities. This complicates the use for large-scale studies and hampers the clinical translatability of these methods.
To account for missing correspondences in pathological regions, an alternative strategy is to estimate a quasi-normal image by learning from population data and use it for registration. Quasi-normal images can, for example, be estimated by a low-rank/sparse (LRS) decomposition [8] or via deep variational encoderdecoder architectures [9]. However, these methods either blur the normal tissue appearance and compromise the registration results or require a large number of training images. Inspired by the LRS decomposition, Han et al. [10] proposed a joint PCA/image-reconstruction model, which also decomposes the pathological image into two parts: (1) normal tissue appearance is captured by a statistical (PCA) model; and (2) large pathologies are captured via a total-variation (TV) term, which avoids blurring of the normal tissue and retains fine details in the quasi-normal image. The reconstructed quasi-normal image is then used for atlas registration. One could directly apply this method independently to the pre and the post scans, and then register the resulting quasi-normal images. However, this strategy would ignore the fact that these scans come from the same patient and the statistical model in the atlas space may not adequately capture the normal appearance for a specific patient; consequently, the registration quality may be impaired. Similarly, Kwon et al. [11] extended their framework [7] by incorporating an inpainting strategy to account for pathological regions. However, prior knowledge about the tumor of each scan, comprising of seed-points with associated radii and initial intensity modeling of each brain tissue type, is required for the algorithm. This manual interactive step, in addition to introducing an extra burden to the method’s usability and increasing the time footprint of the method, also affects the objectivity and repeatability of the obtained results. All these together have a direct impact on the consideration of the method for potential clinical translation, as well as for large research studies. Therefore, a method combining the benefits of pathology modeling with patient-specificity, while eliminating manual interactions, is highly desirable.
Contributions.
In this work, we present an automatic, repeatable, patient-specific registration approach for pre and post brain MRI scans that requires only a single modality. This is accomplished through careful adjustment of the PCA/image-reconstruction model [10]. In particular, we show how to (1) model each patient separately to improve the registration results and (2) leverage the decomposition’s TV term to intrinsically exclude the estimated pathology in case the image is not well-aligned to the target space.
Organization.
Section 2 describes our patient-specific registration framework, Sect. 3 presents the qualitative and quantitative evaluations of our approach, compared against other state-of-the-art methods, and Sect. 4 concludes the paper with a discussion and an outlook on future work.
2. Methodology
We first present an overview of the low-rank/sparse approach [8] and the PCA-TV model [10]. We then propose modifications for patient-specific registration.
2.1. Low-Rank/Sparse (LRS) Decomposition
In the LRS approach, images {Ii : i = 1, 2,..., n} are first arranged as columns of a matrix I = [I1,..., In], where n describes the number of images. This matrix is then decomposed into a low-rank matrix L = [L1,.., Ln] and a sparse matrix S = [S1,..., Sn] by solving the problem:
| (1) |
where is the nuclear norm (i.e., a convex approximation of the rank denotes the norm, and λ weighs the penalty on sparse term. Liu et al. [8] proposed a low-rank-based registration method by alternating the LRS decomposition and registering the low-rank image to an atlas. Upon convergence, the low-rank matrix contains the normal information from all images, while the sparse matrix obtains the estimated pathology. The low-rank images are then used for registration. While effective, the approach suffers two shortcomings: First, it requires optimization over the entire population, which is ineffective and computationally expensive. Second, while it recovers normal appearance in pathological regions, normal tissue areas are blurred which may negatively affect registration results.
2.2. PCA-TV Model
Inspired by the LRS framework and the Rudin-Osher-Fatemi (ROF) image denoising model [12], Han et al. proposed a PCA-TV registration framework [10]. It registers all the “normal” images, i.e., images from healthy controls, to an atlas space only once, followed by a PCA on the warped normal images. The PCA basis is kept fixed, and the PCA-TV model decomposes the image by solving the following problem:
| (2) |
where denotes the “pathological image”, i.e., an image with at least a pathology/tumor, after we subtract the mean. i is the spatial location, {α} are the PCA coefficients and B is the PCA basis. The model consists of (1) a quasi-low-rank part that is close to the PCA space and retains image detail, and (2) a TV term, which captures pathologies that are large, spatially contiguous, and not expressed by the PCA basis. The quasi-normal image is obtained by adding the mean image to the quasi-low-rank image. Overall, this model is more effective than the LRS decomposition, as it works on just one image and explicitly leverages spatial information.
Additionally, an iterative regularization strategy can be used after the decomposition, just as for the ROF model [13]. In particular, after solving (2) and obtaining and , for , one can iteratively solve
| (3) |
where . After N regularization steps, the TV term TN captures the pathology and the quasi-low-rank term can be obtained by subtracting the TV term from the input image, i.e.,
The entire framework iteratively alternates between the image decomposition and atlas registration. Each iteration includes the registration of the quasinormal image to the atlas, the transformation of the input image to the atlas space, and the decomposition of the warped image in the atlas space. In addition, to avoid accumulating deformation errors, the quasi-normal image is always transformed back to the original image space prior to registration.
2.3. Patient-Specific Registration
When registering the pre to the post scan, one could simply apply the PCA-TV model (Sect. 2.2) independently on each scan and then register the corresponding quasi-normal images. However, this ignores that both scans are of the same patient. In addition, both the LRS and the PCA-TV approaches register quasi-normal images to the atlas during each iteration, but never use the sparse/TV information. In case an image contains tumors with large mass effect, it is drastically misaligned with the population images. Hence, the decomposition may not work sufficiently, unless the image is well-aligned with the atlas. This is especially true during the first iteration of registration and decomposition. To overcome these shortcomings and improve the registration of pre and post scans, we propose the following key adjustments to the PCA-TV model.
PCA-TV-Mask Model.
When we compute the decomposition in the first iteration, the image is only affinely aligned to the atlas. We apply Otsu thresholding to the TV image, to obtain a coarse mask of the pathological region (TV-mask). This mask is then used during the registration, i.e., we register the quasi-normal image to the atlas, but use the TV-mask for cost-function masking of the tumor. Once the image is better aligned to the atlas via a deformable registration, we remove the TV-mask and use the entire quasi-normal image for registration. We refer to this improvement as the PCA-TV-mask model.
Patient-Specific PCA.
Considering (i) that the post scan is relatively free from mass effects (e.g., except for scarring) and (ii) that the tumor resection cavity is easily modeled via the TV term, we propose the following two-step strategy. In the first step, we apply the PCA-TV-mask model to the post scan, resulting in a quasi-normal reconstructed image, in addition to registering the post scan to the atlas space. In the second step, we use the inverse transformation of the first step to map all normal images into the post scan space and then construct a new PCA basis from this data. Importantly, we can now use this new PCA basis together with the quasi-normal post image (now warped back to the patient space and used as atlas) to run the PCA-TV-mask model on the pre scan. Overall, this strategy allows direct registration between the pre and the post scans. Another advantage of using this patient-specific strategy is that by running PCA in the patient-specific space, the normal space spanned by the PCA basis is expected to be more consistent with the pre scan, which in turn improves the decomposition and registration results, when compared with the original framework.
3. Experiments
We evaluate our framework on 10 pairs of pre and post clinically-acquired scans of patients diagnosed with de novo (primary) glioblastoma. Each timepoint contains native (T1) and contrast-enhanced Tl-weighted (T1-CE), T2-weighted and FLAIR MRI. All modalities of each patient are skull-stripped, bias-field corrected, and affinely co-registered to the pre Tl-CE scan of this patient that describes a 192 × 256 × 192 volume with voxel size of 0.977 × 0.977 × 1.0 [mm3]. For quantitative evaluation, we use manually seeded landmarks from two clinical experts. The first expert placed 20 landmarks within 30[mm] from the tumor region and 30 landmarks outside the 30[mm] region in each pre scan. Then, both experts independently placed matching landmarks in the post scans. The landmarks placed by the first expert are considered the gold-standard and the ones placed by the second expert serve as a baseline comparison, referred to as RATER. In our experiments, we only use the T1 volumes from each patient and run 6 iterations of registration and decomposition. The remaining 3 modalities were only used by the experts for seeding the landmarks. We pick 100 normal images from OASIS [14] and select 50 as PCA basis. For registration, we use NiftyReg [15] as B-spline registration with the default settings and local normalized cross correlation as similarity measure (--lncc 40). The TV-mask is used in the first iteration when the image is only affinely aligned to the target image. After B-spline registration, we remove the TV-mask for subsequent iterations. We also apply the regularization steps in the last three iterations. γ in (2) and (3) for the decomposition model is chosen as 1 if no regularization step is used and 2 if regularization steps are used. We compare with AFFINE [16], GREEDY [17], DRAMMS [18], ANTS [19], NiftyReg [15] and PCA-TV [10]. Although PORTR [7] was specifically designed for this task, we did not include it in our analysis, as our intent is to compare methods that do not require multiple modalities or manual interaction and hence more easily translate to clinical use.
We compute the mean landmark error for each region of each patient (Fig. 1) and we note that all deformable methods are better than affine registration, but worse than RATER. Compared to other deformable methods, our patient-specific approach improves the results in the close-to-tumor region. We also improve results in the region far away from the tumor, except when comparing with NiftyReg and the original PCA-TV model. In fact, as shown in Table 2, the improvements in the close-to-tumor region are statistically significant, assessed via a one-tailed paired Wilcoxon signed-rank test with a Benjamini-Hochberg procedure to control the false discovery rate at level α = 0.05. For far-from-tumor regions, the results are only significant when compared to AFFINE and GREEDY. We also calculate the effect sizes with each paired rank test. Most of the tests result in large or medium effect sizes.
Fig. 1.
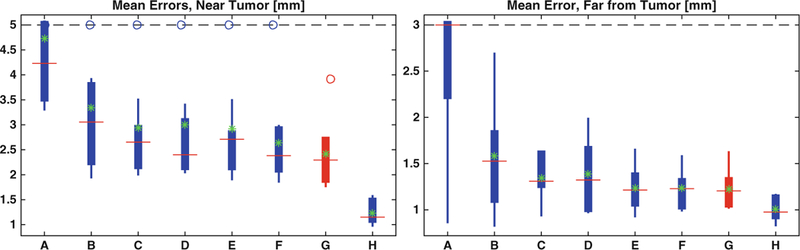
Boxplots of the mean landmark errors. For each method, the landmark errors are computed against the gold-standard. On each box, the red line is the median and the green star is the mean. The bottom and top edges of the box denote the 25th and 75th percentiles, respectively, the whiskers extend to the most extreme datas that are not considered outliers and the outliers are plotted in circle. (A) AFFINE; (B) GREEDY; (C) DRAMMS; (D) ANTs; (E) NiftyReg; (F) PCA-TV; (G) PCA-PS; (H) RATER. Our result is plotted in red. (Color figure online)
Table 2.
p-values and effect sizes for one-tailed paired Wilcoxon signed-rank test. We compare all methods (except for RATER) with our patient specific framework. Green boxes indicate statistically significant results after false discovery rate correction or effect sizes that are at least medium (>0.3).
| AFFINE | GREEDY | DRAMMS | ANTs | NiftyReg | PCA-TV | ||
|---|---|---|---|---|---|---|---|
| p-values | Near | 9.77e-4 | 4.90e-3 | 1.37e-2 | 1.86e-2 | 4.90e-3 | 3.22e-2 |
| Far | 2.00e-3 | 1.37e-2 | 4.20e-2 | 0.116 | 0.423 | 0.385 | |
| effect sizes | Near | 0.6268 | 0.5584 | 0.4900 | 0.4672 | 0.5584 | 0.4217 |
| Far | 0.6040 | 0.4900 | 0.3989 | 0.2849 | 0.0570 | 0.0798 | |
We also evaluate the statistics of the paired landmark errors in both regions (Table 1). For each landmark, we calculate the differences of the errors between our framework and competing methods. Compared to RATER, our method shows worse performance on more than 50% of the landmarks. However, when comparing to other automatic registration methods, although at some landmarks our method performs worse than others by less than 1.5[mm] near the tumor and 1[mm] far away from the tumor, as shown at 5% statistics, it shows better performance on more than 50% of the landmarks. In fact, the improvement, especially near the tumor, can be larger than 5[mm], as shown at 95% statistics in the table. Furthermore, on average, we perform better than other registration methods by 0.5[mm] near the tumor and by less than 0.2[mm] far away from the tumor. This is consistent with the green stars shown in Fig. 1. Our patient-specific method also improves over the PCA-TV model near the tumor which illustrates its utility and the benefit of the patient-specific model.
Table 1.
Statistic results for all paired landmark errors in both regions. For each land-mark, we calculate the paired error; i.e., we subtract the landmark error of compared method from the landmark error of our method. This is to calculate the improvement obtained by our method. For each compared method, we rank the paired landmark errors and show the statistics in the table. The green boxes indicate results where errors from our framework are smaller.
| Near Tumor[mm] | Far from Tumor[mm] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5% | 25% | 50% | 75% | 95% | Mean | 5% | 25% | 50% | 75% | 95% | Mean | |
| AFFINE | −1.03 | 0.22 | 1.65 | 3.71 | 7.58 | 2.32 | −0.60 | 0.79 | 1.35 | 3.64 | 6.90 | 2.11 |
| GREEDY | −1.01 | −0.28 | 0.31 | 1.18 | 6.03 | 0.94 | −0.80 | −0.17 | 0.05 | 0.43 | 2.77 | 0.36 |
| DRAMMS | −1.45 | −0.55 | 0.18 | 0.79 | 4.68 | 0.52 | −1.15 | −0.28 | 0.14 | 0.52 | 1.16 | 0.13 |
| ANTs | −1.44 | −0.31 | 0.17 | 0.80 | 6.10 | 0.59 | −0.68 | −0.18 | 0.08 | 0.37 | 1.32 | 0.17 |
| NiftyReg | −1.21 | −0.19 | 0.12 | 0.60 | 3.35 | 0.51 | −0.50 | −0.14 | −0.02 | 0.12 | 0.55 | 0.01 |
| PCA_TV | −1.06 | −0.29 | 0.11 | 0.57 | 2.08 | 0.23 | −0.45 | −0.14 | 0.00 | 0.15 | 0.55 | 0.01 |
| RATER | −4.67 | −1.86 | −0.79 | 0.07 | 1.06 | −1.18 | −1.99 | −0.74 | −0.14 | 0.44 | 1.18 | −0.21 |
Finally, Fig. 2 shows example results from three patients, where we register the pre to the post scans. For the PCA-TV model and our patient-specific PCA-PS model, we reconstruct the quasi-normal images from each patient which are used to guide the registrations. Although the visual differences between our method and the PCA-TV model are subtle, other results show that by modeling the pathologies registrations are qualitatively more accurate. Note that, Fig. 2(c) illustrates the T2-FLAIR scans for the post images, only for visualization purposes, to better depict the surgically-imposed cavities of these illustrated examples. All the applied registration methods use only the T1 volumes.
Fig. 2.
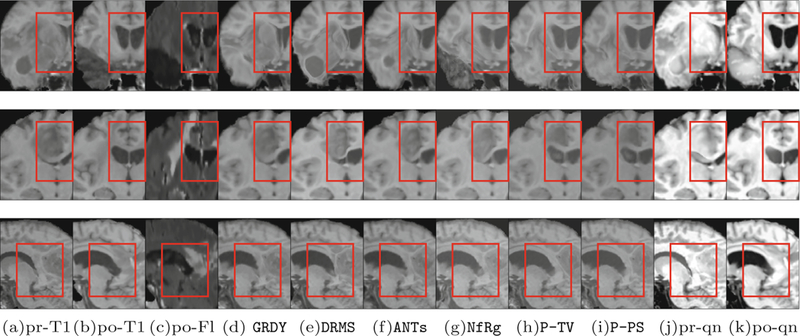
Example registration results from three patients. (a) and (b) show the pre and the post T1 scans. (c) shows the post T2-FLAIR scans, only for visualization purposes. (d)-(i) show registration results of pre to post from GREEDY, DRAMMS, ANTs, NiftyReg, PCA-TV, and our patient-specific model, PCA-PS. In addition, (j) and (k) show the quasi-normal reconstructions of the pre and post scans, respectively. The red box highlights major differences. (Color figure online)
4. Conclusion
We proposed a patient-specific registration framework based on a PCA-TV-mask model, which registers pre-operative and post-recurrence scans of the same patient. The framework uses the post scan, which is relatively free from mass effects, to build a patient-specific PCA basis, and directly registers the pre scan to the patient space. The validation results show that our framework is more effective than the PCA-TV model, as well as other registration methods that do not explicitly model pathologies. In addition, our framework does not require any manual interaction, neither in the form of segmentation nor as tumor seeding, and only requires a single modality. In future work we will explore our method for different diseases, for example, to register acute and chronic image pairs from patients with traumatic brain injuries.
Acknowledgements.
Research reported in this publication was supported by the National Institutes of Health (NIH) and the National Science Foundation (NSF), under award numbers NIH:2R44NS081792, NIH/NINDS:R01NS042645, NIH/NCI:U24CA189523, NSF/ECCS-1148870, and NSF/EECS-1711776. The content of this publication is solely the responsibility of the authors and does not necessarily represent the official views of the NIH, or the NSF.
References
- 1.Price SJ, Jena R, Burnet NG, Carpenter TA, Pickard JD, Gillard JH: Predicting patterns of glioma recurrence using diffusion tensor imaging. Eur. Radiol. 17(7), 1675–1684 (2007) [DOI] [PubMed] [Google Scholar]
- 2.Milano MT, et al. : Patterns and timing of recurrence after temozolomide-based chemoradiation for glioblastoma. Int. J. Rad. Oncol. Biol. Phys. 78(4), 1147–1155 (2010) [DOI] [PubMed] [Google Scholar]
- 3.Brett M, Leff AP, Rorden C, Ashburner J: Spatial normalization of brain images with focal lesions using cost function masking. NeuroImage 14(2), 486–500 (2001) [DOI] [PubMed] [Google Scholar]
- 4.Niethammer M, et al. : Geometric metamorphosis In: Fichtinger G, Martel A, Peters T (eds.) MICCAI 2011. LNCS, vol. 6892, pp. 639–646. Springer, Heidelberg: (2011). 10.1007/978-3-642-23629-7_78 [DOI] [Google Scholar]
- 5.Gooya A, et al. : GLISTR: glioma image segmentation and registration. IEEE TMI 31(10), 1941–1954 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bakas S, et al. : GLISTRboost: combining multimodal MRI segmentation, registration, and biophysical tumor growth modeling with gradient boosting machines for glioma segmentation In: Crimi A, Menze B, Maier O, Reyes M, Handels H (eds.) BrainLes 2015. LNCS, vol. 9556, pp. 144–155. Springer, Cham: (2016). 10.1007/978-3-319-30858-6_13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kwon D, Niethammer M, Akbari H, Bilello M, Davatzikos C, Pohl KM: PORTR: pre-operative and post-recurrence brain tumor registration. IEEE TMI 33(3), 651–667 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu X, Niethammer M, Kwitt R, Singh N, McCormick M, Aylward S: Low-rank atlas image analyses in the presence of pathologies. IEEE TMI 34(12), 2583–2591 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yang X, Han X, Park E, Aylward S, Kwitt R, Niethammer M: Registration of pathological images In: Tsaftaris SA, Gooya A, Frangi AF, Prince JL (eds.) SASHIMI 2016. LNCS, vol. 9968, pp. 97–107. Springer, Cham: (2016). 10.1007/978-3-319-46630-9_10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Han X, Yang X, Aylward S, Kwitt R, Niethammer M: Efficient registration of pathological images: a joint PCA/image-reconstruction approach. In: ISBI (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kwon D, Zeng K, Bilello M, Davatzikos C: Estimating patient specific templates for pre-operative and follow-up brain tumor registration In: Navab N, Hornegger J, Wells WM, Frangi AF (eds.) MICCAI 2015. LNCS, vol. 9350, pp. 222–229. Springer, Cham: (2015). 10.1007/978-3-319-24571-3_27 [DOI] [Google Scholar]
- 12.Rudin LI, Osher S, Fatemi E: Nonlinear total variation based noise removal algorithms. Phys. D: Nonlinear Phenom. 60(1–4), 259–268 (1992) [Google Scholar]
- 13.Osher S, Burger M, Goldfarb D, Xu J, Yin W: An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 4(2), 460–489 (2005) [Google Scholar]
- 14.Marcus DS, Wang TH, Parker J, Csernansky JG, Morris JC, Buckner RL: Open access series of imaging studies (OASIS): cross-sectional MRI data in young, middle aged, nondemented, and demented older adults. J. Cogn. Neurosci. 19(9), 1498–1507 (2007) [DOI] [PubMed] [Google Scholar]
- 15.Modat M, et al. : Fast free-form deformation using graphics processing units. Com-put. Methods Programs Biomed. 98(3), 278–284 (2010) [DOI] [PubMed] [Google Scholar]
- 16.Modat M, Cash DM, Daga P, Winston GP, Duncan JS, Ourselin S: Global image registration using a symmetric block-matching approach. J. Med. Imaging 1(2), 024003 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Avants BB, Epstein CL, Grossman M, Gee JC: Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 12(1), 26–41 (2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ou Y, Sotiras A, Paragios N, Davatzikos C: Dramms: deformable registration via attribute matching and mutual-saliency weighting. Med. Image Anal. 15(4), 622–639 (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Avants BB, Tustison N, Song G: Advanced normalization tools (ANTS). Insight J. 2, 1–35 (2009) [Google Scholar]


