MICROVASCULAR NETWORKS WITH UNIFORM FLOW

Abstract

Within animals, oxygen exchange occurs within vascular transport networks containing potentially billions of microvessels that are distributed throughout the body. By comparison, large blood vessels are theorized to minimize transport costs, leading to tree-like networks that satisfy Murray’s law. We know very little about the principles underlying the organization of healthy micro-vascular networks. Indeed capillary networks must also perfuse tissues with oxygen, and efficient perfusion may be incompatible with minimization of transport costs. While networks that minimize transport costs have been well-studied, other optimization principles have received much less scrutiny. In this work we derive the morphology of networks that uniformize blood flow distribution, inspired by the zebrafish trunk micro-vascular network. To find uniform flow networks, we devise a gradient descent algorithm able to optimize arbitrary differentiable objective functions on transport networks, while exactly respecting arbitrary differentiable constraint functions. We prove that in a class of networks that we call stackable, which includes a model capillary bed, the uniform flow network will have the same flow as a uniform conductance network, i.e. in which all edges have the same conductance. This result agrees with uniform flow capillary bed network found by the algorithm. We also show that the uniform flow completely explains the observed radii within the zebrafish trunk vasculature. In addition to deriving new results on optimization of uniform flow in micro-vascular networks, our algorithm provides a general method for testing hypotheses about possible optimization principles underlying real microvascular networks, including exposing tradeoffs between flow uniformity and transport cost.

1. Introduction.

The large vessels within animal ardiovascular networks are widely believed to be shaped primarily by the necessity of minimizing the cost of transport. This minimization leads to Murray’s law for the relationship between a vessel’s radius and the flow of blood through it, which has been verified in dog intestine microvasculature and plant bundle network [51, 35]. The idea that networks should be organized to optimize transport costs for given amount of material investment provides a powerful tool for understanding the organization of networks, and underpins use of CFD models to optimize vascular geometries in cardiac surgery [33], as well as studies explaining the scaling of metabolic needs with organism size [54, 19]

Work on cardiovascular network optimization has focused primarily on the largest vessels in the network. Do the same optimization principles and constraints apply for finer vessels – arterioles and capillaries? Indeed if we divide the cardiovascular network into levels, we can estimate the total dissipation within each level as the product of the pressure drop between the level and the next and the total volume of blood passing through all vessels in that level per unit time. Now since we expect the same volume blood to be cleared through every level of the network in its passage from the heart to the finest vessels of the network, pressure drops alone become a proxy for the relative dissipations occurring at different levels. In the pressure measurements summarized in guyton and Hall [21], we find the pressure drop from the arteriole level to the capillary level (~ 60 mmHg) accounts for half of the total drop from the heart to the capillary level (~ 120 mmHg).

Mathematical modeling of microvascular networks has illuminated how networks with statistically predictable properties may emerge from the growth of vessels following rules for oxygen taxis and self avoidance [28, 23], the disconnection and reconnection of capillaries [40], and the remodeling of small vessels in response to the blood flows they carry [10]. However, despite the success of these mechanistic models for network formation, there are, to our knowledge, no works that have identified physical principles that may explain microvascular network organization and vessel geometries in the same way that Murray’s law describes the largest vessels within the network. For example, while Hu and Cai [22] have hypothesized that capillary networks minimize transport costs, we are aware of no data that shows that principles of dissipation minimization extend to these vessels. Indeed microvascular networks typically contain abundant loops [7, 55, 5, 52] (also see Fig. 1), but minimally dissipative networks, when subject to constant loads, can be proven to never contain loops [17, 8], at least when supplying steady flows of blood. Hence, the minimization of dissipation alone can not explain organization in microvascular networks [20, 42]. Our study of zebrafish trunk vasculature suggests that blood flows are uniformly distributed among fine vessels at the cost of transport efficiency, that is red blood cells are delivered at identical rates to the finest vessels of the trunk (i.e. the intersegmental vessels) [9]. Maintaining uniform flows across each vessel requires precise tuning of vessel radii. To show that tuning is needed we compare the real zebrafish trunk flow with flows in a ensemble of theoretical zebrafish trunk vasculatures. These theoretical vasculatures are created by simply permuting the radii measured in the real zebrafish trunk vessels. In all of 10, 000 theoretical trunk vasculatures, we found that the partitioning of blood flows between finest vessels, measured by the coefficient of variation (CV) of flow was less uniform than in the real zebrafish trunk (Fig. 2). The same analysis reveals a trade-off between transport efficiency and flow uniformity: All of the simulated networks had lower dissipation than the real network, and in general dissipation decreased as CV of flows increased. Thus, uniform flow is bought at the cost of decreased transport efficiency. Why might microvascular networks, like the zebrafish trunk, be adapted for uniform flow? Blood flow may serve as a proxy for oxygen perfusion; since red blood cells carry oxygen that then diffuses from the vessel into the tissue that surrounds it, uniform delivery of red blood cells to vessels may be an important precondition for uniform perfusion (but see Discussion). Indeed when we simulated oxygen perfusion in a model zerafish trunk in which every fine vessel was assigned the same radius, we found that oxygen entering the trunk from the blood was strongly concentrated around the fine vessels closest to the fish’s heart [9]. The evolutionary adaptation to vessels to create oxygen perfusion [31] may result in microvascular networks with optimally uniform blood flow, but a detailed comparison between networks with uniform blood flow with real microvascular networks is lacking. To determine whether optimization for uniform flow can explain the structure of real microvascular networks, we develop in this paper an algorithm for generating networks that optimize arbitrary functions of flow, going beyond previous works (summarized in Table 1) that have computed networks that optimize transport costs (and in the case of [26] resistance to damage).

Fig. 1.

Examples of complex microvascular networks and the corresponding model networks. (A) Capillary bed in salamander skin [36]. (B) Microvascular network of zebrafish 7.5 days post fertilization (dpf) embryo [25, 9].

Fig. 2.

Zebrafish trunk microvascular network (red square) optimizes uniform flow in fine vessels at a high transport cost, compared to untuned networks (blue dots). The untuned networks are obtained by randomly permuting the conductances of fine vessels in a real zebrafish trunk network [9]. The transport cost is characterized by dissipation [6, 1], and the flow variation is quantified by the coefficient of variation of flows in the fine vessels.

Table 1.

Comparison between previous works on optimal transport networks and the results presented in this work. Previous works focus on optimizing dissipation either alone or in combinations with damage resistance or flow fluctuations (first two rows). They constrain the network by imposing a fixed material cost of vessels. Our work agrees with previous work on the morphologies of minimally dissipative networks under material constraint (first row), but extends the classes of the target functions and constraints. Specifically we study uniform flow networks, under both material constraint and a Murray constraint that includes dissipation (last four rows).

Target functional	Constraint	Method
$\sum \frac{Q_{kl}^2}{{\kappa }_{kl}}$	$\sum {\kappa }_{kl}^{\gamma }$	local topological optimization [16], global optimization [6], structural adaptation [22], growth and structural adaptation [44], Section 3.1
$\sum \frac{Q_{kl}^2}{{\kappa }_{kl}}$ with damage and flow fluctuations	$\sum {\kappa }_{kl}^{\gamma }$	global optimization [26], fluctuating source [13]
$\sum \frac{1}{2}{Q}_{kl}^2$	$\sum {\kappa }_{kl}^{\gamma }$	Section 3.2
$\sum \frac{1}{2}{(Q_{kl}-\stackrel{‒}{Q})}^2$	$\sum {\kappa }_{kl}^{\gamma }$	Section 3.3
$\sum \frac{1}{2}{Q}_{kl}^2$	$\sum \left({\kappa }_{kl}^{\gamma }+a\frac{Q_{kl}^2}{{\kappa }_{kl}}\right)$	Section 3.4
$\sum \frac{1}{2}{(Q_{kl}-\stackrel{‒}{Q})}^2$	$\sum \left({\kappa }_{kl}^{\gamma }+a\frac{Q_{kl}^2}{{\kappa }_{kl}}\right)$	Section 3.4

To find the uniform flow networks we devise a gradient descent algorithm with Lagrange multipliers to tune the hydraulic conductances of vessels and derive uniform flow networks under fixed network topologies. At each step gradient descent algorithms calculate the optimal direction to perturb the variables in a system to optimize a target function, and approach the optimum after several small steps [11]. Lagrange multipliers are used widely to solve constrained optimization problems [39]. In our algorithm they are implemented to impose the laws of flow conservation in the network and to constrain the cost of maintaining the network. We use the algorithm to study uniform flow networks (1) on a model capillary bed consisting of a rectangular grid with single inflow (arteriole) and outflow (venule) (Fig. 1A), and (2) on a model of the zebrafish trunk that includes both main trunk vessel (dorsal aorta) and the fine (intersegmental) vessels that branch off from it (Fig. 1B).

In particular, we compare the morphologies of minimally dissipative and uniform flow networks. We find that uniform flow capillary beds contain loops that are not present in minimally dissipative networks. We are able to analytically show that, in a class of networks we call stackable, the blood flows in uniform flow networks agree with those in uniform conductance networks (See Section 3.2), hence they provably contain loops. Stackable networks include other popular models for capillary beds branching trees and honeycomb grids, as well as square grids. We show that, in zebrafish trunk topology, the real conductances of vessels are in almost exact accordance with the conductances required to create uniform flow. These results suggest that principle of uniform flow explains the zebrafish trunk network geometry. By contrast, minimization of dissipation produces networks with unrealistic morphologies. Our algorithm will then allow the uniform flow to be evaluated as an optimization principle for general microvascular networks.

To explore how uniform flow networks may yet be constrained by transport costs, we calculate networks in the zebrafish trunk while constraining both the total cost of the vessel material and the blood flow dissipation. When the relative importance of transport cost is gradually increased, we observed an abrupt change in both the flow uniformity and network morphology, resembling a phase transition: in particular, up until dissipation reaches a critical point, the optimal network is apparently unconstrained by dissipation. Thus even when a network is actually subject to multiple constraints, it may apparently be organized to ignore all but a subset of these constraints. Thus optimizing a single target function (e.g. dissipation) may be endowed with surprising power to predict shapes of real networks that are, in reality, targeting multiple functions [38].

The rest of this paper is organized as follows: In Section 2.1 we introduce the mathematical notations for describing microvascular networks. In Section 2.2 we describe a gradient descent algorithm to find general optimal networks. In Sections 2.3 - 2.7 we write down the detailed formulation of the algorithm when finding minimally dissipative and uniform flow networks under different topologies and constraints. In Section 3.1 we use the algorithm to calculate minimally dissipative networks and show that they agree with previous work. In Section 3.2 we compare minimally dissipative and uniform flow networks on the capillary bed model (a square grid). In Section 3.3 we extend our results to uniform flow zebrafish trunk networks, and show that the principle of uniform flow produces networks that match experimental data. In Section 3.4 we impose both material cost and dissipation as constraints on uniform flow networks, and describe a phase transition in network morphology that occurs as the relative weight of the two constraints is varied. Finally in Section 4 we summarize our work and discuss its consequences for microvascular network organization and for methods for finding optimal transport networks generally.

2. Methods.

2.1. Physical modeling and notation.

First we mathematically frame the problem of finding optimal networks for general network topology. Consider an undirected graph ($\mathcal{V}$ , $\mathcal{E}$ ) with V vertices k = 1,…, V. For any given 2 vertices k, l we write ⟨k, l⟩ = 1 if there is a edge linking k and l and ⟨k, l⟩ = 0 if k and l are not linked. Each edge in the network is assigned a conductance κ_kl; the flow Q_kl in the edge is then determined by Q_kl = (p_k – p_l)κ_kl, where p_k and p_l are respectively the pressures at the vertices k and l. In typical microvascular networks vessel diameters are on the order of 10 μm, and blood flow velocities are on the order of 1 mm/s, so the Reynolds number, which represents the relative importance of inertia to viscous stresses, is Re = UL/ν ≈ 4 × 10⁻³, using the viscosity of whole blood ν ≈ 2.74 mm²/s. Since Re ≪ 1 inertial effects may be neglected, and the conductances of individual vessels will be obtained by Hagen-Poiseuille’s law [1]:

$$\kappa =\frac{\pi r^4}{8\mu \ell }$$ (1)

where κ is the conductance, μ is the blood viscosity, ℓ is the vessel length, and r is the vessel radius. In ascribing a well-defined pressure to each vertex within the graph, and applying the Hagen-Poiseuille law to compute edge flows from pressures, we assume that there are unidirectional flows within each vessel, ignoring the entrance and exit effects that occur when vessels branch or merge [9]. In capillary networks hydraulic conductances might change with concentration of red blood cells, a physiological effect known as Fahraeus-Lindqvist effect [43], which can change our expression here. Although our method can be generalized to include this effect (see Discussion), we will use our default model (1) throughout this work.

The networks we consider consist of vertices and predescribed edges where conductance may be positive (or zero if required by the algorithm, in which case the vessel is pruned) along with two kinds of boundary conditions on vertices (Fig. 3). At any vertex in the network we can either impose Kirchoff’s first law (conservation of flux)

$$\sum _{l:\langle k,l\rangle =1}{Q}_{kl}=\sum _{l:\langle k,l\rangle =1}{k}_{kl}(p_k-p_l)=q_k\forall 1\le k\le V,$$ (2)

where q_k is the total flow of blood entering the network (or leaving it if q_k < 0) at vertex k, or we impose $p_k={\stackrel{‒}{p}}_k$ (i.e. pressure is specified). We say a vertex is in ${\mathcal{V}}_D$ (or is Dirichlet) if pressure is specified, or in ${\mathcal{V}}_N$ (is Neumann) if Kirchhoff’s first law is imposed (possibly with inflow or outflow). This system of V linear equations forms a discretized Poisson equation with Neumann and Dirichlet boundary conditions imposed on selected vertices, and the flow is uniquely solvable if and only if each connected component of the network (connected by edges with positive conductances) either has at least one Dirichlet vertex or ${\sum }_{k\in {\mathcal{V}}_N}{q}_k=0$ with sum restricted to the component [29, 8]. The uniform flow network has the flows on all edges being as uniform as possible, that is the flows κ_kl(p_k – p_l) on some subset of the edges are close to being identical (See Section 2.4 for a detailed discussion). However, to understand the tradeoffs between perfusion and other network objectives, we may also add e.g. total viscous dissipation as an additional cost. We therefore have the general goal of how to tune the conductances within the network to minimize arbitrary predetermined objective function f({p_k}, {κ_kl}), where {p_k} means the set of all p_k’s and {κ_kl} denotes the set of all κ_kl’s. Previous works (see Table 1) have shown how to generate networks that minimize the total viscous dissipation occurring within the network: $f(\{p_k\},\{{\kappa }_{kl}\})={\sum }_{k>l,\langle k,l\rangle =1}{\kappa }_{kl}{(p_k-p_l)}^2$ .

Fig. 3.

Transport network with the Dirichlet vertices ${\mathcal{V}}_D$ and Newmann vertices ${\mathcal{V}}_N$ . In our representation we imagine Dirichlet vertices connected to fluid reservoirs allowing pressure to be imposed, and Neumann vertices to syringe pumps, allowing inflows or outflows to be imposed [8]. Loops are shown in arrows.

This optimization is complicated by the coupling of the pressures {p_k} and conductances {κ_kl} through Equations (2). Since the relationship between {p_k} and {κ_kl} is holonomic, we may incorporate it into a functional via Lagrange multipliers. Lagrange multipliers are a widely used method to solve optimization problems when the variables are subject to holonomic constraints (i.e. must solve some differentiable equation). They allow us to treat the variables as if they were independent for the purpose of calculating partial derivatives, at the cost of introducing new auxillary variables – one for each constraint [11]. The functional that we want to minimize in this paper will take the form:

$$\begin{gathered} \mathrm{\Theta }=f(\{p_k\},\{{\kappa }_{kl}\})+\lambda \left[\sum _{k>l,\langle k,l\rangle =1}(a{\kappa }_{kl}{(p_k-p_l)}^2+{\kappa }_{kl}^{\gamma }{d}_{kl}^{1+\gamma })-K\right] \\ -\sum _k{\mu }_k\left(\sum _{l,\langle k,l\rangle =1}{\kappa }_{kl}(p_k-p_l)-q_k\right). \end{gathered}$$ (3)

which has V_N +1 Lagrange multipliers: a set $\{{\mu }_k\mid k\in {\mathcal{V}}_N\}$ enforcing Kirchoff’s first law on Neumann vertices (the set ${\mathcal{V}}_N$ with $\mid {\mathcal{V}}_N\mid =V_N$ ), and a single multiplier λ that constrains the amount of energy that the organism can invest in pushing blood through the network and in maintaining the vessels that make up the network. The transport constraint is made up of two terms: ∑κ_kl(p_k – p_l)² represents the total viscous dissipation within the network, while $\sum {\kappa }_{kl}^{\gamma }{d}_{kl}^{\gamma +1}$ represents the total cost of maintaining the network (the material constraint) [38, 6, 26], with d_kl being the vessel length. K is the total amount of material and dissipation to which the network should adhere. The exponent γ can be altered to embody different models for the cost of maintaining a network. In our default model (Equation (1)) conductance of an edge is proportional to the fourth power of its radius, so if the cost of maintaining a particular vessel is proportional to its surface area (and thus to its radius), then we expect γ = 1/4, while if the cost is proportional to volume then γ = 1/2. In general we need γ < 1 to produce well posed optimization problems (otherwise, the cost of building a vessel can be indefinitely reduced by subdividing the vessel into finer parallel vessels). We initially adopt the same material cost function definition as was used in previous work, i.e. a = 0 [26, 6], but in the latter part of the paper we will incorporate a parameter a > 0 that represents the relative importance of network maintenance and dissipation to the cost of maintaining the network. When presenting optimal networks, we will discuss the effect of varying a (as well as asymptotic limits in which a → 0) upon the network geometry. Since Murray’s work on dissipation-minimizing networks [38, 37] is equivalent to minimizing the constraint function [8], we will adopt the shorthand of calling the network cost term the Murray constraint.

Table 1 gives a systematic description of previous work on minimizing functionals across networks, as well as outlining the new results that will be presented here on the optimization of (3).

2.2. A gradient descent method with extended Lagrange multipliers.

At any local minimum of Θ, each of the partial derivatives of (3) must vanish. In order to locate such points, we adopt a gradient descent approach, in which κ_kl are treated as adiabatically changing variables. That is: $\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}$ is calculated, and an optimal perturbation of the form $\delta {\kappa }_{kl}=-\alpha \frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}$ is applied to ensure Θ decreases each time the conductances in the network are updated. At the same time, the other variables in the system, namely {p_k, μ_k, λ}, are assumed to vary much more rapidly, to remain at a local equilibrium, so that:

$$\frac{\partial \mathrm{\Theta }}{\partial p_k}=\frac{\partial \mathrm{\Theta }}{\partial {\mu }_k}=\frac{\partial \mathrm{\Theta }}{\partial \lambda }=0.$$ (4)

Our ability to perform gradient descent therefore hinges on our ability to solve the system of 2V_N + 1 equations (4) for each set of conductances {κ_kl} that the network passes through on its way to the local minimum. Fortunately it turns out that for general target functions f only one nonlinear equation in a single unknown variable needs to be solved for to solve all of the conditions (4); the other equations are linear and can be solved with relatively low computational cost.

Because we will consider multiple variants of the Murray constraint, in what follows we will write the summand that enforces the Murray constraint in the general form: λg({p_k}, {κ_kl}). Then the condition that $\frac{\partial \mathrm{\Theta }}{\partial {\mu }_k}=0$ , $k\in {\mathcal{V}}_N$ , merely enforces the system of mass conservation statements at each Neumann-vertex in the network (2). These equations represent a discretized form of the Poisson equation and can be solved by inverting a sparse V_N × V_N matrix with O(E, V_N) entries [29]. That is, we write:

$$D_p=f$$ (5)

where f_k = q_k is the prescribed inflow at Neumann vertices and $f_k={\tilde{p}}_k$ , the prescribed pressure at Dirichlet vertices. –D is a form of graph Laplacian:

$$D_{kl}\doteq \{\begin{array}{cc}\sum _{l,\langle k,l\rangle =1}{\kappa }_{kl}\hfill & k=l,k\notin {\mathcal{V}}_D\hfill \\ -{\kappa }_{kl}\hfill & \langle k,l\rangle =1,k\notin {\mathcal{V}}_D\hfill \\ {\kappa }^{(1)}\hfill & k=l,k\in {\mathcal{V}}_D\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (6)

where κ⁽¹⁾ = 1. (For any κ⁽¹⁾ ≠ 0 D is full rank; we will make use of other positive constant values for κ⁽¹⁾ later.)

To solve for {μ_k}, we consider the system of equations $\frac{\partial \mathrm{\Theta }}{\partial p_k}=0$ , $k\in {\mathcal{V}}_N$ :

$$0=\left(\frac{\partial f}{\partial p_k}+\lambda \frac{\partial g}{\partial p_k}\right)-\sum _{l,\langle k,l\rangle =1}({\mu }_k-{\mu }_l){\kappa }_{kl}.$$ (7)

If λ, {p_k} and {κ_kl} are all known then these equations again take the form of a discrete Poisson equation, however, just as with the solution of the pressure equation, these equations themselves do not admit unique solutions unless a reference value of μ_k is established. If ${\mathcal{V}}_D\ne \varphi$, i.e. if pressure is specified at least one vertex within ($\mathcal{V}$ , E), then ${\mu }_k=0\forall k\in {\mathcal{V}}_D$ and Eqns. (7) admit a unique solution; otherwise the μ_k’s are determined up to a constant (see Appendix A). For some forms of target function f and constraint function g, we will show that μ_k’s for the minimizer are directly related to the pressures, with no need to solve the Poisson equation by a separate matrix inversion.

However, to use Equation (7) to solve for μ_k it is still necessary to know the Lagrange multiplier that enforces the Murray constraint (i.e. λ). The simplest way to derive λ is to dictate that the variational of the constraint function should vanish when κ_kl is updated, since the constraint function should remain constant under changes in conductances, i.e.:

$$0=\sum _{k\notin {\mathcal{V}}_D}\frac{\partial g}{\partial p_k}\delta p_k+\sum _{k>l,\langle k,l\rangle =1}\frac{\partial g}{\partial {\kappa }_{kl}}\delta {\kappa }_{kl}$$ (8)

(we set δ_pk = 0 if $k\in {\mathcal{V}}_D$ ) where

$$\delta {\kappa }_{kl}=-\alpha \frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}=-\alpha \left(\frac{\partial f}{\partial {\kappa }_{kl}}+\lambda \frac{\partial g}{\partial {\kappa }_{kl}}-{\kappa }_{kl}({\mu }_k-{\mu }_l)(p_k-p_l)\right).$$ (9)

At this point in our calculation {δ_pk} and {μ_k} are undetermined. The Lagrange multipliers {μ_k} can be solved in terms of the still unknown λ from (7) (see Appendix A). The {μ_k} are linear functions of λ since (7) is a linear system. To obtain δ_pk for each $k\in {\mathcal{V}}_N$ we calculate the variational in Kirchhoff’s first law:

$$\sum _{l,\langle l,k\rangle =1}\delta {\kappa }_{kl}(p_k-p_l)+{\kappa }_{kl}(\delta p_k-\delta p_l)=0.$$ (10)

When written in matrix form, the matrix multiplying {δ_pk} is again the negative of the graph Laplacian, –D. Thus {δ_pk} can be solved in terms of λ so long as the original matrix system is solvable for {p_k}. Since {μ_k} are linear in λ, {δ_pk} are also linear in λ, which implies that the right hand side of Equation (8) is linear in λ. Therefore λ can be solved in closed form from Equation (8), and the optimal variation δκ_kl can be determined from equation (9).

With {p_k}, {μ_k}, and λ solvable given {κ_kl} we can perform gradient descent using Equation (9) and numerically approach a minimizer. However our descent method has the following limitations: 1. For finite step sizes α, conductances may drop below 0 when perturbed according to Equation (9). 2. The method only conserves the Murray function up to terms of O(δκ).

To avoid negative conductances we truncate at a small positive value ϵ at each step, i.e. set:

$${\kappa }_{kl}^{(n+\frac{1}{2})}=\max \{{\kappa }_{kl}^{(n)}-\alpha \frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}},ϵ\}.$$ (11)

To ensure that the constraint is exactly obeyed we then project the conductances $\{{\kappa }_{kl}^{(n+\frac{1}{2})}\}$ onto the constraint manifold g({p_k}, {κ_kl}) = 0, via a projection function:

$${\kappa }_{kl}^{(n+1)}=h({\kappa }_{kl}^{(n+\frac{1}{2})})\forall \langle k,l\rangle =1,k>l.$$ (12)

Throughout this work we consider three possible projection functions: One choice is to project according to the normal of the constraint surface:

$${\kappa }_{kl}^{(n+1)}={\kappa }_{kl}^{(n+\frac{1}{2})}-\beta \frac{\partial g}{\partial {\kappa }_{kl}}(\{p_k^{(n+\frac{1}{2})}\},\{{\kappa }_{kl}^{(n+\frac{1}{2})}\}),\forall \langle k,l\rangle =1,k>l$$ (13)

The value of β must be chosen numerically to ensure that $g(\{p_k^{(n+1)}\},\{{\kappa }_{kl}^{(n+1)}\})=0$ exactly. This entails recomputing the pressure distribution $\{p_k^{(n+1)}\}$ for each β value, and secant search on β to obtain the root. Another approach we have followed is varying the parameter λ. This method has comparable complexity to projection on $\{{\kappa }_{kl}^{(n+\frac{1}{2})}\}$ ; since the {μ_k} depend linearly on λ via Equation (7), $\{{\kappa }_{kl}^{(n+1)}\}$ depends linearly on the parameter λ. However, just as with the projection method, we must still recompute the $\{p_k^{(n+1)}\}$ for each trial set of $\{{\kappa }_{kl}^{(n+1)}\}$ . Moreover, for some target functions f or constraint functions g, it is difficult to derive closed-form expressions for λ (i.e. to calculate the partial derivatives $\frac{\partial f}{\partial p_k}$ and $\frac{\partial g}{\partial p_k}$ ). In this case λ may only be computed numerically, by solving $g(\{p_k^{(n+1)}(\lambda )\},\{{\kappa }_{kl}^{(n+1)}(\lambda )\})=0$ . A third approach that we have adopted is to simply scale the conductances:

$${\kappa }_{kl}^{(n+1)}=\beta {\kappa }_{kl}^{(n+\frac{1}{2})},\forall \langle k,l\rangle =1,k>l$$ (14)

where β is chosen to satisfy the Murray constraint. This method produces theoretically suboptimal corrections on the conductances, but it is typically easy to compute a value of β that satisfies the Murray constraint. In particular, under certain boundary conditions, e.g. $p_k=\stackrel{‒}{p}$ , $\forall k\in {\mathcal{V}}_D$ within each connected component of the network (meaning that all pressure vertices within a single connected component have the same imposed pressures, which is trivially true if there is only one Dirichlet vertex in each connected subcomponent of the graph), a rescaling of the conductances throughout the network leaves the fluxes on each edge unaffected. For a uniform flow network, this rescaling affects the constraint function g, but not the target function f.

2.3. Calculating minimally dissipative networks.

To calculate minimally dissipative networks we set the target function to be the dissipation ∑_{⟨k,l⟩=1, k>l} κ_kl(p_k – p_l)² and the constraint to be the total amount of material. Thus the function to minimize becomes:

$$\mathrm{\Theta }=\sum _{\langle k,l\rangle =1,k>l}{\kappa }_{kl}{(p_k-p_l)}^2+\lambda (\sum _{\langle k,l\rangle =1,k>l}{\kappa }_{kl}^{\gamma }-K^{\gamma })-\sum _{k\notin {\mathcal{V}}_D}{\mu }_k\left(\sum _{l,\langle k,l\rangle =1}{\kappa }_{kl}(p_k-p_l)-q_k\right).$$ (15)

Here we ignore d_kl since we assume all the vessels have the same length which may be scaled to 1 by choice of units, but different vessel lengths can be readily incorporated by adding d_kl back in the following equations.

The equations for adiabatic variation of p_k and μ_k are derived from

$$\frac{\partial \mathrm{\Theta }}{\partial p_k}=\sum _{l,\langle k,l\rangle =1}2{\kappa }_{kl}(p_k-p_l)-\sum _{l,\langle k,l\rangle =1}{\kappa }_{kl}({\mu }_k-{\mu }_l),k\notin {\mathcal{V}}_D$$ (16)

and the fixed pressure boundary condition on pressure vertices allows us to specify that:

$${\mu }_i=0\forall i\in {\mathcal{V}}_D$$ (17)

The μ_k are therefore solving a variant of the Kirchhoff flux conservation equations:

$$D\mu =2Dp$$ (18)

with D as defined in Equation 6.

This system can be solved for μ_k under the same conditions as the presure equations being solvable (see Appendix A). In particular if, as in the network topologies we study in this work, the only pressure boundary conditions imposed at vertices in ${\mathcal{V}}_D$ are of the form p = 0, then μ_k = 2p_k, $\forall k\in \mathcal{V}$ , i.e. μ_k’s represent the pressures. Now we calculate the derivatives of Θ with respect to the conductances:

$$\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}={(p_k-p_l)}^2+\lambda \gamma {\kappa }_{kl}^{\gamma -1}-({\mu }_k-{\mu }_l)(p_k-p_l)=\lambda \gamma {\kappa }_{kl}^{\gamma -1}-{(p_k-p_l)}^2.$$ (19)

In general we determine λ from Equations (8,9,10). However the constraint function g is independent of {p_k} in this case, so Equation (8) becomes

$$0=\sum _{k>l,\langle k,l\rangle =1}\frac{\partial g}{\partial {\kappa }_{kl}}\delta {\kappa }_{kl}$$ (20)

and we can solve λ directly in terms of {p_k}, {κ_kl}:

$$\lambda =\frac{\sum _{\langle k,l\rangle =1,k>l}{\kappa }_{kl}^{\gamma -1}{(p_k-p_l)}^2}{\sum _{\langle k,l\rangle =1,k>l}\gamma {\kappa }_{kl}^{2\gamma -2}}$$ (21)

p

As described in Section 2.2 we project {κ_kl} along $\frac{\partial g}{\partial {\kappa }_{kl}}=\gamma {\kappa }_{kl}^{\gamma -1}$ after each step of the algorithm. At each step of the algorithm, we solve for the pressures p_k from the conductances {κ_kl}, then the μ_k, and then descend according to Eqn. (19). Analyzing minimal dissipation on networks allows us to compare the performance of the algorithm described in this paper with previous work [6, 26] (See Section 3.1).

2.4. Calculating microvascular networks with uniform flow.

We now turn to other target functions that have not been extensively studied. At the level of micro-vessels it is likely that uniform flow rather than transport efficiency is the dominant principle underlying network organization, as shown in the comparison between the zebrafish trunk network with its untuned counterparts (Fig. 2). We frame this question more generally, i.e. ask what organization of vessels achieves a given amount of flow $\stackrel{‒}{Q}$ on all edges or equivalently, how the flow variation

$$f(\{p_k\},\{{\kappa }_{kl}\})=\sum _{\langle k,l\rangle =1,k>l}\frac{1}{2}{(Q_{kl}-\stackrel{‒}{Q})}^2$$ (22)

may be minimized by optimal choice of conductances κ_kl

To simplify the target function we expand the function f and abandon the constant term:

$$f(\{p_k\},\{{\kappa }_{kl}\})=\sum _{k>l,\langle k,l\rangle =1}(\frac{1}{2}{Q}_{kl}^2-\stackrel{‒}{Q}{Q}_{kl}).$$ (23)

Under the assumption that the total flow on all edges is conserved, i.e.:

$$\sum _{\langle k,l\rangle =1,k>l}{Q}_{kl}=C$$ (24)

the function f can be reduced to

$$f(\{p_k\},\{{\kappa }_{k,l}\})=\sum _{\langle k,l\rangle =1,k>l}\frac{1}{2}{Q}_{kl}^2$$ (25)

by ignoring constants. The assumption (24) is valid in networks provided that the network may be divided into levels: that is, a series of control surfaces may be constructed between source (inflow to the network) and sink (outflow from the network), with each edge intersected by exactly one control surface and each path from source to sink intersecting all control surfaces (Fig. 4). We call networks with this property stackable. The stackability of a network depends both on its geometry and the positions of sources and sinks: a honeycomb grid is also stackable when source and sink are arranged across the diameter of the network, but the square-grid network is not stackable if the sink were on the bottom instead of the right corner. Then since the total flow across each control surface is the same, the total flow over all network edges is ∑_{k>l,⟨k,l⟩=1} Q_kl = SF where F is the total sink strength and S is the number of control surfaces. Both symmetric branching trees and quadrilateral grids (such as the one shown in Fig. 4) are examples of stackable networks, and both can be used as simplified models of microvascular transport networks [23].

Fig. 4.

A quadrilateral grid (black) can be divided using a set of non-intersecting control surfaces (red dashed lines) such that each edge in the grid is intersected by exactly one control surface.

For the model capillary bed network we have only one pressure vertex, which means that a multiplicative scaling in all the conductances does not affect the flow. Therefore solving unconstrained optimal networks is equivalent to solving those with material constraints. Without any constraint the function to be optimized can now be written as

$$\mathrm{\Theta }=\sum _{\langle k,l\rangle =1,k>l}\frac{1}{2}{(p_k-p_l)}^2{\kappa }_{kl}^2-\sum _{k\in {\mathcal{V}}_D}{\mu }_k\left(\sum _{l,\langle k,l\rangle =1,}{\kappa }_{kl}(p_k-p_l)-q_k\right).$$ (26)

To do the gradient descent we calculate

$$\frac{\partial \mathrm{\Theta }}{\partial p_k}=\sum _{l,\langle k,l\rangle =1}{\kappa }_{kl}^2(p_k-p_l)-\sum _{l,\langle k,l\rangle =1}({\mu }_k-{\mu }_l){\kappa }_{kl},k\notin {\mathcal{V}}_D$$ (27)

$$\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}={\kappa }_{kl}{(p_k-p_l)}^2-({\mu }_k-{\mu }_l)(p_k-p_l).$$ (28)

At each step we can solve for μ_k by setting $\frac{\partial \mathrm{\Theta }}{\partial p_k}=0$ in Eqn. (27), along with μ_k = 0, $k\in {\mathcal{V}}_D$ , and we can calculate the gradient from Eqn. (28). Note that here we have neither Murray nor material constraint, so a numerical projection is not required to ensure that the constraint is being exactly met, and the network can be obtained by repeating the procedure until convergence (See Section 3.2).

2.5. Calculating embryonic zebrafish trunk vasculatures with uniform flow.

To compare putative network optimization principles on the zebrafish trunk vasculature, we start by identifying our model for the trunk network. Blood flows into the trunk of the zebrafish from the heart through the dorsal aorta and then passes into minute vessels called intersegmental (Se) vessels. Blood then returns to the heart via the cardinal vein. These vessels are arranged just like rungs (Se) and parallels (cardinal vein and dorsal aorta) of a ladder (Fig. 8A). Most gas exchange in the network is assumed to occur in the Se vessels. As the zebrafish develops further minute vessels form between the Se vessels, converting the trunk into a dense reticulated network [25]. We focus on the mechanisms underlying flow distribution in the main fine vessels. Since the zebrafish trunk network is symmetric, we can consider only half of the network consisting of the aorta and intersegmental arteries, designated by vertices v₁, …, v_2n+1 and edges e₁, …, e_2n with n being the number of Se vessels. Since this topology does not satisfy the assumption (24) we have to consider the full uniform flow target function:

$$f(\{p_k\},\{{\kappa }_{kl}\})=\sum _{i=1}^n\frac{1}{2}{(Q_{2i}-\stackrel{‒}{Q})}^2,$$ (29)

where $\stackrel{‒}{Q}$ is a predetermined flow for all the capillaries (in the following arguments edge-defined quantities such as Q_i are indexed with the edges, and vertex-defined quantities such as p_i are indexed with the vertices). Using this indexing scheme, the function to be optimized becomes:

$$\begin{gathered} \mathrm{\Theta }=\sum _{i=1}^n\frac{1}{2}{\kappa }_{2i}^2{p}_i^2-\sum _{i=1}^n\stackrel{‒}{Q}{\kappa }_{2i}{p}_i-\sum _{i=2}^{n-1}{\mu }_i[{\kappa }_{2i-3}(p_i-p_{i-1})+{\kappa }_{2i-1}(p_i-p_{i+1})+p_i{\kappa }_{2i}] \\ -{\mu }_1[{\kappa }_1(p_1-p_2)+p_1{\kappa }_2-F]-{\mu }_n[{\kappa }_{2n-3}(p_n-p_{n-1})+p_n{\kappa }_{2n-1}+{\kappa }_{2n}{p}_n]. \end{gathered}$$ (30)

Fig. 8.

Minimal dissipative networks for zebrafish trunk vasculature do not explain observed morphology. (A) The zebrafish trunk vasculature can be simplified into a ladder network with arterial (red) and venous parts (blue). The edges e₁, e₃, …, e_2n-1 are aorta segments and e₂, e₄, …, e_2n are capillaries. We use n = 12 in all the following calculations on zebrafish network. (B) The optimal dissipative network with $\gamma =\frac{1}{2}$ and fixed inflow does not correctly describe the zebrafish trunk network since all the conductances are concentrated on the first capillary (red circle), and the whole aorta is deleted (blue cross). In this calculation we imposed a fixed inflow on v₁ and fixed zero pressure on v_n+1,…,v_2n+1. We started with κ = 20 for aorta segments and κ = 1 for capillaries to reflect the difference in radii in real zebrafish. This initial condition is used for all the following simulations. (C) The optimal dissipative network with $\gamma =\frac{1}{2}$ and fixed outflows has a tapering aorta (blue cross) and capillaries with the same conductances (red circle). We imposed zero pressure on v₁ and fixed outflows on v_n+1, …,v_2n+1 with v_n+1 taking half of the total outflow (i.e. $\frac{1}{2}$ F) and v_n+2,…, v_2n+1 evenly dividing the other half of F. (D) However the pressures on the ends of capillaries are decreasing to maintain uniform flows among capillaries, which is non-physical since this means that the blood flows toward the tail in the principal cardinal vein, due to the aorta-vein symmetry.

Just as in Section 2.4 we do not need to introduce a Lagrange multiplier enforcing the material constraint because the target function only depends on flows, and we can scale all conductances to realize any material constraint without affecting the target function. For performing gradient descent method on this function we calculate the partial derivatives of Θ:

$$\frac{\partial \mathrm{\Theta }}{\partial p_i}=\{\begin{array}{cc}{\kappa }_{2i}^2{p}_i-\stackrel{‒}{Q}{\kappa }_{2i}-({\kappa }_{2i-1}+{\kappa }_{2i-3}+{\kappa }_{2i}){\mu }_i+{\kappa }_{2i-1}{\mu }_{i+1}+{\kappa }_{2i-3}{\mu }_{i-1}\hfill & i\ne 1,n\hfill \\ {\kappa }_2^2{p}_1-\stackrel{‒}{Q}{\kappa }_2-({\kappa }_1+{\kappa }_2){\mu }_1+{\mu }_2{\kappa }_1\hfill & i=1\hfill \\ {\kappa }_{2n}^2{p}_n-\stackrel{‒}{Q}{\kappa }_{2n}-({\kappa }_{2n-3}+{\kappa }_{2n-1}+{\kappa }_{2n}){\mu }_n+{\kappa }_{2n-3}{\mu }_{n-1}\hfill & i=n\hfill \end{array}\phantom{\}}.$$ (31)

$$\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_i}=\{\begin{array}{cc}{\kappa }_i{p}_{i∕2}^2-\stackrel{‒}{Q}{p}_{i∕2}-{\mu }_{i∕2}{p}_{i∕2}\hfill & i\mid 2=0\hfill \\ -({\mu }_{\frac{i+1}{2}}-{\mu }_{\frac{i+3}{2}})(p_{\frac{i+1}{2}}-p_{\frac{i+3}{2}})\hfill & i\mid 2=1,i\ne 2n-1\hfill \\ -{\mu }_n{p}_n\hfill & i=2n-1\hfill \end{array}\phantom{\}}.$$ (32)

Then we impose the physical boundary conditions, i.e. fixed inflow into the network and zero pressure on the ends of the main aorta and the capillaries, and perform gradient descent to find the optimal network (See Section 3.3).

Since no constraint is imposed on the uniform flow zebrafish trunk network the explicit relation between vessel radius and conductance does not need to be specified (see Section 2.1). Therefore when we compare the uniform flow network to experimental data in Section 3.3 we can assume that, instead of the default model (1), the occlusive effect of red blood cells contribute to the effective vessel conductance [9].

2.6. Calculating uniform flow network on capillary beds under Murray’s constraint.

So far we have followed previous work [6, 26] by calculating all of our optimal networks under constraints on the total material (or without constraints if the target function does not involve conductances). However both material investment and transport costs (i.e. dissipation) may contribute to the total cost of a particular network. We modify our cost function, g, to include both costs. In this case $g(\{p_k\},\{{\kappa }_{kl}\})=\sum (a{\kappa }_{kl}{(p_k-p_l)}^2+{\kappa }_{kl}^{\gamma })-K$ depends on both pressure and conductance, and the full mechanism for keeping g constant during the gradient descent needs to be used. Specifically now we are minimizing the function

$$\mathrm{\Theta }=\sum _{\langle k,l\rangle =1,k>l}\frac{1}{2}{Q}_{kl}^2+\lambda \left(\sum _{\langle k,l\rangle =1,k>l}(a{\kappa }_{kl}{(p_k-p_l)}^2+{\kappa }_{kl}^{\gamma })-K\right)-\sum _{k\in {\mathcal{V}}_N}{\mu }_k\left(\sum _{l,\langle k,l\rangle =1}{\kappa }_{kl}(p_k-p_l)-q_k\right)$$ (33)

with $\gamma =\frac{1}{2}$ and a > 0. To calculate the optimal network by this method we need an explicit formula for λ.

We introduce several notations to be used later. Suppose {b_ij} is a set of quantities defined on the edges of the network. For any real constant c we define the matrix for the graph Laplacian with specified boundary conditions as

$$M_b^{(c)}=\{\begin{array}{cc}\sum _{l,\langle k,l\rangle =1}{b}_{kl}\hfill & k=l,k\notin {\mathcal{V}}_D\hfill \\ -b_{kl}\hfill & \langle k,l\rangle =1\hfill \\ c\hfill & k=l,k\in {\mathcal{V}}_D\hfill \\ 0\hfill & \mathit{\text{otherwise}}\hfill \end{array}\phantom{\}}.$$ (34)

We also abbreviate $M_b=M_b^{(1)}$ . In the notation of Equation (6) D = M_κ. We define D⁽ⁿ⁾ = M_κⁿ for notational convenience. For a quantity v that is defined on the vertices of the network (such as pressure) we define the graph difference vector ${\nabla }_v\in {\mathbb{R}}^E$ as

$$\nabla v_{kl}=v_k-v_l(k,l)\in \mathcal{E},$$ (35)

where ε denotes the set of ordered pairs of edges so that each edge only appears once in ε. Now we can derive explicit formulas for λ and δ_κ. From $\frac{\partial \mathrm{\Theta }}{\partial p_k}=0$ we obtain μ = D⁻¹D⁽²⁾p + 2λap (recall here we have $f={\sum }_{k>l,\langle k,l\rangle =1}\frac{1}{2}{\kappa }_{kl}^2{(p_k-p_l)}^2$ , $g={\sum }_{k>l,\langle k,l\rangle =1}a{\kappa }_{kl}{(p_k-p_l)}^2+{\kappa }_{kl}^{\gamma }-K^{\gamma })$ , and so:

$$\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}=\lambda [\gamma {\kappa }_{kl}^{\gamma -1}-a{(\nabla p_{kl})}^2]+{\kappa }_{kl}{(\nabla p_{kl})}^2-\nabla (D^{-1}{D}^{(2)}p{)}_{kl}\nabla p_{kl}.$$ (36)

We determine λ from the variational:

$$\begin{gathered} 0=dg=\sum _{k>l,\langle k,l\rangle =1}\gamma {\kappa }_{kl}^{\gamma -1}\delta {\kappa }_{kl}+a\delta {\kappa }_{kl}\nabla p_{kl}^2+2a{\kappa }_{kl}\nabla \delta p_{kl}\nabla p_{kl} \\ =\sum _{k>l,\langle k,l\rangle =1}-\alpha (\gamma {\kappa }_{kl}^{\gamma -1}+a\nabla p_{kl}^2)\left\{\lambda [\gamma {\kappa }_{kl}^{\gamma -1}-a\nabla p_{kl}^2] \\ +{\kappa }_{kl}\nabla p_{kl}^2-\nabla {(D^{-1}{D}^{(2)}p)}_{kl}\nabla p_{kl}\right\}+2a{\kappa }_{kl}\nabla \delta p_{kl}\nabla p_{kl}. \end{gathered}$$ (37)

This formula depends on δ_p; the change in p produced by the change κ ↦ κ+δ_κ. If we assume $p_i=0\forall i\in {\mathcal{V}}_D$ we can write Equation (10) in matrix form as

$$M_{\delta \kappa }p+D\delta p=0$$ (38)

so

$$\delta p=-D^{-1}{M}_{\delta \kappa }p.$$ (39)

(Equation (38)) can be modified by adding a non-zero vector on the right hand side, if inhomogeneous pressure boundary conditions are applied.) Thus if we define auxiliary variables: β ≐ γκ^γ−1 – a∇p², X ≐ κ∇p² – ∇(D⁻¹ D⁽²⁾p)∇p, so that δκ = –α(λβ + X), then:

$$\begin{gathered} 0=-\alpha \left\{\lambda \sum _{k>l,\langle k,l\rangle =1}(\gamma {\kappa }_{kl}^{\gamma -1}+a\nabla p_{kl}^2){\beta }_{kl}+\sum _{k>l,\langle k,l\rangle =1}(\gamma {\kappa }_{kl}^{\gamma -1}+a\nabla p_{kl}^2){\chi }_{kl}\right\} \\ -2a\sum _{k>l,\langle k,l\rangle =1}{\kappa }_{kl}\nabla p_{kl}\nabla {(D^{-1}{M}_{-\alpha \{\lambda \beta +\chi \}}p)}_{kl}, \\ 0=\lambda \sum _{k>l,\langle k,l\rangle =1}{\gamma }^2{\kappa }_{kl}^{2\gamma -2}-a^2\nabla p_{kl}^4-2a{\kappa }_{kl}\nabla p_{kl}\nabla {(D^{-1}{M}_{\beta }^{(0)}p)}_{kl} \\ +\sum _{k>l,\langle k,l\rangle =1}(\gamma {\kappa }_{kl}^{\gamma -1}+a\nabla p_{kl}^2){\chi }_{kl}-2a{\kappa }_{kl}\nabla p_{kl}\nabla {(D^{-1}{M}_{\chi }^{(-\frac{1}{\alpha })}p)}_{kl.} \end{gathered}$$ (40)

Finally we can write down the formula for λ as

$$\lambda =\frac{-\sum _{k>l,\langle k,l\rangle =1}(\gamma {\kappa }_{kl}^{\gamma -1}+a\nabla p_{kl}^2){\chi }_{kl}-2a{\kappa }_{kl}\nabla p_{kl}\nabla {(D^{-1}{M}_{\chi }^{(-\frac{1}{\alpha })}p)}_{kl}}{\sum _{k>l,\langle k,l\rangle =1}{\gamma }^2{\kappa }_{kl}^{2\gamma -2}-a^2\nabla p_{kl}^4-2a{\kappa }_{kl}\nabla p_{kl}\nabla {(D^{-1}{M}_{\beta }^{(0)}p)}_{kl}}.$$ (41)

The value of λ in Eqn. (41) ensures that g remains constant up to O(δκ_kl) terms. However, we must also adjust {κ_kl} at each step to exactly maintain the constraint following the method given in Section 2.2. In previous applications since g was a function of κ alone this additional projection step did not require perturbation of pressures. Now both the change in κ_kl and the change in flow must be considered when adjusting conductances. We calculate here the additional terms created by the pressure variation. To project along the constraint surface normal we need to calculate the normal vector:

$$\begin{gathered} n_{kl}=\frac{\partial }{\partial {\kappa }_{kl}}\left\{\sum _{i>j,\langle i,j\rangle }\left({\kappa }_{ij}^{\gamma }+a{\kappa }_{ij}{(p_i-p_j)}^2\right)-K^{\gamma }\right\} \\ =\gamma {\kappa }_{kl}^{\gamma -1}+a{(p_k-p_l)}^2-\sum _{\langle i,j\rangle ,i>j}2a{\kappa }_{ij}(\frac{\partial p_i}{\partial {\kappa }_{kl}}-\frac{\partial p_j}{\partial {\kappa }_{kl}})(p_i-p_j). \end{gathered}$$ (42)

To obtain $\frac{\partial p_i}{\partial {\kappa }_{kl}}$ we differentiate Kirchhoff’s first law with respect to κ_kl:

$$\sum _j{\kappa }_{ij}(\frac{\partial p_i}{\partial {\kappa }_{kl}}-\frac{\partial p_j}{\partial {\kappa }_{kl}})+({\delta }_{ik}{\delta }_{jl}-{\delta }_{il}{\delta }_{jk})(p_i-p_j)=0$$ (43)

or:

$$\sum _j{\kappa }_{ij}(\frac{\partial p_i}{\partial {\kappa }_{kl}}-\frac{\partial p_j}{\partial {\kappa }_{kl}})=-(p_k-p_l)({\delta }_{il}+{\delta }_{ik}).$$ (44)

Notice that $\frac{\partial p_i}{\partial {\kappa }_{kl}}=0\forall i\in {\mathcal{V}}_D$ since these p_i are fixed by the boundary conditions. Then we can solve for $\frac{\partial p_i}{\partial {\kappa }_{kl}}$ , 1 ≤ i ≤ V by solving the linear system (solvability was discussed in Appendix A) and calculate the normal vector.

2.7. Calculating uniform flow zebrafish microvascular network under Murray’s constraint.

The gradient descent method with Murray constraint closely follows Section 2.6 with the target function

$$\mathrm{\Theta }=\sum _{(k,l)\in \mathcal{E}}\frac{1}{2}{({\kappa }_{kl}(p_k-p_l)-\stackrel{‒}{Q})}^2{I}_{kl}+\lambda \left(\sum _{\langle k,l\rangle =1,k>l}(a{\kappa }_{kl}{(p_k-p_l)}^2+{\kappa }_{kl}^{\gamma })-K\right)-\sum _{k\in {\mathcal{V}}_N}{\mu }_k\left(\sum _{l,\langle k,l\rangle =1}{\kappa }_{kl}(p_k-p_l)-q_k\right)$$ (45)

where ε = {(k, l : ⟨k, l⟩ = 1, k < l} and the index convention here follows Fig. 8A. Here I_kl = 1 if and only if the edge kl is an intersegmental vessel. To carry out the gradient descent we calculate

$$\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}=({\kappa }_{kl}(p_k-p_l)-\stackrel{‒}{Q})(p_k-p_l)I_{kl}-a\lambda {(\nabla p^2)}_{kl}+\lambda \gamma {\kappa }_{kl}^{\gamma -1}-\nabla {(D^{-1}\zeta )}_{kl}\nabla p_{kl}\doteq \lambda {\beta }_{kl}+{\chi }_{kl}\forall (k,l)\in \mathcal{E}$$ (46)

Now given {κ_kl}, {p_k} we need to solve for {μ_k}, λ for the algorithm. Again from $\frac{\partial \mathrm{\Theta }}{\partial p_k}=0$ we get

$$\mu =2a\lambda p+D^{-1}\zeta$$ (47)

where

$${\zeta }_k\doteq \{\begin{array}{cc}\sum _{l,\langle k,l\rangle =1}({\kappa }_{kl}(p_k-p_l)-\stackrel{‒}{Q})I_{kl}{\kappa }_{kl}\hfill & k\notin {\mathcal{V}}_D\hfill \\ 0\hfill & \kappa \in {\mathcal{V}}_D\hfill \end{array}\phantom{\}}.$$ (48)

To solve for lambda we can use Eqn. (41) if we calculate β, X in Eqn. (46). Since the target function here is the same as that in Section 2.6 we have ${\beta }_{kl}=\gamma {\kappa }_{kl}^{\gamma -1}$ . The χ can be calculated as

$${\chi }_{kl}=({\kappa }_{kl}(p_k-p_l)-\stackrel{‒}{Q})(p_k-p_l)I_{kl}-\nabla {(D^{-1}\zeta )}_{kl}\nabla p_{kl}(k,l)\in \mathcal{E}$$ (49)

With these expressions we can solve for λ by Eqn. (41) and obtain the expression for {μ_k} by Eqn. (47). Then we can carry out the gradient descent by Eqn. (46). Notice that if we set $\stackrel{‒}{Q}=0$ , I_kl = 1 ∀⟨k,l⟩ = 1 then f is the same as in Section 2.6 and the expression of X agrees with the auxiliary variable defined in that section.

3. Results.

3.1. The algorithm finds known minimally dissipative networks.

To evaluate the ability of our algorithm to find optimal networks we start with minimally dissipative networks that have been thoroughly studied. It has been proven that, when the exponent in material constraint γ is less than one, as is the case for vascular networks, the minimally dissipative networks with flow (Neumann) boundary conditions contain no loops [17] (this result was generalized to both flow and pressure (Dirichlet) boundary conditions in [8]). Those networks are also known to satisfy Murray’s law [38, 51], which states that the sum of third power of vessel radii in the same hierarchy is a constant. Although the original derivation by Murray in 1926 was based on local optimization in a network in which flows are unaffected by changes in conductances, Murray’s law is also necessary for a network to be a global minimizer [8]. To see whether our algorithm recovers these theoretical properties we consider a model for the branching vasculature in animals [54] (Fig. 5A). We impose distributed sinks on the bottom and a single source on top (with pressure imposed to ensure solvability [29]). We apply the algorithm described in Section 2.3 starting from a network with no prior knowledge, i.e. all edges have the same uniformly random distribution of conductances. All 20 networks we simulated are trees (Fig. 5B), agreeing with previous theoretical work. To further validate our algorithm we calculate the Murray exponent by minimizing the coefficient of variation (CV) of sums of vessel radii in the same hierarchy to the exponent (Fig. 5C). The Murray exponents cluster tightly around 3 (3.01 ± 0.03, mean ± sd, 20 networks), which is the exponent in Murray’s law [38]. So our algorithm recovers both properties of minimally dissipative networks [6].

Fig. 5.

Minimally dissipative networks agree with previous work (with target junction Σκ_kl(p_k – p_l)² and material constraint $\sum {\kappa }_{kl}^{\gamma }-K^{\gamma }$ with $\gamma =\frac{1}{2}$ ). (A) We use a branching grid as our basic topology. There are N = 20 layers of vertices and a total of 380 edges, connecting a single source (red filled circle) with 8 sinks (red open circles). (B) A minimal dissipative network calculated by gradient descent method exhibits tree structure as predicted in [17]. We imposed a fixed zero pressure on the top vertex and 8 evenly distributed outflows on the bottom. Each edge is initially assigned a positive uniformly random conductance to impose no prior knowledge on the algorithm. (C) Murray’s law [38] is obeyed by the minimal dissipative network, indicated by the nearly constant sum of radius to an exponent 3.004 among different hierarchies in network shown in (B).

3.2. Uniform flow qualitatively explains network structure of capillary beds.

Here we compare these organizing principles on the topology of capillary beds [53, 36] (Fig. 6A). We follow Section 2.3 to calculate minimally dissipative networks, and Section 2.4 to calculate uniform flow networks. We assume that the capillary bed is supplied by a single arteriole and blood leaves from a single venule. Networks formed according to the minimal dissipation principle consist of a single pipe following a geodesic route (Fig. 6B, C), which can be shown theoretically to be the optimal solution. Specifically, since the network cannot contain loops, and connects a single source to a single sink, there can only be one pipe in the network. Longer pipes have less material in each segment but the same flows as shorter pipes, so have higher total dissipation. Finally uneven material distribution has been ruled out by [16]. This morphology contrasts sharply with empirically observed capillary structure [53, 30, 36], suggesting that minimizing dissipation is not the dominant factor for capillary systems.

Fig. 6.

Minimally dissipative networks consist of a single conduit on capillary bed topology (with target function Σ κ_kl (p_k – p_l)² and material constraint $\sum {\kappa }_{kl}^{\gamma }-K^{\gamma }$ with $\gamma =\frac{1}{2}$ on a 10×10 square grid). (A) We represent the capillary bed network by a square grid where a single source and a single sink locate at upper-left and lower-right corners respectively. (B, C) Different initial conductances produce different optimal networks, but all optimal networks are made of a single wide conduit. Here we use a constant step size throughout the process, and at each step we project by surface normal to maintain the material constraint. Each edge is initially assigned a positive uniformly random conductance to impose no prior knowledge on the algorithm.

Uniform flow networks, on the other hand, might explain capillary bed morphology. Starting from a uniformly random configuration, our algorithm finds a network with an apparently random distribution of materials (Fig. 7A). The conductances have a smaller variance compared to the initial configuration, but do not have a clear pattern otherwise (Fig. 7B). While the uniform flow networks more closely resembles a capillary bed than a minimally dissipative network, it is not clear what quantitative characters can be used to compare the networks. As discussed in Section 2.4, the uniform flow target function simplifies to $\frac{1}{2}\sum Q^2$ on capillary bed topology, which allows us to analytically derive properties of uniform flow networks.

Fig. 7.

Uniform flow networks have a seemingly random morphology, but can be shown to have the same flows as a uniform conductance network (Here we show a 20×20 square grid network with 400 vertices). (A) An optimal network has an apparently random distribution of conductances. The edge widths are proportional to the conductances. (B) A closer view reveals that the conductances of the optimal network (blue circle) are quite different from uniform (red cross), and do not seem qualitatively different from initial conductances drawn from a uniform random distribution (green star). The conductances are normalized such that $\sum {\kappa }^{\frac{1}{2}}$ are the same. Each edge is initially assigned a positive uniformly random conductance to impose no prior knowledge on the algorithm. (C) The differences of flows from those in a uniform conductance network (blue circles) are uniformly zero, while the differences of initial flows from those in a uniform conductance network (green stars) are not.

Theorem 1. Any critical point of the target function (26) in which $p_k=0\forall k\in {\mathcal{V}}_D$ has the same set of flows as a uniform, conductance network with the same support on edges. That is, suppose we let κ_kl, Q_kl be the conductances and flows on the stationary network, and ${\kappa }_{kl}^{\prime }$ , $Q_{kl}^{\prime }$ be those on the uniform, conductance network, i.e.

$${\kappa }_{kl}^{\prime }=\{\begin{array}{cc}1\hfill & \mathit{if}\langle k,l\rangle =1\mathit{with}{\kappa }_{kl}>0\hfill \\ 0\hfill & \mathit{if}\langle k,l\rangle =1\mathit{with}{\kappa }_{kl}=0\hfill \end{array}\phantom{\}}.$$ (50)

Then

$$Q_{kl}=Q_{kl}^{\prime }\forall \langle k,l\rangle =1.$$ (51)

(The proof will be presented in the end of this subsection.) The theorem states that a uniform flow network, i.e. a local minimum of target function (26), will have the same flow as the network where all the edges with positive conductances are assigned unit conductance. In order to evenly distribute the flows, networks with all allowed edges present will have higher uniformity than networks in which some subset of edges have been cut (indeed among 100 uniform flow networks those with all edges present have an average value for the target function of 1.9465, compared to 1.9470 for networks with at least one edge cut). Therefore the uniform conductance network can predict the flows in all uniform flow (Fig. 7C). While the flows in uniform flow networks are tightly constrained, many possible configurations can achieve the same uniformity, and there is no visible pattern in the distribution of conductances for those networks, unlike minimally dissipative networks.

Proof of Theorem 1. The assumption that all pressure vertices have pressure zero is really an assumption that all pressure vertices have the same pressure: In the latter case since a constant shift in all pressures does not change the flows. To find the critical points of Θ we recall the derivatives in Eqns. (27, 28), along with ${\mu }_i=0\forall i\in {\mathcal{V}}_D$ by assumption. First we show that a uniform distribution of conductances would result in a critical point ({p_k}, {μ_k}, {κ_kl}), by rewriting the equation $\frac{\partial \mathrm{\Theta }}{\partial p_k}=0$ (27) into the matrix form:

$$D\mu =D^{(2)}p.$$ (52)

Here D_kl is in Equation (6) and –D⁽²⁾ is another graph Laplacian:

$$D_{kl}^{(2)}\doteq \{\begin{array}{cc}\sum _{l,\langle k,l\rangle =1}{\kappa }_{kl}^2\hfill & k=l,k\notin {\mathcal{V}}_D\hfill \\ -{\kappa }_{kl}^2\hfill & \langle k,l\rangle =1,k\notin {\mathcal{V}}_D\hfill \\ {\kappa }^{(2)}\hfill & k=l,k\in {\mathcal{V}}_D\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\phantom{\}}$$ (53)

in which the matrix is made full-rank if κ⁽²⁾ > 0 (similarly to the κ⁽¹⁾ constant in D). The κ⁽¹⁾ entries in D_kl enforce μ_k = 0 at each $k\in {\mathcal{V}}_D$ . The entries in D⁽²⁾ are not needed since p_k = 0 at each $k\in {\mathcal{V}}_D$ , but we add values here to emphasize the symmetry between {μ_k} and {p_k}. Now consider uniform conductances, i.e. κ_kl = a > 0 ∀⟨k, l⟩ = 1. We can set κ⁽¹⁾ = a and κ⁽²⁾ = a². Then we have D = aD⁽²⁾ and since D is invertible (see Appendix A)

$$\mu =D^{-1}{D}^{(2)}p=ap.$$ (54)

Now this set of μ_k’s and p_k’s then also satisfies $\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}=0$ because

$$\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}=a{(p_k-p_l)}^2-a{(p_k-p_l)}^2=0.$$ (55)

Thus the network with uniform conductances along with pressures solved from the Kirchhoff’s first law is indeed a critical point.

Now we show that any interior critical point, i.e. satisfying κ_kl > 0 ∀⟨k, l⟩ = 1, has the same flows as the uniform conductance network. We will see that for any such network the _μk’s represent the pressures of the uniform conductance network. Since all the conductances are positive we have $\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}=0\forall \langle k,l\rangle =1$ . Assume for now p_k – p_l ≠ 0 ∀⟨k, l⟩ = 1. Then from Equation (28) we obtain that the (μ_k} obey a system of equations

$${\kappa }_{kl}(p_k-p_l)-({\mu }_k-{\mu }_l)=0,\forall \langle k,l\rangle =1$$ (56)

which may be rewritten as

$${\mu }_k-{\mu }_l={\kappa }_{kl}(p_k-p_l)=Q_{kl},\forall \langle k,l\rangle =1.$$ (57)

Kirchhoff’s first law in terms of μ_k’s then reads

$$\sum _{l,\langle k,l\rangle =1}({\mu }_k-{\mu }_l)=q_k\forall k\in {\mathcal{V}}_N,{\mu }_k=0\forall k\in {\mathcal{V}}_D.$$ (58)

In matrix form the equations can be written as

$$D\mu =F$$ (59)

where F_k = q_k if $k\in {\mathcal{V}}_N$ and is zero otherwise, and D is defined as for network made up of unit conductances:

$$D_{kl}\doteq \{\begin{array}{cc}\sum _{l,\langle k,l\rangle =1}1\hfill & k=l,k\notin {\mathcal{V}}_D\hfill \\ -1\hfill & \langle k,l\rangle =1,k\notin {\mathcal{V}}_D\hfill \\ 1\hfill & k=l,k\in {\mathcal{V}}_D\hfill \\ 0\hfill & o.w.\hfill \end{array}\phantom{\}}$$ (60)

Because D is invertible we can solve for μ_k’s from Eqn. (59). The {μ_k}’s represent the pressures that would occur at each vertex if all conductances in the network were set equal to 1, creating uniform conductance network. Since the flows Q_kl = μ_k – μ_l are determined by μ_k’s we conclude that the locally optimal networks would have flows the same as in the network of uniform conductances.

To derive (56) from (28) we had to assume that p_k ≠ p_l whenever ⟨k, l⟩ = 1. Consider the case where in the optimal network p_k – p_l = 0 for some ⟨k, l⟩ = 1. For these (k, l)’s Eqn. (56) no longer holds and we have to set $\frac{\partial \mathrm{\Theta }}{\partial p_k}=0$ in Eqn. (27) to obtain extra information. We claim that μ_k = μ_l if p_k – p_l = 0. This can be seen from a loop current argument similar to that used in Appendix A to prove existence and uniqueness of the {μ_k}. Specifically, suppose for contradiction that μ_k1 ≠ μ_k2 for some pair of vertices with p_k1 – p_k2 = 0 and without loss of generosity let μ_k1 > μ_k2. If k₁ and $k_2\in {\mathcal{V}}_D$ then μ_k1 = μ_k2 = 0; so at least one of the two vertices does not lie in ${\mathcal{V}}_D$ . If $k_2\notin {\mathcal{V}}_D$ then $\frac{\partial \mathrm{\Theta }}{\partial p_{k_2}}=0$ implies:

$$\sum _{l,\langle k_2,l\rangle =1}{\kappa }_{k_{2}l}^2(p_{k_2}-p_l)=\sum _{l,\langle k_2,l\rangle =1}{\kappa }_{k_{2}l}({\mu }_{k_2}-{\mu }_l).$$ (61)

Since Eqn. (56) holds when p_k – p_l ≠ 0 we have

$$0=\sum _{l,\langle k_2,l\rangle =1,p_1=p_{k_2}}{\kappa }_{k_{2}l}^2(p_{k_2}-p_l)=\sum _{l,\langle k_2,l\rangle =1,p_{k_2}=p_l}{\kappa }_{k_{2}l}({\mu }_{k_2}-{\mu }_l).$$ (62)

Since κ_kl > 0 ∀⟨k, l⟩ = 1 and the sum includes the negative summand κ_k2k2 (μ_k2 – μ_k1) we can find l for which μ_l < μ_k2 and p_l = p_k2. We let k₃ = l and repeat the process to find a neighbor of k₃ such that p_l = p_k3 but μ_l < p_k3. We then can keep repeating this process until we reach a vertex $k_N\in {\mathcal{V}}_D$ (no vertex may be visited more than once). We have imposed μ_kN = 0. Now we trace through increasing μ_k’s starting from k₂ and k₁ and we get $k_1^{\prime },\dots ,k_{N^{\prime }}^{\prime }$ , such that ${\mu }_{k_n^{\prime }}<{\mu }_{k_{n+1}^{\prime }}\forall n=1,\dots ,N^{\prime }-1$ and ${\mu }_{k_1^{\prime }}>{\mu }_{k_1}$ . By the same reasoning we have $k_{N^{\prime }}\in {\mathcal{V}}_D$ and we reach a contradiction since $0={\mu }_{k_{N^{\prime }}^{\prime }}>{\mu }_{k_{N^{\prime }-1}^{\prime }}>\cdots >{\mu }_{k_1^{\prime }}>{\mu }_{k_1}>\cdots >{\mu }_{k_N}=0$ . Therefore μ_k = μ_l when p_k = p_l and Eqn. (56) actually holds for all ⟨k,l⟩ = 1. Again we conclude that the flows of a locally optimal network with non-zero conductances are the same as the flows in the uniform conductance network.

Finally we discuss the boundary case where κ_kl = 0 for some ⟨k,l⟩ = 1, and we denote this set of edges by I. To avoid ill-posedness of pressures we require that that the matrix D is invertible. In this case we do not have Eqn. (56) for κ_kl = 0 because $\frac{\partial \mathrm{\Theta }}{\partial {\kappa }_{kl}}$ need not be zero on these edges. However since there is no flow through edges with κ_kl = 0 we can write down Kirchhoff’s first law as

$$D\mu =0,$$ (63)

where −D is again the graph Laplacian, but with zero conductance edges removed and other edges with conductance 1:

$$D_{kl}=\{\begin{array}{cc}\sum _{l,\langle k,l\rangle =1,(k,l)\notin I}1\hfill & k=l,k\notin {\mathcal{V}}_D\hfill \\ -1\hfill & \langle k,l\rangle =1,(k,l)\notin I\hfill \\ 1\hfill & k=l,k\in {\mathcal{V}}_D\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (64)

We can safely remove the zero conductance edges from the network because the difference μ_k – μ_l no longer represents the flow Q_kl, and that we know Q_kl = 0 for these edges. By assumption we can solve for μ from Eqn. (63) so {μ_k} represent the pressures within the uniform conductance network, but with edges κ_kl = 0 removed from the network.

3.3. Optimal zebrafish microvasculature.

Comparison of the different organizing principles on our model capillary bed network suggests that uniform flow is prioritized more than transport efficiency for these networks. The comparison remains qualitative because although capillary beds in e.g. salamander skin do resemble square grids [36] (and Fig. 1A), this resemblance is only approximate, so it is difficult to test our theoretical predictions. The embryonic zebrafish trunk vasculature, on the other hand, can be completely mapped, down to the finest vessels. Moreover, the blood flows can be measured by tracking the motion of red blood cells ([49, 32], as well as our previous work [9]), thereby directly testing the flows predicted in optimal networks.

First we show how far the embryonic zebrafish network is from minimizing dissipation. The optimal morphology of the network depends on the boundary conditions we impose, and there are two conceivable ways to assign boundary conditions. One way is to assume a fixed inflow from the heart into the trunk from v₁. If one thinks of the venous part of the trunk as symmetric to the arterial part then the pressures in the middle of fine vessels need to be the same, and we can set p_n+1 = p_n+2 = ⋯ = p_2n+1 = 0 (since a constant shift in the pressure does not change the flow). Under this boundary condition we can find the minimally dissipative network by methods described in Secion 2.3. The minimally dissipative network eliminates all the edges but e₂, on which all the allowed material is used (Fig. 8B). This agrees with prior theoretical predictions since minimally dissipative networks cannot have loops, nor can they connect vertices with the same assigned pressure [8]. Therefore there are only n + 1 possibilities: the flow returns through one of the fine vessels e₂,…, e_2n or the tail e_2n−1. Since the shortest route would be going through the first fine vessel e₂, the minimally dissipative network concentrates all the material on e₂.

Instead of imposing a fixed pressure in the middle of the fine vessels, one can also impose a fixed flow [6, 26, 16] through each vessel. This boundary condition interprets into a uniform flow at each of the vertices v_n+2,…, v_2n+1, and we can find a distribution of conductances that minimizes dissipation from Section 2.3. Now equal amount of flow passes through each fine vessels, leading to a decaying flow in the aorta from head to tail. Therefore the material is concentrated on the rostral part of the aorta, with all the fine vessels having equal amount of material (Fig. 8C). The imposed fixed flow then requires a decrease of pressure in the middle of fine vessels from head to tail, to compensate for the pressure drop in the aorta (Fig. 8D). Under symmetry of arterial and venous parts, this pressure distribution then creates an unrealistic blood flow in the vein toward the tail, i.e. away from the heart.

Since the principle of minimal dissipation is unable to generate networks that resemble the observed zebrafish trunk microvasculature, we look at uniform flow networks and see if they match the observed vasculature. To avoid back flow in the vein we impose fixed pressure in the middle of fine vessels, and a fixed flow into the trunk from v₁. The zebrafish trunk vasculature is not stackable, so we use the square error target function (29) instead of (25), and we use methods described in Section 2.5 to find the uniform flow network. Instead of concentrating all the materials on the first capillary or tapering the aorta, the uniform flow network has constant conductance along the aorta and conductances on the fine vessels that increase exponentially with the distance from the heart (Fig. 9A). If vessels obeyed the Hagen-Poiseuille law (Eqn. (1)) a 20-fold change in conductance would require a 2-fold change in radii of fine vessels, which is not observed in the real zebrafish trunk [25]. However, these fine vessels have radii that match the size of red blood cells; thus red blood cells almost totally occlude the vessels they pass through, adding a large increment to the vessel’s hydraulic resistance [46]. This increment depends sensitively on the gap distance between the cell and the endothelial wall, which is typically on the scale of 10 ~ 300 nm, and is smaller than the optical resolution for fluorescence microscopy [47]. In our previous work, we proposed an indirect method that measures this increment based on the correlation between the flow speed and the number of cells in each fine vessel [9]. When we compare the measured hydraulic resistance with the resistances of fine vessels in the uniform flow network, we see an excellent agreement between the predicted and measured resistances (Fig. 9B). Our results show that the principle of uniform flow quantitatively reproduces the zebrafish trunk geometry.

Fig. 9.

The uniform flow networks quantitatively explains the zebrafish trunk vascular network morphology. (A) The uniform flow network dictates a constant conductance on aorta segments (blue cross) but assigns conductances to Se vessels that increase exponentially from head to tail (red circle). We scale the conductances such that $\sum {\kappa }^{\frac{1}{2}}$ remains the same for comparison with minimal dissipative networks. We started with κ = 20 for aorta segments and κ = 1 for capillaries to reflect the difference in radii in real zebrafish. (B) The predicted hydraulic resistance (blue dashed curve) agrees well with experimentally measured data (red curve, with 95% confidence intervals). The data is obtained from our previous work [9] under the assumption that the volume fraction of the red blood cells is 0.45 [43]. Theoretical resistances are normalized by the mean since optimization only controls the relative resistances of vessels.

3.4. Murray constraint on optimal networks.

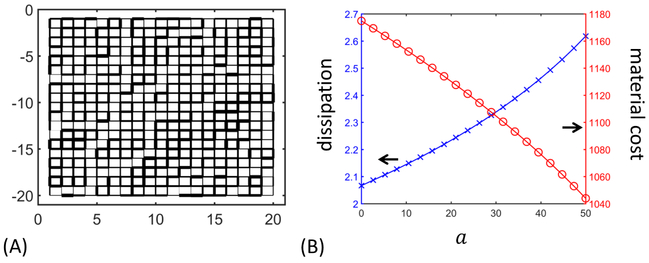
So far we show that capillary networks prioritize uniform flow over minimizing dissipation, but biological networks may be subject to more than one constraint at a time. In capillary networks the total dissipation will be higher when the density of capillaries increases, which in turn requires more energy input. As we noted in the introduction, fine vessels account for half of the cost of blood transport in the human body [21], suggesting that capillaries will be constrained not only in respect to materials but also by dissipation. In this case the function to be optimized takes the full form of (4) with a constant a > 0, representing the relative importance of dissipation compared to material cost. Following Section 2.6 we can calculate uniform flow networks with the model capillary bed geometry under the Murray constraint (Fig. 10A). The uneven distribution of conductances resembles that in Section 3.2, and indeed for 20 networks with a ranges from 0 to 50, the function $\frac{1}{2}\sum Q^2$ clusters closely at the optimal value (1.9461 ±9.25 × 10⁻⁶, mean ± sd, 20 networks), i.e. that of uniform conductance network. This result is counter-intuitive since we would expect that constraining dissipation would prevent the network from achieving the non-constrained optimal uniformity in flows. However, on the capillary bed topology we can reason by a scaling argument. Suppose we find an optimal network under the material constraint. We calculate the total material cost K of this network. Then we calculate the optimal network in which Murray’s constraint is imposed with allowed total energy K including both material costs and dissipation. Denote by κ_kl the conductances in the network under Murray constraint, and by ${\kappa }_{kl}^{\prime }$ the conductances in the optimal network under material constraint. If a is sufficiently close to zero then the target function of Murray network will be lower or equal to that of material network. The reasoning is that although $\sum {\kappa }_{kl}^{\prime \gamma }+a\frac{Q_{kl}^2}{{\kappa }_{kl}^{\prime }}=K$ does not hold, we can try to solve for a multiplicative scaling β > 0 that satisfies $\sum {(\beta {\kappa }_{kl}^{\prime })}^{\gamma }+a\frac{Q_{kl}^2}{\beta {\kappa }_{kl}^{\prime }}=K.$ Notice that Q_kl does not change under the scaling for this class of networks, so the value of target function is unaffected by scaling conductances. Now if a > 0 is small enough we expect to be able to find a solution β and $\{\beta {\kappa }_{kl}^{\prime }\}$ is an admissible network in the sense that it obeys the Murray constraint. Thus the optimal network under the Murray constraint must have equal or smaller target function value than the optimal network obeying only the material constraint. By reversing this argument we can see that the optimal networks for small enough a > 0 actually agree with those with a = 0. The question is how large a has to be so that the Murray network is truly constrained by the total energy cost, and the optimal networks under the Murray constraint and under the material constraint diverge. From our numerical simulations we can see that large changes of a can be accommodated with changing the morphology of the uniform flow networks from its unconstrained counterpart. We observe that increasing a decreases material costs (Fig. 10B), which is unintuitive since increasing a adds weight to dissipation, and we might expect this to encourage the network to decrease its dissipation. If we study the curve of $\sum {(\beta {\kappa }_{kl}^{\prime })}^{\gamma }+a\frac{Q_{kl}^2}{\beta {\kappa }_{kl}^{\prime }}$ as a function of β, the function is U-shaped and diverges when β → 0 or β → ∞. When a increases the total energy increases, and the network has to adjust itself to a low energy state. If the network is on the left side of the U this means increasing β, which increases the material cost to realize the constraint. In contrast when the network is on the right side of the curve, decreasing β will be the only way to lower the total energy, which explains the trends depicted in Fig. 10B. The simulation suggests that, on the capillary bed topology, constraining dissipation seems to have little effect on the morphology of uniform flow network.

Fig. 10.

Uniform flow networks under Murray constraint have the same flows as the analytic solution in Sec 3.2, but exhibit tradeoff between dissipation and material cost as a increases. (A) For small a the uniform flow network with Murray constraint is equivalent to a network with material constraint. The network is constrained with a = 36.8, and the solution is selected from the best network visited during the gradient descent, with relative error in energy cost < 10⁻⁴, as in the following simulations. Widths show the relative conductances. (B) When a is increased, the dissipation in the network increases (blue crosses), while the material cost decreases (red circles). The simulations were carried out in the manner of numerical continuation, i.e. the simulation for each a starts with the solution from previous a, and the simulation for a = 0 starts with a random conductance configuration. All the networks have the same fixed total energy cost K = 1174.9.

Would uniform flow models of the zebrafish trunk follow the same trend? Using methods described in Section 2.7, we can calculate uniform flow networks under Murray constraint, with different values in a. When a is close to zero, the constrained networks have optimal flow uniformity, and dissipation increases as in the case of capillary bed topology (Fig. 11A). However, at a critical value around a_c = 33.3, a phase change occurs; the flows become less uniform and dissipation starts dropping (Fig. 11A). The network morphology changes dramatically, in particular conductances of the fine vessels become non-monotonic, and the flows are concentrated toward the head side of zebrafish (Fig. 11B, C). Our results suggest that, when a biological network has multiple constraints to meet, the network morphology will conform only to the tightest constraint, and then if the relative weight of these constraints is changed, the network changes dramatically only when another constraint becomes dominant.

Fig. 11.

Uniform flow networks on zebrafish trunk topology exhibit a phase transition when a, the relative cost of dissipation to total material, is varied in the Murray constraint. (A) The target function remains zero for small a until a_c = 33.3 where a phase transition occurs and the value of target function suddenly increases (blue crosses). The dissipation (red circles) increases with a for a < a_c just as for the capillary bed, but has a sharp decrease right after the critical value a_c. Here we adopted numerical continuation as in Fig. 10B, but when a local minimum around previous initial condition does not satisfy Murray constraint the initial configuration at a = 0 is reused for the initial conductances. The minimal value for the total energy cost upon scaling of conductances is used whenever the Murray constraint cannot be maintained. The Murray energy K is maintained to be 70.43 in all simulations by the projection method described in Section 2.6. The total energy cost is fixed to that of initial configuration (with uniform conductances in fine vessels being 1 and those in aorta being 20) when a = 1. The solution is selected from the best network visited during the gradient descent, with relative error in energy cost < 10⁻⁴ (B) The conductances of capillaries change qualitatively after the phase transition. The morphology resembles the unconstrained network (Fig. 9A) before the phase transition (blue cross and red circle), but changes qualitatively afterwards (green square). (C) The flows are uniform before the phase transition (blue cross and red circle), but decrease from head to tail afterwards (green square).

4. Discussion and Conclusion.

Microvascular network mapping tools have until recently lagged far behind our ability to measure the morphology of large vessels using e.g. plasticization. However, recent advances in microscopy have created detailed digitization of microvascular networks [7, 5, 18]. For example Knife-Edge Scanning Microscopy (FESM) and Micro-optical Sectioning Tomography (MOST) have been used to map the blood vessels within rodent brains to micron resolution [34, 55]; while mapping the blood vessels in the human brain is one of the central goals of the BRAIN initiative [24]. Meanwhile long working distance two photon microscopes can be used to directly measure blood flows within living rodent brains [7, 15]. But the revolution in microvascular imaging has not been matched by new theorizing about what are the organizing principles for microvascular networks. For large vessels minimization of dissipation and the concomitant laws for vessel radii have proven to be powerful organizing tools with which to understand both the morphology of healthy and pathological cardiovascular networks [42]. By comparison it is not known whether any optimization principles underly real microvascular networks. In this work we explore the principle of uniform flow as a candidate organizing principle for microvascular networks [9] in both an idealized capillary bed geometry and the real embryonic zebrafish trunk. To do so, we devised an algorithm for optimizing general functions on transport networks. On the model capillary bed we showed analytically that the flows in a uniform flow network are identical to a network with constant conductances. In the zebrafish trunk, achieving uniform flow requires careful tuning of vessel conductances, and implies a distribution of conductances that matches the real zebrafish trunk.

Finally we expose a phase transition that occurs if dissipation costs are also modeled, as the relative size of transport and material costs is increased. Surprisingly, networks that are constrained by both material costs and dissipation do not continuously interpolate between optimizing uniformity and optimizing dissipation, but instead are initially invariant under changes in the cost of dissipation, and then undergo a sudden phase transition-like reconfiguration when this cost exceeds a certain threshold. Although further work is needed to show whether such transitions occur for other combinations of functions, it offers two surprising biological insights. First, no two functions will likely shape the network simultaneously, explaining the remarkable power of single target functions to predict the geometry of biological networks. Secondly, the departure of real zebrafish networks from the optimum for creating uniform distributions of fluxes cannot readily be explained as a result of the network needing to balance tradeoffs between multiple target functions. We believe that the non-optimal features of the zebrafish trunk network are more likely due to another cause; for example variability (e.g. due to biological noise) during vessel formation. For example a 10% variation in vessel radius, as has been observed in small arterioles [27], leads to a 40% variation in vessel conductance under the Hagen-Poiseuille model (1), and the variation will be even larger when the occlusion of red blood cells is considered [46]. Under even such mild perturbations, variation in red blood cell flux can reach 0.7 (1/s) standard deviation, comparable to the variations measured for real zebrafish in [9].

The principle of uniform flow may be relevant to other biological transport networks as well. Many organisms build networks for transport, such as plants and slime molds [26, 2]. Previously the loopy structure of leaf vascular networks was attributed to damage resistance [26]. Yet uniform flow also favors loopy structures, and provides an alternative optimal principle for these networks.

Real blood is a multi-phase fluid containing both plasma and cells. By assuming Hagen-Poiseuille law we omit two of the complexities of real blood flow: non-Newtonian viscosities and ZweiFach-Fung effect [43]. Hydraulic conducances depend both on vessel radius (the Fahraeus-Lindqvist effect) and on the concentration of cells due to both the occlusion of red blood cells in narrow capillaries and the disordered flow of cells within large vessels [9, 46, 48]. The Zweifach-Fung effect refers to variation of hematocrit between vessels following uneven partitioning of red blood cells at branching points [56, 14]. Our algorithm has the flexibility to incorporate the Fahraeus-Lindqvist effect by changing the constraint term into a non-power law representation of vessel radius. For simplicity we considered the default model (1) throughout the paper, except when comparing uniform flow zebrafish trunk vasculature to experimental data in Section 3.3. To incorporate the Zweifach-Fung effect the hematocrit has to be re-calculated each time we calculate blood flows which will affect oxygen perfusion. Although [41] proposed an empirical formula for the Zweifach-Fung effect, the effect of vessel radius and cell geometry upon the Zweifach-Fung effect is still under active research [4, 50, 12].

Throughout this work we have used uniformity of flow as a proxy for uniform perfusion. This is defensible if perfusion in limited by the rate of delivery of oxygenated red blood cells to a particular tissue. However it is also affected by the rate at which it subsequently diffuses through the surrounding tissue – which is in turn affected by levels of oxygen saturation and pH in the tissues and blood and may indeed vary in the same tissues due to functional activation of capillaries in response to time varying metabolic demands [3]. Thus although we have previously presented direct evidence of uniform flow across the zebrafish trunk microvasculature, and in this work show that this uniformity results from conductances being close to the unique maximum of a constrained optimization problem, the connection between uniform flow and uniform perfusion is not proven.

Although our algorithm easily handles the relatively small number of vessels in the zebrafish trunk or model capillary, the mouse cortex contains about 14, 000 capillaries per mm³ [5]. Further tool development is needed to determine whether such networks obey the same principles of uniform flow.

There are many other relevant biological functions that have been identified as candidates for optimization in biological transport networks, for example damage resistance [26] and mixing [45]. Our algorithm has the flexibility to find optimal networks for general biological functions that can be represented by closed-form target functions. Previous numerical work focused on dissipation and functions derived from it [6, 26], but we hope that our algorithm will help to catalyze systematic study of other target functions.

Our networks are constrained either by material or total transport cost (i.e. material plus dissipation). However, we could equally impose network cost as a penalty function rather than as a constraint. Indeed, in Murray’s original paper, optimal vessel geometries were derived by minimizing the total energy formed as a sum of material and transport costs (i.e. by a penalty function approach) [38, 51]. In contrast, recent works on minimal dissipation networks impose the material cost as a constraint and minimize dissipation under this constraint. The two approaches carry different physical meanings; and under many, but not all conditions, they produce equivalent networks [8].

Highlights.

• Large blood vessels are organized for transport efficiency, but microvascular networks are not – we explore the hypothesis that uniform flow may explain microvascular morphologies.

• A gradient descent algorithm is devised to find optimal vascular networks with general functions and constraints, comparing transport efficient and uniform flow networks on different microvasculatures.

• On a class of model capillary beds, we prove that uniform flow networks have the same flows as networks in which all vessels are assigned the same conductance.

• Optimizing fine vessels in the zebrafish trunk network for uniform flow produces vessel conductances that match experimental measurements.

• When the cost of transport is incorporated as a constraint with controlled strength, microvascular network morphologies undergo a phase transition, suggesting that networks that optimize multiple functions may be indistinguishable from networks that optimize only one function.

Appendix A. Solvability of {μ_k}.

Here we prove that {μ_k} in Equation (7) are solvable under a general configuration of flow (i.e. Neumann) and pressure (i.e. Dirichlet) boundary conditions (BCs). We assume that κ_kl > 0 ∀⟨k, l⟩ = 1 (since κ_kl = 0 is the same as ⟨k, l⟩ = 0) and that the network is connected. It suffices to show that the matrix D is invertible. This is the same matrix in the linear system for solving {p_k} with the specified boundary conditions, so we only have to show that there exists a unique flow given any flow and pressure boundary conditions, which is a well-known [29]. Since our derivation makes use of multiple invertibility results for different matrices D, D⁽²⁾ and so on, we provide a proof in order to highlight under what conditions invertibility is allowed. The problem is equivalent to showing that

$$Dp=0\Rightarrow p=0.$$ (65)

The solution p for Eqn. (65) corresponds to a network where we do not have any flows into the system except possibly at vertices with pressure boundary conditions, denoted by ${\mathcal{V}}_D$ . The goal is to show that p_k =0 ∀k. Suppose for contradiction that $\exists i\notin {\mathcal{V}}_D$ s.t. p_i ≠ 0 (since we already have p_j = 0 $\forall j\in {\mathcal{V}}_D$ ). Then we would have Q_kl ≠ 0 for some ⟨k, l⟩ = 1 since the network is connected, and without loss of generality let Q_kl > 0. Now we can trace this flow throughout the network in the following procedure:

1. Given that Q_kn−1kn > 0 first check if $k_n\in {\mathcal{V}}_D$ , and stop if this is the case.

2. Consider all vertices l s.t. ⟨k_n, l⟩ = 1. According to Kirchhoff’s first law there must be an l s.t. Q_knl > 0. Since the network is finite we can pick e.g. the smallest l satisfying these conditions and let k_n+1 = l.

3. Repeat the procedure until $k_N\in {\mathcal{V}}_D$ for some N and stop.

If we start with k₁ = k, k₂ = l we can initiate the process since the first condition is satisfied. This procedure has to stop eventually because the network is finite and that k₁,…, k_n are all distinct for any given n > 1. To see this suppose k_n = k_m with m > n. Then we would have p_n > p_n+1 > ⋯ > p_m = p_n, a contradiction. Thus we would end up with a chain of distinct vertices k₁, k₂,…, k_N with ⟨k_n, k_n+1) = 1, Q_knkn+1 > 0 ∀n = 1,…, N – 1, and $N\in {\mathcal{V}}_D$ . Now we repeat the same procedure just with $k_1^{\prime }=l$ , $k_2^{\prime }=k$ to trace the flows upstream, and we would end up with another chain $k_1^{\prime }$ , $k_2^{\prime },\dots ,k_{N^{\prime }}^{\prime }$ , with $\langle k_n^{\prime },k_{n+1}^{\prime }\rangle =1$ , $Q_{k_n^{\prime }{k}_{n+1}^{\prime }}<0\forall n=1,\dots ,N^{\prime }-1$ , and $N^{\prime }\in {\mathcal{V}}_D$. Notice that there is no repetition in the set $\{k_1,\dots ,k_N,k_1^{\prime },\dots ,k_{N^{\prime }}^{}\}$ since $k_n=k_m^{\prime }$ would lead to the same contradiction since pressures must be ordered.