Abstract
We propose a pairwise and readily parallelizable SASA-based nonpolar solvation approach for protein simulations, inspired by our previous pairwise GB polar solvation model development. In this work, we developed a novel function to estimate the atomic and molecular SASAs of proteins, which results in comparable accuracy as the LCPO algorithm in reproducing numerical icosahedral-based SASA values. Implemented in Amber software and tested on consumer GPUs, our pwSASA method reasonably reproduces LCPO simulation results, but accelerates MD simulations up to 30 times compared to the LCPO implementation, which is greatly desirable for protein simulations facing sampling challenges. The value of incorporating the nonpolar term in implicit solvent simulations is explored on a peptide fragment containing the hydrophobic core of HP36, and evaluating thermal stability profiles of four small proteins.
Graphical Abstract
1. INTRODUCTION
Biomolecules such as proteins, carbohydrates, and nucleic acids function in an aqueous environment. Biophysical study of their properties and functions requires an accurate description of their solvation and desolvation processes, i.e. the binding and removal of water1 or solvent. To study how proteins fold or bind, the solvation free energy changes (△Gsol) associated with solute-solvent interactions and water reassembly are essential. In biomolecular modeling, these water molecules can be represented explicitly or implicitly. Explicit solvent models, which compute all the pairwise interactions over all solute and solvent atoms and are thus more detailed and complete in theory, however, can be limited in usage, as water atoms dominate the calculations and friction slows the sampling of large conformational changes2. As an attractive alternative, implicit solvent models possess high efficiency in sampling, which has promoted their wide applications in protein folding3–4, structure prediction5, protein design6 and refinement7 using Molecular Dynamics (MD) simulations, binding free energy estimations such as Monte Carlo (MC) simulations8, molecular mechanics/Poisson Boltzmann surface area (MM/PBSA) and molecular mechanics/generalized Born surface area (MM/GBSA)9.
In implicit solvent models, the solvation process is put in the context of a thermodynamic cycle10 (Figure 1), first solvating the uncharged solute by creating and accommodating a cavity (nonpolar term, △Gnp) and then turning the charges back on by modeling water as a continuum high dielectric (polar term, △Gpol). The polar, or electrostatic part, is typically modeled with Poisson-Boltzmann (PB)11 or Generalized Born (GB)12 equations. The nonpolar part is often further decomposed into cavity (△Gcav ) and van der Waals (△Gvdw) contributions13. The cavity term tends to be unfavorable, while the van der Waals interaction with solvent is typically favorable, thus some cancellation between these contributions gives rise to the overall △Gnp. Both △Gcav and △Gvdw are thought to be proportional to the average number of waters making direct contact with solute (i.e. first solvation shell approximation)14. Thus the nonpolar term is often estimated by a SASA-based method12, although it has been pointed out that SASA is not accurately proportional to solvation energies for small alkane solutes15–16, and the volume term may be more important16–17. While SASA-based implicit solvent incorrectly predicted association stabilities of small molecule amino acid analogues when compared to explicit solvent results14, 18, SASA-based nonpolar solvation has been shown to be useful for accurate prediction of native-like protein conformations19 and protein-ligand binding affinities20–21 such as in MM/PBSA and MM/GBSA.
Figure 1.
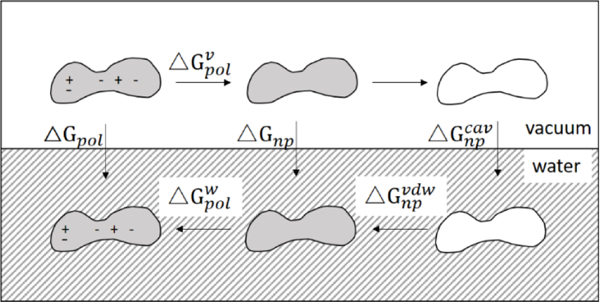
Thermodynamic cycle of the solvation process. Solvation free energy (△Gsol) is decomposed into polar (△Gpol) and nonpolar(△Gnp) contributions. The steps involve uncharging the solute in vacuum , removing the solute-solvent interaction in vacuum (no free energy change), creating a solute cavity (), establishing uncharged solute-solvent interaction in solvent (), and charging the solute in solvent (). The figure is adapted from Levy et al.22
Although PB solvation has been used in MD simulations23-25, GB is typically chosen for MD due to the reduced computational complexity of calculating solvation energies and the associated derivatives. The use of GB in MD applications has also gained in popularity in recent years due to two factors: improved accuracy in simple GB models, and their efficient implementation on fast general purpose Graphics Processing Units (GPUs)26. These GB models27-29 are often trained to reproduce the PB energies, along with the PB-based “perfect” effective radii30, employing additive and pairwise analytical energies and derivatives. This pairwise descreening algorithm31 serves as an ideal platform for GPU parallelization26. When the same instruction is executed for every atom pair in the protein system, massively efficient GPU cores can compute the desired values simultaneously. Compared to parallel performance of CPU implementation with all double precision calculations, a single GPU using the mixed precision model32 can achieve a factor of 2-5 speed up compared to large numbers of CPU cores, as CPU scaling plateaus long before it reaches the GPU performance26.
Although much recent effort has been devoted to improving the polar solvation contribution, less attention has been paid to the nonpolar solvation term. This is likely because of its small magnitude relative to the polar part, questionable accuracy of simple nonpolar models, and significant computational cost. Its two sub-terms are of opposite signs in free energy change, thus this term is often treated as negligible; cavity-creation loses entropy, while formation of attractive solute-solvent interaction gains enthalpy15. Compared to a solvation energy of −5.0 kcal/mol for a polar molecule, this number is only 1.8 kcal/mol for a nonpolar molecule of similar composition (e.g. ethanol vs. ethane)33. In other reported literature, even if nonpolar contributions were considered, the implicit solvent accuracy was not improved with respect to experimental or explicit solvent results34. Even with demonstrated optimizations16, 22, 35–36, the cavity sub-term, particularly the SASA, remains a major resource demanding calculation. Moreover, in contrast to the fact that all the other energy terms can be computed on GPUs in the most recent Amber implementation37, the SASA-based nonpolar approaches can only be calculated on CPUs, producing a bottleneck that severely limits sampling in simulations.
Our motivation to revisit the nonpolar solvation aspect arose from our recent study of protein folding simulations using only polar solvation3. Although we could sample folding for proteins up to nearly 100 amino acids in standard MD on GPUs using only the polar solvation term (GB-neck227, 29), we observed that the proteins tested in our folding studies3 and Perez et al.’s structure predictions5 suffered from poor folding stability compared to experiment. In some of the small proteins (CLN025, Trp-cage, Villin HP36 etc.), even though folding to native conformations is accessible from only sequence data to as close as 1 Å, and correct trends in the melting behavior could be reproduced3, 5, simulated melting temperatures (Tms) were usually off by tens of Kelvin (see Results). We hypothesized3 that this instability might be a result of neglecting nonpolar solvation in our model. It was also suggested by Chen and Brooks14 that a fine tuning non-polar solvation model might be helpful or sufficient for proteins such as HP36. Shell and Dill et al. also suggested38 that more studies are needed to explore the impact of surface area contributions to simulated protein stability. Here, we investigate and quantify the effect of a nonpolar term on protein stability and conformational equilibria in MD with the same protein force field39 and GB model27 that we used for the protein folding study3. Moreover, we study the extent to which a simple SASA-based approach could improve reproduction of experimentally determined properties such as folding free energy.
In our opinion, an analytical, GPU-compatible nonpolar solvation energy term currently is needed before we can carry out thorough investigations on the impact of nonpolar term in MD of larger proteins. Numerical approaches of Lee and Richards40, and other geometric constructions41–42, are computationally costly and not suitable for our purpose, since folding requires many microseconds of MD that remain intractable using these existing methods. Analytical approximations expressed as a function of interatomic distances are more attractive. Wodak and Janin43 developed the first algorithm exploiting a probabilistic method in which atoms or residues are assumed to randomly distributed in space using excluded volumes; the probability that a surface is accessible on one sphere is the product of individual probabilities for all pairwise intersecting spheres. Negative SSA values were forced to be zero. Hasel and Still et al.44 modified this approach for atomic surface areas. Dynerman et al.45 implemented this algorithm on GPU and refit the parameters to calculate SASA changes in protein docking studies. However, their approach is not ideal for MD simulations because when atom pairs are considered, the derivatives are not mutually of the same value and are not pairwise additive. Weiser and Still et al.46 derived an even faster formula approximating atomic surfaces from linear combinations of pairwise overlaps (LCPO), which is the current nonpolar implementation (gbsa=1) for Amber simulations. Along with another pairwise algorithm developed by Vasilyev and Purisima47, it has been implemented on CPUs for MD simulations. These are not optimal for our purpose because we seek for a simple and fast approximation that can be embedded in the same code loops as the other nonbonded energy terms in the current Amber GPU-implementation26, 37, without the need of additional, nested loops for nonpolar term evaluations. Richmond48 and later Wesson and Eisenberg49–50 provided area derivatives with respect to the atomic positions, but they are not pairwise additive and also not suitable for fast parallel GPU implementation. Different approaches taken by Schaefer and Karplus et al.51 make use of the effective Born radii calculated in GB equations, which is not independent of polar term used in solvation. It may also be beneficial to have a method to estimate SASA without the need for the full GB polar solvation calculation, for use in SASA-based methods that also estimate the polar solvation by using atom type specific surface tensions, or atomic solvation parameters (ASP), such used in the work of Eisenberg et al.52 and some preceding work49, 53.
Here, we explore a simple pairwise approach that would be amenable to fast GPU calculations in situ. Similar to previous work by Guvench et al., our pwSASA algorithm is designed to estimate SASA from short-range atom pair distances. For each atom, the SASA equals a maximum value, subtracting the sum of the areas that are buried or shielded due to other neighboring atoms preventing waters from accessing to the atom of interest. The ideal shielding function would re-use terms that are already being calculated for the non-solvation energies and forces. In principle, this could provide a SASA estimate with nearly no additional computational cost. Our approach is inspired by Vasilyev and Purisima47, who employed a recursive Lorentz function to compute the central atom’s SASA from distances to all other atoms, and Guvench et al.54, who used a 4th-order polynomial using pairwise distance data. We adhere to a single function, but without recursive iteration complexity, to maintain its pairwise evaluation and minimal burden in speed. A monotonic and continuously differential function is chosen to best represent the pairwise burial term. Similar to Guvench et al.54, we utilize the unique geometry environments for different protein atoms by defining specific atom types for parameterization. These atom types account for change in SASA due to bonded atoms, and also help us incorporate non-pairwise contributions in a mean-field manner. In our model, each pwSASA type possesses one parameter representing the base maximum SASA value and another two parameters describing how much this atom can shield other atoms’ SASA and how this shielding profile changes over distance. Trained to reproduce numerical SASA values for all the atoms in a novel training set of multiple peptides spanning all 20 amino acids, we validate the 90 resulting parameters on a test set of proteins. In addition to comparing SASA profiles for LCPO and our new method, we also compared the ensembles sampled in MD simulations using both SASA calculation methods, as well as simulations without nonpolar solvation.
In the present work, we use the SASA to estimate only △Gnp, thus a reasonable first approximation is that the same surface tension could be used for all atoms. Since a variety of surface tension values have been suggested from different training sets12, 55–56, we further calibrated the surface tension that best reproduces explicit solvent data in a model system with precisely controlled set-up. In this model system (HC16, a 16-residue hydrophobic core fragment of HP36), the surface tension was empirically adjusted to correct the discrepancy between GB and TIP3P simulation results. The optimized surface tension was then used for GB/SA simulations on additional systems.
Overall, we present a fast algorithm for calculating SASA with parameters optimized against diverse protein ensembles, implement the atomic SASA calculations in Amber software on consumer GPUs, and apply our GPU-encoded GB/SA method on four proteins, CLN025, Trp-cage tc5b, Homeodomain variant and HP36, to explore our hypothesis that incorporation of a nonpolar term could improve the predicted protein stabilities. We compared well-converged ensembles obtained using a consistent protocol except for the inclusion or omission of the nonpolar solvation energy. Our findings suggest a potentially valuable role of this inexpensive nonpolar term in the accuracy of our computational model, particularly in improving the ability to predict native-like structures using the GB solvent model in microsecond-timescale implicit solvent simulations.
2. METHODS
2.1. Theory of nonpolar solvation
A SASA-based nonpolar solvation model12 was used, where the free energy is approximated by taking the product of the surface tension scaling factor (γ) and the Solvent Accessible Surface Area (SASA).
| (1) |
2.2. SASA estimations by ICOSA and LCPO algorithm
ICOSA40, 57 surface area (gbsa=2 in Amber) SASA is a numerical method that recursively rolls a 1.4 Å radius water probe on the van der Waals surface of the molecule, starting from an icosahedron. The current Amber implementation does not include derivatives of the SASA, so it is not possible to use in MD where forces are required.
LCPO46 (Linear Combinations of Pairwise Overlaps, gbsa=1 in Amber) is the algorithm used for GB/SA MD simulations in recent Amber versions. It considers the neighbor list of a central atom and subtracts the pairwise overlaps from its isolated sphere area. In practice, this is a three-body approach, as not only the overlaps between the central atom and its neighbor atoms are calculated, but also the overlaps of the neighbors with each other. This adds to the computational complexity compared to our desired (non-recursive pairwise) approach.
2.3. pwSASA: the proposed fast pairwise analytical SASA estimation algorithm
2.3.1. Physical Rationale
Our first step is to assume that the SASA of the molecule can be approximated by considering only the heavy (non-H) atoms, and that H atoms can also be excluded in the calculation of solvent shielding of the heavy atoms. Estimating SASA just for heavy atoms results in a substantial reduction of atom pairs and computational cost, which also has been exploited in LCPO46 and other algorithms47.
The SASA of each atom in a protein configuration is its maximum surface area (termed max_SASAi) subtracting the patches shielded by close neighbor atoms (termed shielded_SASAi):
| (2) |
The simplest (although impractical) case is solvation of a single atom; both the SASAi and max_SASAi for this atom are the surface area of this isolated sphere. In the context of proteins, all atoms have at least one covalent bond, and thus atoms are never exposed entirely to solvent. We decided to handle the shielding by covalent and non-covalent neighbors differently, since the covalent neighbors (bonds and angles) likely have larger overlaps and closer distances than those sampled by purely non-bonded neighbors. This simplifies our construction of a function to estimate the shielding of an atom based on the distance of each neighbor. We also assume that the shielding by covalent neighbors (1–2 and 1–3 neighbors) is approximately independent of conformation, and thus max_SASAi also is independent of the specific conformation and incorporates the shielding of the 1–2 and 1–3 pairs. Therefore, the max_SASAi absorbs any shielding from covalent neighbors and differences in accessibility due to hybridization variants, and implicitly accounts for multi-body effects such as those from overlaps between covalent neighbors.
In this context, what is an atomic max_SASAi in proteins? The answer is that it depends on the local geometry of an atom, including atoms that are covalently linked (bonds, angles etc.). To describe the protein local geometries by defining 30 pwSASA atom types with each representing one specific local geometry of an atom found in proteins (see the detailed classifications in Supporting Info Table S1 and parameters in Table S2). Each element (C, N, O, S) is divided first into different hybridization states, then further divided based on the number and type of bonded heavy atoms. Some types are subsequently divided further to improve quality of fitting. 30 total atom types, termed “pwSASA types”, were used to describe all the protein local geometries. Guvench et al. also used atom types in their procedure54, with a similar but not identical approach to dividing atoms into 26 types (for example, H atoms were included in that work but are not here).
Each pwSASA atom type has an associated constant max_SASAi that is calculated after the fitting of the second term, shielded_SASAi (i.e. the pairwise burial term, or pairwise shielding effect on each other’s accessible surface area). To adhere to the pairwise decomposability, we make two assumptions that (1) the atomic surface area shielded by all other atoms is a sum of pairwise effect, which only iterates once for all the i,j pairs, when atom j iterates over remaining atoms with respect to atom i; (2) this pairwise effect could be represented as a single function of distance separating this atom pair.
| (3) |
| (4) |
As a result, shielded_SASAi for a specific atom pair i, j contributes the same SASA reduction to both atoms i and j, with symmetric forces. But as every atom in a protein possesses its specific local geometry (as defined by pwSASA types and involving different neighbor atoms), iteratively evaluating all the pairwise atoms results in a unique sum for each central atom in its specific conformation of the protein.
In the next section, we focus on the considerations of the functional form we selected, and the parameters used for pairwise burial term evaluations.
2.3.2. Formula and parameterization design
Given the basic idea elaborated in the physical rationale, to calculate atomic SASA, A term shielded_SASAi is computed from summing pairwise burial terms shielded_SASAi,j considering all close neighbor atoms (Equations 2, 3). The pairwise shielded_SASAi,j is assumed to be a function only of pairwise distances (Equations 4) and is conceptually physical. As depicted in Figure 2A, it varies as the two atoms are apart at different distances: when the distance is beyond a certain cutoff, water can traverse the gap and the SASAs are not shielded by each other; when the distance gets smaller, the SASA shielding increases, until the atom fully displaces solvent and thus the shielded SASA reaches its maximum at contact distance. Therefore, a sigmoid-like function with pairwise combinatory parameters is desirable.
Figure 2.
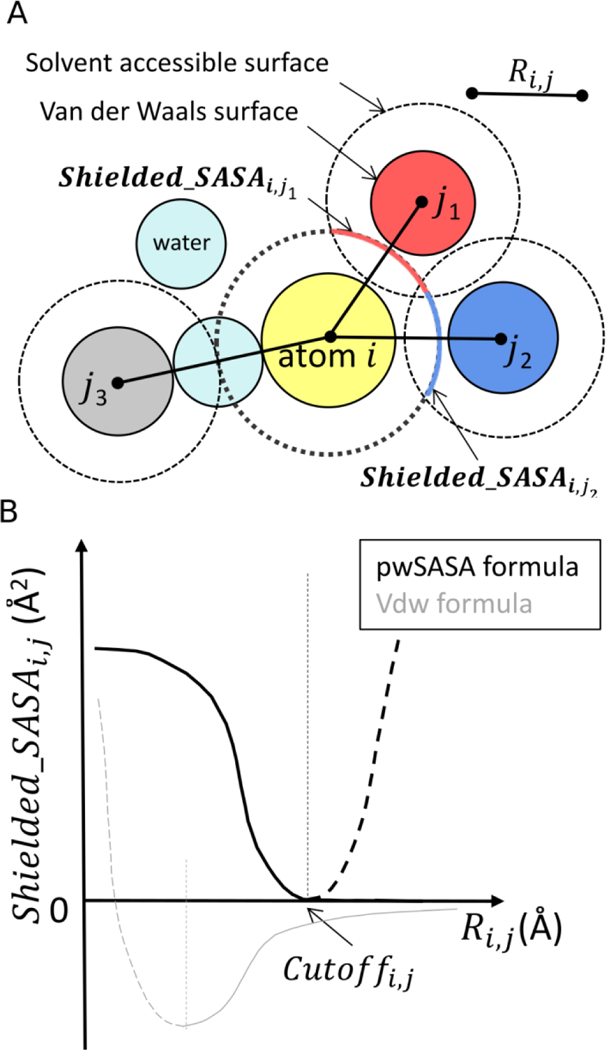
2D illustration of the proposed pwSASA approach for calculating shielded_SASAi,j.
(A) atom i in yellow is the central atom of interest; its SASA (central dotted circle) shielded by atom j1 in red and atom j2 in blue are calculated, respectively, using the pairwise distances Ri,j. Atom j3 in gray is beyond the cutoff distance to atom i thus contributes zero to shielded_SASAi,j.
(B) Our formula (black) is a transformation of the standard Lennard-Jones 6–12 formula (gray), by a reflection over the y-axis followed by an up-right shift. Dashed lines indicate the repulsive Lennard-Jones region that is eliminated in our function through application of a distance cutoff that also ensures force continuity. Details of the derivation are provided in Figure S1 and Equation S1–6.
Many options for a sigmoidal form are possible, including adapting some of the values calculated for the GB polar term for the nonpolar calculation51. Guvench et al. used 4th-order polynomial fitting to estimate screening contributions.54 Our choice of formula is inspired by the Lennard-Jones function (depicted in gray in Figure 2B) that is already being calculated during the simulation, further minimizing the additional computational overhead. The curve is monotonic and continuously differential at all points, and importantly, the pairwise approach of Lennard-Jones parameters can be adapted to generate pair-specific shielded_SASAi,j parameters. Some transformations (a reflection of the Lennard-Jones curve over the y-axis followed by an up/right shift) result in a curve that fits our conceptual goals (black curve in Figure 2B). When the distance of an atom pair Ri,j exceeds a certain point, the resulting shielded_SASAi,j is zero; as Ri,j gets smaller, the burial term gets larger before it reaches a plateau and sensitivity to distance decreases as water is fully displaced. The cutoffi,j values are also taken in a pairwise combinatory way (Equation 8).
The stepwise derivation of the pairwise burial term shielded_SASAi,j is provided in Equations S1-S6, with the final equation as a function of Ri,j shown below:
| (5) |
where σi,j and εi,j are calculated from pwSASA-type specific parameters discussed below. The values of m and n are also discussed below. Cutoffi,j is a pairwise constant calculated from atomic radii. We note that the function and its derivatives with respect to atomic coordinates are continuous across the cutoff point, differing from the Guvench et al. work where a force discontinuity is present at the cutoff point.54 We evaluated energy conservation with and without the pwSASA energy term, and found that addition of pwSASA had neglible impact on the energy conservation (Figure S4; additional details provided in Supporting Information).
For each atom of a given pwSASA type, two parameters σi, and εi, are needed to describe its ability to shield other atoms (hence 60 total). For each atom pair, we use the Lorentz-Berthelot combination rules to obtain the σi,j and εi,j values:
| (6) |
| (7) |
The cutoff distance is employed to ensure that when two atoms are far enough apart (Ri,j ≥ Cutoffi,j) they do not contribute to each other’s shielded_SASA. This eliminates the repulsive portion originally present in the Lennard-Jones-type function (dashed lines in Figure 2B) and ensures force continuity through the cutoff distance. Cutoff distances are the sum of the atomic radius and the water probe radius (1.4 Å). The same atomic radii for four elements (C 1.7 Å, O 1.5 A, N 1.55 Å and S 1.8 Å) were used both here and in ICOSA. Different radii were used with LCPO (C 1.7 Å, O 1.6 Å, N 1.65 Å and S 1.9 Å) to be consistent with the values used during the original training of the 54 LCPO parameters58.
| (8) |
| (9) |
The exponents m and n determine the steepness of the shielded_SASi,j transition as the two atoms approach. Values for n were tested among 2, 4, 6 and 8; n = 4 gave the best atomic SASA correlation (data not shown). Correlation was less affected by the choice of m when 10 and 12 were used for comparison, so m = 10 was initially used in the optimization. As other values for m and n did not improve the accuracy of the algorithm (data not shown), and parameterizations of σi and εi values also affect the depth and steepness of the pairwise curves, we kept m = 10 and n = 4 for all atom pairs.
2.3.3. Training set and Fitting strategy
The 60 parameters for pwSASA atom type specific shielding were fit against ICOSA SASAs (also calculated using only heavy atoms) on a training set of 10 peptides. To cover a broad spectrum of atomic environments and possible atomic pairwise contacts and extents of burial, we designed a set of 10 sequences (Table S3); each is a scrambled sequence made of all 20 natural amino acids (using all 3 protonation variants for the His side chain, thus each peptide was 22 amino acids in length). Together, conformational ensembles for these scrambled peptides provide significant statistics for atomic SASA ranges, and they encompass the distributions of pairwise distance distributions expected in real proteins (Figure S2).
For each sequence, 50 geometries of diverse structures were included in the training set ensembles. Ensembles were generated as follows: initial conformations were generated from fully extended structures constructed using tleap, with 1000 steps of minimization to ensure reasonable initial geometries. This was followed by 1 μs of unrestrained MD simulation at 300K (using a Langevin thermostat, the ff14SBonlysc39 force field in GB-Neck227 solvent without SA term) producing 5000 conformations equally spaced in time. The cpptraj program59 was used to separate each trajectory into 50 clusters using the hierarchical agglomerative algorithm, based on all 22 Cα atoms. These 50 representative structures from each peptide sequence comprised the training set ensembles. Table S3 shows the representative structure of the most populated cluster for each peptide. We calculated reference atomic SASA values for each heavy atom in each structure using a modified version of sander (where Atom_Radius for hydrogen was set to zero in the icosa subroutine) in Amber 1637.
Fitting of parameters was done as follows (for further details, see Supporting Information). Initial guesses for all 60 parameters were randomly generated, then were optimized using the l_bfgs_b algorithm60 in the Python Scipy package61. The objective function used for optimization was:
| (10) |
where:
| (11) |
where frame_a and frame_b represent two different conformations from the training set for that peptide. As Vasilyev and Purisima pointed out47, the change in the accessible surface area is often of more interest than the absolute value. In addition, as max_SASAi is a constant for one specific pwSASA type, fitting to ΔSASAi results in isolation of the 30 max_SASAi parameters since they cancel in the target ΔSASAi values. For these reasons, we fit the 30 sets of σi and εi parameters to the SASA difference between pairs of conformations.
Instead of iterating over all combinations of conformation pairs, we sorted the atomic SASA of all 500 representatives, picked the 2 conformations with largest and smallest SASA as the first pair, then the second largest and the second smallest as the second pair, and so on. The reasons not to include all pairs of 500 conformations are (1) all 250,000 conformation pairs per atom for one evaluation of optimization is more time-consuming, (2) many data are redundant if each conformation to every other conformation is included, and (3) most importantly, most of the SASA differences are quite small if all conformation pairs are included, and the squared differences would weigh even less in the optimization function (Equation 10), resulting in inefficient data use. In the end, we adopted a sorted pair scheme that included 250 pairs of conformations for each atom in optimizations, and a flatter distribution of SASA difference values compared to the more costly all pairs scheme (Figure S3).
As discussed above, fitting the changes in SASA results in cancellation of the max_SASAi in the scoring function. Calculating the 30 max_SASAi values was done after optimizing the 60 σi and εi values. For each SASA type, the max_SASA was obtained by taking the arithmetic average of the difference between the icosahedral SASA and the calculated shielded_SASA, over all atoms of that SASA type:
| (12) |
where N equals to the total number of atoms of that pwSASA type.
2.3.4. Test set
18 proteins were used as a test set to validate SASA estimation. This set of proteins of diverse topologies ranging from 10 to 92 amino acids corresponds to the set we previously used for ab initio protein folding3. The structural ensembles for the test set were extracted from the protein folding trajectories in that work to get a set of structures spanning diverse atomic and molecular SASA values to evaluate the new pairwise model. The model system HC16 was also included. Reference data were calculated for each structure using the ICOSA and LCPO algorithms.
2.4. Simulated protein systems
2.4.1. HC16 with helical restraints
HC16 (16-residues with ACE and NHE caps, with sequence DEDFKAVFGMTRSAFA) consists of the hydrophobic core of HP21 (a Villin headpiece HP36 fragment). HP21 was reported to transiently adopt a native-like conformation similar to that in full-length HP3662, retaining the core of three phenylalanine residues, Phe47, Phe51, and Phe58 (we adopt the widely used numbering of residues derived from intact Villin headpiece). HC16 retains the structured region of HP21.
To facilitate obtaining converged data in explicit solvent, and also to maximally isolate the difference between simulations to the presence or absence of nonpolar solvation, we restrained 7 hydrogen bonds in the backbone of HC16 with 50 kcal/(mol Å2) force constant: ace.O-Phe47.H (1.94 Å), Asp44.O-Lys48.H (1.95 Å), Glu45.O-Ala49.H (2.41 Å), Phe47.O-Val50.H (1.87 Å), Thr54.O-Phe58.H (1.67 Å), Arg55.O-Ala59.H (2.24 Å), Ala57.O-nhe.H (2.07 Å). The distances for the restraints (listed respectively in the parentheses and depicted in Figure 3A) were selected as those present in the NMR structure63 of HP36. The HC16 model system is precisely controlled by setting the nonpolar term as the single variable in benchmark simulations; we hypothesize that when the two helices in HC16 are rigorously restrained to the secondary structures adopted in folded conformations, the thermodynamic stability in hydrophobic core formation and breakdown is dominated by the effectiveness of nonpolar term. Restraining the helices has the double benefit of (1) simplifying sampling in explicit solvent (still highly challenging to fully converge for 16 amino acids), and (2) reducing the potential influence of differences in secondary structure propensity from the polar portion of the implicit/explicit solvent64 (although we note that the GBneck2 model used here has excellent agreement with TIP3P in this respect27).
Figure 3.
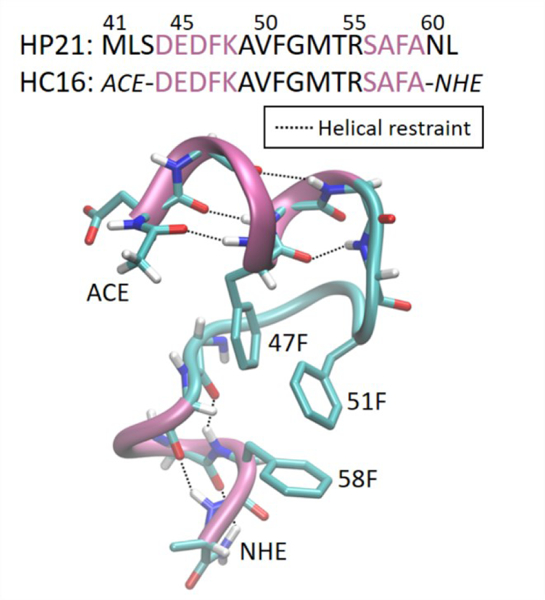
HC16 (Hydrophobic-Core 16-residue) sequence and conformation as adopted in the NMR structure of HP36 (PDB code: 1VII63). The sequence of HP21 which has been characterized in experiment62 is also listed for comparison. The two helices shown in pink were restrained with hydrogen bonds shown in black dotted lines. Side chains of three Phe (comprising the hydrophobic core of HP36) and capped termini are denoted.
2.4.2. Unrestrained Cln025, Trp-cage, HP36 and Homeodomain
Chignolin variant CLN025 is a 10-residue mini-protein with sequence YYDPETGTWY. CLN025 adopts a stable hairpin conformation, determined by both crystallography (PDB code: 5AWL65) and aqueous state NMR (PDB code: 2RVD65).
Trp-cage variant tc5b is a 20-residue mini-protein with sequence NLYIQWLKDGGPSSGRPPPS. Designed and solved via NMR (PDB code: 1L2Y66) in 2002, it is designated as the ‘Trp-cage’ motif because the burial of a hydrophobic Tryptophan side chain is thought to be a driving force of its folding. It contains secondary structure of an α-helix, a short 310-helix and the Trp indole ring encapsulated in a cluster of Pro rings.
HP36 is the naturally found 36-residue Villin headpiece subdomain with a full sequence MLSDEDFKAVFGMTRSAFANLPLWKQQNLKKEKGLF. It is recognized to fold into a compact native state with three α-helices as solved by NMR (PDB code: 1VII63).
Homeodomain is a 52-residue computationally re-designed variant of Drosophila melanogaster engrailed homeodomain, with sequence MKQWSENVEEKLKEFVKRHδQRITQEELHδQYAQRLGLNEEAIRQFFEEFEQRK. The NMR-solved native structure (PDB code:2P6J67) is thermally stable, and like HP36 consists of three a-helices but with a different overall fold.
Experimental melting curves for CLN02565, Trp-cage66 and HP3668 were obtained from CD experiments. The melting temperature of the Homeodomain variant was measured from CD67. All 4 systems were previously studied in our ab initio folding experiments3 using the same force field and solvent model used here, providing an excellent reference to quantify the possible improvement by addition of a nonpolar solvation term.
2.5. MD simulation and analysis details
2.5.1. Explicit solvent simulations of restrained HC16
Helical distance restraints described in 2.4.1 were applied to the HC16 system in explicit solvent simulations. Two sets of simulations were initiated from two conformations: one “restrained unfolded” and the other as observed in HP36 NMR structure. The “restrained unfolded” conformation was generated from a short high-temperature MD simulation starting from the NMR structure; after this 1 ns short MD run at 500K with chirality and helical distance restraints, the conformation of maximal end-to-end distance (25.9 Å vs. 16.0 Å as in NMR structure) was equilibrated with helical restraints at 300K as the “restrained unfolded” structure. HC16 was parameterized in ff14SBonlysc39 and solvated with 2187 TIP3P69 water molecules in a truncated octahedral periodic box. The distance from solute to the edge of the box was at least 9 Å for the “restrained unfolded” structure, and increased to 11.061 Å for the NMR structure so that the total number of atoms was equivalent for the two simulations. For the equilibration, 10000 steps of energy minimization were first done with 100 kcal/(mol Å2) positional restraints on all heavy atoms, followed by 100 ps of MD heating from 100 to 300K at constant volume. Next, 100 ps and 250 ps of constant pressure MD simulations were done with 100 and 10 kcal/(mol Å2) force constant, respectively. Another 10000 steps of minimization with backbone positional restraints of 10 kcal/(mol Å2) were followed by 100 ps of MD simulation at constant pressure and temperature. Then three 100 ps simulations (with 1, 0.1, 0 kcal/(mol Å2) backbone restraints, respectively) were done with helical restraints as described in 2.4.1. The helical restraints were maintained throughout the production runs. Replica Exchange Molecular Dynamics (REMD) simulations were performed to help overcome viscosity barriers in explicit solvent, using 32 replicas in the NVT ensemble; 8.0 Â was used as the nonbonded direct space cutoff; Langevin dynamics with 1 ps−1 collision frequency was used; thermostat temperatures ranged from 294.4 K to 394.4 K (the full temperature ladder is reported in Table S5). Each replica was simulated for > 2.6 μs, giving a cumulative 83 μs of simulation time and requiring ~15 days on Tesla K20X using the Amber 16 GPU (CUDA) version of PMEMD. The PMF profile at 300K was calculated with the temperature-biased weighted histogram analysis method (TWHAM)70.
2.5.2. GB and GB/SA simulations
SHAKE constraints71 were applied on all bonds involving hydrogen. Langevin dynamics used 1 ps−1 collision frequency (ntt=3) and 4 fs time step via hydrogen mass repartitioning (following the published protocol72 in which masses of H atoms are scaled by a factor of 3, with the extra mass being subtracted from that of the bonded heavy atom).
Restrained HC16 model system.
Restrained HC16 parameterized in ff14SBonlysc39 was simulated in GBNeck2 (igb=8) with mbondi3 radii27. GB simulations without nonpolar solvation used gbsa=0. Two runs of Langevin dynamics simulations starting from the two conformations were run at 300K, each for 16 μs. Cluster analysis comparing pairwise RMSD between structures was performed on the last 8 μs of simulations (2 runs of 8000 frames, 16000 frames in total). The hierarchical agglomerative algorithm in cpptraj program59 was used for clustering, based on all 16 Ca atoms at a 2 Å cutoff.
REMD was used to enhance the sampling efficiency for all GB/SA simulations since compact conformations were stabilized relative to unfolded states, and simulations at 300K sampled high RMSD conformations too rarely for precise quantification of stability. In Amber, gbsa=1 was used for LCPO algorithm and gbsa=3 was used for our new pairwise model. Surface tension values (surften flag) of 5, 7, 10 and 12 cal/(mol Å2) were tested. For each surface tension, two production runs starting from the “restrained unfolded” and NMR structures were simulated to 4 μs per replica of REMD with 6 replicas to obtain well-converged data; thermostat temperatures ranged from 279.5 K to 397.9 K (see Table S5). It took > 60 days for GB/(LCPO)SA to generate 4 μs of simulations on 4 cpu cores for each replica, while 4 days were sufficient to collect the same amount of data for GB/(pairwise)SA, on 1 GXT680 GPU for each replica.
PMF structure equilibrium profiles were calculated using a collective variable of RMSD of all Cα atoms, against native structure as in HP36. This can be interpreted as the reconstructed free energy landscape projection onto the RMSD space. We first histogrammed the RMSD values for all sampled structures at 300 K (either directly from MD simulations running at 300 K or extracting 300 K trajectories from REMD simulations), using a bin size of 0.1, in the range 0–7 Å. We then defined the relative free energy for each bin, using Equation 13:
| (13) |
where R is the gas constant (1.9858775×10−3 kcal-K−1-mol−1), T is 300 K, and N is the largest bin population. The error bars on PMF plots reflect the absolute deviation of free energies for each bin calculated from the two independent simulations starting from different conformations.
Unrestrained proteins.
CLN025, Trp-cage, HP36 and Homeodomain variant were simulated without restraints in REMD, employing ff14SBonlysc and GBNeck2 with mbondi3 radii; both LCPO and our pairwise SA were used in separate simulations. Surface tension was 7 cal/(mol Å2) unless otherwise specified. For each system, two production runs starting from fully extended or experimental structure were simulated. For CLN025, 6 replicas (252.3 K – 389.1 K, see Table S5) REMD were done for 1.3 μs in GB, 1.5 μs in LCPO and 8 μs in pairwise SASA. A backbone RMSD cutoff of 2.2 Å was used for calculating fraction of folded, consistent with our previous study3. For Trp-cage, 8 replicas (247.7 K – 387.3 K, see Table S5) REMD were simulated for 1.7 μs in GB, 1.4 μs in LCPO and 4 μs in pairwise SASA. A backbone RMSD cutoff of 2.0 Å was used for calculating fraction of folded27. In both CLN025 and Trp-cage, the last half of the trajectories of the two runs were used for melting curve plotting. For Homeodomain variant, 12 replicas (288.7 K – 440.3 K, see Table S5) REMD were simulated for 4 μs for GB and pairwise GB/SA. A backbone RMSD cutoff of 5.0 Å was used for fraction of folded calculations. For HP36, 8 replicas (250.0 K – 349.0 K, see Table S5) REMD were simulated for 4.2 μs in GB. As simulations in LCPO used a surface tension of 10 cal/(mol Å2) for 650 ns, the pairwise SASA used the same surface tension to be consistent. REMD simulations were run for 24 μs to converge. Cluster analysis was done on the lowest temperature trajectories (250K) using the same protocol as for HC16 GB trajectories, based on all 36 Cα atoms. Another set of HP36 REMD simulations were carried out in ff14SB39 with GBNeck2 for 20 μs to explore whether the observed misfolding of HP36 could arise from force field inaccuracies.
3. RESULTS
3.1. SASA estimation by the proposed algorithm
3.1.1. Parameterization on atomic SASA of training set
As stated in Methods, we defined 30 pwSASA types, each with two parameters σ and ε, to characterize variation of SASA with the possible pairwise atomic contacts found in proteins. All 60 parameters were optimized to minimize least square errors with respect to the ICOSA-based SASA numerical changes for all the heavy atoms in the scrambled peptide training set. The optimization took multiple rounds to best reproduce in Equation 10. We verified that reducing the pwSASA types or the peptide species worsens the fit quality, but using fewer frames for each peptide ensemble made less difference. The resulting σ and ε values are provided in Table S2, along with the calculated max-SASA parameters.
The final set of parameters reasonably reproduces the atomic SASA for heavy atoms in the trained peptides, shown separately for each of the 30 pwSASA types in Figure 4. Among all the types, hydrogen atoms are defined as ‘1H’ type and excluded in both reference and estimation. Nitrogen atoms ‘4NCC’ that bond with 3 other heavy atoms in sp3 hybridization were set to zero SASA, for they are highly buried in trained peptides and test proteins. The estimated atomic SASA values scatter around the diagonals that represent perfect fittings. In particular, the diagonals go through the densest data (dark red) regions for all atom types, which indicates excellent agreement for the most frequently sampled atomic SASA values. The coefficients of determination (R2 for the linear regression between ICOSA values and our estimations) vary from 0.28 (‘5CCN2’) to 0.91 (‘1SC’). However, those with lower correlation tend to adopt a small range of SASA values (e.g. ‘2NCC’, “3CCC”); the R2 for atom types sampling atomic SASA over 20 Å are all above 0.50. For the atom types that are seldom exposed to solvent (e.g. “4xxx”, 5xxx”), the pairwise estimate also indicates burial with close to 0 Å atomic SASA.
Figure 4.
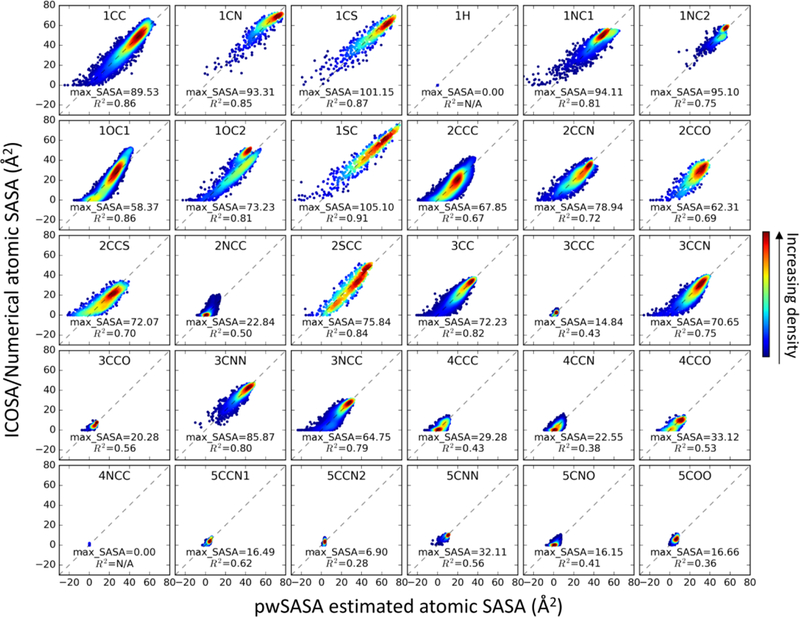
2D histograms of pairwise atomic SASA of each pwSASA type, versus ICOSA-based numerical values in the training set. Perfect agreement would coincide with the diagonal dashed lines. The color indicates the kernel density estimated using scipy gaussian_kde73.
For the totally buried heavy atoms, our algorithm sometimes produces negative SASA values. The appearance of a small number of negate atomic SASA values also was previously observed by Guvench at al54. Our pairwise burial algorithm assumes the mutually buried surface areas could be averaged to a pairwise fashion, which can be captured by one monotonic function. While our fitting works well for the more exposed instances of a pwSASA type, the accuracy suffers for the most buried examples of that pwSASA type. For example, for the ‘1SC’ type atoms that have SASA > 30 Å2, data points fall closely around the diagonal and visually correlate well, compared with lower accuracy for the instances with SASA < 30 Å2. This observation applies to almost all other pwSASA types. When atoms become deeply buried, our current algorithm continues to assign (small) shielding contributions from atoms in the tail of the sigmoidal function. A better-designed switching function might eliminate these negative SASA values, but in the current implementation we did not explore this more since our goal was to develop a simple, fast approach, and the frequency of observing the slightly negative SASA values is quite low overall. Furthermore, the changes in the SASA are more important than the absolute values.
3.1.1. Accuracy of atomic SASA values in protein ensemble test set
We next used the pwSASA parameters that were fit on the scrambled peptides to calculate atomic SASA values for the diverse structures in the ensembles for the test set of 18 proteins. As seen in Figure S5, the results are highly similar to those from the peptide training data (Figure 4). For some pwSASA types (such as 1CC and 1OC2), the data appear to cluster into 2 groups, suggesting that the fit could be improved somewhat by additional splitting of these pwSASA types and refitting. This may be explored in a future update to the parameters.
As discussed above, our approach to estimating atomic SASA through a pairwise calculations has significant similarity to that of Guvench et al.54 A direct comparison of performance by SASA type is not possible since their atom types differ from ours. Moreover, the Guvench types include H atoms, leading to significantly different absolute atomic SASA values for most heavy atoms. However, we tested the Guvench method on our protein ensemble test set. As seen in Figure S6, accuracy of the Guvench atomic SASA values for each SASA type are generally of comparable accuracy as our pwSASA, with the exception of three SASA types for which the accuracy of SASA estimation is significantly lower. These calculations employed the default parameters reported by Guvench et al.; examination of the polynomial curves estimating the atomic SASAs shows that the curves for these three atom types significantly deviate from the exact SASA values (Figure S7). We retrained their c0-c4 parameters data and obtained polynomial curves that reflect an improved match to the atomic SASA values (Figure S7, with additional details, methods and new parameters provided in Supporting Information).
3.1.3. Estimation of molecular SASA in the protein ensemble test set
Generally, we would expect that high correlations of the atomic SASA values (calculated to obtain forces) would also result in accurate molecular SASA values when the atomic values are summed. However, we observed that the sum of estimated atomic SASA values systematically deviates from the numerical molecular values, which was also encountered in Dynerman et al.’s work where computed SASA values (desolvation energy changes calculated from SASA, to be specific) systematically deviate from numerical numbers in a proportional manner45. We ascribe it to be a negative consequence of tolerating inaccuracies in atomic SASA pairwise estimation. The occurrence of negative SASAs, along with correlation in errors for different atoms, attribute to cumulative errors in molecular SASA estimations, which was further adjusted by linear transformations described below.
Given the systematic error from summing our simple pairwise atomic SASA estimates, we decided to empirically adjust the sum of our atomic estimations to more closely match molecular values. By comparing total SASA values we found that a universal scaling factor 0.6 worked well in terms of energy and forces; this is equivalent to scaling the designated surface tension γ by 0.6. It is recommended for users to bear in mind that molecular SASA values for the test set directly estimated as sums of atomic SASA values systematically deviate from numerical ICOSA calculations (Figure S8). The total SASA shown in Figure 5 were obtained from summed atomic SASA through scaling by 0.6 and adding an offset, which compensates for the difference of ICOSA SASA and the scaled shielded sums (see details in Supporting Info, Equations S7-S11 and Figure S9). In Amber, we encoded the scaling factor directly so users could obtain comparable results for different SASA algorithms when setting a particular surface tension value.
Figure 5.
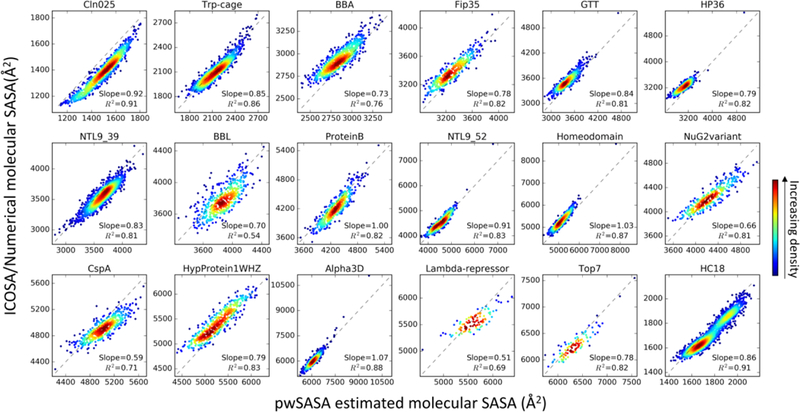
2D histograms for each protein, showing fitted molecular SASA versus ICOSA numerical values for the test set. Perfect agreement is indicated by the diagonal dashed lines. The color indicates the kernel density estimated using scipy gaussian_kde73.
After transformations, the estimated molecular SASA values become better estimates of the numerical values for the 18 test protein systems in Figure 5. The coefficients of determination range from 0.54 for BBL, 0.69 for λ-repressor, to above 0.8 for CLN025, Trp-cage, Fip35, GTT, HP36, HC16, NTL9 (39 and 52 residues), ProteinB, Homeodomain, NuG2variant, Hypothetical protein 1WHZ, α3D, and Top7. Overall, in 15 out of the 18 protein test systems, we can estimate the SASA to well correlate with numerical calculations (Pearson correlation efficient, R2 > 0.81) across the range of sampled conformations. This is encouraging given that the parameters were trained on short peptides with scrambled sequences; even though the local pairwise atom contacts are similar between the training and test sets, the transferability to larger proteins is still reassuring.
In most cases, our fast estimations tend to slightly overestimate the ICOSA molecular SASA differences (indicated by slope < 1), but the same effect is also observed in LCPO-based SASA predictions for the same test set (Figure S10); this can be attenuated by decreasing the chosen surface tension. Notably, the cases for which our estimation qualities are worse than average (BBA, BBL, NuG2variant and λ-repressor) are also challenging and among the worst predictions for LCPO. This suggests there may be some specificities in these proteins, where local geometric features are insufficient for predicting solvation properties.
It is possible that pwSASA estimation accuracy could be further improved by refining the functional forms for our pairwise estimates, or fitting pair-dependent shielding parameters and avoiding the approximations invoked by using combining rules. . However, a SASA-only nonpolar term is itself a crude estimation of non-electrostatic solvation, perhaps suggesting that adding further complexity and computation cost may not be worthwhile. However, before this work, except nonpolar term, all the other energy terms were accessible on GPUs. Having the nonpolar term left out hindered the possibility of extensive tests with a more complete description of solvation, and quantitative analysis of the impact of SASA-based nonpolar solvation on well-converged ensembles for non-trivial systems. Thus our focus here is not on an ideal SASA calculation, but what benefits, if any, can be obtained from simple SASA-based approaches amenable for generating very long protein MD simulations. Once these are implemented in a form fast enough to converge ensembles for non-trivial proteins, it will become possible to examine the extent to which further optimization can improve agreement with experiment. In the next section, the acceleration in MD simulations achieved by GPU implementation is illustrated and described in detail. The efficiency of the pwSASA algorithm is compared to LCPO. Convergence is comparable within the same simulation time, but the overall wallclock speed (computational cost) of the simulations is sped up by more than an order of magnitude using pwSASA.
3.2. Speed up in MD simulations
The parameter set for pwSASA was coded in a modified version of Amber version 1637. Setting the gbsa flag to 3 in GB simulations activates GB/SA using pwSASA in the sander, pmemd or pmemd.cuda (all precisions) programs. Compared with the existing hybrid GPU/CPU algorithm74 needing the CPUs for the LCPO algorithm and GPU for remaining terms in the force field, pwSASA calculates all energy/force terms on GPUs, if designated, and thus accelerates the MD production run by tens of times.
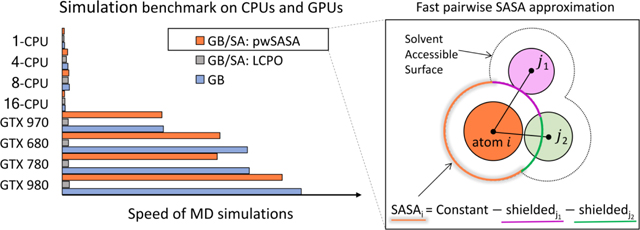
After implementation in the Amber software, simulation benchmarks establishing the performance of simulating unrestrained HP36 are shown in Figure 6 below. On CPUs, simulations using GB, GB/SA (LCPO) and GB/SA (pwSASA) are similar in speed, with LCPO being slightly slower. However, pwSASA was really targeted to GPU-style massive parallelism. Compared to less than 40 ns/day with 8-core CPU clusters, the slowest GPU calculation (GTX 970) provides 665 ns/day using pwSASA. Importantly, adding pwSASA calculations incurs little additional overhead compared to simulations without it (676 ns/day). As the compute capability of GPU increases, the speed accelerations over LCPO reached 31× (single GTX 980). These accelerations are comparable to standard Amber GPU performance26, and are also consistent with our design of the algorithm. The only information needed is how far each central heavy atom is from its close neighbor atoms within the solvent accessible distances, and with no recursive neighbor-neighbor calculations required. These distances have already been pre-calculated and cached for the electrostatic, van der Waals, and polar part of solvation computations, and the pwSASA calculation can be embedded in the same loops and parallel decomposition schemes. Our nonpolar calculation is also implemented fully on the GPU, without the need to transfer back and forth between GPUs and CPUs, as is necessary by the current LCPO code.
Figure 6.
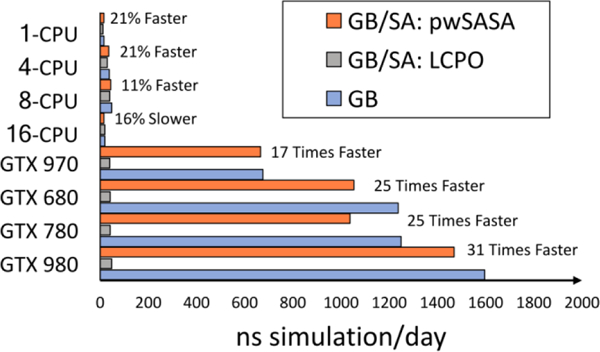
Performance benchmarks on CPUs and single gaming GPUs, simulating HP36 in GB and GB/SA (LCPO and pwSASA) models. The speed up multiples (percentages) denoted are calculated from the respective ns simulation/day achieved in our method divided by that obtained using LCPO on the same architecture.
An efficient GPU-parallelizable algorithm requires the same instructions be executed for every neighbor atom j of i indistinguishably. In LCPO (gbsa=1), the SASA of a central atom i is dependent on not only the neighbors of i, but also the overlaps of the neighbors with each other. For example, in Figure 2, atom j1 and j2 are both neighbors of atom i. In determination of the SASA for atom i, not only atom pair (i,j1) and (i,j2) are involved, but atom pair (j1,j2) also contributes. This extra consideration makes LCPO a many-body algorithm and not as suitable for GPU parallelization. Therefore, even if GPU devices are employed for GB/(LCPO)SA simulations, the SA portion becomes a major bottleneck. In pwSASA, the same Equation 5 is used for all two atom pairs (with different corresponding parameters), thus it is an ideal fit for GPU parallelization. Importantly, we could still get reasonable results by adopting the two-body algorithm, because our 30 pwSASA atom types provide pre-adjustments estimating three-body effects in a mean-field way, without impacting parallel performance.
3.3. Stability of the hydrophobic core in the HC16 model system
3.3.1. Calibration model system and rationale
We next carried out a quantitative comparison of explicit and implicit solvent results on a controlled peptide fragment, in which the role of the solvent model could be isolated from other variables that confound direct comparison to experiment such as protein force field accuracy. We use the hydrophobic core of HP36, a peptide of 16 residues termed “HC16” (Figure 3), with a packed hydrophobic core made of side chains protruding from two α-helices.
In the restrained HC16 model system, we used consistent computational methods and simulation protocols except for the nonpolar term: (GB) GB as the polar term and no nonpolar term used; (TIP3P) TIP3P as a full solvation description of both polar and nonpolar terms; and (GB/SA) GB as the polar term and nonpolar term incorporated through SASA, modulated by scaling the surface tension. Comparing ensembles from LCPO and pwSASA evaluates our SASA approximation, and comparing the TIP3P, GB and GB/SA simulations allows tuning of an appropriate surface tension value and evaluation of the extent to which this approximation can improve reproduction of explicit solvent results.
3.3.2. Quantification of discrepancies between GB and TIP3P
As stated earlier, proteins solvated in the GBneck2 model alone exhibit low folding stability3. We hypothesized that this is due to lack of nonpolar solvation stabilizing the hydrophobic core, and that an explicit solvent model like TIP3P may produce a more accurate result. Therefore, we first investigate structurally and energetically the conformational equilibrium of HC16 in both GB and TIP3P to see if expected stability differences are recapitulated, by comparing well-converged simulations that are largely identical except for nonpolar solvation.
Although the PMF profiles all exhibit dominant global minima at low RMSD values as shown in Figure 7A, differences manifest as discrepancies in the sampled structural ensembles. Without the nonpolar term, GB predicts a smaller energy gap and flatter energy surface for the unfolded conformations. The GB PMF falls below the TIP3P PMF as soon as the RMSD advances beyond the native-like minimum, with maximum energy difference close to 2 kcal/mol (at around 4 Å Cα-RMSD). Furthermore, the cluster analysis (see Table S7) of the simulated GB trajectory manifests in the compositions of three dominant conformations of various SASA values as shown in Figure 7B. Compared to the second dominant cluster (4.1 Å Cα-RMSD, cluster 2), the native cluster (1.0 Å Cα-RMSD, cluster 1) has smaller SASA, suggesting that a nonpolar term could stabilize the native-like cluster. The third cluster (5.4 Å Cα-RMSD), with SASA falling between cluster 1 and 2, could also be modestly stabilized with respect to cluster 2. The combination of the lower hydrophobic core stability in GB MD, along with the difference in SASA between the clusters with and without hydrophobic core suggests that a SASA-based algorithm might appropriately stabilize the native cluster and improve agreement between implicit and explicit solvent.
Figure 7.
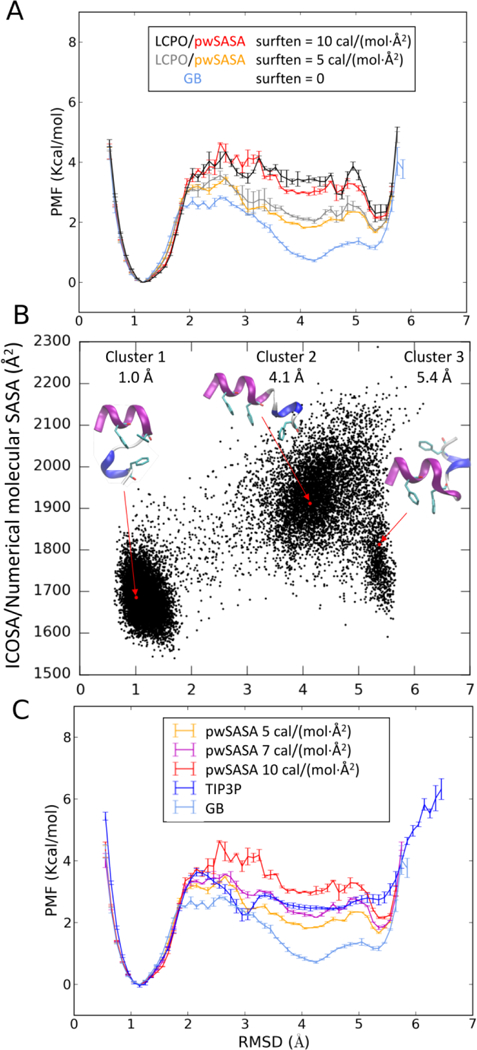
Structural equilibria of restrained HC16 simulated in GB, TIP3P and GB/SA water models at 300K. (A) PMFs for structural equilibria of HC16 measured by Cα-RMSD, by varying the effectiveness of nonpolar solvation, from no nonpolar effect (pure GB), to increased nonpolar effect as surface tensions in GB/SA simulations increase, and to full solvation with TIP3P. (B) 2D scatter plot of ICOSA/numerical SASA versus Cα-RMSD against NMR structure fragment of HC16. The top three cluster representative structures are indicated in the figure. (C) PMFs for structural equilibria of HC16 measured by Cα-RMSD comparing two GB/SA methods (LCPO and pwSASA) and GB.
3.3.3. The pwSASA PMF closely matches LCPO
Before we compare the effect of SASA-based nonpolar solvation (GB/SA) to explicit solvent result, we first compared the effects obtained using two different GB/SA methods in Amber: gbsa=1 and 3 for LCPO and our pairwise method, respectively. This allows us to evaluate the ability of our pairwise approximation to recapitulate the ensemble shifts obtained with LCPO, as compared to the analysis in 3.1.2 that focused solely on the accuracy with which we could reproduce LCPO-based SASA values.
As shown in Figure 7C, the PMFs illustrating the free energy landscape profiles using LCPO and our method agree quite well (within +/− 0.3 kcal/mol) when the same surface tension value is used for both methods. Using either model, increasing the surface tension results in less unfolded structures in the structural ensemble, which suggests that at least for this peptide, the nonpolar term plays a modulating role in hydrophobic core stability in implicit solvent.
There are still small local disagreements between our method and LCPO, at the scale of <0.3 kcal/mol. These are reasonable for two reasons: (1) the SASA estimations for atoms and molecules are of somewhat different accuracies compared with the numerical references, (2) although the PMF uncertainties appear small when using the RMSD as collective variable, these may underestimate the true uncertainty in the data. In Figure 8 we show an alternate convergence analysis in which the population of native-like structures (< 2.0 Å all Cα-RMSD) is accumulated as a function of time for two independent REMD simulations for each of the two GB/SA methods. Even after several microseconds of REMD, the fractions of native-like for LCPO vary by ~ 10% depending on the initial structure. pwSASA MD appears to converge more quickly than LCPO MD, but more extensive testing would be needed to determine the generality of this observation.
Figure 8.
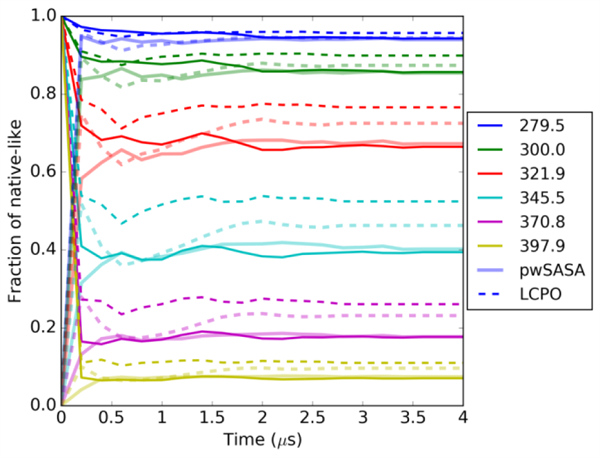
Fraction of folded calculated on HC16 for each temperature trajectory throughout the REMD simulations. Convergences from two different initial starting structures (NMR: opaque lines, unfolded: semi-transparent lines) are observed in pwSASA (solid lines) and LCPO (dashed lines), both using surface tension of 5 cal/(mol Å2).
3.3.4. GB/SA solvation with reasonable surface tension can reproduce TIP3P profile
When nonpolar solvation energy is incorporated, GB/SA models could resurface the energy profile of HC16 towards the TIP3P result, by stabilizing the dominant native-like conformation while sampling less of the unfolded conformations (Figure 7B). A surface tension γ of 7 cal/(mol Å2) is found to agree best with the TIP3P result, although as expected the details do not agree exactly. This choice of the calibrated surface tension is close to the value of 7.2 cal/(mol Å2) used in MM/PBSA and MM/GBSA methods implemented in Amber as the Free Energy Workflow (FEW75); this is encouraging that the good agreement obtained with our method is not simply a result of empirical fitting.
Further consistency in GB/SA and TIP3P simulations is evident with closer examination of the PMF profiles shown in Figure 7A. When the nonpolar term is absent, the cluster 2, which is an extended helical structural ensemble, appears on the GB energy surface with a Cα-RMSD at around 4.1 Å in Figure 7B with an occurrence of 15.0 % (see occurrence data in Table S7) at 300K, measured by within 2 Å from this 4.1 Å misfolded structure. This structural ensemble is not abundant in TIP3P solvent results, with occurrence < 0.2% in the TIP3P ensemble. In GB/SA simulations, this misfolded structure is also diminished to < 2% (in two GB/SA methods with γ = 7 cal/(mol Å2)). But we also noticed that by increasing surface tension, in both LCPO algorithm and our method, another energy minimum appears at around 5.4 Å as cluster 3 in Figure 7B with close to 3% occurrence, with respect to <0.2% in explicit solvent results. This 5.4 Å misfolded structure inversely orients the two helices of HC16 with misplacement of core Phenylalanine residues, and of relatively smaller SASA values. It is hard to attribute the cause as it could be a force field or solvent inaccuracy, or it may also be the convergence is still challenging in explicit solvent simulations and the population of this misfolded structure is difficult to calculate with high precision.
3.4. Application to unrestrained proteins
Our algorithm provides a fast way to estimate the SASA of atoms and molecules in various conformations. Validated on a carefully controlled short peptide, we demonstrated that the nonpolar term is beneficial for core stability. With GPU compatibility, it is now possible to rapidly evaluate the extent to which a simple SASA-based nonpolar term can improve prediction of protein structure and stability in the context of complex conformational ensembles. Such analyses on multiple systems were largely out of reach in the past due to the computational cost of SASA calculations on larger peptides and proteins during MD.
We included the GPU-compatible nonpolar solvation term while simulating the four proteins (CLN025, Trp-cage tc5b, HP36 and Homeodomain variant) without restraints. The simulated ensembles, with nonpolar term (pwSASA and LCPO) or without (GB polar solvation only), were compared to experimental measures (CD or NMR). As always, one must use caution in such comparisons, since inaccuracies in the solute force field also impact agreement with experiment. Furthermore, the accuracy of the solvent models employed here is likely less reliable away from 300K. Nevertheless, the trends in the data may provide useful insight within these limitations.
As shown in Figure 9A, compared with CLN025 GB-only simulations, conformational ensembles across the simulated temperature range show higher population of native-like conformations using pwSASA, which also agrees reasonably with LCPO results. While still not as thermally stable as measured in CD65, the improvement in stabilizing β-hairpin structures is encouraging; experimentally, the fraction of native folded hairpin is over 90% at 300K, while it is less than 20% in our Amber ff14SBonlysc and GB-Neck2 results here (without SASA). By incorporating the nonpolar solvation term, this value is elevated to ~70% in our method and ~80% in LCPO. This discrepancy between these two nonpolar methods corresponds to only ~0.30 kcal/mol, consistent with the differences observed for HC16. It is likely that better agreement with experiment could be obtained by increasing surface tension from 7 cal/(mol Å2) to a larger value, but we decided to only test the value optimized using TIP3P with HC16 as discussed above.
Figure 9.
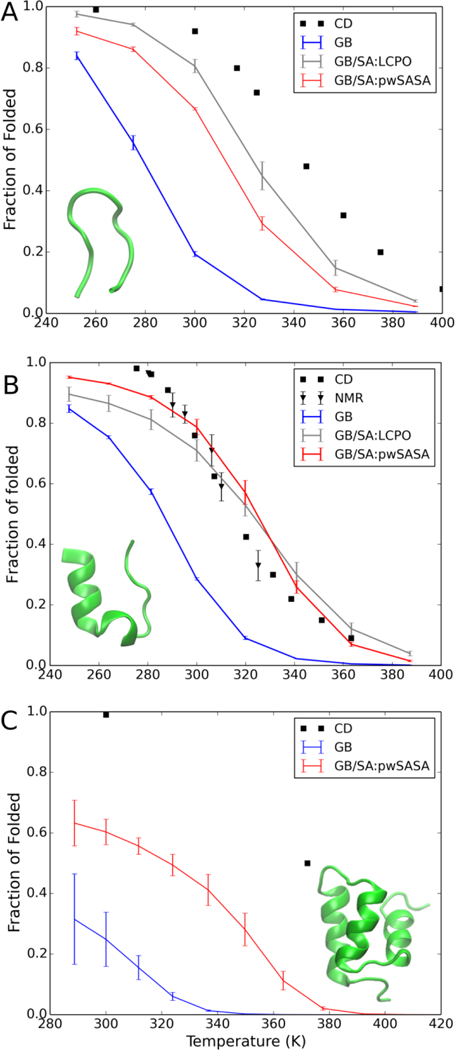
Thermal stability profiles for (A) CLN025, (B) Trp-cage tc5b and (C) Homeodomain, respectively in GB and GB/SA REMD simulations, compared to experimental data65–67.
We next simulated Trp-cage tc5b, and again observed a significantly better agreement with experiment when the nonpolar term was added (Figure 9B). With GB/SA, we obtained near-quantitative agreement between our simulated Trp-cage tc5b and experimental thermal stability profiles. This further suggests that the ability to perform GB/SA with adequate sampling may significantly improve protein modeling efforts. At 300K, our method and LCPO both accurately reproduce the experimental value of ~80%, compared to less accurate < 30% fraction of folded as seen in the GB-only result. Higher fractions of native structure can significantly improve the performance of methods5, 76 that use GB MD to model protein structure. Our predicted Tm of 323K also is close to the experimental value of around 317K66. This thermal stability of Trp-cage shows better accuracy than the GB-only model (predicted Tm at 283K) and other models, compared with predicted Tm down-shifted to 206K77 using Charmm22* force field and modified TIP3P water model, or up-shifted to above 400K using ff94 force field and GB-HCT model78, or OPLS-AA force field and TIP3P water79.
When pwSASA-based nonpolar term is incorporated in Homeodomain variant simulations, the increase of thermal stability with respect to GB-only result is again observed (Figure 9C). With pwSASA, native structures at all simulated temperatures are of higher stability compared to with GB-only simulations that are in worse agreement with experimental data. Accordingly, the simulated melting temperature for Homeodomain is elevated to over 320K, compared to GB-only that is under 50% folded even at the lowest simulated temperature. Compared with experimental measured Tm beyond 372K, better agreement with GB/SA is possibly achievable with a larger surface tension, similar to CLN025. However, as the fold and topology of a protein gets more complicated, it is less reasonable to ascribe the simulated thermal instability to solely the lack of nonpolar term, as the inaccuracies in computational models are likely to be magnified with more atoms and degrees of freedom. The errors compared to experiment can arise from errors in the force field as well as from solvent models. These challenging issues need further investigation.
In the case of HP36 Villin headpiece, when only polar solvation with GB is included, at 300K, less than 5% of conformations adopt folded structures (measured by fractions of conformations < 3.5 Å Cα-RMSD excluding flexible termini), see Figure 10A. With pwSASA, the stability of native-like conformations is predicted to be over 20% at 300K, in better agreement with experiment. At 300K, two native-like conformations are populated in the GB-only trajectory that have occurrences of 1.4% and 1.7%; with GB/SA, both are stabilized to 18.1% and 14.1%, shown as cluster 1 and cluster 3 in Figure 10B (see detailed measurements in Supporting Info Table S8).
Figure 10.
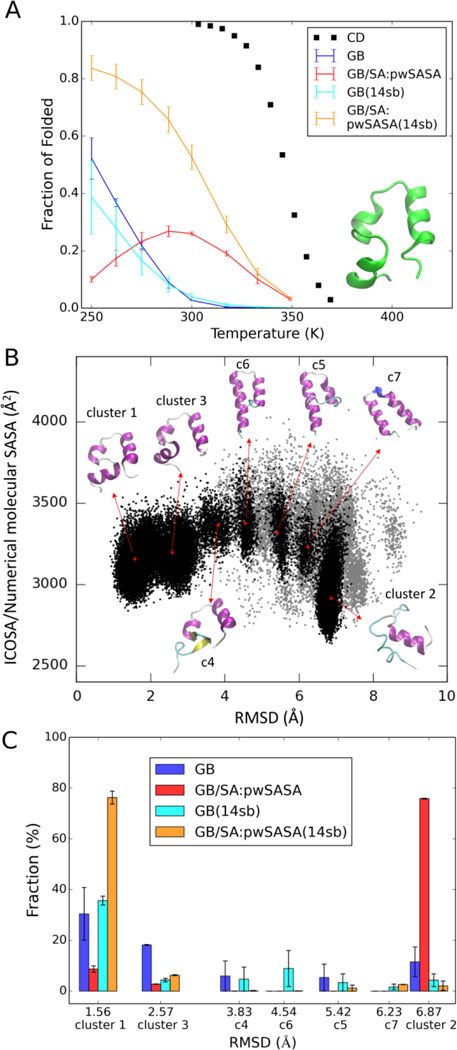
HP36 melting curves and simulated structural equilibria using four models. (A) Thermal stability profiles for HP36 from experiment and calculated from GB and pairwise GB/SA REMD simulations using ff14SBonlysc and ff14SB. GB with ff14SBonlysc (denoted: GB) in blue, GB/SA with ff14SBonlysc (denoted: GB/SA: our method) in red, GB with ff14SB (denoted: GB(14sb)) in cyan, and GB/SA with ff14SB (denoted: GB/SA: our method (14sb) in orange. (B) 2D scatter plot of SASA versus Cα-RMSD excluding flexible termini for all structures in the combined 250K trajectories simulated using four models. Structures from the 7 most populated clusters are indicated with black dots; other structures are in gray. Representative structures from the top 7 clusters are colored by secondary structure and illustrated with arrows pointing from their corresponding (RMSD, SASA) coordinates shown as red dots. (C) Comparison of the top 7 cluster populations across four models. Each bar in the chart refers to the fraction (population) of a certain cluster in the simulated 250K trajectory using a certain model. The color scheme is the same as in (A). Cα-RMSD excluding flexible termini values and the cluster order are denoted on the x-axis. The error bars are calculated from the first and second halves of trajectories.
Looking across the temperature range, the native-like structure is significantly increased in stability at 300K and above when the SASA term is added (Figure 10A), as we observed for CLN025 and Trp-cage. However, decreasing fractions of folded at 288.4K and below result in a melting curve with a downward bell shape, suggesting a cold denaturation, which is unexpected in implicit solvent. We analyzed the lower temperature ensembles to gain more insight. At 250K, the native-like structures populated in GB3 (cluster 1, 30.4% and cluster 3, 18.3%) are diminished to 8.7% and 2.8% respectively in GB/SA simulations (see Figure 10C and more details in Table S8). The native structures are displaced by a misfolded structure ensemble (cluster 2 in Figure 10B) that occupies 75.9% of the GB/SA ensemble. Being significantly more compact and of smaller SASA (see Figure 10B and data in Table S8), this 6.87 Å misfolded structure ensemble is stabilized by ~ 2 kcal/mol in nonpolar solvation energy relative to the native-like structures.
Consequently, in all temperature trajectories of REMD simulations starting from the NMR structure, the fractions of native-like structure decrease in the first hundreds of nanoseconds, which is not only observed with our method, but also with LCPO (Figure S11). There are two reasonable explanations for GB/SA methods destabilizing the native structure of HP36. The most obvious is that the SASA-based nonpolar solvation term fails to accurately recapitulate the missing nonpolar effect. The solute-solvent dispersive interactions might be indispensable for HP36 stability in simulations; as suggested by Gallicchio et al.15, this dispersive term is almost independent of SASA but depends strongly on atomic composition. Alternatively, although the SASA term stabilizes the misfolded structure, it is possible that this accurately reflects the true nonpolar solvation preference, and the observation of large amounts of misfolded structure in the ensemble is due to force field inaccuracy, providing insufficient penalization to counteract the nonpolar solvation effect.
The ff14SBonlysc force field was employed throughout all the training (HC16) and test cases (CLN025, Trp-cage and Homeodomain), as it was previously demonstrated to be capable of folding small proteins3 with GBNeck227 implicit solvent. The ff14SB force field39 added empirical adjustment in the backbone φ parameters to improve agreement80 between experimental data and simulations in TIP3P explicit solvent. Since our tests here employ GB and not TIP3P, we initially did not use ff14SB, but it provides an opportunity to explore the sensitivity of the misfolding to the protein force field in addition to the SASA role described above. As seen in Figure 10A, using the ff14SB force field produces a dramatically different view of the influence of the SASA term on HP36 simulations. GB-only simulations using ff14SBonlysc and ff14SB predict similar melting behavior for HP36 across the simulated temperature range; the predicted Tm is ~100 K lower than experiment68. When the pwSASA term is added, ff14SB elevates the stability of HP36 at all simulated temperatures and reflects a significantly improved match with experimental melting data68, as seen for the other 3 systems discussed above. Importantly, the misfolded structures that dominated the low-temperature ensembles using ff14SBonlysc are no longer highly populated with ff14SB. Figure 10C illustrates and Table S8 summarizes the predicted structural ensembles at 250K compared across four models. The divergence of the observed impact of adding SASA to the two force field variants is a frustrating reminder of the complexity of using comparisons to experiment as a method to evaluate the accuracy of one component of the overall energy function (and a strong argument against using experimental results to empirically adjust a single component of a model).
4. CONCLUSIONS
In this work, we propose a fast, GPU-friendly pairwise SASA-based nonpolar solvation approach for protein simulations on GPUs. In this pwSASA approach, we estimate the atomic and molecular SASAs of proteins using a simple function inspired by the Lennard-Jones function already being used during MD, which result in comparable accuracy as LCPO algorithm46 in reproducing numerical ICOSA40 SASA values. Accuracy is also similar to prior work by Guvench et al., who proposed a pairwise approach that is very similar to that described here, but with a 4th-order polynomial approach to SASA estimation. By calculating pairwise burial SASA from atom distances, our method accelerates MD simulations up to 30 times compared to the LCPO implementation, with only ~ 20% overhead compared to CPU or GPU simulations that omit the SASA term. The main speed advance arises from employing GPU devices for SASA calculations and reducing constant communications with CPUs; the previous Amber CPU/GPU implementation74 using LCPO suffers from dramatic speed loss when the SASA calculation for every time integration step is still done on CPUs, even though all other energy terms are evaluated on the GPU26. Compared with other analytical approaches43–44, 46, 48–49 including LCPO, our two-body algorithm is suitable for inexpensive gaming GPU devices that are built for highly parallel calculations.
To ensure that our purely two-body algorithm is able to capture reasonably the SASA values in proteins, we pre-treat all protein atoms by grouping them into SASA types. This allows implicit incorporation of many-body contributions based on local geometry, and the remaining neighbor shielding is calculated using the non-recursive pair distances. Parameters were optimized on a peptide library covering all of the defined protein SASA types, sampling diverse conformations and SASA ranges. The objective function for training was designed to reproduce the SASA changes in atomic numerical ICOSA values, instead of the absolute atomic or molecular SASA numbers. The accuracy of this simple approach is encouraging, though it falls short of more complex algorithms for estimating SASA during MD81. The resulting 90 parameters are encoded in a new implementation as gbsa=3 in Amber version 18.
The evaluation of our nonpolar term and the calibration of surface tension were done in a helically restrained model system which is derived from the hydrophobic core of HP36. This small peptide was also simulated in LCPO and TIP3P explicit solvent. Our method achieves similar outcomes as LCPO as well as TIP3P solvent when surface tension values of 7 cal/(mol Å2) were used.
Three small proteins (CLN025, Trp-cage, and HP36) without restraints were simulated and compared to experimental results. The simulated melting curves for CLN025 and Trp-cage, with nonpolar term, are more consistent with experimental measures as compared to without this term. Our method reasonably reproduces LCPO-based MD results. In the case of HP36, results were more complicated. Adding SASA-based nonpolar solvation for HP36 destabilized the NMR structure for both LCPO and pwSASA, but we showed that this apparent negative impact was not observed when using a different variant of the protein force field. Further work on more systems will be needed to isolate these two variables when comparing to experimental results.
Although clear weaknesses have been recognized, the SASA-based nonpolar model has been shown to work reasonably well with extensive parameterization against experimental solvation free energies of small nonpolar molecules55, 82. The application in biomolecules faces more challenges due to the tradeoff between computational cost and accuracy issues. Complete nonpolar solvation is a combination of solute-solvent dispersion energy (△Gvdw)16, 22, along with the hydrophobic effect and surface tension that depend on the size scale and shape of molecules55, 83–85, the curvature, and temperature85. Methods to accurately calculate these contributions have not reached a consensus and are not readily calculated on GPUs to test impact on complex protein ensembles. But with the implementation of our new algorithm, despite its relative crudeness, the bottleneck in computational cost is reduced with order of magnitude accelerations for peptide and protein modeling. This can permit a greater exploration of success and failure cases for more complex biomolecules, possibly improving structure prediction and refinement, and also providing insight into future, more accurate nonpolar solvation models.
It is promising that protein modeling in implicit solvent continues to gain in physical accuracy as well as increase in speed. This is an important distinction since current protein simulations are typically limited by conformational sampling, rather than accuracy (especially for protein folding/misfolding, aggregation, intrinsically disordered proteins and more). Fast and accurate implicit solvation treatments may provide a valuable alternative to explicit solvent for such systems, but it remains to be seen how well these simple SASA-based approaches can improve modeling of the entire free energy landscape, as compared to just modeling native conformations as shown here.
Supplementary Material
ACKNOWLEDGMENT
This work was supported by NIH grant GM107104 and an NSF Petascale Computational Resource (PRAC) Award from the NSF (0CI-1036208). We gratefully acknowledge support from Henry and Marsha Laufer.
Supporting Information.
The supporting information file contains detailed methods for the derivation of functional form from Lennard-Jones formula, definitions of SASA types and final parameters, process of parameter fitting and optimization, sequences and features of peptide training set, comparison of pairwise distance distributions for training and test set, comparison of distributions for all pairs and sorted pairs of frames, refit parameters for the Guvench at al. estimator, temperature ladders for all REMD simulations, atomic and molecular SASA estimations of test set proteins, transformations to correct molecular SASA estimations, LCPO molecular SASA estimations of test set proteins, clustering details for HC16 and HP36, fraction of folded for HP36 REMD simulations starting from NMR structure using two GB/SA solvents (our method and LCPO). This material is available free of charge via the Internet at http://pubs.acs.org.
ABBREVIATIONS
- GPU
Graphics Processing Unit
- SASA
Solvent Accessible Surface Area
- LCPO
Linear Combinations of Pairwise Overlap
- GB
Generalized Born
- GB/SA
Generalized Born/Surface Area
- REMD
Replica Exchange Molecular Dynamics
- PMF
Potential of Mean Force
Footnotes
ASSOCIATED CONTENT
REFERENCES
- 1.Fennell CJ; Dill KA, Physical Modeling of Aqueous Solvation. Journal of Statistical Physics 2011, 145 (2), 209–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Anandakrishnan R; Drozdetski A; Walker RC; Onufriev AV, Speed of Conformational Change: Comparing Explicit and Implicit Solvent Molecular Dynamics Simulations. Biophysical Journal 2015, 108 (5), 1153–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nguyen H; Maier J; Huang H; Perrone V; Simmerling C, Folding simulations for proteins with diverse topologies are accessible in days with a physics-based force field and implicit solvent. J Am Chem Soc 2014, 136 (40), 13959–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lei H; Duan Y, Two-stage folding of HP-35 from ab initio simulations. J Mol Biol 2007, 370 (1), 196–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Perez A; Morrone JA; Brini E; MacCallum JL; Dill KA, Blind protein structure prediction using accelerated free-energy simulations. Science Advances 2016, 2 (11). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Archontis G; Simonson T, A residue-pairwise generalized born scheme suitable for protein design calculations. J Phys Chem B 2005, 109 (47), 22667–73. [DOI] [PubMed] [Google Scholar]
- 7.Terashi G; Kihara D, Protein structure model refinement in CASP12 using short and long molecular dynamics simulations in implicit solvent. Proteins 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Michel J; Taylor RD; Essex JW, Efficient Generalized Born Models for Monte Carlo Simulations. J Chem Theory Comput 2006, 2 (3), 732–9. [DOI] [PubMed] [Google Scholar]
- 9.Kollman PA; Massova I; Reyes C; Kuhn B; Huo SH; Chong L; Lee M; Lee T; Duan Y; Wang W; Donini O; Cieplak P; Srinivasan J; Case DA; Cheatham TE, Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Accounts of Chemical Research 2000, 33 (12), 889–897. [DOI] [PubMed] [Google Scholar]
- 10.Sitkoff D; Sharp KA; Honig B, Accurate Calculation of Hydration Free-Energies Using Macroscopic Solvent Models. Journal of Physical Chemistry 1994, 98 (7), 1978–1988. [Google Scholar]
- 11.Honig B; Nicholls A, Classical Electrostatics in Biology and Chemistry. Science 1995, 268 (5214), 1144–1149. [DOI] [PubMed] [Google Scholar]
- 12.Still WC; Tempczyk A; Hawley RC; Hendrickson T, Semianalytical Treatment of Solvation for Molecular Mechanics and Dynamics. Journal of the American Chemical Society 1990, 112 (16), 6127–6129. [Google Scholar]
- 13.Pratt LR; Chandler D, Theory of Hydrophobic Effect. Journal of Chemical Physics 1977, 67 (8), 3683–3704. [Google Scholar]
- 14.Chen J; Brooks CL 3rd, Implicit modeling of nonpolar solvation for simulating protein folding and conformational transitions. Phys Chem Chem Phys 2008, 10 (4), 471–81. [DOI] [PubMed] [Google Scholar]
- 15.Gallicchio E; Kubo MM; Levy RM, Enthalpy-entropy and cavity decomposition of alkane hydration free energies: Numerical results and implications for theories of hydrophobic solvation. Journal of Physical Chemistry B 2000, 104 (26), 6271–6285. [Google Scholar]
- 16.Wagoner JA; Baker NA, Assessing implicit models for nonpolar mean solvation forces: The importance of dispersion and volume terms. Proceedings of the National Academy of Sciences of the United States of America 2006, 103 (22), 8331–8336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lee MS; Olson MA, Comparison of volume and surface area nonpolar solvation free energy terms for implicit solvent simulations (vol 139, 044119, 2013). Journal of Chemical Physics 2013, 139 (7). [DOI] [PubMed] [Google Scholar]
- 18.Chen JH; Brooks CL, Critical importance of length-scale dependence in implicit modeling of hydrophobic interactions. Journal of the American Chemical Society 2007, 129 (9), 2444-+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Arnautova YA; Vorobjev YN; Vila JA; Scheraga HA, Identifying native-like protein structures with scoring functions based on all-atom ECEPP force fields, implicit solvent models and structure relaxation. Proteins 2009, 77 (1), 38–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Michel J; Verdonk ML; Essex JW, Protein-ligand binding affinity predictions by implicit solvent simulations: A tool for lead optimization? Journal of Medicinal Chemistry 2006, 49 (25), 7427–7439. [DOI] [PubMed] [Google Scholar]
- 21.Genheden S; Ryde U, The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opinion on Drug Discovery 2015, 10 (5), 449–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Levy RM; Zhang LY; Gallicchio E; Felts AK, On the nonpolar hydration free energy of proteins: Surface area and continuum solvent models for the solute-solvent interaction energy. Journal of the American Chemical Society 2003, 125 (31), 9523–9530. [DOI] [PubMed] [Google Scholar]
- 23.Tironi IG; Sperb R; Smith PE; Vangunsteren WF, A Generalized Reaction Field Method for Molecular-Dynamics Simulations. Journal of Chemical Physics 1995, 102 (13), 5451–5459. [Google Scholar]
- 24.Luo R; David L; Gilson MK, Accelerated Poisson-Boltzmann calculations for static and dynamic systems. J Comput Chem 2002, 23 (13), 1244–1253. [DOI] [PubMed] [Google Scholar]
- 25.Wang J; Tan CH; Chanco E; Luo R, Quantitative analysis of Poisson-Boltzmann implicit solvent in molecular dynamics. Physical Chemistry Chemical Physics 2010, 12 (5), 1194–1202. [DOI] [PubMed] [Google Scholar]
- 26.Gotz AW; Williamson MJ; Xu D; Poole D; Le Grand S; Walker RC, Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. Journal of Chemical Theory and Computation 2012, 8 (5), 1542–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nguyen H; Roe DR; Simmerling C, Improved Generalized Born Solvent Model Parameters for Protein Simulations. J Chem Theory Comput 2013, 9 (4), 2020–2034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Onufriev A; Bashford D; Case DA, Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins-Structure Function and Bioinformatics 2004, 55 (2), 383–394. [DOI] [PubMed] [Google Scholar]
- 29.Mongan J; Simmerling C; McCammon JA; Case DA; Onufriev A, Generalized Born model with a simple, robust molecular volume correction. Journal of Chemical Theory and Computation 2007, 3 (1), 156–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Onufriev A; Case DA; Bashford D, Effective Born radii in the generalized Born approximation: The importance of being perfect. J Comput Chem 2002, 23 (14), 1297–1304. [DOI] [PubMed] [Google Scholar]
- 31.Hawkins GD; Cramer CJ; Truhlar DG, Pairwise Solute Descreening of Solute Charges from a Dielectric Medium. Chemical Physics Letters 1995, 246 (1–2), 122–129. [Google Scholar]
- 32.Le Grand S; Gotz AW; Walker RC, SPFP: Speed without compromise-A mixed precision model for GPU accelerated molecular dynamics simulations. Computer Physics Communications 2013, 184 (2), 374–380. [Google Scholar]
- 33.Du QH; Beglov D; Roux B, Solvation free energy of polar and nonpolar molecules in water: An extended interaction site integral equation theory in three dimensions. Journal of Physical Chemistry B 2000, 104 (4), 796–805. [Google Scholar]
- 34.Liu H; Chen F; Sun HY; Li D; Hou TJ, Improving the Efficiency of Non-equilibrium Sampling in the Aqueous Environment via Implicit-Solvent Simulations. Journal of Chemical Theory and Computation 2017, 13 (4), 1827–1836. [DOI] [PubMed] [Google Scholar]
- 35.Tan C; Tan YH; Luo R, Implicit nonpolar solvent models. Journal of Physical Chemistry B 2007, 111 (42), 12263–12274. [DOI] [PubMed] [Google Scholar]
- 36.Gallicchio E; Paris K; Levy RM, The AGBNP2 Implicit Solvation Model. Journal of Chemical Theory and Computation 2009, 5 (9), 2544–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.DA. Case, D. S. C., Cheatham TE III Darden TA, Duke RE, Giese TJ, Gohlke H, Goetz AW, Greene D, Homeyer N, Izadi S, Kovalenko A, Lee TS, LeGrand S, Li P, Lin C, Liu J, Luchko T, Luo R, Mermelstein D, Merz KM, Monard G, Nguyen H, Omelyan I, Onufriev A, Pan F, Qi R, Roe DR, Roitberg A, Sagui C, Simmerling CL, Botello-Smith WM, Swails J, Walker RC, Wang J, Wolf RM, Wu X, Xiao L, York DM and Kollman PA, AMBER 2016. 2017. [Google Scholar]
- 38.Shell MS; Ritterson R; Dill KA, A test on peptide stability of AMBER force fields with implicit solvation. Journal of Physical Chemistry B 2008, 112 (22), 6878–6886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C, ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. Journal of Chemical Theory and Computation 2015, 11 (8), 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lee BK; Richards FM, The Interpretation of Protein Structures: Estimation of Static Accessibility. Journal of Molecular Biology 1971, 55, 379. [DOI] [PubMed] [Google Scholar]
- 41.Durham E; Dorr B; Woetzel N; Staritzbichler R; Meiler J, Solvent accessible surface area approximations for rapid and accurate protein structure prediction. Journal of Molecular Modeling 2009, 15 (9), 1093–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Juba D; Varshney A, Parallel, stochastic measurement of molecular surface area. Journal of Molecular Graphics & Modelling 2008, 27 (1), 82–87. [DOI] [PubMed] [Google Scholar]
- 43.Wodak SJ; Janin J, Analytical Approximation to the Accessible Surface-Area of Proteins. Proceedings of the National Academy of Sciences of the United States of America-Physical Sciences 1980, 77 (4), 1736–1740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hasel W; Hendrickson TF; Still WC, A Rapid Approximation to the Solvent Accessible Surface Areas of Atoms. Tetrahedron Computer Methodology 1988, 1 (2), 103–116. [Google Scholar]
- 45.Dynerman D; Butzlaff E; Mitchell JC, CUSA and CUDE: GPU-Accelerated Methods for Estimating Solvent Accessible Surface Area and Desolvation. Journal of Computational Biology 2009, 16 (4), 523–537. [DOI] [PubMed] [Google Scholar]
- 46.Weiser J; Shenkin PS; Still WC, Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J Comput Chem 1999, 20 (2), 217–230. [Google Scholar]
- 47.Vasilyev V; Purisima EO, A fast pairwise evaluation of molecular surface area. J Comput Chem 2002, 23 (7), 737–745. [DOI] [PubMed] [Google Scholar]
- 48.Richmond TJ, Solvent Accessible Surface-Area and Excluded Volume in Proteins-Analytical Equations for Overlapping Spheres and Implications for the Hydrophobic Effect. Journal of Molecular Biology 1984, 178 (1), 63–89. [DOI] [PubMed] [Google Scholar]
- 49.Wesson L; Eisenberg D, Atomic Solvation Parameters Applied to Molecular-Dynamics of Proteins in Solution. Protein Science 1992, 1 (2), 227–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Klenin KV; Tristram F; Strunk T; Wenzel W, Derivatives of Molecular Surface Area and Volume: Simple and Exact Analytical Formulas. J Comput Chem 2011, 32 (12), 2647–2653. [DOI] [PubMed] [Google Scholar]
- 51.Schaefer M; Bartels C; Karplus M, Solution conformations and thermodynamics of structured peptides: molecular dynamics simulation with an implicit solvation model. J Mol Biol 1998, 284 (3), 835–48. [DOI] [PubMed] [Google Scholar]
- 52.Eisenberg D; Mclachlan AD, Solvation Energy in Protein Folding and Binding. Nature 1986, 319 (6050), 199–203. [DOI] [PubMed] [Google Scholar]
- 53.Qiu D; Shenkin PS; Hollinger FP; Still WC, The GB/SA continuum model for solvation. A fast analytical method for the calculation of approximate Born radii. Journal of Physical Chemistry A 1997, 101 (16), 3005–3014. [Google Scholar]
- 54.Guvench O; Brooks CL, Efficient approximate all-atom solvent accessible surface area method parameterized for folded and denatured protein conformations. J Comput Chem 2004, 25 (8), 1005–1014. [DOI] [PubMed] [Google Scholar]
- 55.Simonson T; Brunger AT, Solvation Free-Energies Estimated from Macroscopic Continuum Theory-an Accuracy Assessment. Journal of Physical Chemistry 1994, 98 (17), 4683–4694. [Google Scholar]
- 56.Sitkoff D; Sharp KA; Honig B, Correlating solvation free energies and surface tensions of hydrocarbon solutes. Biophys Chem 1994, 51 (2–3), 397–403; discussion 404–9. [DOI] [PubMed] [Google Scholar]
- 57.Shrake A; Rupley JA, Environment and Exposure to Solvent of Protein Atoms-Lysozyme and Insulin. Journal of Molecular Biology 1973, 79 (2), 351–371. [DOI] [PubMed] [Google Scholar]
- 58.Weiser J; Weiser AA; Shenkin PS; Still WC, Neighbor-list reduction: Optimization for computation of molecular van der Waals and solvent-accessible surface areas (vol 19, pg 797, 1998). J Comput Chem 1998, 19 (9), 1110–1110. [Google Scholar]
- 59.Roe DR; Cheatham TE, PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. Journal of Chemical Theory and Computation 2013, 9 (7), 3084–3095. [DOI] [PubMed] [Google Scholar]
- 60.Morales JL; Nocedal J, Remark on “algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound constrained optimization”. ACM Trans. Math. Softw. 2011, 38 (1), 1–4. [Google Scholar]
- 61.Jones E; Oliphant T; Peterson P, {SciPy}: open source scientific tools for {Python}. 2014. [Google Scholar]
- 62.Meng WL; Shan B; Tang YF; Raleigh DP, Native like structure in the unfolded state of the villin headpiece helical subdomain, an ultrafast folding protein. Protein Science 2009, 18 (8), 1692–1701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.McKnight CJ; Matsudaira PT; Kim PS, NMR structure of the 35-residue villin headpiece subdomain. Nature Structural Biology 1997, 4 (3), 180–184. [DOI] [PubMed] [Google Scholar]
- 64.Roe DR; Okur A; Wickstrom L; Hornak V; Simmerling C, Secondary structure bias in generalized Born solvent models: comparison of conformational ensembles and free energy of solvent polarization from explicit and implicit solvation. J Phys Chem B 2007, 111 (7), 1846–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Honda S; Akiba T; Kato YS; Sawada Y; Sekijima M; Ishimura M; Ooishi A; Watanabe H; Odahara T; Harata K, Crystal Structure of a Ten-Amino Acid Protein. Journal of the American Chemical Society 2008, 130 (46), 15327–15331. [DOI] [PubMed] [Google Scholar]
- 66.Neidigh JW; Fesinmeyer RM; Andersen NH, Designing a 20-residue protein. Nature Structural Biology 2002, 9 (6), 425–430. [DOI] [PubMed] [Google Scholar]
- 67.Shah PS; Hom GK; Ross SA; Lassila JK; Crowhurst KA; Mayo SL, Full-sequence computational design and solution structure of a thermostable protein variant. Journal of Molecular Biology 2007, 372 (1), 1–6. [DOI] [PubMed] [Google Scholar]
- 68.Xiao SF; Patsalo V; Shan B; Bi Y; Green DF; Raleigh DP, Rational modification of protein stability by targeting surface sites leads to complicated results. Proceedings of the National Academy of Sciences of the United States of America 2013, 110 (28), 11337–11342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML, Comparison of simple potential functions for simulating liquid water. The Journal of chemical physics 1983, 79 (2), 926–935. [Google Scholar]
- 70.Sindhikara DJ, Modular reweighting software for statistical mechanical analysis of biased equilibrium data. Computer Physics Communications 2011, 182 (10), 2227–2231. [Google Scholar]
- 71.Ryckaert JP; Ciccotti G; Berendsen HJC, Numerical-Integration of Cartesian Equations of Motion of a System with Constraints-Molecular-Dynamics of N-Alkanes. Journal of Computational Physics 1977, 23 (3), 327–341. [Google Scholar]
- 72.Hopkins CW; Le Grand S; Walker RC; Roitberg AE, Long-Time-Step Molecular Dynamics through Hydrogen Mass Repartitioning. Journal of Chemical Theory and Computation 2015, 11 (4), 1864–1874. [DOI] [PubMed] [Google Scholar]
- 73.Scott DW, Multivariate Density Estimation: Theory, Practice, and Visualization, 2nd Edition. Multivariate Density Estimation: Theory, Practice, and Visualization, 2nd Edition 2015, 1–350. [Google Scholar]
- 74.Tanner DE; Phillips JC; Schulten K, GPU/CPU Algorithm for Generalized Born/Solvent-Accessible Surface Area Implicit Solvent Calculations. Journal of Chemical Theory and Computation 2012, 8 (7), 2521–2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Homeyer N; Gohlke H, FEW: a workflow tool for free energy calculations of ligand binding. J Comput Chem 2013, 34 (11), 965–73. [DOI] [PubMed] [Google Scholar]
- 76.MacCallum JL; Perez A; Dill KA, Determining protein structures by combining semireliable data with atomistic physical models by Bayesian inference. Proceedings of the National Academy of Sciences 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Lindorff-Larsen K; Piana S; Dror RO; Shaw DE, How Fast-Folding Proteins Fold. Science 2011, 334 (6055), 517–520. [DOI] [PubMed] [Google Scholar]
- 78.Pitera JW; Swope W, Understanding folding and design: Replica-exchange simulations of “Trp-cage” fly miniproteins. Proceedings of the National Academy of Sciences of the United States of America 2003, 100 (13), 7587–7592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Zhou R, Trp-cage: folding free energy landscape in explicit water. Proc Natl Acad Sci U S A 2003, 100 (23), 13280–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Wickstrom L; Okur A; Simmerling C, Evaluating the Performance of the ff99SB Force Field Based on NMR Scalar Coupling Data. Biophysical Journal 2009, 97 (3), 853–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Im WP; Lee MS; Brooks CL, Generalized born model with a simple smoothing function. J Comput Chem 2003, 24 (14), 1691–1702. [DOI] [PubMed] [Google Scholar]
- 82.Cramer CJ; Truhlar DG, Implicit solvation models: Equilibria, structure, spectra, and dynamics. Chemical Reviews 1999, 99 (8), 2161–2200. [DOI] [PubMed] [Google Scholar]
- 83.Bennaim A; Mazo RM, Size Dependence of the Solvation Free-Energies of Large Solutes. Journal of Physical Chemistry 1993, 97 (41), 10829–10834. [Google Scholar]
- 84.Sharp KA; Nicholls A; Fine RF; Honig B, Reconciling the Magnitude of the Microscopic and Macroscopic Hydrophobic Effects. Science 1991, 252 (5002), 106–109. [DOI] [PubMed] [Google Scholar]
- 85.Huang DM; Chandler D, Temperature and length scale dependence of hydrophobic effects and their possible implications for protein folding. Proceedings of the National Academy of Sciences of the United States of America 2000, 97 (15), 8324–8327. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


